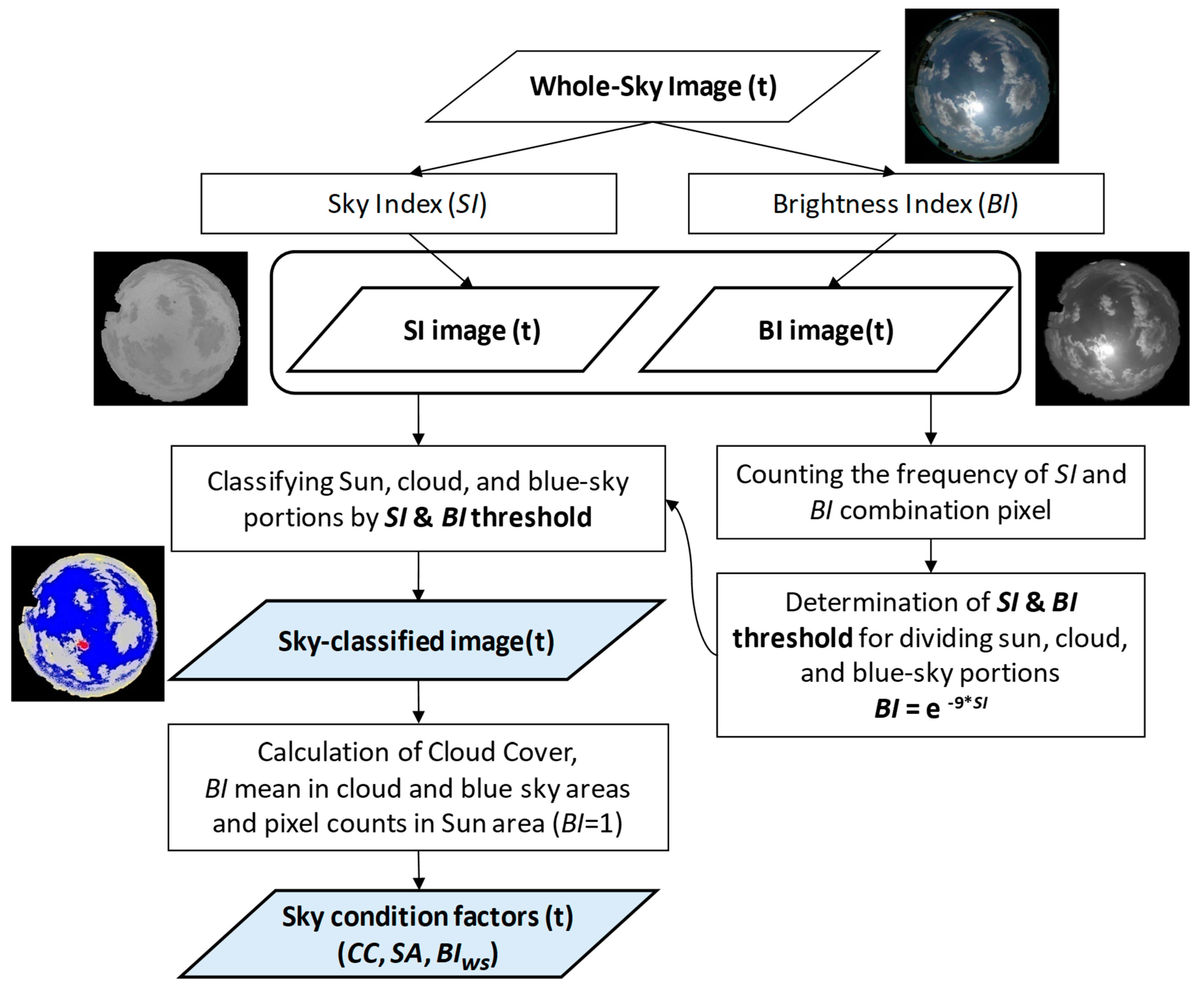
3.1. Instability of PF and Q/E
Recent studies have highlighted that the
PF and
Q/E are not constants but that they depend on the weather conditions and season because of the different processes of absorption, scattering, and transmittance in the atmosphere [
2,
6,
7,
8,
9,
10,
11,
12,
13,
14,
15]. To illustrate the seasonal variability of the
PF and
Q/E under different sky conditions,
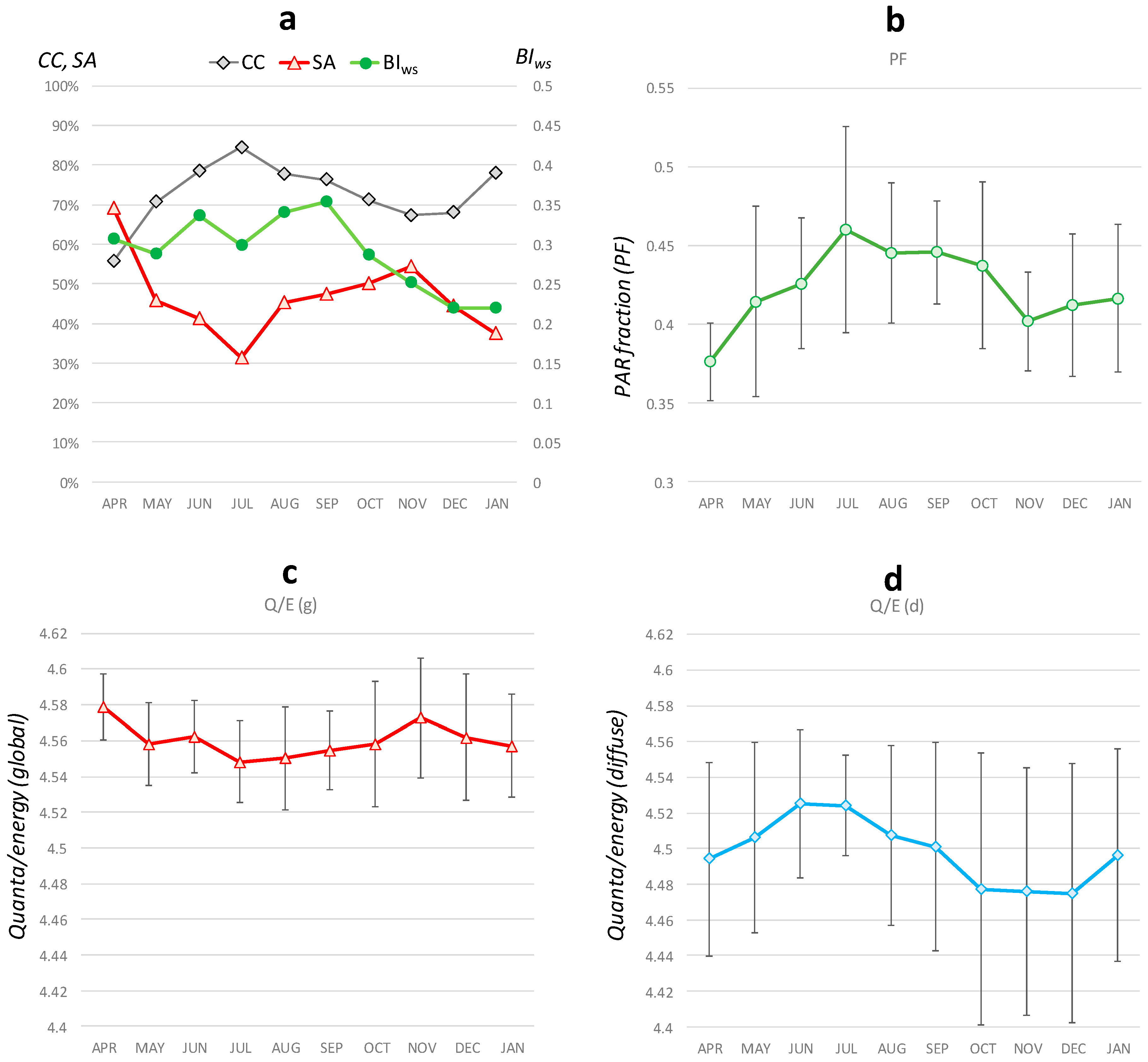
Figure 2 shows the monthly means of
PF,
Q/E(g), and
Q/E(d) with sky-condition factors of
CC,
SA, and
BIws. It can be seen that the monthly means of
PF,
Q/E(g), and
Q/E(d) clearly change over the course of a year.
The annual mean and standard deviation (St.Dev.) of the
PF were 0.430 and 0.052, respectively, and the mean of the
PF was approximately 7% lower than the constant value of 0.5 that is commonly used in the field [
4]. The monthly difference in the mean
PF was highest (0.456) in summer (July) (
Figure 2b), when the
CC was the highest and the
SA the lowest (i.e., the cloudy season) (
Figure 2a) and relatively low in spring (April: 0.377) and autumn (November: 0.402), when the
CC was low and the
SA was high (i.e., the sunny season) (
Figure 2a). The
PF at the TOA, where there is no influence by the atmosphere, can be calculated as 0.387 using a solar constant of 1367 W m
−2 and PAR
0 (529 W m
−2). The difference in values between the ground surface and the TOA is due to atmospheric absorption. In particular, water vapor and clouds absorb infrared rays well, and the absorption of solar radiation, including the infrared wavelength band, is therefore greater than the absorption of the PAR. Akitsu et al. [
2] found a similar seasonal variation between the
PF and water vapor pressure.
As for the
Q/E(g) and
Q/E(d), the annual means (St.Dev.) of the
Q/E(g) and
Q/E(d) were 4.558 (0.040) and 4.497 (0.064), respectively. The mean of the
Q/E(g) was almost the same as the commonly used constant value of 4.57 [
5]. The theoretical value of the
Q/E at the PAR wavelength is 4.600, calculated using Planck’s constant, the speed of light, and Avogadro’s number; i.e., the blue component is larger than the red component in the case where the
Q/E is less than 4.600. The value of the
Q/E(d) was found to be less than the
Q/E(g) for the present results, which means that the diffuse PAR had much more of the blue component than of the red component. This is due to the processes of Rayleigh and Mie scattering in the atmosphere that depend on the particle size (i.e., wavelength); i.e., the spectral components are imbalanced under different sky conditions. Thus, the
Q/E should be lower under a clear sky and higher under a cloudy sky for the diffuse component. In particular, the different seasonal characteristics of the
Q/E(g) and
Q/E(d) are shown (
Figure 2c,d). It can be seen that the
Q/E(g) and
Q/E(d) were respectively the lowest and highest in July and the highest and lowest in April. The monthly differences in the
Q/E(d) were similar to the changes in the
CC.
3.2. Effects of Sky-Condition Factors on PF, Q/E, DR, and CI on an Hourly Timescale
Previous studies have proposed methods for estimating the
PF using the
CI [
8,
9], estimating the
Q/E(g) and
Q/E(d) using the
DR [
7], and estimating the
DR using the
CI [
10,
14,
23] on a daily or hourly timescale. Both the
CI and
DR have been used as indices of clearness and cloudiness [
7,
10]. Here, to clarify the effects of actual sky-condition factors on the
PF,
Q/E,
DR, and
CI, including
CIpar on an hourly timescale, we performed a multiregression analysis (MRA) using the four sky-condition factors
CC,
SA,
BIws, and
SEA as explanatory variables. In this analysis, we used 2707 samples as hourly data (6–18, 5–19, and 7–17 h in spring and autumn, summer, and winter respectively) over 257 days from 18 April 2005 to 1 February 2006.
Table 2 lists the MRA results of the partial regression coefficient (
p.r.c.) and standard partial regression coefficient (
s.p.r.c.), together with the coefficient of determination (
R2). The effects of the sky-condition factors on the estimation parameters
PF,
Q/E,
DR, and
CI are described as follows.
The
PF is affected negatively by the
BIws and affected positively by the
SEA. When the
BIws is low (i.e., when the sky is covered by dark clouds, or when the sun is setting or rising (low
SEA)), the
PF is high because infrared rays are absorbed more easily into the atmosphere than when there is a clear blue sky. However, when the
SEA is low (i.e., the passage through the air mass is longer), the
PF should also be high (which is not a positive effect). Meanwhile, in the season in which the
SEA is high (i.e., summer), the humidity is also high; i.e., the
PF would be high [
9]. The result of our measurement shows that the
PF is higher in summer (
Figure 2b). However, the value of
R2 is not high (0.375). Finch et al. [
8] and Jacovides et al. [
9] obtained results of
R2 = 0.32 and 0.31, respectively, by modeling the
PF using the
CI on a daily scale. It might be difficult to explain the
PF using limited factors because of the dependence on the balance between absorption in the infrared range and transmission in the visible range.
The
Q/E(g) is affected mainly by the
SA with a positive effect. When the
SA is high, the direct component should be greater than the diffuse component; i.e., the
Q/E(g) would be high because the red component tends to reach the ground. However, the global PAR is the sum of the direct and diffuse components such that the
Q/E(g) also depends on the balance of the spectral components in the direct and diffuse PAR. Therefore, the
CC,
BIws, and
SEA interactively affect the
Q/E(g). Our value of
R2 is not high (0.343) because the
Q/E(g) for hourly data has a small St.Dev. of 0.040. Additionally, Dye [
8] identified that the
Q/E(g) has a representative value of 4.56 (μmol J
−1) on a daily timescale. In contrast, the
Q/E(d) is affected strongly and positively by the
CC (
s.p.r.c.: 0.883) with a high value of
R2 (0.834). This is because, when the
CC is low (i.e., a clear sky), the blue component is greater than the red component in the diffuse component; i.e., the
Q/E(d) should be low.
The
DR can be explained by the positive effect of the
CC (
s.p.r.c: 0.474) and the negative effect of the
SA (
s.p.r.c: −0.556) with a very high value of
R2 (0.919). There is no effect by the
BIws. The diffuse PAR is close to the global PAR under overcast conditions (i.e., when there is almost no direct component) because the
DR is the ratio of the diffuse PAR to the global PAR observed at the ground, not the PAR at the TOA. Therefore, the brightness over the whole sky would not be reflected by the
DR. The
DR has been modeled using an nth-degree function of the
CIpar in previous studies [
10,
14,
23]. Adopting this method, the quadratic function (
DR = −1.342
CIpar2 + 0.146
CIpar + 0.995) was derived with
R2 = 0.852. Thus, our result using sky-condition factors might be more reproducible than the results obtained using the
CIpar.
Both the CI and CIpar have been used to estimate the PF and DR in previous studies, as mentioned earlier. Our MRA clarified that the CI and CIpar can be explained interactively by the four sky-condition factors with high values of R2 (0.851 and 0.873); i.e., with the positive effects of the SA and BIws and the negative effects of the CC and SEA. This result shows that, in a case where SR data are unavailable, it would be possible to estimate the CI or CIpar using these sky-condition factors. Thus, the SR or PAR could be estimated subsequently from the CI or CIpar.
3.3. Estimation of Global and Diffuse PPFD with Instantaneous Values
The results of the MRA using the hourly data show the possibility of explaining the estimation parameters for the global and diffuse PPFD using the sky-condition factors. We estimated the global and diffuse PPFD using the sky-condition factors. The timescale of the estimation was set as an instantaneous value at the time of the acquisition of the whole-sky images with 2-min intervals. There were 91,511 instantaneous values (i.e., samples) recorded on 300 days from 24 February 2005 to 7 February 2006. To include the data observed under various sky conditions in all seasons in the samples for the model derivation and its validation, we first separated 17,438 samples obtained on 59 days (i.e., day 5, 10, 15, 20, 25, and 30 of each month) for the validation of our estimation models. Thus, we used 74,073 samples obtained on 241 days for the model derivation of the estimation parameters. We also applied an MRA to derive each estimation model of the CIpar, DR, Q/E(g), and Q/E(d) as response variables using the sky-condition factors as explanatory variables. In this analysis, we separated the 74,073 samples into two classes of SA = 1 and SA = 0 because the instantaneous value of the PPFD is affected most by the appearance of the sun. The number of samples in the group with SA = 1 and SA = 0 was 30,894 and 43,179, respectively.
The estimation models of the global and diffuse PPFD were constructed using four functions for
SA = 1 and
SA = 0 each. Here, the
PF was not needed because it is possible to estimate the global PAR directly by estimating the
CIpar. The models for the case of the sun appearing (i.e.,
SA = 1) are as follows:
The models for the case of the sun hidden by cloud (i.e.,
SA = 0) are written as follows:
These model equations were created using only explanatory variables that are considered statistically significant (i.e., having a p-value of <0.001). However, we could not derive the multiregression model for the Q/E(g) using only sky-condition factors. Therefore, similarly to the estimation models of the Q/E(g) shown in Equations (16) and (20), the DR was used as one of the explanatory variables. In the case of estimating the Q/E(g), we used the DR estimated using Equations (15) and (19), together with the CC, BIws, and SEA.
To evaluate the contribution of each explanatory variable in the MRA,
Table 3 and
Table 4 list the standard partial regression coefficients of the
CC,
BIws,
SEA, and
DR (used only for the
Q/E(g)) with the multiple coefficient of determination (
R2) of each model, for
SA = 1 and
SA = 0 respectively.
The values of
R2 of the
CIpar in the case of
SA = 1 and of the
DR in the case of
SA = 0 are low, i.e., 0.156 and 0.273, respectively. This is because the values of the
CIpar when the sun appears (
SA = 1) and of the
DR when the sun is hidden (
SA = 0) do not change greatly when distinguishing samples for
SA = 1 and
SA = 0. Overall, the
CC has a positive effect on the
DR,
Q/E(g), and
Q/E(d) in the two cases where
SA = 1 and
SA = 0. In the case of
SA = 0, the
BIws contributes positively to the
CIpar, while the
SEA affects the
CIpar negatively. On the hourly timescale, the
BIws and
SEA are not adopted as explanatory variables for the
DR and
Q/E(d), respectively (
Table 2), but in the data samples with the instantaneous values, the
BIws contributes to the
DR positively (
SA = 1) and negatively (
SA = 0), while the
SEA contributes slightly to the
Q/E(d). By separating the two cases of the sun appearing and being hidden, the sky-condition factors seem to function interactively in explaining each estimation parameter.
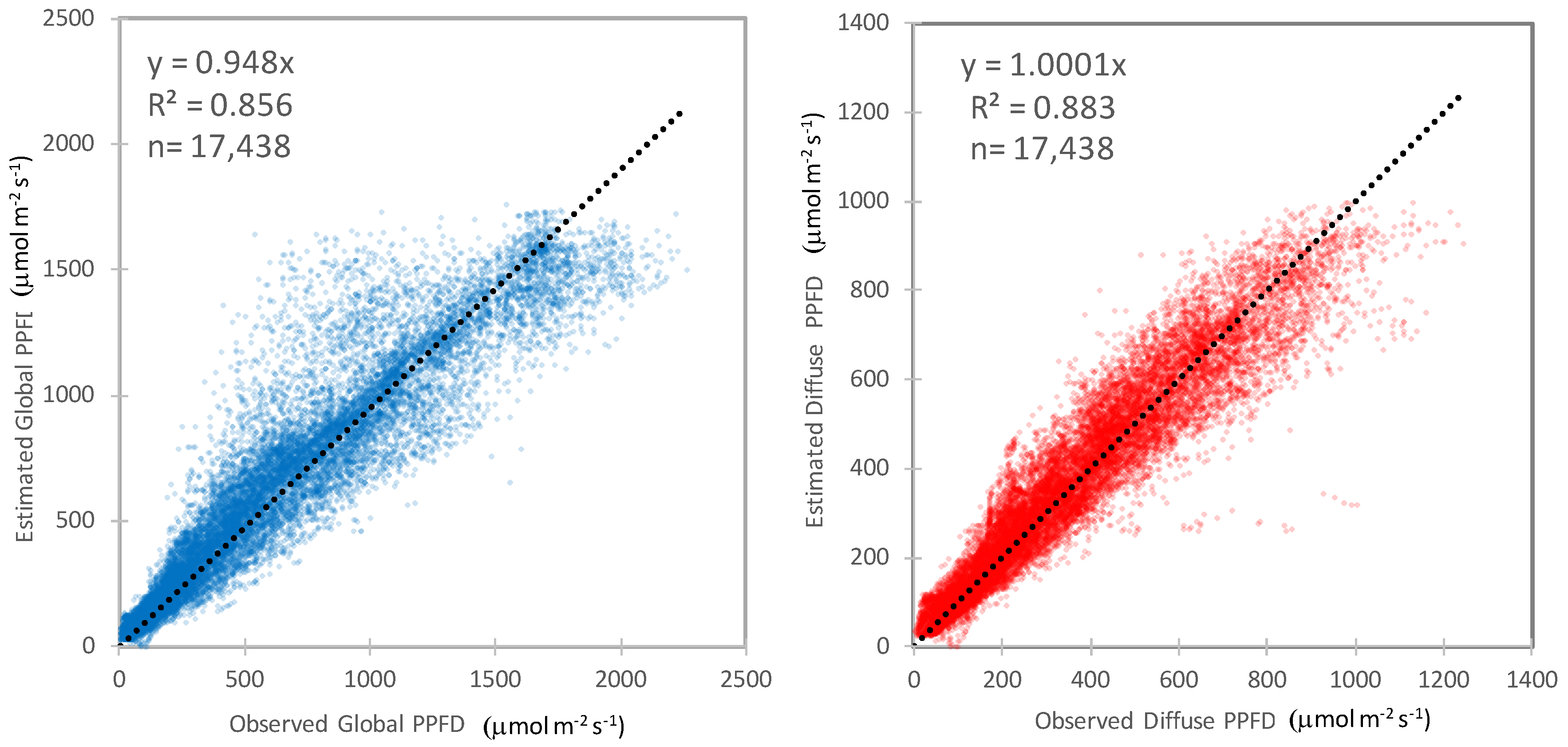
We then applied the estimation models expressed as Equations (14)–(21) to the sky-condition factors of the validation samples (
n = 17,438), and calculated the estimated global PPFD (
PPFDg_e) and diffuse PPFD (
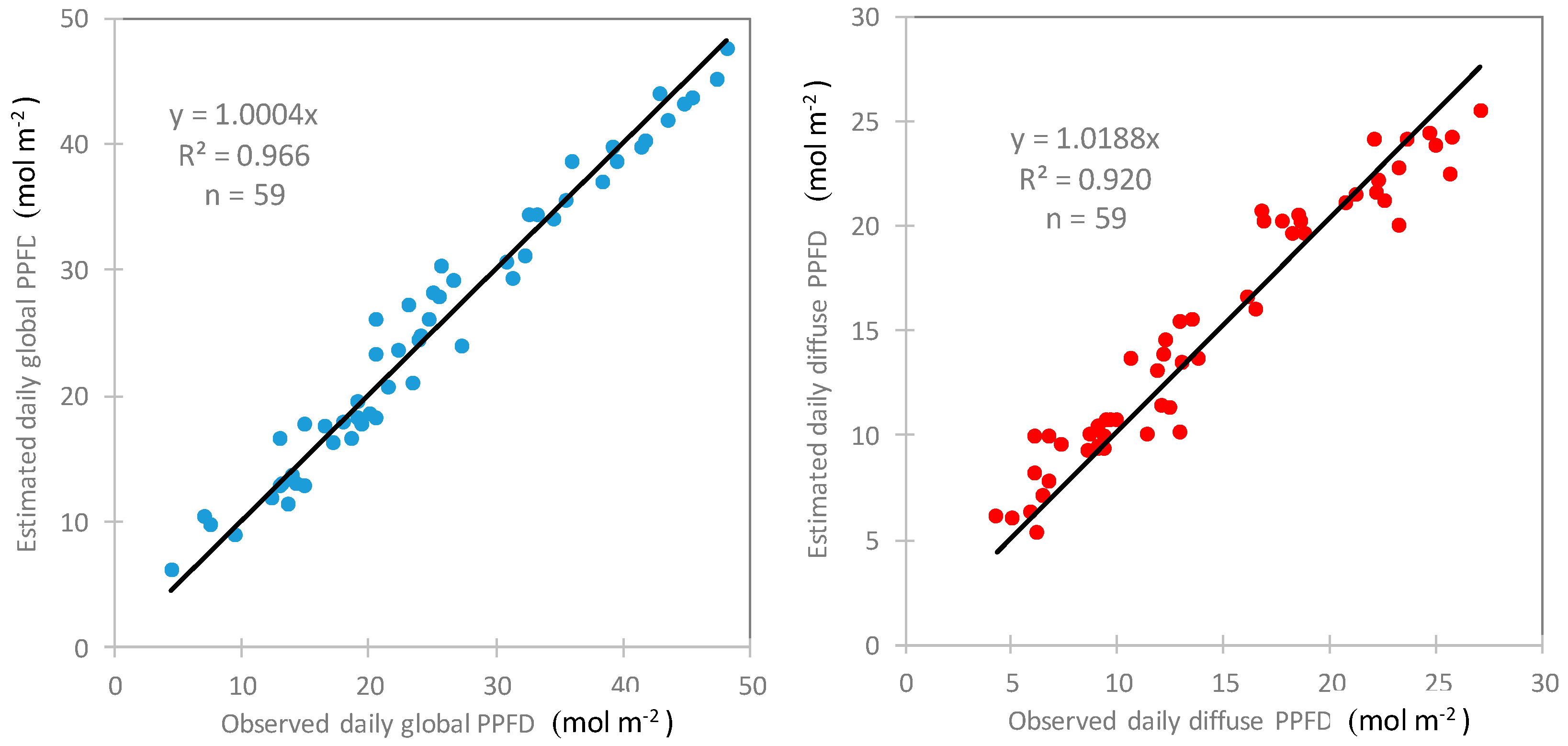
PPFDd_e) using Equations (10) and (11). To evaluate our estimation, the relationship between the observed global and diffuse PPFD and the estimations derived using the instantaneous values is shown in the left and right panels of
Figure 3, respectively. A linear approximation with a zero intercept is shown in each panel of the figure. The coefficient for the global and diffuse PPFD is 0.948 and 1.0001, respectively, i.e., both coefficients are close to 1.0. The coefficient of determination (
R2) for both relationships is >0.85.
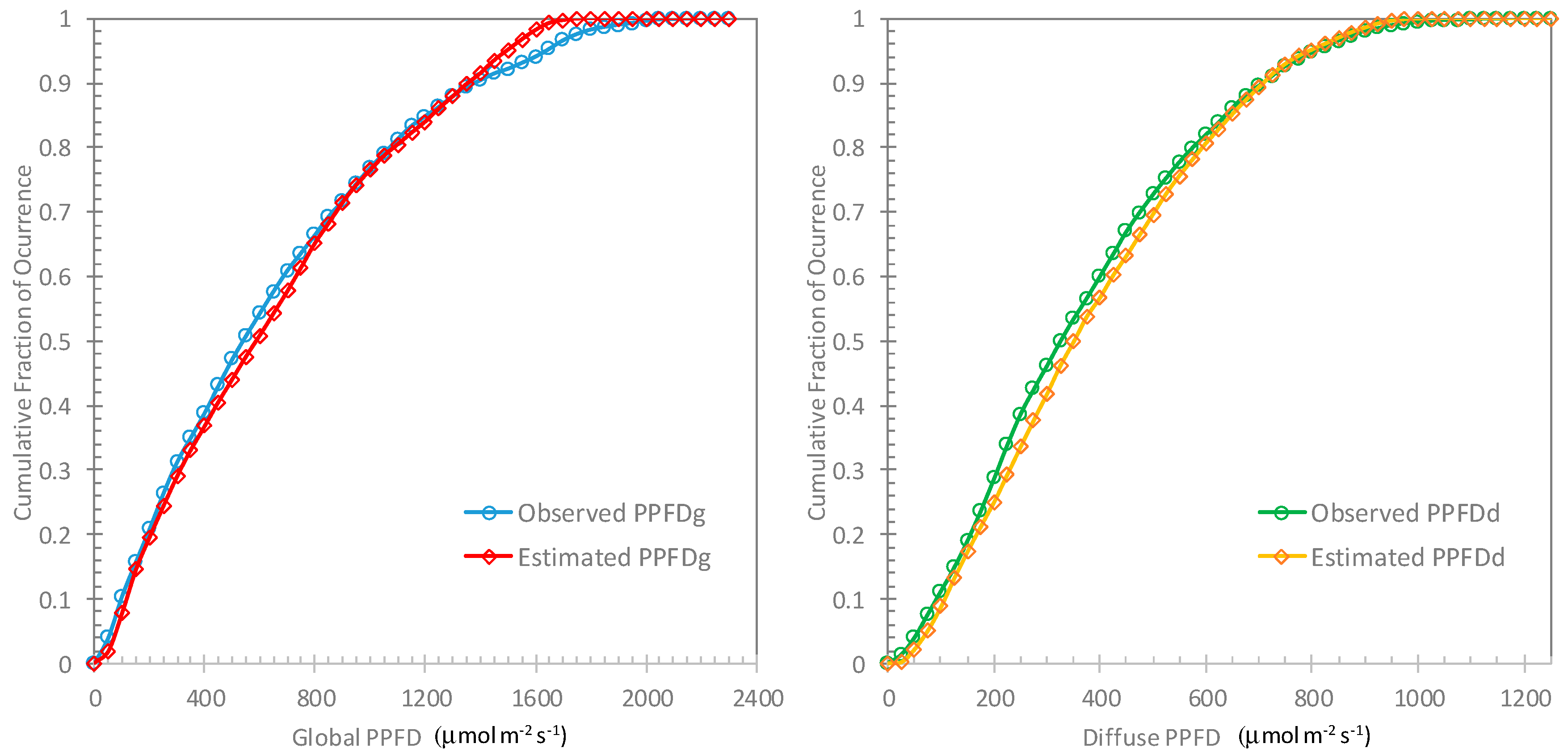
Figure 4 shows the cumulative frequency distribution curves [
35] of the estimated and the observed PPFD. For the global PPFD (
Figure 4; left), a difference of about 3% between the estimated value and the observed value was found at around 500–700 μmol m
−2 s
−1. Moreover, the curves of both agree well until 800–1400 μmol m
−2 s
−1. A difference of 3–4% can again be seen at around 1450–1750 μmol m
−2 s
−1. The global PPFD with instantaneous values over 1750 might be difficult to estimate in this model. As for the diffuse PPFD (
Figure 4; right), a difference of 3–5% can be seen at around 200–500 μmol m
−2 s
−1; however, the two curves are otherwise in good agreement.
To compare our results with the results of existing methods, the estimation accuracy of the global and diffuse PAR and PPFD is summarized in
Table 5. The mean bias errors of the global and diffuse PAR (PPFD) were 0.51 W m
−2 (1.77 μmol m
−2 s
−1) and 3.16 W m
−2 (14.0 μmol m
−2 s
−1), respectively. The diffuse components of the PAR and PPFD tend to be somewhat overestimated in comparison with the global PAR and PPFD. However, the relative root mean square error (RMSE) of the diffuse component is less than the global RMSE. The most remarkable point is that the relative RMSEs of the global PAR and PPFD and diffuse PAR and PPFD are almost the same, indicating that our models of the
Q/E(g) and
Q/E(d) contribute much to the estimation of the PPFD.
Wang et al. [
36] estimated the global PPFD using hourly data of the
CI and a cosine
SEA function with a relative RMSE of 7.0–12.5% at meteorological stations in China. In the case of estimating the global PPFD using instantaneous values of the
CI, Sun et al. [
37] obtained an RMSE of 40%. In the case of the diffuse PPFD estimation, Jacovides et al. [
38] performed estimations using the
CIpar and
DR with a relative RMSE of 27% on an hourly timescale. Wang et al. [
39] estimated the hourly global and diffuse PPFD under clear sky conditions at sites having a complex terrain using the ratios of the global and diffuse PAR to extraterrestrial PAR, and they reported relative RMSEs of 8–26% and 23–26%, respectively. Our estimations of the global and diffuse PPFD using instantaneous values under various sky conditions with relative RMSEs of 27% and 20%, respectively, have good accuracy in comparison with the results of existing methods.
3.4. Validity of PPFD Estimation with Instantaneous Values
The incident global and diffuse PPFDs on a short timescale are important input parameters for the precise modeling of plant physiological processes in the estimation of the carbon gain, biomass, and yields during vegetation growth [
1,
7,
39,
40]. To verify the validity of the estimations of the global and diffuse PPFD with instantaneous values, we examined our estimation results at daily and diurnal levels.
First, the relationships between the estimated and observed daily accumulated values of the global and diffuse PPFD are shown in
Figure 5. The validation data for all 59 days produce a mean relative error and relative RMSE of the daily accumulated global (diffuse) PPFD of +0.9% (+4.4%) and 8.2% (11.5%), respectively (
Table 6). Those days that show a low accumulation of the PPFD tend to have a large relative error of approximately 20–30%. There were 2 days on which the daily global PPFD had a relative error of >30%. The daily global PPFD on these days was low, i.e., 7.1 and 4.5 mol m
−2 d
−1. The whole-sky images acquired on these days showed a persistent dark cloud.
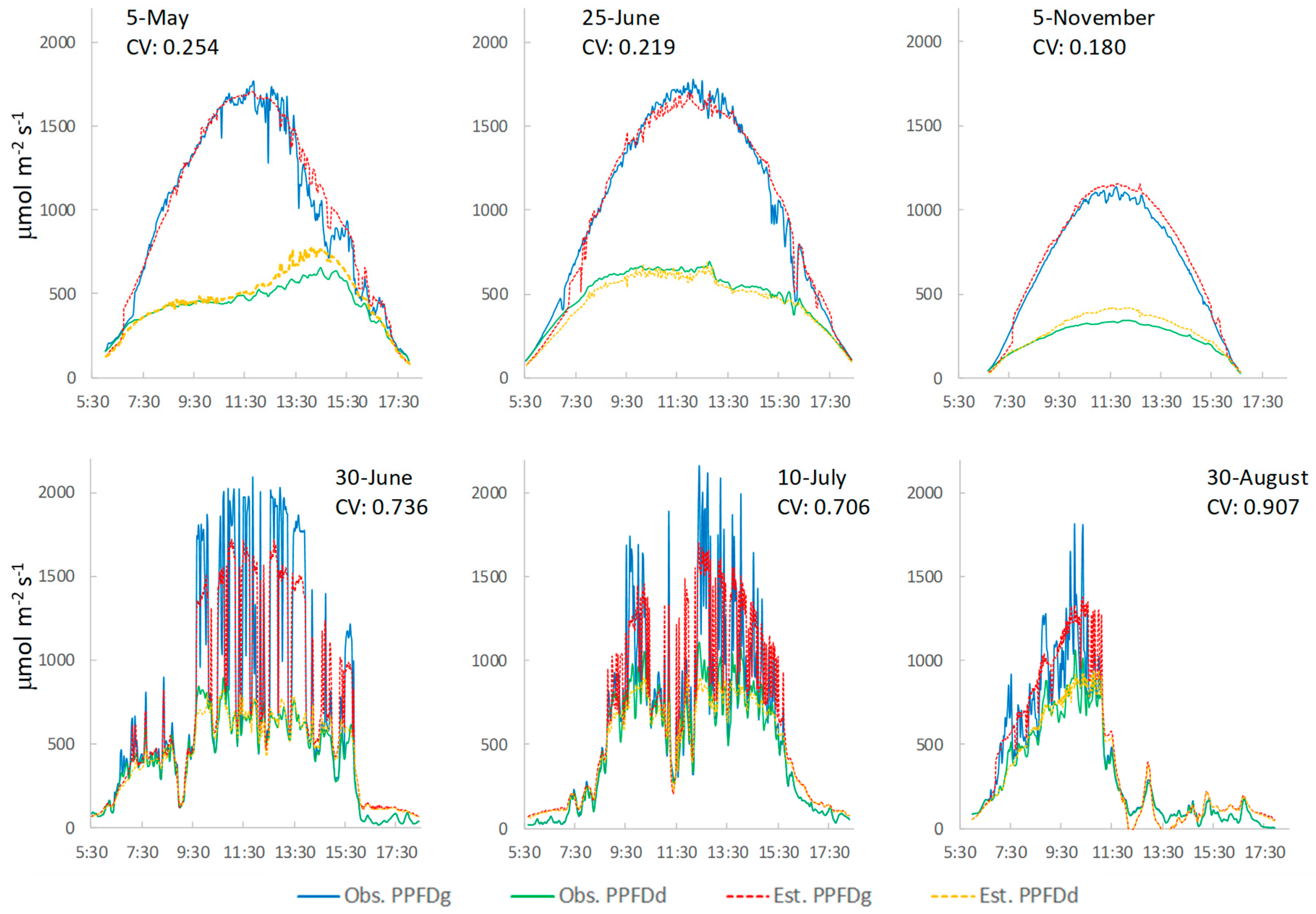
Second, we examined whether the diurnal fluctuation of the PPFD due to a change of sky condition could be estimated using instantaneous values. Using the coefficient of variation (CV = St.Dev./Mean) of the
CIpar per day for all 59 days, it was assumed that a day with a large CV was a day on which sky conditions fluctuated, whereas a day with a small CV was a day on which sky conditions were clear. We selected 3 days with the lowest (0.180, 0.219, and 0.254) and 3 days with the highest (0.907, 0.736, and 0.706) CV values as days with clear and fluctuating sky conditions, respectively. The CV mean (St.Dev.) of all 59 days was 0.433 (0.147).
Figure 6 shows the diurnal changes in the observed global and diffuse PPFD and the estimations made with instantaneous values for the 3 days with clear sky conditions (5 May, 25 June 5, and 5 November) and for the 3 days with fluctuating sky conditions (30 June, 10 July, and 30 August). The daily accumulated values of the observed and estimated PPFD are given in
Table 7.
On the 3 days when the weather was clear, both the global and the diffuse PPFD increased in the morning and decreased in the afternoon in response to the sun elevation, because there were no cloud effects. On the afternoon of 5 May, as the
CC increased and the
BIws was high, it seems that the diffuse component was greater owing to the presence of thin clouds. There were occasional differences between the observed and estimated values of the diffuse PPFD in the afternoon of 5 May and around noon on 5 November, with relative errors of the daily accumulated PPFD of +7.6% and +13.5%, respectively. In contrast, for the 3 days with fluctuating sky conditions, it can be seen that the diurnal global and diffuse PPFD changed drastically in a short time owing to the changing sky conditions, especially when the sun emerged from or disappeared behind a moving cloud. These fluctuations almost have the same pattern for the observed and estimated values, i.e., the estimated PPFD values reflect the drastic changes in sky condition at the times when the whole-sky images were acquired. However, when the observed
PPFDg becomes instantaneously high, a large difference from the estimated
PPFDg is evident. The absolute error in the instantaneous value is large when the sun emerges from or disappears behind a cloud. In terms of the daily accumulated values (
Table 7), the relative errors of the global and diffuse PPFD are small (ranging from −0.4 to +9.0%), even on the 3 days with fluctuating sky conditions.
From
Table 7 it can be seen that there were no marked differences in the relative error of the daily accumulated value between the clear days and days with fluctuating sky conditions. The process models of ecosystems are generally inputs with a time series of parameters, and they predict accumulated values. In the case of the process of photosynthesis, daily accumulating values are affected by diurnal changes in the PPFD [
1,
40]. Therefore, it is not possible to reflect the diurnal variation of sky conditions using only a daily value of the PPFD [
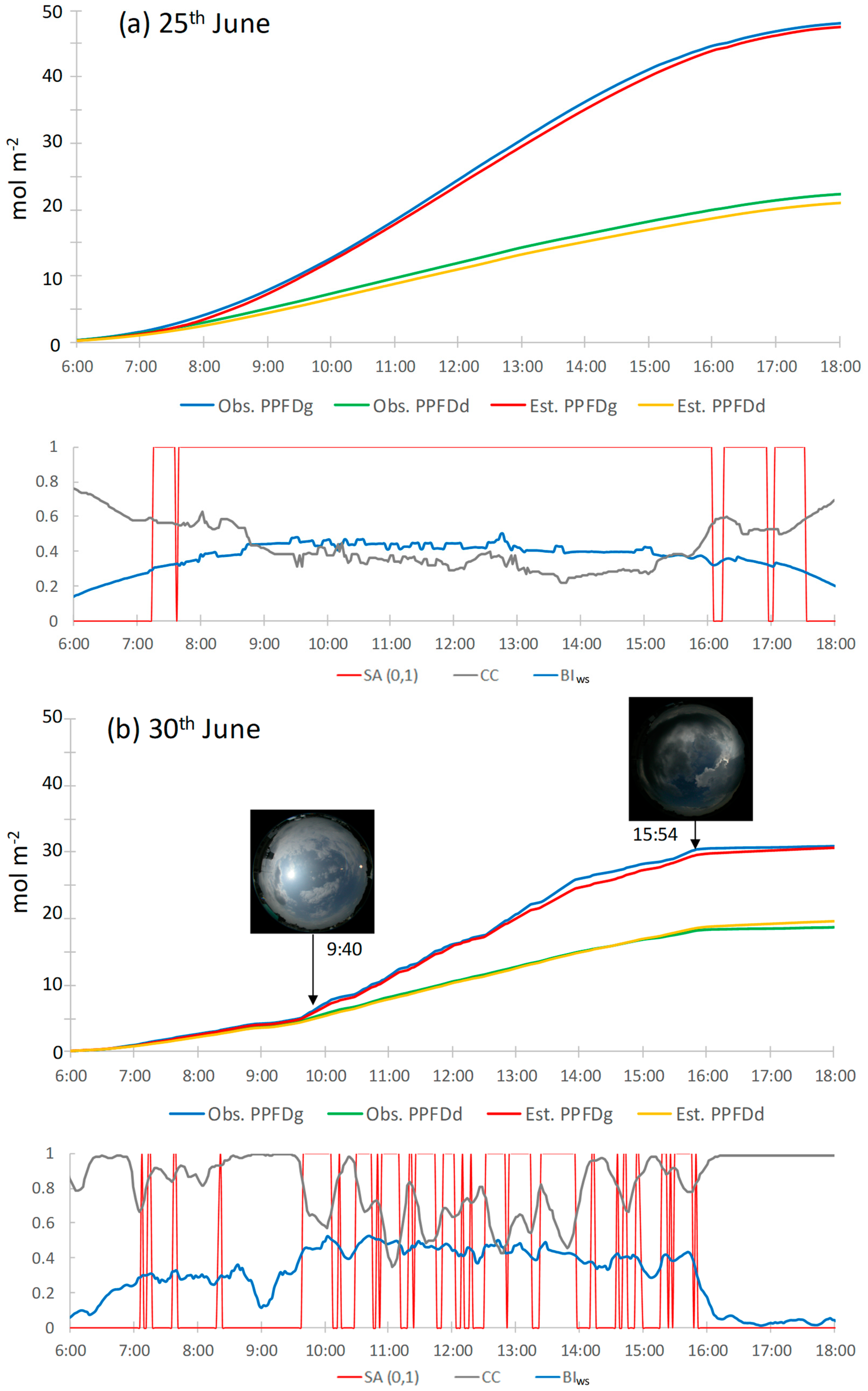
1]. Here, to compare the diurnal accumulating values between the observed and estimated PPFD,
Figure 7 shows the accumulating values for a time series of global and diffuse PPFD on 25 and 30 June (as an example of a clear day and a day with fluctuating sky conditions, respectively) when the
SEA was high. The diurnal changes of the
SA,
CC, and
BIws are also shown.
On 25 June, when the sky conditions were reasonably clear (CV = 0.219), both the global and the diffuse PPFD produced smooth curves (
Figure 7a). The difference between the global and diffuse PPFD is the direct component. On this day, there was direct sunlight from early morning, and the relative errors of the daily estimated global and diffuse PPFD were −1.2% and −6.8%, respectively (
Table 7). The sky conditions on 30 June were variable (CV = 0.736), i.e., after being cloudy in the early morning, it was sunny until early evening when it became cloudy again. The values of the global and diffuse PPFD were almost the same until around 09:40 local time (LT). The global PPFD increased with the appearance of the sun (i.e., the direct component increased) from 09:40 LT until around 16:00 LT. The traces of the global and diffuse PPFD were almost parallel after 16:00 LT (
Figure 7b). The diurnal accumulated values of the estimated global and diffuse PPFD were always close to the observations at all times. The relative errors of the global and diffuse PPFD were −0.4% and +4.2%, respectively (
Table 7). This result reflects the effects of the sky conditions well.
The above verification shows that our PPFD estimation using instantaneous values could be effective for precise process models of vegetation photosynthesis. Additionally, we expect our proposed methodology for PPFD estimation using whole-sky images to be used not only at existing weather stations but also at any point where a whole-sky camera system could be installed.