Rubber Tree Crown Segmentation and Property Retrieval Using Ground-Based Mobile LiDAR after Natural Disturbances
Abstract
:1. Introduction
2. Materials and Methods
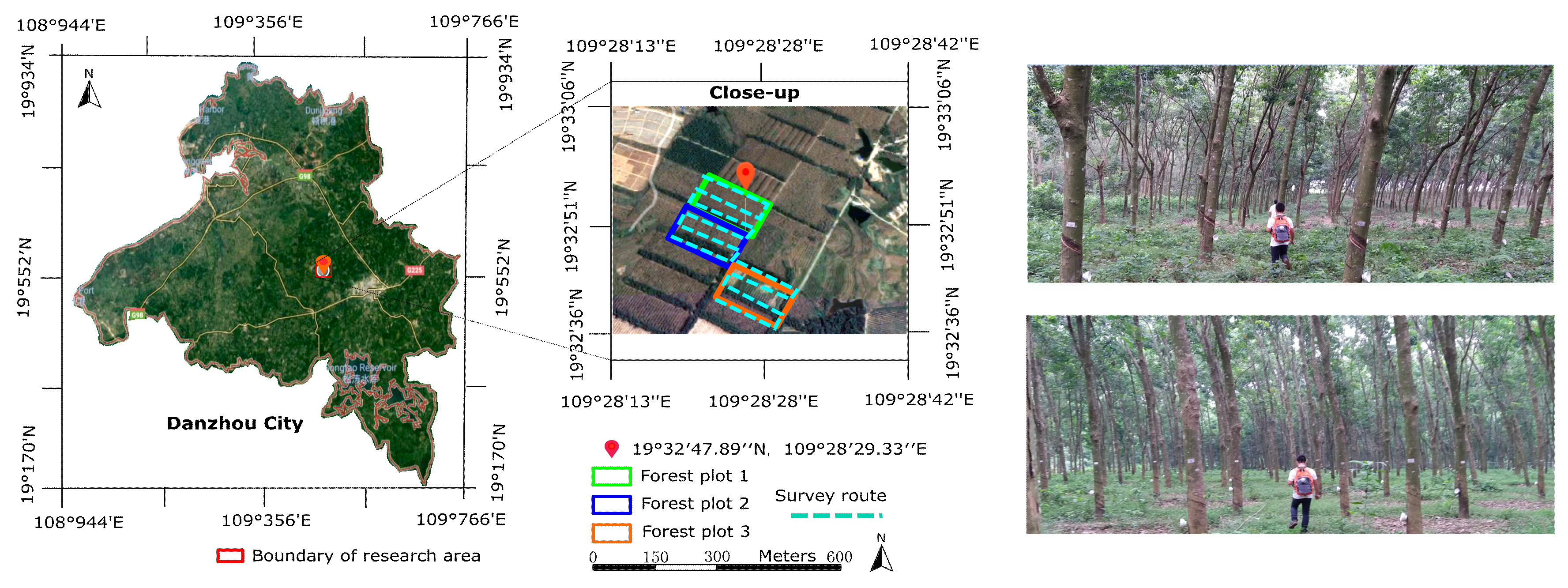
2.1. Study Area
2.2. Laser Data Acquisition
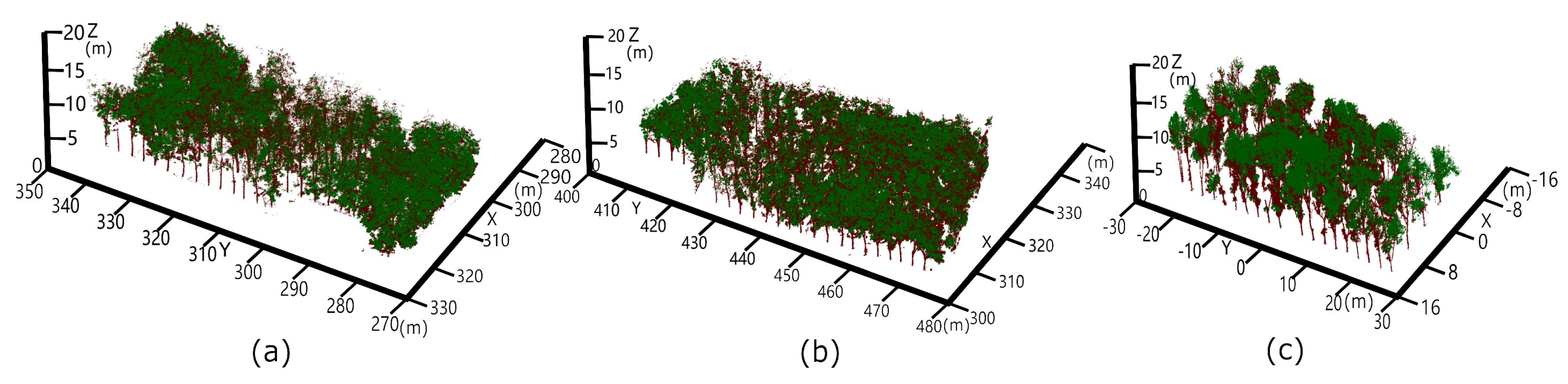
2.3. Field Data
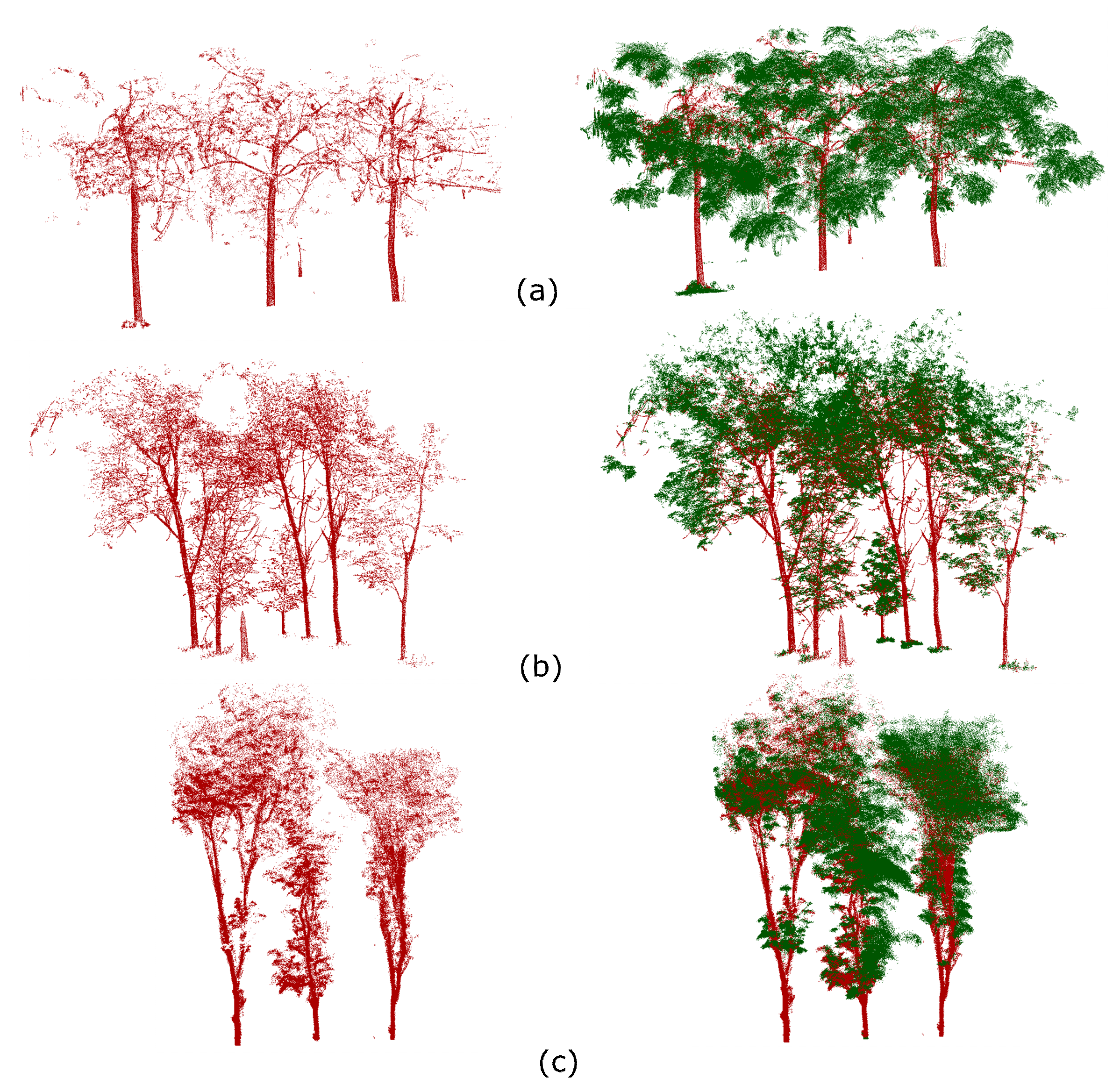
2.4. Pre-Processing of the Scanned Data
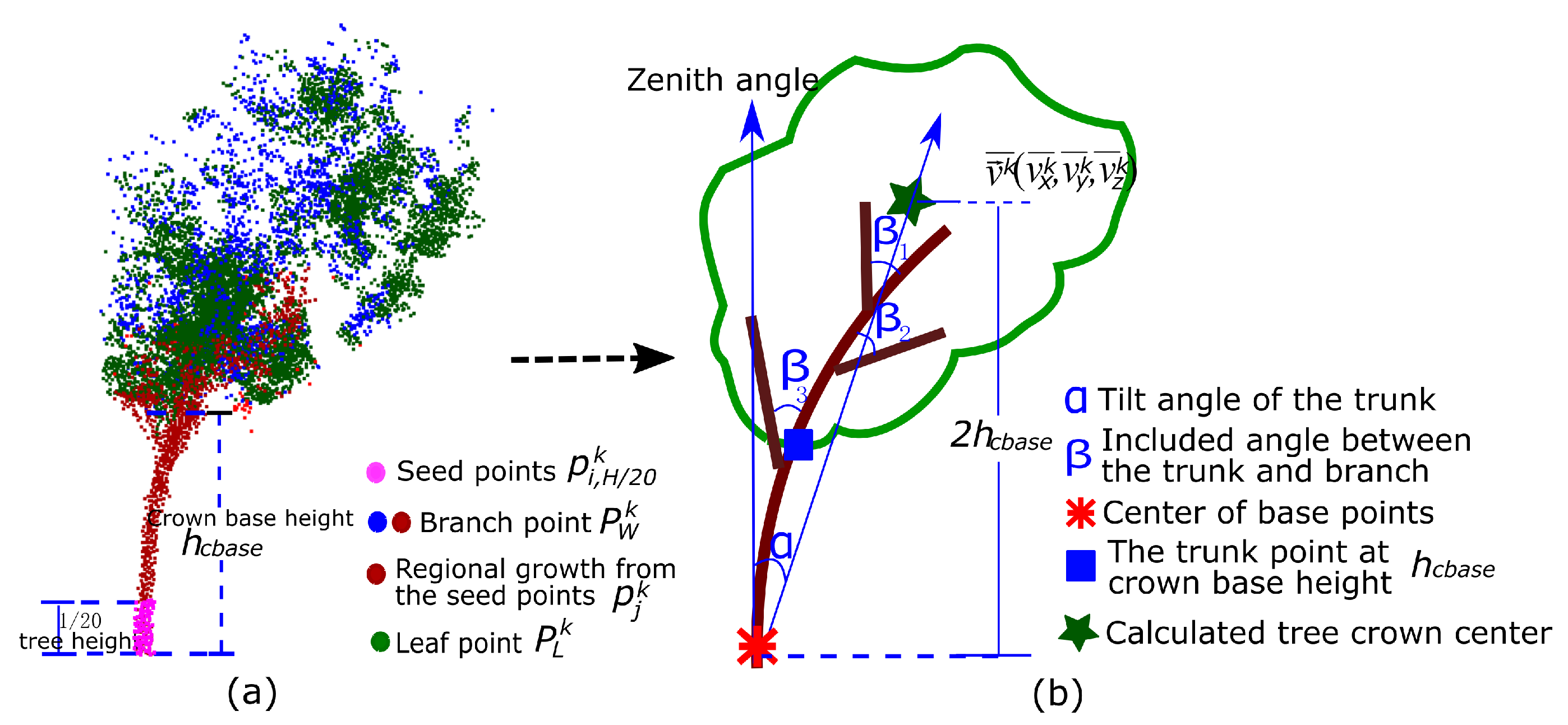
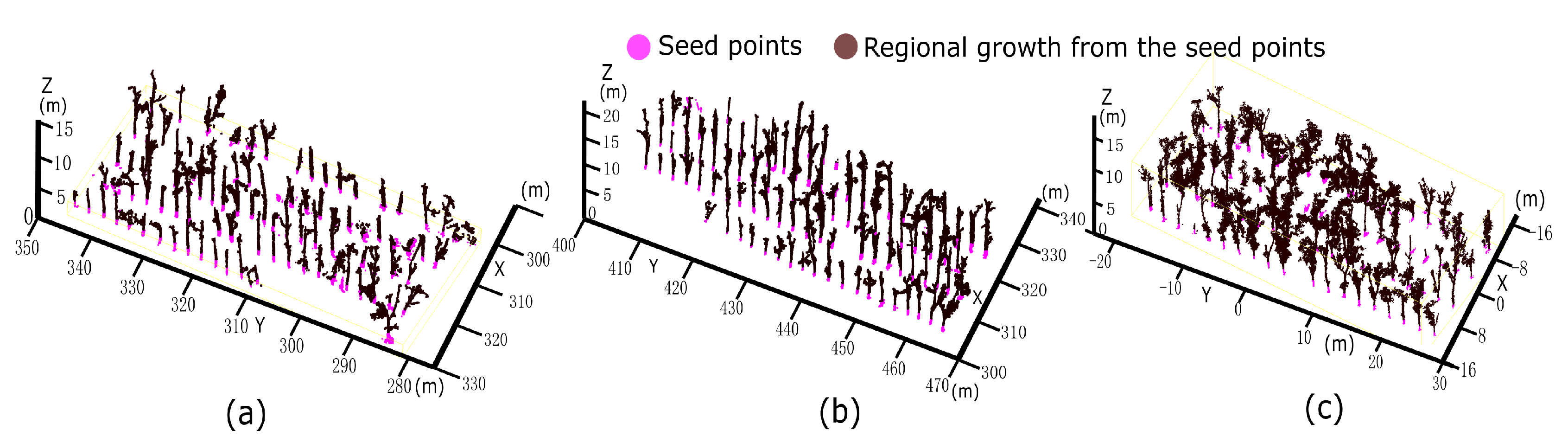
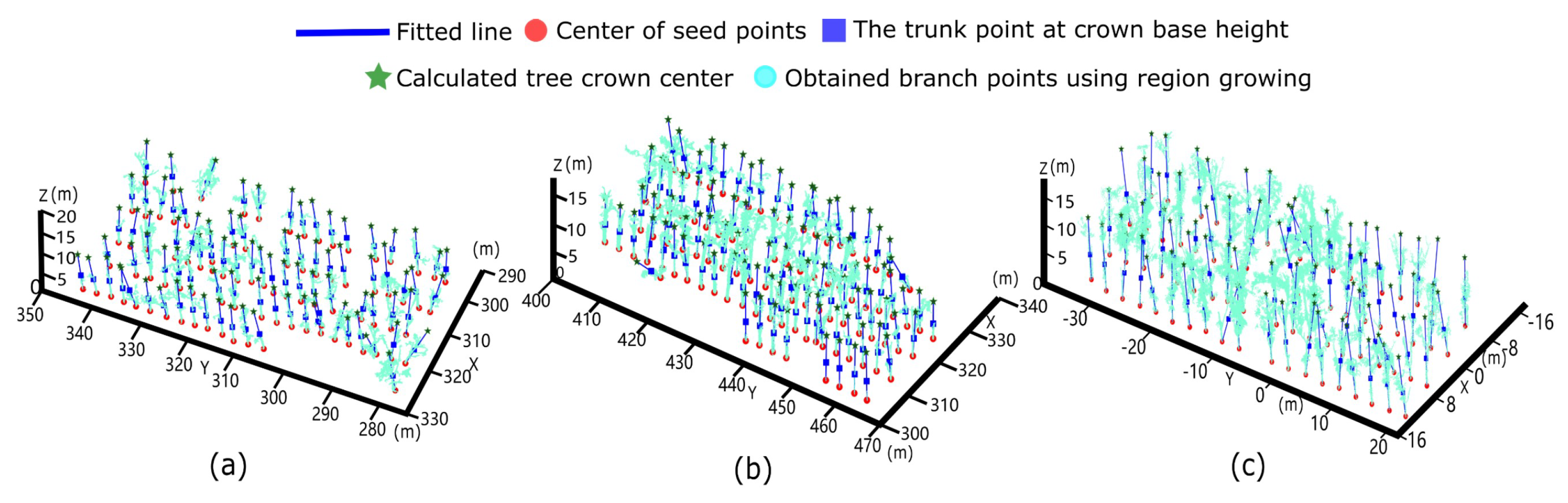
2.5. Positioning the Centre of the Tree Crown
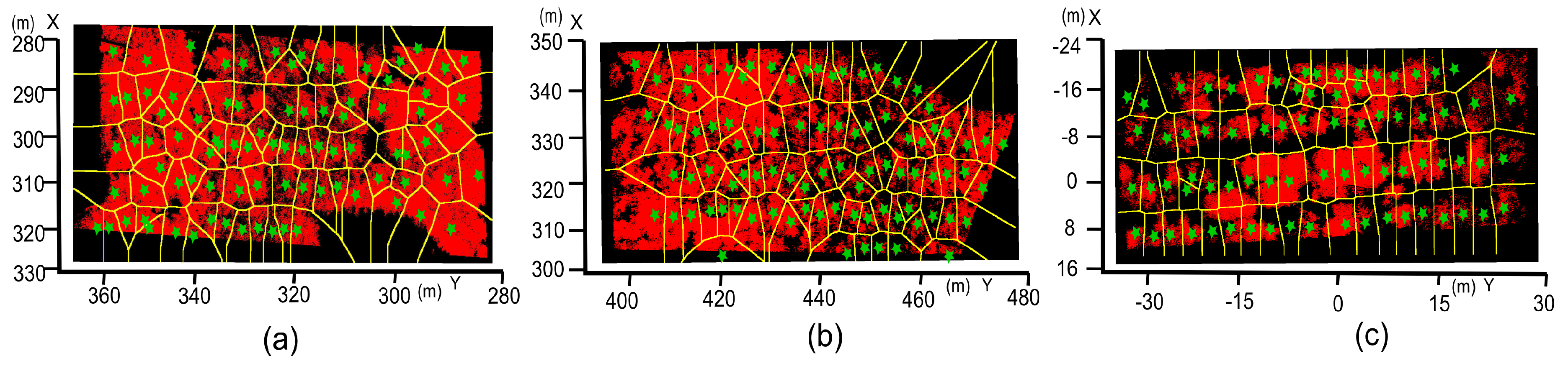
2.6. Tree Crown Delineation Based on the Watershed Algorithm
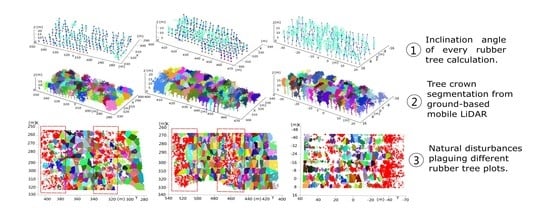
3. Results
4. Discussion
4.1. Specific Uses of Our Approach
4.2. Impact of Hurricane Propagation through the Rubber Tree Forests
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Hakeem, K.R.; Jawaid, M.; Rashid, U. Biomass and Bioenergy: Processing and Properties; Springer: New York, NY, USA, 2014; ISBN 3319076418. [Google Scholar]
- Korhonen, L.; Korhonen, K.T.; Rautiainen, M.; Stenberg, P. Estimation of Forest Canopy Cover: A Comparison of Field Measurement Techniques. Available online: https://bit.ly/2P4WjIt (accessed on 13 April 2019).
- Cao, L.; Coops, N.C.; Sun, Y.; Ruan, H.; Wang, G.; Dai, J.; She, G. Estimating canopy structure and biomass in bamboo forests using airborne LiDAR data. ISPRS J. Photogramm. Remote Sens. 2019, 148, 114–129. [Google Scholar] [CrossRef]
- Cao, L.; Liu, H.; Fu, X.; Zhang, Z.; Shen, X.; Ruan, H. Comparison of UAV LiDAR and digital aerial photogrammetry point clouds for estimating forest structural attributes in subtropical planted forests. Forests 2019, 10, 145. [Google Scholar]
- Hancock, S.; Essery, R.; Reid, T.; Carle, J.; Baxter, R.; Rutter, N.; Huntley, B. Characterising forest gap fraction with terrestrial lidar and photography: An examination of relative limitations. Agric. For. Meteorol. 2014, 189–190, 105–114. [Google Scholar] [CrossRef]
- Xu, Q.; Cao, L.; Xue, L.; Chen, B.; An, F.; Yun, T. Extraction of Leaf Biophysical Attributes Based on a Computer Graphic-based Algorithm Using Terrestrial Laser Scanning Data. Remote Sens. 2019, 11, 15. [Google Scholar] [CrossRef]
- Hu, C.; Pan, Z.; Li, P. A 3D Point Cloud Filtering Method for Leaves Based on Manifold Distance and Normal Estimation. Remote Sens. 2019, 11, 198. [Google Scholar] [CrossRef]
- Côté, J.-F.; Fournier, R.A.; Egli, R. An architectural model of trees to estimate forest structural attributes using terrestrial LiDAR. Environ. Model. Softw. 2011, 26, 761–777. [Google Scholar] [CrossRef]
- Sun, Y.; Liang, X.; Liang, Z.; Welham, C.; Li, W. Deriving merchantable volume in poplar through a localized tapering function from non-destructive terrestrial laser scanning. Forests 2016, 7, 87. [Google Scholar] [CrossRef]
- Xu, S.; Xu, S.; Ye, N.; Zhu, F. Automatic extraction of street trees’ nonphotosynthetic components from MLS data. Int. J. Appl. Earth Obs. Geoinf. 2018, 69, 64–77. [Google Scholar] [CrossRef]
- Bauwens, S.; Bartholomeus, H.; Calders, K.; Lejeune, P. Forest inventory with terrestrial LiDAR: A comparison of static and hand-held mobile laser scanning. Forests 2016, 7, 127. [Google Scholar] [CrossRef]
- Polewski, P.; Yao, W.; Cao, L.; Gao, S. Marker-free coregistration of UAV and backpack LiDAR point clouds in forested areas. ISPRS J. Photogramm. Remote Sens. 2019, 147, 307–318. [Google Scholar] [CrossRef]
- Zhang, Z.; Cao, L.; Mulverhill, C.; Liu, H.; Pang, Y.; Li, Z. Prediction of Diameter Distributions with Multimodal Models Using LiDAR Data in Subtropical Planted Forests. Forests 2019, 10, 125. [Google Scholar] [CrossRef]
- Dalponte, M.; Ørka, H.O.; Ene, L.T.; Gobakken, T.; Næsset, E. Tree crown delineation and tree species classification in boreal forests using hyperspectral and ALS data. Remote Sens. Environ. 2014, 140, 306–317. [Google Scholar] [CrossRef]
- Morsdorf, F.; Meier, E.; Kötz, B.; Itten, K.I.; Dobbertin, M.; Allgöwer, B. LIDAR-based geometric reconstruction of boreal type forest stands at single tree level for forest and wildland fire management. Remote Sens. Environ. 2004, 92, 353–362. [Google Scholar] [CrossRef]
- Brandtberg, T.; Warner, T.A.; Landenberger, R.E.; McGraw, J.B. Detection and analysis of individual leaf-off tree crowns in small footprint, high sampling density lidar data from the eastern deciduous forest in North America. Remote Sens. Environ. 2003, 85, 290–303. [Google Scholar] [CrossRef]
- Hu, X.; Chen, W.; Xu, W. Adaptive Mean Shift-Based Identification of Individual Trees Using Airborne LiDAR Data. Remote Sens. 2017, 9, 148. [Google Scholar] [CrossRef]
- Jung, S.-E.; Kwak, D.-A.; Park, T.; Lee, W.-K.; Yoo, S. Estimating crown variables of individual trees using airborne and terrestrial laser scanners. Remote Sens. 2011, 3, 2346–2363. [Google Scholar] [CrossRef]
- Ke, Y.; Quackenbush, L.J. A review of methods for automatic individual tree-crown detection and delineation from passive remote sensing. Int. J. Remote Sens. 2011, 32, 4725–4747. [Google Scholar] [CrossRef]
- Duncanson, L.I.; Cook, B.D.; Hurtt, G.C.; Dubayah, R.O. An efficient, multi-layered crown delineation algorithm for mapping individual tree structure across multiple ecosystems. Remote Sens. Environ. 2014, 154, 378–386. [Google Scholar] [CrossRef]
- Weinmann, M.; Mallet, C.; Brédif, M. Segmentation and localization of individual trees from MMS point cloud data acquired in urban areas. In Proceedings of the Tagungsband der Dreiländertagung der DGPF, der OVG und der SGPF, Bern, Switzerland, 14–16 September 2016; pp. 7–9. [Google Scholar]
- Mongus, D.; Žalik, B. An efficient approach to 3D single tree-crown delineation in LiDAR data. ISPRS J. Photogramm. Remote Sens. 2015, 108, 219–233. [Google Scholar] [CrossRef]
- Pitkänen, J.; Maltamo, M.; Hyyppä, J.; Yu, X. Adaptive methods for individual tree detection on airborne laser based canopy height model. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2004, 36, 187–191. [Google Scholar]
- Lin, C.; Thomson, G.; Lo, C.-S.; Yang, M.-S. A multi-level morphological active contour algorithm for delineating tree crowns in mountainous forest. Photogramm. Eng. Remote Sens. 2011, 77, 241–249. [Google Scholar] [CrossRef]
- Jing, L.; Hu, B.; Noland, T.; Li, J. An individual tree crown delineation method based on multi-scale segmentation of imagery. ISPRS J. Photogramm. Remote Sens. 2012, 70, 88–98. [Google Scholar] [CrossRef]
- Lu, X.; Guo, Q.; Li, W.; Flanagan, J. A bottom-up approach to segment individual deciduous trees using leaf-off lidar point cloud data. ISPRS J. Photogramm. Remote Sens. 2014, 94, 1–12. [Google Scholar] [CrossRef]
- Yun, T.; Li, W.; Sun, Y.; Xue, L. Study of Subtropical Forestry Index Retrieval Using Terrestrial Laser Scanning and Hemispherical Photography. Math. Probl. Eng. 2015, 2015, 206108. [Google Scholar] [CrossRef]
- Yun, T.; An, F.; Li, W.; Sun, Y.; Cao, L.; Xue, L. A novel approach for retrieving tree leaf area from ground-based LiDAR. Remote Sens. 2016, 8, 942. [Google Scholar] [CrossRef]
- Tao, S.; Wu, F.; Guo, Q.; Wang, Y.; Li, W.; Xue, B.; Hu, X.; Li, P.; Tian, D.; Li, C. Segmenting tree crowns from terrestrial and mobile LiDAR data by exploring ecological theories. ISPRS J. Photogramm. Remote Sens. 2015, 110, 66–76. [Google Scholar] [CrossRef]
- Maurer, C.R.; Qi, R.; Raghavan, V. A linear time algorithm for computing exact Euclidean distance transforms of binary images in arbitrary dimensions. IEEE Trans. Pattern Anal. Mach. Intell. 2003, 25, 265–270. [Google Scholar] [CrossRef]
- Zheng, G.; Moskal, L.M. Computational-geometry-based retrieval of effective leaf area index using terrestrial laser scanning. IEEE Trans. Geosci. Remote Sens. 2012, 50, 3958–3969. [Google Scholar] [CrossRef]
- Wang, Z.; Zhang, L.; Fang, T.; Tong, X.; Mathiopoulos, P.T.; Zhang, L.; Mei, J. A local structure and direction-aware optimization approach for three-dimensional tree modeling. IEEE Trans. Geosci. Remote Sens. 2016, 54, 4749–4757. [Google Scholar] [CrossRef]
- Yen, T.-M. Relationships of Chamaecyparis formosensis crown shape and parameters with thinning intensity and age. Ann. For. Res. 2015, 58, 323–332. [Google Scholar] [CrossRef]
- Baldwin, V.; Clark, J.; Peterson, K.D. Predicting the crown shape of loblolly pine trees. Can. J. For. Res. 1997, 27, 102–107. [Google Scholar] [CrossRef]
- Shen, X.; Cao, L.; Yang, B.; Xu, Z.; Wang, G. Estimation of Forest Structural Attributes Using Spectral Indices and Point Clouds from UAS-Based Multispectral and RGB Imageries. Remote Sens. 2019, 11, 800. [Google Scholar] [CrossRef]
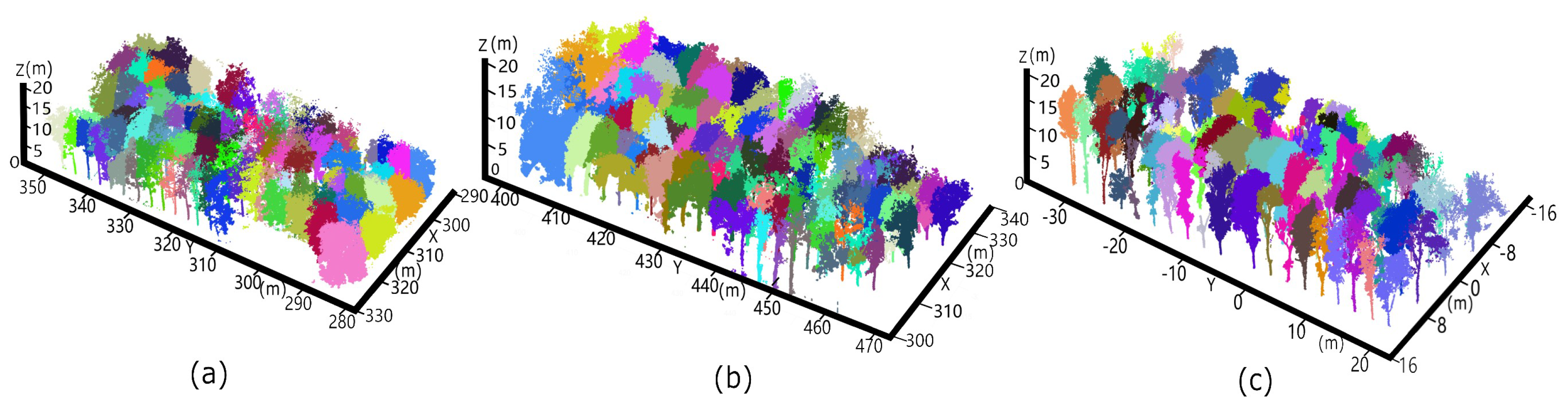
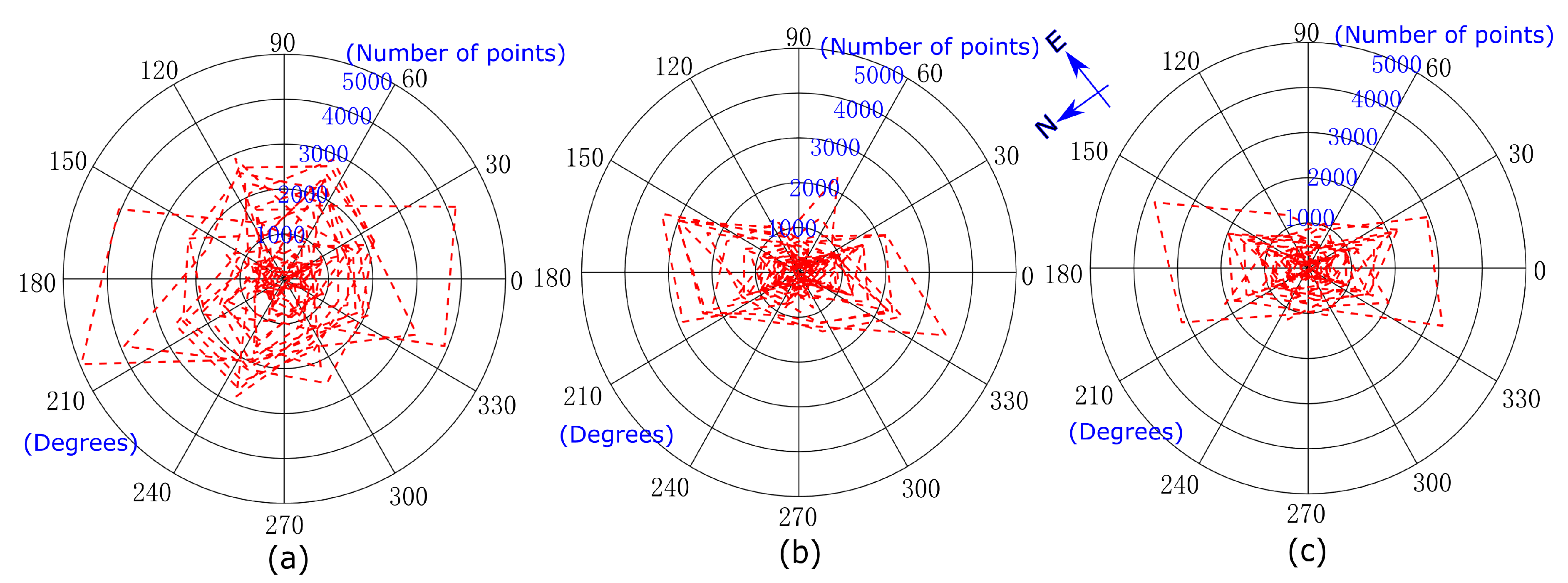
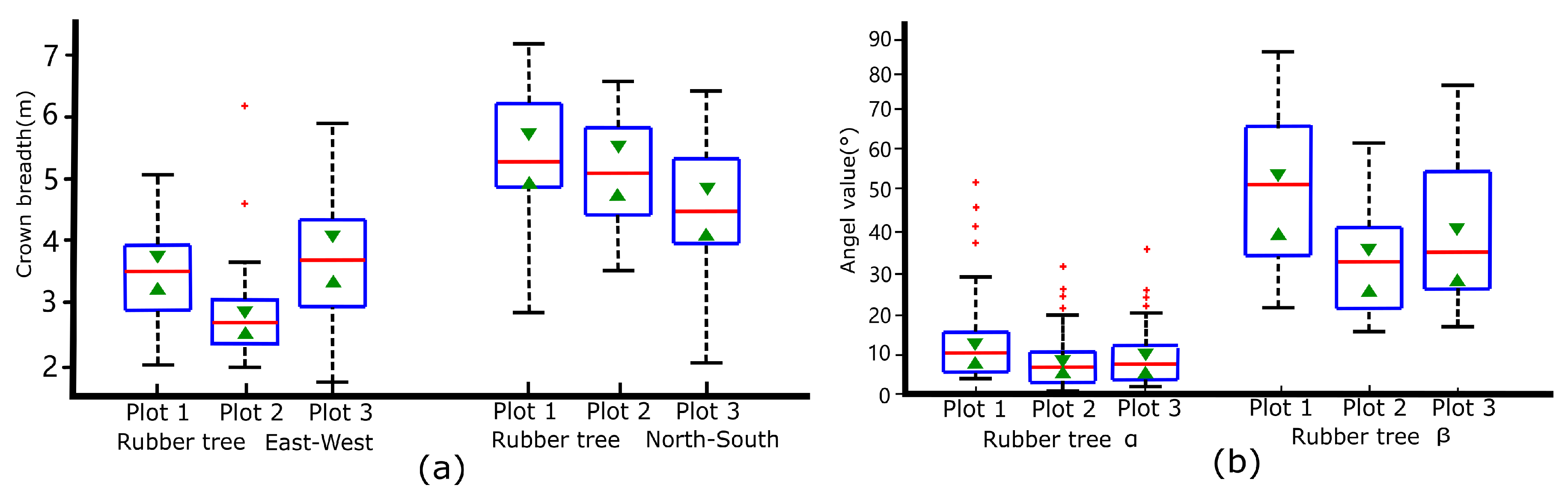
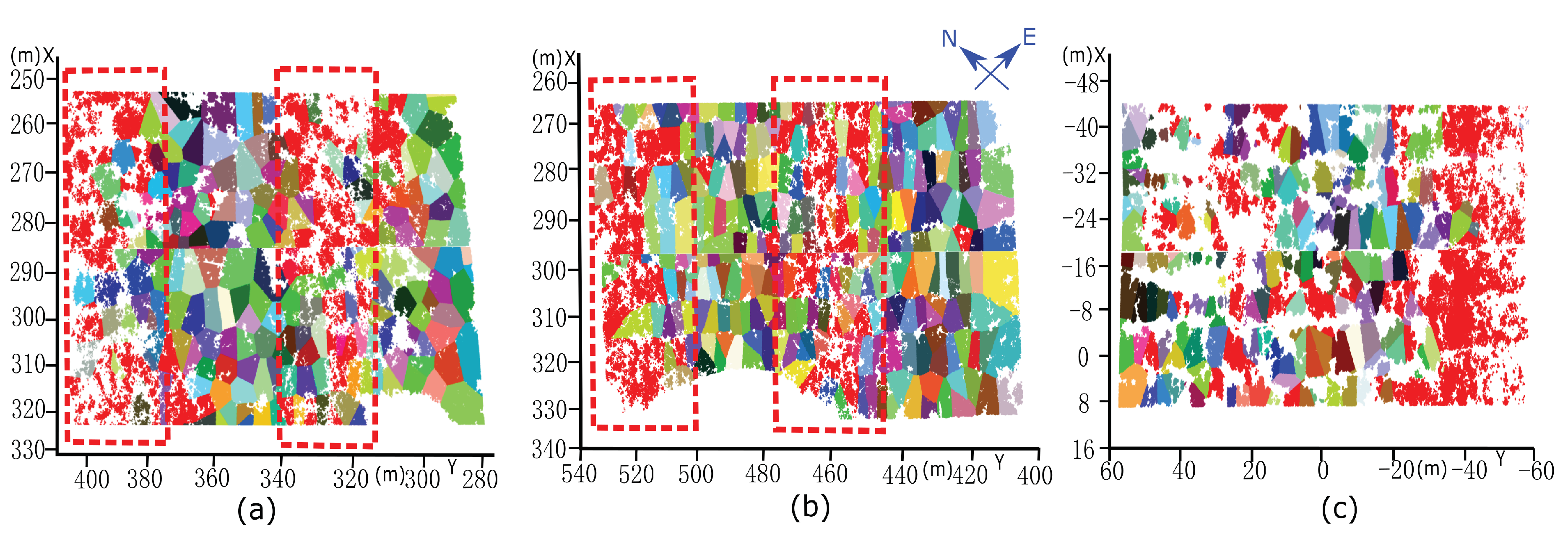
| Rubber Tree Plot 1 (PR107) | Rubber Tree Plot 2 (CATAS 7-20-59) | Rubber Tree Plot 3 (CATAS 8-7-9) | |
|---|---|---|---|
| Number of scanned points/Number of trees | 1359879/138 | 1325866/148 | 922628/191 |
| Number of scanned points (Leaf/Wood) | 1039143/320736 | 958631/367235 | 660558/262070 |
| Plant spacing (m) | 6.08 Vertical 2.52 Horizontal | 6.13 Vertical 2.52 Horizontal | 6.14 Vertical 2.62 Horizontal |
| Retrieved parameters | (Our method/Field measurement), Correlation degree | (Our method/Field measurement), Correlation degree | (Our method/Field measurement), Correlation degree |
| Average tree height (m) | (13.23/13.17), 96.34% | (14.95/15.10), 98.32% | (12.92/13.11), 97.15% |
| Average breast diameter (cm) | (27.12/26.21), 97.21% | (33.10/33.29), 98.43% | (21.91/21.06), 96.32% |
| Average crown volume (m3) | (205.45/200.98), 92.82% | (182.00/184.48), 91.71% | (99.47/ 103.82), 90.31% |
| Crown length (m) | (3.74/3.95), 93.72% E-W (5.59/5.78), 95.13% N-S | (3.07/3.08), 98.72% E-W (5.48/5.70), 96.12% N-S | (3.92/3.96), 97.81% E-W (4.87/4.69), 96.30% N-S |
| Average trunk inclined angle α (degree) | (13.08°/12.97°), 97.16% | 8.14°/8.49°, 95.92% | 8.87°/9.17°, 94.74% |
| The angle β between the first-order branch and trunk (degree) | (35.06°–67.73°/36.62°–66.49°) | (20.29°–43.20°/21.34°–41.18°) | (23.14°–54.36°/24.28°–55.38°) |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yun, T.; Jiang, K.; Hou, H.; An, F.; Chen, B.; Jiang, A.; Li, W.; Xue, L. Rubber Tree Crown Segmentation and Property Retrieval Using Ground-Based Mobile LiDAR after Natural Disturbances. Remote Sens. 2019, 11, 903. https://doi.org/10.3390/rs11080903
Yun T, Jiang K, Hou H, An F, Chen B, Jiang A, Li W, Xue L. Rubber Tree Crown Segmentation and Property Retrieval Using Ground-Based Mobile LiDAR after Natural Disturbances. Remote Sensing. 2019; 11(8):903. https://doi.org/10.3390/rs11080903
Chicago/Turabian StyleYun, Ting, Kang Jiang, Hu Hou, Feng An, Bangqian Chen, Anna Jiang, Weizheng Li, and Lianfeng Xue. 2019. "Rubber Tree Crown Segmentation and Property Retrieval Using Ground-Based Mobile LiDAR after Natural Disturbances" Remote Sensing 11, no. 8: 903. https://doi.org/10.3390/rs11080903
APA StyleYun, T., Jiang, K., Hou, H., An, F., Chen, B., Jiang, A., Li, W., & Xue, L. (2019). Rubber Tree Crown Segmentation and Property Retrieval Using Ground-Based Mobile LiDAR after Natural Disturbances. Remote Sensing, 11(8), 903. https://doi.org/10.3390/rs11080903