Temporal Up-Sampling of Planar Long-Range Doppler LiDAR Wind Speed Measurements Using Space-Time Conversion
Abstract
1. Introduction
2. Planar LiDAR Data
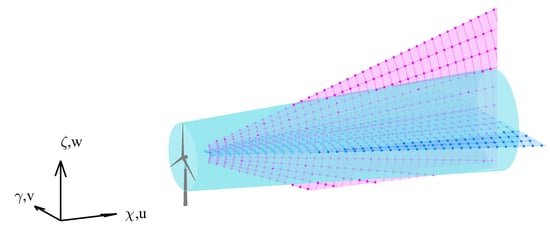
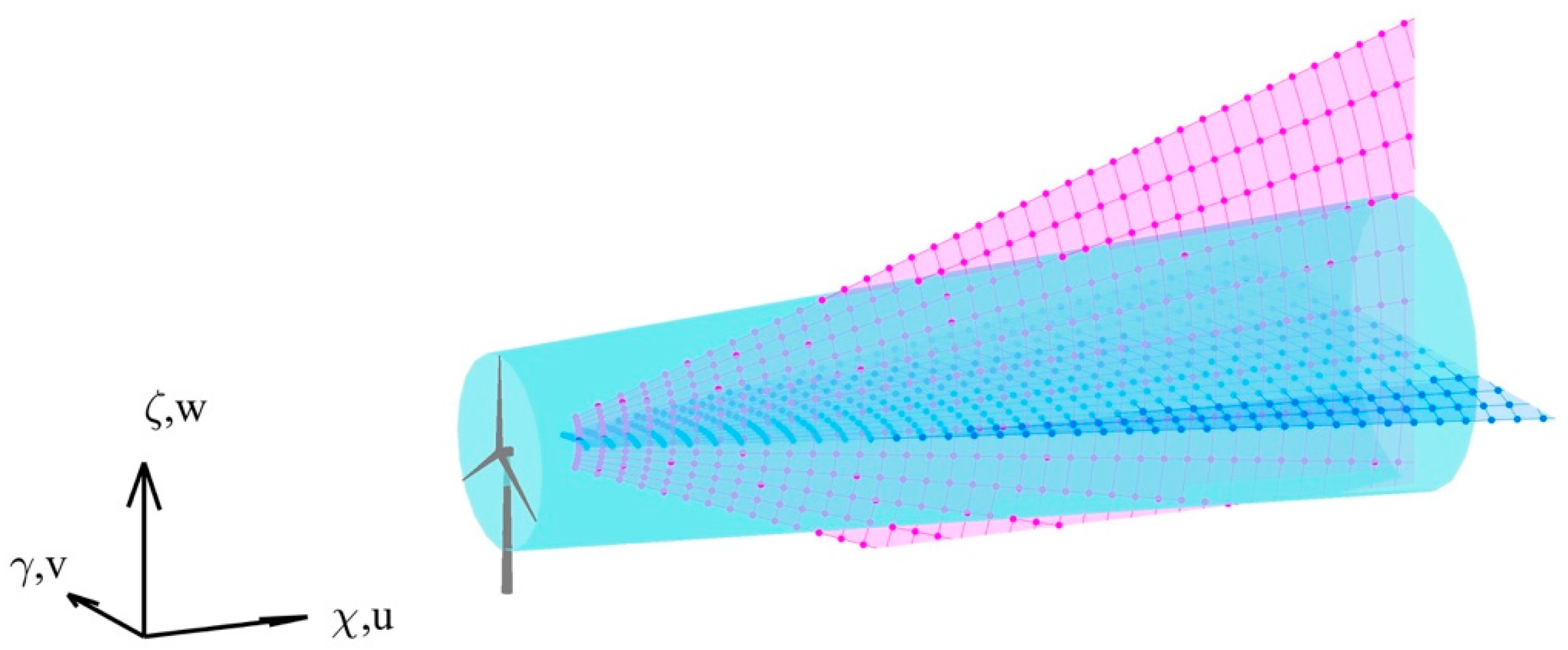
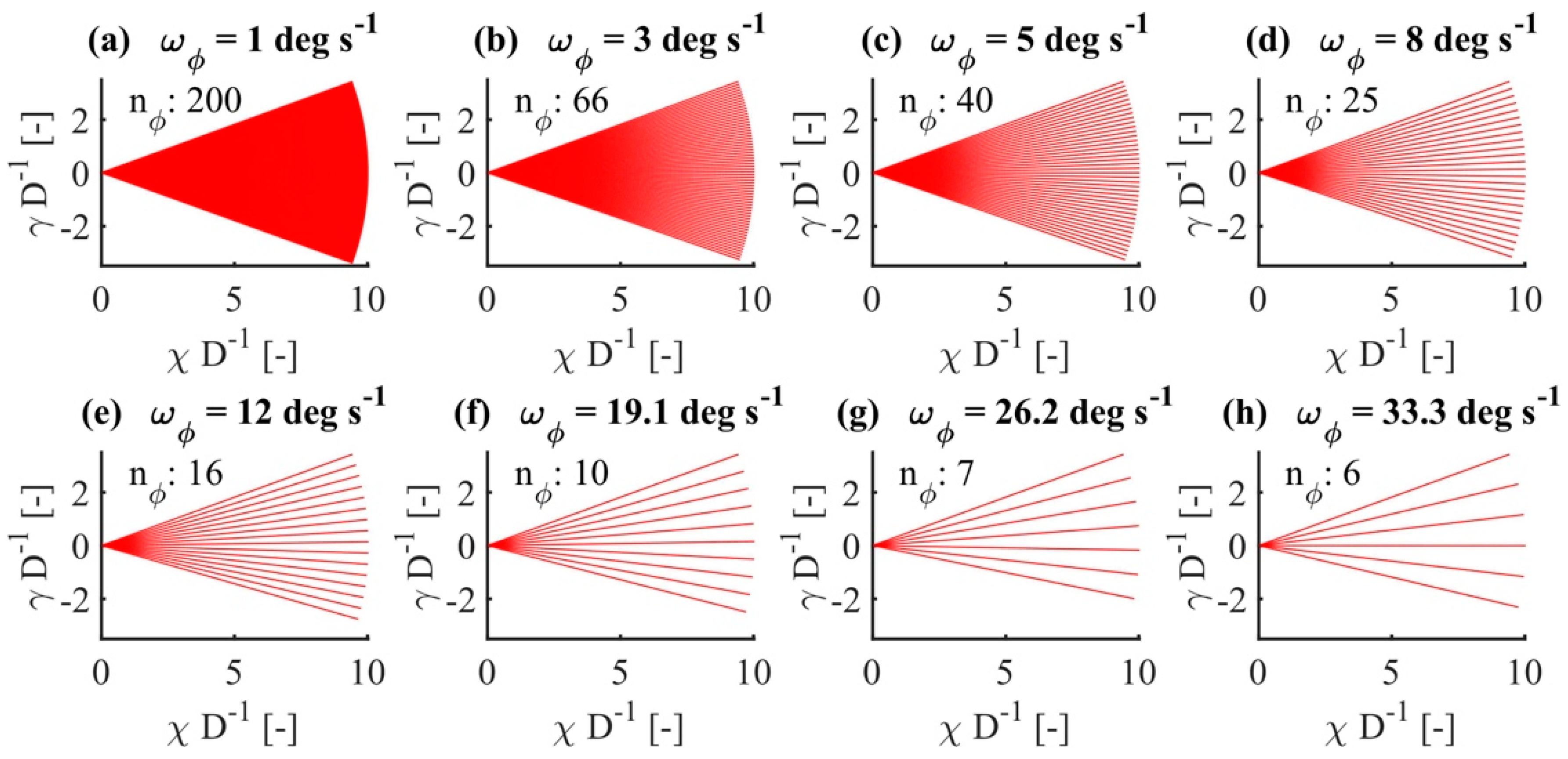
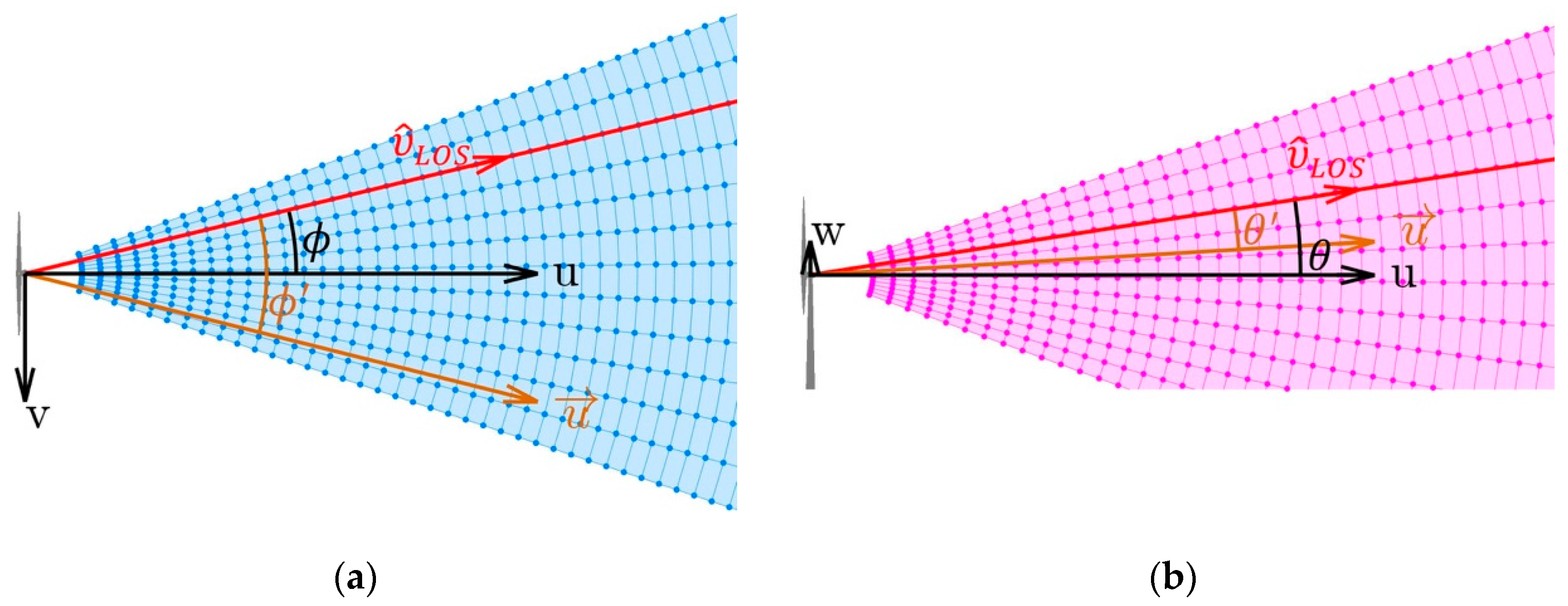
2.1. Measurement Trajectories
2.2. Synthetic LiDAR Data
3. Method
3.1. Wind-Speed Reconstruction
3.2. Wind-Field Propagation
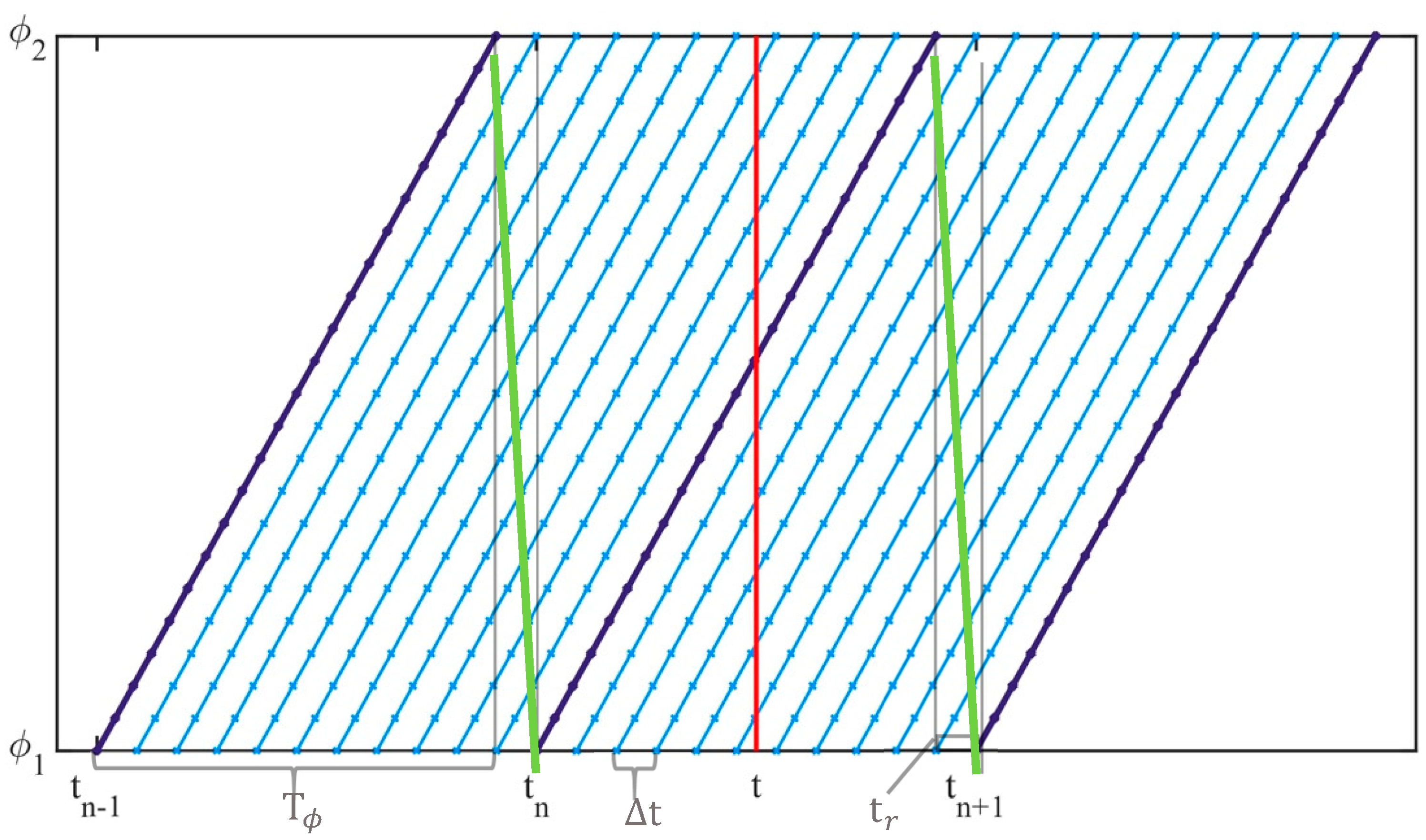
3.3. Temporal Correction and Data Synchronisation
4. Results
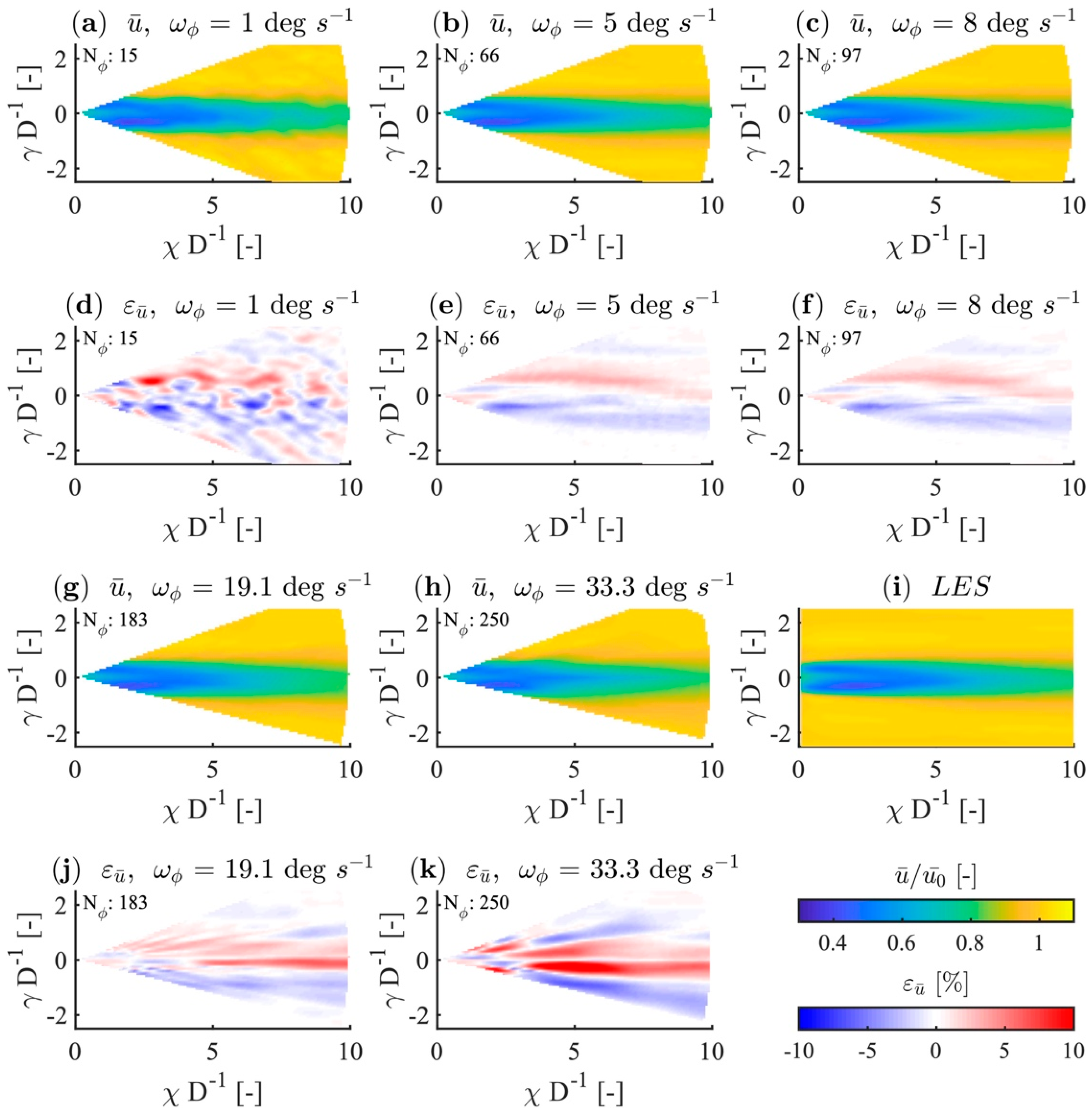
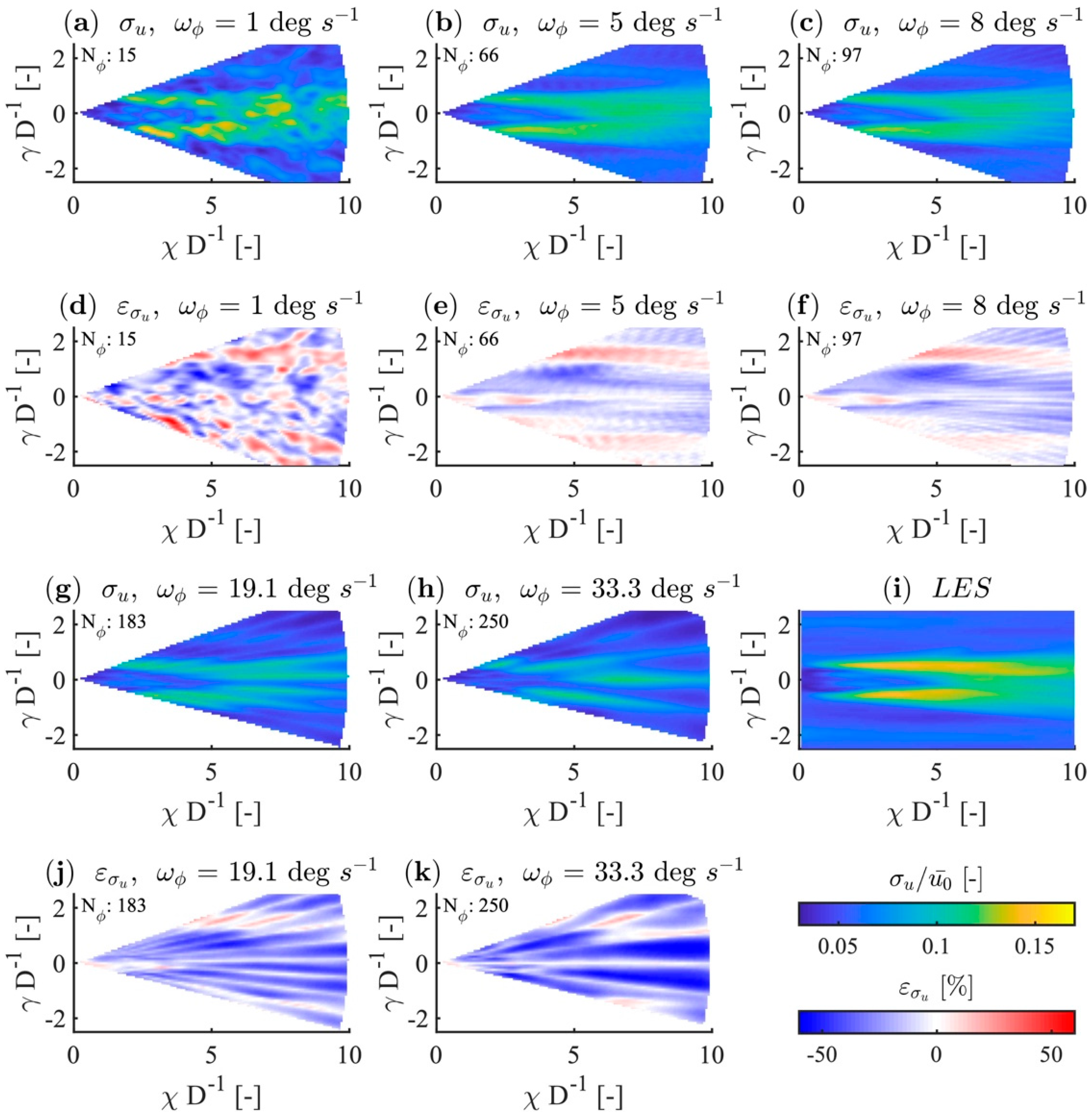
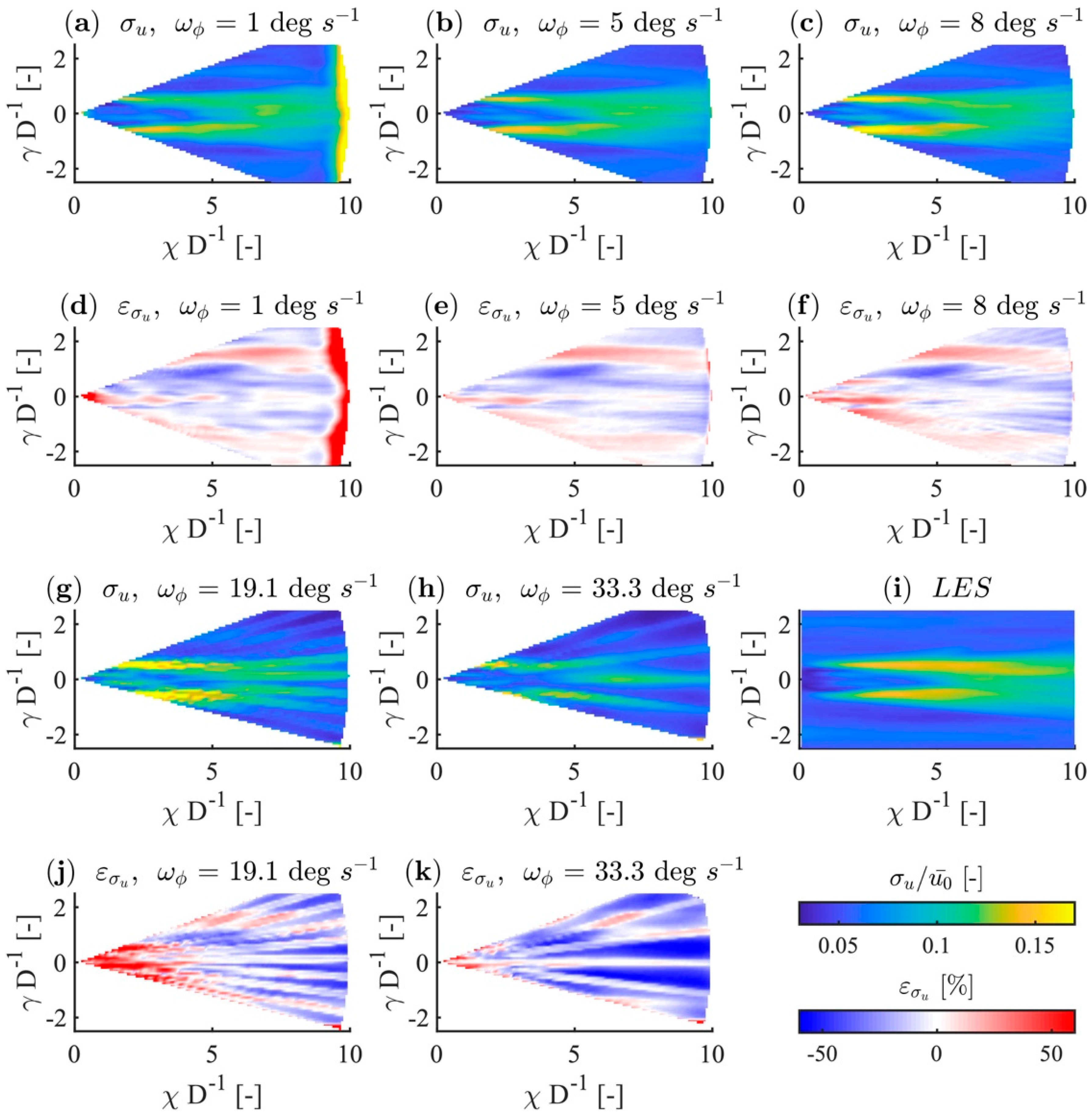
4.1. Calculation of Synthetic LiDAR Data
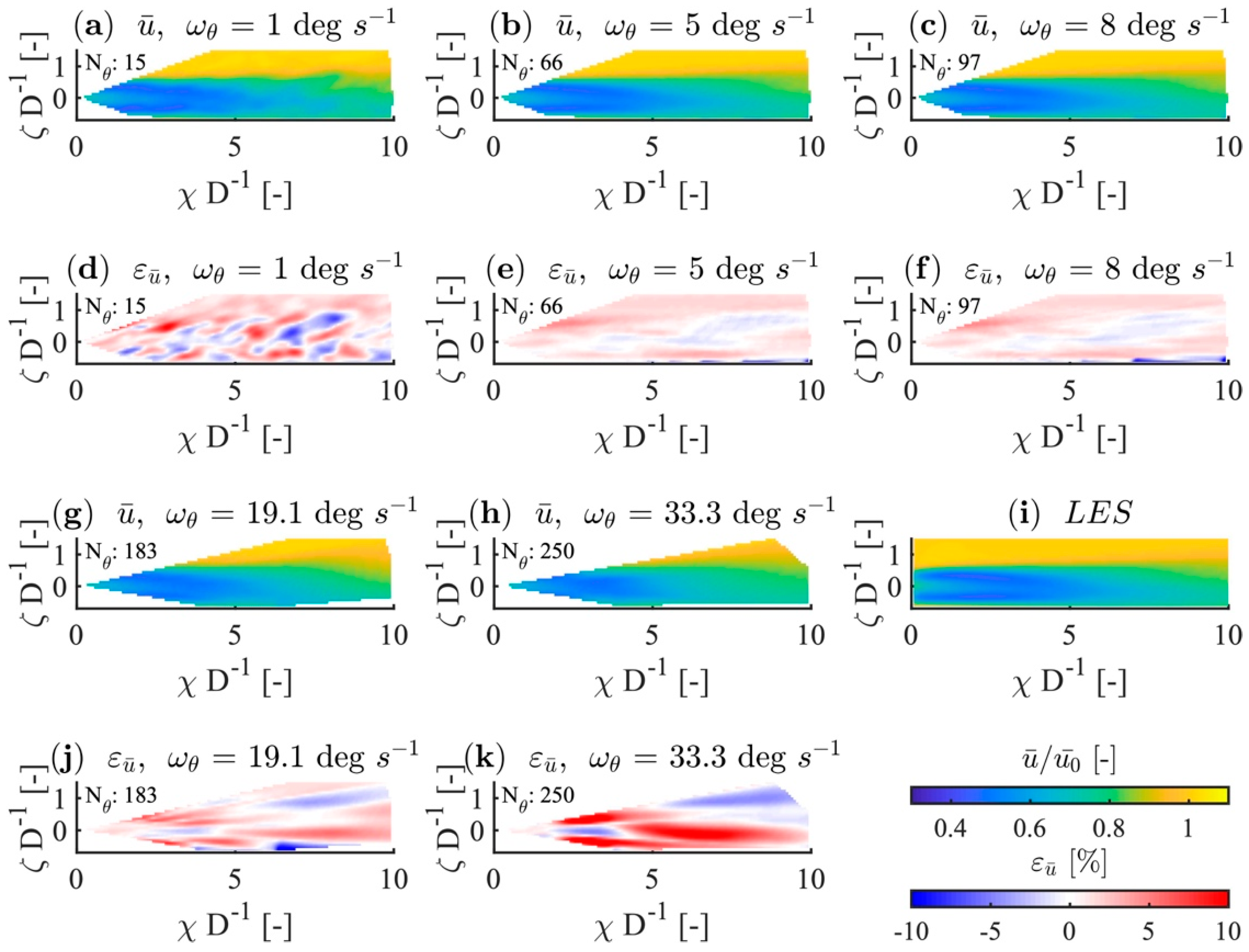
4.1.1. Error Case Discrimination
- Error at the centreline in the wake: and .
- Planar wake error: and .
- Error in the free stream outside of the wake (opposite the planar wake case).
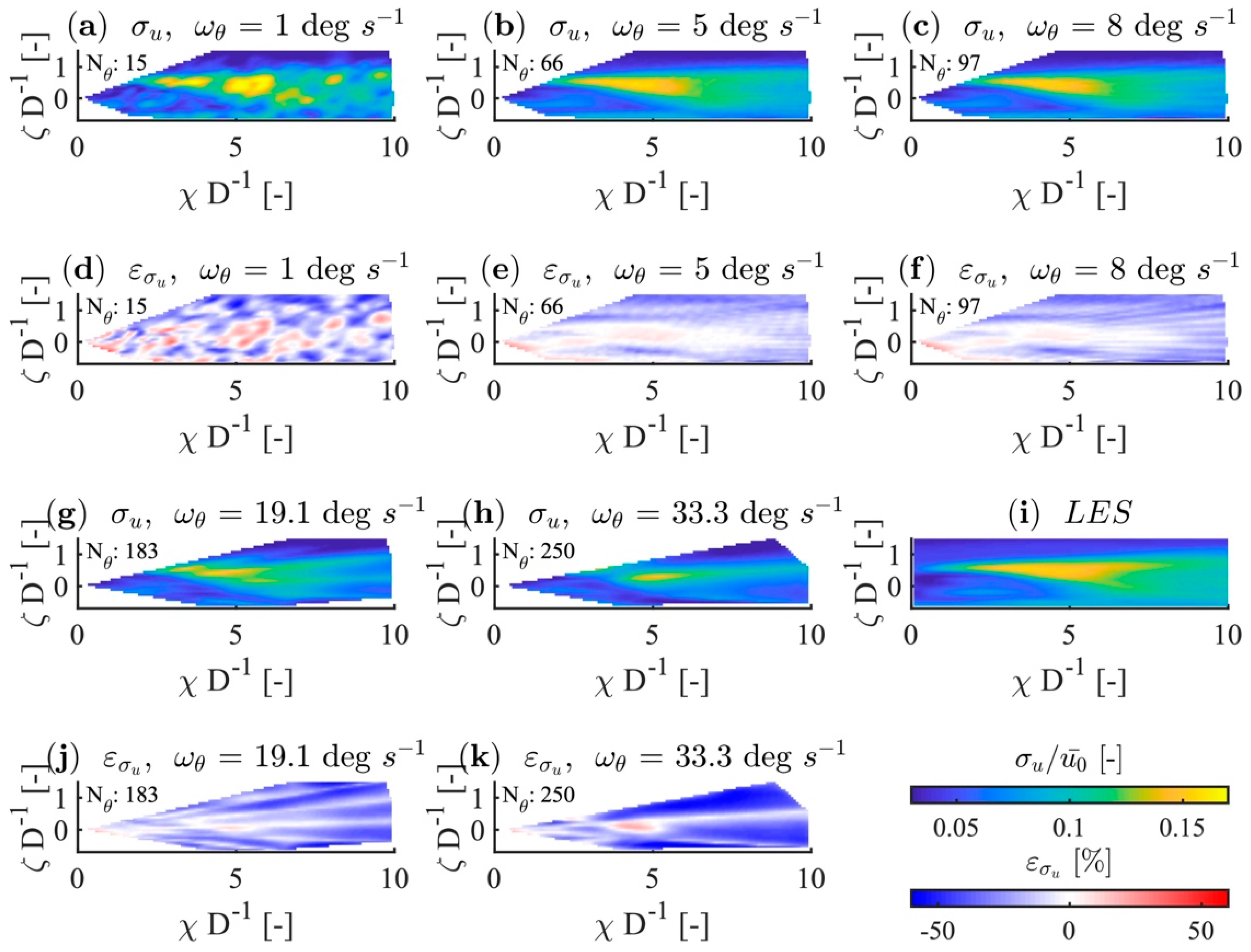
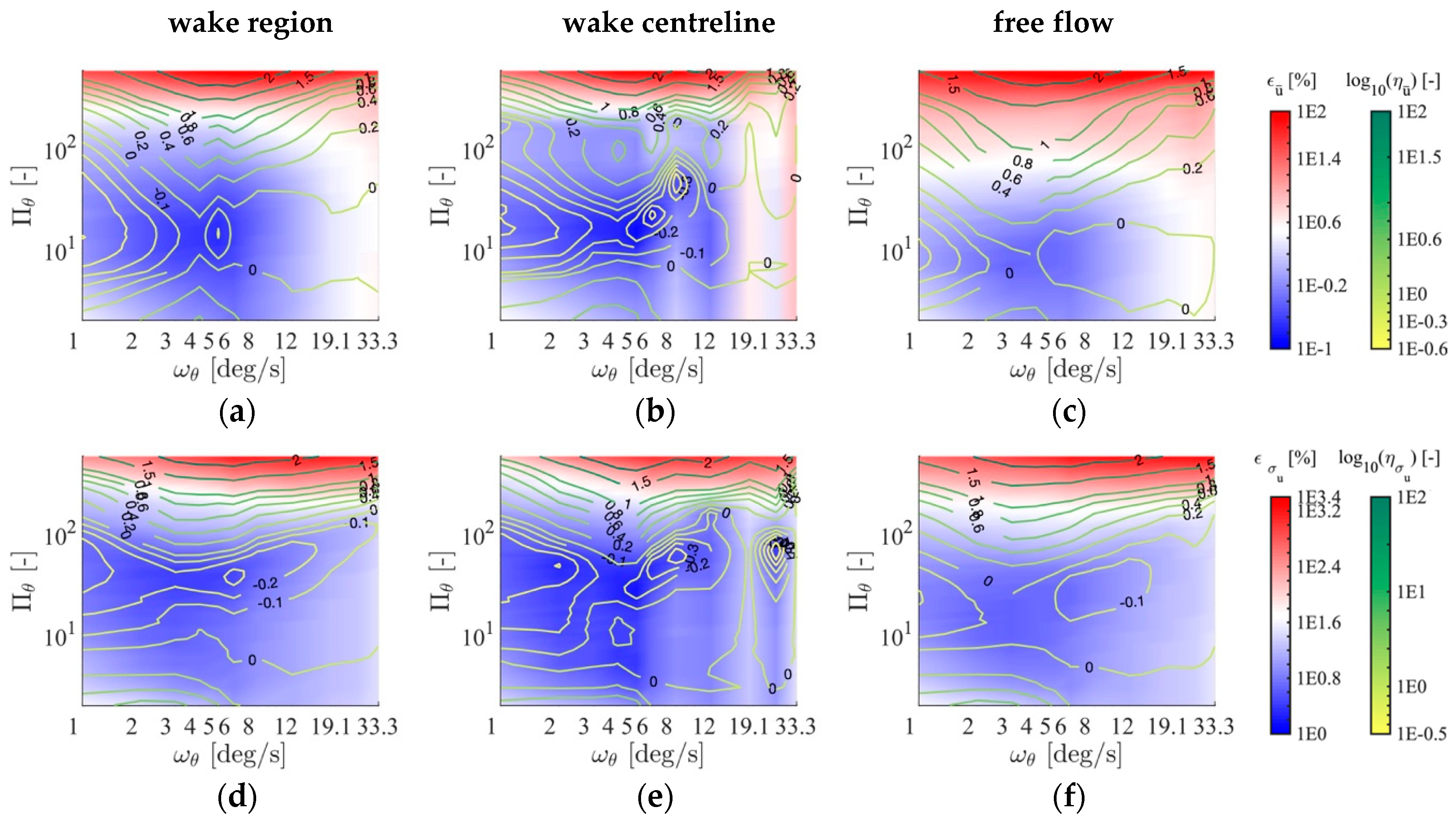
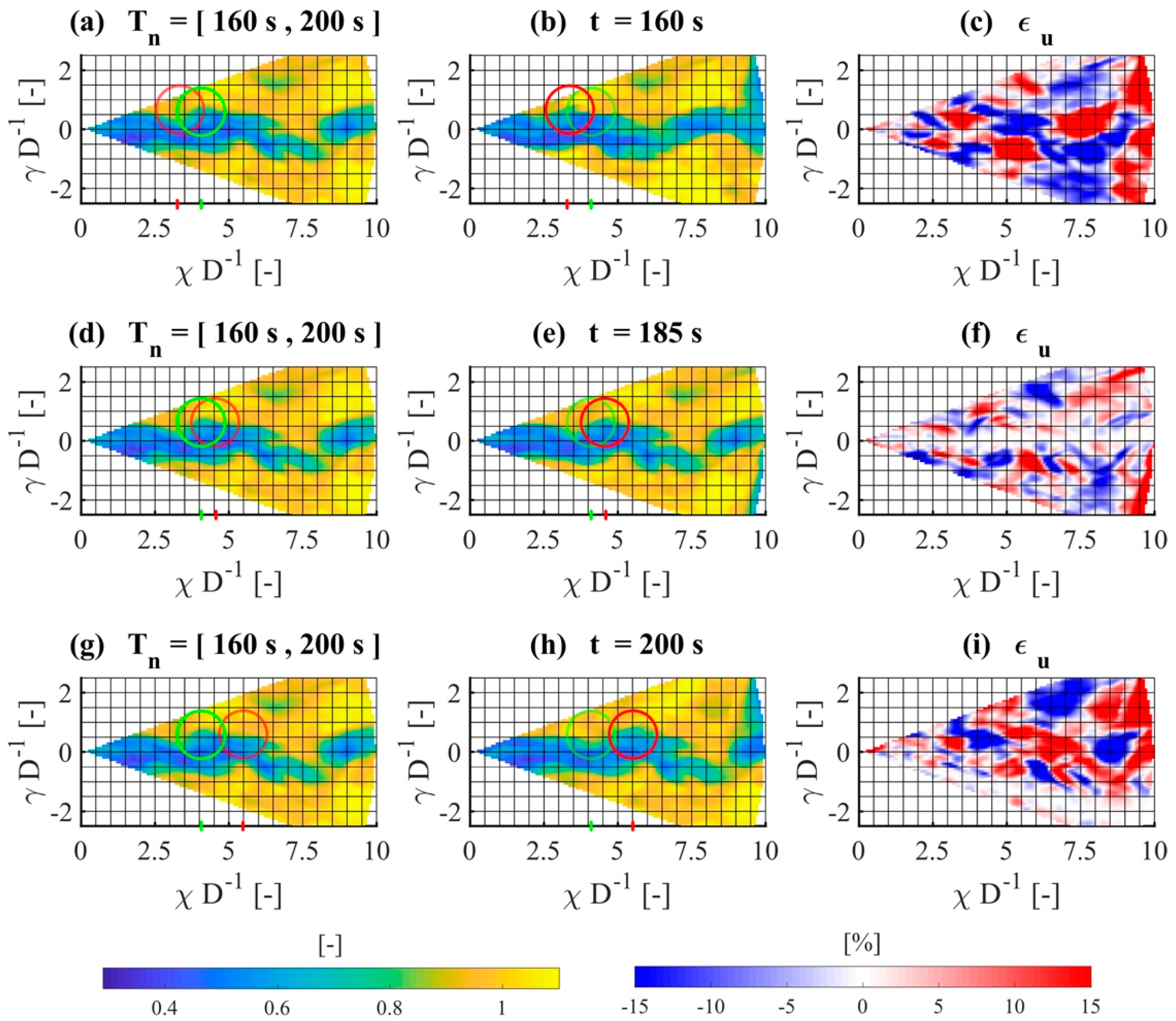
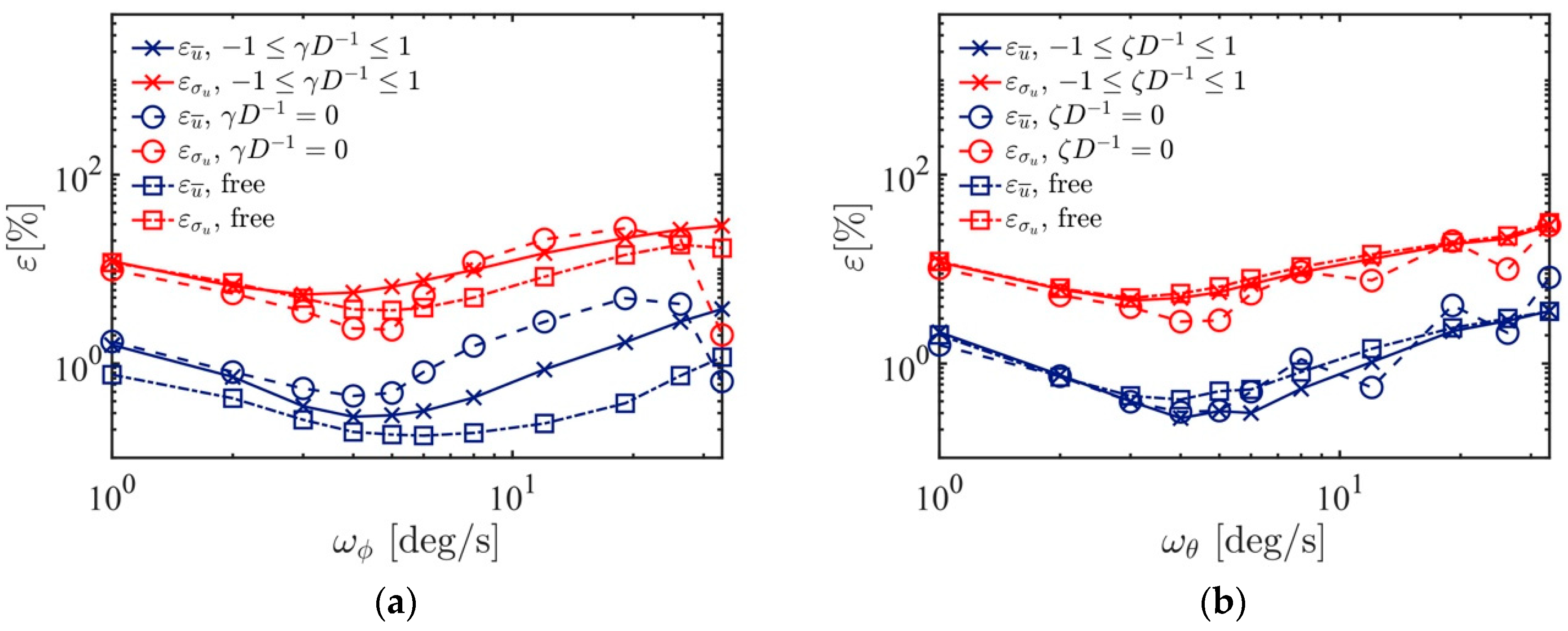
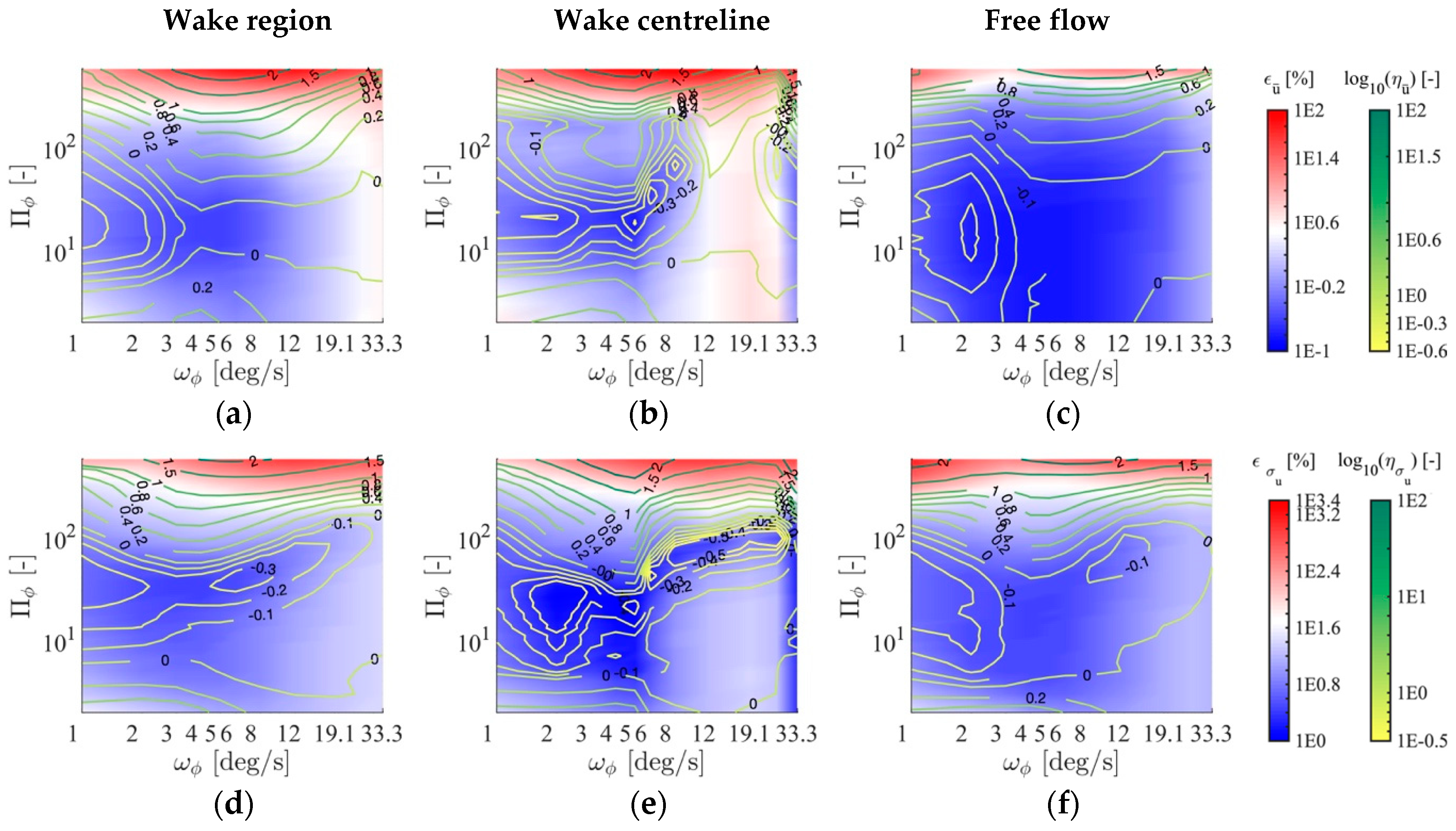
4.2. Time-Resolution Improvement
4.3. Influence of the Interpolation Time Step, Δt, on the Statistical Error
- Inside the wake for and .
- Along the centreline for and .
- In the free flow.
5. Discussion
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
Appendix B
| 1°/s | 2°/s | 3°/s | 4°/s | 5°/s | 6°/s | 8°/s | 12°/s | 19.1°/s | 27.2°/s | 33.3°/s | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| wake region | |||||||||||
| 1.68% | 0.72% | 0.36% | 0.29% | 0.31% | 0.35% | 0.49% | 0.99% | 1.99% | 3.17% | 4.21% | |
| 12.61% | 5.71% | 4.81% | 5.00% | 5.93% | 7.06% | 9.43% | 14.83% | 21.04% | 25.63% | 27.85% | |
| wake centreline | |||||||||||
| 1.71% | 0.81% | 0.54% | 0.46% | 0.49% | 0.81% | 1.54% | 2.77% | 4.91% | 4.27% | 0.65% | |
| 9.81% | 5.54% | 3.59% | 2.36% | 2.29% | 5.23% | 11.87% | 20.65% | 27.09% | 20.72% | 2.01% | |
| free flow | |||||||||||
| 0.77% | 0.43% | 0.25% | 0.19% | 0.18% | 0.17% | 0.18% | 0.23% | 0.38% | 0.74% | 1.17% | |
| 11.78% | 7.19% | 4.91% | 3.77% | 3.68% | 3.90% | 5.00% | 8.34% | 14.22% | 18.15% | 16.69% | |
| 1°/s | 2°/s | 3°/s | 4°/s | 5°/s | 6°/s | 8°/s | 12°/s | 19.1°/s | 27.2°/s | 33.3°/s | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| wake region | |||||||||||
| 2.15% | 0.76% | 0.40% | 0.26% | 0.31% | 0.30% | 0.54% | 1.04% | 2.21% | 2.84% | 3.59% | |
| 11.87% | 6.15% | 4.66% | 4.96% | 5.70% | 6.94% | 9.24% | 12.87% | 18.43% | 21.02% | 29.30% | |
| wake centreline | |||||||||||
| 1.58% | 0.73% | 0.39% | 0.31% | 0.32% | 0.50% | 1.11% | 0.56% | 4.13% | 2.11% | 8.20% | |
| 10.28% | 5.29% | 3.97% | 2.78% | 2.87% | 5.47% | 9.37% | 7.58% | 19.78% | 10.00% | 28.98% | |
| free flow | |||||||||||
| 2.01% | 0.72% | 0.45% | 0.42% | 0.51% | 0.53% | 0.81% | 1.44% | 2.39% | 3.00% | 3.58% | |
| 12.02% | 6.27% | 4.98% | 5.51% | 6.48% | 7.92% | 10.60% | 14.26% | 19.26% | 22.48% | 30.87% | |
Appendix C

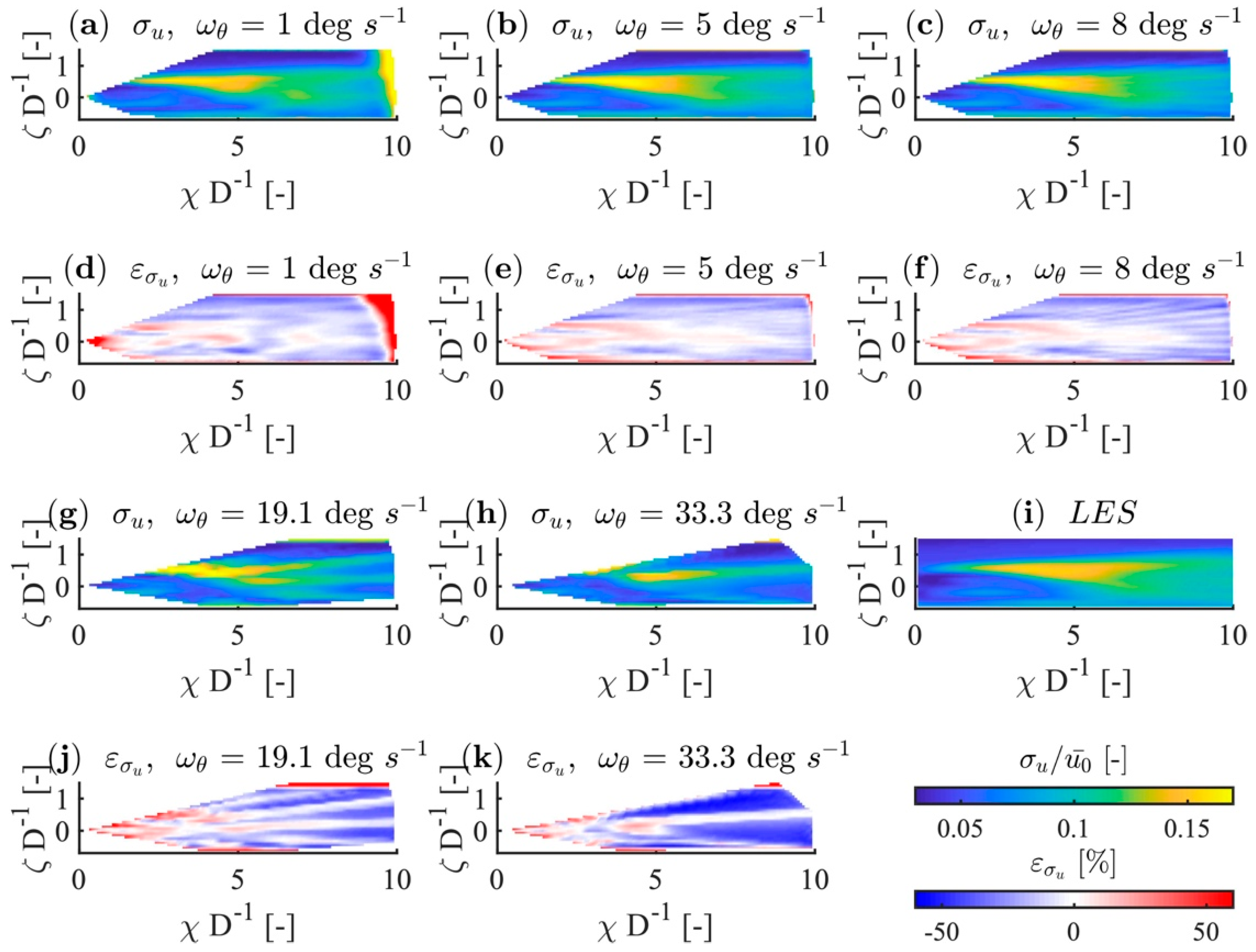
Appendix D
References
- Crespo, A.; Hernández, J.; Frandsen, S. Survey of modelling methods for wind turbine wakes and wind farms. Wind Energy 1999, 2, 1–24. [Google Scholar] [CrossRef]
- Vermeer, L.J.; Sørensen, J.N.; Crespo, A. Wind turbine wake aerodynamics. Prog. Aerosp. Sci. 2003, 39, 467–510. [Google Scholar] [CrossRef]
- Kelley, N.; Osgood, R.; Bialasiewicz, J.; Jakubowski, A. Using wavelet analysis to assess turbulence/rotor interactions. Wind Energy 2000, 3, 121–134. [Google Scholar] [CrossRef]
- Hand, M. Mitigation of Wind Turbine/Vortex Interaction Using Disturbance Accommodating Control. Ph.D. Thesis, National Renewable Energy Lab., Golden, CO, USA, 2003. [Google Scholar] [CrossRef]
- Manwell, J.F.; McGowan, J.G.; Rogers, A.L. Wind Energy Explained: Theory, Design and Application; John Wiley & Sons: Hoboken, NJ, USA, 2010. [Google Scholar]
- Ainslie, J.F. Calculating the flow field in the wake of wind turbines. J. Wind Eng. Ind. Aerodyn. 1988, 27, 213–224. [Google Scholar] [CrossRef]
- Jensen, N.O. A Note on Wind Generator Interaction Tech. Rep. Risø-M-2411(EN); Risø National Laboratory: Roskilde, Denmark, 1983. [Google Scholar]
- Frandsen, S.; Barthelmie, R.; Pryor, S.; Rathmann, O.; Larsen, S.; Højstrup, J.; Thøgersen, M. Analytical modelling of wind speed deficit in large offshore wind farms. Wind Energy 2006, 9, 39–53. [Google Scholar] [CrossRef]
- Larsen, G.; Madsen, H.; Thomsen, K.; Larsen, T. Wake meandering: A pragmatic approach. Wind Energy 2008, 11, 377–395. [Google Scholar] [CrossRef]
- Larsen, T.; Madsen, H.; Larsen, G.; Hansen, K.S. Validation of the dynamic wake meander model for loads and power production in the Egmond aan Zee wind farm. Wind Energy 2013, 16, 605–624. [Google Scholar] [CrossRef]
- Churchfield, M.J.; Lee, S.; Moriarty, P.J.; Hao, Y.; Lackner, M.A.; Barthelmie, R.; Lundquist, J.; Oxley, G. A Comparison of the Dynamic Wake Meandering Model, Large-Eddy Simulation, and Field Data at the Egmond aan Zee Offshore Wind Plant. In Proceedings of the 33rd Wind Energy Symposium 2015, Kissimmee, FL, USA, 5–9 January 2015. [Google Scholar] [CrossRef]
- Keck, R.-E.; de Maré, M.; Churchfield, M.J.; Lee, S.; Larsen, G.; Aagaard Madsen, H. On atmospheric stability in the dynamic wake meandering model. Wind Energy 2014, 17, 1689–1710. [Google Scholar] [CrossRef]
- Cheynet, E.; Jakobsen, J.B.; Snæbjörnsson, J.; Angelou, N.; Mikkelsen, T.; Sjöholm, M.; Svardal, B. Full-scale observation of the flow downstream of a suspension bridge deck. J. Wind Eng. Ind. Aerodyn. 2017, 171, 261–272. [Google Scholar] [CrossRef]
- Trabucchi, D.; Trujillo, J.J.; Schneemann, J.; Bitter, M.; Kühn, M. Application of staring LiDARs to study the dynamics of wind turbine wakes. Meteorol. Z. 2015, 6, 557–564. [Google Scholar] [CrossRef]
- van Dooren, M.F.; Campagnolo, F.; Sjöholm, M.; Angelou, N.; Mikkelsen, T.; Floris, M. Demonstration and uncertainty analysis of synchronised scanning LiDAR measurements of 2-D velocity fields in a boundary-layer wind tunnel. Wind Energy Sci. 2017, 2, 329–341. [Google Scholar] [CrossRef]
- Bartl, J.; Mühle, F.; Schottler, J.; Sætran, L.; Peinke, J.; Adaramola, M.; Hölling, M. Wind tunnel experiments on wind turbine wakes in yaw: Effects of inflow turbulence and shear. Wind Energy Sci. 2018, 3, 329–343. [Google Scholar] [CrossRef]
- Machefaux, E.; Larsen, G.C.; Troldborg, N.; Gaunaa, M.; Rettenmeier, A. Empirical modeling of single-wake advection and expansion using full-scale pulsed LiDAR-based measurements. Wind Energy 2015, 18, 2085–2103. [Google Scholar] [CrossRef]
- IEC 61400-1:2015. Assessment of a Wind Turbine for Site-Specific Conditions; IEC: Geneva, Switzerland, 2015. [Google Scholar]
- Bingöl, F.; Mann, J.; Larsen, G.C. Light detection and ranging measurements of wake dynamics part I: One-dimensional scanning. Wind Energy 2010, 13, 51–61. [Google Scholar] [CrossRef]
- Trujillo, J.-J.; Bingöl, F.; Mann, J.; Larsen, G.C.; Kühn, M. Light detection and ranging measurements of wake dynamics part II: Two-dimensional scanning. Wind Energy 2011, 14, 61–75. [Google Scholar] [CrossRef]
- Bromm, M.; Rott, A.; Beck, H.; Vollmer, L.; Steinfeld, G.; Kühn, M. Field investigation on the influence of yaw misalignment on the propagation of wind turbine wakes. Wind Energy 2018, 21, 1011–1028. [Google Scholar] [CrossRef]
- Goyer, G.G.; Watson, R. The Laser and its Application to Meteorology. Bull. Am. Meteorol. Soc. 1963, 44, 564–575. [Google Scholar] [CrossRef]
- Gal-Chen, T.; Xu, M.; Eberhard, W.L. Estimation of atmospheric boundary layer fluxes and other turbulence parameters from Doppler LiDAR data. J. Geophys. Res. 1992, 97, 18409–18423. [Google Scholar] [CrossRef]
- Frehlich, R. Coherent Doppler LiDAR signal covariance including wind shear and wind turbulence. Appl. Opt. 1994, 33, 6472–6481. [Google Scholar] [CrossRef]
- Frehlich, R. Effects of wind turbulence on coherent Doppler LiDAR performance. J. Atmos. Ocean. Technol. 1997, 14, 54–75. [Google Scholar] [CrossRef]
- Beck, H.; Kühn, M. Dynamic data filtering of long-range Doppler LiDAR wind speed measurements. Remote Sens. 2017, 9, 561. [Google Scholar] [CrossRef]
- Fuertes, F.; Porté-Agel, F. Using a Virtual LiDAR Approach to Assess the Accuracy of the Volumetric Reconstruction of a Wind Turbine Wake. Remote Sens. 2018, 10, 721. [Google Scholar] [CrossRef]
- Stenger, H. Mehrstufige Stichprobenverfahren. Metrika 1974, 21, 7. [Google Scholar] [CrossRef]
- Raasch, S.; Schröter, M. PALM—A Large-Eddy Simulation Model Performing on Massively Parallel 419 Computers. Meteorol. Z. 2001, 10, 363–372. [Google Scholar] [CrossRef]
- Troldborg, N. Actuator Line Modeling of Wind Turbine Wakes. Ph.D. Thesis, Technical University of 421 Denmark—Department of Wind Energy, Risø Campus, Roskilde, Denmark, 2008. [Google Scholar]
- Jonkman, J.; Butterfield, S.; Musial, W.; Scott, G. Definition of a 5-MW Reference Wind Turbine for Offshore System Development (No. NREL/TP-500-38060); National Renewable Energy Lab. (NREL): Golden, CO, USA, 2009. [Google Scholar]
- Trabucchi, D.; Trujillo, J.J.; Steinfeld, G.; Schneemann, J.; Machtaa, M.; Cariou, J.P.; Kühn, M. Numerical Assessment of Performance of LiDAR WindScanners for Wake Measurements; EWEA: Brussel, Belgium, 2011. [Google Scholar]
- van Dooren, M.F.; Trabucchi, D.; Kühn, M. A Methodology for the Reconstruction of 2D Horizontal Wind Fields of Wind Turbine Wakes Based on Dual-Doppler LiDAR Measurements. Remote Sens. 2016, 8, 809. [Google Scholar] [CrossRef]
- Stawiarski, C.; Traumner, K.; Knigge, C.; Calhoun, R. Scopes and challenges of dual-doppler LiDAR wind measurements-an error analysis. J. Atmos. Ocean. Technol. 2013, 30, 2044–2062. [Google Scholar] [CrossRef]
- Träumner, K.; Stawiarski, C.; Kottmeier, C.; Knigge, C.; Raasch, S. Assessment of surface-layer coherent structure detection in dual-Doppler LiDAR data based on virtual measurements. Bound.-Layer Meteorol. 2015, 156, 371–393. [Google Scholar] [CrossRef]
- Peña Diaz, A.; Hasager, C.B.; Lange, J.; Anger, J.; Badger, M.; Bingöl, F.; Bischoff, O.; Cariou, J.P.; Dunne, F.; Emeis, S.; et al. Remote Sensing for Wind Energy; Number DTU Wind Energy-E-Report-0029(EN), DTU 385 Wind Energy; DTU: Lyngby, Denmark, 2013; Chapter 5; pp. 131–148. [Google Scholar]
- Mann, J.; Cariou, J.P.C.; Parmentier, R.M.; Wagner, R.; Lindelöw, P.; Sjöholm, M.; Enevoldsen, K. Comparison of 3D turbulence measurements using three staring wind LiDARs and a sonic anemometer. Meteorol. Z. 2009, 135–140. [Google Scholar] [CrossRef]
- Lindelöw, P. Fiber Based Coherent LiDARs for Remote Wind Sensing. Ph.D. Thesis, Danish Technical University, Lyngby, Denmak, 2008. [Google Scholar]
- Fuertes, F.C.; Iungo, G.V.; Porté-Agel, F. 3D Turbulence Measurements Using Three Synchronous Wind LiDARs: Validation against Sonic Anemometry. J. Atmos. Oceanic Technol. 2014, 31, 1549–1556. [Google Scholar] [CrossRef]
- Sibson, R. A brief description of natural neighbour interpolation. In Interpreting Multivariate Data; Barnett, V., Ed.; Wiley: New York, NY, USA, 1981; pp. 21–36. [Google Scholar]
- Schneiders, J.; Scarano, F. Dense velocity reconstruction from tomographic PTV with material derivatives. Exp. Fluids 2016, 57, 139. [Google Scholar] [CrossRef]
- Rott, A.; Boersma, S.; van Wingerden, J.W.; Kühn, M. Dynamic flow model for real-time application in wind farm control. J. Phys. Conf. Ser. 2017, 854. [Google Scholar] [CrossRef]
- Valldecabres, L.; Peña, A.; Courtney, M.; von Bremen, L.; Kühn, M. Very short-term forecast of near-coastal flow using scanning LiDARs. Wind Energy Sci. 2018, 3, 313–327. [Google Scholar] [CrossRef]
- Taylor, G.I. The spectrum of turbulence. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1938, 164, 476–490. [Google Scholar] [CrossRef]
- Cheynet, E.; Jakobsen, J.B.; Snæbjörnsson, J.; Mann, J.; Courtney, M.; Lea, G.; Svardal, B. Measurements of surface-layer turbulence in a wide Norwegian fjord using synchronized long- range Doppler wind LiDARs. Remote Sens. 2017, 9, 977. [Google Scholar] [CrossRef]
- Käsler, Y.; Rahm, S.; Simmet, R.; Kühn, M. Wake measurements of a multi-MW wind turbine with coherent long-range pulsed Doppler wind LiDAR. J. Atmos. Ocean. Technol. 2010, 27, 1529–1532. [Google Scholar] [CrossRef]
- Smalikho, I.N.; Banakh, V.A.; Pichugina, Y.L.; Brewer, W.A.; Banta, R.M.; Lundquist, J.K.; Kelley, N.D. LiDAR investigation of atmosphere effect on a wind turbine wake. J. Atmos. Ocean. Technol. 2013, 30, 2554–2570. [Google Scholar] [CrossRef]
- Aitken, M.L.; Banta, R.M.; Pichugina, Y.L.; Lundquist, J.K. Quantifying Wind Turbine Wake Characteristics from Scanning Remote Sensor Data. J. Atmos. Ocean. Technol. 2014, 31, 765–787. [Google Scholar] [CrossRef]
- Iungo, G.V.; Porté-Agel, F. Volumetric LiDAR scanning of wind turbine wakes under convective and neutral atmospheric stability regimes. J. Atmos. Ocean. Technol. 2014, 31, 2035–2048. [Google Scholar] [CrossRef]
- Banta, R.M.; Pichugina, Y.L.; Brewer, W.A.; Lundquist, J.K.; Kelley, N.D.; Sandberg, S.P.; Alvarez, R.J.; Hardesty, R.M.; Weickmann, A.M. 3D volumetric analysis of wind turbine wake properties in the atmosphere using high-resolution Doppler LiDAR. J. Atmos. Ocean. Technol. 2015, 32, 904–914. [Google Scholar] [CrossRef]
- Aitken, M.L.; Lundquist, J.K. Utility-Scale Wind Turbine Wake Characterization Using Nacelle-Based Long-Range Scanning LiDAR. J. Atmos. Ocean. Technol. 2014, 31, 1529–1539. [Google Scholar] [CrossRef]


| , | , | , | , | , | ||||
| 1°/s | 40° | 15 | 36000 | 200 | 0.2° | 40.0 s | 0.024 Hz | 97.2 % |
| 2°/s | 40° | 29 | 18000 | 100 | 0.4° | 20.0 s | 0.047 Hz | 94.2 % |
| 3°/s | 40° | 42 | 11880 | 66 | 0.6° | 13.3 s | 0.068 Hz | 91.0 % |
| 4°/s | 40° | 54 | 9000 | 50 | 0.8° | 10.0 s | 0.089 Hz | 89.2 % |
| 5°/s | 40° | 66 | 7920 | 40 | 1.0° | 8.0 s | 0.011 Hz | 86.8 % |
| 6°/s | 40° | 77 | 6840 | 33 | 1.2° | 6.7 s | 0.127 Hz | 84.6 % |
| 8°/s | 40° | 97 | 4500 | 25 | 1.6° | 5.0 s | 0.161 Hz | 80.6 % |
| 12°/s | 40° | 133 | 2880 | 16 | 2.5° | 3.3 s | 0.221 Hz | 73.4 % |
| 19.11°/s | 40° | 183 | 1800 | 10 | 4.0° | 2.1 s | 0.303 Hz | 63.4 % |
| 26.22°/s | 40° | 221 | 1260 | 7 | 5.7° | 1.5 s | 0.370 Hz | 55.8 % |
| 33.33°/s | 40° | 250 | 1080 | 6 | 6.7° | 1.2 s | 0.417 Hz | 50.0 % |
| PPI | RHI | |||||
|---|---|---|---|---|---|---|
| Wake Region | Wake Centreline | Free Flow | Wake Region | Wake Centreline | Free Flow | |
| 5°/s | 5°/s | 5°/s | 5°/s | 5°/s | 3°/s | |
| 16 | 18 | 9 | 14 | 16 | 7 | |
| 0.24% | 0.15% | 0.14% | 0.20% | 0.13% | 0.40% | |
| 4°/s | 5°/s | 4°/s | 4°/s | 5°/s | 3°/s | |
| 33 | 21 | 16 | 33 | 26 | 13 | |
| 2.89% | 0.60% | 3.02% | 2.79% | 1.61% | 4.53% | |
| PPI | RHI | |||||
|---|---|---|---|---|---|---|
| Wake Region | Wake Centreline | Free Flow | Wake Region | Wake Centreline | Free Flow | |
| 1°/s | 2°/s | 2°/s | 1°/s | 1°/s | 1°/s | |
| 16 | 21 | 13 | 13 | 16 | 8 | |
| 35.5% | 31.0% | 36.9% | 30.5% | 31.2% | 46.5% | |
| 1°/s | 1°/s | 1°/s | 1°/s | 1°/s | 1°/s | |
| 33 | 42 | 37 | 67 | 60 | 26 | |
| 42.8% | 43.6% | 45.6% | 43.9% | 42.0% | 60.5% | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Beck, H.; Kühn, M. Temporal Up-Sampling of Planar Long-Range Doppler LiDAR Wind Speed Measurements Using Space-Time Conversion. Remote Sens. 2019, 11, 867. https://doi.org/10.3390/rs11070867
Beck H, Kühn M. Temporal Up-Sampling of Planar Long-Range Doppler LiDAR Wind Speed Measurements Using Space-Time Conversion. Remote Sensing. 2019; 11(7):867. https://doi.org/10.3390/rs11070867
Chicago/Turabian StyleBeck, Hauke, and Martin Kühn. 2019. "Temporal Up-Sampling of Planar Long-Range Doppler LiDAR Wind Speed Measurements Using Space-Time Conversion" Remote Sensing 11, no. 7: 867. https://doi.org/10.3390/rs11070867
APA StyleBeck, H., & Kühn, M. (2019). Temporal Up-Sampling of Planar Long-Range Doppler LiDAR Wind Speed Measurements Using Space-Time Conversion. Remote Sensing, 11(7), 867. https://doi.org/10.3390/rs11070867