Numerical Assessments of Leaf Area Index in Tropical Savanna Rangelands, South Africa Using Landsat 8 OLI Derived Metrics and In-Situ Measurements
Abstract
1. Introduction
2. Materials and Methods
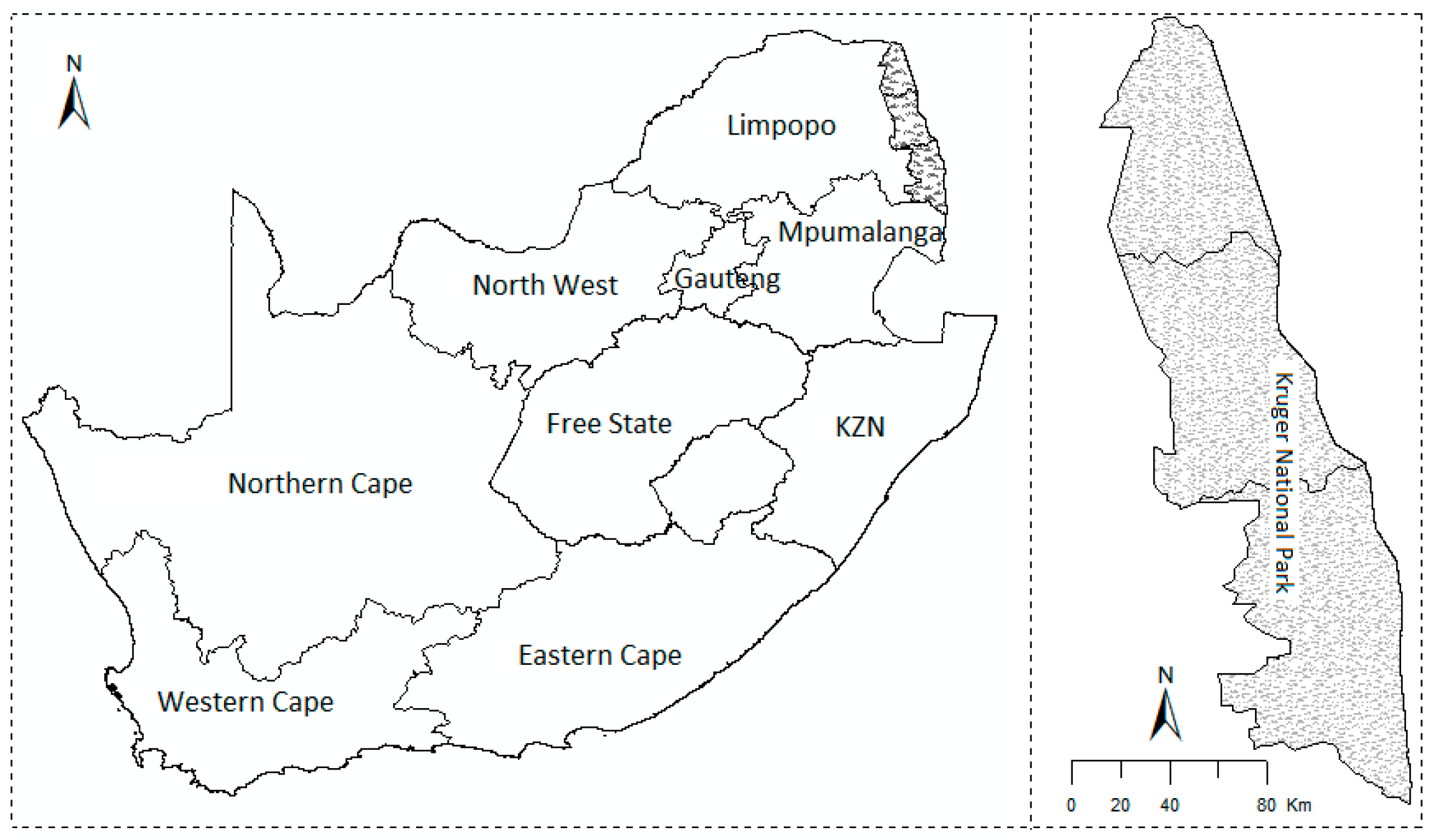
2.1. Study Area
2.2. LAI Field Measurements
2.3. Satellite Acquisition and Pre-Processing
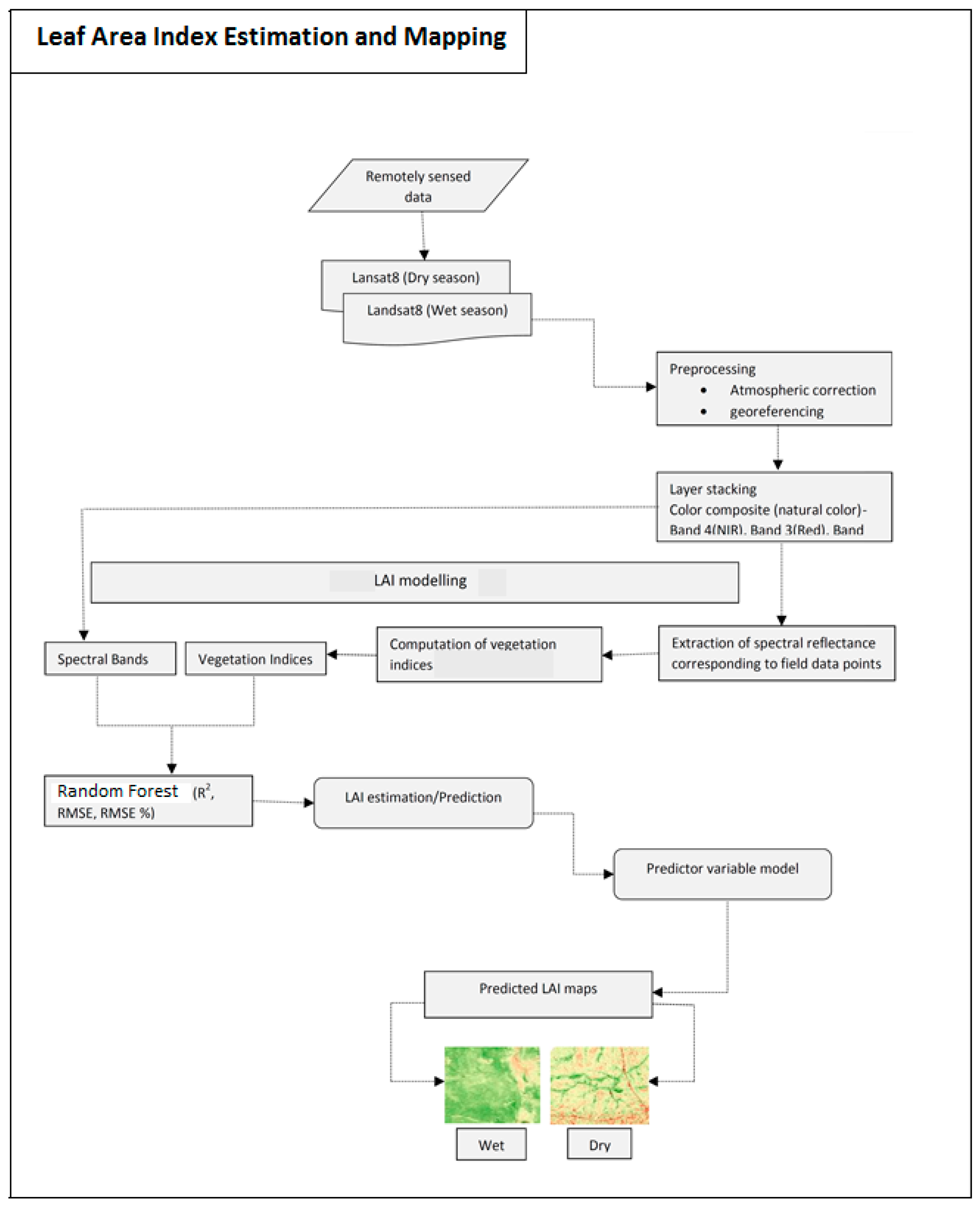
2.4. Random Forest Algorithm for LAI Estimates
3. Results
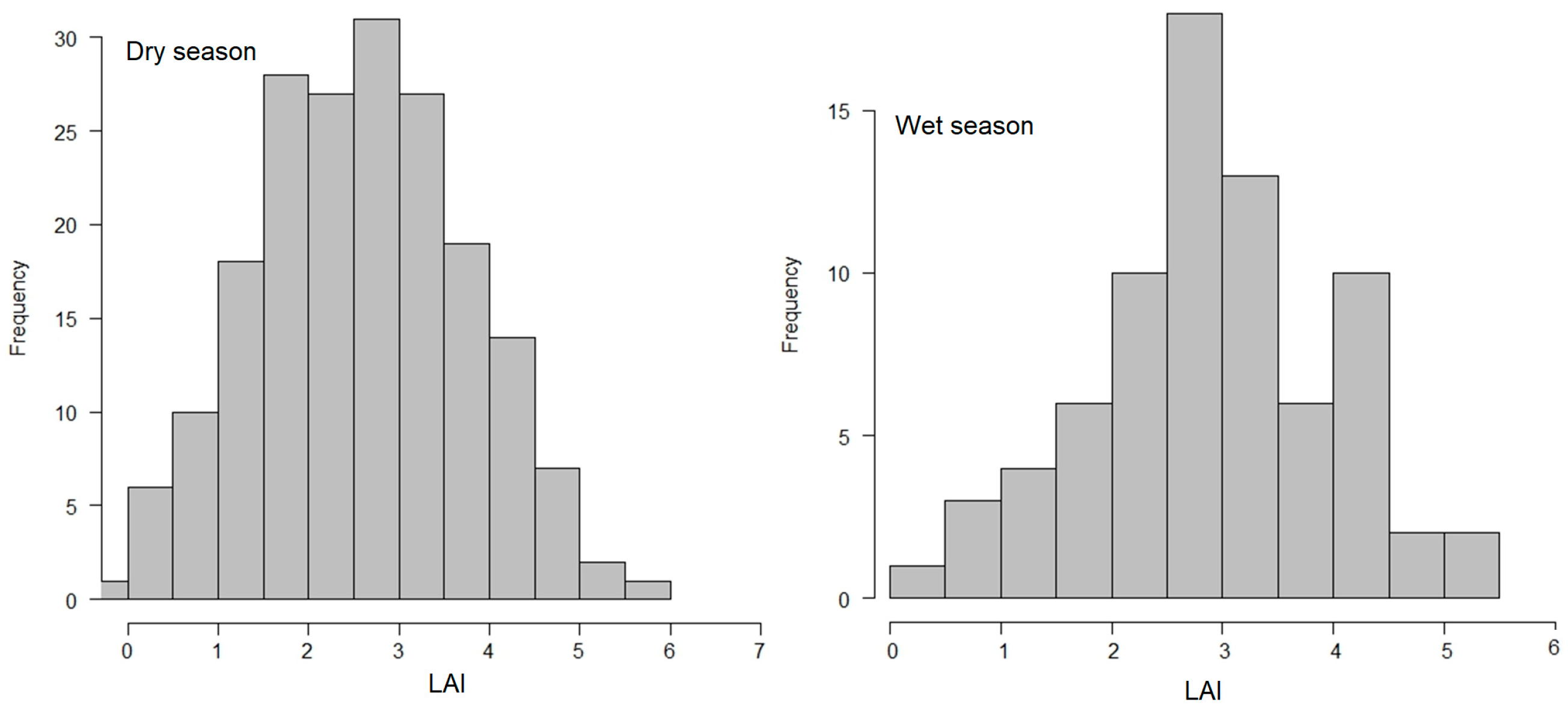
3.1. Statistical Summary of the Measured LAI
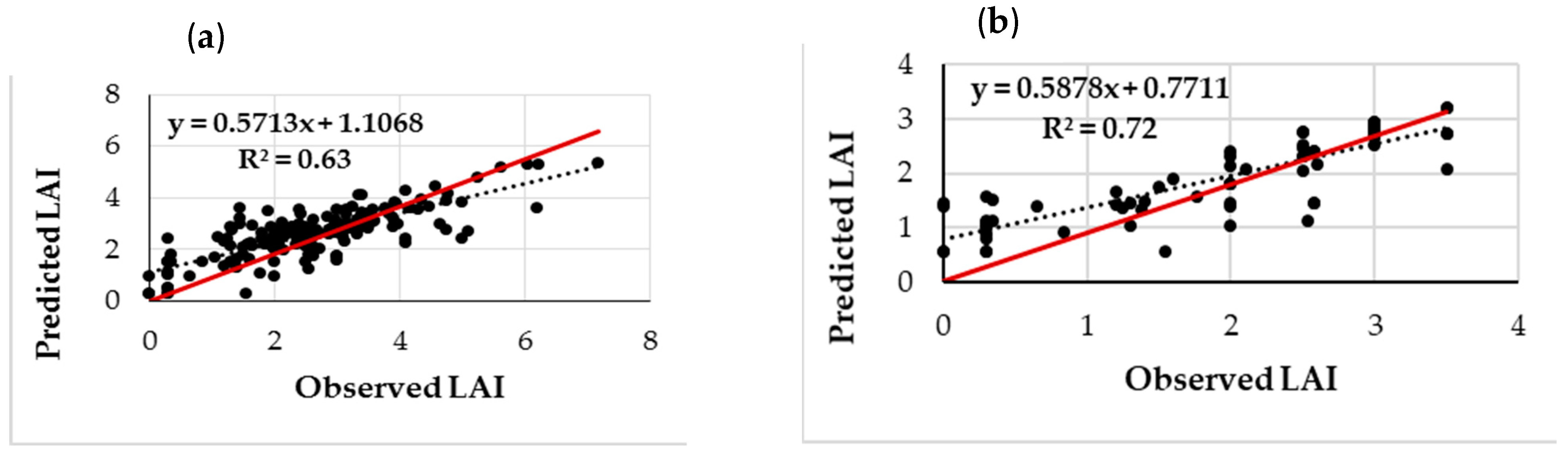
3.2. LAI Estimates Using RF Algorithm
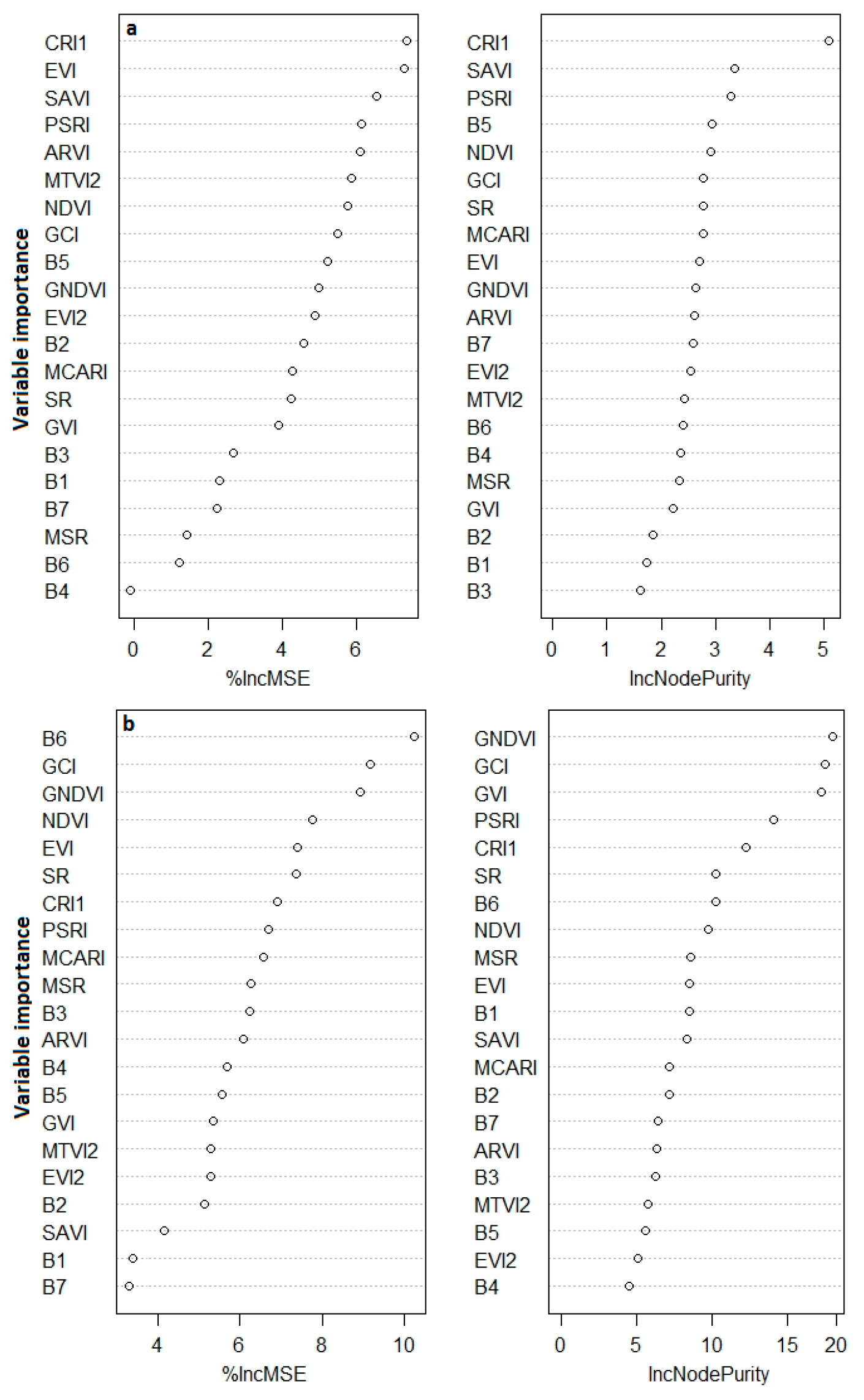
3.3. RF Important Variables Selection
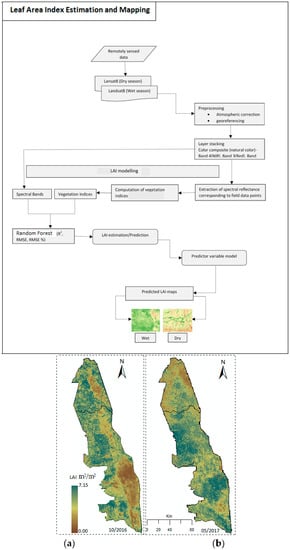
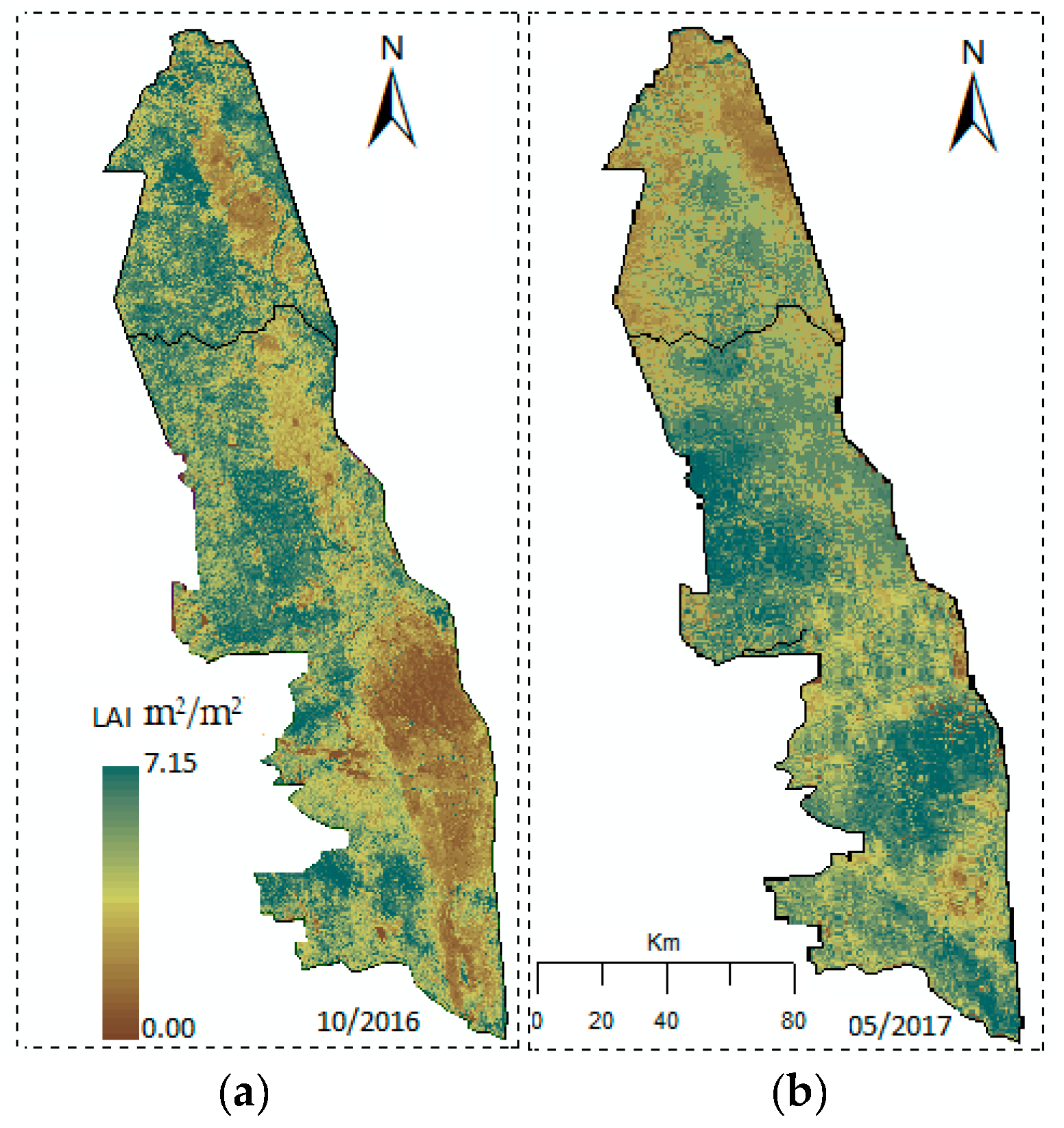
3.4. Derived LAI Thematic Maps
4. Discussion
4.1. Variations in LAI between Wet and Dry Season
4.2. Performance of Landsat 8 Variables in Characterizing Seasonal LAI
4.3. The Implications of Seasonal LAI Estimations for Reserve
5. Conclusions
- With its improved sensing characteristics, the Landsat 8 OLI has the ability to explain and predict the spatio-temporal dynamics in LAI in tropical savanna rangelands with acceptable accuracy.
- LAI could be estimated with high accuracy during the wet season when compared to the dry season using RF model—a previously challenging task with traditional linear techniques.
- The derived KNP LAI thematic maps indicate that forage productivity varied significantly (α = 0.05) between the wet and dry seasons, hence the need for monitoring wildlife movements and grazing patterns so that degradation can be minimal.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Munyati, C.; Shaker, P.; Phasha, M.G. Using remotely sensed imagery to monitor savanna rangeland deterioration through woody plant proliferation: A case study from communal and biodiversity conservation rangeland sites in Mokopane, South Africa. Environ. Monit. Assess. 2011, 176, 293–311. [Google Scholar] [CrossRef] [PubMed]
- Palmer, A.R.; Samuels, I.; Cupido, C.; Finca, A.; Kangombe, W.F.; Yunusa, I.A.; Vetter, S.; Mapaure, I. Aboveground biomass production of a semi-arid southern African savanna: Towards a new model. Afr. J. Range Forage Sci. 2016, 33, 43–51. [Google Scholar] [CrossRef]
- Ramoelo, A.; Cho, M.A.; Mathieu, R.S.; Skidmore, A.; Schlerf, M.; Heitkönig, I. Estimating grass nutrients and biomass as an indicator of rangeland (forage) quality and quantity using remote sensing in Savanna ecosystems. In Proceedings of the 9th International Conference of the African Association of Remote Sensing and the Environment (AARSE), El-Jadida, Morroco, 28 October–2 November 2012. [Google Scholar]
- Department of Environmental Affairs and Tourism. White Paper on the Conservation and Sustainable Use of South Africa’s Biological Diversity: Draft for Discussion; Department of Environmental Affairs and Tourism: Pretoria, South Africa, 1997; Available online: https://searchworks.stanford.edu/view/4445125 (accessed on 13 November 2018).
- Alkemade, R.; Reid, R.S.; van den Berg, M.; de Leeuw, J.; Jeuken, M. Assessing the impacts of livestock production on biodiversity in rangeland ecosystems. Proc. Natl. Acad. Sci. USA 2013, 110, 20900–20905. [Google Scholar] [CrossRef] [PubMed]
- Zheng, G.; Moskal, L.M. Retrieving leaf area index (LAI) using remote sensing: Theories, methods and sensors. Sensors 2009, 9, 2719–2745. [Google Scholar] [CrossRef] [PubMed]
- Dube, T.; Mutanga, O. Evaluating the utility of the medium-spatial resolution Landsat 8 multispectral sensor in quantifying aboveground biomass in uMgeni catchment, South Africa. ISPRS J. Photogramm. Remote Sens. 2015, 101, 36–46. [Google Scholar] [CrossRef]
- Rouse, J.W., Jr. Monitoring the Vernal Advancement and Retrogra-Dation (Green Wave Effect) of Natural Vegetation; NASA/GSFC Final Report; Texas A and M University, Remote Sensing Center: College Station, TX, USA, 1974. [Google Scholar]
- Jordan, C.F. Derivation of leaf-area index from quality of light on the forest floor. Ecology 1969, 50, 663–666. [Google Scholar] [CrossRef]
- Huete, A.R. A soil-adjusted vegetation index (SAVI). Remote Sens. Environ. 1988, 25, 295–309. [Google Scholar] [CrossRef]
- Huete, A.; Didan, K.; Miura, T.; Rodriguez, E.P.; Gao, X.; Ferreira, L.G. Overview of the Radiometric and Biophysical Performance of the MODIS Vegetation Indices. Remote Sens. Environ. 2002, 83, 195–213. [Google Scholar] [CrossRef]
- Merzlyak, M.N.; Gitelson, A.A.; Chivkunova, O.B.; Rakitin, V.Y. Non-destructive Optical Detection of Pigment Changes During Leaf Senescence and Fruit Ripening. Physiol. Plant. 1999, 106, 135–141. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Zur, Y.; Chivkunova, O.B.; Merzlyak, M.N. Assessing Carotenoid Content in Plant Leaves with Reflectance Spectroscopy. Photochem. Photobiol. 2002, 75, 272–281. [Google Scholar] [CrossRef]
- Kauth, R.; Thomas, G.S. The tasselled cap—A graphic description of the spectral-temporal development of agricultural crops as seen by Landsat. In LARS Symposia; Purdue University: West Lafayette, Indiana, 1976; p. 159. Available online: http://docs.lib.purdue.edu/lars_symp (accessed on 12 October 2018).
- Gitelson, A.; Merzlyak, M.N. Remote Sensing of Chlorophyll Concentration in Higher Plant Leaves. Adv. Space Res. 1998, 22, 689–692. [Google Scholar] [CrossRef]
- Gitelson, A.; Gritz, Y.; Merzlyak, M.N. Relationships Between Leaf Chlorophyll Content and Spectral Reflectance and Algorithms for Non-Destructive Chlorophyll Assessment in Higher Plant Leaves. J. Plant Physiol. 2003, 160, 271–282. [Google Scholar] [CrossRef] [PubMed]
- Qi, J.; Chehbouni, A.; Huete, A.R.; Kerr, Y.H.; Sorooshian, S. A modified soil adjusted vegetation index. Remote Sens. Environ. 1994, 48, 119–126. [Google Scholar] [CrossRef]
- Kaufman, Y.; Tanre, D. Atmospherically Resistant Vegetation Index (ARVI) for EOS-MODIS. IEEE Trans. Geosci. Remote Sens. 1992, 30, 261–270. [Google Scholar] [CrossRef]
- Daughtry, C.S.T.; Walthall, C.L.; Kim, M.S.; De Colstoun, E.B.; McMurtrey, J.E., III. Estimating Corn Leaf Chlorophyll Concentration from Leaf and Canopy Reflectance. Remote Sens Environ. 2000, 74, 229–239. [Google Scholar] [CrossRef]
- Haboudane, D.; Miller, J.R.; Pattey, E.; Zarco-Tejada, P.J.; Strachan, I.B. Hyperspectral Vegetation Indices and Novel Algorithms for Predicting Green LAI of Crop Canopies: Modeling and Validation in the Context of Precision Agriculture. Remote Sens. Environ. 2004, 90, 337–352. [Google Scholar] [CrossRef]
- Pandit, S.; Tsuyuki, S.; Dube, T. Estimating above-ground biomass in sub-tropical buffer zone community Forests, Nepal, using Sentinel-2 data. Remote Sens. 2018, 10, 601. [Google Scholar] [CrossRef]
- Jeong, J.H.; Resop, J.P.; Mueller, N.D.; Fleisher, D.H.; Yun, K.; Butler, E.E.; Timlin, D.J.; Shim, K.M.; Gerber, J.S.; Reddy, V.R.; et al. Random Forests for Global and Regional Crop Yield Predictions. PLoS ONE 2016, 11, e0156571. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Dube, T.; Mutanga, O.; Elhadi, A.; Ismail, R. Intra-and-inter species biomass prediction in a plantation forest: Testing the utility of high spatial resolution space borne multispectral RapidEye sensor and advance machine learning algorithms. Remote Sens. 2014, 14, 15348–15370. [Google Scholar] [CrossRef]
- Scornet, E.; Biau, G.; Vert, J.P. Consistency of random forests. Ann. Stat. 2015, 43, 1716–1741. [Google Scholar] [CrossRef]
- R Development Core Team. R: A Language and Environment for Statistical Computing. Available online: www.R-project.org (accessed on 12 October 2018).
- Liaw, A.; Matthew, W. Classification and regression by randomforest. R News 2002, 2, 18–22. [Google Scholar]
- Kuhn, M. Building Predictive Models in R Using the caret Package. J. Stat. Softw. 2008, 28, 1–26. [Google Scholar] [CrossRef]
- Horning, N. Random Forests: An algorithm for image classification and generation of continuous fields data sets. In Proceedings of the International Conference on Geoinformatics for Spatial Infrastructure Development in Earth and Allied Sciences, Osaka, Japan, 22 October 2010; Volume 911. [Google Scholar]
- Adam, E.M.; Mutanga, O.; Abdel-Rahman, E.M.; Ismail, R. Estimating standing biomass in papyrus (Cyperus papyrus L.) swamp: Exploratory of in situ hyperspectral indices and random forest regression. Int. J. Remote Sens. 2014, 35, 693–714. [Google Scholar] [CrossRef]
- Wong, V.C.W. Optimizing Digital Aerial Photogrammetry for Forestry Applications in Tropical Montane Forest Environment. Ph.D. Thesis, University of Tokyo, Tokyo, Japan, 2016. [Google Scholar]
- Genuer, R.; Poggi, J.M.; Tuleau-Malot, C. Variable selection using random forests. Pattern Recognit. Lett. 2010, 31, 2225–2236. [Google Scholar] [CrossRef]
- Oshiro, T.M.; Perez, P.S.; Baranauskas, J.A. How many trees in a random forest? In International Workshop on Machine Learning and Data Mining in Pattern Recognition; Springer: Berlin/Heidelberg, Germany, 2012; pp. 154–168. [Google Scholar] [CrossRef]
- Biau, G.; Scornet, E. A random forest guided tour. Test 2016, 25, 197–227. [Google Scholar] [CrossRef]
- Grömping, U. Variable importance assessment in regression: Linear regression versus random forest. Am. Stat. 2009, 63, 308–319. [Google Scholar] [CrossRef]
- Nackaerts, K.; Coppin, P.; Muys, B.; Hermy, M. Sampling methodology for LAI measurements with LAI-2000 in small forest stands. Agric. For. Meteorol. 2000, 101, 247–250. [Google Scholar] [CrossRef]
- Manssour, K.M.Y. Rangeland Degradation Assessment Using Remote Sensing and Vegetation Species. Ph.D. Thesis, University of KwaZulu-Natal, Pietermaritzburg, South Africa, 2011. Available online: http://hdl.handle.net/10413/8583 (accessed on 12 October 2018).
- Bulcock, H.; Jewitt, G. Spatial mapping of leaf area index using hyperspectral remote sensing for hydrological applications with a particular focus on canopy interception. Hydrol. Earth Syst. Sci. 2010, 14, 383–392. [Google Scholar] [CrossRef]
- Baret, F.; Guyot, G. Potentials and limits of vegetation indices for LAI and APAR assessment. Remote Sens. Environ. 1991, 35, 161–173. [Google Scholar] [CrossRef]
- Papadavid, G.C.; Hadjimitsis, D.G.; Toulios, L.; Michaelides, S. Mapping potato crop height and leaf area index through vegetation indices using remote sensing in Cyprus. J. Appl. Remote Sens. 2011, 5, 053526. [Google Scholar] [CrossRef]
- Yoder, B.J.; Waring, R.H. The normalized vegetation index of small douglas-fir canopies with varying chlorophyll concentration. Remote Sens. Environ. 1994, 49, 81–91. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Stark, R.; Grits, U.; Rundquist, D.; Kaufman, Y.; Derry, D. Vegetation and soil lines in visible spectral space: A concept and technique for remote estimation of vegetation fraction. Int. J. Remote Sens. 2002, 23, 2537–2562. [Google Scholar] [CrossRef]
- Wang, F.M.; Huang, J.F.; Tang, Y.L.; Wang, X.Z. New vegetation index and its application in estimating leaf area index of rice. Rice Sci. 2007, 14, 195–203. [Google Scholar] [CrossRef]
- Zhang, C. The evaluation of broadband vegetation indices on monitoring Northern mixed grassland. Prairie Perspect. 2005, 8, 23–36. Available online: http://pcag.uwinnipeg.ca/Prairie-Perspectives/PP-Vol08/Zhang.pdf (accessed on 12 November 2018).
- He, Y.; Guo, X. Leaf Area Index estimation using remotely sensed data in mixed grassland ecosystem. Prairie Perspect. 2006, 9, 105–117. Available online: http://hdl.handle.net/1807/69335 (accessed on 15 October 2018).
- Wanjura, D.F.; Hatfield, J.L. Sensitivity of spectral vegetative indices to crop biomass. Trans. ASAE 1987, 30, 0810–0816. [Google Scholar] [CrossRef]
- Gray, J.; Song, C. Mapping leaf area index using spatial, spectral, and temporal information from multiple sensors. Remote Sens. Environ. 2012, 119, 173–183. [Google Scholar] [CrossRef]
- Shen, L.; Li, Z.; Guo, X. Remote sensing of leaf area index (LAI) and a spatiotemporally parameterized model for mixed grasslands. Int. J. Appl. Sci. Technol. 2014, 4. Available online: http://ijastnet.com/journals/Vol_4_No_1_January_2014/5.pdf (accessed on 13 January 2019).
- Rutherford, M.; Powrie, L. Impacts of heavy grazing on plant species richness: A comparison across rangeland biomes of South Africa. S. Afr. J. Bot. 2013, 87, 146–156. [Google Scholar] [CrossRef]

| Season | Image Scene Detail | Date of Acquisition |
|---|---|---|
| Dry | LC08_L1TP_168077_20161022_20170319_01_T1 | 22 October 2016 |
| LC08_L1TP_169076_20161029_20170319_01_T1 | 29 October 2016 | |
| Wet | LC08_L1TP_168077_20170518_20170525_01_T1 | 18 May 2017 |
| LC08_L1TP_169076_20170525_20170614_01_T1 | 25 May 2017 |
| Vegetation Indices | Algorithm | Reference |
|---|---|---|
| NDVI | NIR − RED/NIR + RED | [8] |
| SR | NIR/RED | [9] |
| SAVI | ((NIR − RED)/(NIR + R + L)) × (1 + L) | [10] |
| EVI | 2.5 × (NIR − RED)/(NIR + 6RED − 7.5 × BLUE + 1) | [11] |
| EVI2 | 2.4 × (NIR − RED)/(NIR + RED + 1) | [11] |
| PSRI | (RED − GREEN)/NIR | [12] |
| CRI1 | (1/BLUE) − (1/GREEN) | [13] |
| GVI | NIR/GREEN | [14] |
| GNDVI | (NIR − GREEN)/(NIR + GREEN) | [15] |
| GCI | (NIR/GREEN) − 1 | [16] |
| MSR | (NIR/RED) − 1/√((NIR/RED)) +1 | [17] |
| ARVI | NIR − (RED − 1 × (BLUE − RED))/NIR + (RED − 1 × (BLUE − RED)) where, 1 = γ | [18] |
| MCARI | 1.5 × (2.5 × (NIR − RED) − 1.3 × (NIR − BLUE))/√((2 × NIR + 1)^2 − (6 × NIR − 5 × RED) − 0.5) | [19] |
| MTVI2 | 1.5 × (1.2 × (NIR − GREEN) − 2.5 × (RED − GREEN))/√((2 × NIR + 1)^2 − (6 × NIR − 5 × √(RED) − 0.5)) | [20] |
| No. of Variables Used | Eliminated Variable (Backward) | R2 | RMSE m2/m2 | relRMSE% |
|---|---|---|---|---|
| 21 | full predictors | 0.63 | 0.70 | 37.63 |
| 20 | B3 | 0.70 | 0.63 | 33.82 |
| 19 | B1 | 0.69 | 0.63 | 33.97 |
| 18 | B2 | 0.69 | 0.62 | 33.67 |
| 17 | GVI | 0.68 | 0.63 | 34.08 |
| 16 | MSR | 0.69 | 0.63 | 34.07 |
| 15 | B4 | 0.72 | 0.60 | 32.48 |
| 14 | B6 | 0.68 | 0.64 | 34.33 |
| 13 | MTVI2 | 0.68 | 0.64 | 33.33 |
| 12 | EVI2 | 0.68 | 0.63 | 34.34 |
| 11 | B7 | 0.68 | 0.63 | 34.14 |
| 10 | ARVI | 0.68 | 0.63 | 34.20 |
| 9 | GNDVI | 0.68 | 0.63 | 34.23 |
| 8 | EVI | 0.67 | 0.64 | 34.57 |
| 7 | MCARI | 0.67 | 0.64 | 34.56 |
| 6 | SR | 0.66 | 0.65 | 34.92 |
| 5 | GCI | 0.65 | 0.66 | 35.36 |
| 4 | NDVI | 0.59 | 0.70 | 38.03 |
| 3 | B5 | 0.63 | 0.67 | 36.19 |
| No. of Variables Used | Eliminated Variable (Backward) | R2 | RMSE m2/m2 | relRMSE% |
|---|---|---|---|---|
| 21 | full predictors | 0.62 | 0.81 | 37.63 |
| 20 | B4 | 0.61 | 0.80 | 33.82 |
| 19 | EVI2 | 0.61 | 0.80 | 33.97 |
| 18 | B5 | 0.61 | 0.80 | 33.67 |
| 17 | MTVI2 | 0.61 | 0.80 | 34.08 |
| 16 | B3 | 0.61 | 0.80 | 34.07 |
| 15 | ARVI | 0.61 | 0.80 | 32.48 |
| 14 | B7 | 0.62 | 0.79 | 34.33 |
| 13 | B2 | 0.62 | 0.79 | 33.33 |
| 12 | MCARI | 0.62 | 0.80 | 34.34 |
| 11 | SAVI | 0.62 | 0.80 | 34.14 |
| 10 | B1 | 0.62 | 0.79 | 34.20 |
| 9 | EVI | 0.63 | 0.79 | 34.23 |
| 8 | MSR | 0.63 | 0.79 | 34.57 |
| 7 | NDVI | 0.63 | 0.79 | 34.56 |
| 6 | B6 | 0.62 | 0.79 | 34.92 |
| 5 | SR | 0.62 | 0.79 | 35.36 |
| 4 | CRI1 | 0.61 | 0.80 | 38.03 |
| 3 | PSRI | 0.59 | 0.86 | 36.19 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dube, T.; Pandit, S.; Shoko, C.; Ramoelo, A.; Mazvimavi, D.; Dalu, T. Numerical Assessments of Leaf Area Index in Tropical Savanna Rangelands, South Africa Using Landsat 8 OLI Derived Metrics and In-Situ Measurements. Remote Sens. 2019, 11, 829. https://doi.org/10.3390/rs11070829
Dube T, Pandit S, Shoko C, Ramoelo A, Mazvimavi D, Dalu T. Numerical Assessments of Leaf Area Index in Tropical Savanna Rangelands, South Africa Using Landsat 8 OLI Derived Metrics and In-Situ Measurements. Remote Sensing. 2019; 11(7):829. https://doi.org/10.3390/rs11070829
Chicago/Turabian StyleDube, Timothy, Santa Pandit, Cletah Shoko, Abel Ramoelo, Dominic Mazvimavi, and Tatenda Dalu. 2019. "Numerical Assessments of Leaf Area Index in Tropical Savanna Rangelands, South Africa Using Landsat 8 OLI Derived Metrics and In-Situ Measurements" Remote Sensing 11, no. 7: 829. https://doi.org/10.3390/rs11070829
APA StyleDube, T., Pandit, S., Shoko, C., Ramoelo, A., Mazvimavi, D., & Dalu, T. (2019). Numerical Assessments of Leaf Area Index in Tropical Savanna Rangelands, South Africa Using Landsat 8 OLI Derived Metrics and In-Situ Measurements. Remote Sensing, 11(7), 829. https://doi.org/10.3390/rs11070829