Improving Aboveground Forest Biomass Maps: From High-Resolution to National Scale
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
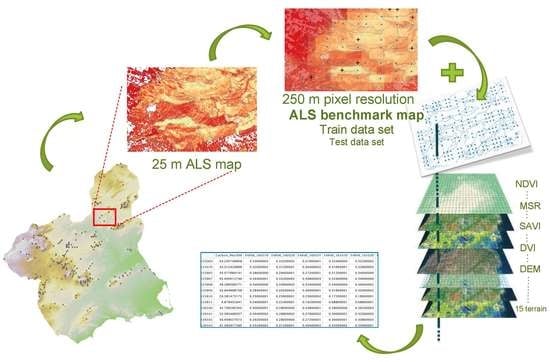
2.2. From Field Plots to ALS Benchmark Map
2.2.1. Field Data
2.2.2. ALS Data Acquisition and Processing
2.2.3. ALS Benchmark Map: Model, Spatial Prediction, and Resampling
2.3. From ALS Benchmark Map to MODIS Map
2.3.1. Optical Remote Sensing and Topographic Variables
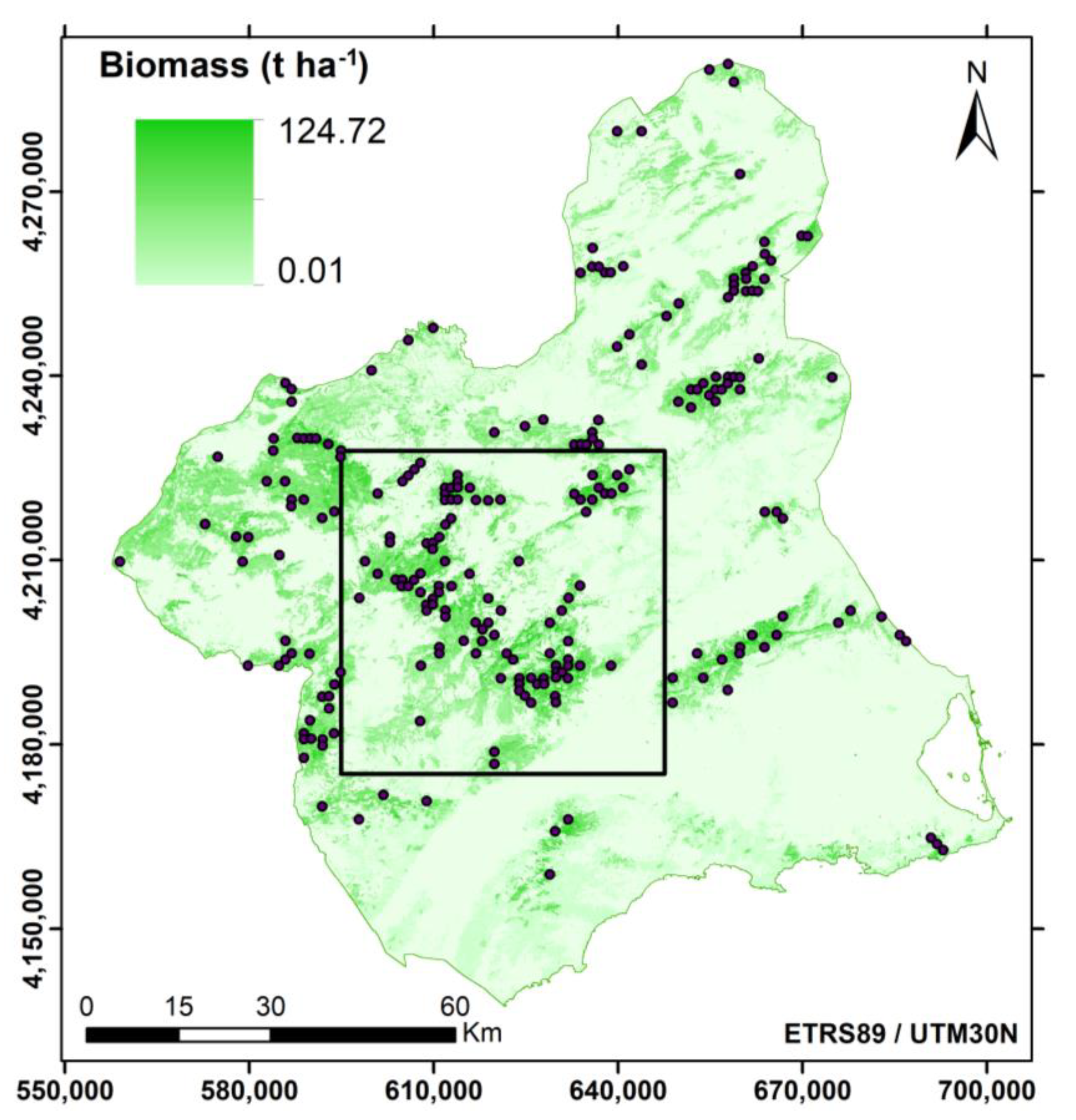
2.3.2. NDVI Annual Profile per Vegetation Type
2.3.3. MODIS Map: Spatial Predictive Model and Associated Uncertainty
3. Results
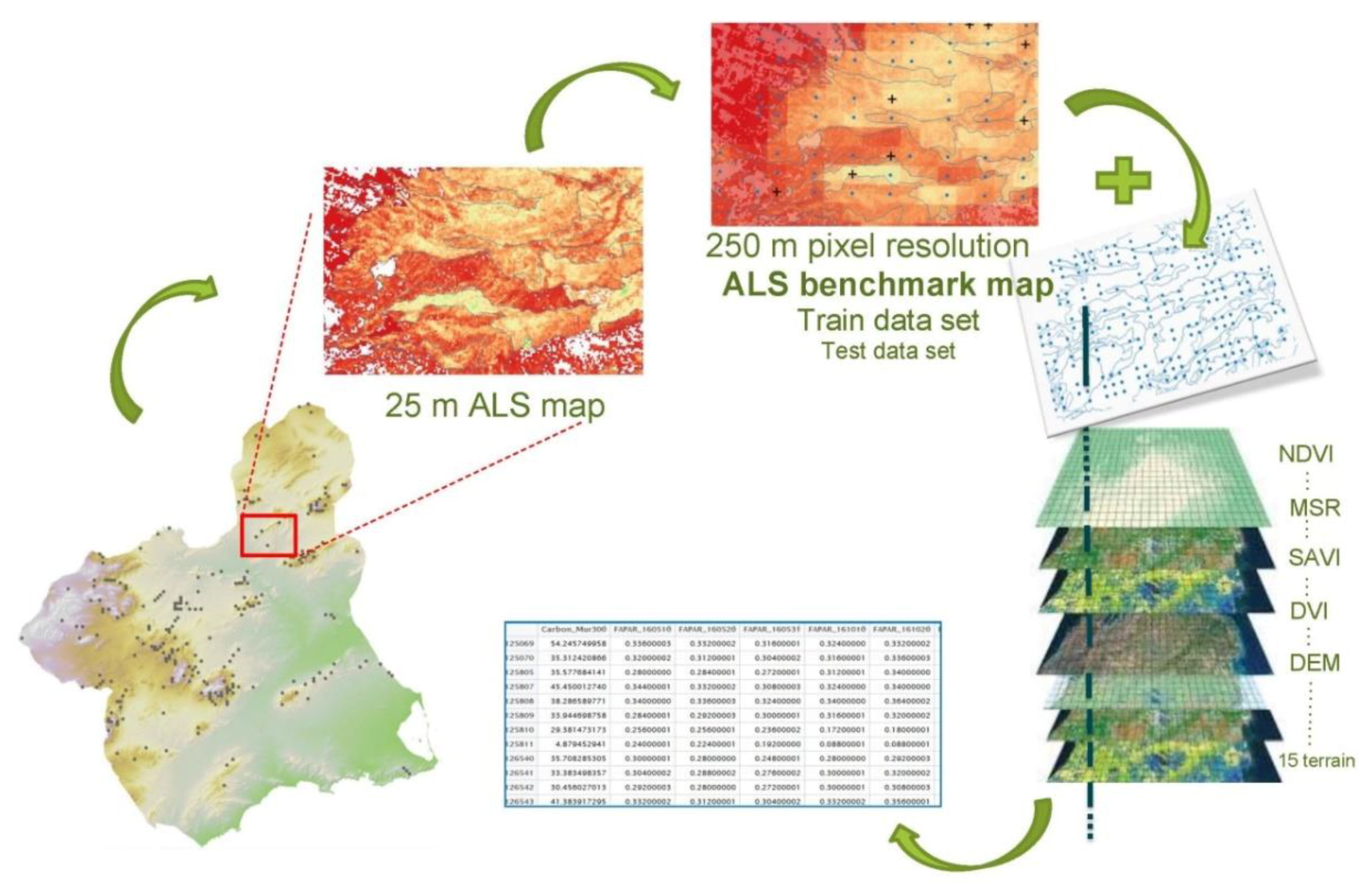
3.1. ALS-Based Forest AGB Assessment
3.2. From ALS Benchmark Map to MODIS Map
3.2.1. NDVI Annual Mean Profile per Vegetation Type
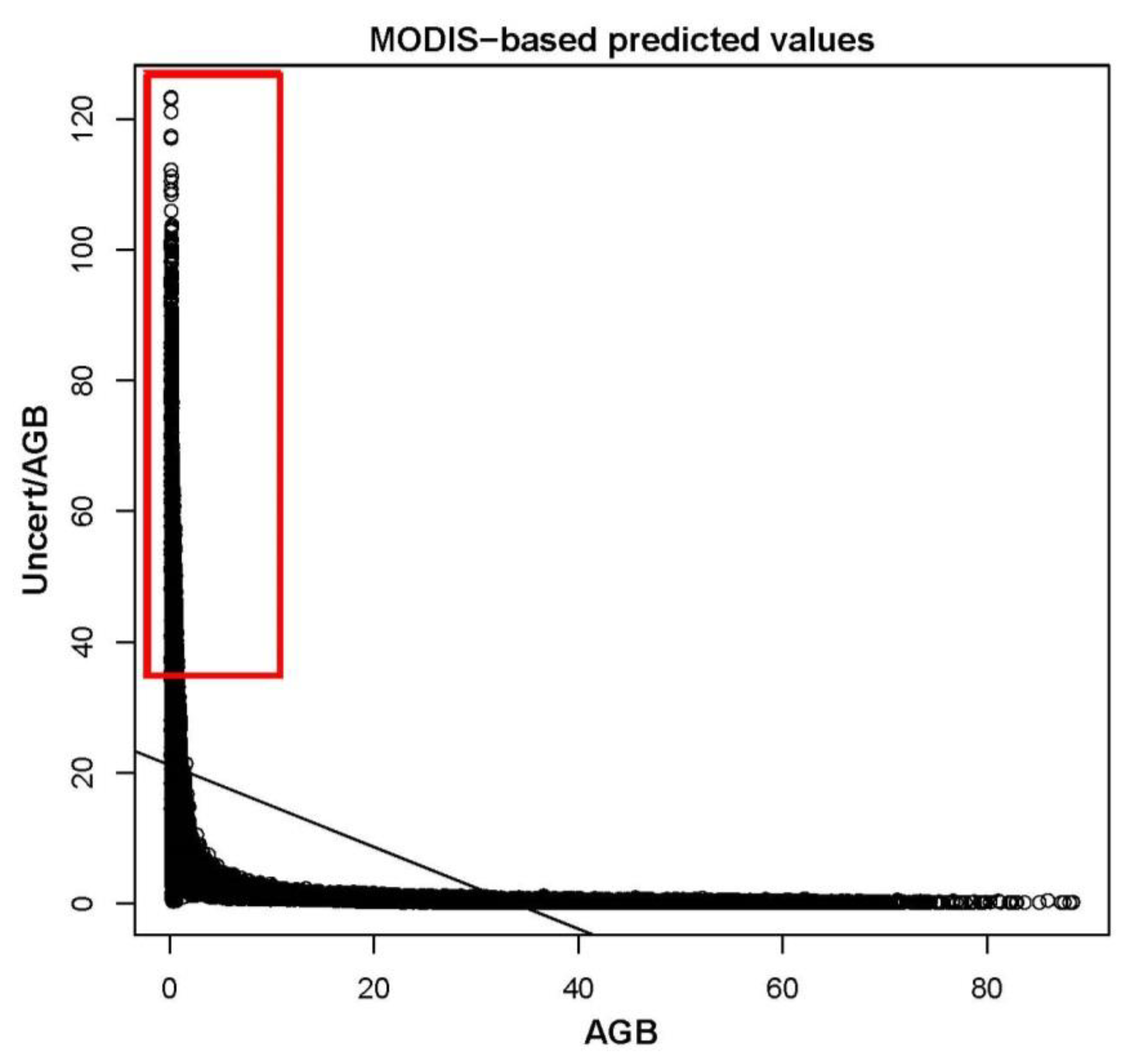
3.2.2. Model Fitting, Spatial Prediction, and Uncertainty Assessment
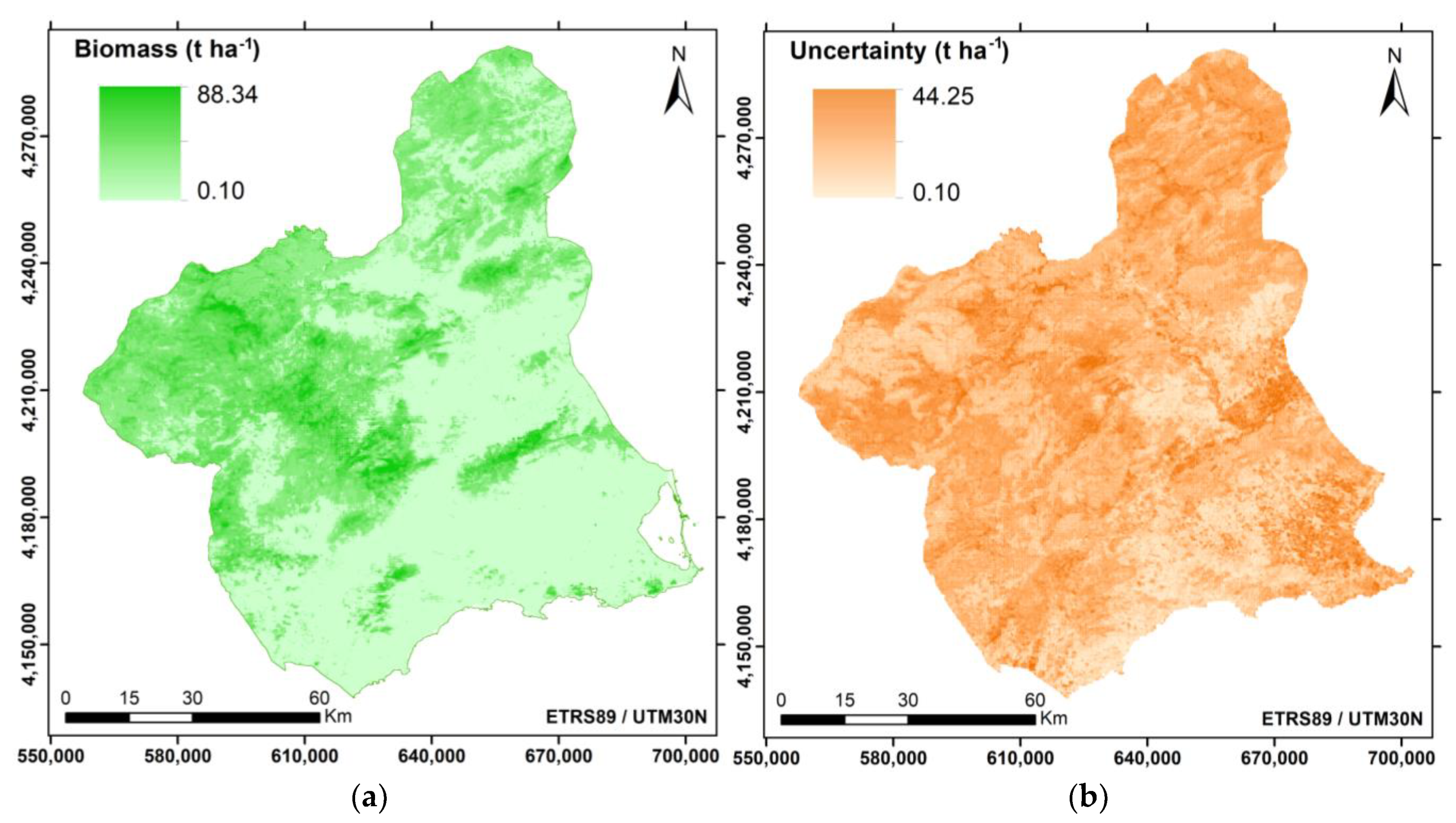
3.2.3. Final Predicted MODIS Map and Validation
4. Discussion
4.1. Forest AGB Estimate from Local to National Scale
4.2. Environmental Drivers of Forest AGB Spatial Variability
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Barredo, J.I.; Mauri, A.; Caudullo, G. Assessing Shifts of Mediterranean and Arid Climates Under RCP4.5 and RCP8.5 Climate Projections in Europe. Pure Appl. Geophys. 2018, 175, 3955–3971. [Google Scholar] [CrossRef]
- Ometto, J.P.; Aguiar, A.P.; Assis, T.; Soler, L.; Valle, P.; Tejada, G.; Lapola, D.M.; Meir, P. Amazon forest biomass density maps: Tackling the uncertainty in carbon emission estimates. Clim Chang. 2014, 124, 545–560. [Google Scholar] [CrossRef]
- Saatchi, S.; Houghton, R.A.; Dos Santos Alvalá, R.C.; Soares, J.V.; Yu, Y. Distribution of aboveground live biomass in the Amazon basin. Glob. Chang. Biol. 2007, 13, 816–837. [Google Scholar] [CrossRef]
- Canadell, J.G.; Raupach, M.R. Managing forests for climate change mitigation. Science 2008, 320, 1456–1457. [Google Scholar] [CrossRef]
- González-Jaramillo, V.; Fries, A.; Zeilinger, J.; Homeier, J.; Paladines-Benitez, J.; Bendix, J. Estimation of Above Ground Biomass in a Tropical Mountain Forest in Southern Ecuador Using Airborne LiDAR Data. Remote Sens. 2018, 10, 660. [Google Scholar] [CrossRef]
- Navarro Cerrillo, R.M.; González Ferreiro, E.; García Gutiérrez, J.; Ceacero Ruiz, C.J.; Hernández Clemente, R. Impact of plot size and model selection on forest biomass estimation using airborne LiDAR: A case study of pine plantations in southern Spain. J. For. Sci. 2017, 63, 88–97. [Google Scholar] [CrossRef]
- Næsset, E.; Gobakken, T. Estimation of above-and below-ground biomass across regions of the boreal forest zone using airborne laser. Remote Sens. Environ. 2008, 112, 3079–3090. [Google Scholar] [CrossRef]
- White, J.C.; Coops, N.C.; Wulder, M.A.; Vastaranta, M.; Hilker, T.; Tompalski, P. Remote sensing technologies for enhancing forest inventories: A review. Can. J. Remote Sens. 2016, 42, 619–641. [Google Scholar] [CrossRef]
- Valbuena, R.; De Blas, A.; Martín Fernández, S.; Maltamo, M.; Nabuurs, G.J.; Manzanera, J.A. Within-Species Benefits of Back-projecting Laser Scanner and Multispectral Sensors in Monospecific P. sylvestris Forests. Eur. J. Remote Sens. 2013, 46, 491–509. [Google Scholar] [CrossRef]
- Bottalico, F.; Chirici, G.; Giannini, R.; Mele, S.; Mura, M.; Puxeddu, M.; McRoberts, R.E.; Valbuena, R.; Travaglini, D. Modeling Mediterranean Forest Structure Using Airborne Laser Scanning Data. Int. J. Appl. Earth Obs. 2017, 57, 145–153. [Google Scholar] [CrossRef]
- Kauranne, T.; Joshi, A.; Gautam, B.; Manandhar, U.; Nepal, S.; Peuhkurinen, J.; Hämäläinen, J.; Junttila, V.; Gunia, K.; Latva-Käyrä, P.; et al. LiDAR-Assisted Multi-Source Program (LAMP) for Measuring Above Ground Biomass and Forest Carbon. Remote Sens. 2017, 9, 154. [Google Scholar] [CrossRef]
- Molina, P.X.; Asner, G.P.; Farjas Abadía, M.; Ojeda Manrique, J.C.; Sánchez Diez, L.A.; Valencia, R. Spatially-Explicit Testing of a General Aboveground Carbon Density Estimation Model in a Western Amazonian Forest Using Airborne LiDAR. Remote Sens. 2016, 8, 9. [Google Scholar] [CrossRef]
- Maltamo, M.; Packalén, P.; Suvanto, A.; Korhonen, K.T.; Mehtätalo, L.; Hyvönen, P. Combining ALS and NFI training data for forest management planning: A case study in Kuortane, Western Finland. Eur. J. For. Res. 2009, 128, 305. [Google Scholar] [CrossRef]
- Nelson, R.; Gobakken, T.; Næsset, E.; Gregoire, T.; Ståhl, G.; Holm, S.; Flewelling, J. Lidar sampling—Using an airborne profiler to estimate forest biomass in Hedmark County, Norway. Remote Sens. Environ. 2012, 123, 563–578. [Google Scholar] [CrossRef]
- Fassnacht, F.E.; Latifi, H.; Hartig, F. Using synthetic data to evaluate the benefits of large field plots for forest biomass estimation with LiDAR. Remote Sens. Environ. 2018, 213, 115–128. [Google Scholar] [CrossRef]
- Hudak, A.T.; Strand, E.K.; Vierling, L.A.; Byrne, J.C.; Eitel, J.U.H.; Martinuzzi, S.; Falkowski, M.J. Quantifying aboveground forest carbon pools and fluxes from repeat LiDAR surveys. Remote Sens. Environ. 2012, 123, 25–40. [Google Scholar] [CrossRef]
- Cash, D.W.; Moser, S.C. Linking global and local scales: Designing dynamic assessment and management processes. Glob. Environ. Chang. 2000, 10, 109–120. [Google Scholar] [CrossRef]
- Lu, D. The potential and challenge of remote sensing-based biomass estimation. Int. J. Remote Sens. 2006, 27, 1297–1328. [Google Scholar] [CrossRef]
- Xiao, J.; Moody, A. Photosynthetic activity of US biomes: Responses to the spatial variability and seasonality of precipitation and temperature. Glob Chang Biol. 2004, 10, 437–451. [Google Scholar] [CrossRef]
- Blackard, J.A.; Finco, M.V.; Helmer, E.H.; Holden, G.R.; Hoppus, M.L.; Jacobs, D.M.; Lister, A.J.; Moisen, G.G.; Nelson, M.D.; Riemann, R.; et al. Mapping U.S. forest biomass using nationwide forest inventory data and moderate resolution information. Remote Sens. Environ. 2008, 112, 1658–1677. [Google Scholar] [CrossRef]
- Chi, H.; Sun, G.; Huang, J.; Guo, Z.; Ni, W.; Fu, A. National Forest Aboveground Biomass Mapping from ICESat/GLAS Data and MODIS Imagery in China. Remote Sens. 2015, 7, 5534–5564. [Google Scholar] [CrossRef]
- Jin, Y.; Yang, X.; Qiu, J.; Li, J.; Gao, T.; Wu, Q.; Zhao, F.; Ma, H.; Yuand, H.; Xu, B. Remote sensing-based biomass estimation and its spatio-temporal variations in temperate grassland, Northern China. Remote Sens. 2014, 6, 1496–1513. [Google Scholar] [CrossRef]
- Didan, K. MOD13Q1 MODIS/Terra Vegetation Indexes 16-Day L3 Global 250 m SIN Grid V006 [Data Set]; NASA EOSDIS LP DAAC: Sioux Falls, SD, USA, 2015. [CrossRef]
- Reed, B.C.; Schwartz, M.D.; Xiangming, X. Remote sensing phenology: Status and the way forward. In Phenology of Ecosystem Processes; Noormets, A., Ed.; Springer: New York, NY, USA, 2009; pp. 231–246. ISBN 978-1-4419-0026-5. [Google Scholar]
- Le, L.; Guo, Q.; Tao, S.; Kelly, M.; Xu, G. Lidar with multi-temporal MODIS provide a means to upscale predictions of forest biomass. ISPRS J. Photogramm. Remote Sens. 2015, 102, 198–208. [Google Scholar] [CrossRef]
- Tucker, C.J. Red and photographic infrared linear combinations for monitoring vegetation. Remote Sens. Environ. 1979, 8, 127–150. [Google Scholar] [CrossRef]
- Paruelo, J.M.; Epstein, H.E.; Lauenroth, W.K.; Burke, I.C. ANPP estimates from NDVI for the central grassland region of the United States. Ecology 1997, 78, 953–958. [Google Scholar] [CrossRef]
- Piao, S.; Friedlingstein, P.; Ciais, P.; de Noblet-Ducoudré, N.; Labat, D.; Zaehle, S. Changes in climate and land use have a larger direct impact than rising CO2 on global river runoff trends. Proc. Natl. Acad. Sci. USA 2007, 4, 15242–15247. [Google Scholar] [CrossRef] [PubMed]
- Yan, F.; Wu, B.; Wang, Y. Estimating spatiotemporal patterns of aboveground biomass using Landsat TM and MODIS images in the Mu Us Sandy Land, China. Agric. For. Meteorol. 2015, 200, 119–128. [Google Scholar] [CrossRef]
- Alcaraz-Segura, D.; Cabello, J.; Paruelo, J.; Delibes, M. Use of Descriptors of Ecosystem Functioning for Monitoring a National Park Network: A Remote Sensing Approach. Environ. Manag. 2009, 43, 38–48. [Google Scholar] [CrossRef]
- Tenkabail, P.S.; Smith, R.B.; Pauw, E.D. Hyperspectral vegetation indices and their relationships with agricultural crop characteristics. Remote Sens. Environ. 2000, 75, 158–182. [Google Scholar] [CrossRef]
- Liu, Q.; Huete, A. A feedback based modification of the NDVI to minimize canopy background and atmospheric noise. IEEE Trans. Geosci. Remote Sens. 1995, 33, 457–465. [Google Scholar] [CrossRef]
- Huete, A.R. A soil adjusted vegetation index (SAVI). Remote Sens. Environ. 1988, 25, 295–309. [Google Scholar] [CrossRef]
- Mutanga, O.; Skidmore, A.K. Narrow band vegetation indices solve the saturation problem in biomass estimation. Int. J. Remote Sens. 2004, 25, 3999–4014. [Google Scholar] [CrossRef]
- Rougean, J.L.; Breon, F.M. Estimating PAR absorbed by vegetation from bidirectional reflectance measurements. Remote Sens. Environ. 1995, 51, 375–384. [Google Scholar] [CrossRef]
- Jordan, C.F. Derivation of leaf area index from quality of light on the forest floor. Ecology 1969, 50, 663–666. [Google Scholar] [CrossRef]
- Chen, J. Evaluation of vegetation indexes and modified simple ratio for boreal applications. Can. J. Remote Sens. 1996, 22, 229–242. [Google Scholar] [CrossRef]
- Matasci, G.; Hermosilla, T.; Wulder, M.A.; White, J.C.; Coops, N.C.; Hobart, G.W.; Zald, H.S. Large-area mapping of Canadian boreal forest cover, height, biomass and other structural attributes using Landsat composites and lidar plots. Remote Sens. Environ. 2018, 209, 90–106. [Google Scholar] [CrossRef]
- Moore, I.D.; Grayson, R.B.; Ladson, A.R. Digital terrain modelling: A review of hydrological, geomorphological, and biological applications. Hydrol. Process. 1991, 5, 3–30. [Google Scholar] [CrossRef]
- Mendoza Ponce, A.; Corona Núñez, R.; Kraxnera, F.; Leduca, S.; Patrizioa, P. Identifying effects of land use cover changes and climate change on terrestrial ecosystems and carbon stocks in Mexico. Glob. Environ. Chang. 2018, 53, 12–23. [Google Scholar] [CrossRef]
- Wulder, M.A.; White, J.C.; Nelson, R.F.; Næsset, E.; Ørka, H.O.; Coops, N.C.; Hilker, T.; Bater, C.B.; Gobakken, T. Lidar sampling for large-area forest characterization: A review. Remote Sens. Environ. 2012, 121, 196–209. [Google Scholar] [CrossRef]
- Navarro, J.A.; Algeet, N.; Fernández-Landa, A.; Esteban, J.; Rodríguez-Noriega, P.; Guillén-Climent, M.L. Integration of UAV, Sentinel-1, and Sentinel-2 Data for Mangrove Plantation Aboveground Biomass Monitoring in Senegal. Remote Sens. 2019, 11, 77. [Google Scholar] [CrossRef]
- Saarela, S.; Holm, S.; Grafström, A.; Schnell, S.; Næsset, E.; Gregoire, T.G.; Nelson, R.F.; Ståhl, G. Hierarchical model-based inference for forest inventory utilizing three sources of information. Ann. For. Sci. 2016, 73, 895–910. [Google Scholar] [CrossRef]
- Papadakis, J. Climates of the World and their Agricultural Potentialities; J. Papadakis: Buenos Aires, Argentina, 1966; ISBN 19670701017. [Google Scholar]
- Ministerio de Agricultura, Alimentación y Medio Ambiente (MAGRAMA). Cuarto Inventario Forestal Nacional. Región de Murcia; Organismo Autónomo Parques Nacionales: Madrid, Spain, 2012; 44p, ISBN 978-84-8014-820-7. [Google Scholar]
- Murgaš, V.; Sačkov, I.; Sedliak, M.; Tunák, D.; Chudý, F. Assessing horizontal accuracy of inventory plots in forests with different mix of tree species composition and development stage. J. For. Sci. 2018, 64, 478–485. [Google Scholar] [CrossRef]
- Mauro, F.; Valbuena, R.; Manzanera, J.A.; García-Abril, A. Influence of Global Navigation Satellite System errors in positioning inventory plots for tree-height distribution studies. Can. J. For. Res. 2011, 41, 11–23. [Google Scholar] [CrossRef]
- Fernández-Landa, A.; Fernández-Moya, J.; Tomé, J.L.; Algeet-Abarquero, N.; Guillén-Climent, M.L.; Vallejo, R.; Marchamalo, M. High resolution forest inventory of pure and mixed stands at regional level combining National Forest Inventory field plots, Landsat, and low density lidar. Int. J. of Rem. Sen. 2018, 39, 4830–4844. [Google Scholar] [CrossRef]
- Magnussen, S.; Boudewyn, P. Derivations of stand heights from airborne laser scanner data with canopy-based quantile estimators. Can. J. For. Res. 1998, 28, 1016–1031. [Google Scholar] [CrossRef]
- Montero, G.; Ruiz-Peinado, R.; Muñoz, M. Producción de Biomasa y fijación de CO2 por los Bosques Españoles; INIA (MEC): Madrid, Spain, 2005; ISBN 9788474985122. [Google Scholar]
- Montero, G.; Pasalodos-Tato, M.; López-Senespleda, E.; Onrubia, R.; Madrigal, G. Ecuaciones para la Estimación de la Biomasa en Matorrales y arbustedos mediterráneos. 6º Congreso Forestal Español; Sociedad Española de Ciencias Forestales: Vitoria-Gasteiz, Spain, 2013. [Google Scholar]
- Domingo, D.; Alonso, R.; Lamelas, M.T.; Montealegre, A.L.; Rodríguez, F.; de la Riva, J. Temporal Transferability of Pine Forest Attributes Modeling Using Low-Density Airborne Laser Scanning Data. Remote Sens. 2019, 11, 261. [Google Scholar] [CrossRef]
- McGaughey, R.J.; Carson, W.W. Fusing LIDAR data, photographs, and other data using 2D and 3D visualization techniques. Proc. Terrain Data Appl. Vis.—Mak. Connect. 2003, 28–30. Available online: https://bit.ly/2UaNGlm (accessed on 18 November 2018).
- Næsset, E. Predicting Forest Stand Characteristics with Airborne Scanning Laser Using a Practical Two-Stage Procedure and Field Data. Remote Sens. Environ. 2002, 80, 88–99. [Google Scholar] [CrossRef]
- Pike, R.J.; Wilson, S.E. Elevation-Relief Ratio, Hypsometric Integral, and Geomorphic Area-Altitude Analysis. GSA Bull. 1971, 82, 1079–1084. [Google Scholar] [CrossRef]
- Parker, G.G.; Russ, M.E. The Canopy Surface and Stand Development: Assessing Forest Canopy Structure and Complexity with near-Surface Altimetry. For. Ecol. Manag. 2004, 189, 307–315. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Liaw, A.; Wiener, M. Classification and regression by random forest. R News 2002, 2, 18–22. [Google Scholar]
- Genuer, R.; Poggi, J.M.; Tuleau-Malot, C.; Genuer, M.R. Package ‘vsurf’. Pattern Recognit. Lett. 2015, 14, 2225–2236. [Google Scholar]
- Evans, J.S.; Murphy, M.A. rfUtilities. R Package Version 2.1-3. 2018. Available online: https://cran.r-project.org/web/packages/rfUtilities/index.html (accessed on 18 November 2018).
- R Development Core Team. R: A Language and Environment for Statistical Computing; R Development Core Team: Vienna, Austria, 2014. [Google Scholar]
- Hijmans, R.J. Package ‘raster’. R Package Version 2.8-4. 2018. Available online: https://cran.r-project.org/web/packages/raster/index.html (accessed on 20 November 2018).
- Vermote, E. MOD09Q1 MODIS/Terra Surface Reflectance 8-Day L3 Global 250 m SIN Grid V006 [Data Set]; NASA EOSDIS LP DAAC: Sioux Falls, SD, USA, 2015.
- NASA Land Processes Distributed Active Archive Center. Available online: https://lpdaac.usgs.gov/ (accessed on 25 October 2018).
- Gao McNairn, H.; Protz, R. Mapping corn residue cover on agricultural fields in Oxford County, Ontario, using Thematic Mapper. Can. J. Remote Sens. 1993, 19, 152–159. [Google Scholar] [CrossRef]
- Qi, J.; Chehbouni, A.; Huete, A.R.; Kerr, Y.H.; Sorooshian, S. A modified soil adjusted vegetation index. Remote Sens. Environ. 1994, 48, 119–126. [Google Scholar] [CrossRef]
- Pettorelli, N.; Vik, J.O.; Mysterud, A.; Gaillard, J.M.; Tucker, C.J.; Stenseth, N.C. Using the satellite-derived NDVI to assess ecological responses to environmental change. Trends Ecol. Evol. 2005, 20, 503–510. [Google Scholar] [CrossRef] [PubMed]
- Holben, B.N. Characteristics of maximum value composite images for temporal AVHRR data. Int. J. Remote Sens. 1986, 7, 1417–1437. [Google Scholar] [CrossRef]
- Wilson, D.S.; Jamieson, S.S.; Barrett, P.J.; Leitchenkov, G.; Gohl, K.; Larter, R.D. Antarctic topography at the Eocene–Oligocene boundary. Palaeogeogr. Palaeoclimatol. Palaeoecol. 2012, 335–336, 24–34. [Google Scholar] [CrossRef]
- Conrad, O.; Bechtel, B.; Bock, M.; Dietrich, H.; Fischer, E.; Gerlitz, L.; Wehberg, J.; Wichmann, V.; Böhner, J. System for Automated Geoscientific Analyses (SAGA) v. 2.1.4. Geosci. Model Dev. 2015, 8, 1991–2007. [Google Scholar] [CrossRef]
- Fox, J. Applied Regression Analysis and Generalized Linear Models, 3rd ed.; SAGE: Thousand Oaks, CA, USA, 2016; ISBN 978-1-4522-0566. [Google Scholar]
- Do, T.N.; Lenca, P.; Lallich, S.; Pham, N.K. Classifying very-high-dimensional data with random forests of oblique decision trees. In Advances in Knowledge Discovery and Management; Guillet, F., Pinaud, B., Venturini, G., Zighed, D.A., Eds.; Springer: Berlin/Heidelberg, Germany, 2010; pp. 39–55. ISBN 978-3-642-00580-0. [Google Scholar]
- Xu, B.; Huang, J.Z.; Williams, G.; Wang, Q.; Ye, Y. Classifying very high-dimensional data with random forests built from small subspaces. Int. J. Data Wareh. Min. 2012, 8, 44–63. [Google Scholar] [CrossRef]
- Meinshausen, N. quantregForest: Quantile Regression Forests. R Package version 1.3-7, 2017. Available online: https://CRAN.R-project.org/package=quantregForest (accessed on 22 November 2018).
- Flilnt, R.; Gregory, P.A.; Baldwine, J.A.; Mascaroc, J.; Bufild, L.K.K.; Knappb, D.E. Estimating aboveground carbon density across forest landscapes of Hawaii: Combining FIA plot-derived estimates and airborne LiDAR. For. Ecol. Manag. 2018, 424, 323–337. [Google Scholar] [CrossRef]
- Urbazaev, M.; Thiel, C.; Cremer, F.; Dubayah, R.; Migliavacca, M.; Reichstein, M.; Schmullius, C. Estimation of forest aboveground biomass and uncertainties by integration of field measurements, airborne lidar, and sar and optical satellite data in México. Carbon Balance Manag. 2018, 13, 5. [Google Scholar] [CrossRef]
- Chirici, G.; Mura, M.; Mcinerney, D.; Py, N.; Tomppo, E.O.; Waser, L.T.; Travaglini, D.; Mcroberts, R.E. A meta-analysis and review of the literature on the k-Nearest Neighbors technique for forestry applications that use remotely sensed data. Remote Sens. Environ. 2016, 176, 282–294. [Google Scholar] [CrossRef]
- Domingo, D.; Lamelas, M.T.; Montealegre, A.L.; García-Martín, A.; De la Riva, J. Estimation of Total Biomass in Aleppo Pine Forest Stands Applying Parametric and Nonparametric Methods to Low-Density Airborne Laser Scanning Data. Forests 2018, 9, 158. [Google Scholar] [CrossRef]
- Beaudoin, A.; Bernier, P.Y.; Guindon, L.; Villemaire, P.; Guo, X.J.; Stinson, G.; Magnussen, S.; Hall, R.J. Mapping attributes of Canada’s forests at moderate resolution through kNN and MODIS imagery. Can. J. For. Res. 2014, 44, 521–532. [Google Scholar] [CrossRef]
- Nguyen, T.H.; Jones, S.; Soto-Berelov, M.; Haywood, A.; Hislop, S. A Comparison of Imputation Approaches for Estimating Forest Biomass Using Landsat Time-Series and Inventory Data. Remote Sens. 2018, 10, 1825. [Google Scholar] [CrossRef]
- Hancock, S. Measurement of fine-spatial-resolution 3D vegetation structure with airborne waveform lidar: Calibration and validation with voxelised terrestrial lidar. Remote Sens. Environ. 2016, 188, 37–50. [Google Scholar] [CrossRef]
- Ozdemir, I. Linear transformation to minimize the effects of variability in understory to estimate percent tree canopy cover using RapidEye data. GIsci. Remote Sens. 2014, 51, 288–300. [Google Scholar] [CrossRef]
- Li, A.; Dhakal, S.; Glenn, N.F.; Spaete, L.P.; Shinneman, D.J.; Pilliod, D.S.; Arkle, R.S.; McIlroy, S.K. Lidar aboveground vegetation biomass estimates in shrublands: Prediction, uncertainties and application to coarser scales. Remote Sens. 2017, 9, 903. [Google Scholar] [CrossRef]
- Glenn, N.F.; Neuenschwander, A.; Vierling, A.A.; Spaete, L.P.; Li, A.; Shinneman, D.; Pilliod, D.S.; Arkle, R.; McIlroy, S. Landsat 8 and ICESat-2: Performance and potential synergies for quantifying dryland ecosystem vegetation cover and biomass. Remote Sens. Environ. 2016, 185, 233–242. [Google Scholar] [CrossRef]
- He, S.H.; Ventura, J.S.; Mladenoff, J.D. Effects of spatial aggregation approaches on classified satellite imagery. Int. J. Geogr. Inf. Syst. 2002, 16, 93–109. [Google Scholar] [CrossRef]
- Doblas-Miranda, E.; Martínez-Vilalta, J.; Lloret, F.; Álvarez, A.; Ávila, A.; Bonet, F.J.; Brotons, L.; Castro, J.; Curiel Yuste, J.; Díaz, M.; et al. Reassessing global change research priorities in Mediterranean terrestrial ecosystems: How far have we come and where do we go from here? Glob. Ecol. Biogeogr. 2014, 24, 25–43. [Google Scholar] [CrossRef]
- Duane, A.; Aquilué, N.; Gil-Tena, A.; Brotons, L. Integrating fire spread patterns in fire modelling at landscape scale. Environ. Model. Softw. 2016, 86, 219–231. [Google Scholar] [CrossRef]
- Mura, M.; Bottalico, F.; Giannetti, F.; Bertani, R.; Giannini, R.; Mancini, M.; Orlandini, S.; Travaglini, D.; Chirici, G. Exploiting the capabilities of the Sentinel-2 multi spectral instrument for predicting growing stock volume in forest ecosystems. Int. J. Appl. Earth Obs. Geoinf. 2018, 66, 126–134. [Google Scholar] [CrossRef]
- Huete, A.; Didan, K.; Miura, T.; Rodriguez, E.P.; Gao, X.; Ferreira, L.G. Overview of the radiometric and biophysical performance of the MODIS vegetation indexes. Remote Sens. Environ. 2002, 83, 195–213. [Google Scholar] [CrossRef]
| Group | Variable | Min | Max | Mean | SD |
|---|---|---|---|---|---|
| Response | Aboveground forest biomass (t·ha−1) | 6.88 | 143.51 | 57.20 | 28.03 |
| *ALS metrics | Hmean | 2.75 | 13.34 | 6.38 | 1.98 |
| Hsd | 0.55 | 4.86 | 1.99 | 0.73 | |
| Hvar | 0.30 | 23.61 | 4.49 | 3.55 | |
| Hcv | 0.16 | 0.50 | 0.31 | 0.06 | |
| Hiq | 0.76 | 8.13 | 2.90 | 1.15 | |
| Hkur | 1.43 | 4.77 | 2.51 | 0.56 | |
| Hp01 | 2.02 | 5.00 | 2.39 | 0.52 | |
| Hp05 | 2.04 | 6.97 | 3.07 | 1.00 | |
| Hp10 | 2.06 | 8.06 | 3.66 | 1.28 | |
| Hp25 | 2.27 | 10.94 | 4.93 | 1.73 | |
| Hp50 | 2.48 | 14.00 | 6.44 | 2.17 | |
| Hp75 | 3.10 | 17.64 | 7.83 | 2.45 | |
| Hp90 | 3.51 | 19.24 | 8.94 | 2.67 | |
| Hp95 | 3.77 | 19.59 | 9.50 | 2.78 | |
| Hp99 | 4.24 | 20.15 | 10.25 | 2.94 | |
| CRR | 0.29 | 0.73 | 0.48 | 0.09 | |
| TCC | 1.88 | 93.86 | 44.55 | 19.87 | |
| Hmean_LS | 0.55 | 1.77 | 1.07 | 0.21 | |
| TCC_LS | 0.00 | 95.49 | 50.40 | 20.64 |
| Vegetation Index | Equation 1 | |
|---|---|---|
| Normalized difference vegetation index (NDVI) | [26] | |
| Enhanced Vegetation Index (EVI) | [32] | |
| Normalized Difference Index 7 (NDI7) | [65] | |
| Modified Simple Ratio (MSR) | [37] | |
| Difference vegetation index (DVI) | [36] | |
| Renormalized difference vegetation index (RDVI) | [35] | |
| Soil adjusted vegetation index (SAVI) | [33] | |
| Modified soil adjusted vegetation index (MSAVI) | [66] |
| Covariate | Description (Time Period) | Product | |
|---|---|---|---|
| Dynamic 1 | NDVI MSR DVI RDVI SAVI MSAVI | 8-day composite time series (2015–2017) | MOD09Q1 |
| 8-day composite mean annual profile (2015–2017) | |||
| Maximum-value composite (2015–2017) | |||
| NDVI EVI NDI7 | 16-day composite time series (2015–2017) | MOD13Q1 | |
| 16-day composite mean annual profile (2015–2017) | |||
| NDVI mean | Mean value (2001–2016) | MOD13Q1 | |
| NDVI sd | Standard deviation (2001–2016) | ||
| Static | Topographic | Digital elevation model (DEM), analytical hillshading, slope, aspect, cross-section curvature, longitudinal curvature, convergence index, closed depressions, catchment area, topographic wetness index, Ls factor, channel network base level, vertical distance to channel network, valley depth, relative slope position, multiresolution valley bottom flatness index, multiresolution ridge top flatness index. | Terrain Analyst function in SAGA GIS software |
| Description | Selected | Covariates 1 |
|---|---|---|
| 8-day composite time series (2015–2017) | 14/04/2016; 5&29/09/2016 | NDVI, |
| 15/10/2016 | MSR | |
| 8-day composite mean annual profile (2015–2017) | 9/05; 21/08 | NDVI, |
| 16-day composite mean annual profile (2015–2017) | 9/05; 13/08 | EVI, NDW7 |
| Mean value and standard deviation (2001–2016) | 2 indices | NDVImean, NDVIsd |
| Maximum value (2015–2017) | 6 indices | NDVI, MSR, DVI, RDVI, SAVI, MSAVI |
| Topographic variables | 17 parameters | DEM, and 16 derived parameters included in Terrain Analyst functions (SAGA GIS software) |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Durante, P.; Martín-Alcón, S.; Gil-Tena, A.; Algeet, N.; Tomé, J.L.; Recuero, L.; Palacios-Orueta, A.; Oyonarte, C. Improving Aboveground Forest Biomass Maps: From High-Resolution to National Scale. Remote Sens. 2019, 11, 795. https://doi.org/10.3390/rs11070795
Durante P, Martín-Alcón S, Gil-Tena A, Algeet N, Tomé JL, Recuero L, Palacios-Orueta A, Oyonarte C. Improving Aboveground Forest Biomass Maps: From High-Resolution to National Scale. Remote Sensing. 2019; 11(7):795. https://doi.org/10.3390/rs11070795
Chicago/Turabian StyleDurante, Pilar, Santiago Martín-Alcón, Assu Gil-Tena, Nur Algeet, José Luis Tomé, Laura Recuero, Alicia Palacios-Orueta, and Cecilio Oyonarte. 2019. "Improving Aboveground Forest Biomass Maps: From High-Resolution to National Scale" Remote Sensing 11, no. 7: 795. https://doi.org/10.3390/rs11070795
APA StyleDurante, P., Martín-Alcón, S., Gil-Tena, A., Algeet, N., Tomé, J. L., Recuero, L., Palacios-Orueta, A., & Oyonarte, C. (2019). Improving Aboveground Forest Biomass Maps: From High-Resolution to National Scale. Remote Sensing, 11(7), 795. https://doi.org/10.3390/rs11070795