Altimeter Observation-Based Eddy Nowcasting Using an Improved Conv-LSTM Network
Abstract
:1. Introduction
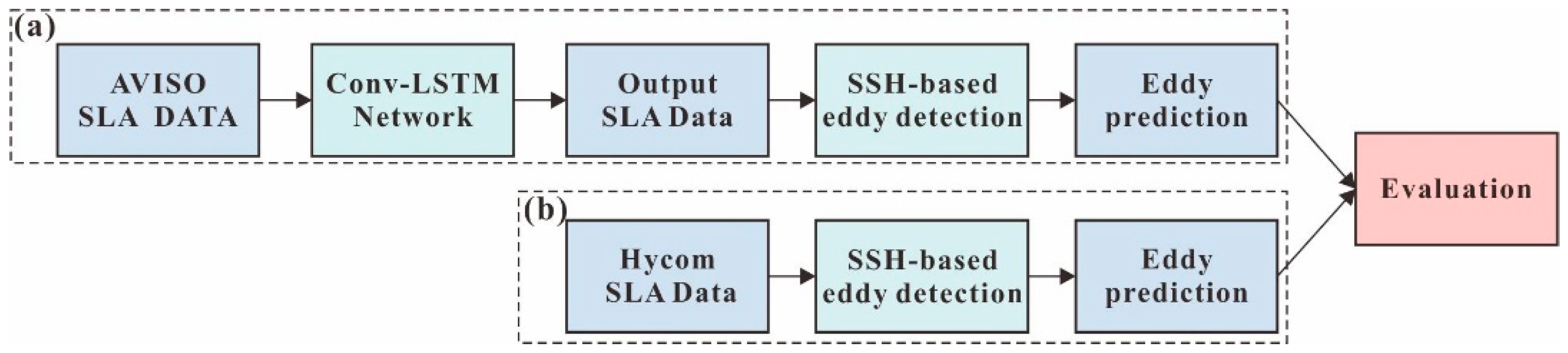
2. Materials and Methods
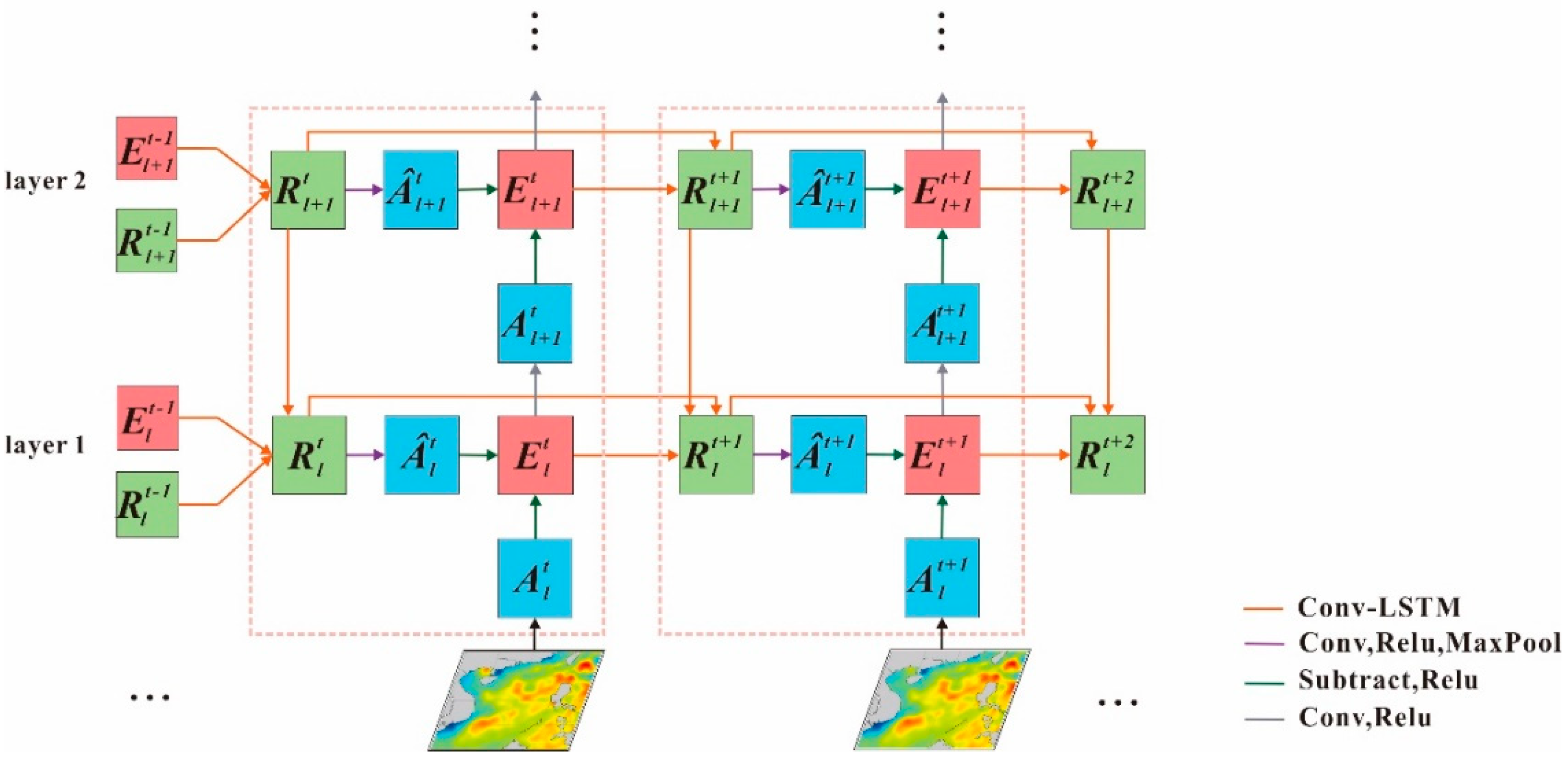
2.1. An Improved Conv-LSTM Network
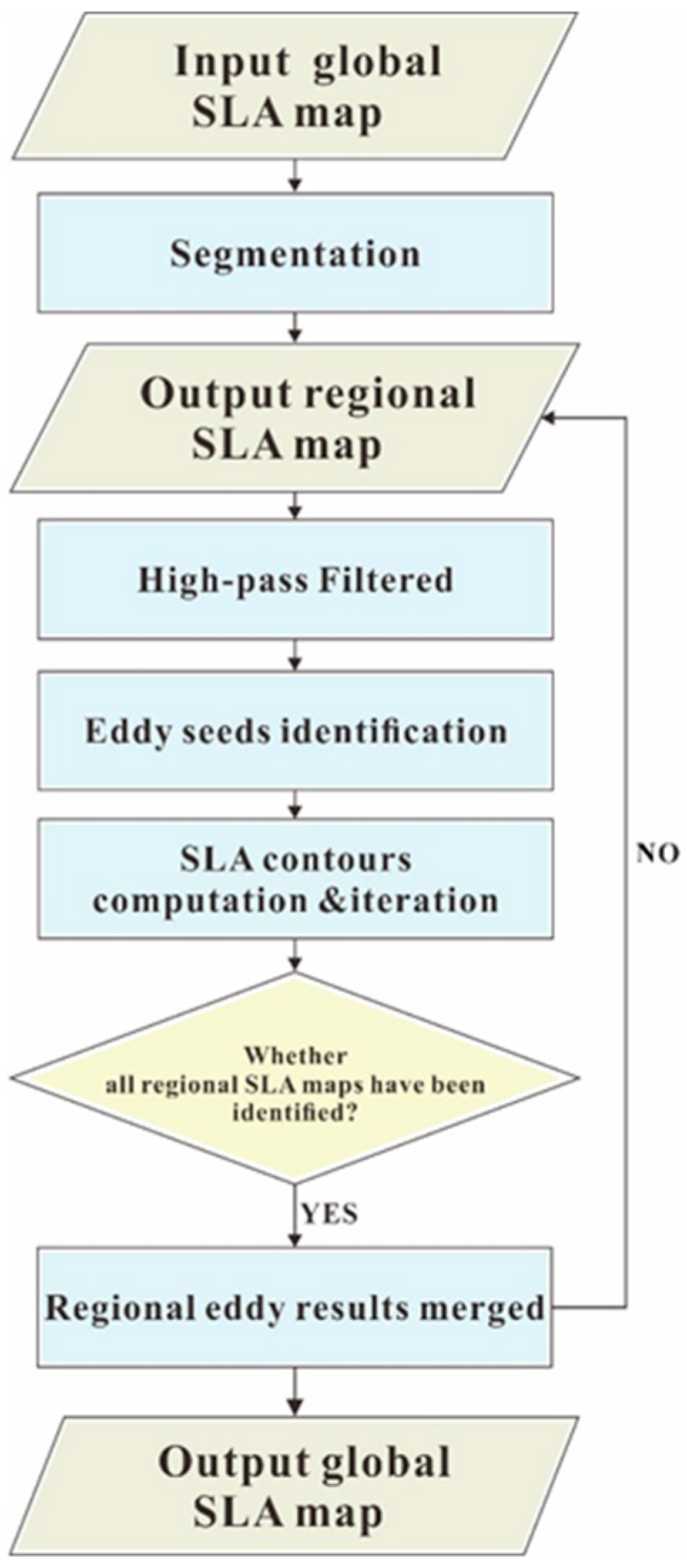
2.2. Eddy Detection
3. Experiment and Results
3.1. Model Training and Testing
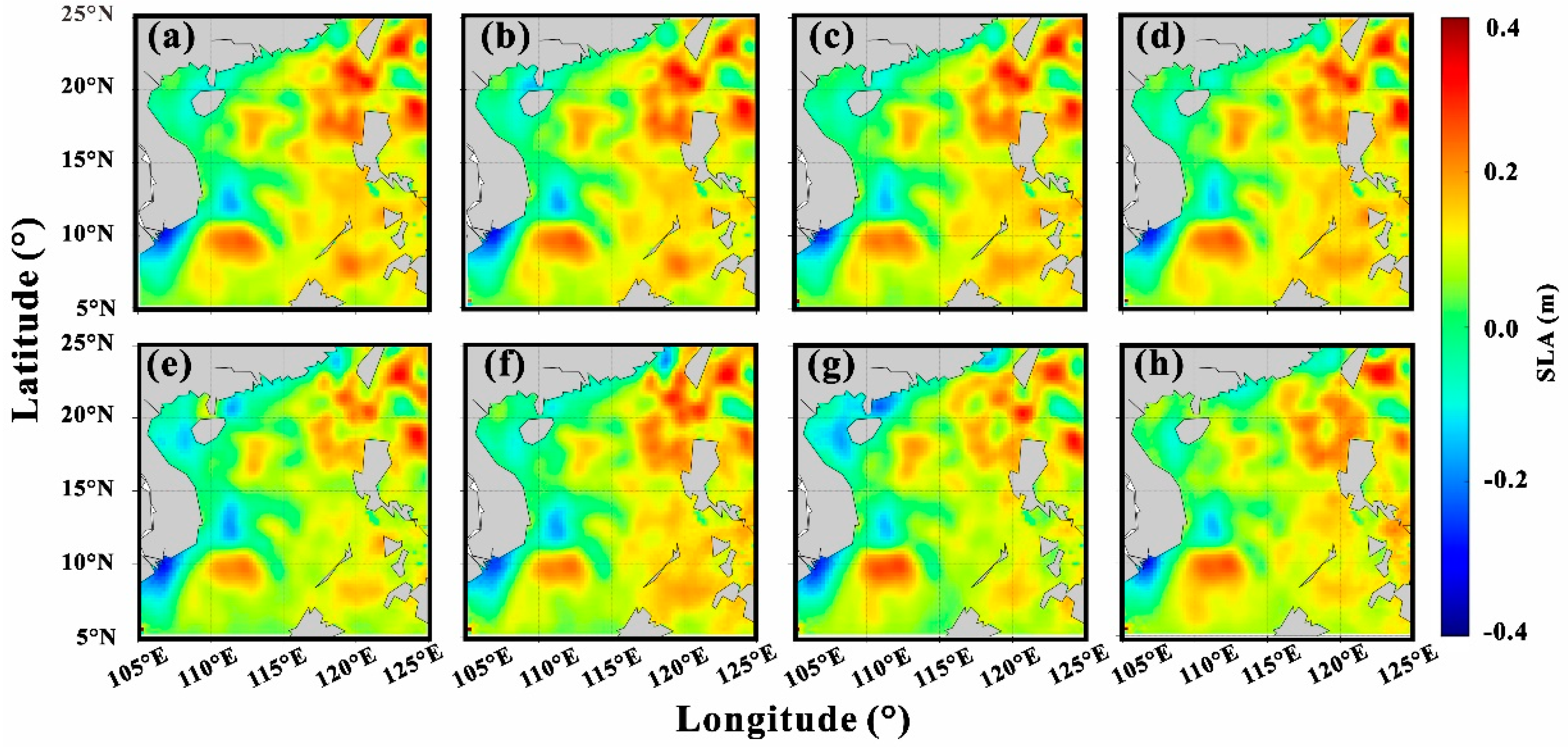
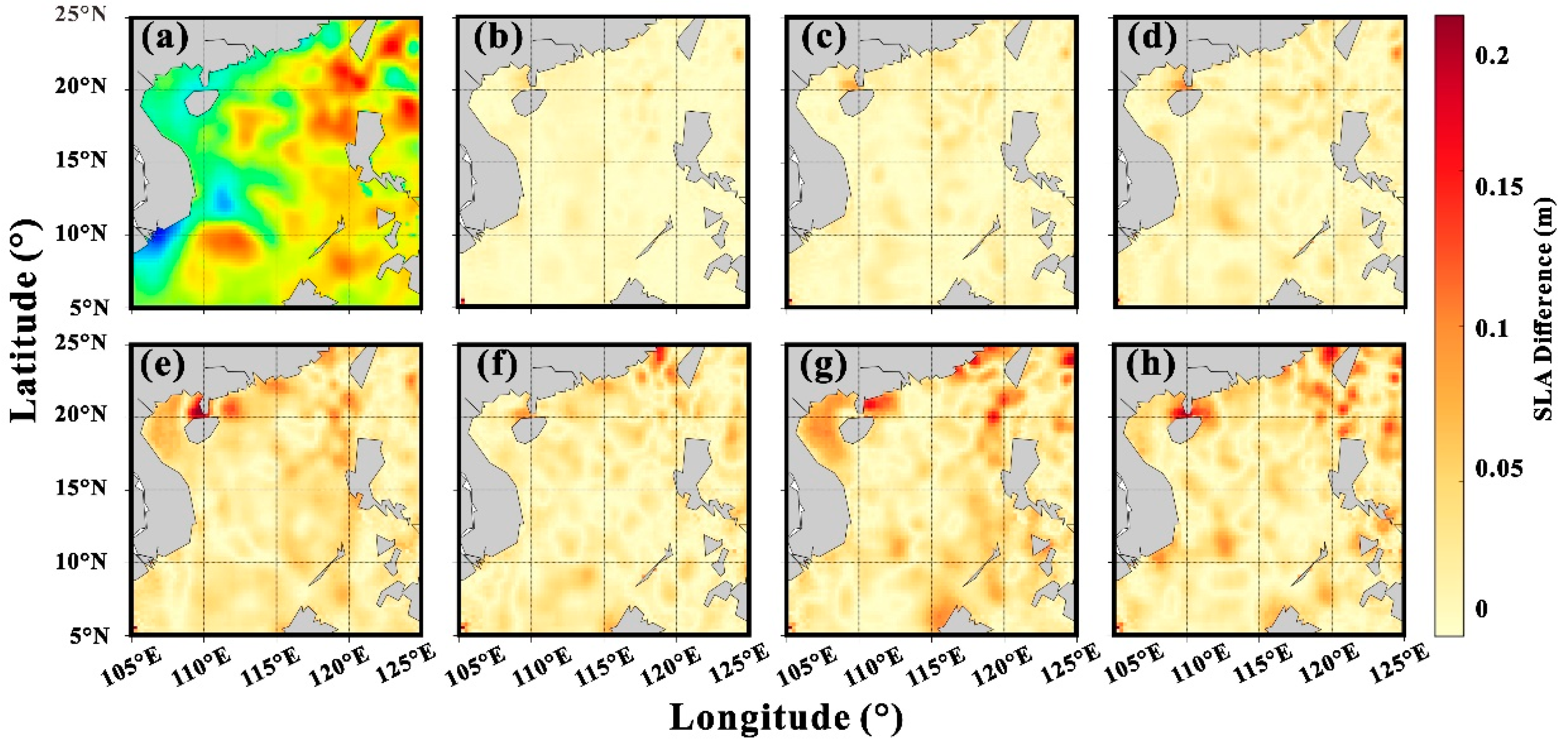
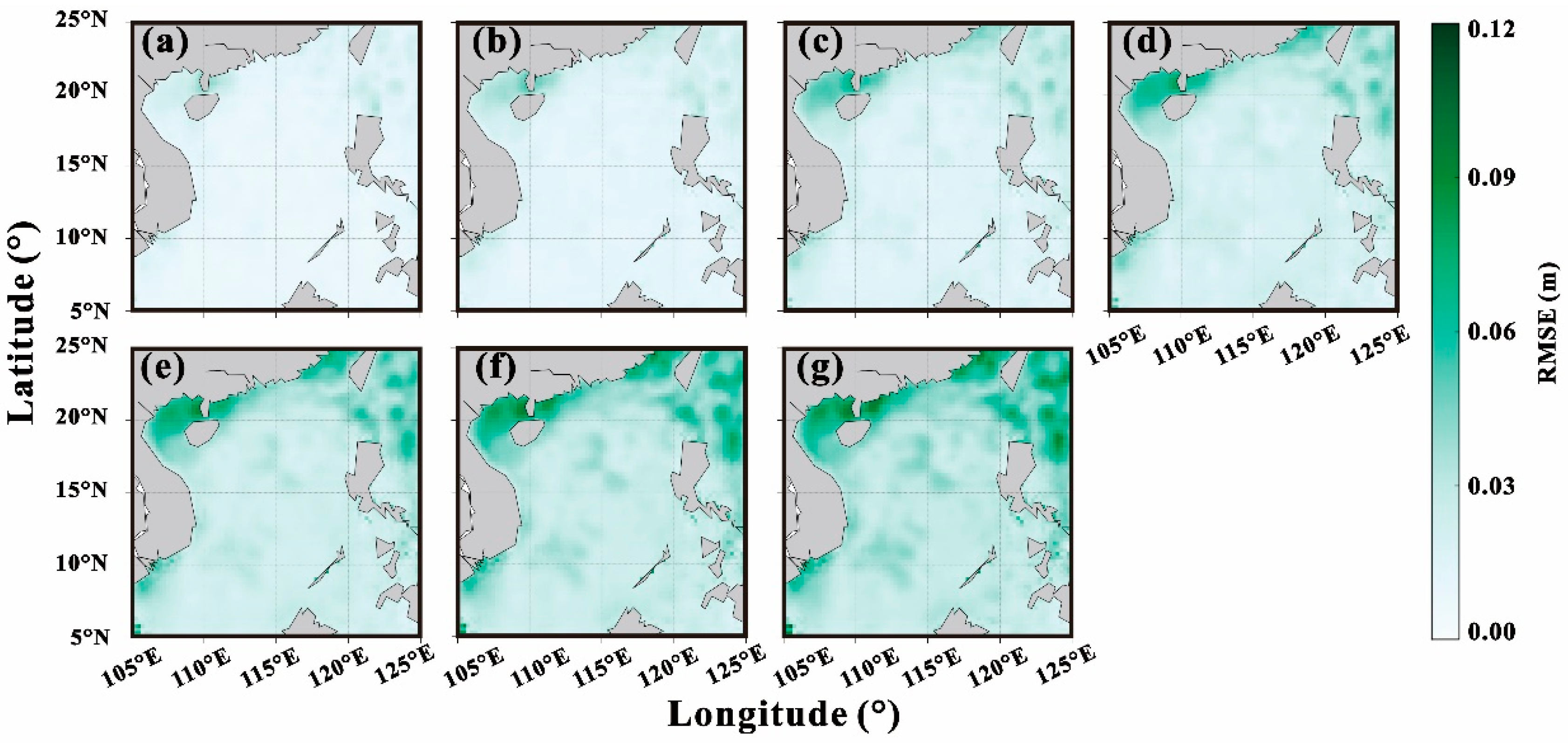
3.2. SLA Prediction Evaluation
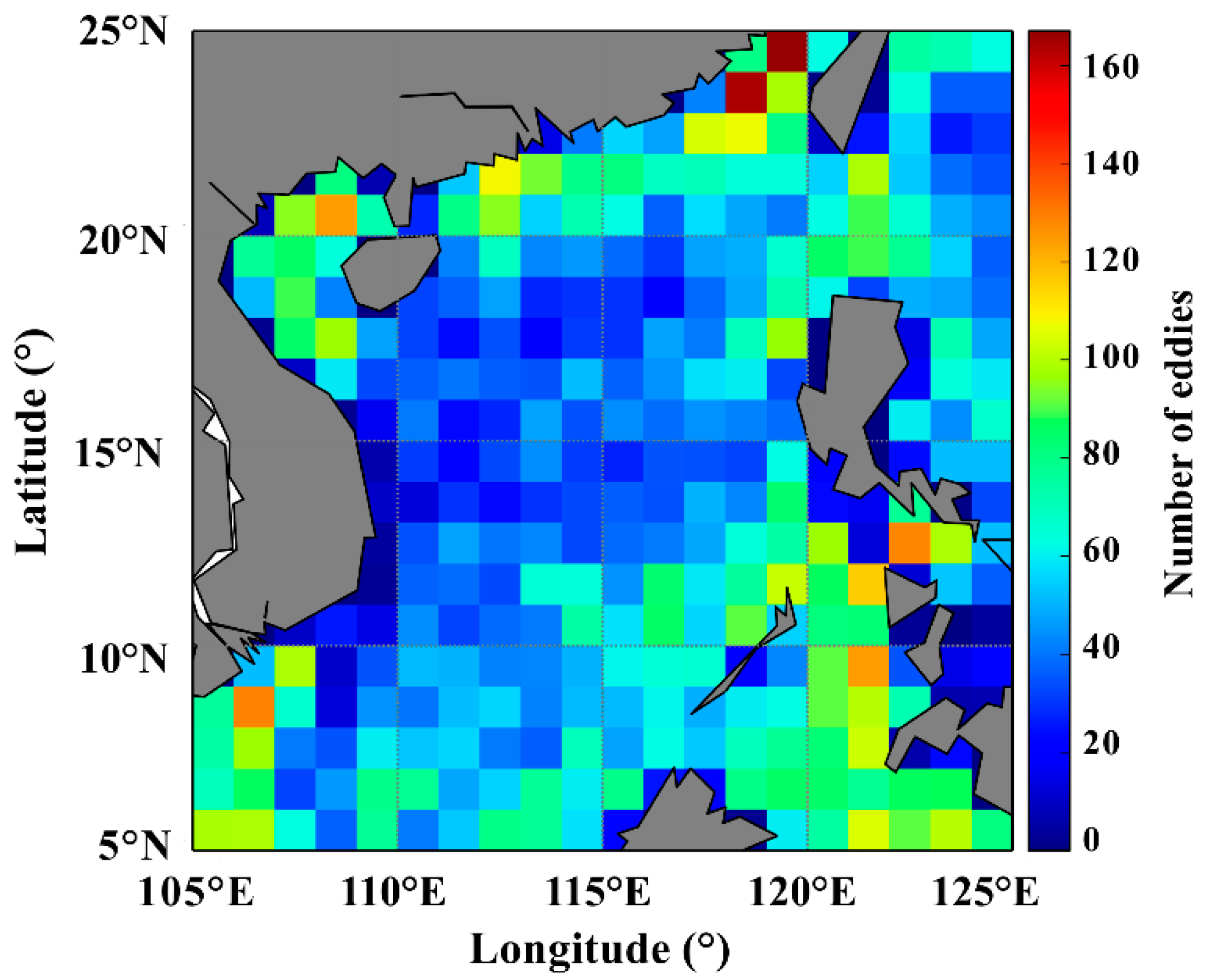
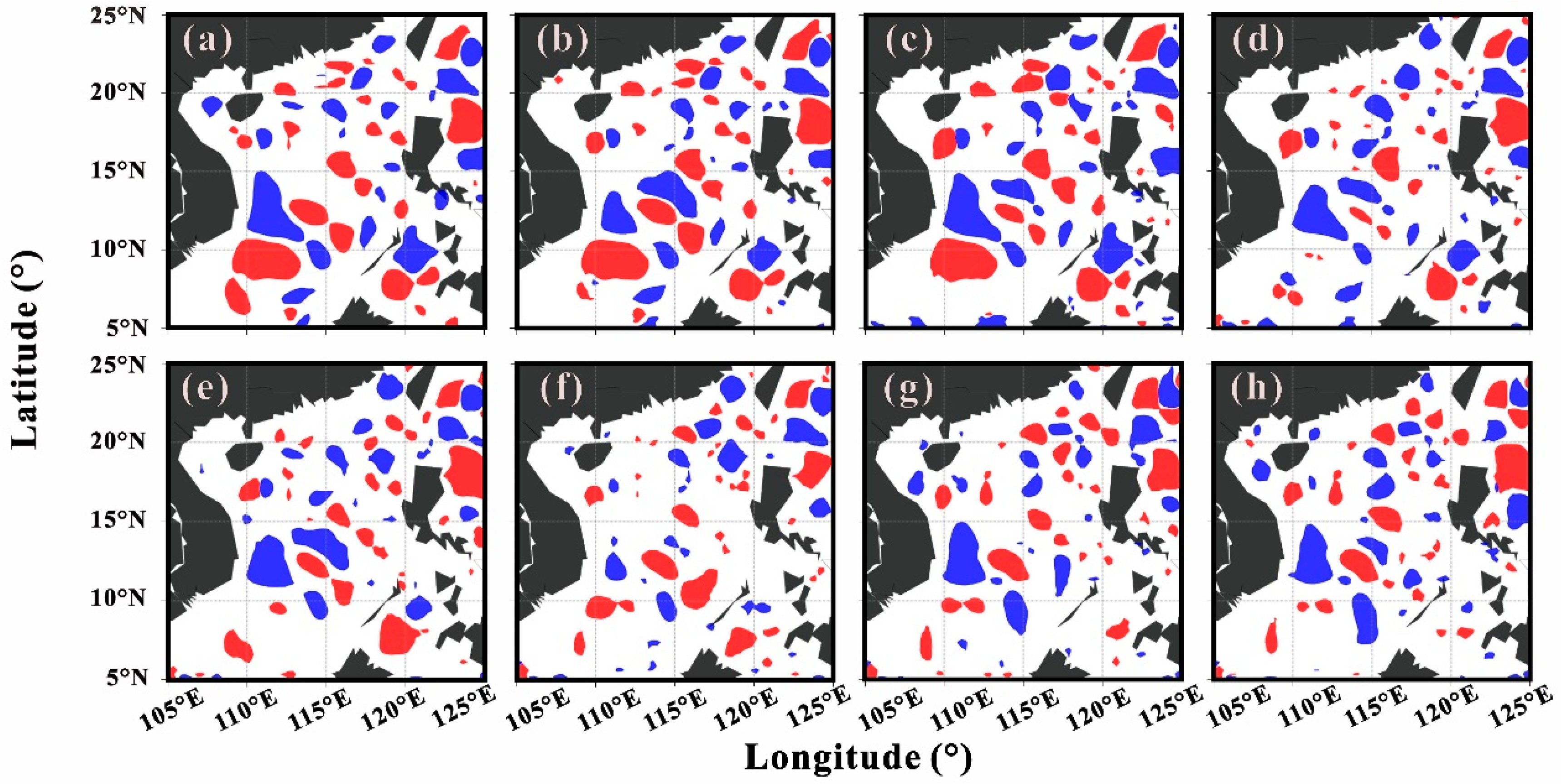
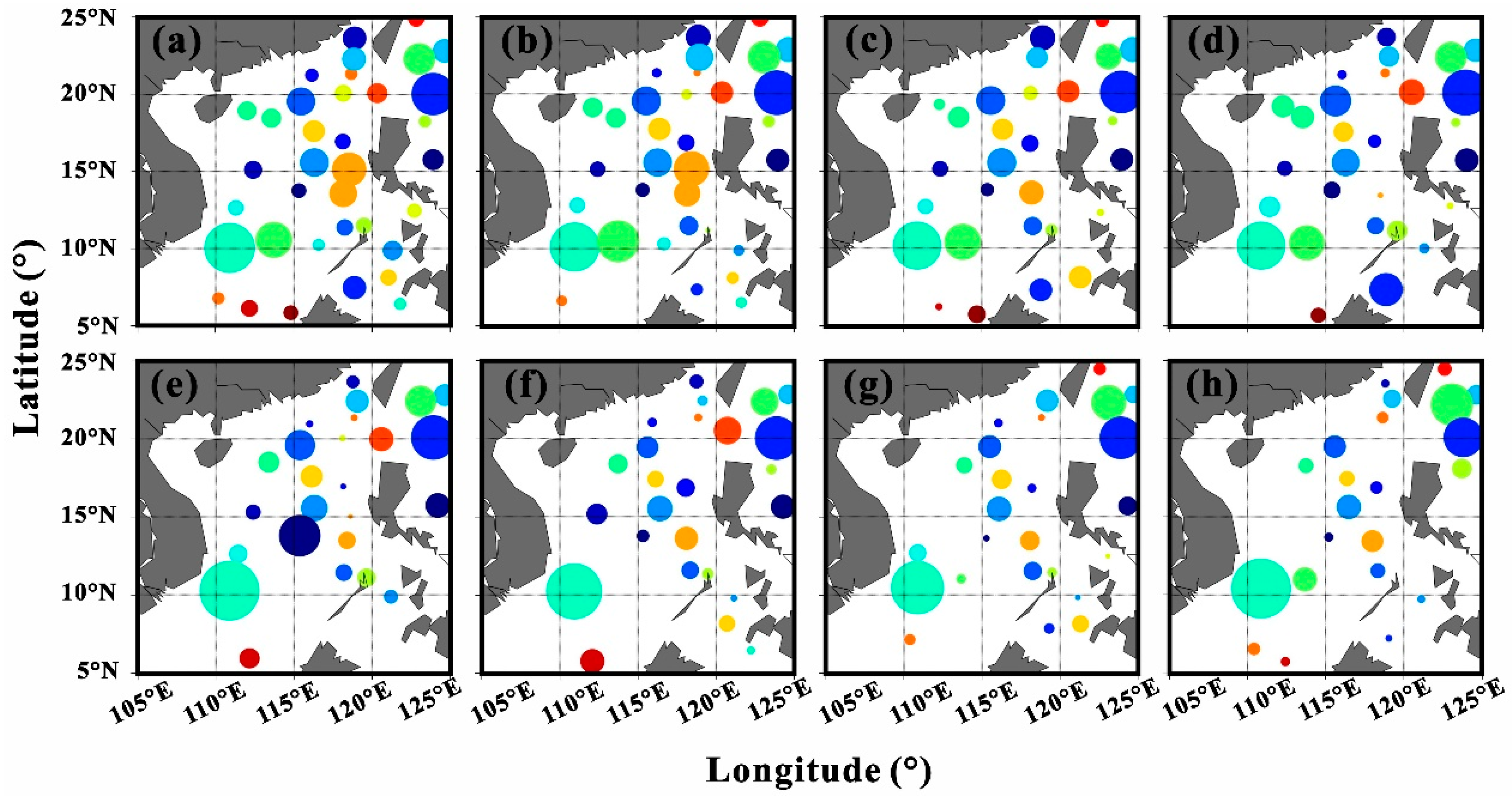
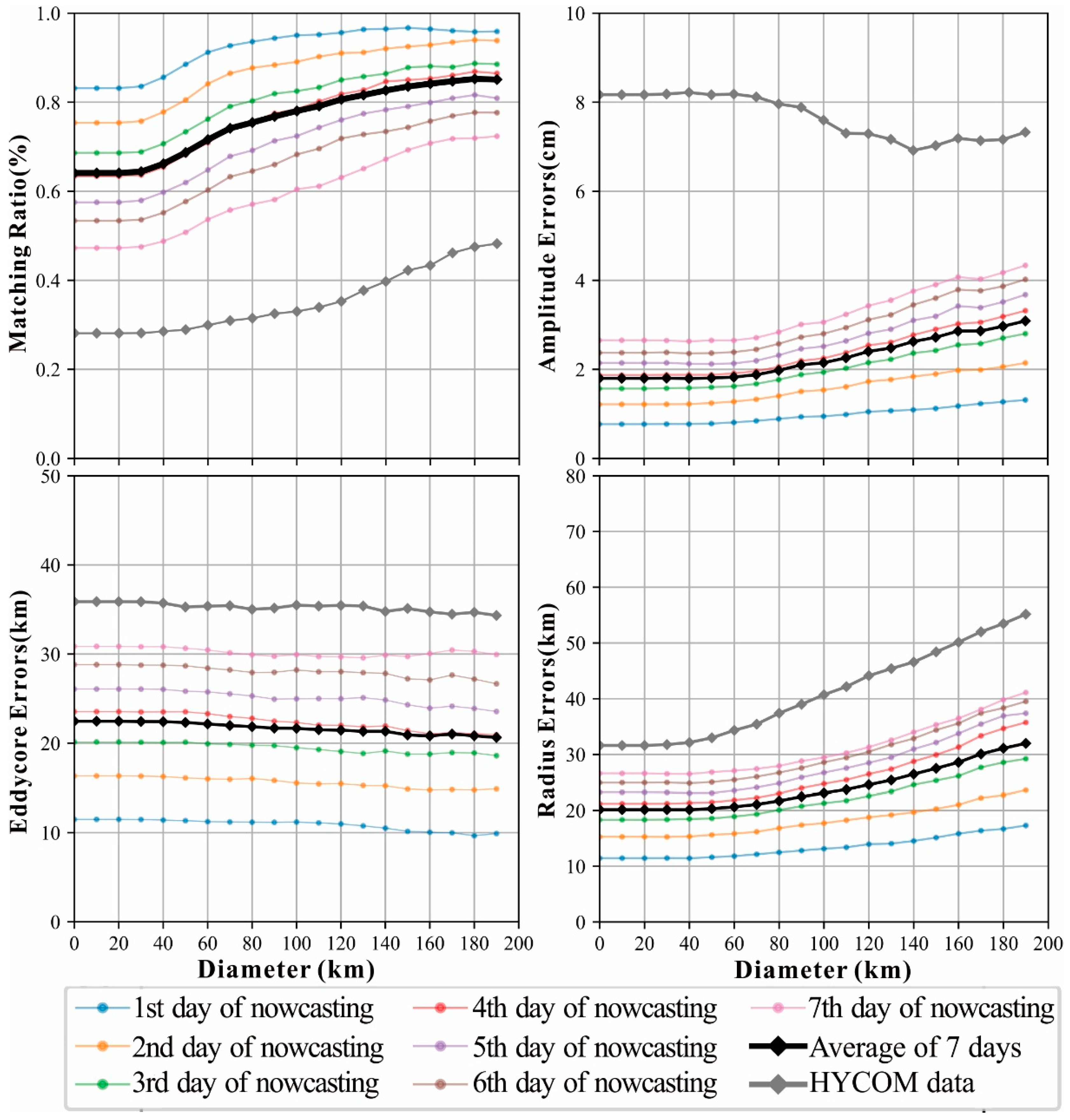
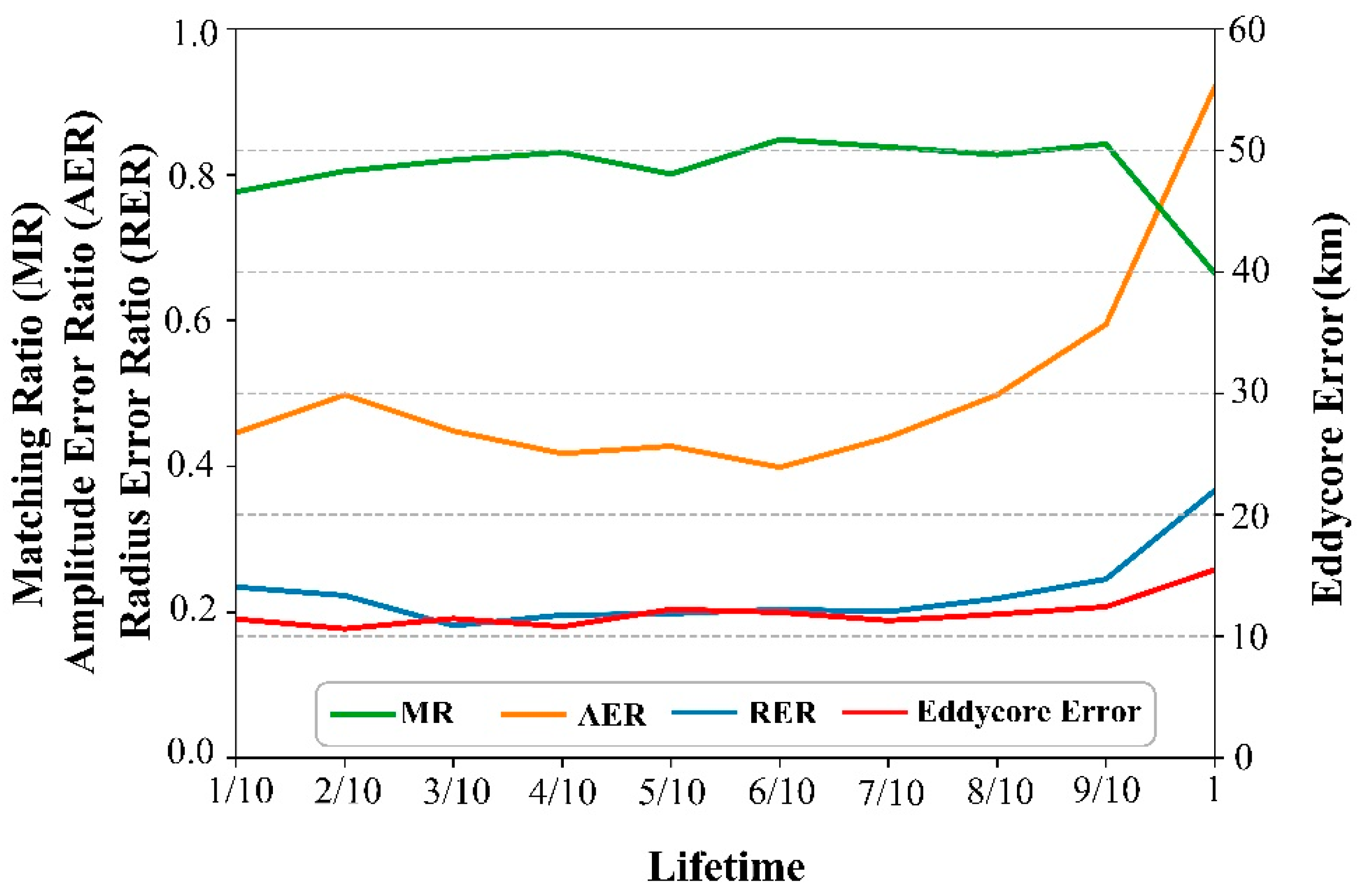
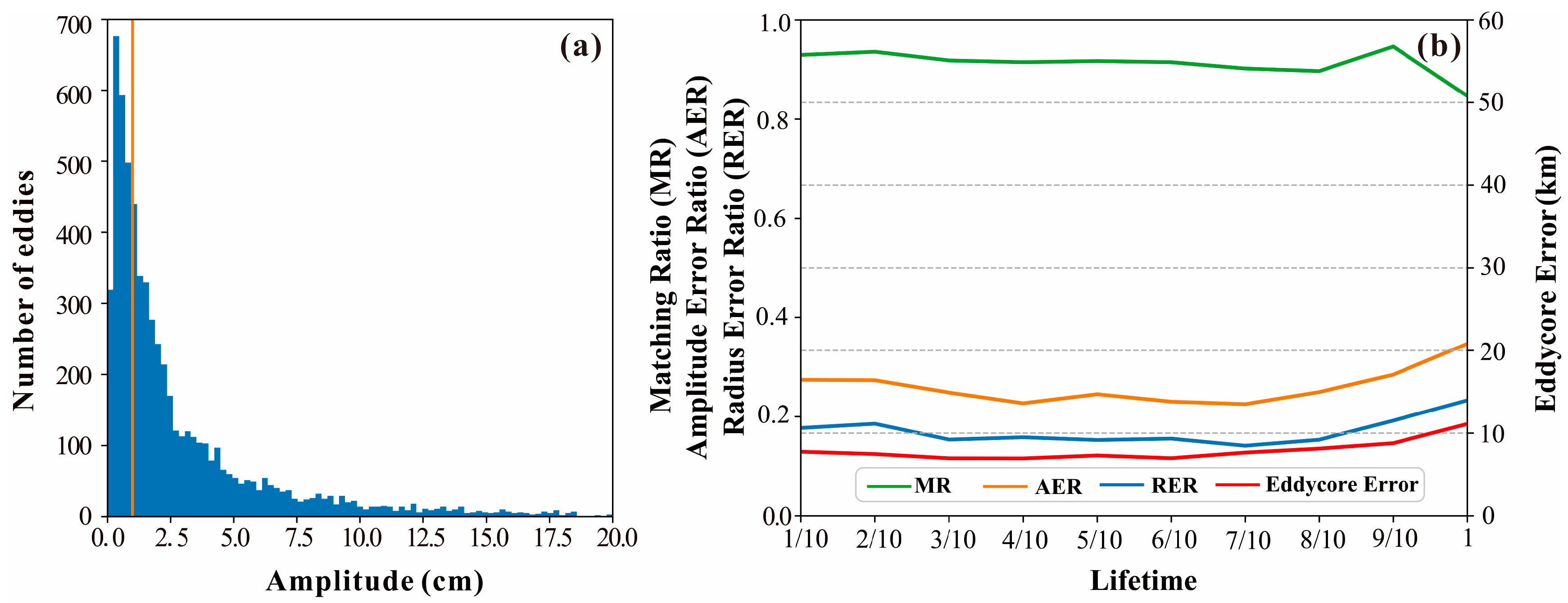
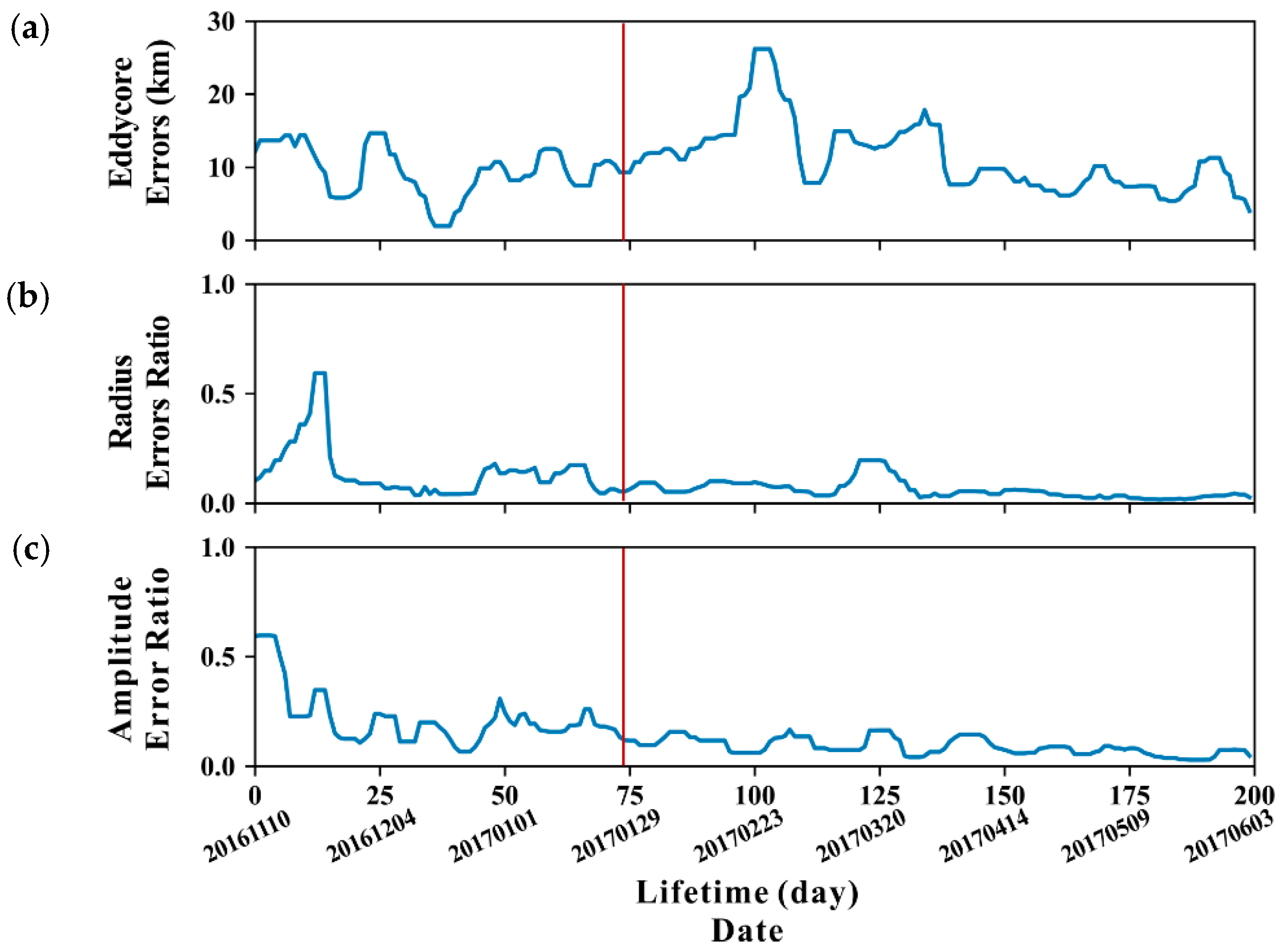
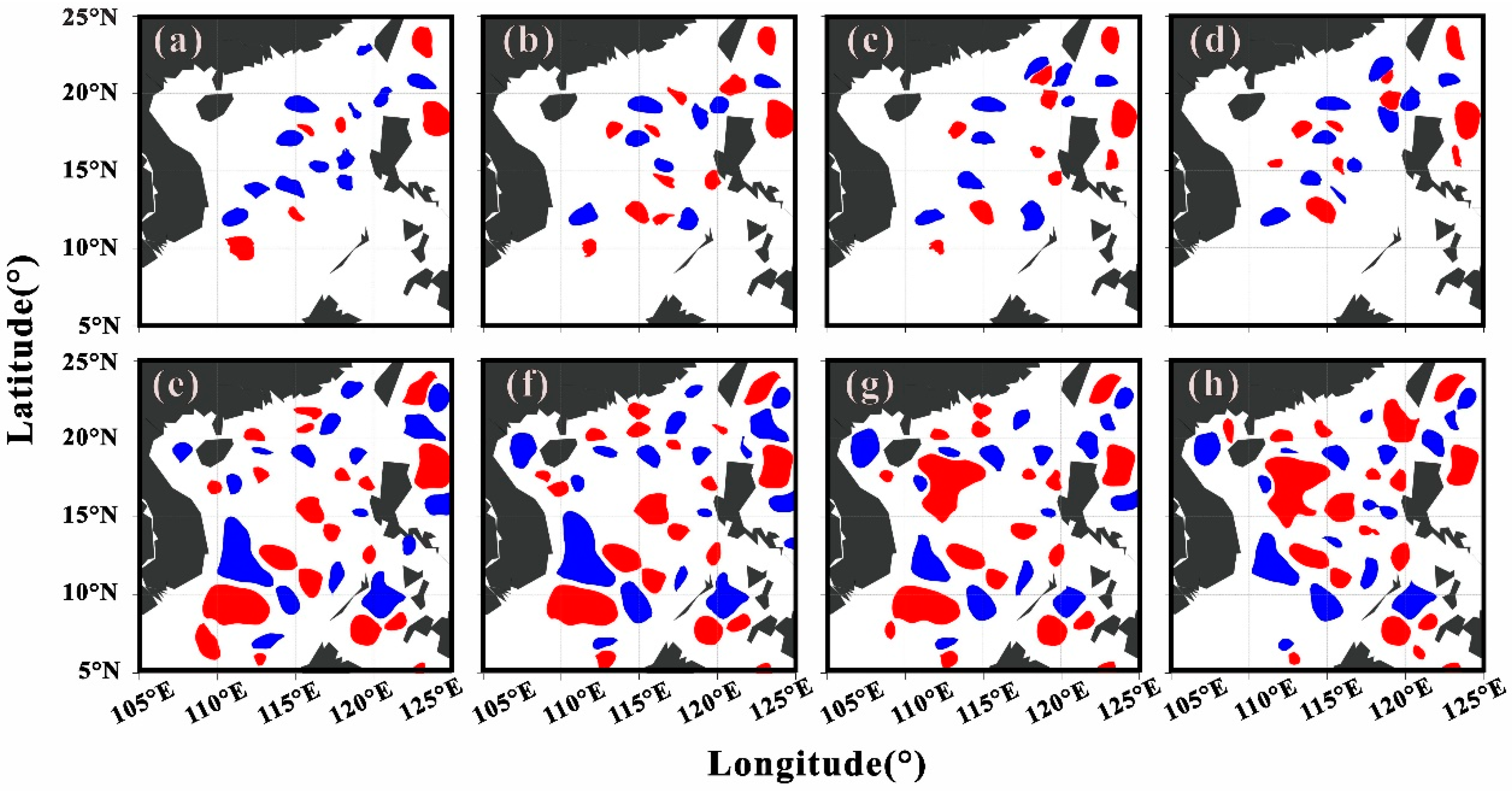
3.3. Eddy Nowcasting Evaluation
4. Discussion
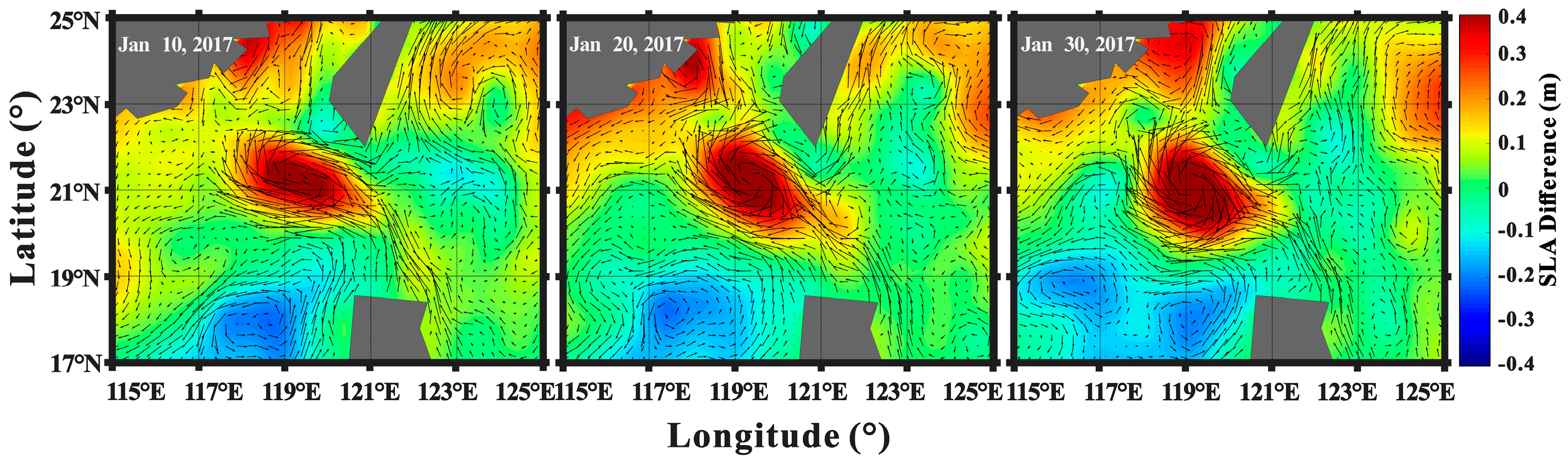
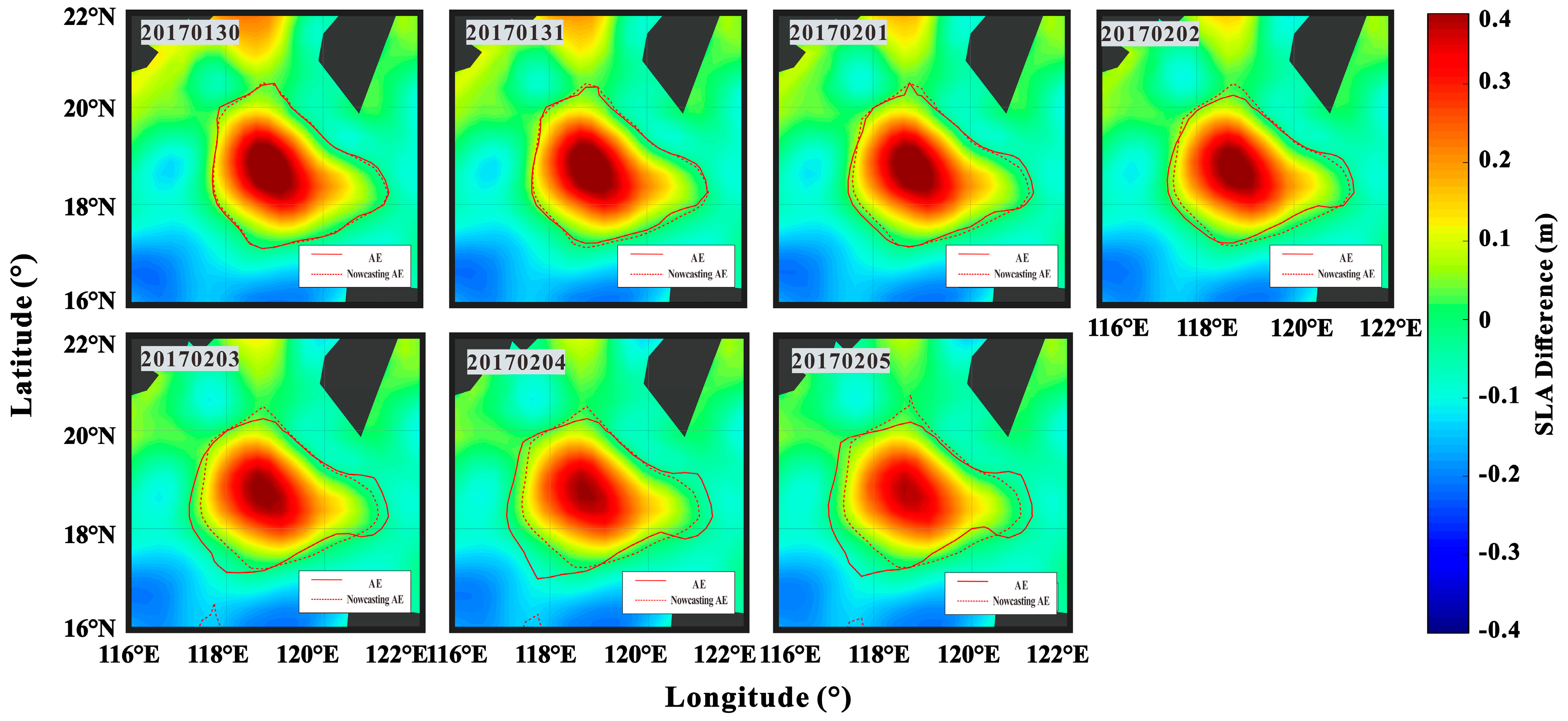
4.1. Verification with an Anticyclonic Eddy Shedding from Kuroshio
4.2. Comparison with HYCOM Data
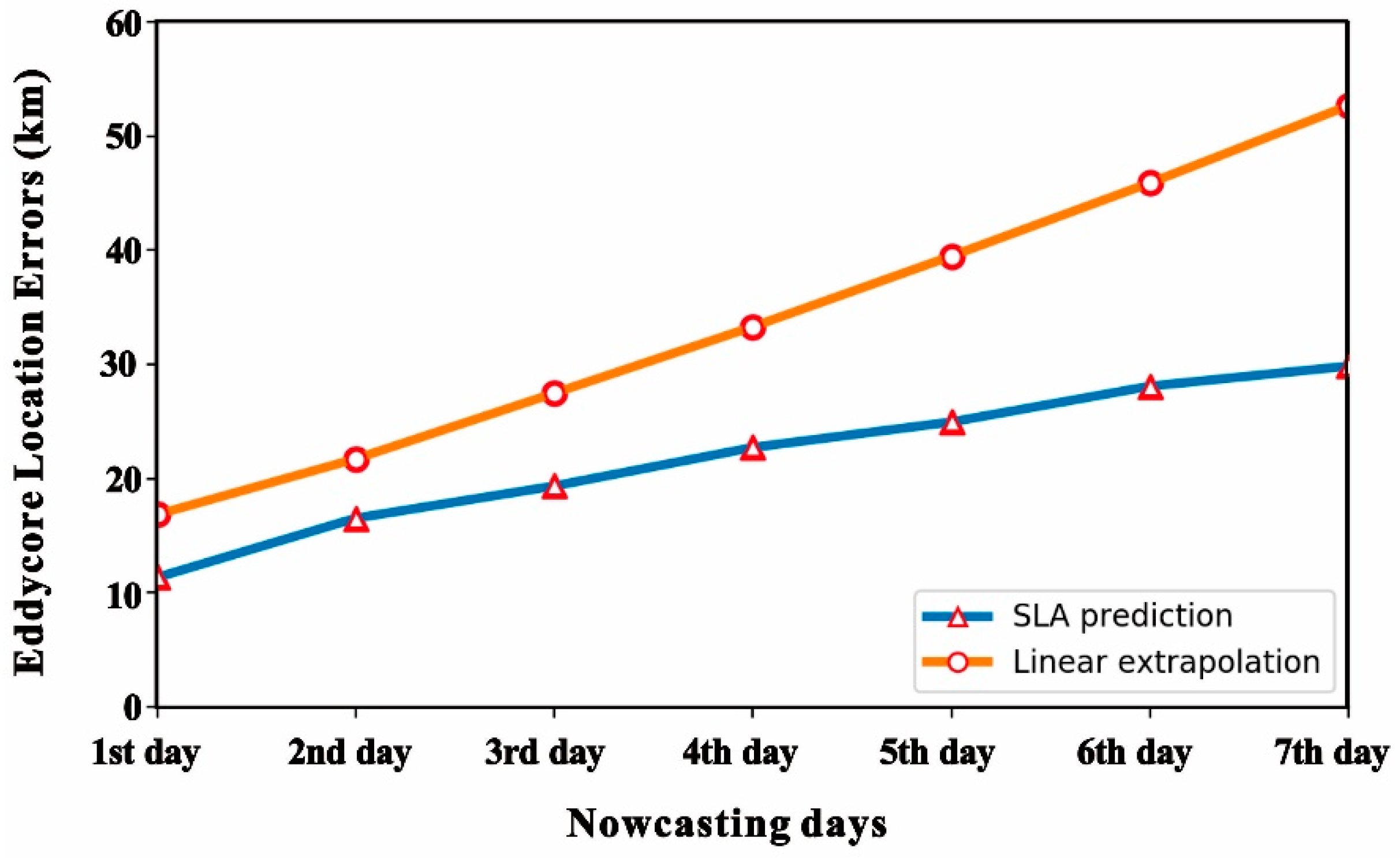
4.3. Comparison with Trajectory Extrapolation
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Zhang, Y.; Liu, Z.; Zhao, Y.; Wang, W.; Li, J.; Xu, J. Mesoscale eddies transport deep-sea sediments. Sci. Rep. 2014, 4, 5937. [Google Scholar] [CrossRef] [PubMed]
- Cotroneo, Y.; Aulicino, G.; Ruiz, S.; Pascual, A.; Budillon, G.; Fusco, G.; Tintore, J. Glider and satellite high resolution monitoring of a mesoscale eddy in the Algerian basin: Effects on the mixed layer depth and biochemistry. J. Mar. Syst. 2015, 162, 72–88. [Google Scholar] [CrossRef]
- Font, J.; Isern-Fontanet, J.; Salas, J.J. Tracking a big anticyclonic eddy in theWestern Mediterranean Sea. Sci. Mar. 2004, 68, 331–342. [Google Scholar] [CrossRef]
- Olita, A.; Ribotti, A.; Sorgente, R.; Fazioli, L.; Perilli, A. SLA-chlorophyll-a variability and covariability in the Algero-Proven çal Basin (1997–2007) through combined use of EOF and wavelet analysis of satellite data. Ocean Dyn. 2011, 61, 89–102. [Google Scholar] [CrossRef]
- Pujol, M.I.; Larnicol, G. Mediterranean Sea eddy kinetic energy variability from 11 years of altimetric data. J. Mar. Syst. 2005, 58, 121–142. [Google Scholar] [CrossRef]
- Aulicino, G.; Cotroneo, Y.; Lacava, T.; Sileo, G.; Fusco, G.; Carlon, R.; Satriano, V.; Pergola, N.; Tramutoli, V.; Budillon, G. Results of the first wave glider experiment inthe southern Tyrrhenian Sea. Adv. Oceanogr. Limnol. 2016, 7, 16–35. [Google Scholar] [CrossRef]
- Aulicino, G.; Cotroneo, Y.; Ruiz, S.; Sánchez Román, A.; Pascual, A.; Fusco, G.; Tintor e, J.; Budillon, G. Monitoring the Algerian Basin through glider observations, satellitealtimetry and numerical simulations along a SARAL/AltiKa track. J. Mar. Syst. 2018, 179, 55–71. [Google Scholar] [CrossRef]
- Pessini, F.; Olita, A.; Cotroneo, Y.; Perilli, A. Mesoscale eddies in the Algerian Basin: Do they differ as a function of their formation site? Ocean Sci. 2018, 14, 669–688. [Google Scholar] [CrossRef]
- Cotroneo, Y.; Aulicino, G.; Ruiz, S.; Sánchez Román, A.; Torner Tomàs, M.; Pascual, A.; Fusco, G.; Heslop, E.; Tintoré, J.; Budillon, G. Glider data collected during the Algerian Basin Circulation Unmanned Survey. Earth Syst. Sci. Data 2019, 11, 147–161. [Google Scholar] [CrossRef]
- Ansorge, I.; Jackson, J.; Reid, K.; Durgadoo, J.; Swart, S.; Eberen, S. Evidence of a southward eddy corridor in the south-west Indian ocean. Deep-Sea Res. 2014, 119, 69–76. [Google Scholar] [CrossRef]
- Cotroneo, Y.; Budillon, G.; Fusco, G.; Spezie, G. Cold core eddies and fronts of the Antarctic Circumpolar Current south of New Zealand from in situ and satellite data. J. Geophys. Res. Ocean. 2013, 118, 2653–2666. [Google Scholar] [CrossRef]
- Holland, W. The role of mesoscale eddies in the general circulation of the ocean—Numerical experiments using a wind-driven quasigeo-strophic model. J. Phys. Oceanogr. 1978, 8, 363–392. [Google Scholar] [CrossRef]
- Holland, W.R.; Lin, L.B. On the origin of mesoscale eddies and their contribution to the general circulation of the ocean. I. A preliminary numerical experiment. J. Phys. Oceanogr. 1975, 5, 642–657. [Google Scholar] [CrossRef]
- Keffer, T.; Holloway, G. Estimating Southern Ocean eddy flux of heat and salt from satellite altimetry. Nature 1988, 332, 624–626. [Google Scholar] [CrossRef]
- Morrow, R.; Donguy, J.R.; Chaigneau, A.; Rintoul, S.R. Cold core anomalies at the subantarctic front, south of Tasmania. Deep Sea Res. 2004, 51, 1417–1440. [Google Scholar] [CrossRef]
- Robinson, A.R.; Carton, J.A.; Mooers, C.N.K.; Walstad, L.J.; Carter, E.F.; Rienecker, M.M.; Smith, J.A.; Leslie, W.G. A real-time dynamical forecast of ocean synoptic/mesoscale eddies. Nature 1984, 309, 781. [Google Scholar] [CrossRef]
- Masina, S.; Pinardi, N. Mesoscale data assimilation studies in the Middle Adriatic Sea. Cont. Shelf Res. 1994, 14, 1293–1310. [Google Scholar] [CrossRef]
- Shriver, J.F.; Hurlburt, H.E.; Smedstad, O.M.; Wallcraft, A.J.; Rhodes, R.C. 1/32 real-time global ocean prediction and value-added over 1/16 resolution. J. Mar. Syst. 2007, 65, 3–26. [Google Scholar] [CrossRef]
- Smedstad, O.M.; Hurlburt, H.E.; Metzger, E.J.; Rhodes, R.C.; Shriver, J.F.; Wallcraft, A.J.; Kara, A.B.; Murray, C.P. An operational real-time eddy-resolving 1/16° global ocean nowcast/forecast system. In Proceedings of the OCEANS’02 MTS/IEEE, Biloxi, MI, USA, 29–31 October 2002; Volume 2, pp. 769–774. [Google Scholar]
- Isern-Fontanet, J.; García-Ladona, E.; Font, J. Identification of marine eddies from altimetric maps. J. Atmos. Ocean. Technol. 2003, 20, 772–778. [Google Scholar] [CrossRef]
- Isern-Fontanet, J.; García-Ladona, E.; Font, J. Vortices of the Mediterranean Sea: An altimetric perspective. J. Phys. Oceanogr. 2006, 36, 87–103. [Google Scholar] [CrossRef]
- Chelton, D.B.; Schlax, M.G.; Samelson, R.M. Global observations of nonlinear mesoscale eddies. Prog. Oceanogr. 2011, 91, 167–216. [Google Scholar] [CrossRef]
- Lima, E.; Sun, X.; Dong, J.; Wang, H.; Yang, Y.; Liu, L. Learning and transferring convolutional neural network knowledge to ocean front recognition. IEEE Geosci. Remote Sens. Lett. 2017, 14, 354–358. [Google Scholar] [CrossRef]
- Yang, Y.; Dong, J.; Sun, X.; Lima, E.; Mu, Q.; Wang, X. A CFCC-LSTM model for sea surface temperature prediction. IEEE Geosci. Remote Sens. Lett. 2018, 15, 207–211. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Karpathy, A.; Li, F. Deep visual-semantic alignments for generating image descriptions. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 664–676. [Google Scholar] [CrossRef]
- Donahue, J.; Anne Hendricks, L.; Guadarrama, S.; Rohrbach, M.; Venugopalan, S.; Saenko, K.; Darrell, T. Long-term recurrent convolutional networks for visual recognition and description. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 677–691. [Google Scholar] [CrossRef]
- Xingjian, S.H.I.; Chen, Z.; Wang, H.; Yeung, D.Y.; Wong, W.K.; Woo, W.C. Convolutional LSTM Network: A machine learning approach for precipitation nowcasting. In Proceedings of the Advances in Neural Information Processing Systems, Montreal, QC, Canada, 7–12 December 2015; pp. 802–810. [Google Scholar]
- Liu, Y.; Chen, G.; Sun, M.; Liu, S.; Tian, F. A Parallel SLA-Based Algorithm for Global Mesoscale Eddy Identification. J. Atmos. Ocean. Technol. 2016, 33, 2743–2754. [Google Scholar] [CrossRef]
- Wang, G.; Su, J.; Chu, P.C. Mesoscale eddies in the South China Sea observed with altimeter data. Geophys. Res. Lett. 2003, 30. [Google Scholar] [CrossRef]
- Chen, G.; Hou, Y.; Chu, X.; Qi, P. Vertical structure and evolution of the Luzon Warm Eddy. Chin. J. Oceanol. Limnol. 2010, 28, 955–961. [Google Scholar] [CrossRef]
- Du, Y.; Wu, D.; Liang, F.; Yi, J.; Mo, Y.; He, Z.; Pei, T. Major migration corridors of mesoscale ocean eddies in the South China Sea from 1992 to 2012. J. Mar. Syst. 2016, 158, 173–181. [Google Scholar] [CrossRef]
- Chen, G.; Hou, Y.; Chu, X. Mesoscale eddies in the South China Sea: Mean properties, spatiotemporal variability, and impact on thermohaline structure. J. Geophys. Res. Ocean. 2011, 116. [Google Scholar] [CrossRef]
- Lotter, W.; Kreiman, G.; Cox, D. Deep Predictive Coding Networks for Video Prediction and Unsupervised Learning. arXiv, 2016; arXiv:1605.08104. [Google Scholar]
- Jia, Y.; Liu, Q.; Liu, W. Primary study of the mechanism of eddy shedding from the Kuroshio bend in Luzon Strait. J. Oceanogr. 2005, 61, 1017–1027. [Google Scholar] [CrossRef]
- Nan, F.; Xue, H.; Yu, F. Kuroshio intrusion into the South China Sea: A review. Prog. Oceanogr. 2015, 137, 314–333. [Google Scholar] [CrossRef]
- Cummings, J.A.; Smedstad, O.M. Variational Data Assimilation for the Global Ocean. In Data Assimilation for Atmospheric, Oceanic and Hydrologic Applications (Vol. II); Springer-Verlag: Berlin/Heidelberg, Germany, 2013; pp. 303–343. [Google Scholar]
| Nowcasting Days | HYCOM | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 1st | 2nd | 3rd | 4th | 5th | 6th | 7th | |||
| Matching Ratio (%) | Anticyclonic eddies | 79.8 | 70.4 | 64.6 | 58.0 | 52.2 | 47.3 | 40.4 | 21.9 |
| Cyclonic eddy | 76.1 | 67.7 | 59.6 | 51.4 | 44.8 | 40.4 | 35.0 | 19.0 | |
| Amplitude Errors (cm) | Anticyclonic eddies | 0.8 | 1.3 | 1.7 | 2.0 | 2.3 | 2.6 | 2.9 | 8.7 |
| Cyclonic eddy | 0.7 | 1.1 | 1.4 | 1.7 | 2.0 | 2.1 | 2.4 | 7.7 | |
| Eddycore Errors (km) | Anticyclonic eddies | 11.3 | 16.0 | 20.2 | 23.8 | 26.1 | 28.6 | 30.6 | 36.5 |
| Cyclonic eddy | 11.7 | 16.7 | 20.1 | 23.2 | 26.0 | 29.1 | 31.2 | 35.2 | |
| Radius errors (km) | Anticyclonic eddies | 11.9 | 15.9 | 19.0 | 21.4 | 23.3 | 25.5 | 27.4 | 30.7 |
| Cyclonic eddy | 10.9 | 14.6 | 17.6 | 20.9 | 23.1 | 24.3 | 25.6 | 32.5 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, C.; Li, S.; Wang, A.; Yang, J.; Chen, G. Altimeter Observation-Based Eddy Nowcasting Using an Improved Conv-LSTM Network. Remote Sens. 2019, 11, 783. https://doi.org/10.3390/rs11070783
Ma C, Li S, Wang A, Yang J, Chen G. Altimeter Observation-Based Eddy Nowcasting Using an Improved Conv-LSTM Network. Remote Sensing. 2019; 11(7):783. https://doi.org/10.3390/rs11070783
Chicago/Turabian StyleMa, Chunyong, Siqing Li, Anni Wang, Jie Yang, and Ge Chen. 2019. "Altimeter Observation-Based Eddy Nowcasting Using an Improved Conv-LSTM Network" Remote Sensing 11, no. 7: 783. https://doi.org/10.3390/rs11070783
APA StyleMa, C., Li, S., Wang, A., Yang, J., & Chen, G. (2019). Altimeter Observation-Based Eddy Nowcasting Using an Improved Conv-LSTM Network. Remote Sensing, 11(7), 783. https://doi.org/10.3390/rs11070783





