Identifying 2010 Xynthia Storm Signature in GNSS-R-Based Tide Records
Abstract
:1. Introduction
2. Study Area
3. Datasets
3.1. GNSS Data
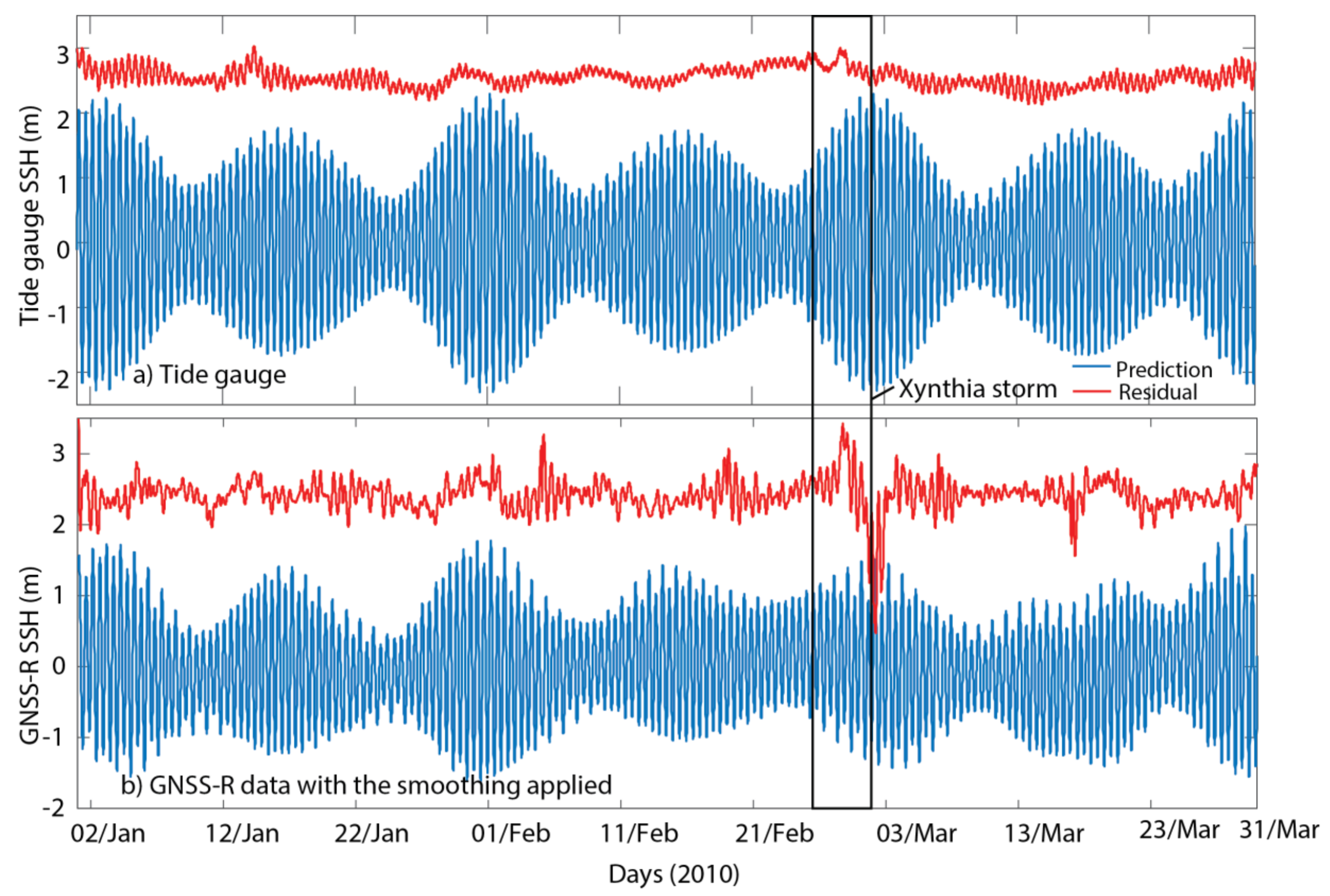
3.2. Tide Gauge Data
3.3. Meteorological Data
3.4. Significant Wave Height Data
4. Methods
4.1. Inversion of the SNR Data
4.2. Analysis of the GNSS-R-Based Water Levels
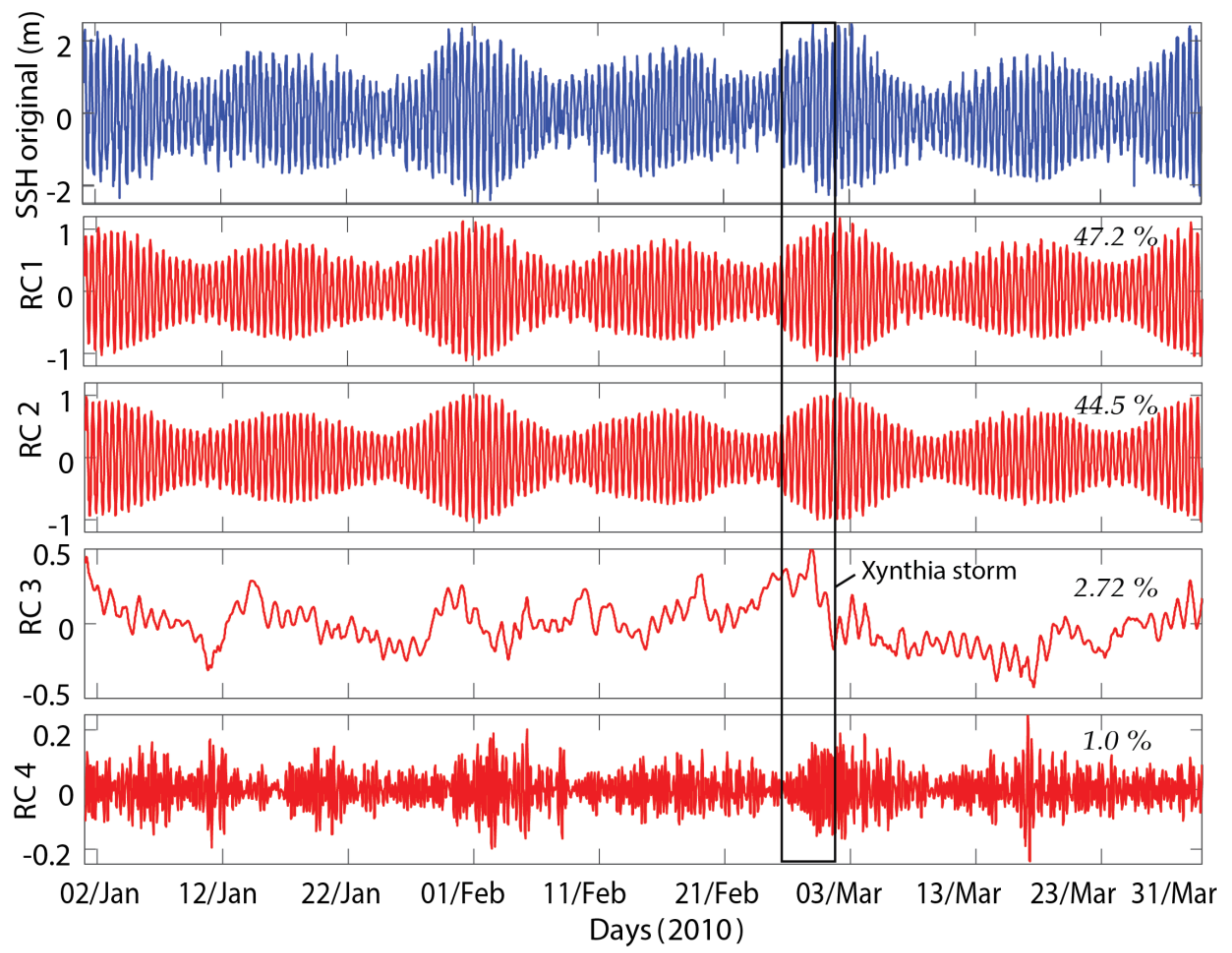
4.2.1. Singular Spectrum Analysis
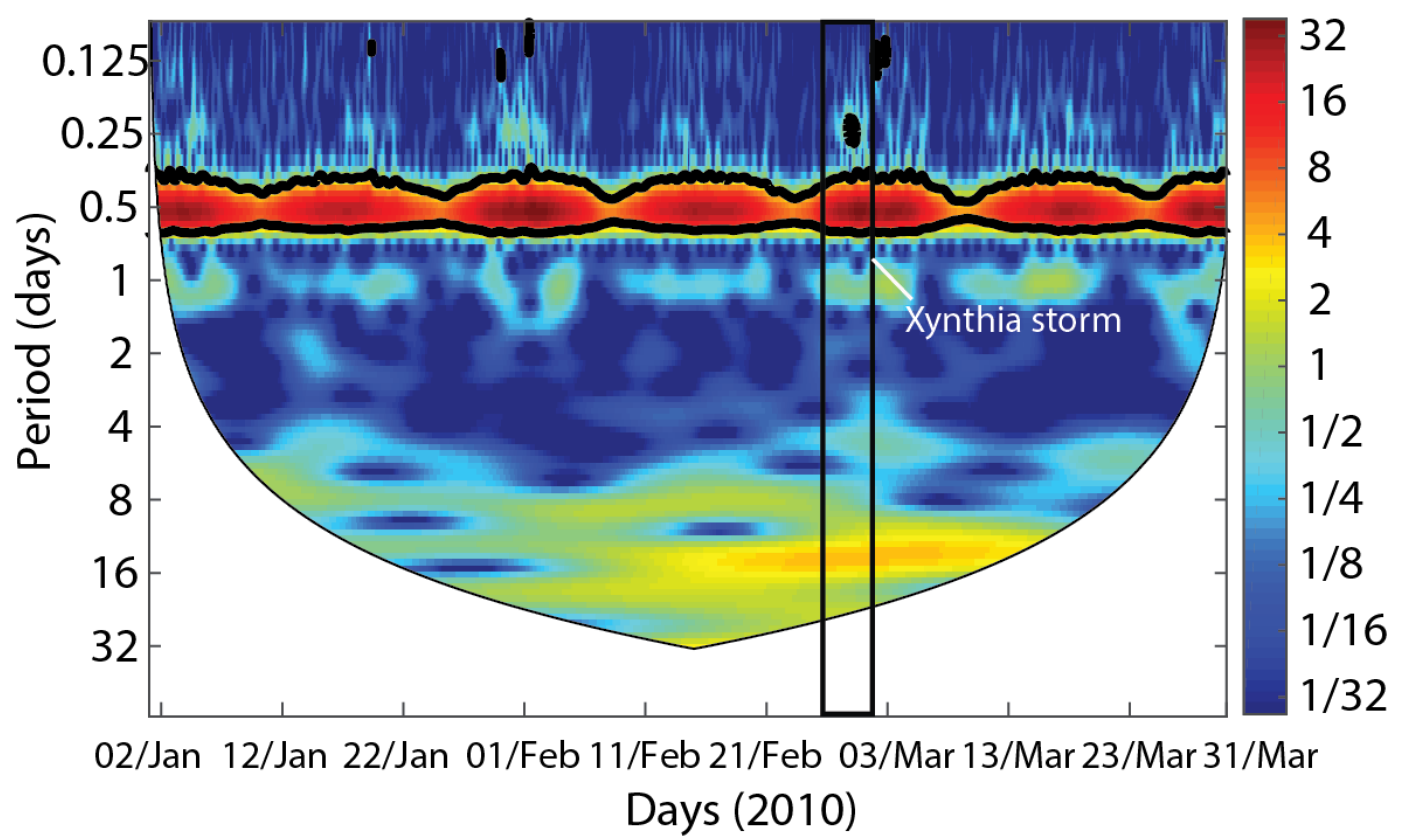
4.2.2. Continuous Wavelet Transform
5. Results
5.1. GNSS-R SSH Time Series Analysis Using the SSA Method
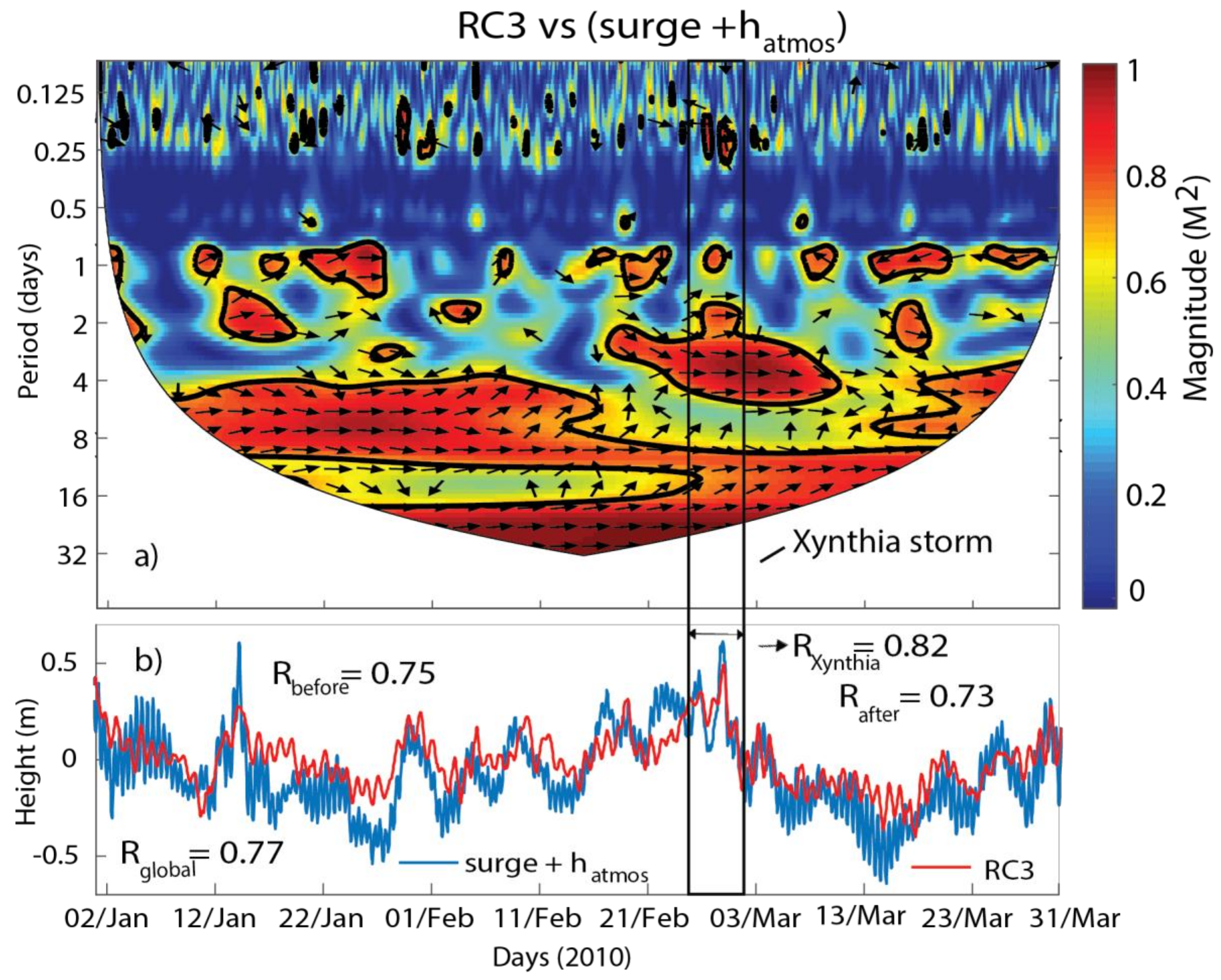
5.2. GNSS-R SSH Time Series Analysis Using CWT Method
6. Discussion
6.1. The Accidental Tide Gauge and More
- -
- the presence of several buildings, dikes, which mask part of the GNSS satellite and are likely to cause parasite multi-paths (more than one reflection), and
- -
- the presence of boats in the bay that are likely to also cause other parasite multi-paths.
- -
- many other GNSS geodetic stations from permanent networks around the world can also be used as accidental tide gauges to complement or improve the existing tide gauge networks,
- -
- GNSS geodetic stations offer the opportunity to record other geophysical phenomena such SWH (e.g., Roussel et al., (2015) [22]) or surge or inverted barometer (this study), and
- -
- if located on a better environment as the top of a hill or a mast, better accuracy can be reached (e.g., 0.12 m see [47]). The choice of the location and the altitude of deployment can be facilitated by the use of dedicated softwares, such as GNSS Reflected Signals Simulations (GRESS) [48] or the GPS tool box [49], which provide a simulation of the position of the reflection points depending on the location of the GNSS geodetic station.
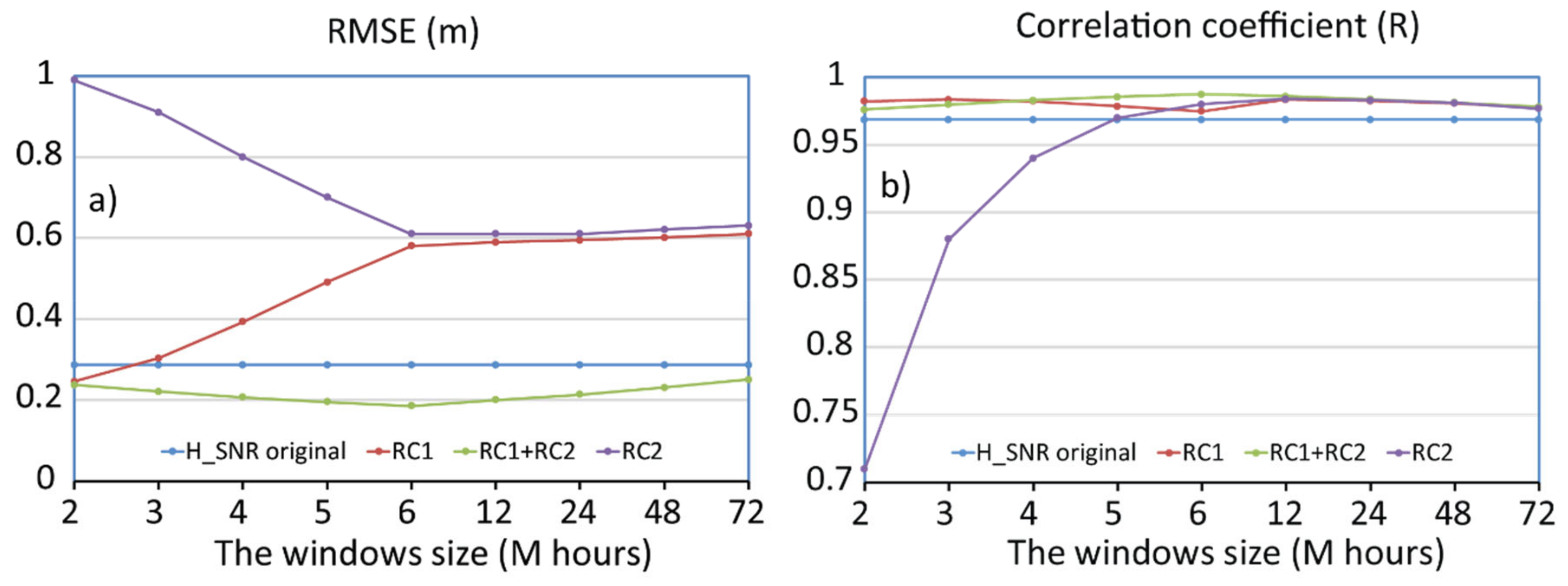
6.2. The Choice of the SSA and CWT for Separating Tides from Other Geophysical Parameters
6.3. The Complementarity Between SSA and Inverse CWT (iCWT) to Separate Tides from Other Geophysical Signals
6.4. Is Each SSA Mode Related to a Single Geophysical Phenomena?
7. Conclusions
Author Contributions
Acknowledgments
Funding
Conflicts of Interest
References
- Cooper, M.J.P.; Beevers, M.D.; Oppenheimer, M. The potential impacts of sea level rise on the coastal region of New Jersey, USA. Clim. Chang. 2008, 90, 475–492. [Google Scholar] [CrossRef]
- FitzGerald, D.M.; Fenster, M.S.; Argow, B.A.; Buynevich, I.V. Coastal Impacts Due to Sea-Level Rise. Annu. Rev. Earth Planet. Sci. 2008, 36, 601–647. [Google Scholar] [CrossRef]
- Kirshen, P.; Knee, K.; Ruth, M. Climate change and coastal flooding in Metro Boston: Impacts and adaptation strategies. Clim. Chang. 2008, 90, 453–473. [Google Scholar] [CrossRef]
- Karim, M.F.; Mimura, N. Impacts of climate change and sea level rise on cyclonis storm surge floods in Bangladesh. Glob. Environ. Chang. 2008, 18, 490–500. [Google Scholar] [CrossRef]
- Bondesanf, M.; Castiglioni, G.B.; Elmis, C.; Pirazzolift, P.A.; Tomasin, A. Coastal areas at risk from storm surges and sea level rise in northestern Italy. J. Coast. Res. 1995, 11, 1354–1379. [Google Scholar]
- Tebaldi, C.; Strauss, B.H.; Zervas, C.E. Modelling sea level rise impacts on storm surges along US coasts. Environ. Res. Lett. 2012, 7, 014032. [Google Scholar] [CrossRef]
- McGranahan, G.; Balk, D.; Anderson, B. The rising tide: Assessing the risks of climate change and human settlements in low elevation coastal zones. Environ. Urban. 2007, 19, 17–37. [Google Scholar] [CrossRef]
- Bode, L.; Hardy, T.A. Progress and recent developments in storm surge modeling. J. Hydraul. Eng. 1997, 123, 315–331. [Google Scholar] [CrossRef]
- Olbert, A.L.; Hartnett, M. Storms and surges in Irish coastal waters. Ocean Model. 2010, 34, 50–62. [Google Scholar] [CrossRef]
- McRobie, A.; Spencer, T.; Gerritsen, H. The Big Flood: North Sea storm surge. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2005, 363, 1263–1270. [Google Scholar] [CrossRef]
- De Zolt, S.; Lionello, P.; Nuhu, A.; Tomasin, A. The disastrous storm of 4 November 1966 on Italy. Nat. Hazards Earth Syst. Sci. 2006, 6, 861–879. [Google Scholar] [CrossRef]
- Bertin, X.; Bruneau, N.; Breilh, J.F.; Fortunato, A.B.; Karpytchev, M. Importance of wave age and resonance in storm surges: The case Xynthia, Bay of Biscay. Ocean Model. 2012, 42, 16–30. [Google Scholar] [CrossRef]
- Pineau-Guillou, L.; Lathuiliere, C.; Magne, R.; Louazel, S.; Corman, D.; Perherin, C. Sea levels analysis and surge modelling during storm Xynthia. Eur. J. Environ. Civ. Eng. 2012, 16, 943–952. [Google Scholar] [CrossRef]
- Vinet, F.; Defossez, S.; Rey, T.; Boissier, L. The production process of flooding risk in coastal area: The example of “Xynthia” areas. Norois 2012, 222, 10–26. [Google Scholar]
- André, C.; Monfort, D.; Bouzit, M.; Vinchon, C. Contribution of insurance data to cost assessment of coastal flood damage to residential buildings: Insights gained from Johanna (2008) and Xynthia (2010) storm events. Nat. Hazards Earth Syst. Sci. 2013, 13, 2003–2012. [Google Scholar] [CrossRef]
- Genovese, E.; Przyluski, V. Storm surge disaster risk management: The Xynthia case study in France. J. Risk Res. 2013, 16, 825–841. [Google Scholar] [CrossRef]
- Przyluski, V.; Hallegatte, S. Gestion des risques naturels- Lecons de la tempête Xynthia; Matière de débattre et décider; Editions Quae: Versailles, France, 2012; ISBN 978-2-7592-2008-3. [Google Scholar]
- Wöppelmann, G.; Zerbini, S.; Marcos, M. Tide gauges and Geodesy: A secular synergy illustrated by three present-day case studies. Intern. Geophys. Geod. 2006, 338, 980–991. [Google Scholar] [CrossRef]
- Martin-neira, M. A Passive Reflectometry and Interferometry System (PARIS): Application to ocean altimetry. ESA J. 1993, 17, 331–355. [Google Scholar]
- Martin-neira, M.; Caparrini, M.; Font-Rossello, J.; Lannelongue, S.; Vallmitjana, C.S. The PARIS Concept: An Experimental Demonstration of Sea Surface Altimetry Using GPS Reflected Signals. IEEE Trans. Geosci. Remote Sens. 2001, 39, 142–150. [Google Scholar] [CrossRef]
- Lowe, S.T.; Zuffada, C.; Chao, Y.; Kroger, P.; Young, L.E.; LaBrecque, J.L. 5-cm-Precision aircraft ocean altimetry using GPS reflections. Geophys. Res. Lett. 2002, 29. [Google Scholar] [CrossRef]
- Roussel, N.; Ramillien, G.; Frappart, F.; Darrozes, J.; Gay, A.; Biancale, R.; Striebig, N.; Hanquiez, V.; Bertin, X.; Allain, D. Sea level monitoring and sea state estimate using a single geodetic receiver. Remote Sens. Environ. 2015, 171, 261–277. [Google Scholar] [CrossRef]
- Jeinking, J. GNSS-SNR water level estimation using global optimization based on interval analysis. J. Geodet. Sci. 2016, 6, 80–92. [Google Scholar]
- Larson, K.M.; Löfgren, J.S.; Haas, R. Coastal sea level measurements using a single geodetic GPS receiver. Adv. Space Res. 2013, 51, 1301–1310. [Google Scholar] [CrossRef]
- Lestarquit, L.; Peyrezabes, M.; Darrozes, J.; Motte, E.; Roussel, N.; Wautelet, G.; Frappart, F.; Ramillien, G.; Biancale, R.; Zribi, M. Reflectometry with an Open-Source Software GNSS Receiver: Use Case with Carrier Phase Altimetry. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 4843–4853. [Google Scholar] [CrossRef]
- Roussel, N.; Frappart, F.; Ramillien, G.; Darrozes, J.; Baup, F.; Lestarquit, L.; Ha, M.C. Detection of soil moisture variations using gps and glonass snr data for elevation angles ranging from 2° to 70°. IEEE IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 4781–4794. [Google Scholar] [CrossRef]
- Abadie, S.; Butel, R.; Dupuis, H.; Brière, C. Statistical parameters of waves on the south Aquitaine Coast. Comptes Rendus Geosci. 2005, 337, 769–776. [Google Scholar] [CrossRef]
- Delpey, M.T.; Ardhuin, F.; Otheguy, P.; Jouon, A. Effects of waves on coastal water dispersion in a small estuarine bay. J. Geophys. Res. Oceans 2014, 119, 70–86. [Google Scholar] [CrossRef]
- Platel, J.P. Atlas cartographique des phénomènes naturels et des caractéristiques physiques du littoral de la Cote Basque; Geosciences pour une Tere durable (BRGM), Observatoire de la Côte Aquitaine: Orléans, France, Rapport Final BRGM/RP-55262-FR; 2007. [Google Scholar]
- Pingree, R.D.; Mardell, G.T.; New, A.L. Propagation of internal tides from the upper slopes of the Bay of Biscay. Nature 1986, 321, 154–158. [Google Scholar] [CrossRef]
- New, A.L. Internal tidal mixing in the Bay of Biscay. Deep Sea Res. Part A Oceanogr. Res. Pap. 1988, 35, 691–709. [Google Scholar] [CrossRef]
- Wunsch, C.; Stammer, D. Atmospheric loading and the oceanic “Inverted barometer” effect. Rev. Geophys. 1997, 35, 79–107. [Google Scholar] [CrossRef]
- Motte, E.; Egido, A.; Roussel, N.; Boniface, K.; Frappart, F. Applications of GNSS-R in continental hydrology. Land Surf. Remote Sens. Cont. Hydrol. 2016, 281–322. [Google Scholar] [CrossRef]
- Larson, K.M.; Small, E.E.; Gutmann, E.; Bilich, A.; Axelrad, P.; Braun, J. Using GPS multipath to measure soil moisture fluctuations: Initial results. GPS Solut. 2008, 12, 173–177. [Google Scholar] [CrossRef]
- Löfgren, J.S.; Haas, R.; Scherneck, H.G.; Bos, M.S. Three months of local sea level derived from reflected: GNSS signals. Radio Sci. 2011, 46, 1–10. [Google Scholar] [CrossRef]
- Bishop, G.J.; Klobuchar, J.A.; Doherty, P.H. Multipath effects on the determination of absolute ionospheric time delay from GPS signals. Radio Sci. 1985, 20, 388–396. [Google Scholar] [CrossRef]
- Larson, K.M.; Ray, R.D.; Nievinski, F.G.; Freymueller, J.T. The Accidental Tide Gauge: A GPS ReRflection Case study from Kachemak Bay, Alaska. IEEE Geosci. Remote Sens. Lett. 2013, 10, 1200–1204. [Google Scholar] [CrossRef]
- Broomhead, D.S.; King, G.P. Extracting qualitative dynamics from experimental data. Phys. D Nonlinear Phenom. 1986, 20, 217–236. [Google Scholar] [CrossRef]
- Vautard, R.; Yiou, P.; Ghil, M. Singular-spectrum analysis: A toolkit for short, noisy, chaotic signals. Phys. D Nonlinear Phenom. 1992, 58, 95–126. [Google Scholar] [CrossRef]
- Schoellhamer, D.H. Singular spectrum analysis for time series with missing data. Geophys. Res. Lett. 2001, 28, 3187–3190. [Google Scholar] [CrossRef]
- Claessen, D.; Groth, A. A Beginner’s Guide to SSA; CERES, Ecole Normale Supérieure: Paris, France, 2002. [Google Scholar]
- Daubechies, I. The Wavelet Transform, Time-Frequency Localization and Signal Analysis. IEEE Trans. Inf. Theory 1990, 36, 961–1005. [Google Scholar] [CrossRef]
- Torrence, C.; Compo, G.P. A Practical Guide to Wavelet Analysis. Am. Meteorol. Soc. 1998, 79, 61–78. [Google Scholar] [CrossRef]
- Grinsted, A.; Moore, J.C.; Jevrejeve, S. Application of the cross wavelet transform and wavelet coherence to geophysical time series. Nonlinear Process. Geophys. 2004, 11, 561–566. [Google Scholar] [CrossRef]
- Pingree, R.D.; Le Cann, B. Structure, strength, and seasonality of the slope current in the Bay of Biscay region. J. Mar. Biol. Assoc. UK 2009, 70, 857–885. [Google Scholar] [CrossRef]
- Ponte, R.M. Low-Frequency Sea Level Variability and the Inverted Barometer Effect. J. Atmos. Ocean. Technol. 2006, 23, 619–629. [Google Scholar] [CrossRef]
- Larson, K.M.; Ray, R.D.; Williams, S.D. A 10-Year Comparison of Water Levels Measured with a Geodetic GPS Receiver versus a Conventional Tide Gauge. J. Atmos. Ocean. Technol. 2017, 34, 295–307. [Google Scholar] [CrossRef]
- Roussel, N.; Frappart, F.; Ramillien, G.; Darrozes, J.; Desjardins, C.; Gegout, P.; Pérosanz, F.; Biancale, R. Simulations of direct and reflected wave trajectories for ground-based GNSS-R experiments. Geosci. Model Dev. 2014, 7, 2261–2279. [Google Scholar] [CrossRef]
- Roesler, C.; Larson, K.M. Software tools for GNSS interferometric reflectometry (GNSS-IR). GPS Solut. 2018, 22, 80. [Google Scholar] [CrossRef]
- Pawlowicz, R.; Beardsley, B.; Lentz, S. Classical tidal harmonic analysis including error estimates in MATLAB using T_TIDE. Comput. Geosci. 2002, 28, 929–937. [Google Scholar] [CrossRef]

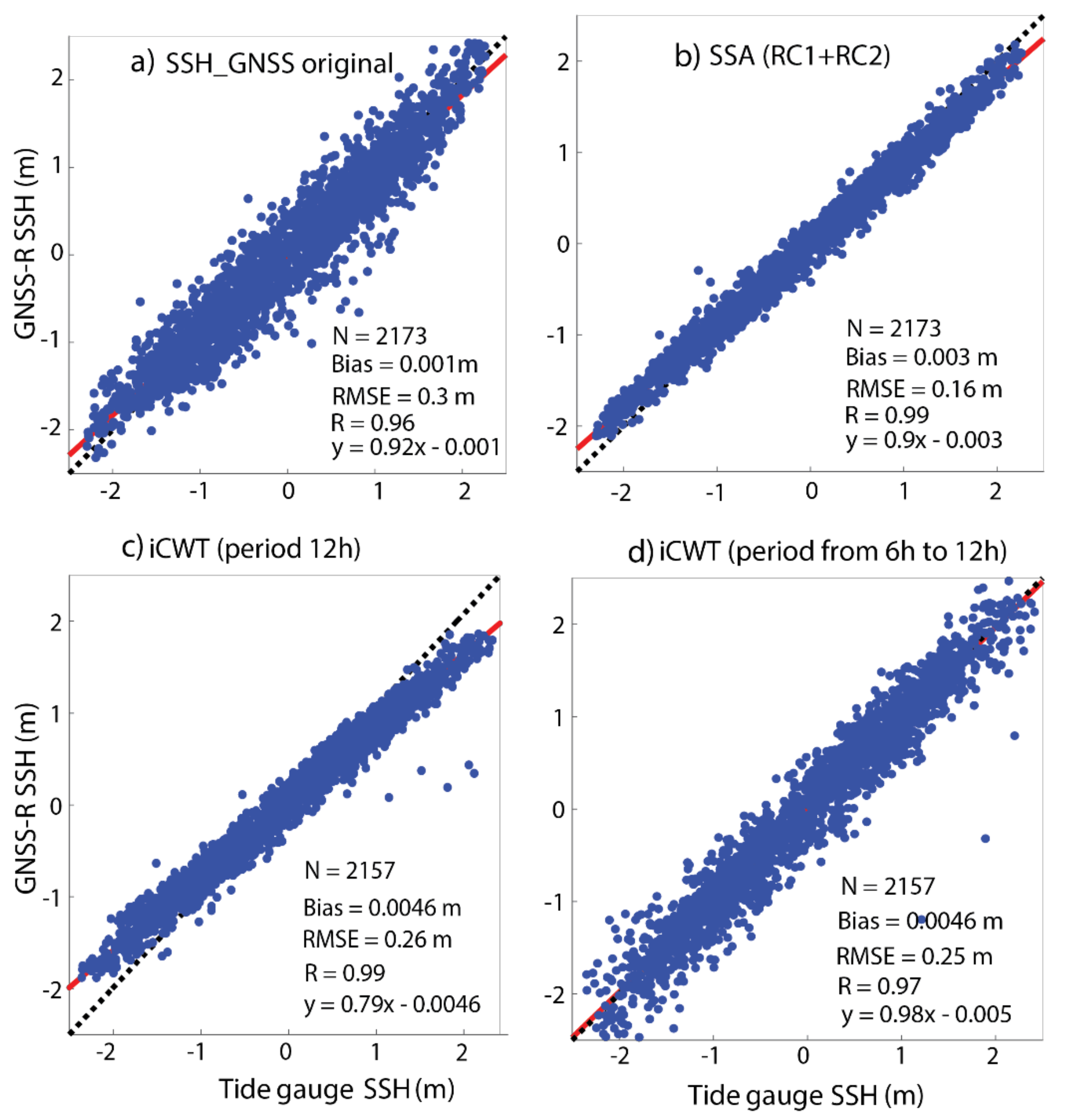
| Bias (m) | RMSE (m) | R | |
|---|---|---|---|
| SSH GNSS-R | 0.001 | 0.30 | 0.96 |
| RC1 + RC2 | 0.003 | 0.16 | 0.99 |
| iCWT at 12 h | 0.005 | 0.26 | 0.99 |
| iCWT from 6 h to 12 h | 0.005 | 0.25 | 0.97 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vu, P.L.; Ha, M.C.; Frappart, F.; Darrozes, J.; Ramillien, G.; Dufrechou, G.; Gegout, P.; Morichon, D.; Bonneton, P. Identifying 2010 Xynthia Storm Signature in GNSS-R-Based Tide Records. Remote Sens. 2019, 11, 782. https://doi.org/10.3390/rs11070782
Vu PL, Ha MC, Frappart F, Darrozes J, Ramillien G, Dufrechou G, Gegout P, Morichon D, Bonneton P. Identifying 2010 Xynthia Storm Signature in GNSS-R-Based Tide Records. Remote Sensing. 2019; 11(7):782. https://doi.org/10.3390/rs11070782
Chicago/Turabian StyleVu, Phuong Lan, Minh Cuong Ha, Frédéric Frappart, José Darrozes, Guillaume Ramillien, Grégory Dufrechou, Pascal Gegout, Denis Morichon, and Philippe Bonneton. 2019. "Identifying 2010 Xynthia Storm Signature in GNSS-R-Based Tide Records" Remote Sensing 11, no. 7: 782. https://doi.org/10.3390/rs11070782
APA StyleVu, P. L., Ha, M. C., Frappart, F., Darrozes, J., Ramillien, G., Dufrechou, G., Gegout, P., Morichon, D., & Bonneton, P. (2019). Identifying 2010 Xynthia Storm Signature in GNSS-R-Based Tide Records. Remote Sensing, 11(7), 782. https://doi.org/10.3390/rs11070782








