Remote Sensing of Water Use Efficiency and Terrestrial Drought Recovery across the Contiguous United States
Abstract
1. Introduction
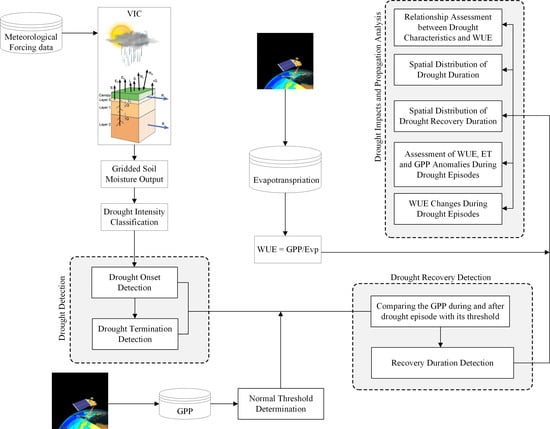
2. Materials and Method
2.1. Remotely Sensed Data
2.2. Simulated Data
2.3. Drought Detection
2.4. Drought Recovery Duration
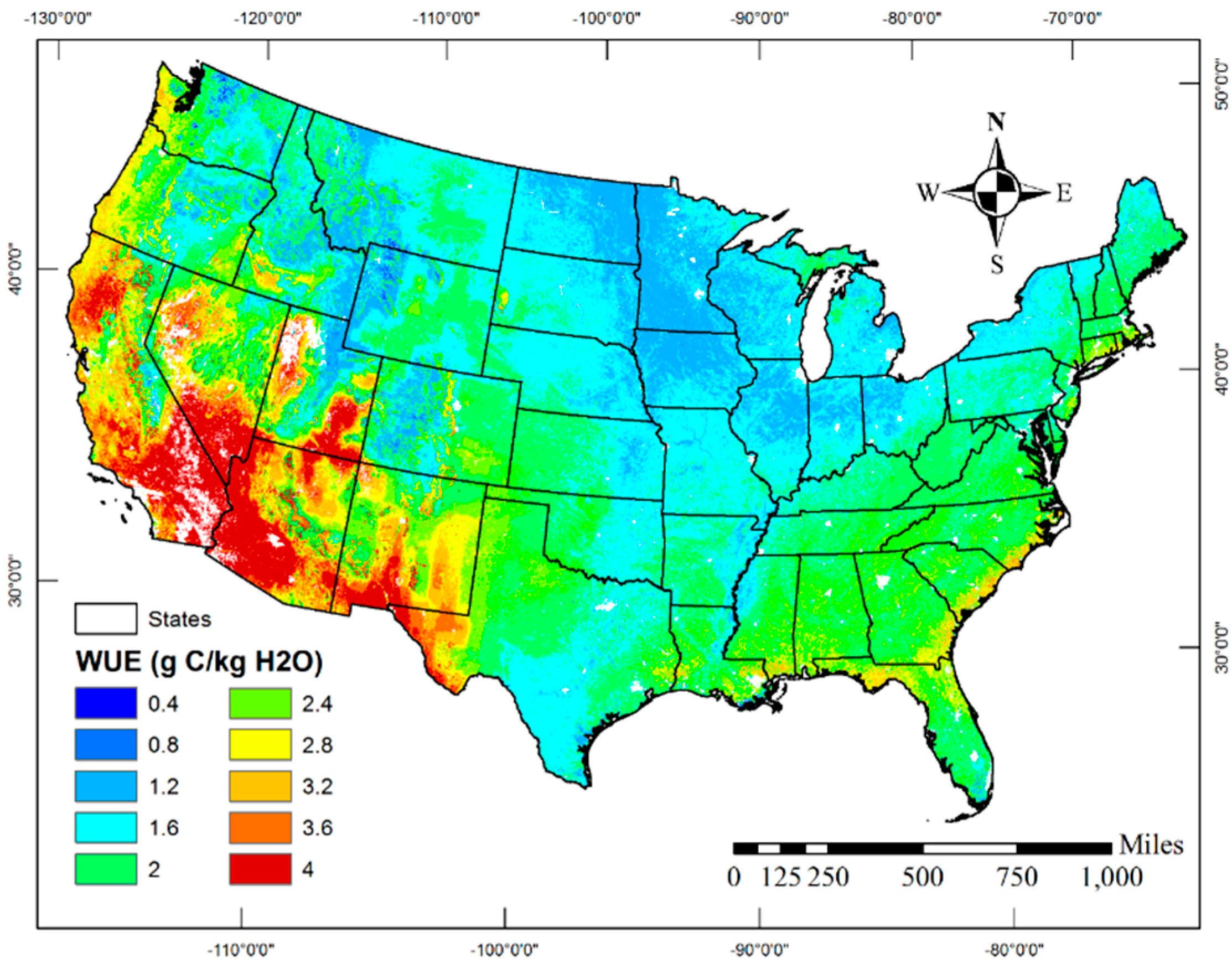
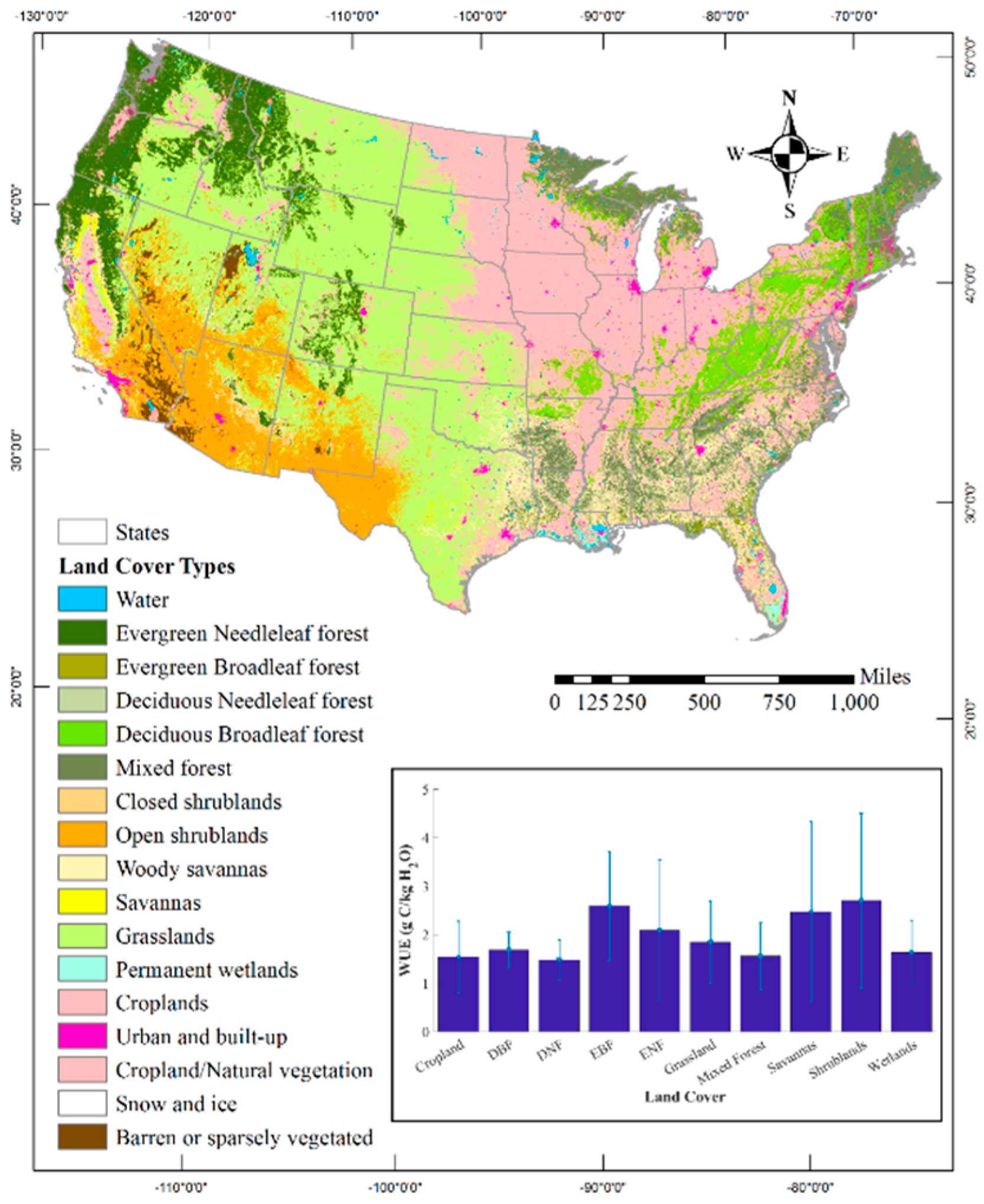
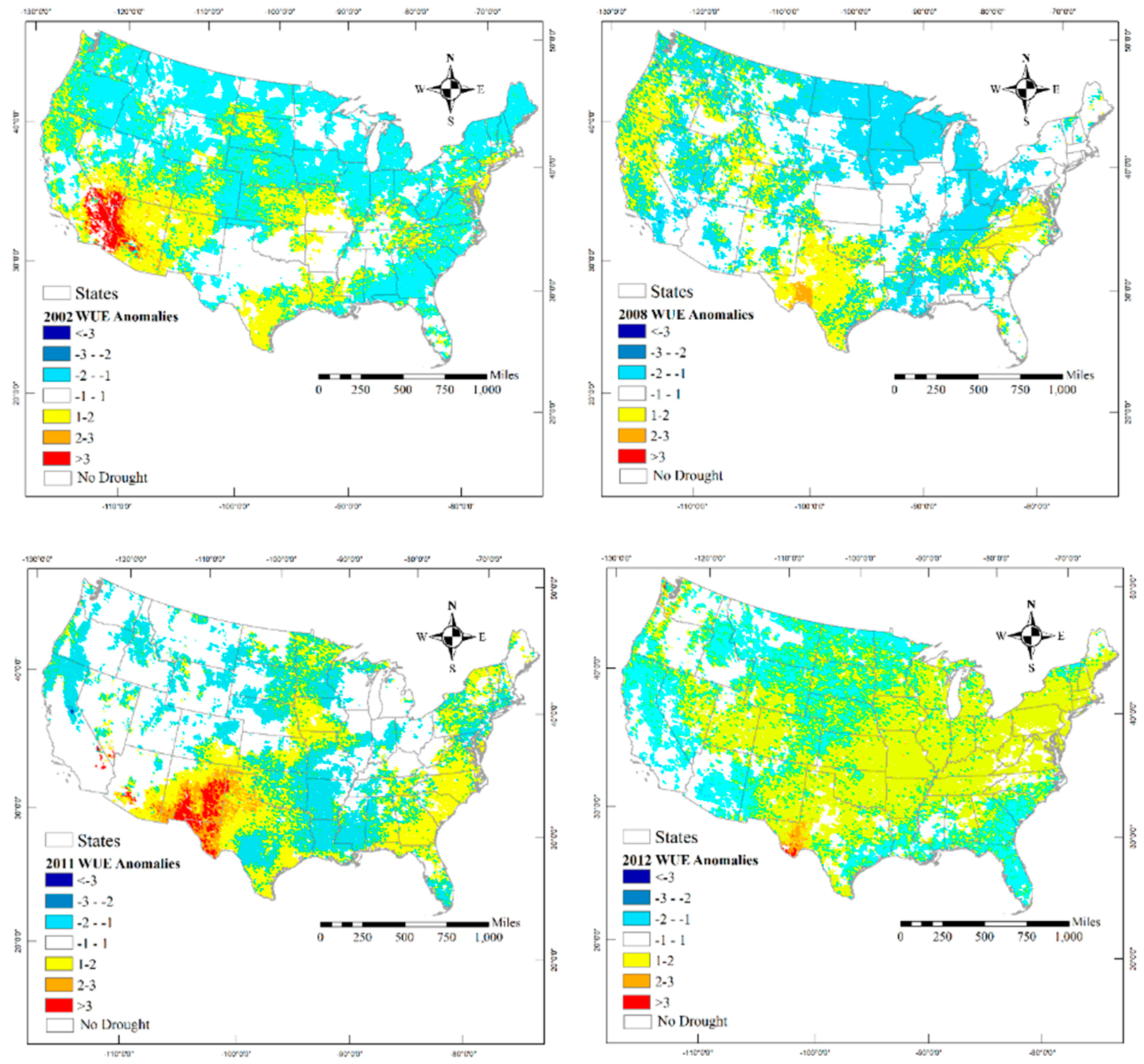
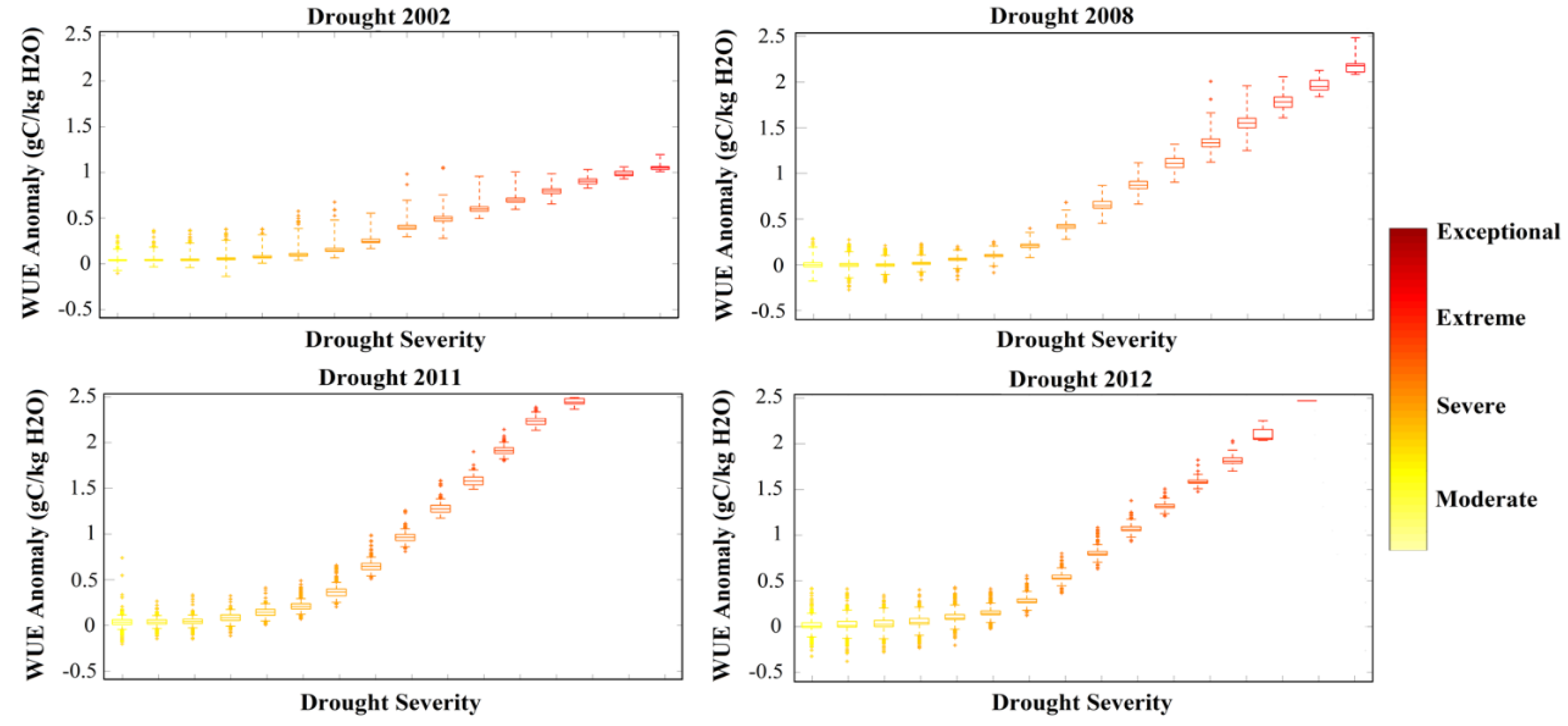
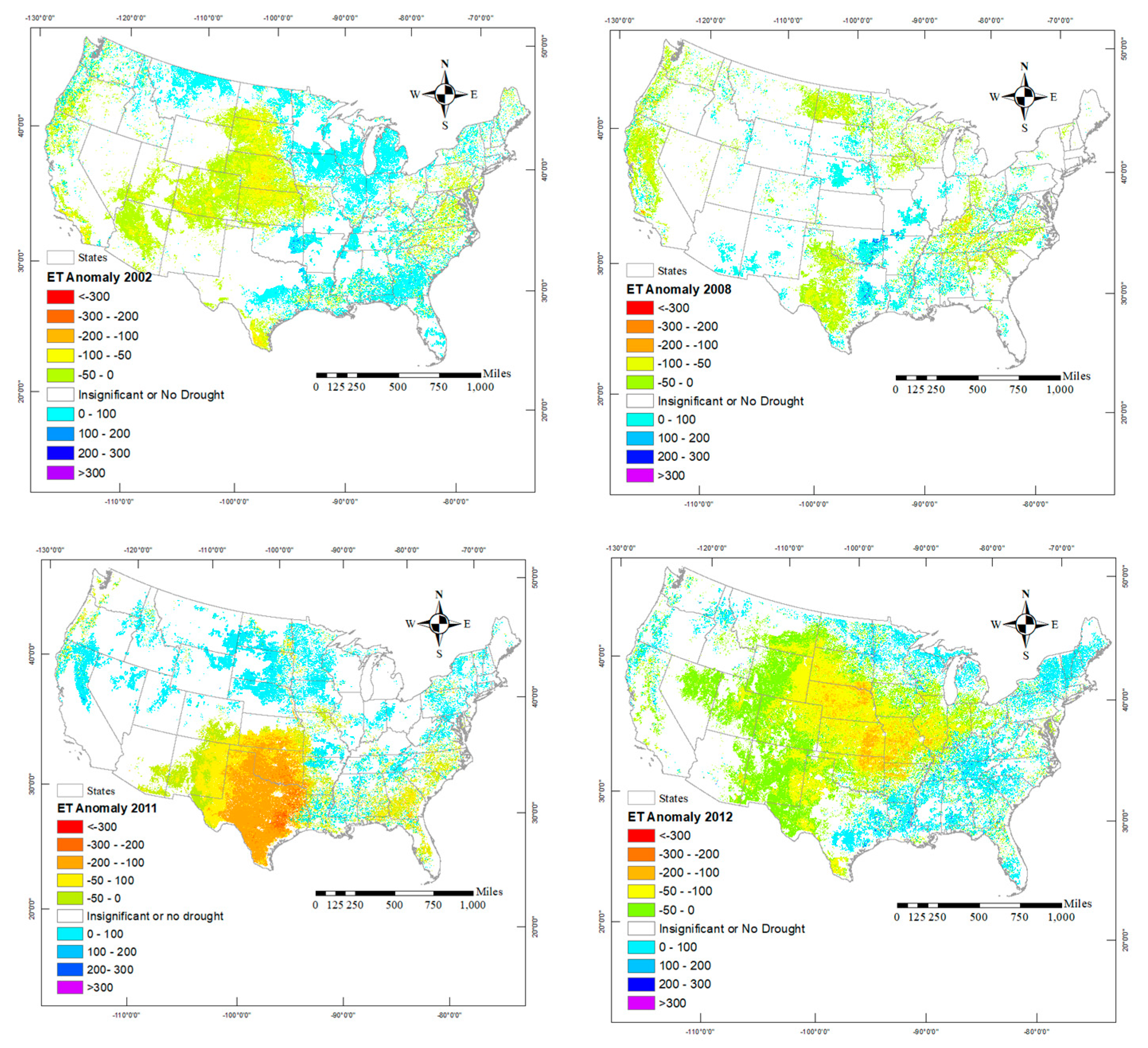
3. Results
4. Discussion
5. Summary and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Huang, L.; He, B.; Han, L.; Liu, J.; Wang, H.; Chen, Z. A global examination of the response of ecosystem water-use efficiency to drought based on MODIS data. Sci. Total Environ. 2017, 601–602, 1097–1107. [Google Scholar] [CrossRef] [PubMed]
- Yu, Z.; Wang, J.; Liu, S.; Rentch, J.S.; Sun, P.; Lu, C. Global gross primary productivity and water use efficiency changes under drought stress. Environ. Res. Lett. 2017, 12, 014016. [Google Scholar] [CrossRef]
- Yang, Y.; Guan, H.; Batelaan, O.; Mcvicar, T.R.; Long, D.; Piao, S.; Liang, W.; Liu, B.; Jin, Z.; Simmons, C.T. Contrasting responses of water use efficiency to drought across global terrestrial ecosystems. Sci. Rep. 2016, 6, 23284. [Google Scholar] [CrossRef] [PubMed]
- Karamouz, M.; Yazdi, M.S.; Ahmadi, B.; Zahraie, B. A System Dynamics Approach to Economic Assessment of Water Supply and Demand Strategies. In Proceedings of the World Environmental and Water Resources Congress 2011, Palm Springs, CA, USA, 22–26 May 2011. [Google Scholar]
- IPCC. Climate Change 2014—Impacts, Adaptation and Vulnerability: Regional Aspects; Cambridge University Press: New York, NY, USA, 2014; ISBN 1107058163. [Google Scholar]
- Zeng, N.; Qian, H.; Munoz, E.; Iacono, R. How strong is carbon cycle-climate feedback under global warming? Geophys. Res. Lett. 2004, 31, 5. [Google Scholar] [CrossRef]
- Karamouz, M.; Ahmadi, A.; Semsar, Y.M.S.; Ahmadi, B. Economic Assessment of Water Resources Management Strategies. J. Irrig. Drain. Eng. 2014, 140, 4013005. [Google Scholar] [CrossRef]
- Ahmadalipour, A.; Moradkhani, H.; Svoboda, M. Centennial drought outlook over the CONUS using NASA-NEX downscaled climate ensemble. Int. J. Climatol. 2016, 37, 2477–2491. [Google Scholar] [CrossRef]
- Karamouz, M.; Ahmadi, B.; Zahmatkesh, Z. Developing an Agricultural Planning Model in a Watershed Considering Climate Change Impacts. J. Water Resour. Plan. Manag. 2013, 139, 349–363. [Google Scholar] [CrossRef]
- Irannezhad, M.; Ahmadi, B.; Kløve, B.; Moradkhani, H. Atmospheric circulation patterns explaining climatological drought dynamics in the boreal environment of Finland, 1962–2011. Int. J. Climatol. 2017, 37, 801–817. [Google Scholar] [CrossRef]
- Ahmadi, B.; Ahmadalipour, A.; Moradkhani, H. Hydrological drought persistence and recovery over the CONUS: A multi-stage framework considering water quantity and quality. Water Res. 2019, 150, 97–110. [Google Scholar] [CrossRef]
- Keyantash, J.; Dracup, J.A. The Quantification of Drought: An Evaluation of Drought Indices. Bull. Am. Meteorol. Soc. 2002, 83, 1167–1180. [Google Scholar] [CrossRef]
- Sheffield, J.; Wood, E.F. Global Trends and Variability in Soil Moisture and Drought Characteristics, 1950–2000, from Observation-Driven Simulations of the Terrestrial Hydrologic Cycle. J. Clim. 2008, 21, 432–458. [Google Scholar] [CrossRef]
- Mishra, A.; Vu, T.; Veettil, A.V.; Entekhabi, D. Drought monitoring with soil moisture active passive (SMAP) measurements. J. Hydrol. 2017, 552, 620–632. [Google Scholar] [CrossRef]
- Vereecken, H.; Huisman, J.A.; Bogena, H.; Vanderborght, J.; Vrugt, J.A.; Hopmans, J.W. On the value of soil moisture measurements in vadose zone hydrology: A review. Water Resour. Res. 2008, 44, W00D06. [Google Scholar] [CrossRef]
- Escorihuela, M.J.; Quintana-Seguí, P. Comparison of remote sensing and simulated soil moisture datasets in Mediterranean landscapes. Remote Sens. Environ. 2016, 180, 99–114. [Google Scholar] [CrossRef]
- Narasimhan, B.; Srinivasan, R. Development and evaluation of Soil Moisture Deficit Index (SMDI) and Evapotranspiration Deficit Index (ETDI) for agricultural drought monitoring. Agric. For. Meteorol. 2005, 133, 69–88. [Google Scholar] [CrossRef]
- Ceppi, P.; Zelinka, M.D.; Hartmann, D.L. The response of the Southern Hemispheric eddy-driven jet to future changes in shortwave radiation in CMIP5. Geophys. Res. Lett. 2014, 41, 3244–3250. [Google Scholar] [CrossRef]
- Qin, Y.; Yang, D.; Lei, H.; Xu, K.; Xu, X. Comparative analysis of drought based on precipitation and soil moisture indices in Haihe basin of North China during the period of 1960–2010. J. Hydrol. 2015, 526, 55–67. [Google Scholar] [CrossRef]
- Ahmadalipour, A.; Moradkhani, H.; Yan, H.; Zarekarizi, M. Remote Sensing of Drought: Vegetation, Soil Moisture, and Data Assimilation BT. In Remote Sensing of Hydrological Extremes; Lakshmi, V., Ed.; Springer International Publishing: Cham, Switzerland, 2017; pp. 121–149. ISBN 978-3-319-43744-6. [Google Scholar]
- Rebel, K.T.; de Jeu, R.A.M.; Ciais, P.; Viovy, N.; Piao, S.L.; Kiely, G.; Dolman, A.J. A global analysis of soil moisture derived from satellite observations and a land surface model. Hydrol. Earth Syst. Sci. 2012, 16, 833–847. [Google Scholar] [CrossRef]
- Xu, X.; Li, J.; Tolson, B.A. Progress in integrating remote sensing data and hydrologic modeling. Prog. Phys. Geogr. Earth Environ. 2014, 38, 464–498. [Google Scholar] [CrossRef]
- Champagne, C.; McNairn, H.; Berg, A.A. Monitoring agricultural soil moisture extremes in Canada using passive microwave remote sensing. Remote Sens. Environ. 2011, 115, 2434–2444. [Google Scholar] [CrossRef]
- Kang, C.S.; Kanniah, K.D.; Kerr, Y.H.; Cracknell, A.P. Analysis of in-situ soil moisture data and validation of SMOS soil moisture products at selected agricultural sites over a tropical region. Int. J. Remote Sens. 2016, 37, 3636–3654. [Google Scholar] [CrossRef]
- Martínez-Fernández, J.; González-Zamora, Á.; Sanchez, N.; Gumuzzio, A.; Herrero-Jiménez, C. Satellite soil moisture for agricultural drought monitoring: Assessment of the SMOS derived Soil Water Deficit Index. Remote Sens. Environ. 2016, 177, 277–286. [Google Scholar] [CrossRef]
- Wagner, W.; Scipal, K.; Pathe, C.; Gerten, D.; Lucht, W.; Rudolf, B. Evaluation of the agreement between the first global remotely sensed soil moisture data with model and precipitation data. J. Geophys. Res. Atmos. 2003, 108. [Google Scholar] [CrossRef]
- Liu, Y.Y.; Parinussa, R.M.; Dorigo, W.A.; De Jeu, R.A.M.; Wagner, W.; van Dijk, A.I.J.M.; McCabe, M.F.; Evans, J.P. Developing an improved soil moisture dataset by blending passive and active microwave satellite-based retrievals. Hydrol. Earth Syst. Sci. 2011, 15, 425–436. [Google Scholar] [CrossRef]
- Yan, H.; Zarekarizi, M.; Moradkhani, H. Toward improving drought monitoring using the remotely sensed soil moisture assimilation: A parallel particle filtering framework. Remote Sens. Environ. 2018, 216, 456–471. [Google Scholar] [CrossRef]
- Yan, H.; Moradkhani, H.; Zarekarizi, M. A probabilistic drought forecasting framework: A combined dynamical and statistical approach. J. Hydrol. 2017, 548, 291–304. [Google Scholar] [CrossRef]
- Liu, Y.; Xiao, J.; Ju, W.; Zhou, Y.; Wang, S.; Wu, X. Water use efficiency of China’s terrestrial ecosystems and responses to drought. Sci. Rep. 2015, 5, 13799. [Google Scholar] [CrossRef]
- Tang, X.; Li, H.; Desai, A.R.; Nagy, Z.; Luo, J.; Kolb, T.E.; Olioso, A.; Xu, X.; Yao, L.; Kutsch, W.; et al. How is water-use efficiency of terrestrial ecosystems distributed and changing on Earth? Sci. Rep. 2014, 4, 7483. [Google Scholar] [CrossRef] [PubMed]
- Yang, F.; Ichii, K.; White, M.A.; Hashimoto, H. Developing a continental-scale measure of gross primary production by combining MODIS and AmeriFlux data through Support Vector Machine approach. Remote Sens. Environ. 2007, 110, 109–122. [Google Scholar] [CrossRef]
- He, M.; Kimball, J.S.; Running, S.; Ballantyne, A.; Guan, K.; Huemmrich, F. Remote Sensing of Environment Satellite detection of soil moisture related water stress impacts on ecosystem productivity using the MODIS-based photochemical re fl ectance index. Remote Sens. Environ. 2016, 186, 173–183. [Google Scholar] [CrossRef]
- Lawrence, D.M.; Thornton, P.E.; Oleson, K.W.; Bonan, G.B. The Partitioning of Evapotranspiration into Transpiration, Soil Evaporation, and Canopy Evaporation in a GCM: Impacts on Land–Atmosphere Interaction. J. Hydrometeorol. 2007, 8, 862–880. [Google Scholar] [CrossRef]
- Zhang, X.; Moran, M.S.; Zhao, X.; Liu, S.; Zhou, T.; Ponce-Campos, G.E.; Liu, F. Remote Sensing of Environment Impact of prolonged drought on rainfall use ef fi ciency using MODIS data across China in the early 21st century. Remote Sens. Environ. 2014, 150, 188–197. [Google Scholar] [CrossRef]
- Ponce-Campos, G.E.; Moran, M.S.; Huete, A.; Zhang, Y.; Bresloff, C.; Huxman, T.E.; Eamus, D.; Bosch, D.D.; Buda, A.R.; Gunter, S.A.; et al. Ecosystem resilience despite large-scale altered hydroclimatic conditions. Nature 2013, 494, 349–352. [Google Scholar] [CrossRef] [PubMed]
- Tang, X.; Li, H.; Xu, X.; Luo, J.; Li, X.; Ding, Z.; Xie, J. Potential of MODIS data to track the variability in ecosystem water-use efficiency of temperate deciduous forests. Ecol. Eng. 2016, 91, 381–391. [Google Scholar] [CrossRef]
- Mazdiyasni, O.; Aghakouchak, A. Substantial increase in concurrent droughts and heatwaves in the United States. Proc. Natl. Acad. Sci. USA 2015, 112, 11484–11489. [Google Scholar] [CrossRef]
- Chiang, F.; Mazdiyasni, O.; Aghakouchak, A. Amplified warming of droughts in southern United States in observations and model simulations. Sci. Adv. 2018, 4, eaat2380. [Google Scholar] [CrossRef]
- Teuling, A.J.; Van Loon, A.F.; Seneviratne, S.I.; Lehner, I.; Aubinet, M.; Heinesch, B.; Bernhofer, C.; Grünwald, T.; Prasse, H.; Spank, U. Evapotranspiration ampli fi es European summer drought. Geophys. Res. Lett. 2015, 40, 2071–2075. [Google Scholar] [CrossRef]
- Huntington, T. Evidence for Intensification of the Global Water Cycle: Review and Synthesis. J. Hydrol. 2006, 319, 83–95. [Google Scholar] [CrossRef]
- Dan, L.I.U.; Chenglong, Y.U.; Fang, Z. Response of the water use efficiency of natural vegetation to drought in Northeast China. J. Geogr. Sci. 2018, 28, 611–628. [Google Scholar]
- Pan, M.; Yuan, X.; Wood, E.F. A probabilistic framework for assessing drought recovery. Geophys. Res. Lett. 2013, 40, 3637–3642. [Google Scholar] [CrossRef]
- Dechant, C.M.; Moradkhani, H. Analyzing the sensitivity of drought recovery forecasts to land surface initial conditions. J. Hydrol. 2015, 526, 89–100. [Google Scholar] [CrossRef]
- Secchi, F.; Zwieniecki, M.A. Down-Regulation of Plasma Intrinsic Protein1 Aquaporin in Poplar Trees Is Detrimental to Recovery from Embolism. Plant Physiol. 2014, 164, 1789–1799. [Google Scholar] [CrossRef] [PubMed]
- Martorell, S.; Diaz-espejo, A.; Medrano, H.; Ball, M.C.; Choat, B. Rapid hydraulic recovery in Eucalyptus pauciflora after drought: Linkages between stem hydraulics and leaf gas exchange. Plant Cell Environ. 2014, 37, 617–626. [Google Scholar] [CrossRef] [PubMed]
- Parry, S.; Prudhomme, C.; Wilby, R.L.; Wood, P.J. Drought termination: Concept and characterisation. Prog. Phys. Geogr. 2016, 40, 743–767. [Google Scholar] [CrossRef]
- Schwalm, C.R.; Anderegg, W.R.L.; Michalak, A.M.; Fisher, J.B.; Biondi, F.; Koch, G.; Litvak, M.; Ogle, K.; Shaw, J.D.; Wolf, A.; et al. Global patterns of drought recovery. Nature 2017, 548, 202–205. [Google Scholar] [CrossRef] [PubMed]
- Connor, J.D.; Crossman, N.D.; Banerjee, O.; Bark, R.; Connor, J.; Crossman, N.D. An ecosystem services approach to estimating economic losses associated with drought an ecosystem services approach to estimating economic losses associated with drought. Ecol. Econ. 2013, 91, 19–27. [Google Scholar]
- Nepstad, D.C.; Stickler, C.M.; Soares-filho, B.; Merry, F.; Nin, E. Interactions among Amazon land use, forests and climate: Prospects for a near-term forest tipping point. Philos. Trans. R. Soc. B Biol. Sci. 2008, 363, 1737–1746. [Google Scholar] [CrossRef]
- Running, S.W.; Nemani, R.R.; Heinsch, F.A.N.N.; Zhao, M.; Reeves, M.; Hashimoto, H.A. Continuous Satellite-Derived Measure of Global Terrestrial Primary Production. Bioscience 2004, 54, 547–560. [Google Scholar] [CrossRef]
- Zhao, M.; Heinsch, F.A.; Nemani, R.R.; Running, S.W. Improvements of the MODIS terrestrial gross and net primary production global data set. Remote Sens. Environ. 2005, 95, 164–176. [Google Scholar] [CrossRef]
- Mu, Q.; Heinsch, F.A.; Zhao, M.; Running, S.W. Development of a global evapotranspiration algorithm based on MODIS and global meteorology data. Remote Sens. Environ. 2007, 111, 519–536. [Google Scholar] [CrossRef]
- Mu, Q.; Zhao, M.; Running, S.W. Improvements to a MODIS global terrestrial evapotranspiration algorithm. Remote Sens. Environ. 2011, 115, 1781–1800. [Google Scholar] [CrossRef]
- Heinsch, F.; Reeves, M.; Votava, P.; Kang, S.; Cristina, M.; Zhao, M.; Glassy, J.; Jolly, W.; Loehman, R.; Bowker, C.F.; et al. User’s Guide GPP and NPP (MOD17A2/A3) Products NASA MODIS Land Algorithm; The University of Montana: Missoula, MT, USA, 2003. [Google Scholar]
- Cohen, W.B.; Maiersperger, T.K.; Turner, D.P.; Ritts, W.D.; Pflugmacher, D.; Kennedy, R.E.; Kirschbaum, A.; Running, S.W.; Costa, M.; Gower, S.T. MODIS land cover and LAI collection 4 product quality across nine sites in the western hemisphere. IEEE Trans. Geosci. Remote Sens. 2006, 44, 1843–1857. [Google Scholar] [CrossRef]
- Heinsch, F.A.; Zhao, M.; Running, S.W.; Kimball, J.S.; Nemani, R.R.; Davis, K.J.; Bolstad, P.V.; Cook, B.D.; Desai, A.R.; Ricciuto, D.M.; et al. Evaluation of Remote Sensing Based Terrestrial Productivity from MODIS Using Regional Tower Eddy Flux Network Observations. IEEE Trans. Geosci. Remote Sens. 2006, 44, 1908–1925. [Google Scholar] [CrossRef]
- Turner, D.P.; Ritts, W.D.; Cohen, W.B.; Gower, S.T.; Running, S.W.; Zhao, M.; Costa, M.H.; Kirschbaum, A.A.; Ham, J.M.; Saleska, S.R.; et al. Evaluation of MODIS NPP and GPP products across multiple biomes. Remote Sens. Environ. 2006, 102, 282–292. [Google Scholar] [CrossRef]
- Zargar, A.; Sadiq, R.; Naser, B.; Khan, F.I. A review of drought indices. Environ. Rev. 2011, 19, 333–349. [Google Scholar] [CrossRef]
- Xiao, J.; Zhuang, Q.; Law, B.E.; Chen, J.; Baldocchi, D.D.; Cook, D.R.; Oren, R.; Richardson, A.D.; Wharton, S.; Ma, S.; et al. Remote Sensing of Environment A continuous measure of gross primary production for the conterminous United States derived from MODIS and AmeriFlux data. Remote Sens. Environ. 2010, 114, 576–591. [Google Scholar] [CrossRef]
- Xue, B.-L.; Guo, Q.; Otto, A.; Xiao, J.; Tao, S.; Li, L. Global patterns, trends, and drivers of water use efficiency from 2000 to 2013. Ecosphere 2015, 6, art174. [Google Scholar] [CrossRef]
- Zhang, K.; Kimball, J.S.; Running, S.W. A review of remote sensing based actual evapotranspiration estimation. Wiley Interdiscip. Rev. Water 2016, 3, 834–853. [Google Scholar] [CrossRef]
- Wolf, S.; Keenan, T.F.; Fisher, J.B.; Baldocchi, D.D.; Desai, A.R.; Richardson, A.D.; Scott, R.L.; Law, B.E.; Litvak, M.E.; Brunsell, N.A.; et al. Warm spring reduced carbon cycle impact of the 2012 US summer drought. Proc. Natl. Acad. Sci. USA 2016, 113, 5880–5885. [Google Scholar] [CrossRef]
- Zscheischler, J.; Mahecha, M.D.; von Buttlar, J.; Harmeling, S.; Jung, M.; Rammig, A.; Randerson, J.T.; Schölkopf, B.; Seneviratne, S.I.; Tomelleri, E.; et al. A few extreme events dominate global interannual variability in gross primary production. Environ. Res. Lett. 2014, 9, 35001. [Google Scholar] [CrossRef]
- Mu, Q.; Zhao, M.; Running, S.W. Numerical Terradynamic Simulation Group MODIS Global Terrestrial Evapotranspiration (ET) Product (NASA MOD16A2/A3) Collection 5. NASA Headquarters; Numerical Terradynamic Simulation Group Publications: Missoula, MT, USA, 2013. [Google Scholar]
- Velpuri, N.M.; Senay, G.B.; Singh, R.K.; Bohms, S.; Verdin, J.P. A comprehensive evaluation of two MODIS evapotranspiration products over the conterminous United States: Using point and gridded FLUXNET and water balance ET. Remote Sens. Environ. 2013, 139, 35–49. [Google Scholar] [CrossRef]
- Xia, Y.; Mitchell, K.; Ek, M.; Cosgrove, B.; Sheffield, J.; Luo, L.; Alonge, C.; Wei, H.; Meng, J.; Livneh, B.; et al. Continental-scale water and energy flux analysis and validation for North American Land Data Assimilation System project phase 2 (NLDAS-2): 2. Validation of model-simulated streamflow. J. Geophys. Res. Atmos. 2012, 117. [Google Scholar] [CrossRef]
- Liang, X.; Lettenmaier, D.P.; Wood, E.F.; Burges, S.J. A simple hydrologically based model of land surface water and energy fluxes for general circulation models. J. Geophys. Res. Atmos. 1994, 99, 14415–14428. [Google Scholar] [CrossRef]
- Wood, E.F.; Lettenmaier, D.; Liang, X.; Nijssen, B.; Wetzel, S.W. Hydrological modeling of continental-scale basins. Annu. Rev. Earth Planet. Sci. 1997, 25, 279–300. [Google Scholar] [CrossRef]
- Maurer, E.P.; Wood, A.W.; Adam, J.C.; Lettenmaier, D.P.; Nijssen, B. A Long-Term Hydrologically Based Dataset of Land Surface Fluxes and States for the Conterminous United States. J. Clim. 2002, 15, 3237–3251. [Google Scholar] [CrossRef]
- Livneh, B.; Rosenberg, E.A.; Lin, C.; Nijssen, B.; Mishra, V.; Andreadis, K.M.; Maurer, E.P.; Lettenmaier, D.P. A Long-Term Hydrologically Based Dataset of Land Surface Fluxes and States for the Conterminous United States: Update and Extensions. J. Clim. 2013, 26, 9384–9392. [Google Scholar] [CrossRef]
- Shukla, S.; Steinemann, A.C.; Lettenmaier, D.P. Drought Monitoring for Washington State: Indicators and Applications. J. Hydrometeorol. 2011, 12, 66–83. [Google Scholar] [CrossRef]
- Zhao, M.; Running, S.W. Drought-Induced Reduction in Global Terrestrial Net Primary Production from 2000 through 2009. Science 2010, 329, 940–943. [Google Scholar] [CrossRef]
- Beer, C.; Reichstein, M.; Tomelleri, E.; Ciais, P.; Jung, M.; Carvalhais, N.; Rödenbeck, C.; Arain, M.A.; Baldocchi, D.; Bonan, G.B.; et al. Terrestrial Gross Carbon Dioxide Uptake: Global Distribution and Covariation with Climate. Science 2010, 329, 834–838. [Google Scholar] [CrossRef] [PubMed]
- Breshears, D.D.; Cobb, N.S.; Rich, P.M.; Price, K.P.; Allen, C.D.; Balice, R.G.; Romme, W.H.; Kastens, J.H.; Floyd, M.L.; Belnap, J.; et al. Regional vegetation die-off in response to global-change-type drought. Proc. Natl. Acad. Sci. USA 2005, 102, 15144–15148. [Google Scholar] [CrossRef]
- Seager, R.; Goddard, L.; Nakamura, J.; Henderson, N.; Lee, D.E. Dynamical Causes of the 2010/11 Texas–Northern Mexico Drought. J. Hydrometeorol. 2013, 15, 39–68. [Google Scholar] [CrossRef]
- Long, D.; Scanlon, B.R.; Longuevergne, L.; Sun, A.Y.; Fernando, D.N.; Save, H. GRACE satellite monitoring of large depletion in water storage in response to the 2011 drought in Texas. Geophys. Res. Lett. 2013, 40, 3395–3401. [Google Scholar] [CrossRef]
- Rippey, B.R. The U.S. drought of 2012. Weather Clim. Extrem. 2015, 10, 57–64. [Google Scholar] [CrossRef]
- Hoerling, M.; Eischeid, J.; Kumar, A.; Leung, R.; Mariotti, A.; Mo, K.; Schubert, S.; Seager, R. Causes and Predictability of the 2012 Great Plains Drought. Bull. Am. Meteorol. Soc. 2013, 95, 269–282. [Google Scholar] [CrossRef]
- Wang, H.; Schubert, S.; Koster, R.; Ham, Y.-G.; Suarez, M. On the Role of SST Forcing in the 2011 and 2012 Extreme U.S. Heat and Drought: A Study in Contrasts. J. Hydrometeorol. 2014, 15, 1255–1273. [Google Scholar] [CrossRef]
- Otkin, J.A.; Svoboda, M.; Hunt, E.D.; Ford, T.W.; Anderson, M.C.; Hain, C.; Basara, J.B. Flash Droughts: A Review and Assessment of the Challenges Imposed by Rapid-Onset Droughts in the United States. Bull. Am. Meteorol. Soc. 2017, 99, 911–919. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.M.; Gouveia, C.; Camarero, J.J.; Begueria, S.; Trigo, R.; López-Moreno, J.I.; Azorin-Molina, C.; Pasho, E.; Lorenzo-Lacruz, J.; Revuelto, J.; et al. Response of vegetation to drought time-scales across global land biomes. Proc. Natl. Acad. Sci. USA 2013, 110, 52–57. [Google Scholar] [CrossRef]
- Schwingshackl, C.; Hirschi, M.; Seneviratne, S.I. Quantifying Spatiotemporal Variations of Soil Moisture Control on Surface Energy Balance and Near-Surface Air Temperature. J. Clim. 2017, 30, 7105–7124. [Google Scholar] [CrossRef]
- Haghighi, E.; Short Gianotti, D.J.; Akbar, R.; Salvucci, G.D.; Entekhabi, D. Soil and Atmospheric Controls on the Land Surface Energy Balance: A Generalized Framework for Distinguishing Moisture-Limited and Energy-Limited Evaporation Regimes. Water Resour. Res. 2018, 54, 1831–1851. [Google Scholar] [CrossRef]
- Frank, D.; Reichstein, M.; Bahn, M.; Thonicke, K.; Frank, D.; Mahecha, M.D.; Smith, P.; Velde, M.; Vicca, S.; Babst, F.; et al. Effects of climate extremes on the terrestrial carbon cycle: Concepts, processes and potential future impacts. Glob. Chang. Biol. 2015, 21, 2861–2880. [Google Scholar] [CrossRef] [PubMed]
- Schwalm, C.R.; Williams, C.A.; Schaefer, K.; Baldocchi, D.; Black, T.A.; Goldstein, A.H.; Law, B.E.; Oechel, W.C.; Paw, K.T.; Scott, R.L. Reduction in carbon uptake during turn of the century drought in western North America. Nat. Geosci. 2012, 5, 551–556. [Google Scholar] [CrossRef]
- Liao, C.; Zhuang, Q. Reduction of Global Plant Production due to Droughts from 2001 to 2010: An Analysis with a Process-Based Global Terrestrial Ecosystem Model. Earth Interact. 2015, 19, 1–21. [Google Scholar] [CrossRef]
- Rodell, M.; Beaudoing, H.K.; L’Ecuyer, T.S.; Olson, W.S.; Famiglietti, J.S.; Houser, P.R.; Adler, R.; Bosilovich, M.G.; Clayson, C.A.; Chambers, D.; et al. The Observed State of the Water Cycle in the Early Twenty-First Century. J. Clim. 2015, 28, 8289–8318. [Google Scholar] [CrossRef]
- L’Ecuyer, T.S.; Beaudoing, H.K.; Rodell, M.; Olson, W.; Lin, B.; Kato, S.; Clayson, C.A.; Wood, E.; Sheffield, J.; Adler, R. The observed state of the energy budget in the early twenty-first century. J. Clim. 2015, 28, 8319–8346. [Google Scholar] [CrossRef]
- Ford, T.W.; Labosier, C.F. Meteorological conditions associated with the onset of flash drought in the Eastern United States. Agric. For. Meteorol. 2017, 247, 414–423. [Google Scholar] [CrossRef]
- Mo, K.C.; Lettenmaier, D.P. Heat wave flash droughts in decline. Geophys. Res. Lett. 2015, 42, 2823–2829. [Google Scholar] [CrossRef]
- Hobbins, M.; Wood, A.; McEvoy, D.; Huntington, J.; Morton, C.; Verdin, J.; Anderson, M.; Hain, C. The Evaporative Demand Drought Index: Part I-Linking Drought Evolution to Variations in Evaporative Demand. J. Hydrometeorol. 2016, 17, 1745–1761. [Google Scholar] [CrossRef]
- Stegehuis, A.I.; Vautard, R.; Ciais, P.; Teuling, A.J.; Jung, M.; Yiou, P. Summer temperatures in Europe and land heat fluxes in observation-based data and regional climate model simulations. Clim. Dyn. 2013, 41, 455–477. [Google Scholar] [CrossRef]
- Teuling, A.J.; Seneviratne, S.I.; Stöckli, R.; Reichstein, M.; Moors, E.; Ciais, P.; Luyssaert, S.; van den Hurk, B.; Ammann, C.; Bernhofer, C.; et al. Contrasting response of European forest and grassland energy exchange to heatwaves. Nat. Geosci. 2010, 3, 722. [Google Scholar] [CrossRef]
- Seneviratne, S.I.; Lehner, I.; Gurtz, J.; Teuling, A.J.; Lang, H.; Moser, U.; Grebner, D.; Menzel, L.; Schroff, K.; Vitvar, T.; et al. Swiss prealpine Rietholzbach research catchment and lysimeter: 32 year time series and 2003 drought event. Water Resour. Res. 2012, 48. [Google Scholar] [CrossRef]
- Liu, Y.; Parolari, A.J.; Kumar, M.; Huang, C.-W.; Katul, G.G.; Porporato, A. Increasing atmospheric humidity and CO2 concentration alleviate forest mortality risk. Proc. Natl. Acad. Sci. USA 2017, 114, 9918–9923. [Google Scholar] [CrossRef] [PubMed]
- Ahmadi, B.; Moradkhani, H. Revisiting Hydrological Drought Propagation and Recovery Considering Water Quantity and Quality. Hydrol. Proc. 2019, 1–14. [Google Scholar] [CrossRef]


| Data | Original Spatial Resolution | Temporal Resolution | Unit | Type |
|---|---|---|---|---|
| Gross Primary Productivity (GPP) (MOD17A2) | 1 km | 8 days | kgC/m2 | Remotely sensed by MODIS |
| Evapotranspiration (ET) (MOD16A2) | 1 km | 8 days | mm | Remotely sensed by MODIS |
| Land Cover (MCD12Q1) | 500 m | monthly | -------- | Remotely sensed by MODIS |
| Soil Moisture (NLDAS-2) | 1/8° (~12 km) | 8 days | cm/cm | Simulated by VIC |
| Category | Description | Percentiles (%) |
|---|---|---|
| N | Normal/wet condition | 31 to 100 |
| D0 | Abnormally dry | 21 to 30 |
| D1 | Moderate drought | 11 to 20 |
| D2 | Severe drought | 6 to 10 |
| D3 | Extreme drought | 3 to 5 |
| D4 | Exceptional drought | 0 to 2 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ahmadi, B.; Ahmadalipour, A.; Tootle, G.; Moradkhani, H. Remote Sensing of Water Use Efficiency and Terrestrial Drought Recovery across the Contiguous United States. Remote Sens. 2019, 11, 731. https://doi.org/10.3390/rs11060731
Ahmadi B, Ahmadalipour A, Tootle G, Moradkhani H. Remote Sensing of Water Use Efficiency and Terrestrial Drought Recovery across the Contiguous United States. Remote Sensing. 2019; 11(6):731. https://doi.org/10.3390/rs11060731
Chicago/Turabian StyleAhmadi, Behzad, Ali Ahmadalipour, Glenn Tootle, and Hamid Moradkhani. 2019. "Remote Sensing of Water Use Efficiency and Terrestrial Drought Recovery across the Contiguous United States" Remote Sensing 11, no. 6: 731. https://doi.org/10.3390/rs11060731
APA StyleAhmadi, B., Ahmadalipour, A., Tootle, G., & Moradkhani, H. (2019). Remote Sensing of Water Use Efficiency and Terrestrial Drought Recovery across the Contiguous United States. Remote Sensing, 11(6), 731. https://doi.org/10.3390/rs11060731