Metrics of Lidar-Derived 3D Vegetation Structure Reveal Contrasting Effects of Horizontal and Vertical Forest Heterogeneity on Bird Species Richness
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Field-Based Vegetation Structure Data
2.3. Lidar Data
2.4. Lidar-Derived Metrics
2.4.1. Canopy Height Metrics
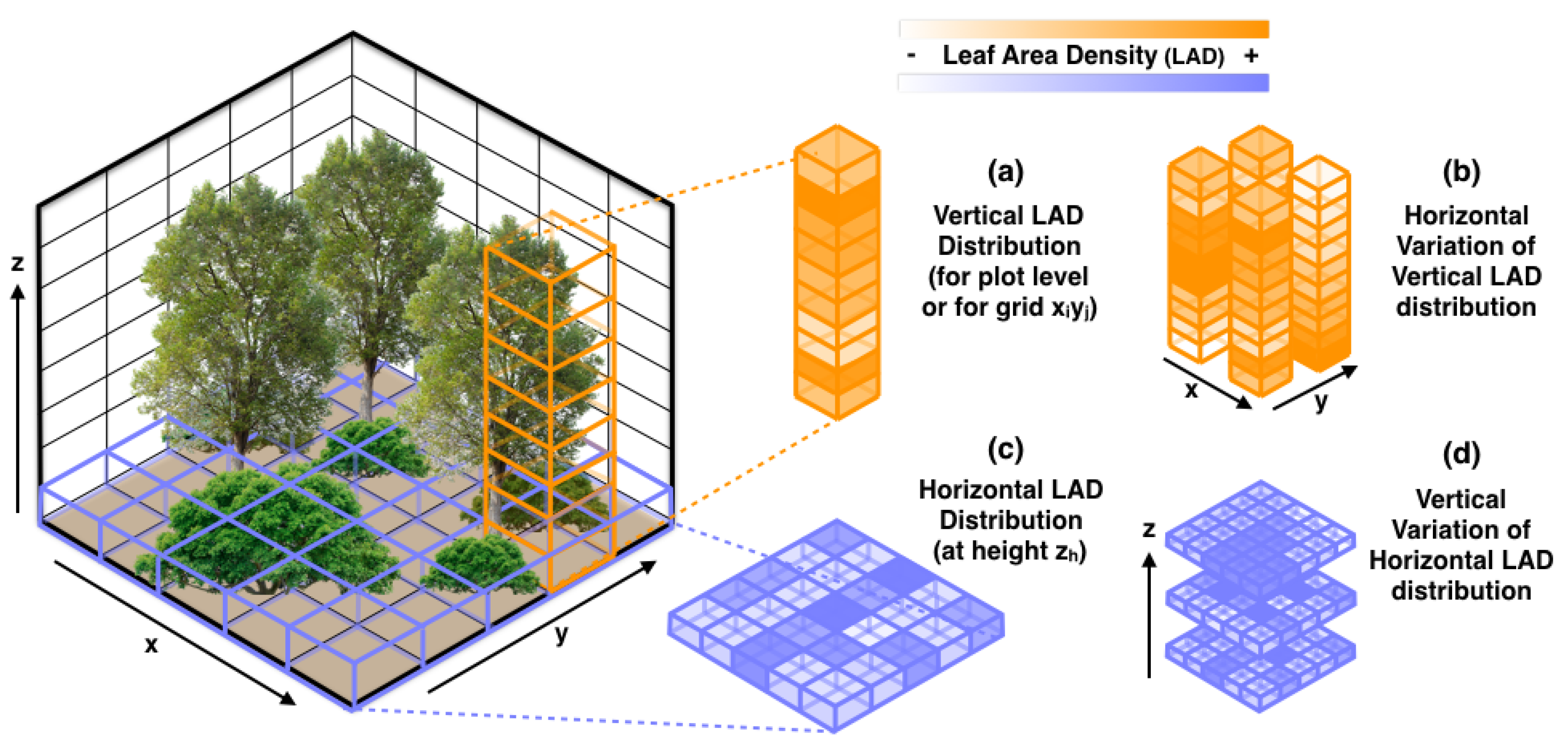
2.4.2. LAD-Based Metrics
2.5. Bird Species Richness
2.6. Statistical Analysis
3. Results
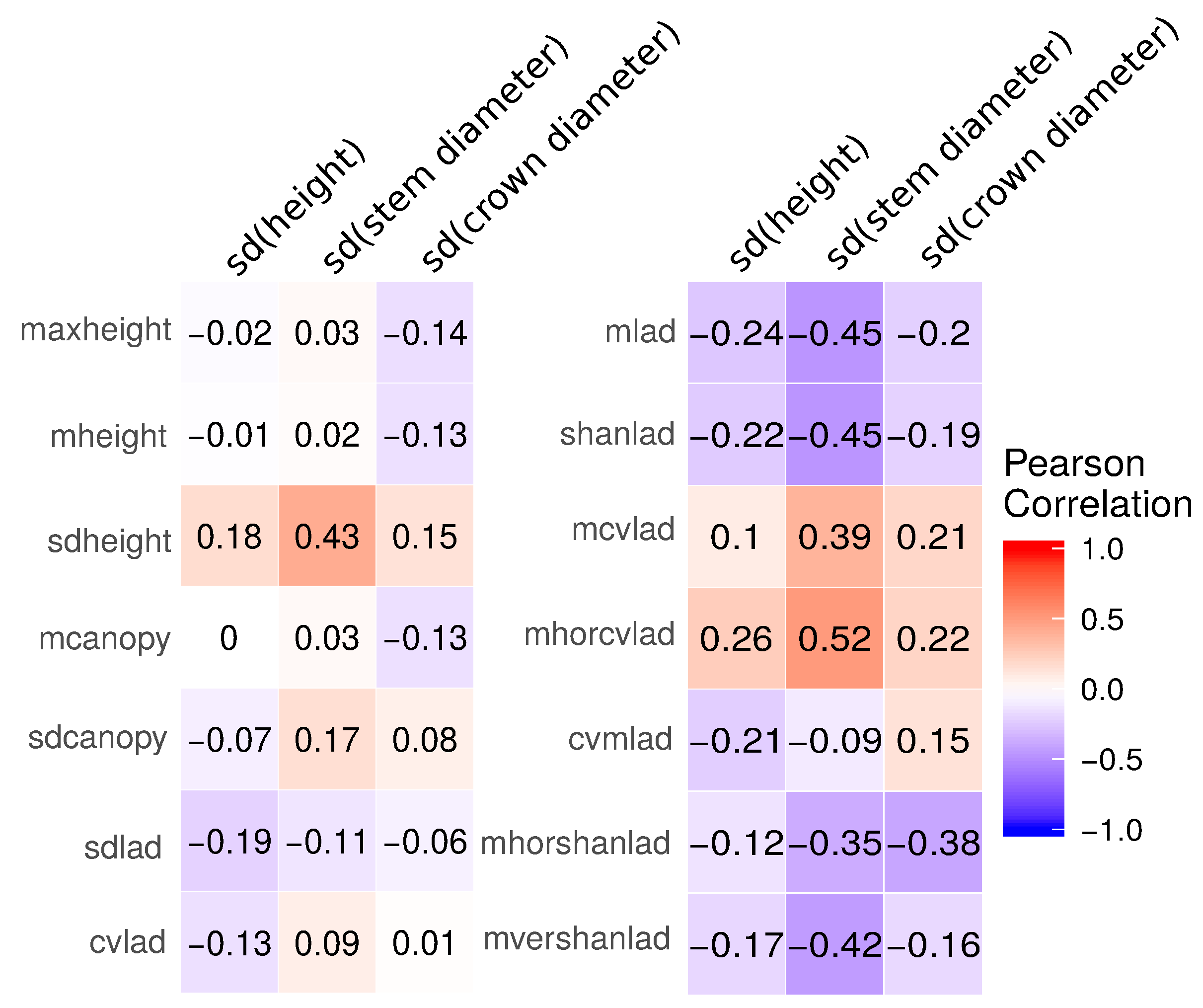
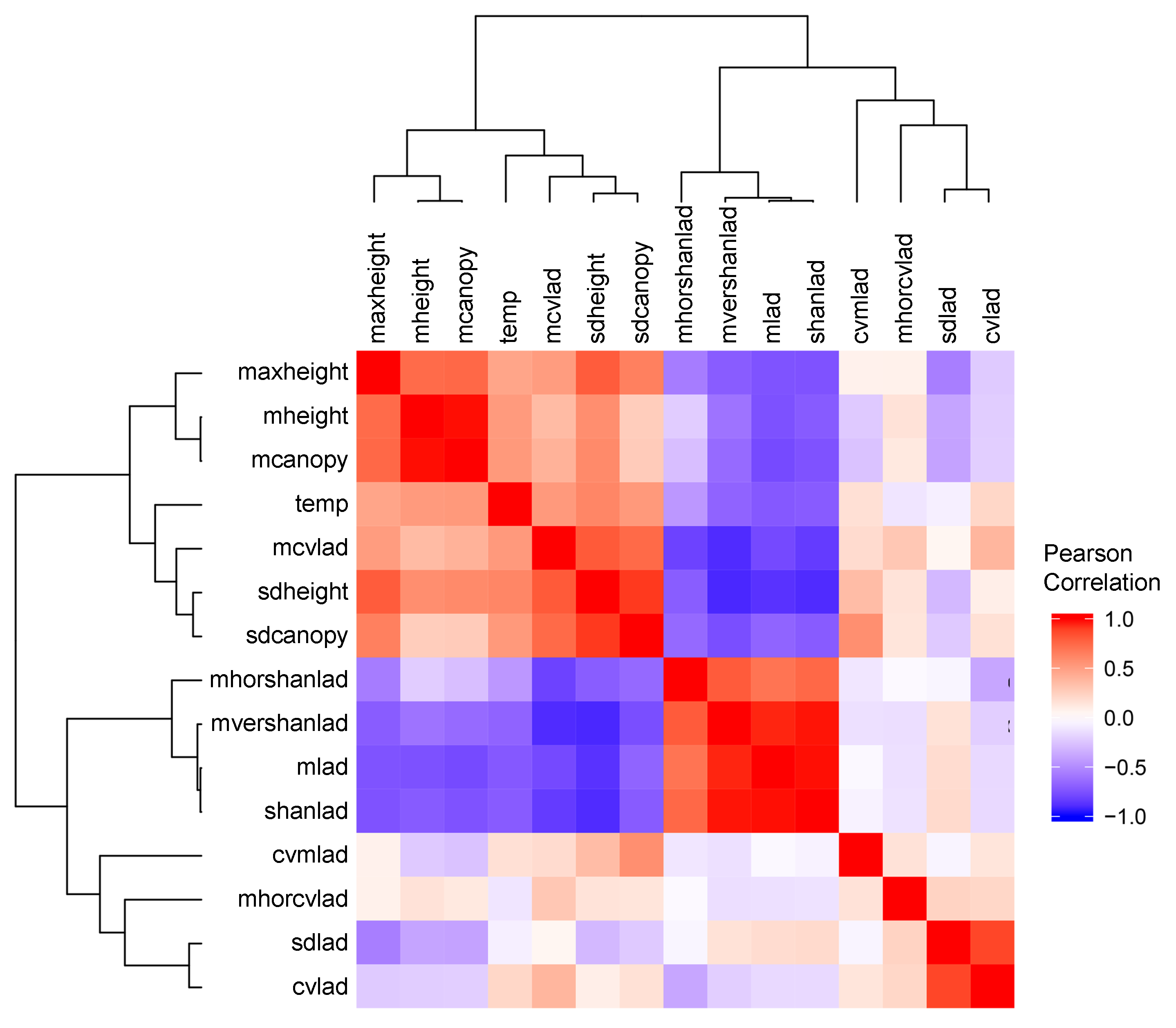
3.1. Field-Based Vegetation Structure and Lidar-Derived Metrics
3.2. Bird Plots
3.2.1. Lidar-Derived Metrics
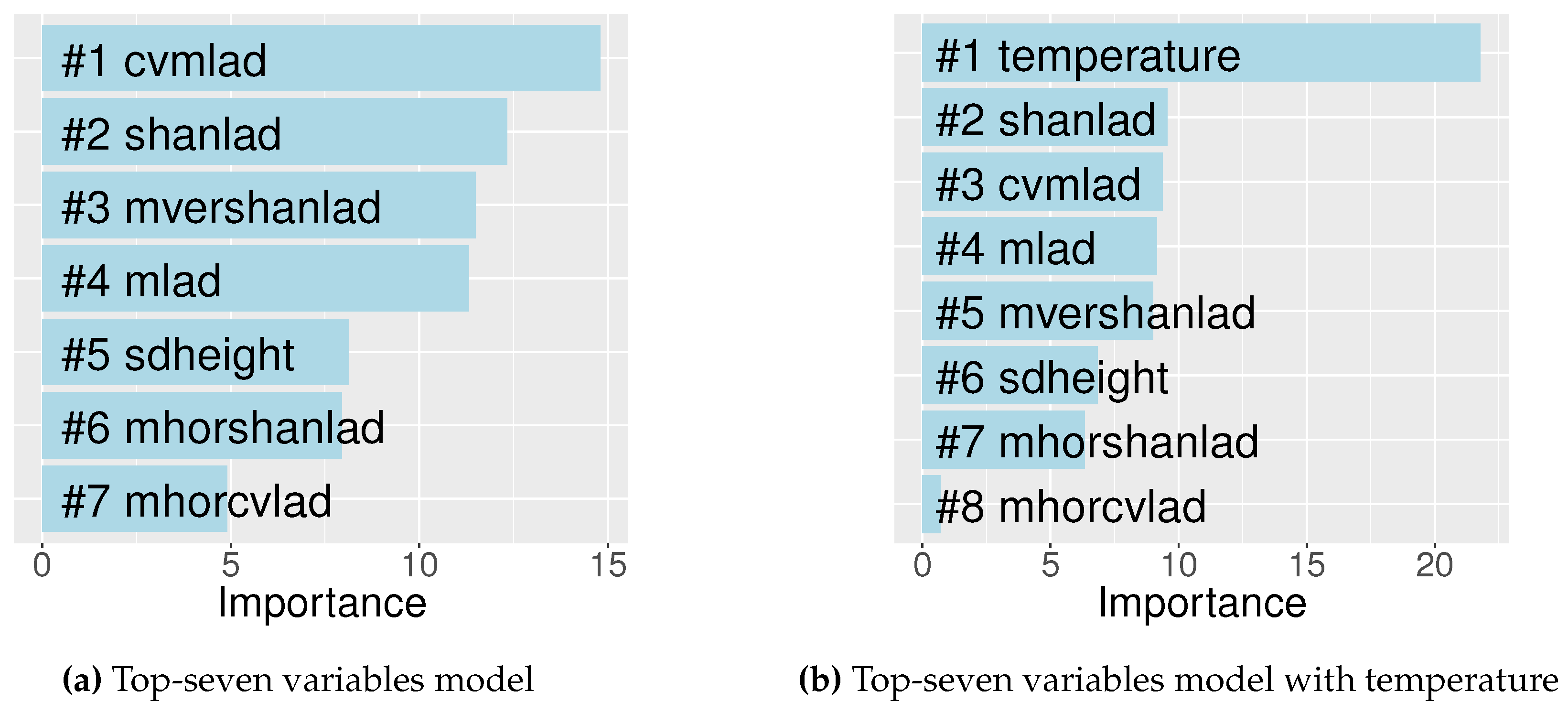
3.2.2. Bird Species Richness Models
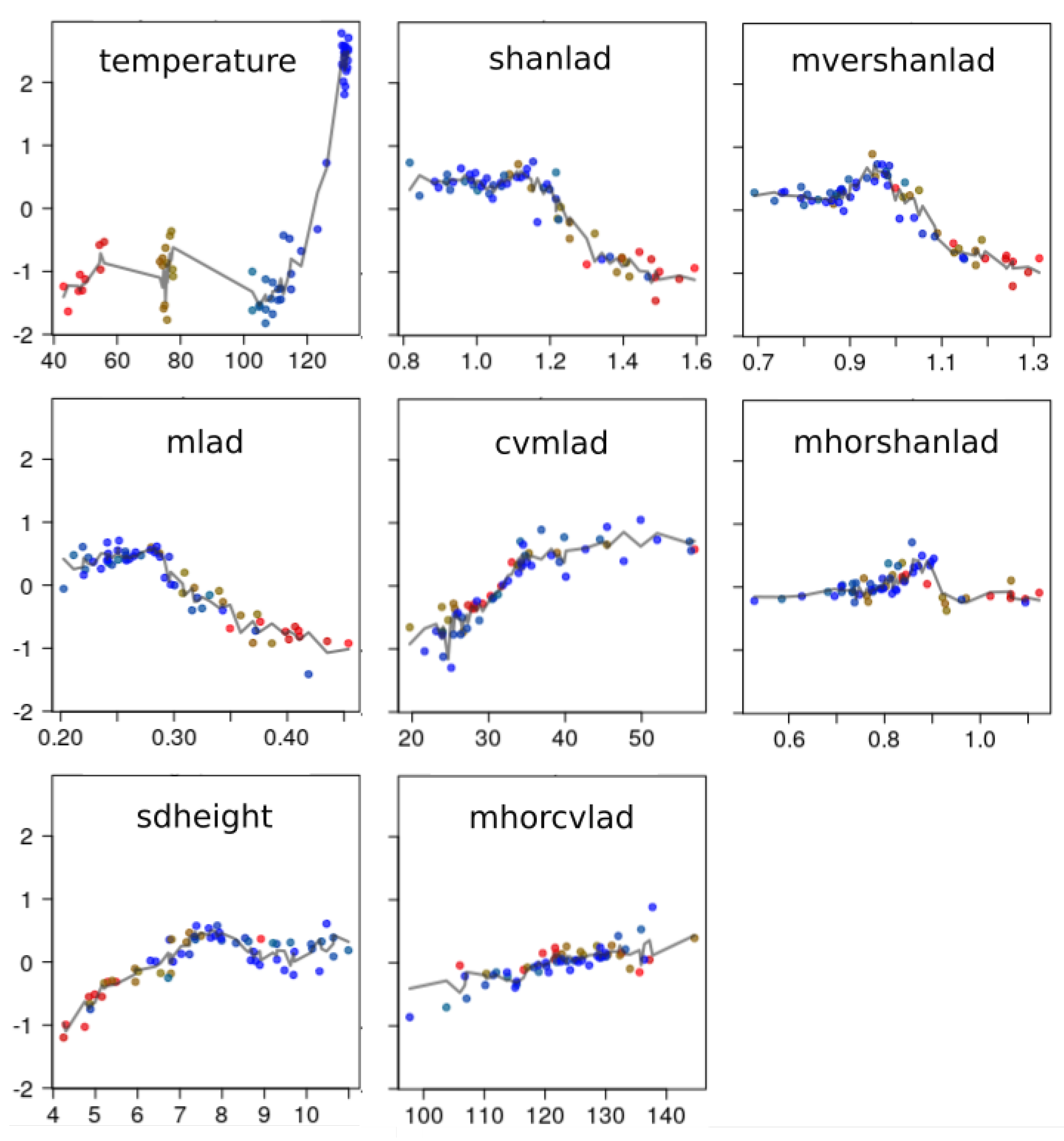
3.2.3. Shapes of Bird Richness Response
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- MacArthur, R.H.; MacArthur, J.W. On bird species diversity. Ecology 1961, 42, 594–598. [Google Scholar] [CrossRef]
- Lack, D. The numbers of bird species on islands. Bird Study 1969, 16, 193–209. [Google Scholar] [CrossRef]
- Tews, J.; Brose, U.; Grimm, V.; Tielbörger, K.; Wichmann, M.; Schwager, M.; Jeltsch, F. Animal species diversity driven by habitat heterogeneity/diversity: The importance of keystone structures. J. Biogeogr. 2004, 31, 79–92. [Google Scholar] [CrossRef]
- Bramer, I.; Anderson, B.J.; Bennie, J.; Bladon, A.J.; De Frenne, P.; Hemming, D.; Hill, R.A.; Kearney, M.R.; Körner, C.; Korstjens, A.H.; et al. Advances in Monitoring and Modelling Climate at Ecologically Relevant Scales. Adv. Ecol. Res. 2018, 58, 101–161. [Google Scholar]
- Bergen, K.; Goetz, S.; Dubayah, R.; Henebry, G.; Hunsaker, C.; Imhoff, M.; Nelson, R.; Parker, G.; Radeloff, V. Remote sensing of vegetation 3-D structure for biodiversity and habitat: Review and implications for lidar and radar spaceborne missions. J. Geophys. Res. Biogeosci. 2009, 114. [Google Scholar] [CrossRef]
- Vogeler, J.C.; Hudak, A.T.; Vierling, L.A.; Evans, J.; Green, P.; Vierling, K.T. Terrain and vegetation structural influences on local avian species richness in two mixed-conifer forests. Remote Sens. Environ. 2014, 147, 13–22. [Google Scholar] [CrossRef]
- Hinsley, S.A.; Hill, R.A.; Bellamy, P.E.; Balzter, H. The Application of Lidar in Woodland Bird Ecology. Photogramm. Eng. Remote Sens. 2006, 72, 1399–1406. [Google Scholar] [CrossRef]
- Müller, J.; Stadler, J.; Brandl, R. Composition versus physiognomy of vegetation as predictors of bird assemblages: The role of lidar. Remote Sens. Environ. 2010, 114, 490–495. [Google Scholar] [CrossRef]
- Müller, J.; Brandl, R.; Buchner, J.; Pretzsch, H.; Seifert, S.; Strätz, C.; Veith, M.; Fenton, B. From ground to above canopy—Bat activity in mature forests is driven by vegetation density and height. For. Ecol. Manag. 2013, 306, 179–184. [Google Scholar] [CrossRef]
- Gouveia, S.F.; Villalobos, F.; Dobrovolski, R.; Beltrão-Mendes, R.; Ferrari, S.F. Forest structure drives global diversity of primates. J. Anim. Ecol. 2014, 83, 1523–1530. [Google Scholar] [CrossRef] [PubMed]
- Shine, R.; Barrott, E.G.; Elphick, M.J. Some like it hot: Effects of forest clearing on nest temperatures of montane reptiles. Ecology 2002, 83, 2808–2815. [Google Scholar] [CrossRef]
- Müller, J.; Bae, S.; Röder, J.; Chao, A.; Didham, R.K. Airborne LiDAR reveals context dependence in the effects of canopy architecture on arthropod diversity. For. Ecol. Manag. 2014, 312, 129–137. [Google Scholar] [CrossRef]
- Listopad, C.M.; Masters, R.E.; Drake, J.; Weishampel, J.; Branquinho, C. Structural diversity indices based on airborne LiDAR as ecological indicators for managing highly dynamic landscapes. Ecol. Indic. 2015, 57, 268–279. [Google Scholar] [CrossRef]
- Davies, A.B.; Asner, G.P. Advances in animal ecology from 3D-LiDAR ecosystem mapping. Trends Ecol. Evolut. 2014, 29, 681–691. [Google Scholar] [CrossRef]
- Simonson, W.D.; Allen, H.D.; Coomes, D.A. Applications of airborne lidar for the assessment of animal species diversity. Methods Ecol. Evolut. 2014, 5, 719–729. [Google Scholar] [CrossRef]
- Goetz, S.; Steinberg, D.; Dubayah, R.; Blair, B. Laser remote sensing of canopy habitat heterogeneity as a predictor of bird species richness in an eastern temperate forest, USA. Remote Sens. Environ. 2007, 108, 254–263. [Google Scholar] [CrossRef]
- Goetz, S.J.; Steinberg, D.; Betts, M.G.; Holmes, R.T.; Doran, P.J.; Dubayah, R.; Hofton, M. Lidar remote sensing variables predict breeding habitat of a Neotropical migrant bird. Ecology 2010, 91, 1569–1576. [Google Scholar] [CrossRef]
- Stein, A.; Gerstner, K.; Kreft, H. Environmental heterogeneity as a universal driver of species richness across taxa, biomes and spatial scales. Ecol. Lett. 2014, 17, 866–880. [Google Scholar] [CrossRef] [PubMed]
- De Araújo, W.S. Different relationships between galling and non-galling herbivore richness and plant species richness: A meta-analysis. Arthropod-Plant Interact. 2013, 7, 373–377. [Google Scholar] [CrossRef]
- Richter, K.; Stelling, N.; Maas, H. Correcting attenuation effects caused by interactions in the forest canopy in full-waveform airborne laser scanner data. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2014, 40, 273. [Google Scholar] [CrossRef]
- Weiss, M.; Baret, F.; Smith, G.; Jonckheere, I.; Coppin, P. Review of methods for in situ leaf area index (LAI) determination: Part II. Estimation of LAI, errors and sampling. Agric. For. Meteorol. 2004, 121, 37–53. [Google Scholar] [CrossRef]
- Waring, R.H. Estimating forest growth and efficiency in relation to canopy leaf area. Adv. Ecol. Res. 1983, 13, 327–354. [Google Scholar]
- Kamoske, A.G.; Dahlin, K.M.; Stark, S.C.; Serbin, S.P. Leaf area density from airborne LiDAR: Comparing sensors and resolutions in a temperate broadleaf forest ecosystem. For. Ecol. Manag. 2019, 433, 364–375. [Google Scholar] [CrossRef]
- Almeida, D.R.A.d.; Stark, S.C.; Shao, G.; Schietti, J.; Nelson, B.W.; Silva, C.A.; Gorgens, E.B.; Valbuena, R.; Papa, D.d.A.; Brancalion, P.H.S. Optimizing the Remote Detection of Tropical Rainforest Structure with Airborne Lidar: Leaf Area Profile Sensitivity to Pulse Density and Spatial Sampling. Remote Sens. 2019, 11, 92. [Google Scholar] [CrossRef]
- Bouvier, M.; Durrieu, S.; Fournier, R.A.; Renaud, J.P. Generalizing predictive models of forest inventory attributes using an area-based approach with airborne LiDAR data. Remote Sens. Environ. 2015, 156, 322–334. [Google Scholar] [CrossRef]
- White, J.C.; Coops, N.C.; Wulder, M.A.; Vastaranta, M.; Hilker, T.; Tompalski, P. Remote sensing technologies for enhancing forest inventories: A review. Can. J. Remote Sens. 2016, 42, 619–641. [Google Scholar] [CrossRef]
- Kampe, T.U.; Johnson, B.R.; Kuester, M.A.; Keller, M. NEON: The first continental-scale ecological observatory with airborne remote sensing of vegetation canopy biochemistry and structure. J. Appl. Remote Sens. 2010, 4, 043510. [Google Scholar] [CrossRef]
- National Ecological Observatory Network. Data Product NEON.DOM.SITE.DP1.10098.001; Battelle: Boulder, CO, USA, 2016; Available online: http://data.neonscience.org (accessed on 20 January 2019).
- National Ecological Observatory Network. Data Product NEON.DOM.SITE.DP1.30003.001; Battelle: Boulder, CO, USA, 2016; Available online: http://data.neonscience.org (accessed on 1 November 2018).
- Roussel, J.; Auty, D. lidR: Airborne LiDAR Data Manipulation and Visualization for Forestry Applications. 2018. Available online: https://rdrr.io/cran/lidR/ (accessed on 15 January 2019).
- R Development Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2013. [Google Scholar]
- Hijmans, R. Raster: Geographic Analysis and Modeling with Raster Data, 2nd ed.; R Foundation for Statistical Computing: Vienna, Austria, 2010; pp. 1–204. Available online: https://CRAN.R-project.org/package=raster (accessed on 15 December 2018).
- Detto, M.; Asner, G.P.; Muller-Landau, H.C.; Sonnentag, O. Spatial variability in tropical forest leaf area density from multireturn lidar and modeling. J. Geophys. Res. Biogeosci. 2015, 120, 294–309. [Google Scholar] [CrossRef]
- Jonckheere, I.; Fleck, S.; Nackaerts, K.; Muys, B.; Coppin, P.; Weiss, M.; Baret, F. Review of methods for in situ leaf area index determination: Part I. Theories, sensors and hemispherical photography. Agric. For. Meteorol. 2004, 121, 19–35. [Google Scholar] [CrossRef]
- Hopkinson, C.; Lovell, J.; Chasmer, L.; Jupp, D.; Kljun, N.; van Gorsel, E. Integrating terrestrial and airborne lidar to calibrate a 3D canopy model of effective leaf area index. Remote Sens. Environ. 2013, 136, 301–314. [Google Scholar] [CrossRef]
- Bréda, N.J. Ground-based measurements of leaf area index: a review of methods, instruments and current controversies. J. Exp. Bot. 2003, 54, 2403–2417. [Google Scholar] [CrossRef] [PubMed]
- Tang, H.; Brolly, M.; Zhao, F.; Strahler, A.H.; Schaaf, C.L.; Ganguly, S.; Zhang, G.; Dubayah, R. Deriving and validating Leaf Area Index (LAI) at multiple spatial scales through lidar remote sensing: A case study in Sierra National Forest, CA. Remote Sens. Environ. 2014, 143, 131–141. [Google Scholar] [CrossRef]
- Pluim, J.P.; Maintz, J.A.; Viergever, M.A. Mutual-information-based registration of medical images: A survey. IEEE Trans. Med. Imaging 2003, 22, 986–1004. [Google Scholar] [CrossRef] [PubMed]
- National Ecological Observatory Network. Data Product NEON.DOM.SITE.DP1.10003.001; Battelle: Boulder, CO, USA, 2016; Available online: http://data.neonscience.org (accessed on 20 January 2019).
- Ralph, C.J.; Geupel, G.R.; Pyle, P.; Martin, T.E.; DeSante, D.F. Handbook of Field Methods for Monitoring Landbirds; USDA Forest Service/UNL Faculty Publications: Berkeley, CA, USA, 1993; p. 105.
- Hijmans, R.J.; Cameron, S.E.; Parra, J.L.; Jones, P.G.; Jarvis, A. Very high resolution interpolated climate surfaces for global land areas. Int. J. Climatol. 2005, 25, 1965–1978. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Prasad, A.M.; Iverson, L.R.; Liaw, A. Newer classification and regression tree techniques: Bagging and random forests for ecological prediction. Ecosystems 2006, 9, 181–199. [Google Scholar] [CrossRef]
- Cutler, D.R.; Edwards, T.C., Jr.; Beard, K.H.; Cutler, A.; Hess, K.T.; Gibson, J.; Lawler, J.J. Random forests for classification in ecology. Ecology 2007, 88, 2783–2792. [Google Scholar] [CrossRef]
- Carrasco, L.; Mashiko, M.; Toquenaga, Y. Application of random forest algorithm for studying habitat selection of colonial herons and egrets in human-influenced landscapes. Ecol. Res. 2014, 29, 483–491. [Google Scholar] [CrossRef]
- Genuer, R.; Poggi, J.M.; Tuleau-Malot, C. Variable selection using random forests. Pattern Recognit. Lett. 2010, 31, 2225–2236. [Google Scholar] [CrossRef]
- Palczewska, A.; Palczewski, J.; Robinson, R.M.; Neagu, D. Interpreting random forest classification models using a feature contribution method. Integr. Reusable Syst. 2014, 193–218. [Google Scholar]
- Asner, G.P.; Mascaro, J.; Muller-Landau, H.C.; Vieilledent, G.; Vaudry, R.; Rasamoelina, M.; Hall, J.S.; Van Breugel, M. A universal airborne LiDAR approach for tropical forest carbon mapping. Oecologia 2012, 168, 1147–1160. [Google Scholar] [CrossRef] [PubMed]
- Palace, M.W.; Sullivan, F.B.; Ducey, M.J.; Treuhaft, R.N.; Herrick, C.; Shimbo, J.Z.; Mota-E-Silva, J. Estimating forest structure in a tropical forest using field measurements, a synthetic model and discrete return lidar data. Remote Sens. Environ. 2015, 161, 1–11. [Google Scholar] [CrossRef]
- Deo, R.K.; Russell, M.B.; Domke, G.M.; Woodall, C.W.; Falkowski, M.J.; Cohen, W.B. Using Landsat time-series and LiDAR to inform aboveground forest biomass baselines in northern Minnesota, USA. Can. J. Remote Sens. 2017, 43, 28–47. [Google Scholar] [CrossRef]
- Parker, G.G.; Tibbs, D.J. Structural phenology of the leaf community in the canopy of a Liriodendron tulipifera L. forest in Maryland, USA. For. Sci. 2004, 50, 387–397. [Google Scholar]
- Raich, J.W.; Russell, A.E.; Kitayama, K.; Parton, W.J.; Vitousek, P.M. Temperature influences carbon accumulation in moist tropical forests. Ecology 2006, 87, 76–87. [Google Scholar] [CrossRef]
- Stegen, J.C.; Swenson, N.G.; Enquist, B.J.; White, E.P.; Phillips, O.L.; Jørgensen, P.M.; Weiser, M.D.; Mendoza, A.M.; Vargas, P.N. Variation in above-ground forest biomass across broad climatic gradients. Glob. Ecol. Biogeogr. 2011, 20, 744–754. [Google Scholar] [CrossRef]
- Korhonen, L.; Korpela, I.; Heiskanen, J.; Maltamo, M. Airborne discrete-return LIDAR data in the estimation of vertical canopy cover, angular canopy closure and leaf area index. Remote Sens. Environ. 2011, 115, 1065–1080. [Google Scholar] [CrossRef]
- Liu, J.; Skidmore, A.K.; Jones, S.; Wang, T.; Heurich, M.; Zhu, X.; Shi, Y. Large off-nadir scan angle of airborne LiDAR can severely affect the estimates of forest structure metrics. ISPRS J. Photogramm. Remote Sens. 2018, 136, 13–25. [Google Scholar] [CrossRef]
- Disney, M.I.; Kalogirou, V.; Lewis, P.; Prieto-Blanco, A.; Hancock, S.; Pfeifer, M. Simulating the impact of discrete-return lidar system and survey characteristics over young conifer and broadleaf forests. Remote Sens. Environ. 2010, 114, 1546–1560. [Google Scholar] [CrossRef]
- Graf, R.F.; Mathys, L.; Bollmann, K. Habitat assessment for forest dwelling species using LiDAR remote sensing: Capercaillie in the Alps. For. Ecol. Manag. 2009, 257, 160–167. [Google Scholar] [CrossRef]
- Smart, L.; Swenson, J.; Christensen, N.; Sexton, J. Three-dimensional characterization of pine forest type and red-cockaded woodpecker habitat by small-footprint, discrete-return lidar. For. Ecol. Manag. 2012, 281, 100–110. [Google Scholar] [CrossRef]
- Hancock, S.; Anderson, K.; Disney, M.; Gaston, K.J. Measurement of fine-spatial-resolution 3D vegetation structure with airborne waveform lidar: Calibration and validation with voxelised terrestrial lidar. Remote Sens. Environ. 2017, 188, 37–50. [Google Scholar] [CrossRef]
- Ferger, S.W.; Schleuning, M.; Hemp, A.; Howell, K.M.; Böhning-Gaese, K. Food resources and vegetation structure mediate climatic effects on species richness of birds. Glob. Ecol. Biogeogr. 2014, 23, 541–549. [Google Scholar] [CrossRef]
- Carrasco, L.; Norton, L.; Henrys, P.; Siriwardena, G.M.; Rhodes, C.J.; Rowland, C.; Morton, D. Habitat diversity and structure regulate British bird richness: Implications of non-linear relationships for conservation. Biol. Conserv. 2018, 226, 256–263. [Google Scholar] [CrossRef]
- Flaspohler, D.J.; Giardina, C.P.; Asner, G.P.; Hart, P.; Price, J.; Lyons, C.K.; Castaneda, X. Long-term effects of fragmentation and fragment properties on bird species richness in Hawaiian forests. Biol. Conserv. 2010, 143, 280–288. [Google Scholar] [CrossRef]
- Huang, Q.; Swatantran, A.; Dubayah, R.; Goetz, S.J. The influence of vegetation height heterogeneity on forest and woodland bird species richness across the United States. PLoS ONE 2014, 9, e103236. [Google Scholar] [CrossRef]
- Ding, T.S.; Liao, H.C.; Yuan, H.W. Breeding bird community composition in different successional vegetation in the montane coniferous forests zone of Taiwan. For. Ecol. Manag. 2008, 255, 2038–2048. [Google Scholar] [CrossRef]
- Falkowski, M.J.; Evans, J.S.; Martinuzzi, S.; Gessler, P.E.; Hudak, A.T. Characterizing forest succession with lidar data: An evaluation for the Inland Northwest, USA. Remote Sens. Environ. 2009, 113, 946–956. [Google Scholar] [CrossRef]
- Brawn, J.D.; Robinson, S.K.; Thompson, F.R., III. The role of disturbance in the ecology and conservation of birds. Ann. Rev. Ecol. Syst. 2001, 32, 251–276. [Google Scholar] [CrossRef]
- Wolf, A.T.; Howe, R.W.; Davis, G.J. Detectability of forest birds from stationary points in northern Wisconsin. In Monitoring Bird Populations by Point Counts; Gen. Tech. Rep. PSW-GTR-149; Ralph, C.J., Sauer, J.R., Droege, S., Eds.; US Department of Agriculture, Forest Service, Pacific Southwest Research Station: Albany, CA, USA, 1995; Volume 149, pp. 19–24. [Google Scholar]
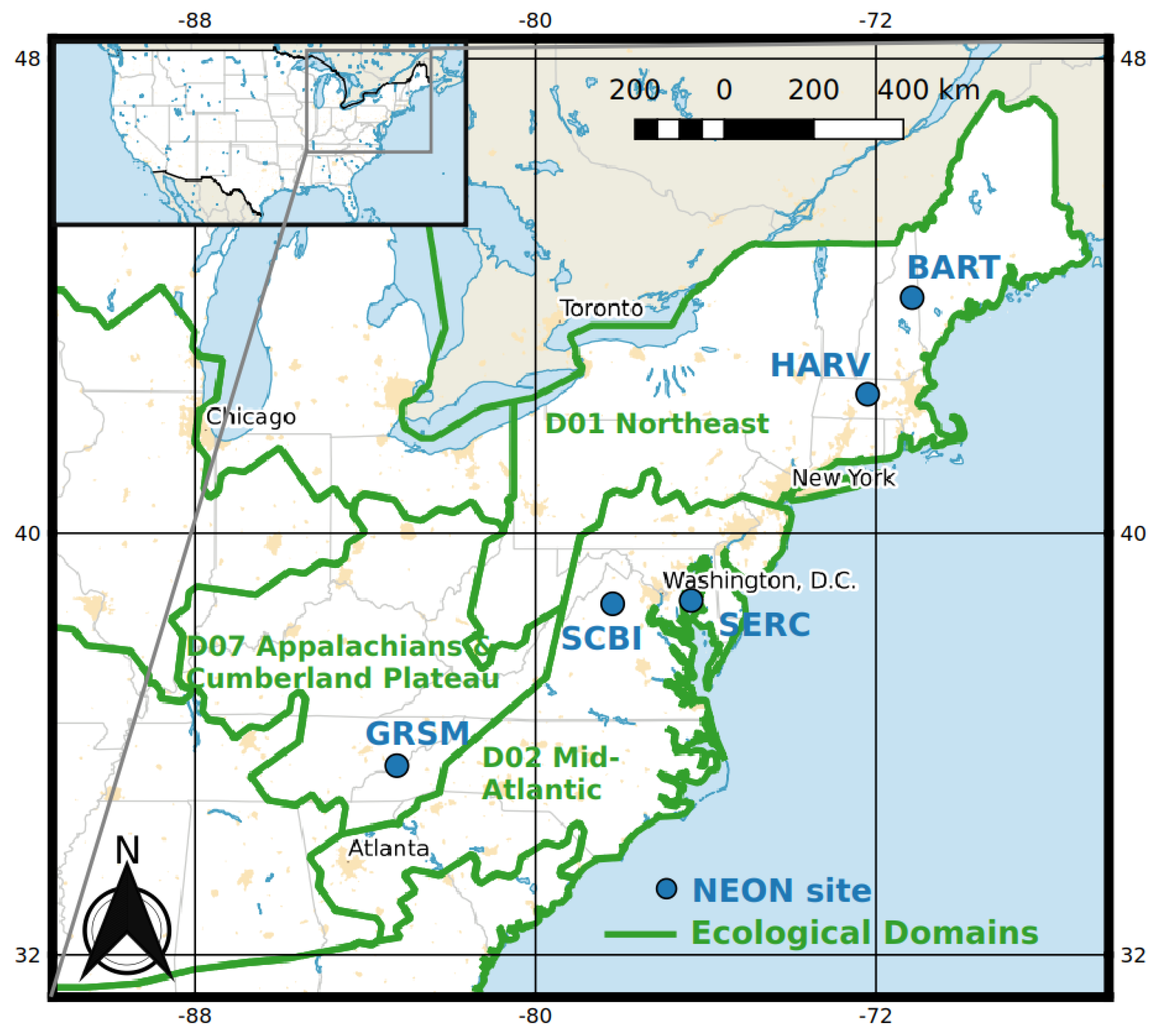
| Domain | Site | Description | N° of WPVS Plots (20 m × 20 m or 40 m × 40 m) | N° of Bird Plots (200 m × 200 m) |
|---|---|---|---|---|
| D01 Northeast | Harvard forest (HARV) | Northern, central, and transition forests with patches of conifer-dominated bogs and forest plantations. | 16 | 12 |
| Barlett Experimental Forest (BART) | Thirty percent of the forest is managed. Includes a wide range of forest patch sizes and structural distributions. | 30 | 9 | |
| D02 Mid-Atlantic | Smithsonian Conservation Biology Institute (SBCI) | Mainly deciduous forest with a well-defined ground cover and understory strata. | 19 | 18 |
| Smithsonian Environmental Research Center (SERC) | Mainly deciduous forest with abundant patches of cultivated fields. | 37 | 19 | |
| D07 Appalachians & Cumberland Plateau | Great Smoky Mountains National Park (GRSM) | Mainly deciduous forest with coniferous forest at higher altitudes. Thirty-six percent of the forest is old growth with more than 5000 plant species. | 4 | 3 |
| Type | Variable | Description |
|---|---|---|
| First return | maxheight | Maximum height from first returns |
| mheight | Mean height from first returns | |
| sdheight | Variation of height from first returns | |
| Canopy model | mcanopy | Mean height from the canopy model |
| sdcanopy | Variation of height from the canopy model | |
| LAD—plot level | sdlad | Vertical variation of LAD |
| cvlad | Vertical coefficient of variation of LAD | |
| LAD—grid level | mlad | Mean LAD across all voxels |
| shanlad | Shannon index of LAD variation across all voxels | |
| mcvlad | Mean vertical LAD coefficient of variation | |
| mhorcvlad | Mean horizontal LAD coefficient of variation | |
| cvmlad | Coefficient of variation of vertical LAD mean | |
| mhorshanlad | Mean Shannon index of horizontal LAD variation | |
| mvershanlad | Mean Shannon index of vertical LAD variation |
| Model | Variables | Variance Explained (%) |
|---|---|---|
| Top-seven variables | cvmlad, shanlad, mvershanlad, mlad, sdheight, mhorshanlad, mhorcvlad | 43.82 |
| Top-seven + temperature | cvmlad, shanlad, mvershanlad, sdheight, mlad, mhorshanlad, mhorcvlad, temperature | 61.34 |
| Top of canopy | maxheight, mheight, sdheight, mcanopy, sdcanopy | 32.10 |
| LAD-derived | All LAD derived variables (see Table 2) | 44.41 |
| LAD-derived (grid based) | All LAD grid based variables (see Table 2) | 42.71 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Carrasco, L.; Giam, X.; Papeş, M.; Sheldon, K.S. Metrics of Lidar-Derived 3D Vegetation Structure Reveal Contrasting Effects of Horizontal and Vertical Forest Heterogeneity on Bird Species Richness. Remote Sens. 2019, 11, 743. https://doi.org/10.3390/rs11070743
Carrasco L, Giam X, Papeş M, Sheldon KS. Metrics of Lidar-Derived 3D Vegetation Structure Reveal Contrasting Effects of Horizontal and Vertical Forest Heterogeneity on Bird Species Richness. Remote Sensing. 2019; 11(7):743. https://doi.org/10.3390/rs11070743
Chicago/Turabian StyleCarrasco, Luis, Xingli Giam, Monica Papeş, and Kimberly S. Sheldon. 2019. "Metrics of Lidar-Derived 3D Vegetation Structure Reveal Contrasting Effects of Horizontal and Vertical Forest Heterogeneity on Bird Species Richness" Remote Sensing 11, no. 7: 743. https://doi.org/10.3390/rs11070743
APA StyleCarrasco, L., Giam, X., Papeş, M., & Sheldon, K. S. (2019). Metrics of Lidar-Derived 3D Vegetation Structure Reveal Contrasting Effects of Horizontal and Vertical Forest Heterogeneity on Bird Species Richness. Remote Sensing, 11(7), 743. https://doi.org/10.3390/rs11070743





