Analysis of Retrackers’ Performances and Water Level Retrieval over the Ebro River Basin Using Sentinel-3
Abstract
:1. Introduction
2. Study Area and Database
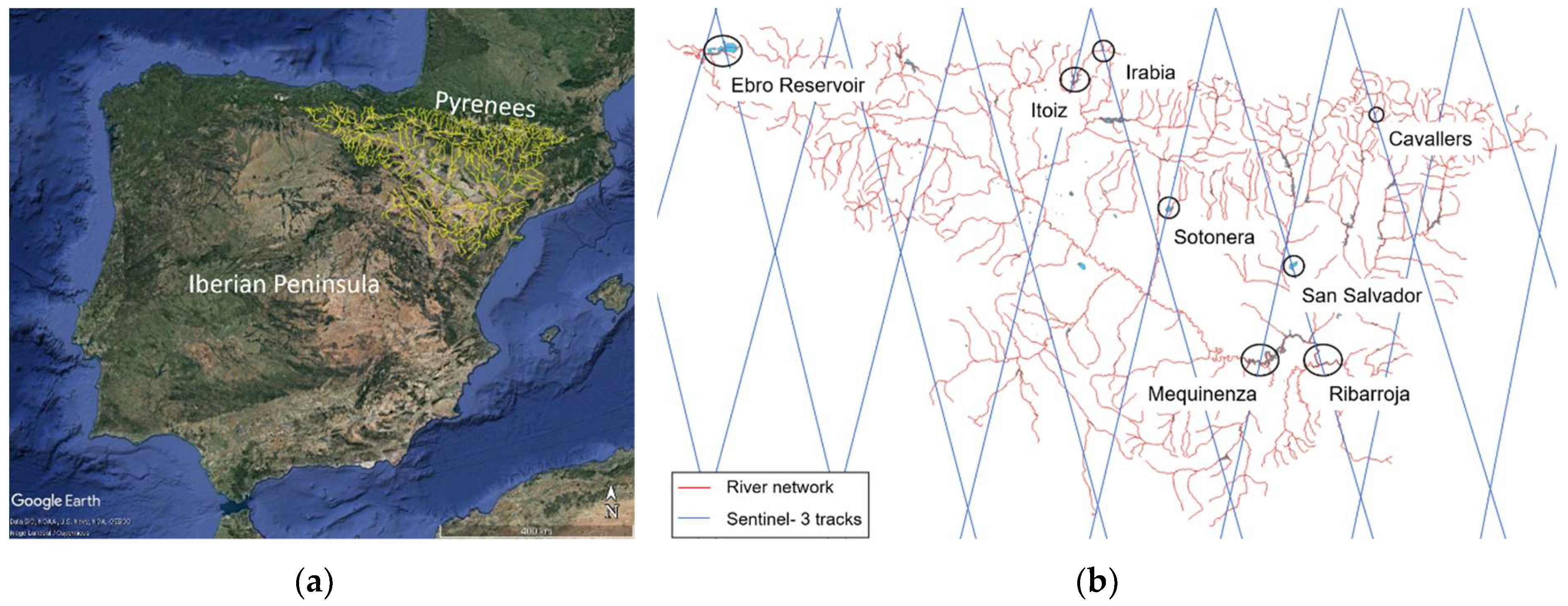
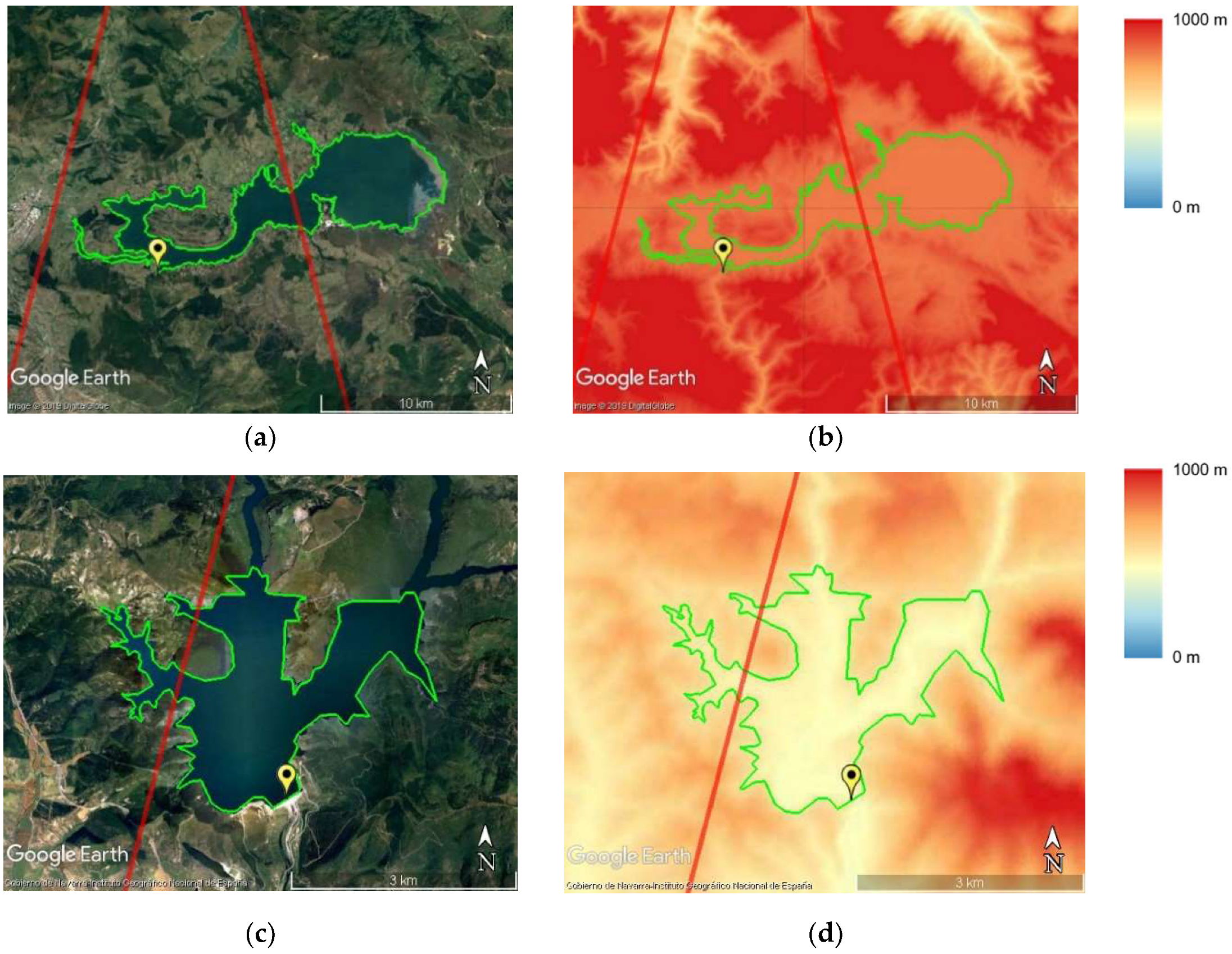
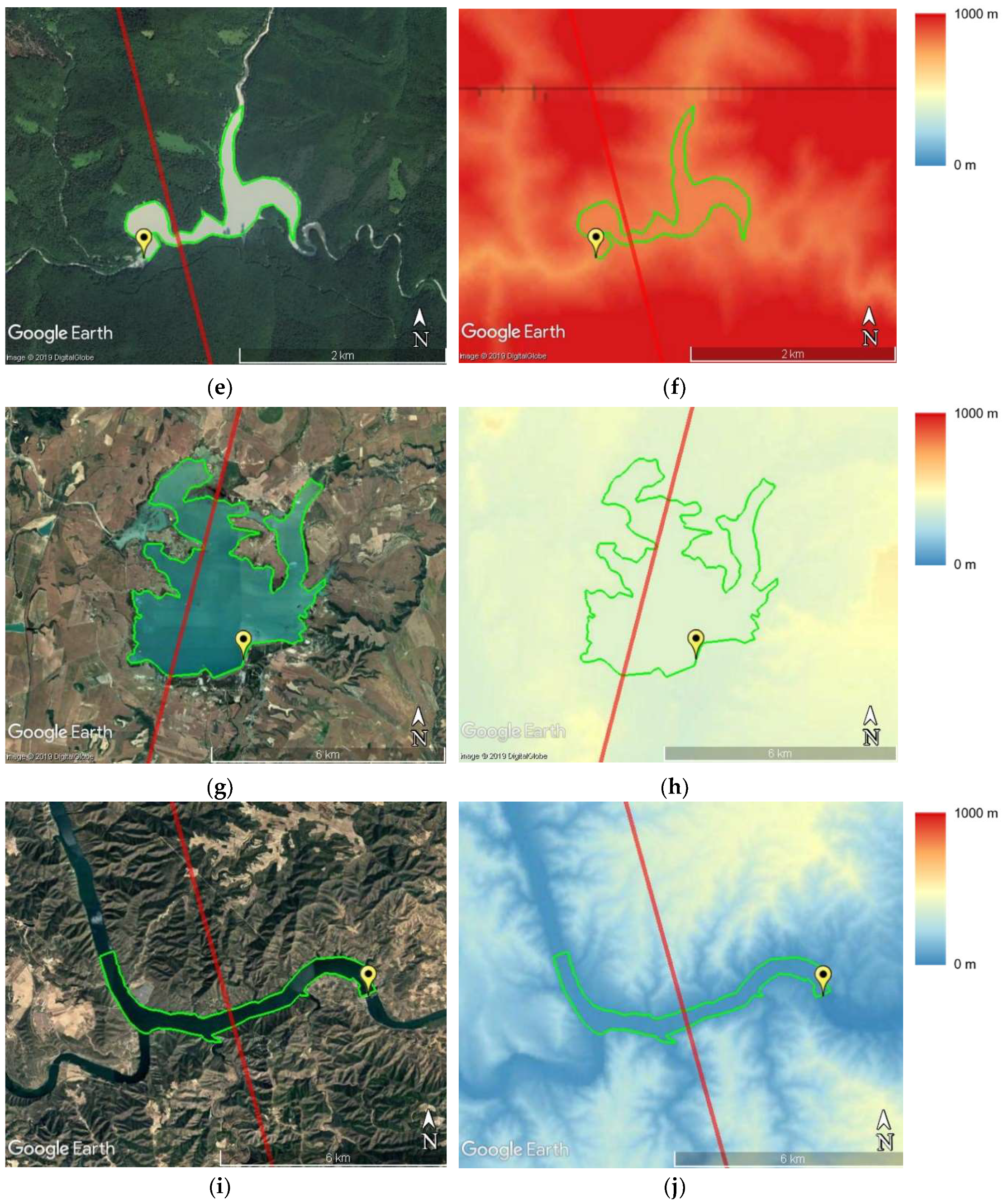
2.1. Study Area
2.2. Data Base
2.2.1. Sentinel-3
2.2.2. In Situ Data
2.2.3. Digital Elevation Model
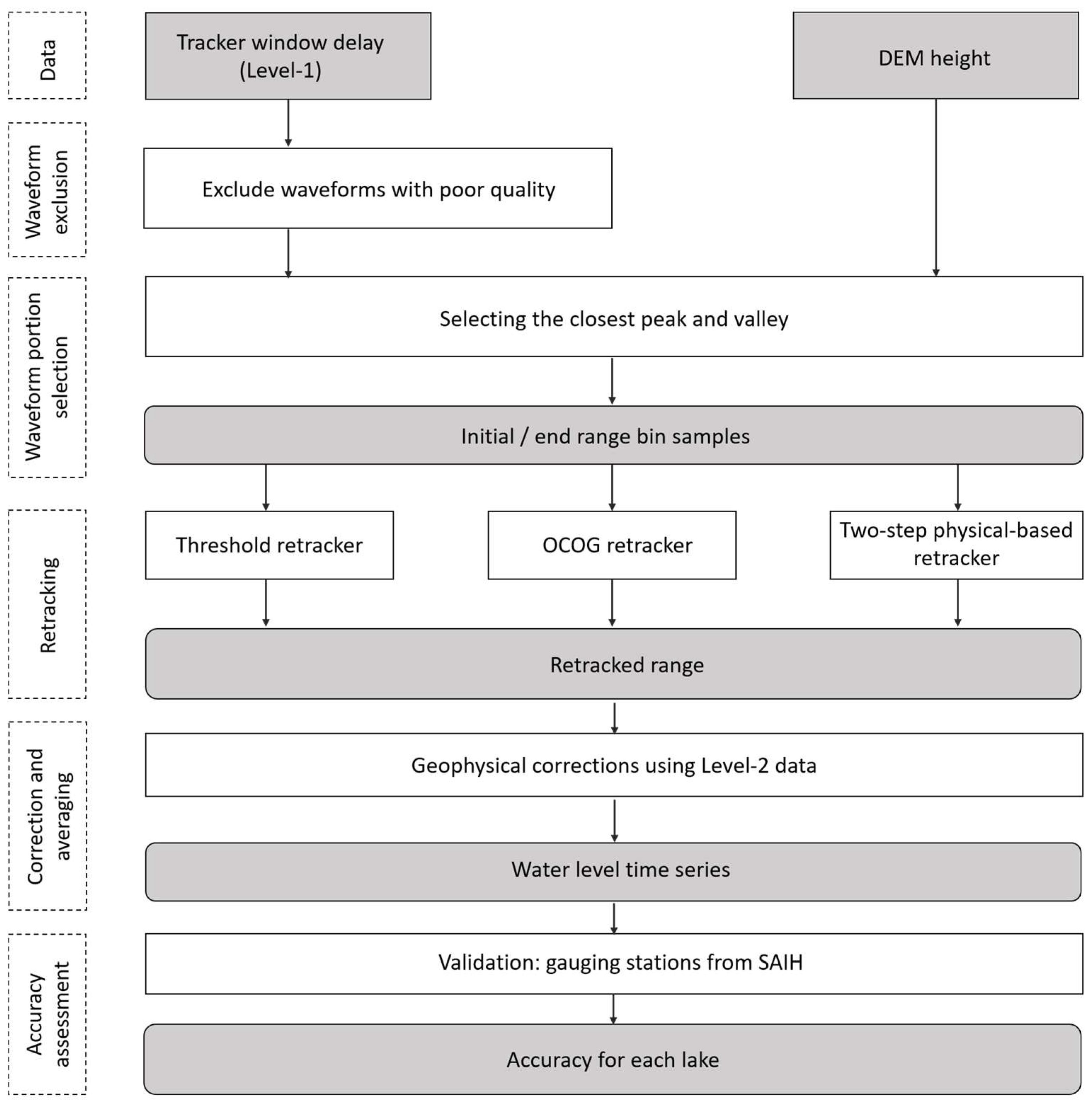
3. Methodology
3.1. Geophysical Corrections
3.2. Retrackers
3.2.1. Threshold Retracker
3.2.2. Offset Center of Gravity (OCOG) Retracker
3.2.3. Two-Step Physical-Based Retracker
3.3. Waveform Exclusion
- The epoch of the reference SRTM DEM must be within the waveform window
- Number of outstanding peaks < 5
- Sigma_0 (backscatter coefficient) > 50 dB
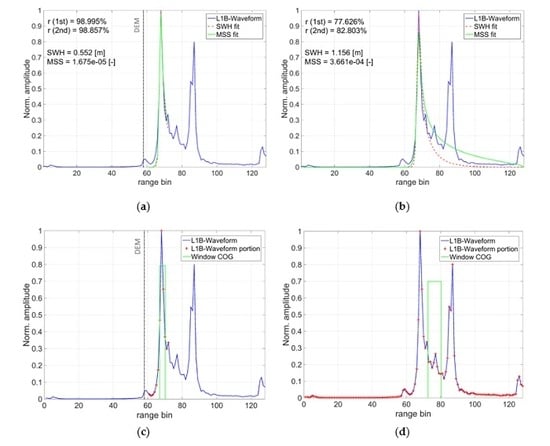
3.4. Selection of the Waveform Portion
- From the geo-located surface of interest within the water body and beneath the satellite track, the associated height was interpolated from the DEM information and referred to the geodetic ellipsoid, .
- This height was subtracted from the satellite height () at the geo-located surface to obtain a rough estimation of the range (or equivalently window delay) from where the nadir returns were expected.
- This range was linked to a specific bin within the received waveform, by comparing it with the vector of ranges associated to each bin in the receiving window, which could be obtained from the measured range by the radar and the range sampling.
- The peak location closest to the previous range bin position was taken, and the portion of the waveform was selected around this peak considering the valley positions to the left and right of the peak plus some guard samples on top:
- ○
- A built-in Matlab function (findpeaks) was used to compute the prominent or outstanding peaks within the waveform. Prominent peaks are those peaks that drop more than a given threshold value on either side of the peak before the signal attains a higher value.
- ○
- The associated valley locations can be extracted using this built-in function, but taking as input the maximum of the whole waveform minus the waveform itself.
4. Results
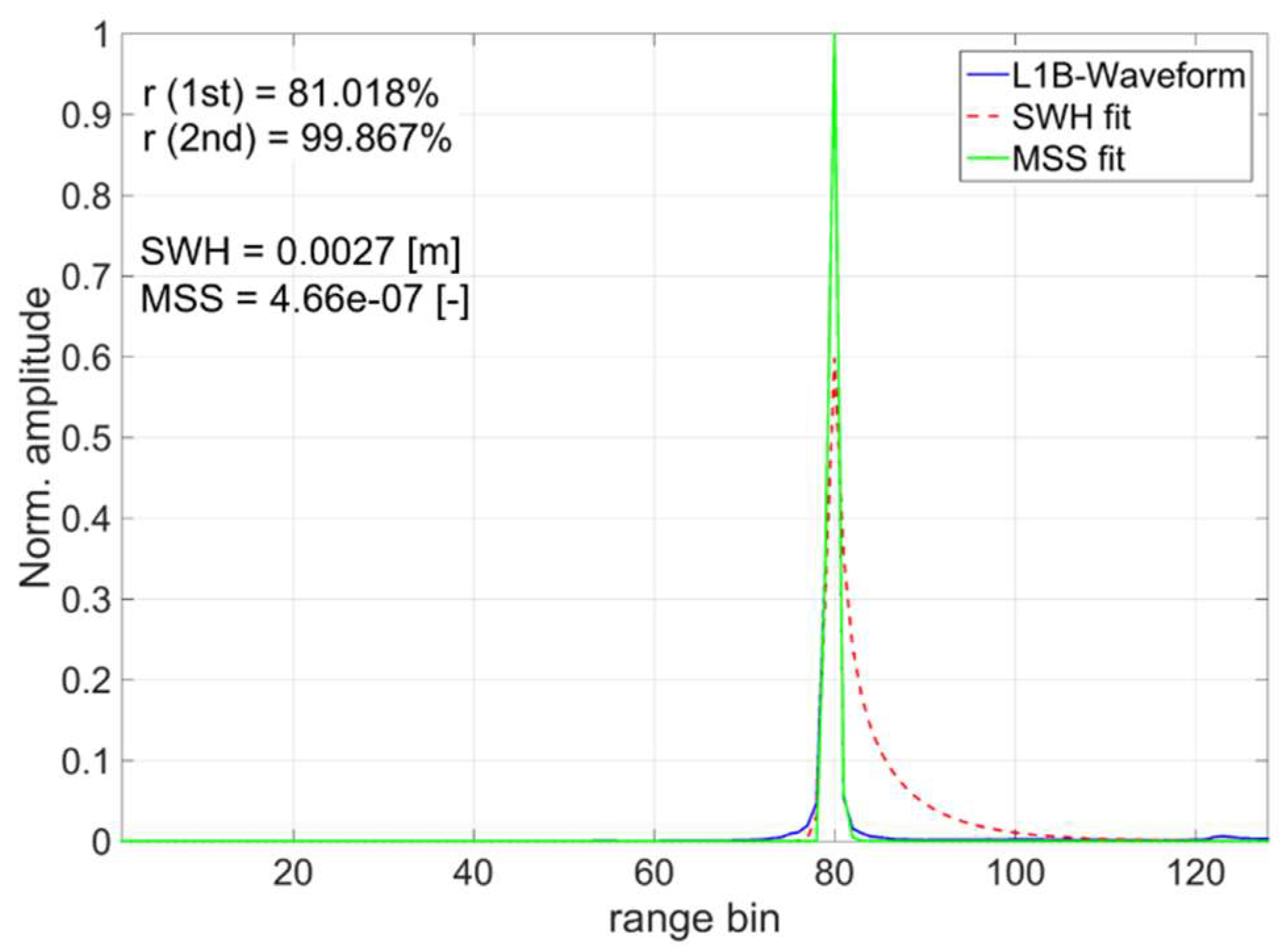
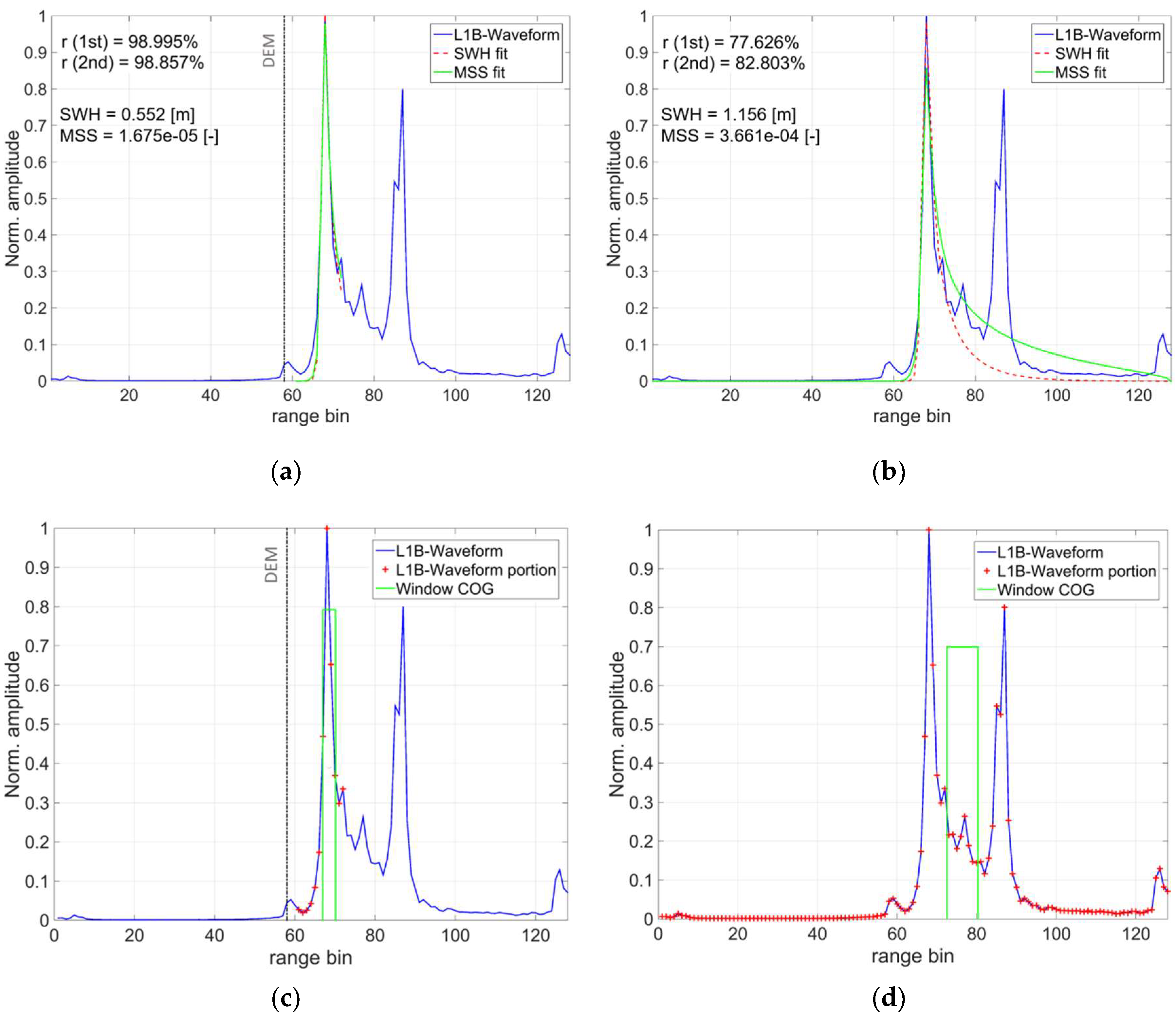
4.1. Selecting the Waveform Portion Using a DEM
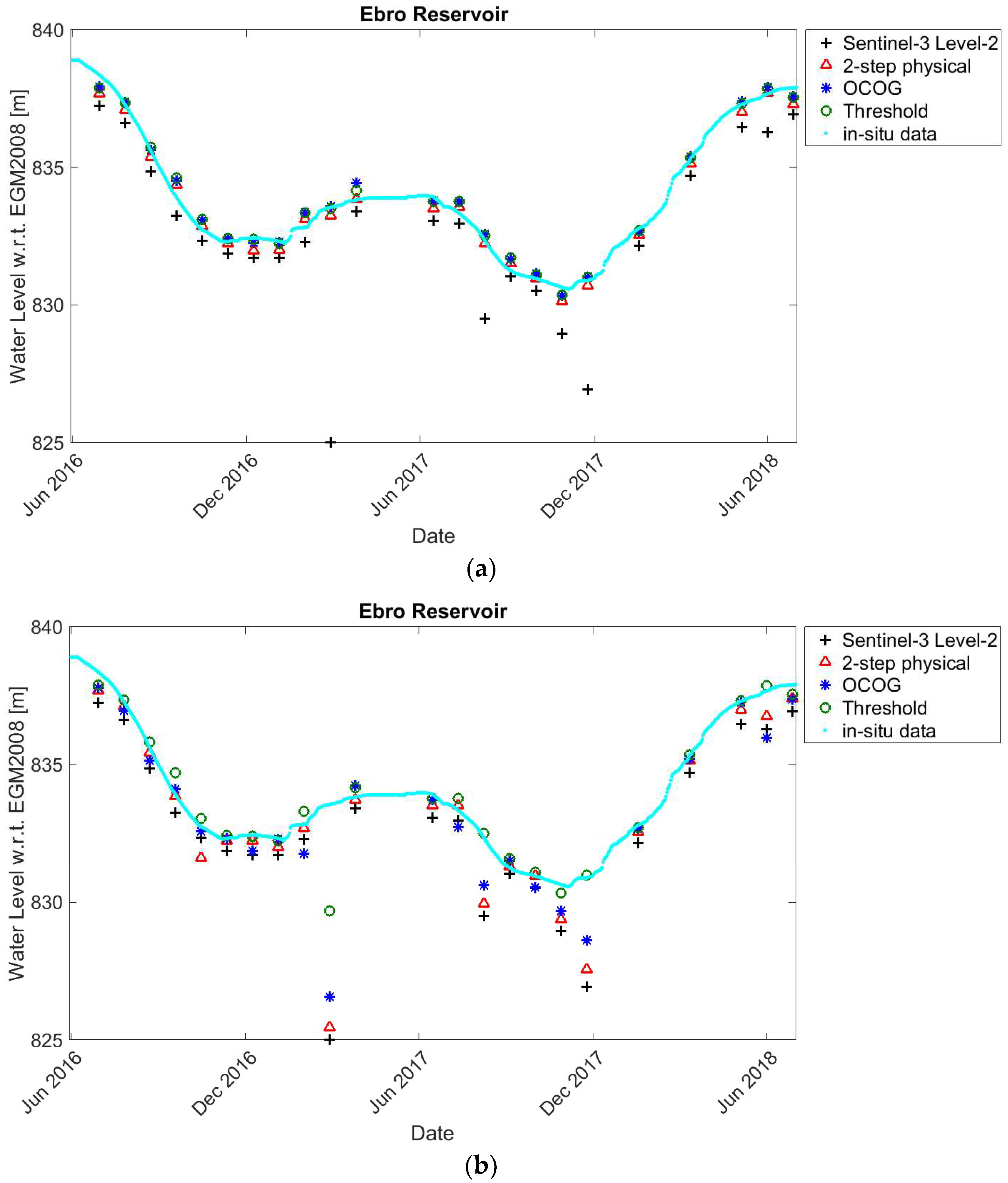
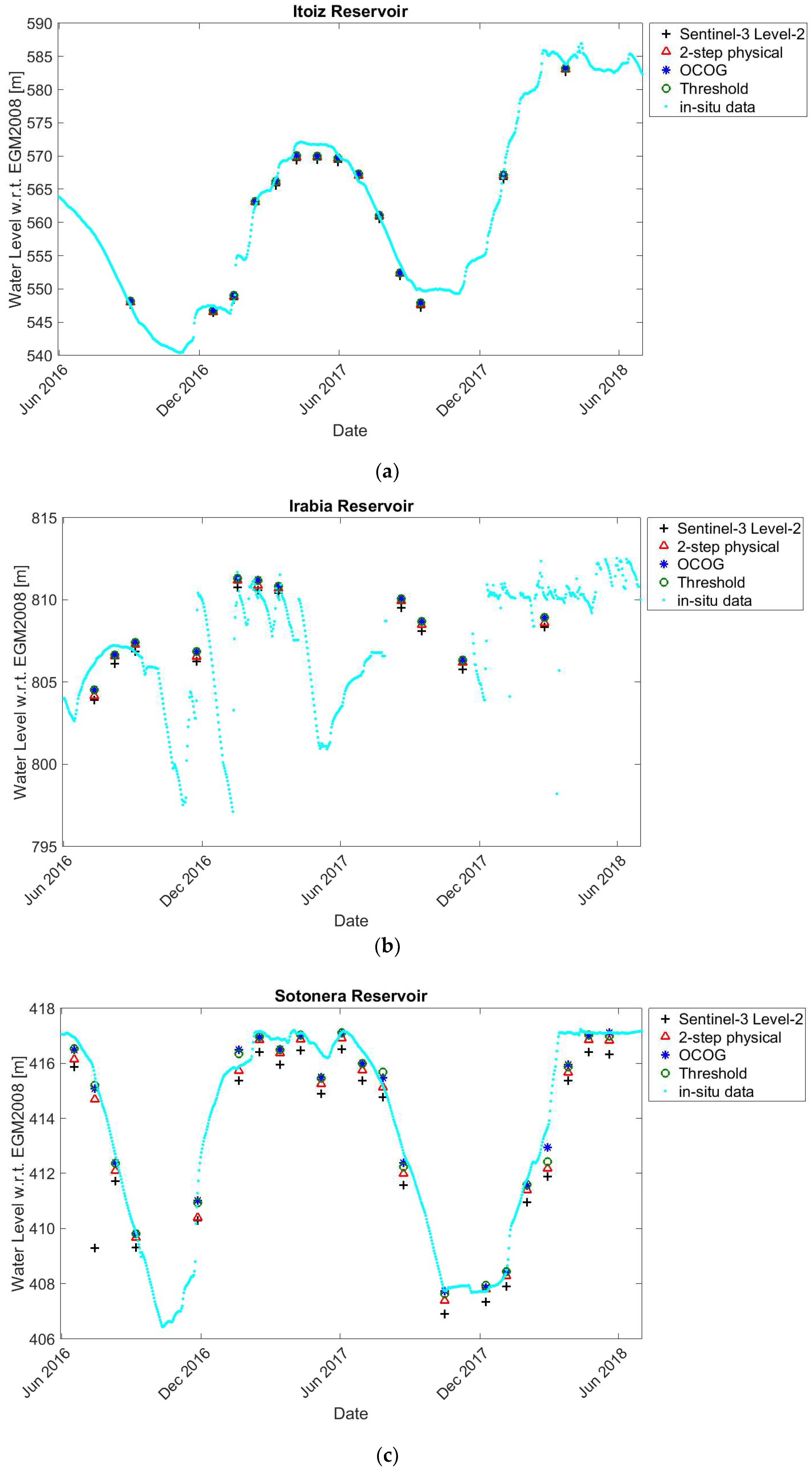
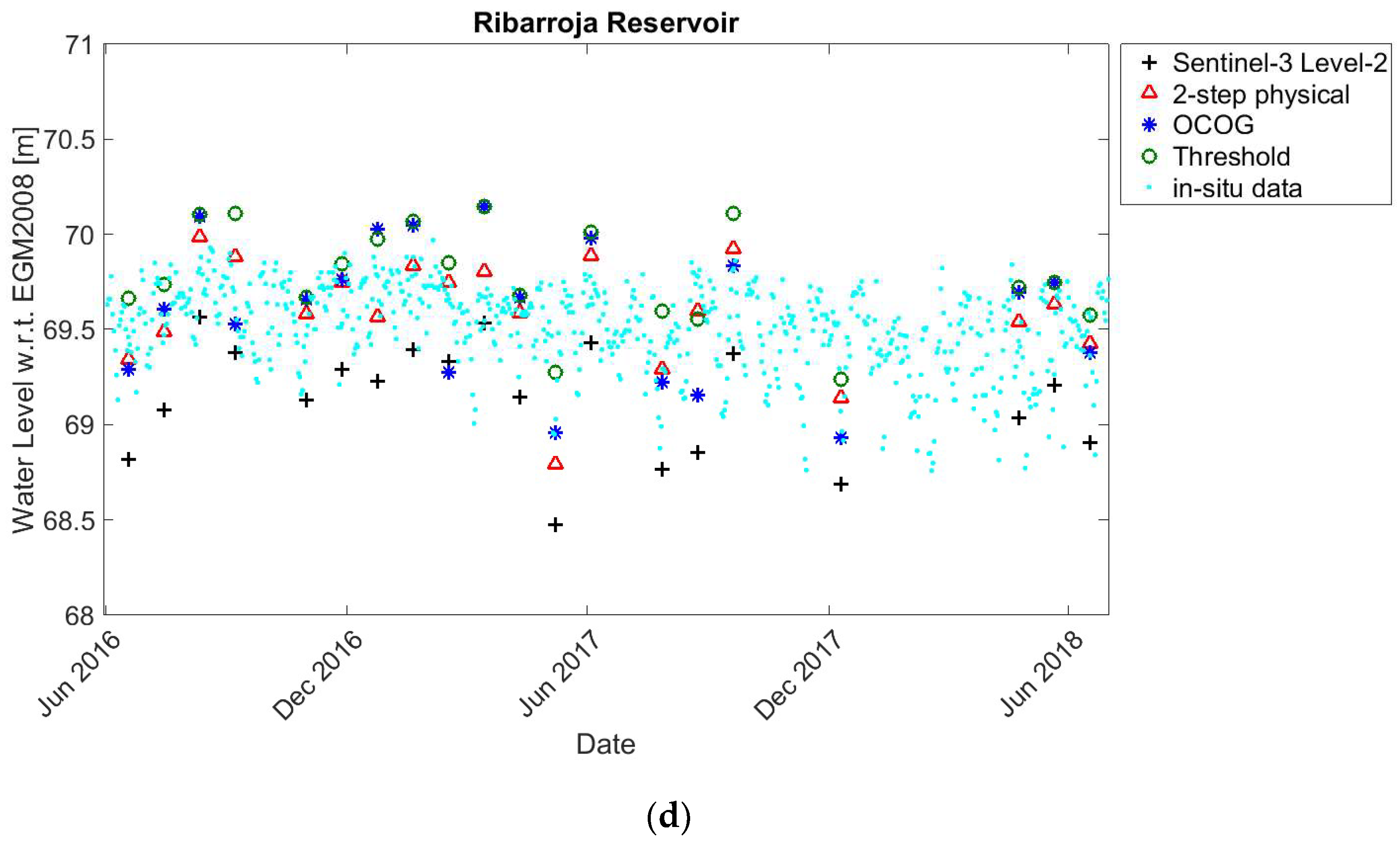
4.2. Time Series Validation
5. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Postel, S.L.; Carpenter, S.R. Freshwater Ecosystem Services. In Nature’s Services; Daily, G., Ed.; Island Press: Washington, DC, USA, 1997; pp. 195–214. [Google Scholar]
- Döll, P.; Hoffmann-Dobrev, H.; Portmann, F.T.; Siebert, S.; Eicker, A.; Rodell, M.; Strassberg, G.; Scanlon, B.R. Impact of water withdrawals from groundwater and surface water on continental water storage variations. J. Geodyn. 2012, 59, 143–156. [Google Scholar] [CrossRef]
- Alsdorf, D.E.; Rodriguez, E.; Lettenmaier, D.P. Measuring surface water from space. Rev. Geophys. 2007, 45, RG2002. [Google Scholar] [CrossRef]
- Gleick, P.H. Global freshwater resources: Soft-path solutions for the 21st century. Science 2003, 302, 1524–1528. [Google Scholar] [CrossRef] [PubMed]
- Bogning, S.; Frappart, F.; Blarel, F.; Niño, F.; Mahé, G.; Bricquet, J.-P.; Seyler, F.; Onguéné, R.; Etamé, J.; Paiz, M.-C.; et al. Monitoring Water Levels and Discharges Using Radar Altimetry in an Ungauged River Basin: The Case of the Ogooué. Remote Sens. 2018, 10, 350. [Google Scholar] [CrossRef]
- Benveniste, J. Radar Altimetry: Past, Present and Future. In Coastal Altimetry; Vignudelli, S., Kostianoy, A., Cipollini, P., Benveniste, J., Eds.; Springer: Berlin/Heidelberg, Germany, 2011; ISBN 978-3-642-12795-3. [Google Scholar] [CrossRef]
- Calman, S.; Seyler, F. Continental surface water from satellite altimetry. C. R. Geosci. 2006, 338, 1113–1122. [Google Scholar] [CrossRef]
- Cretaux, J.F.; Birkett, C. Lake studies from satellite radar altimetry. C. R. Geosci. 2006, 338, 1098–1112. [Google Scholar] [CrossRef]
- Radar Altimetry Tutorial and Toolbox—A Collaborative Portal for Altimetry Users. Available online: http://www.altimetry.info/ (accessed on 3 November 2018).
- Raney, R.K. The delay/Doppler radar altimeter. IEEE Trans. Geosci. Remote Sens. 1998, 36, 1578–1588. [Google Scholar] [CrossRef]
- Wingham, D.J.; Phalippou, L.; Mavrocordatos, C.; Wallis, D. The mean echo and echo cross-product from a beam forming, interferometric altimeter and their application to elevation measurement. IEEE Trans. Geosci. Remote Sens. 2004, 10, 10–2323. [Google Scholar] [CrossRef]
- Koblinsky, C.J.; Clarke, R.T.; Brenner, A.C.; Frey, H. Measurement of river level variations with satellite altimetry. Water Resour. Res. 1993, 29, 1839–1848. [Google Scholar] [CrossRef]
- Birkett, C. The contribution of TOPEX/POSEIDON to the global monitoring of climatically sensitive lakes. J. Geophys. Res. Ocean. 1995, 100, 25179–25204. [Google Scholar] [CrossRef]
- Birkett, C.M. Contribution of the TOPEX NASA radar altimeter to the global monitoring of large rivers and wetlands. Water Resour. Res. 1998, 34, 1223–1239. [Google Scholar] [CrossRef]
- Jarihani, A.A.; Callow, J.N.; Johansen, K.; Gouweleeuw, B. Evaluation of multiple satellite altimetry data for studying inland water bodies and river floods. J. Hydrol. 2013, 505, 78–90. [Google Scholar] [CrossRef]
- Yi, Y.; Kouraev, A.V.; Shum, C.K.; Vuglinsky, V.S.; Cretaux, J.F.; Calmant, S. The performance of altimeter waveform retrackers at Lake Baikal. Terr. Atmos. Ocean. Sci. 2013, 24, 513–519. [Google Scholar] [CrossRef]
- Nielsen, K.; Stenseng, L.; Andersen, O.B.; Villadsen, H.; Knudsen, P. Validation of CryoSat-2 SAR mode based lake levels. Remote Sens. Environ. 2015, 171, 162–170. [Google Scholar] [CrossRef]
- Schwatke, C.; Dettmering, D.; Boergens, E.; Bosch, W. Potential of SARAL/AltiKa for inland water applications. Mar. Geod. 2015, 38, 626–643. [Google Scholar] [CrossRef]
- Villadsen, H.; Andersen, O.; Stenseng, L.; Nielsen, K.; Knudsen, P. CryoSat-2 altimetry for river level monitoring—Evaluation in the Ganges-Brahmaputra River basin. Remote Sens. Environ. 2015, 168, 80–89. [Google Scholar] [CrossRef]
- Moore, P.; Birkinshaw, S.J.; Ambrózio, A.; Restano, M.; Benveniste, J. CryoSat-2 Full Bit Rate Level 1A processing and validation for inland water applications. Adv. Space Res. 2018, 62, 1497–1515. [Google Scholar] [CrossRef]
- Song, C.; Huang, B.; Ke, L. Inter-annual changes of alpine inland lake water storage on the Tibetan Plateau: Detection and analysis by integrating satellite altimetry and optical imagery. Hydrol. Process. 2014, 28, 2411–2418. [Google Scholar] [CrossRef]
- Song, C.; Ye, Q.; Sheng, Y.; Gong, T. Combined ICESat and CryoSat-2 altimetry for accessing water level dynamics of Tibetan lakes over 2003–2014. Water 2015, 7, 4685–4700. [Google Scholar] [CrossRef]
- Song, C.; Ye, Q.; Cheng, X. Shifts in water-level variation of Namco in the central Tibetan Plateau from ICESat and CryoSat-2 altimetry and station observations. Sci. Bull. 2015, 60, 1287–1297. [Google Scholar] [CrossRef]
- Frappart, F.; Calmant, S.; Cauhop, M.; Seyler, F.; Cazenave, A. Preliminary results of ENVISAT RA-2-derived water levels validation over the Amazon Basin. Remote Sens. Environ. 2006, 100, 252–264. [Google Scholar] [CrossRef]
- Villadsen, H.; Deng, X.; Andersen, O.B.; Stenseng, L.; Nielsen, K.; Knudsen, P. Improved inland water levels from SAR altimetry using novel empirical and physical retrackers. J. Hydrol. 2016, 537, 234–247. [Google Scholar] [CrossRef]
- Jiang, L.; Nielsen, K.; Andersen, O.B.; Bauer-Gottwein, P. Monitoring recent lake level variations on the Tibetan Plateau using CryoSat-2 SARin mode data. J. Hydrol. 2017, 544, 109–124. [Google Scholar] [CrossRef]
- Kleinherenbrink, M.; Ditmar, P.G.; Lindenbergh, R.C. Retracking CryoSat data in the SARIn mode and robust lake level extraction. Remote Sens. Environ. 2014, 152, 38–50. [Google Scholar] [CrossRef]
- Schwatke, C.; Dettmering, D.; Bosch, W.; Seitz, F. DAHITI—An innovative approach for estimating water level time series over inland waters using multi-mission satellite altimetry. Hydrol. Earth Syst. Sci. 2015, 19, 4345–4364. [Google Scholar] [CrossRef]
- Crétaux, J.-F.; Jelinski, W.; Calmant, S.; Kouraev, A.; Vuglinski, V.; Bergé-Nguyen, M.; Gennero, M.-C.; Nino, F.; Abarca Del Rio, R.; Cazenave, A.; et al. SOLS: A Lake database to monitor in Near Real Time water level and storage variations from remote sensing data. J. Adv. Space Res. 2011, 47, 1497–1507. [Google Scholar] [CrossRef]
- Birkett, C.M.; Reynolds, C.; Beckley, B.; Doorn, B. From Research to Operations: The USDA Global Reservoir and Lake Monitor; Vignudelli, S., Kostianoy, A.G., Cipollini, P., Benveniste, J., Eds.; Chapter 2 in Coastal Altimetry, Springer Publications; Springer: Berlin/Heidelberg, Germany, 2010; ISBN 978-3-642-12795-3. [Google Scholar]
- Gustafsson, D.; Andersson, J.; Brito, F.; Martinez, B.; Arheimer, B. New tool to share data and models in hydrological forecasting, based on the ESA TEP. In Proceedings of the EGU 2018 Symposium, Vienna, Austria, 8–13 April 2018. [Google Scholar]
- Dinardo, S.; Restano, M.; Ambrózio, A.; Benveniste, J. SAR Altimetry Processing on Demand Service for Cryosat-2 and Sentinel-3 at Esa G-Pod. In Proceedings of the 2016 conference on Big Data from Space (BiDS’16), Santa Cruz de Tenerife, Spain, 15–17 March 2016. [Google Scholar] [CrossRef]
- Birkinshaw, S.J.; O’Donnell, G.M.; Moore, P.; Kilsby, C.G.; Fowler, H.J.; Berry, P.A.M. Using satellite altimetry data to augment flow estimation techniques on the Mekong River. Hydrol. Process. 2010, 24, 3811–3825. [Google Scholar] [CrossRef]
- Da Silva, J.S.; Calmant, S.; Seyler, F.; Rotunno Filho, O.C.; Cochonneau, G.; Mansur, W.J. Water levels in the Amazon basin derived from the ERS 2 and ENVISAT radar altimetry missions. Remote Sens. Environ. 2010, 114, 2160–2181. [Google Scholar] [CrossRef]
- Michailovsky, C.I.; McEnnis, S.; Berry, P.A.M.; Smith, R.; Bauer-Gottwein, P. River monitoring from satellite radar altimetry in the Zambezi River Basin. Hydrol. Earth Syst. Sci. 2012, 9, 3203–3235. [Google Scholar] [CrossRef]
- Maillard, P.; Bercher, N.; Calmant, S. New processing approaches on the retrieval of water levels in Envisat and SARAL radar altimetry over rivers: A case study of the Sao Francisco River, Brazil. Remote Sens. Environ. 2015, 156, 226–241. [Google Scholar] [CrossRef]
- Boergens, E.; Nielsen, K.; Andersen, O.B.; Dettmering, D.; Seitz, F. River Levels Derived with CryoSat-2 SAR Data Classification—A Case Study in the Mekong River Basin. Remote Sens. 2017, 9, 1238. [Google Scholar] [CrossRef]
- Schneider, R.; Tarpanelli, A.; Nielsen, K.; Madsen, H.; Bauer-Gottwein, P. Evaluation of multi-mode CryoSat-2 altimetry data over the Po River against in situ data and a hydrodynamic model. Adv. Water Resour. 2018, 112, 17–26. [Google Scholar] [CrossRef]
- Huang, Q.; Long, D.; Du, M.; Zeng, C.; Li, X.; Hou, A.; Hong, Y. An improved approach to monitoring Brahmaputra River water levels using retracked altimetry data. Remote Sens. Environ. 2018, 211, 112–128. [Google Scholar] [CrossRef]
- Biancamaria, S.; Frappart, F.; Leleu, A.-S.; Marieu, V.; Blumstein, D.; Desjonquères, J.D.; Boy, F.; Sottolichio, A.; Valle-Levinson, A. Satellite altimetry water elevations performance over a 200 m wide river: Evaluation over the Garonne River. Adv. Space Res. 2017, 59, 128–146. [Google Scholar] [CrossRef]
- Becker, M.; da Silva, J.; Calmant, S.; Robinet, V.; Linguet, L.; Seyler, F. Water level fluctuations in the Congo Basin derived from ENVISAT satellite altimetry. Remote Sens. 2014, 6, 9340–9358. [Google Scholar] [CrossRef]
- Birkett, C.M.; Mertes, L.A.K.; Dunne, T.; Costa, M.H.; Jasinski, M.J. Surface water dynamics in the Amazon Basin: Application of satellite radar altimetry. J. Geophys. Res. 2002, 107, 8059. [Google Scholar] [CrossRef]
- Birkinshaw, S.J.; Moore, P.; Kilsby, C.G.; O’Donnell, G.M.; Hardy, A.J.; Berry, P.A.M. Daily discharge estimation at ungauged river sites using remote sensing. Hydrol. Process. 2014, 28, 1043–1054. [Google Scholar] [CrossRef]
- Cretaux, J.-F.; Calmant, S. Spatial Altimetry and Continental Waters. In Land Surface Remote Sensing in Continental Hydrology; Baghdadi, N., Zribi, M., Eds.; Elsevier: Amsterdam, The Netherlands, 2016. [Google Scholar] [CrossRef]
- Gommenginger, C.; Martin-Puig, C.; Amarouche, L.; Raney, R.K. Review of State of Knowledge for SAR Altimetry over Ocean; Report of the EUMETSAT JASON-CS SAR Mode Error Budget Study; National Oceanography Centre: Southampton, UK, 2013; Available online: https://eprints.soton.ac.uk/366765/ (accessed on 1 September 2018).
- Davis, C.H. A robust threshold retracking algorithm for measuring ice-sheet surface elevation change from satellite radar altimeter. IEEE Trans. Geosci. Remote Sens. 1997, 35, 974–979. [Google Scholar] [CrossRef]
- Martin, T.V.; Zwally, H.J.; Brenner, A.C.; Bindschadler, R.A. Analysis and retracking of continental ice sheet radar altimeter waveforms. J. Geophys. Res. Ocean. 1983, 88, 1608–1616. [Google Scholar] [CrossRef]
- Wingham, D.J.; Rapley, C.G.; Griffiths, H. New techniques in satellite tracking system. In Proceedings of the IGARSS’ 86 Symposium, Zurich, Switzerland, 8–11 September 1986; pp. 1339–1344. [Google Scholar]
- Bamber, J.L. Ice sheet altimeter processing scheme. Int. J. Remote Sens. 1994, 15, 925–938. [Google Scholar] [CrossRef]
- Brown, G.S. The average impulse response of a rough surface and its applications. IEEE Trans. Antennas Propag. 1977, 25, 67–74. [Google Scholar] [CrossRef]
- Legrésy, B.; Rémy, F. Altimetric observations of surface characteristics of the Antarctic ice sheet. J. Glaciol. 1997, 43, 265–275. [Google Scholar] [CrossRef]
- Legrésy, B.; Papa, F.; Remy, F.; Vinay, G.; Bosch, M.V.D.; Zanife, O.Z. ENVISAT radar altimeter measurements over continental surfaces and ice caps using the Ice-2 retracking algorithm. Remote Sens. Environ. 2005, 95, 150–163. [Google Scholar] [CrossRef]
- Ray, C.; Martin-Puig, C.; Clarizia, M.P.; Ruffini, G.; Dinardo, S.; Gommenginger, C.; Benveniste, J. SAR altimeter backscattered waveform model. IEEE Trans. Geosci. Remote Sens. 2015, 53, 911–919. [Google Scholar] [CrossRef]
- Fenoglio-Marc, L.; Dinardo, S.; Scharroo, R.; Roland, A.; Dutour Sikiric, M.; Lucas, B.; Becker, M.; Benveniste, J.; Weiss, R. The German Bight: A validation of CryoSat-2 altimeter data in SAR mode. Adv. Space Res. 2015, 55, 2641–2656. [Google Scholar] [CrossRef]
- Wingham, D.J.; Francis, C.R.; Baker, S.; Bouzinac, C.; Brockley, D.; Cullen, R.; de Chateau-Thierry, P.; Laxon, S.W.; Mallow, U.; Mavrocordatos, C.; et al. CryoSat: A mission to determine the fluctuations in Earth’s land and marine ice fields. Adv. Space Res. 2006, 37, 841–871. [Google Scholar] [CrossRef]
- Mavrocordatos, C.; Berruti, B.; Aguirre, M.; Drinkwater, M. The Sentinel-3 mission and its topography element. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS 2007), Barcelona, Spain, 23–27 July 2007; pp. 3529–3532. [Google Scholar] [CrossRef]
- Chander, S.; Ganguly, D.; Dubey, A.K.; Gupta, P.K.; Singh, R.P.; Chauhan, P. Inland Water Bodies Monitoring Using Satellite Altimetry Over Indian Region. ISPRS-Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2014, 1035–1041. [Google Scholar] [CrossRef]
- Martin-Puig, C.; García, P. A new SAR altimetry waveform model in combination with phase information for coastal altimetry. In Proceedings of the 8th Coastal Altimetry Workshop, Lake Constance, Germany, 23–24 October 2014. [Google Scholar]
- Martin-Puig, C.; García, P. Synthetic Aperture Radar (SAR) altimetry for hydrology. In Proceedings of the ESA Living Planets Symposium, Edinburgh, Scotland, UK, 9–13 September 2013. [Google Scholar]
- Roca, M.; Martínez, D.; Reche, M. Preliminary results obtained using the EnviSat RA-2 individual echoes (full-rate waveforms with phase information). In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Seoul, Korea, 25–29 July 2005. [Google Scholar] [CrossRef]
- Roca, M.; Martinez, D.; Reche, M. The RA-2 individual echoes processing description and some scientific results. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Barcelona, Spain, 23–27 July 2007; pp. 3541–3546. [Google Scholar] [CrossRef]
- Bramer, S.M.S.; Berry, P.A.M.; Freeman, J.A.; Rommen, B. Global Analysis of Envisat Ku and S Band Sigma0 over All Surfaces. In Proceedings of the Envisat Symposium, Montreux, Switzerland, 23–27 April 2007. [Google Scholar]
- Abileah, R.; Scozzari, A.; Vignudelli, S. Envisat RA-2 Individual Echoes: A Unique Dataset for a Better Understanding of Inland Water Altimetry Potentialities. Remote Sens. 2017, 9, 605. [Google Scholar] [CrossRef]
- Egido, A.; Smith, W.H.F. Fully Focused SAR Altimetry: Theory and Applications. IEEE Trans. Geosci. Remote Sens. 2017, 55, 392–406. [Google Scholar] [CrossRef]
- Makhoul, E.; Roca, M.; Ray, C.; Escolà, R.; Garcia-Mondéjar, A. Evaluation of the precision of different Delay-Doppler Processor (DDP) algorithms using CryoSat-2 data over open ocean. Adv. Space Res. 2018, 62, 1464–1478. [Google Scholar] [CrossRef]
- Li, S.; Zhao, D.; Zhou, L.; Liu, B. Dependence of mean square slope on wave state and its application in altimeter wind speed retrieval. Int. J. Remote Sens. 2013, 34, 264–275. [Google Scholar] [CrossRef]
- Valenzuela, G.R. Theories for the interaction of electromagnetic and oceanic waves—A review. Bound.-Layer Meteorol. 1978, 13, 61–85. [Google Scholar] [CrossRef]
- Romaní, A.M.; Sabater, S.; Muñoz, I. The Physical Framework and Historic Human Influences in the Ebro River. In The Ebro River Basin; The Handbook of Environmental Chemistry; Barceló, D., Petrovic, M., Eds.; Springer: Berlin/Heidelberg, Germany, 2010; Volume 13. [Google Scholar] [CrossRef]
- Cruzado, A.; Velasquez, Z.; Perez, M.; Bahamon, N.; Grimaldo, N.S.; Ridolfi, F. Nutrient fluxes from the Ebro River and subsequent across-shelf dispersion. Cont. Shelf Res. 2002, 22, 349–360. [Google Scholar] [CrossRef]
- Sentinel-3 Team. SentinSentinel-3 User Handbook. European Space Agency. Available online: https://earth.esa.int/documents/247904/685236/Sentinel-3_User_Handbook-iss1_v1_20170113/960ff616-87f5-43cc-b23e-3e96030bd13a (accessed on 15 March 2018).
- Re-Tracking Estimates. Available online: https://sentinel.esa.int/web/sentinel/technical-guides/sentinel-3-altimetry/level-2/re-tracking-estimates (accessed on 3 October 2018).
- SAIH Ebro. Available online: http://www.saihebro.com (accessed on 1 July 2018).
- Farr, T.G.; Rosen, P.A.; Caro, E.; Crippen, R.; Duren, R.; Hensley, S.; Kobrick, M.; Paller, M.; Rodriguez, E.; Roth, L.; et al. The Shuttle Radar Topography Mission. Rev. Geophys. 2007, 45. [Google Scholar] [CrossRef]
- Mukul, M.; Srivastava, V.; Mukul, M. Analysis of the accuracy of shuttle radar topography mission (SRTM) height models using international global navigation satellite system service (IGS) network. J. Earth Syst. Sci. 2015, 124, 1343–1357. [Google Scholar] [CrossRef]
- Mukul, M.; Srivastava, V.; Mukul, M. Uncertainties in the Shuttle Radar Topography Mission (SRTM) heights: Insights from the Indian Himalaya and Peninsula. Sci. Rep. 2017, 7, 41672. [Google Scholar] [CrossRef]
- Rabus, B.; Eineder, M.; Roth, A.; Bamler, R. The shuttle radar topography mission—A new class of digital elevation models acquired by space borne radar. J. Photogramm. Remote Sens. 2003, 57, 241–262. [Google Scholar] [CrossRef]
- Elkhrachy, I. Vertical accuracy assessment for SRTM and ASTER Digital Elevation Models: A case study of Najran city, Saudi Arabia. Ain Shams Eng. J. 2017. [Google Scholar] [CrossRef]
- Calmant, S.; Seyler, F.; Cretaux, J.F. Monitoring continental surface waters by satellite altimetry. Surv. Geophys. 2008, 29, 247–269. [Google Scholar] [CrossRef]
- Fernandes, M.J.; Lázaro, C.; Nunes, A.L.; Scharroo, R. Atmospheric Corrections for Altimetry Studies over Inland Water. Remote Sens. 2014, 6, 4952–4997. [Google Scholar] [CrossRef]
- Sentinel-3A L2P SLA Product Handbook. Available online: https://www.aviso.altimetry.fr/fileadmin/documents/data/tools/hdbk_L2P_S3.pdf (accessed on 1 November 2017).
- Pavlis, N.K.; Holmes, S.A.; Kenyon, S.C.; Factor, J.K. The development and evaluation of the Earth Gravitational Model 2008 (EGM2008). J. Geophys. Res. Solid Earth 2012, 117, B4. [Google Scholar] [CrossRef]
- Boehm, J.; Kouba, J.; Schuh, H. Forecast Vienna Mapping Functions 1 for real-time analysis of space geodetic observations. J. Geod. 2009, 83, 397. [Google Scholar] [CrossRef]
- Scharroo, R.; Smith, W.H.F. Global positioning system-based climatology for the total electron content in the ionosphere. J. Geophys. Res. 2010, 115. [Google Scholar] [CrossRef]
- Cartwright, D.E.; Edden, A.C. Corrected Tables of Tidal Harmonics. Geophys. J. Int. 1973, 33, 253–264. [Google Scholar] [CrossRef]
- Wahr, J.M. Deformation of the Earth induced by polar motion. J. Geophys. Res. (Solid Earth) 1985, 90, 9363–9368. [Google Scholar] [CrossRef]
- Ray, R.D.; Ponte, R.M. Barometric tides from ECMWF operational analyses. Ann. Geophys. 2003, 21, 1897–1910. [Google Scholar] [CrossRef]
- Deng, X.; Featherstone, W.E. A coastal retracking system for satellite radar altimeter waveforms: Application to ERS-2 around Australia. J. Geophys. Res. 2006, 111. [Google Scholar] [CrossRef]
- Davis, C.H. Growth of the Greenland ice sheet: A performance assessment of altimeter retracking algorithms. IEEE Trans Geosci Remote Sens. 1995, 33, 1108–1116. [Google Scholar] [CrossRef]
- Jain, M.; Martin-Puig, C.; Andersen, O.B.; Stenseng, L.; Dall, J. Evaluation of SAMOSA3 adapted retracker using Cryosat-2 SAR altimetry data over the Arctic ocean. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Quebec City, QC, Canada, 13–18 July 2014; pp. 5115–5118. [Google Scholar] [CrossRef]
- Crétaux, J.F.; Calmant, S.; Del Rio, R.A.; Kouraev, A.; Bergé-Nguyen, M.; Maisongrande, P. Lakes Studies from Satellite Altimetry. In Coastal Altimetry; Vignudelli, S., Kostianoy, A.G., Cipollini, P., Benveniste, J., Eds.; Springer: Berlin/Heidelberg, Germany, 2011; pp. 509–533. [Google Scholar]
- Zhang, M.M.; Lee, H.; Shum, C.K.; Alsdorf, D.; Schwartz, F.; Tseng, K.H.; Yi, Y.C.; Kuo, C.Y.; Tseng, H.Z.; Braun, A.; et al. Application of retracked satellite altimetry for inland hydrologic studies. Int. J. Remote Sens. 2010, 31, 3913–3929. [Google Scholar] [CrossRef]
| Satellite Mission | Mission Period | Inclination (deg) | Revisit Time (Days) | Along-Track Resolution (km) | Ground Track Separation at Equator (km) |
|---|---|---|---|---|---|
| Geosat 1 | 1985–1990 | 108 | 17 | 1.7 | 16 |
| ERS 2 1 and 2 | 1991–2011 | 98.5 | 35 | 1.7 (ocean mode) 3.4 (ice mode) | 80 |
| TOPEX/Poseidon 3 | 1992–2006 | 66 | 10 | 2.2 | 315 |
| GFO 4 | 1998–2008 | 108 | 17 | 1.7 km | 164 |
| Jason 1, 2, and 3 | 2001–present | 66 | 10 | 2.2 | 315 |
| Envisat 5 | 2002–2012 | 98.55 | 30-35 | 1.7 | 80 |
| CryoSat-2 6 | 2010–present | 92 | 369 | 0.25 (SAR and SARIN) 1.6 (LRM) | 7.7 |
| HY-2 7 | 2011–present | 99.3 | Two phases (14 and 168) | 1.9 | 100 |
| SARAL 8 | 2013–present | 98.55 | 35 | 1.4 | 75 |
| Sentinel-3 | 2016–present | 98.6 | 27 | 0.3 | 104 |
| SWOT 9 | Planned on 2021 | 77.6 | 21 | 0.1 | 0 |
| JASON-CS 10/SENTINEL-6 | Planned on 2022 | 66 | 10 | 0.3 | 315 |
| Water Bodies | Coordinates | Width | Satellite Tracks | Tracking Mode | Gauging Station Distance | Average Slope (5 km) |
|---|---|---|---|---|---|---|
| Ebro Reservoir | (43.0°N, 3.96°W) | 1.8 km | 014 | Closed loop | 8 km | 4% |
| Itoiz Reservoir | (42.81°N, 1.37°W) | 400 m–2.7 km depends on satellite tracks | 165 | Closed loop | 2 km | 19% |
| Irabia Reservoir | (42.99°N, 1.15°W) | 130 m | 186 | Closed loop | 450 m | 20% |
| Sotonera Reservoir | (42.12°N, 0.68°W) | 4.5 km | 222 | Closed loop | 1.5 km | 3% |
| Ribarroja Reservoir | (41.24°N, 0.40°E) | 400 m | 242 | Open loop | 3.5 km | 24% |
| Mequinenza Reservoir | (41.26°N, 0.04°W) | 600 m | 279 | Open loop | 30 km | 3.5% |
| Cavallers Reservoir | (42.59°N, 0.86°E) | 800 m | 299 | Open loop | 500 m | 27% |
| San Salvador Reservoir | (41.78°N, 0.20°E) | 1.2 km | 242 | Open loop | 2.5 km | 4.5% |
| Correction | Model | Variable of Level-2 Product | Range of Correction |
|---|---|---|---|
| Dry troposphere | European Center for Medium-Range Weather Forecasts (ECMWF) model [82] | Mod_dry_tropo_cor_meas_altitude_01 | 1.7–2.5 m |
| Wet troposphere | ECMWF model [82] | Mod_wet_tropo_cor_meas_altitude_01 | 0–50 cm |
| Ionosphere | Global Ionospheric Map (GIM) [83] | Iono_cor_gim_01_ku | 6–12 cm |
| Solid earth tide | Cartwright model [84] | Solid_earth_tide_01 | −30 to +30 cm |
| Geocentric polar tide | Historical pole location [85] | Pole_tide_01 | −2 to +2 cm |
| Ocean loading tide | GOT00.2 model [86] | Ocean_tide_sol1_01 | −2 to +2 cm |
| Parameter | Definition | Formulation |
|---|---|---|
| 1 | Receive Bandwidth | - |
| PRF | Pulse Repetition Frequency | - |
| Number of Pulses in a burst | - | |
| Carrier frequency | - | |
| Speed of light | - | |
| Range to the surface (distance from satellite to the surface) | - | |
| Orbit Height | - | |
| SWH | - | |
| Standard deviation of the height PDF | ||
| Orbital factor | ||
| Along-track resolution | ||
| Across-track resolution | ||
| Vertical resolution |
| Water Bodies | Width | Tracking Mode | RMSE/ubRMSE (m) | |||
|---|---|---|---|---|---|---|
| Two-Step Physical | OCOG | Threshold | Level-2 Ocean | |||
| Ebro Reservoir | 1.8 km | Closed loop | 0.32/0.29 | 0.30/0.28 | 0.30/0.28 | 2.18/1.76 |
| Itoiz Reservoir | 400 m–2.7 km | Closed loop | 1.18/1.02 | 1.10/1.00 | 1.10/1.00 | 1.41/1.03 |
| Irabia Reservoir | 130 m | Closed loop | 1.39/1.39 | 1.39/1.38 | 1.39/1.38 | 1.44/1.39 |
| Sotonera Reservoir | 4.5 km | Closed loop | 0.60/0.43 | 0.49/0.38 | 0.48/0.44 | 1.65/1.19 |
| Ribarroja Reservoir | 400 m | Open loop | 0.18/0.16 | 0.29/0.28 | 0.31/0.16 | 0.44/0.20 |
| Mequinenza Reservoir | 600 m | Open loop | Off-track | |||
| Cavallers Reservoir | 800 m | Open loop | Off-track | |||
| San Salvador Reservoir | 1.2 km | Open loop | Off-track | |||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, Q.; Makhoul, E.; Escorihuela, M.J.; Zribi, M.; Quintana Seguí, P.; García, P.; Roca, M. Analysis of Retrackers’ Performances and Water Level Retrieval over the Ebro River Basin Using Sentinel-3. Remote Sens. 2019, 11, 718. https://doi.org/10.3390/rs11060718
Gao Q, Makhoul E, Escorihuela MJ, Zribi M, Quintana Seguí P, García P, Roca M. Analysis of Retrackers’ Performances and Water Level Retrieval over the Ebro River Basin Using Sentinel-3. Remote Sensing. 2019; 11(6):718. https://doi.org/10.3390/rs11060718
Chicago/Turabian StyleGao, Qi, Eduard Makhoul, Maria Jose Escorihuela, Mehrez Zribi, Pere Quintana Seguí, Pablo García, and Mònica Roca. 2019. "Analysis of Retrackers’ Performances and Water Level Retrieval over the Ebro River Basin Using Sentinel-3" Remote Sensing 11, no. 6: 718. https://doi.org/10.3390/rs11060718
APA StyleGao, Q., Makhoul, E., Escorihuela, M. J., Zribi, M., Quintana Seguí, P., García, P., & Roca, M. (2019). Analysis of Retrackers’ Performances and Water Level Retrieval over the Ebro River Basin Using Sentinel-3. Remote Sensing, 11(6), 718. https://doi.org/10.3390/rs11060718