Fusion of GNSS and Satellite Radar Interferometry: Determination of 3D Fine-Scale Map of Present-Day Surface Displacements in Italy as Expressions of Geodynamic Processes
Abstract
:1. Introduction
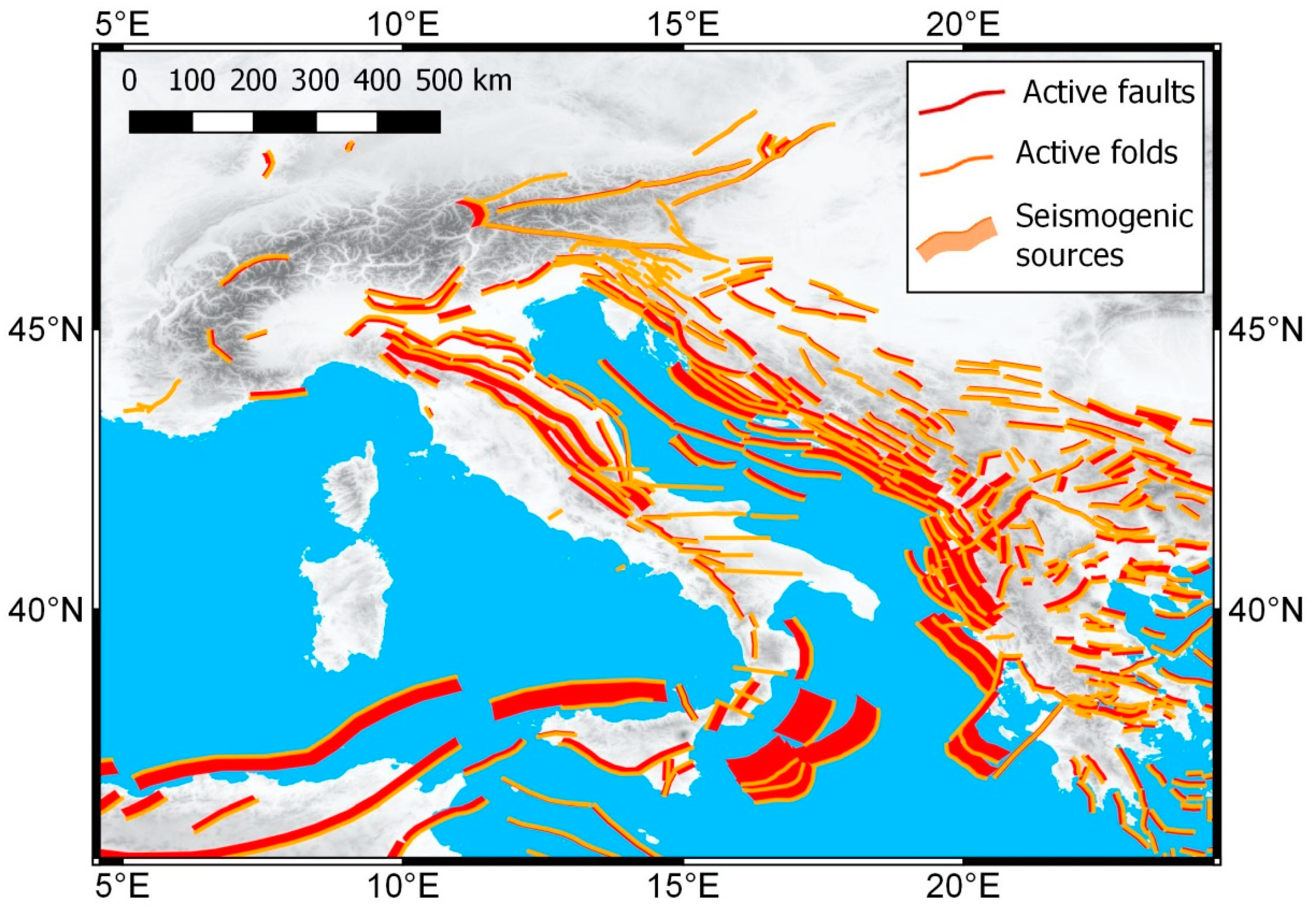
2. Area of Study—The Italian Geological Framework
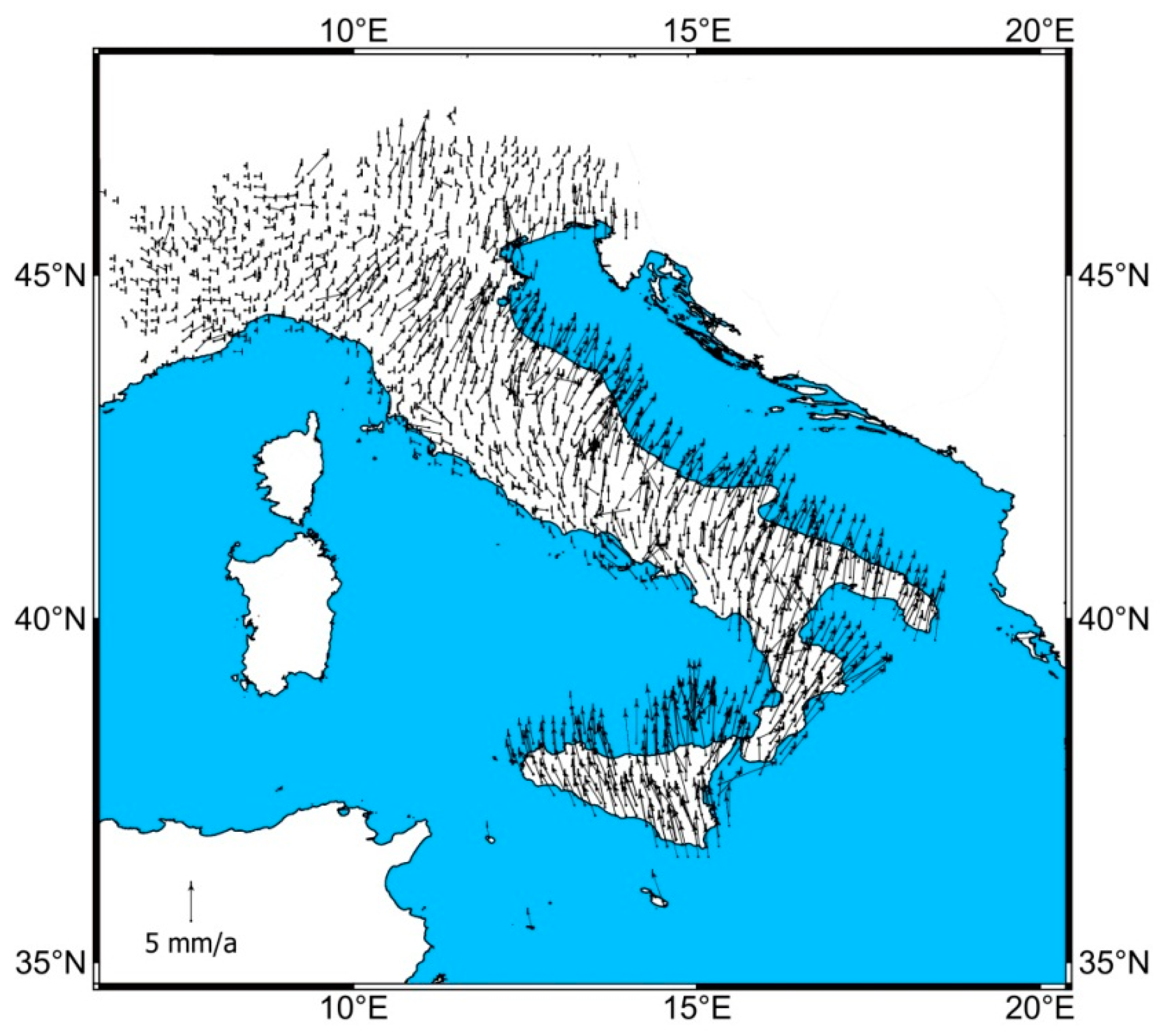
3. Current Tectonics of Italy
4. Comparison of Techniques
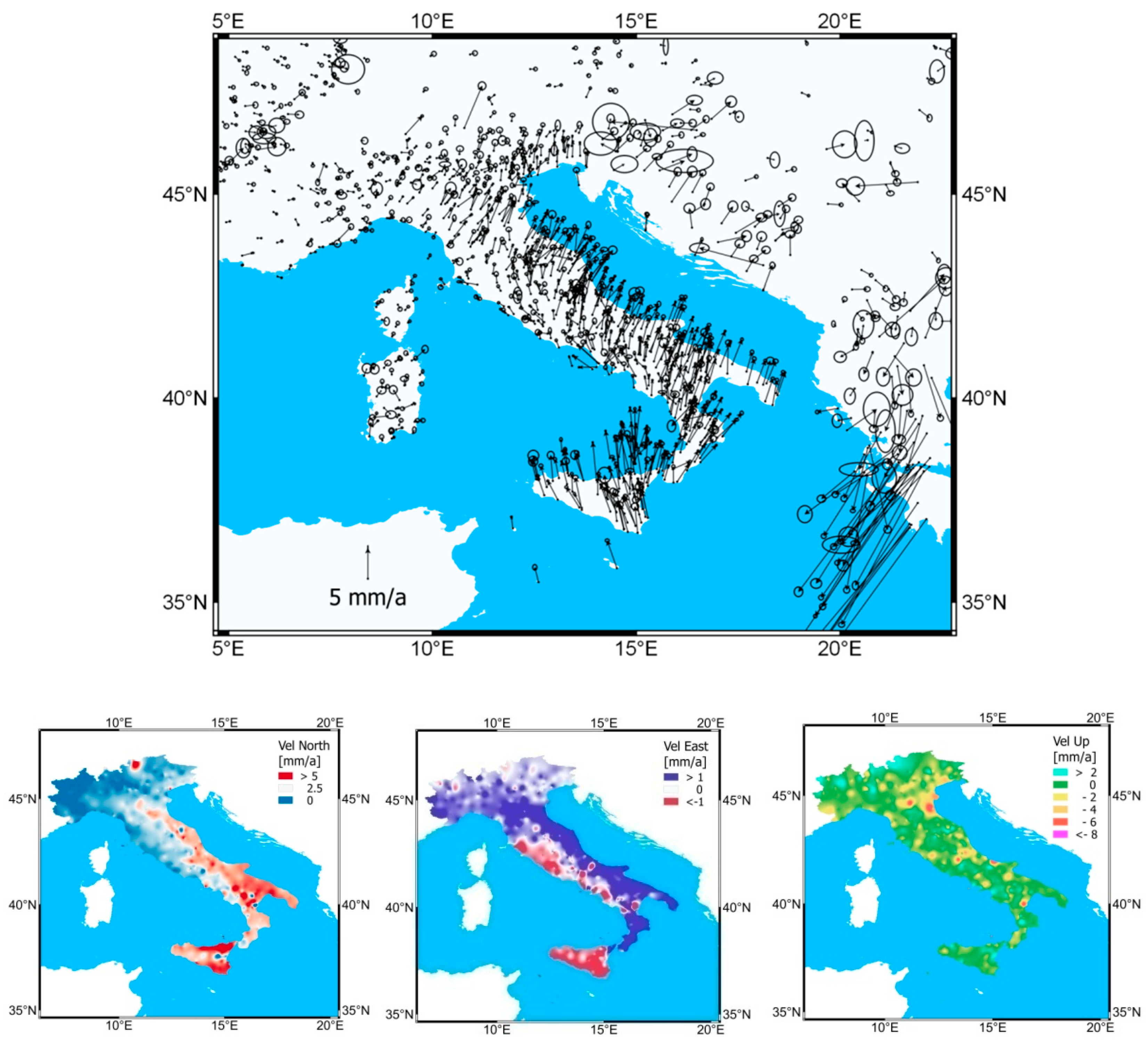
5. GNSS and PSI Datasets
5.1. GNSS
5.2. PSI
6. PS Velocity Transformation from LOS to Local Geodetic Systems
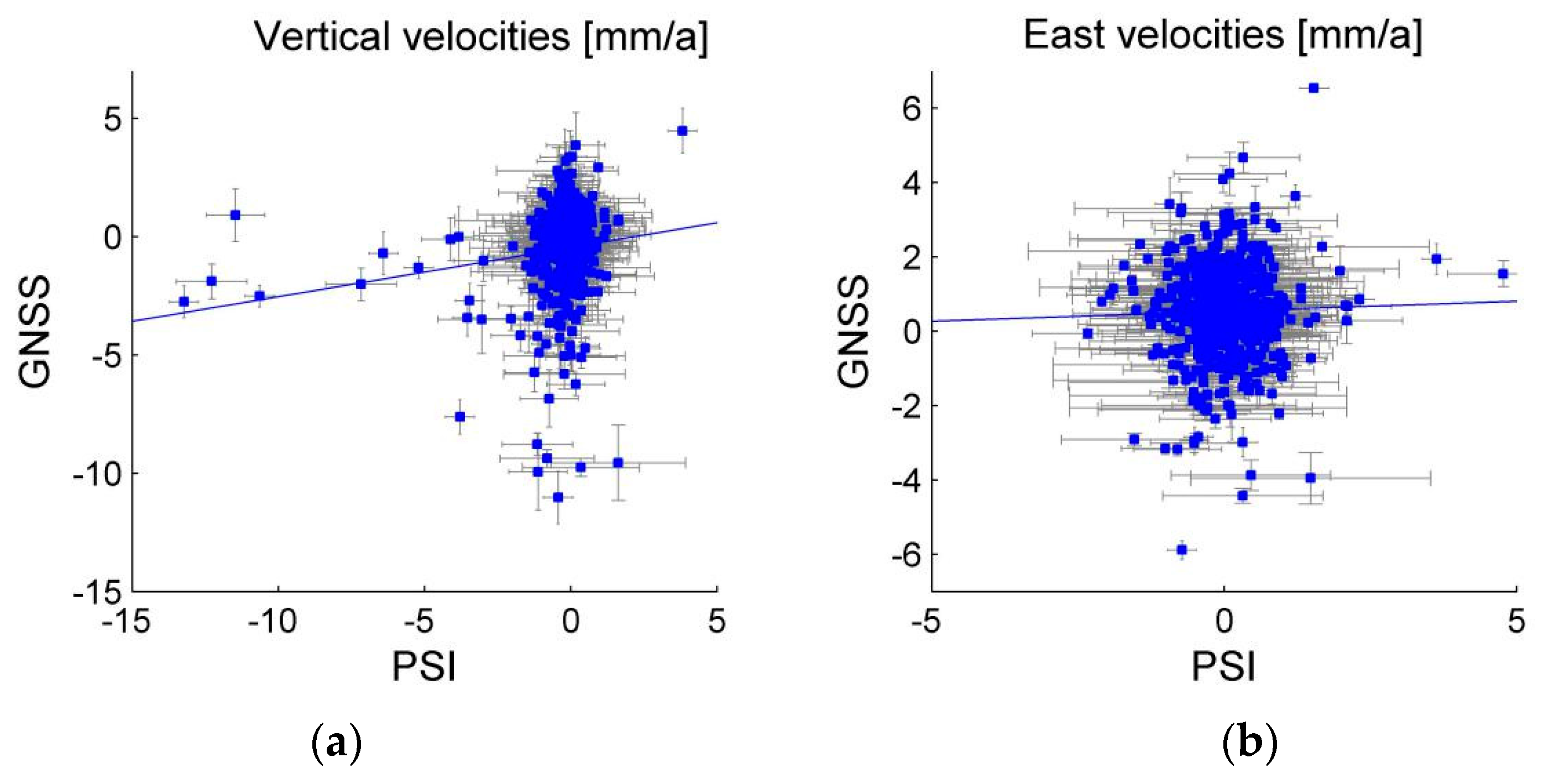
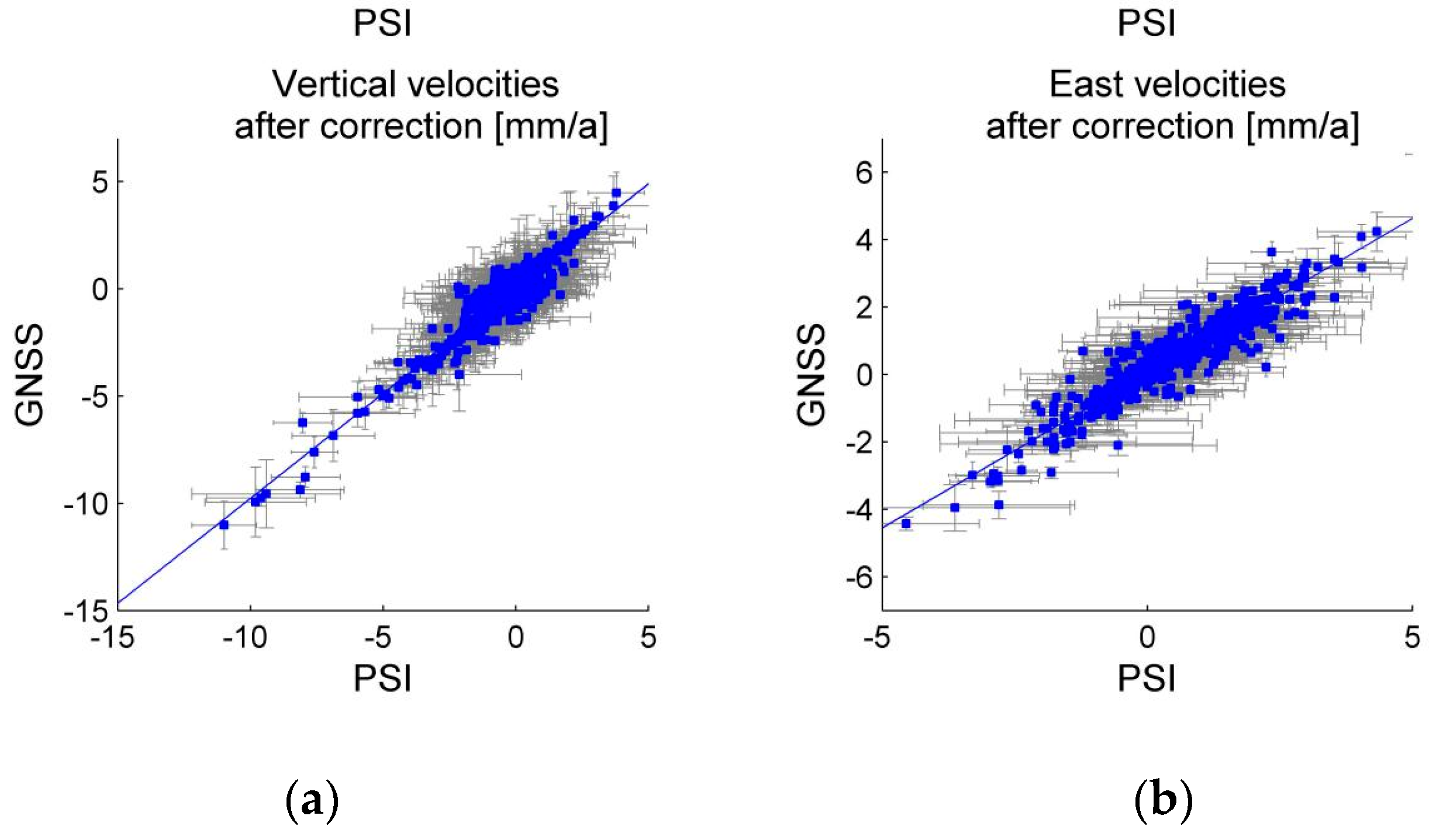
7. PS Velocity Calibration and Calibration
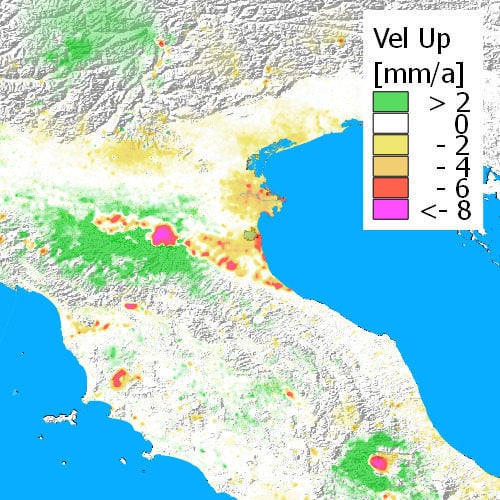
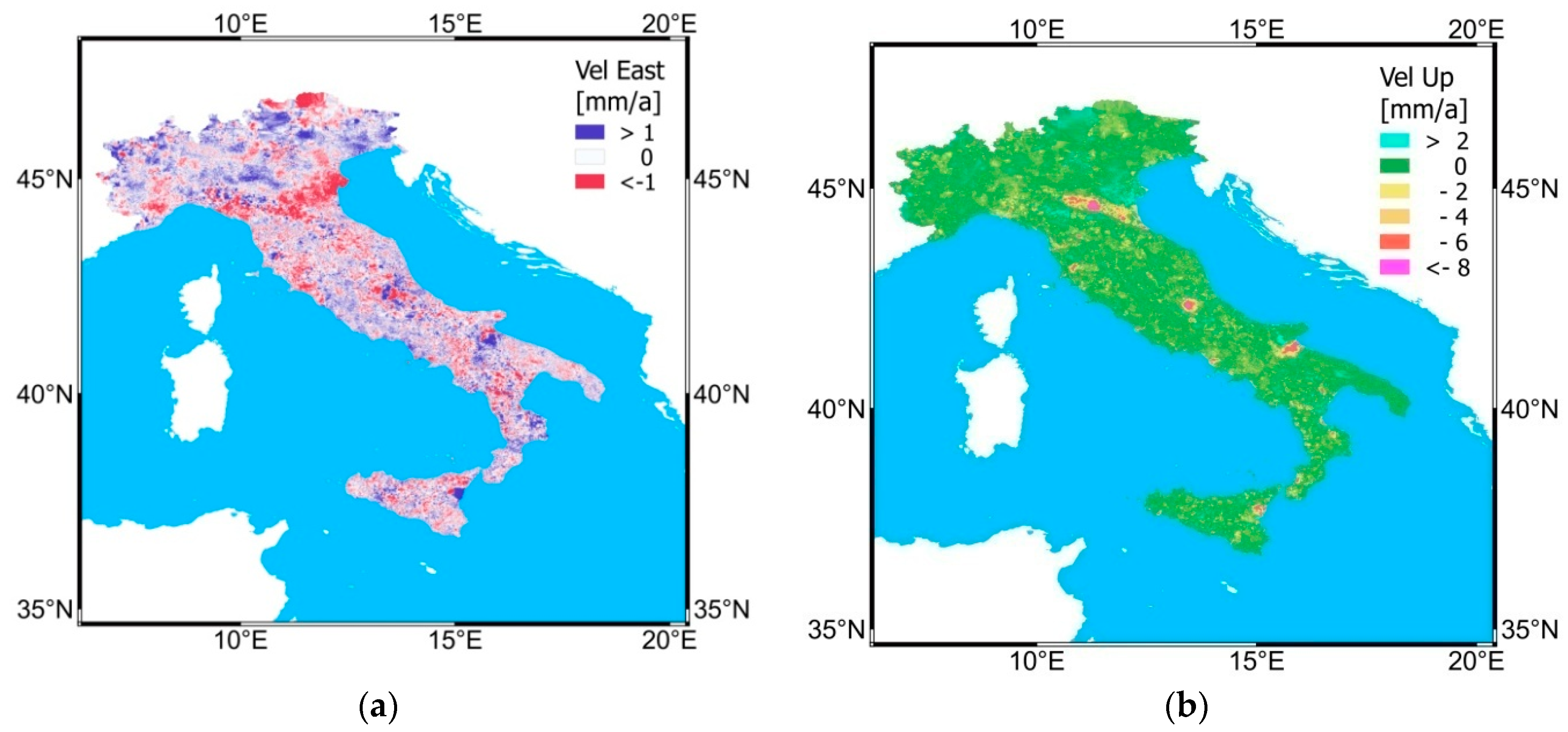
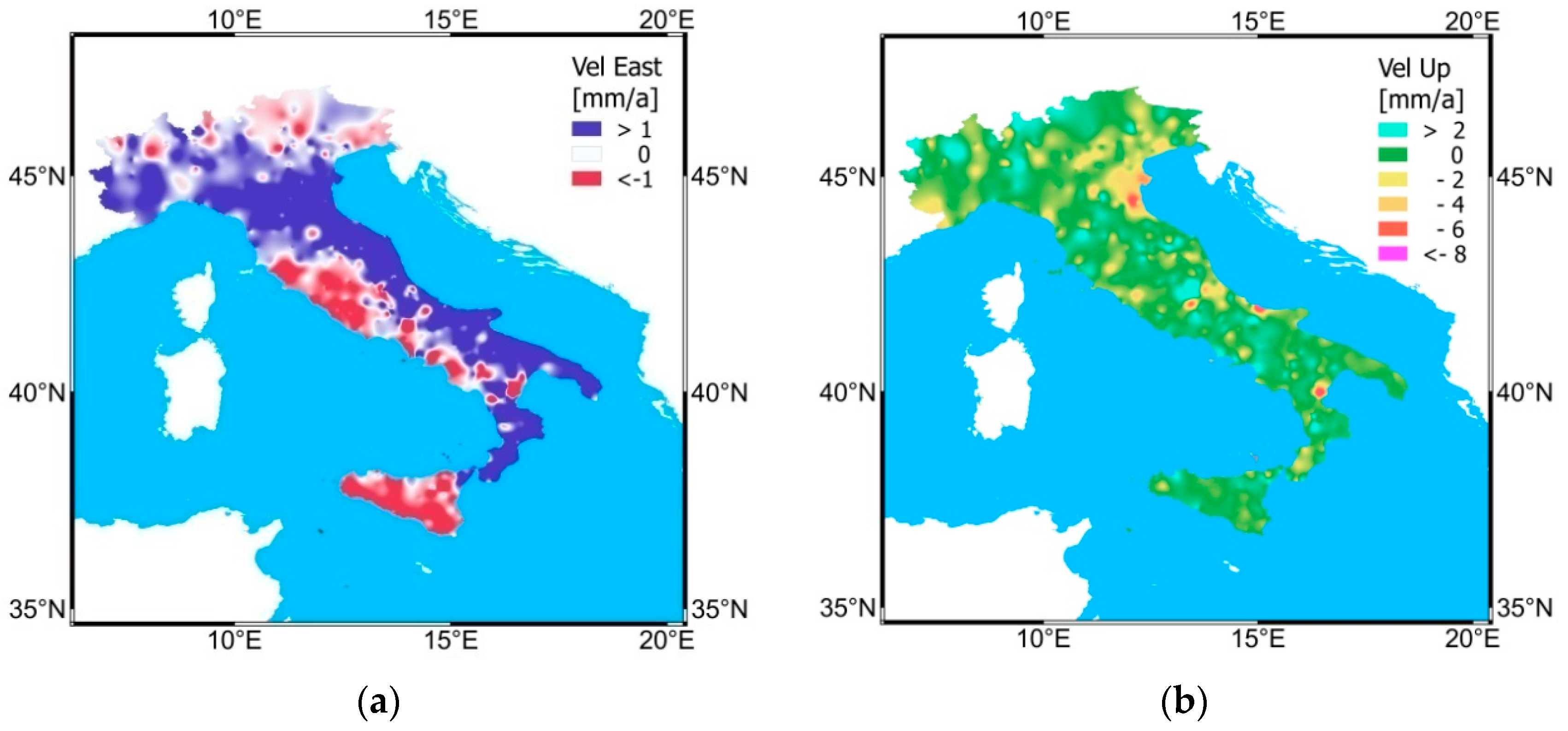
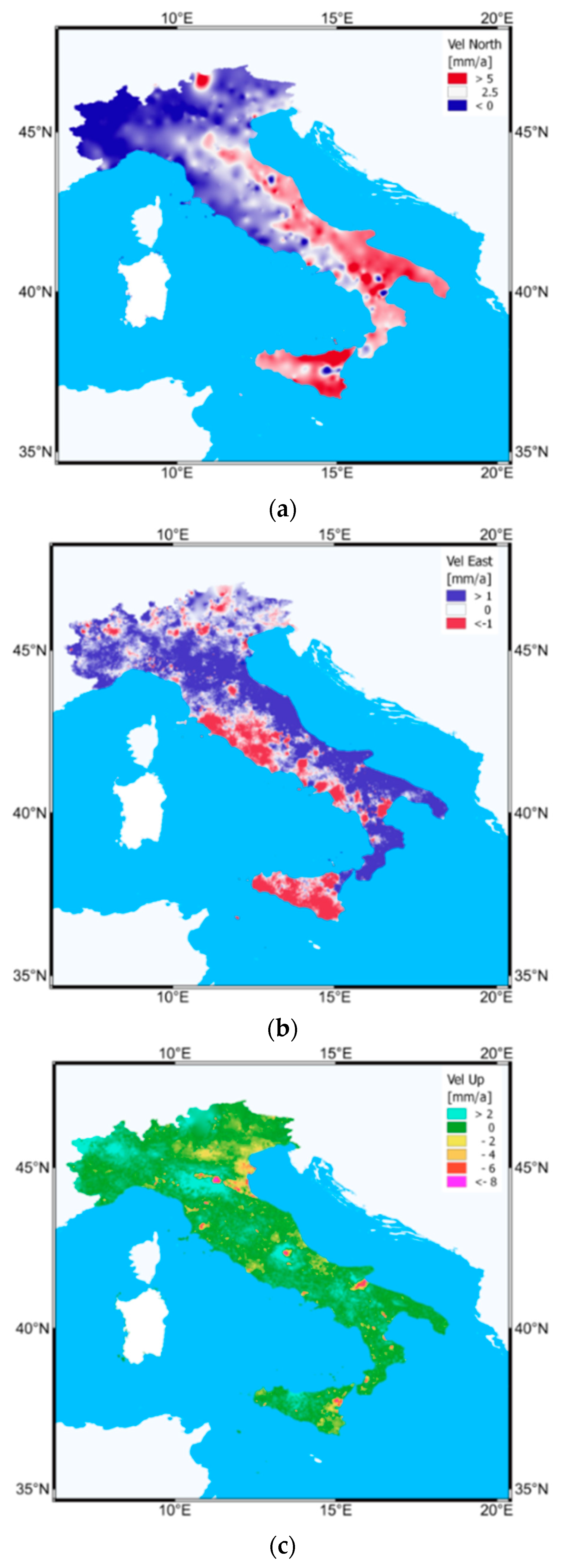
8. Results—Current Italian Geological Characteristics
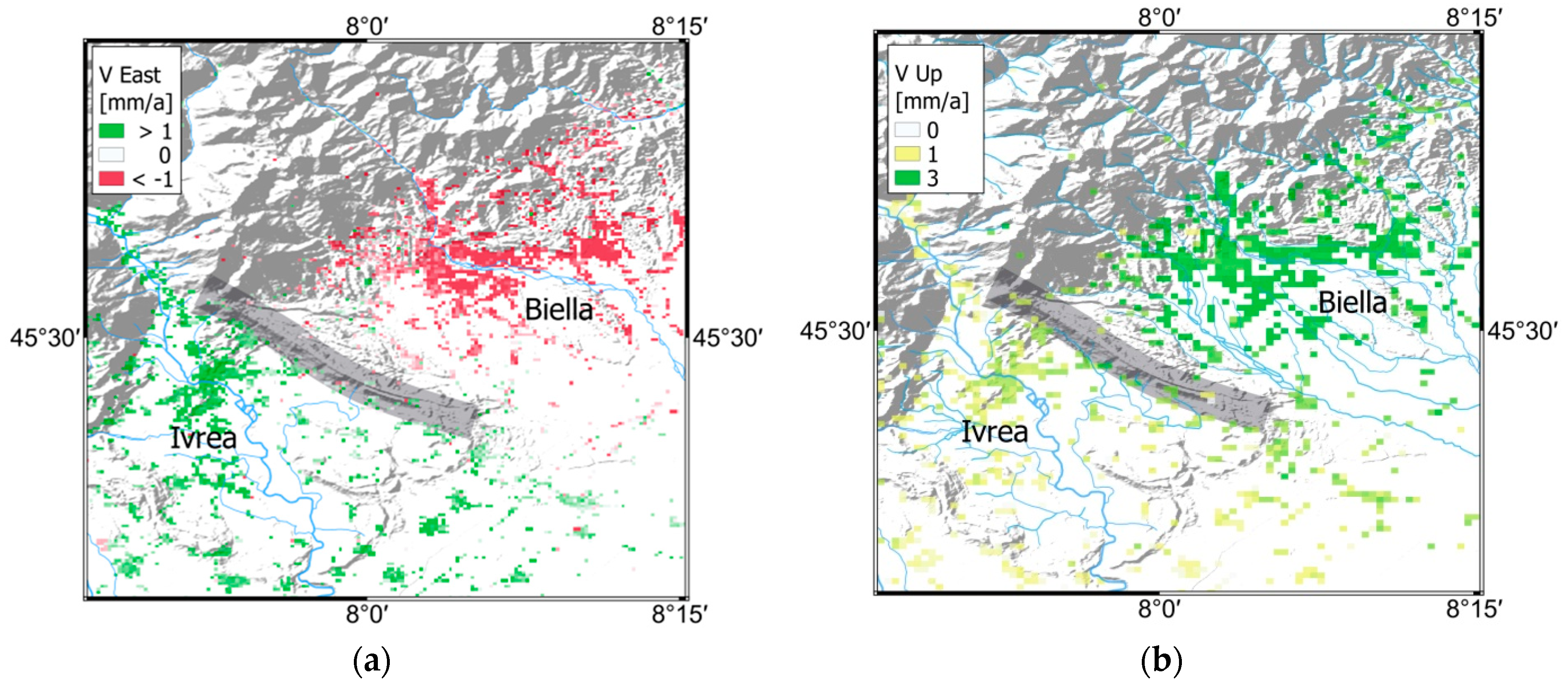
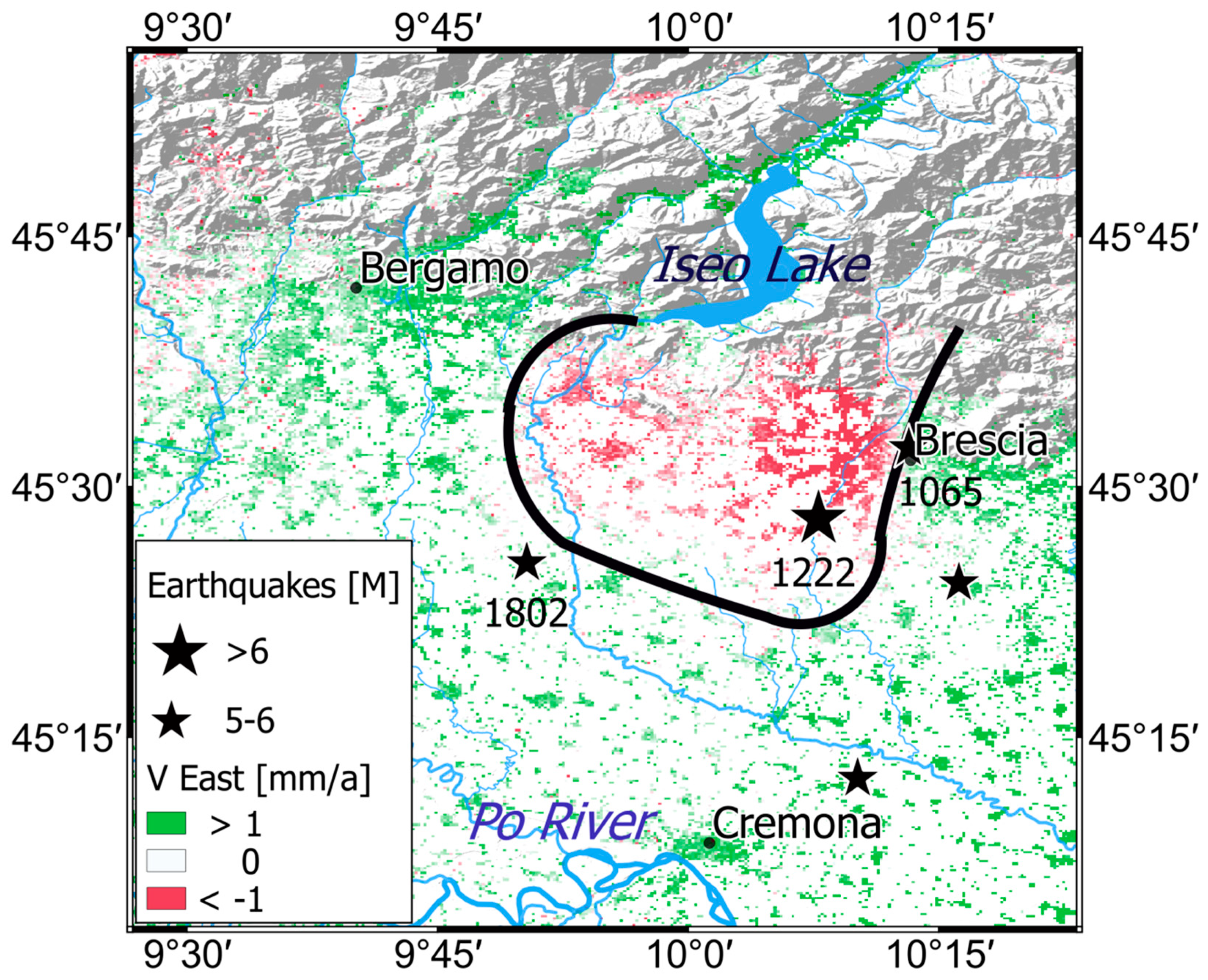
8.1. Northern Italy
8.1.1. Biella—OrtaWestern Kinematic Zone
8.1.2. Brescia
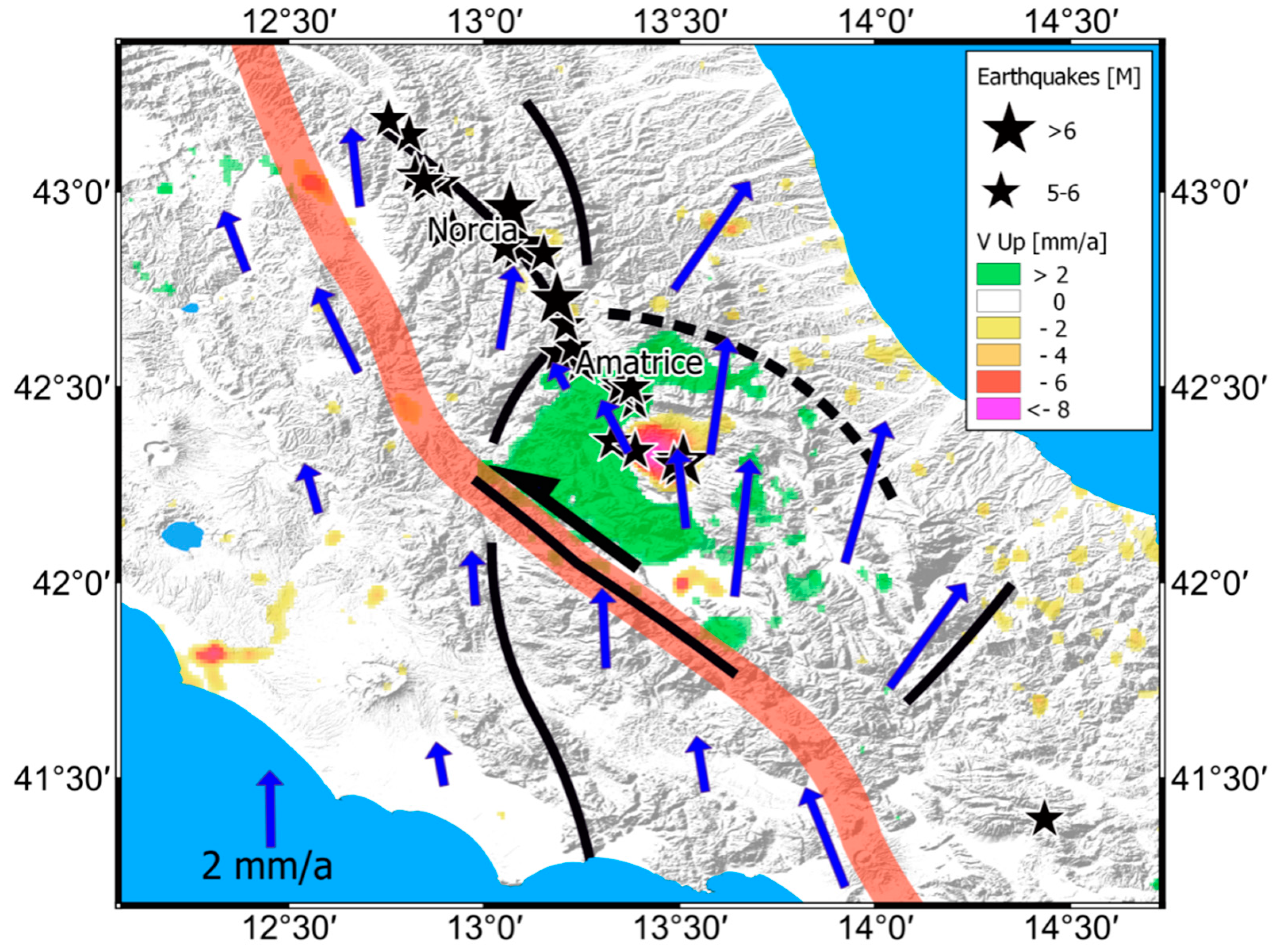
8.2. Central Italy
8.2.1. Abruzzi
8.2.2. Southern Latium
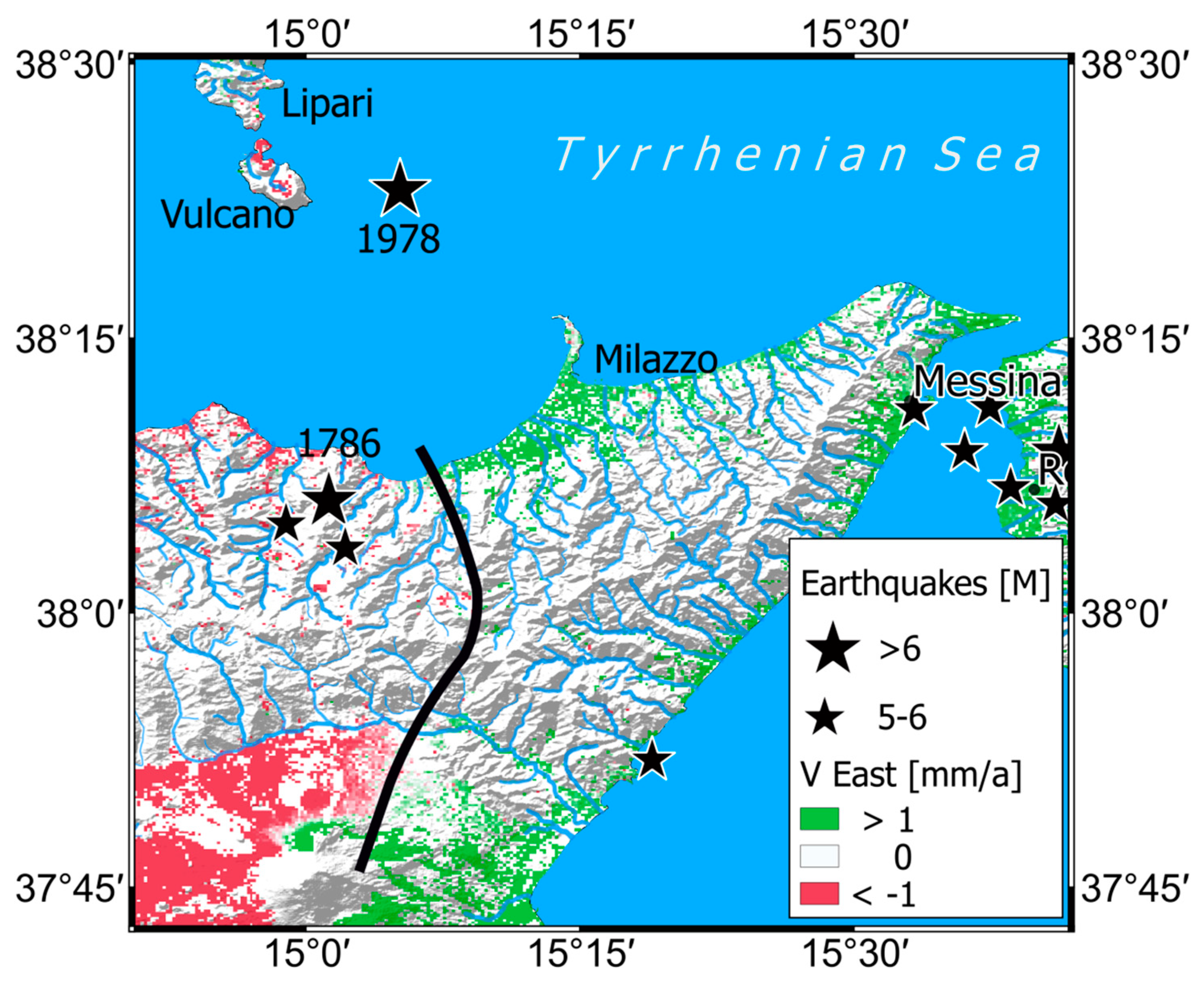
8.3. Southern Italy
9. Conclusions
- The surface movement maps present detailed and correct information that is coherent at a wider scale. It improves knowledge of geodynamic processes such as crustal dynamics, subsidence and uplift.
- The geodynamics can be improved by SAR data that verify the stability of GNSS sites. In fact, it can be used to check and highlight possible local movement involving a given GNSS site and then exclude it for geodetic purposes (i.e., crustal dynamics and reference frame).
- The SAR interferometry maps can be corrected for constant movements and for the low wave number components of the velocity field before being aligned to geodetic data.
- Because the different systems of acquisition used in SAR satellite missions produce velocity surfaces with different characteristics, it is necessary to create a unique surface motion map. Geodesy plays a fundamental role in the alignment of data before stacking SAR maps. The method of data analysis presented in this work should be applied taking account of other technologies such as LIDAR and leveling networks and particularly for validating DInSAR from newer SAR systems such as Sentinel-1, Cosmo-SkyMed SAR, and TerraSAR-X.
- The present work can be the base for the determination of a detail strain rate map of the Italian peninsula that plays an important role for a better understanding of geodynamical and geophysical processes [73].
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Bruyninx, C.; Becker, M.; Stangl, G. Regional densification of the IGS in Europe using the EUREF permanent GPS network (EPN). Phys. Chem. Earth Part A Solid Earth Geod. 2001, 26, 531–538. [Google Scholar] [CrossRef]
- Falchi, U.; Parente, C.; Prezioso, G. Global geoid adjustment on local area for GIS applications using GNSS permanent station coordinates. Geod. Cartogr. 2018, 44, 80–88. [Google Scholar] [CrossRef]
- Farolfi, G.; Del Ventisette, C. Monitoring the Earth’s ground surface movements using satellite observations: Geodinamics of the Italian peninsula determined by using GNSS networks. In Proceedings of the 2016 IEEE Metrology for Aerospace (MetroAeroSpace), Florence, Italy, 22–23 June 2016; pp. 479–483. [Google Scholar] [CrossRef]
- Del Soldato, M.; Riquelme, A.; Bianchini, S.; Tomàs, R.; Di Martire, D.; De Vita, P.; Calcaterra, D. Multisource data integration to investigate one century of evolution for the Agnone landslide (Molise, southern Italy). Landslides 2018, 15, 2113–2128. [Google Scholar] [CrossRef]
- Bianchini, S.; Raspini, F.; Solari, L.; Del Soldato, M.; Ciampalini, A.; Rosi, A.; Casagli, N. From Picture to Movie: Twenty Years of Ground Deformation recording over Tuscany Region (Italy) with Satellite InSAR. Front. Earth Sci. 2018, 6, 177. [Google Scholar] [CrossRef]
- Colesanti, C.; Ferretti, A.; Prati, C.; Rocca, F. Monitoring landslides and tectonic motions with the Permanent Scatterers Technique. Eng. Geol. 2003, 68, 3–14. [Google Scholar] [CrossRef]
- Raspini, F.; Bianchini, S.; Ciampalini, A.; Del Soldato, M.; Solari, L.; Novali, F.; Casagli, N. Continuous, semi-automatic monitoring of ground deformation using Sentinel-1 satellites. Sci. Rep. 2018, 8, 7253. [Google Scholar] [CrossRef] [PubMed]
- Santoro, M.; Askne, J.I.; Wegmuller, U.; Werner, C.L. Observations, modelling, and applications of ERS-ENVISAT coherence over land surfaces. IEEE Trans. Geosci. Remote Sens. 2007, 45, 2600–2611. [Google Scholar] [CrossRef]
- Crosetto, M.; Monserrat, O.; Cuevas-González, M.; Devanthéry, N.; Crippa, B. Persistent Scatterer Interferometry: A review. Int. J. Photogramm. Remote Sens. 2016, 115, 78–89. [Google Scholar] [CrossRef]
- Ferretti, A.; Prati, C.; Rocca, F. Permanent Scatterers in SAR Interferometry. IEEE Trans. Geosci. Remote Sens. 2001, 39, 8–20. [Google Scholar] [CrossRef]
- Goel, K.; Adam, N. A distributed scatterer interferometry approach for precision monitoring of known surface deformation phenomena. IEEE Trans. Geosci. Remote Sens. 2014, 52, 5454–5468. [Google Scholar] [CrossRef]
- Even, M.; Schulz, K. InSAR deformation analysis with distributed scatterers: A review complemented by new advances. Remote Sens. 2018, 10, 744. [Google Scholar] [CrossRef]
- Tofani, V.; Raspini, F.; Catani, F.; Casagli, N. Persistent Scatterer Interferometry (PSI) technique for landslide characterization and monitoring. Remote Sens. 2013, 5, 1045–1065. [Google Scholar] [CrossRef]
- Bekaert, D.P.S.; Segall, P.; Wright, T.J.; Hooper, A.J. A network inversion filter combining GNSS and InSAR for tectonic slip modeling. J. Geophys. Res. Solid Earth 2016, 121, 2069–2086. [Google Scholar] [CrossRef]
- Komac, M.; Holley, R.; Mahapatra, P.; van der Marel, H.; Bavec, M. Coupling of GPS/GNSS and radar interferometric data for a 3D surface displacement monitoring of landslides. Landslides 2015, 12, 241–257. [Google Scholar] [CrossRef]
- Del Soldato, M.; Farolfi, G.; Rosi, A.; Raspini, F.; Casagli, N. Subsidence Evolution of the Firenze–Prato–Pistoia Plain (Central Italy) Combining PSI and GNSS Data. Remote Sens. 2018, 10, 1146. [Google Scholar] [CrossRef]
- Bertotti, G.; Mosca, P.; Juez, J.; Polino, R.; Dunai, T. Oligocene to Present kilometres scale subsidence and exhumation of the Ligurian Alps and the Tertiary Piedmont Basin (NW Italy) revealed by apatite (U–Th)/He thermochronology: Correlation with regional tectonics. Terra Nova 2006, 18, 18–25. [Google Scholar] [CrossRef]
- Lustrino, M.; Morra, V.; Melluso, L.; Brotzu, P.; D’Amelio, F.; Fedele, L.; Franciosi, L.; Lonis, R.; Petteruti-Liebercknecht, A.M. The Cenozoic igneous activity of Sardinia. Period. Mineral. 2004, 73, 105–134. [Google Scholar]
- Spakman, W.; Wortel, M.J.R. A tomographic view on western Mediterranean geodynamics. In The TRANSMED Atlas, the Mediterranean Region from Crust to Mantle; Cavazza, W., Roure, F., Spakman, W., Stampfli, G.M., Ziegler, P., Eds.; Springer: Berlin/Heidelberg, Germany, 2004; pp. 31–52. [Google Scholar]
- Wortel, M.J.R.; Spakman, W. Structure and dynamics of subducted lithosphere in the Mediterranean region. Proc. van de Koninklijke NederlandseAcademie van Wetenschappen 1992, 95, 325–347. [Google Scholar]
- Rosenbaum, G.; Lister, G.S. Formation of arcuateorogenic belts in the western Mediterranean region. Geol. Soc. Am. Spec. Pap. 2004, 383, 41–56. [Google Scholar]
- Cocchi, L.; Passaro, S.; Caratori Tontini, F.; Ventura, G. Volcanism in slab tear faults is larger than in island-arcs and back-arcs. Nat. Commun. 2017, 8, 1451. [Google Scholar] [CrossRef]
- Serpelloni, E.; Bürgmann, R.; Anzidei, M.; Baldi, P.; Mastrolembo Ventura, B.; Boschi, E. Strain accumulation across the Messina Straits and kinematics of Sicily and Calabria from GPS data and dislocation modeling. Earth Planet. Sci. Lett. 2010, 298, 347–360. [Google Scholar] [CrossRef]
- Worth, J.R.; Spakman, W. Subduction and Slab Detachment in the Mediterranean-Carpathian Region. Science 2000, 290, 1910–1917. [Google Scholar]
- DISS Working Group. Database of Individual Seismogenic Sources (DISS), Version 3.2.1: A compilation of potential sources for earthquakes larger than M 5.5 in Italy and surrounding areas. 2018. Available online: http://diss.rm.ingv.it/diss/ (accessed on 10 February 2019). [CrossRef]
- Ustaszewski, K.; Schmid, S.M.; Fügenschuh, B.; Tischler, M.; Kissling, E.; Spakman, W. A map-view restoration of the Alpine-Carpathian-Dinaridic system for the Early Miocene. Swiss J. Geosci. 2008, 101 (Suppl. 1), S273–S294. [Google Scholar] [CrossRef]
- Fodor, L.; Jelen, B.; Marton, E.; Skaberne, D.; Car, J.; Vrabec, M. Miocene-Pliocene tectonic evolution of the Slovenian Periadriatic fault: Implications for Alpine-Carpathian extrusion models. Tectonics 1998, 17, 690–709. [Google Scholar] [CrossRef]
- Sani, F.; Vannucci, G.; Boccaletti, M.; Bonini, M.; Corti, G.; Serpelloni, E. Insights into the fragmentation of the Adria Plate. J. Geodyn. 2016, 102, 121–138. [Google Scholar] [CrossRef]
- Hooper, A. A multi-temporal InSAR method incorporating both persistent scatterer and small baseline approaches. Geophys. Res. Lett. 2018, 35. [Google Scholar] [CrossRef]
- Werner, C.L.; Hensley, S.; Goldstein, R.M.; Rosen, P.A.; Zebker, H.A. Techniques and applications of SAR interferometry for ERS-1: Topographic mapping, change detection, and slope measurement. In Proceedings of the First ERS-1 Symposium on Space at the Service of Our Environment, Cannes, France, 4–6 November 1996; Volume 1, pp. 205–210. [Google Scholar]
- Farolfi, G.; Del Ventisette, C. Contemporary crustal velocity field in Alpine Mediterranean area of Italy from new geodetic data. GPS Solut. 2015, 20, 715–722. [Google Scholar] [CrossRef]
- Farolfi, G.; Del Ventisette, C. Strain rates in the Alpine Mediterranean region: Insights from advanced techniques of data processing. GPS Solut. 2016, 21, 1027–1036. [Google Scholar] [CrossRef]
- Dach, R.; Hugentobler, U.; Fridez, P.; Meindl, M. The Bernese GPS Software Version 5.0; Astronomical Institute of University of Bern (AIUB): Bern, Switzerland, 2007. [Google Scholar]
- Böhm, J.; Heinkelmann, R.; Schuh, H.A. Global Model of Pressure and Temperature for Geodetic Applications. J. Geod. 2007, 81, 679–683. [Google Scholar] [CrossRef]
- Williams, S.D.P. CATS: GPS coordinate time series analysis software. GPS Solut. 2008, 12, 147–153. [Google Scholar] [CrossRef]
- Palano, M. On the present-day crustal stress, strain-rate fields and mantle anisotropypattern of Italy. Geophys. J. Int. 2015, 200, 969–985. [Google Scholar] [CrossRef]
- Herring, T.A.; King, R.W.; McClusky, S.C. Introduction to GAMIT/GLOB. Release 10.4; Massachusetts Institute of Technology: Cambridge, MA, USA, 2010; pp. 1–48. [Google Scholar]
- Herring, T. MATLAB Tools for viewing GPS velocities and time series. GPS Solut. 2003, 7, 194. [Google Scholar] [CrossRef]
- Zafiri, Z.; Nilfouroushan, F.; Raeesi, M. Crustal stress Map of Iran: Insight from seismic and geodetic computations. Pure Appl. Geophys. 2014, 171, 1219–1236. [Google Scholar] [CrossRef]
- Italian Geoportale Nazionale. Available online: www.pcn.minambiente.it (accessed on 20 December 2017).
- Shepard, D. A two-dimensional interpolation function for irregularly-spaced data. In Proceedings of the 1968 ACM National Conference, Las Vegas, NV, USA, 27–29 August 1968. [Google Scholar] [CrossRef]
- Bartier, P.; Keller, P. Multivariate interpolation to incorporate thematic surface data using inverse distance weighting (IDW). Comput. Geosci. 1996, 22, 795–799. [Google Scholar] [CrossRef]
- Lee, S.; Wolberg, G.; Shin, S.Y. Scattered Data Interpolation with Multilevel B-Splines. IEEE Trans. Vis. Comput. Graph. 1997, 3, 228–244. [Google Scholar] [CrossRef]
- Morelli, M.; Piana, F.; Mallen, L.; Nicolò, G.; Fioraso, G. Iso-Kinematic Maps from statistical analysis of PS-InSAR data of Piemonte, NW Italy. Comparison with geological kinematic trends. Remote Sens. Environ. 2011, 115, 1188–1201. [Google Scholar] [CrossRef]
- Farolfi, G.; Bianchini, S.; Casagli, N. Integration of GNSS and satellite InSARdta: Derivation of fine-scale vertical surface motion maps of Po Plain, Northern Apennines and Southern Alps, Italy. IEEE Trans. Geosci. Remote Sens. (TGRS) 2018. [Google Scholar] [CrossRef]
- Guidoboni, E.; Comastri, A. The “exceptional” earthquake of 3 January 1117 in the Verona area (northern Italy): A critical time review and detection of two lost earthquakes (lower Germany and Tuscany). J. Geophys. Res. 2005, 110, B12309. [Google Scholar] [CrossRef]
- Galli, P.; Galadini, F.; Pantosti, D. Twenty years of paleoseismology in Italy. Earth-Sci. Rev. 2008, 88, 89–117. [Google Scholar] [CrossRef]
- Nocquet, J.-M.; Calais, E. Geodetic Measurements of Crustal Deformation in the Western Mediterranean and Europe. Pure Appl. Geophys. 2004, 161, 661–681. [Google Scholar] [CrossRef]
- Albini, P.; Rovida, A. The 12 May 1802 earthquake (N Italy) in its historical and seismological context. J. Seismol. 2010, 14, 629–651. [Google Scholar] [CrossRef]
- Desio, A. I rilievi isolati della Pianura Lombarda e di movimenti tettonici del Quaternario. Rend. Ist. Lomb. Acc. Sci. Lett. Sez. A 1965, 99, 881–894. [Google Scholar]
- Livio, F.A.; Berlusconi, A.; Michetti, A.M.; Sileo, G.; Zerboni, A.; Trombino, L.; Cremaschi, M.; Mueller, K.; Vittori, E.; Carcano, C.; et al. Active fault-related folding in the epicentral area of the December 25, 1222 (Io=IXMCS) Brescia earthquake (Northern Italy): Seismotectonic implications. Tectonophysics 2009, 476, 320–335. [Google Scholar] [CrossRef]
- Mantovani, E.; Viti, M.; Cenni, N.; Babbucci, D.; Tamburelli, C.; Baglione, M.; D’Intinosante, V. Seismotectonics and present seismic hazard in the Tuscany–Romagna–Marche–Umbria Apennines (Italy). J. Geodyn. 2015, 89, 1–14. [Google Scholar] [CrossRef]
- Di Bucci, D.; Corrado, S.; Naso, G. Active faults at the boundary between Central and Southern Apennines (Isernia, Italy). Tectonophysics 2002, 359, 47–63. [Google Scholar] [CrossRef]
- Rovida, A.; Locati, M.; Camassi, R.; Lolli, B.; Gasperini, P. (Eds.) CPTI15, the 2015 version of the Parametric Catalogue of Italian Earthquakes; Istituto Nazionale di Geofisica e Vulcanologia: Rome, Italy, 2016. [Google Scholar] [CrossRef]
- Bonardi, G.; Cavazza, W.; Perrone, V.; Rossi, S. Calabria-Peloritaniterrane and northern Ionian Sea. In Anatomy of an Orogen: The Apennines and Adjacent Mediterranean Basins; Vai, G.B., Martini, I.P., Eds.; Springer: Dordrecht, The Netherland, 2001. [Google Scholar] [CrossRef]
- Roure, F.; Howell, D.G.; Muller, C.; Moretti, I. Late Cenozoicsubduction complex of Sicily. J. Struct. Geol. 1990, 12, 259–266. [Google Scholar] [CrossRef]
- Lentini, F.; Carbone, S.; Guarnieri, P. Collisional and post collisional tectonics of the Apenninic-Maghrebianorogen (southern Italy). GSA Spec. Pap. 2006, 409, 57–81. [Google Scholar] [CrossRef]
- Gallais, F.; Graindorge, D.; Gutscher, M.A.; Klaeschen, D. Propagation of a lithospheric tear fault (STEP) through the western boundary of the Calabrian accretionary wedge offshore eastern Sicily (Southern Italy). Tectonophysics 2013, 602, 141–152. [Google Scholar] [CrossRef]
- Billi, A.; Barberi, G.; Faccenna, C.; Neri, G.; Pepe, F.; Sulli, A. Tectonics and seismicity of the Tindari Fault System, southern Italy: Crustal deformations at the transition between on going contractional and extensional domains located above the edge of a subducting slab. Tectonics 2006, 25, TC2006. [Google Scholar] [CrossRef]
- Ghisetti, F.; Pezzino, A.; Atzori, P.; Vezzani, L. Un approccio strutturale per la definizione della Linea di Taormina: Risultati preliminari. Mem. Soc. Geol. Ital. 1991, 47, 272–283. [Google Scholar]
- Palano, M.; Ferranti, L.; Monaco, C.; Mattia, M.; Aloisi, M.; Bruno, V.; Cannavò, F.; Siligato, G. GPS velocity and strain fields in Sicily and southern Calabria, Italy: Updated geodetic constraints on tectonic block interaction in the central Mediterranean. J. Geophys. Res. 2012, 117, B07401. [Google Scholar] [CrossRef]
- Cultrera, F.; Barreca, G.; Ferranti, L.; Monaco, C.; Pepe, F.; Passaro, S.; Graziella, B.; Bruno, V.; Burrato, P.; Mattia, M.; et al. Structural architecture and active deformation pattern in the northern sector of the Aeolian-Tindari-Letojanni fault system (SE Tyrrhenian Sea-NE Sicily) from integrated analysis of eld, marine geophysical, seismological and geodetic data. Ital. J. Geosci. 2017, 136, 399–417. [Google Scholar] [CrossRef]
- Di Stefano, A.; Lentini, R. Ricostruzione stratigrafica e significato paleotettonico dei depositi plio-pleistocenici del margine tirrenico tra Villafranca Tirrena e Faro (Sicilia nordorientale). Stud. Geol. Camerti 1995, 2, 219–237. [Google Scholar]
- Doglioni, C.; Innocenti, F.; Mariotti, G. Why Mt Etna? Terra Nova 2001, 13, 25–31. [Google Scholar] [CrossRef]
- Neri, M.; Rivalta, E.; Maccaferri, F.; Acocella, V.; Cirrincione, R. Etnean and Hyblean volcanism shifted away from the Malta Escarpment by crustal stresses. Earth Planet. Sci. Lett. 2018, 486, 15–22. [Google Scholar] [CrossRef]
- Del Carlo, P.; Branca, S.; De Beni, E.; Lo Castro, M.D.; Wijbrans, J.R. The Mt. Moio eruption (Etna): Stratigraphy, petrochemistry and 40Ar/39Ar age determination with inferences on the relationship between structural setting and magma intrusion. J. Volcanol. Geotherm. Res. 2012, 241–242, 49–60. [Google Scholar] [CrossRef]
- Govers, R.; Wortel, M.J.R. Lithosphere tearing at STEP faults: Response to edges of subduction zones. Earth Planet. Sci. Lett. 2005, 236, 505–523. [Google Scholar] [CrossRef]
- Argnani, A. The Southern Tyrrhenian subduction system: Recent evolution and neotectonic implications. Ann. Geophys. 2000, 43, 585–607. [Google Scholar]
- Polonia, A.; Torelli, L.; Gasperini, L.; Cocchi, L.; Muccini, L.; Bonatti, E.; Hensen, C.; Schmidt, M.; Romano, A.; Artoni, A.; et al. Lower plate serpentinite diapirism in the Calabrian Arc subduction complex. Nat. Commun. 2017, 8, 2172. [Google Scholar] [CrossRef]
- Di Pasquale, A.; Nico, G.; Pitullo, A.; Prezioso, G. Monitoring Strategies of Earth Dams by Ground-Based Radar Interferometry: How to Extract Useful Information for Seismic Risk Assessment. Sensors 2018, 18, 244. [Google Scholar] [CrossRef]
- Narayan, A.B.; Tiwari, A.; Devara, M.; Dwivedi, R.; Dikshit, O. Monitoring landslides in the Mussoorie region, Uttarakhand using multi-temporal SAR interferometry with Sentinel-1 images. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2008, XLII-5, 849–853. [Google Scholar] [CrossRef]
- Tiwari, A.; Narayan, A.B.; Devara, M.; Dwivedi, R.; Dikshit, O. Multi-sensor geodetic approach for landslide detection and monitoring. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2018, IV-5, 287–292. [Google Scholar] [CrossRef]
- Neres, M.; Custódio, C.; Custódio, S.; Palano, M.; Fernandes, R.; Matias, L.; Carafa, M.; Terrinha, P. Gravitational Potential Energy in Iberia: A Driver of Active Deformation in High-Topography Regions. J. Geophys. Res. Solid Earth 2017, 123, 10277–10296. [Google Scholar] [CrossRef]
- QGIS Development Team. QGIS Geographic Information System. Open Source Geospatial Foundation, 2009. Available online: http://qgis.org (accessed on 10 February 2019).
- Ramsey, P. Postgis Manual; Refractions Research Inc.: Victoria, BC, Canada, 2005. [Google Scholar]
- Conrad, O.; Bechtel, B.; Bock, M.; Dietrich, H.; Fischer, E.; Gerlitz, L.; Wehberg, J.; Wichmann, V.; Böhner, J. System for Automated Geoscientific Analyses (SAGA) v. 2.1.4. Geosci. Model. Dev. 2015, 8, 1991–2007. [Google Scholar] [CrossRef]
- Farr, T.G.; Rosen, P.A.; Caro, E.; Crippen, R.; Duren, R.; Hensley, S.; Kobrick, M.; Paller, M.; Rodriguez, E.; Roth, L.; et al. The Shuttle Radar Topography Mission. Rev. Geophys. 2007, 45, RG2004. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Farolfi, G.; Piombino, A.; Catani, F. Fusion of GNSS and Satellite Radar Interferometry: Determination of 3D Fine-Scale Map of Present-Day Surface Displacements in Italy as Expressions of Geodynamic Processes. Remote Sens. 2019, 11, 394. https://doi.org/10.3390/rs11040394
Farolfi G, Piombino A, Catani F. Fusion of GNSS and Satellite Radar Interferometry: Determination of 3D Fine-Scale Map of Present-Day Surface Displacements in Italy as Expressions of Geodynamic Processes. Remote Sensing. 2019; 11(4):394. https://doi.org/10.3390/rs11040394
Chicago/Turabian StyleFarolfi, Gregorio, Aldo Piombino, and Filippo Catani. 2019. "Fusion of GNSS and Satellite Radar Interferometry: Determination of 3D Fine-Scale Map of Present-Day Surface Displacements in Italy as Expressions of Geodynamic Processes" Remote Sensing 11, no. 4: 394. https://doi.org/10.3390/rs11040394
APA StyleFarolfi, G., Piombino, A., & Catani, F. (2019). Fusion of GNSS and Satellite Radar Interferometry: Determination of 3D Fine-Scale Map of Present-Day Surface Displacements in Italy as Expressions of Geodynamic Processes. Remote Sensing, 11(4), 394. https://doi.org/10.3390/rs11040394