Modeling and Precise Processing for Spaceborne Transmitter/Missile-Borne Receiver SAR Signals
Abstract
:1. Introduction
- (1)
- The large-maneuver and receiving-only features of the missile-borne receiver reduce the detection probability. The corresponding anti-interference and anti-interception are greatly improved in the ST/MR SAR system.
- (2)
- The radar antenna, installed on the missile-borne platform, is used to receive the echo signals without a transmitting function, which indicates that a large power device can be avoided in the missile system to greatly save space and costs.
- (3)
- Spaceborne transmitter has the characteristics of wide coverage, unrestricted geography, net flexibility, and a high revisiting-frequency, which could provide some degrees of freedom (DOFs) in target area selection, flight trajectories, and number of missile-borne receivers.
- (4)
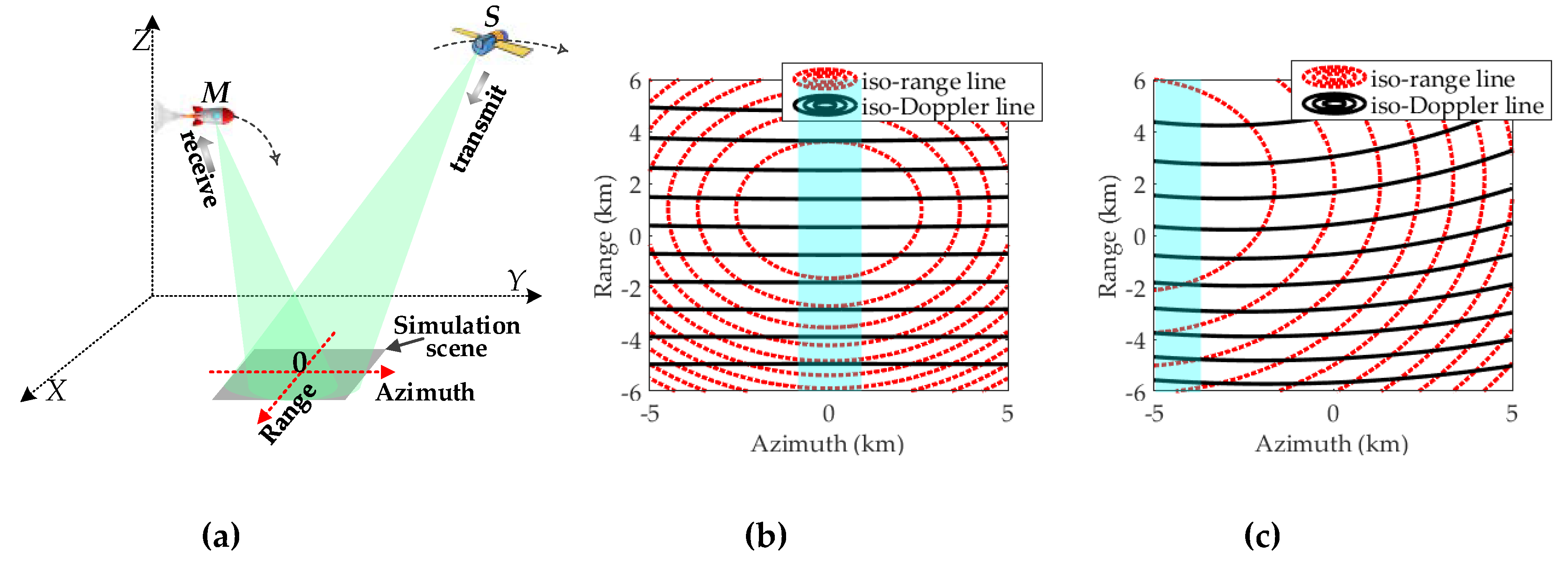
- By setting the transmitter and receiver on different platforms with a special style, the non-complete coupling areas between iso-range and iso-Doppler lines could be formed in front of missile, which means that the missile has the capability of forwarding-looking imaging.
2. Modeling
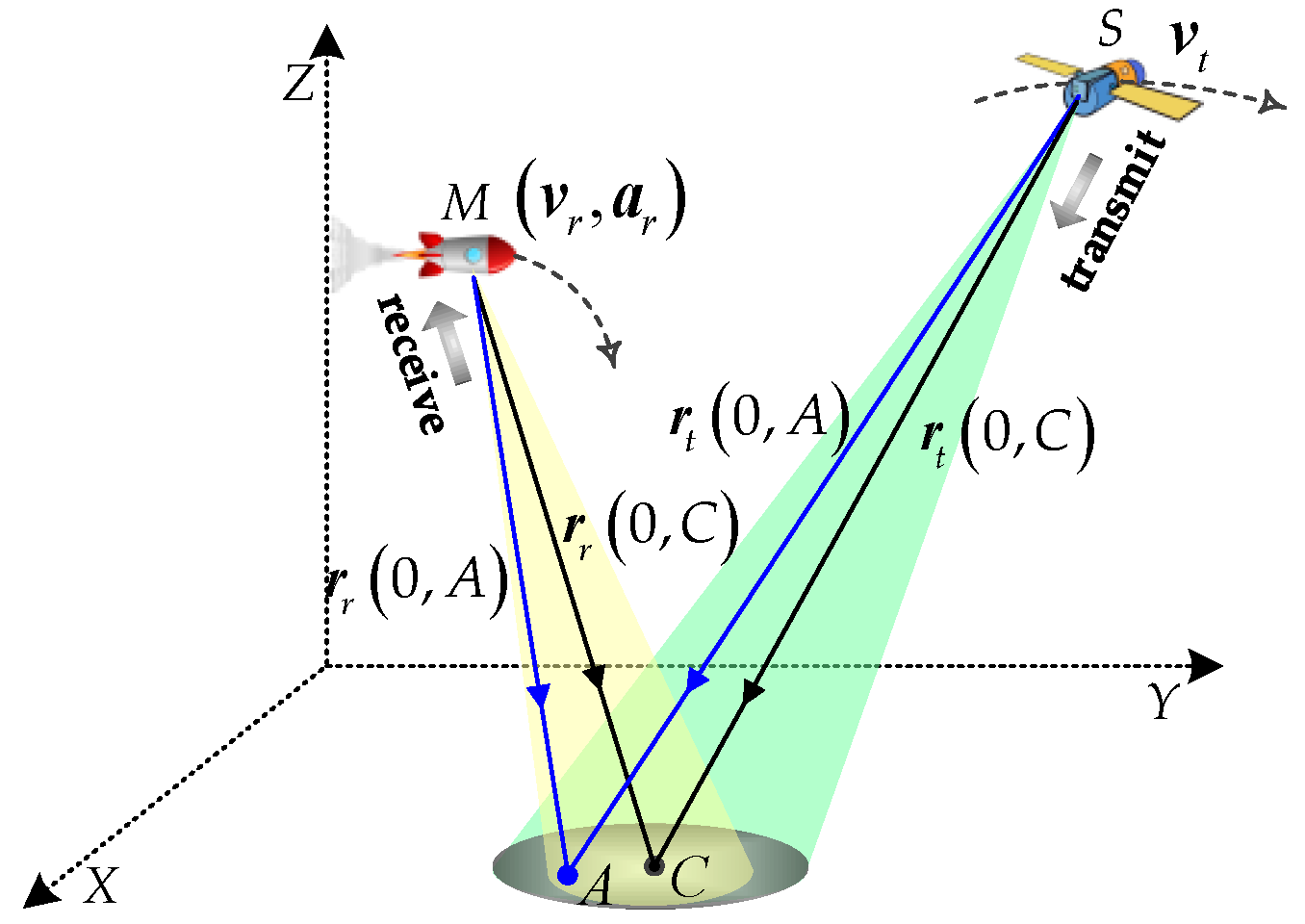
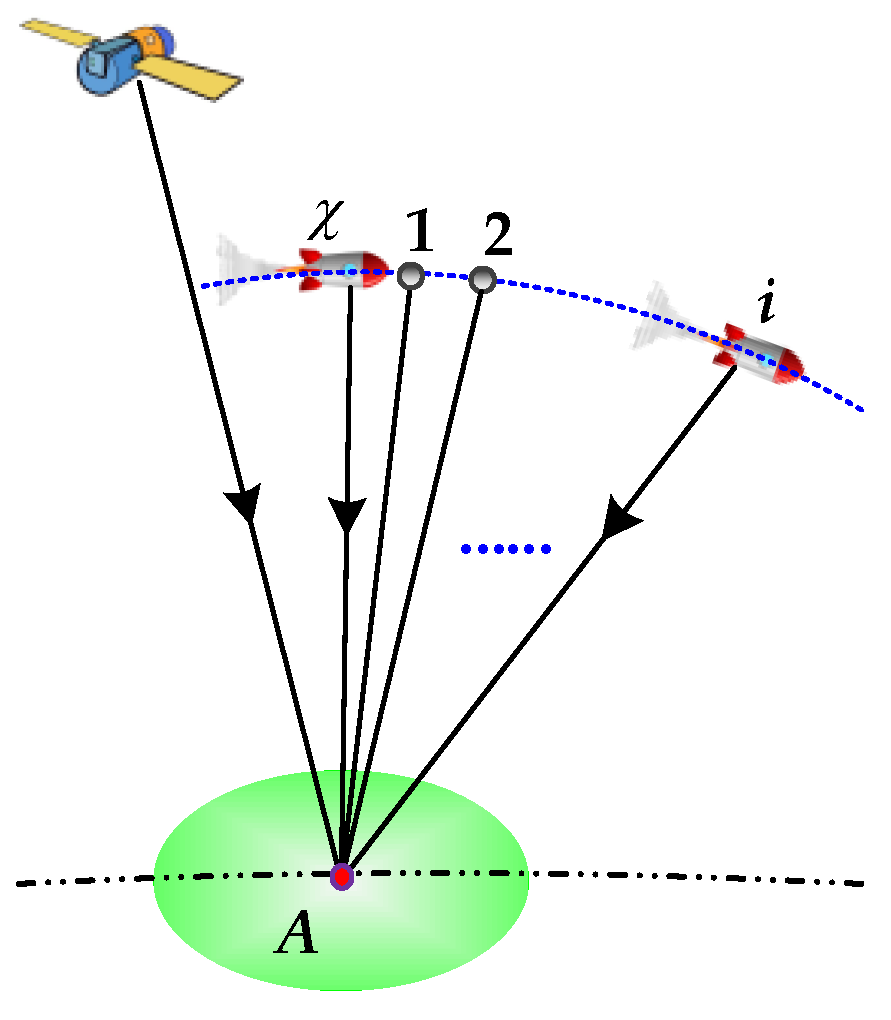
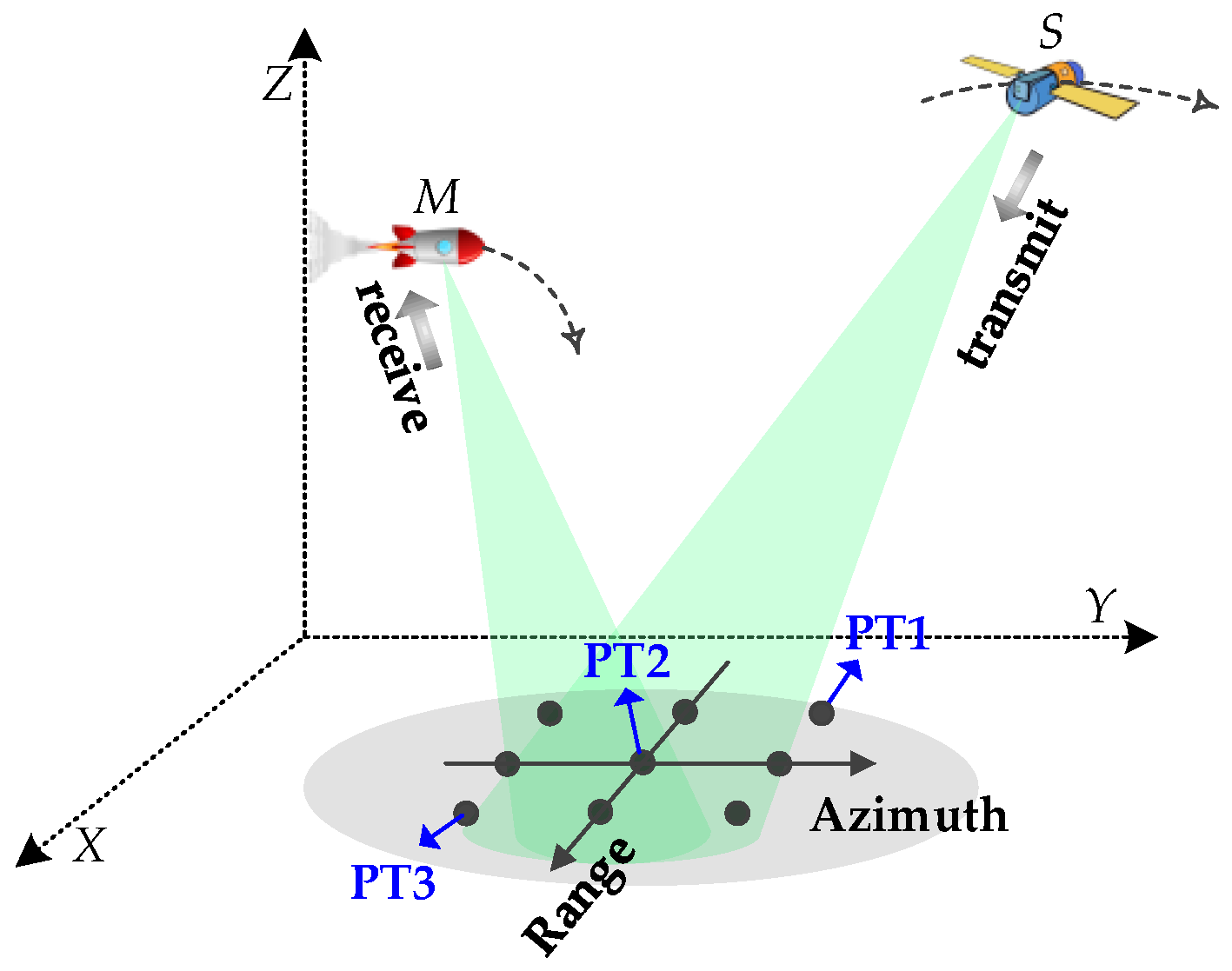
2.1. Geometric Model
2.2. Flight-Path Constraint
2.3. Flight-Path Constraint
| Algorithm 1. Basic procedure. |
| 1: Fixed input parameters: , , , , , , 2: Initialization (i=0): 3: Iterations (i≥1): 4: Calculate the delay: 5: Calculate the slant range of the receiver: 6: If , return and stop. 7: Calculate the time of the receiver: 8: Set . |
3. Imaging Approach
- ➢
- Cross-couplings. Traditionally, the cross-coupling phases in the 2-D spectrum derived by using the principle of stationary point (POSP) and MSR are divided into two parts, i.e., the range- and azimuth-dependent ones, and they are eliminated separately, which would introduce errors in the final image. The 2-D scaling algorithm in this work can avoid this division and make the processing more accurate than that of the traditional methods.
- ➢
- Spatial variations. Generally, the range, azimuth, and cross-coupling spatial variations in the 2-D spectrum are difficult to be removed simultaneously and entirely because of the complex phase expressions. In the 2-D scaling algorithm, two perturbation functions performed in the hybrid domains can eliminate the range, azimuth, and cross-coupling spatially variant terms simultaneously and entirely, which can avoid the defect of the traditional methods that the range and cross-coupling spatial variations cannot be removed.
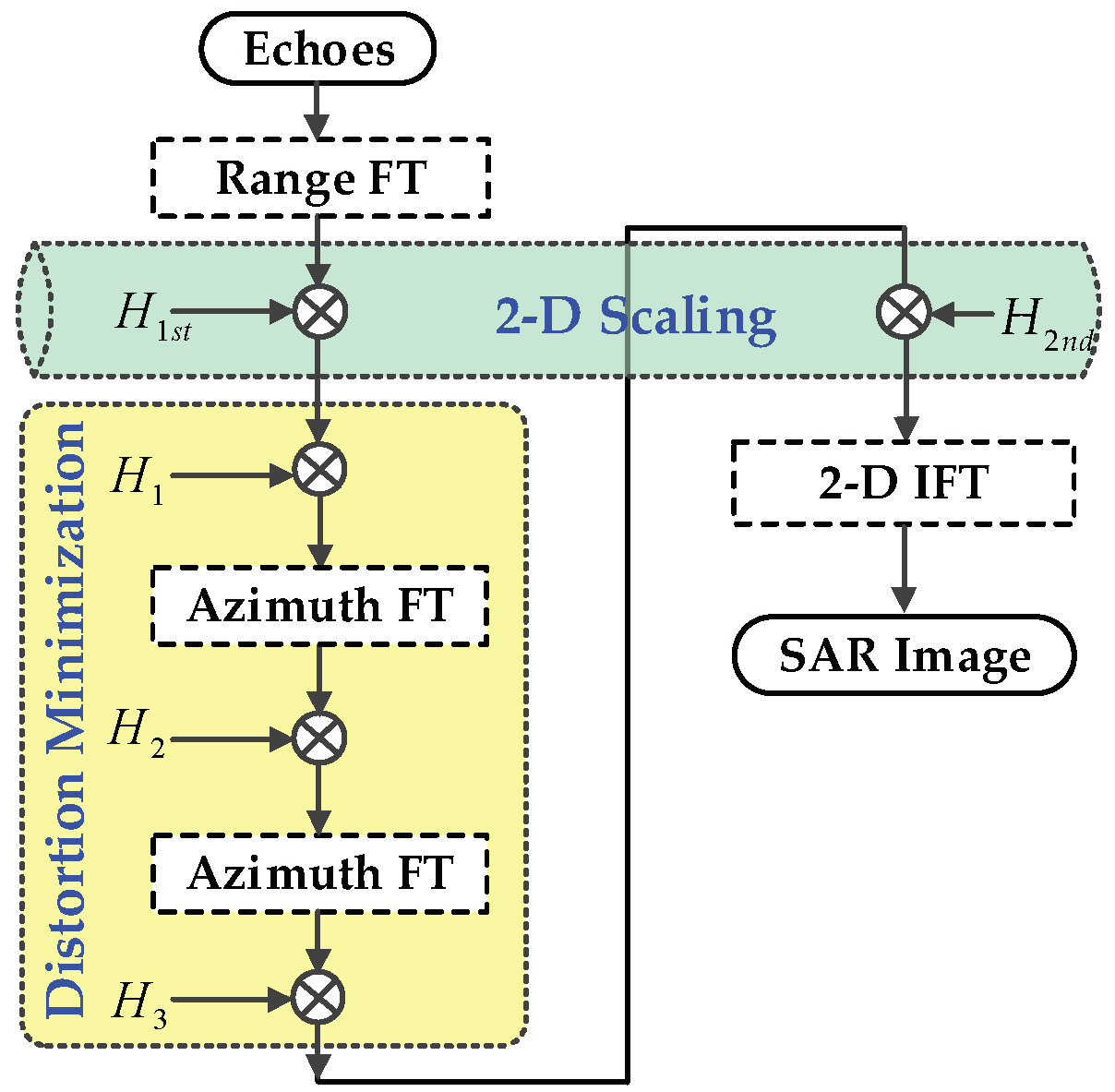
3.1. 2-D Scaling in Range Frequency/Azimuth Time Domain
3.2. Distortion Minimization
- ➢
- ➢
- ➢
- After multiplying Equation (6) with echoes, the rate of the Doppler FM becomes , which means that the azimuth bandwidth may display a big change. Thus, the possible spectral distortion should be eliminated before the azimuth FT of the signal.
3.3. 2-D Scaling in Range Frequency/Azimuth Frequency Domain
4. Simulation Results
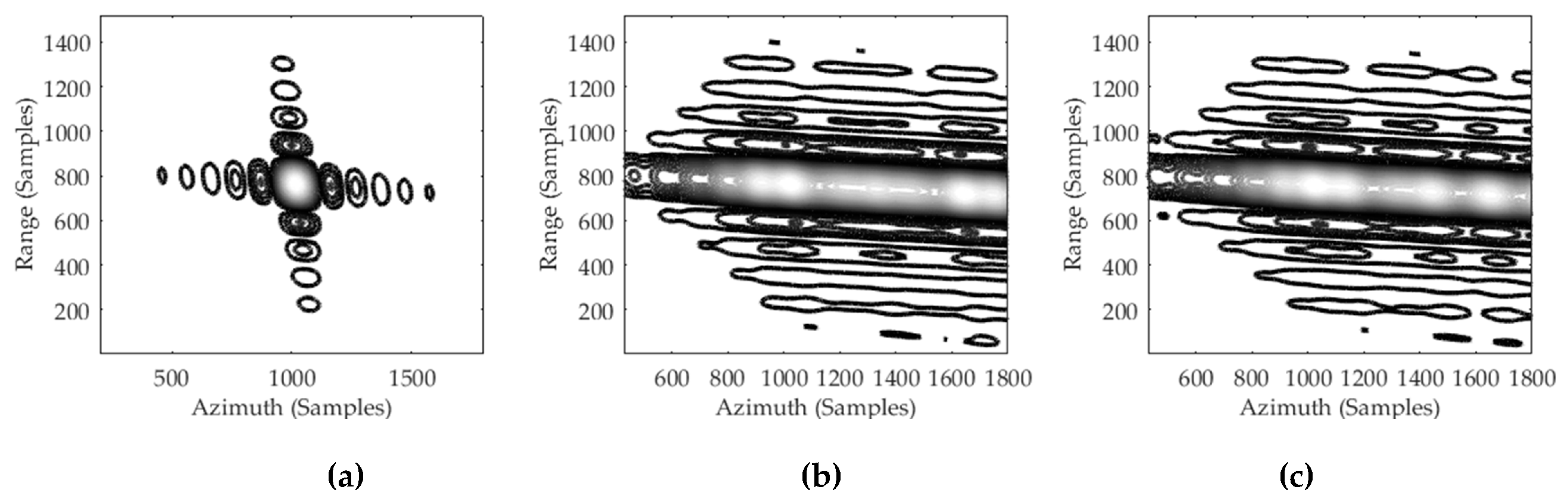
4.1. Case I
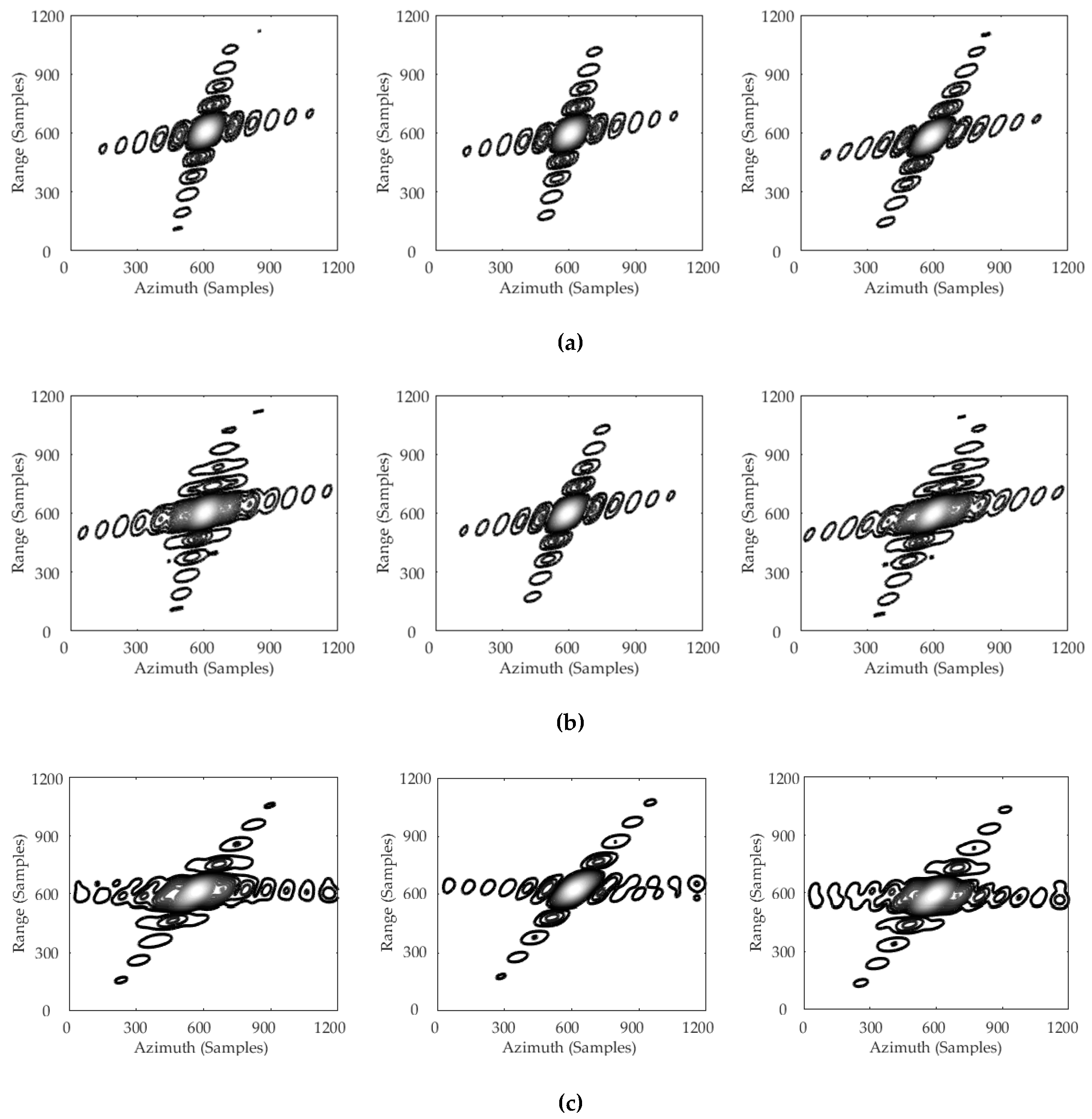
4.2. Case II
5. Discussion
5.1. 2-D Range Compression
5.2. Computational Load
6. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
Appendix A
| Coefficient | Transmitter | Coefficients | Receiver |
|---|---|---|---|
Appendix B
Appendix C
References
- Ender, J.H.; Walterscheid, I.; Brennner, A. New Aspects of Bistatic SAR: Processing and Experiments. Proc. IGARSS 2004, 9, 1758–1762. [Google Scholar]
- Loffeld, O.; Nies, H.; Peters, V.; Knedlik, S. Models and Useful Relations for Bistatic SAR Processing. IEEE Trans. Geosci. Remote Sens. 2004, 10, 2031–2038. [Google Scholar] [CrossRef]
- Wu, J.; Sun, Z.; Li, Z.; Huang, Y.; Yang, J.; Liu, Z. Focusing Translational Variant Bistatic Forward-Looking SAR Using Keystone Transform and Extended Nonlinear Chirp Scaling. Remote Sens. 2016, 8, 840. [Google Scholar] [CrossRef]
- Nies, H.; Loffeld, O.; Natroshvili, K. Analysis and Focusing of Bistatic Airborne SAR Data. IEEE Trans. Geosci. Remote Sens. 2007, 11, 3342–3349. [Google Scholar] [CrossRef]
- Rodriguez-Cassola, M.; Prats, P.; Schulze, D.; Tous-Ramon, N.; Steinbrecher, U.; Marotti, L.; Nannini, M.; Younis, M.; Lopez-Dekker, P.; López-Dekker, P.; et al. First Bistatic Spaceborne SAR Experiments with TanDEM-X. Proc. IGARSS 2011, 7, 1393–1396. [Google Scholar]
- Buckreuss, S.; Schattler, B.; Fritz, T.; Mittermayer, J.; Kahle, R.; Maurer, E.; Boer, J.; Bachmann, M.; Mrowka, F.; Schwarz, E.; et al. TenYears of TerraSAR-X Operations. Remote Sens. 2018, 6, 873. [Google Scholar] [CrossRef]
- Espeter, T.; Walterscheid, I.; Klare, J.; Ender, J.H.G. Synchronization Techniques for the Bistatic Spaceborne/Airborne SAR Experiment with TerraSAR-X and PAMIR. Proc. IGARSS 2007, 7, 2160–2163. [Google Scholar]
- Walterscheid, I.; Espeter, T.; Brenner, A.R.; Klare, J.; Ender, J.H.G.; Nies, H.; Wang, R.; Loffeld, O. Bistatic SAR Experiments with PAMIR and TerraSAR-X Setup, Processing, and Image Results. IEEE Trans. Geosci. Remote Sens. 2010, 8, 3268–3279. [Google Scholar] [CrossRef]
- Saeedi, J. Feasibility Study and Conceptual Design of Missile-Borne Synthetic Aperture Radar. IEEE Trans. Syst. Man Cybern. Syst. 2018. in Press. [Google Scholar] [CrossRef]
- Tang, S.; Zhang, L.; Guo, P.; Zhao, Y. An Omega-K Algorithm for Highly Squinted Missile-Borne SAR With Constant Acceleration. IEEE Geosci. Remote Sens. Lett. 2014, 9, 1569–1573. [Google Scholar] [CrossRef]
- Li, Y.; Meng, Z.; Xing, M.; Bao, Z. Configuration Study of Missile-borne Bistatic Forward-looking SAR. Proc. ChinaSIP 2014, 7, 184–188. [Google Scholar]
- Moreira, A. A Golden Age for Spaceborne SAR Systems. Proc. ICMRWC 2014, 1–4. [Google Scholar]
- Li, T.; Chen, K.; Jin, M. Analysis and Simulation on Imaging Performance of Backward and Forward Bistatic Synthetic Aperture Radar. Remote Sens. 2018, 11, 1676. [Google Scholar] [CrossRef]
- Jun, S.; Zhang, X.; Yang, J. Principle and Methods on Bistatic SAR Signal Processing via Time Correlation. IEEE Geosci. Remote Sens. 2008, 10, 3163–3178. [Google Scholar] [CrossRef]
- Walterscheid, I.; Ender, J.H.G.; Brenner, A.R.; Loffeld, O. Bistatic SAR Processing and Experiments. IEEE Geosci. Remote Sens. 2006, 10, 2710–2717. [Google Scholar] [CrossRef]
- Tang, S.; Deng, H.; Guo, P.; Li, Y.; Zhang, L. Generalized PFA for Air-Missile Borne Bistatic Forward-Looking Beam-Steering SAR With Accelerations. IEEE Access. 2019, 1, 74616–74627. [Google Scholar] [CrossRef]
- Meng, Z.; Li, Y.; Xing, M.; Bao, Z. Imaging of Missile-borne Bistatic Forward-looking SAR. Proc. ChinaSIP 2014, 7, 179–183. [Google Scholar]
- Meta, A.; Hoogeboom, P.; Lighthart, L.P. Signal Processing for FMCW SAR. IEEE Trans. Geosci. Remote Sens. 2007, 11, 3519–3532. [Google Scholar] [CrossRef]
- Curlander, J.C.; McDonough, R.N. Synthetic Aperture Radar: System and Signal Processing; Willey: New York, NY, USA, 1991. [Google Scholar]
- Liu, Y.; Xing, M.; Sun, G.; Lv, X.; Bao, Z.; Hong, W.; Wu, Y. Echo Model Analyses and Imaging Algorithm for High-resolution SAR on High-speed Platform. IEEE Trans. Geosci. Remote Sens. 2012, 3, 933–950. [Google Scholar] [CrossRef]
- Yan, H.; Wang, Y.; Yu, H.; Li, L. An Imaging Method of Distributed Small Satellites Bistatic SAR Based on Range Distance Compensation. J. Electron. Inf. Technol. 2005, 5, 771–774. [Google Scholar]
- Qiu, X.; Hu, D.; Ding, C. Focusing Bistatic Images use RDA based on Hyperbolic Approximating. Proc. Int. Conf. Radar, CIE 2006, 1323–1326. [Google Scholar]
- Neo, Y.L.; Wong, F.; Cumming, I.G. A Two-dimensional Spectrum for Bistatic SAR Processing using Series Reversion. IEEE Geosci. Remote Sens. Lett. 2007, 1, 93–96. [Google Scholar] [CrossRef]
- Bamler, R.; Boerner, E. On the Use of Numerically Computed Transfer Functions for Processing of Data from Bistatic SARs and High Squint Orbital SARs. Proc. IGARSS 2005, 2, 1051–1055. [Google Scholar]
- Bamler, R.; Meyer, R.; Liebhart, L. No math: Bistatic SAR Processing Using Numerically Computed Transfer Functions. Proc. IGARSS 2006, 1844–1847. [Google Scholar]
- Neo, Y.L.; Wong, F.H.; Cumming, I.G. Processing of Azimuth-invariant Bistatic SAR Data using the Range Doppler Algorithm. IEEE Geosci. Remote Sens. 2008, 1, 14–21. [Google Scholar] [CrossRef]
- Wang, R.; Deng, Y.K.; Loffeld, O.; Nies, H.; Walterscheid, I.; Espeter, T.; Klare, J.; Ender, J.H.G. Processing the Azimuth-variant Bistatic SAR Data by using Monostatic Imaging Algorithms based on Two-dimensional Principle of Stationary Phase. IEEE Geosci. Remote Sens. 2011, 10, 3504–3520. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, Z.; Xing, M.; Bao, Z. Bistatic Spotlight SAR Processing using the Frequency-scaling Algorithm. IEEE Geosci. Remote Sens. Lett. 2008, 1, 48–52. [Google Scholar] [CrossRef]
- Liu, B.; Wang, T.; Wu, Q.; Bao, Z. Bistatic SAR Data Focusing using an Omega-K Algorithm based on Method of Series Reversion. IEEE Geosci. Remote Sens. 2009, 8, 2899–2912. [Google Scholar]
- Zhong, H.; Liu, X. An Extended Nonlinear Chirp-scaling Algorithm for Focusing Large-baseline Azimuth-invariant Bistatic SAR Data. IEEE Geosci. Remote Sens. Lett. 2009, 3, 548–552. [Google Scholar] [CrossRef]
- Qiu, X.; Hu, D.; Ding, C. An Improved NLCS Algorithm with Capability Analysis for One-stationary BiSAR. IEEE Geosci. Remote Sens. 2008, 10, 3179–3186. [Google Scholar] [CrossRef]
- Zhang, Q.; Wu, J.; Yang, J.; Huang, Y.; Du, K.; Yang, G. Extended Nonlinear Chirp Scaling Algorithm with Topography Compensation for Manueuvering-platform Bistatic Forward-looking SAR. Proc. IGARSS 2017, 1047–1050. [Google Scholar]
- Peng, X.; Wang, Y.; Hong, W.; Wu, Y. Autonomous Navigation Airborne Forward-Looking SAR High Precision Imaging with Combination of Pseudo-Polar Formatting and Overlapped Sub-Aperture Algorithm. Remote Sens. 2013, 11, 6063–6078. [Google Scholar] [CrossRef]
- Carrara, W.G.; Goodman, R.S.; Ricoy, M.A. New Algorithms for Widefield SAR Image Formation. Proc. Radar Conf. 2004, 38–43. [Google Scholar]
- Rodriguez-Cassola, M.; Parts, P.; Krieger, G.; Moreira, A. Efficient Time-domain Image Formation with Precise Topography Accommodation for General Bistatic SAR Configurations. IEEE Trans. Aerosp. Electron. Syst. 2011, 4, 2949–2966. [Google Scholar] [CrossRef]
- Lin, C.; Tang, S.; Zhang, L.; Guo, P. Focusing High-Resolution Airborne SAR with Topography Variations Using an Extended BPA Based on a Time/Frequency Rotation Principle. Remote Sens. 2018, 8, 1275. [Google Scholar] [CrossRef]
- Yang, L.; Zhou, S.; Zhao, L.; Xing, M. Coherent Auto-Calibration of APE and NsRCM under Fast Back-Projection Image Formation for Airborne SAR Imaging in Highly-Squint Angle. Remote Sens. 2018, 10, 321. [Google Scholar] [CrossRef]
- Eldhuset, K. Ultra high resolution spaceborne SAR processing with EETF4. Proc. IEEE IGARSS 2001, 7, 2689–2691. [Google Scholar]
- Wu, C.; Liu, K.Y.; Jin, M. Modeling and a correlation algorithm for spaceborne SAR signals. IEEE Trans. Aerosp. Electron. Syst. 1982, 5, 563–575. [Google Scholar] [CrossRef]
- Mims, J.H.; Farrell, J.L. Synthetic Aperture Imaging with Maneuvers. IEEE Trans. Aerosp. Electron. Syst. 1972, 4, 410–418. [Google Scholar] [CrossRef]
- Wang, P.; Liu, W.; Chen, J.; Niu, M.; Yang, W. A High-order Imaging Algorithm for High-resolution Spaceborne SAR Based on a Modified Equivalent Squint Range Model. IEEE Trans. Geosci. Remote Sens. 2015, 3, 1225–1235. [Google Scholar] [CrossRef]
- Bao, M.; Xing, M.; Li, Y.; Wang, Y. Two-dimensional Spectrum for MEO SAR Processing using a Modified Advanced Hyperbolic Range Equation. Electronic Lett. 2011, 8, 1043–1045. [Google Scholar] [CrossRef]
- Tobin, M.; Greenspan, M. Smuggling Interdiction using an Adaptation of the AN/APG-76 Multimode Radar. IEEE Aerosp. Electron. Syst. Mag. 1996, 11, 19–24. [Google Scholar] [CrossRef]
- Moccia, A.; Renga, A. Spatial Resolution of Bistatic Synthetic Aperture Radar: Impact of Acquisition Geometry on Imaging Performance. IEEE Trans. Geosci. Remote Sens. 2011, 10, 3487–3503. [Google Scholar] [CrossRef]
- Lanari, R.; Tesauro, M.; Sansosti, E.; Fornaro, G. Spotlight SAR Data Focusing based on a Two-step Processing Approach. IEEE Trans. Geosci. Remote Sens. 2001, 9, 1993–2004. [Google Scholar] [CrossRef]
- Lanari, R.; Zoffoli, S.; Sansosti, E.; Fornaro, G.; Serafino, F. New Approach for Hybrid Strip-map/spotlight SAR Data Focusing. Proc. Inst. Elect. Eng.-Radar Sonar Navig. 2001, 6, 363–372. [Google Scholar] [CrossRef]
- Tang, S.; Zhang, L.; Guo, P.; Liu, G.; Sun, G.-C. Acceleration Model Analyses and Imaging Algorithm for Highly Squinted Airborne Spotlight Mode SAR with Maneuvers. IEEE J. Sel. Topics Appl. Earth Observat. Remote Sens. 2015, 3, 1120–1131. [Google Scholar] [CrossRef]
- Tang, S.; Zhang, L.; Guo, P.; Liu, G.; Zhang, Y.; Li, Q.; Gu, Y.; Lin, C. Processing of Monostatic SAR Data with General Configurations. IEEE Trans. Geosci. Remote Sens. 2012, 9, 3595–3609. [Google Scholar] [CrossRef]
- Lanari, R.; Tesauro, M.; Sansosti, E.; Fornaro, G. Spotlight SAR Data Focusing Based on a Two-step Processing Approach. IEEE Trans. Geosci. Remote Sens. 2001, 9, 1993–2004. [Google Scholar] [CrossRef]
- Lanari, R.; Zoffoli, S.; Sansosti, E.; Fornaro, G.; Serafino, F. New Approach for Hybrid Strip-map/spotlight SAR Data Focusing. Proc. Inst. Elect. Eng.-Radar Sonar Navig. 2001, 6, 363–372. [Google Scholar] [CrossRef]
- Raney, R.K.; Runge, H.; Bamler, R.; Cumming, I.G.; Wong, F.H. Precision SAR Processing using Chirp Scaling. IEEE Trans. Geosci. Remote Sens. 1994, 4, 786–799. [Google Scholar] [CrossRef]
| Platform | Transmitter | Receiver 1 | Receiver 2 | |
|---|---|---|---|---|
| Parameter | ||||
| Radar Position at ACM | (0, 1000, 500) km | (12.5, −4, 25) km | (−6, −4, 30) km | |
| Velocity Vector | (0, 7600, 0) m/s | (0, 1000, 0) m/s | (−100, −1200, 800) m/s | |
| Acceleration Vector | / | (10, −30, −50) m/s2 | (50, −60, −35) m/s2 | |
| Elevation Angle | 84.1° | 45.8° | 32.3° | |
| Platform | Transmitter | Receiver | |
|---|---|---|---|
| Parameter | |||
| Radar Position at ACM | (0, 0, 754) km | (132, 0, 15) km | |
| Velocity Vector | (0, 7600, 0) m/s | (300, 1200, −200) m/s | |
| Acceleration Vector | / | (30, 54, −26) m/s2 | |
| Elevation Angle | 74.1° | 44.6° | |
| Carrier Frequency | 9.65 GHz | ||
| Pulse Width | 20 μs | ||
| Pulse Bandwidth | 200 MHz | ||
| Sampling Frequency | 300 MHz | ||
| Azimuth Resolution | 0.823 m | ||
| Platform | Transmitter | Receiver | |
|---|---|---|---|
| Parameter | |||
| Radar Position at ACM | (0, 0, 510) km | (112, −78, 25) km | |
| Velocity Vector | (0, 7600, 0) m/s | (−170, 800, −640) m/s | |
| Acceleration Vector | / | (13, −34, −68) m/s2 | |
| Elevation Angle | 81.3° | 27.7° | |
| Carrier Frequency | 9.65 GHz | ||
| Pulse Width | 20 μs | ||
| Pulse Bandwidth | 240 MHz | ||
| Sampling Frequency | 360 MHz | ||
| Azimuth Resolution | 0.716 | ||
| Range | Azimuth | ||||||
|---|---|---|---|---|---|---|---|
| Method | Target | IRW (m) | PSLR (dB) | ISLR (dB) | IRW (m) | PSLR (dB) | ISLR (dB) |
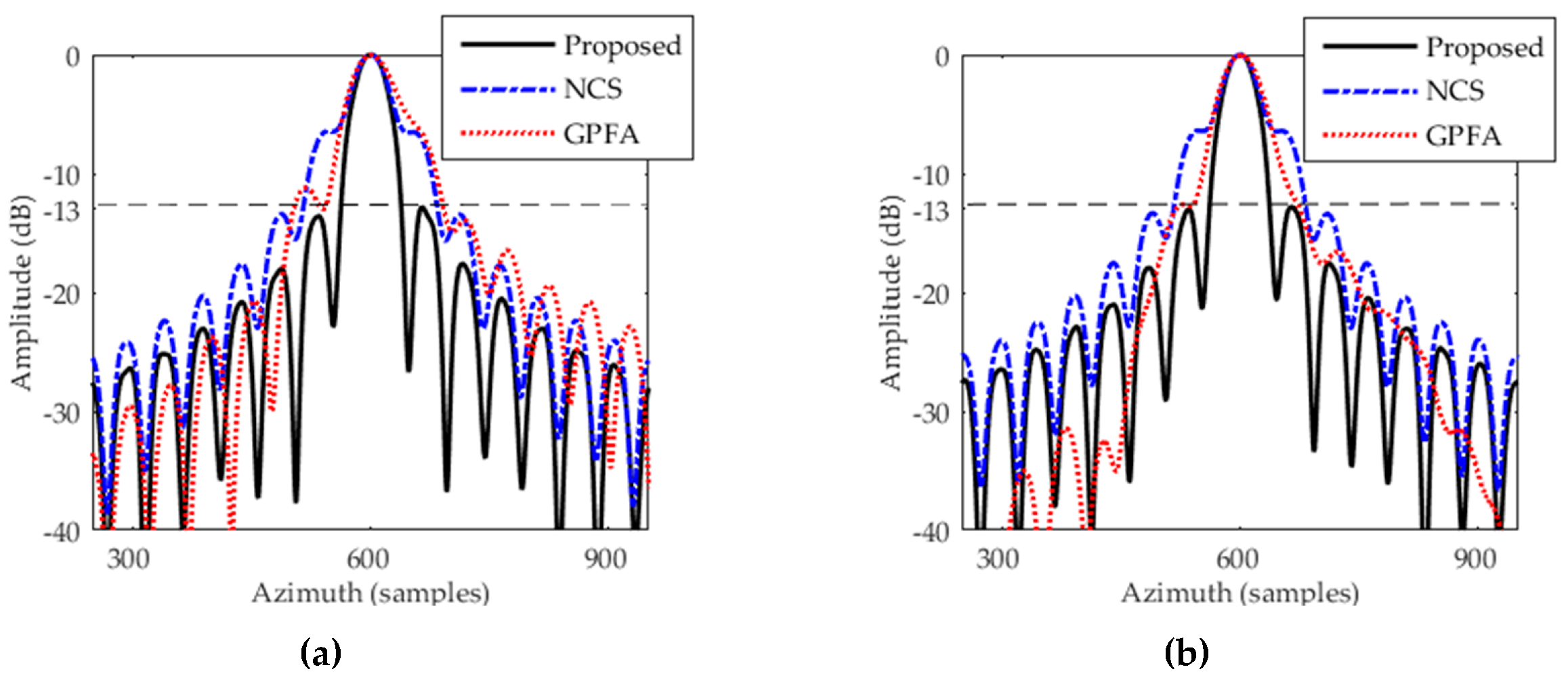
| Proposed | PT1 | 0.626 | −13.21 | −9.97 | 0.723 | −13.09 | −9.91 |
| PT3 | 0.625 | −13.19 | −10.01 | 0.712 | −13.04 | −9.84 | |
| NCSA | PT1 | 0.625 | −13.20 | −9.99 | 0.983 | −7.04 | −7.36 |
| PT3 | 0.627 | −13.18 | −9.98 | 0.965 | −6.83 | −7.28 | |
| GPFA | PT1 | 0.626 | −13.20 | −10.02 | 1.124 | −10.12 | −8.07 |
| PT3 | 0.628 | −13.19 | −9.99 | 1.059 | −12.25 | −6.63 | |
| Data Size in Samples (×103) | 1 | 2 | 4 | 8 | 16 |
|---|---|---|---|---|---|
| CSA/Proposed | 0.793 | 0.794 | 0.794 | 0.795 | 0.795 |
| BPA/Proposed | 35.59 | 91.25 | 194.81 | 387.78 | 750.61 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, S.; Guo, P.; Zhang, L.; Lin, C. Modeling and Precise Processing for Spaceborne Transmitter/Missile-Borne Receiver SAR Signals. Remote Sens. 2019, 11, 346. https://doi.org/10.3390/rs11030346
Tang S, Guo P, Zhang L, Lin C. Modeling and Precise Processing for Spaceborne Transmitter/Missile-Borne Receiver SAR Signals. Remote Sensing. 2019; 11(3):346. https://doi.org/10.3390/rs11030346
Chicago/Turabian StyleTang, Shiyang, Ping Guo, Linrang Zhang, and Chunhui Lin. 2019. "Modeling and Precise Processing for Spaceborne Transmitter/Missile-Borne Receiver SAR Signals" Remote Sensing 11, no. 3: 346. https://doi.org/10.3390/rs11030346
APA StyleTang, S., Guo, P., Zhang, L., & Lin, C. (2019). Modeling and Precise Processing for Spaceborne Transmitter/Missile-Borne Receiver SAR Signals. Remote Sensing, 11(3), 346. https://doi.org/10.3390/rs11030346





