A Cuboid Model for Assessing Surface Soil Moisture
Abstract
1. Introduction
2. Materials and Methods
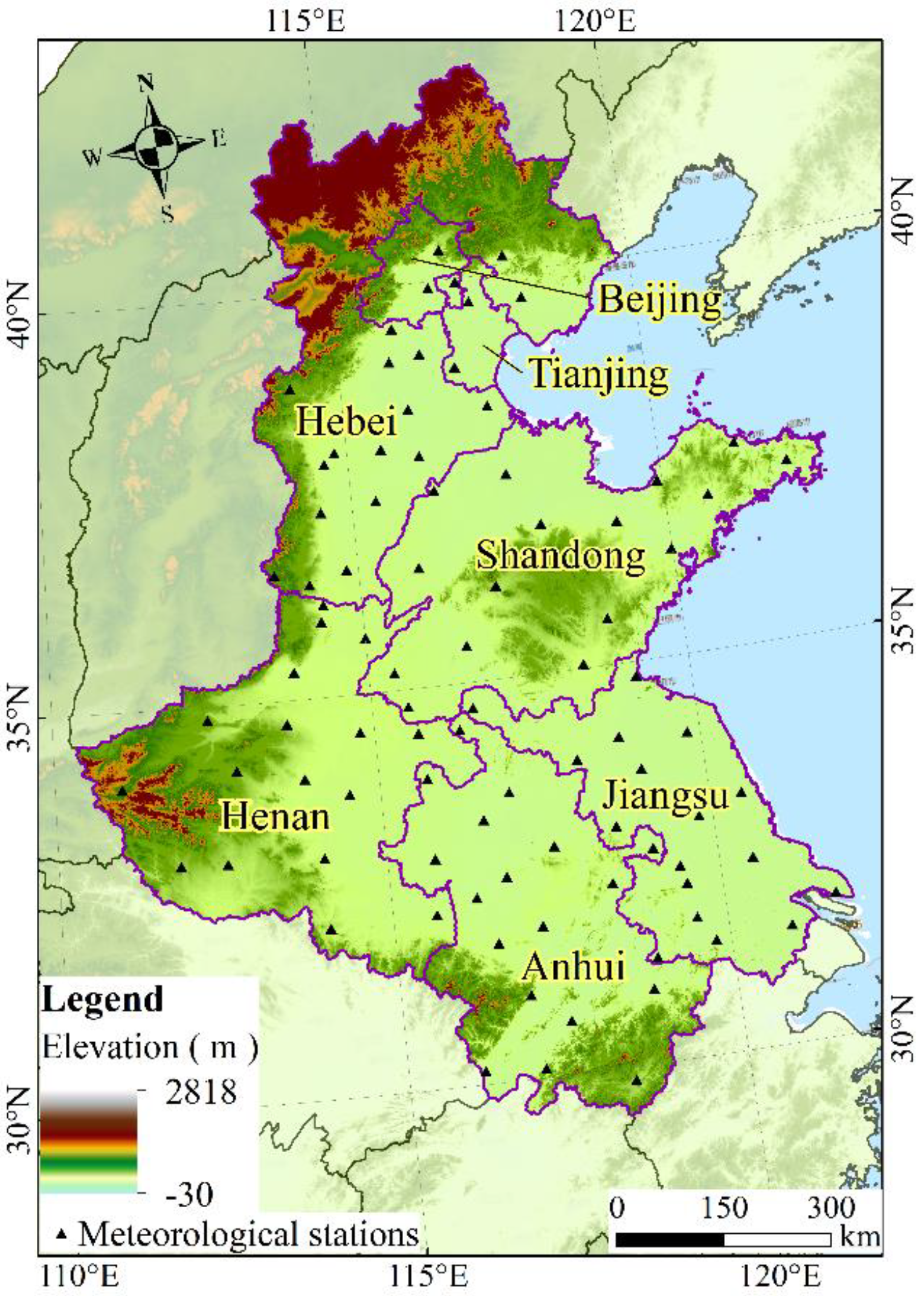
2.1. Study Areas
2.2. Data
2.3. Method
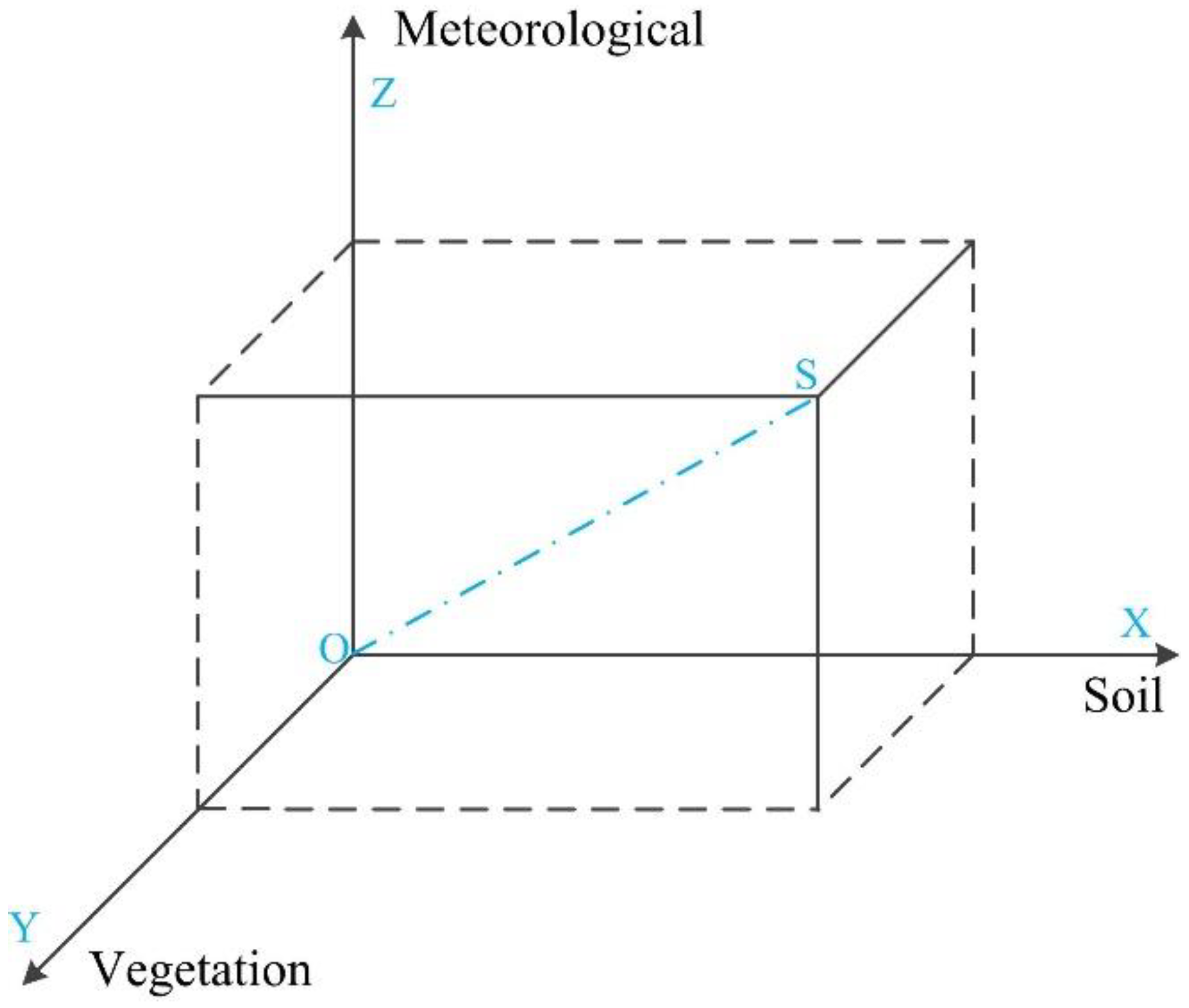
2.3.1. Cuboid Soil Moisture Index (CSMI)
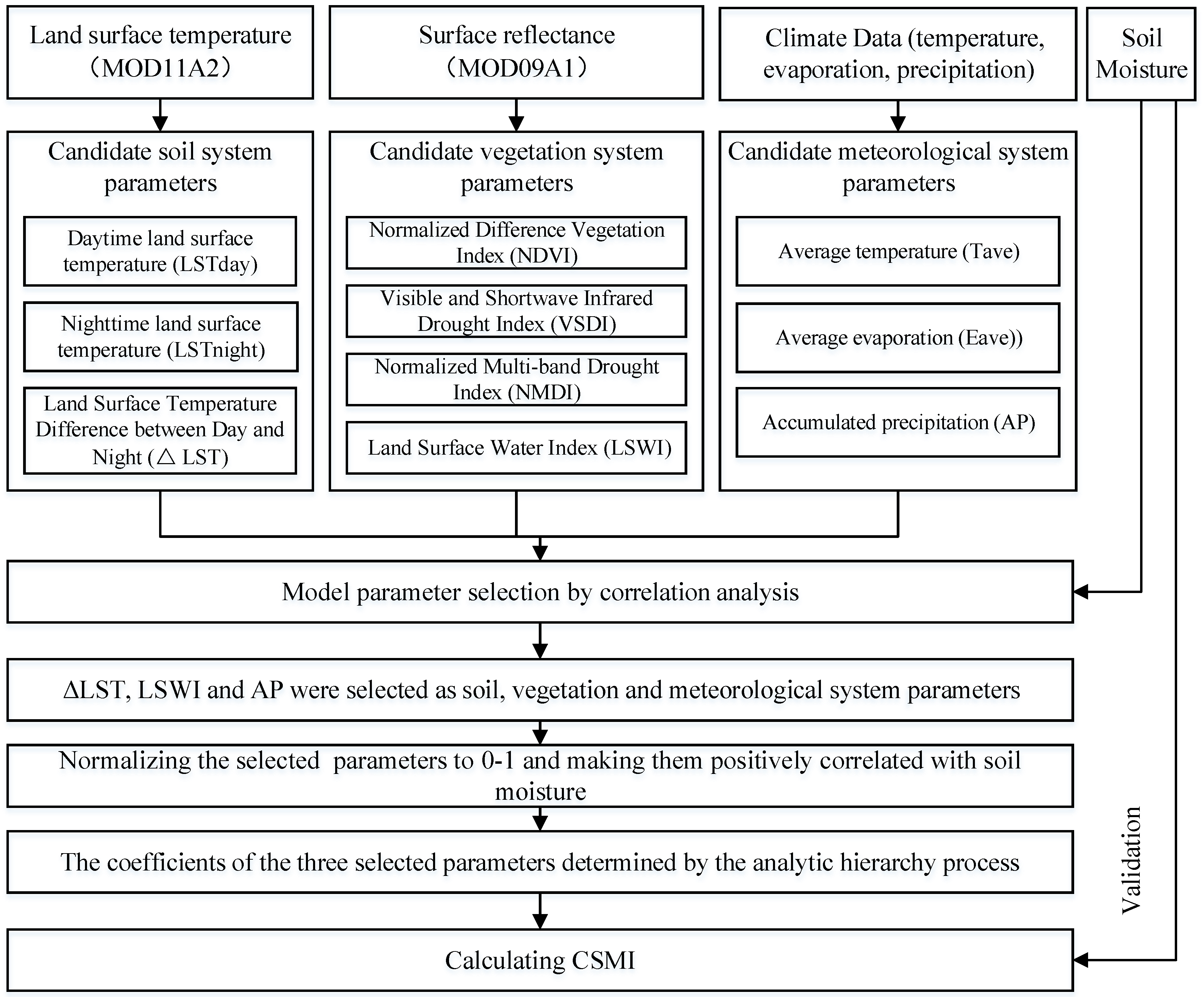
2.3.2. Cuboid Soil Moisture Index Calculation
Model Parameter Selection
Parametric Standardization
Edge Length Coefficient Determination
3. Results
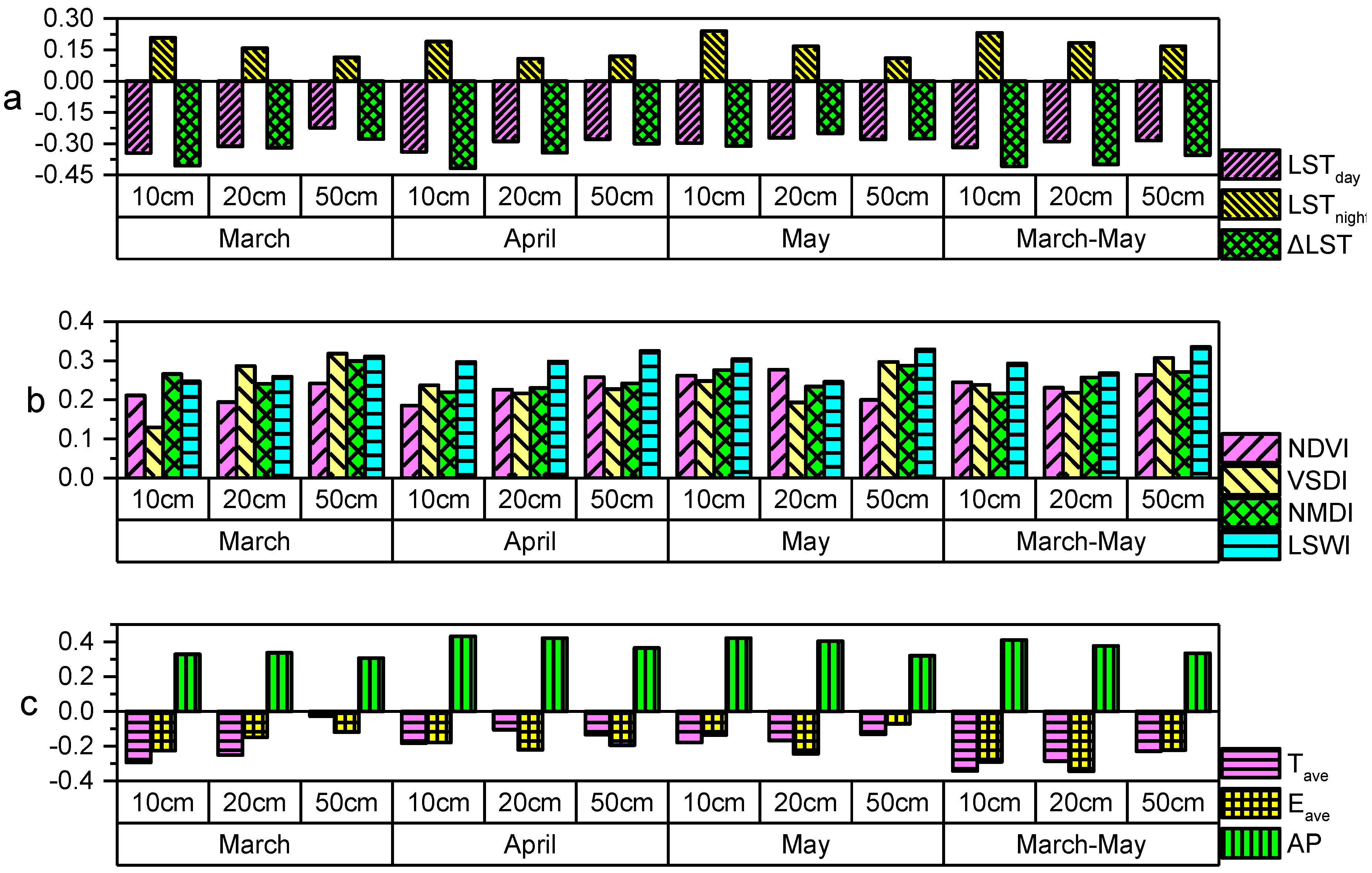
3.1. Model Parameters and Edge Length Coefficient
3.2. CSMI of Study Area
4. Discussion
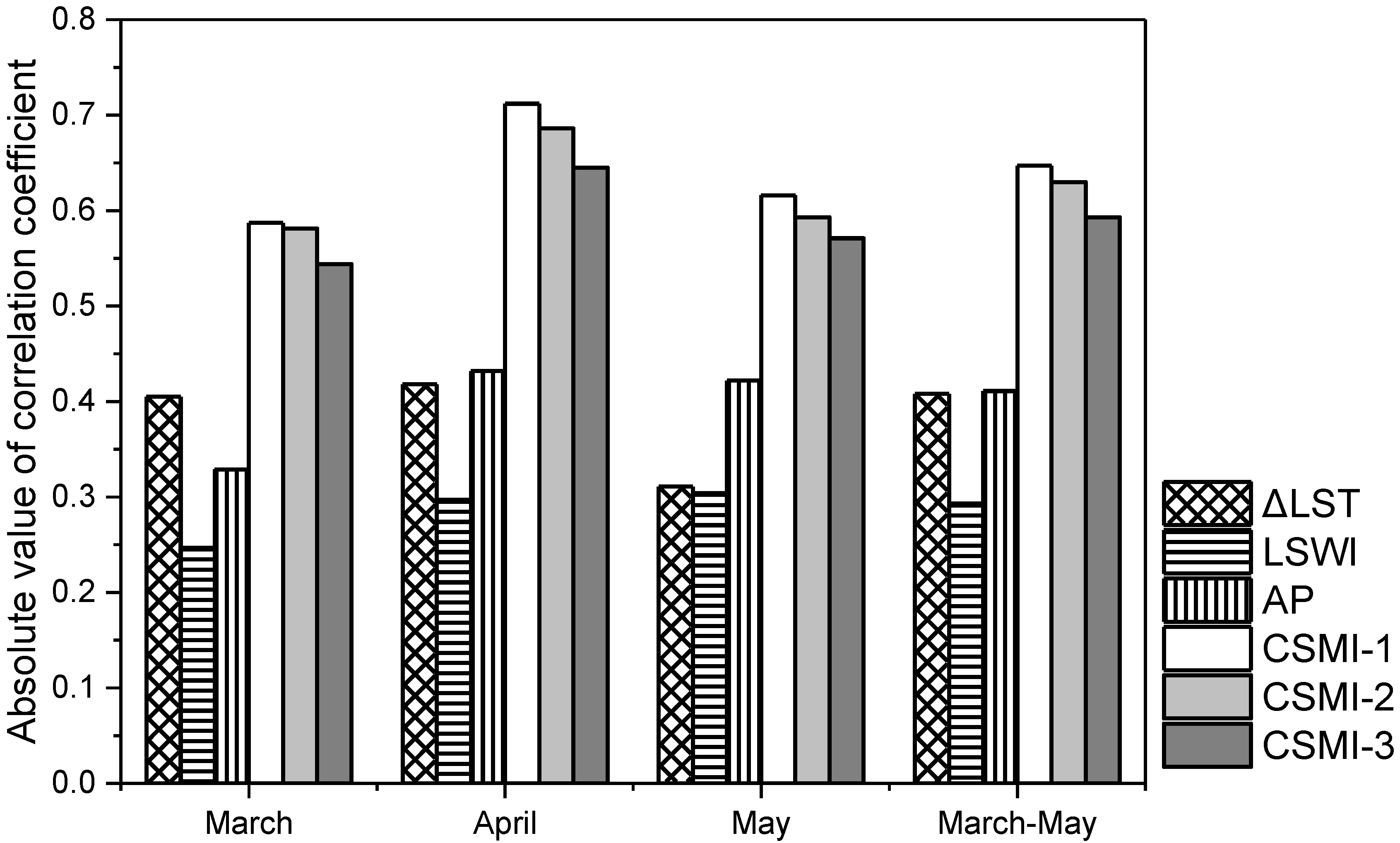
4.1. Impacts of Edge Length Coefficient on CSMI
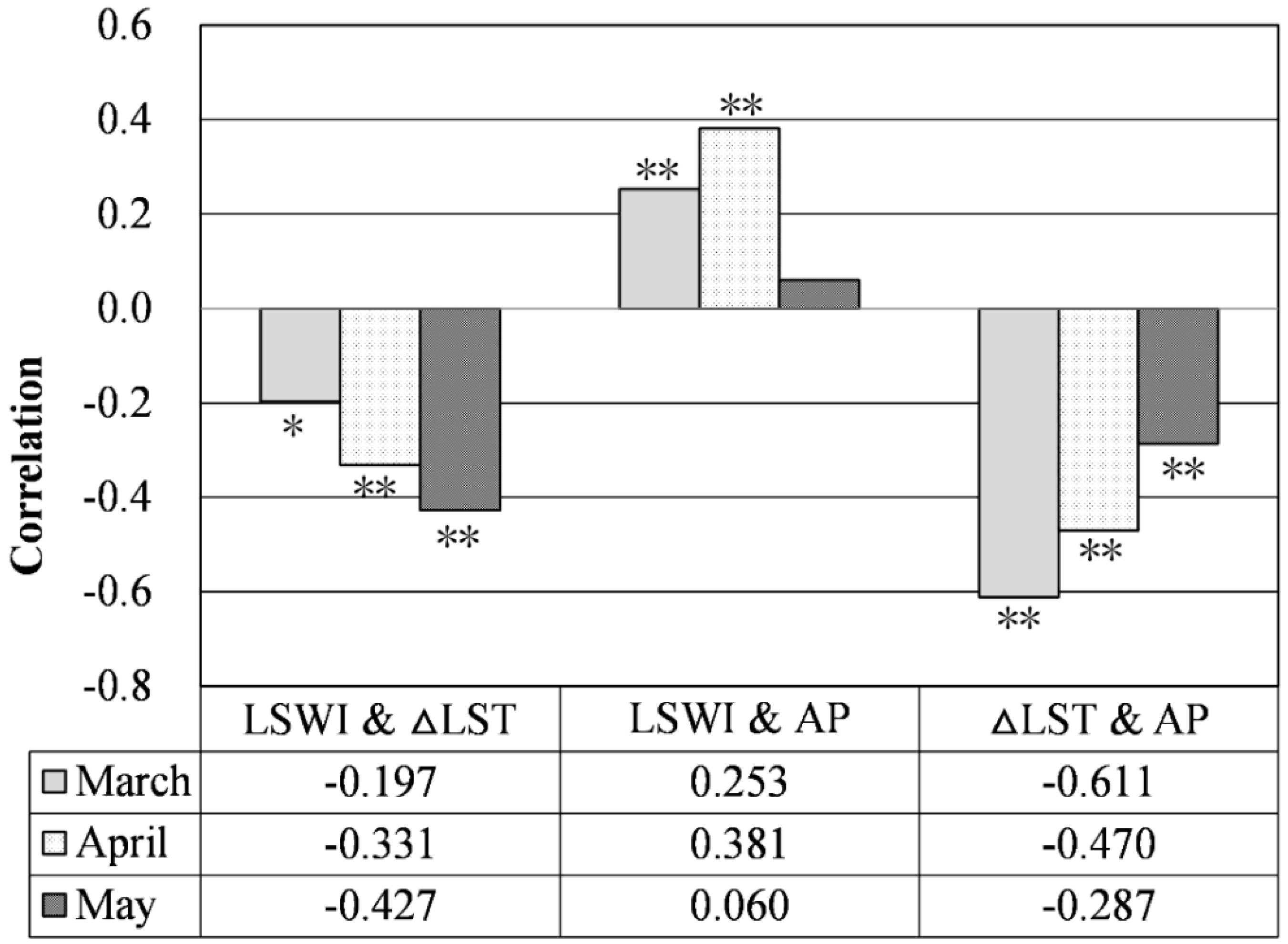
4.2. Impacts of Surface Temperature Difference, Crop Growth, and Accumulated Precipitation on CSMI
4.3. Limitations and Potential Improvement of This Study
4.4. Significance of This Study
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Heathman, G.C.; Cosh, M.H.; Han, E.; Jackson, T.J.; McKee, L.; McAfee, S. Field scale spatiotemporal analysis of surface soil moisture for evaluating point-scale in situ networks. Geoderma 2012, 170, 195–205. [Google Scholar] [CrossRef]
- Holzman, M.E.; Rivas, R.; Piccolo, M.C. Estimating soil moisture and the relationship with crop yield using surface temperature and vegetation index. Int. J. Appl. Earth Obs. Geoinf. 2014, 28, 181–192. [Google Scholar] [CrossRef]
- Petropoulos, G.P.; Ireland, G.; Barrett, B. Surface soil moisture retrievals from remote sensing: Current status, products & future trends. Phys. Chem. Earth Parts A/B/C 2015, 83–84, 36–56. [Google Scholar] [CrossRef]
- Champagne, C.; Davidson, A.; Cherneski, P.; L’Heureux, J.; Hadwen, T. Monitoring agricultural risk in Canada using L-band passive microwave soil moisture from SMOS. J. Hydrometeorol. 2014, 16, 5–18. [Google Scholar] [CrossRef]
- Liu, X.F.; Zhu, X.F.; Pan, Y.Z.; Li, S.S.; Liu, Y.X.; Ma, Y.Q. Agricultural drought monitoring: Progress, challenges, and prospects. J. Geogr. Sci. 2016, 26, 750–767. [Google Scholar] [CrossRef]
- Wang, L.; Qu, J.J. Satellite remote sensing applications for surface soil moisture monitoring: A review. Front. Earth Sci. China 2009, 3, 237–247. [Google Scholar] [CrossRef]
- Ceccato, P.; Flasse, S.; Tarantola, S.; Jacquemoud, S.; Grégoire, J.M. Detecting vegetation leaf water content using reflectance in the optical domain. Remote Sens. Environ. 2001, 77, 22–33. [Google Scholar] [CrossRef]
- Liu, W.D.; Baret, F.; Gu, X.F.; Tong, Q.X.; Zheng, L.F.; Zhang, B. Relating soil surface moisture to reflectance. Remote Sens. Environ. 2002, 81, 238–246. [Google Scholar] [CrossRef]
- Sandholt, I.; Rasmussen, K.; Andersen, J. A simple interpretation of the surface temperature/vegetation index space for assessment of surface moisture status. Remote Sens. Environ. 2002, 79, 213–224. [Google Scholar] [CrossRef]
- Price, J.C. On the analysis of thermal infrared imagery: The limited utility of apparent thermal inertia. Remote Sens. Environ. 1985, 18, 59–73. [Google Scholar] [CrossRef]
- Njoku, E.G.; Li, L. Retrieval of land surface parameters using passive microwave measurements at 6–18 GHz. IEEE Trans. Geosci. Remote Sens. 1999, 37, 79–93. [Google Scholar] [CrossRef]
- Wigneron, J.P.; Waldteufel, P.; Chanzy, A.; Calvet, J.C.; Kerr, Y. Two-dimensional microwave interferometer retrieval capabilities over land surfaces (SMOS Mission). Remote Sens. Environ. 2000, 73, 270–282. [Google Scholar] [CrossRef]
- Brian, W.B.; Edward, D.; Pádraig, W. Soil Moisture retrieval from active spaceborne microwave observations: An evaluation of current techniques. Remote Sens. 2009, 1, 210–242. [Google Scholar] [CrossRef]
- Whiting, M.L.; Li, L.; Ustin, S.L. Predicting water content using Gaussian model on soil spectra. Remote Sens. Environ. 2004, 89, 535–552. [Google Scholar] [CrossRef]
- Rouse, J.W.; Hass, R.H.; Schell, J.A.; Deering, D.W. Monitoring vegetation systems in the great plains with ERTS. NASA Spec. Publ. 1974, 351, 309. [Google Scholar]
- Kogan, F.N. Application of vegetation index and brightness temperature for drought detection. Adv. Space Res. 1995, 15, 91–100. [Google Scholar] [CrossRef]
- Liu, W.T.; Kogan, F.N. Monitoring regional drought using the vegetation condition index. Int. J. Remote Sens. 1996, 17, 2761–2782. [Google Scholar] [CrossRef]
- Singh, R.P.; Roy, S.; Kogan, F. Vegetation and temperature condition indices from NOAA AVHRR data for drought monitoring over India. Int. J. Remote Sens. 2003, 24, 4393–4402. [Google Scholar] [CrossRef]
- Bajgiran, P.R.; Darvishsefat, A.A.; Khalili, A.; Makhdoum, M.F. Using AVHRR-based vegetation indices for drought monitoring in the Northwest of Iran. J. Arid Environ. 2008, 72, 1086–1096. [Google Scholar] [CrossRef]
- Quiring, S.M.; Ganesh, S. Evaluating the utility of the Vegetation Condition Index (VCI) for monitoring meteorological drought in Texas. Agric. For. Meteorol. 2010, 150, 330–339. [Google Scholar] [CrossRef]
- Xu, H.Q. Modification of normalised difference water index NDWI to enhance open water features in remotely sensed imagery. Int. J. Remote Sens. 2006, 27, 3025–3033. [Google Scholar] [CrossRef]
- Ceccato, P.; Flasse, S.; Grégoire, J.M. Designing a spectral index to estimate vegetation water content from remote sensing data: Part 1: Theoretical approach. Remote Sens. Environ. 2002, 82, 188–197. [Google Scholar] [CrossRef]
- Chandrasekar, K.; Sesha Sai, M.V.R.; Roy, P.S.; Dwevedi, R.S. Land Surface Water Index (LSWI) response to rainfall and NDVI using the MODIS vegetation index product. Int. J. Remote Sens. 2010, 31, 3987–4005. [Google Scholar] [CrossRef]
- Zhang, N.; Hong, Y.; Qin, Q.M.; Liu, L. VSDI: A visible and shortwave infrared drought index for monitoring soil and vegetation moisture based on optical remote sensing. Int. J. Remote Sens. 2013, 34, 4585–4609. [Google Scholar] [CrossRef]
- Wang, L.; Qu, J.J. NMDI: A normalized multi-band drought index for monitoring soil and vegetation moisture with satellite remote sensing. Geophys. Res. Lett. 2007, 34, L20405. [Google Scholar] [CrossRef]
- Wan, Z.M.; Dozier, J. A generalized split-window algorithm for retrieving land-surface temperature from space. IEEE Trans. Geosci. Remote Sens. 1996, 34, 892–905. [Google Scholar] [CrossRef]
- Li, Z.L.; Tang, B.H.; Wu, H.; Ren, H.; Yan, G.; Wan, Z.; Trigo, I.F.; Sobrino, J.A. Satellite-derived land surface temperature: Current status and perspectives. Remote Sens. Environ. 2013, 131, 14–37. [Google Scholar] [CrossRef]
- McVicar, T.R.; Jupp, D.L.B.; Yang, X.; Tian, G. Linking regional water balance models with remote sensing. In Proceedings of the 13th Asian Conference on Remote Sensing, Ulaanbaatar, Mongolia, 7 October 1992; p. B6. [Google Scholar]
- Yu, F.; Zhao, Y.; Li, H. Soil moisture retrieval based on GA-BP neural networks algorithm. J. Infrared Millim. Waves 2012, 31, 283–288. [Google Scholar] [CrossRef]
- Zhuo, W.; Huang, J.; Li, L.; Zhang, X.; Ma, H.; Gao, X.; Huang, H.; Xu, B.; Xiao, X. Assimilating soil moisture retrieved from Sentinel-1 and Sentinel-2 data into WOFOST model to improve winter wheat yield estimation. Remote Sens. 2019, 11, 1618. [Google Scholar] [CrossRef]
- Wang, H.; Li, X.; Long, H.; Xu, X.; Bao, Y. Monitoring the effects of land use and cover type changes on soil moisture using remote-sensing data: A case study in China’s Yongding River basin. Catena 2010, 82, 135–145. [Google Scholar] [CrossRef]
- Goward, S.N.; Cruickshanks, G.D.; Hope, A.S. Observed relation between thermal emission and reflected spectral radiance of a complex vegetated landscape. Remote Sens. Environ. 1985, 18, 137–146. [Google Scholar] [CrossRef]
- Gillies, R.R.; Carlson, T.N. Thermal remote sensing of surface soil water content with partial vegetation cover for incorporation into climate models. J. Appl. Meteorol. 1995, 34, 745–756. [Google Scholar] [CrossRef]
- Zhang, D.; Tang, R.; Zhao, W.; Tang, B.; Wu, H.; Shao, K.; Li, Z.L. Surface soil water content estimation from thermal remote sensing based on the temporal variation of land surface temperature. Remote Sens. 2014, 6, 3170–3187. [Google Scholar] [CrossRef]
- Amani, M.; Salehi, B.; Mahdavi, S.; Masjedi, A.; Dehnavi, S. Temperature-vegetation-soil moisture dryness index (TVMDI). Remote Sens. Environ. 2017, 197, 1–14. [Google Scholar] [CrossRef]
- Zhang, X.; Zhao, J.; Tian, J. A robust coinversion model for soil moisture retrieval from multisensor Data. IEEE Trans. Geosci. Remote Sens. 2014, 52, 5230–5237. [Google Scholar] [CrossRef]
- Hupet, F.; Vanclooster, M. Intraseasonal dynamics of soil moisture variability within a small agricultural maize cropped field. J. Hydrol. 2002, 261, 86–101. [Google Scholar] [CrossRef]
- Lookingbill, T.; Urban, D. An empirical approach towards improved spatial estimates of soil moisture for vegetation analysis. Landsc. Ecol. 2004, 19, 417–433. [Google Scholar] [CrossRef]
- Berretta, C.; Poë, S.; Stovin, V. Reprint of “Moisture content behaviour in extensive green roofs during dry periods: The influence of vegetation and substrate characteristics”. J. Hydrol. 2014, 516, 37–49. [Google Scholar] [CrossRef]
- Saaty, T.L.; Kearns, K.P. Systems characteristics and the analytic hierarchy process. In Analytical Planning; Pergamon: New York, NY, USA, 1985; pp. 63–86. ISBN 978-0-08-032599-6. [Google Scholar]
- Rahmati, O.; Samani, A.N.; Mahdavi, M.; Pourghasemi, H.R.; Zeinivand, H. Groundwater potential mapping at Kurdistan region of Iran using analytic hierarchy process and GIS. Arab. J. Geosci. 2015, 8, 7059–7071. [Google Scholar] [CrossRef]
- Wang, L.; Wang, P.X.; Li, L.; Xun, L.; Kong, Q.L.; Liang, S.L. Developing an integrated indicator for monitoring maize growth condition using remotely sensed vegetation temperature condition index and leaf area index. Comput. Electron. Agric. 2018, 152, 340–349. [Google Scholar] [CrossRef]
- Pedrycz, W.; Song, M. Analytic Hierarchy Process (AHP) in group decision making and its optimization with an allocation of information granularity. IEEE Trans. Fuzzy Syst. 2011, 19, 527–539. [Google Scholar] [CrossRef]
- Dolan, J.G. Shared decision-making-transferring research into practice: The Analytic Hierarchy Process (AHP). Patient Educ. Couns. 2008, 73, 418–425. [Google Scholar] [CrossRef] [PubMed]
- Zhu, X.F.; Zhu, W.Q.; Zhang, J.S.; Pan, Y.Z. Mapping irrigated areas in China from remote sensing and statistical data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 4490–4504. [Google Scholar] [CrossRef]
- Wang, X.W.; Xie, H.J.; Guan, H.D.; Zhou, X.B. Different responses of MODIS-derived NDVI to root-zone soil moisture in semi-arid and humid regions. J. Hydrol. 2007, 340, 12–24. [Google Scholar] [CrossRef]

| Name | Spatial Resolution | Temporal Resolution | Source | Utility |
|---|---|---|---|---|
| Surface reflectance (MOD09A1) | 500 m | 8-day | United States Geological Survey (USGS) | Model input |
| Land surface temperature (MOD11A2) | 1000 m | 8-day | USGS | Model input |
| Daily precipitation rate (TRMM3B42) | 0.25° | 1-day | National Aeronautics and Space Administration (NASA) | Model input |
| Daily Data Set of Surface Climate Data (temperature, evaporation, precipitation) | − | 1-day | China meteorological information center (CMIC) | Model input |
| Soil Moisture | − | 10-day | CMIC | Accuracy verification |
| Land use land cover map | 1000 m | yearly | Resource and environment data cloud platform, institute of geographic science and natural resources research | Extracting the distribution of cultivated land |
| Provincial boundary | − | − | National fundamental geographic information system in national geomatics center of China | Obtaining the boundary of the research area |
| Scale Value | Compare Factors i and j |
|---|---|
| 1 | Factor i is as important as j, and the scale value is 1. |
| 3 | Factor i is obviously more important than j, and the scale value is 3 |
| 5 | Factor i is much more important than j, and the scale value is 5. |
| 2, 4 | The median value of the above two adjacent judgments |
| Reciprocal of 1–5 | The scale value of factor i compared with factor j is equal to the reciprocal of the scale value of factor j compared with factor i. |
| CSMI | X | Y | Z | |
|---|---|---|---|---|
| CSMI-1 | X | 1 | 2 | 1 |
| Y | 1/2 | 1 | 1/2 | |
| Z | 1 | 1/2 | 1 | |
| CSMI-2 | X | 1 | 2 | 1/2 |
| Y | 1/2 | 1 | 1/3 | |
| Z | 2 | 3 | 1 | |
| CSMI-3 | X | 1 | 3 | 1/2 |
| Y | 1/3 | 1 | 1/4 | |
| Z | 2 | 4 | 1 | |
| CSMI | a | b | c | CR |
|---|---|---|---|---|
| CSMI-1 | 0.4 | 0.2 | 0.4 | 0.0032 |
| CSMI-2 | 0.3 | 0.2 | 0.5 | 0.0088 |
| CSMI-3 | 0.3 | 0.1 | 0.6 | 0.0176 |
| CSMI | Soil Moisture | ||
|---|---|---|---|
| 10 cm | 20 cm | 50 cm | |
| CSMI-1 | 0.647 ** | 0.600 ** | 0.518 ** |
| CSMI-2 | 0.630 ** | 0.585 ** | 0.507 ** |
| CSMI-3 | 0.593 ** | 0.554 ** | 0.482 ** |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, X.; Pan, Y.; Wang, J.; Liu, Y. A Cuboid Model for Assessing Surface Soil Moisture. Remote Sens. 2019, 11, 3034. https://doi.org/10.3390/rs11243034
Zhu X, Pan Y, Wang J, Liu Y. A Cuboid Model for Assessing Surface Soil Moisture. Remote Sensing. 2019; 11(24):3034. https://doi.org/10.3390/rs11243034
Chicago/Turabian StyleZhu, Xiufang, Yaozhong Pan, Junxia Wang, and Ying Liu. 2019. "A Cuboid Model for Assessing Surface Soil Moisture" Remote Sensing 11, no. 24: 3034. https://doi.org/10.3390/rs11243034
APA StyleZhu, X., Pan, Y., Wang, J., & Liu, Y. (2019). A Cuboid Model for Assessing Surface Soil Moisture. Remote Sensing, 11(24), 3034. https://doi.org/10.3390/rs11243034





