Spaceborne EO and a Combination of Inverse and Forward Modelling for Monitoring Lava Flow Advance
Abstract
1. Introduction
2. Materials and Methods
2.1. Rock Samples
2.2. Laboratory-Based Data Acquisition
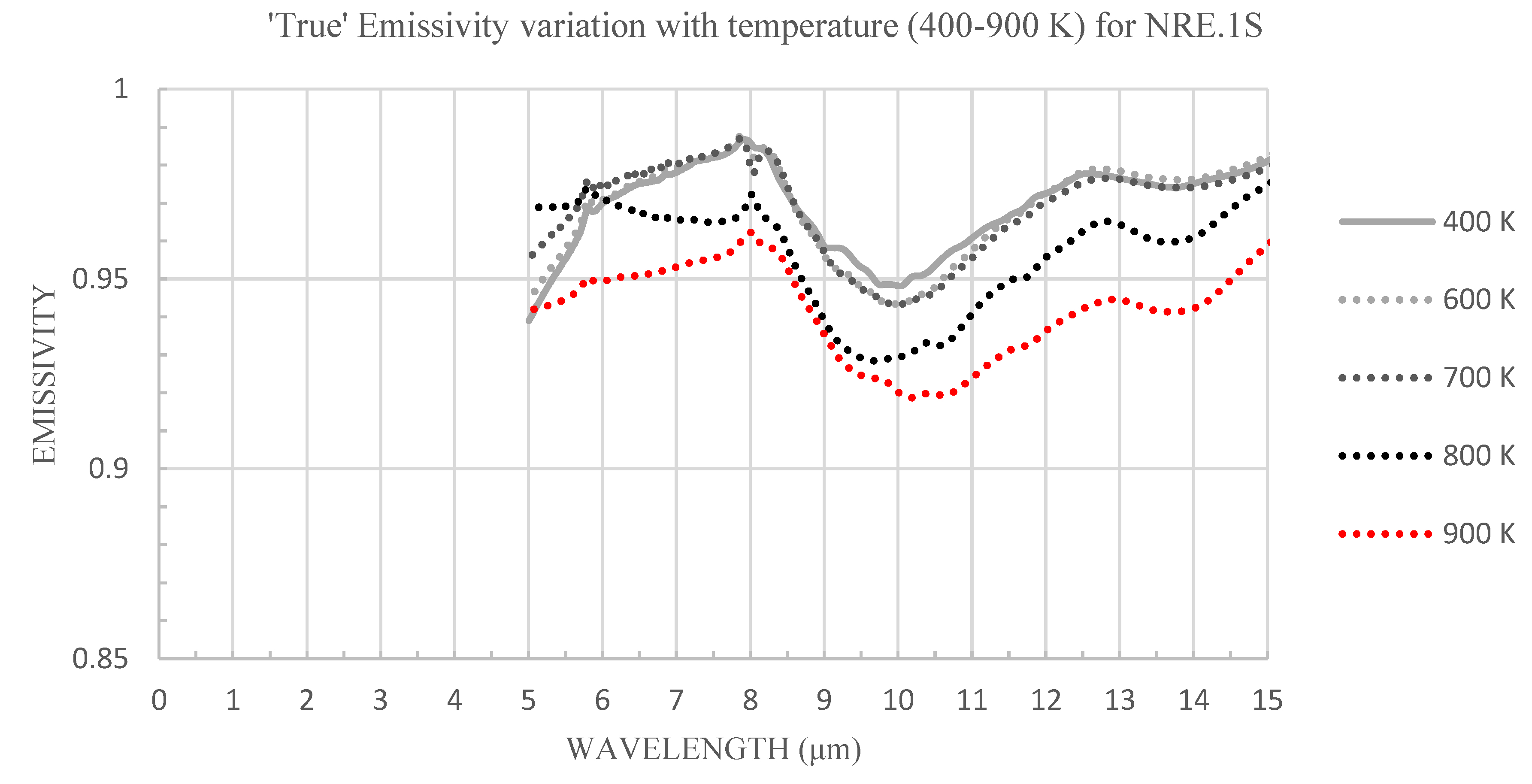
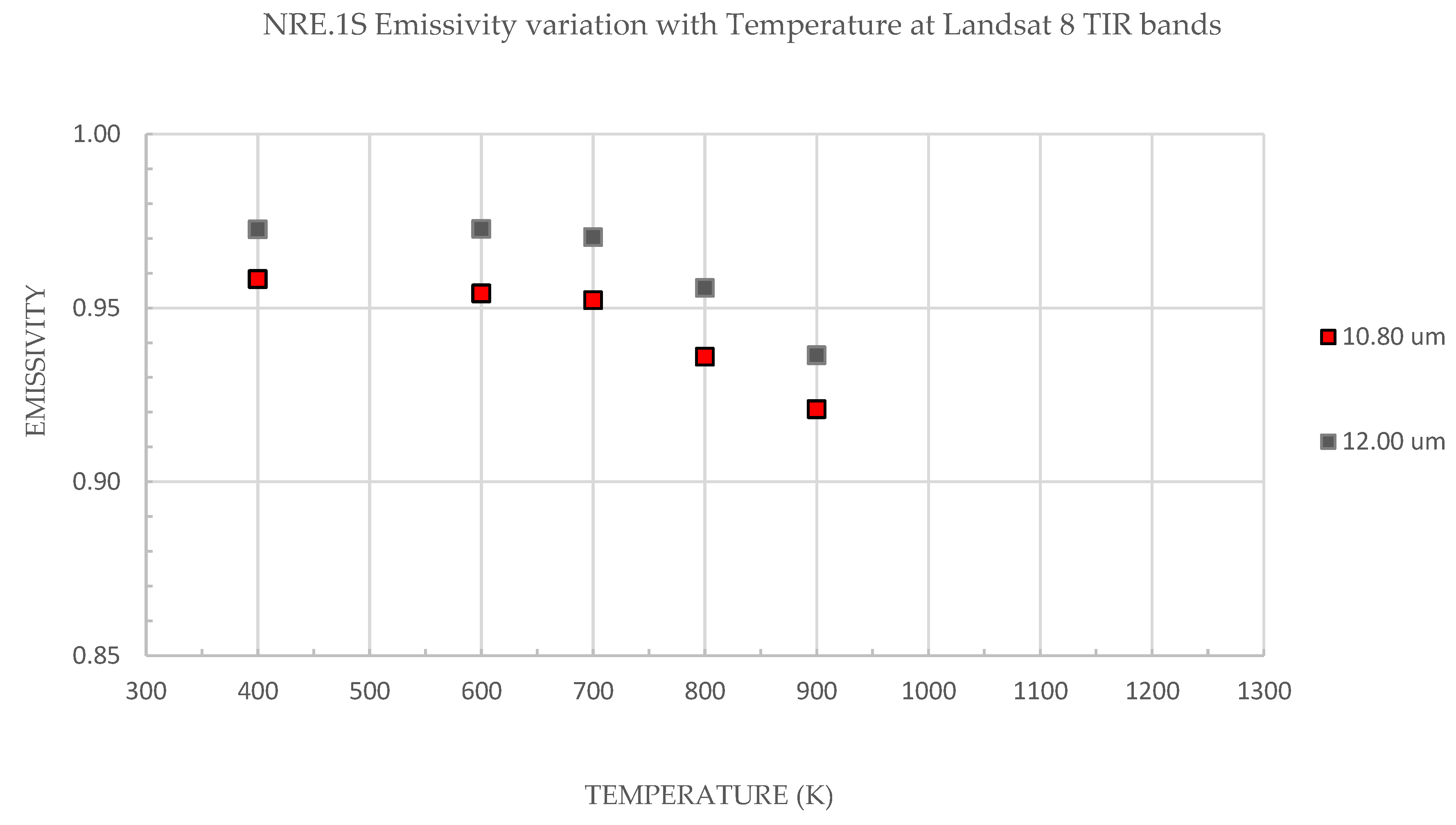
2.2.1. Emissivity from Surface Radiance Spectra
2.3. Thermal Surveillance Using Spaceborne Data
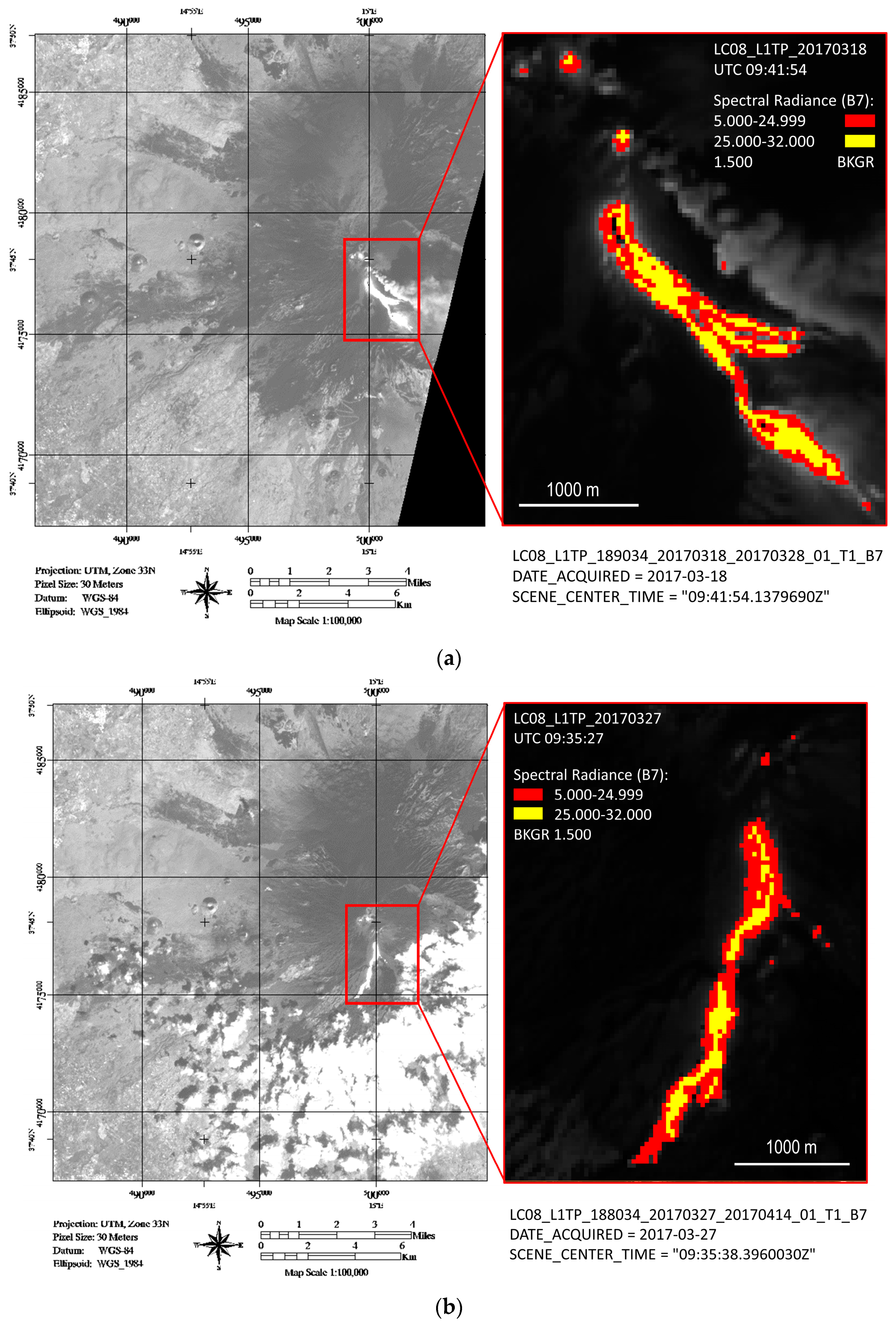
2.3.1. High-Spatial Resolution Data
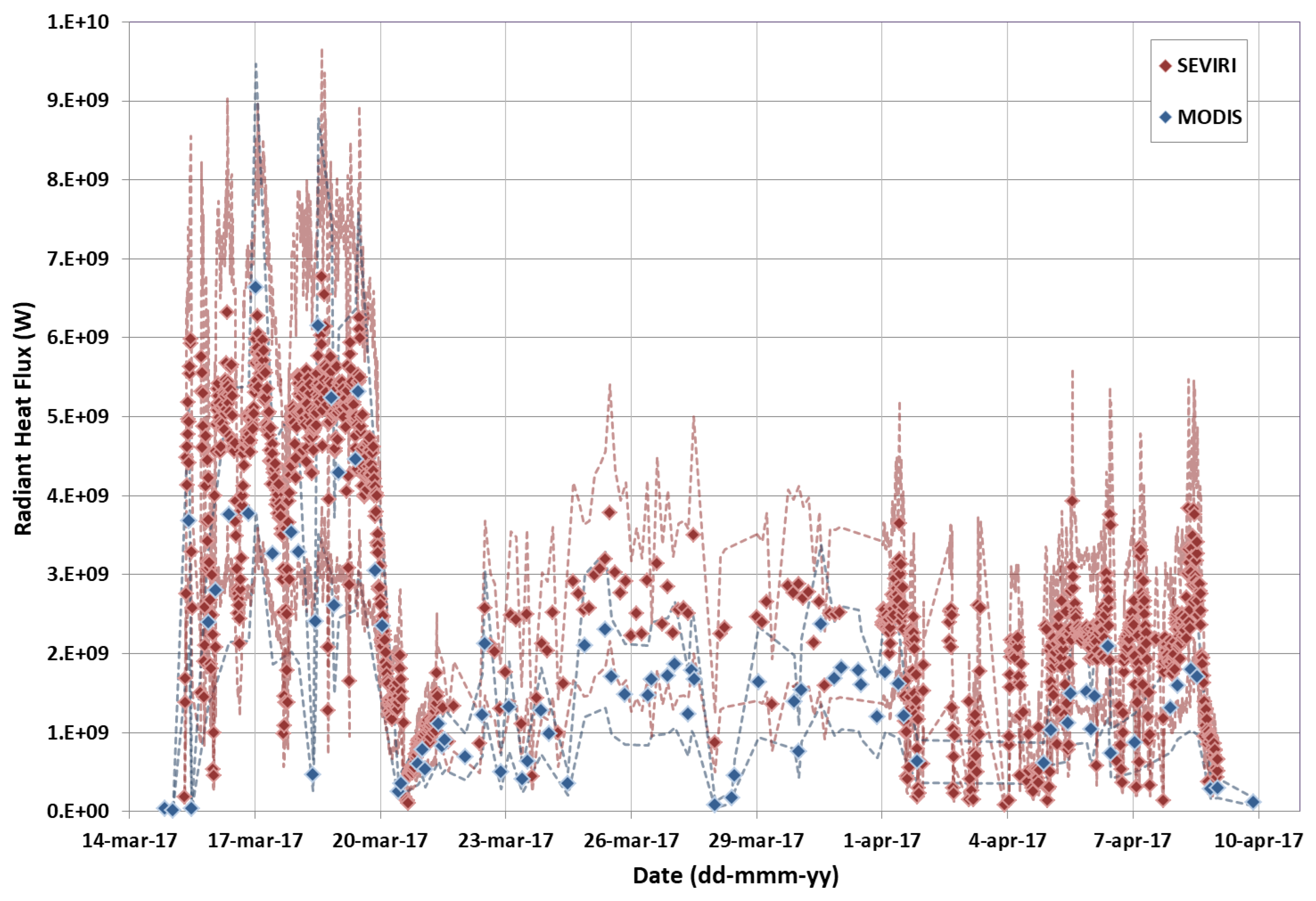
2.3.2. Moderate-to-High Temporal Resolution Data
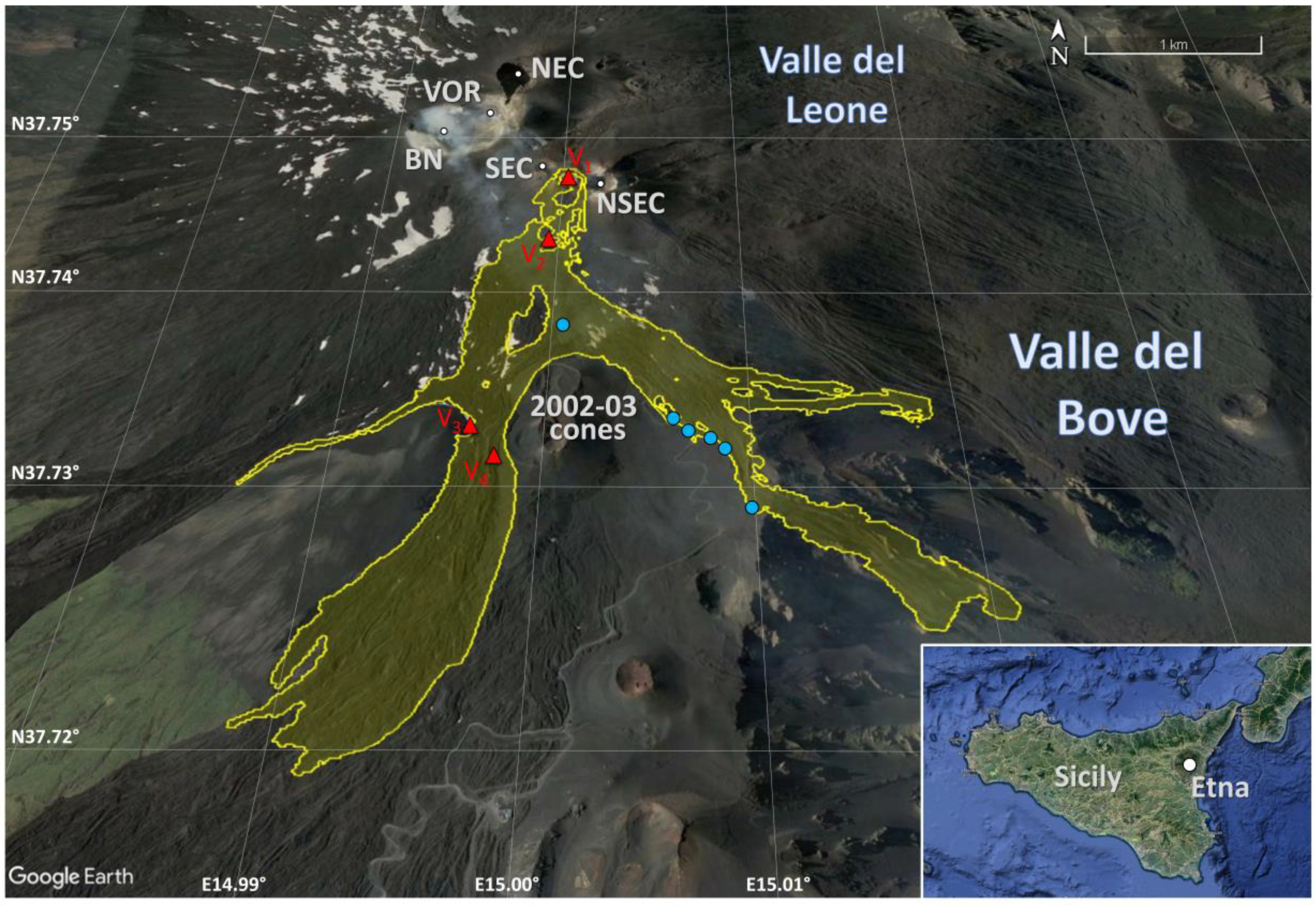
2.4. Numerical Modelling Approach
2.4.1. MAGFLOW
3. Results
3.1. Emissivity from Radiance
3.2. From Spaceborne Data
3.2.1. High-Spatial (Low-Temporal) Resolution Data
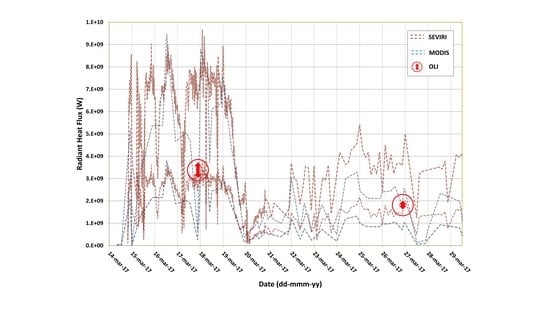
3.2.2. Moderate-to-High Temporal Resolution
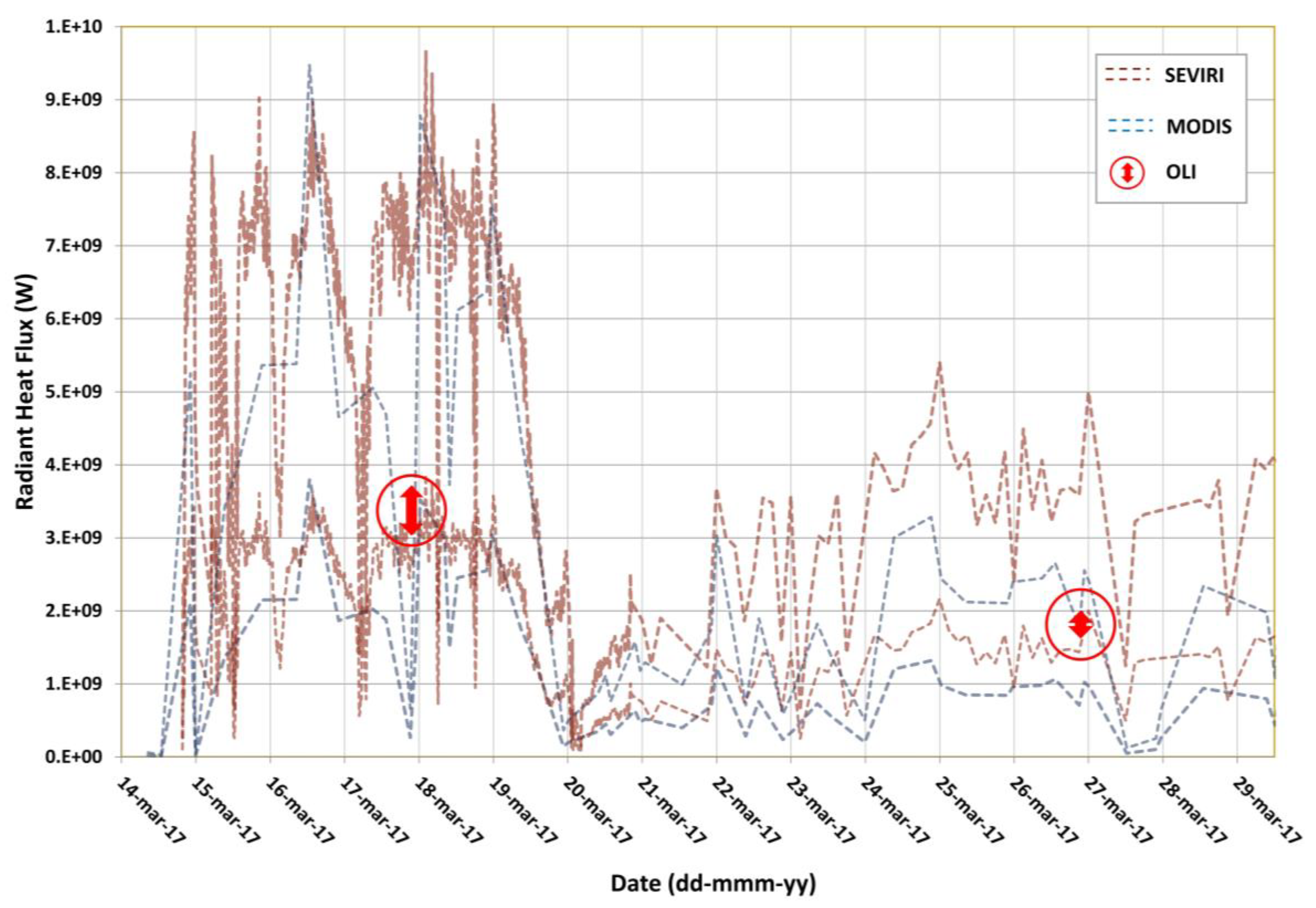
3.2.3. Spaceborne Data Comparison and Validation
3.2.4. From Straightforward Modelling
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Sigurdsson, H.; McNutt, S.R.; Rymer, H.; Stix, J.; Houghton, B. The Encyclopedia of Volcanoes, 2nd ed.; Sigurdsson, H., Houghton, B., McNutt, S.R., Rymer, H., Stix, J., Eds.; Academic Press: Cambridge, MA, USA, 2015. [Google Scholar]
- Sparks, R.S.; Aspinall, W.P.; Crosweller, H.S.; Hincks, T.K. Risk and Uncertainty Assessment of Volcanic Hazards; 2011; Volume 9781107006, ISBN 9781139047562. [Google Scholar]
- Ramsey, M.S.; Harris, A.J.L. Volcanology 2020: How will thermal remote sensing of volcanic surface activity evolve over the next decade? J. Volcanol. Geotherm. Res. 2013, 249, 217–233. [Google Scholar] [CrossRef]
- Tait, S.; Ferrucci, F. A real-time, space borne volcano observatory to support decision making during eruptive crises: European volcano observatory space services. In Proceedings of the 2013 UKSim 15th International Conference on Computer Modelling and Simulation, Cambridge, UK, 10–12 April 2013; pp. 283–289. [Google Scholar]
- Komorowski, J.C.; Jenkins, S.; Baxter, P.J.; Picquout, A.; Lavigne, F.; Charbonnier, S.; Gertisser, R.; Preece, K.; Cholik, N.; Budi-Santoso, A.; et al. Paroxysmal dome explosion during the Merapi 2010 eruption: Processes and facies relationships of associated high-energy pyroclastic density currents. J. Volcanol. Geotherm. Res. 2013, 261, 260–294. [Google Scholar] [CrossRef]
- Pallister, J.; Papale, P.; Eichelberger, J.; Newhall, C.; Mandeville, C.; Nakada, S.; Marzocchi, W.; Loughlin, S.; Jolly, G.; Ewert, J.; et al. Volcano observatory best practices (VOBP) workshops—A summary of findings and best-practice recommendations. J. Appl. Volcanol. 2019, 8. [Google Scholar] [CrossRef]
- Hill, L.J.; Sparks, R.S.; Rougier, J.C. Risk assessment and uncertainty in natural hazards. Risk Uncertain. Assess. Nat. Hazards 2011, 9781107006, 1–18. [Google Scholar]
- Cappello, A.; Ganci, G.; Bilotta, G.; Herault, A.; Zago, V.; Del Negro, C. Satellite-driven modeling approach for monitoring lava flow hazards during the 2017 Etna eruption. Ann. Geophys. Geophys. 2018, 61. [Google Scholar] [CrossRef]
- Ganci, G.; Cappello, A.; Bilotta, G.; Corradino, C.; Del Negro, C. Satellite-Based Reconstruction of the Volcanic Deposits during the December 2015 Etna Eruption. MDPI J. Data 2019, 4, 120. [Google Scholar] [CrossRef]
- Corradino, C.; Ganci, G.; Cappello, A.; Bilotta, G.; Herault, A.; Del Negro, C. Mapping Recent Lava Flows at Mount Etna Using Multispectral Sentinel-2 Images and Machine Learning Techniques. Remote Sens. 2019, 11, 1916. [Google Scholar] [CrossRef]
- Cappello, A.; Geshi, N.; Neri, M.; Del Negro, C. Lava flow hazards—An impending threat at Miyakejima volcano, Japan. J. Volcanol. Geotherm. Res. 2015, 308, 1–9. [Google Scholar] [CrossRef]
- Cappello, A.; Zanon, V.; Del Negro, C.; Ferreira, T.J.L.; Queiroz, M.G.P.S. Exploring lava-flow hazards at Pico Island, Azores Archipelago (Portugal). Terra Nov. 2015, 27, 156–161. [Google Scholar] [CrossRef]
- Bilotta, G.; Cappello, A.; Herault, A.; Ganci, G.; Del Negro, C. MAGFLOW: a physics-based model for the dynamics of lava-flow emplacement. Geol. Soc. Spec. Publ. 2016, 357–373. [Google Scholar]
- Del Negro, C.; Cappello, A.; Neri, M.; Bilotta, G.; Hérault, A.; Ganci, G. Lava flow hazards at Mount Etna: Constraints imposed by eruptive history and numerical simulations. Sci. Rep. 2013, 3, 1–8. [Google Scholar]
- Del Negro, C.; Cappello, A.; Ganci, G. Quantifying lava flow hazards in response to effusive eruption. Bull. Geol. Soc. Am. 2016, 128, 1–13. [Google Scholar] [CrossRef]
- Ramsey, M.; Dehn, J. Spaceborne observations of the 2000 Bezymianny, Kamchatka eruption: The integration of high-resolution ASTER data into near real-time monitoring using AVHRR. J. Volcanol. Geotherm. Res. 2004, 135, 127–146. [Google Scholar] [CrossRef]
- Solikhin, A.; Thouret, J.C.; Gupta, A.; Harris, A.J.L.; Liew, S.C. Geology, tectonics, and the 2002-2003 eruption of the Semeru volcano, Indonesia: Interpreted from high-spatial resolution satellite imagery. Geomorphology 2012, 138, 364–379. [Google Scholar] [CrossRef]
- Wright, R.; Flynn, L.P.; Garbeil, H.; Harris, A.J.L.; Pilger, E. MODVOLC: Near-real-time thermal monitoring of global volcanism. J. Volcanol. Geotherm. Res. 2004, 135, 29–49. [Google Scholar] [CrossRef]
- Wooster, M.J.; Rothery, D.A. Time-series analysis of effusive volcanic activity the using ERS Along Track Scanning Radiometer: The 1995 eruption of Fernandina Volcano, Galapagos Islands. Remote Sens. Environ. 1997, 62, 109–117. [Google Scholar] [CrossRef]
- Oppenheimer, C. Thermal distributions of hot volcanic surfaces constrained using three infrared bands of remote sensing data. Geophys. Res. Lett. 1993, 20, 431–434. [Google Scholar] [CrossRef]
- Harris, A.; Steffke, A.; Calvari, S.; Spampinato, L. Thirty years of satellite-derived lava discharge rates at Etna: Implications for steady volumetric output. J. Geophys. Res. Solid Earth 2011, 116, 1–15. [Google Scholar] [CrossRef]
- Harris, A.J.L. Thermal Remote Sensing of Active Volcanoes: A User’s Manual; Cambridge University Press: Cambridge, UK, 2013; Volume 9780521859, ISBN 9781139029346. [Google Scholar]
- Hirn, B.; Di Bartola, C.; Ferrucci, F. Spaceborne monitoring 2000-2005 of the Pu’u ’O’o-Kupaianaha (Hawaii) eruption by synergetic merge of multispectral payloads ASTER and MODIS. IEEE Trans. Geosci. Remote Sens. 2008, 46, 2848–2856. [Google Scholar] [CrossRef]
- Rothery, D.A.; Francis, P.W.; Wood, C.A. Volcano monitoring using short wavelength infrared data from satellites. J. Geophys. Res. 1988, 93, 7993–8008. [Google Scholar] [CrossRef]
- Ramsey, M.; Chevrel, M.; Coppola, D.; Harris, A. The influence of emissivity on the thermo-rheological modeling of the channelized lava flows at Tolbachik volcano. Ann. Geophys. 2019, 61. [Google Scholar] [CrossRef]
- Marchese, F.; Neri, M.; Falconieri, A.; Lacava, T.; Mazzeo, G.; Pergola, N.; Tramutoli, V. The contribution of multi-sensor infrared satellite observations to monitor Mt. Etna (Italy) Activity during May to August 2016. Remote Sens. 2018, 10, 1948. [Google Scholar] [CrossRef]
- Lee, R.J.; Ramsey, M.S.; King, P.L. Development of a new laboratory technique for high-temperature thermal emission spectroscopy of silicate melts. J. Geophys. Res. Solid Earth 2013, 118, 1968–1983. [Google Scholar] [CrossRef]
- Rogic, N.; Cappello, A.; Ferrucci, F. Role of Emissivity in Lava Flow ‘Distance-to-Run’ Estimates from Satellite-Based Volcano Monitoring. Remote Sens. 2019, 11, 662. [Google Scholar] [CrossRef]
- Cappello, A.; Bilotta, G.; Neri, M.; Del Negro, C. Probabilistic modeling of future volcanic eruptions at Mount Etna. J. Geophys. Res. Solid Earth 2013, 118, 1925–1935. [Google Scholar] [CrossRef]
- Cappello, A.; Ganci, G.; Bilotta, G.; Corradino, C.; Hérault, A.; Del Negro, C. Changing Eruptive Styles at the South-East Crater of Mount Etna: Implications for Assessing Lava Flow Hazards. Front. Earth Sci. 2019, 7, 1–10. [Google Scholar] [CrossRef]
- Del Negro, C.; Currenti, G.; Napoli, R.; Vicari, A. Volcanomagnetic changes accompanying the onset of the 2002-2003 eruption of Mt. Etna (Italy). Earth Planet. Sci. Lett. 2004, 229, 1–14. [Google Scholar] [CrossRef]
- Giordano, D.; Dingwell, D.B. Viscosity of hydrous Etna basalt: Implications for Plinian-style basaltic eruptions. Bull. Volcanol. 2003, 65, 8–14. [Google Scholar] [CrossRef]
- Maturilli, A.; Helbert, J.; D’Amore, M.; Varatharajan, I.; Rosas Ortiz, Y. The Planetary Spectroscopy Laboratory (PSL): wide spectral range, wider sample temperature range. Infrared Remote Sens. Instrum. 2018, 11. [Google Scholar]
- Maturilli, A.; Helbert, J. Characterization, testing, calibration, and validation of the Berlin emissivity database. J. Appl. Remote Sens. 2014, 8. [Google Scholar] [CrossRef]
- World Metheorological Organisation Observing Systems Capability Analysis and Review Tool—Landsat 8. Available online: https://www.wmo-sat.info/oscar/satellites/view/227 (accessed on 25 September 2019).
- U.S. Department of the Interior. U.S. Geological Survey Global Visualisation (GloVis) Viewer. Available online: https://glovis.usgs.gov/ (accessed on 1 September 2019).
- Barsi, J.A.; Barker, J.L.; Schott, J.R. An Atmospheric Correction Parameter Calculator for a Single Thermal Band Earth-Sensing Instrument. Int. Geosci. Remote Sens. Symp. 2003, 5, 3014–3016. [Google Scholar]
- Barsi, J.A.; Barker, J.L.; Schott, J.R. Web-Based Atmospheric Correction Tool for Single Thermal Band Instrument. Available online: https://atmcorr.gsfc.nasa.gov/ (accessed on 25 September 2019).
- Barsi, J.A.; Schott, J.R.; Palluconi, F.D.; Hook, S.J. Validation of a web-based atmospheric correction tool for single thermal band instruments. Earth Obs. Syst. X 2005, 5882, 58820E. [Google Scholar]
- Dozier, J. A method for satellite identification of surface temperature fields of subpixel resolution. Remote Sens. Environ. 1981, 11, 221–229. [Google Scholar] [CrossRef]
- Francis, P.W.; Rothery, D.A. Using the Landsat Thematic Mapper to detect and monitor active volcanoes: an example from Lascar volcano, northern Chile. Geology 1987, 15, 614–617. [Google Scholar] [CrossRef]
- Glaze, L.; Francis, P.W.; Rothery, D.A. Measuring thermal budgets of active volcanoes by satellite remote sensing. Nature 1989, 338, 144–146. [Google Scholar] [CrossRef]
- Flynn, L.P.; Harris, A.J.L.; Wright, R. Improved identification of volcanic features using Landsat 7 ETM+. Remote Sens. Environ. 2001, 78, 180–193. [Google Scholar] [CrossRef]
- Pieri, D.C.; Glaze, L.S.; Abrams, M.J. Thermal radiance observations of an active lava flow during the June 1984 eruption of Mount Etna. Geology 1990, 18, 1018–1022. [Google Scholar] [CrossRef]
- Wright, R.; Pilger, E. Radiant flux from Earth’s subaerially erupting volcanoes. Int. J. Remote Sens. 2008, 29, 6443–6466. [Google Scholar] [CrossRef]
- USGS Landsat 8 Data Users Handbook. Available online: https://www.usgs.gov/land-resources/nli/landsat/landsat-8-data-users-handbook (accessed on 1 November 2019).
- Ganci, G.; Bilotta, G.; Cappello, A.; Herault, A.; Del Negro, C. HOTSAT: A multiplatform system for the thermal monitoring of volcanic activity using satellite data. Geol. Soc. Spec. Publ. 2016, 426, 207–221. [Google Scholar] [CrossRef]
- Ganci, G.; Vicari, A.; Fortuna, L.; del Negro, C. The HOTSAT volcano monitoring system based on combined use of SEVIRI and MODIS multispectral data. Ann. Geophys. 2011, 54, 544–550. [Google Scholar]
- Ganci, G.; Vicari, A.; Bonfiglio, S.; Gallo, G.; del Negro, C. A texton-based cloud detection algorithm for MSG-SEVIRI multispectral images. Geomat. Nat. Hazards Risk 2011, 2, 279–290. [Google Scholar] [CrossRef]
- Wooster, M.J.; Zhukov, B.; Oertel, D. Fire radiative energy for quantitative study of biomass burning: Derivation from the BIRD experimental satellite and comparison to MODIS fire products. Remote Sens. Environ. 2003, 86, 83–107. [Google Scholar] [CrossRef]
- Ramsey, M.S.; Harris, A.J.L. Modelling the thermal and infrared spectral properties of active vents: Comparing basaltic lava flows of Tolbachik, Russia to Arsia Mons, Mars. In Proceedings of the AGU Fall Meeting, San Francisco, CA, USA, 12–16 December 2016. [Google Scholar]
- Lee, R.J.; Ramsey, M.S. What is the emissivity of active basaltic lava flows? In Proceedings of the AGU Fall Meeting, San Francisco, CA, USA, 12–16 December 2016. [Google Scholar]
- Lee, R.J.; King, P.L.; Ramsey, M.S. Spectral analysis of synthetic quartzofeldspathic glasses using laboratory thermal infrared spectroscopy. J. Geophys. Res. Solid Earth 2010, 115, n/a-n/a. [Google Scholar] [CrossRef]
- Ganci, G.; Vicari, A.; Cappello, A.; Del Negro, C. An emergent strategy for volcano hazard assessment: From thermal satellite monitoring to lava flow modeling. Remote Sens. Environ. 2012, 119, 197–207. [Google Scholar] [CrossRef]
- Bilotta, G.; Rustico, E.; Hérault, A.; Vicari, A.; Russo, G.; del Negro, C.; Gallo, G. Porting and optimizing MAGFLOW on CUDA. Ann. Geophys. 2011, 54, 580–591. [Google Scholar]
- Vicari, A.; Ganci, G.; Behncke, B.; Cappello, A.; Neri, M.; Del Negro, C. Near-real-time forecasting of lava flow hazards during the 12–13 January 2011 Etna eruption. Geophys. Res. Lett. 2011, 38, 1–7. [Google Scholar] [CrossRef]
- Vicari, A.; Bilotta, G.; Bonfiglio, S.; Cappello, A.; Ganci, G.; Hérault, A.; Rustico, E.; Gallo, G.; del Negro, C. Lav@hazard: A web-gis interface for volcanic hazard assessment. Ann. Geophys. 2011, 54, 662–670. [Google Scholar]
- Ganci, G.; Cappello, A.; Bilotta, G.; Herault, A.; Zago, V.; Del Negro, C. Mapping volcanic deposits of the 2011–2015 etna eruptive events using satellite remote sensing. Front. Earth Sci. 2018, 6, 1–12. [Google Scholar] [CrossRef]
- Ganci, G.; Cappello, A.; Zago, V.; Bilotta, G.; Hérault, A.; Del Negro, C. 3D lava flow mapping of the 17–25 may 2016 ETNA eruption using tri-stereo optical satellite data. Ann. Geophys. 2019, 62, 1–6. [Google Scholar] [CrossRef]
- French Institut Géographique National MicMac Photogrammetric Library. Available online: http://micmac.ensg.eu (accessed on 1 November 2019).
- Hamilton, V.E.; Wyatt, M.B.; McSween, H.Y.; Christensen, P.R. Analysis of terrestrial and Martian volcanic compositions using thermal emission spectroscopy 2. Application to Martian surface spectra from the Mars Global Surveyor Thermal Emission Spectrometer. J. Geophys. Res. E Planets 2001, 106, 14733–14746. [Google Scholar] [CrossRef]
- Kereszturi, G.; Cappello, A.; Ganci, G.; Procter, J.; Németh, K.; Del Negro, C.; Cronin, S.J. Numerical simulation of basaltic lava flows in the auckland volcanic field, New Zealand—implication for volcanic hazard assessment. Bull. Volcanol. 2014, 76, 1–17. [Google Scholar] [CrossRef]
- Kereszturi, G.; Németh, K.; Moufti, M.R.; Cappello, A.; Murcia, H.; Ganci, G.; Del Negro, C.; Procter, J.; Zahran, H.M.A. Emplacement conditions of the 1256 AD Al-Madinah lava flow field in Harrat Rahat, Kingdom of Saudi Arabia—Insights from surface morphology and lava flow simulations. J. Volcanol. Geotherm. Res. 2016, 309, 14–30. [Google Scholar] [CrossRef]
- Bilotta, G.; Cappello, A.; Hérault, A.; Del Negro, C. Influence of topographic data uncertainties and model resolution on the numerical simulation of lava flows. Environ. Model. Softw. 2019, 112, 1–15. [Google Scholar] [CrossRef]
- Sobrino, J.A.; Jiménez-Muñoz, J.C.; Sòria, G.; Romaguera, M.; Guanter, L.; Moreno, J.; Plaza, A.; Martínez, P. Land surface emissivity retrieval from different VNIR and TIR sensors. IEEE Trans. Geosci. Remote Sens. 2008, 46, 316–327. [Google Scholar] [CrossRef]
- King, P.L.; Ramsey, M.S.; McMillan, P.F.; Swayze, G. Laboratory Fourier transform infrared spectroscopy methods for geologic samples. Infrared Spectrosc. Geochem. Explor. Geochem. Remote Sens. 2004, 33, 57–91. [Google Scholar]
- Pieri, D.C.; Baloga, S.M. Eruption Rate, Area, and Length relationships for some Hawaiian lava flows. J. Volcanol. Geotherm. Res. 1986, 30, 29–45. [Google Scholar] [CrossRef]
- Wright, R.; Blake, S.; Harris, A.J.L.; Rothery, D.A. A simple explanation for the space-based calculation of lava eruption rates. Earth Planet. Sci. Lett. 2001, 192, 223–233. [Google Scholar] [CrossRef]
- Bailey, J.E.; Harris, A.J.L.; Dehn, J.; Calvari, S.; Rowland, S.K. The changing morphology of an open lava channel on Mt. Etna. Bull. Volcanol. 2006, 68, 497–515. [Google Scholar] [CrossRef]
- Wadge, G. The variation of magma discharge during basaltic eruptions. J. Volcanol. Geotherm. Res. 1981, 11, 139–168. [Google Scholar] [CrossRef]
- Harris, A.J.L.; Murray, J.B.; Aries, S.E.; Davies, M.A.; Flynn, L.P.; Wooster, M.J.; Wright, R.; Rothery, D.A. Effusion rate trends at Etna and Krafla and their implications for eruptive mechanisms. J. Volcanol. Geotherm. Res. 2000, 102, 237–269. [Google Scholar] [CrossRef]
- Lautze, N.C.; Harris, A.J.L.; Bailey, J.E.; Ripepe, M.; Calvari, S.; Dehn, J.; Rowland, S.K.; Evans-Jones, K. Pulsed lava effusion at Mount Etna during 2001. J. Volcanol. Geotherm. Res. 2004, 137, 231–246. [Google Scholar] [CrossRef]

| MnO | MgO | CaO | LOl | Total | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 47.49 | 1.63 | 17.71 | 11.26 | 0.17 | 4.81 | 10.362 | 3.65 | 1.72 | 0.55 | −0.35 | 99.02 |
| Date/Time | Emissivity | # Radiant Pixels | ||
|---|---|---|---|---|
| Constant | 0.95 | 672 | 3.12 | |
| 18/03/2017 | Constant | 0.60 | 672 | 3.68 |
| 09:41:54 | Two | 0.95 * | 379 | |
| Components | 0.60 ** | 293 | 3.41 | |
| Constant | 0.95 | 421 | 1.68 | |
| 27/03/2017 | Constant | 0.60 | 421 | 1.97 |
| 09:35:38 | Two | 0.95 * | 263 | |
| Components | 0.60 ** | 158 | 1.82 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rogic, N.; Cappello, A.; Ganci, G.; Maturilli, A.; Rymer, H.; Blake, S.; Ferrucci, F. Spaceborne EO and a Combination of Inverse and Forward Modelling for Monitoring Lava Flow Advance. Remote Sens. 2019, 11, 3032. https://doi.org/10.3390/rs11243032
Rogic N, Cappello A, Ganci G, Maturilli A, Rymer H, Blake S, Ferrucci F. Spaceborne EO and a Combination of Inverse and Forward Modelling for Monitoring Lava Flow Advance. Remote Sensing. 2019; 11(24):3032. https://doi.org/10.3390/rs11243032
Chicago/Turabian StyleRogic, Nikola, Annalisa Cappello, Gaetana Ganci, Alessandro Maturilli, Hazel Rymer, Stephen Blake, and Fabrizio Ferrucci. 2019. "Spaceborne EO and a Combination of Inverse and Forward Modelling for Monitoring Lava Flow Advance" Remote Sensing 11, no. 24: 3032. https://doi.org/10.3390/rs11243032
APA StyleRogic, N., Cappello, A., Ganci, G., Maturilli, A., Rymer, H., Blake, S., & Ferrucci, F. (2019). Spaceborne EO and a Combination of Inverse and Forward Modelling for Monitoring Lava Flow Advance. Remote Sensing, 11(24), 3032. https://doi.org/10.3390/rs11243032