Crustal Deformation of Northeastern China Following the 2011 Mw 9.0 Tohoku, Japan Earthquake Estimated from GPS Observations: Strain Heterogeneity and Seismicity
Abstract
1. Introduction
2. Seismotectonic Setting
3. Method
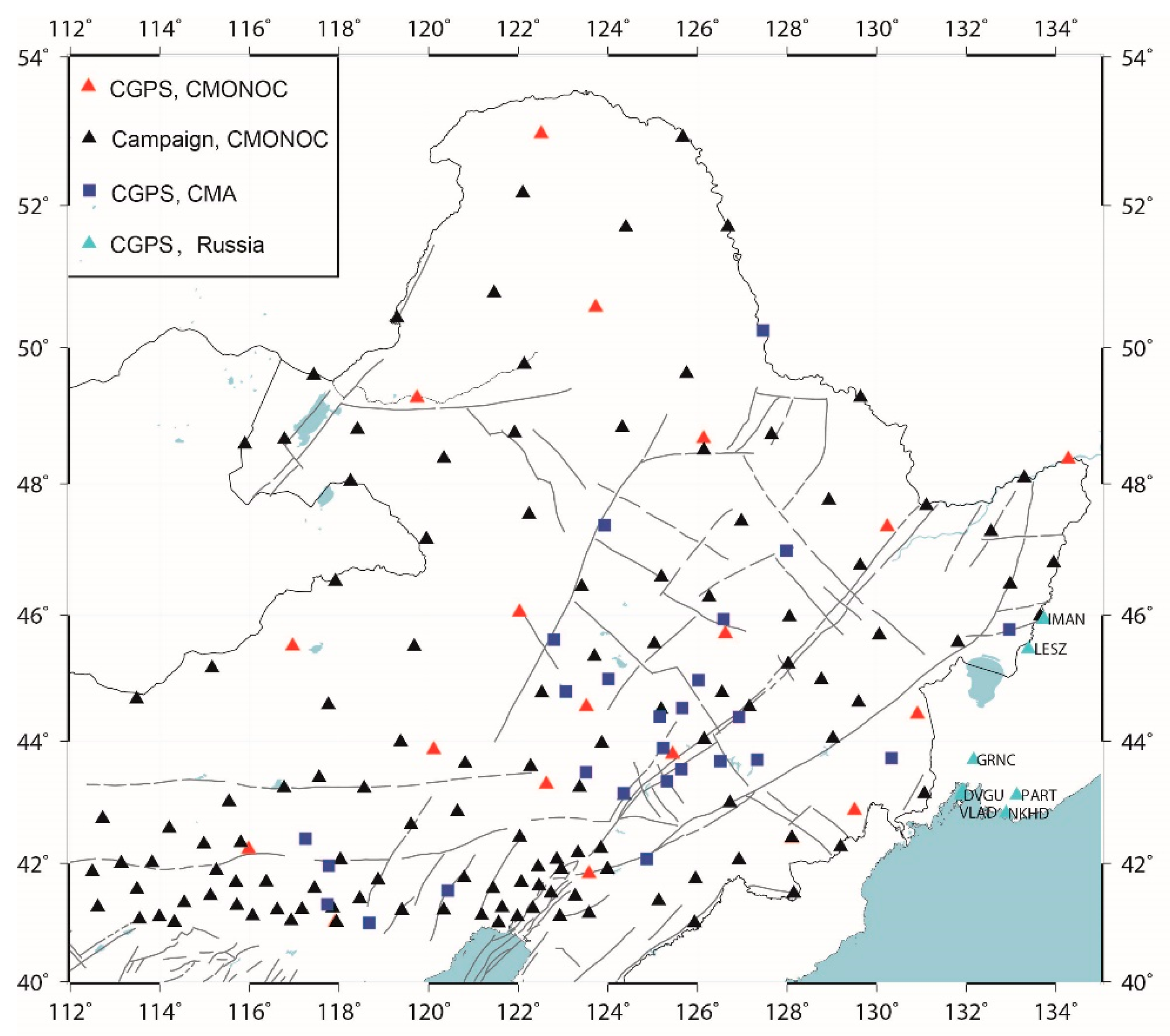
3.1. The Processing of GPS Data
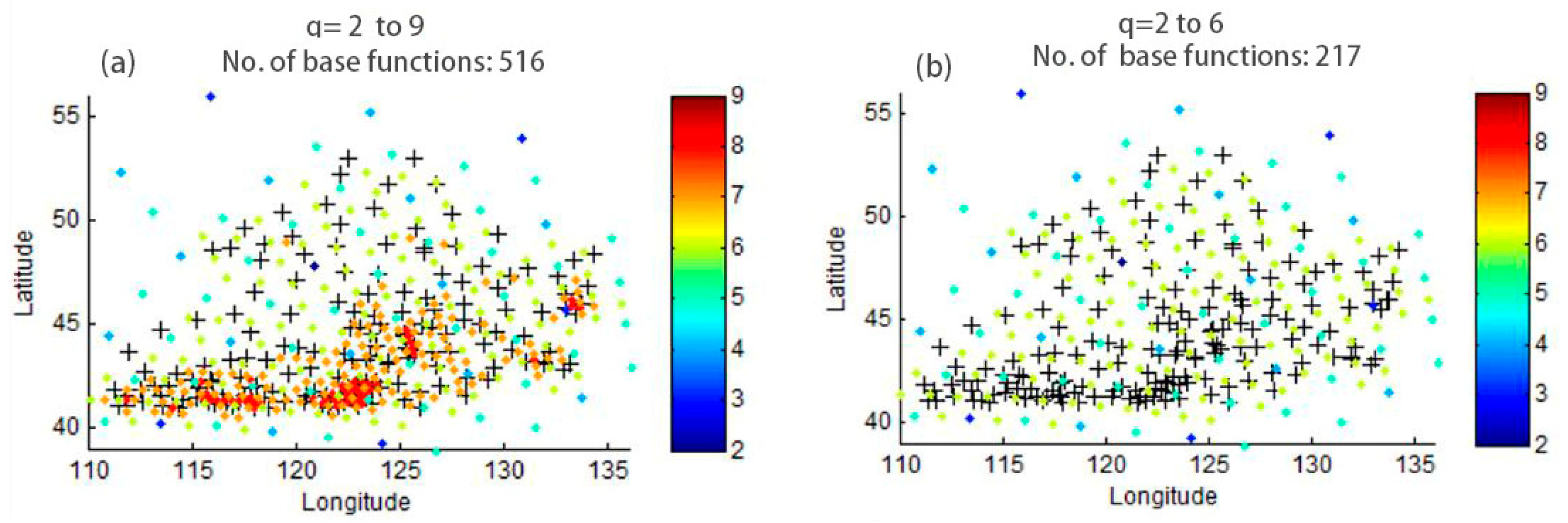
3.2. Strain Rate Estimation
4. Results
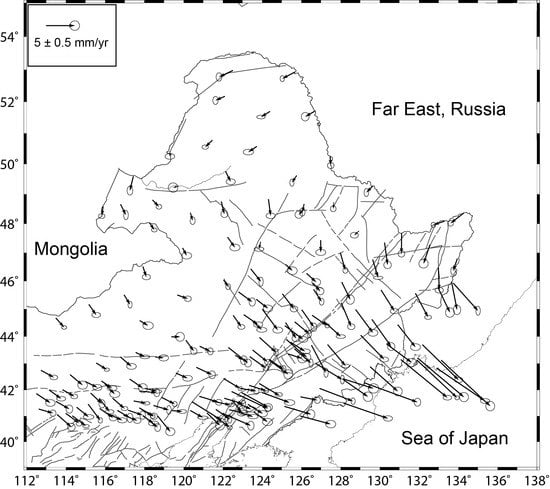
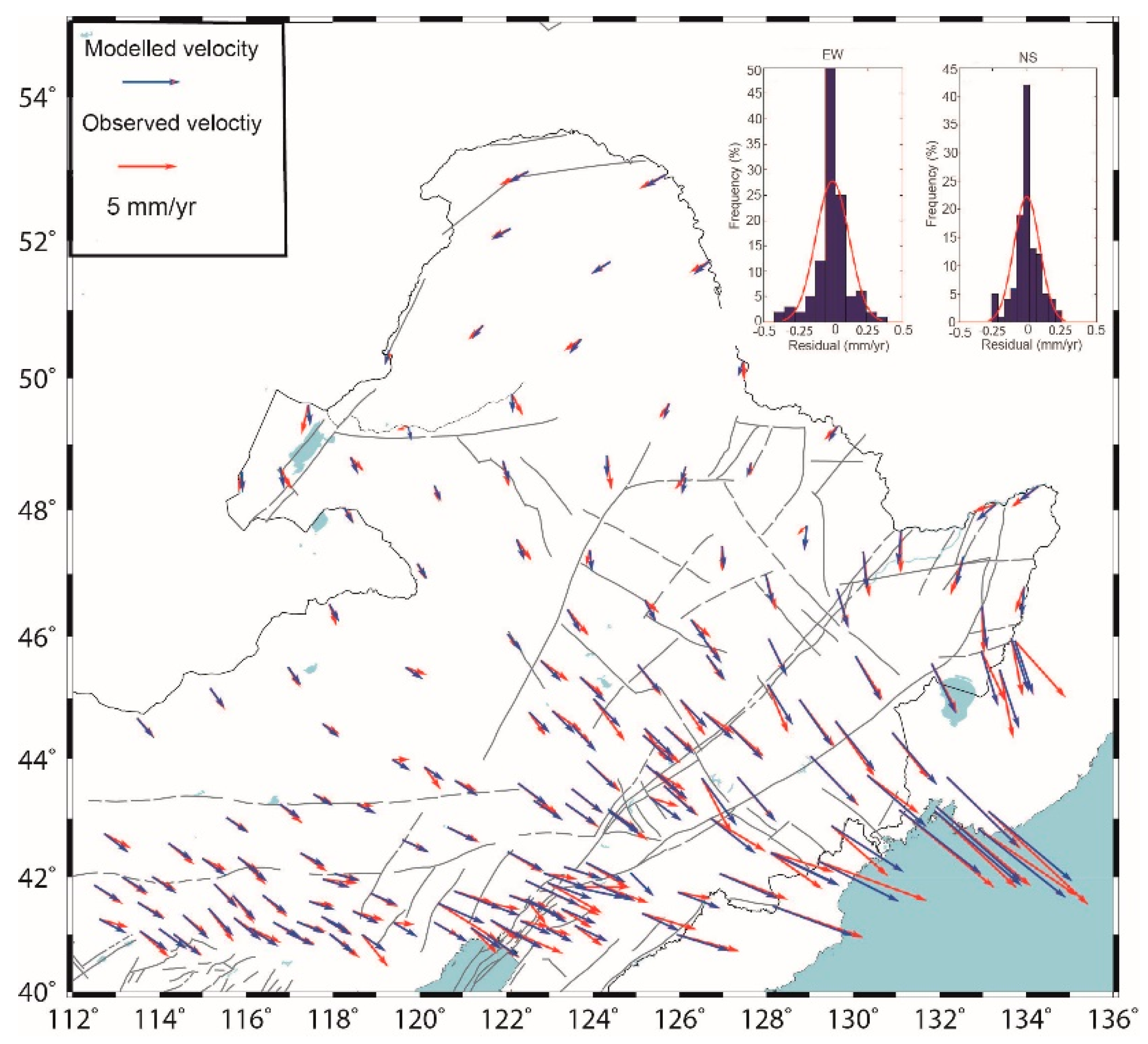
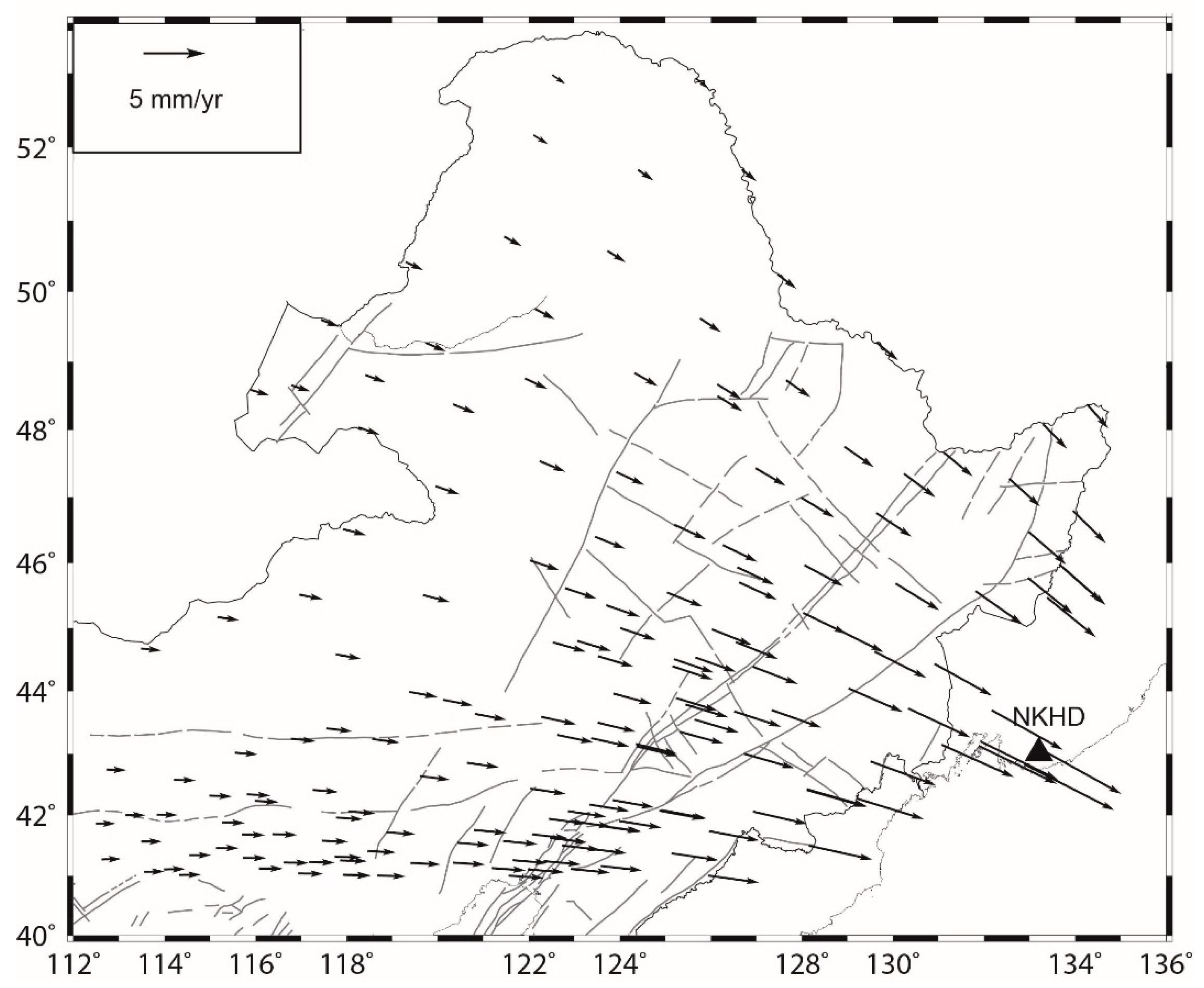
4.1. Horizontal Velocities
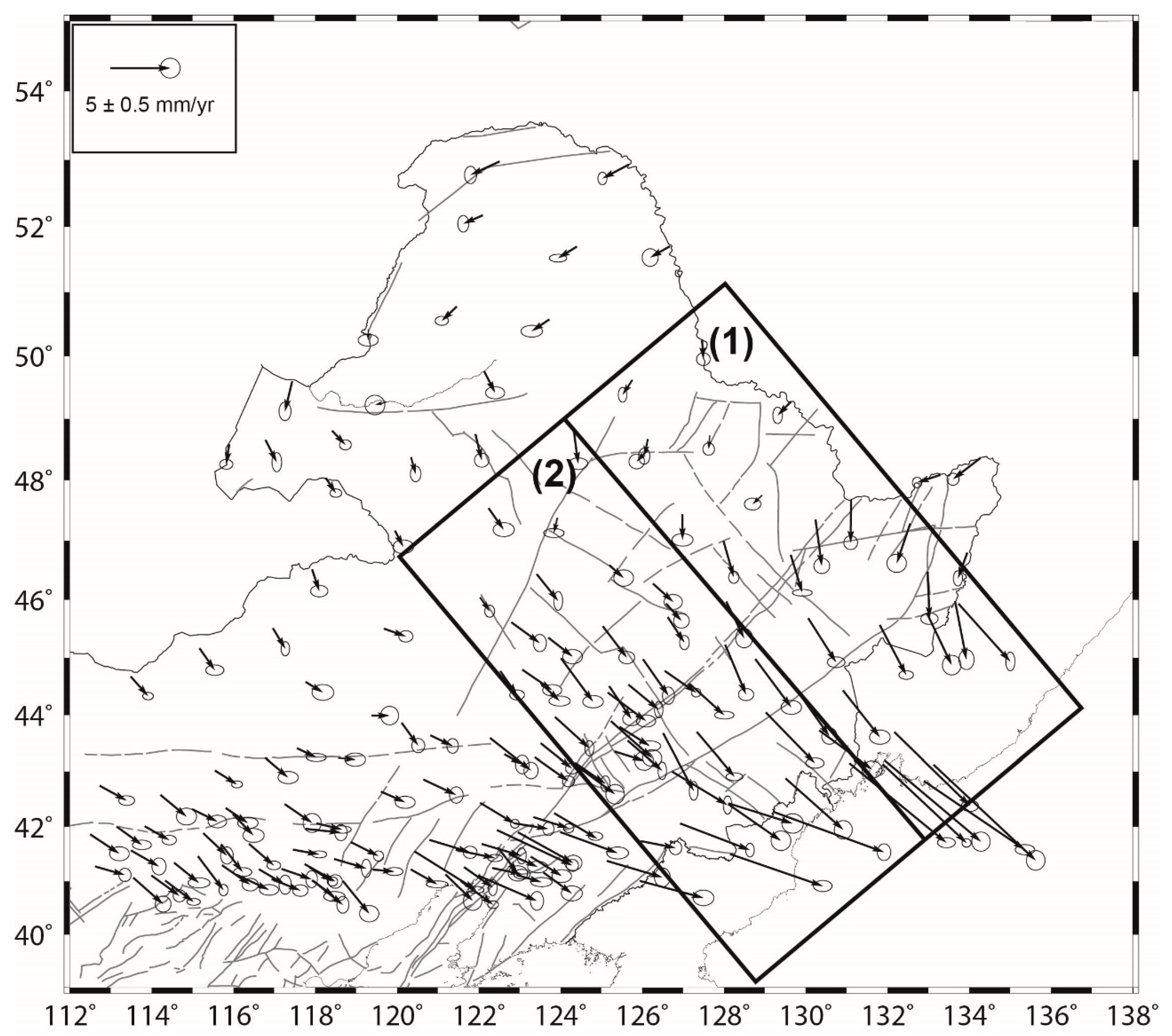
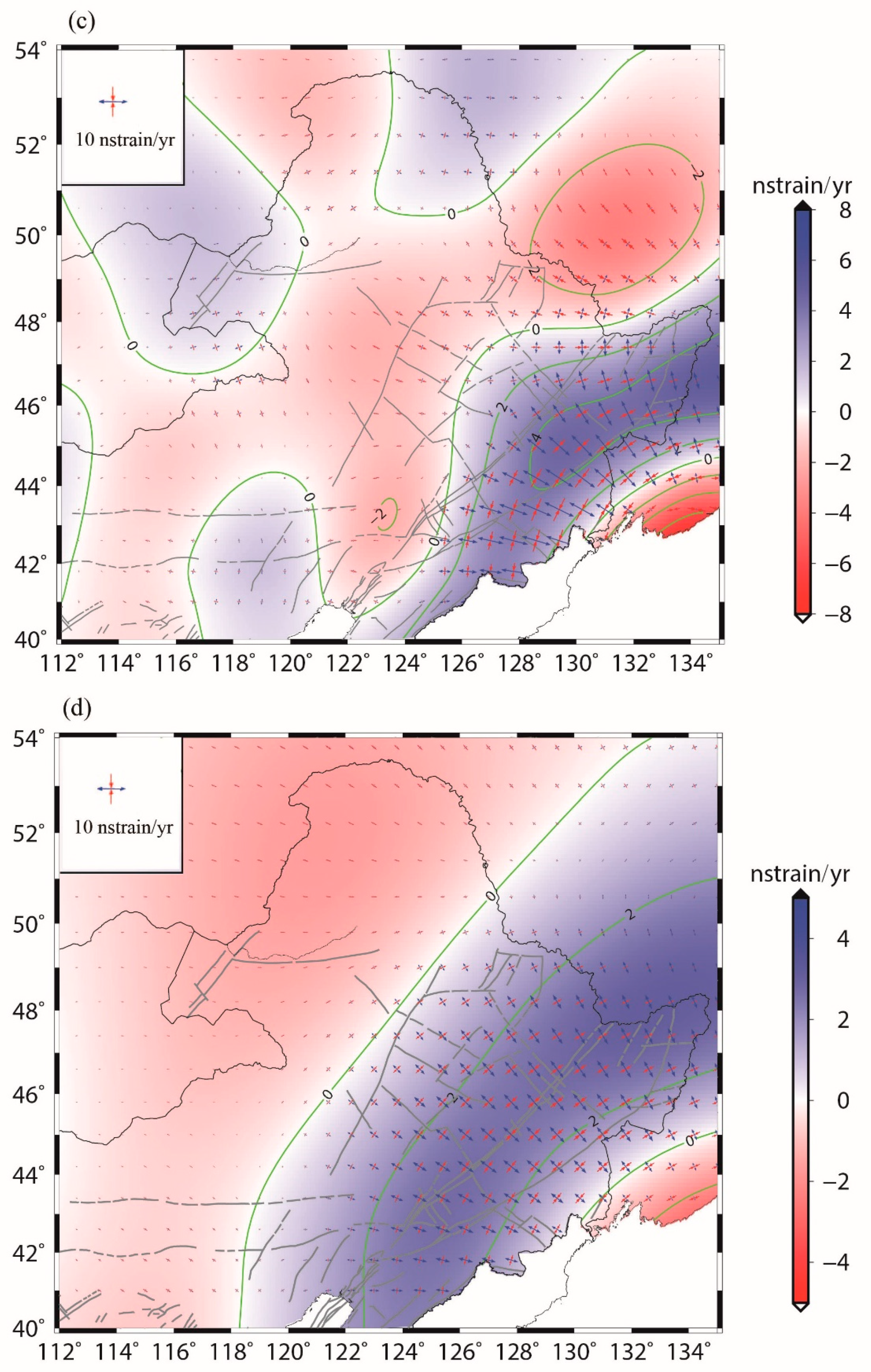
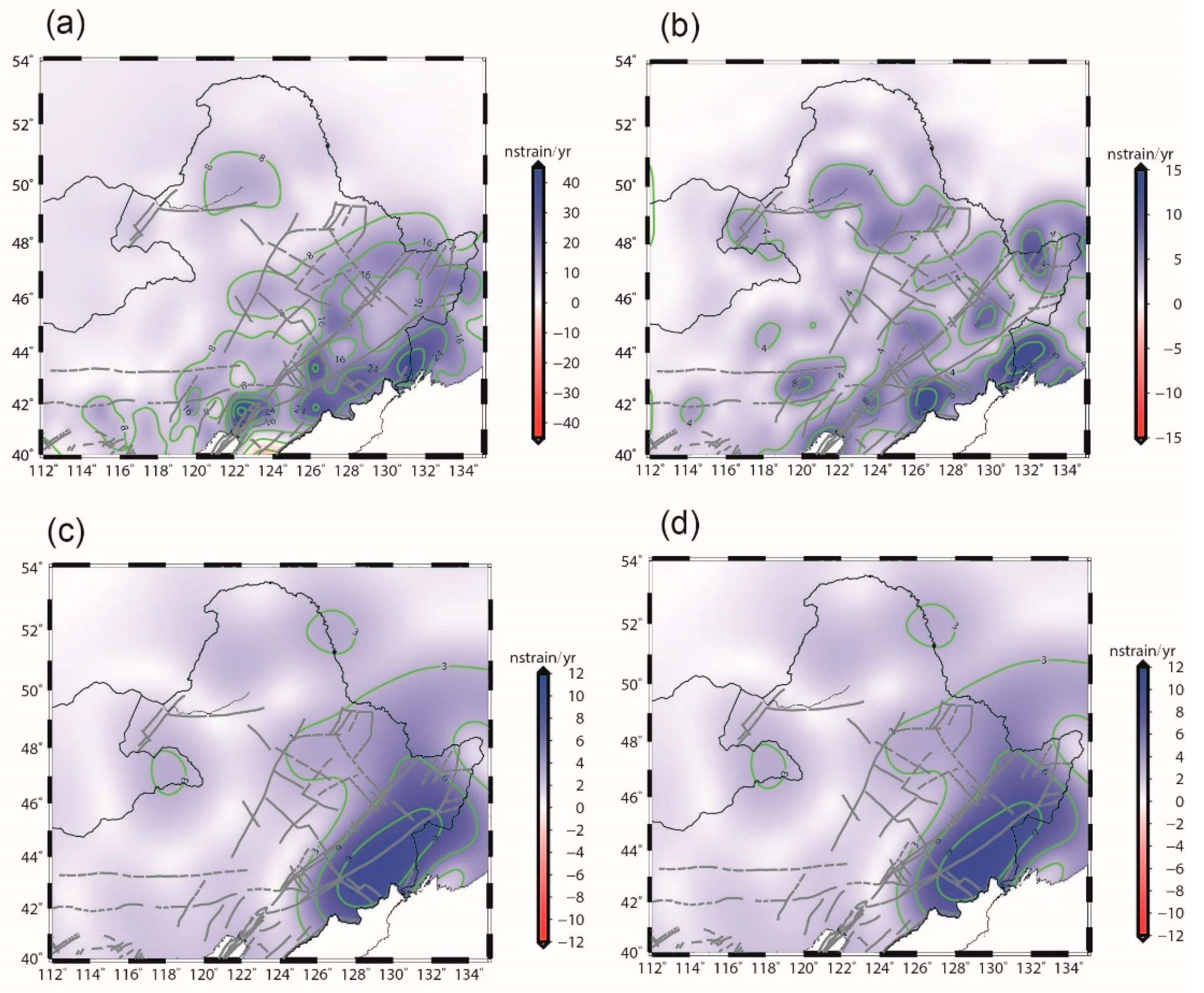
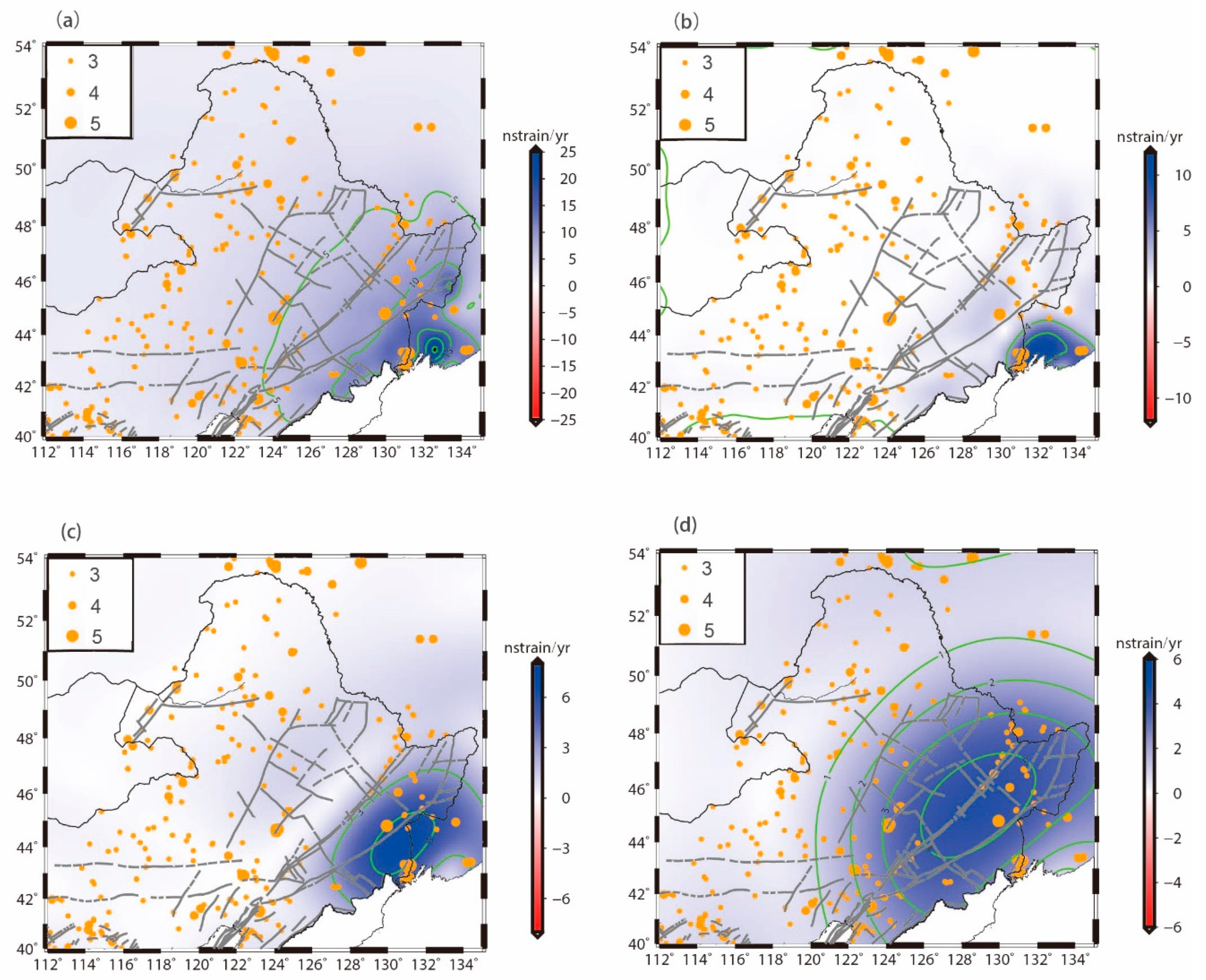
4.2. Heterogeneous Strain Rates
5. Discussion
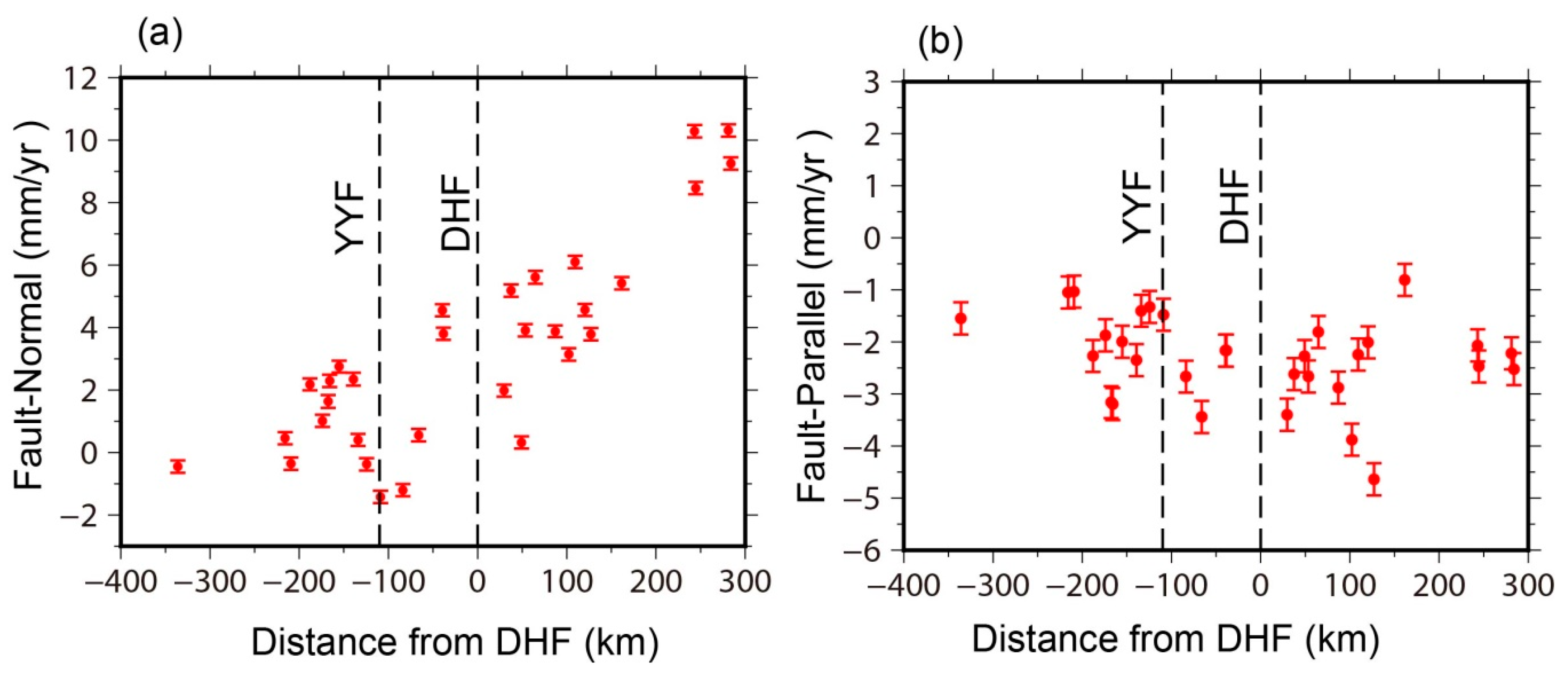
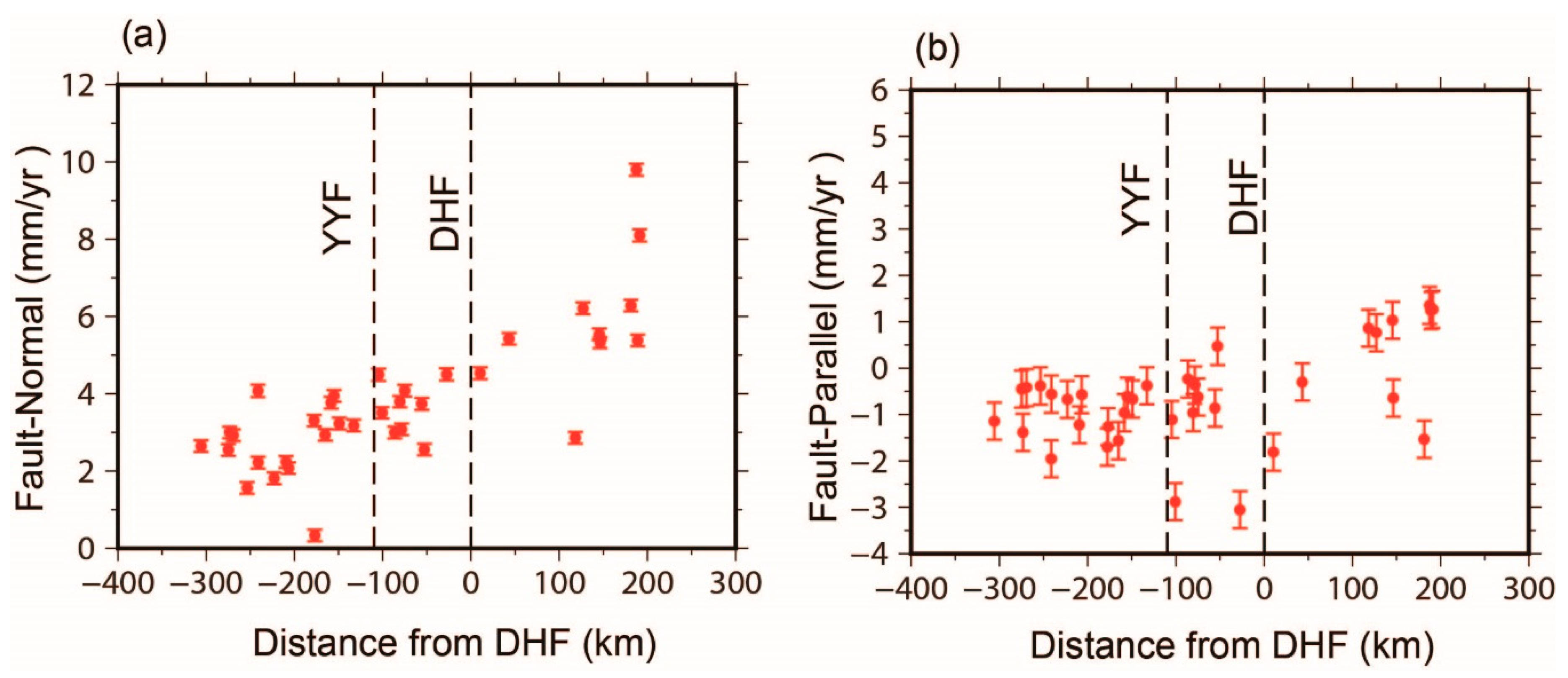
5.1. Impact of the 2011 Tohoku Earthquake
5.2. Comparison of Strain Rate and Seismicity
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Shestakov, N.; Takahashi, H.; Ohzono, M.; Prytkov, A.; Bykov, V.; Gerasimenko, M.; Luneva, M.; Gerasimov, G.; Kolomiets, A.; Bormotov, V.; et al. Analysis of the far-field crustal displacementscaused by the 2011 Great Tohoku earthquake inferred from continuous GPS observations. Tectonophysics 2012, 524–525, 76–86. [Google Scholar] [CrossRef]
- Wang, M.; Li, Q.; Wang, F.; Zhang, R.; Wang, Y.; Shi, H. Far-field coseismic displacements associated with the 2011 Tohoku earthquake in Japan observed by Global Positioning System. Chin. Sci. Bull. 2011, 56, 2419–2424. [Google Scholar] [CrossRef]
- Ozawa, S.; Nishimura, T.; Munekane, H.; Suito, H.; Kobayashi, T.; Tobita, M.; Imakiire, T. Preceding, coseismic, and postseismic slips of the 2011 Tohoku earthquake, Japan. J. Geophys. Res. 2012, 117. [Google Scholar] [CrossRef]
- Pollitz, F.; Burgmann, R.; Banerjee, P. Geodetic slip model of the 2011 M9.0 Tohoku earthquake. Geophys. Res. Lett. 2011, 38. [Google Scholar] [CrossRef]
- Baek, J.; Shin, Y.H.; Na, S.H.; Shestakov, N.V.; Park, P.H.; Cho, S. Coseismic and postseismic crustal deformations of the Korean Peninsula caused by the 2011 Mw 9.0 Tohoku earthquake, Japan, from Global Positioning System data. Terra Nova 2012, 24, 295–300. [Google Scholar] [CrossRef]
- Hwang, J.S.; Yun, H.S.; Huang, H.; Jung, T.J.; Lee, D.H.; We, K.J. The 2011 Tohoku earthquake’s influence on the Asian plates and Korean geodetic network. Chin. J. Geophys. 2012, 55, 1884–1893. [Google Scholar]
- Zhao, Q.; Fu, G.; Wu, W.; Liu, T.; Su, L.; Su, X.; Shestakov, N. Spatial-temporal evolution and corresponding mechanism of the far-field post-seismic displacements following the 2011 Mw 9.0 Tohoku earthquake. Geophys. J. Int. 2018, 214, 1774–1782. [Google Scholar] [CrossRef]
- Cheng, J.; Liu, M.; Gan, W.; Xu, X.; Huang, F.; Liu, J. Seismic impact of the Mw 9.0 Tohoku earthquake in Eastern China. Bull. Seis. Soc. Am. 2014, 104, 1258–1267. [Google Scholar] [CrossRef]
- Wang, L.; Liu, J.; Zhao, J.; Zhao, J. Tempo-spatial impact of the 2011 M 9 Tohoku earthquake on eastern china. Pure Appl. Geophys. 2016, 173, 35–47. [Google Scholar] [CrossRef]
- Hirose, F.; Miyaoka, K.; Hayashimoto, N.; Yamazaki, T.; Nakamura, M. Outline of the 2011 Off the Pacific Coast of Tohoku earthquake (Mw 9.0)—Seismicity: Foreshocks, mainshock, aftershocks, and induced activity. Earth Planets Space 2011, 63, 513–518. [Google Scholar] [CrossRef]
- Kato, A.; Sakai, S.; Obara, K.A. normal-faulting seismic sequence triggered by the 2011 Off the Pacific Coast of Tohoku earthquake: Wholesale stress regime changes in the upper plate. Earth Planets Space 2011, 63, 745–748. [Google Scholar] [CrossRef]
- Feng, C.; Zhang, P.; Sun, W.; Qin, X.; Che, Q.; Tan, C. A dicussion on the impact of Japan Mw 9.0 earthquake on the main active fault zone in north-and northereast China continent and the seismic risk. Earth Sci. Front. 2013, 20, 123–140. [Google Scholar]
- Tan, C.; Hu, Q.; Zhang, P.; Feng, C.; Qin, X. Present tectonic stres adjustment process before and after Japan Mw 9.0 earthquake in North and Northeast China and its research significance. Earth Sci. Front. 2015, 22, 345–359. [Google Scholar]
- Ogata, Y. Statistical models for earthquake occurrences and residual analysis for point processes. J. Am. Stat. Assoc. 1988, 83, 9–27. [Google Scholar] [CrossRef]
- Ogata, Y. Seismicity analysis through point-process modeling: A review. Pure Appl. Geophys. 1999, 155, 471–507. [Google Scholar] [CrossRef]
- Su, X.N.; Meng, G.J.; Wang, Z. Methodology and application of GPS strain field estimation based on spherical wavelet. Chin. J. Geophys. 2016, 59, 1585–1595. [Google Scholar] [CrossRef]
- Zonenshain, L.P.; Savostin, L.A. Geodynamics of the Baikal rift zone and plate tectonics of Asia. Tectonophysics 1981, 76, 1–45. [Google Scholar] [CrossRef]
- Apel, E.V.; Bürgmann, R.; Steblov, G.; Vasilenko, N.; King, R.; Prytkov, A. Independent active microplate tectonics of northeast asia from gps velocities and block modeling. Geophys. Res. Lett. 2006, 33, L11303. [Google Scholar] [CrossRef]
- Chen, B.; Jahn, B.M.; Wilde, S.; Xu, B. Two contrasting Paleozoic magmatic belts in northern Inner Mongolia, China. Tectonophysics 2000, 328, 157–182. [Google Scholar] [CrossRef]
- Shi, Y.; Liu, D.; Zhang, Q. SHRIMP geochronology of dioritic-granitic intrusions in Sunidzuoqi area, Inner Mongolia. Acta Geol. Sin. 2004, 78, 789–799. [Google Scholar]
- Meng, Q.R. What drove late Mesozoic extension of the northern China–Mongolia tract? Tectonophysics 2003, 369, 155–174. [Google Scholar] [CrossRef]
- Kravchinsky, V.A.; Halim, N.; Hankard, F. Late Jurassic–Early Cretaceous closure of the Mongol–Okhotsk Ocean demonstrated by new Mesozoic paleomagnetic results from the Trans-Baikalarea (SE Siberia). Geophys. J. Int. 2005, 163, 813–832. [Google Scholar] [CrossRef]
- Ren, J.; Tamaki, K.; Li, S.; Zhang, J. Late Mesozoic and Cenozoic rifting and its dynamic setting in eastern China and adjacent areas. Tectonophysics 2002, 344, 175–205. [Google Scholar] [CrossRef]
- Watson, M.P.; Hayward, A.B.; Parkinson, D.N.; Zhang, Z.M. Plate tectonic history, basin development and petroleum source rock deposition onshore China. Mar. Pet. Geol. 1987, 4, 205–225. [Google Scholar] [CrossRef]
- Davis, G.A.; Xu, B.; Zheng, Y.; Zhang, W. Indosinian extension in the Solonker suture zone: The Sonid Zuoqi metamorphic core complex, Inner Mongolia, China. Earth Sci. Front. 2004, 11, 135–144. [Google Scholar]
- Molnar, P.; Houseman, G.A.; Conrad, C.P. Rayleigh–Taylor instability and convective thinning of mechanically thickened lithosphere: Effects of non-linear viscosity decreasing exponentially with depth and of horizontal shortening of the layer. Geophys. J. Int. 1998, 133, 568–584. [Google Scholar] [CrossRef]
- Wang, F.; Zhou, X.; Zhang, L.; Ying, J.; Zhang, Y.; Wu, F.; Zhu, R. Late Mesozoic volcanism in the Great Xing’an Range (NE China): Timing and implications for the dynamic setting of NE Asia. Earth Planet. Sci. Lett. 2006, 251, 179–198. [Google Scholar] [CrossRef]
- Tao, K.; Niu, F.; Ning, J.; Chen, Y.J.; Grand, S.; Kawakatsu, H.; Satoru, T.; Masayuki, O.; Ni, J. Crustal structure beneath NE China imaged by NECESSArray receiver function data. Earth Planet. Sci. Lett. 2014, 398, 48–57. [Google Scholar] [CrossRef]
- Yin, A.; Nie, S. An indentation model for the North and South China collision and the development of the Tan-Lu and Honam Fault Systems, eastern Asia. Tectonics 1993, 12, 801–813. [Google Scholar] [CrossRef]
- Wang, F.; Xu, W.; Ge, W.; Yang, H.; Pei, F.; Wu, W. The offset distance of the Dunhua-Mishuan Fault: Constraints from Paleozoic Mesozoic magmatism within the Songnen Zhangguancai Range, Jiamusi, and Khanka massifs. Acta Petrol. Sin. 2016, 32, 1129–1140. [Google Scholar]
- Min, W.; Liu, Y.; Jiao, D.; Shen, J.; Pan, X. Evidence for holocene activity of the yilan-yitong fault, northeastern section of the Tan-lu fault zone in northeast china. J. Asian Earth Sci. 2013, 67–68, 207–216. [Google Scholar] [CrossRef]
- Sun, W.; Wang, X.; Chang, Z.; Chen, H.; He, Y.S. Discussion on time-space evolutionary characteristics of seismicity in northeast of China and dynamic mechanism. Seismol. Res. Northeast China 2005, 21, 1–8. [Google Scholar]
- Sun, W.; He, Y. The Feature of Seismicity in Northeast China and its relation to the suduction of the Japan Sea plate. Seismol. Geol. 2004, 26, 122–132. [Google Scholar]
- Herring, T.A.; King, R.W.; Floyd, M.A.; McClusky, S.C. GAMIT Reference Manual, Version 10.6; Massachusetts Institute of Technology: Cambridge, MA, USA, 2015; Available online: http://geoweb.mit.edu/gg/GAMIT_Ref.pdf (accessed on 16 June 2019).
- Herring, T.A.; King, R.W.; Floyd, M.A.; McClusky, S.C. GLOBK Reference Manual, Version 10.6; Massachusetts Institute of Technology: Cambridge, MA, USA, 2015; Available online: http://geoweb.mit.edu/gg/GLOBK_Ref.pdf (accessed on 16 June 2019).
- Wu, W.W.; Su, X.N.; Meng, G.J.; Li, C.T. Crustal deformation prior to the 2017 Jiuzhaigou, northeastern Tibetan Plateau (China), Ms 7.0 earthquake derived from GPS observations. Remote Sens. 2018, 10, 2028. [Google Scholar] [CrossRef]
- Su, X.N.; Yao, L.B.; Wu, W.W.; Meng, G.J.; Su, L.N.; Xiong, R.W.; Hong, S.Y. Crustal deformation on the northeastern margin of the Tibetan Plateau from continuous GPS observations. Remote Sens. 2019, 11, 34. [Google Scholar] [CrossRef]
- Altamimi, Z.; Rebischung, P.; Métivier, L.; Collilieux, X. ITRF2014: A new release of the International Terrestrial Reference Frame modeling nonlinear station motions. J. Geophys. Res. 2016, 121, 6109–6131. [Google Scholar] [CrossRef]
- Nikolaidis, R. Observation of Geodetic and Seismic Deformation with the Global Positioning System. Ph.D. Thesis, University of California, San Diego, CA, USA, January 2002. [Google Scholar]
- Tape, C.; Musé, P.; Simons, M.; Dong, D.; Webb, F. Multiscale estimation of GPS velocity fields. Geophys. J. Int. 2009, 179, 945–971. [Google Scholar] [CrossRef]
- Bao, B.C.; Hu, W.; Liu, Z.D.; Kang, Z.S.; Xu, J.P. Dynamic analysis of the DOG wavelet mapping with dilation and translation. Acta Phys. Sinca 2009, 58, 2240–2247. [Google Scholar]
- Golub, G.H.; Hansen, P.C.; O’Leary, D.P. Tikhonov regularization and total least squares. Siam J. Matrix Anal. Appl. 1997, 21, 185–194. [Google Scholar] [CrossRef]
- Golub, G.H.; Wahba, H.G. Generalized cross-validation as a method for choosing a good ridge parameter. Technometrics 1979, 21, 215–223. [Google Scholar] [CrossRef]
- Johnson, K.M.; Bürgmann, R.; Larson, K. Frictional properties on the San Andreas fault near Parkfield, California, inferred from models of afterslip following the 2004 earthquake. Bull. Seismol. Soc. Am. 2006, 96, 321–338. [Google Scholar] [CrossRef]
- Bürgmann, R.; Dresen, G. Rheology of the lower crust and upper mantle: Evidence from rock mechanics, geodesy and field observations. Annu. Rev. Earth Planet. Sci. 2008, 36, 531–567. [Google Scholar] [CrossRef]
- Jónsson, S.; Segall, P.; Pedersen, R.; Björnsson, G. Post-earthquake ground movements correlated to pore-pressure transients. Nature 2003, 424, 179–183. [Google Scholar] [CrossRef] [PubMed]
- Savage, J.C.; Svarc, J.L. Postseismic relaxation following the 1989 Ms 7.1 Loma Prieta earthquake, central California. J. Geophys. Res. 2010, 115, B08404. [Google Scholar] [CrossRef]
- Freed, A.M.; Hirth, G.; Behn, M.D. Using short-term postseismic displacements to infer the ambient deformation conditions of the upper mantle. J. Geophys. Res. 2012, 117, B01409. [Google Scholar] [CrossRef]
- Yamagiwa, S.; Miyazaki, S.I.; Hirahara, K.; Fukahata, Y. Afterslip and viscoelastic relaxation following the 2011 Tohoku earthquake (Mw9.0) inferred from inland GPS and seafloor GPS/Acoustic data. Geophys. Res. Lett. 2015, 42, 66–73. [Google Scholar] [CrossRef]
- Wei, S.J.; Graves, R.; Helmberger, D.; Avouac, J.P.; Jiang, J. Sources of shaking and flooding during the Tohoku earthquake: A mixture of rupture styles. Earth Planet. Sci. Lett. 2012, 333–334, 91–100. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Meng, G.; Su, X.; Wu, W.; Nikolay, S.; Takahashi, H.; Ohzono, M.; Gerasimenko, M. Crustal Deformation of Northeastern China Following the 2011 Mw 9.0 Tohoku, Japan Earthquake Estimated from GPS Observations: Strain Heterogeneity and Seismicity. Remote Sens. 2019, 11, 3029. https://doi.org/10.3390/rs11243029
Meng G, Su X, Wu W, Nikolay S, Takahashi H, Ohzono M, Gerasimenko M. Crustal Deformation of Northeastern China Following the 2011 Mw 9.0 Tohoku, Japan Earthquake Estimated from GPS Observations: Strain Heterogeneity and Seismicity. Remote Sensing. 2019; 11(24):3029. https://doi.org/10.3390/rs11243029
Chicago/Turabian StyleMeng, Guojie, Xiaoning Su, Weiwei Wu, Shestakov Nikolay, Hiroaki Takahashi, Mako Ohzono, and Mikhail Gerasimenko. 2019. "Crustal Deformation of Northeastern China Following the 2011 Mw 9.0 Tohoku, Japan Earthquake Estimated from GPS Observations: Strain Heterogeneity and Seismicity" Remote Sensing 11, no. 24: 3029. https://doi.org/10.3390/rs11243029
APA StyleMeng, G., Su, X., Wu, W., Nikolay, S., Takahashi, H., Ohzono, M., & Gerasimenko, M. (2019). Crustal Deformation of Northeastern China Following the 2011 Mw 9.0 Tohoku, Japan Earthquake Estimated from GPS Observations: Strain Heterogeneity and Seismicity. Remote Sensing, 11(24), 3029. https://doi.org/10.3390/rs11243029