Long-Term Change of the Secchi Disk Depth in Lake Maninjau, Indonesia Shown by Landsat TM and ETM+ Data
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Data Collection
2.2.1. The In Situ SD Data Collection
2.2.2. The Satellite Data Collection
2.3. The Preprocessing of the Landsat TM and ETM+ Images
2.3.1. The Removal of Non-Water Pixels
2.3.2. The Reduction of Noise Effects on the Remaining Water Pixels
2.3.3. The Conversion of the DN Values to Radiance and the Minimization of Atmospheric Effects
2.4. SD Estimation Model Development and Accuracy Assessment
2.4.1. The Development of the Empirical SD Estimation Models
2.4.2. The Accuracy Assessment
3. Results
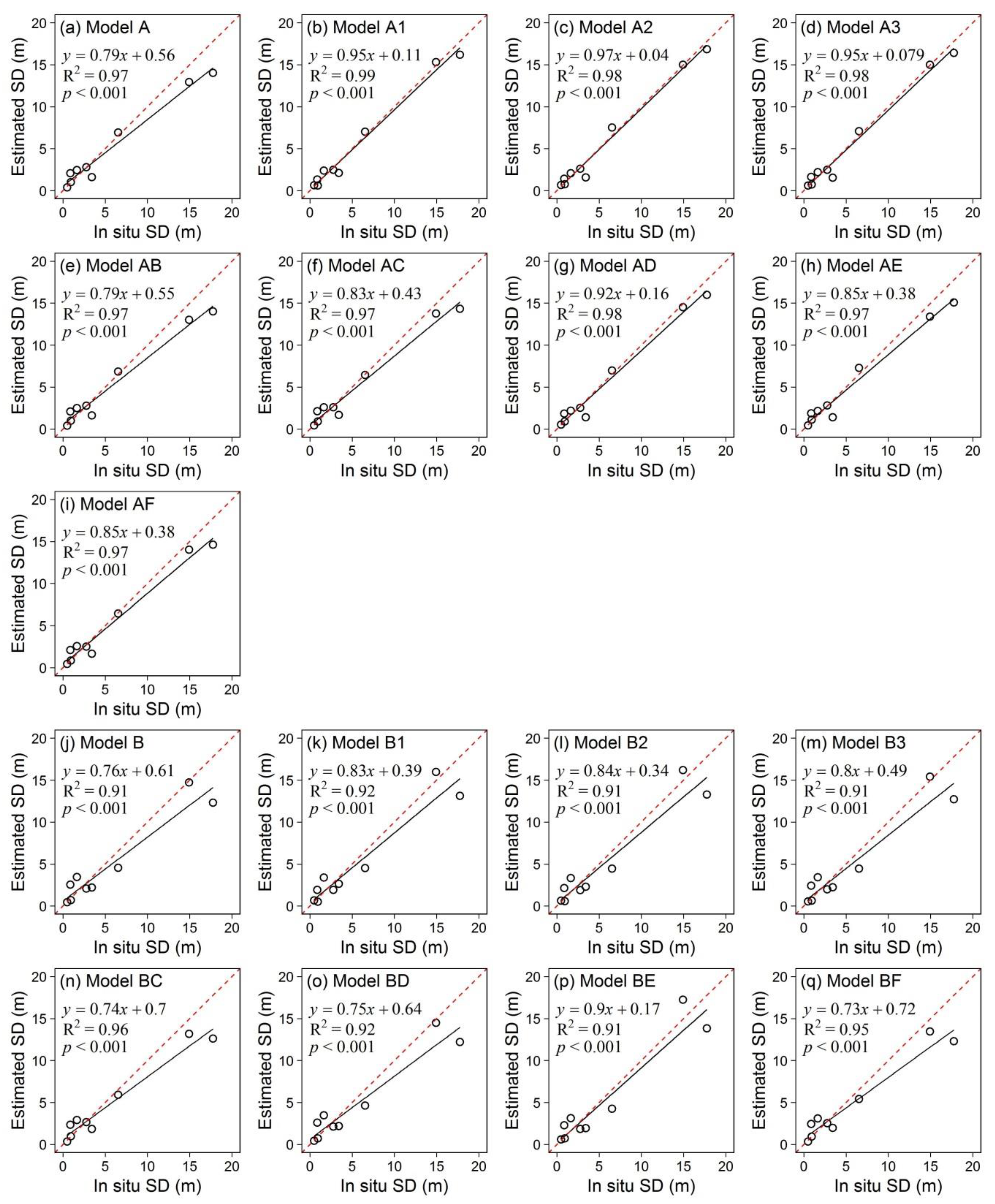
3.1. The Empirical Models for Estimating the SD from Landsat TM/ETM+ Data
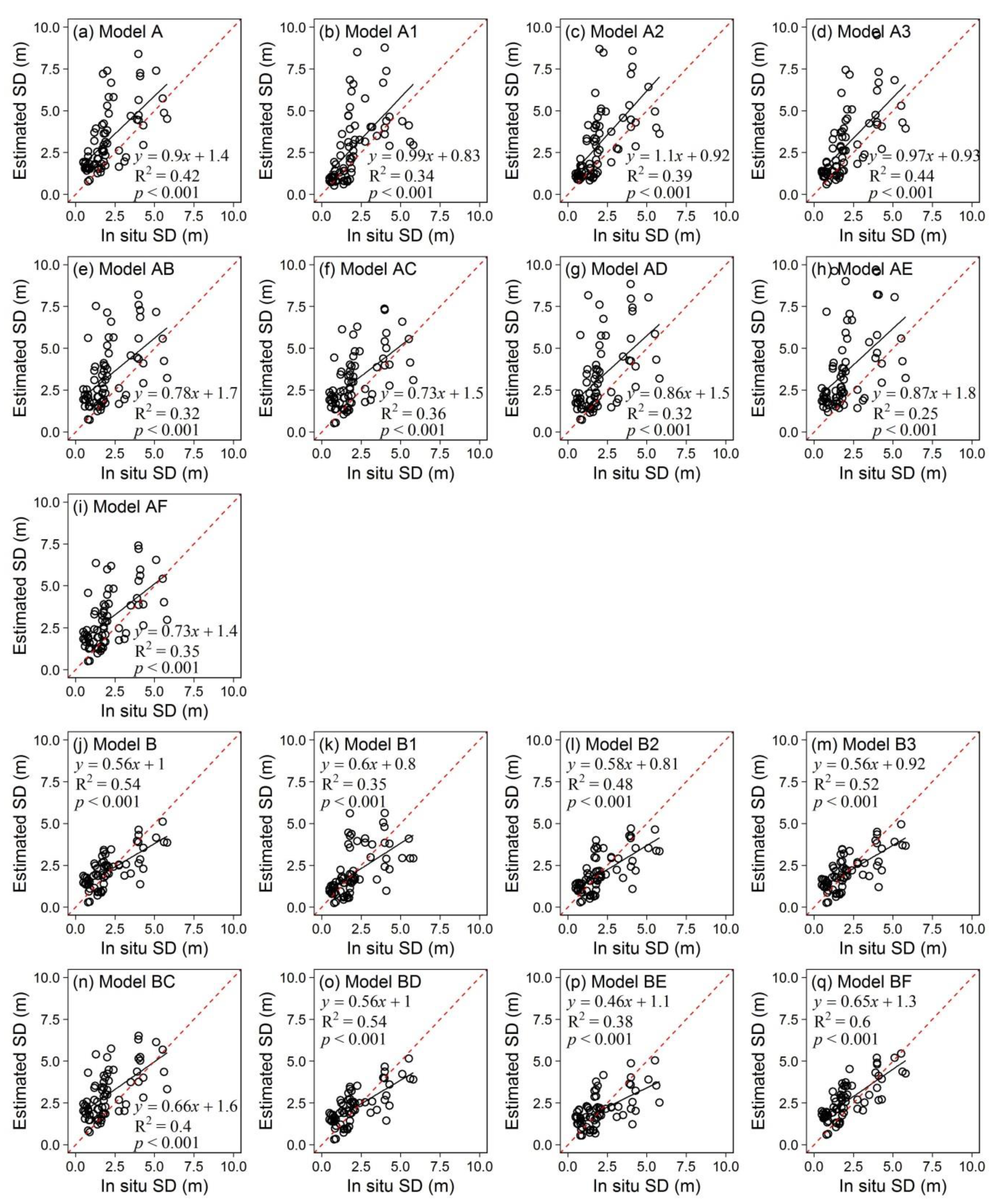
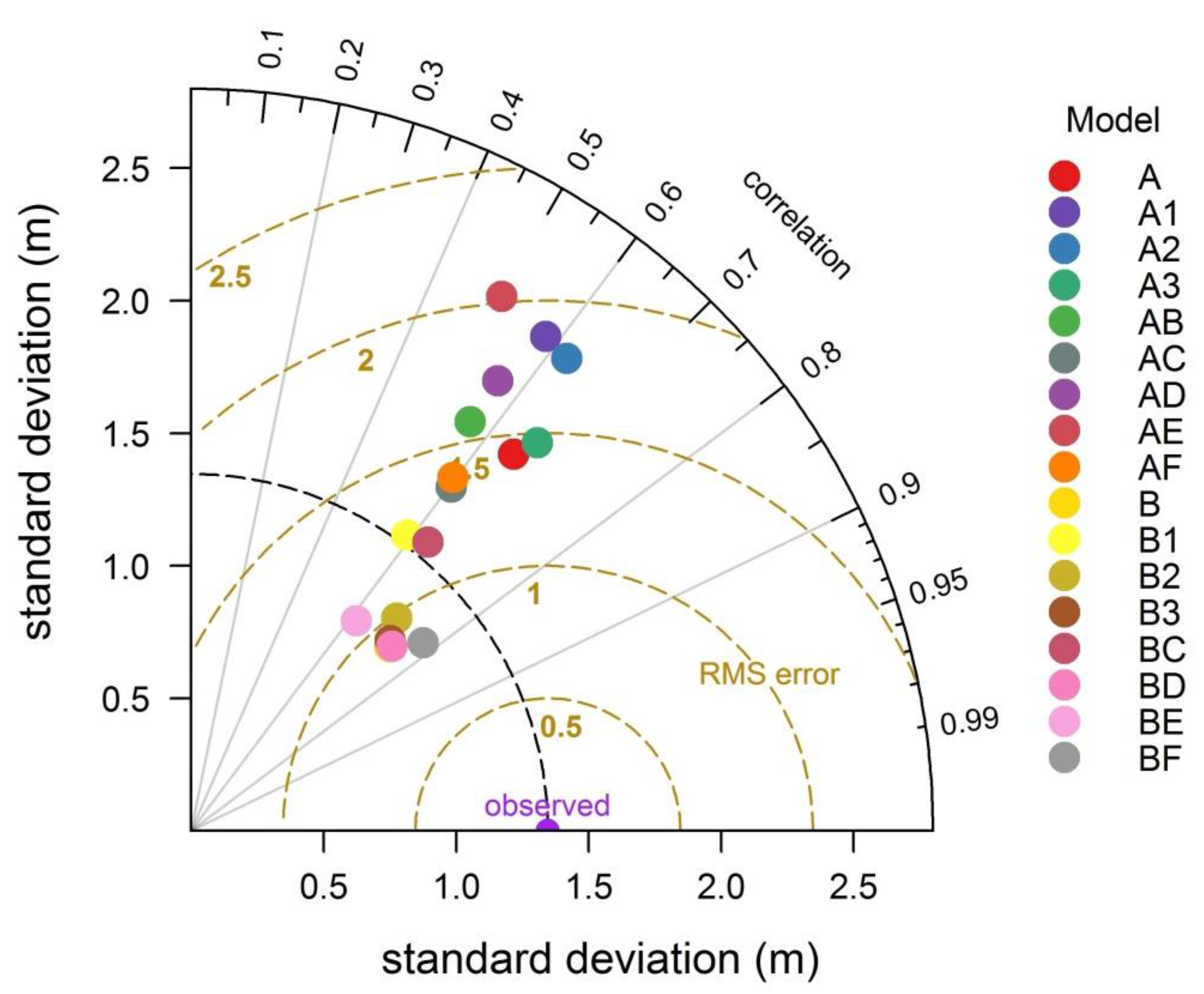
3.2. The Validation of the 17 Selected SD Estimation Models in Lake Maninjau
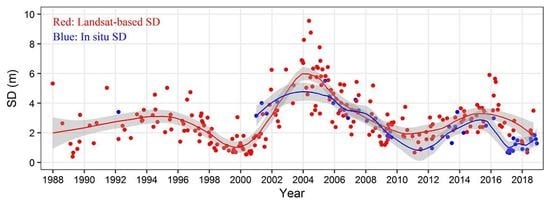
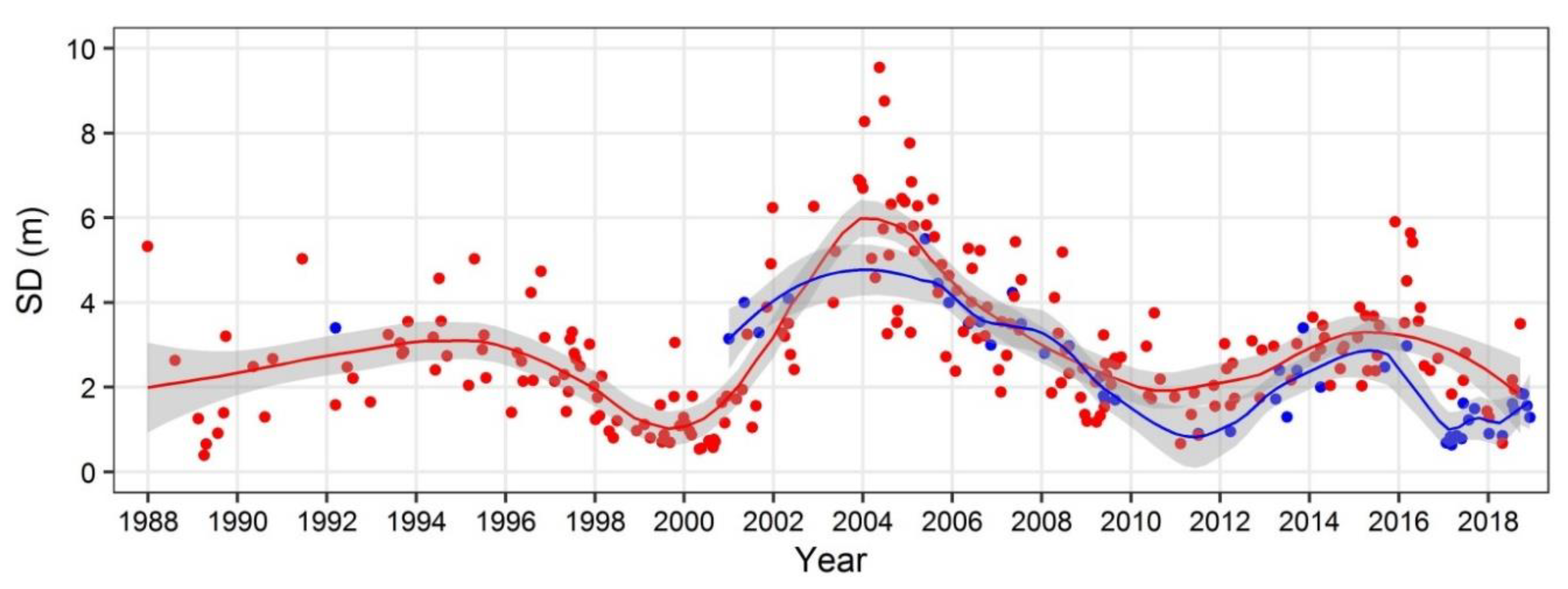
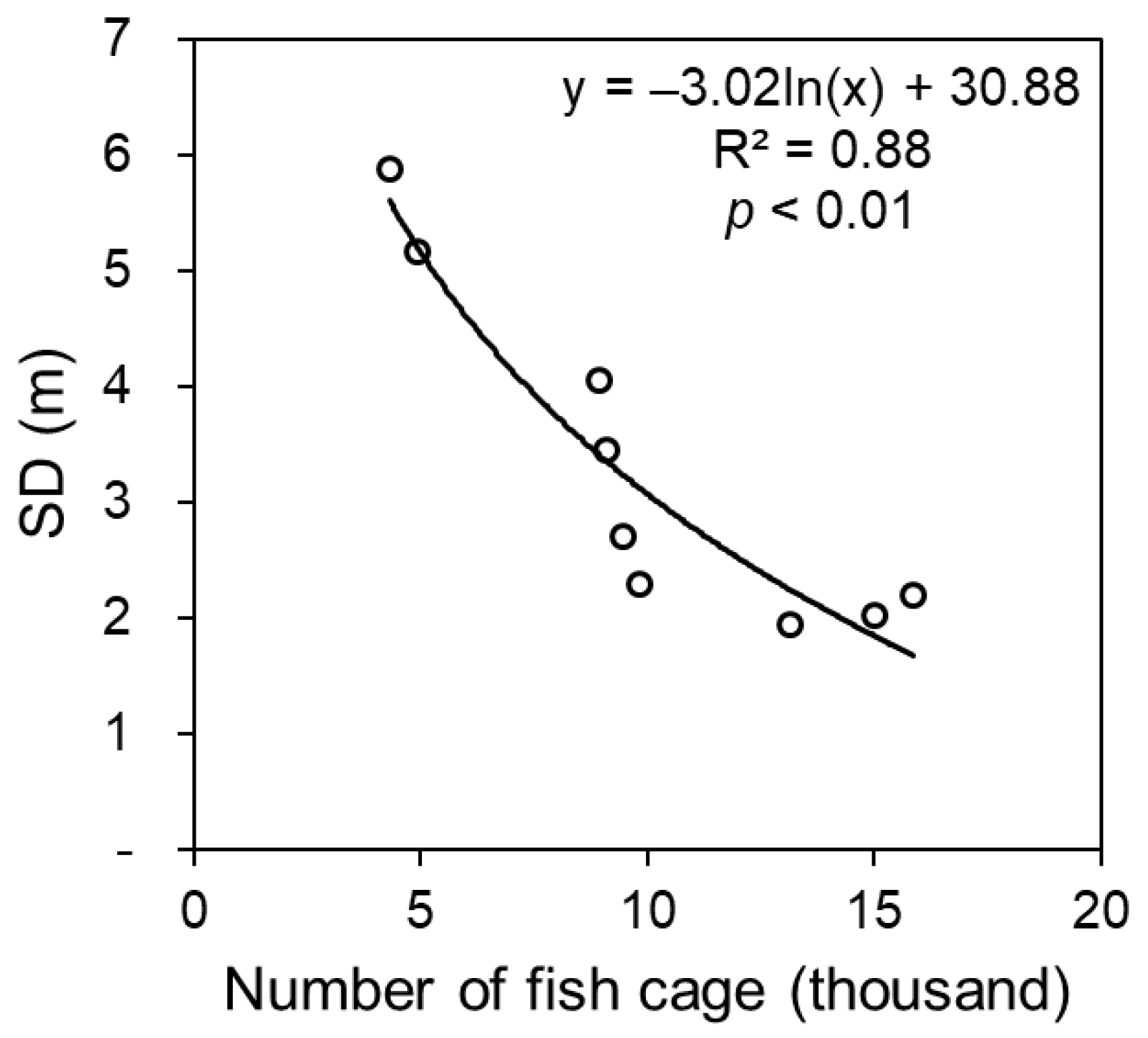
3.3. Long-Term SD Changes in Lake Maninjau from the Landsat TM/ETM+ Time Series
4. Discussion
4.1. The Applicability of the Developed SD Estimation Model
4.2. The Reliability of the Estimated SD Values from Landsat Data
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Sulastri. Inland water resources and limnology in Indonesia. Tropics 2006, 15, 285–295. Available online: https://www.jstage.jst.go.jp/article/tropics/15/3/15_3_285/_pdf/-char/en (accessed on 19 April 2018). [CrossRef]
- Ministry of Environment of the Republic of Indonesia. Profil 15 Danau Prioritas Nasional; Kementerian Lingkungan Hidup Republik Indonesia: Jakarta, Indonesia, 2011; pp. 1–148. [Google Scholar]
- Ruttner, F. Hydrographische und Hydrochemishe Beobachtungen auf Java, Sumatera und Bali. Arch. Hydrobiol. Suppl. 1930, 8, 197–454. [Google Scholar]
- Lehmusluoto, P.; Machbub, B.; Terangna, N.; Rusmiputro, S.; Achmad, F.; Boer, L.; Brahmana, S.; Priadi, B.; Setiadji, B.; Sayuman, O.; et al. National Inventory of the Major Lakes and Reservoirs in Indonesia. General Limnology, Revised ed.; Research Institute for Water Resources Development, Ministry of Public Works, Agency for Research and Development: Bandung, Indonesia, 1997; pp. 1–71.
- Giardino, C.; Pepe, M.; Brivio, P.A.; Ghezzi, P.; Zilioli, E. Detecting chlorophyll, Secchi disk depth and surface temperature in a sub-alpine lake using Landsat imagery. Sci. Total Environ. 2001, 268, 19–29. [Google Scholar] [CrossRef]
- Kloiber, S.M.; Brezonik, P.L.; Bauer, M.E. Application of Landsat imagery to regional-scale assessment of lake clarity. Water Res. 2002, 26, 4330–4340. [Google Scholar] [CrossRef]
- Olmanson, L.G.; Bauer, M.E.; Brezonik, P.L. A 20-year Landsat water clarity census of Minnesota’s 10,000 Lakes. Remote Sens. Environ. 2008, 112, 4086–4097. [Google Scholar] [CrossRef]
- Olmanson, L.G.; Brezonik, P.L.; Bauer, M.E. Evaluation of medium to low resolution satellite imagery for regional lake water quality assessments. Water Resour. Res. 2011, 47, W09515. [Google Scholar] [CrossRef]
- Bonansea, M.; Ledesma, C.; Rodríguez, C.; Pinotti, L.; Antunes, H.M. Effects of atmospheric correction of Landsat imagery on lake water clarity assessment. Adv. Space Res. 2015, 56, 2345–2355. [Google Scholar] [CrossRef]
- Dörnhöfer, K.; Oppelt, N. Remote sensing for lake research and monitoring. Recent Adv. Ecol. Indic. 2016, 64, 105–122. [Google Scholar] [CrossRef]
- Gholizadeh, M.H.; Melesse, A.M.; Reddi, L. A Comprehensive Review on Water Quality Parameters Estimation Using Remote Sensing Techniques. Sensors 2016, 16, 1298. [Google Scholar] [CrossRef]
- Olmanson, L.G.; Brezonik, P.L.; Finlay, J.C.; Bauer, M.E. Comparison of Landsat 8 and Landsat 7 for regional measurements of CDOM and water clarity in lakes. Remote Sens. Environ. 2016, 185, 119–128. [Google Scholar] [CrossRef]
- Blondeau-Patissier, D.; Gower, J.F.; Dekker, A.G.; Phinn, S.R.; Brando, V.E. A review of ocean color remote sensing methods and statistical techniques for the detection, mapping and analysis of phytoplankton blooms in coastal and open oceans. Prog. Oceanogr. 2014, 123, 123–144. [Google Scholar] [CrossRef]
- Oyama, Y.; Matsushita, B.; Fukushima, T.; Matsushige, K.; Imai, A. Application of spectral decomposition algorithm for mapping water quality in a turbid lake (Lake Kasumigaura, Japan) from Landsat TM data. ISPRS J. Photogramm. Remote Sens. 2009, 64, 73–85. [Google Scholar] [CrossRef]
- Kutser, T. The possibility of using the Landsat image archive for monitoring long time trends in coloured dissolved organic matter concentration in lake waters. Remote Sens. Environ. 2012, 123, 334–338. [Google Scholar] [CrossRef]
- Zheng, Z.; Li, Y.; Guo, Y.; Xu, Y.; Liu, G.; Du, C. Landsat-Based Long-Term Monitoring of Total Suspended Matter Concentration Pattern Change in the Wet Season for Dongting Lake, China. Remote Sens. 2015, 7, 13975–13999. [Google Scholar] [CrossRef]
- Lobo, F.L.; Costa, M.P.F.; Novo, E.M.L.M. Time-series analysis of Landsat-MSS/TM/OLI images over Amazonian waters impacted by gold mining activities. Remote Sens. Environ. 2015, 157, 170–184. [Google Scholar] [CrossRef]
- Lee, Z.; Shang, S.; Qi, L.; Yan, J.; Lin, G. A semi-analytical scheme to estimate Secchi-disk depth from Landsat-8 measurements. Remote Sens. Environ. 2016, 177, 101–106. [Google Scholar] [CrossRef]
- Rodrigues, T.; Alcantara, E.; Watanabe, F.; Imai, N. Retrieval of Secchi disk depth from a reservoir using a semi-analytical scheme. Remote Sens. Environ. 2017, 198, 213–228. [Google Scholar] [CrossRef]
- Lee, Z.; Shang, S.; Hu, C.; Du, K.; Weidemann, A.; Hou, W.; Lin, J.; Lin, G. Secchi disk depth: A new theory and mechanistic model for underwater visibility. Remote Sens. Environ. 2015, 169, 139–149. [Google Scholar] [CrossRef]
- Lee, Z.; Carder, K.L.; Arnone, R.A. Deriving inherent optical properties from water color: A multiband quasi-analytical algorithm for optically deep waters. Appl. Opt. 2002, 41, 5755–5772. [Google Scholar] [CrossRef]
- Yang, W.; Matsushita, B.; Chen, J.; Yoshimura, K.; Fukushima, T. Retrieval of inherent optical properties for turbid inland waters from remote-sensing reflectance. IEEE Trans. Geosci. Remote Sens. 2013, 51, 3761–3773. [Google Scholar] [CrossRef]
- Lathrop, R.G. Landsat thematic mapper monitoring of turbid inland water quality. Photogramm. Eng. Remote Sens. 1992, 58, 465–470. [Google Scholar]
- Lavery, P.; Pattiaratchi, C.; Wyllie, A.; Hick, P. Water quality monitoring in estuarine waters using the Landsat thematic mapper. Remote Sens. Environ. 1993, 46, 268–280. [Google Scholar] [CrossRef]
- Cox, R.M.; Forsythe, R.D.; Vaughan, G.E.; Olmsted, L.L. Assessing water quality in the Catawba river reservoirs using Landsat thematic mapper satellite data. Lake Reserv. Manag. 1998, 14, 405–416. [Google Scholar] [CrossRef]
- Brezonik, P.; Menken, K.D.; Bauer, M. Landsat-based Remote Sensing of Lake Water Quality Characteristics, Including Chlorophyll and Colored Dissolved Organic Matter (CDOM). Lake Reserv. Manag. 2005, 21, 373–382. [Google Scholar] [CrossRef]
- Zhao, D.; Cai, Y.; Jiang, H.; Xu, D.; Zhang, W.; An, S. Estimation of water clarity in Taihu Lake and surrounding rivers using Landsat imagery. Adv. Water Resour. 2011, 34, 165–173. [Google Scholar] [CrossRef]
- Sriwongsitanon, N.; Surakit, K.; Thianpopirug, S. Influence of atmospheric correction and number of sampling points on the accuracy of water clarity assessment using remote sensing application. J. Hydrol. 2011, 401, 203–220. [Google Scholar] [CrossRef]
- Bonansea, M.; Rodríguez, C.; Pinotti, L.; Ferrero, S. Using multi-temporal Landsat imagery and Linear mixed models for assessing water quality parameters in Rio Tercero reservoir (Argentina). Remote Sens. Environ. 2015, 158, 28–41. [Google Scholar] [CrossRef]
- Butt, M.J.; Nazeer, M. Landsat ETM+ Secchi Disc Transparency (SDT) retrievals for Rawal Lake, Pakistan. Adv. Space Res. 2015, 56, 1428–1440. [Google Scholar] [CrossRef]
- Nichol, J.E.; Vohora, V. Noise over water surface in Landsat TM images. Int. J. Remote Sens. 2004, 25, 2087–2094. [Google Scholar] [CrossRef]
- Fakhrudin, M.; Wibowo, H.; Subehi, L.; Ridwansyah, I. Karakterisasi Hidrologi Danau Maninjau Sumatera Barat. In Proceedings of the Seminar Nasional Limnologi 2002, Bogor, Indonesia, 22 April 2002; Pusat Penelitian Limnologi—LIPI: Bogor, Indonesia, 2002; pp. 65–75. [Google Scholar]
- Syandri, H. Loading and Distribution of Organic Materials in Maninjau Lake West Sumatra Province-Indonesia. J. Aquac. Res. Dev. 2014, 5, 1–4. [Google Scholar] [CrossRef]
- Badan Pusat Statistik Kabupaten Agam. Agam in Figures 2015. Available online: https://agamkab.bps.go.id/publication/2016/01/27/9e1bdfeacc59787c00e6a53e/kabupaten-agam-dalam-angka-2015.html (accessed on 15 February 2019).
- Badan Pusat Statistik Kabupaten Agam. Agam in Figures 2016. Available online: https://agamkab.bps.go.id/publication/2016/07/15/3a4ed5ae43c41906b939bf50/kabupaten-agam-dalam-angka-2016.html (accessed on 15 February 2019).
- Badan Pusat Statistik Kabupaten Agam. Agam in Figures 2017. Available online: https://agamkab.bps.go.id/publication/2017/08/11/2ef8e1564e24faf29cd9ebd4/kabupaten-agam-dalam-angka-2017.html (accessed on 15 February 2019).
- Badan Pusat Statistik Kabupaten Agam. Agam in Figures 2018. Available online: https://agamkab.bps.go.id/publication/2018/08/16/61f234670dec4ca6f38c0024/kabupaten-agam-dalam-angka-2018.html (accessed on 15 February 2019).
- Ridwansyah, I.; Subehi, L.; Yulianti, M.; Triwisesa, E.; Nasahara, K. Impact of LULC Change on Hydrological Response in Lake Maninjau Catchment Area. In Proceedings of the 17th World Lake Conference, Lake Kasumigaura, Ibaraki, Japan, 15–19 October 2018; pp. 289–291. [Google Scholar]
- Landsat Science—Landsat 5. Available online: https://landsat.gsfc.nasa.gov/landsat-5/ (accessed on 16 April 2018).
- Landsat Science—Landsat 7. Available online: https://landsat.gsfc.nasa.gov/landsat-7/ (accessed on 16 April 2018).
- USGS Earth Explorer. Available online: https://earthexplorer.usgs.gov/ (accessed on 11 March 2019).
- McFeeters, S.K. The use of normalized difference water index (NDWI) in the delineation of open water features. Int. J. Remote Sens. 1996, 17, 1425–1432. [Google Scholar] [CrossRef]
- Xu, H. Modification of normalized difference water index (NDWI) to enhance open water features in remotely sensed imagery. Int. J. Remote Sens. 2006, 27, 3025–3033. [Google Scholar] [CrossRef]
- Poros, D.J.; Petersen, C.J. A method for destriping Landsat Thematic Mapper images: A feasibility study for an online destriping process in the Thematic Mapper image processing System (TIPS). Photogramm. Eng. Remote Sens. 1985, 51, 1371–1378. [Google Scholar]
- Chander, G.; Markham, B.; Dennis, D.L. Summary of current radiometric calibration coefficients for Landsat MSS, TM, ETM+, and EO-1 ALI sensors. Remote Sens. Environ. 2009, 113, 893–903. [Google Scholar] [CrossRef]
- Wang, S.; Li, J.; Zhang, B.; Spyrakos, E.; Tyler, A.N.; Shen, Q.; Zhang, F.; Kuster, T.; Lehmann, M.K.; Wu, Y.; et al. Trophic state assessment of global inland waters using a MODIS-derived Forel-Ule index. Remote Sens. Environ. 2018, 217, 444–460. [Google Scholar] [CrossRef]
- Vermote, E.F.; Tanré, D.; Deuzé, J.L.; Herman, M.; Morcrette, J.L. Second Simulation of the Satellite Signal in the Solar Spectrum, 6S: An Overview. IEEE Trans. Geosci. Remote Sens. 1997, 35, 675–686. [Google Scholar] [CrossRef]
- Feng, L.; Hou, X.; Li, J.; Zheng, Y. Exploring the potential of Rayleigh-corrected reflectance in coastal and inland water applications: A simple aerosol correction method and its merits. ISPRS J. Photogramm. Remote Sens. 2018, 146, 52–64. [Google Scholar] [CrossRef]
- R Core Team. R: A language and environment for statistical computing. In R Foundation for Statistical Computing; Vienna, Austria, 2018; Available online: https://www.R-project.org/ (accessed on 5 March 2019).
- Zambrano-Bigiarini, M. hydroGOF: Goodness-of-fit functions for comparison of simulated and observed hydrological time series. In R Package Version 0.3-10; 2017; Available online: http://hzambran.github.io/hydroGOF/ (accessed on 15 November 2019). [CrossRef]
- Willmott, C.J. On the Validation of Models. Phys. Geogr. 1981, 2, 184–194. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River Flow Forecasting Through Conceptual Models Part I: A Discussion of Prinicples. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Carslaw, D.C.; Ropkins, K. Openair—An R package for air quality data analysis. Environ. Model. Softw. 2012, 27–28, 52–61. [Google Scholar] [CrossRef]
- Taylor, K.E. Summarizing multiple aspect of model performance in a single diagram. J. Geophys. Res. Atmos. 2001, 106, 7183–7192. [Google Scholar] [CrossRef]
- Wickham, H. Ggplot2: Elegant Graphics for Data Analysis; Springer: New York, NY, USA, 2016. [Google Scholar]
- Cristina, S.; Cordeiro, C.; Lavender, S.; Costa Goela, P.; Icely, J.; Newton, A. MERIS phytoplankton time series products from the SW Iberian Peninsula (Sagres) using seasonal-trend decomposition based on loess. Remote Sens. 2016, 8, 449. [Google Scholar] [CrossRef]
- Lu, H.; Raupach, M.R.; McVicar, T.R.; Barrett, D.J. Decomposition of vegetation cover into woody and herbaceous components using AVHRR NDVI time series. Remote Sens. Environ. 2003, 86, 1–18. [Google Scholar] [CrossRef]
- Jiang, B.; Liang, S.; Wang, J.; Xiao, Z. Modeling MODIS LAI time series using three statistical methods. Remote Sens. Environ. 2010, 114, 1432–1444. [Google Scholar] [CrossRef]
- Doxaran, D.; Froidefond, J.M.; Castaing, P. A reflectance band ratio used to estimate suspended matter concentrations in sediment-dominated coastal waters. Int. J. Remote Sens. 2002, 23, 5079–5085. [Google Scholar] [CrossRef]
- Doxaran, D.; Froidefond, J.M.; Castaing, P. Remote-sensing reflectance of turbid sediment-dominated waters. Reduction of sediment type variations and changing illumination conditions effects by use of reflectance ratios. Appl. Opt. 2003, 42, 2623–2634. [Google Scholar] [CrossRef]
- Febrianti. Attack of the Algae at Lake Maninjau. Tempo: Indonesia's Weekly News Magazine. 19 November 2000. Available online: https://search.proquest.com/docview/198798412?accountid=25225 (accessed on 20 February 2019).
- Sulastri. Spatial and Temporal Distribution of Phytoplankton in Lake Maninjau, West Sumatera. In Proceedings of the International Symposium on Land Management and Biodiversity in South East Asia, Bali, Indonesia, 17–20 September 2002; pp. 403–408. [Google Scholar]
- Henny, C.; Nomosatryo, S. Changes in water quality and trophic status associated with aquaculture in Lake Maninjau, Indonesia. IOP Conf. Ser. Earth Environ. Sci. 2016, 31, 012027. [Google Scholar] [CrossRef]
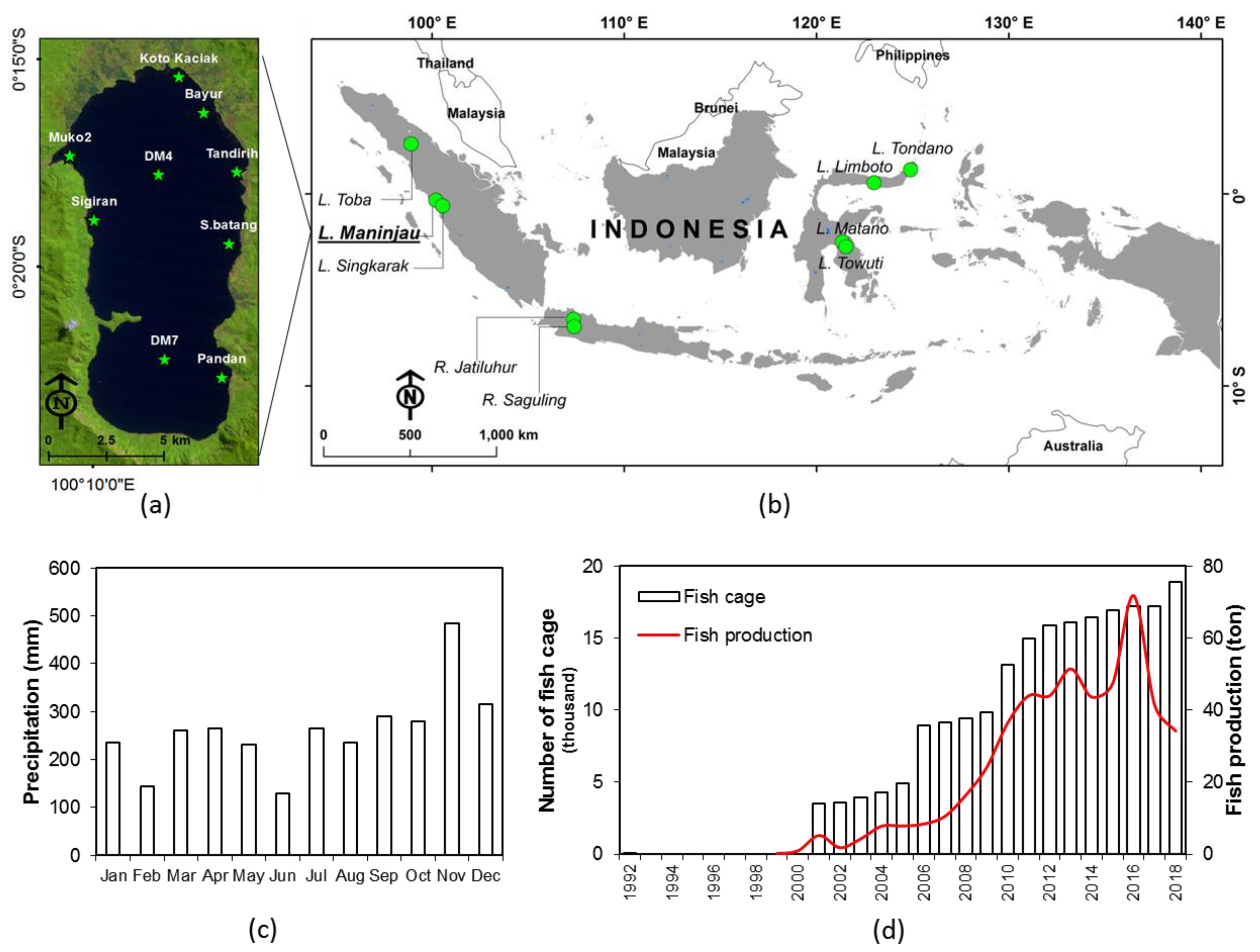
| No. | Name and Site | Area (km2) | Max Depth (m) | Altitude (m) | Coordinate | Investigation Date | SD (m) | |
|---|---|---|---|---|---|---|---|---|
| Longitude | Latitude | |||||||
| 1 | Singkarak st.1 | 108 | 268 | 362 | 100.5062 | −0.5432 | 20 July 2011 | 3.70 |
| 2 | Singkarak st.2 | 100.5061 | −0.5434 | 4.00 | ||||
| 3 | Singkarak st.3 | 100.5446 | −0.6228 | 3.05 | ||||
| 4 | Singkarak st.4 | 100.5722 | −0.6741 | 3.00 | ||||
| 5 | Maninjau st.1 | 98 | 165 | 459 | 100.2234 | −0.2879 | 21 July 2011 | 0.90 |
| 6 | Maninjau st.2 | 100.2173 | −0.2879 | 0.97 | ||||
| 7 | Maninjau st.3 | 100.2234 | −0.2879 | 0.91 | ||||
| 8 | Saguling st.1 | 53 | 99 | 645 | 107.4828 | −6.9133 | 18 July 2012 | 0.94 |
| 9 | Saguling st.2 | 107.4948 | −6.9177 | 0.86 | ||||
| 10 | Saguling st.3 | 107.5349 | −6.9333 | 0.88 | ||||
| 11 | Saguling st.4 | 107.5546 | −6.9025 | 0.79 | ||||
| 12 | Tondano st.1 | 50 | 20 | 600 | 124.8862 | 1.2268 | 18 March 2013 | 2.80 |
| 13 | Tondano st.2 | 124.8857 | 1.2165 | 2.80 | ||||
| 14 | Tondano st.3 | 124.8997 | 1.2461 | 2.90 | ||||
| 15 | Tondano st.4 | 124.9034 | 1.2560 | 2.60 | ||||
| 16 | Limboto st.1 | 56 | 3 | 25 | 122.9897 | 0.5877 | 20 March 2013 | 0.48 |
| 17 | Limboto st.2 | 122.9797 | 0.5910 | 0.46 | ||||
| 18 | Limboto st.3 | 122.9929 | 0.5634 | 0.55 | ||||
| 19 | Toba st.1 | 1124 | 529 | 905 | 98.6586 | 2.7674 | 19 March 2014 | 6.54 |
| 20 | Toba st.2 | 98.9271 | 2.4147 | 6.50 | ||||
| 21 | Toba st.3 | 98.9611 | 2.4410 | 6.22 | ||||
| 22 | Jatiluhur st.1 | 83 | 105 | 111 | 107.3665 | −6.5260 | 15 July 2014 | 1.37 |
| 23 | Jatiluhur st.2 | 107.3236 | −6.5393 | 1.83 | ||||
| 24 | Jatiluhur st.3 | 107.3024 | −6.5805 | 1.74 | ||||
| 25 | Jatiluhur st.4 | 107.3297 | −6.5139 | 1.71 | ||||
| 26 | Matano st.1 | 164 | 590 | 382 | 121.3001 | −2.4843 | 7 October 2014 | 15.10 |
| 27 | Matano st.2 | 121.3690 | −2.4943 | 18.60 | ||||
| 28 | Matano st.3 | 121.4154 | −2.5179 | 16.90 | ||||
| 29 | Towuti st.1 | 561 | 203 | 293 | 121.5430 | −2.6990 | 8 October 2014 | 15.30 |
| 30 | Towuti st.2 | 121.5104 | −2.7989 | 17.10 | ||||
| 31 | Towuti st.3 | 121.4607 | −2.8633 | 12.40 | ||||
| No | Acquisition Date | Path | Row | Sensor | Lake/Reservoir | Days between Satellite and Field Data |
|---|---|---|---|---|---|---|
| 1 | 6 July 2011 | 127 | 60 | 5 TM | Singkarak and Maninjau | –14 days and –15 days |
| 2 | 29 July 2012 | 122 | 65 | 7 ETM+ | Saguling | 11 days |
| 3 | 13 March 2013 | 111 | 59 | 7 ETM+ | Tondano | 5 days |
| 4 | 27 March 2013 | 113 | 60 | 7 ETM+ | Limboto | 7 days |
| 5 | 30 March 2014 | 129 | 58 | 7 ETM+ | Toba | 11 days |
| 6 | 19 July 2014 | 122 | 65 | 7 ETM+ | Jatiluhur | 3 days |
| 7 | 8 October 2014 | 113 | 62 | 7 ETM+ | Matano and Towuti | 1 day and same day |
| No. | Acquisition Date | Sensor | Days between Satellite and Field Data |
|---|---|---|---|
| 1 | 31 May 2001 | 7 ETM+ | Within 30 days |
| 2 | 18 May 2002 | 7 ETM+ | Within 30 days |
| 3 | 3 June 2005 | 5 TM | Within 30 days |
| 4 | 4 December 2005 | 7 ETM+ | Within 30 days |
| 5 | 29 May 2006 | 7 ETM+ | Within 30 days |
| 6 | 17 August 2006 | 7 ETM+ | Within 30 days |
| 7 | 24 May 2007 | 5 TM | Within 30 days |
| 8 | 3 July 2007 | 7 ETM+ | Within 30 days |
| 9 | 14 August 2008 | 5 TM | Within 30 days |
| 10 | 29 May 2009 | 5 TM | Within 30 days |
| 11 | 25 August 2009 | 7 ETM+ | Within 30 days |
| 12 | 19 November 2011 | 7 ETM+ | Within 30 days |
| 13 | 26 March 2012 | 7 ETM+ | Within 30 days |
| 14 | 13 March 2013 | 7 ETM+ | Within 30 days |
| 15 | 1 April 2014 | 7 ETM+ | 20 days |
| 16 | 8 March 2017 | 7 ETM+ | –9 days |
| 17 | 12 June 2017 | 7 ETM+ | Same day |
| 18 | 6 January 2018 | 7 ETM+ | –9 days |
| 19 | 28 April 2018 | 7 ETM+ | Same day |
| 20 | 17 July 2018 | 7 ETM+ | –2 days |
| 21 | 19 September 2018 | 7 ETM+ | Same day |
| Variable | Name | ln (SD) = | R2 | WIA * | NSME ** | RMSE (m) | MNB (%) | NMAE (%) |
|---|---|---|---|---|---|---|---|---|
| Single band | 1 | –0.04 + 29.35(TM1) | 0.02 | 0.39 | –0.17 | 6.6 | 89.7 | 140.5 |
| 2 | 2.77 – 47.99(TM2) | 0.32 | 0.44 | 0.07 | 5.9 | 58.8 | 111.0 | |
| 3 | 2.24 – 53.91(TM3) | 0.33 | 0.45 | 0.06 | 5.9 | 55.2 | 107.5 | |
| Band ratio | A | –2.45 + 1.81(TM1/TM3) | 0.97 | 0.98 | 0.93 | 1.6 | 10.1 | 34.7 |
| B | –3.29 + 3.93(TM1/TM2) | 0.91 | 0.96 | 0.88 | 2.1 | 16.6 | 50.7 | |
| C | –5.77 + 3.95(TM2/TM3) | 0.27 | 0.53 | 0.16 | 5.6 | 43.2 | 86.9 | |
| D | 3.33 – 3.88(TM3/TM1) | 0.78 | 0.69 | 0.43 | 4.6 | 29.3 | 74.5 | |
| E | 4.55 – 3.60(TM2/TM1) | 0.85 | 0.80 | 0.57 | 4.0 | 28.2 | 68.3 | |
| F | 6.97 – 10.07(TM3/TM2) | 0.29 | 0.49 | 0.14 | 5.6 | 45.7 | 91.1 | |
| Band ratio and single band | A1 | –4.36 + 1.87(TM1/TM3) + 49.01(TM1) | 0.99 | 1.00 | 0.98 | 0.8 | 4.4 | 25.0 |
| A2 | –4.48 + 2.33TM1/TM3) + 28.22(TM2) | 0.98 | 1.00 | 0.98 | 0.8 | 5.4 | 24.3 | |
| A3 | –3.85 + 2.24(TM1/TM3) + 25.83(TM3) | 0.98 | 0.99 | 0.98 | 0.9 | 6.6 | 27.2 | |
| B1 | –4.43 + 3.94(TM1/TM2) + 30.99(TM1) | 0.92 | 0.97 | 0.90 | 1.9 | 12.5 | 46.7 | |
| B2 | –4.47 + 4.52(TM1/TM2) + 14.93(TM2) | 0.92 | 0.97 | 0.90 | 1.9 | 13.9 | 49.4 | |
| B3 | –3.71 + 4.18(TM1/TM2) + 7.18(TM3) | 0.91 | 0.97 | 0.89 | 2.0 | 15.8 | 50.3 | |
| C1 | –13.60 + 5.85(TM2/TM3) + 124.11(TM1) | 0.54 | 0.81 | 0.52 | 4.2 | 15.8 | 56.6 | |
| C2 | –4.17 + 3.28(TM2/TM3) – 12.07(TM2) | 0.34 | 0.53 | 0.18 | 5.5 | 42.9 | 88.9 | |
| C3 | –4.80 + 3.49(TM2/TM3) – 8.40(TM3) | 0.30 | 0.52 | 0.17 | 5.6 | 43.3 | 88.2 | |
| D1 | 0.21 – 4.84(TM3/TM1) + 100.49(TM1) | 0.93 | 0.92 | 0.79 | 2.8 | 8.2 | 34.5 | |
| D2 | 4.53 – 11.87(TM3/TM1) + 146.26(TM2) | 0.94 | 0.89 | 0.74 | 3.1 | 17.5 | 50.5 | |
| D3 | 4.27 – 10.20(TM3/TM1) + 125.67(TM3) | 0.93 | 0.92 | 0.78 | 2.8 | 9.8 | 36.8 | |
| E1 | 2.75 – 3.78(TM2/TM1) + 53.86(TM1) | 0.90 | 0.89 | 0.72 | 3.2 | 17.4 | 53.4 | |
| E2 | 4.80 – 5.10(TM2/TM1) + 33.83(TM2) | 0.89 | 0.86 | 0.68 | 3.4 | 21.0 | 57.0 | |
| E3 | 4.90 – 4.47(TM2/TM1) + 22.52(TM3) | 0.87 | 0.84 | 0.64 | 3.7 | 25.4 | 63.9 | |
| F1 | 5.46 – 16.59(TM3/TM2) + 146.02(TM1) | 0.68 | 0.86 | 0.64 | 3.6 | 10.3 | 42.9 | |
| F2 | 6.63 – 9.10(TM3/TM2) – 6.16(TM2) | 0.33 | 0.49 | 0.15 | 5.6 | 45.5 | 92.3 | |
| F3 | 7.11 – 10.37(TM3/TM2) + 2.01(TM3) | 0.29 | 0.49 | 0.14 | 5.6 | 45.7 | 90.9 | |
| Two band ratios | AB | –2.49 + 1.76(TM1/TM3) + 0.12(TM1/TM2) | 0.97 | 0.98 | 0.93 | 1.6 | 10.2 | 34.6 |
| AC | –1.80 + 1.95(TM1/TM3) – 0.53(TM2/TM3) | 0.97 | 0.98 | 0.94 | 1.4 | 10.2 | 34.3 | |
| AD | –4.34 + 2.35(TM1/TM3) + 1.45(TM3/TM1) | 0.98 | 0.99 | 0.97 | 1.0 | 8.1 | 26.4 | |
| AE | –4.17 + 2.22(TM1/TM3) + 0.96(TM2/TM1) | 0.97 | 0.99 | 0.95 | 1.3 | 8.6 | 30.5 | |
| AF | –3.94 + 2.00(TM1/TM3) + 1.89(TM3/TM2) | 0.97 | 0.99 | 0.95 | 1.3 | 9.9 | 33.7 | |
| BC | –4.84 + 3.37(TM1/TM2) + 1.26(TM2/TM3) | 0.96 | 0.96 | 0.89 | 2.0 | 13.0 | 42.0 | |
| BD | –3.05 + 3.80(TM1/TM2) – 0.16(TM3/TM1) | 0.92 | 0.96 | 0.87 | 2.2 | 16.7 | 51.1 | |
| BE | –6.78 + 5.60(TM1/TM2) + 1.70(TM2/TM1) | 0.91 | 0.97 | 0.90 | 1.9 | 14.2 | 48.8 | |
| BF | –1.18 + 3.45(TM1/TM2) – 2.67(TM3/TM2) | 0.95 | 0.96 | 0.88 | 2.1 | 14.4 | 45.2 | |
| CD | 2.53 + 0.38(TM2/TM3) – 3.62(TM3/TM1) | 0.77 | 0.69 | 0.43 | 4.6 | 28.6 | 73.8 | |
| CE | 1.48 + 1.41(TM2/TM3) – 2.94(TM2/TM1) | 0.86 | 0.81 | 0.60 | 3.9 | 22.3 | 60.8 | |
| CF | –10.31 + 5.34(TM2/TM3) + 3.64(TM3/TM2) | 0.26 | 0.53 | 0.16 | 5.6 | 42.6 | 86.6 | |
| DE | 4.49 – 0.28(TM3/TM1) – 3.36(TM2/TM1) | 0.85 | 0.80 | 0.57 | 4.0 | 28.0 | 67.9 | |
| DF | 2.72 – 4.27(TM3/TM1) + 1.43(TM3/TM2) | 0.79 | 0.69 | 0.43 | 4.6 | 29.9 | 74.4 | |
| EF | 5.65 – 3.07(TM2/TM1) – 2.74(TM3/TM2) | 0.87 | 0.80 | 0.58 | 3.9 | 24.7 | 64.1 |
| Name | ln (SD) = | R2 | WIA * | NSME ** | RMSE (m) | MNB (%) | NMAE (%) |
|---|---|---|---|---|---|---|---|
| A | –2.45 + 1.81(TM1/TM3) | 0.42 | 0.68 | –0.88 | 1.83 | 83.46 | 89.83 |
| A1 | –4.36 + 1.87(TM1/TM3) + 49.01(TM1) | 0.34 | 0.65 | –1.29 | 2.02 | 45.98 | 63.67 |
| A2 | –4.48 + 2.33TM1/TM3) + 28.22(TM2) | 0.39 | 0.66 | –1.35 | 2.05 | 61.35 | 73.23 |
| A3 | –3.85 + 2.24(TM1/TM3) + 25.83(TM3) | 0.44 | 0.72 | –0.61 | 1.70 | 57.25 | 69.72 |
| AB | –2.49 + 1.76(TM1/TM3) + 0.12(TM1/TM2) | 0.32 | 0.62 | –1.24 | 2.00 | 98.44 | 106.40 |
| AC | –1.80 + 1.95(TM1/TM3) – 0.53(TM2/TM3) | 0.36 | 0.69 | –0.52 | 1.65 | 81.22 | 93.08 |
| AD | –4.34 + 2.35(TM1/TM3) + 1.45(TM3/TM1) | 0.32 | 0.63 | –1.37 | 2.06 | 88.98 | 99.28 |
| AE | –4.17 + 2.22(TM1/TM3) + 0.96(TM2/TM1) | 0.25 | 0.54 | –2.63 | 2.55 | 115.41 | 122.65 |
| AF | –3.94 + 2.00(TM1/TM3) + 1.89(TM3/TM2) | 0.36 | 0.69 | –0.51 | 1.64 | 76.59 | 90.17 |
| B | –3.29 + 3.93(TM1/TM2) | 0.54 | 0.83 | 0.53 | 0.92 | 30.67 | 54.19 |
| B1 | –4.43 + 3.94(TM1/TM2) + 30.99(TM1) | 0.35 | 0.76 | 0.16 | 1.23 | 13.44 | 48.66 |
| B2 | –4.47 + 4.52(TM1/TM2) + 14.93(TM2) | 0.48 | 0.82 | 0.46 | 0.98 | 14.80 | 45.81 |
| B3 | –3.71 + 4.18(TM1/TM2) + 7.18(TM3) | 0.52 | 0.83 | 0.52 | 0.93 | 22.72 | 50.20 |
| BC | –4.84 + 3.37(TM1/TM2) + 1.26(TM2/TM3) | 0.40 | 0.71 | –0.29 | 1.52 | 84.90 | 92.43 |
| BD | –3.05 + 3.80(TM1/TM2) – 0.16(TM3/TM1) | 0.54 | 0.83 | 0.53 | 0.92 | 33.19 | 55.38 |
| BE | –6.78 + 5.60(TM1/TM2) + 1.70(TM2/TM1) | 0.38 | 0.76 | 0.37 | 1.07 | 26.62 | 55.97 |
| BF | –1.18 + 3.45(TM1/TM2) – 2.67(TM3/TM2) | 0.60 | 0.83 | 0.43 | 1.01 | 56.47 | 67.43 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Setiawan, F.; Matsushita, B.; Hamzah, R.; Jiang, D.; Fukushima, T. Long-Term Change of the Secchi Disk Depth in Lake Maninjau, Indonesia Shown by Landsat TM and ETM+ Data. Remote Sens. 2019, 11, 2875. https://doi.org/10.3390/rs11232875
Setiawan F, Matsushita B, Hamzah R, Jiang D, Fukushima T. Long-Term Change of the Secchi Disk Depth in Lake Maninjau, Indonesia Shown by Landsat TM and ETM+ Data. Remote Sensing. 2019; 11(23):2875. https://doi.org/10.3390/rs11232875
Chicago/Turabian StyleSetiawan, Fajar, Bunkei Matsushita, Rossi Hamzah, Dalin Jiang, and Takehiko Fukushima. 2019. "Long-Term Change of the Secchi Disk Depth in Lake Maninjau, Indonesia Shown by Landsat TM and ETM+ Data" Remote Sensing 11, no. 23: 2875. https://doi.org/10.3390/rs11232875
APA StyleSetiawan, F., Matsushita, B., Hamzah, R., Jiang, D., & Fukushima, T. (2019). Long-Term Change of the Secchi Disk Depth in Lake Maninjau, Indonesia Shown by Landsat TM and ETM+ Data. Remote Sensing, 11(23), 2875. https://doi.org/10.3390/rs11232875