Monitoring Within-Field Variability of Corn Yield using Sentinel-2 and Machine Learning Techniques
Abstract
1. Introduction
- (1)
- to examine different vegetation indices for corn yield estimation;
- (2)
- to define the suitable crop age for predicting yield variability within the field scale;
- (3)
- to develop a corn yield prediction model based on Sentinel-2 images and the best performing machine learning technique and compare the results with VIs.
2. Materials and Methods
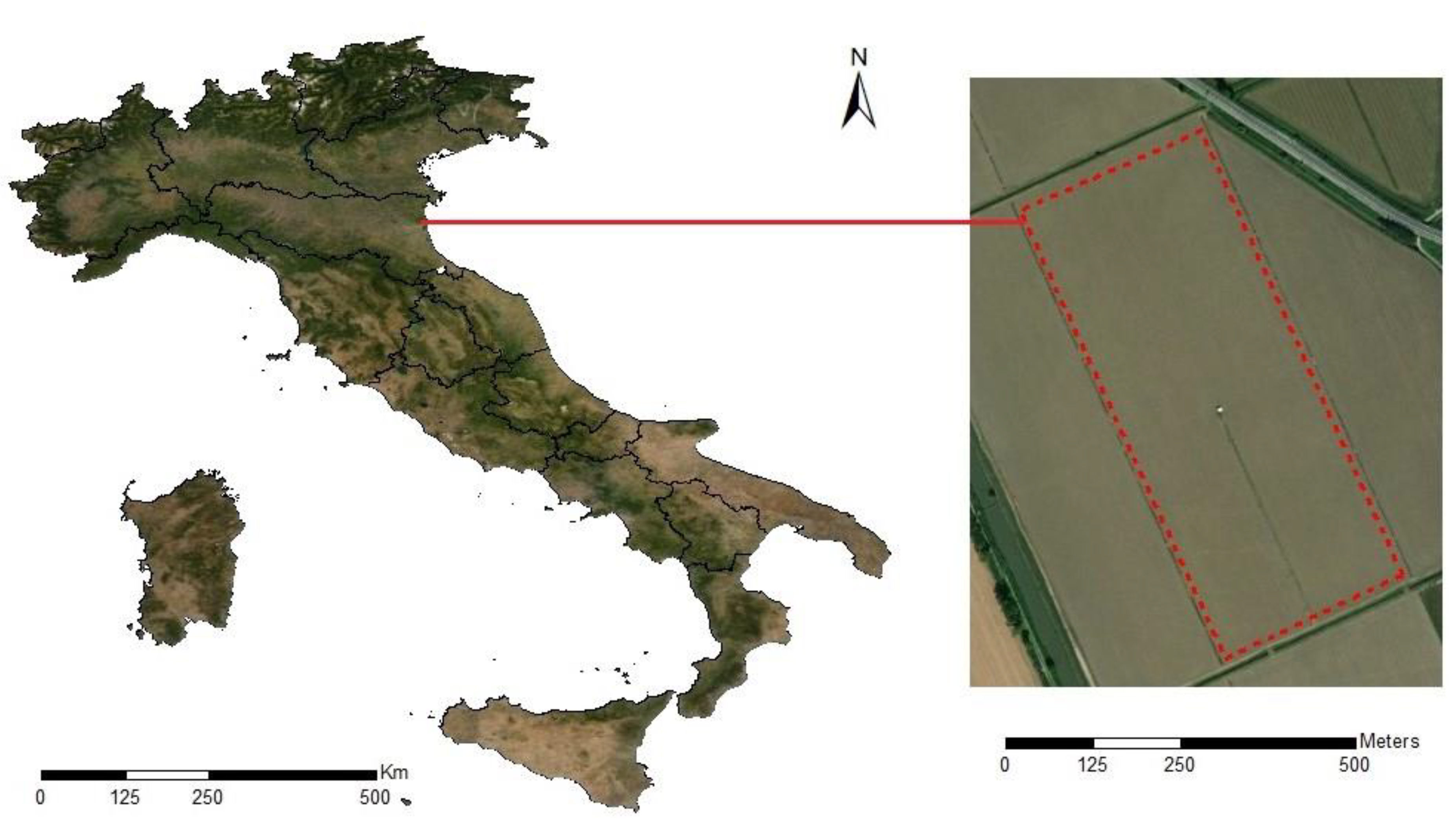
2.1. Study Area
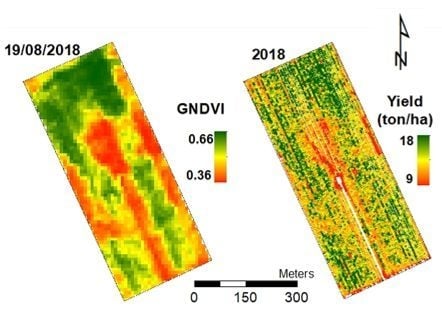
2.2. Measured Yield Data
2.3. Satellite Imagery
2.4. Vegetation Indices
2.5. Yield Prediction with Machine Learning
3. Results
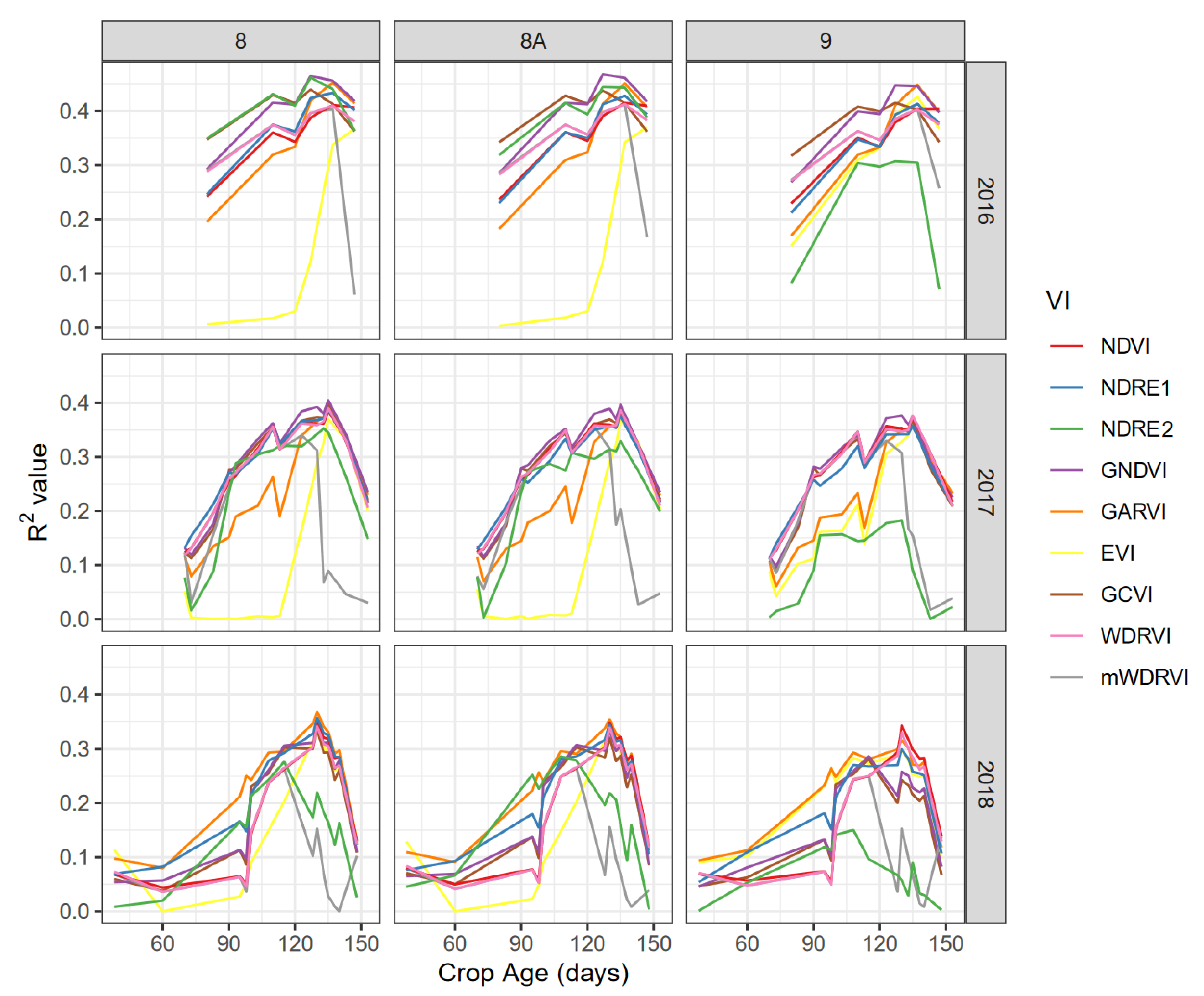
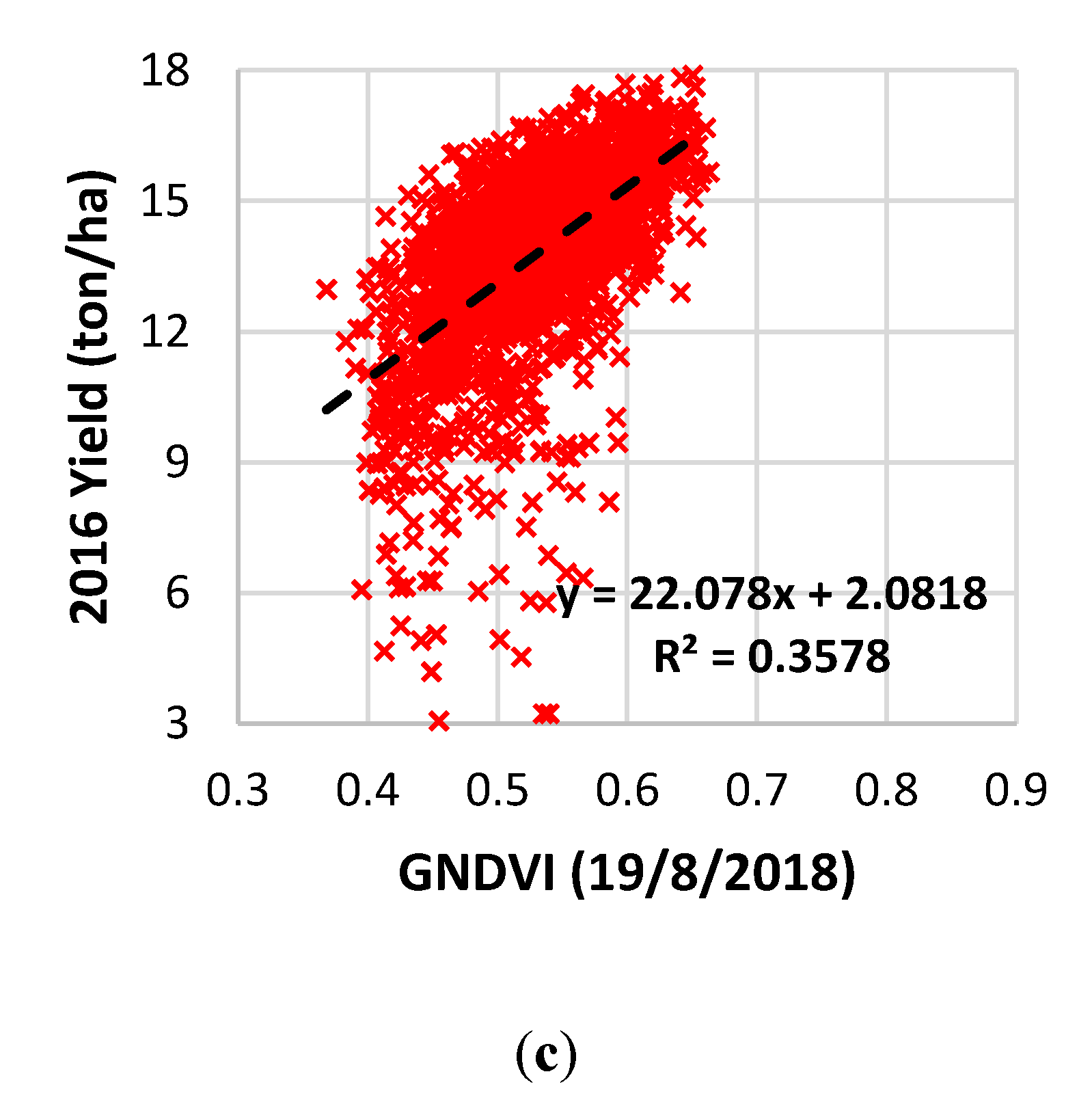
3.1. Vegetation Indices
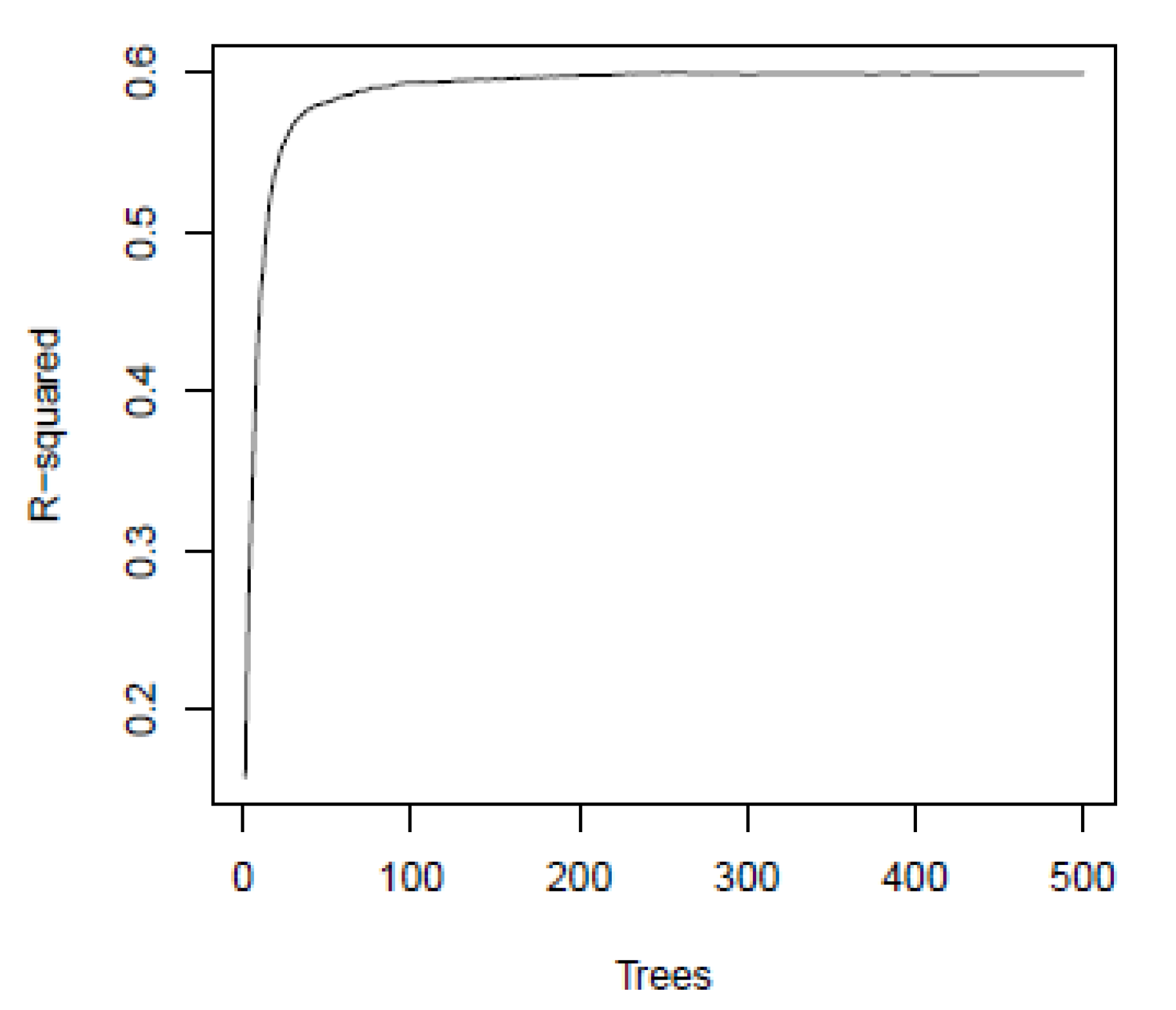
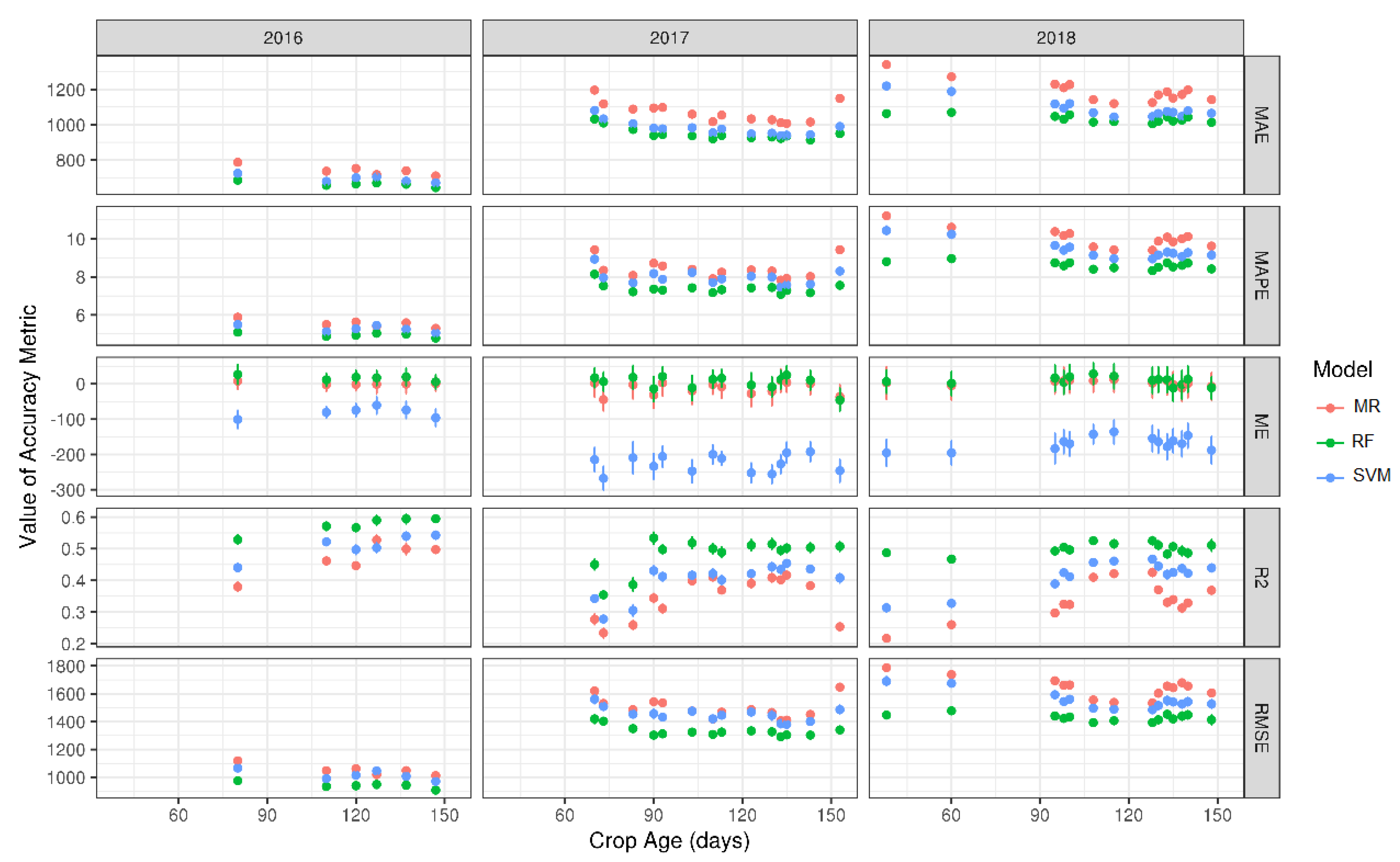
3.2. Machine Learning Models
4. Discussion
5. Conclusions
- -
- GNDVI was the most correlated VI with corn grain yield at the field scale;
- -
- the most suitable time for corn yield forecasting was during the physiological maturity stages (R4–R6) between 105 and 135 days from the planting date, i.e., between mid-July and mid-August;
- -
- this period is not only the most correlated, but also is provides a higher number of satellite images due to reduced cloud events in the area considered;
- -
- Random Forests was the most accurate machine learning technique in corn yield monitoring with R2 values almost reaching 0.6 in an independent validation set;
- -
- the Random Forests method works best when trained with imagery close to the above-mentioned most suitable time for forecasting; applying it to images at different crop stages is not advised.
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Ross, K.W.; Morris, D.K.; Johannsen, C.J. A Review of Intra-Field Yield Estimation from Yield Monitor Data. Appl. Eng. Agric. 2008, 24, 309–317. [Google Scholar] [CrossRef]
- Trotter, T.F.; Fraizer, P.S.; Mark, G.T.; David, W.L. Objective Biomass Assessment Using an Active Plant Sensor (Crop circletm)—Preliminary Experiences on a Variety of Agricultural Landscapes. In Proceedings of the 9th International Conference on Precision Agriculture (ICPA), Denver, CO, USA, 20–23 July 2008. [Google Scholar]
- Pezzuolo, A.; Basso, B.; Marinello, F.; Sartori, L. Using SALUS model for medium and long term simulations of energy efficiency in different tillage systems. Appl. Math. Sci. 2014, 8, 6433–6445. [Google Scholar] [CrossRef]
- Al-Gaadi, K.A.; Hassaballa, A.A.; Tola, E.; Kayad, A.; Madugundu, R.; Assiri, F.; Alblewi, B. Characterization of the spatial variability of surface topography and moisture content and its influence on potato crop yield. Int. J. Remote Sens. 2018, 39, 8572–8590. [Google Scholar] [CrossRef]
- Lobell, D.B.; Thau, D.; Seifert, C.; Engle, E.; Little, B. A scalable satellite-based crop yield mapper. Remote Sens. Environ. 2015, 164, 324–333. [Google Scholar] [CrossRef]
- Kross, A.; McNairn, H.; Lapen, D.; Sunohara, M.; Champagne, C. Assessment of RapidEye vegetation indices for estimation of leaf area index and biomass in corn and soybean crops. Int. J. Appl. Earth Obs. Geoinf. 2015, 34, 235–248. [Google Scholar] [CrossRef]
- Blackmore, S. The Role of Yield Maps in Precision Farming. Ph.D. Thesis, Cranfiled University at Silsoe, Cranfiled, UK, 2003. [Google Scholar]
- Bouman, B.M. Crop modelling and remote sensing for yield prediction. Neth. J. Agric. Sci. 1995, 43, 143–161. [Google Scholar]
- Yao, F.; Tang, Y.; Wang, P.; Zhang, J. Estimation of maize yield by using a process-based model and remote sensing data in the Northeast China Plain. Phys. Chem. Earth 2015, 87–88, 142–152. [Google Scholar] [CrossRef]
- Huang, Y.; Zhu, Y.; Li, W.; Cao, W.; Tian, Y. Assimilating Remotely Sensed Information with the WheatGrow Model Based on the Ensemble Square Root Filter forImproving Regional Wheat Yield Forecasts. Plant Prod. Sci. 2013, 16, 352–364. [Google Scholar] [CrossRef]
- Morel, J.; Todoroff, P.; Bégué, A.; Bury, A.; Martiné, J.F.; Petit, M. Toward a satellite-based system of sugarcane yield estimation and forecasting in smallholder farming conditions: A case study on reunion island. Remote Sens. 2014, 6, 6620–6635. [Google Scholar] [CrossRef]
- Bala, S.K.; Islam, A.S. Correlation between potato yield and MODIS-derived vegetation indices. Int. J. Remote Sens. 2009, 30, 2491–2507. [Google Scholar] [CrossRef]
- Mkhabela, M.S.; Bullock, P.; Raj, S.; Wang, S.; Yang, Y. Crop yield forecasting on the Canadian Prairies using MODIS NDVI data. Agric. For. Meteorol. 2011, 151, 385–393. [Google Scholar] [CrossRef]
- Gao, F.; Anderson, M.; Daughtry, C.; Johnson, D. Assessing the variability of corn and soybean yields in central Iowa using high spatiotemporal resolution multi-satellite imagery. Remote Sens. 2018, 10, 1489. [Google Scholar] [CrossRef]
- Lobell, D.B.; Ortiz-Monasterio, J.I.; Asner, G.P.; Naylor, R.L.; Falcon, W.P. Combining field surveys, remote sensing, and regression trees to understand yield variations in an irrigated wheat landscape. Agron. J. 2005, 97, 241–249. [Google Scholar]
- Kayad, A.G.; Al-Gaadi, K.A.; Tola, E.; Madugundu, R.; Zeyada, A.M.; Kalaitzidis, C. Assessing the spatial variability of alfalfa yield using satellite imagery and ground-based data. PLoS ONE 2016, 11, e0157166. [Google Scholar] [CrossRef]
- Al-Gaadi, K.A.; Hassaballa, A.A.; Tola, E.; Kayad, A.; Madugundu, R.; Alblewi, B.; Assiri, F. Prediction of potato crop yield using precision agriculture techniques. PLoS ONE 2016, 11, e0162219. [Google Scholar] [CrossRef]
- Peralta, N.R.; Assefa, Y.; Du, J.; Barden, C.J.; Ciampitti, I.A. Mid-season high-resolution satellite imagery for forecasting site-specific corn yield. Remote Sens. 2016, 8, 848. [Google Scholar] [CrossRef]
- Schwalbert, R.A.; Amado, T.J.C.; Nieto, L.; Varela, S.; Corassa, G.M.; Horbe, T.A.N.; Rice, C.W.; Peralta, N.R.; Ciampitti, I.A. Forecasting maize yield at field scale based on high-resolution satellite imagery. Biosyst. Eng. 2018, 171, 179–192. [Google Scholar] [CrossRef]
- Asrar, G.; Kanemasu, E.T.; Yoshida, M. Estimates of leaf area index from spectral reflectance of wheat under different cultural practices and solar angle. Remote Sens. Environ. 1985, 17, 1–11. [Google Scholar] [CrossRef]
- Patel, N.K.; Patnaik, C.; Dutta, S.; Shekh, A.M.; Dave, A.J. Study of crop growth parameters using Airborne Imaging Spectrometer data. Int. J. Remote Sens. 2001, 22, 2401–2411. [Google Scholar] [CrossRef]
- Tucker, C.J.; Holben, B.N.; Elgin, J.H.; McMurtrey, J.E. Remote sensing of total dry-matter accumulation in winter wheat. Remote Sens. Environ. 1981, 11, 171–189. [Google Scholar] [CrossRef]
- Ferencz, C.; Bognár, P.; Lichtenberger, J.; Hamar, D.; Tarcsai, G.; Timár, G.; Molnár, G.; Pásztor, S.; Steinbach, P.; Székely, B.; et al. Crop yield estimation by satellite remote sensing. Int. J. Remote Sens. 2004, 25, 4113–4149. [Google Scholar] [CrossRef]
- Sibley, A.M.; Grassini, P.; Thomas, N.E.; Cassman, K.G.; Lobell, D.B. Testing remote sensing approaches for assessing yield variability among maize fields. Agron. J. 2014, 106, 24–32. [Google Scholar] [CrossRef]
- Dubbini, M.; Pezzuolo, A.; De Giglio, M.; Gattelli, M.; Curzio, L.; Covi, D.; Yezekyan, T.; Marinello, F. Last generation instrument for agriculture multispectral data collection. Agric. Eng. Int. CIGR J. 2017, 19, 87–93. [Google Scholar]
- Báez-González, A.D.; Chen, P.; Tiscareño-López, M.; Srinivasan, R. Using Satellite and Field Data with Crop Growth Modeling to Monitor and Estimate Corn Yield in Mexico. Crop Sci. 2002, 42, 1943–1949. [Google Scholar] [CrossRef]
- Lobell, D.B. The use of satellite data for crop yield gap analysis. Field Crop. Res. 2013, 143, 56–64. [Google Scholar] [CrossRef]
- Tucker, C.J. Red and photographic infrared linear combinations for monitoring vegetation. Remote Sens. Environ. 1979, 8, 127–150. [Google Scholar] [CrossRef]
- Huete, A.R. A soil-adjusted vegetation index (SAVI). Remote Sens. Environ. 1988, 25, 295–309. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Kaufman, Y.J.; Merzlyak, M.N. Use of a green channel in remote sensing of global vegetation from EOS- MODIS. Remote Sens. Environ. 1996, 58, 289–298. [Google Scholar] [CrossRef]
- Panda, S.S.; Ames, D.P.; Panigrahi, S. Application of vegetation indices for agricultural crop yield prediction using neural network techniques. Remote Sens. 2010, 2, 673–696. [Google Scholar] [CrossRef]
- Xue, J.; Su, B. Significant Remote Sensing Vegetation Indices: A Review of Developments and Applications. J. Sensors 2017, 2017, 1–17. [Google Scholar] [CrossRef]
- Sakamoto, T.; Gitelson, A.A.; Wardlow, B.D.; Verma, S.B.; Suyker, A.E. Estimating daily gross primary production of maize based only on MODIS WDRVI and shortwave radiation data. Remote Sens. Environ. 2011, 115, 3091–3101. [Google Scholar] [CrossRef]
- Sakamoto, T.; Gitelson, A.A.; Arkebauer, T.J. MODIS-based corn grain yield estimation model incorporating crop phenology information. Remote Sens. Environ. 2013, 131, 215–231. [Google Scholar] [CrossRef]
- Burke, M.; Lobell, D.B. Satellite-based assessment of yield variation and its determinants in smallholder African systems. Proc. Natl. Acad. Sci. USA 2017, 114, 2189–2194. [Google Scholar] [CrossRef] [PubMed]
- Bu, H.; Sharma, L.K.; Denton, A.; Franzen, D.W. Comparison of satellite imagery and ground-based active optical sensors as yield predictors in sugar beet, spring wheat, corn, and sunflower. Agron. J. 2017, 109, 299–308. [Google Scholar] [CrossRef]
- Liao, C.; Wang, J.; Dong, T.; Shang, J.; Liu, J.; Song, Y. Using spatio-temporal fusion of Landsat-8 and MODIS data to derive phenology, biomass and yield estimates for corn and soybean. Sci. Total Environ. 2019, 650, 1707–1721. [Google Scholar] [CrossRef]
- Fieuzal, R.; Marais Sicre, C.; Baup, F. Estimation of corn yield using multi-temporal optical and radar satellite data and artificial neural networks. Int. J. Appl. Earth Obs. Geoinf. 2016, 57, 14–23. [Google Scholar] [CrossRef]
- Rojas, O. Operational maize yield model development and validation based on remote sensing and agro-meteorological data in Kenya. Int. J. Remote Sens. 2007, 28, 3775–3793. [Google Scholar] [CrossRef]
- Maestrini, B.; Basso, B. Predicting spatial patterns of within-field crop yield variability. F. Crop. Res. 2018, 219, 106–112. [Google Scholar] [CrossRef]
- Shanahan, J.F.; Schepers, J.S.; Francis, D.D.; Varvel, G.E.; Wilhelm, W.W.; Tringe, J.M.; Schlemmer, M.R.; Major, D.J. Use of remote-sensing imagery to estimate corn grain yield. Agron. J. 2001, 93, 583–589. [Google Scholar] [CrossRef]
- Bognár, P.; Ferencz, C.; Pásztor, S.Z.; Molnár, G.; Timár, G.; Hamar, D.; Lichtenberger, J.; Székely, B.; Steinbach, P.; Ferencz, O.E. Yield forecasting for wheat and corn in Hungary by satellite remote sensing. Int. J. Remote Sens. 2011, 32, 4759–4767. [Google Scholar] [CrossRef]
- Rahman, M.M.; Robson, A.; Bristow, M. Exploring the potential of high resolution worldview-3 Imagery for estimating yield of mango. Remote Sens. 2018, 10, 1866. [Google Scholar] [CrossRef]
- Mas, J.F.; Flores, J.J. The application of artificial neural networks to the analysis of remotely sensed data. Int. J. Remote Sens. 2008, 29, 617–663. [Google Scholar] [CrossRef]
- Yuan, H.; Yang, G.; Li, C.; Wang, Y.; Liu, J.; Yu, H.; Feng, H.; Xu, B.; Zhao, X.; Yang, X. Retrieving soybean leaf area index from unmanned aerial vehicle hyperspectral remote sensing: Analysis of RF, ANN, and SVM regression models. Remote Sens. 2017, 9, 309. [Google Scholar] [CrossRef]
- Russell, S.; Norvig, P. Artificial Intelligence A Modern Approach, 3rd ed.; Prentice Hall: Upper Saddle River, NJ, USA, 2010; ISBN 9780136042594. [Google Scholar]
- Liakos, K.G.; Busato, P.; Moshou, D.; Pearson, S.; Bochtis, D. Machine learning in agriculture: A review. Sensors 2018, 18, 2674. [Google Scholar] [CrossRef] [PubMed]
- Ali, I.; Greifeneder, F.; Stamenkovic, J.; Neumann, M.; Notarnicola, C. Review of machine learning approaches for biomass and soil moisture retrievals from remote sensing data. Remote Sens. 2015, 7, 16398–16421. [Google Scholar] [CrossRef]
- Yue, J.; Feng, H.; Yang, G.; Li, Z. A comparison of regression techniques for estimation of above-ground winter wheat biomass using near-surface spectroscopy. Remote Sens. 2018, 10, 66. [Google Scholar] [CrossRef]
- Karimi, Y.; Prasher, S.O.; Patel, R.M.; Kim, S.H. Application of support vector machine technology for weed and nitrogen stress detection in corn. Comput. Electron. Agric. 2006, 51, 99–109. [Google Scholar] [CrossRef]
- Han, L.; Yang, G.; Dai, H.; Xu, B.; Yang, H.; Feng, H.; Li, Z.; Yang, X. Modeling maize above-ground biomass based on machine learning approaches using UAV remote-sensing data. Plant Methods 2019, 15, 1–19. [Google Scholar] [CrossRef]
- EUROSTAT. European Statistics on Agriculture, Forestry and Fisheries. Available online: https://ec.europa.eu/eurostat/data/database (accessed on 5 April 2019).
- Drusch, M.; Del Bello, U.; Carlier, S.; Colin, O.; Fernandez, V.; Gascon, F.; Hoersch, B.; Isola, C.; Laberinti, P.; Martimort, P.; et al. Sentinel-2: ESA’s Optical High-Resolution Mission for GMES Operational Services. Remote Sens. Environ. 2012, 120, 25–36. [Google Scholar] [CrossRef]
- Louis, J. S2 MPC—L2A Product Definition Document. Available online: https://sentinel.esa.int/documents/247904/685211/S2+L2A+Product+Definition+Document/2c0f6d5f-60b5-48de-bc0d-e0f45ca06304 (accessed on 1 December 2019).
- Gitelson, A.A. Wide Dynamic Range Vegetation Index for Remote Quantification of Biophysical Characteristics of Vegetation. J. Plant Physiol. 2004, 161, 165–173. [Google Scholar] [CrossRef]
- Pirotti, F.; Sunar, F.; Piragnolo, M. Benchmark of Machine Learning Methods for Classification of a Sentinel-2 Image. ISPRS Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, XLI-B7, 335–340. [Google Scholar] [CrossRef]
- Piragnolo, M.; Masiero, A.; Pirotti, F. Open source R for applying machine learning to RPAS remote sensing images. Open Geospat. Data Softw. Stand. 2017, 2, 16. [Google Scholar] [CrossRef]
- Kim, N.; Lee, Y.W. Machine learning approaches to corn yield estimation using satellite images and climate data: A case of Iowa State. J. Korean Soc. Surv. Geod. Photogramm. Cartogr. 2016, 34, 383–390. [Google Scholar] [CrossRef]
- Jeong, J.H.; Resop, J.P.; Mueller, N.D.; Fleisher, D.H.; Yun, K.; Butler, E.E.; Timlin, D.J.; Shim, K.M.; Gerber, J.S.; Reddy, V.R.; et al. Random forests for global and regional crop yield predictions. PLoS ONE 2016, 11, e0156571. [Google Scholar] [CrossRef] [PubMed]
- Hunt, M.L.; Blackburn, G.A.; Carrasco, L.; Redhead, J.W.; Rowland, C.S. High resolution wheat yield mapping using Sentinel-2. Remote Sens. Environ. 2019, 233, 111410. [Google Scholar] [CrossRef]
- Cortez, P. Package ‘rminer’. Available online: https://cran.r-project.org/web/packages/rminer/index.html (accessed on 1 December 2019).
- Cortez, P. Package ‘Rminer’; Teaching Report; Department of Information System, ALGORITMI Research Centre, Engineering School: Guimares, Portugal, 2016; p. 59. [Google Scholar]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Tan, C.; Samanta, A.; Jin, X.; Tong, L.; Ma, C.; Guo, W.; Knyazikhin, Y.; Myneni, R.B. Using hyperspectral vegetation indices to estimate the fraction of photosynthetically active radiation absorbed by corn canopies. Int. J. Remote Sens. 2013, 34, 8789–8802. [Google Scholar] [CrossRef]
- Patil, V.C.; Al-Gaadi, K.A.; Madugundu, R.; Tola, E.K.H.M.; Marey, S.A.; Al-Omran, A.M.; Khosla, R.; Upadhyaya, S.K.; Mulla, D.J.; Al-Dosari, A. Delineation of management zones and response of spring wheat (Triticum aestivum) to irrigation and nutrient levels in Saudi Arabia. Int. J. Agric. Biol. 2014, 16, 104–110. [Google Scholar]
- Colaço, A.F.; Bramley, R.G.V. Do crop sensors promote improved nitrogen management in grain crops? Field Crop. Res. 2018, 218, 126–140. [Google Scholar] [CrossRef]
- Mulla, D.J. Twenty five years of remote sensing in precision agriculture: Key advances and remaining knowledge gaps. Biosyst. Eng. 2013, 114, 358–371. [Google Scholar] [CrossRef]
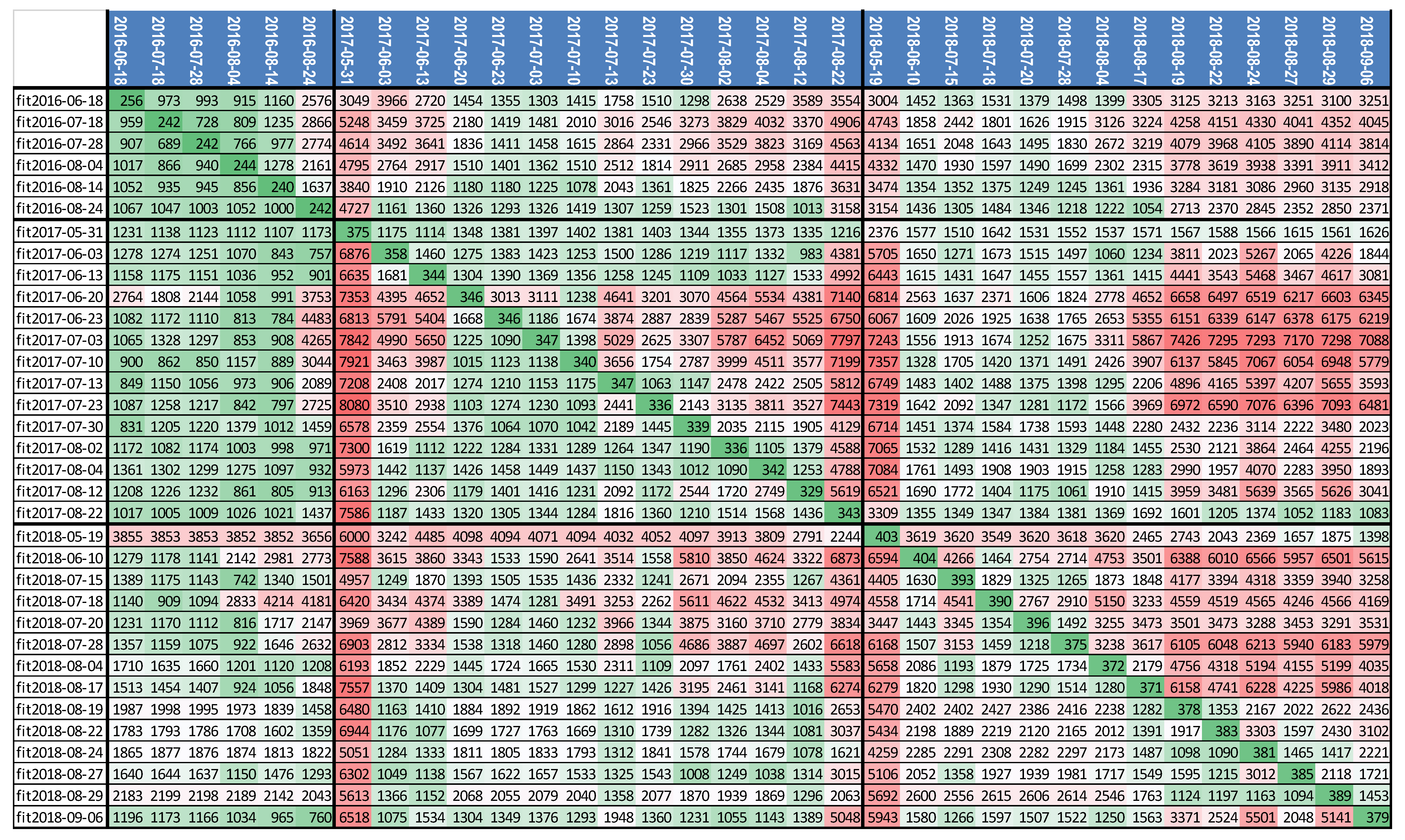
| 2016 Season | 2017 Season | 2018 Season | ||||||
|---|---|---|---|---|---|---|---|---|
| Planting Date: 30 March 2016 | Planting Date: 22 March 2017 | Planting Date: 11 April 2018 | ||||||
| Harvesting Date: 14 September 2016 | Harvesting Date: 25 August 2017 | Harvesting Date: 18 September 2018 | ||||||
| I | Date | Age (Stage) | I | Date | Age (Stage) | I | Date | Age (Stage) |
| 1 | 18 June 2016 | 80 (R3) | 1 | 31 May 2017 | 70 (R2) | 1 | 19 May 2018 | 38 (V10) |
| 2 | 18 July 2016 | 110 (R4) | 2 | 03 June 2017 | 73 (R2) | 2 | 10 June 2018 | 60 (R1) |
| 3 | 28 July 2016 | 120 (R5) | 3 | 13 June 2017 | 83 (R3) | 3 | 15 July 2018 | 95 (R3) |
| 4 | 04 August 2016 | 127 (R6) | 4 | 20 June 2017 | 90 (R3) | 4 | 18 July 2018 | 98 (R4) |
| 5 | 14 August 2016 | 137 (R6) | 5 | 23 June 2017 | 93 (R3) | 5 | 20 July 2018 | 100 (R4) |
| 6 | 24 August 2016 | 147 (R6) | 6 | 03 July 2017 | 103 (R4) | 6 | 28 July 2018 | 108 (R4) |
| 7 | 10 July 2017 | 110 (R4) | 7 | 04 August 2018 | 115 (R6) | |||
| 8 | 13 July 2017 | 113 (R5) | 8 | 17 August 2018 | 128 (R6) | |||
| 9 | 23 July 2017 | 123 (R6) | 9 | 19 August 2018 | 130 (R6) | |||
| 10 | 30 July 2017 | 130 (R6) | 10 | 22 August 2018 | 133 (R6) | |||
| 11 | 02 August 2017 | 133 (R6) | 11 | 24 August 2018 | 135 (R6) | |||
| 12 | 04 August 2017 | 135 (R6) | 12 | 27 August 2018 | 138 (R6) | |||
| 13 | 12 August 2017 | 143 (R6) | 13 | 29 August 2018 | 140 (R6) | |||
| 14 | 22 August 2017 | 153 (R6) | 14 | 06 September 2018 | 148 (R6) | |||
| Cloudy Sky Confidence | ||||
|---|---|---|---|---|
| Image Date | N. Pixels * | Min | Mean | Max |
| 18 June 2016 | 6 | 1 | 1.83 | 2 |
| 18 July 2016 | 4 | 1 | 1.00 | 1 |
| 28 July 2016 | 4 | 1 | 1.00 | 1 |
| 24 August 2016 | 4 | 1 | 1.00 | 1 |
| 31 May 2017 | 70 | 1 | 1.17 | 3 |
| 3 June 2017 | 690 | 1 | 1.08 | 5 |
| 13 June2017 | 619 | 1 | 1.05 | 5 |
| 23 June 2017 | 4 | 2 | 2.00 | 2 |
| 10 July 2017 | 4 | 1 | 1.00 | 1 |
| 13 July 2017 | 4 | 4 | 4.00 | 4 |
| 2 August 2017 | 12 | 1 | 1.00 | 1 |
| 4 August 2017 | 4 | 1 | 1.00 | 1 |
| 12 August 2017 | 4 | 1 | 1.00 | 1 |
| 10 June 2018 | 4 | 3 | 3.00 | 3 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kayad, A.; Sozzi, M.; Gatto, S.; Marinello, F.; Pirotti, F. Monitoring Within-Field Variability of Corn Yield using Sentinel-2 and Machine Learning Techniques. Remote Sens. 2019, 11, 2873. https://doi.org/10.3390/rs11232873
Kayad A, Sozzi M, Gatto S, Marinello F, Pirotti F. Monitoring Within-Field Variability of Corn Yield using Sentinel-2 and Machine Learning Techniques. Remote Sensing. 2019; 11(23):2873. https://doi.org/10.3390/rs11232873
Chicago/Turabian StyleKayad, Ahmed, Marco Sozzi, Simone Gatto, Francesco Marinello, and Francesco Pirotti. 2019. "Monitoring Within-Field Variability of Corn Yield using Sentinel-2 and Machine Learning Techniques" Remote Sensing 11, no. 23: 2873. https://doi.org/10.3390/rs11232873
APA StyleKayad, A., Sozzi, M., Gatto, S., Marinello, F., & Pirotti, F. (2019). Monitoring Within-Field Variability of Corn Yield using Sentinel-2 and Machine Learning Techniques. Remote Sensing, 11(23), 2873. https://doi.org/10.3390/rs11232873