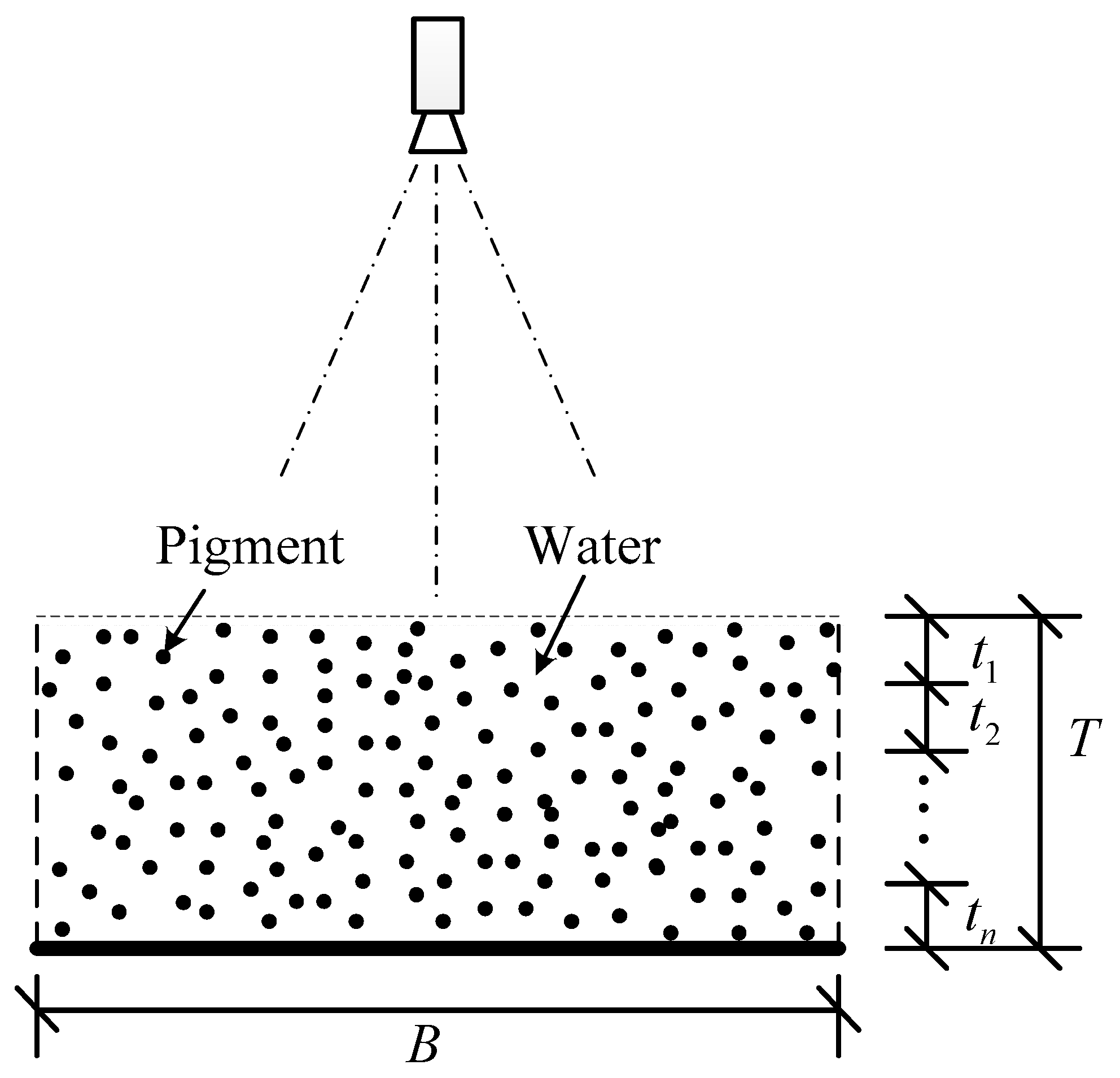
Thickness Measurement of Water Film/Rivulets Based on Grayscale Index
Abstract
1. Introduction
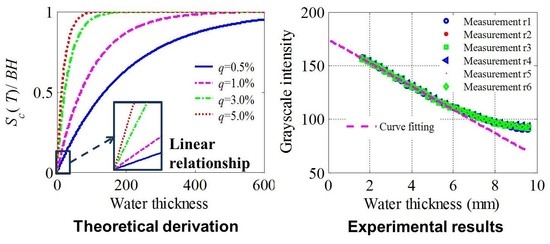
2. Theoretical Analysis
3. Experimental Validation
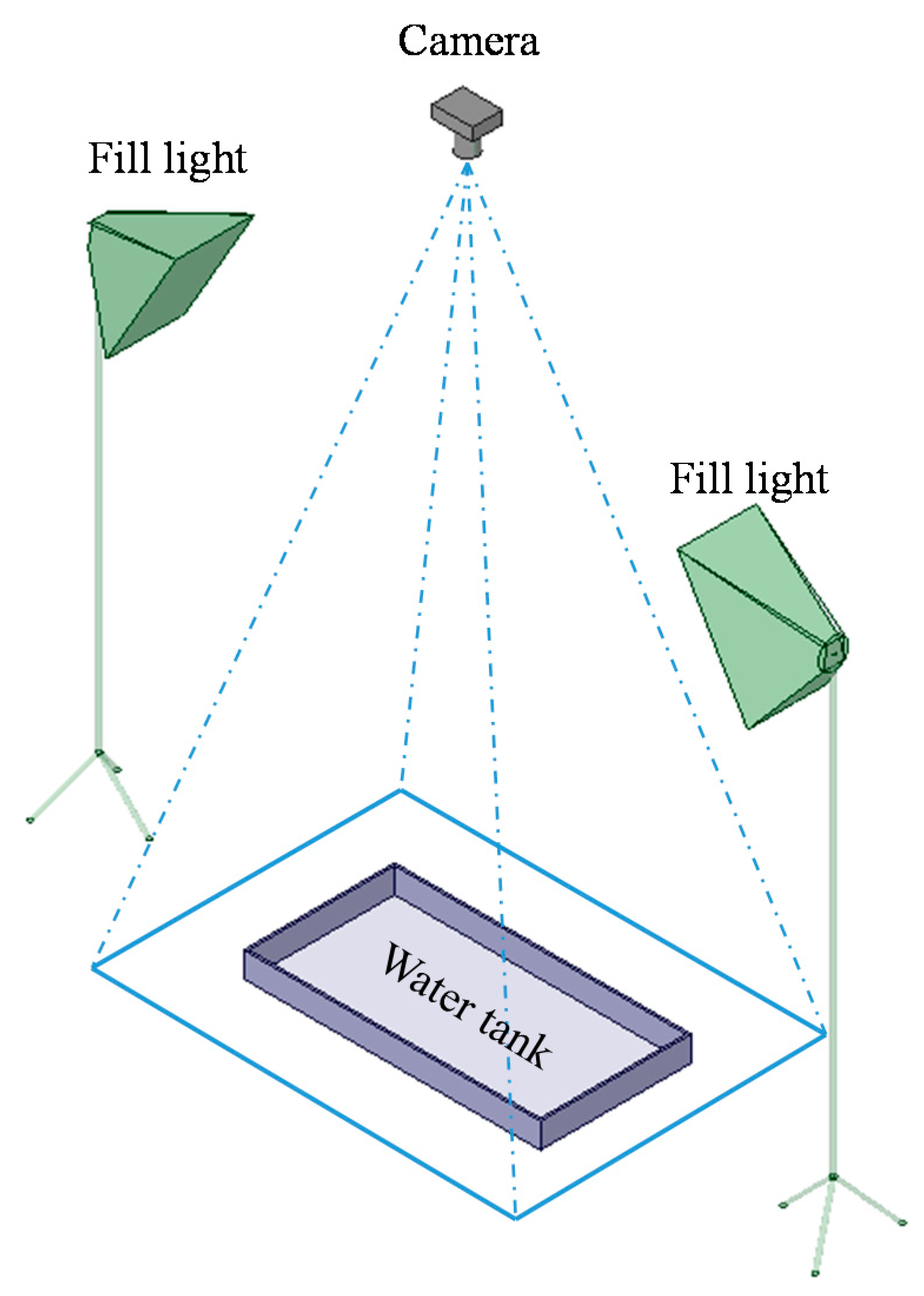
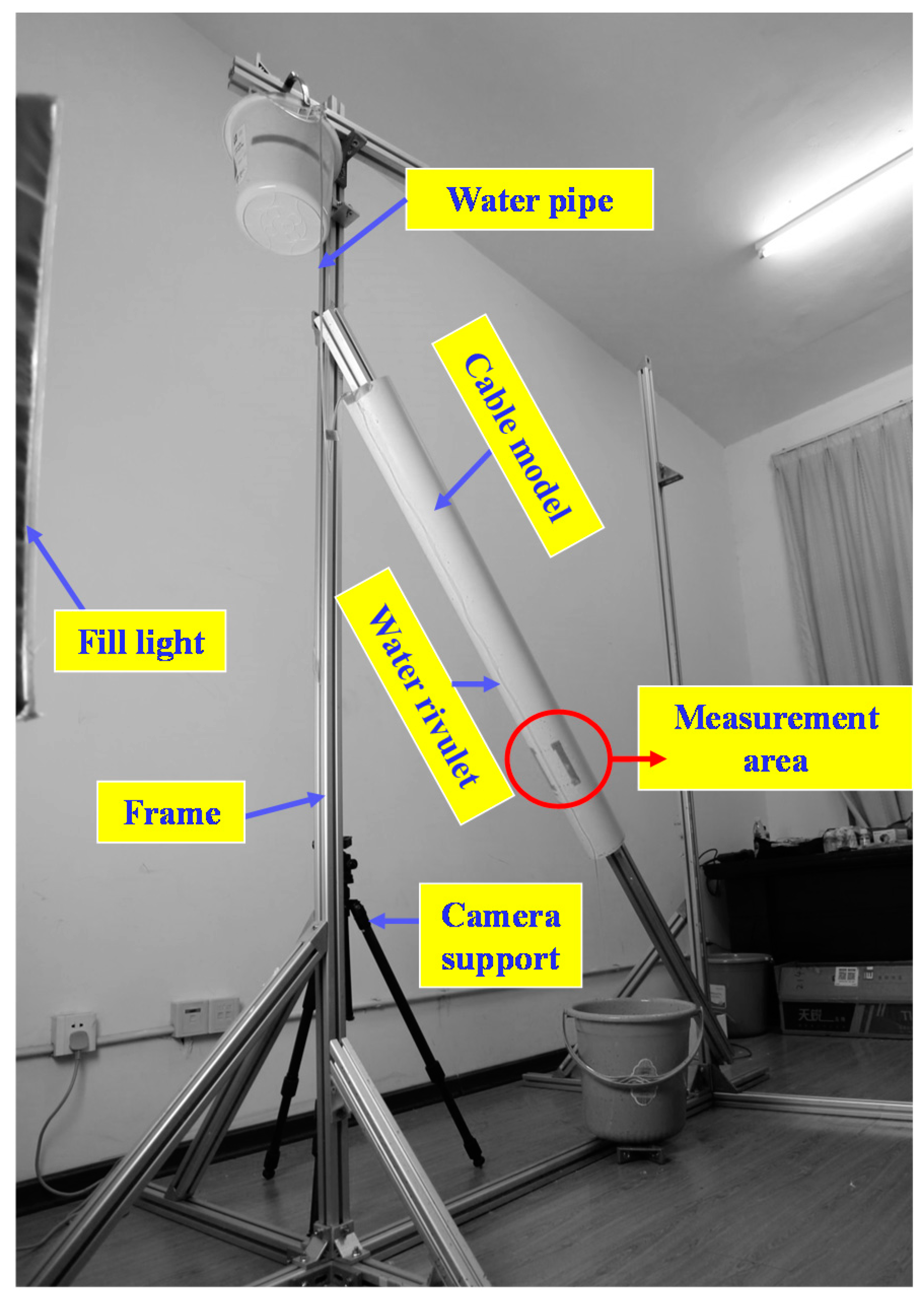
3.1. Experimental Setup
3.2. Data Processing Method
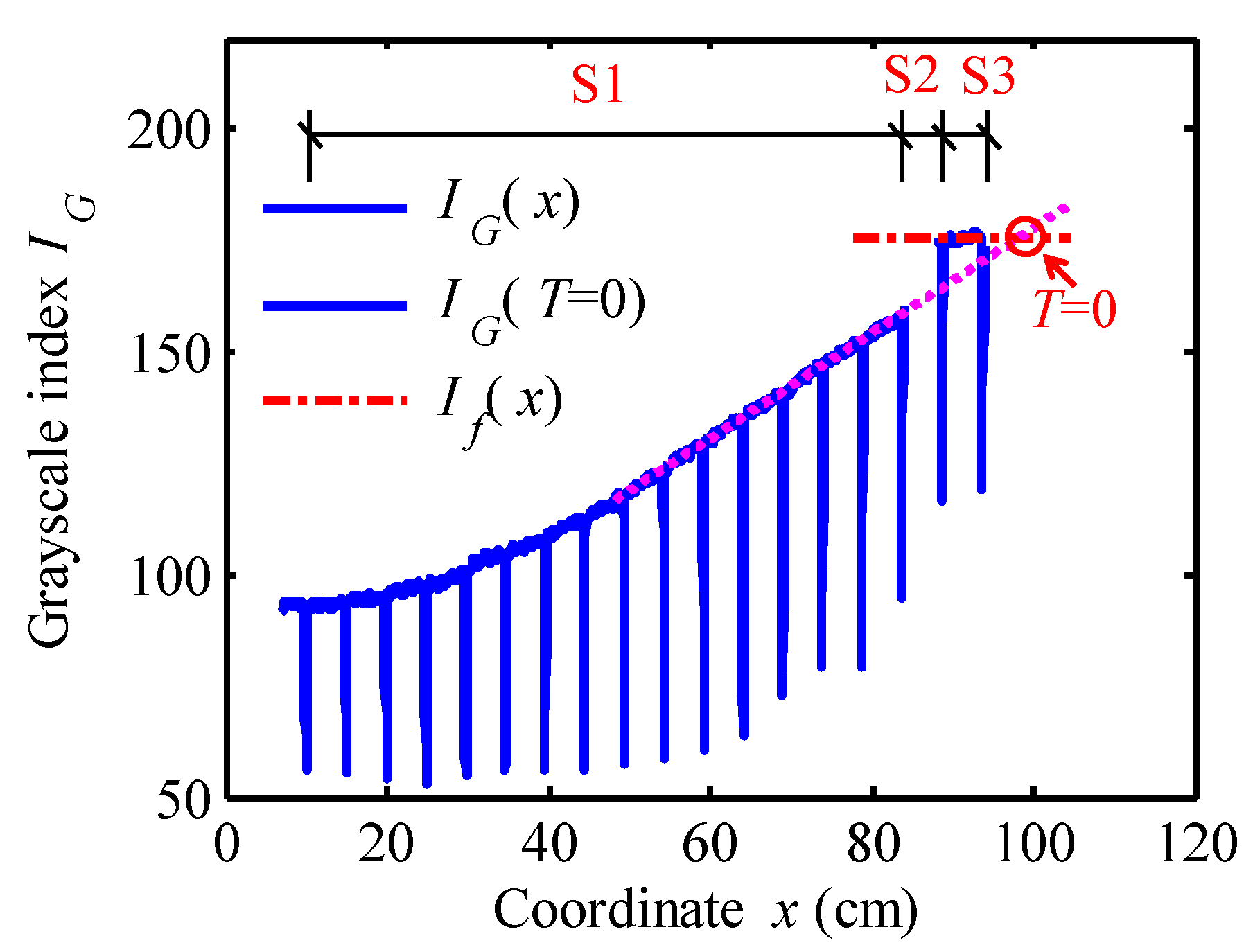
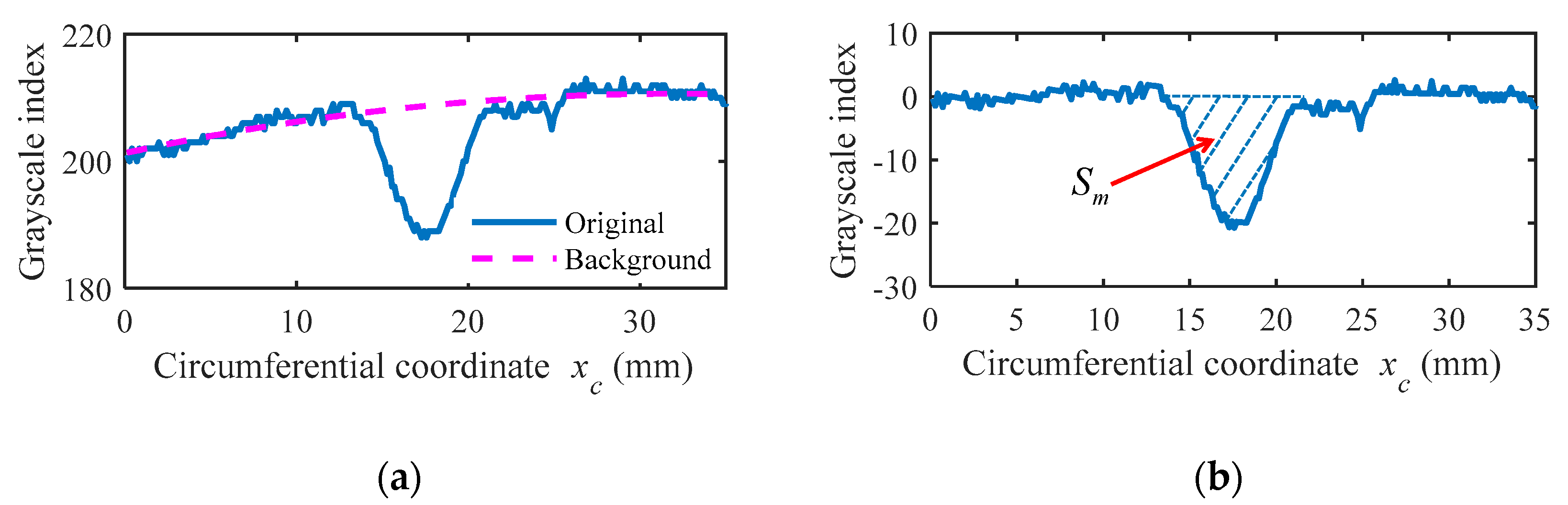
3.2.1. Image Processing
3.2.2. Identification of
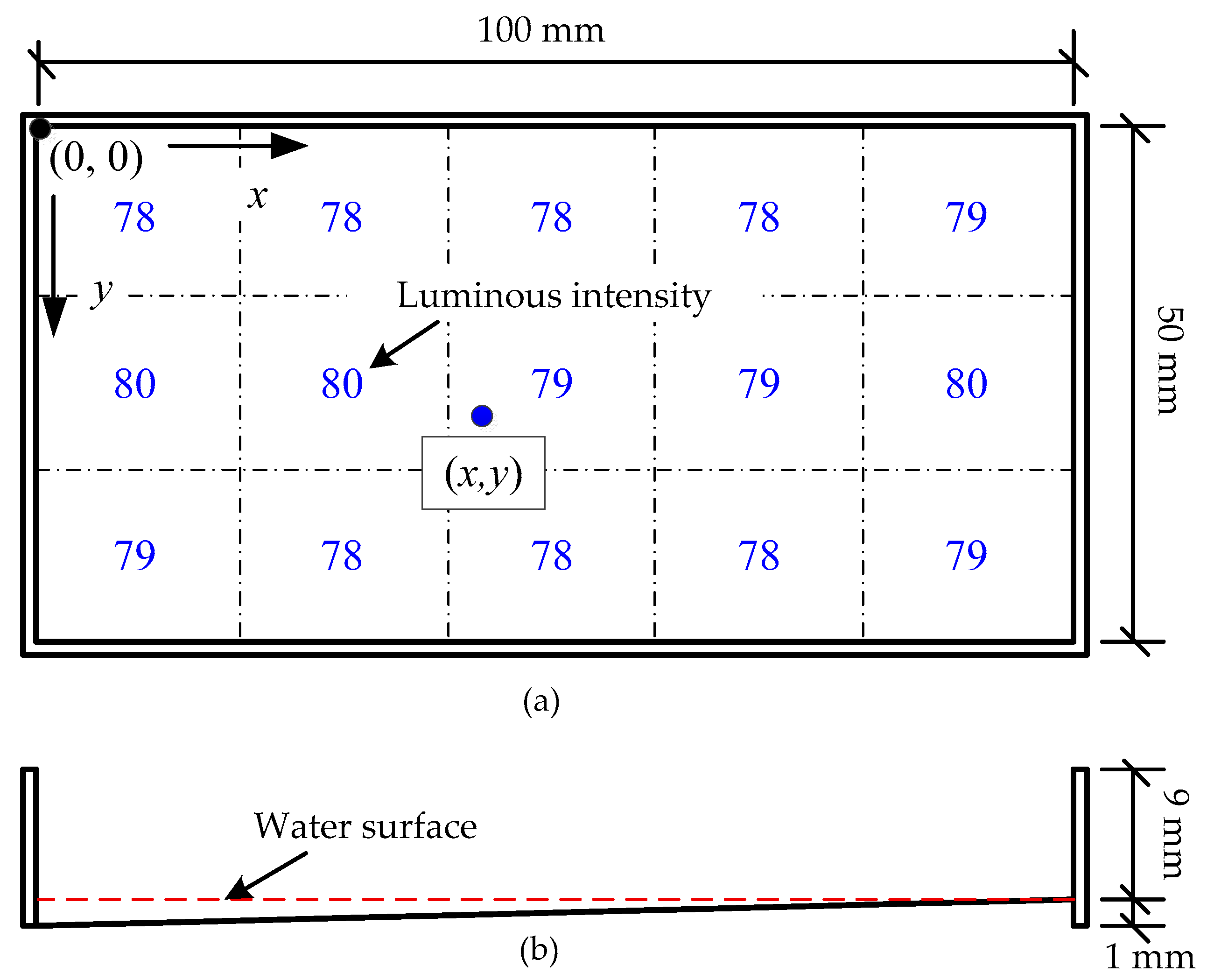
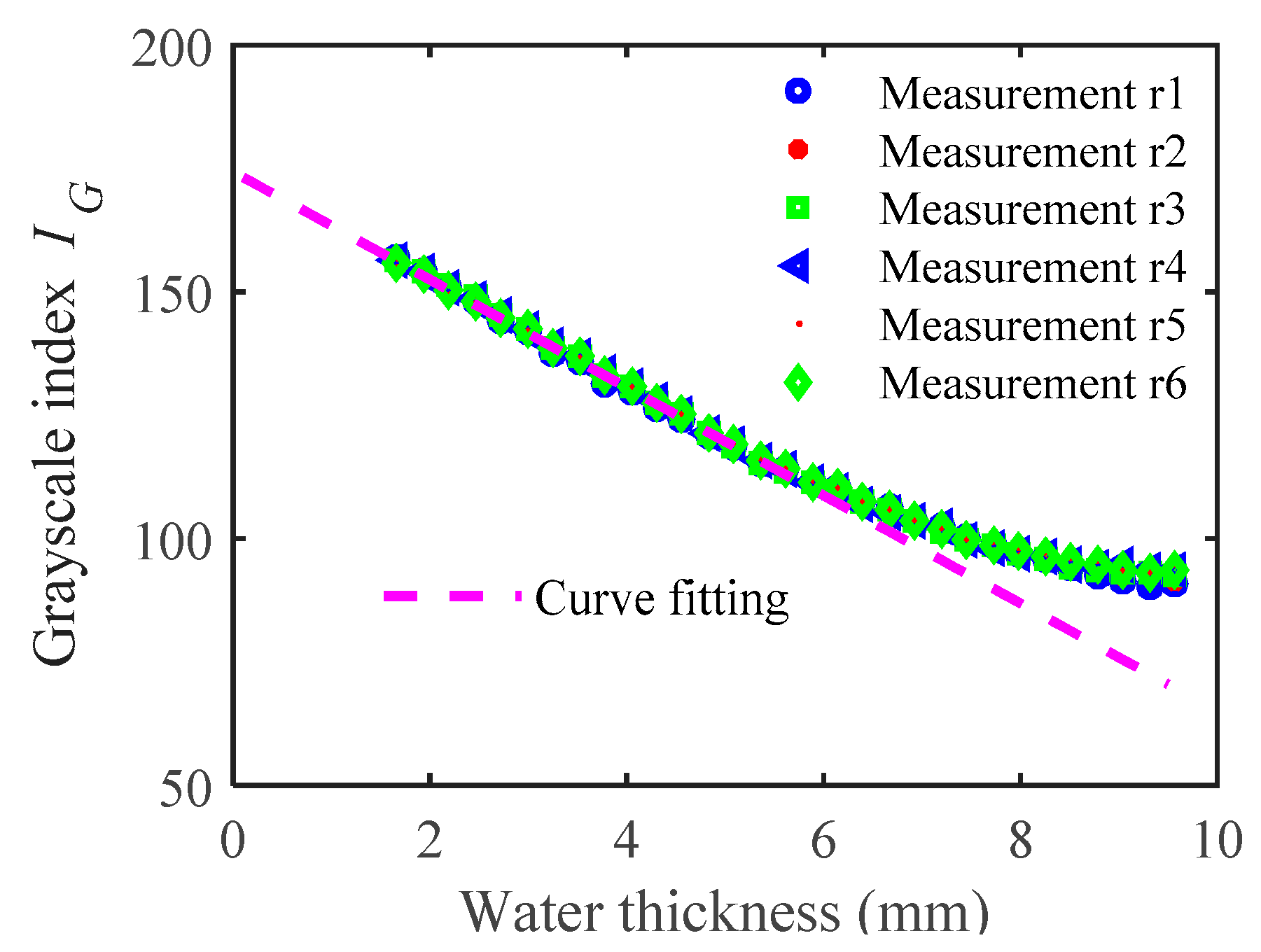
3.3. Calibration Results
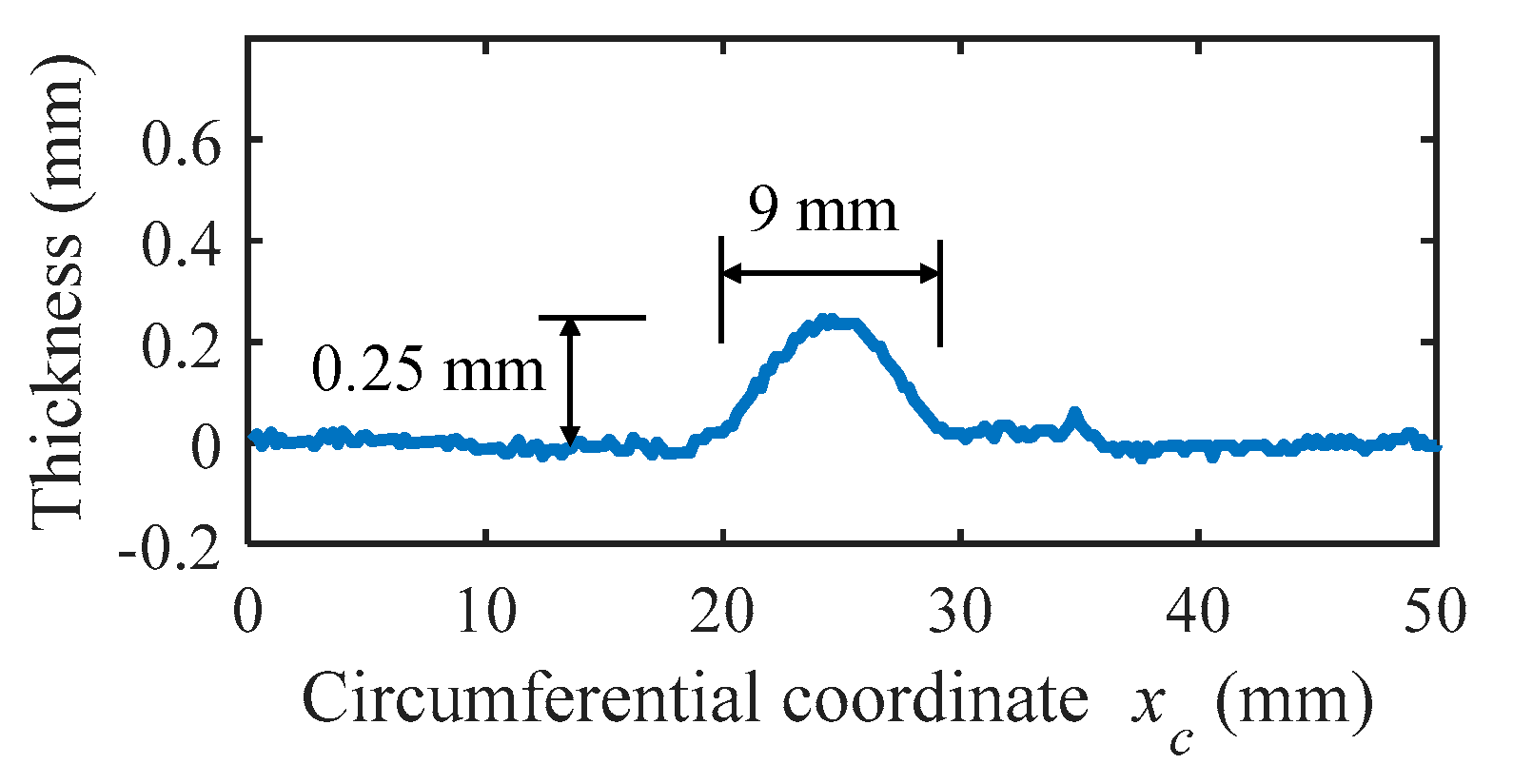
4. Measurement of the Profile of a Water Rivulet Flowing on a Cable Surface
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Zhang, K.; Wei, T.; Hu, H. An experimental investigation on the surface water transport process over an airfoil by using a digital image projection technique. Exp. Fluids 2015, 56, 173. [Google Scholar] [CrossRef]
- Flamand, O. Rain-wind induced vibration of cables. J. Wind Eng. Ind. Aerodyn. 1995, 57, 353–362. [Google Scholar] [CrossRef]
- Li, F.C.; Chen, W.L.; Li, H.; Zhang, R. An ultrasonic transmission thickness measurement system for study of water rivulets characteristics of stay cables suffering from wind–rain-induced vibration. Sens. Actuators A Phys. 2010, 159, 12–23. [Google Scholar] [CrossRef]
- Li, Y.; Jing, H.; Xia, Y.; Xu, Y.; Xiang, H. Measurement of rivulet movement on inclined cables during rain–wind induced vibration. Sens. Actuators A Phys. 2015, 231, 17–24. [Google Scholar] [CrossRef]
- Jing, H.; Xia, Y.; Xu, Y.; Li, Y. Measurement of rivulet movement and thickness on inclined cable using videogrammetry. Smart Struct. Syst. 2016, 18, 485–500. [Google Scholar] [CrossRef]
- Jing, H.; Xia, Y.; Li, H.; Xu, Y.; Li, Y. Excitation mechanism of rain–wind induced cable vibration in a wind tunnel. J. Fluids Struct. 2017, 68, 33–47. [Google Scholar] [CrossRef]
- Liu, J. Three-dimensional instabilities of film flows. Phys. Fluids 1995, 7, 55–67. [Google Scholar] [CrossRef]
- Johnson, M.F.G.; Schluter, R.A.; Bankoff, S.G. Fluorescent imaging system for global measurement of liquid film thickness and dynamic contact angle in free surface flows. Rev. Sci. Instrum. 1997, 68, 4097–4102. [Google Scholar] [CrossRef]
- Johnson, M.F.G.; Schluter, R.A.; Miksis, M.J.; Bankoff, S.G. Experimental study of rivulet formation on an inclined plate by fluorescent imaging. J. Fluid Mech. 1999, 394, 339–354. [Google Scholar] [CrossRef]
- He, X.H.; Yu, X.D.; Chen, Z.Q. Nonstationarity analysis in wind-rain-induced vibration of stay cables. J. Civ. Eng. Manag. 2012, 18, 821–827. [Google Scholar] [CrossRef]
- Cobelli, P.J.; Maurel, A.; Pagneux, V.; Petitjeans, P. Global measurement of water waves by Fourier transform profilometry. Exp. Fluids 2009, 46, 1037. [Google Scholar] [CrossRef]
- Hu, H.; Wang, B.; Zhang, K.; Lohry, W.; Zhang, S. Quantification of transient behavior of wind-driven surface droplet/rivulet flows using a digital fringe projection technique. J. Vis. 2014, 18, 1–14. [Google Scholar] [CrossRef]
- Salvi, J.; Fernandez, S.; Pribanic, T.; Llado, X. A state of the art in structured light patterns for surface profilometry. Pattern Recognit. 2010, 43, 2666–2680. [Google Scholar] [CrossRef]
- Zhang, Q.C.; Su, X.Y. An optical measurement of vortex shape at a free surface. Opt. Laser Technol. 2002, 34, 107–113. [Google Scholar] [CrossRef]
- Chen, W.L.; Tang, S.R.; Li, H.; Hu, H. Influence of dynamic properties and position of rivulet on rain–wind-induced vibration of stay cables. J. Bridge Eng. 2013, 18, 1021–1032. [Google Scholar] [CrossRef][Green Version]
- Liu, Y.; Chen, W.L.; Bond, L.J.; Hu, H. An experimental study on the characteristics of wind-driven surface water film flows by using a multi-transducer ultrasonic pulse-echo technique. Phys. Fluids 2017, 30, 012102. [Google Scholar] [CrossRef]
- Benetazzo, A. Measurements of short water waves using stereo matched image sequences. Coast. Eng. 2006, 53, 1013–1033. [Google Scholar] [CrossRef]
- Benetazzo, A.; Barbariol, F.; Bergamasco, F.; Torsello, A.; Carniel, S.; Sclavo, M. Stereo wave imaging from moving vessels: Practical use and applications. Coast. Eng. 2016, 109, 114–127. [Google Scholar] [CrossRef]
- Wright, W.B.; Budakian, R.; Putterman, S.J. Diffusing light photography of fully developed isotropic ripple turbulence. Phys. Rev. Lett. 1996, 76, 4528–4532. [Google Scholar] [CrossRef]
- Zhang, X.; Dabiri, D.; Gharib, M. Optical mapping of fluid density interfaces: Concepts and implementations. Rev. Sci. Instrum. 1996, 67, 1858–1868. [Google Scholar] [CrossRef]
- Lel, V.V.; Al-Sibai, F.; Leefken, A.; Renz, U. Local thickness and wave velocity measurement of wavy films with a chromatic confocal imaging method and a fluorescence intensity technique. Exp. Fluids 2005, 39, 856–864. [Google Scholar] [CrossRef]
- Chinnov, E.A.; Kharlamov, S.M.; Saprykina, A.V.; Zhukovskaya, O.V. Measuring deformations of the heated liquid film by the fluorescence method. Thermophys. Aeromech. 2007, 14, 241–246. [Google Scholar] [CrossRef]
- Schagen, A.; Modigell, M. Local film thickness and temperature distribution measurement in wavy liquid films with a laser-induced luminescence technique. Exp. Fluids 2007, 43, 209–221. [Google Scholar] [CrossRef]
- Xue, T.; Lin, X.; Yang, L. Measurement of circumferential liquid film based on LIF and virtual stereo vision sensor. J. Sens. 2016, 2872947. [Google Scholar] [CrossRef]
- Cochard, S.; Ancey, C. Tracking the free surface of time-dependent flows: Image processing for the dam-break problem. Exp. Fluids 2008, 44, 59–71. [Google Scholar] [CrossRef]
- Tsubaki, R.; Fujita, I. Stereoscopic measurement of a fluctuating free surface with discontinuities. Meas. Sci. Technol. 2005, 16, 1894. [Google Scholar] [CrossRef]
- Ye, X.-W.; Dong, C.-Z.; Liu, T. Image-based structural dynamic displacement measurement using different multi-object tracking algorithms. Smart Struct. Syst. 2016, 17, 935–956. [Google Scholar] [CrossRef]
- Ye, X.-W.; Yi, T.-H.; Dong, C.-Z.; Liu, T. Vision-based structural displacement measurement: System performance evaluation and influence factor analysis. Measurement 2016, 88, 372–384. [Google Scholar] [CrossRef]
- Ye, X.-W.; Ni, Y.-Q.; Wai, T.-T.; Wong, K.-Y.; Zhang, X.-M.; Xu, F. A vision-based system for dynamic displacement measurement of long-span bridges: Algorithm and verification. Smart Struct. Syst. 2013, 12, 363–379. [Google Scholar] [CrossRef]
- Zhou, X.-Q.; Xia, Y.; Wei, Z.-L.; Wu, Q.-X. A videogrammetric technique for measuring the vibration displacement of stay cables. Geo Spat. Inf. Sci. 2012, 15, 135–141. [Google Scholar] [CrossRef]
- Ferraz, A.; Carvalho, V.; Soares, F.; Leão, C.P. Characterization of blood samples using image processing techniques. Sens. Actuators A Phys. 2011, 172, 318–324. [Google Scholar] [CrossRef]
- Qu, Y.; Huang, J.; Zhang, X. Rapid 3D Reconstruction for Image Sequence Acquired from UAV Camera. Sensors 2018, 18, 225. [Google Scholar]
- Li, H.; Yang, M. A nonlinear inverse perspective transform based method for camera distortion calibration. J. Shanghai Jiaotong Univ. 2008, 42, 1736–1739. [Google Scholar]
- Mao, J.X.; Wang, H.; Feng, D.M.; Tao, T.Y.; Zheng, W.Z. Investigation of dynamic properties of long-span cable-stayed bridges based on one-year monitoring data under normal operating condition. Struct Control Health Monit. 2018, e2146. [Google Scholar] [CrossRef]
 q = 0.5%,
q = 0.5%,  q = 1.0%,
q = 1.0%,  q = 3.0%,
q = 3.0%,  q = 5.0%).
q = 5.0%).
 q = 0.5%,
q = 0.5%,  q = 1.0%,
q = 1.0%,  q = 3.0%,
q = 3.0%,  q = 5.0%).
q = 5.0%).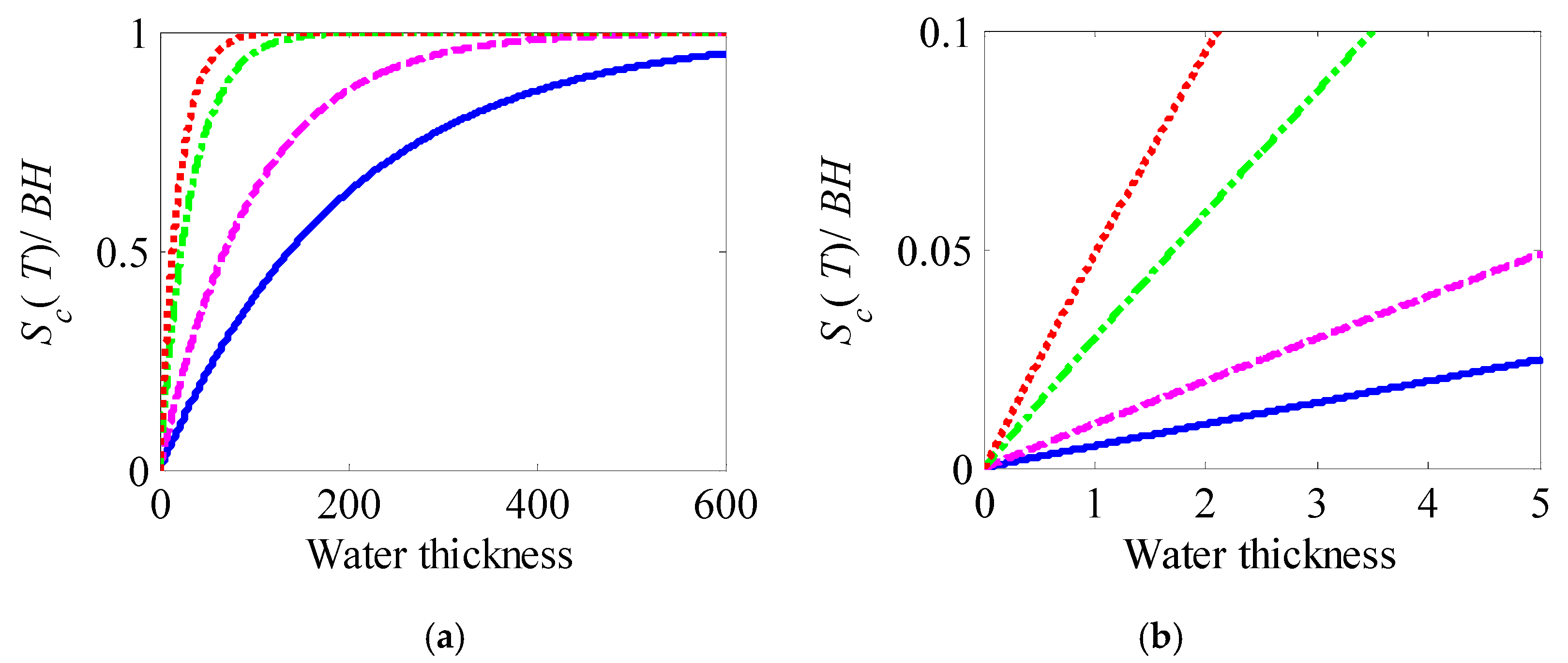




© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jing, H.; Cheng, Y.; He, X.; Zhou, X.; He, J. Thickness Measurement of Water Film/Rivulets Based on Grayscale Index. Remote Sens. 2019, 11, 2871. https://doi.org/10.3390/rs11232871
Jing H, Cheng Y, He X, Zhou X, He J. Thickness Measurement of Water Film/Rivulets Based on Grayscale Index. Remote Sensing. 2019; 11(23):2871. https://doi.org/10.3390/rs11232871
Chicago/Turabian StyleJing, Haiquan, Yi Cheng, Xuhui He, Xu Zhou, and Jia He. 2019. "Thickness Measurement of Water Film/Rivulets Based on Grayscale Index" Remote Sensing 11, no. 23: 2871. https://doi.org/10.3390/rs11232871
APA StyleJing, H., Cheng, Y., He, X., Zhou, X., & He, J. (2019). Thickness Measurement of Water Film/Rivulets Based on Grayscale Index. Remote Sensing, 11(23), 2871. https://doi.org/10.3390/rs11232871