1.1. Background
Image classification has always been an important basic problem in computer vision, and it is also the basis of other high-level visual tasks such as image detection, image segmentation, object tracking, and behavior analysis [
1]. To propose an effective method to extract features which can represent the characteristics of the image is always critical in image classification [
2]. The methods of extracting features can be divided into hand-crafted feature based methods and deep feature based methods. Before the rise of feature learning, people mostly used hand-crafted feature based methods to extract the essential features of the image such as edge, corner, texture, and other information [
3]. For example, Laplacian of Gaussian (LoG) operator [
4] and Difference of Gaussian (DoG) operator [
5] are designed for detecting blobs in the image, scale invariant feature transform (SIFT) [
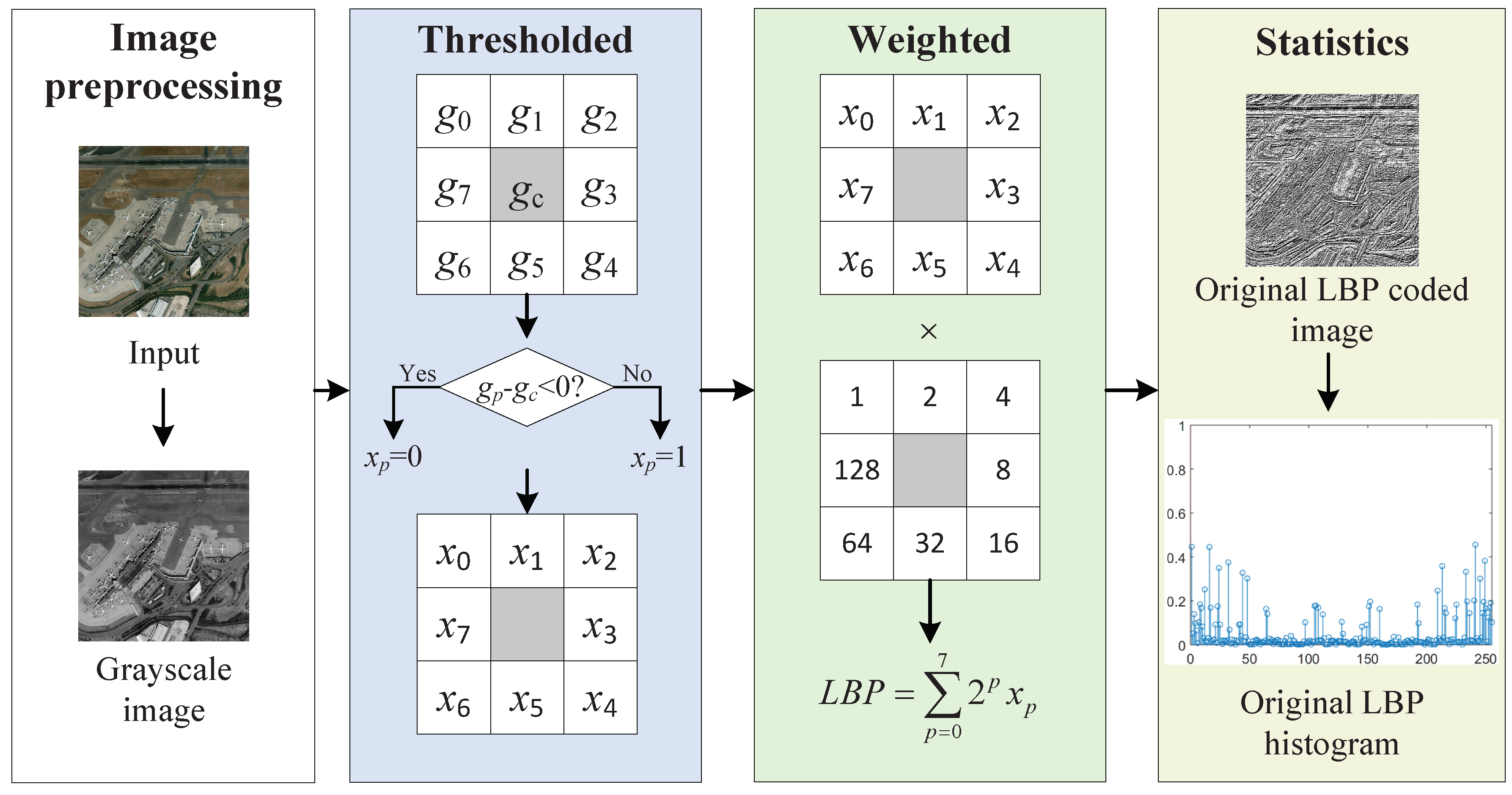
6] is independent of the size and rotation of the object, local binary pattern (LBP) [
7] has rotation invariance and gray invariance, features from accelerated segment test (FAST) operator [
8] has high computational performance and high repeatability, bag of visual words model [
9] pays more attention to the statistical information of features, Fisher vector [
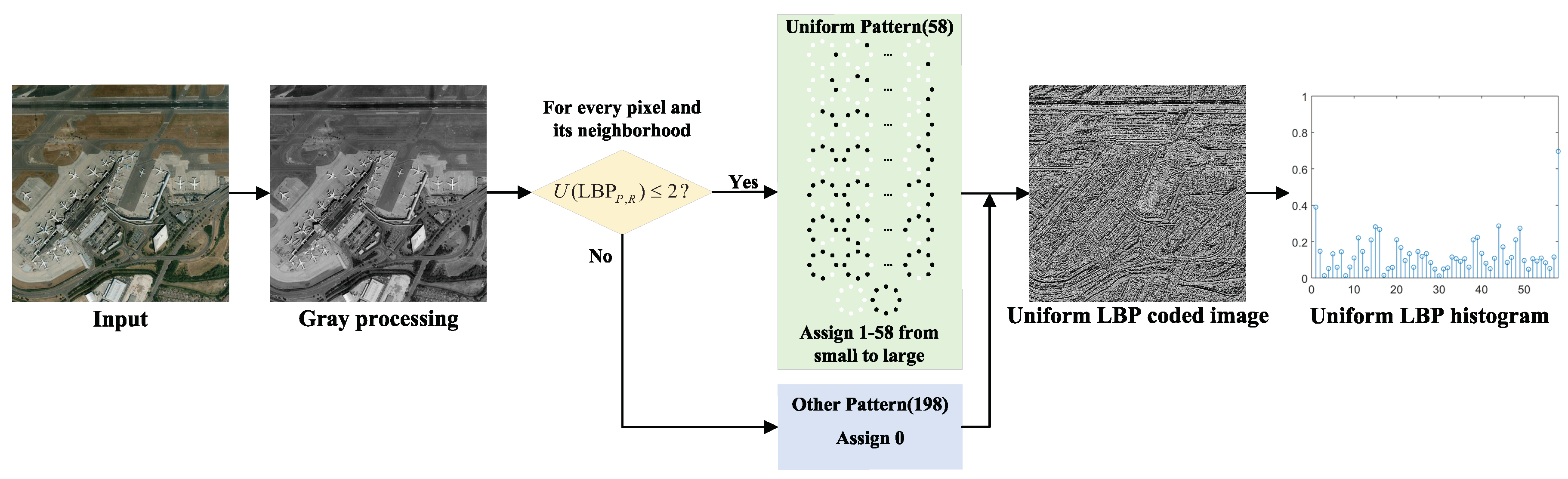
10] expresses an image with a gradient vector of likelihood functions, etc. A few of the most successful methods of texture description are the LBP and its variants such as uniform local binary pattern (ULBP) [
11], COVariance and LBP Difference (COV-LBPD) [
12], median robust extended LBP (MRELBP) [
13], fast LBP histograms from three orthogonal planes (fast LBP-TOP) [
14]. The ULBP proposed by Ahonen et al. reduces the number of binary patterns of LBP and is robust for high frequency noise. Hong et al. proposed the LBP difference (LBPD) descriptor and the COV-LBPD descriptor. The LBPD characterizes the extent to which one LBP varies from the average local structure of an image region of interest, and the COV-LBPD is able to capture the intrinsic correlation between the LBPD and other features in a compact manner. The MRELBP descriptor proposed by Liu et al. was computed by comparing image medians over a novel sampling scheme, which can capture both microstructure and macrostructure texture information and has attractive properties of strong discriminativeness, grayscale and rotation invariance, and computational efficiency. Hong et al. proposed the fast LBP-TOP descriptor which fastens the computational efficiency of LBP-TOP on spatial-temporal information and introduced the concept of tensor unfolding to accelerate the implementation process from three-dimensional space to two-dimensional space.
Since the rise of feature learning, deep learning methods have become a research hotspot and have broad application prospects and research value in many fields such as speech recognition and image classification [
15]. Deep learning architectures mainly include four types: the autoencoder (AE), deep belief networks (DBNs), convolutional neural network (CNN), and recurrent neural network (RNN) [
16]. Among these four deep learning architectures, CNN is the most popular and most published to date. For example, neural networks such as GoogLeNet [
17], VGGNet [
18], and residual neural network (ResNet) [
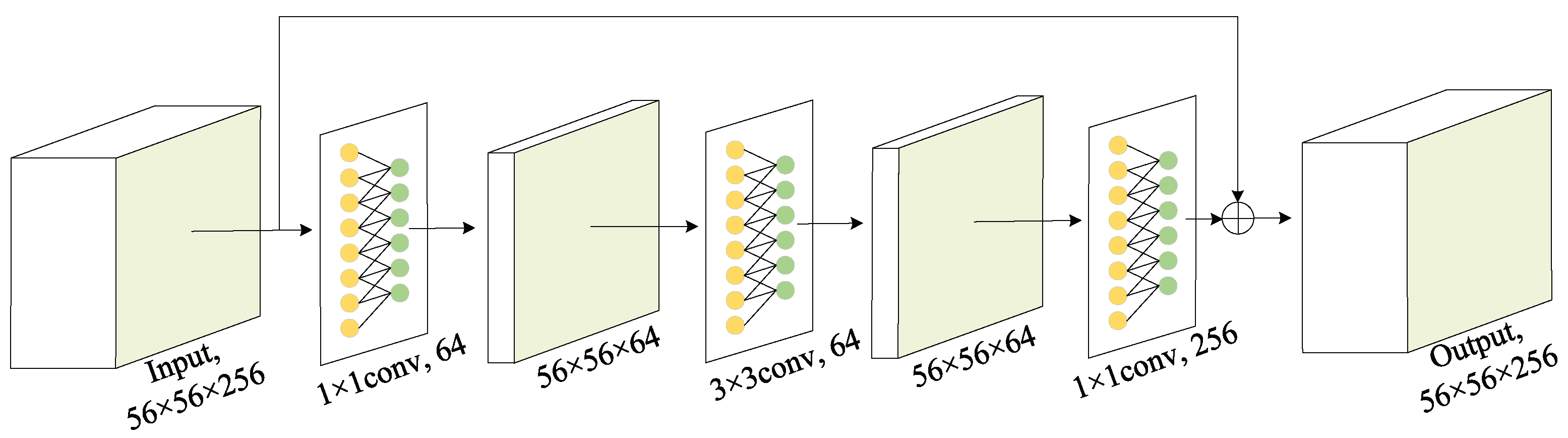
19] have performed well in the field of image classification. GoogLeNet proposes an inception module, VGGNet explores the effects of the depth of deep neural network, and ResNet solves the problem of degradation of deep networks. These deep learning algorithms build the reasonable model by simulating a multi-layer neural network. High-level layers pay more attention to semantic information and less attention to detail information, while low-level layers are more concerned with detailed information and less with semantic information.
The deep learning algorithms have automatic feature learning capabilities for image data relying on large training sets and large models [
20], while traditional methods rely primarily on hand-crafted features. Despite the success of deep features, the hand-crafted LBP texture descriptor and its variants have proven to provide competitive performance compared to deep learning methods in recent texture recognition performance evaluation, especially when there are rotations and multiple types of noise [
21]. The LBP method introduces the priori information by presetting thresholds, so it can directly extract useful features through a manually designed algorithm, while the acquisition of deep features with excellent performance requires large training sets and large models. Therefore, there are aspects where hand-crafted features and deep features can learn from each other. For example, Courbariaux et al. proposed the BinaryConnect, which means training a DNN with binary weights during the forward and backward propagations, while retaining precision of the stored weights [
22]. Hubara et al. introduced a method to train binarized neural networks (BNNs)—neural networks with binary weights and activations at run-time, and the binary weights and activations are used for computing the parameter gradients at train-time [
23]. Inspired by the characteristics of hand-crafted features and deep features, this paper mainly studies the complementary performance between deep features and binary coded features and proposes a more effective feature description method.
During the training of the model, the loss function is used to assess the degree to which a specific algorithm models the given data [
24]. The better the loss function, the better the performance of the algorithm. The design of the loss function can be guided by two strategies: empirical risk minimization and structural risk minimization. The average loss of the model on the training data set is called empirical risk, and the strategy of minimizing empirical risk is that the model with the least empirical risk is the best model. The related loss functions include center loss [
25] and large-margin softmax loss [
26], which are typical improved versions of softmax loss. When the size of training set is small or the model is complex, the model with the least empirical risk makes it easy to overfit the data. The strategy of structural risk minimization adds a regularization term based on the empirical risk minimization strategy. The structural risk minimization strategy means that the model with the least structural risk is the optimal model. The commonly used regularization terms include L1-regularization and L2-regularization. Sinkhorn distance [
27] is the approximation of Earth mover’s distance (EMD) [
28] which can be used as a loss function. Different from other distance functions, EMD solves the correlation between two distributions by a distance matrix and a coupling matrix related to the predicted probability distribution and the actual probability distribution. The presetting distance matrix can increase the influence of the inter-class distance on the loss value, thereby improving the performance of the model. However, when EMD is used as loss function, there will be the problem of excessive computational complexity. Thus, as an approximate representation of EMD, the Sinkhorn distance which adds an entropic regularization term based on EMD is introduced as the loss function of the proposed model. The added entropic constraint turns the transport problem between distributions into a strictly convex problem that can be solved with matrix scaling algorithms and avoids the overfitting program.
This paper mainly verifies the performance of the proposed image classification algorithm in texture classification and remote sensing scene classification. Texture classification is an important basic problem in the field of computer vision and pattern recognition as well as the basis of other visual tasks such as image segmentation, object recognition, and scene understanding. However, texture is only the feature of the surface of an object, which cannot fully reflect the essential properties of the object. High-level image features cannot be obtained using only texture features [
29]. Remote sensing scene classification is challenging due to several factors, such as large intra-class variations, small inter-class differences, scale changes, and illumination changes [
30]. With the rise of remote sensing instruments, a large amount of satellite data has appeared in the field of remote sensing. Therefore, deep learning is gradually introduced into the image classification of remote sensing scenes. There are wild applications receiving more and more attention, such as land cover classification and target detection.
1.3. Contributions and Structure
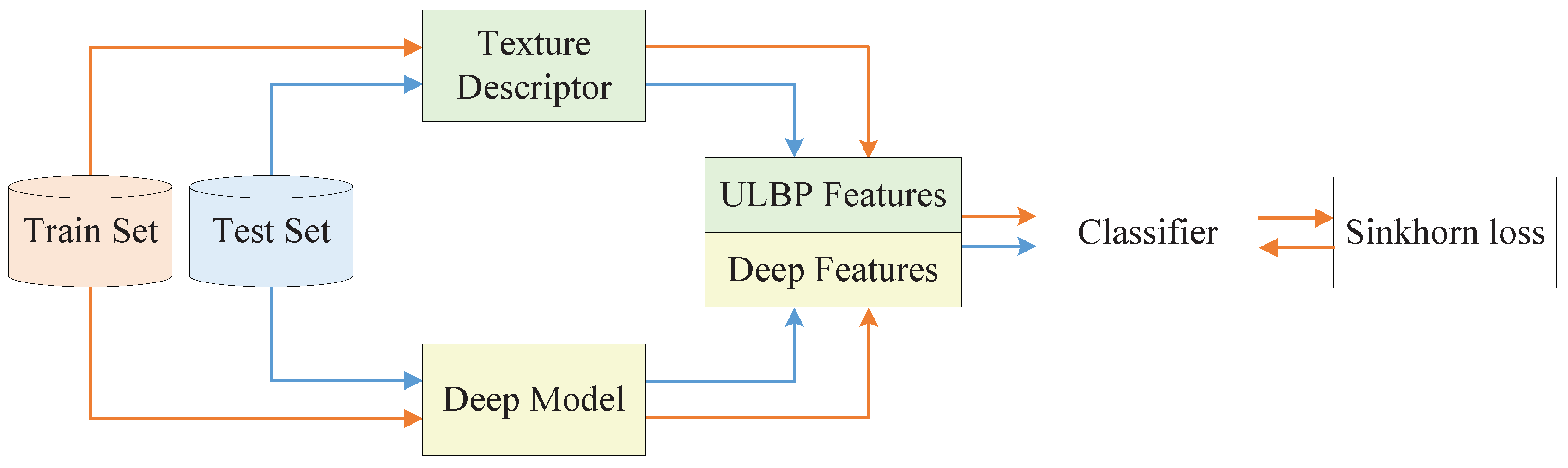
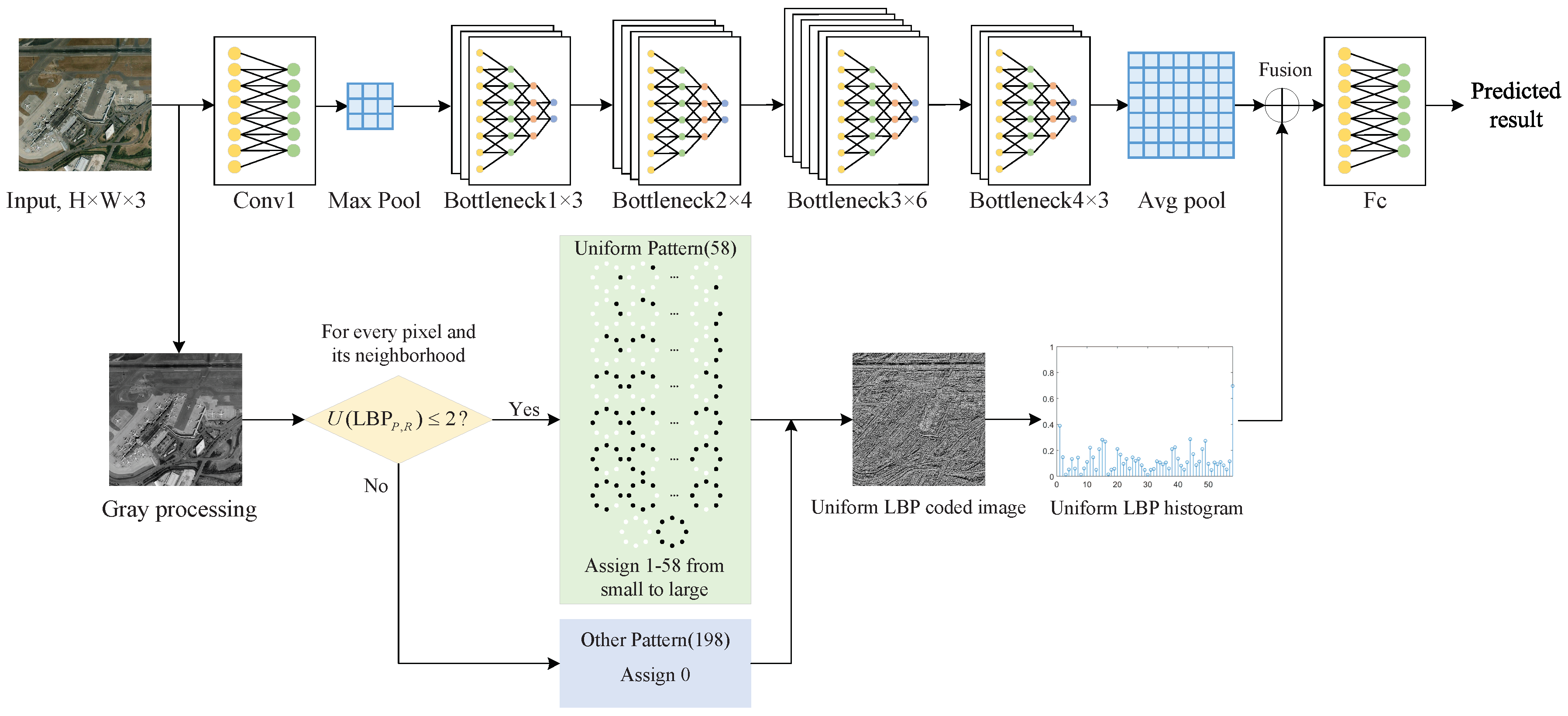
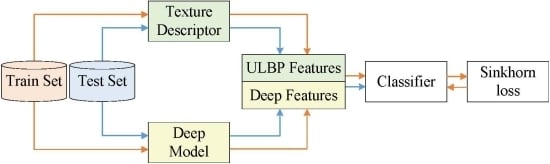
This paper presents a remote sensing and texture image classification network, which is based on deep learning integrated with binary coding and Sinkhorn distance. The general framework of the proposed algorithm is shown in
Figure 1.
The contributions of this paper are summarized as follows.
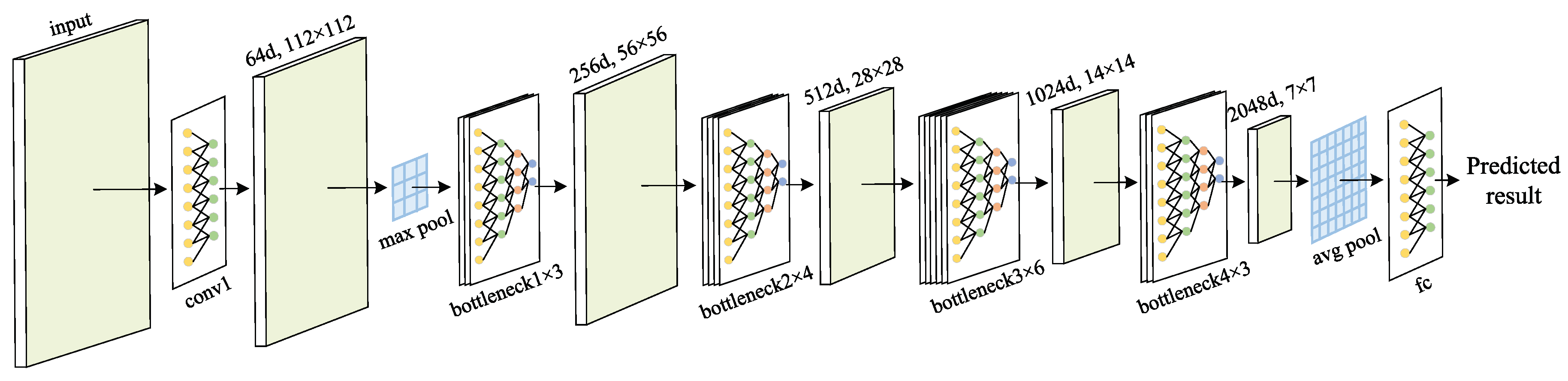
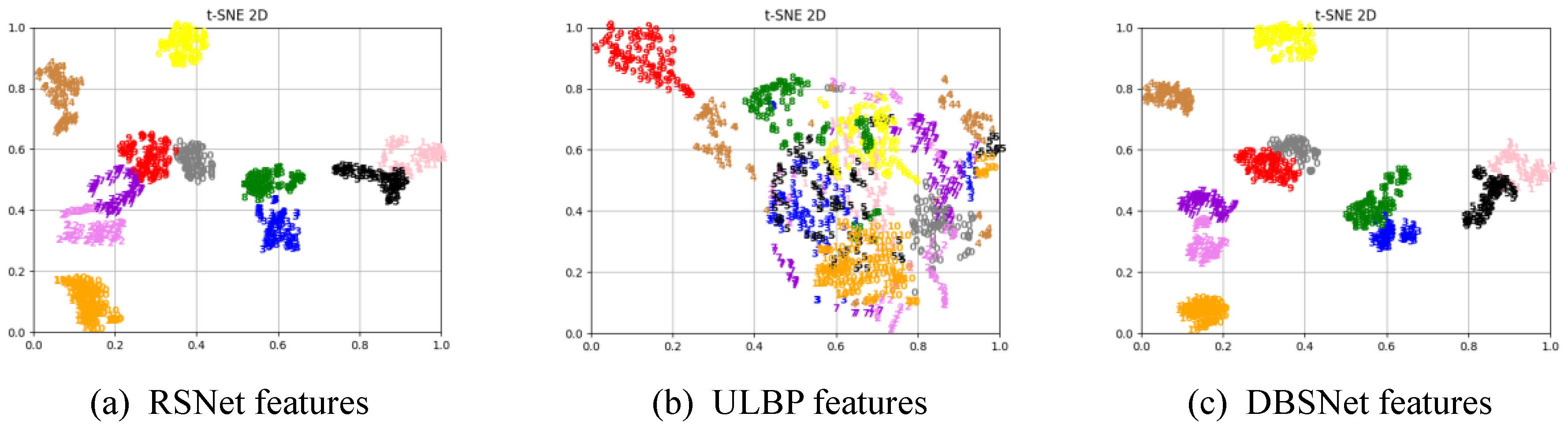
Firstly, since the deep feature based methods and hand-crafted feature based methods are complementary in some aspects, we combine these two kinds of features to obtain better features to characterize the image. Specifically, the hand-crafted binary coding features extracted by ULBP are introduced to supplement the deep features extracted by representative ResNet-50 in classification, which makes the image features more accurate and comprehensive.
Secondly, a new loss function is proposed, which combines the score function with the Sinkhorn distance to predict the class. Sinkhorn loss analyzes the loss value between distributions from the perspective of doing work and removes the redundancy of the fused features with an entropic regularization term. Since the Sinkhorn distance is bounded from below by the distance between the centers of mass of the two signatures when the ground distance is induced by a norm, we can increase the impact of the inter-class distance on the loss value by presetting the distance matrix to guide the optimization process of the model.
The following sections are arranged as follows:
Section 2 introduces the related work;
Section 3 shows the proposed image classification algorithm;
Section 4 introduces the experiments on texture datasets and remote sensing scene datasets;
Section 5 introduces the summary of this paper.