Detection of New Zealand Kauri Trees with AISA Aerial Hyperspectral Data for Use in Multispectral Monitoring
Abstract
1. Introduction
1.1. Research Context
1.2. Objectives and Approach
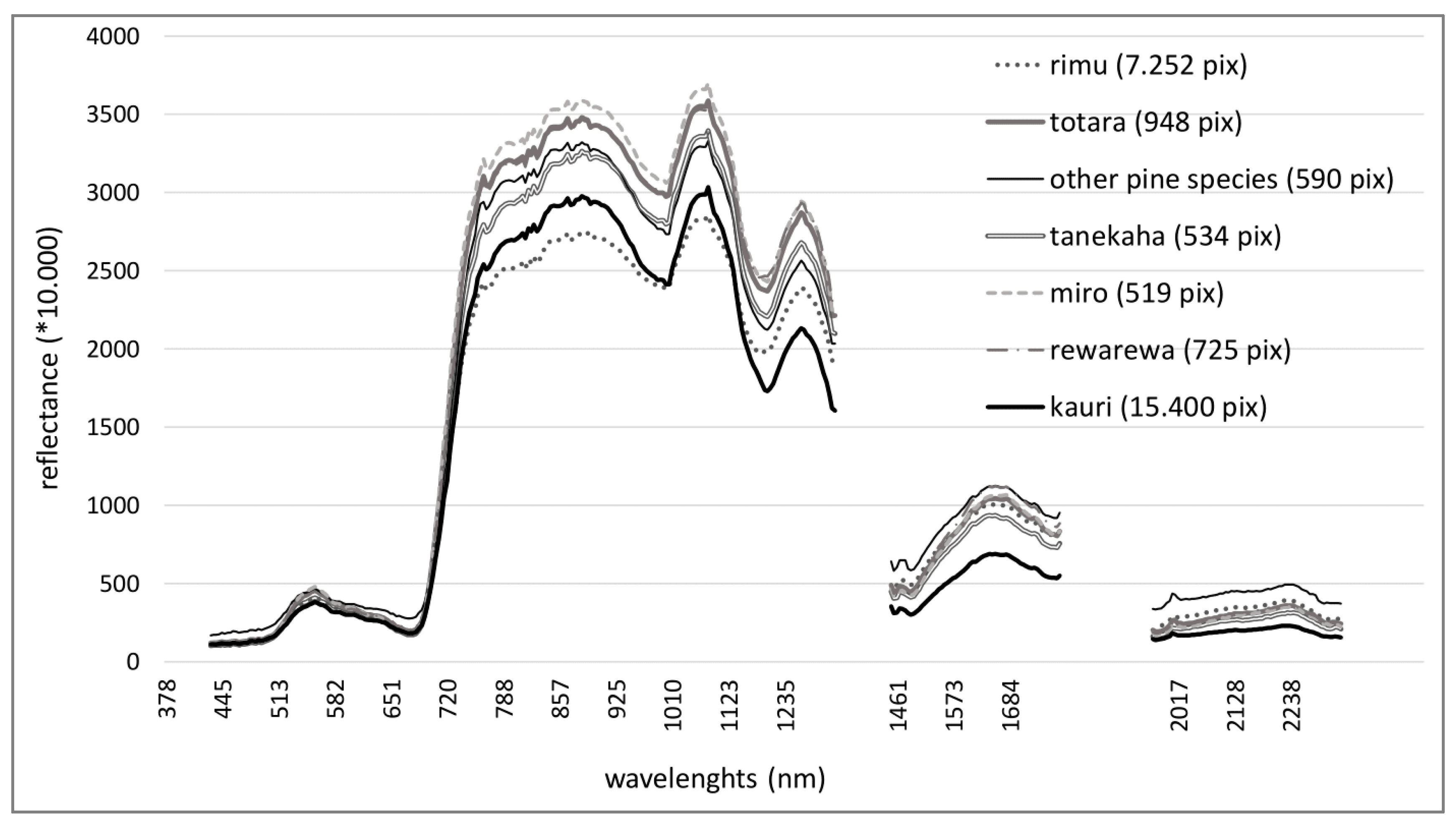
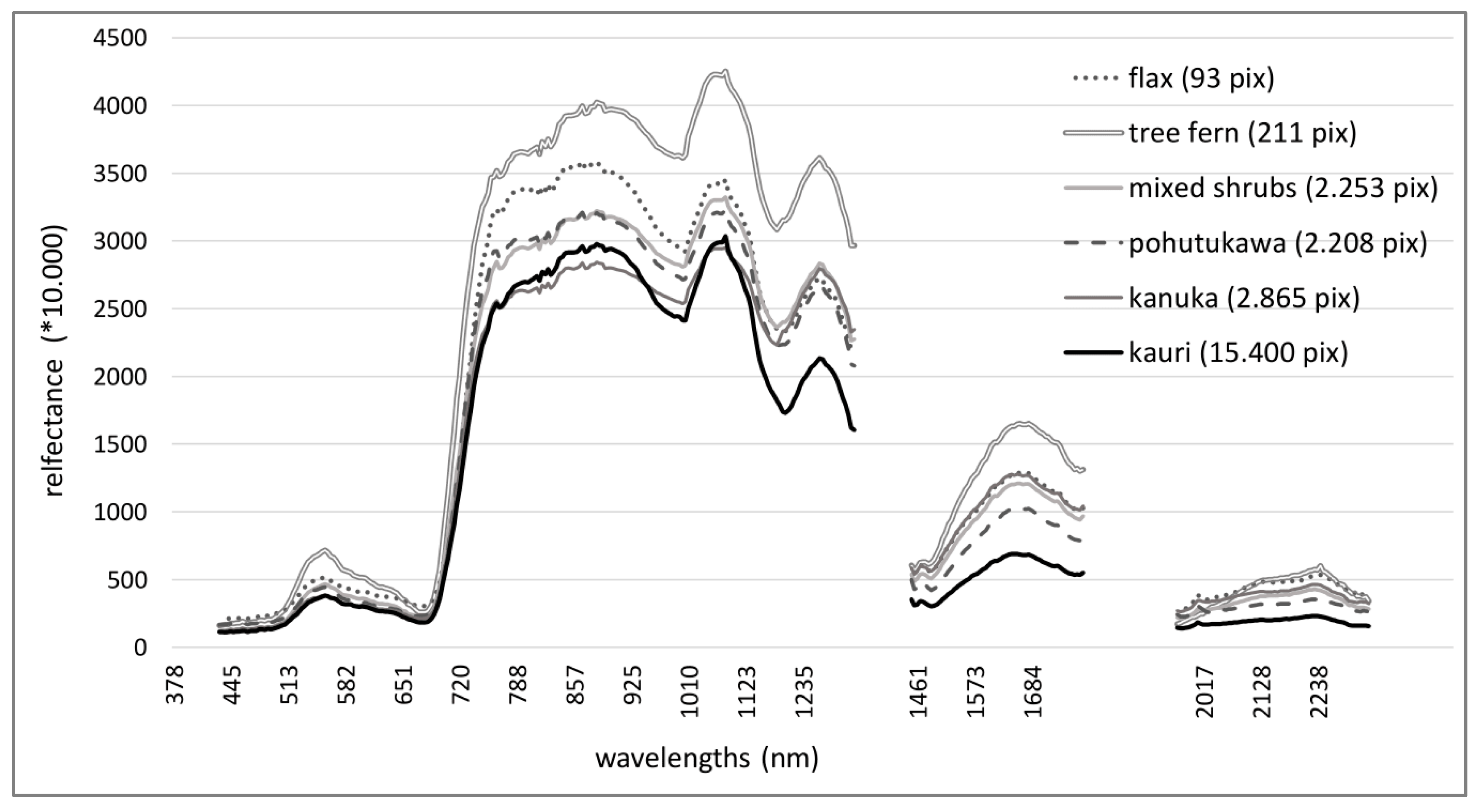
- Objective 1: Identify and compare the spectra of kauri and associated canopy tree species with no to medium stress symptoms and analyse their spectral characteristics and separability.
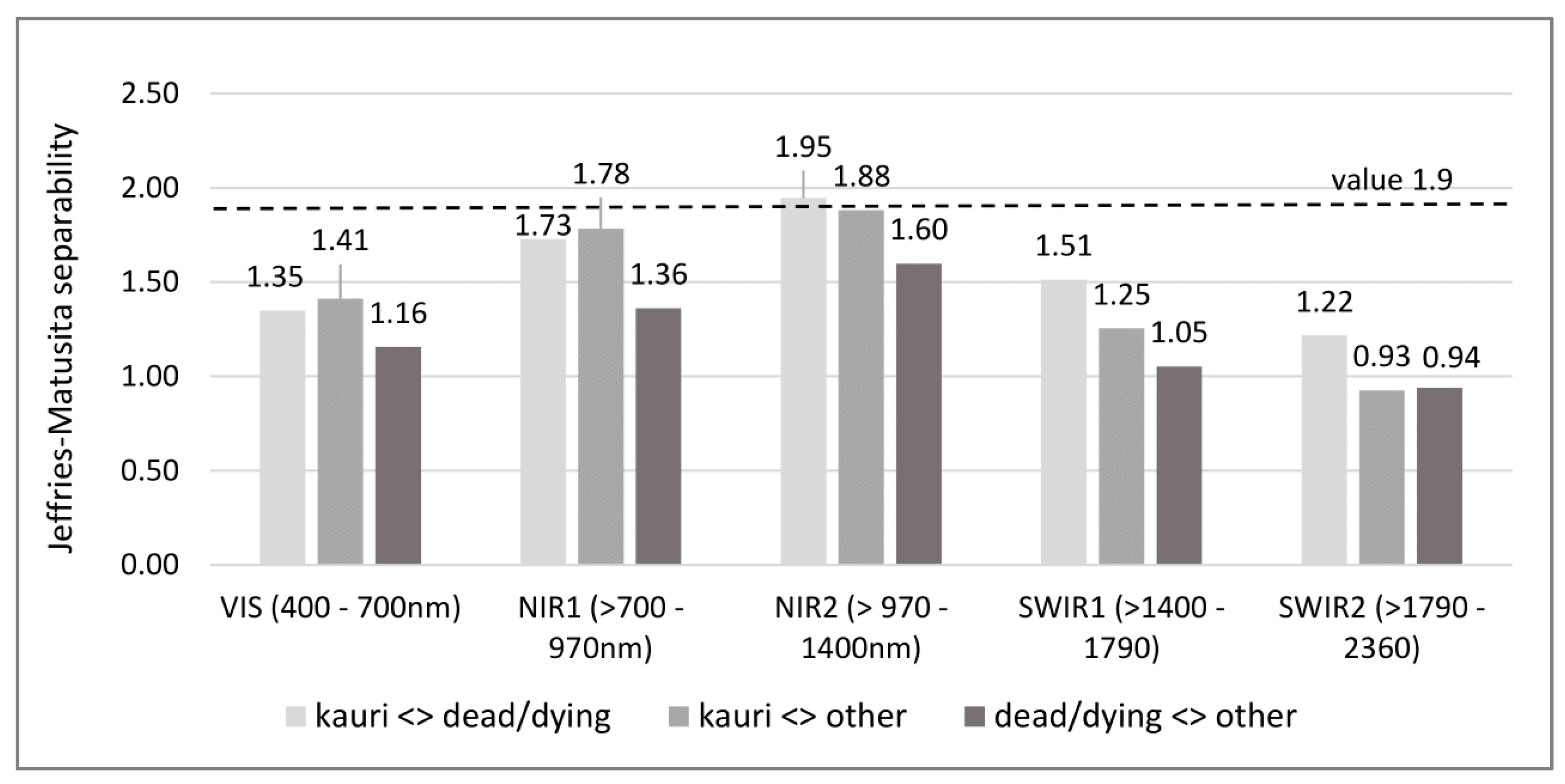
- Objective 2: Identify and describe the best spectral indices for the separation of the three target classes “kauri”, “dead/dying trees” and “other” canopy vegetation (see class description below).
- Objective 3: Define an efficient non-parametric classification method to differentiate the three target classes that is applicable for large area monitoring with multispectral sensors.
2. Materials and Methods
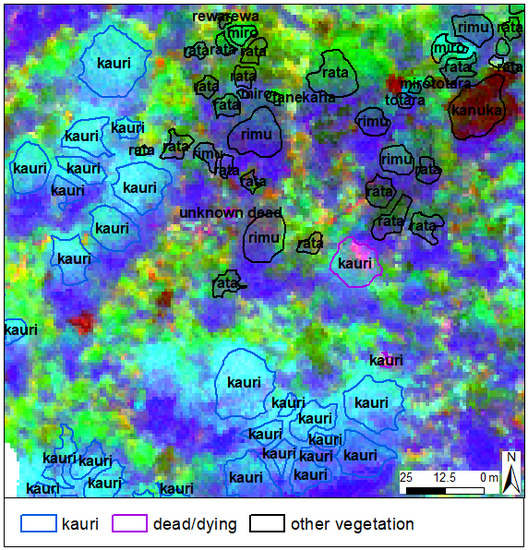
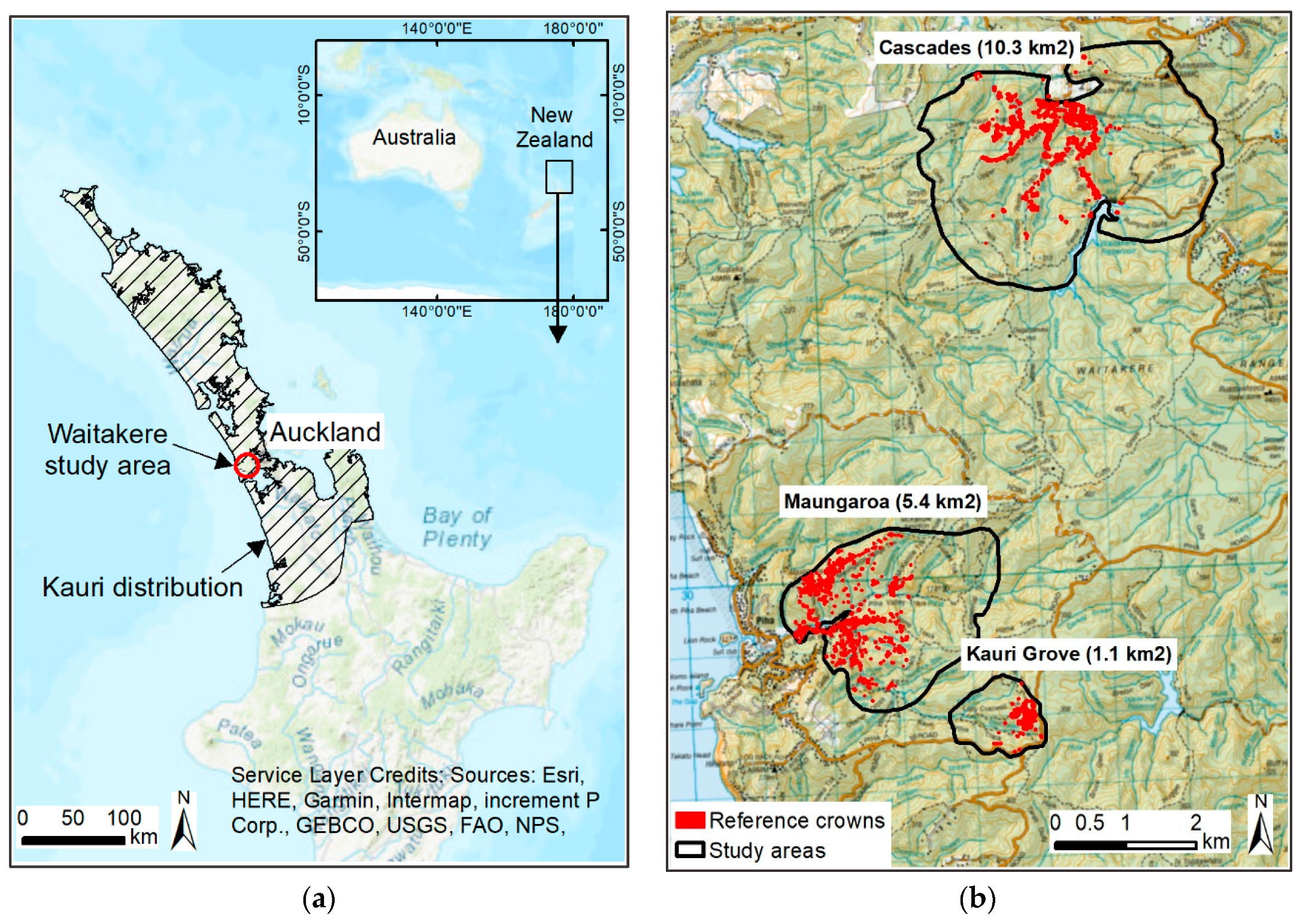
2.1. Study Area
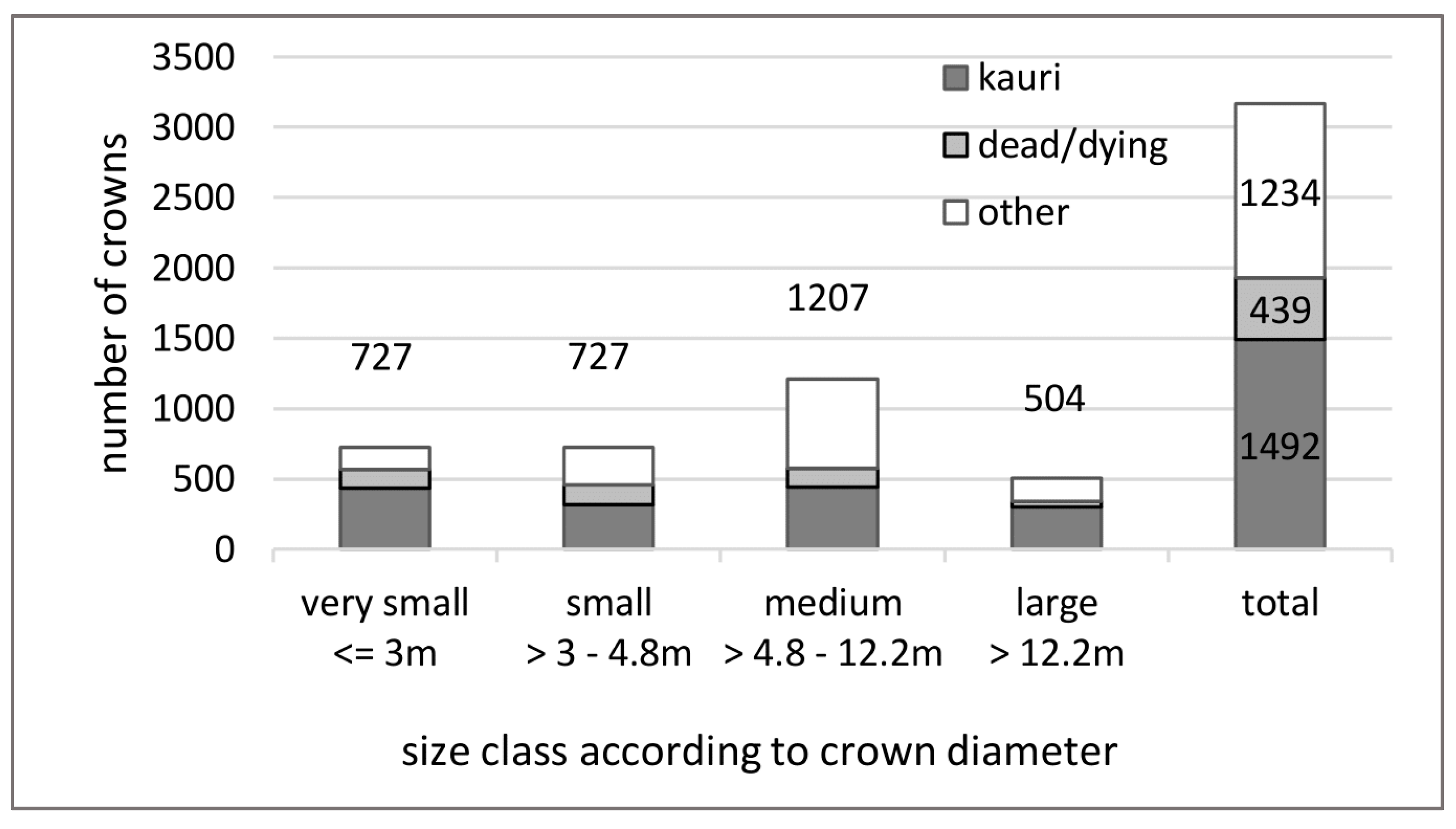
2.2. Data and Data Preparation
- “dead/dying trees” with a minimum of 40% visible dead branches in the aerial image;
- “kauri” that were not classified as “dead/dying”; and
- “other” canopy vegetation that was not classified as “dead/dying”.
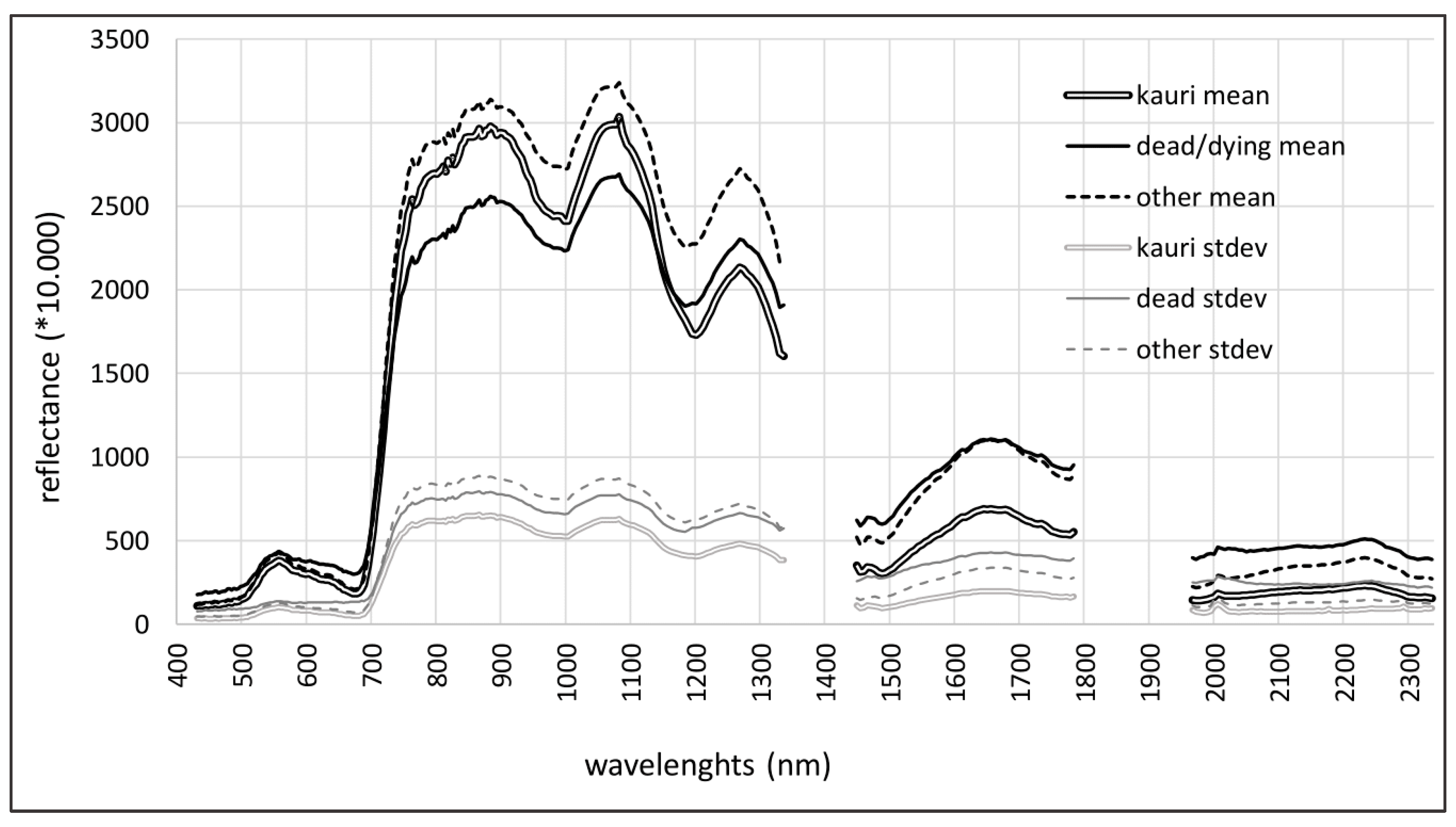
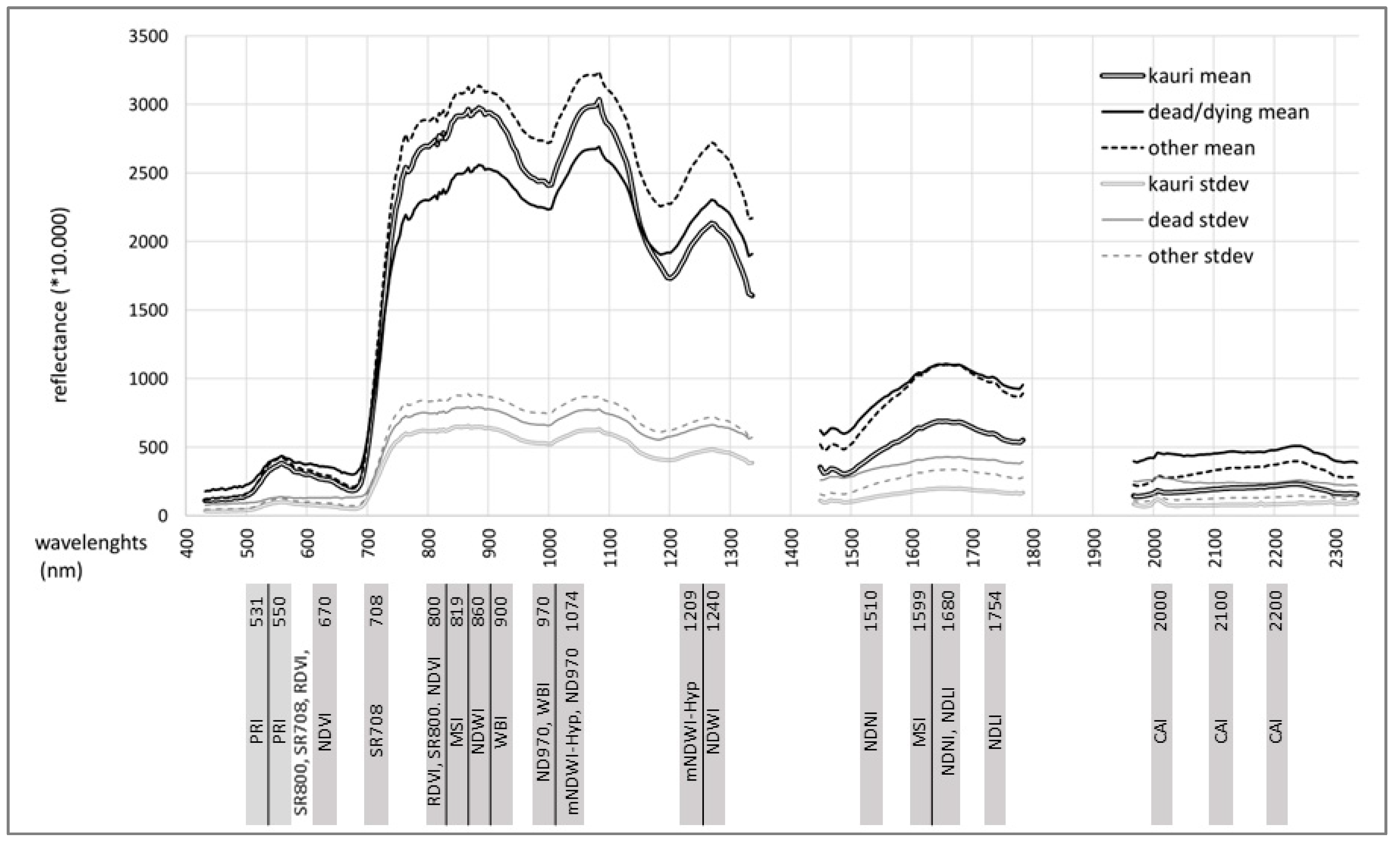
2.3. Extraction and Analysis of Spectra and Spectral Separabilities
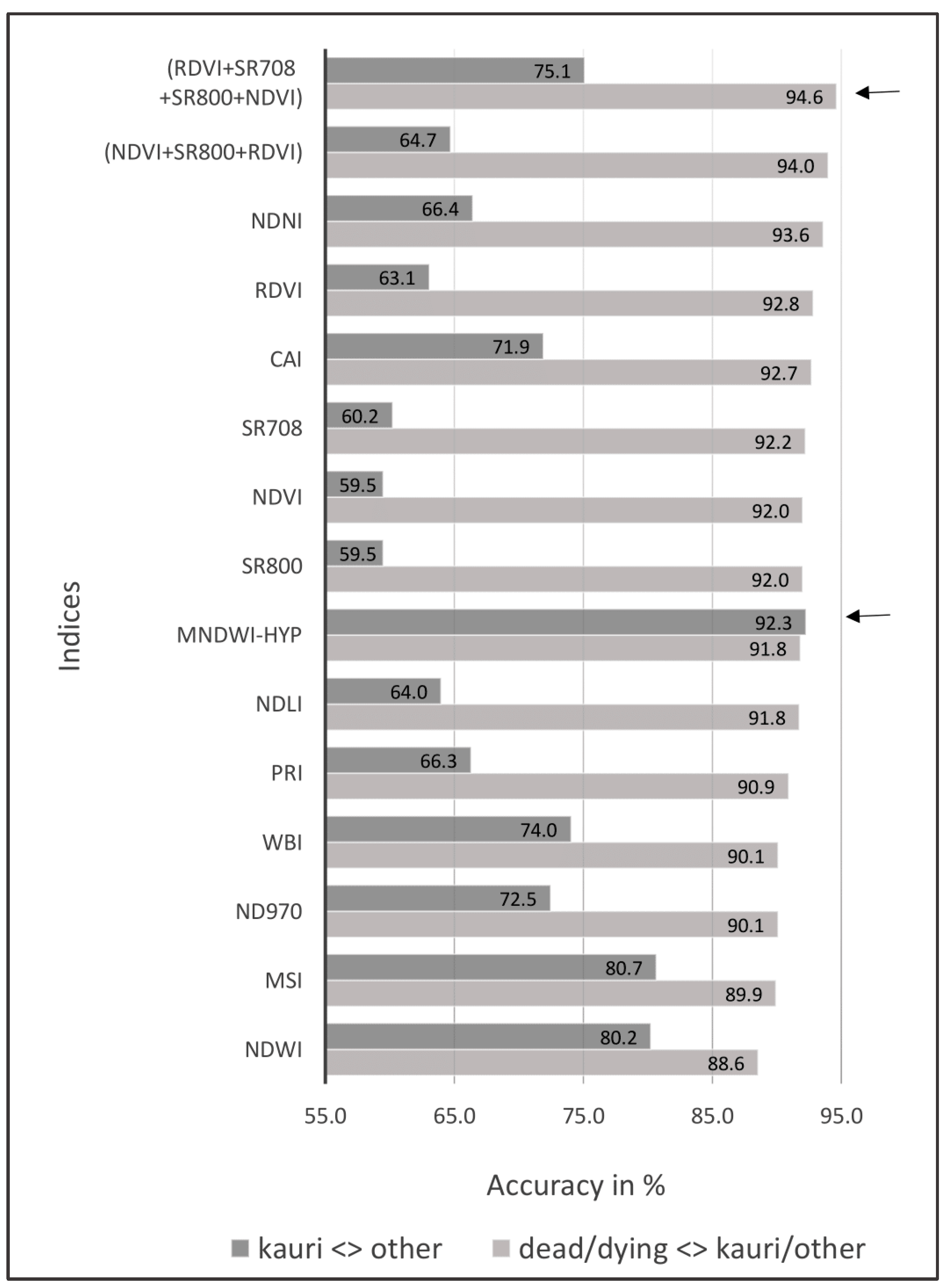
2.4. Band and Indices Selection
- separate “dead/dying trees” from less symptomatic “kauri” and “other” canopy vegetation; and
- distinguish “kauri” from “other” canopy vegetation.
2.5. Selection and Parametrisation of the Classifier
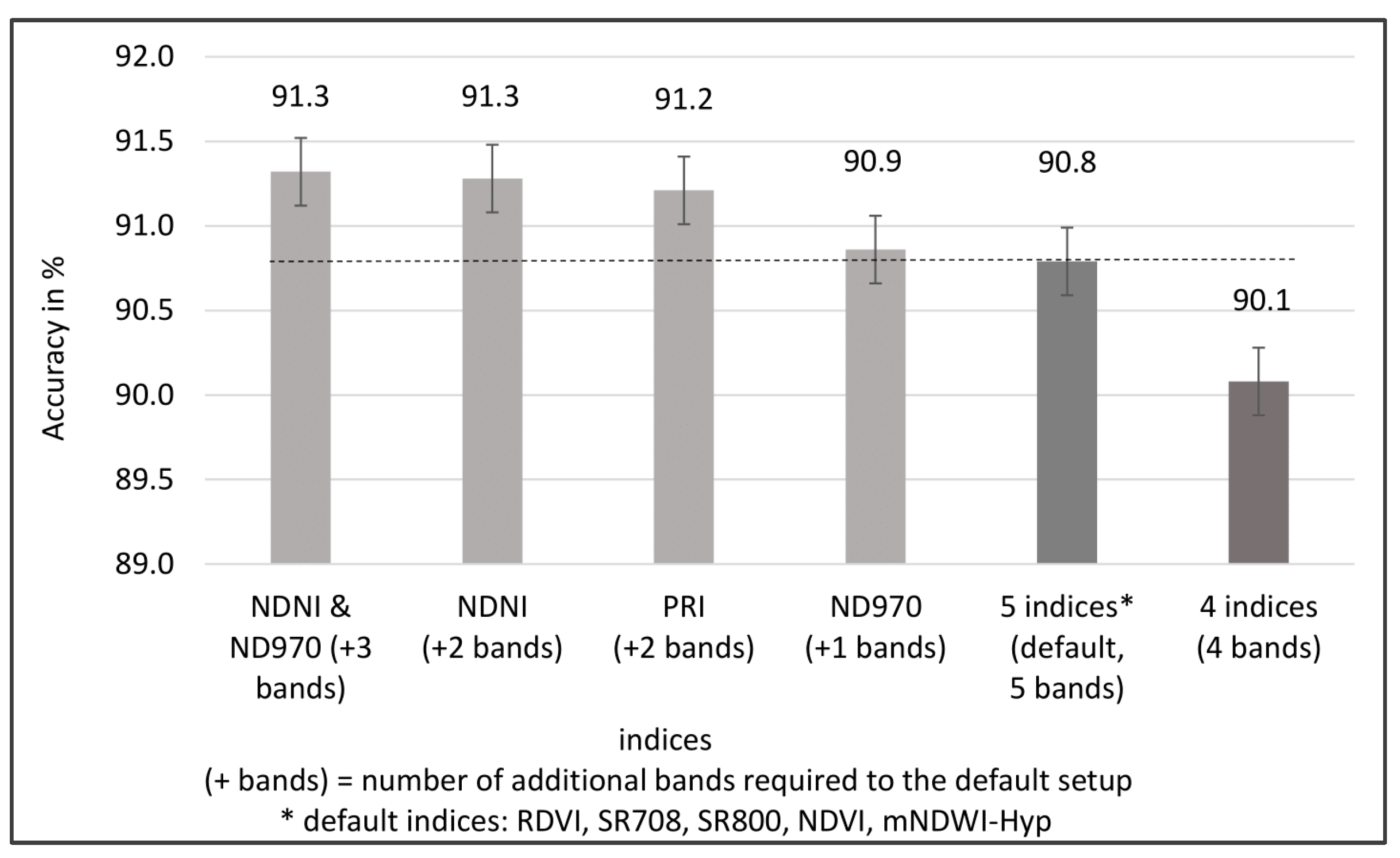
2.6. Tests to Further Improve the Accuracy
- resampling of the original bandwidths to 10 nm, 20 nm and 30 nm;
- addition of three selected texture values on the 800 nm band (data range (7 kernel (k)), variance (7 k) and second moment (3 k)), following the procedure for the indices’ selection;
- addition of a LiDAR CHM as a layer for the classification;
- separate classifications for low and high stands; and
- removal or reclassification of outlier pixels in the training set.
3. Results and Interpretations
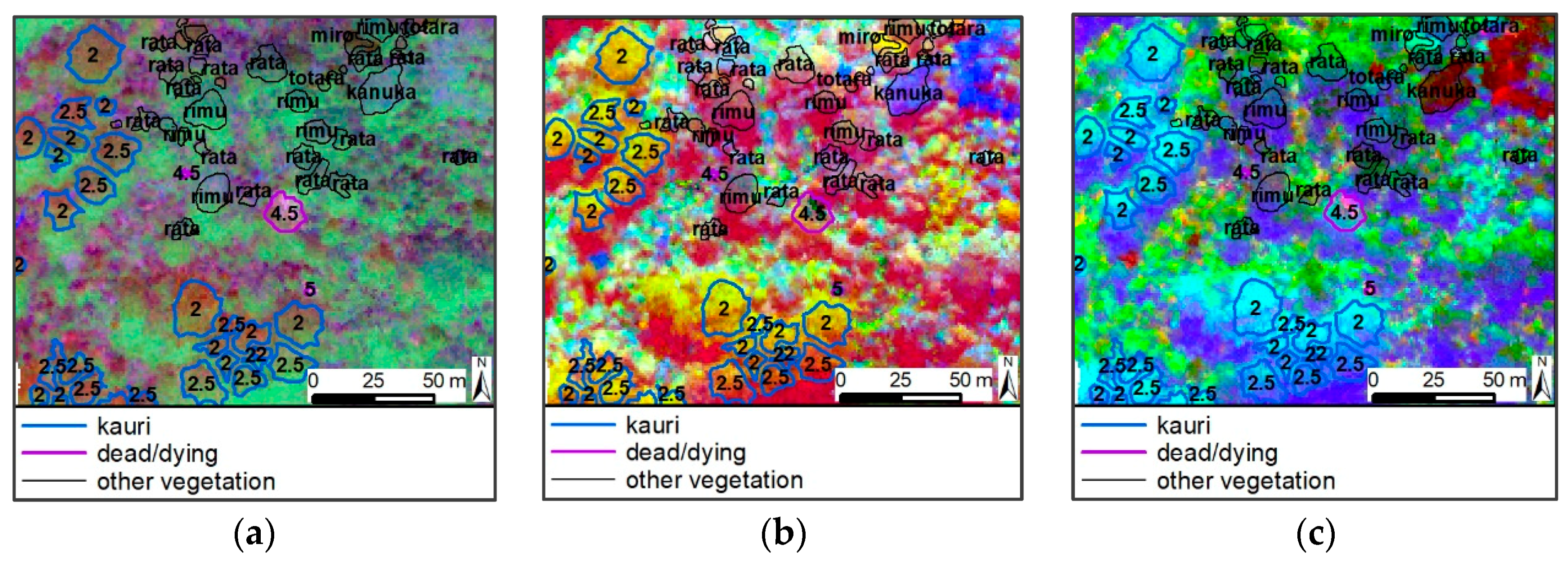
3.1. Results Objective 1: Kauri Spectrum
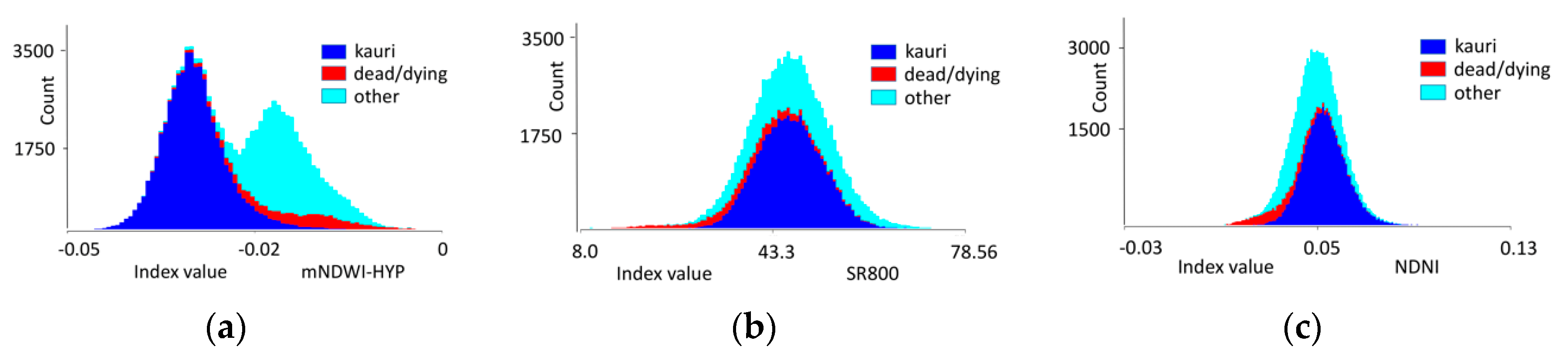
3.2. Results Objective 2: Indices Selection
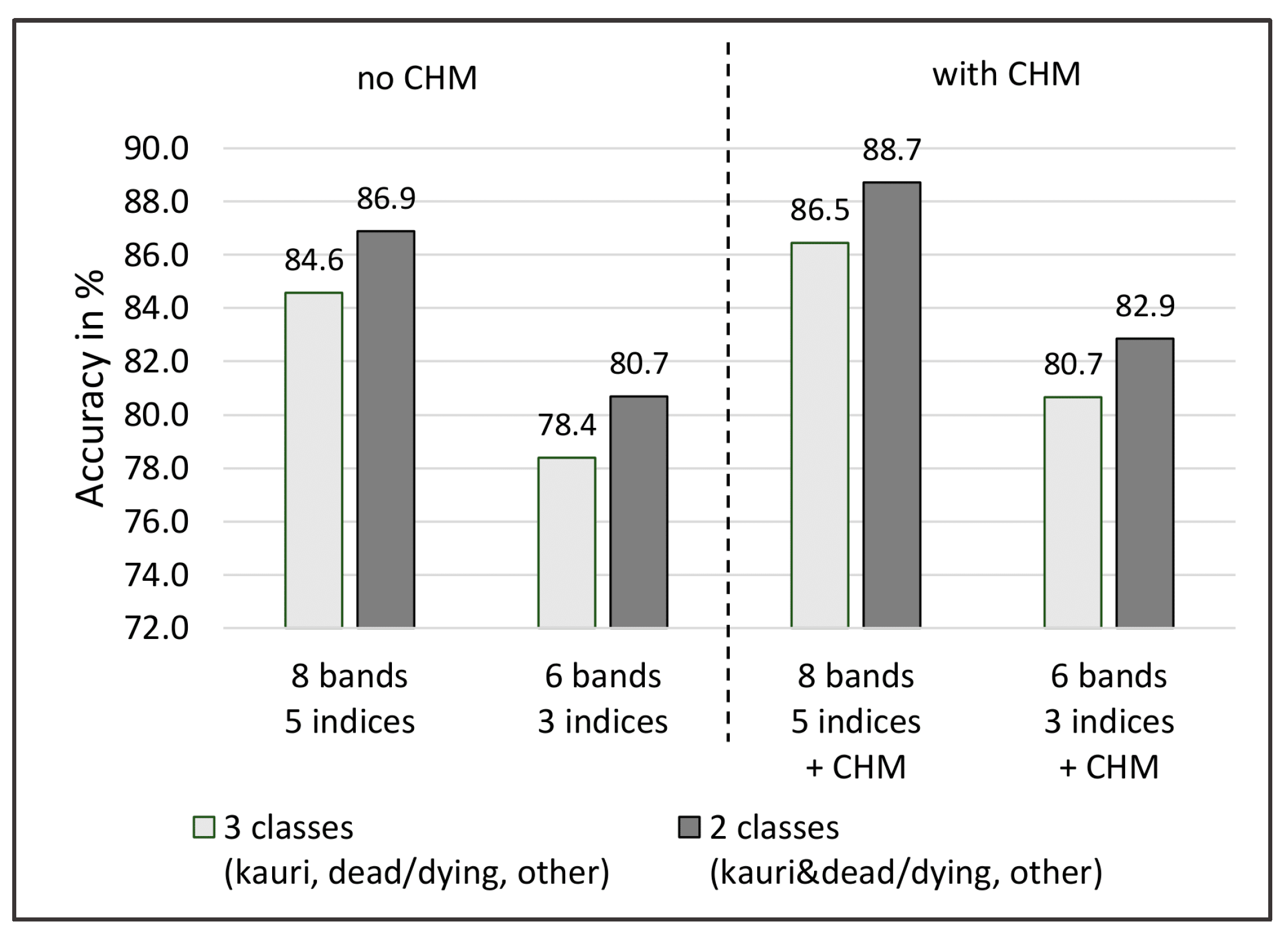
3.3. Results Objective 3: Method Development
4. Discussion and Recommendations for Further Analysis
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| Common Name | Scientific Name | Crowns | Pixels (1) | |
|---|---|---|---|---|
| kauri | kauri | Agathis australis (D.Don) Lindl. ex Loudon | 1483 | 57,700 |
| kauri group/stand | Agathis australis (D.Don) Lindl. ex Loudon | 9 | 850 | |
| dead/dying | kauri dead/dying | Agathis australis (D.Don) Lindl. ex Loudon | 326 | 5329 |
| unknown dead/dying | NN | 91 | 1937 | |
| other dead/dying | NN | 22 | 839 | |
| other 1. priority | kahikatea | Dacrycarpus dacrydioides (A.Rich.) de Laub. | 87 | 2932 |
| kanuka | Kunzea spp. | 218 | 4224 | |
| miro | Prumnopitys ferruginea (D.Don) de Laub. | 21 | 780 | |
| pohutukawa | Metrosideros excelsa Sol. ex Gaertn. | 52 | 2273 | |
| puriri | Vitex lucens Kirk | 40 | 1741 | |
| rata | Metrosideros robusta A.Cunn. | 102 | 6504 | |
| rewarewa | Knightia excelsa R.Br. | 93 | 1082 | |
| rimu | Dacrydium cupressinum Sol. ex G.Forst | 226 | 10,841 | |
| tanekaha | Phyllocladus trichomanoides G.Benn ex D.Don | 126 | 964 | |
| taraire | Beilschmiedia tarairi (A.Cunn.) Benth. & Hook.f. ex Kirk | 11 | 253 | |
| taraire/puriri | NN | 3 | 79 | |
| tōtara | Podocarpus totara D.Don | 37 | 1761 | |
| other 2. priority | broadleaf mix | NN | 16 | 370 |
| cabbage tree | Cordyline australis (G.Forst.) Endl. | 25 | 302 | |
| coprosma sp. | Coprosma spp. | 56 | 790 | |
| flax | Phormium tenax J.R.Forst. & G.Forst. | 3 | 91 | |
| karaka | Corynocarpus laevigatus J.R.Forst. & G.Forst. | 4 | 73 | |
| kowhai | Sophora spp. | 5 | 119 | |
| kawaka | Libocedrus plumosa (D.Don) Sarg. | 4 | 84 | |
| matai | Prumnopitys taxifolia (Sol. ex D.Don) de Laub. | 3 | 103 | |
| nikau | Rhopalostylis sapida H.Wendl. & Drude | 27 | 431 | |
| other pine trees | NN | 4 | 360 | |
| pukatea | Laurelia novae-zelandiae A.Cunn. | 8 | 215 | |
| shrub mix (nikau, tree fern, cabbage…) | NN | 13 | 1346 | |
| tawa | Beilschmiedia tawa (A.Cunn.) Benth. & Hook.f. ex Kirk | 23 | 965 | |
| tree fern | Cyathea spp. | 20 | 294 | |
| other species (not kauri) | NN | 7 | 406 | |
| Total | 3165 | 106,028 |
Appendix B
| “Other” Classified as “Kauri” | Jeffries–Matusita Separability to the Kauri Spectrum | Confusion of Kauri with other Species (2) | |||
|---|---|---|---|---|---|
| Outliers Removed | All Sunlit Pixels | Mean No. of Confused Pixels | Mean Percent Confused | Mean No. of Test Pixels | |
| rimu (1) | 1.948 | 1.995 | 73.3 | 0.2% | 1821.1 |
| totara (1) | 1.929 | 1.979 | 50.3 | 1.1% | 321.6 |
| other pine species (1) (3) | 1.997 | 2.000 | 34.2 | 4.3% | 88.6 |
| tanekaha (1) | 1.860 | 1.992 | 27.7 | 2.1% | 169.5 |
| rata | 1.989 | 1,998 | 25.9 | 0.3% | 1189.3 |
| rewarewa (1) | 1.968 | 1.995 | 8.8 | 2.1% | 175.6 |
| miro | 1.960 | 1.995 | 8.4 | 2.6% | 139.8 |
| kahikatea | 1.983 | 1.993 | 6.4 | 0.7% | 530.5 |
| pohutukawa | 1.997 | 1.999 | 4.6 | 0.8% | 441.8 |
| coprosma sp. | NN | NN | 4.3 | 3.4% | 143.3 |
| kawaka | 1.999 | 2.000 | 3.6 | 4.1% | 709 |
| tawa | 1.996 | 2.000 | 1 | 1.6% | 114.9 |
| puriri | 1.990 | 1.999 | 0.9 | 0.9% | 235.7 |
| scrub mix | 1.988 | 1.997 | 0.9 | 4.9% | 62.6 |
| karaka | 2.000 | 2.000 | 0.7 | 15.8% | 9 |
| nikau | 1.998 | 2.000 | 0.6 | 1.6% | 28.1 |
| pukatea | NN | NN | 0.6 | 3.9% | 18.4 |
| tree fern | 2.000 | 2.000 | 0.3 | 2.1% | 8.7 |
| taraire | 1.990 | 1.999 | 0.2 | 2.1% | 7.7 |
| broadleaf mix | NN | NN | 0.1 | 0.2% | 5.8 |
| other (not kauri) | NN | NN | 0.1 | 0.4% | 2.6 |
| kanuka | 1.996 | 2.000 | no confusion of kauri with these species | ||
| flax | 2.000 | 2.000 | |||
| kanuka flowering | 2.000 | 2.000 | |||
| kowhai | 2.000 | 2.000 | |||
Appendix C
| Name | Equation | Name, Description (Sensitive to…) | Literature |
|---|---|---|---|
| Selected indices for a 5-band sensor | |||
| SR800 (1) | Simple Ratio 800/670 …chlorophyll concentration and Leaf Area Index (LAI) | [73] | |
| SR708 | Simple Ratio 670/800 …chlorophyll concentration and LAI | [66] (modified) | |
| RDVI (1) | Renormalised Difference Vegetation Index …chlorophyll concentration and LAI | [64] | |
| NDVI (1) | Normalised Difference Vegetation Index …chlorophyll concentration and LAI | [74] | |
| mNDWI-Hyp | Modified Normalised Difference Water Index – Hyperion …vegetation canopy water content and canopy structure | [75] | |
| Additional indices for a 6–8-band sensor | |||
| ND970 | Normalised Difference 1074/970 …vegetation canopy water content and canopy structure | This study | |
| PRI | Photochemical Reflectance Index …photosynthetic light use efficiency of carotenoid pigments | [63] | |
| NDNI | Normalised Nitrogen Index …canopy nitrogen | [76] | |
| Other selected indices | |||
| WBI | Water Band Index …relative water content at leaf level | [67] | |
| MSI | Moisture Stress Index …moisture stress in vegetation | [77] | |
| NDWI | Normalised Difference Water Index …total water content | [78] | |
| NDLI | Normalised Difference Lignin Index …leaf and canopy lignin content | [79] | |
| CAI | =0.5*(2000 + 2200) − 2100 | Cellulose Absorption Index …cellulose, dried plant material | [80] |
References
- MPI. Kauri Dieback Sampling Locations; Ministry of Primary Industries: Wellington, New Zealand, 2018.
- Ecroyd, C. Biological flora of New Zealand 8. Agathis australis (D. Don) Lindl.(Araucariaceae) Kauri. N. Z. J. Bot. 1982, 20, 17–36. [Google Scholar] [CrossRef]
- Waipara, N.W.; Hill, S.; Hill, L.M.W.; Hough, E.G.; Horner, I.J. Surveillance methods to determine tree health, distribution of kauri dieback disease and associated pathogens. N. Z. Plant Prot. 2013, 66, 235–241. [Google Scholar] [CrossRef]
- Jamieson, A.; Bassett, I.E.; Hill, L.M.W.; Hill, S.; Davis, A.; Waipara, N.W.; Hough, E.G.; Horner, I.J. Aerial surveillance to detect kauri dieback in New Zealand. N. Z. Plant Prot. 2014, 67, 60–65. [Google Scholar] [CrossRef]
- Bock, C.H.; Poole, G.H.; Parker, P.E.; Gottwald, T.R. Plant disease severity estimated visually, by digital photography and image analysis, and by hyperspectral imaging. Crit. Rev. Plant Sci. 2010, 29, 59–107. [Google Scholar] [CrossRef]
- Jones, H.G.; Vaughan, R.A. Remote Sensing of Vegetation: Principles, Techniques, and Applications; Oxford University Press: New York, NY, USA, 2010. [Google Scholar]
- Thenkabail, P.S.; Lyon, J.G.; Huete, A. Fundamentals, Sensor Systems, Spectral Libraries, and Data Mining for Vegetation; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Sandau, R. Digital Airborne Camera: Introduction and Technology; Springer Science & Business Media: New York, NY, USA, 2009. [Google Scholar]
- Petrie, G.; Walker, A.S. Airborne digital imaging technology: A new overview. Photogramm. Rec. 2007, 22, 203–225. [Google Scholar] [CrossRef]
- Hagen, N.A.; Gao, L.S.; Tkaczyk, T.S.; Kester, R.T. Snapshot advantage: A review of the light collection improvement for parallel high-dimensional measurement systems. Opt. Eng. 2012, 51, 111702. [Google Scholar] [CrossRef]
- Asner, G.P. Hyperspectral remote sensing of canopy chemistry, physiology, and biodiversity in tropical rainforests. In Hyperspectral Remote Sensing of Tropical and Sub-Tropical Forests; CRC Press: Boca Raton, FL, USA, 2008; pp. 261–296. [Google Scholar]
- Dalponte, M.; Ørka, H.O.; Ene, L.T.; Gobakken, T.; Næsset, E. Tree crown delineation and tree species classification in boreal forests using hyperspectral and ALS data. Remote Sens. Environ. 2014, 140, 306–317. [Google Scholar] [CrossRef]
- Jones, T.G.; Coops, N.C.; Sharma, T. Assessing the utility of airborne hyperspectral and LiDAR data for species distribution mapping in the coastal Pacific Northwest, Canada. Remote Sens. Environ. 2010, 114, 2841–2852. [Google Scholar] [CrossRef]
- Richter, R.; Schläpfer, D. ATCOR-4 User Guide, Version 7.3.0, April 2019. In Atmospheric/Topographic Correction for Airborne Imagery; ReSe Applications LLC: Wil, Switzerland, 2019. [Google Scholar]
- Trier, Ø.D.; Salberg, A.-B.; Kermit, M.; Rudjord, Ø.; Gobakken, T.; Næsset, E.; Aarsten, D. Tree species classification in Norway from airborne hyperspectral and airborne laser scanning data. Eur. J. Remote Sens. 2018, 51, 336–351. [Google Scholar] [CrossRef]
- Asner, G.P.; Martin, R.E. Airborne spectranomics: Mapping canopy chemical and taxonomic diversity in tropical forests. Front. Ecol. Environ. 2009, 7, 269–276. [Google Scholar] [CrossRef]
- Carlson, K.M.; Asner, G.P.; Hughes, R.F.; Ostertag, R.; Martin, R.E. Hyperspectral remote sensing of canopy biodiversity in Hawaiian lowland rainforests. Ecosystems 2007, 10, 536–549. [Google Scholar] [CrossRef]
- Clark, M.L. Identification of Canopy Species in Tropical Forests Using Hyperspectral Data. In Huete, Hyperspectral Remote Sensing of Vegetation, 2nd ed.; Thenkabail, P.S., Lyon, J.G., Eds.; Biophysical and Biochemical Characterisation and Plant Species Studies; CRC Press: Boca Raton, FL, USA, 2018; Volume 3, p. 423. [Google Scholar]
- Féret, J.-B.; Asner, G.P. Tree species discrimination in tropical forests using airborne imaging spectroscopy. IEEE Trans. Geosci. Remote Sens. 2013, 51, 73–84. [Google Scholar] [CrossRef]
- Ferreira, M.P.; Zortea, M.; Zanotta, D.C.; Shimabukuro, Y.E.; de Souza Filho, C.R. Mapping tree species in tropical seasonal semi-deciduous forests with hyperspectral and multispectral data. Remote Sens. Environ. 2016, 179, 66–78. [Google Scholar] [CrossRef]
- Dalponte, M.; Bruzzone, L.; Gianelle, D. Fusion of hyperspectral and LIDAR remote sensing data for classification of complex forest areas. IEEE Trans. Geosci. Remote Sens. 2008, 46, 1416–1427. [Google Scholar] [CrossRef]
- Peerbhay, K.Y.; Mutanga, O.; Ismail, R. Commercial tree species discrimination using airborne AISA Eagle hyperspectral imagery and partial least squares discriminant analysis (PLS-DA) in KwaZulu–Natal, South Africa. ISPRS J. Photogramm. Remote Sens. 2013, 79, 19–28. [Google Scholar] [CrossRef]
- Shen, X.; Cao, L. Tree-species classification in subtropical forests using airborne hyperspectral and LiDAR data. Remote Sens. 2017, 9, 1180. [Google Scholar] [CrossRef]
- Asner, G.P.; Warner, A.S. Canopy shadow in IKONOS satellite observations of tropical forests and savannas. Remote Sens. Environ. 2003, 87, 521–533. [Google Scholar] [CrossRef]
- Kempeneers, P.; Vandekerkhove, K.; Devriendt, F.; van Coillie, F. Propagation of shadow effects on typical remote sensing applications in forestry. In Proceedings of the 2013 5th Workshop on Hyperspectral Image and Signal Processing: Evolution in Remote Sensing (WHISPERS), Gainesville, FL, USA, 26–28 June 2013. [Google Scholar]
- Blaschke, T. Object based image analysis for remote sensing. ISPRS J. Photogramm. Remote Sens. 2010, 65, 2–16. [Google Scholar] [CrossRef]
- Heumann, B.W. An object-based classification of mangroves using a hybrid decision tree—Support vector machine approach. Remote Sens. 2011, 3, 2440–2460. [Google Scholar] [CrossRef]
- Machala, M.; Zejdová, L. Forest mapping through object-based image analysis of multispectral and LiDAR aerial data. Eur. J. Remote Sens. 2014, 47, 117–131. [Google Scholar] [CrossRef]
- Leckie, D.; Gougeon, F.; Hill, D.; Quinn, R.; Armstrong, L.; Shreenan, R. Combined high-density lidar and multispectral imagery for individual tree crown analysis. Can. J. Remote Sens. 2003, 29, 633–649. [Google Scholar] [CrossRef]
- Ghosh, A.; Ewald Fassnacht, F.; Joshi, P.K.; Koch, B. A framework for mapping tree species combining hyperspectral and LiDAR data: Role of selected classifiers and sensor across three spatial scales. Int. J. Appl. Earth Obs. Geoinf. 2014, 26, 49–63. [Google Scholar] [CrossRef]
- Zhang, C.; Qiu, F. Mapping individual tree species in an urban forest using airborne lidar data and hyperspectral imagery. Photogramm. Eng. Remote Sens. 2012, 78, 1079–1087. [Google Scholar] [CrossRef]
- Buddenbaum, H.; Schlerf, M.; Hill, J. Classification of coniferous tree species and age classes using hyperspectral data and geostatistical methods. Int. J. Remote Sens. 2005, 26, 5453–5465. [Google Scholar] [CrossRef]
- Baldeck, C.A.; Asner, G.P.; Martin, R.E.; Anderson, C.B.; Knapp, D.E.; Kellner, J.R.; Wright, S.J. Operational tree species mapping in a diverse tropical forest with airborne imaging spectroscopy. PLoS ONE 2015, 10, e0118403. [Google Scholar] [CrossRef] [PubMed]
- Fassnacht, F.E.; Latifi, H.; Stereńczak, K.; Modzelewska, A.; Lefsky, M.; Waser, L.T.; Straub, C.; Ghosh, A. Review of studies on tree species classification from remotely sensed data. Remote Sens. Environ. 2016, 186, 64–87. [Google Scholar] [CrossRef]
- Holmgren, J.; Persson, Å.; Söderman, U. Species identification of individual trees by combining high resolution LiDAR data with multi-spectral images. Int. J. Remote Sens. 2008, 29, 1537–1552. [Google Scholar] [CrossRef]
- Singers, N.; Osborne, B.; Lovegrove, T.; Jamieson, A.; Boow, J.; Sawyer, J.; Hill, K.; Andrews, J.; Hill, S.; Webb, C. Indigenous terrestrial and wetland ecosystems of Auckland; Auckland Council: Auckland, New Zealand, 2017. Available online: http://www.knowledgeauckland.org.nz (accessed on 20 July 2019).
- Steward, G.A.; Beveridge, A.E. A review of New Zealand kauri (Agathis australis (D. Don) Lindl.): Its ecology, history, growth and potential for management for timber. N. Z. J. For. Sci. 2010, 40, 33–59. [Google Scholar]
- Macinnis-Ng, C.; Schwendenmann, L. Litterfall, carbon and nitrogen cycling in a southern hemisphere conifer forest dominated by kauri (Agathis australis) during drought. Plant Ecol. 2015, 216, 247–262. [Google Scholar] [CrossRef]
- Meiforth, J. Photos, Waitakere Ranges. Photos taken during fieldwork in January to March 2016. 2016. [Google Scholar]
- Jongkind, A.; Buurman, P. The effect of kauri (Agathis australis) on grain size distribution and clay mineralogy of andesitic soils in the Waitakere Ranges, New Zealand. Geoderma 2006, 134, 171–186. [Google Scholar] [CrossRef]
- Chappell, P.R. The Climate and Weather of Auckland; Niwa Science and Technology Series; NIWA: Auckland, New Zealand, 2012. [Google Scholar]
- LINZ. NZ Topo50. Topographical Map for New Zealand. 2019. Available online: https://www.linz.govt.nz/land/maps/topographic-maps/topo50-maps (accessed on 20 July 2019).
- Khosravipour, A.; Skidmore, A.K.; Isenburg, M. Generating spike-free digital surface models using LiDAR raw point clouds: A new approach for forestry applications. Int. J. Appl. Earth Obs. Geoinf. 2016, 52, 104–114. [Google Scholar] [CrossRef]
- Auckland Council, A. Auckland 0.075m Urban Aerial Photos (2017), RGB, Waitakere Ranges. 2017. Available online: https://data.linz.govt.nz/layer/95497-auckland-0075m-urban-aerial-photos-2017/ (accessed on 12 April 2019).
- Datt, B.; McVicar, T.R.; van Niel, T.G.; Jupp, D.L.B.; Pearlman, J.S. Preprocessing EO-1 Hyperion hyperspectral data to support the application of agricultural indexes. IEEE Trans. Geosci. Remote Sens. 2003, 41, 1246–1259. [Google Scholar] [CrossRef]
- Schlaepfer, D. PARGE—Parametric Geocoding & Orthorectification for Airborne Optical Scanner Data. Available online: http://www.rese.ch/products/parge/ (accessed on 21 March 2019).
- Adeline, K.R.M.; Chen, M.; Briottet, X.; Pang, S.K.; Paparoditis, N. Shadow detection in very high spatial resolution aerial images: A comparative study. ISPRS J. Photogramm. Remote Sens. 2013, 80, 21–38. [Google Scholar] [CrossRef]
- Trimble. eCognition® Developer 9.3. User Guide; Trimble Germany GmbH: Munich, Germany, 2018. [Google Scholar]
- Green, A.A.; Berman, M.; Switzer, P.; Craig, M.D. A transformation for ordering multispectral data in terms of image quality with implications for noise removal. IEEE Trans. Geosci. Remote Sens. 1988, 26, 65–74. [Google Scholar] [CrossRef]
- Witten, I.H.; Frank, E.; Hall, M.A.; Pal, C.J. Data Mining: Practical Machine Learning Tools and Techniques; Morgan Kaufmann: San Francisco, CA, USA, 2016. [Google Scholar]
- Belgiu, M.; Drăguţ, L. Random forest in remote sensing: A review of applications and future directions. ISPRS J. Photogramm. Remote Sens. 2016, 114, 24–31. [Google Scholar] [CrossRef]
- Dalponte, M.; Ørka, H.O.; Gobakken, T.; Gianelle, D.; Næsset, E. Tree species classification in boreal forests with hyperspectral data. IEEE Trans. Geosci. Remote Sens. 2013, 51, 2632–2645. [Google Scholar] [CrossRef]
- Fassnacht, F.E.; Neumann, C.; Förster, M.; Buddenbaum, H.; Ghosh, A.; Clasen, A.; Joshi, P.K.; Koch, B. Comparison of feature reduction algorithms for classifying tree species with hyperspectral data on three central European test sites. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 2547–2561. [Google Scholar] [CrossRef]
- Raczko, E.; Zagajewski, B. Comparison of support vector machine, random forest and neural network classifiers for tree species classification on airborne hyperspectral APEX images. Eur. J. Remote Sens. 2017, 50, 144–154. [Google Scholar] [CrossRef]
- Bollandsås, O.M.; Maltamo, M.; Gobakken, T.; Næsset, E. Comparing parametric and non-parametric modelling of diameter distributions on independent data using airborne laser scanning in a boreal conifer forest. Forestry 2013, 86, 493–501. [Google Scholar] [CrossRef]
- James, G.; Witten, D.; Hastie, T.; Tibshirani, R. An Introduction to Statistical Learning; Springer: New York, NY, USA, 2013; Volume 112. [Google Scholar]
- Bruzzone, L.; Chi, M.; Marconcini, M. A novel transductive SVM for semisupervised classification of remote-sensing images. IEEE Trans. Geosci. Remote Sens. 2006, 44, 3363–3373. [Google Scholar] [CrossRef]
- Chang, C.-C.; Lin, C.-J. LIBSVM: A Library for Support Vector Machines [EB/OL]. 2001. Available online: https://www.csie.ntu.edu.tw/~cjlin/libsvm/ (accessed on 6 May 2019).
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Richards, J.A. Remote Sensing Digital Image Analysis; Springer: Berlin/Heidelberg, Germany, 1999; Volume 3. [Google Scholar]
- Jeffreys, H. An invariant form for the prior probability in estimation problems. Proc. R. Soc. Lond. Ser. A. Math. Phys. Sci. 1946, 186, 453–461. [Google Scholar]
- Serrano, L.; Penuelas, J.; Ustin, S.L. Remote sensing of nitrogen and lignin in Mediterranean vegetation from AVIRIS data: Decomposing biochemical from structural signals. Remote Sens. Environ. 2002, 81, 355–364. [Google Scholar] [CrossRef]
- Gamon, J.; Penuelas, J.; Field, C. A narrow-waveband spectral index that tracks diurnal changes in photosynthetic efficiency. Remote Sens. Environ. 1992, 41, 35–44. [Google Scholar] [CrossRef]
- Roujean, J.-L.; Breon, F.-M. Estimating PAR absorbed by vegetation from bidirectional reflectance measurements. Remote Sens. Environ. 1995, 51, 375–384. [Google Scholar] [CrossRef]
- Datt, B. A new reflectance index for remote sensing of chlorophyll content in higher plants: Tests using Eucalyptus leaves. J. Plant Physiol. 1999, 154, 30–36. [Google Scholar] [CrossRef]
- Datt, B. Remote sensing of chlorophyll a, chlorophyll b, chlorophyll a + b, and total carotenoid content in eucalyptus leaves. Remote Sens. Environ. 1998, 66, 111–121. [Google Scholar] [CrossRef]
- Peñuelas, J.; Filella, I.; Biel, C.; Serrano, L.; Savé, R. The reflectance at the 950–970 nm region as an indicator of plant water status. Int. J. Remote Sens. 1993, 14, 1887–1905. [Google Scholar] [CrossRef]
- Asner, G.P. Biophysical and biochemical sources of variability in canopy reflectance. Remote Sens. Environ. 1998, 64, 234–253. [Google Scholar] [CrossRef]
- Clark, M.L.; Roberts, D.; Clark, D. Hyperspectral discrimination of tropical rain forest tree species at leaf to crown scales. Remote Sens. Environ. 2005, 96, 375–398. [Google Scholar] [CrossRef]
- Hill, J. State-of-the-Art and Review of Algorithms with Relevance for Retrieving Biophysical and Structural Information on Forests and Natural Vegetation with Hyper-Spectral Remote Sensing Systems. In Hyperspectral algorithms: report in the frame of EnMAP Preparation Activities; Kaufmann, H., Ed.; Scientific Technical Report (STR); 10/08; Deutsches GeoForschungsZentrum GFZ: Potsdam, Germany, 2010. [Google Scholar]
- Loizzo, R.; Guarini, R.; Longo, F.; Scopa, T.; Formaro, R.; Facchinetti, C.; Varacalli, G. PRISMA: The Italian hyperspectral mission. In Proceedings of the IGARSS 2018—2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018. [Google Scholar]
- Guanter, L.; Kaufmann, H.; Segl, K.; Foerster, S.; Rogass, C.; Chabrillat, S.; Kuester, T.; Hollstein, A.; Rossner, G.; Chlebek, C.; et al. The EnMAP spaceborne imaging spectroscopy mission for earth observation. Remote Sens. 2015, 7, 8830–8857. [Google Scholar] [CrossRef]
- Birth, G.S.; McVey, G.R. Measuring the Color of Growing Turf with a Reflectance Spectrophotometer 1. Agron. J. 1968, 60, 640–643. [Google Scholar] [CrossRef]
- Rouse, J.W., Jr.; Haas, R.H.; Schell, J.A.; Deering, D.W. Monitoring the Vernal Advancement and Retrogradation (Green Wave Effect) of Natural Vegetation; NASA Technical Report; Texas A&M University: College Station, TX, USA, 1973. [Google Scholar]
- Ustin, S.L.; Roberts, D.A.; Gardner, M.; Dennison, P. Evaluation of the potential of Hyperion data to estimate wildfire hazard in the Santa Ynez Front Range, Santa Barbara, California. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Toronto, ON, Canada, 24–28 June 2002. [Google Scholar]
- Fourty, T.; Baret, F.; Jacquemoud, S.; Schmuck, G.; Verdebout, J. Leaf optical properties with explicit description of its biochemical composition: Direct and inverse problems. Remote Sens. Environ. 1996, 56, 104–117. [Google Scholar] [CrossRef]
- Hunt, E.R., Jr.; Rock, B.N. Detection of changes in leaf water content using near-and middle-infrared reflectances. Remote Sens. Environ. 1989, 30, 43–54. [Google Scholar]
- Gao, B.-C. NDWI—A normalized difference water index for remote sensing of vegetation liquid water from space. Remote Sens. Environ. 1996, 58, 257–266. [Google Scholar] [CrossRef]
- Melillo, J.M.; Aber, J.D.; Muratore, J.F. Nitrogen and lignin control of hardwood leaf litter decomposition dynamics. Ecology 1982, 63, 621–626. [Google Scholar] [CrossRef]
- Nagler, P.L.; Inoue, Y.; Glenn, E.P.; Russ, A.L.; Daughtry, C.S.T. Cellulose absorption index (CAI) to quantify mixed soil–plant litter scenes. Remote Sens. Environ. 2003, 87, 310–325. [Google Scholar] [CrossRef]

| Spectral Range | Electromagnetic Wavelengths |
|---|---|
| Visible (VIS) | 437–700 nm 1 |
| 1st near-infrared (NIR1) | 700–ca. 970 nm 2 |
| 2nd near-infrared (NIR2) | 970–1327 nm |
| 1st short wave infrared (SWIR1) | 1467–1771 nm |
| 2nd short wave infrared (SWIR2) | 1994–2337 nm 1 |
| Classified | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Classified As --> | Kauri | Kahikatea | Totara | Kanuka | Rimu | Rewarewa | Tanekaha | Rata | Miro | Puriri | Pohutu-kawa | Total | Producers Accuracy | |
| Reference | Kauri | 7412 | 1 | 2 | 0 | 50 | 0 | 1 | 13 | 0 | 0 | 0 | 7479 | 99.1 |
| Kahikatea | 4 | 2043 | 1 | 10 | 65 | 3 | 0 | 11 | 4 | 7 | 0 | 2148 | 95.1 | |
| Totara | 22 | 11 | 903 | 5 | 49 | 2 | 1 | 182 | 6 | 5 | 8 | 1194 | 75.6 | |
| Kanuka | 3 | 6 | 1 | 3191 | 21 | 0 | 2 | 65 | 0 | 1 | 17 | 3307 | 96.5 | |
| Rimu | 25 | 36 | 6 | 14 | 4446 | 5 | 0 | 97 | 8 | 7 | 0 | 4644 | 95.7 | |
| Rewarewa | 13 | 38 | 5 | 7 | 18 | 229 | 0 | 81 | 1 | 6 | 4 | 402 | 57.0 | |
| Tanekaha | 6 | 9 | 11 | 3 | 15 | 0 | 204 | 38 | 0 | 0 | 0 | 286 | 71.3 | |
| Rata | 6 | 7 | 4 | 2 | 41 | 1 | 0 | 4988 | 15 | 24 | 11 | 5099 | 97.8 | |
| Miro | 9 | 6 | 21 | 1 | 25 | 3 | 0 | 49 | 381 | 1 | 4 | 500 | 76.2 | |
| Puriri | 0 | 8 | 0 | 5 | 2 | 3 | 0 | 34 | 1 | 1440 | 22 | 1515 | 95.0 | |
| Pohutukawa | 7 | 0 | 0 | 45 | 3 | 0 | 0 | 46 | 0 | 44 | 1964 | 2109 | 93.1 | |
| Total | 7507 | 2165 | 954 | 3283 | 4735 | 246 | 208 | 5604 | 416 | 1535 | 2030 | 28,683 | ||
| Users Accuracy | 98.7 | 94.4 | 94.7 | 97.2 | 93.9 | 93.1 | 98.1 | 89.0 | 91.6 | 93.8 | 96.7 | 94.8 | ||
| Index Abbrev. | Name | Equation | Wavelengths | Literature | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| RDVI (1) (2) | Renormalised Difference Vegetation Index | RDVI = (R800-R675)/ √(R800+R675) | 675 | 800 | [64] | ||||||
| GM1 | Gitelson and Merzlyak Index 1 | GM1 = R750/R550 | 550 | 750 | [65] | ||||||
| SRb2 (2) | Simple Ratio Chlorophyll b2 | SRchlb2 = R675/R710 | 675 | 710 | [66] | ||||||
| LCI (1) (2) | Leaf Chlorophyll Index | LCI = (R850-R710)/ (R850+R675) | 675 | 710 | 850 | [65] | |||||
| WBI (1) | Water Band Index | WBI = 900/970 | 900 | 970 | [67] | ||||||
| 2 Classes | 3 Classes | User’s Accuracy | Producer’s Accuracy | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| All DM | ≥3 m | <3 m | All DM | ≥3 m | <3 m | Kauri | Dead/Dying | Other | Kauri | Dead/Dying | Other | ||
| Default | |||||||||||||
| Test A | Training and test: all outliers included. Image on original bandwidths for the default 5 indices on 5 bands | 92.1 (0.1) | 92.5 (0.1) | 66.9 (1.7) | 89.9 (0.2) | 90.3 (0.2) | 64.6 (1.7) | 93.1 (0.9) | 78.7 (1.6) | 86.7 (0.8) | 94.3 (0.3) | 45.0 (1.3) | 93.0 (1.0) |
| Test B1 | Resampling to 10 nm | 93.0 (0.1) | 93.4 (0.1) | 67.2 (1.1) | 91.0 (0.1) | 91.4 (0.1) | 65.0 (1.5) | ||||||
| Test B2 | Resampling to 20 nm | 92.8 (0.2) | 93.2 (0.2) | 67.0 (2.8) | 90.7 (0.2) | 91.1 (0.2) | 64.7 (3.0) | ||||||
| Test C | Separate classification for low and high stands | 93.4 (0.1) | 93.7 (0.1) | 70.8 (1.9) | 91.4 (0.1) | 91.7 (0.1) | 67.5 (1.8) | ||||||
| Test D | Outliers removed in the training set that confuse “kauri” with “other” and pixels that cause confusion with “dead/dying” < 3 m diameter | 92.6 (0.1) | 93.0 (0.1) | 68.3 (1.4) | 90.6 (0.1) | 91.0 (0.1) | 65.8 (1.3) | ||||||
| Final | |||||||||||||
| Test E | Training and test: all outliers included. 5 bands (10 nm), 5 indices; no textures, low and high stands separated. No post-processing | 93.4 (0.1) | 93.8 (0.1) | 69.0 (2.1) | 91.3 (0.1) | 91.7 (0.1) | 66.6 (2.0) | 94.6 (0.2) | 80.3 (0.7) | 88.3 (0.3) | 94.8 (0.2) | 52.1 (1.4) | 94.7 (0.3) |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Meiforth, J.J.; Buddenbaum, H.; Hill, J.; Shepherd, J.; Norton, D.A. Detection of New Zealand Kauri Trees with AISA Aerial Hyperspectral Data for Use in Multispectral Monitoring. Remote Sens. 2019, 11, 2865. https://doi.org/10.3390/rs11232865
Meiforth JJ, Buddenbaum H, Hill J, Shepherd J, Norton DA. Detection of New Zealand Kauri Trees with AISA Aerial Hyperspectral Data for Use in Multispectral Monitoring. Remote Sensing. 2019; 11(23):2865. https://doi.org/10.3390/rs11232865
Chicago/Turabian StyleMeiforth, Jane J., Henning Buddenbaum, Joachim Hill, James Shepherd, and David A. Norton. 2019. "Detection of New Zealand Kauri Trees with AISA Aerial Hyperspectral Data for Use in Multispectral Monitoring" Remote Sensing 11, no. 23: 2865. https://doi.org/10.3390/rs11232865
APA StyleMeiforth, J. J., Buddenbaum, H., Hill, J., Shepherd, J., & Norton, D. A. (2019). Detection of New Zealand Kauri Trees with AISA Aerial Hyperspectral Data for Use in Multispectral Monitoring. Remote Sensing, 11(23), 2865. https://doi.org/10.3390/rs11232865