Transferred Multi-Perception Attention Networks for Remote Sensing Image Super-Resolution
Abstract
1. Introduction
- Present MPSR, a parallel two-branch structure, which achieves multi-perception learning in image patterns and multi-level information adaptive weighted fusion simultaneously.
- Propose residual channel attention group (RCAG), where the enhanced residual block (ERB) serves as the main building block to fully capture the prior information from diverse perception levels and the attention mechanism allows the group to focus on more informative feature maps adaptively.
- Train the proposed model with a supervised transfer learning strategy to cope with the lack of real HR remote sensing training samples and further boost the reconstruction ability of the proposed network toward remote sensing images.
2. Materials and Methods
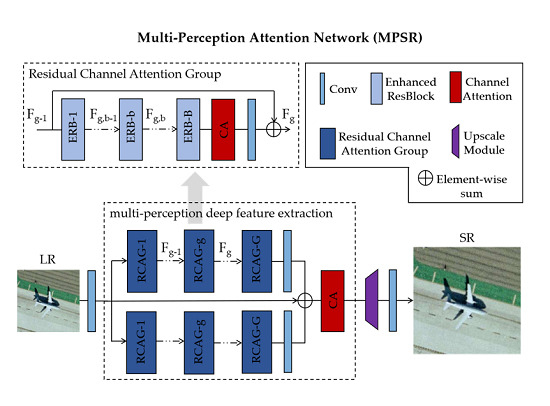
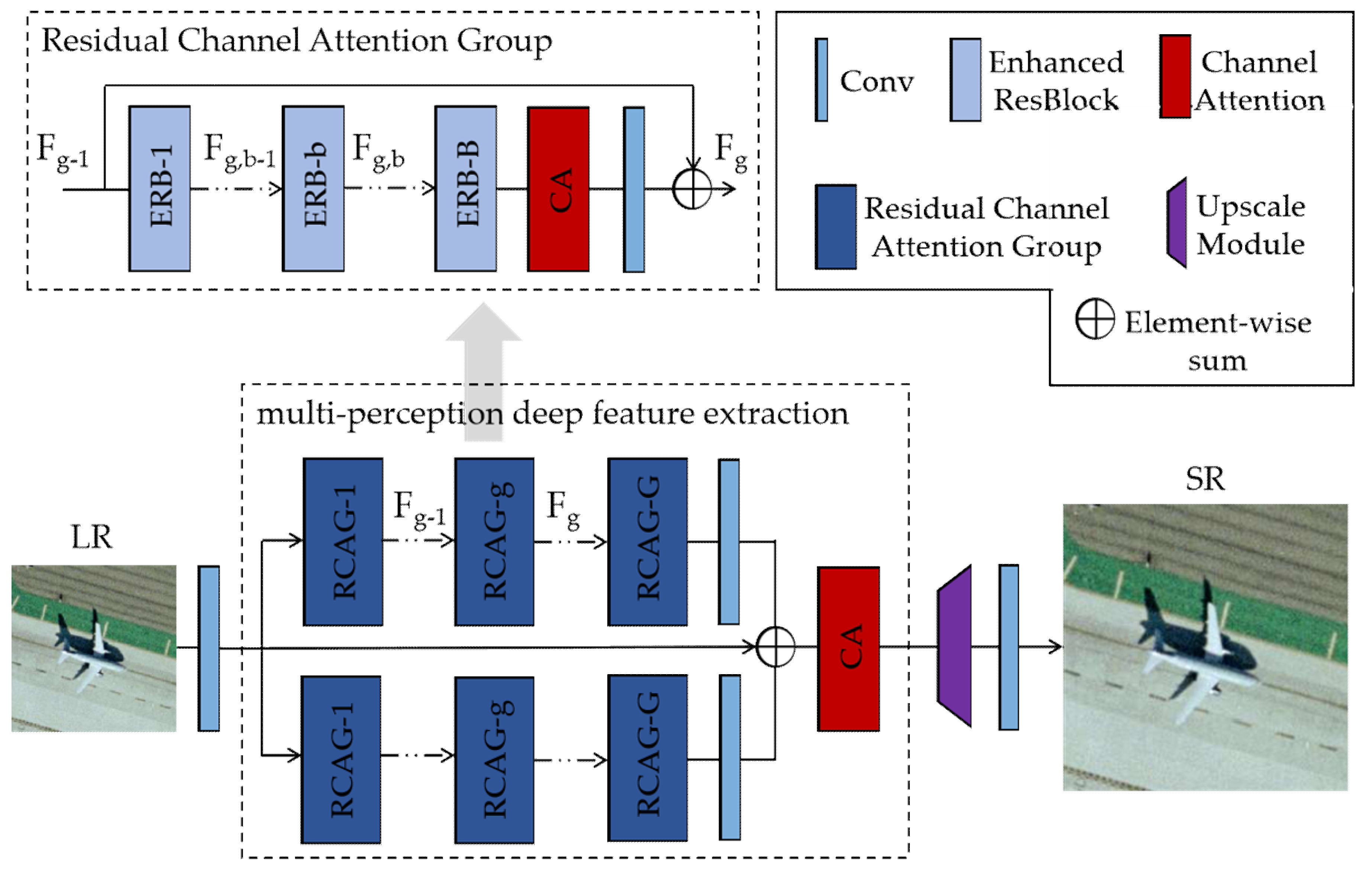
2.1. Network Architecture
2.2. Loss Function
2.3. Multi-Perception Learning
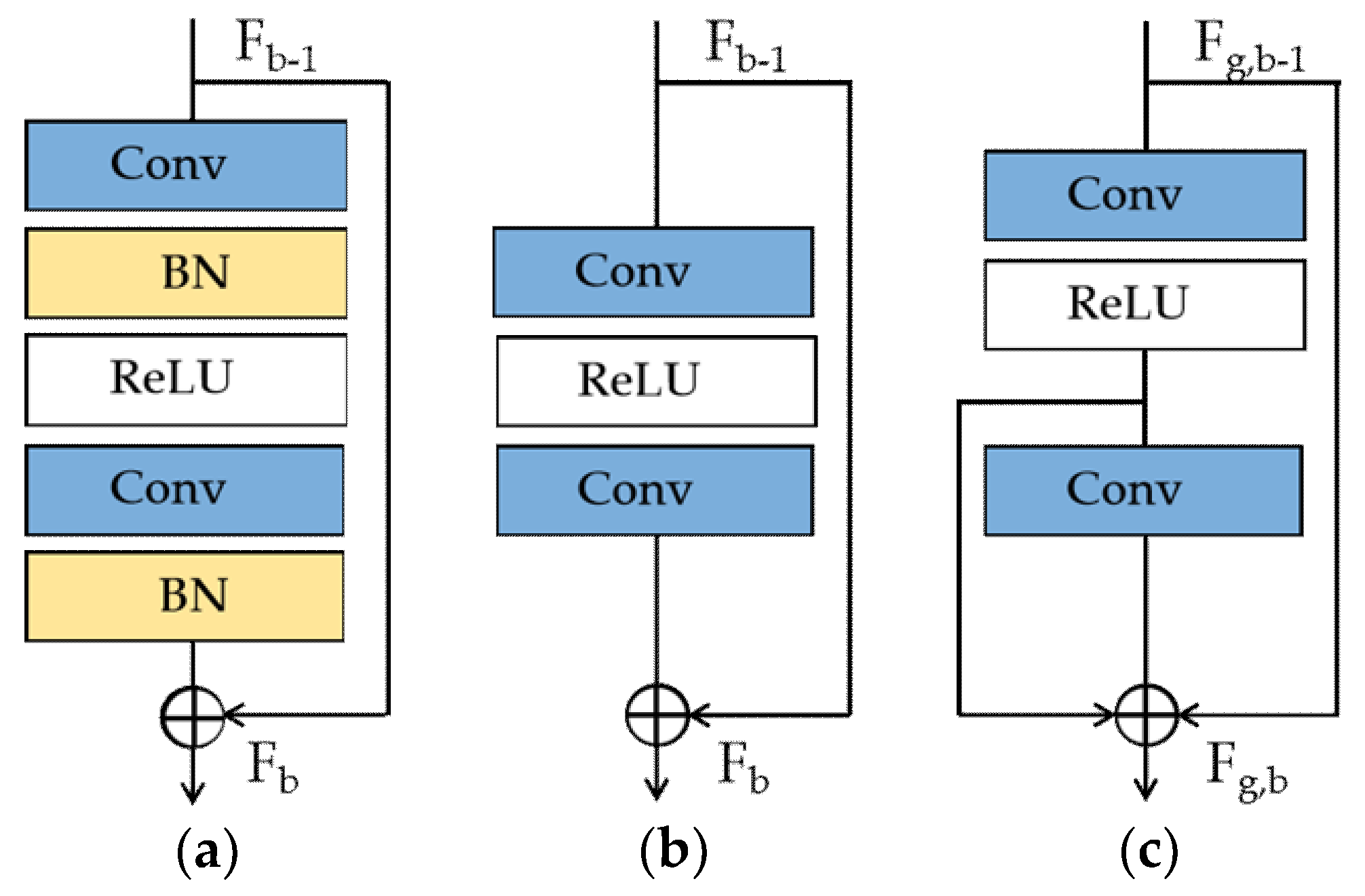
2.3.1. Enhanced Residual Block
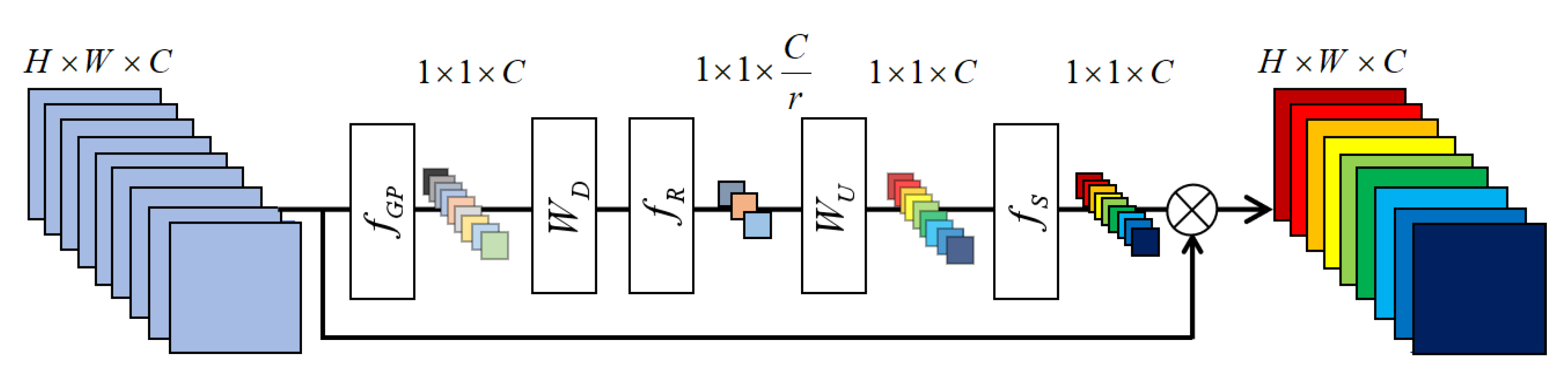
2.3.2. Residual Channel Attention Group
2.3.3. Multi-Perception Learning Overview
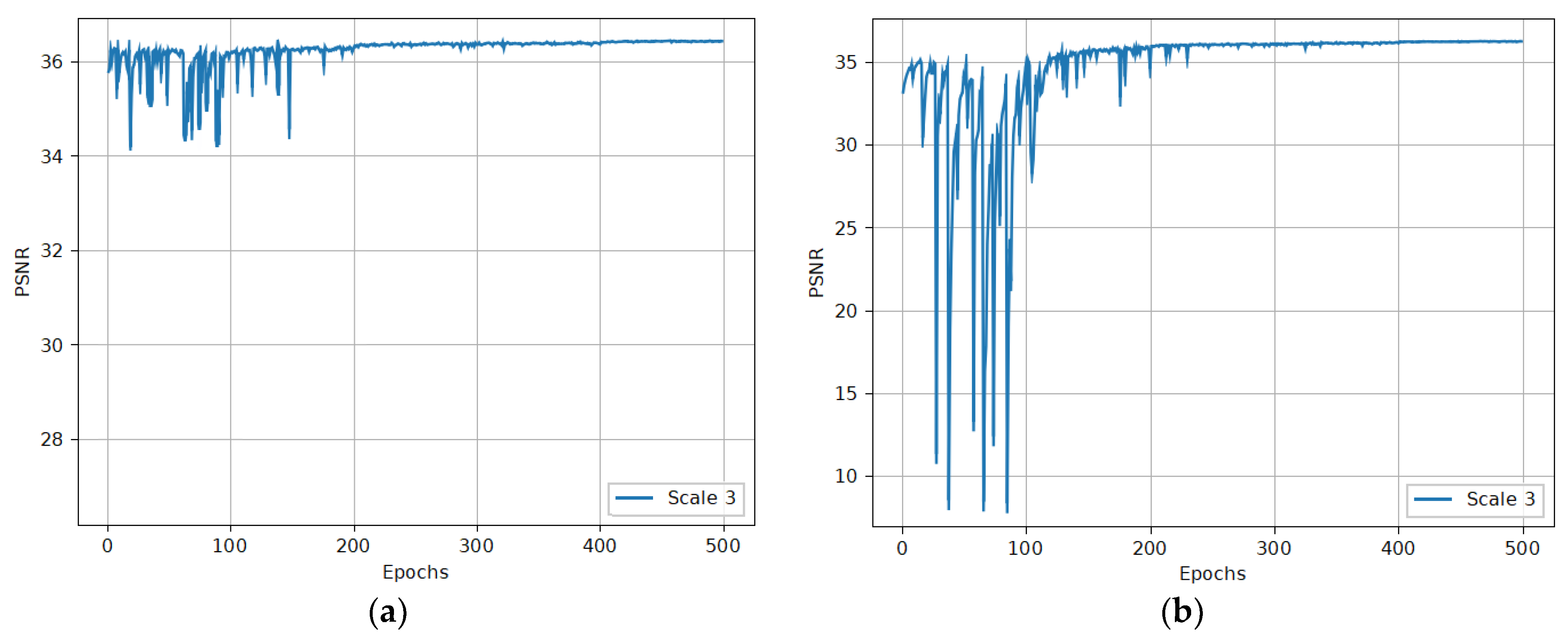
2.4. Transfer Training Strategy
3. Results
3.1. Experiment Settings
- DIV2K [34] contains 800 natural images for training. The image resolution is of around 2K.
- UC MERCED [35] contains 2100 images in size of 256 × 256 pixel. The pixel resolution is 0.3 m.
- Set5 [36] is a classical dataset which only consists of 5 test images.
- Set14 [37] has 14 test images which contain more categories compared to Set5.
- BSD100 [38] has 100 rich and delicate images ranging from natural to object-specific.
- Urban100 [39] is a relatively more recent dataset composed of 100 images, the focus of which is on urban scenes.
3.2. Model Design and Performance
3.3. Comparisons to State-of-the-Art Methods
4. Discussion
5. Conclusions
6. Patents
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Beaulieu, M.; Foucher, S.; Haberman, D.; Stewart, C. Deep image-to-image transfer applied to resolution enhancement of Sentinel-2 images. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018; pp. 2611–2614. [Google Scholar]
- Huang, N.; Yang, Y.; Liu, J.; Gu, X.; Cai, H. Single-image super-resolution for remote sensing data using deep residual-learning neural network. In Proceedings of the International Conference on Neural Information Processing, Guangzhou, China, 14–18 November 2017. [Google Scholar]
- Liebel, L.; Körner, M. Single-image super resolution for multispectral remote sensing data using convolutional neural networks. In Proceedings of the International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, Prague, Czech Republic, 12–19 July 2016. [Google Scholar]
- Li, F.; Xin, L.; Guo, Y.; Gao, D.; Kong, X.; Jia, X. Super-resolution for GaoFen-4 remote sensing images. IEEE Geosci. Remote Sens. Lett. 2018, 15, 28–32. [Google Scholar] [CrossRef]
- Li, F.; Xin, L.; Guo, Y.; Gao, J.; Jia, X. A framework of mixed sparse representations for remote sensing images. IEEE Trans. Geosci. Remote Sens. 2017, 55, 1210–1221. [Google Scholar] [CrossRef]
- Yuan, Q.; Zhang, L.; Shen, H. Multiframe super-resolution employing a spatially weighted total variation model. IEEE Trans. Circuits Syst. Video Technol. 2012, 22, 379–392. [Google Scholar] [CrossRef]
- Dong, C.; Loy, C.C.; He, K.; Tang, X. Image super-resolution using deep convolutional networks. IEEE Trans. Pattern Anal. Mach. Intell. 2016, 38, 295–307. [Google Scholar] [CrossRef] [PubMed]
- Shi, W.; Caballero, J.; Huszár, F.; Totz, J.; Aitken, A.P.; Bishop, R.; Rueckert, D.; Wang, Z. Real-time single image and video super-resolution using an efficient sub-pixel convolutional neural network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 1874–1883. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Kim, J.; Lee, J.K.; Lee, K.M. Accurate image super-resolution using very deep convolutional networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 1646–1654. [Google Scholar]
- Kim, J.; Lee, J.K.; Lee, K.M. Deeply-recursive convolutional network for image super-resolution. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 1637–1645. [Google Scholar]
- Tai, Y.; Yang, J.; Liu, X. Image super-resolution via deep recursive residual network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 2790–2798. [Google Scholar]
- Tai, Y.; Yang, J.; Liu, X.; Xu, C. MemNet: A Persistent Memory Network for Image Restoration. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 4549–4557. [Google Scholar]
- Ledig, C.; Theis, L.; Huszar, F.; Caballero, J.; Cunningham, A.; Acosta, A.; Aitken, A.; Tejani, A.; Totz, J.; Wang, Z.; et al. Photo-realistic single image super-resolution using a generative adversarial network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 105–114. [Google Scholar]
- Lai, W.S.; Huang, J.B.; Ahuja, N.; Yang, M.H. Deep laplacian pyramid networks for fast and accurate super-resolution. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 5835–5843. [Google Scholar]
- Hui, Z.; Wang, X.; Gao, X. Fast and accurate single image super-resolution via information distillation network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 723–731. [Google Scholar]
- Zhang, K.; Zuo, W.; Zhang, L. Learning a single convolutional super-resolution network for multiple degradations. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 3262–3271. [Google Scholar]
- Ahn, N.; Kang, B.; Sohn, K.A. Fast, accurate, and lightweight super-resolution with cascading residual network. In Proceedings of the European Conference on Computer Vision, Munich, Germany, 8–14 September 2018. [Google Scholar]
- Luo, Y.; Zhou, L.; Wang, S.; Wang, Z. Video satellite imagery super resolution via convolutional neural networks. IEEE Geosci. Remote Sens. Lett. 2017, 14, 2398–2402. [Google Scholar] [CrossRef]
- Lei, S.; Shi, Z.; Zou, Z. Super-resolution for remote sensing images via local–global combined network. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1243–1247. [Google Scholar] [CrossRef]
- Xu, W.; Xu, G.; Wang, Y.; Sun, X.; Lin, D.; Wu, Y. High quality remote sensing image super-resolution using deep memory connected network. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018; pp. 8889–8892. [Google Scholar]
- Mario, H.J.; Ruben, F.B.; Paoletti, M.E.; Javier, P.; Antonio, P.; Filiberto, P. A new deep generative network for unsupervised remote sensing single-image super-resolution. IEEE Trans. Geosci. Remote Sens. 2018, 56, 6792–6810. [Google Scholar]
- Li, J.; Fang, F.; Mei, K.; Zhang, G. Multi-scale residual network for image super-resolution. In Proceedings of the European Conference on Computer Vision, Munich, Germany, 8–14 September 2018; pp. 527–542. [Google Scholar]
- Hu, J.; Shen, L.; Albanie, S.; Sun, G.; Wu, E. Squeeze-and-excitation networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 7132–7141. [Google Scholar]
- Choi, J.S.; Kim, M. A deep convolutional neural network with selection units for super-resolution. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Honolulu, HI, USA, 21–26 July 2017; pp. 1150–1156. [Google Scholar]
- Kim, J.H.; Choi, J.H.; Cheon, M.; Lee, J.S. Ram: Residual attention module for single image super-resolution. arXiv 2018, arXiv:1811.12043. [Google Scholar]
- Zhang, Y.; Li, K.; Li, K.; Wang, L.; Zhong, B.; Fu, Y. Image super-resolution using very deep residual channel attention networks. In Proceedings of the European Conference on Computer Vision, Munich, Germany, 8–14 September 2018; pp. 286–301. [Google Scholar]
- Zhao, H.; Gallo, O.; Frosio, I.; Kautz, J. Loss functions for image restoration with neural networks. IEEE Trans. Comput. Imaging 2017, 3, 47–57. [Google Scholar] [CrossRef]
- Lim, B.; Son, S.; Kim, H.; Nah, S.; Lee, K.M. Enhanced deep residual networks for single image super-resolution. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Honolulu, HI, USA, 21–26 July 2017; pp. 1132–1140. [Google Scholar]
- Tong, T.; Li, G.; Liu, X.; Gao, Q. Image super-resolution using dense skip connections. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 4809–4817. [Google Scholar]
- Nair, V.; Hinton, G.E. Rectified linear units improve restricted Boltzmann machines. In Proceedings of the 27th International Conference on Machine Learning, Haifa, Israel, 21–25 June 2010. [Google Scholar]
- Dong, C.; Loy, C.C.; Tang, X. Accelerating the super-resolution convolutional neural network. In Proceedings of the European Conference on Computer Vision, Berlin, Germany, 27–30 June 2016; pp. 391–407. [Google Scholar]
- Pan, S.J.; Qiang, Y. A survey on transfer learning. IEEE Trans. Knowl. Data Eng. 2010, 22, 1345–1359. [Google Scholar] [CrossRef]
- Timofte, R.; Lee, K.M.; Wang, X.; Tian, Y.; Ke, Y.; Zhang, Y.; Wu, S.; Dong, C.; Lin, L.; Qiao, Y.; et al. NTIRE 2017 challenge on single image super-resolution: Methods and results. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Honolulu, HI, USA, 21–26 July 2017; pp. 1110–1121. [Google Scholar]
- Yang, Y.; Newsam, S. Bag-of-visual-words and spatial extensions for land-use classifification. In Proceedings of the 18th SIGSPATIAL International Conference On Advances in Geographic Information Systems, Seattle, WA, USA, 2–5 November 2010; pp. 270–279. [Google Scholar]
- Bevilacqua, M.; Roumy, A.; Guillemot, C.; Morel, M.L.A. Low-complexity single-image super-resolution based on nonnegative neighbor embedding. In Proceedings of the British Machine Vision Conference, Guildford, UK, 3–7 September 2012. [Google Scholar]
- Zeyde, R.; Elad, M.; Protter, M. On single image scale-up using sparse-representations. In Proceeding of the 7th International Conference on Curves and Surfaces, Avignon, France, 24–30 June 2010. [Google Scholar]
- Martin, D.; Fowlkes, C.; Tal, D.; Malik, J. A database of human segmented natural images and its application to evaluating segmentation algorithms and measuring ecological statistics. In Proceedings of the 8th IEEE International Conference on Computer Vision, Vancouver, BC, Canada, 7–14 July 2001. [Google Scholar]
- Huang, J.B.; Singh, A.; Ahuja, N. Single image super-resolution from transformed self-exemplars. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 8–10 June 2015; pp. 5197–5206. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. In Proceedings of the 3rd International Conference for Learning Representations, San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- Paszke, A.; Gross, S.; Chintala, S.; Chanan, G.; Yang, E.; DeVito, Z.; Lin, Z.; Desmaison, A.; Antiga, L.; Lerer, A. Automatic differentiation in pytorch. In Proceedings of the 31st Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef] [PubMed]
- Bulat, A.; Yang, J.; Tzimiropoulos, G. To learn image super-resolution, use a gan to learn how to do image degradation first. In Proceedings of the European Conference on Computer Vision, Munich, Germany, 8–14 September 2018; pp. 185–200. [Google Scholar]










| ERB | RCAG | Transferred | PSNR |
|---|---|---|---|
| × | × | × | 39.510 |
| √ | × | × | 39.540 |
| √ | √ | × | 39.604 |
| √ | √ | √ | 39.728 |
| B = 6 | B = 7 | B = 8 | B = 9 | B = 10 | |
|---|---|---|---|---|---|
| PSNR | 39.604 | 39.621 | 39.627 | 39.570 | 39.573 |
| TIME | 0.14 | 0.16 | 0.18 | 0.20 | 0.21 |
| G = 3 | G = 4 | G = 5 | |
|---|---|---|---|
| PSNR | 39.627 | 39.608 | 39.630 |
| TIME | 0.18 | 0.23 | 0.28 |
| Bicubic | IDN | SRMDNF | CARN | MSRN | MPSR | MPSR-T | |
|---|---|---|---|---|---|---|---|
| ×2 | 35.05 | 39.20 | 39.03 | 39.22 | 39.55 | 39.63 | 39.78 |
| 0.9450 | 0.9696 | 0.9695 | 0.9695 | 0.9704 | 0.9705 | 0.9709 | |
| ×3 | 29.92 | 33.35 | 32.99 | 33.38 | 33.47 | 33.71 | 33.93 |
| 0.8627 | 0.9154 | 0.9131 | 0.9156 | 0.9163 | 0.9183 | 0.9199 | |
| ×4 | 27.07 | 29.95 | 29.71 | 29.96 | 29.90 | 30.20 | 30.34 |
| 0.7739 | 0.8528 | 0.8498 | 0.8533 | 0.8527 | 0.8571 | 0.8584 |
| Method | Set5 | Set14 | BSD100 | Urban100 | ||||
|---|---|---|---|---|---|---|---|---|
| PSNR | SSIM | PSNR | SSIM | PSNR | SSIM | PSNR | SSIM | |
| × 2 | ||||||||
| Bicubic | 33.66 | 0.9299 | 30.24 | 0.8688 | 29.56 | 0.8431 | 26.88 | 0.8403 |
| SRCNN | 36.66 | 0.9542 | 32.45 | 0.9067 | 31.36 | 0.8879 | 29.50 | 0.8946 |
| VDSR | 37.53 | 0.9587 | 33.05 | 0.9127 | 31.90 | 0.8960 | 30.77 | 0.9141 |
| DRCN | 37.63 | 0.9588 | 33.06 | 0.9121 | 31.85 | 0.8942 | 30.76 | 0.9133 |
| DRRN | 37.74 | 0.9591 | 33.23 | 0.9136 | 32.05 | 0.8973 | 31.23 | 0.9188 |
| LapSRN | 37.52 | 0.9591 | 33.08 | 0.9124 | 31.80 | 0.8949 | 30.41 | 0.9101 |
| MemNet | 37.78 | 0.9597 | 33.28 | 0.9142 | 32.08 | 0.8978 | 31.31 | 0.9195 |
| IDN | 37.83 | 0.9600 | 33.30 | 0.9148 | 32.08 | 0.8985 | 31.27 | 0.9196 |
| SRMDNF | 37.79 | 0.9601 | 33.32 | 0.9159 | 32.05 | 0.8985 | 31.33 | 0.9204 |
| CARN | 37.76 | 0.9590 | 33.52 | 0.9166 | 32.09 | 0.8978 | 31.92 | 0.9256 |
| SelNet | 37.89 | 0.9598 | 33.61 | 0.9160 | 32.08 | 0.8984 | - | - |
| SRRAM | 37.82 | 0.9592 | 33.48 | 0.9171 | 32.12 | 0.8983 | 32.05 | 0.9264 |
| MSRN | 38.08 | 0.9605 | 33.74 | 0.9170 | 32.23 | 0.9013 | 32.22 | 0.9326 |
| MPSR (ours) | 38.09 | 0.9607 | 33.73 | 0.9187 | 32.25 | 0.9005 | 32.49 | 0.9314 |
| × 3 | ||||||||
| Bicubic | 30.39 | 0.8682 | 27.55 | 0.7742 | 27.21 | 0.7385 | 24.46 | 0.7349 |
| SRCNN | 32.75 | 0.9090 | 29.29 | 0.8215 | 28.41 | 0.7863 | 26.24 | 0.7991 |
| VDSR | 33.66 | 0.9213 | 29.78 | 0.8318 | 28.83 | 0.7976 | 27.14 | 0.8279 |
| DRCN | 33.82 | 0.9226 | 29.77 | 0.8314 | 28.80 | 0.7963 | 27.15 | 0.8277 |
| DRRN | 34.03 | 0.9244 | 29.96 | 0.8349 | 28.95 | 0.8004 | 27.53 | 0.8377 |
| LapSRN | 33.82 | 0.9227 | 29.79 | 0.8320 | 28.82 | 0.7973 | 27.07 | 0.8271 |
| MemNet | 34.09 | 0.9248 | 30.00 | 0.8350 | 28.96 | 0.8001 | 27.56 | 0.8376 |
| IDN | 34.11 | 0.9253 | 29.99 | 0.8354 | 28.95 | 0.8013 | 27.42 | 0.8359 |
| SRMDNF | 34.12 | 0.9254 | 30.04 | 0.8382 | 28.97 | 0.8025 | 27.57 | 0.8398 |
| CARN | 34.29 | 0.9255 | 30.29 | 0.8407 | 29.06 | 0.8034 | 28.06 | 0.8493 |
| SelNet | 34.27 | 0.9257 | 30.30 | 0.8399 | 28.97 | 0.8025 | - | - |
| SRRAM | 34.30 | 0.9256 | 30.32 | 0.8417 | 29.07 | 0.8039 | 28.12 | 0.8507 |
| MSRN | 34.38 | 0.9262 | 30.34 | 0.8395 | 29.08 | 0.8041 | 28.08 | 0.8554 |
| MPSR (ours) | 34.55 | 0.9284 | 30.47 | 0.8450 | 29.18 | 0.8072 | 28.57 | 0.8606 |
| × 4 | ||||||||
| Bicubic | 28.43 | 0.8104 | 26.00 | 0.7027 | 25.96 | 0.6675 | 23.14 | 0.6577 |
| SRCNN | 30.48 | 0.8628 | 27.50 | 0.7513 | 26.90 | 0.7103 | 24.52 | 0.7226 |
| VDSR | 31.35 | 0.8838 | 28.02 | 0.7678 | 27.29 | 0.7252 | 25.18 | 0.7525 |
| DRCN | 31.53 | 0.8854 | 28.03 | 0.7673 | 27.24 | 0.7233 | 25.14 | 0.7511 |
| DRRN | 31.68 | 0.8888 | 28.21 | 0.7720 | 27.38 | 0.7284 | 25.44 | 0.7638 |
| LapSRN | 31.54 | 0.8866 | 28.19 | 0.7694 | 27.32 | 0.7264 | 25.21 | 0.7553 |
| MemNet | 31.74 | 0.8893 | 28.26 | 0.7723 | 27.40 | 0.7281 | 25.50 | 0.7630 |
| SRDenseNet | 32.02 | 0.8934 | 28.50 | 0.7782 | 27.53 | 0.7337 | 26.05 | 0.7819 |
| IDN | 31.82 | 0.8903 | 28.25 | 0.7730 | 27.41 | 0.7297 | 25.41 | 0.7632 |
| SRMDNF | 31.96 | 0.8925 | 28.35 | 0.7787 | 27.49 | 0.7337 | 25.68 | 0.7731 |
| CARN | 32.13 | 0.8937 | 28.60 | 0.7806 | 27.58 | 0.7349 | 26.07 | 0.7837 |
| SelNet | 32.00 | 0.8931 | 28.49 | 0.7783 | 27.44 | 0.7325 | - | - |
| SRRAM | 32.13 | 0.8932 | 28.54 | 0.7800 | 27.56 | 0.7350 | 26.05 | 0.7834 |
| MSRN | 32.07 | 0.8903 | 28.60 | 0.7751 | 27.52 | 0.7273 | 26.04 | 0.7896 |
| MPSR (ours) | 32.30 | 0.8968 | 28.74 | 0.7856 | 27.66 | 0.7389 | 26.43 | 0.7969 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dong, X.; Xi, Z.; Sun, X.; Gao, L. Transferred Multi-Perception Attention Networks for Remote Sensing Image Super-Resolution. Remote Sens. 2019, 11, 2857. https://doi.org/10.3390/rs11232857
Dong X, Xi Z, Sun X, Gao L. Transferred Multi-Perception Attention Networks for Remote Sensing Image Super-Resolution. Remote Sensing. 2019; 11(23):2857. https://doi.org/10.3390/rs11232857
Chicago/Turabian StyleDong, Xiaoyu, Zhihong Xi, Xu Sun, and Lianru Gao. 2019. "Transferred Multi-Perception Attention Networks for Remote Sensing Image Super-Resolution" Remote Sensing 11, no. 23: 2857. https://doi.org/10.3390/rs11232857
APA StyleDong, X., Xi, Z., Sun, X., & Gao, L. (2019). Transferred Multi-Perception Attention Networks for Remote Sensing Image Super-Resolution. Remote Sensing, 11(23), 2857. https://doi.org/10.3390/rs11232857