Land Cover Change Detection from High-Resolution Remote Sensing Imagery Using Multitemporal Deep Feature Collaborative Learning and a Semi-supervised Chan–Vese Model
Abstract
:1. Introduction
- (1)
- This paper proposed a new schema for solving CD problems for high-resolution multispectral remote sensing images, which has the ability to measure changes accurately and efficiently.
- (2)
- The multitemporal deep feature collaborative learning can transform the original multitemporal images into the same high-level feature space, obtaining the abstract representation of difference in intensities and improving the separability between changed and unchanged objects.
- (3)
- The pseudo-training set containing changed and unchanged patterns derived by uncertainty analysis of object labels is incorporated into the level set evolution process to efficiently drive the level curves towards the accurate boundaries of changed objects.
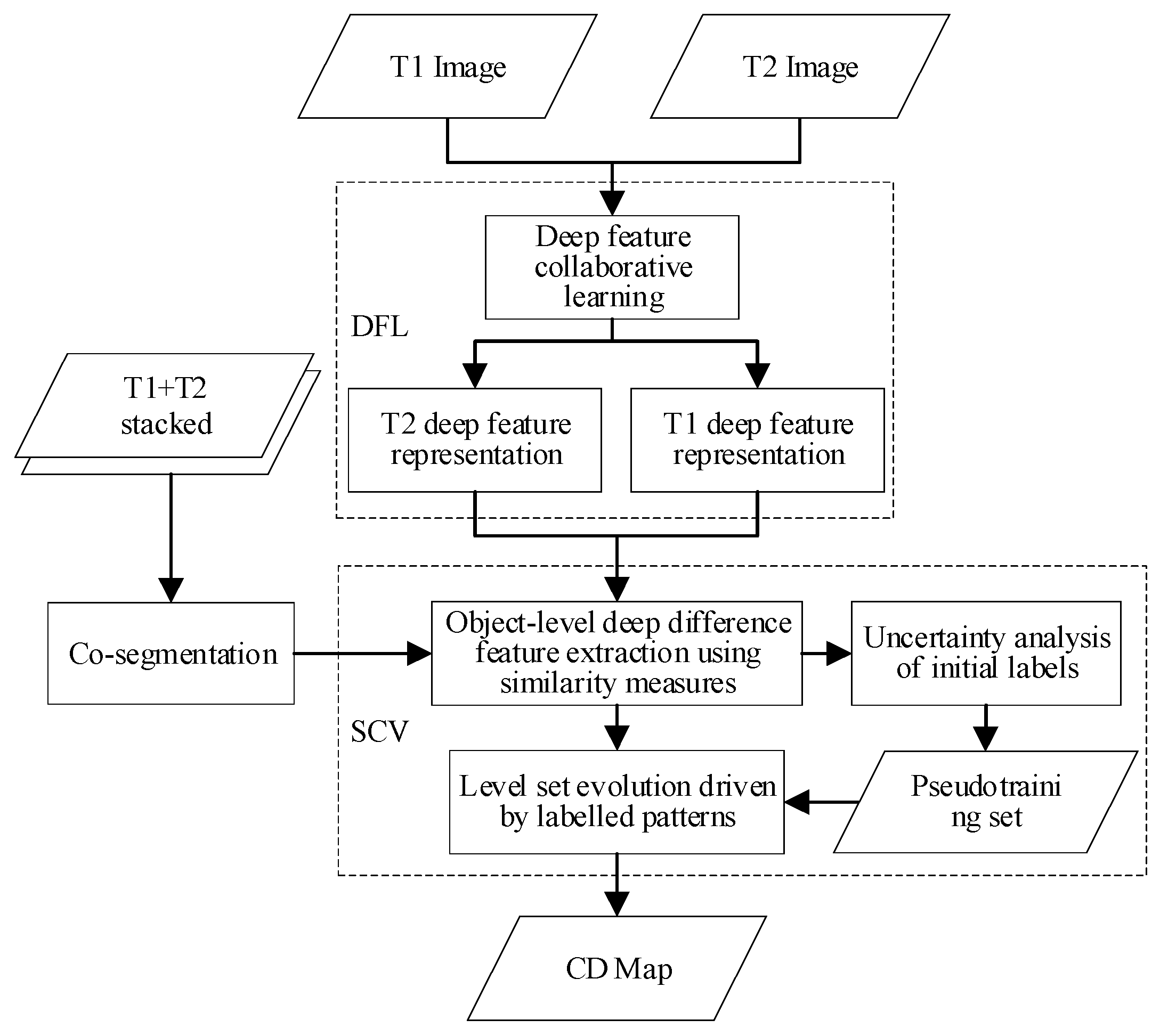
2. Methodology
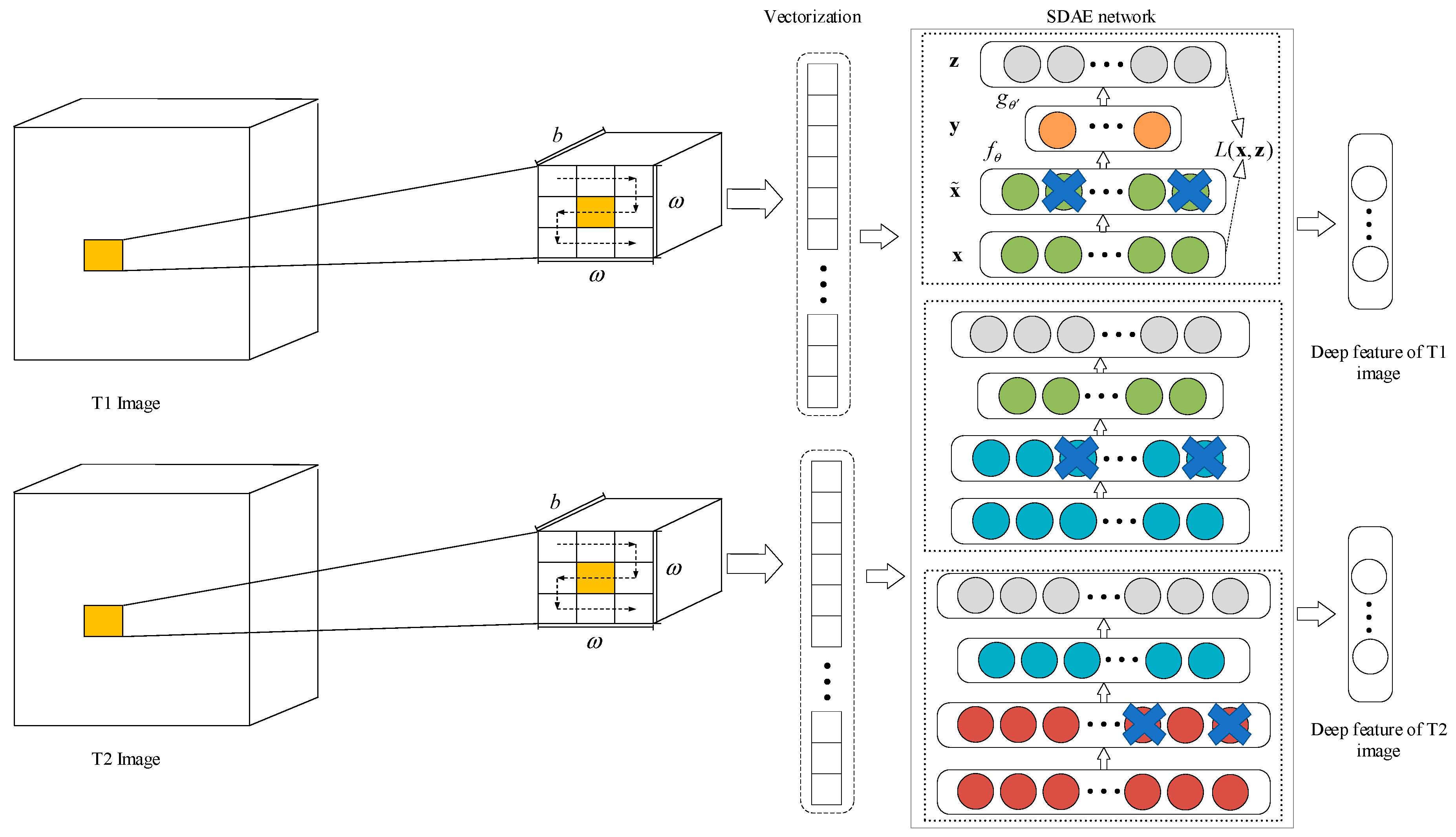
2.1. Multitemporal Deep Feature Collaborative Learning
2.2. Deep Difference Feature Extraction
2.3. Uncertainty Analysis
2.4. SCV Model
3. Experiments and Analysis
3.1. Datasets
3.2. Evaluation Criteria and Experimental Settings
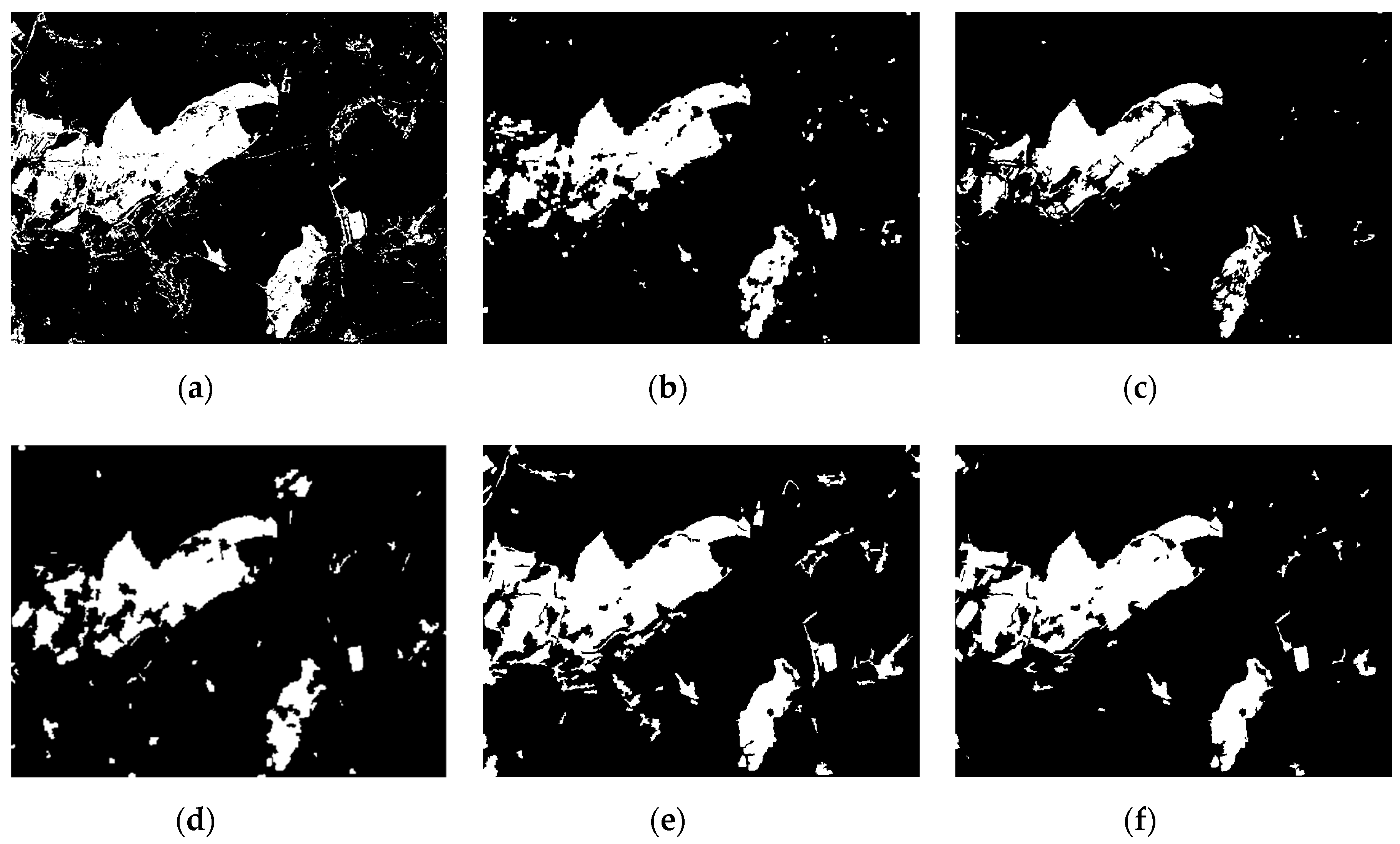
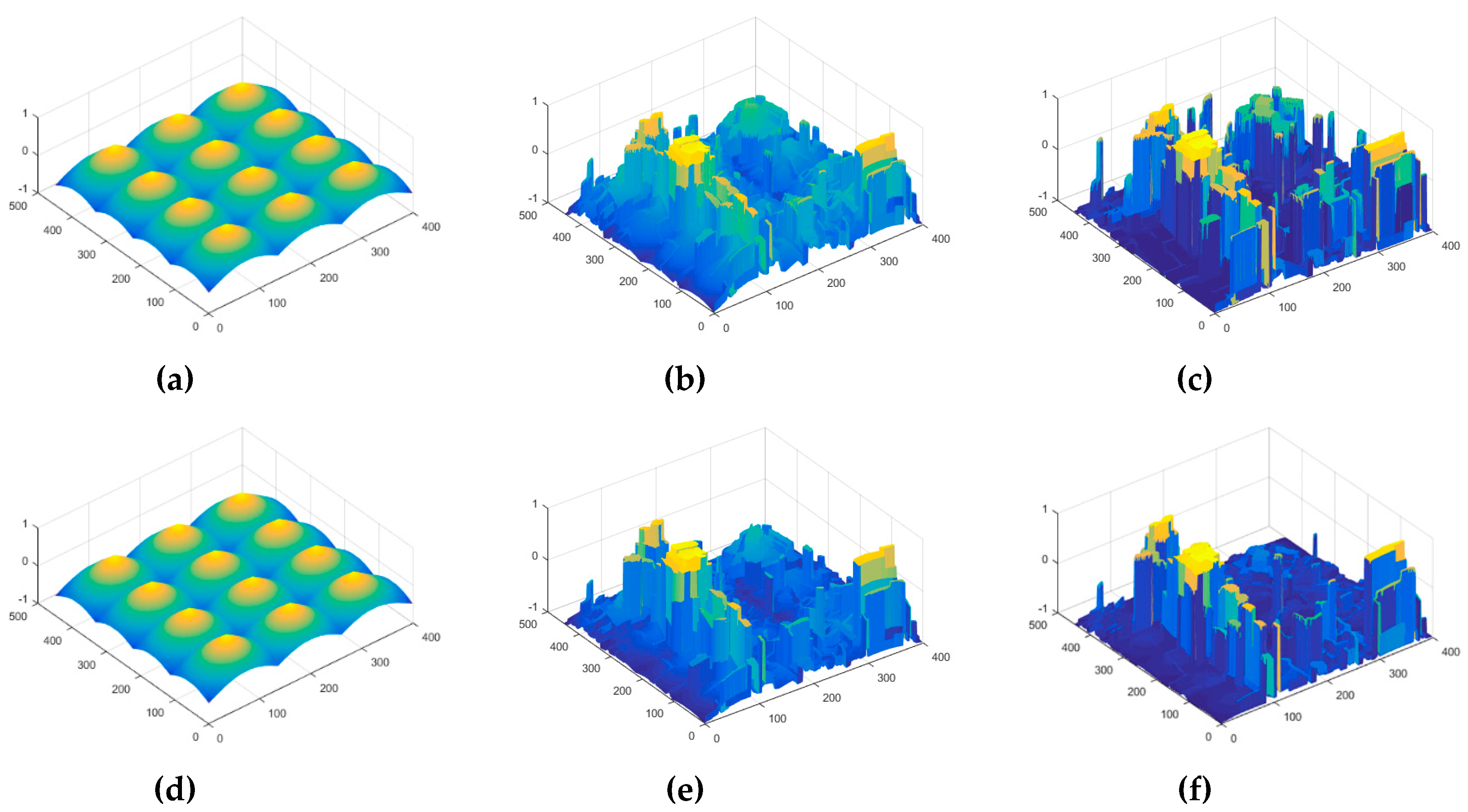
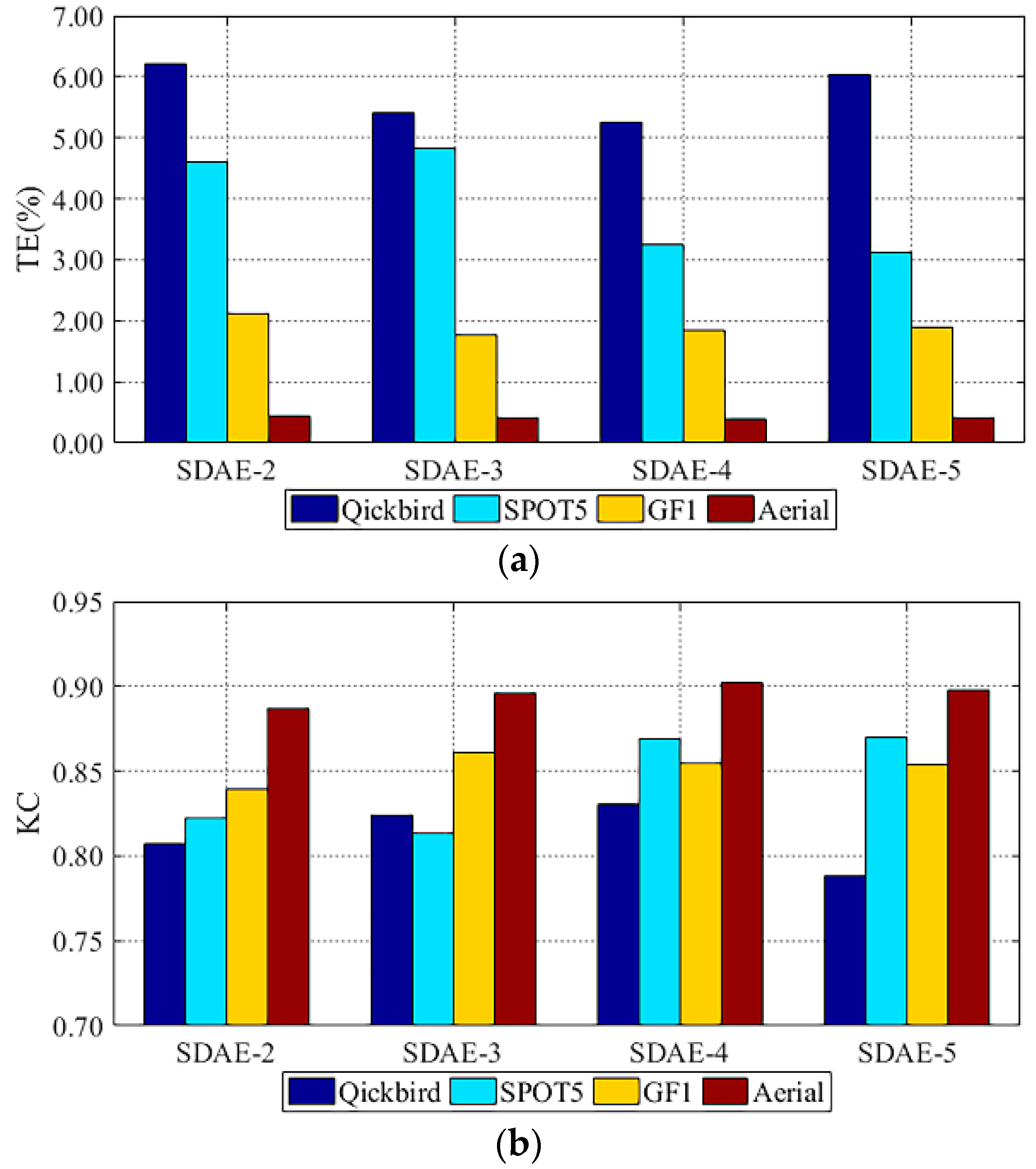
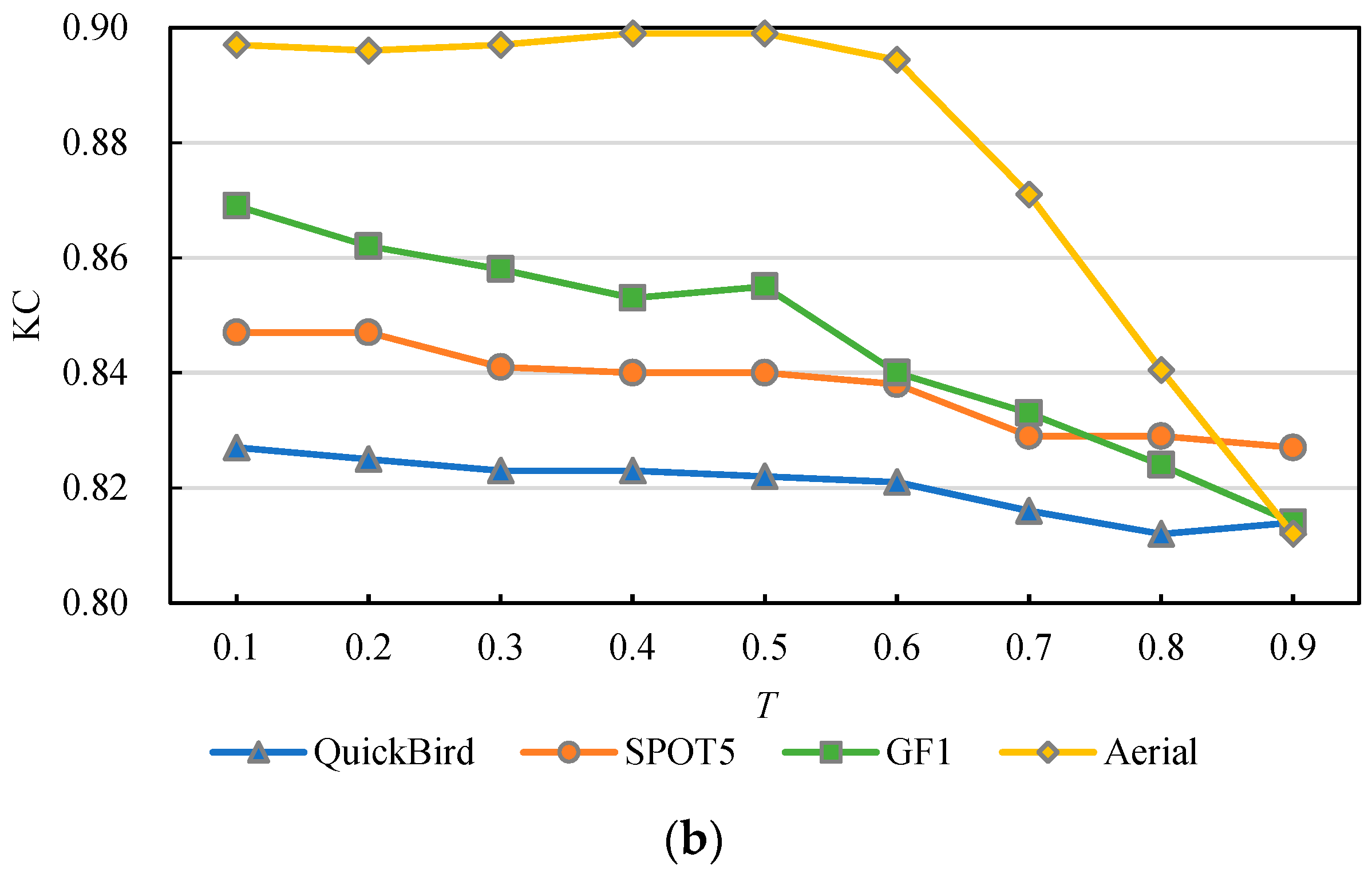
3.3. Experimental Analysis
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Hansen, M.C.; Loveland, T.R. A review of large area monitoring of land cover change using Landsat data. Remote Sens. Environ. 2012, 122, 66–74. [Google Scholar] [CrossRef]
- Stramondo, S.; Bignami, C.; Chini, M.; Pierdicca, N.; Tertulliani, A. Satellite radar and optical remote sensing for earthquake damage detection: Results from different case studies. Int. J. Remote Sens. 2006, 27, 4433–4447. [Google Scholar] [CrossRef]
- Foley, J.A.; DeFries, R.; Asner, G.P.; Barford, C.; Bonan, G.; Carpenter, S.R.; Chapin, F.S.; Coe, M.T.; Daily, G.C.; Gibbs, H.K. Global consequences of land use. Science 2005, 309, 570–574. [Google Scholar] [CrossRef]
- Coppin, P.; Jonckheere, I.; Nackaerts, K.; Muys, B.; Lambin, E. Review ArticleDigital change detection methods in ecosystem monitoring: A review. Int. J. Remote Sens. 2004, 25, 1565–1596. [Google Scholar] [CrossRef]
- Lu, D.; Mausel, P.; Brondizio, E.; Moran, E. Change detection techniques. Int. J. Remote Sens. 2004, 25, 2365–2401. [Google Scholar] [CrossRef]
- Tewkesbury, A.P.; Comber, A.J.; Tate, N.J.; Lamb, A.; Fisher, P.F. A critical synthesis of remotely sensed optical image change detection techniques. Remote Sens. Environ. 2015, 160, 1–14. [Google Scholar] [CrossRef]
- Lv, Z.Y.; Liu, T.F.; Zhang, P.; Benediktsson, J.A.; Lei, T.; Zhang, X. Novel Adaptive Histogram Trend Similarity Approach for Land Cover Change Detection by Using Bitemporal Very-High-Resolution Remote Sensing Images. IEEE Trans. Geosci. Remote Sens. 2019, 57, 9554–9574. [Google Scholar] [CrossRef]
- Saha, S.; Bovolo, F.; Bruzzone, L. Unsupervised Deep Change Vector Analysis for Multiple-Change Detection in VHR Images. IEEE Trans. Geosci. Remote Sens. 2019, 57, 3677–3693. [Google Scholar] [CrossRef]
- Zhan, Y.; Fu, K.; Yan, M.; Sun, X.; Wang, H.; Qiu, X. Change Detection Based on Deep Siamese Convolutional Network for Optical Aerial Images. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1845–1849. [Google Scholar] [CrossRef]
- Hussain, M.; Chen, D.; Cheng, A.; Wei, H.; Stanley, D. Change detection from remotely sensed images: From pixel-based to object-based approaches. ISPRS J. Photogramm. Remote Sens. 2013, 80, 91–106. [Google Scholar] [CrossRef]
- Blaschke, T.; Hay, G.J.; Weng, Q.; Resch, B. Collective Sensing: Integrating Geospatial Technologies to Understand Urban Systems—An Overview. Remote Sens. 2011, 3, 1743–1776. [Google Scholar] [CrossRef]
- Im, J.; Rhee, J.; Jensen, J.R.; Hodgson, M.E. An automated binary change detection model using a calibration approach. Remote Sens. Environ. 2007, 106, 89–105. [Google Scholar] [CrossRef]
- Serra, P.; Pons, X.; Sauri, D. Post-classification change detection with data from different sensors: Some accuracy considerations. Int. J. Remote Sens. 2003, 24, 3311–3340. [Google Scholar] [CrossRef]
- Bruzzone, L.; Prieto, D. Automatic analysis of the difference image for unsupervised change detection. IEEE Trans. Geosci. Remote Sens. 2000, 38, 1171–1182. [Google Scholar] [CrossRef]
- Zhang, X.; Shi, W.; Hao, M.; Shao, P.; Lyu, X. Level set incorporated with an improved MRF model for unsupervised change detection for satellite images. Eur. J. Remote Sens. 2017, 50, 202–210. [Google Scholar] [CrossRef]
- Lv, Z.; Liu, T.; Wan, Y.; Benediktsson, J.A.; Zhang, X. Post-Processing Approach for Refining Raw Land Cover Change Detection of Very High-Resolution Remote Sensing Images. Remote Sens. 2018, 10, 472. [Google Scholar] [CrossRef]
- Celik, T. Unsupervised Change Detection in Satellite Images Using Principal Component Analysis and k-Means Clustering. IEEE Geosci. Remote Sens. Lett. 2009, 6, 772–776. [Google Scholar] [CrossRef]
- Zhang, Y.; Peng, D.; Huang, X. Object-Based Change Detection for VHR Images Based on Multiscale Uncertainty Analysis. IEEE Geosci. Remote Sens. Lett. 2018, 15, 13–17. [Google Scholar] [CrossRef]
- Leichtle, T.; Geiß, C.; Wurm, M.; Lakes, T.; Taubenböck, H. Unsupervised change detection in VHR remote sensing imagery—An object-based clustering approach in a dynamic urban environment. Int. J. Appl. Earth Obs. Geoinf. 2017, 54, 15–27. [Google Scholar] [CrossRef]
- Ma, L.; Li, M.; Blaschke, T.; Ma, X.; Tiede, D.; Cheng, L.; Chen, Z.; Chen, D. Object-based change detection in urban areas: The effects of segmentation strategy, scale, and feature space on unsupervised methods. Remote Sens. 2016, 8, 761. [Google Scholar] [CrossRef]
- Cai, L.; Shi, W.; Zhang, H.; Hao, M. Object-oriented change detection method based on adaptive multi-method combination for remote-sensing images. Int. J. Remote Sens. 2016, 37, 5457–5471. [Google Scholar] [CrossRef]
- Wang, B.; Choi, S.; Byun, Y.; Lee, S.; Choi, J. Object-Based Change Detection of Very High Resolution Satellite Imagery Using the Cross-Sharpening of Multitemporal Data. IEEE Geosci. Remote Sens. Lett. 2015, 12, 1151–1155. [Google Scholar] [CrossRef]
- Shao, P.; Shi, W.; He, P.; Hao, M.; Zhang, X. Novel Approach to Unsupervised Change Detection Based on a Robust Semi-Supervised FCM Clustering Algorithm. Remote Sens. 2016, 8, 264. [Google Scholar] [CrossRef]
- Ardila, J.P.; Bijker, W.; Tolpekin, V.A.; Stein, A. Multitemporal change detection of urban trees using localized region-based active contours in VHR images. Remote Sens. Environ. 2012, 124, 413–426. [Google Scholar] [CrossRef]
- Cao, G.; Li, Y.; Liu, Y.; Shang, Y. Automatic change detection in high-resolution remote-sensing images by means of level set evolution and support vector machine classification. Int. J. Remote Sens. 2014, 35, 6255–6270. [Google Scholar] [CrossRef]
- Li, Z.; Shi, W.; Myint, S.W.; Lu, P.; Wang, Q. Semi-automated landslide inventory mapping from bitemporal aerial photographs using change detection and level set method. Remote Sens. Environ. 2016, 175, 215–230. [Google Scholar] [CrossRef]
- Zhang, X.; Shi, W.; Liang, P.; Hao, M. Level set evolution with local uncertainty constraints for unsupervised change detection. Remote Sens. Lett. 2017, 8, 811–820. [Google Scholar] [CrossRef]
- Li, H.; Gong, M.; Liu, J. A local statistical fuzzy active contour model for change detection. IEEE Geosci. Remote Sens. Lett. 2015, 12, 582–586. [Google Scholar] [CrossRef]
- Blaschke, T.; Hay, G.J.; Kelly, M.; Lang, S.; Hofmann, P.; Addink, E.; Feitosa, R.Q.; Van Der Meer, F.; Van Der Werff, H.; Van Coillie, F.; et al. Geographic Object-Based Image Analysis—Towards a new paradigm. ISPRS J. Photogramm. Remote Sens. 2014, 87, 180–191. [Google Scholar] [CrossRef]
- Blaschke, T. Object based image analysis for remote sensing. ISPRS J. Photogramm. Remote Sens. 2010, 65, 2–16. [Google Scholar] [CrossRef]
- Lv, Z.Y.; Shi, W.; Zhang, X.; Benediktsson, J.A. Landslide Inventory Mapping From Bitemporal High-Resolution Remote Sensing Images Using Change Detection and Multiscale Segmentation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 1520–1532. [Google Scholar] [CrossRef]
- Im, J.; Jensen, J.R.; Tullis, J.A. Object-based change detection using correlation image analysis and image segmentation. Int. J. Remote Sens. 2008, 29, 399–423. [Google Scholar] [CrossRef]
- Volpi, M.; Tuia, D.; Bovolo, F.; Kanevski, M.; Bruzzone, L. Supervised change detection in VHR images using contextual information and support vector machines. Int. J. Appl. Earth Obs. Geoinf. 2013, 20, 77–85. [Google Scholar] [CrossRef]
- Bovolo, F.; Bruzzone, L.; Marconcini, M. A Novel Approach to Unsupervised Change Detection Based on a Semisupervised SVM and a Similarity Measure. IEEE Trans. Geosci. Remote Sens. 2008, 46, 2070–2082. [Google Scholar] [CrossRef] [Green Version]
- Huo, C.; Zhou, Z.; Lu, H.; Pan, C.; Chen, K. Fast Object-Level Change Detection for VHR Images. IEEE Geosci. Remote Sens. Lett. 2009, 7, 118–122. [Google Scholar] [CrossRef]
- Neagoe, V.-E.; Stoica, R.-M.; Ciurea, A.-I.; Bruzzone, L.; Bovolo, F. Concurrent Self-Organizing Maps for Supervised/Unsupervised Change Detection in Remote Sensing Images. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 3525–3533. [Google Scholar] [CrossRef]
- Ghosh, S.; Roy, M.; Ghosh, A. Semi-supervised change detection using modified self-organizing feature map neural network. Appl. Soft Comput. 2014, 15, 1–20. [Google Scholar] [CrossRef]
- Homer, C.; Dewitz, J.; Yang, L.; Jin, S.; Danielson, P.; Xian, G.; Coulston, J.; Herold, N.; Wickham, J.; Megown, K. Completion of the 2011 National Land Cover Database for the conterminous United States–representing a decade of land cover change information. Photogramm. Eng. Remote Sens. 2015, 81, 345–354. [Google Scholar]
- Im, J.; Jensen, J.R. A change detection model based on neighborhood correlation image analysis and decision tree classification. Remote Sens. Environ. 2005, 99, 326–340. [Google Scholar] [CrossRef]
- Sesnie, S.E.; Gessler, P.E.; Finegan, B.; Thessler, S. Integrating Landsat TM and SRTM-DEM derived variables with decision trees for habitat classification and change detection in complex neotropical environments. Remote Sens. Environ. 2008, 112, 2145–2159. [Google Scholar] [CrossRef]
- Xu, X.; Li, W.; Ran, Q.; Du, Q.; Gao, L.; Zhang, B. Multisource remote sensing data classification based on convolutional neural network. IEEE Trans. Geosci. Remote Sens. 2017, 56, 937–949. [Google Scholar] [CrossRef]
- Wu, H.; Prasad, S. Convolutional Recurrent Neural Networks for Hyperspectral Data Classification. Remote Sens. 2017, 9, 298. [Google Scholar] [CrossRef] [Green Version]
- Zhang, C.; Sargent, I.; Pan, X.; Li, H.; Gardiner, A.; Hare, J.; Atkinson, P.M. An object-based convolutional neural network (OCNN) for urban land use classification. Remote Sens. Environ. 2018, 216, 57–70. [Google Scholar] [CrossRef] [Green Version]
- Lei, T.; Zhang, Y.; Lv, Z.; Li, S.; Liu, S.; Nandi, A.K. Landslide Inventory Mapping from Bitemporal Images Using Deep Convolutional Neural Networks. IEEE Geosci. Remote Sens. Lett. 2019, 16, 982–986. [Google Scholar] [CrossRef]
- Bischke, B.; Helber, P.; Folz, J.; Borth, D.; Dengel, A. Multi-Task Learning for Segmentation of Building Footprints with Deep Neural Networks. In Proceedings of the 2019 IEEE International Conference on Image Processing (ICIP), Taipei, Taiwan, 22–25 September 2019; pp. 1480–1484. [Google Scholar]
- Liu, W.; Cheng, D.; Yin, P.; Yang, M.; Li, E.; Xie, M.; Zhang, L. Small Manhole Cover Detection in Remote Sensing Imagery with Deep Convolutional Neural Networks. ISPRS Int. J. Geo-Inf. 2019, 8, 49. [Google Scholar] [CrossRef] [Green Version]
- Mahdianpari, M.; Salehi, B.; Rezaee, M.; Mohammadimanesh, F.; Zhang, Y. Very Deep Convolutional Neural Networks for Complex Land Cover Mapping Using Multispectral Remote Sensing Imagery. Remote Sens. 2018, 10, 1119. [Google Scholar] [CrossRef] [Green Version]
- Khan, S.H.; He, X.; Porikli, F.; Bennamoun, M. Forest Change Detection in Incomplete Satellite Images with Deep Neural Networks. IEEE Trans. Geosci. Remote Sens. 2017, 55, 5407–5423. [Google Scholar] [CrossRef]
- Mou, L.; Bruzzone, L.; Zhu, X.X. Learning Spectral-Spatial-Temporal Features via a Recurrent Convolutional Neural Network for Change Detection in Multispectral Imagery. IEEE Trans. Geosci. Remote Sens. 2018, 57, 924–935. [Google Scholar] [CrossRef] [Green Version]
- Wang, Q.; Yuan, Z.; Du, Q.; Li, X. GETNET: A General End-to-End 2-D CNN Framework for Hyperspectral Image Change Detection. IEEE Trans. Geosci. Remote Sens. 2018, 57, 3–13. [Google Scholar] [CrossRef] [Green Version]
- Zhang, P.; Gong, M.; Su, L.; Liu, J.; Li, Z. Change detection based on deep feature representation and mapping transformation for multi-spatial-resolution remote sensing images. ISPRS J. Photogramm. Remote Sens. 2016, 116, 24–41. [Google Scholar] [CrossRef]
- Gong, M.; Zhan, T.; Zhang, P.; Miao, Q. Superpixel-Based Difference Representation Learning for Change Detection in Multispectral Remote Sensing Images. IEEE Trans. Geosci. Remote Sens. 2017, 55, 2658–2673. [Google Scholar] [CrossRef]
- Xie, J.; Xu, L.; Chen, E. Image denoising and inpainting with deep neural networks. In Proceedings of the Advances in Neural Information Processing Systems, Lake Tahoe, NV, USA, 3–6 December 2012; pp. 341–349. [Google Scholar]
- Vincent, P.; Larochelle, H.; Lajoie, I.; Bengio, Y.; Manzagol, P.-A. Stacked denoising autoencoders: Learning useful representations in a deep network with a local denoising criterion. J. Mach. Learn. Res. 2010, 11, 3371–3408. [Google Scholar]
- Zhang, X.; Chen, G.; Wang, W.; Wang, Q.; Dai, F. Object-Based Land-Cover Supervised Classification for Very-High-Resolution UAV Images Using Stacked Denoising Autoencoders. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 3373–3385. [Google Scholar] [CrossRef]
- Vincent, P.; LaRochelle, H.; Bengio, Y.; Manzagol, P.-A. Extracting and composing robust features with denoising autoencoders. In Proceedings of the 25th International Conference on Machine Learning, Helsinki, Finland, 5–9 July 2008; pp. 1096–1103. [Google Scholar]
- Lv, Z.; Liu, T.; Benediktsson, J.A.; Lei, T.; Wan, Y. Multi-Scale Object Histogram Distance for LCCD Using Bi-Temporal Very-High-Resolution Remote Sensing Images. Remote Sens. 2018, 10, 1809. [Google Scholar] [CrossRef] [Green Version]
- Gu, H.; Han, Y.; Yang, Y.; Li, H.; Liu, Z.; Soergel, U.; Blaschke, T.; Cui, S. An Efficient Parallel Multi-Scale Segmentation Method for Remote Sensing Imagery. Remote Sens. 2018, 10, 590. [Google Scholar] [CrossRef] [Green Version]
- Lei, T.; Jia, X.; Zhang, Y.; He, L.; Meng, H.; Nandi, A.K. Significantly Fast and Robust Fuzzy C-Means Clustering Algorithm Based on Morphological Reconstruction and Membership Filtering. IEEE Trans. Fuzzy Syst. 2018, 26, 3027–3041. [Google Scholar] [CrossRef]
- Lei, T.; Xue, D.; Lv, Z.; Li, S.; Zhang, Y.; Nandi, A.K. Unsupervised change detection using fast fuzzy clustering for landslide mapping from very high-resolution images. Remote Sens. 2018, 10, 1381. [Google Scholar] [CrossRef] [Green Version]
- Lei, Y.; Liu, X.; Shi, J.; Lei, C.; Wang, J. Multiscale superpixel segmentation with deep features for change detection. IEEE Access 2019, 7, 36600–36616. [Google Scholar] [CrossRef]
- Yetgin, Z. Unsupervised change detection of satellite images using local gradual descent. IEEE Trans. Geosci. Remote Sens. 2012, 50, 1919–1929. [Google Scholar] [CrossRef]
- Shi, W.; Zhang, X.; Hao, M.; Shao, P.; Cai, L.; Lyu, X. Validation of land cover products using reliability evaluation methods. Remote Sens. 2015, 7, 7846–7864. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.; Shi, W.; Lv, Z. Uncertainty Assessment in Multitemporal Land Use/Cover Mapping with Classification System Semantic Heterogeneity. Remote Sens. 2019, 11, 2509. [Google Scholar] [CrossRef] [Green Version]






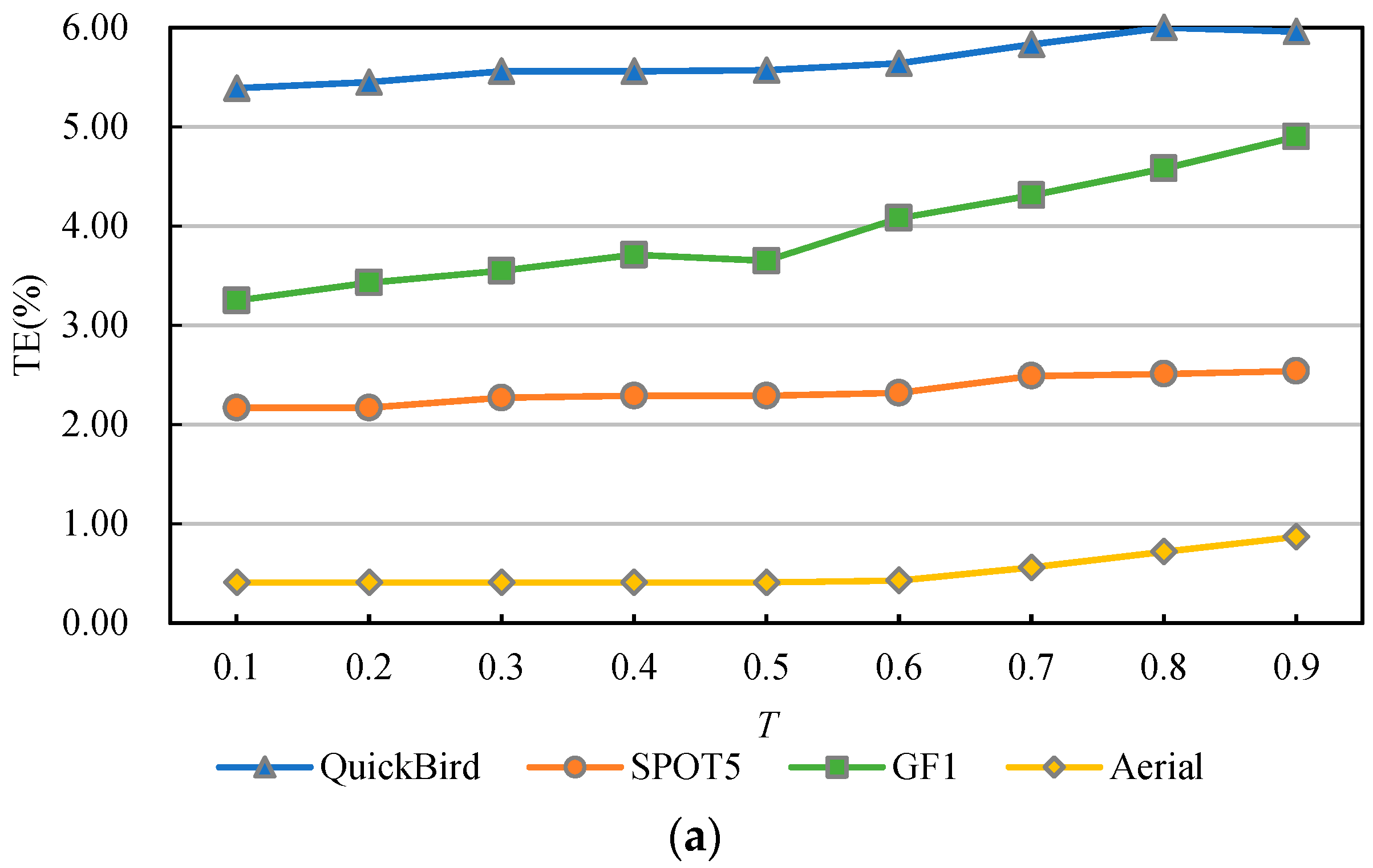
| Input: Deep difference feature map Q Time step Threshold of uncertainty T Initial zero level curve Output: Binary result of CD |
| 1: Initialize as a signed distance function, 2: Initial clustering 3: Get the pseudo-training set H through uncertainty analysis 4: Repeat 5: Compute and 6: Solve the partial differential equation in 7: Update the level set function 8: Until convergence criterion is satisfied 9: Return , i.e., the binary result of CD |
| Method | FA (%) | MD (%) | TE (%) | KC |
|---|---|---|---|---|
| PCA-K-Means | 13.29 | 44.39 | 19.23 | 0.40 |
| MSDNN | 3.66 | 23.63 | 7.47 | 0.75 |
| RLSE | 1.61 | 45.77 | 10.04 | 0.62 |
| MOHD | 12.79 | 20.46 | 14.25 | 0.59 |
| OSVM | 1.11 | 32.80 | 7.16 | 0.74 |
| Proposed approach | 2.99 | 14.64 | 5.23 | 0.83 |
| Method | FA (%) | MD (%) | TE (%) | KC |
|---|---|---|---|---|
| PCA-K-Means | 5.20 | 8.36 | 5.65 | 0.79 |
| MSDNN | 1.26 | 18.90 | 3.71 | 0.83 |
| RLSE | 0.33 | 33.91 | 5.13 | 0.76 |
| MOHD | 1.86 | 25.07 | 5.09 | 0.77 |
| OSVM | 5.45 | 6.14 | 5.55 | 0.80 |
| Proposed approach | 2.45 | 8.05 | 3.23 | 0.87 |
| Method | FA (%) | MD (%) | TE (%) | KC |
|---|---|---|---|---|
| PCA-K-Means | 2.80 | 7.62 | 3.14 | 0.79 |
| MSDNN | 1.89 | 14.64 | 2.78 | 0.80 |
| RLSE | 0.18 | 37.23 | 2.77 | 0.75 |
| MOHD | 0.82 | 23.12 | 2.38 | 0.81 |
| OSVM | 4.62 | 6.67 | 4.76 | 0.71 |
| Proposed approach | 1.84 | 6.54 | 2.17 | 0.85 |
| Method | FA (%) | MD (%) | TE (%) | KC |
|---|---|---|---|---|
| PCA-K-Means | 19.56 | 9.26 | 19.34 | 0.13 |
| MSDNN | 0.92 | 20.80 | 1.33 | 0.71 |
| RLSE | 0.12 | 28.82 | 0.73 | 0.80 |
| MOHD | 0.15 | 18.42 | 0.54 | 0.86 |
| OSVM | 0.90 | 5.09 | 0.99 | 0.80 |
| Proposed approach | 0.12 | 13.42 | 0.41 | 0.90 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Shi, W.; Lv, Z.; Peng, F. Land Cover Change Detection from High-Resolution Remote Sensing Imagery Using Multitemporal Deep Feature Collaborative Learning and a Semi-supervised Chan–Vese Model. Remote Sens. 2019, 11, 2787. https://doi.org/10.3390/rs11232787
Zhang X, Shi W, Lv Z, Peng F. Land Cover Change Detection from High-Resolution Remote Sensing Imagery Using Multitemporal Deep Feature Collaborative Learning and a Semi-supervised Chan–Vese Model. Remote Sensing. 2019; 11(23):2787. https://doi.org/10.3390/rs11232787
Chicago/Turabian StyleZhang, Xiaokang, Wenzhong Shi, Zhiyong Lv, and Feifei Peng. 2019. "Land Cover Change Detection from High-Resolution Remote Sensing Imagery Using Multitemporal Deep Feature Collaborative Learning and a Semi-supervised Chan–Vese Model" Remote Sensing 11, no. 23: 2787. https://doi.org/10.3390/rs11232787
APA StyleZhang, X., Shi, W., Lv, Z., & Peng, F. (2019). Land Cover Change Detection from High-Resolution Remote Sensing Imagery Using Multitemporal Deep Feature Collaborative Learning and a Semi-supervised Chan–Vese Model. Remote Sensing, 11(23), 2787. https://doi.org/10.3390/rs11232787









