Establishment of Plot-Yield Prediction Models in Soybean Breeding Programs Using UAV-Based Hyperspectral Remote Sensing
Abstract
1. Introduction
2. Materials and Methods
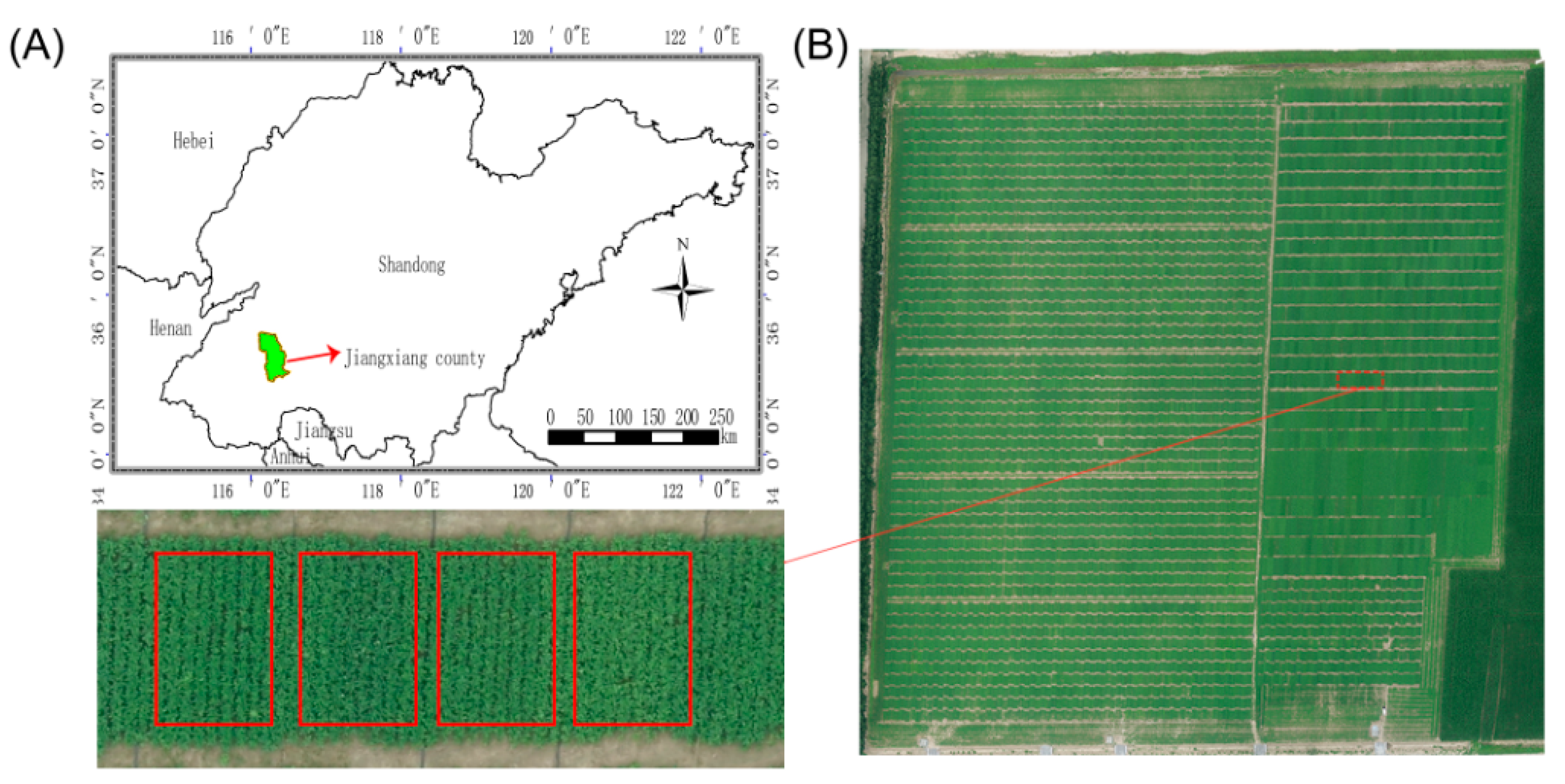
2.1. Plant Materials and Field Experiments
2.2. Assembly of the Unmanned Aerial Vehicle (UAV)-Based Hyperspectral Remote-Sensing System
2.3. Processing of the UAV Hyperspectral Reflectance and Determination of the Reflectance-Sampling Unit-Size in Plots
2.4. Optimization of the Vegetation Indices along with Corresponding Hyperspectral Bands
2.5. Establishment and Verification of the Yield Prediction Models
2.6. Superior Plot-Yield Prediction Models Selected for Breeding Programs
3. Results
3.1. Field Experiment Precision and Variation among the Tested Breeding Lines
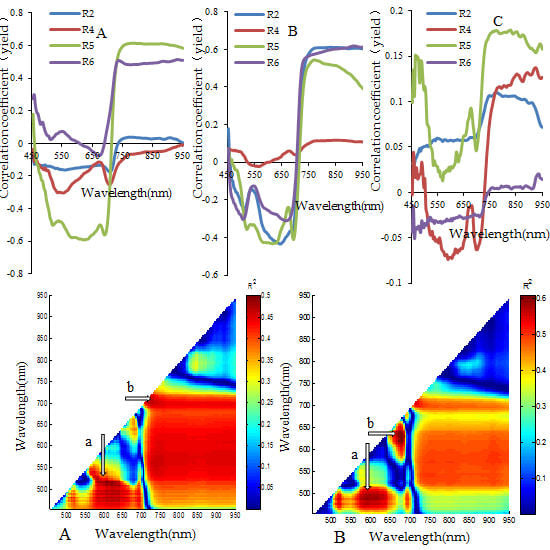
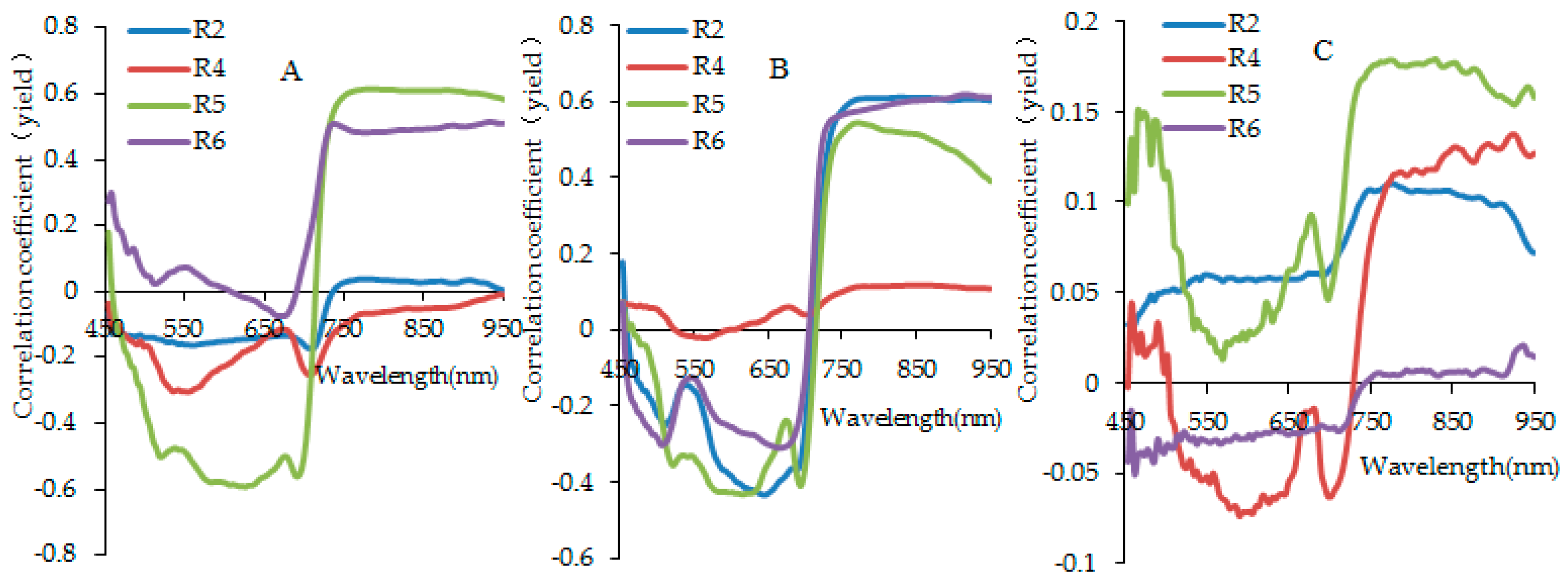
3.2. Analysis for Sensitive Wavebands and Optimal Vegetation Indices for Breeding Line Yield-Prediction
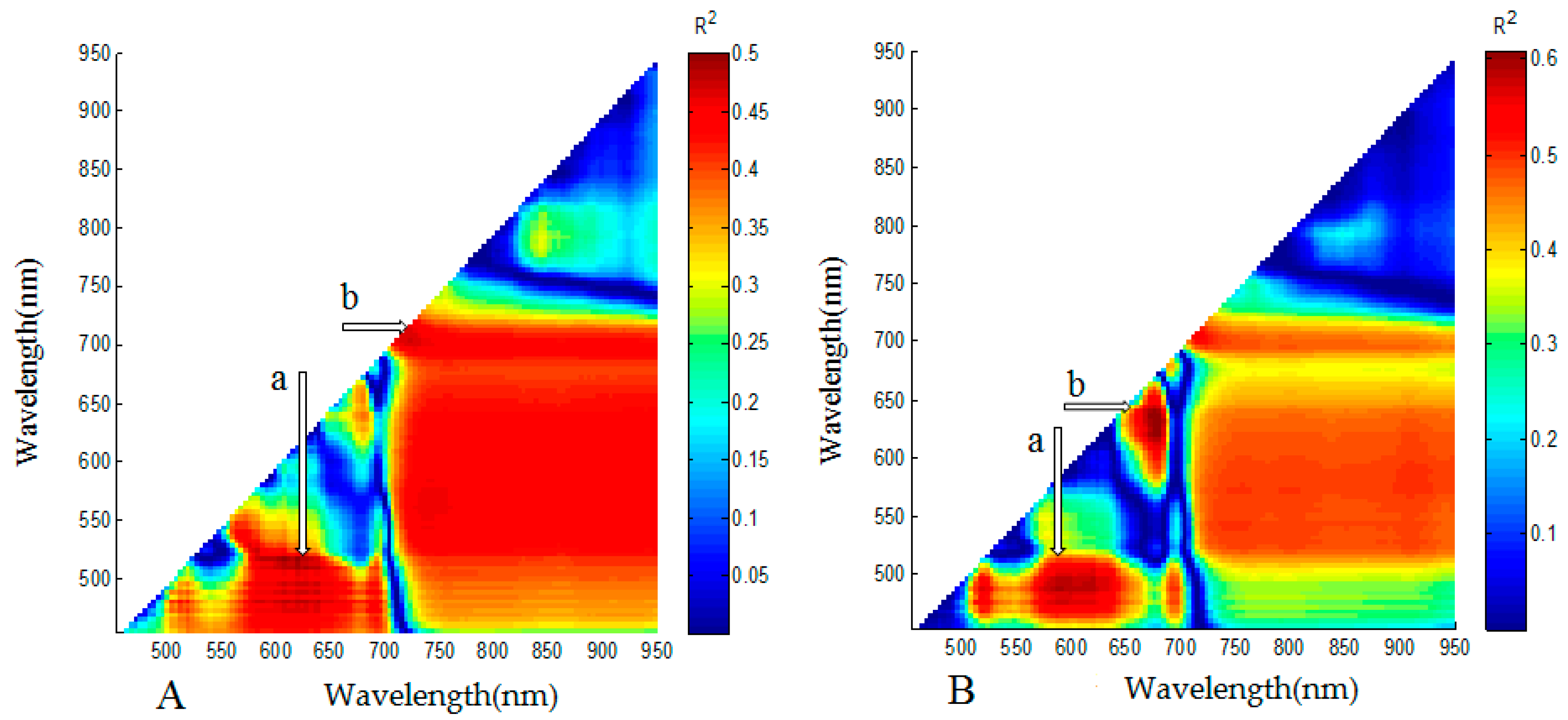
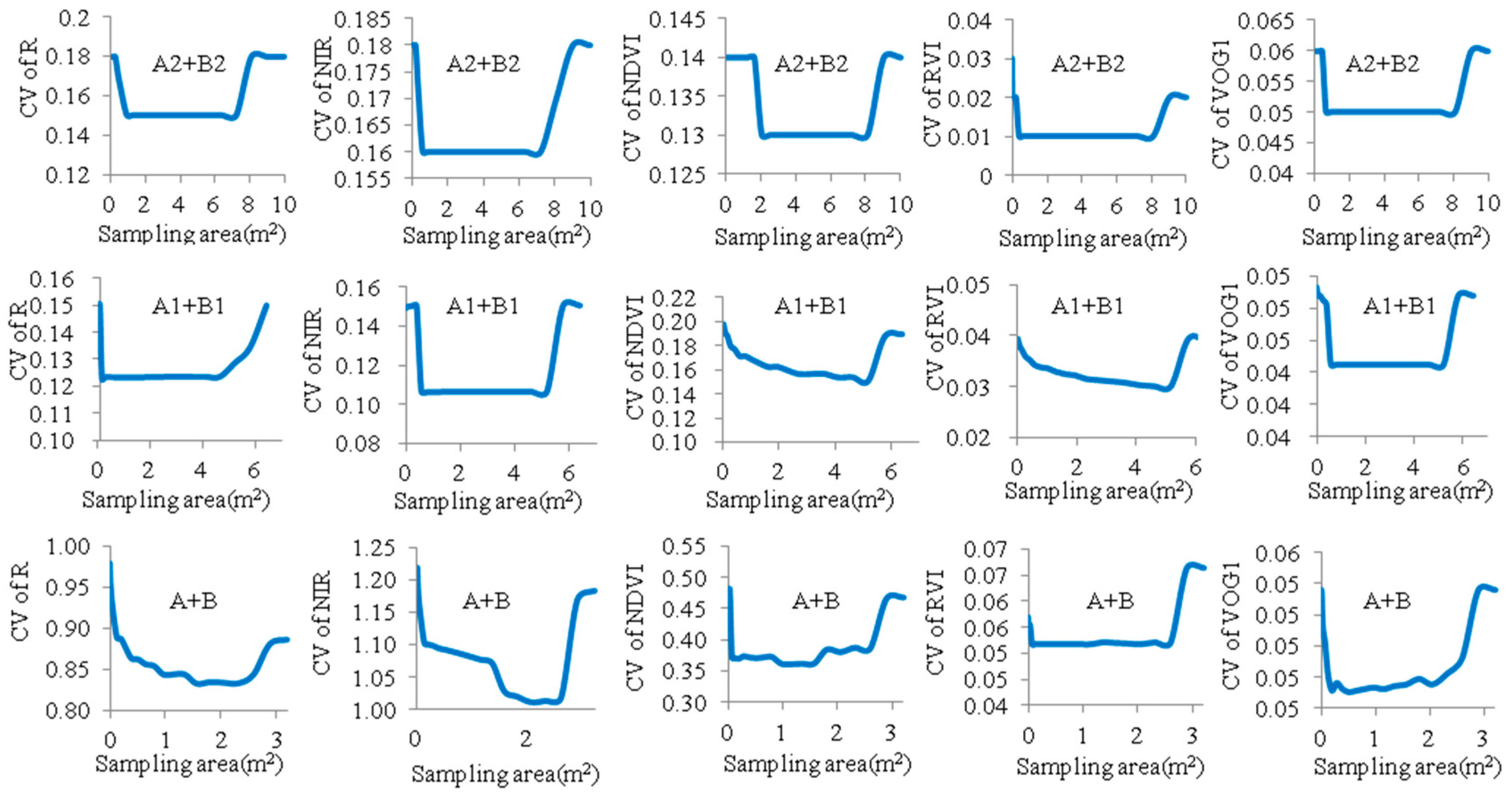
3.3. Optimized Reflectance-Sampling Unit-Size for Organizing the UAV Hyperspectral Reflectance Data
3.4. Identification of Major Factors for the Establishment of Plot-Yield Prediction Models
3.5. Establishment and Evaluation of Yield-Prediction Models Using Normalized Difference Vegetation Index (NDVI) and Ration Vegetation Index (RVI) at R5
3.6. Establishment and Evaluation of Yield-Prediction Models Using NDVI and RVI at Multiple Stages
3.7. Further Comparison and Selection of Best-Fitted Plot-Yield Prediction Models for Yield Breeding Programs
4. Discussion
4.1. The Major Elements and Potential Utilization of the Established Plot-Yield Prediction Models
4.2. Potential Improvement of Plot-Yield Prediction Models in Soybean Breeding Program
4.3. Innovation Potential of Plant Breeding Nursery System Using UAV-Based Hyperspectral Reflectance Techniques
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Zaman-Allah, M.; Vergara, O.; Araus, J.; Tarekegne, A.; Magorokosho, C.; Zarco-Tejada, P.; Hornero, A.; Alba, A.; Das, B.; Craufurd, P.; et al. Unmanned aerial platform-based multi-spectral imaging for field phenotyping of maize. Plant Methods 2015, 11, 35. [Google Scholar] [CrossRef] [PubMed]
- Yu, N.; Li, L.; Schmitz, N.; Tian, L.; Greenberg, J.; Diers, B. Development of methods to improve soybean yield estimation and predict plant maturity with an unmanned aerial vehicle based platform. Remote Sens. Environ. 2016, 187, 91–101. [Google Scholar] [CrossRef]
- Gai, J. Experiment Statistics; China Agriculture Press: Beijing, China, 2014. [Google Scholar]
- Clevers, J. A simplified approach for yield prediction of sugar beet based on optical remote sensing data. Remote Sens. Environ. 1997, 61, 221–228. [Google Scholar] [CrossRef]
- Wei, X.; Xu, J.; Guo, H.; Jiang, L.; Chen, S.; Yu, C.; Zhou, Z.; Hu, P.; Zhai, H.; Wan, J. DTH8 suppresses flowering in rice, influencing plant height and yield potential simultaneously. Plant Physiol. 2010, 153, 1747–1758. [Google Scholar] [CrossRef] [PubMed]
- Ilker, E.; Tonk, F.A.; Tosun, M.; Tatar, O. Effects of direct selection process for plant height on some yield components in common wheat (Triticum aestivum) genotypes. Int. J. Agric. Biol. 2013, 15, 795–797. [Google Scholar]
- Alheit, K.; Busemeyer, L.; Liu, W.; Maurer, H.; Gowda, M.; Hahn, V.; Weissmann, S.; Ruckelshausen, A.; Reif, J.; Würschum, T. Multiple-line cross QTL mapping for biomass yield and plant height in triticale (×Triticosecale Wittmack). Theor. Appl. Genet. 2014, 127, 251–260. [Google Scholar] [CrossRef]
- Nigon, T.; Mulla, D.; Rosen, C.; Cohen, Y.; Alchanatis, V.; Knight, J.; Rud, R. Hyperspectral aerial imagery for detecting nitrogen stress in two potato cultivars. Comput. Electron. Agric. 2015, 112, 36–46. [Google Scholar] [CrossRef]
- Jay, S.; Maupas, F.; Bendoula, R.; Gorretta, N. Retrieving LAI, chlorophyll and nitrogen contents in sugar beet crops from multi-angular optical remote sensing: Comparison of vegetation indices and PROSAIL inversion for field phenotyping. Field Crops Res. 2017, 210, 33–46. [Google Scholar] [CrossRef]
- Yang, G.; Liu, J.; Zhao, C. Unmanned Aerial Vehicle Remote Sensing for Field-Based Crop Phenotyping: Current Status and Perspectives.Front. Plant Sci. 2017, 8, 1111. [Google Scholar] [CrossRef]
- Babar, M.; Reynolds, M.; Ginkel, M.; Klatt, A.; Raun, W.; Stone, M. Spectral Reflectance to Estimate Genetic Variation for In-Season Biomass, Leaf Chlorophyll, and Canopy Temperature in Wheat. Crop Sci. 2006, 46, 1046–1057. [Google Scholar] [CrossRef]
- Waddington, S.; Ransom, J.; Osmanzai, M.; Saunders, D. Improvement in the yield potential of bread wheat adapted to Northwest Mexico. Crop Sci. 1986, 26, 698–703. [Google Scholar] [CrossRef]
- Calderini, D.; Dreccer, M.; Slafer, G. Genetic improvement in wheat yield and associated traits. A re-examination of previous results and the latest trends. Plant Breed. 1995, 114, 108–112. [Google Scholar] [CrossRef]
- Sayre, K.; Rajaram, S.; Fischer, R. Yield potential progress in short bread wheat in Northern Mexico. Crop Sci. 1997, 37, 36–42. [Google Scholar] [CrossRef]
- Reynolds, M.; Rajaram, S.; Sayre, K. Physiological and genetic changes of irrigated wheat in the post-green revolution period and approaches for meeting projected global demand. Crop Sci. 1999, 39, 1611–1621. [Google Scholar] [CrossRef]
- Hansen, P.; Schjoering, J. Reflectance measurement of canopy biomass and nitrogen status in wheat crops using normalized difference vegetation indices and partial least squares regression. Remote Sens. Environ. 2003, 86, 542–553. [Google Scholar] [CrossRef]
- Pimstein, A.; Karnieli, A.; Bansal, S.; Bonfil, D. Exploring remotely sensed technologies for monitoring wheat potassium and phosphorus using field spectroscopy. Field Crops Res. 2011, 121, 125–135. [Google Scholar] [CrossRef]
- Lobos, G.; Matus, I.; Rodriguez, A.; Romero-Bravo, S.; Araus, J.; Pozo, D. Wheat genotypic variability in grain yield and carbon isotope discrimination under Mediterranean conditions assessed by spectral reflectance. J. Integr. Plant Biol. 2014, 56, 470–479. [Google Scholar] [CrossRef]
- Weber, V.; Araus, J.; Cairns, J.; Sanchez, C.; Melchinger, A.; Orsini, E. Prediction of grain yield using reflectance spectra of canopy and leaves in maize plants grown under different water regimes. Field Crops Res. 2012, 128, 82–90. [Google Scholar] [CrossRef]
- Lin, W.; Yang, C.; Kuo, B. Classifying cultivars of rice (Oryza sativa L.) based on corrected canopy reflectance spectra data using the orthogonal projections of latent structures (O- PLS) method. Chemom. Intell. Lab. Syst. 2012, 115, 25–36. [Google Scholar] [CrossRef]
- Zhao, D.; Reddy, K.; Kakani, V.; Read, J.; Koti, S. Canopy reflectance in cotton for growth assessment and lint yield prediction. Europ. J. Agronomy. 2007, 26, 335–344. [Google Scholar] [CrossRef]
- Kaul, M.; Hill, R.L.; Walthall, C. Artificial neural networks for corn and soybean yield prediction. Agric. Syst. 2005, 85, 1–18. [Google Scholar] [CrossRef]
- Christenson, B.; Schapaugh, W.; An, N.; Price, K.; Fritz, A. Characterizing changes in soybean spectral response curves with breeding advancements. Crop Sci. 2014, 54, 1585–1597. [Google Scholar] [CrossRef]
- Liu, J.; Zhao, C.; Yang, G.; Yu, H.; Zhao, X.; Xu, B.; Niu, Q. Review of field-based phenotyping by unmanned aerial vehicle remote sensing platform. Trans. Chin. Soc. Agric. Eng. 2016, 32, 98–106. [Google Scholar] [CrossRef]
- Li, D.; Cheng, T.; Jia, M.; Zhou, K.; Lu, N.; Yao, X.; Tian, Y.; Zhu, Y.; Cao, W. PROCWT: Coupling PROSPECT with continuous wavelet transform to improve the retrieval of foliar chemistry from leaf bidirectional reflectance spectra. Remote Sens. Environ. 2018, 3, 1–14. [Google Scholar] [CrossRef]
- Miller, J.; Schepers, J.; Shapiro, C.; Arneson, N.; Eskridge, K.; Oliveira, M.; Giesler, L. Characterizing soybean vigor and productivity using multiple crop canopy sensor readings. Field Crops Res. 2018, 216, 22–31. [Google Scholar] [CrossRef]
- Wu, Q.; Qi, B.; Gai, J. A tentative study on utilization of canopy hyperspectral reflectance to estimate anopy growth and seed yield in soybean. Ronomica Sini. 2013, 39, 309–318. [Google Scholar] [CrossRef]
- Zhang, N.; Qi, B.; Zhao, J. Prediction for soybean grain yield using active sensor greenseeker. Acta Agron. Sin. 2014, 40, 657–666. [Google Scholar] [CrossRef]
- Duan, T.; Chapman, S.; Guo, Y.; Zheng, B. Dynamic monitoring of NDVI in wheat agronomy and breeding trials using an unmanned aerial vehicle. Field Crops Res. 2017, 210, 71–80. [Google Scholar] [CrossRef]
- Walter, J.; Edwards, J.; McDonald, G.; Kuchel, H. Photogrammetry for the estimation of wheat biomass and harvest index. Field Crops Res. 2018, 216, 165–174. [Google Scholar] [CrossRef]
- Zheng, H.; Cheng, T.; Yao, X.; Deng, X.; Tian, Y.; Cao, W.; Zhu, Y. Detection of rice phenology through time series analysis of ground-based spectral index data. Field Crops Res. 2016, 198, 131–139. [Google Scholar] [CrossRef]
- Atzberger, C.; Darvishzadeh, R.; Immitzer, M.; Schlerf, M.; Skidmore, A.; Maire, G. Comparative analysis of different retrieval methods for mapping grassland leaf area index using airborne imaging spectroscopy. Int. J. Appl. Earth Obs. Geoinf. 2015, 43, 19–31. [Google Scholar] [CrossRef]
- Campos, I.; González-Gómez, L.; Villodre, J.; González-Piqueras, J.; Suyker, A.; Calera, A. Remote sensing-based crop biomass with water or light-driven crop growth models in wheat commercial fields. Field Crops Res. 2018, 216, 175–188. [Google Scholar] [CrossRef]
- Chapman, S.; Merz, T.; Chan, A.; Jackway, P.; Hrabar, S.; Dreccer, M.; Holland, E.; Zheng, B.; Ling, T.; Jimenez-Berni, J. Pheno-Copter: A Low-Altitude, Autonomous Remote-Sensing Robotic Helicopter for High-Throughput Field-Based Phenotyping. Agronomy 2014, 4, 279–301. [Google Scholar] [CrossRef]
- Sankaran, S.; Khot, L.; Espinoza, C.; Jarolmasjed, S.; Sathuvalli, V.; Vandemark, G.; Miklas, P.; Carter, A.; Pumphrey, M.; Knowles, N.; et al. Low-altitude, high-resolution aerial imaging systems for row and field crop phenotyping: A review. Eur. J. Agron. 2015, 70, 112–123. [Google Scholar] [CrossRef]
- Ballesteros, R.; Ortega, J.; Hernández, D.; Moreno, M. Applications of georeferenced high-resolution images obtained with unmanned aerial vehicles. Part I: Description of image acquisition and processing. Precis. Agric. 2014, 15, 579–592. [Google Scholar] [CrossRef]
- Candiago, S.; Remondino, F.; Giglio, D.; Dubbini, M.; Gattelli, M. Evaluating Multispectral Images and Vegetation Indices for Precision Farming Applications from UAV Images. Remote Sens. 2015, 7, 4026–4047. [Google Scholar] [CrossRef]
- Tucker, C. A comparison of satellite sensors for monitoring vegetation. Photogramm. Eng. Remote Sens. 1978, 44, 1369–1380. [Google Scholar]
- Huete, A.; Didan, K.; Miura, T.; Rodriguez, E.; Gao, X.; Ferreira, L. Overview of the radiometric and biophysical performance of the MODIS vegetation indices. Remote Sens. Environ. 2002, 83, 195–213. [Google Scholar] [CrossRef]
- Hatfield, J.; Prueger, J. Value of using different vegetative indices to quantify agricultural crop characteristics at different growth stages under varying management practices. Remote Sens. 2010, 2, 562–578. [Google Scholar] [CrossRef]
- Samseemoung, G.; Soni, P.; Jayasuriya, H.; Salokhe, V. Application of low altitude remote sensing (LARS) platform for monitoring crop growth and weed infestation in a soybean plantation. Precis. Agric. 2012, 13, 611–627. [Google Scholar] [CrossRef]
- Wiegand, C.; Richardson, A.; Escobar, D.; Gerbermann, A. Vegetation indexes in crop assessment. Remote Sens. Environ. 1991, 35, 105–119. [Google Scholar] [CrossRef]
- Peñuelas, J.; Isla, R.; Filella, I.; Araus, J. Visible and near infrared reflectance assessment of salinity effects on barley. Science 1997, 37, 198–202. [Google Scholar] [CrossRef]
- Lewis, J.; Rowland, J.; Nadeau, A. Estimating maize production in Kenya using NDVI: Some statistical considerations. Int. J. Remote Sens. 1998, 19, 2609–2617. [Google Scholar] [CrossRef]
- Aparicio, N.; Villegas, D.; Casadesus, J.; Araus, J.; Royo, C. Spectral vegetation indices as nondestructive tools for determining durum wheat yield. Agron. J. 2000, 92, 83–91. [Google Scholar] [CrossRef]
- Ma, B.; Dwyer, L.; Costa, C.; Cober, E.; Morrison, M. Early prediction of soybean yield from canopy reflectance measurements. Agron. J. 2001, 93, 1227–1234. [Google Scholar] [CrossRef]
- Shanahan, J.; Schepers, J.; Francis, D.; Varvel, G.; Wilhelm, W.; Tringe, J.S.; Schlemmer, M.; Major, D. Use of remote-sensing imagery to estimate corn grain yield. Agron. J. 2001, 93, 583–589. [Google Scholar] [CrossRef]
- Royo, C.; Villegas, D.; Garcia, D.; Moral, L.; Elhani, S.; Aparicio, N.; Rharrabti, Y.; Araus, J. Comparative performance of carbon isotope discrimination and canopy temperature depression as predictors of genotype differences in durum wheat yield in Spain. Aust. J. Agric. Res. 2002, 53, 561–569. [Google Scholar] [CrossRef]
- Royo, C.; Aparicio, N.; Villegas, D.; Casadesus, J.; Monneveux, P.; Araus, J. Usefulness of spectral reflectance indices as durum wheat yield predictors under contrasting Mediterranean conditions. Int. J. Remote Sens. 2003, 24, 4403–4419. [Google Scholar] [CrossRef]
- Prasad, B.; Carver, B.; Stone, M.; Babar, M.; Raun, W.; Klatt, A. Genetic analysis of indirect selection for winter wheat grain yield using spectral reflectance indices. Crop Sci. 2007, 47, 1416–1425. [Google Scholar] [CrossRef]
- Prasad, B.; Carver, B.; Stone, M.; Babar, M.; Raun, W.; Klatt, A. Potential use of spectral reflectance indices as a selection tool for grain yield in winter wheat under great plains conditions. Crop Sci. 2007, 47, 1426–1440. [Google Scholar] [CrossRef]
- Marti, J.; Bort, J.; Slafer, G.; Araus, J. Can wheat yield be assessed by early measurements of normalized difference vegetation index? Ann. Appl. Biol. 2007, 150, 253–257. [Google Scholar] [CrossRef]
- Koester, R.; Skoneczka, J.; Cary, T.; Diers, B.; Ainsworth, E. Historical gains in soybean (Glycine max Merr.) seed yield are driven by linear increases in light interception, energy conversion, and partitioning efficiencies. Exp. Bot. 2014, 65, 3311–3321. [Google Scholar] [CrossRef] [PubMed]
- Qi, B. A Study on Prediction Technology of Yield and Vegetative Growth Using Hyperspectral Remote Sensing in Soybean Breeding. Ph.D. Thesis, Nanjing Agricultural University, Nanjing, China, 2014. (In Chinese with English Abstract). [Google Scholar]
- Turner, D.; Lucieer, A.; Watson, C. An automated technique for generating georectified mosaics from ultra-high resolution Unmanned Aerial Vehicle (UAV) imagery, based on Structure from Motion (SFM) point clouds. Remote Sens. 2012, 4, 1392–1410. [Google Scholar] [CrossRef]
- Zhao, X.; Yang, G.; Liu, J.; Zhang, X. Estimation of soybean breeding yield based on optimization of spatial scale of UAV hyperspectral image. Trans. Chin. Soc. Agric. Eng. 2017, 33, 110–116. [Google Scholar] [CrossRef]
- Rouse, J., Jr.; Haas, R.; Schell, J.; Deering, D. Monitoring vegetationsystems in the great plains with Erts. NASA 1974, 351, 309–317. [Google Scholar]
- Pearson, R.L.; Miller, L.D. Remote mapping of standing crop biomass for estimation of the productivity of the short-grass Prairie, Pawnee National Grasslands, Colorado[C]//1371146123. In Proceedings of the Eighth International Symposium on Remote Sensing of Environment, Ann Arbor, MI, USA, 2–6 October 1972; Willow Run Laboratories, Environmental Research Institute of Michigan. pp. 1357–1381. [Google Scholar]
- Vogelmann, J.; Rock, B.; Moss, D. Red edge spectral measurements from sugar maple leaves. Title Remote Sens. 1993, 14, 1563–1575. [Google Scholar] [CrossRef]
- Gitelson, A.; Merzlyak, M.; Lichtenthaler, H. Detection of red edge position and chlorophyll content by reflectance measurements near 700 nm. J. Plant Physiol. 1996, 148, 501–508. [Google Scholar] [CrossRef]
- Gitelson, A.; Merzlyak, M. Spectral reflectance changes associated with autumn senescence of aesculus hippocastanum, L. and acer platanoides, L. leaves. spectral features and relation to chlorophyll estimation. J. Physiol. 1994, 143, 286–292. [Google Scholar] [CrossRef]
- Richardson, A.; Wiegand, C. Distinguishing vegetation from soil background information. Photogramm. Eng. Remote Sens. 1977, 43, 1541–1552. [Google Scholar]
- Roujean, J.; Breon, F. Estimating PAR absorbed by vegetation from bidirectional reflectance measurements. Remote Sens. Environ. 1995, 51, 375–384. [Google Scholar] [CrossRef]
- Rondeaux, G.; Steven, M.; Baret, F. Optimization of soil-adjusted vegetation indices. Remote Sens. Environ. 1996, 55, 95–107. [Google Scholar] [CrossRef]
- Huete, A.; Justice, C.; Liu, H. Development of vegetation and soil indices for MODIS-EOS. Remote Sens. Environ. 1994, 49, 224–234. [Google Scholar] [CrossRef]
- Broge, N.; Mortensen, J. Deriving green crop area index and canopy chlorophyll density of winter wheat from spectral reflectance data. Remote Sens. Environ. 2002, 81, 45–57. [Google Scholar] [CrossRef]
- Sankaran, S.; Khot, L.R.; Carter, A. Field-based crop phenotyping: Multispectral aerial imaging for evaluation of winter wheat emergence and spring stand. Comput. Electron. Agric. 2015, 118, 372–379. [Google Scholar] [CrossRef]
- Gonzalez-Dugo, V.; Hernandez, P.; Solis, I.; Zarco-Tejada, P. Using High-Resolution Hyperspectral and Thermal Airborne Imagery to Assess Physiological Condition in the Context of Wheat Phenotyping. Remote Sens. 2015, 7, 13586–13605. [Google Scholar] [CrossRef]
- Overgaard, S.; Isaksson, T.; Kvaal, K.; Korsaeth, A. Comparisons of two hand-held, multispectral field radiometers and a hyperspectral airborne imager in terms of predicting spring wheat grain yield and quality by means of powered partial least squares regression. J. Near Infrared Spectrosc. 2010, 18, 247–261. [Google Scholar] [CrossRef]
- Yu, K.; Kirchgessner, N.; Grieder, C.; Walter, A.; Hund, A. An image analysis pipeline for automated classification of imaging light conditions and for quantification of wheat canopy cover time series in field phenotyping. Plant Methods 2017, 13. [Google Scholar] [CrossRef]
- Araus, J.; Cairns, J. Field high-throughput phenotyping: The new crop breeding frontier. Trends Plant Sci. 2014, 19, 52–61. [Google Scholar] [CrossRef]
- White, J.; Andrade-Sanchez, P.; Gore, M.; Bronson, K.; Coffelt, T.; Conley, M.; Feldmann, K.; French, A.; Heun, J.; Hunsaker, D. Field-based phenomics for plant genetics research. Field Crop Res. 2012, 133, 101–112. [Google Scholar] [CrossRef]
- Deery, D.; Jimenez-Berni, J.; Jones, H.; Sirault, X.; Furbanks, R. Proximal remote sensing buggies and potential applications for field-based phenotyping. Agronomy 2014, 5, 349–379. [Google Scholar] [CrossRef]
- Pinter, P.J., Jr.; Hatfield, J.; Schepers, J.; Barnes, E.; Moran, M.; Daughtry, C.; Upchurch, D. Remote sensing for crop management. Photogramm. Eng. Remote Sens. 2003, 69, 647–664. [Google Scholar] [CrossRef]
- Zhao, C. Advances of Research and Application in Remote Sensing for Agriculture. Trans. Chin. Soc. Agric. Mach. 2014, 45, 277–293. [Google Scholar] [CrossRef]

| Vegetation Index | Full Name of Index | Algorithm Formula | Reference |
|---|---|---|---|
| NDVI | Normalized Difference Vegetation Index | (Rx1 − Rx2)/(Rx1 + Rx2) | [57] |
| RVI | Ratio Vegetation Index | Rx1/Rx2 | [58] |
| VOG1 | Vogelmann Red Edge Index 1 | R740/R720 | [59] |
| GNDVI | Green Normalized Difference Vegetation Index | (R780 − R550)/(R780 + R550) | [60] |
| NDVI705 | Normalized Difference Vegetation Index705 | (R750 − R705)/(R750 + R705) | [61] |
| PVI | Perpendicular Vegetation Index | (RNIR − aRRed − b)/(1 + a2) | [62] |
| RDVI | Renormalized Difference Vegetation Index | (R800 − R670)/(R800 + R670) | [63] |
| OSAVI | Optimized Soil-Adjusted Vegetation Index | (1 + 0.16)(R800 − R670)/(R800 + R670 + 0.16) | [64] |
| EVI | Enhanced Vegetation Index | 2.5(RNIR − R680)/(1 + RNIR + 6R680 − 7.5R460) | [65] |
| DVI | Difference Vegetation Index | RNIR − RRed | [66] |
| Material Data Set | Class Limit (t ha−1) | Range (t ha−1) | Mean (t ha−1) | GCV (%) | CV (%) | F-Value | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| <2.0 | 2.0–2.3 | 2.3–2.6 | 2.6–2.9 | 2.9–3.2 | 3.2–3.5 | 3.5–3.8 | 3.8–4.1 | >4.1 | Σ | ||||||
| 1stYYT 2015 | 6 | 28 | 53 | 59 | 83 | 80 | 86 | 72 | 65 | 532 | 1.83–4.99 | 3.32 | 34.85 | 19.18 | 3.30 ** |
| 2ndYYT 2015 | 1 | 2 | 17 | 25 | 42 | 44 | 53 | 51 | 39 | 274 | 1.65–4.91 | 3.50 | 29.35 | 15.89 | 3.41 ** |
| 2ndYYT 2016 | 6 | 9 | 31 | 58 | 80 | 59 | 35 | 16 | 3 | 297 | 1.72–4.41 | 3.06 | 26.90 | 12.81 | 4.87 ** |
| NJRIKY2015 | 166 | 121 | 101 | 37 | 11 | 5 | 0 | 0 | 0 | 441 | 1.08–3.39 | 2.14 | 33.15 | 33.31 | 0.99 ** |
| Item | R2 | R4 | R5 | R6 | |||||
|---|---|---|---|---|---|---|---|---|---|
| Breeding line yield-test | 1s tYYT | 2nd YYT | 1s tYYT | 2nd YYT | 1st YYT | 2nd YYT | 1st YYT | 2nd YYT | |
| Sensitive band (nm) | λ1 | 750 | 482 | 750 | 514 | 634 | 514 | 550 | 550 |
| λ2 | 770 | 590 | 770 | 606 | 674 | 606 | 710 | 710 | |
| Vegetation index | NDVI | 1 | 1 | 2 | 2 | 2 | 1 | 2 | 2 |
| RVI | 2 | 2 | 1 | 1 | 1 | 2 | 1 | 1 | |
| GNDVI | 4 | 4 | 4 | 4 | 9 | 9 | 3 | 9 | |
| PVI | 5 | 9 | 9 | 10 | 10 | 10 | 10 | 3 | |
| OSASI | 3 | 7 | 3 | 5 | 4 | 4 | 5 | 4 | |
| EVI | 9 | 10 | 5 | 6 | 7 | 5 | 4 | 6 | |
| RDVI | 6 | 3 | 6 | 9 | 3 | 8 | 6 | 5 | |
| VOG1 | 8 | 8 | 8 | 8 | 8 | 7 | 7 | 8 | |
| DVI | 10 | 6 | 10 | 3 | 5 | 3 | 9 | 10 | |
| NDVI705 | 7 | 5 | 7 | 7 | 6 | 6 | 8 | 7 | |
| Maximum R2 | 0.58 | 0.08 | 0.36 | 0.19 | 0.68 | 0.50 | 0.54 | 0.33 | |
| Model Code | Sensitive Band (nm) | Material No. | Model Precision | Verification Precision | Sum Precision | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| λ1 | λ2 | Model | Verifi-Cation | RM2 | RMSEM (t ha−1) | RV2 | RMSEV (t ha−1) | RS2 | RMSES (t ha−1) | |
| MA1+B1 | 618 | 674 | 266 | 266 | 0.68 | 0.410 | 0.53 | 0.241 | 1.21 | 0.651 |
| MA1 | 638 | 674 | 133 | 133 | 0.72 | 0.300 | 0.58 | 0.241 | 1.30 | 0.541 |
| MB1 | 634 | 678 | 133 | 133 | 0.70 | 0.387 | 0.49 | 0.353 | 1.19 | 0.740 |
| MA2+B2 | 514 | 606 | 137 | 137 | 0.60 | 0.382 | 0.42 | 0.261 | 1.02 | 0.643 |
| MA2 | 514 | 614 | 68 | 69 | 0.70 | 0.331 | 0.43 | 0.172 | 1.13 | 0.503 |
| MB2 | 514 | 582 | 68 | 69 | 0.45 | 0.420 | 0.25 | 0.411 | 0.70 | 0.831 |
| MA3+B3 | 534 | 570 | 148 | 149 | 0.25 | 0.405 | 0.13 | 0.407 | 0.38 | 0.812 |
| MA3 | 538 | 570 | 74 | 74 | 0.33 | 0.373 | 0.22 | 0.407 | 0.55 | 0.780 |
| MB3 | 490 | 754 | 74 | 75 | 0.35 | 0.382 | 0.05 | 0.391 | 0.40 | 0.773 |
| MA4+B4 | 486 | 618 | 551 | 552 | 0.46 | 0.454 | 0.45 | 0.355 | 0.91 | 0.809 |
| MA4 | 570 | 730 | 275 | 276 | 0.52 | 0.377 | 0.39 | 0.347 | 0.91 | 0.724 |
| MB4 | 494 | 618 | 276 | 276 | 0.51 | 0.465 | 0.40 | 0.348 | 0.91 | 0.812 |
| MA5 | 486 | 586 | 1651 | 1651 | 0.70 | 0.356 | 0.49 | 0.224 | 1.19 | 0.580 |
| MB5 | 478 | 738 | 48 1 | 48 1 | 0.68 | 0.378 | 0.38 | 0.296 | 1.06 | 0.674 |
| MA6+B6 | 554 | 730 | 213 | 213 | 0.50 | 0.429 | 0.39 | 0.338 | 0.89 | 0.767 |
| MA6 | 638 | 666 | 106 | 107 | 0.61 | 0.301 | 0.51 | 0.218 | 1.12 | 0.519 |
| MB6 | 694 | 722 | 106 | 107 | 0.30 | 0.362 | 0.11 | 0.370 | 0.41 | 0.732 |
| Model | Sensitive Bands (nm) | Material No. | Model Precision | Verification Precision | Sum Precision | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| R5 λ1 | R5 λ2 | R4 λ1 | R4 λ2 | Mo-del | Verification | RM2 | RMSEM (t ha−1) | P | RV2 | RMSEV (t ha−1) | P | RS2 | RMSEs (t ha−1) | |
| MA1+B1-2 (R5 + R4) | 618 | 674 | 750 | 770 | 266 | 266 | 0.71 | 0.364 | 2.68E-63 | 0.51 | 0.267 | 1.84E-47 | 1.22 | 0.631 |
| MA1-1 (R5 + R2) | 638 | 674 | 722 | 730 | 133 | 133 | 0.74 | 0.315 | 2.36E-35 | 0.67 | 0.142 | 8.98E-33 | 1.41 | 0.457 |
| MA1-2 (R5 + R4) | 638 | 674 | 554 | 850 | 133 | 133 | 0.71 | 0.308 | 1.57E-34 | 0.63 | 0.232 | 6.98E-28 | 1.34 | 0.540 |
| MA1-3 (R5 + R6) | 638 | 674 | 586 | 698 | 133 | 133 | 0.73 | 0.333 | 1.53E-34 | 0.59 | 0.208 | 5.62E-28 | 1.32 | 0.541 |
| MB1-2 (R5 + R4) | 634 | 678 | 754 | 770 | 133 | 133 | 0.71 | 0.385 | 1.94E-33 | 0.53 | 0.255 | 4.44E-23 | 1.24 | 0.640 |
| MA2+B2-2 (R5 + R4) | 514 | 606 | 618 | 670 | 137 | 137 | 0.65 | 0.348 | 9.88E-28 | 0.63 | 0.355 | 2.91E-15 | 1.28 | 0.703 |
| MA2-2 (R5 + R4) | 514 | 614 | 518 | 570 | 68 | 69 | 0.68 | 0.293 | 2.73E-15 | 0.49 | 0.313 | 2.40E-09 | 1.17 | 0.606 |
| MB2-2 (R5 + R4) | 514 | 582 | 786 | 850 | 68 | 69 | 0.61 | 0.374 | 9.93E-13 | 0.39 | 0.229 | 8.72E-09 | 1.00 | 0.603 |
| MA3+B3-2 (R5 + R4) | 534 | 570 | 706 | 714 | 148 | 149 | 0.29 | 0.431 | 1.62E-10 | 0.12 | 0.337 | 0.0001 | 0.41 | 0.768 |
| MA3-2 (R5 + R4) | 538 | 570 | 634 | 730 | 74 | 74 | 0.42 | 0.425 | 9.76E-08 | 0.31 | 0.113 | 0.003 | 0.73 | 0.538 |
| MB3-2 (R5 + R4) | 490 | 754 | 702 | 714 | 74 | 75 | 0.29 | 0.411 | 3.22E-05 | 0.19 | 0.325 | 0.0001 | 0.48 | 0.736 |
| MA4+B4-2 (R5 + R4) | 486 | 618 | 554 | 742 | 551 | 552 | 0.52 | 0.445 | 1.41E-85 | 0.42 | 0.316 | 8.75E-65 | 0.94 | 0.761 |
| MA4-2 (R5 + R4) | 570 | 730 | 554 | 742 | 275 | 276 | 0.55 | 0.381 | 1.24E-40 | 0.39 | 0.272 | 2.76E-34 | 0.94 | 0.653 |
| MB4-2 (R5 + R4) | 494 | 618 | 642 | 678 | 276 | 276 | 0.50 | 0.475 | 3.08E-40 | 0.43 | 0.339 | 5.58-34 | 0.93 | 0.814 |
| MA5-2 (R5 + R4) | 486 | 586 | 622 | 742 | 165 1 | 165 1 | 0.67 | 0.359 | 1.42E-37 | 0.53 | 0.263 | 1.75E-27 | 1.26 | 0.622 |
| MB5-2 (R5 + R4) | 478 | 738 | 634 | 738 | 48 1 | 48 1 | 0.68 | 0.345 | 2.93E-10 | 0.41 | 0.270 | 7.49E-07 | 1.09 | 0.615 |
| MA6+B6-2 (R5 + R4) | 554 | 730 | 622 | 738 | 213 | 213 | 0.57 | 0.402 | 2.90E-37 | 0.46 | 0.278 | 1.09E-30 | 1.03 | 0.680 |
| MA6-1 (R5 + R2) | 638 | 666 | 754 | 770 | 106 | 107 | 0.63 | 0.303 | 1.88E-21 | 0.54 | 0.214 | 1.86E-19 | 1.17 | 0.517 |
| MA6-2 (R5 + R4) | 638 | 666 | 754 | 774 | 106 | 107 | 0.63 | 0.290 | 4.71E-21 | 0.52 | 0.260 | 4.35E-17 | 1.15 | 0.550 |
| MA6-3 (R5 + R6) | 638 | 666 | 554 | 710 | 106 | 107 | 0.64 | 0.301 | 5.77E-22 | 0.53 | 0.249 | 1.89E-19 | 1.17 | 0.550 |
| MB6-2 (R5 + R4) | 694 | 722 | 706 | 774 | 106 | 107 | 0.33 | 0.397 | 1.67E-08 | 0.11 | 0.312 | 0.0004 | 0.44 | 0.709 |
| Model | Growth Period Range (d) | Yield Range/ (t ha−1) | RMSEV of (A1 + B1) (t ha−1) | RMSEV of (A2 + B2) (t ha−1) | RMSEV of (A3 + B3) (t ha−1) | RMSEV of (A4 + B4) (t ha−1) |
|---|---|---|---|---|---|---|
| MA1+B1-2 | 99~113 | 1.831~4.995 | 0.440 | 0.536 | 0.932 | 0.632 |
| MA1-1 | 99~112 | 1.836~4.680 | 0.473 | 1.037 | - | - |
| MA1-2 | 99~112 | 1.836~4.680 | 0.433 | 0.486 | 0.663 | 0.517 |
| MA1-3 | 99~112 | 1.836~4.680 | 0.463 | 0.509 | - | - |
| MB1-2 | 99.7~113 | 1.831~4.995 | 0.460 | 0.547 | 1.620 | 0.940 |
| MA2+B2-2 | 103~116 | 1.656~4.917 | 0.587 | 0.428 | 0.561 | 0.545 |
| MA2-2 | 106~116 | 1.656~4.757 | 0.545 | 0.421 | 1.137 | 0.732 |
| MB2-2 | 103~116 | 2.043~4.917 | 1.555 | 1.635 | 1.655 | 1.604 |
| MA3+B3-2 | 96~116 | 1.724~4.410 | 6.651 | 6.940 | 5.260 | 6.390 |
| MA3-2 | 96~116 | 1.724~4.304 | 1.881 | 2.029 | 1.694 | 1.873 |
| MB3-2 | 99~115 | 1.820~4.410 | 0.843 | 3.795 | 0.437 | 1.996 |
| MA4+B4-2 | 96~116 | 1.656~4.995 | 0.442 | 0.462 | 0.475 | 0.457 |
| MA4-2 | 96~116 | 1.656~4.757 | 0.475 | 0.456 | 0.454 | 0.465 |
| MB4-2 | 99~116 | 1.820~4.995 | 0.456 | 0.471 | 0.471 | 0.464 |
| MA5-2 | 99~114 | 2.380~4.925 | 0.956 | 1.346 | 2.214 | 1.488 |
| MB5-2 | 96~116 | 3.283~4.558 | 0.708 | 1.385 | 0.501 | 0.888 |
| MA6+B6-2 | 96~116 | 2.380~4.925 | 0.581 | 0.533 | 0.444 | 0.536 |
| MA6-1 | 101~116 | 2.380~4.925 | 0.522 | 0.553 | - | - |
| MA6-2 | 101~116 | 2.380~4.925 | 0.501 | 0.547 | 1.022 | 0.690 |
| MA6-3 | 101~116 | 2.380~4.925 | 0.568 | 0.702 | - | - |
| MB6-2 | 96~116 | 2.380~4.925 | 0.862 | 2.071 | 0.428 | 1.215 |
| Model | A1 + B1 | A2 + B2 | A3 + B3 | A4 + B4 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Eli | Res | Pro | Sum | Eli | Res | Pro | Sum | Eli | Res | Pro | Sum | Eli | Res | Pro | Sum | |
| Actual selection | 177 | 203 | 152 | 532 | 60 | 118 | 96 | 274 | 142 | 131 | 24 | 297 | 379 | 452 | 272 | 1103 |
| MA1+B1-2 | 69.5 | 56.7 | 63.2 | 62.8 | 31. 7 | 49.2 | 65.6 | 51.1 | 20.4 | 9.1 | 0 | 13.8 | 45.1 | 40.9 | 58.5 | 46.7 |
| MA1-1 | 81.4 | 58.6 | 15.1 | 53.8 | 40.0 | 48.3 | 38.5 | 43.1 | - | - | - | - | 44.3 | 38.9 | 22.1 | 36.6 |
| MA1-2 | 66.7 | 56.2 | 71.7 | 64.1 | 33.3 | 53.4 | 734.0 | 56.2 | 59.2 | 33.6 | 16. 7 | 44.4 | 58.6 | 48. 9 | 67.75 | 56.8 |
| MA1-3 | 100.0 | 0 | 0 | 33.3 | 100.0 | 0 | 0 | 21.9 | - | - | - | - | 100.0 | 0 | 0 | 55.2 |
| MB1-2 | 84.2 | 54.2 | 52.0 | 63.5 | 33.3 | 44.9 | 80.2 | 54.7 | 99.3 | 0 | 0 | 47.5 | 81.8 | 36.1 | 57.4 | 57.0 |
| MA2+B2-2 | 23.2 | 45.8 | 71.7 | 45.7 | 35.0 | 60.2 | 78.1 | 61.0 | 11.3 | 84.9 | 34. 8 | 45.8 | 20.6 | 61.1 | 70.6 | 49.5 |
| MA2-2 | 29.4 | 68.0 | 48.7 | 49.6 | 40.0 | 73.7 | 55.2 | 59.9 | 1.4 | 18.9 | 95.7 | 16.5 | 20.6 | 55.3 | 54. 8 | 43.3 |
| MB2-2 | 1.1 | 0 | 99.3 | 28.8 | 0 | 0 | 100.0 | 35.0 | 0 | 0 | 100.0 | 7.7 | 0.5 | 0 | 99.3 | 24.7 |
| MA3+B3-2 | 0 | 0 | 100.0 | 28.6 | 0 | 0 | 100.0 | 35.0 | 0 | 0 | 100.0 | 7.7 | 0 | 0 | 99.6 | 24.6 |
| MA3-2 | 9.0 | 60.1 | 24.3 | 32.9 | 38.3 | 27.1 | 66.7 | 43.4 | 44.4 | 62.9 | 30.4 | 51.5 | 26.9 | 52.4 | 39.7 | 40.5 |
| MB3-2 | 91.0 | 8.4 | 0 | 33.5 | 56.7 | 59.3 | 7.3 | 40.5 | 73.2 | 41.7 | 17.4 | 54.9 | 78.9 | 31.4 | 4.0 | 41.0 |
| MA4+B4-2 | 64.4 | 60.6 | 62.5 | 62.4 | 71.7 | 55.9 | 38.5 | 53.3 | 41.6 | 70. 5 | 8.7 | 51.9 | 57.0 | 62.4 | 49.3 | 57.3 |
| MA4-2 | 61.6 | 68.0 | 39.5 | 57.7 | 50.0 | 55.9 | 83.3 | 64.2 | 33.1 | 87.8 | 0 | 54.6 | 49.1 | 70.6 | 51.5 | 58.5 |
| MB4-2 | 63.3 | 60.1 | 61.8 | 61.7 | 70.0 | 54.2 | 50.0 | 56.2 | 47.9 | 60.6 | 8.7 | 50.5 | 58.6 | 58.9 | 52.9 | 57.3 |
| MA5-2 | 94.4 | 33.5 | 27.6 | 52.1 | 96.7 | 14.4 | 7.3 | 29.9 | 97.2 | 0.8 | 0 | 46.8 | 95.8 | 19.0 | 18.0 | 45.2 |
| MB5-2 | 0 | 81.8 | 4.0 | 32.3 | 0 | 0 | 100 | 35.0 | 33.8 | 73.5 | 13.0 | 49.8 | 12.7 | 58.2 | 38.6 | 37.7 |
| MA6+B6-2 | 17.5 | 47.3 | 76.3 | 45.7 | 16. 7 | 43.2 | 94.8 | 55.5 | 47.2 | 65.9 | 0 | 51.9 | 28.5 | 51.8 | 76.1 | 49.8 |
| MA6-1 | 2.3 | 35.5 | 94.1 | 41.2 | 0 | 38.1 | 91.7 | 48.5 | - | - | - | - | 1.1 | 25.9 | 84.9 | 31.9 |
| MA6-2 | 42.9 | 47.3 | 82.9 | 56.0 | 16.7 | 44.9 | 82.3 | 51.8 | 95.8 | 1.5 | 0 | 46.5 | 58.6 | 33.4 | 75.4 | 52.4 |
| MA6-3 | 31.1 | 51.7 | 84.9 | 54.3 | 10.0 | 42.4 | 87.5 | 51.1 | - | - | - | - | 16.1 | 34.3 | 78.3 | 38.9 |
| MB6-2 | 94.4 | 19.2 | 0 | 38.7 | 73.3 | 39.8 | 8.3 | 36.1 | 66.2 | 59.9 | 30.4 | 60.6 | 80.5 | 36.5 | 5.5 | 44.0 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Zhao, J.; Yang, G.; Liu, J.; Cao, J.; Li, C.; Zhao, X.; Gai, J. Establishment of Plot-Yield Prediction Models in Soybean Breeding Programs Using UAV-Based Hyperspectral Remote Sensing. Remote Sens. 2019, 11, 2752. https://doi.org/10.3390/rs11232752
Zhang X, Zhao J, Yang G, Liu J, Cao J, Li C, Zhao X, Gai J. Establishment of Plot-Yield Prediction Models in Soybean Breeding Programs Using UAV-Based Hyperspectral Remote Sensing. Remote Sensing. 2019; 11(23):2752. https://doi.org/10.3390/rs11232752
Chicago/Turabian StyleZhang, Xiaoyan, Jinming Zhao, Guijun Yang, Jiangang Liu, Jiqiu Cao, Chunyan Li, Xiaoqing Zhao, and Junyi Gai. 2019. "Establishment of Plot-Yield Prediction Models in Soybean Breeding Programs Using UAV-Based Hyperspectral Remote Sensing" Remote Sensing 11, no. 23: 2752. https://doi.org/10.3390/rs11232752
APA StyleZhang, X., Zhao, J., Yang, G., Liu, J., Cao, J., Li, C., Zhao, X., & Gai, J. (2019). Establishment of Plot-Yield Prediction Models in Soybean Breeding Programs Using UAV-Based Hyperspectral Remote Sensing. Remote Sensing, 11(23), 2752. https://doi.org/10.3390/rs11232752