Annual Green Water Resources and Vegetation Resilience Indicators: Definitions, Mutual Relationships, and Future Climate Projections
Abstract
1. Introduction
- Protect from erosion and landslides.
- Protect from inland flooding.
- Buffer natural resources against drier and more variable climates.
- Reduce risks and impacts of wildfires.
- Protect from coastal hazards and sea level rise.
- Moderate urban heatwaves and heat island effects.
- Managing stormwater and flooding in urban areas.
- Validity of the fundamental principle of the resilience indicator [27] applied to precipitation, i.e., its proportionality with drought return times.
- Relationship between the water resource resilience indicator and the vegetation primary production resilience.
- Changes of green water resource resilience due to global warming.
2. Materials and Methods
2.1. Annual Crop Production Resilience Indicator (RC): Definition and Properties
- It is formally derived from the ecological definition of resilience, thus, theoretically more grounded than similar indicators based on different functions of the μ over σ ratio such as the coefficient of variance.
- It is inversely/directly proportional to the frequency / return period of the extreme events leading to large production losses.
- It takes into account spatial heterogeneities and diversity in a simple and intuitive manner i.e., RC computed on the sum of n uncorrelated time series with same μ and σ is exactly n-times RC of the individual time series.
- It is simple to compute, and it can take into account the effects of non-linear long-term trends easily e.g., by normalizing the time series by the running mean baseline values prior to the indicator computation.
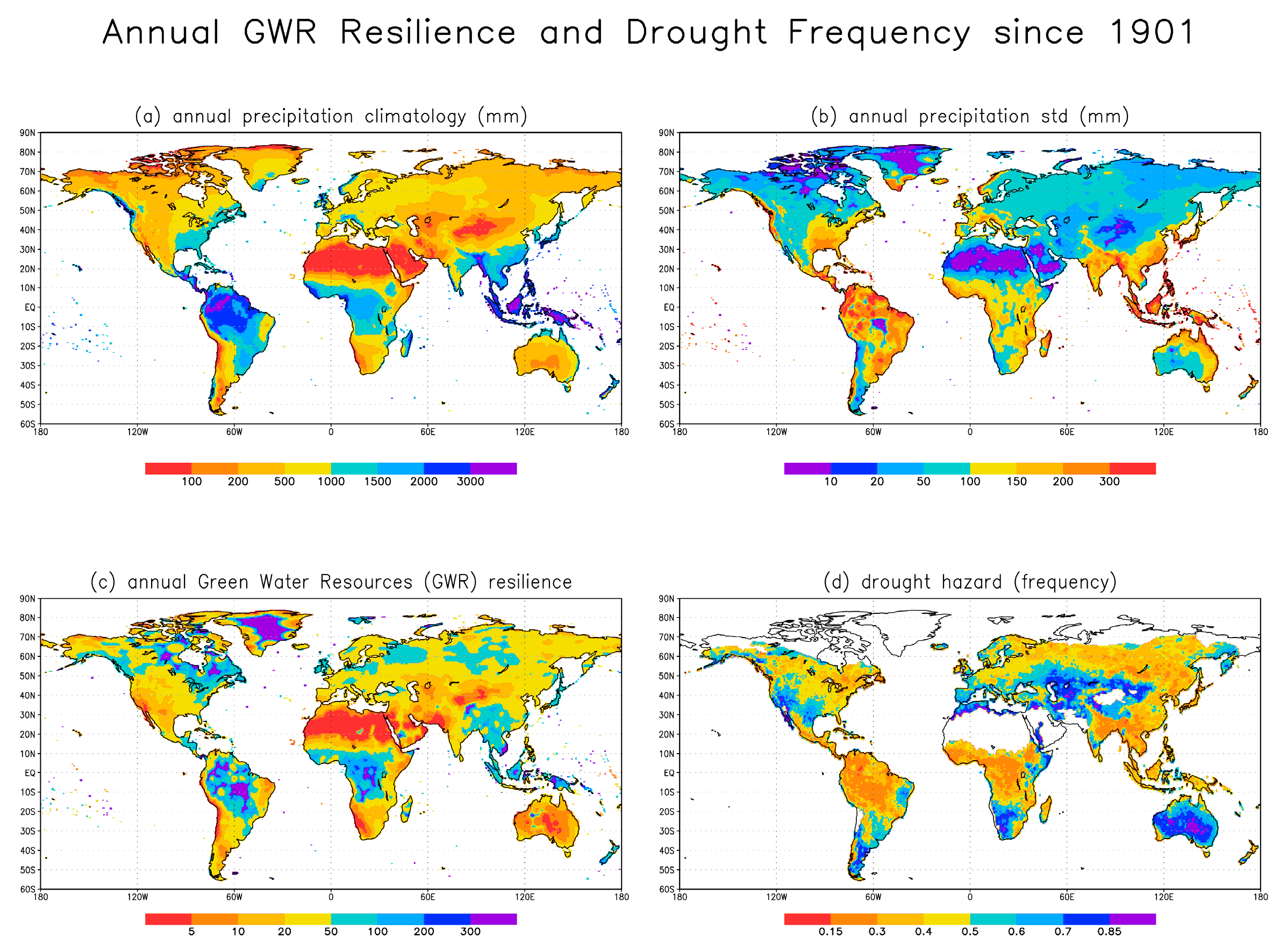
2.2. Annual Green Water Resources Resilience Indicator (RP): Definition and Data
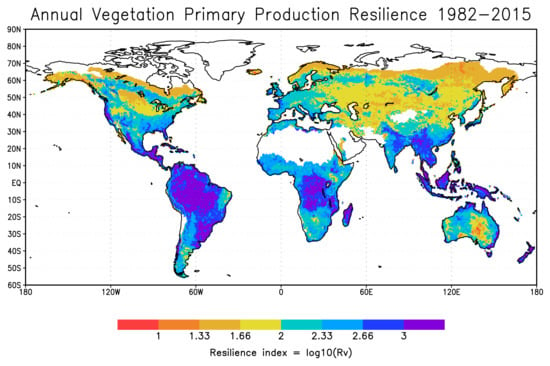
2.3. Annual Vegetation Primary Production Resilience Indicator (RV): Definition and Data
2.4. Properties of RP and RV
3. Results
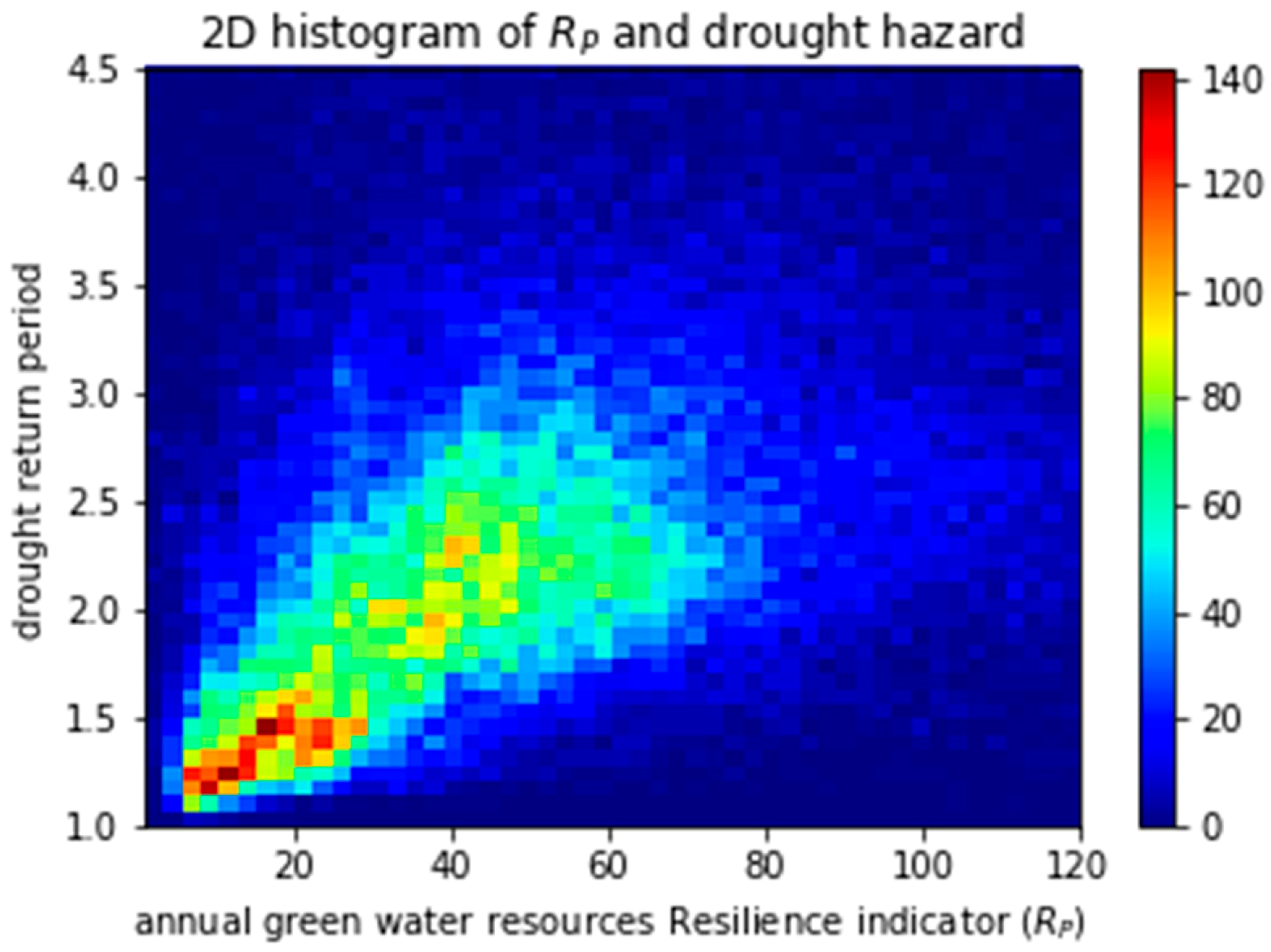
- The test of the annual resilience indicator applied to precipitation to be inversely proportional to drought frequency (Section 3.1–2nd property).
- The effects of climate change on RP (Section 3.3).
3.1. Annual Green Water Resources Resilience Indicator (RP) and Drought Frequency Since 1901
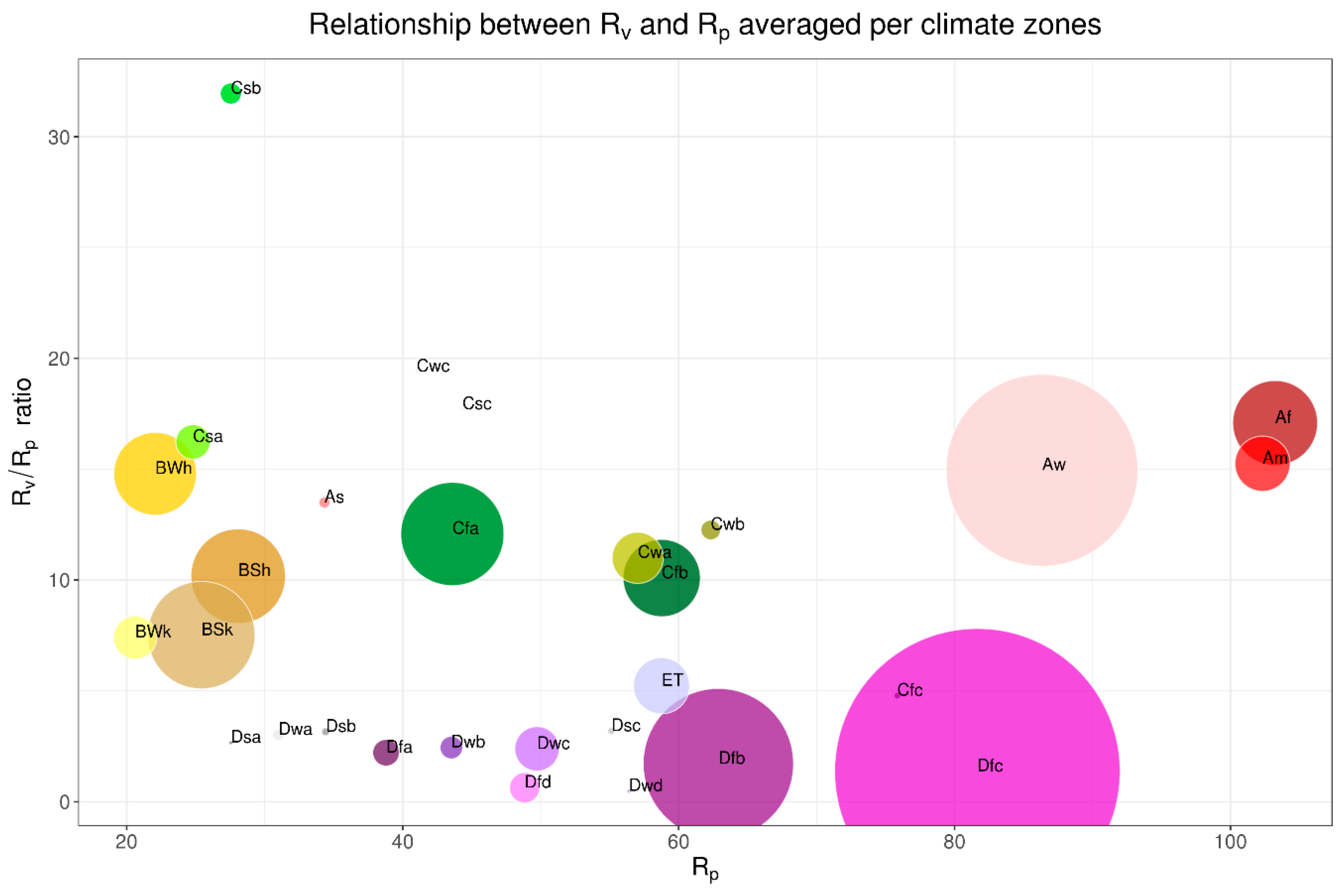
3.2. Precipitation and Vegetation Resilience Indicator Since 1982
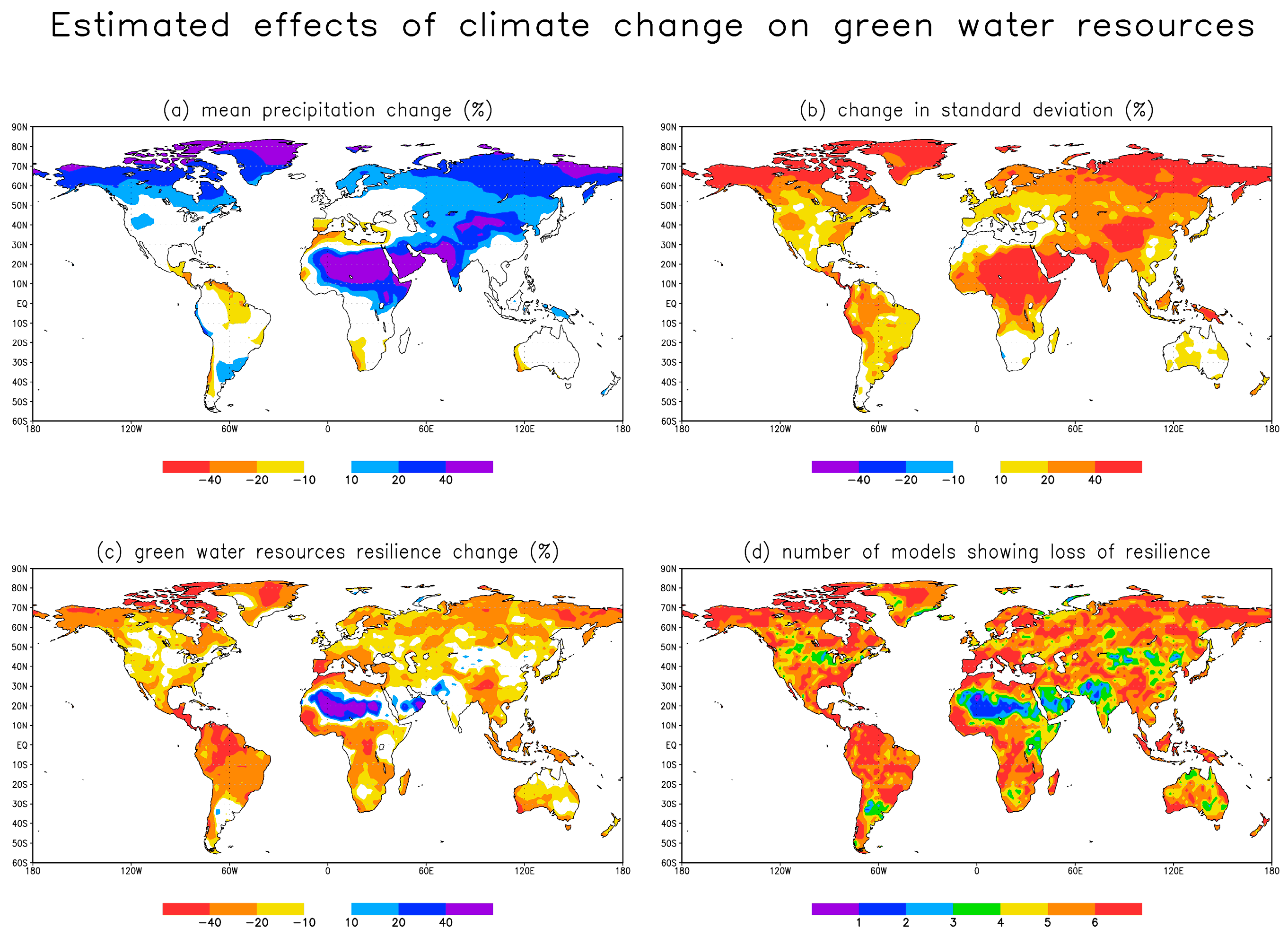
3.3. Effects of Climate Change on Annual Green Water Resources Resilience Indicator (RP)
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- United Nations Economic and Social Council. Report of the Inter-Agency and Expert Group on Sustainable Development Goal Indicators. In Proceedings of the Statistical Commission Forty-Seventh Session, New York, NY, USA, 8–11 March 2016. [Google Scholar]
- Millennium Ecosystem Assessment. Ecosystems and Human Well-Being: Synthesis; Island Press: Washington, DC, USA, 2005. [Google Scholar]
- The Economics of Ecosystems and Biodiversity. Ecological and Economic Foundation; Routledge: London, UK, 2010. [Google Scholar]
- Davis, A.S.; Hill, J.D.; Chase, C.A.; Johanns, A.M.; Liebman, M. Increasing Cropping System Diversity Balances Productivity, Profitability and Environmental Health. PLoS ONE 2012, 7, e47149. [Google Scholar] [CrossRef] [PubMed]
- Seddon, N.; Turner, B.; Berry, P.; Chausson, A.; Girardin, C.A.J. Grounding nature-based climate solutions in sound biodiversity science. Nat. Clim. Chang. 2019, 9, 84–87. [Google Scholar] [CrossRef]
- Costanza, R.; de Groot, R.; Sutton, P.; van der Ploeg, S.; Anderson, S.J.; Kubiszewski, I.; Farber, S.; Turner, R.K. Changes in the global value of ecosystem services. Glob. Environ. Chang. 2014, 26, 152–158. [Google Scholar] [CrossRef]
- Pascual, U.; Balvanera, P.; Díaz, S.; Pataki, G.; Roth, E.; Stenseke, M.; Watson, R.T.; Başak Dessane, E.; Islar, M.; Kelemen, E.; et al. Valuing nature’s contributions to people: The IPBES approach. Curr. Opin. Environ. Sustain. 2017, 26–27, 7–16. [Google Scholar] [CrossRef]
- Maes, J.; Liquete, C.; Teller, A.; Erhard, M.; Paracchini, M.L.; Barredo, J.I.; Grizzetti, B.; Cardoso, A.; Somma, F.; Petersen, J.-E.; et al. An indicator framework for assessing ecosystem services in support of the EU Biodiversity Strategy to 2020. Ecosyst. Serv. 2016, 17, 14–23. [Google Scholar] [CrossRef]
- Santos-Martín, F.; Zorrilla-Miras, P.; Palomo, I.; Montes, C.; Benayas, J.; Maes, J. Protecting nature is necessary but not sufficient for conserving ecosystem services: A comprehensive assessment along a gradient of land-use intensity in Spain. Ecosyst. Serv. 2019, 35, 43–51. [Google Scholar] [CrossRef]
- Dunford, R.; Harrison, P.; Smith, A.; Dick, J.; Barton, D.N.; Martin-Lopez, B.; Kelemen, E.; Jacobs, S.; Saarikoski, H.; Turkelboom, F.; et al. Integrating methods for ecosystem service assessment: Experiences from real world situations. Ecosyst. Serv. 2018, 29, 499–514. [Google Scholar] [CrossRef]
- Shi, L.; Wang, Y.; Jia, Y.; Lu, C.; Lei, G.; Wen, L. Vegetation Cover Dynamics and Resilience to Climatic and Hydrological Disturbances in Seasonal Floodplain: The Effects of Hydrological Connectivity. Front. Plant Sci. 2017, 8, 2196. [Google Scholar] [CrossRef]
- Cui, X.; Gibbes, C.; Southworth, J.; Waylen, P. Using Remote Sensing to Quantify Vegetation Change and Ecological Resilience in a Semi-Arid System. Land 2013, 2, 108–130. [Google Scholar] [CrossRef]
- Myneni, R.B.; Keeling, C.D.; Tucker, C.J.; Asrar, G.; Nemani, R.R. Increase plant growth in the northern high latitudes from 1981 to 1991. Nature 1997, 386, 698–702. [Google Scholar] [CrossRef]
- Pettorelli, N.; Vik, J.O.; Mysterud, A.; Gaillard, J.; Tucker, C.J.; Stenseth, N.C.; Lyon, C.B. Using the satellite-derived NDVI to assess ecological responses to environmental change. Trends Ecol. Evol. 2005, 20, 503–510. [Google Scholar] [CrossRef] [PubMed]
- Hilker, T.; Lyapustin, A.I.; Tucker, C.J.; Hall, F.G.; Myneni, R.B.; Wang, Y.; Bi, J.; de Moura, Y.; Sellers, P.J. Vegetation dynamics and rainfall sensitivity of the Amazon. Proc. Natl. Acad. Sci. USA 2014, 111, 16041–16046. [Google Scholar] [CrossRef] [PubMed]
- Krishnaswamy, J.; Bawa, K.S.; Ganeshaiah, K.N.; Kiran, M.C. Quantifying and mapping biodiversity and ecosystem services: Utility of a multi-season NDVI based Mahalanobis distance surrogate. Remote Sens. Environ. 2009, 113, 857–867. [Google Scholar] [CrossRef]
- Roces-Díaz, J.V.; Díaz-Varela, R.A.; Álvarez-Álvarez, P.; Recondo, C.; Díaz-Varela, E.R. A multiscale analysis of ecosystem services supply in the NW Iberian Peninsula from a functional perspective. Ecol. Indic. 2015, 50, 24–34. [Google Scholar] [CrossRef]
- Paruelo, J.M.; Texeira, M.; Staiano, L.; Mastrángelo, M.; Amdan, L.; Gallego, F. An integrative index of Ecosystem Services provision based on remotely sensed data. Ecol. Indic. 2016, 71, 145–154. [Google Scholar] [CrossRef]
- Calderón-Contreras, R.; Quiroz-Rosas, L.E. Analysing scale, quality and diversity of green infrastructure and the provision of Urban Ecosystem Services: A case from Mexico City. Ecosyst. Serv. 2017, 23, 127–137. [Google Scholar] [CrossRef]
- De Carvalho, R.M.; Szlafsztein, C.F. Urban vegetation loss and ecosystem services: The influence on climate regulation and noise and air pollution. Environ. Pollut. 2019, 245, 844–852. [Google Scholar] [CrossRef]
- De Araujo Barbosa, C.C.; Atkinson, P.M.; Dearing, J.A. Remote sensing of ecosystem services: A systematic review. Ecol. Indic. 2015, 52, 430–443. [Google Scholar] [CrossRef]
- Liquete, C.; Udias, A.; Conte, G.; Grizzetti, B.; Masi, F. Integrated valuation of a nature-based solution for water pollution control. Highlighting hidden benefits. Ecosyst. Serv. 2016, 22, 392–401. [Google Scholar] [CrossRef]
- De Keersmaecker, W.; Lhermitte, S.; Honnay, O.; Farifteh, J.; Somers, B.; Coppin, P. How to measure ecosystem stability? An evaluation of the reliability of stability metrics based on remote sensing time series across the major global ecosystems. Glob. Chang. Biol. 2014, 20, 2149–2161. [Google Scholar] [CrossRef]
- Oliver, T.H.; Isaac, N.J.B.; August, T.A.; Woodcock, B.A.; Roy, D.B.; Bullock, J.M. Declining resilience of ecosystem functions under biodiversity loss. Nat. Commun. 2015, 6, 10122. [Google Scholar] [CrossRef] [PubMed]
- Maes, J.; Egoh, B.; Willemen, L.; Liquete, C.; Vihervaara, P.; Schägner, J.P.; Grizzetti, B.; Drakou, E.G.; Notte, A.L.; Zulian, G.; et al. Mapping ecosystem services for policy support and decision making in the European Union. Ecosyst. Serv. 2012, 1, 31–39. [Google Scholar] [CrossRef]
- Brandl, S.J.; Rasher, D.B.; Côté, I.M.; Casey, J.M.; Darling, E.S.; Lefcheck, J.S.; Duffy, J.E. Coral reef ecosystem functioning: Eight core processes and the role of biodiversity. Front. Ecol. Environ. 2019, 17, 445–454. [Google Scholar] [CrossRef]
- Zampieri, M.; Weissteiner, C.; Grizzetti, B.; Toreti, A.; Van Den Berg, M.; Dentener, F. Estimating resilience of annual crop production systems: Theory and limitations. arXiv 2019, arXiv:1902.02677. [Google Scholar]
- Holling, C.S. Resilience and stability of ecological systems. Annu. Rev. Ecol. Syst. 1973, 4, 1–23. [Google Scholar] [CrossRef]
- Falkenmark, M.; Rockström, J. Rain: The Neglected Resource: Embracing Green Water Management Solutions; Stockholm International Water Institute (SIWI): Stockholm, Sweden, 2005. [Google Scholar]
- Holling, C.S. Engineering Resilience versus Ecological Resilience; The National Academy of Sciences: Washington, DC, USA, 1996. [Google Scholar]
- Harris, I.; Jones, P.D.; Osborn, T.J.; Lister, D.H. Updated high-resolution grids of monthly climatic observations—The CRU TS3. 10 Dataset. Int. J. Climatol. 2014, 34, 623–642. [Google Scholar] [CrossRef]
- Lyon, B.; Barnston, A.G. ENSO and the Spatial Extent of Interannual Precipitation Extremes in Tropical Land Areas. J. Clim. 2005, 18, 5095–5109. [Google Scholar] [CrossRef]
- Carrão, H.; Naumann, G.; Barbosa, P. Mapping global patterns of drought risk: An empirical framework based on sub-national estimates of hazard, exposure and vulnerability. Glob. Environ. Chang. 2016, 39, 108–124. [Google Scholar] [CrossRef]
- O’Neill, B.C.; Kriegler, E.; Riahi, K.; Ebi, K.L.; Hallegatte, S.; Carter, T.R.; Mathur, R.; van Vuuren, D.P. A new scenario framework for climate change research: The concept of shared socioeconomic pathways. Clim. Chang. 2014, 122, 387–400. [Google Scholar] [CrossRef]
- Pinzon, J.E.; Tucker, C.J. A Non-Stationary 1981–2012 AVHRR NDVI3g Time Series. Remote Sens. 2014, 6, 6929–6960. [Google Scholar] [CrossRef]
- Holben, B.N. Characteristics of maximum-value composite images from temporal AVHRR data. Int. J. Remote Sens. 1986, 7, 1417–1434. [Google Scholar] [CrossRef]
- Savitzky, A.; Golay, M.J.E. Smoothing and differentiation of data by simplified least squares procedures. Anal. Chem. 1964, 36, 1627–1639. [Google Scholar] [CrossRef]
- Chen, J.; Jonsson, P.; Tamura, M.; Gu, Z.; Matsushita, B.; Eklundh, L. A simple method for reconstructing a high-quality NDVI time-series data set based on the Savitzky-Golay filter. Remote Sens. Environ. 2004, 91, 332–344. [Google Scholar] [CrossRef]
- Jones, P.W. First- and Second-Order Conservative Remapping Schemes for Grids in Spherical Coordinates. Mon. Weather. Rev. 1999, 127, 2204–2210. [Google Scholar] [CrossRef]
- Kottek, M.; Grieser, J.; Beck, C.; Rudolf, B.; Rubel, F. World Map of the Köppen-Geiger climate classification updated. Meteorol. Z. 2006, 15, 259–263. [Google Scholar] [CrossRef]
- Toreti, A.; Naveau, P.; Zampieri, M.; Schindler, A.; Scoccimarro, E.; Xoplaki, E.; Dijkstra, H.A.; Gualdi, S.; Luterbacher, J. Projections of global changes in precipitation extremes from Coupled Model Intercomparison Project Phase 5 models. Geophys. Res. Lett. 2013, 40, 4887–4892. [Google Scholar] [CrossRef]
- Scoccimarro, E.; Gualdi, S.; Bellucci, A.; Zampieri, M.; Navarra, A. Heavy precipitation events in a warmer climate: Results from CMIP5 models. J. Clim. 2013, 26, 7902–7911. [Google Scholar] [CrossRef]
- Grizzetti, B.; Liquete, C.; Pistocchi, A.; Vigiak, O.; Zulian, G.; Bouraoui, F.; Roo, A.D.; Cardoso, A.C. Relationship between ecological condition and ecosystem services in European rivers, lakes and coastal waters. Sci. Total Environ. 2019, 671, 452–465. [Google Scholar] [CrossRef]
- Smith, A.C.; Harrison, P.A.; Pérez Soba, M.; Archaux, F.; Blicharska, M.; Egoh, B.N.; Erős, T.; Fabrega Domenech, N.; György, Á.I.; Haines-Young, R.; et al. How natural capital delivers ecosystem services: A typology derived from a systematic review. Ecosyst. Serv. 2017, 26, 111–126. [Google Scholar] [CrossRef]
- Seddon, A.W.R.; Macias-Fauria, M.; Long, P.R.; Benz, D.; Willis, K.J. Sensitivity of global terrestrial ecosystems to climate variability. Nature 2016, 531, 229. [Google Scholar] [CrossRef]
- De Keersmaecker, W.; Lhermitte, S.; Hill, M.J.; Tits, L.; Coppin, P.; Somers, B. Assessment of Regional Vegetation Response to Climate Anomalies: A Case Study for Australia Using GIMMS NDVI Time Series between 1982 and 2006. Remote Sens. 2017, 9, 34. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.M.; Gouveia, C.; Camarero, J.J.; Begueria, S.; Trigo, R.; Lopez-Moreno, J.I.; Azorin-Molina, C.; Pasho, E.; Lorenzo-Lacruz, J.; Revuelto, J.; et al. Response of vegetation to drought time-scales across global land biomes. Proc. Natl. Acad. Sci. USA 2013, 110, 52–57. [Google Scholar] [CrossRef] [PubMed]
- Liu, L.; Zhang, Y.; Wu, S.; Li, S.; Qin, D. Water memory effects and their impacts on global vegetation productivity and resilience. Sci. Rep. 2018, 8, 2962. [Google Scholar] [CrossRef] [PubMed]
- Müller, C.; Elliott, J.; Pugh, T.A.M.; Ruane, A.C.; Ciais, P.; Balkovic, J.; Deryng, D.; Folberth, C.; Izaurralde, R.C.; Jones, C.D.; et al. Global patterns of crop yield stability under additional nutrient and water inputs. PLoS ONE 2018, 13, e0198748. [Google Scholar] [CrossRef] [PubMed]
- Baho, D.L.; Allen, C.R.; Garmestani, A.; Fried-Petersen, H.; Renes, S.E.; Gunderson, L.; Angeler, D.G. A quantitative framework for assessing ecological resilience. Ecol. Soc. 2017, 22, 17. [Google Scholar] [CrossRef]
- Enright, N.J.; Fontaine, J.B.; Lamont, B.B.; Miller, B.P.; Westcott, V.C. Resistance and resilience to changing climate and fire regime depend on plant functional traits. J. Ecol. 2014, 102, 1572–1581. [Google Scholar] [CrossRef]
- Reyer, C.P.O.; Brouwers, N.; Rammig, A.; Brook, B.W.; Epila, J.; Grant, R.F.; Holmgren, M.; Langerwisch, F.; Leuzinger, S.; Lucht, W.; et al. Forest resilience and tipping points at different spatio-temporal scales: Approaches and challenges. J. Ecol. 2015, 103, 5–15. [Google Scholar] [CrossRef]
- Ma, Z.; Liu, H.; Mi, Z.; Zhang, Z.; Wang, Y.; Xu, W.; Jiang, L.; He, J.-S. Climate warming reduces the temporal stability of plant community biomass production. Nat. Commun. 2017, 8, 15378. [Google Scholar] [CrossRef]
- Ivits, E.; Cherlet, M.; Tóth, G.; Sommer, S.; Mehl, W.; Vogt, J.; Micale, F. Combining satellite derived phenology with climate data for climate change impact assessment. Glob. Planet. Chang. 2012, 88–89, 85–97. [Google Scholar] [CrossRef]
- Gessner, U.; Naeimi, V.; Klein, I.; Kuenzer, C.; Klein, D.; Dech, S. The relationship between precipitation anomalies and satellite-derived vegetation activity in Central Asia. Glob. Planet. Chang. 2013, 110, 74–87. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.M.; Beguería, S.; López-Moreno, J.I. A Multiscalar Drought Index Sensitive to Global Warming: The Standardized Precipitation Evapotranspiration Index. J. Clim. 2010, 23, 1696–1718. [Google Scholar] [CrossRef]
- Naumann, G.; Alfieri, L.; Wyser, K.; Mentaschi, L.; Betts, R.A.; Carrao, H.; Spinoni, J.; Vogt, J.; Feyen, L. Global Changes in Drought Conditions under Different Levels of Warming. Geophys. Res. Lett. 2018, 45, 3285–3296. [Google Scholar] [CrossRef]
- Zampieri, M.; Garcia, G.C.; Dentener, F.; Gumma, M.K.; Salamon, P.; Seguini, L.; Toreti, A. Surface freshwater limitation explains worst rice production anomaly in India in 2002. Remote Sens. 2018, 10, 244. [Google Scholar] [CrossRef]
- Zampieri, M.; Ceglar, A.; Manfron, G.; Toreti, A.; Duveiller, G.; Romani, M.; Rocca, C.; Scoccimarro, E.; Podrascanin, Z.; Djurdjevic, V. Adaptation and sustainability of water management for rice agriculture in temperate regions: The Italian case study. L Degrad. Dev. 2019, 39, 2033–2047. [Google Scholar] [CrossRef]
- Grizzetti, B.; Pistocchi, A.; Liquete, C.; Udias, A.; Bouraoui, F.; Van De Bund, W. Human pressures and ecological status of European rivers. Sci. Rep. 2017, 7, 205. [Google Scholar] [CrossRef]
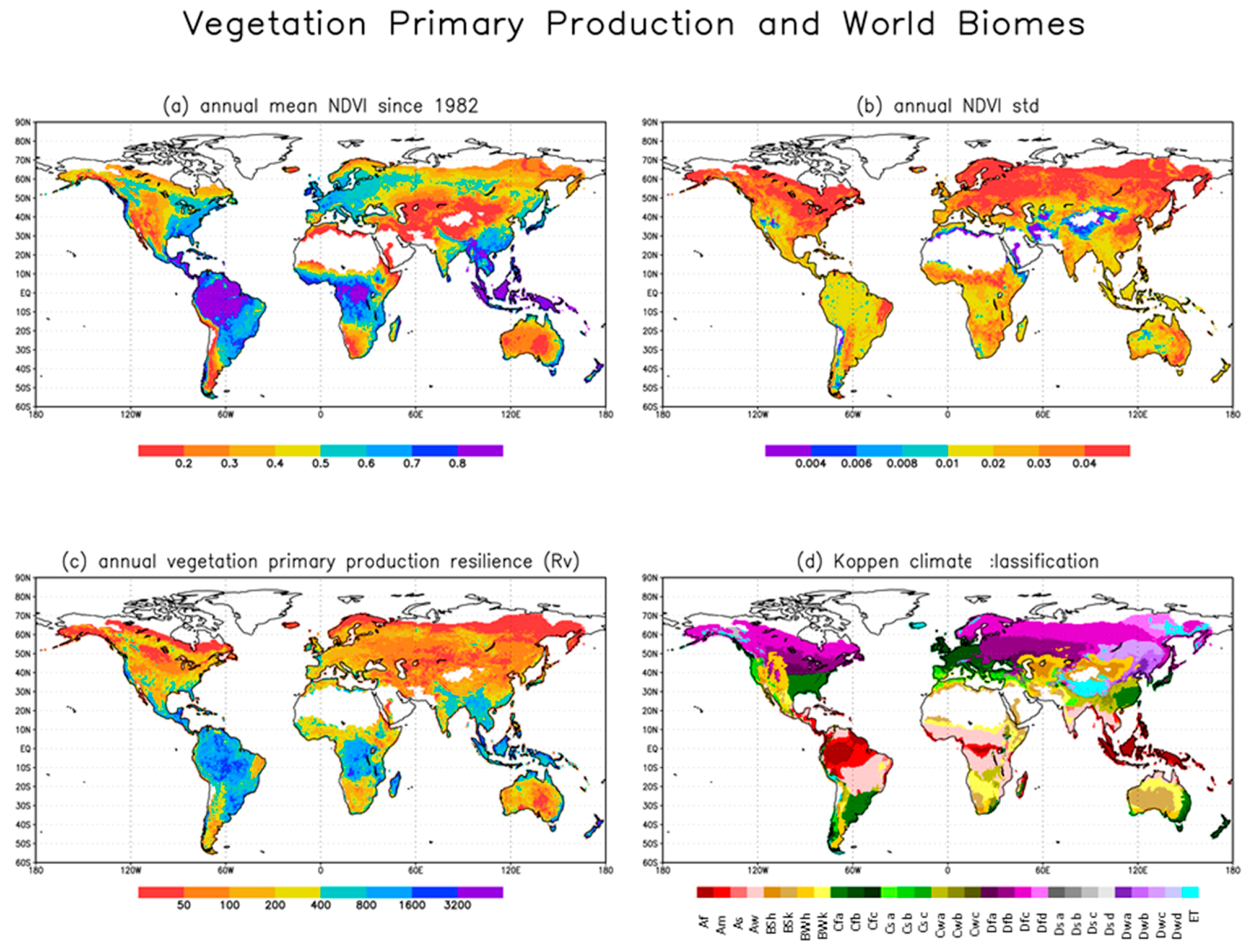
| Main Climates | Precipitation 1 | Temperature 1 | |
|---|---|---|---|
| A: equatorial | W: desert | h: hot arid | E: polar frost |
| B: arid | S: steppe | k: cold arid | T: polar tundra |
| C: warm temperate | f: fully humid | a: hot summer | |
| D: snow | s: summer dry | b: warm summer | |
| E: polar | w: winter dry | c: cool summer | |
| m: monsoonal | d: extremely continental |
| KG | n.grid 1 | P (mm) | RP | WASP 2 | NDVI | RV |
|---|---|---|---|---|---|---|
| Af | 2531 | 2629 ± 748 | 103 ± 86 | 0.35 ± 0.09 | 0.83 ± 0.06 | 1100 ± 628 |
| Am | 1632 | 2162 ± 545 | 102 ± 86 | 0.32 ± 0.08 | 0.77 ± 0.11 | 955 ± 562 |
| As | 302 | 1042 ± 483 | 34 ± 32 | 0.46 ± 0.12 | 0.55 ± 0.15 | 353 ± 337 |
| Aw | 5762 | 1335 ± 418 | 86 ± 84 | 0.37 ± 0.10 | 0.63 ± 0.12 | 705 ± 544 |
| BSh | 2822 | 519 ± 208 | 28 ± 26 | 0.58 ± 0.15 | 0.35 ± 0.12 | 224 ± 164 |
| BSk | 3208 | 291 ± 133 | 25 ± 11 | 0.61 ± 0.13 | 0.23 ± 0.10 | 147 ± 161 |
| BWh | 2465 | 227 ± 95 | 22 ± 41 | 0.71 ± 0.16 | 0.19 ± 0.06 | 174 ± 160 |
| BWk | 1272 | 159 ± 86 | 21 ± 11 | 0.71 ± 0.12 | 0.13 ± 0.06 | 107 ± 87 |
| Cfa | 3084 | 1179 ± 419 | 44 ± 17 | 0.49 ± 0.10 | 0.59 ± 0.12 | 470 ± 458 |
| Cfb | 2302 | 985 ± 521 | 59 ± 29 | 0.47 ± 0.11 | 0.60 ± 0.13 | 464 ± 651 |
| Cfc | 166 | 1418 ± 857 | 76 ± 41 | 0.44 ± 0.14 | 0.59 ± 0.14 | 297 ± 389 |
| Csa | 1008 | 552 ± 224 | 25 ± 10 | 0.55 ± 0.14 | 0.38 ± 0.14 | 302 ± 327 |
| Csb | 602 | 777 ± 456 | 28 ± 13 | 0.48 ± 0.12 | 0.50 ± 0.19 | 510 ± 514 |
| Csc | 9 | 693 ± 214 | 44 ± 23 | 0.58 ± 0.15 | 0.45 ± 0.18 | 275 ± 147 |
| Cwa | 1509 | 1146 ± 536 | 57 ± 45 | 0.37 ± 0.10 | 0.58 ± 0.13 | 543 ± 457 |
| Cwb | 558 | 1104 ± 525 | 62 ± 33 | 0.33 ± 0.10 | 0.56 ± 0.17 | 624 ± 403 |
| Cwc | 10 | 568 ± 389 | 41 ± 29 | 0.47 ± 0.15 | 0.31 ± 0.29 | 472 ± 200 |
| Dfa | 768 | 589 ± 300 | 39 ± 11 | 0.55 ± 0.11 | 0.38 ± 0.11 | 80 ± 42 |
| Dfb | 4508 | 649 ± 290 | 63 ± 29 | 0.46 ± 0.09 | 0.46 ± 0.12 | 96 ± 61 |
| Dfc | 8591 | 574 ± 270 | 82 ± 55 | 0.43 ± 0.09 | 0.41 ± 0.10 | 94 ± 86 |
| Dfd | 877 | 292 ± 55 | 49 ± 11 | 0.42 ± 0.06 | 0.28 ± 0.07 | 30 ± 12 |
| Dsa | 79 | 393 ± 80 | 28 ± 4 | 0.57 ± 0.10 | 0.23 ± 0.06 | 71 ± 22 |
| Dsb | 207 | 502 ± 274 | 34 ± 16 | 0.53 ± 0.12 | 0.26 ± 0.14 | 93 ± 70 |
| Dsc | 188 | 494 ± 358 | 55 ± 27 | 0.50 ± 0.11 | 0.34 ± 0.12 | 115 ± 120 |
| Dwa | 315 | 598 ± 226 | 31 ± 6 | 0.37 ± 0.06 | 0.39 ± 0.08 | 90 ± 47 |
| Dwb | 649 | 565 ± 196 | 44 ± 21 | 0.37 ± 0.06 | 0.42 ± 0.11 | 105 ± 122 |
| Dwc | 1307 | 459 ± 172 | 50 ± 23 | 0.36 ± 0.11 | 0.39 ± 0.11 | 108 ± 127 |
| Dwd | 100 | 315 ± 43 | 56 ± 7 | 0.36 ± 0.04 | 0.27 ± 0.06 | 27 ± 9 |
| ET | 1662 | 583 ± 414 | 59 ± 45 | 0.52 ± 0.13 | 0.26 ± 0.14 | 116 ± 158 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zampieri, M.; Grizzetti, B.; Meroni, M.; Scoccimarro, E.; Vrieling, A.; Naumann, G.; Toreti, A. Annual Green Water Resources and Vegetation Resilience Indicators: Definitions, Mutual Relationships, and Future Climate Projections. Remote Sens. 2019, 11, 2708. https://doi.org/10.3390/rs11222708
Zampieri M, Grizzetti B, Meroni M, Scoccimarro E, Vrieling A, Naumann G, Toreti A. Annual Green Water Resources and Vegetation Resilience Indicators: Definitions, Mutual Relationships, and Future Climate Projections. Remote Sensing. 2019; 11(22):2708. https://doi.org/10.3390/rs11222708
Chicago/Turabian StyleZampieri, Matteo, Bruna Grizzetti, Michele Meroni, Enrico Scoccimarro, Anton Vrieling, Gustavo Naumann, and Andrea Toreti. 2019. "Annual Green Water Resources and Vegetation Resilience Indicators: Definitions, Mutual Relationships, and Future Climate Projections" Remote Sensing 11, no. 22: 2708. https://doi.org/10.3390/rs11222708
APA StyleZampieri, M., Grizzetti, B., Meroni, M., Scoccimarro, E., Vrieling, A., Naumann, G., & Toreti, A. (2019). Annual Green Water Resources and Vegetation Resilience Indicators: Definitions, Mutual Relationships, and Future Climate Projections. Remote Sensing, 11(22), 2708. https://doi.org/10.3390/rs11222708