Infrastructure Safety Oriented Traffic Load Monitoring Using Multi-Sensor and Single Camera for Short and Medium Span Bridges
Abstract
:1. Introduction
2. Traffic Sensing Technologies
2.1. Visual Sensing
2.1.1. Computer Vision Technique
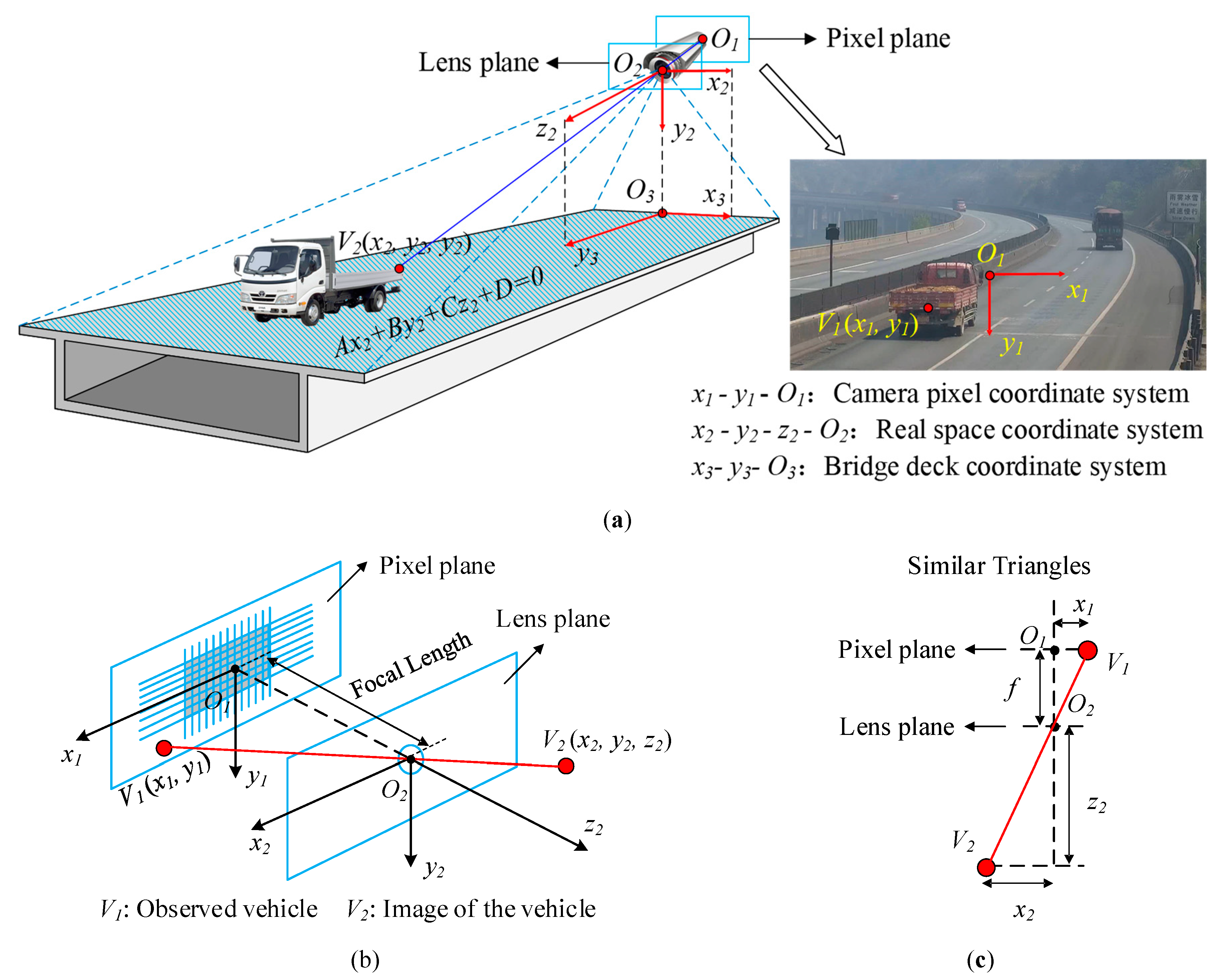
2.1.2. Coordinate Transformation
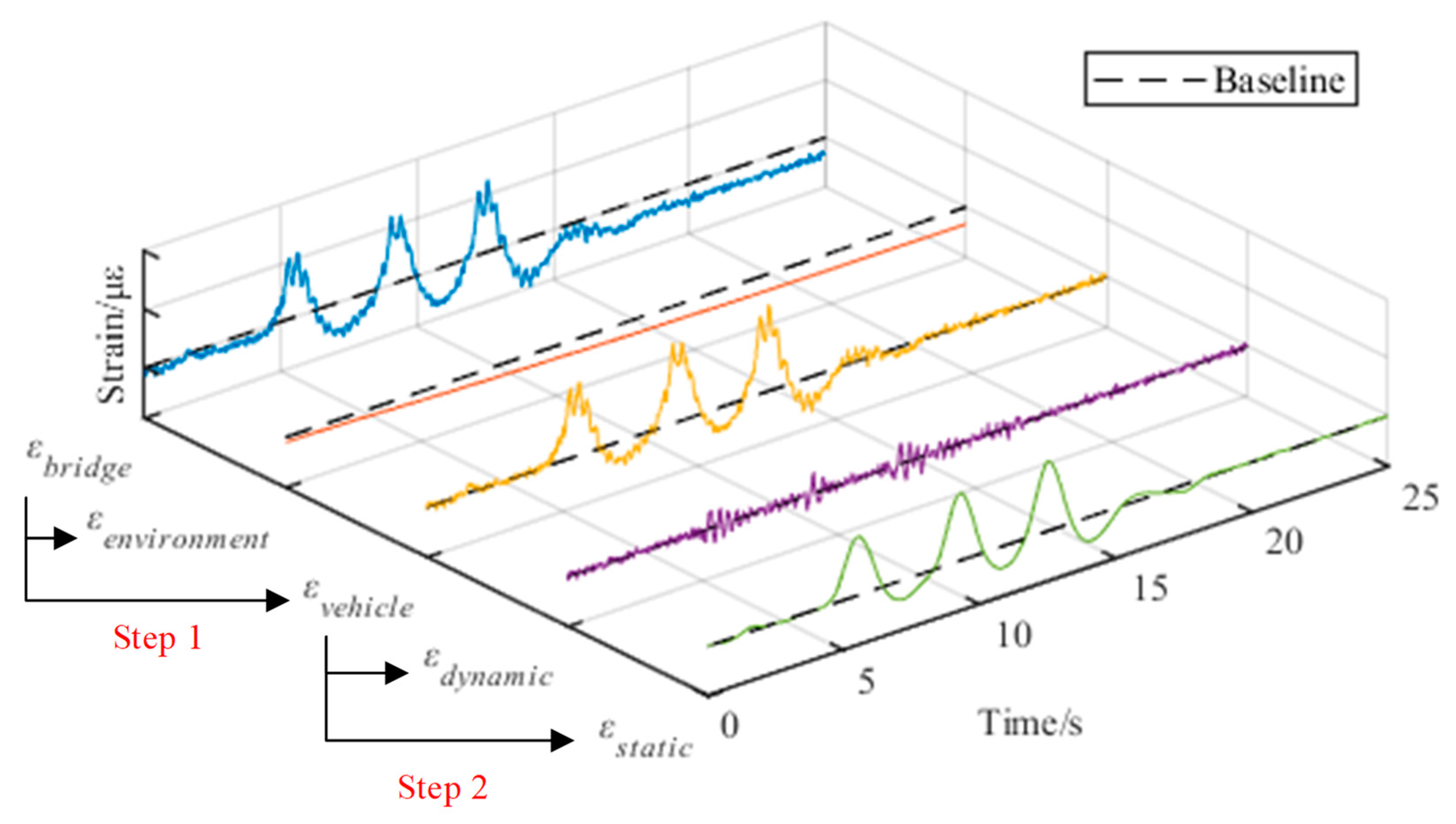
2.2. Bridge Strain Sensing
3. Traffic Load Identification with Redundant Measurements
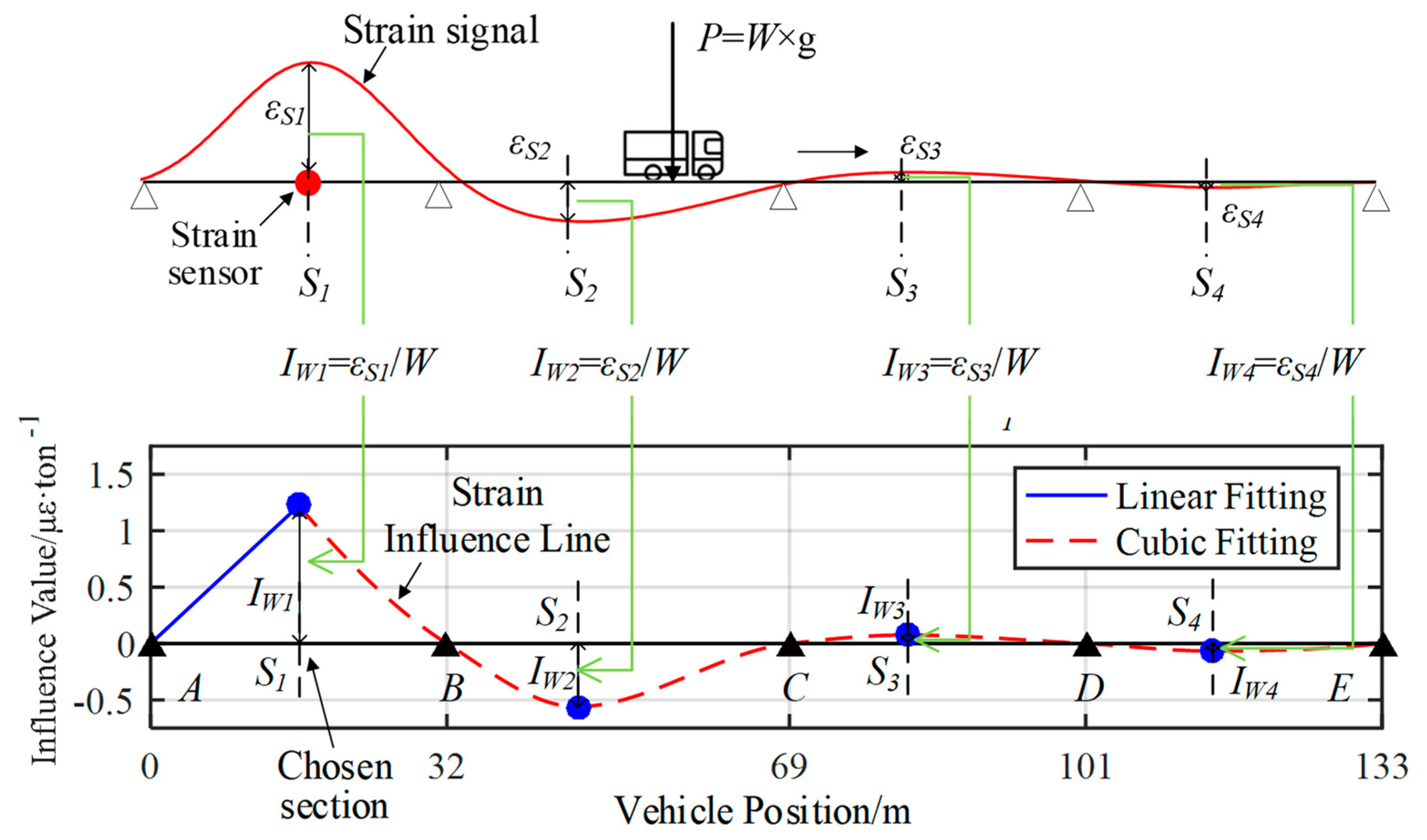
3.1. Traffic Load and Bridge Reaction
3.2. Identification with Irredundant Measurement
3.3. Least Square Based Identification with Redundant Measurements
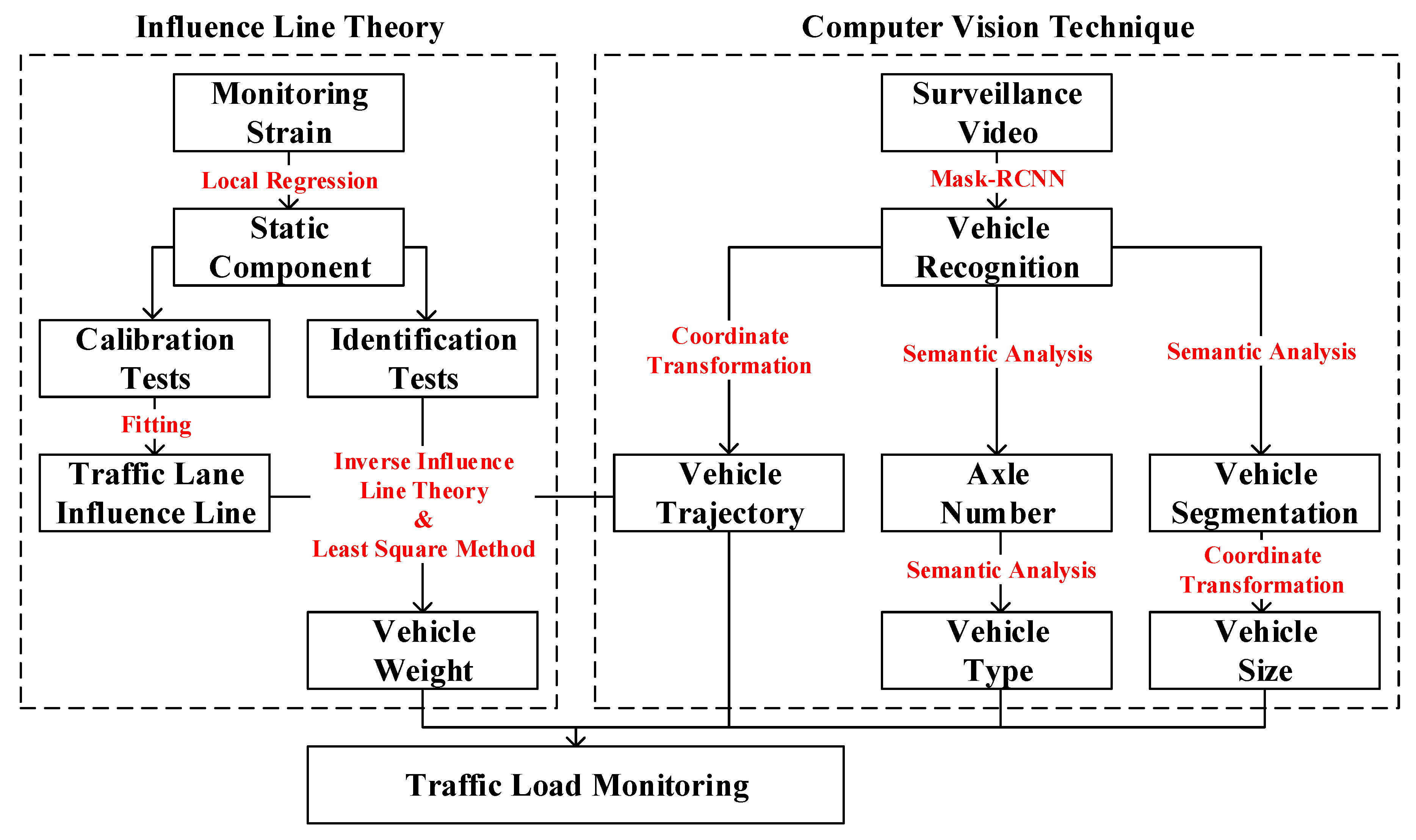
4. Traffic Load Monitoring Framework
5. Field Tests Validation
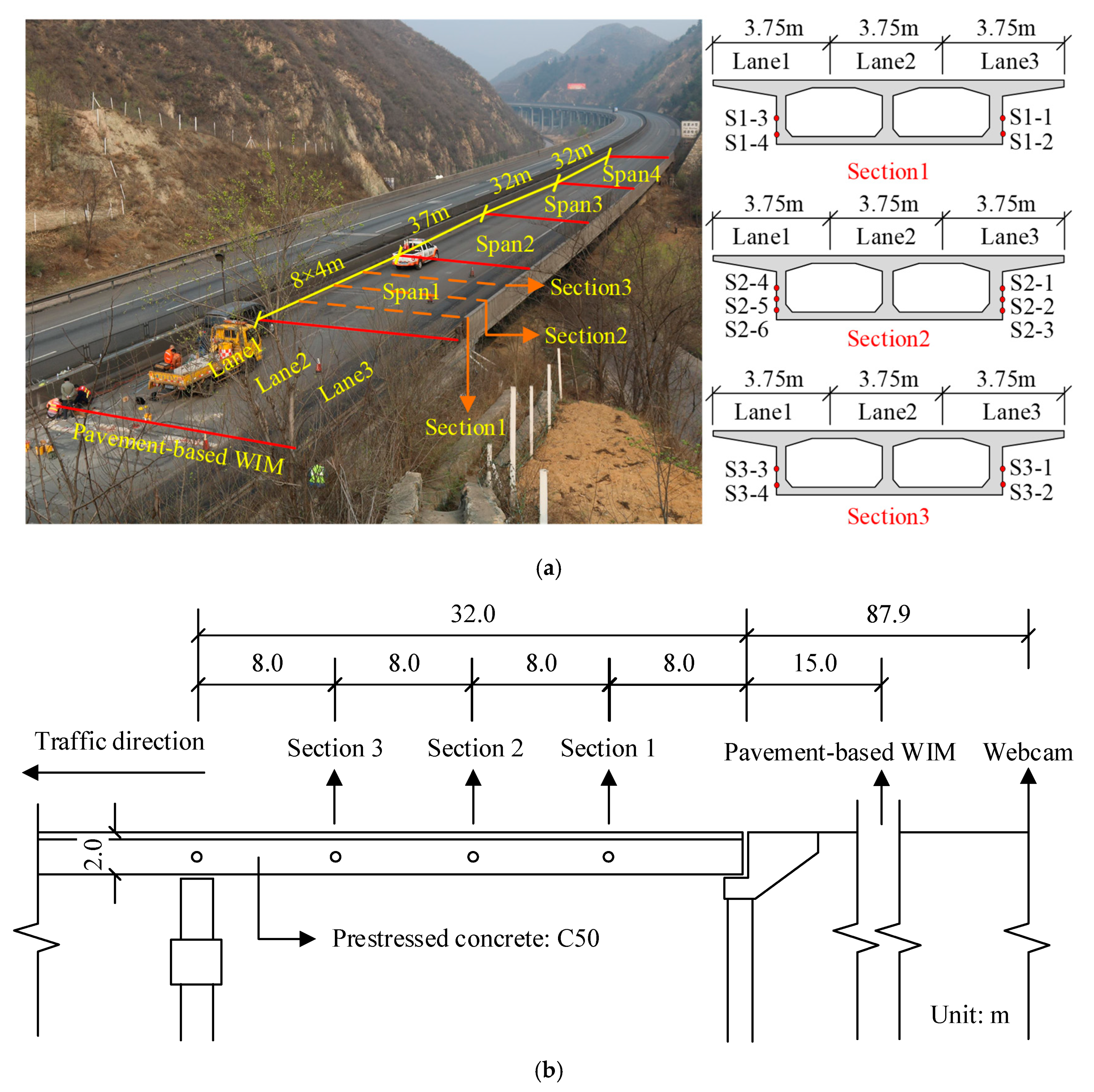
5.1. Instrumentation and Test Setup
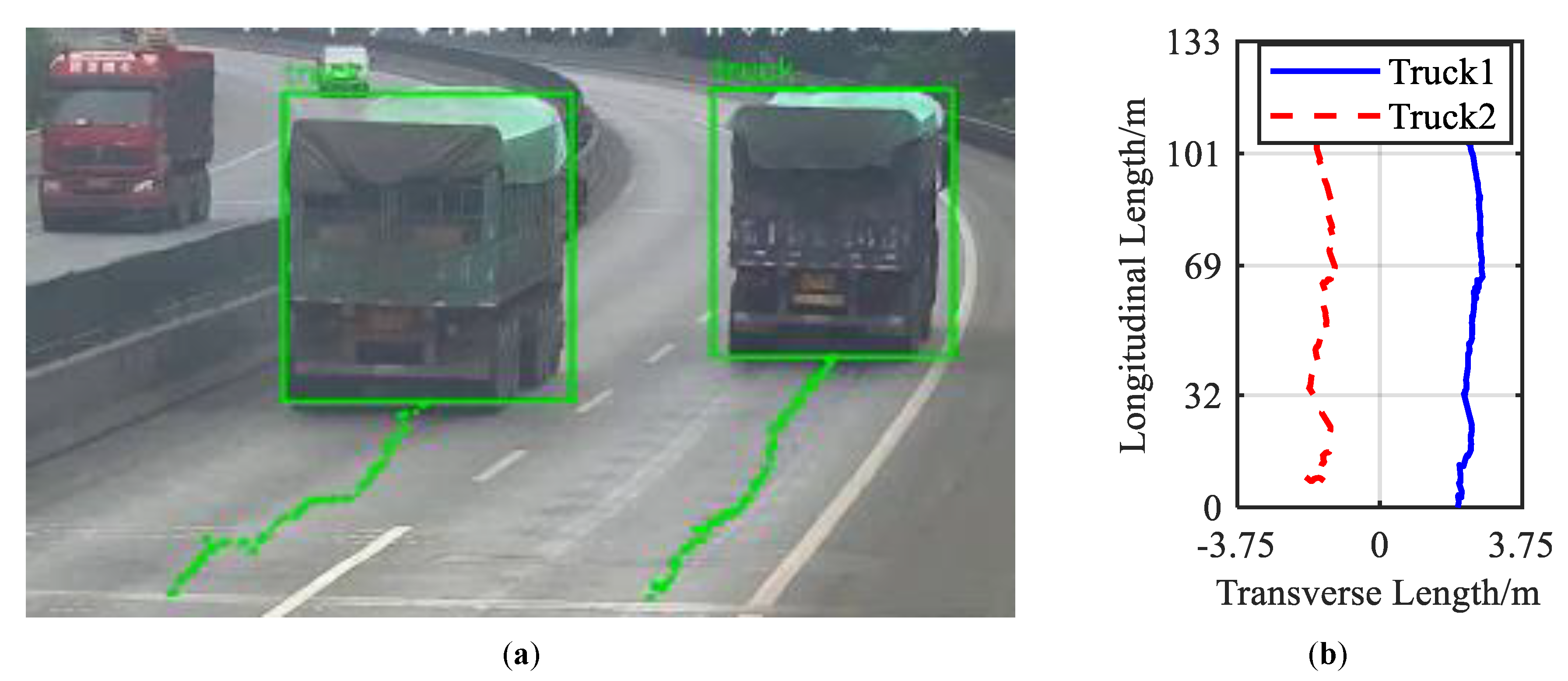
5.2. Vehicle Trajectory Recognition
5.3. Identification Results for Complex Scenarios
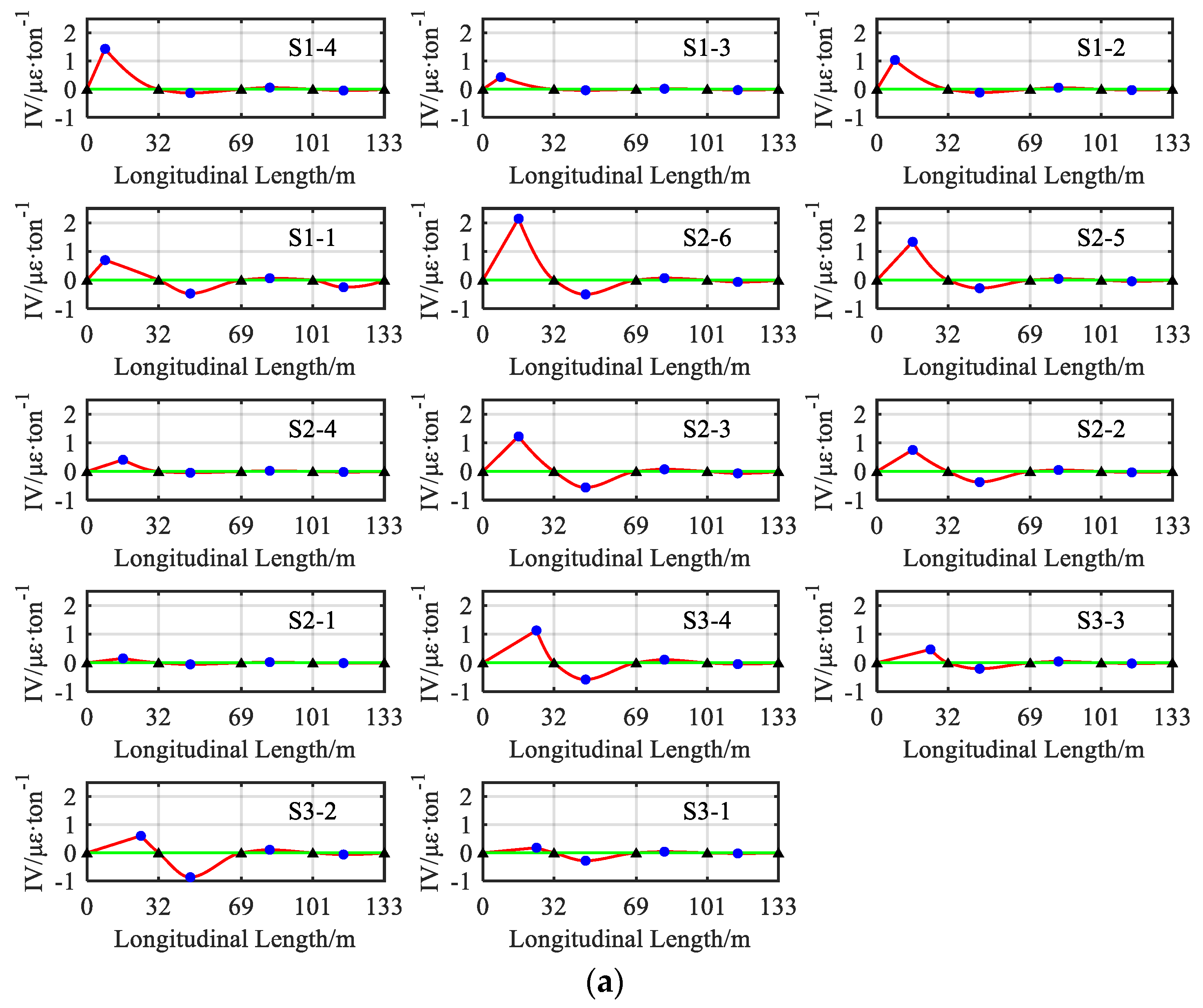
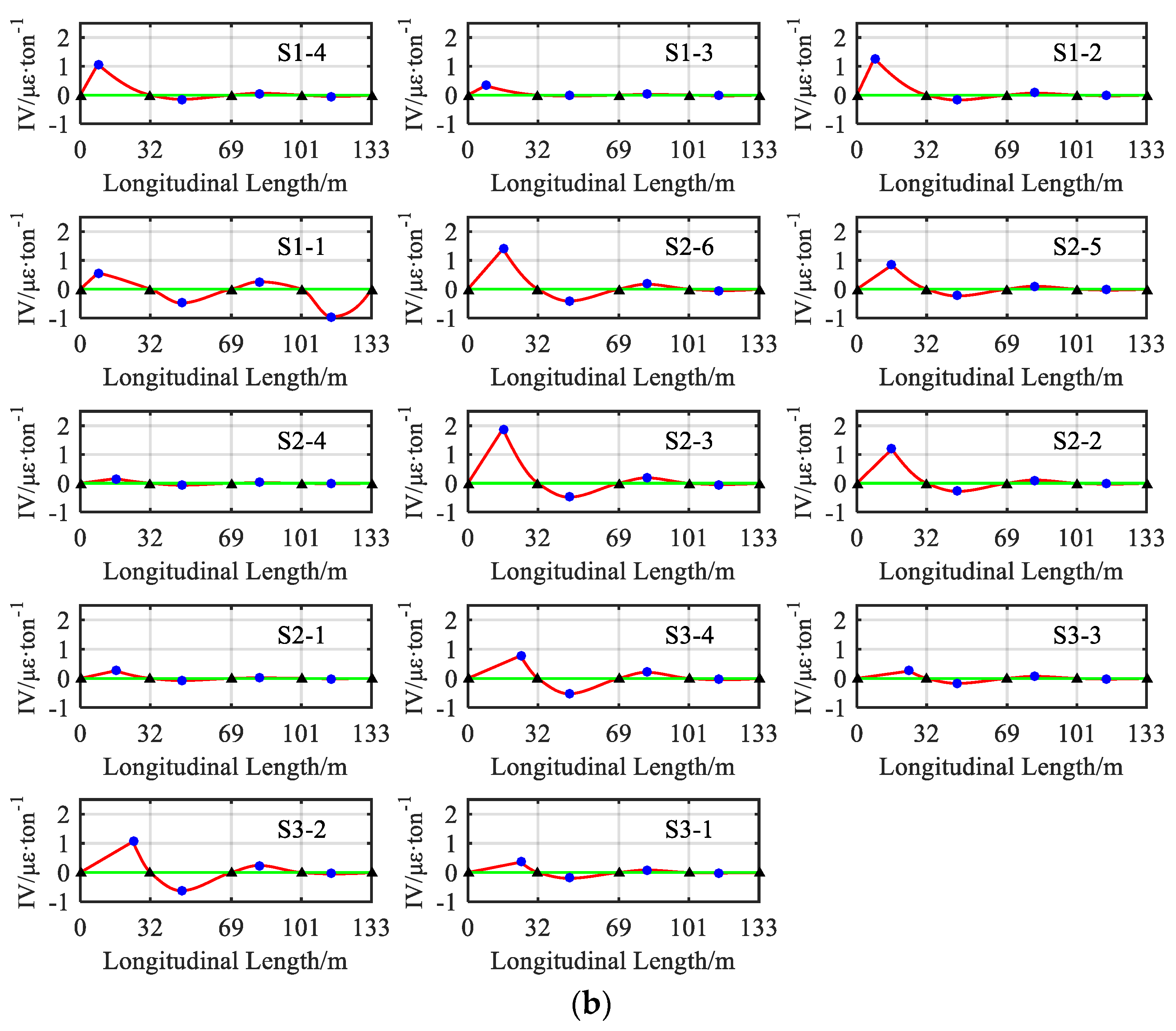
5.3.1. Scenario: One-By-One Vehicles
5.3.2. Scenario: Side-By-Side Vehicles
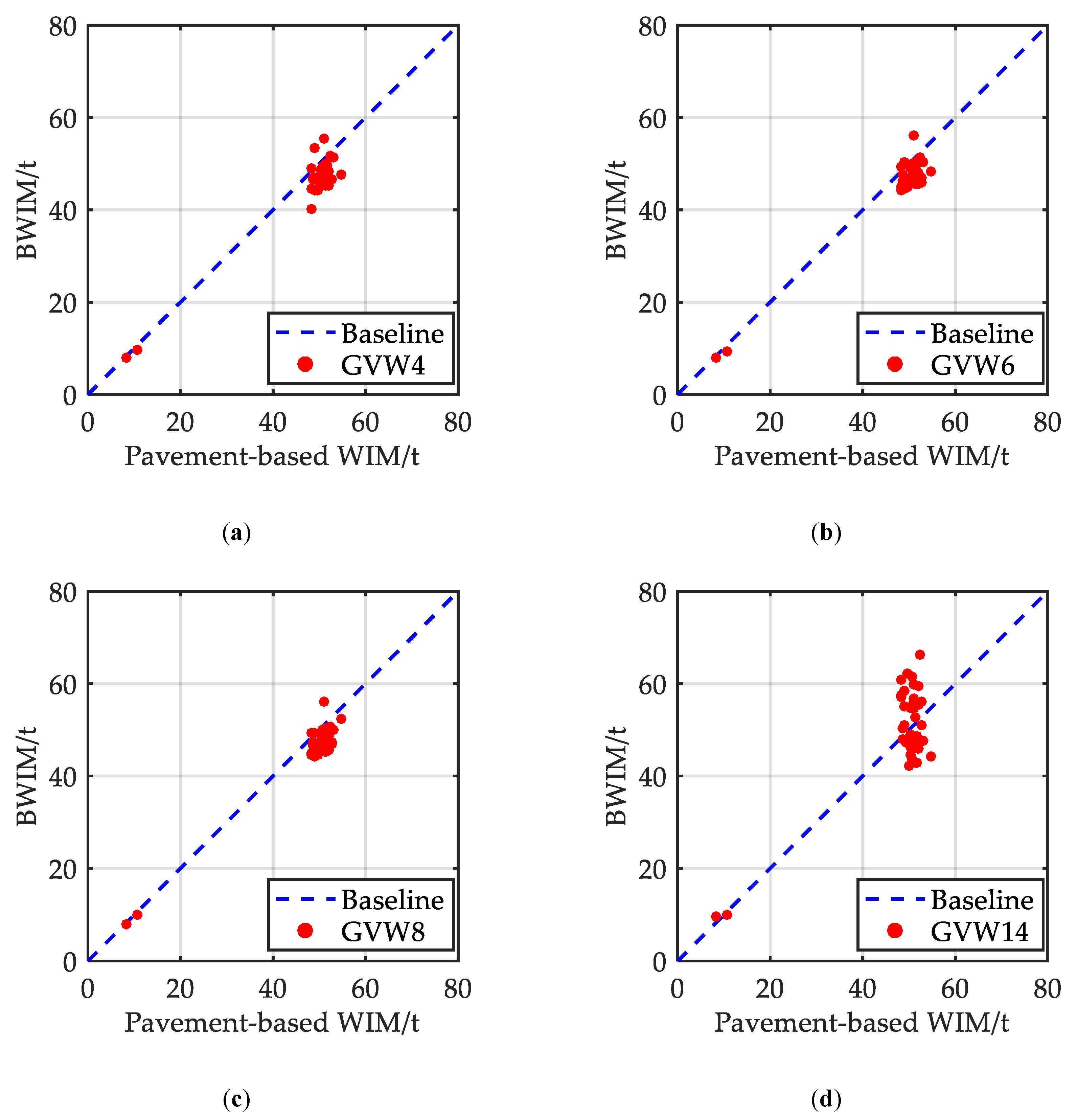
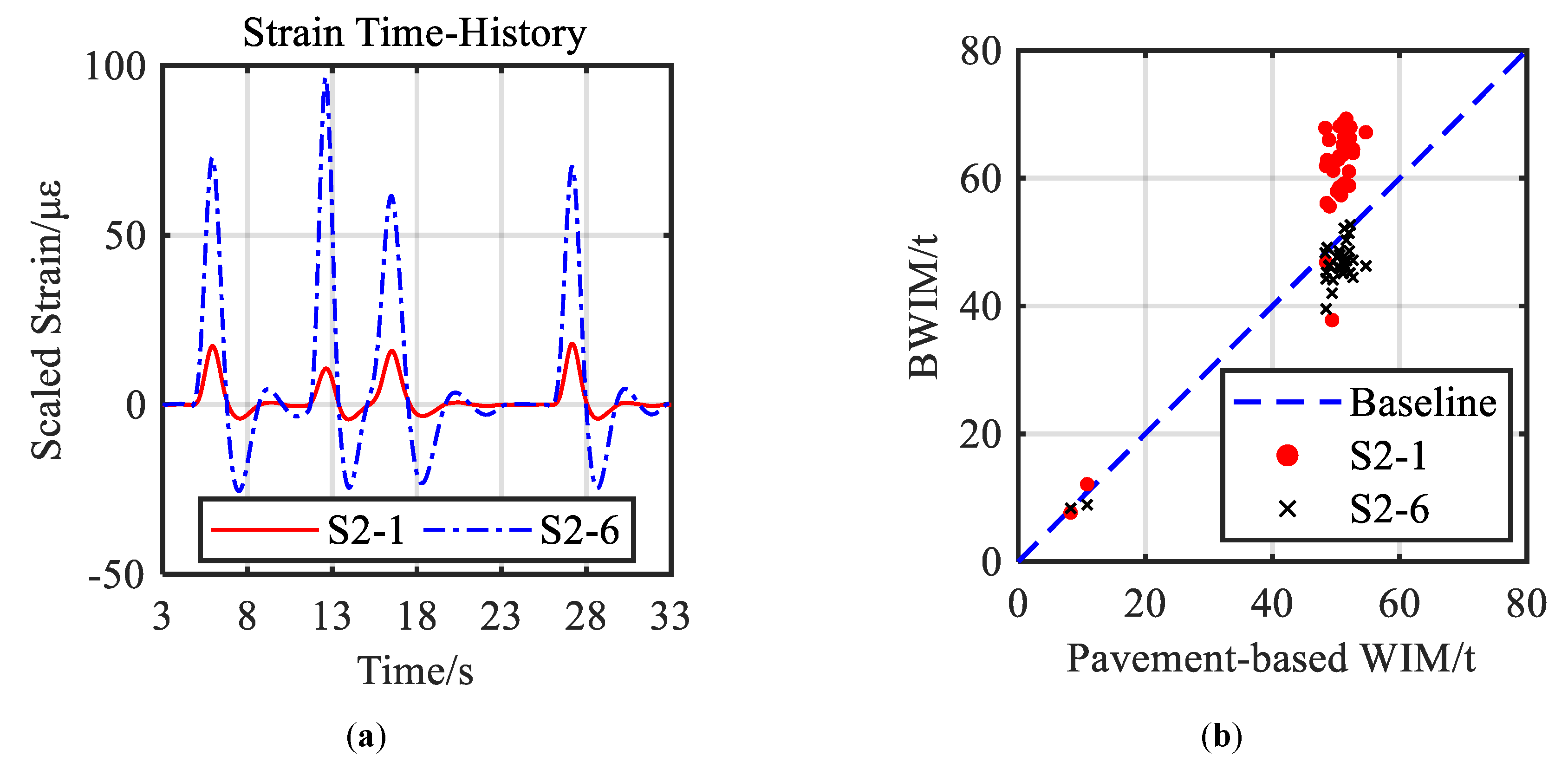
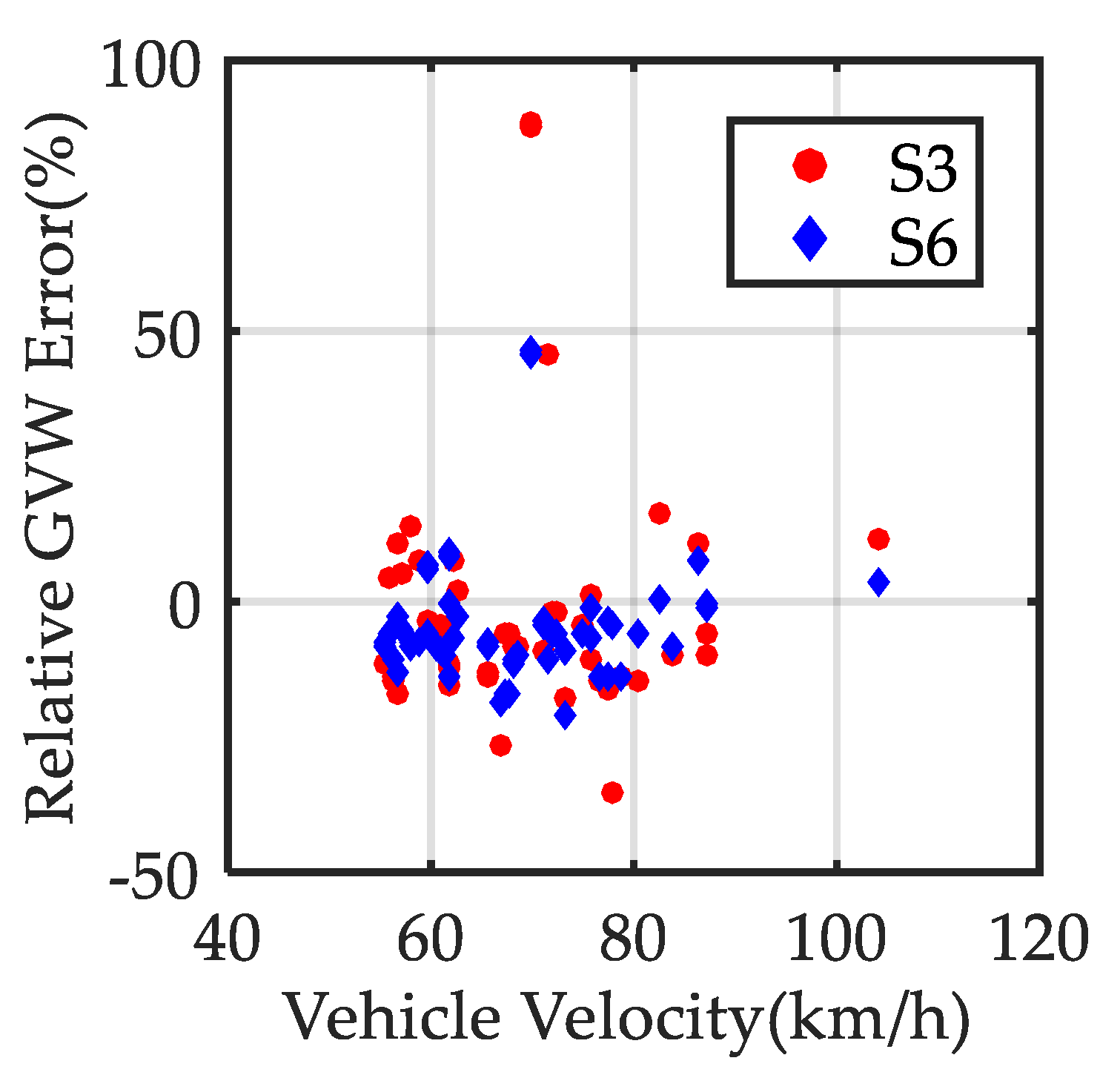
5.3.3. Statistical Analysis for Identification Results
- The recognition results of the GVW are of acceptable accuracy when using data from less than eight strain sensors;
- Errors in one-by-one and side-by-side vehicle scenarios are slightly larger in contrast to the single vehicle scenario. The difference is reasonable because the position of vehicles is essential to obtain their influence value when recognizing the GVW in complicated traffic scenarios, and the positioning error is inevitable in the process of coordinate transformation.
- An interesting phenomenon is the obvious larger error when using the data from all 14 strain sensors. Detailed reason would be particularly discussed later.
6. Conclusions
- Deep learning based computer vision technique is a practical tool to extract the key parameters from traffic video in real time manner, such as position, size, axle number and type of passing vehicles over bridge. Moreover, traffic mode of multi-vehicle problem is equally important to be identified as one-by-one, side-by-side or mixed mode.
- By utilizing the redundant strain measurements, the proposed least square based identification method is capable of: i) distinguishing complicated traffic mode such as side-by-side vehicles, which is theoretically unidentifiable with single measurement and ii) solving the overdetermined inverse influence equations effectively, and hence, reducing the GVW recognition errors.
- Under the condition that vehicle parameters (especially positions) are identified and available, the proposed framework successfully recognizes the vehicle weight in spite of the presence of one-by-one and side-by-side vehicles, with an average weighing error less than 8%. Thus, the elementary scenarios of the multiple-vehicle problem for BWIM research are solved with an overall improvement with respect to cost and accuracy.
- The usage of strain sensors installed at locations with larger response results in smaller recognition error of vehicle weight. It is suggested that strain sensors for BWIM purposes should be installed far from the neutral axis of cross-sections for the sake of higher accuracy.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Hu, X.; Wang, B.; Ji, H. A wireless sensor network-based structural health monitoring system for highway bridges. Comput.-Aided Civ. Infrastruct. Eng. 2013, 28, 193–209. [Google Scholar] [CrossRef]
- Farrar, C.R.; Park, G.; Allen, D.W.; Todd, M.D. Sensor network paradigms for structural health monitoring. Struct. Control Health Monit. 2006, 13, 210–225. [Google Scholar] [CrossRef]
- Cheng, L.; Pakzad, S.N. Agility of Wireless Sensor Networks for Earthquake Monitoring of Bridges. In Proceedings of the Sixth International Conference on Networked Sensing Systems (INSS), Pittsburgh, PA, USA, 17–19 June 2009; pp. 1–4. [Google Scholar]
- Jo, H.; Sim, S.H.; Mechitov, K.A.; Kim, R.; Li, J.; Moinzadeh, P.; Spencer, B.F., Jr.; Park, J.W.; Cho, S.; Jung, H.J.; et al. Hybrid wireless smart sensor network for full-scale structural health monitoring of a cable-stayed bridgeSensors and Smart Structures Technologies for Civil, Mechanical, and Aerospace Systems 2011. Int. Soc. Opt. Photonics 2011, 7981, 798105. [Google Scholar]
- Feng, D.M.; Feng, M.Q. Identification of structural stiffness and excitation forces in time domain using noncontact vision-based displacement measurement. J. Sound Vib. 2017, 406, 15–28. [Google Scholar] [CrossRef]
- Feng, D.M.; Feng, M.Q. Experimental validation of cost-effective vision-based structural health monitoring. Mech. Syst. Signal Process. 2017, 88, 199–211. [Google Scholar] [CrossRef]
- Fraser, M.; Elgamal, A.; He, X.; Conte, J.P. Sensor network for structural health monitoring of a highway bridge. J. Comput. Civ. Eng. 2009, 24, 11–24. [Google Scholar] [CrossRef]
- Rutherford, G.; McNeill, D.K. Statistical vehicle classification methods derived from girder strains in bridges. Can. J. Civ. Eng. 2010, 38, 200–209. [Google Scholar] [CrossRef]
- Gonzalez, I.; Karoumi, R. Traffic monitoring using a structural health monitoring system. Proc. ICE-Bridge Eng. 2014, 168, 13–23. [Google Scholar]
- Yu, Y.; Cai, C.S.; Deng, L. State-of-the-art review on bridge weigh-in-motion technology. Adv. Struct. Eng. 2016, 19, 1514–1530. [Google Scholar] [CrossRef]
- Moses, F. Weigh-in-motion system using instrumented bridges. J. Transp. Eng. 1979, 105, 233–249. [Google Scholar]
- Lydon, M.; Taylor, S.E.; Robinson, D.; Mufti, A.; Brien, E.J. Recent developments in bridge weigh in motion (B-WIM). J. Civ. Struct. Health Monit. 2016, 6, 69–81. [Google Scholar] [CrossRef]
- Zhu, X.Q.; Law, S.S. Recent developments in inverse problems of vehicle–bridge interaction dynamics. J. Civ. Struct. Health Monit. 2016, 6, 107–128. [Google Scholar] [CrossRef]
- Schmidt, F.; Jacob, B.; Servant, C.; Marchadour, Y. Experimentation of a Bridge WIM System in France and Applications for Bridge Monitoring and Overload Detection. In Proceedings of the 6th International Conference on Weigh-In-Motion (ICWIM 6), Dallas, TX, USA, 4–7 June 2012. [Google Scholar]
- Snyder, R.; Moses, F. Application of in-motion weighing using instrumented bridges. Transp. Res. Rec. 1985, 1048, 83–88. [Google Scholar]
- Yu, Y.; Cai, C.S.; Deng, L. Nothing-on-road bridge weigh-in-motion considering the transverse position of the vehicle. Struct. Infrastruct. Eng. 2018, 14, 1108–1122. [Google Scholar] [CrossRef]
- Deng, L.; He, W.; Yu, Y.; Cai, C.S. Equivalent shear force method for detecting the speed and axles of moving vehicles on bridges. J. Bridge Eng. 2018, 23, 04018057. [Google Scholar] [CrossRef]
- He, W.; Ling, T.; OBrien, E.J.; Deng, L. Virtual Axle Method for Bridge Weigh-in-Motion Systems Requiring No Axle Detector. J. Bridge Eng. 2019, 24, 04019086. [Google Scholar] [CrossRef]
- Basharat, A.; Catbas, N.; Shah, M. A Framework for Intelligent Sensor Network with Video Camera for Structural Health Monitoring of Bridges. In Proceedings of the Third IEEE International Conference on Pervasive Computing and Communications Workshops, Kauai Island, HI, USA, 8–12 March 2005; pp. 385–389. [Google Scholar]
- Chen, Z.; Li, H.; Bao, Y.; Li, N.; Jin, Y. Identification of spatio-temporal distribution of vehicle loads on long-span bridges using computer vision technology. Struct. Control Health Monit. 2016, 23, 517–534. [Google Scholar] [CrossRef]
- Hou, R.; Jeong, S.; Wang, Y.; Law, K.H.; Lynch, J.P. Camera-based Triggering of Bridge Structural Health Monitoring Systems using a Cyber-physical System Framework. In Proceedings of the 11th International Workshop on Structural Health Monitoring, Stanford, CA, USA, 12–14 September 2017. [Google Scholar]
- Feng, D.M.; Feng, M.Q. Computer vision for SHM of civil infrastructure: From dynamic response measurement to damage detection—A review. Eng. Struct. 2018, 156, 105–117. [Google Scholar] [CrossRef]
- Dan, D.; Ge, L.; Yan, X. Identification of moving loads based on the information fusion of weigh-in-motion system and multiple camera machine vision. Measurement 2019, 144, 155–166. [Google Scholar] [CrossRef]
- Rawat, W.; Wang, Z. Deep convolutional neural networks for image classification: A comprehensive review. Neural Comput. 2017, 29, 2352–2449. [Google Scholar] [CrossRef]
- Kaushal, M.; Khehra, B.S.; Sharma, A. Soft Computing based object detection and tracking approaches: State-of-the-Art survey. Appl. Soft Comput. 2018, 70, 423–464. [Google Scholar] [CrossRef]
- Schmidhuber, J. Deep learning in neural networks: An overview. Neural Netw. 2015, 61, 85–117. [Google Scholar] [CrossRef] [PubMed]
- Girshick, R.; Donahue, J.; Darrell, T.; Malik, J. Rich Feature Hierarchies for Accurate Object Detection and Semantic Segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 24–27 January 2014; pp. 580–587. [Google Scholar]
- He, K.; Gkioxari, G.; Dollár, P.; Girshick, R. Mask R-CNN. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 2961–2969. [Google Scholar]
- Xu, G.; Zhang, Z. Epipolar Geometry in Stereo, Motion and Object Recognition: A Unified Approach, 1st ed.; Kluwer Academic Publisher: Dordrecht, The Netherlands, 1996. [Google Scholar]
- Jian, X.; Xia, Y.; Lozano-Galant, J.A.; Sun, L. Traffic Sensing Methodology Combining Influence Line Theory and Computer Vision Techniques for Girder Bridges. J. Sens. 2019, 2019, 3409525. [Google Scholar] [CrossRef]
- Cleveland, W.S.; Devlin, S.J. Locally weighted regression: An approach to regression analysis by local fitting. J. Am. Stat. Assoc. 1988, 83, 596–610. [Google Scholar] [CrossRef]
- Ma, H.Y.; Shi, X.F.; Zhang, Y. Long-Term Behavior of Precast Concrete Deck Using Longitudinal Prestressed Tendons in Composite I-Girder Bridge. Appl. Sci. 2018, 8, 2598. [Google Scholar] [CrossRef]
- Znidaric, A.; Baumgartner, W. Bridge Weigh-in-Motion Systems-an Overview. In Proceedings of the Second European Conference on Weigh-in-Motion of Road Vehicles, Lisbon, Portugal, 14–16 September 1998. [Google Scholar]
- McNulty, P.; O’Brien, E.J. Testing of bridge weigh-in-motion system in a sub-Arctic climate. J. Test. Eval. 2003, 31, 497–506. [Google Scholar]
- O’Brien, E.J.; Quilligan, M.; Karoumi, R. Calculating an influence line from direct measurements. Bridge Eng. Proc. Inst. Civ. Eng. 2006, 159, 31–34. [Google Scholar] [CrossRef]
- Zhao, H.; Uddin, N.; Shao, X.; Zhu, P.; Tan, C. Field-calibrated influence lines for improved axle weight identification with a bridge weigh-in-motion system. Struct. Infrastruct. Eng. 2015, 11, 721–743. [Google Scholar] [CrossRef]
- Young, D.H.; Timoshenko, S.P. Theory of Structures; McGraw-Hill: New York, NY, USA, 1965. [Google Scholar]
- Lawson, C.L.; Hanson, R.J. Solving Least Squares Problems, 1st ed.; Prentice-Hall Inc.: Englewood Cliffs, NJ, USA, 1974. [Google Scholar]
- Timoshenko, S.P.; Gere, J.M. Mechanics of Materials; Van Nordstrand Reinhold Company: New York, NY, USA, 1972. [Google Scholar]
- Leming, S.K.; Stalford, H.L. Bridge Weigh-in-Motion System Development Using Superposition of Dynamic Truck/Static Bridge Interaction. In Proceedings of the IEEE 2003 American Control Conference, Denver, CO, USA, 4–6 June 2003; Volume 1, pp. 815–820. [Google Scholar]


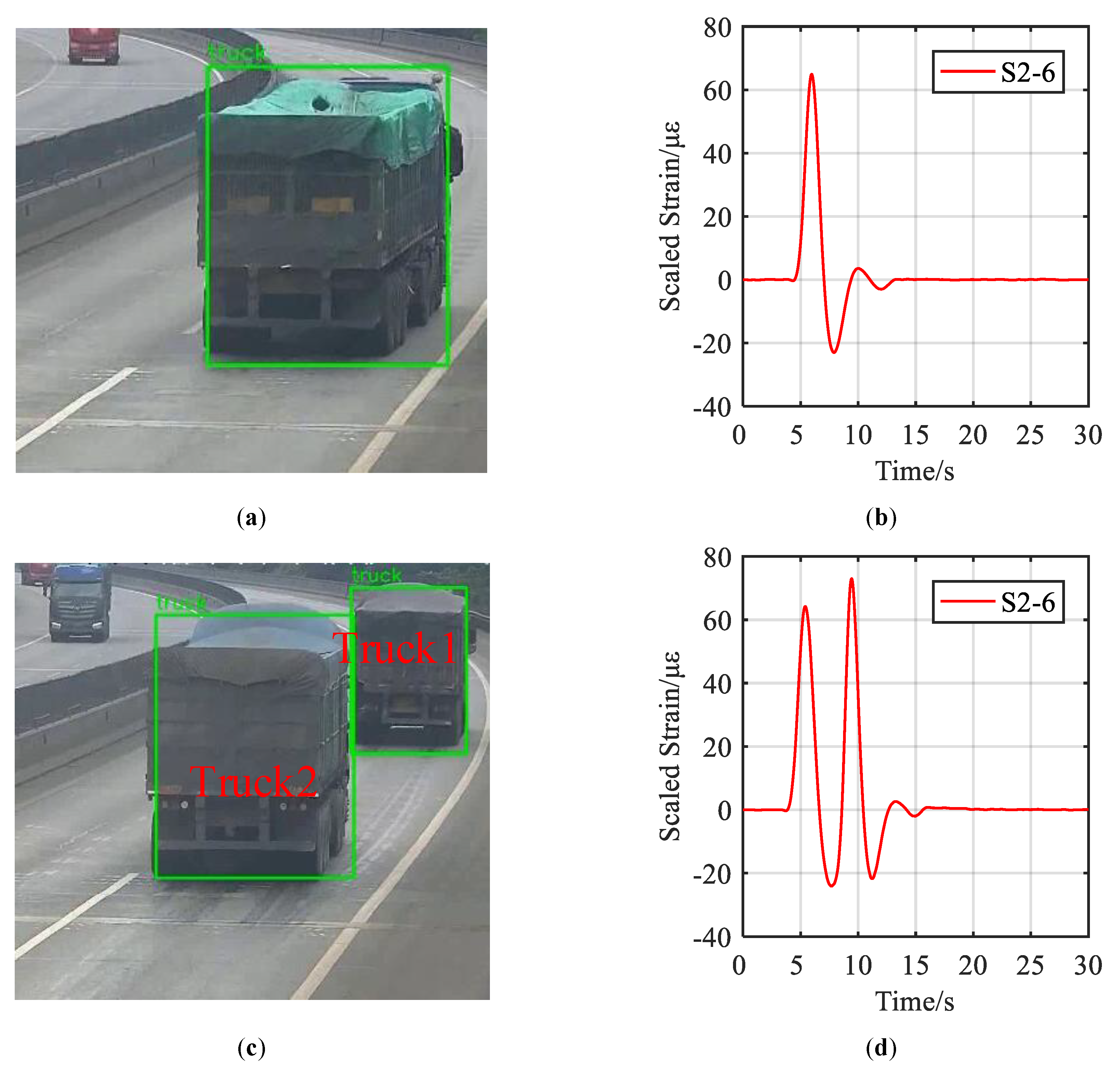
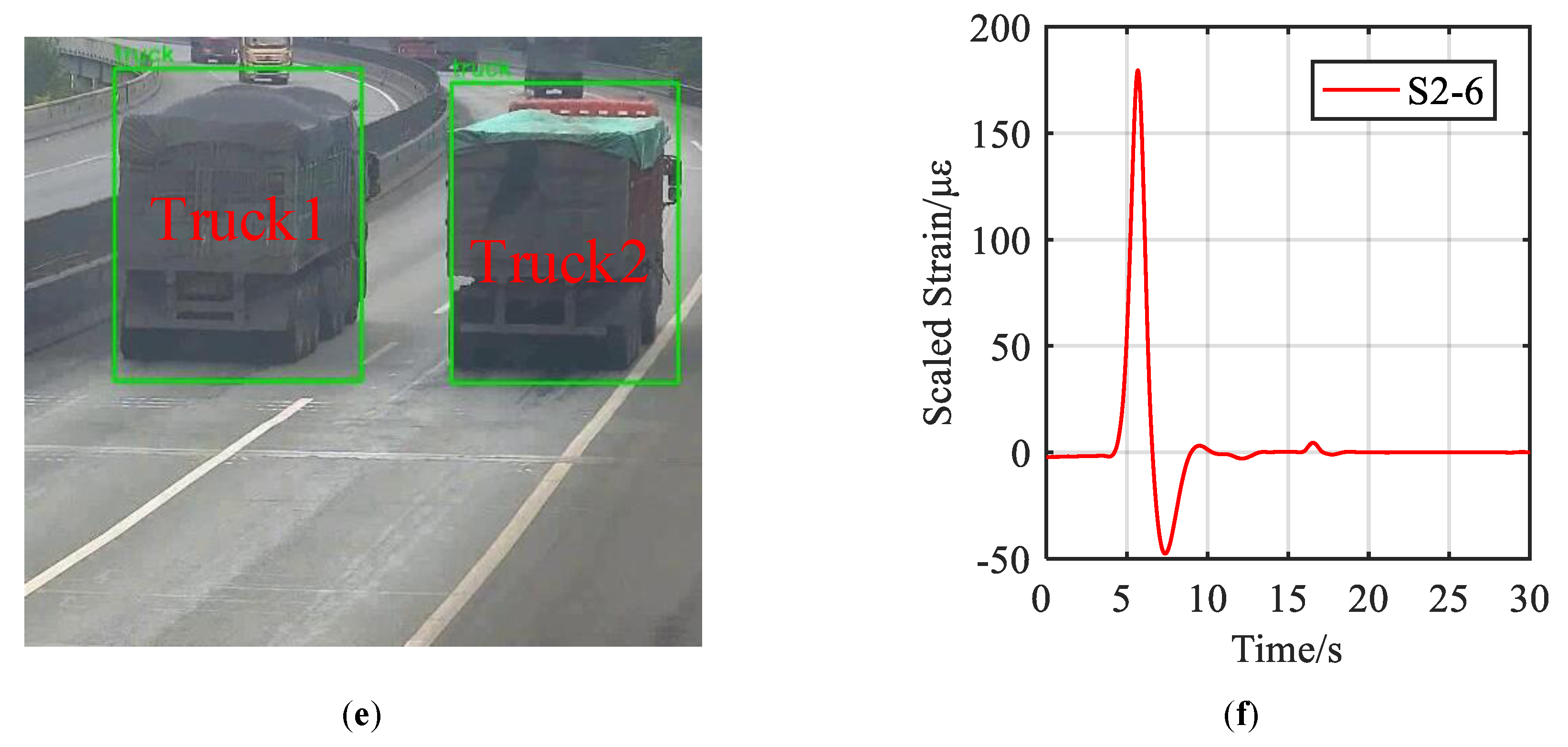
| Vehicle Name | Truck1 | Truck2 |
|---|---|---|
| ①Maximum strain | 64.21 | 73.00 |
| ②Maximum influence value of sensor S2-6 | 1.396 | 1.396 |
| ③GVW = ①/② | 46.00 t | 52.29 t |
| ④GVW measured by pavement-based WIM | 50.37 t | 50.69 t |
| Error = (③−④)/④ | −8.67% | 3.16% |
| Sensor Name | Strain (με) | Influence Value (με/ton) | |
|---|---|---|---|
| Truck1 | Truck2 | ||
| S2-2 | 94.3 | 1.01 | 0.75 |
| S2-3 | 158.5 | 1.62 | 1.22 |
| S2-5 | 112.8 | 0.71 | 1.33 |
| S2-6 | 179.6 | 1.20 | 2.14 |
| Truck Number | Scenario | GVW-WIM(t) | GVW-BWIM-4 Sensors(t) | GVW-BWIM-6 Sensors(t) | GVW-BWIM-8 Sensors(t) | GVW-BWIM-14 Sensors(t) |
|---|---|---|---|---|---|---|
| 1 | single | 53.12 | 51.48 | 50.49 | 49.84 | 47.72 |
| 2 | single | 50.93 | 48.29 | 49.02 | 47.95 | 47.13 |
| 3 | side-by-side | 51.12 | 55.56 | 56.22 | 56.15 | 56.64 |
| 4 | side-by-side | 49.12 | 53.33 | 50.27 | 49.37 | 50.91 |
| 5 | one-by-one | 50.37 | 48.59 | 49.04 | 48.85 | 49.15 |
| 6 | one-by-one | 50.69 | 47.31 | 47.39 | 48.09 | 61.60 |
| 7 | single | 51.29 | 50.13 | 50.44 | 50.39 | 56.04 |
| 8 | single | 51.09 | 47.92 | 47.83 | 48.14 | 54.91 |
| 9 | single | 49.54 | 44.27 | 45.01 | 44.67 | 62.34 |
| 10 | single | 51.61 | 49.83 | 50.06 | 49.93 | 48.66 |
| 11 | single | 8.23 | 8.03 | 8.01 | 8.02 | 9.70 |
| 12 | single | 48.42 | 44.66 | 44.80 | 44.74 | 56.98 |
| 13 | single | 48.58 | 46.96 | 47.49 | 47.18 | 48.11 |
| 14 | single | 50.49 | 45.85 | 46.00 | 45.95 | 54.73 |
| 15 | single | 51.33 | 47.77 | 47.74 | 47.73 | 43.01 |
| 16 | single | 51.65 | 47.99 | 48.47 | 48.34 | 42.72 |
| 17 | side-by-side | 52.16 | 47.01 | 47.33 | 47.12 | 55.57 |
| 18 | side-by-side | 48.43 | 40.17 | 44.19 | 45.06 | 57.61 |
| 19 | single | 52.25 | 51.57 | 51.46 | 50.58 | 66.20 |
| 20 | one-by-one | 50.55 | 49.17 | 49.91 | 49.94 | 43.72 |
| 21 | one-by-one | 50.78 | 47.10 | 46.09 | 47.06 | 55.06 |
| 22 | single | 48.51 | 46.66 | 46.12 | 46.49 | 50.20 |
| 23 | single | 54.68 | 47.61 | 48.24 | 52.44 | 44.07 |
| 24 | single | 52.67 | 46.68 | 45.87 | 47.39 | 51.01 |
| 25 | single | 52.05 | 45.39 | 45.50 | 45.49 | 45.86 |
| 26 | side-by-side | 48.88 | 46.89 | 46.95 | 46.87 | 58.51 |
| 27 | side-by-side | 49.37 | 46.87 | 45.91 | 46.96 | 47.18 |
| 28 | one-by-one | 52.66 | 46.67 | 46.90 | 46.91 | 56.05 |
| 29 | one-by-one | 50.35 | 45.38 | 45.68 | 45.62 | 44.45 |
| 30 | single | 51.06 | 46.62 | 46.71 | 46.60 | 56.21 |
| 31 | single | 10.83 | 9.58 | 9.46 | 9.94 | 10.09 |
| 32 | single | 48.97 | 44.12 | 44.48 | 44.29 | 55.19 |
| 33 | single | 52.01 | 48.21 | 48.09 | 48.73 | 59.53 |
| 34 | single | 51.06 | 46.76 | 46.96 | 46.82 | 59.95 |
| 35 | single | 51.28 | 45.24 | 45.62 | 45.37 | 52.58 |
| 36 | single | 50.14 | 45.13 | 45.76 | 45.30 | 42.21 |
| 37 | single | 50.46 | 45.43 | 45.81 | 45.66 | 46.14 |
| 38 | single | 48.30 | 48.88 | 49.49 | 49.48 | 60.69 |
| Number of Sensors | Mean of Errors (%) | Standard Deviation of Errors (%) | Maximum Error (%) |
|---|---|---|---|
| 4 | −7.66 | 4.07 | +1.20/−17.06 |
| 6 | −7.20 | 3.80 | +2.46/−12.91 |
| 8 | −6.69 | 3.46 | +2.44/−12.60 |
| 14 | 3.69 | 13.41 | +26.70/−19.40 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xia, Y.; Jian, X.; Yan, B.; Su, D. Infrastructure Safety Oriented Traffic Load Monitoring Using Multi-Sensor and Single Camera for Short and Medium Span Bridges. Remote Sens. 2019, 11, 2651. https://doi.org/10.3390/rs11222651
Xia Y, Jian X, Yan B, Su D. Infrastructure Safety Oriented Traffic Load Monitoring Using Multi-Sensor and Single Camera for Short and Medium Span Bridges. Remote Sensing. 2019; 11(22):2651. https://doi.org/10.3390/rs11222651
Chicago/Turabian StyleXia, Ye, Xudong Jian, Bin Yan, and Dan Su. 2019. "Infrastructure Safety Oriented Traffic Load Monitoring Using Multi-Sensor and Single Camera for Short and Medium Span Bridges" Remote Sensing 11, no. 22: 2651. https://doi.org/10.3390/rs11222651
APA StyleXia, Y., Jian, X., Yan, B., & Su, D. (2019). Infrastructure Safety Oriented Traffic Load Monitoring Using Multi-Sensor and Single Camera for Short and Medium Span Bridges. Remote Sensing, 11(22), 2651. https://doi.org/10.3390/rs11222651






