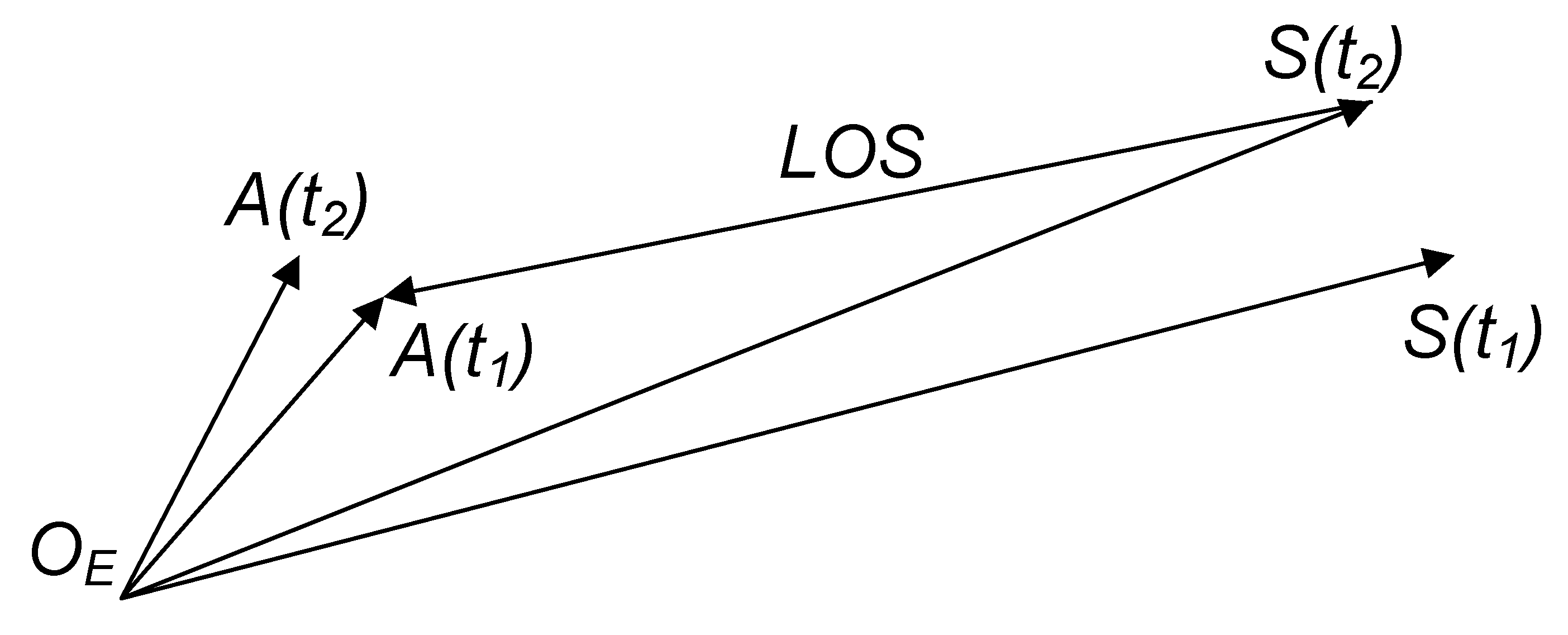1. Introduction
No matter how far humans want to travel in the universe, the Moon, the only natural satellite of the Earth and our nearest neighbor, is the first place we need to colonize. Since 1958, satellites and spacecrafts have visited the Moon more than 100 times. Countries and institutions including the Soviet Union-Russia, USA, ESA, China, Japan, and India have been involved in these explorations. In this century, more than 10 missions have been successfully launched, and tens of missions are scheduled. With technological progress and increases in our understanding of the Moon, the colonization of the Moon is no longer an envisaged possibility but is a real challenge humans face. Recently, the ESA proposed a “moon village” program, which is a Moon base under international collaboration among spacefaring nations for science, business, mining, and even tourism [
1]. NASA also started its new lunar mission, named Artemis, to return astronauts to the lunar surface by 2024 [
2]. Similar plans have emerged over past few decades, but until now, humans have not truly had the ability to realize these plans. Such a permanent settlement on the lunar surface will be significant to scientific studies and deep space exploration. For Earth science, it will also provide an opportunity to complete our Earth observation system. China’s Lunar Exploration Program (CLEP) officially began in 2004, and one of its three overall objectives is to develop the Moon as an Earth observation satellite for monitoring global climate change, eco-environment evolution, pollutant diffusion, natural disaster evolution, and other processes [
3]. Recent research has shown that Moon-based Earth observation is characterized by longevity, integrity, stability, and uniqueness [
4]. In addition, Moon-based Earth observation is a good complement to existing satellite Earth observation systems, which usually run in low Earth orbit or geostationary orbit. Remote sensors on the lunar surface can be used to monitor solid Earth dynamics, the global energy budget, climate and environmental change, and the near-Earth space environment. An Earth’s radiation budget measurement system is planned to land on the lunar surface with Chang’E follow-up mission in ten years [
5]. It consists of a radiometry to measure the outgoing solar and thermal radiation of the earth and an array imaging spectrometry to map the atmospheric and surface composition of the earth disk. Concerning the large distance between the Earth and the Moon, a slight change in the angular parameter is expected to bring in a large deviation on the ground. Therefore, it is necessary to present a high-accuracy geometric model establishing the connection between the Moon-based sensor’s pointing and positioning parameters and a target on the Earth’s surface.
Two scientific Earth observation experiments have been carried out on the lunar surface. During the first Moon-based Earth observation experiment in 1972, Apollo 16 astronauts used a far-ultraviolet camera/spectrograph to observe the Earth’s atmosphere and corona [
6]. Forty-one years later, a one-year Earth plasma observation experiment were successfully carried out by the Extreme Ultraviolet (EUV) camera on the Chang’E-3 mission lander [
7]. These two experiments were mainly related to space science, independent of geographic coordinates. A simplified geometric model, which only consider the earth’s rotation but ignore the revolution of the moon, was presented for synthetic aperture radar (SAR) system performance analysis [
8]. At the same time, ELP2000, a semi-analytic theory, was also selected to construct the geometry for the similar purpose [
9]. These two models are good at analyzing the system performance without referring to the sensor’s pointing direction and its position on lunar surface, which are the only designable parameters in the geometry model. Ding et al. introduced the JPL ephemeris in geometry and built connections among sensor’s seleno-graphic position, point direction, and the doppler parameters of moon-based SAR [
10]. Recently, a simplified geometric model is widely used for spatial and temporal scope analysis [
11,
12] and the simulation of earth’s outgoing radiation [
13,
14,
15]. The moon-based SAR imaging geometry is also improved [
16,
17,
18]. However, for the mission design of moon-based Earth’s radiation budget measurement and moon-based SAR imaging simulation, the model is still made with too much simplification. Although the satellite tool kit (STK) provides us with a powerful function library for most space applications, the tools for moon-based sensors is not so fully functional as the spaceborne ones.
Compared with former studies, the geometric model presented in this paper is characterized by: (1) a general geometric frame compatible with both passive optic sensors and SAR system, (2) reversable simulation flow, (3) minimum approximation to fulfill the stringent requirements and give reference to the simplification, (4) the analysis and compensation of the aberration effect and light time effect, and (5) first accuracy evaluation of moon-based earth observation geometric model. Moreover, the geometric model can be used to: (1) reveal the direct geometry relationship for mission design, SAR focusing processing, image correction etc.; (2) simulate data to develop data processing algorithms and software systems; and (3) forecast the sensor’s pointing direction for the mission operation, especially for the non-imaging radiometry and SAR.
A brief discussion about the moon-based sensors will be presented in
Section 2. Then, in
Section 3, we introduce, in detail, the geometric model and the method of simulation. The definition of spatial coordinate systems and temporal coordinate systems are presented in
Section 3.1 and
Section 3.2, respectively. The data referring to the position of the Sun, the position and attitude of the Earth, and the position, velocity, and libration of the Moon are introduced in
Section 3.3.
Section 3.4 and
Section 3.5 show the transformation matrices and the process of transformation from a sensor-fixed coordinate to a geocentric coordinate system. The corrections of aberration and light time are shown in
Section 3.6 and
Section 3.7, respectively, for two passive optic sensors. The geometry simulation, as well as an attempt of validation, is described in
Section 4. Then, the model accuracy is evaluated in
Section 5. Two examples of application are given before the conclusion. One is predicting the pointing direction of a moon-based sensor and derived constraints on site selection. Another is the simulation of range history of moon-based SAR and its comparison with former approximation.
2. Brief Considerations Concerning Moon-Based Earth Observation Sensors
In 2006, NASA suggested 12 scientific objectives for Earth observation among a total of 160 lunar exploration objectives [
19]. Although the ambitious plan to return to the Moon was abandoned due to the transfer of political power, scientists have not lost their enthusiasm for relative studies. In the decade after 2006, scientific objectives were elaborated, and sensor configurations were put forth [
8,
9,
20,
21,
22]. We chose seven geo-scientific objectives from NASA’s list and rearranged them into three categories: (1) use of multispectral passive sensors at the disk scale for global mapping of atmospheric composition and surface composition, determining the Earth’s bidirectional reflectance distribution function (BRDF) and monitoring the Earth’s hot spots; (2) use of radiometers to measure radiance directed toward the Moon for Earth radiation budget research; and (3) use of SAR for topography, tomography, altimetry, vegetation mapping, and ice dynamics observations in polar regions.
At present, both the radiometry and the array imaging spectrometry are technically feasible to observe the Earth from the Moon. Due to their cost, size, weight, and energy consumption, Moon-based sensors are quite limited. In view of the trade-off between costs and scientific significance, the horizontal resolution in the visible spectrum was initially set at 1–10 km. However, if a permanent manned Moon base is established in the future, the transport, construction, and maintenance costs of the observation system will be greatly reduced by cost allocation, especially for long-lasting missions. A high-resolution optical system for land mapping, source investigation, and target monitoring is also a candidate of the observatory in the future. In long-term planning, a Moon-based SAR can be used to image the global dynamics of the solid Earth. The antenna size and power requirements of such a SAR are very high, so it can only be attached to a permanent Moon base over a certain scale. The suggested spatial resolution is 10–100 m. An L-band system is better for some geoscience applications, but an X-band or C-band system is smaller in size [
22].
To improve efficiency and reduce the possibility of contamination, it is better to use a field of view (FOV) just fit to the Earth disk. The diameter of the Earth disk including the atmosphere is slightly smaller than 13,000 km. Therefore, for the closest case, the FOV or footprint must have a diameter of approximately 2.1° with 1%, or, equivalently 75.6″ tolerance. However, if a smaller FOV or footprint is used to cover a target area on the Earth’s surface, especially for SAR, the requirements will become much more stringent. For example, a footprint with a width of approximately 300 km and a 3% tolerance of deviation will allow a maximum deviation of only 9 km, corresponding to 5.2″. The accuracy of presented geometric model is expected to be better than this value.
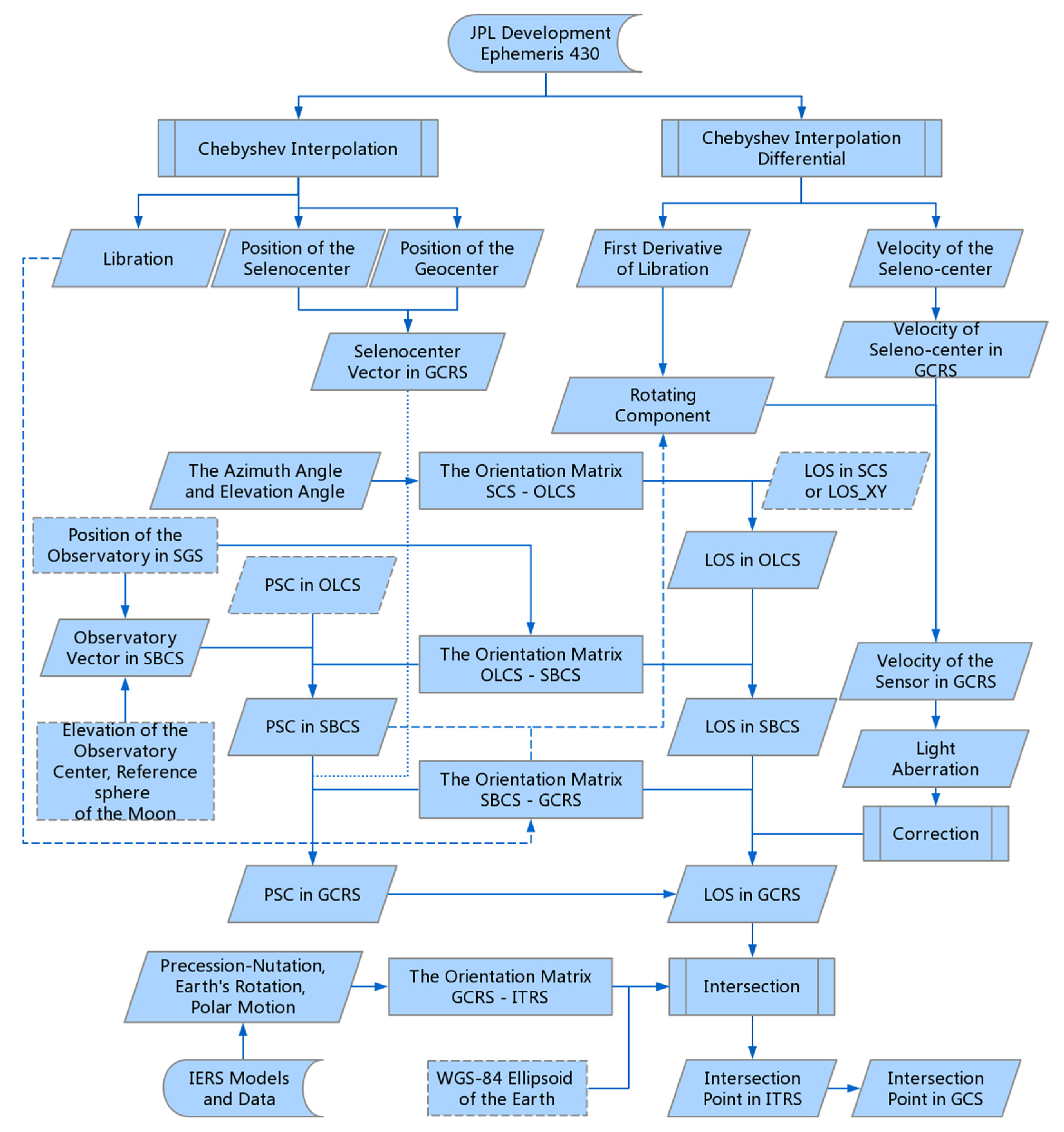
3. Model and Simulation
3.1. The Spatial Coordinate Systems
The four coordinate systems used in this paper, namely, the International Celestial Reference System (ICRS), International Terrestrial Reference System (ITRS), Barycentric Celestial Reference System (BCRS) and Geocentric Celestial Reference System (GCRS), are rigorously defined by the International Astronomical Union (IAU) and the International Union of Geodesy and Geophysics (IUGG). Their definitions are presented in the Nomenclature for Fundamental Astronomy (NFA) glossary. The BCRS and GCRS are assumed to be oriented with the ICRS axes according to the IAU 2006 Resolution B2. To validate most equations in this paper, the time-space distortion will not be taken into consideration.
In addition, the meanings of several other coordinate systems have to be specified. Similar to the geographic coordinate system (GCS), the seleno-graphic coordinate system (SGS) is set up to define Lat-Lon positions on the lunar surface, and its origin is considered the intersection point of the X-axis of the body-fixed coordinate system and the lunar reference sphere. The lunar reference ellipsoid is a sphere with a radius of 1737.4 km. In addition, the three other right-handed three-dimensional space coordinate systems used in the following sections are:
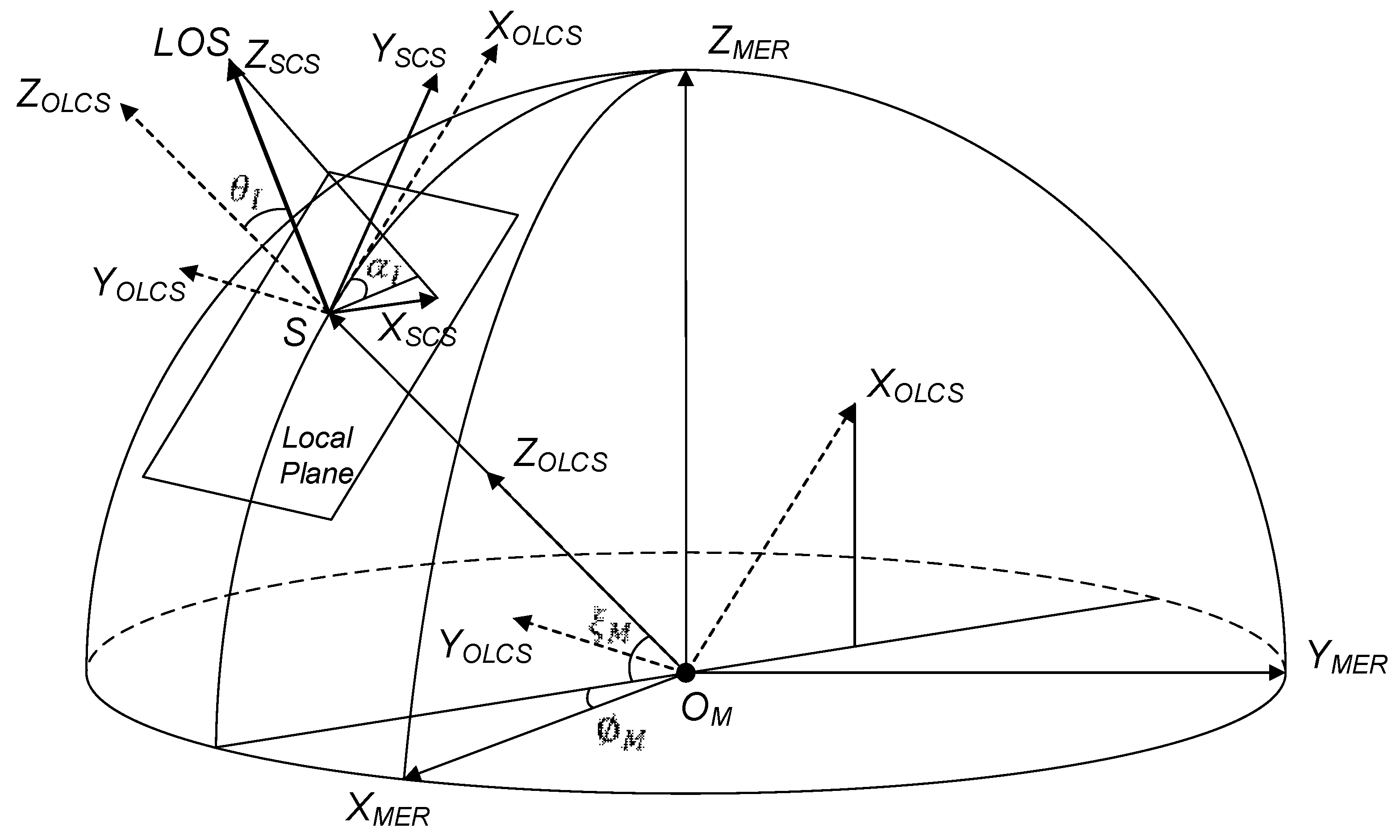
Sensor Coordinate System (SCS): The SCS is a sensor-fixed reference frame. The origin is the optical center for the camera or the phase center for the antenna. The Z-axis is the optical axis or the direction of the main lobe, namely, the line of sight (LOS) in the following sections. The XY plane is perpendicular to Z. The directions of the X-axis and Y-axis refer to the antenna shape or the image coordinates. In this paper, they are implicitly defined by the zenith angle and azimuth angle.
Observatory Local Coordinate System (OLCS): The origin of the OLCS is an artificially defined center of the observatory with an elevation of H. The Z-axis is the same as the local normal vector, while the XY plane is the local tangent plane. The X-axis points to the north. The zenith angle- and the azimuth angle-related SCS and OLCS will be introduced in
Section 3.4.
Selenocentric Body-fixed Coordinate System (SBCS): The coordinate origin is the lunar mass center. Principle axis (PA) coordinates and mean-Earth/rotation-axis (MER) coordinates, which are related by a constant three-angle rotation, are two commonly used body-fixed coordinate systems [
23]. The PA coordinates are directly linked with the ICRS by physical librations [
24], while lunar cartography customarily refers to MER [
25].
3.2. Considerations Concerning the Time Coordinates
The Earth orientation parameter (EOP) data and JPL ephemeris used in this paper are presented in different time coordinates. The terrestrial time (TT) coordinating the Earth’s attitude has a mean rate close to the proper time of the rotating Earth and can accurately be represented by International Atomic Time (TAI), an idealized atomic time system with the SI second on the geoid as the unit of measurement [
26]:
Barycentric dynamical time (TDB) serves as an independent time argument of barycentric ephemerides, such as the JPL ephemeris. The relationship between TDB and TT is given by [
27]:
where
is a periodic term with a main component with an approximately 1.7 ms amplitude and a one-year period.
leads to periodic geometry deviation during the Earth’s orbital cycles; however, its amplitude is too small for the Earth observation application. The maximum space deviation of the lunar mass center is less than 2 m, much smaller than other errors analyzed by
Section 5.3. Universal Time Coordinated (UTC) system, which is the standard for all civil time systems, is different from TAI because the former has integer leap seconds forecasted by the International Earth Rotation Service (IERS). The time conversion is realized by the Standards of Fundamental Astronomy (SOFA) time scale and calendar tools in this paper.
3.3. JPL Development Ephemeris and Earth’s Attitude
The JPL ephemeris is in good agreement with lunar laser ranging (LLR), which now achieves millimeter-scale accuracy [
28]. In this paper, we use DE430 to calculate the positions and velocities of the helio-center, geocenter, and seleno-center in the ICRS, as well as the amplitude and derivative of the libration. The position vector should be translated from the ICRS to the GCRS for the next step.
Usually, the position of the reflector on the Earth is given in the GCS, defined on the Earth’s reference ellipsoid. The coordinates in the ITRS can be calculated by using the geographic coordinates and parameters of the ellipsoid. Since the center of the Sun, Earth, and Moon are given in the GCRS, we need to understand the orientation matrix between the ITRS and GCRS that describes the Earth’s attitude in the universe. According to IERS conventions, the orientation matrix
is presented by [
29]:
where the
is the transform matrix of the precession and nutation,
is the transform matrix of the Earth’s rotation, and
is the transform matrix of the polar motion. The matrix
transforms the position vector from the ITRS to the GCRS. The IERS conventions shows how to use the models and data to calculate
. The SOFA tools for Earth attitude provide the program that implements the official IAU algorithms based on EOP data.
3.4. Orientation Matrices
The relation between the sensor’s position and pointing direction is given by a series of transformation and an intersection. The flow chart of simulation is presented in
Section 4. The orientation matrices for transformation are introduced in this section, and the process of transformation will be introduced in the next section. Assuming the coordinate system rotates
clockwise around the
,
, and
axes, the rotation matrices are:
The vector in the new coordinate system can be calculated by pre-multiplying the unit rotation matrix to the vector in the original coordinates system.
For clarity, we assumed the sensor is on a two-dimensional altazimuth turntable [
30,
31]. In its initial state, the SCS and OLCS are the same. When controlling the direction of the LOS, we first rotate the azimuth angle
clockwise around the Z-axis and then rotate the zenith angle
clockwise around the Y-axis. In some cases, a third rotation is needed. For example, if we use a rectangular antenna, the long side of the footprint is expected to be parallel with the meridian, and an extra
should be added. The rotation angle
is the clockwise angle around the Z-axis, and it is zero for circular aperture. Thus, the orientation matrix
(
Figure 1) can be written as:
If the observatory position is
in the SGS, we can get the orientation matrix
(
Figure 1).
The orientation matrix
connecting the MER to PA is:
The angles
,
, and
refer to the constant parts of the three libration parameters. Their values compatible with DE430 are 67.573″, 78.580″, and 0.285″ [
24]. If the position of the observatory is directly given by PA coordinates
, such as the coordinates of the LLR retroreflectors, the orientation matrix from the OLCS to the PA can be directly expressed by substituting the PA latitude and longitude for the MER latitude and longitude in Equation (6).
The three Euler angles of libration are
,
, and
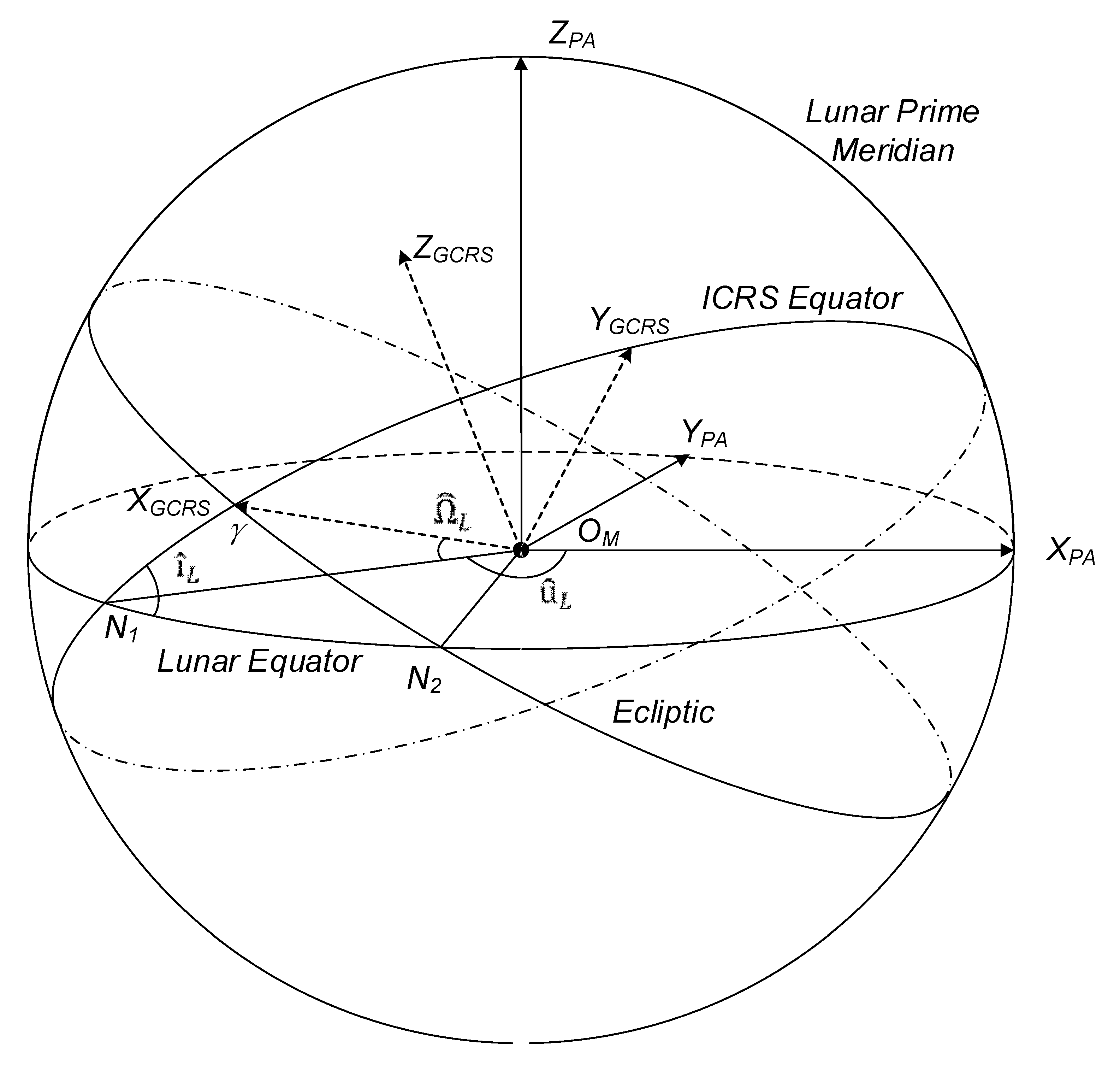
. On the celestial sphere, let
stand for the ascending node of the lunar mantle equator to the ICRS equator (
Figure 2). Thus, it can be inferred that the three Euler angles are the angle from the X-axis of the inertial frame along the ICRS equator to the intersection of the lunar mantle equator, the inclination of the lunar mantle equator from the ICRS equator, and the longitude from
to the lunar prime meridian along the lunar mantle equator [
25,
32]. Thus, the orientation matrix
can be presented by:
The orientation matrix
is already given in
Section 3.4 and is calculated by SOFA. Note that the orientation matrix is orthogonal and has the following property:
3.5. Transformation from the SCS to the GCRS
In the SCS, the LOS can be presented by:
In the OLCS, the LOS can be presented by:
The position of the sensor center (PSC) in the OLCS is . This vector relies upon the system design. For simplicity, we assume the two centers coincide in the simulation.
In the MER, the LOS can be presented by:
And the PSC can be presented by:
where the
is the radius of the Moon, and
is the elevation of the observatory center.
In the PA, the LOS and PSC can be presented by:
In the GCRS, they are presented by:
where
is the position of the Moon in the GCRS.
3.6. The Light Aberration
Light takes approximately 1.3 s to travel from the Earth to the Moon, which is much longer than the spaceborne observation. Thus, an obvious geolocation problem for Moon-based Earth observation is that the geometry changes from the time when the light leaves the Earth to the time when the light arrives at the sensor. This phenomenon, known as light aberration in astronomy, results from the relative motion between the reflector and the observer. Recently, high-resolution remote sensing processing has taken aberration compensation into consideration [
33,
34]. This effect is calibrated by introducing a corrective rotation. Intrinsically and more precisely, a two-step method is developed for moon-based earth observation, and it also can be used in spaceborne cases [
35]. For Earth observation, the aberration can be divided into two parts. The part related to the motion of the sensor will be discussed in this section, and the part caused by the Earth’s rotation, called the light time effect, will be discussed in
Section 3.7. The aberration angle can be approximately presented by:
where
is the viewing angle related to the speed vector,
is the speed of light, and
is the speed of the observer. If the observing angle is perpendicular to the relative speed, the angular aberration can easily be derived and is
. For example, if the orbital speed of the Moon is 1.02 km/s, the viewing angle is 90°, and the distance between the reflector and the seleno-center is 380,000 km; thus, the light aberration is approximately 3.4 × 10
−6 rad (0.7″), corresponding to a 1.3 km deviation on the Earth’s surface.
In the GCRS, the velocity of the sensor is
, and the real received light is
. The calculated received light is
and is in the moving system that has the same axis directions as the GCRS but moves with the SBCS. Let the received light in the GCRS be
, the received light in the moving system be
, and the relative speed of the GCRS in the moving system be
. Therefore, the speed addition can be described by the Lorentz transformation:
where
is the magnitude of
and the factor
. Then, the real received light is:
It can be easily deduced that the sensor speed vectors in the coordinates fixed on the Moon, i.e.,
,
,
, and
, are all 0. Therefore, the GCRS speed vector is:
where
is the velocity of the seleno-center in the GCRS, and:
Formulating Equation (22) is a complex task [
36,
37]. For some applications,
and
can be considered approximately 0, and
can be considered 13.2 degrees per day [
10]. In this paper, the result is numerically computed by using the Chebyshev polynomial to interpolate the JPL ephemeris.
3.7. The Intersection Point
In the previous calculation, the time-variant parameters refer to the receiving time
, so
is not explicitly written out in the equations. However, the position of the reflector refers to the ‘departure time’
, namely, the time when light leaves the reflector, in the geometry. Thus, the time difference should be clearly represented in the following equations. The departure time can hardly be measured by an Earth observation system, but the relationship below stands (
Figure 3):
where
is the length of the LOS.
Meanwhile, at
in the GCRS,
is on the terrestrial ellipsoid, so we get:
where
represents the coordinates
of the intersection point of the LOS and the terrestrial reference ellipsoid in the GCRS at time
, and
is the length of the LOS. The major semi-axis
is 6378.137 km and the minor semi-axis
is 6356.752 km in terms of WGS84 ellipsoid. By solving the equation, we can determine the position of the reflector
by substituting the estimated
into
.
Because
is inexplicit, Equation (24) only has numerical solutions. Here, a simple approximation with a max error less than 10 m is presented. Note that if the LOS and the ellipsoid intersect, the range of
is less than 21.5 ms because:
where
is the length of
. We can estimate
by replacing
with
or
in Equation (24). In this time window, the ITRF is under- or over-rotated with a 10 m max error (the Earth’s mean rotation speed is approximately
) corresponding to an error of
in the estimation of
. In this paper,
is chosen because the case wherein the LOS is pointed to the geocenter is mainly discussed.
In particular, imaging spectrometer models are usually described by the colinear equation, which is an effective planar approximation within limits. To address the whole disk, we follow the same procedure but substitute
for
in Equation (10):
where
is the focal length. Then, all image coordinates
are connected to geographic coordinates. This method is computationally inefficient but has a high accuracy.
4. Geometry Simulation
The simulation procedure follows the model specified from
Section 3.4,
Section 3.5,
Section 3.6 and
Section 3.7. DE430 from JPL and EOP 14 C04 from IERS are two input data tables. Usually, times are initially presented in UTC and should be converted to TDB and TT to interpolate the two input tables. The calculated results are tested by the attached test data and the results from the IERS Rapid Service/Prediction Center (
http://maia.usno.navy.mil/t2crequest/t2crequest.html). Due to the libration and the ellipticity of the orbit of the Moon, the LOS will shift out of the Earth disk if the azimuth angle and zenith angle do not change with the revolution of the Moon. To make Equation (24) always solvable, a simple strategy is to point the LOS to the geocenter:
Then, the coordinates of the intersection point and corresponding azimuth angle and zenith angle can be calculated by a slight adjustment of the proposed method (
Figure 4). The coordinates of the lunar surface are directly given in the PA. The following analyses use these criteria, unless otherwise specified.
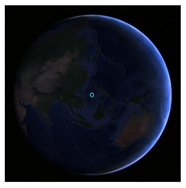
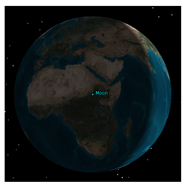
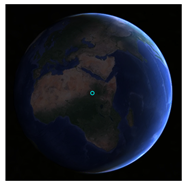
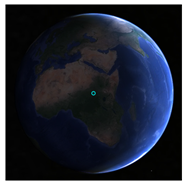
A lack of experimental data makes it very hard to validate simulation results. Optically imaging the Earth is not one of the objectives of the Chang’E-3 mission. Although the Terrain Camera (TCAM) lander did take several photos of the Earth, the spatial resolution is only approximately 70 km. Since these images are the only measured data accessible to us, we compromise with a comparison of the imaged Earth disk and the simulated Earth disk (
Table 1). The elevation of the lander is
2632.0 m, and the location is
in MER.DE421 [
38], i.e.,
in PA.DE430. The orientation angles differ slightly from the angles in Equation (7) [
32]. In addition, the simulation results from the STK 11 are introduced as mutual authentication data. A more credible validation method will only rely on field measurements in future missions.
A qualitative comparison is shown in
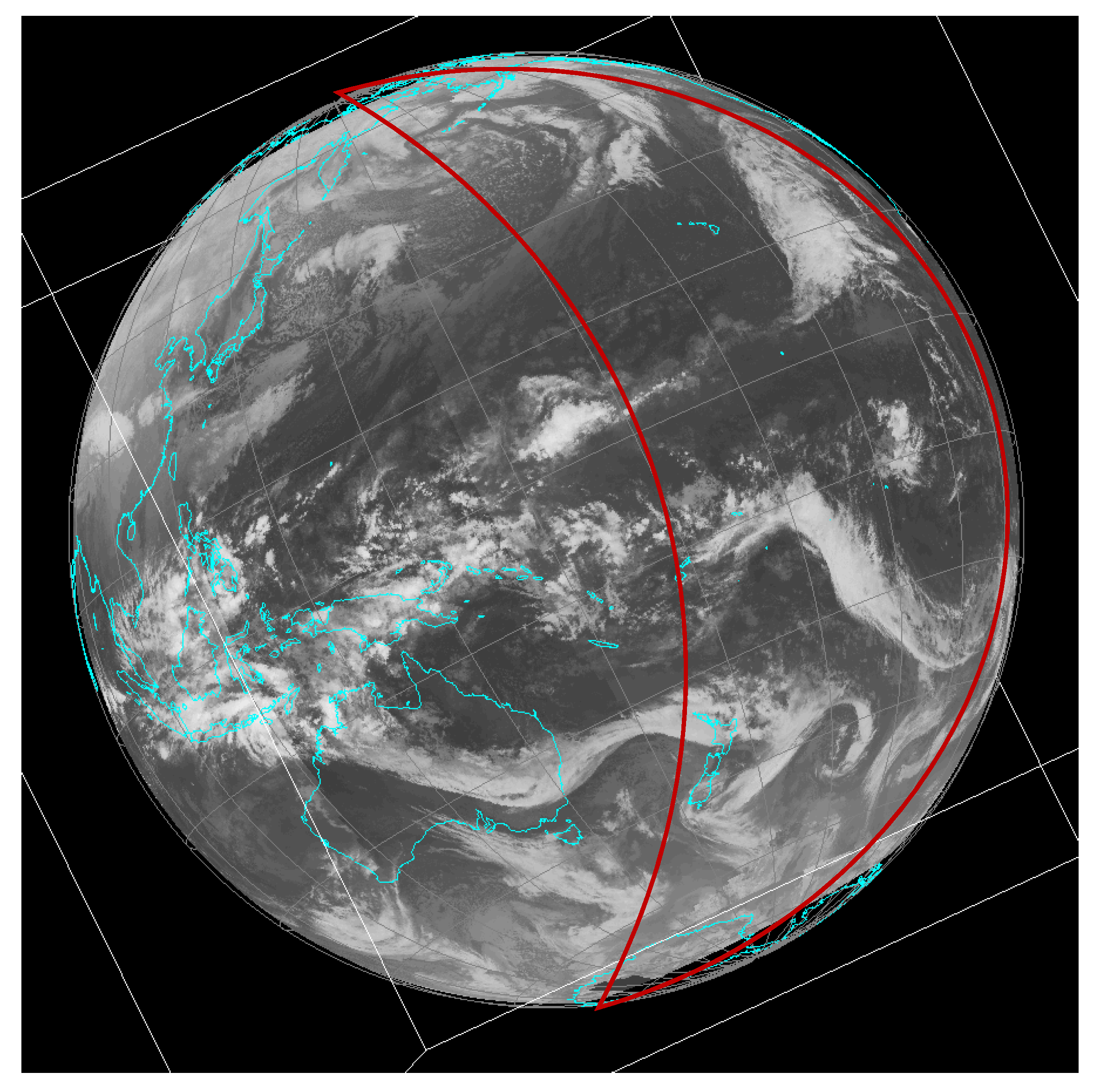
Table 1. The time is given in UTC +8. The STK results are the views from lunar center, while the images of Chang’E-3 and the simulation results of this paper are viewing from the lander. It can be inferred that the twilight arcs from three sources are largely the same (note that the attitude of the Earth and the rendering effect are slightly different). The disk views from the STK and this paper are similar, but the disk views from the Chang’E-3 lander are unidentifiable due to the low spatial resolution and high cloud coverage.
Figure 5 shows infrared global geostationary composite v1 at UTC 2013/12/24 18:15. The cloud texture in the red crescent is very close to that in the Chang’E image acquired four minutes later.
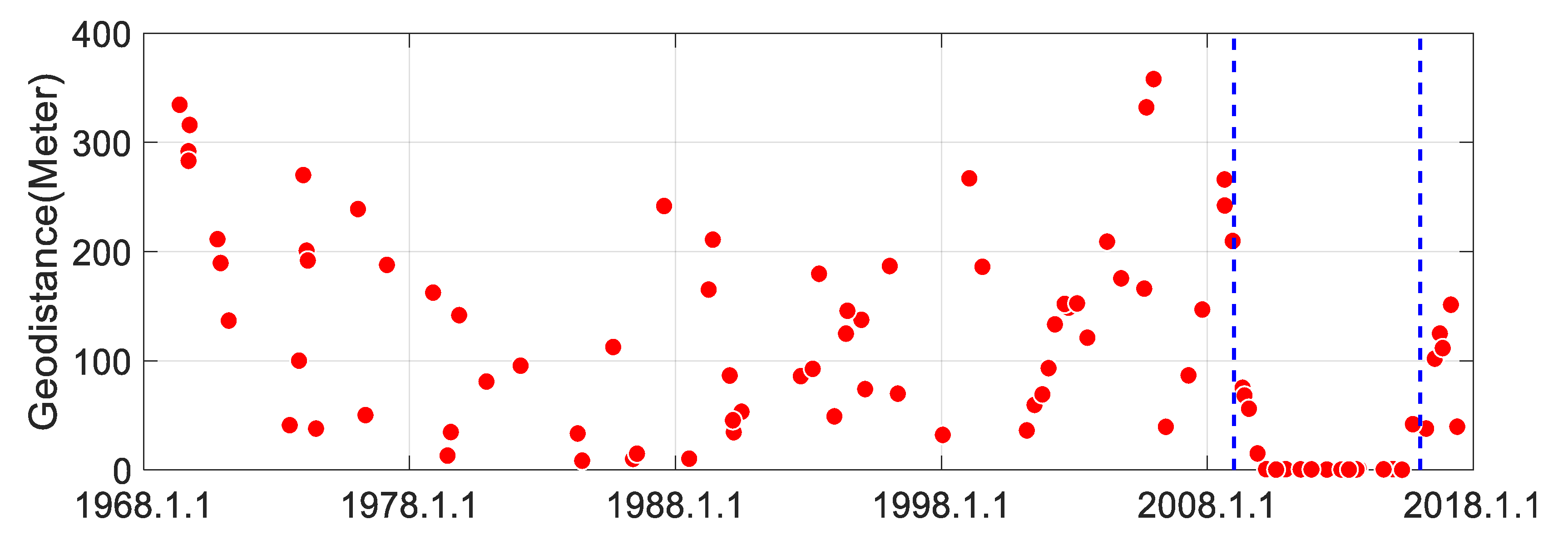
A quantitative comparison between the intermediate result and the STK outputs is also made. Five groups of random numbers corresponding to the timestamp, lunar latitude, lunar longitude, azimuth bias, and zenith bias are combined to generate 100 check points. The aberration correction and light time compensation are not made in this comparison to keep pace with the software. Because the STK does not give built-in functions to report the results for a Moon-based sensor, we estimate the intersection position manually in the 3D interface point by point by using a conic beam as narrow as 2 × 10
−9 degrees. This method is very time-consuming. The comparison results are shown in
Figure 6. All geo-distance deviations are smaller than 400 m and have no significant correlation to any parameters. The mean value and standard deviation are 108.6 m and 95.6 m, respectively. Interestingly, the data between 2009/01/01 and 2016/01/01 obviously fit much better than the data from other times (between two blue dashed lines). Even from 2010/01/01 to 2015/07/01, all the differences are smaller than 2 m. We think that this result may be related to the release date of the used software version and the operation of the ICRF since 2009/01/01, according to the STK help document.
7. Conclusions
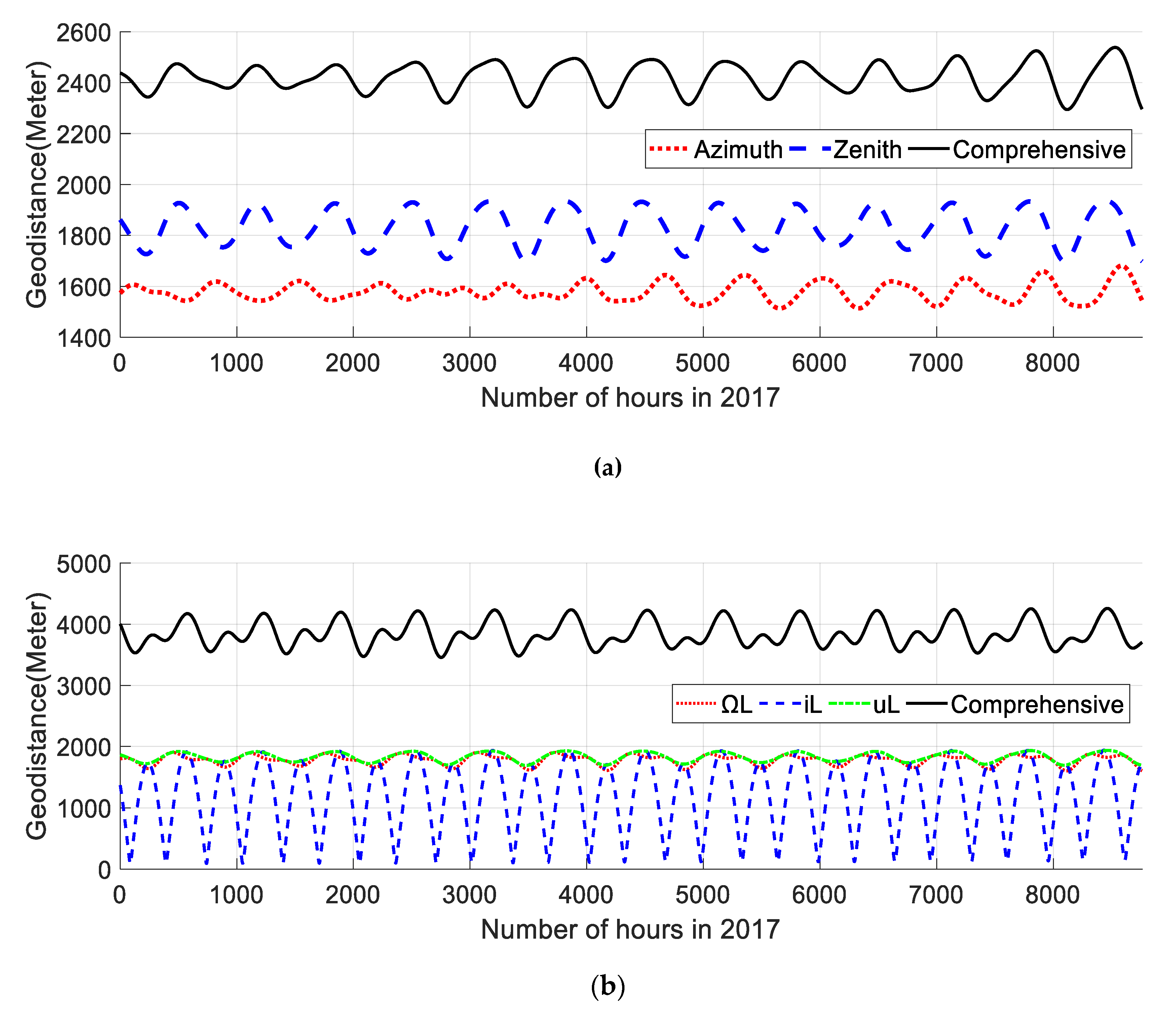
The correspondence between the intersection point and sensor attitude is given by the proposed geometric model. The simulated disk view is in good accordance with the image from the Chang’E lander and STK output. The analysis of the forecasted sensor’s attitude suggests that most places at the near side of the Moon are geometrically suitable for Earth observation, except for the marginal areas of the lunar disk and the neighborhood around the seleno-graphic origin. An observatory at the edge of the disk will likely experience view blocking by the topography or even by the lunar sphere itself, while an observatory near the lunar disk center will have a relatively high frequency of operation. The periodical approach between the Earth and the Sun on the celestial sphere requires a small FOV to prevent direct radiation. The analyses show that the areas near Cater Krafft have relatively low possibility of direct sunlit.
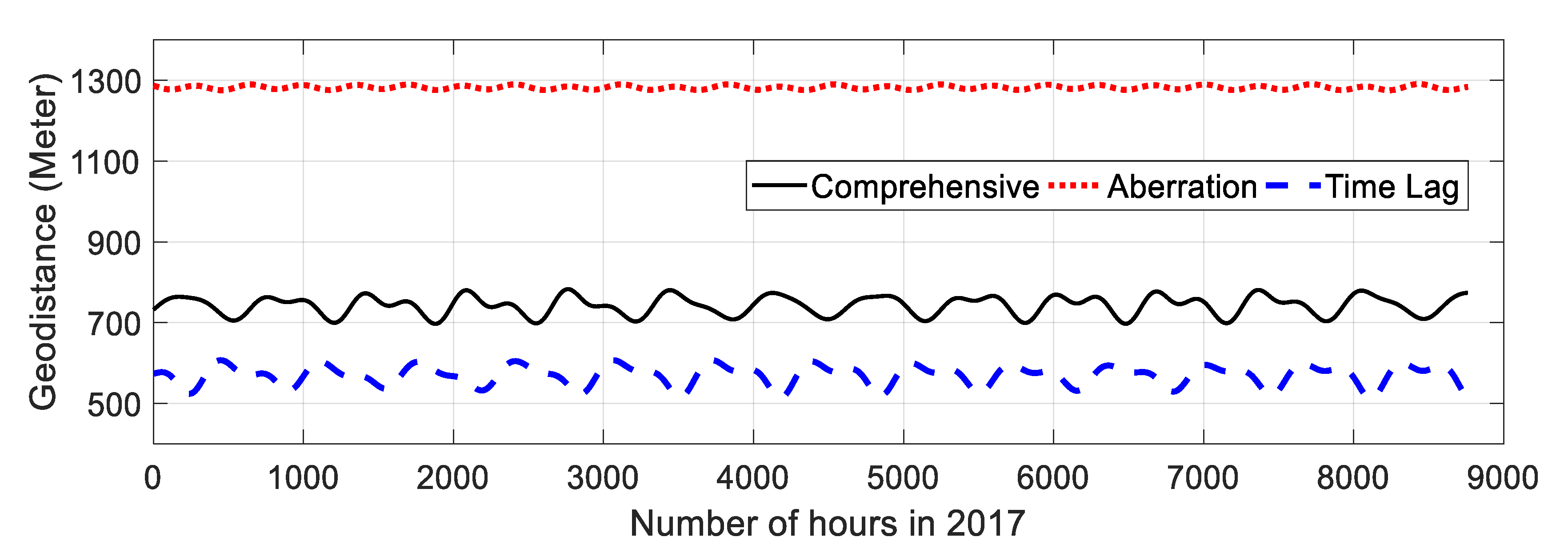
The light aberration scale is approximately 3.4 × 10−6 rad, corresponding to a deviation of 1.3 km on the Earth’s surface, while the light time scale is approximately 0.6 km in the opposite direction. As a result of neutralization, the combined effect is approximately 0.7 km, which is in the same order of magnitude as the pointing error. The light time also causes an error greater that the wavelength in moon-based SAR range history. In a 600s SAT around the time of closest range, the linear error can be as large as 44 m, but the high order error is at least one order smaller than the wavelength. The overall model accuracy is evaluated to be better than 4″ at current stage and will increase to be better than 1.5″ when the lunar positioning error is restricted to the level of the LLR reflector seleno-location accuracy.