1. Introduction
Tropical cyclones (TCs) can induce storm surges and intense rainfall during landfall, thereby causing serious damage to society and affecting the safety of residents in coastal areas. Therefore, in operational forecast centers, risk evaluation of potential TC damage is becoming increasingly significant. Obtaining key parameters is vital for TC forecasts, including the maximum wind speed (MWS), radius of maximum wind (RMW), and wind field distribution. Meteorologists usually determine TC intensity by identifying the MWS; thus, understanding the two-dimensional surface wind structure has great importance.
Over the past decades, efforts have been made to understand the possible reasons for TC surface wind asymmetry by considering large-scale environmental impacts, such as the beta effect, vertical shear of environmental flow, and uniform environmental flows, on storm intensity. Thus, it is suggested that these environmental effects induce quasi-stationary asymmetries near the TC eyewall and exert inhibitory actions on storm intensity [
1]. Moreover, previous studies have shown that other factors may affect TC structural asymmetries, including variations in surface friction [
2], Rossby waves [
3], and blocking actions [
4].
Storm motion is one of the major impact factors on an asymmetric structure in the TC surface wind field. The effect of storm movement induces the wind field to be asymmetric on two sides of the storm motion direction, with higher winds in the right forward quadrant than in the left, and the effect of surface friction leads to front-rear asymmetry due to the storm motion [
5]. However, TC surface wind fields are axisymmetric when simulated with the traditional parametric hurricane wind profile model [
6]. An asymmetric parametric wind profile model was later developed when the impact of storm movement was considered, which maximizes the wind asymmetry to the right side of the forward storm movement [
7]. Moreover, early studies found that the effect of storm motion contributes to convective asymmetries, with updrafts being stronger in the right forward quadrant, based on a linear analytical boundary layer flow model in a moving TC [
8].
Vertical wind shear also has an important effect on hurricane structural asymmetry [
9]. Although the storm motion is traditionally considered to be the primary factor that contributes to the TC structural asymmetry, its effect is significantly weaker than the influence of vertical wind shear on TC convection, based on lightning data in TCs [
10]. Recent studies have shown that large environmental vertical wind shear can induce strong asymmetric structures observed in hurricanes and typhoons [
11,
12]. Moreover, two kinds of rain-rate data have been used to investigate TC rainfall asymmetry; these data show that precipitation asymmetry is much more associated with wind shear than storm motion [
13]. Mesoscale analysis data from four typhoon seasons between 2004 and 2007 acquired from the Japan Meteorological Agency (JMA) were used to investigate the azimuthal wavenumber −1 asymmetry [
14] of surface winds in the typhoon core region, suggesting that the phenomenon of asymmetric surface wind is related to both the vertical wind shear and also to the storm motion. Moreover, a previous study has reported that the maximum surface wind speed occurs on the left side of the storm motion when the direction of shear is approximately identical to the storm heading [
15].
Airborne stepped-frequency microwave radiometer (S-FMR) hurricane wind observations at the surface and flight level have been used to study the effect of storm movement and vertical wind shear on surface wind asymmetry in hurricanes [
16]. At the flight level, the wavenumber −1 wind speed asymmetry amplitude increases with storm translation speed, while no obvious increasing tendency can be found at the surface. SFMR can only observe along-track wind speeds in TCs, not the complete two-dimensional surface wind field of an individual storm [
17]. Satellite scatterometers, such as Ku-band QuikSCAT, have the potential to measure TC surface wind fields [
18]. Scientists have used QuikSCAT winds to qualitatively investigate the link between typhoon surface wind asymmetry, as well as both the vertical wind shear and storm motion [
19]. The highest wind speeds tend to arise favorably on the left side of the shear and on the right side of the storm movement. However, QuikSCAT cannot accurately provide the maximum winds in the eyewall region of most TCs because of radar signal saturation and attenuation by rain [
20]. By conducting a composite analysis of TC wind fields in each TC-inclined region and different TC intensity conditions, based on rain-corrected scatterometer surface winds, a recent investigation has shown that the entire TC surface wind asymmetry is located to the left side of the storm movement, in a motion-relative frame, for all areas and for weaker TCs, when the movement velocity is removed [
21]. For the purpose of further study of the effect of wind shear and storm motion on TC surface wind asymmetry, a low-wavenumber analysis method [
16] was adopted to quantify the asymmetry index; thus, it was shown that tropical storms exhibit the most obvious surface wind asymmetry characteristics among all TC intensity groups [
22]. However, whether the vertical wind shear or the storm motion dominantly affects TC surface wind asymmetry remains an open question.
The L-band spaceborne radiometer is an excellent passive microwave sensor for remotely measuring the wind speed in TCs, because it is much less susceptible to rain attenuation than Ku-band scatterometers. Recent investigation has shown that there is a good relation between the wind-induced brightness temperatures from the SMAP L-band radiometer and TC wind speeds, and that brightness temperatures are not saturated under extreme weather conditions [
23], thereby providing an opportunity for remote sensing of ocean surface winds during severe storms [
24,
25]. Compared to Ku-band scatterometers, the L-band radiometer can provide more accurate measurements of high winds in extreme weather conditions. Although aircraft-based platforms, such as SFMR, are useful instruments to measure TC-force wind speeds in the along-track direction, they cannot provide comprehensive wind speed measurements over the entire two-dimensional spatial domain. However, the SMAP L-band radiometer has a wide swath and therefore has the capability of providing complete and accurate wind speed measurements in severe storms. Thus, it is possible to study TC wind asymmetry using SMAP winds.
In this paper, our focus was the study of surface wind asymmetry in relation to both factors, namely storm motion and vertical wind shear, for the first time, using SMAP wind measurements of TCs between 2015 and 2017 over the Northwest Pacific Ocean. Our motivation was to probe the roles of storm motion and vertical wind shear in affecting the surface wind speed asymmetry degree under differing TC intensity conditions. The sensitivity of the surface wind asymmetry to the difference between the storm motion direction and wind shear direction was also investigated. The remaining part of this paper is organized as follows. The data and the methodology are described in
Section 2 and
Section 3. The results and discussion are presented in
Section 4 and
Section 5. Conclusions are summarized in
Section 6.
3. Methodology
3.1. Asymmetry Parameter
The SMAP wind speeds were used to estimate the degree of TC wind speed asymmetry by using an asymmetry parameter (ε). Following [
4], the dimensionless asymmetry parameter was defined as
where
is the maximum wind speed, and
is the average azimuthal wind speed at the location of the radius of the maximum wind (RMW). In this study,
and
were derived from the SMAP surface wind data. Larger values of the asymmetry parameter correspond to a larger degree of asymmetry for the TC wind field.
The asymmetry parameter for each TC case was estimated following Equation (1). All TCs were divided into two groups according to the asymmetry degree parameter. Strong or weak asymmetry was denoted by the asymmetry parameter, corresponding to larger or smaller values than 0.2, respectively.
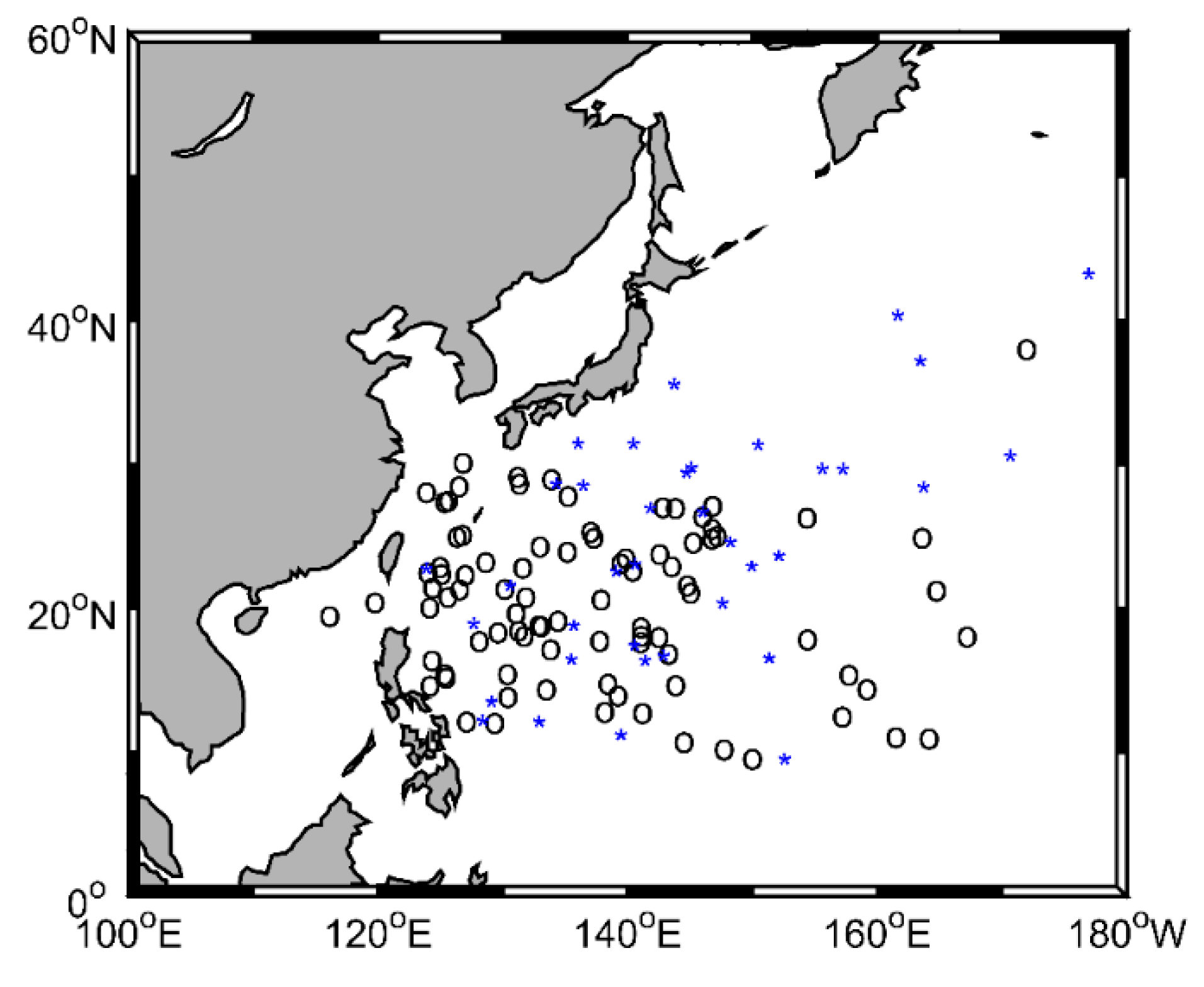
Figure 1 shows the geographical locations of these two groups of TCs, indicating no apparent difference in spatial distributions between the two groups. The linear effect of storm motion was removed by subtracting half of the TC translation speed [
27] from the SMAP surface wind speed data, and the asymmetry parameter was recalculated.
3.2. Composite Wind Field Analysis
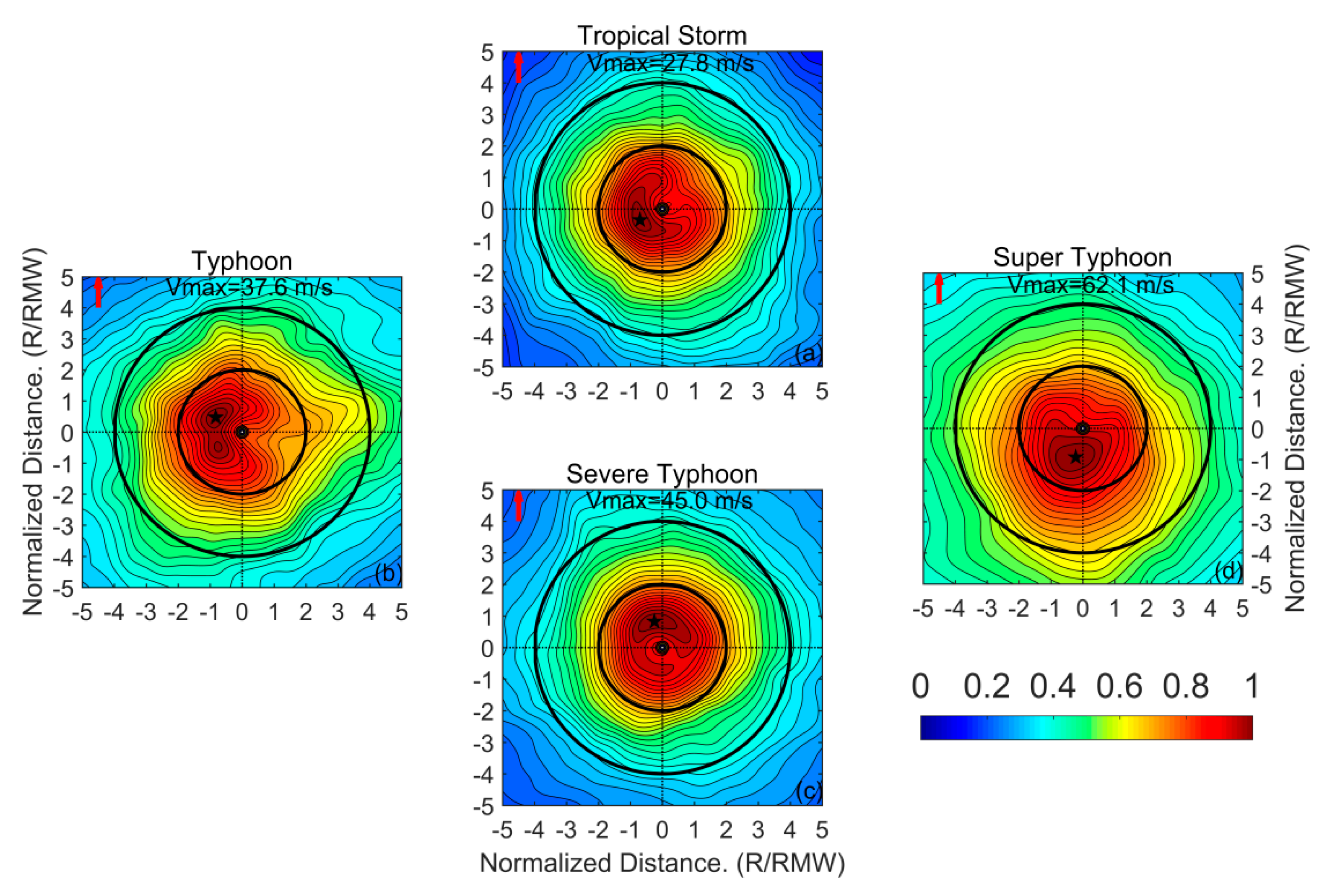
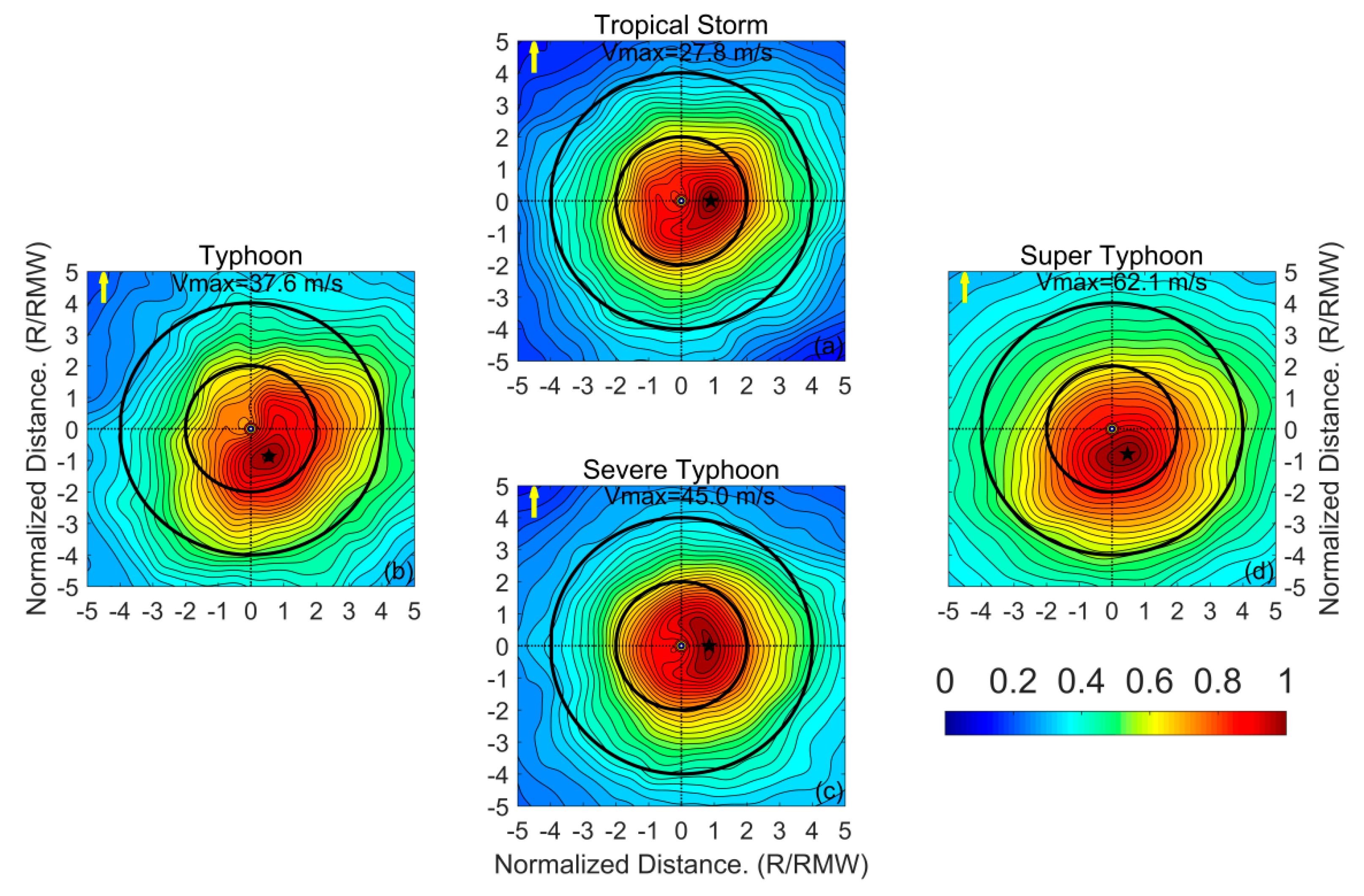
A composite wind field analysis method was used to investigate TC surface wind asymmetry. Compared to an individual case analysis, composite wind field analysis of a group of TCs can directly reveal the overall characteristics of the surface wind field, including the average intensity and asymmetric structure. Since the composite field is derived from the average of the individual fields, the noise in the SMAP wind data is eliminated, to a certain extent. Accordingly, TC asymmetric structure can be elucidated, based on composite analysis, which thus enabled us to explore the effect of various factors on TC surface wind asymmetry.
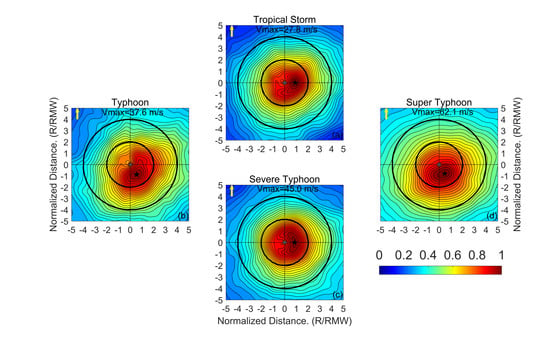
The basic steps for the composite analysis were as follows: (1) Select the SMAP wind field within a radius of 250 km from the TC center to ensure that the composite wind fields can exhibit the essential asymmetric structural features; (2) rotate the TC wind fields so that the forward direction of the composite field coincides with the direction of the wind shear or storm motion; and (3) bin average the TC wind fields as a function of the distance from the TC center and normalize, by using the radius of maximum wind speed (RMW) and the maximum wind speed (MWS).
3.3. Grouping Approach and Coordinate Systems
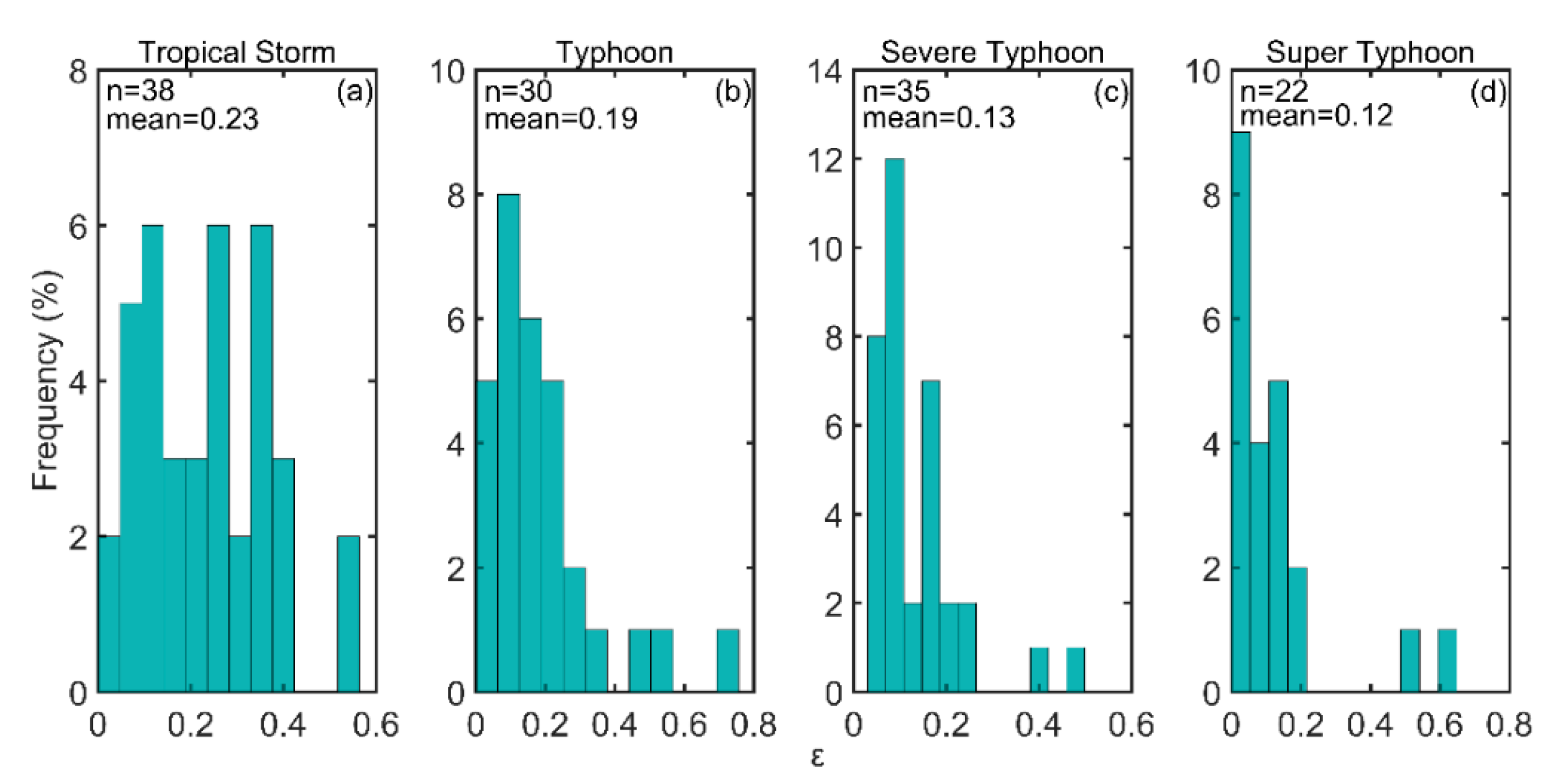
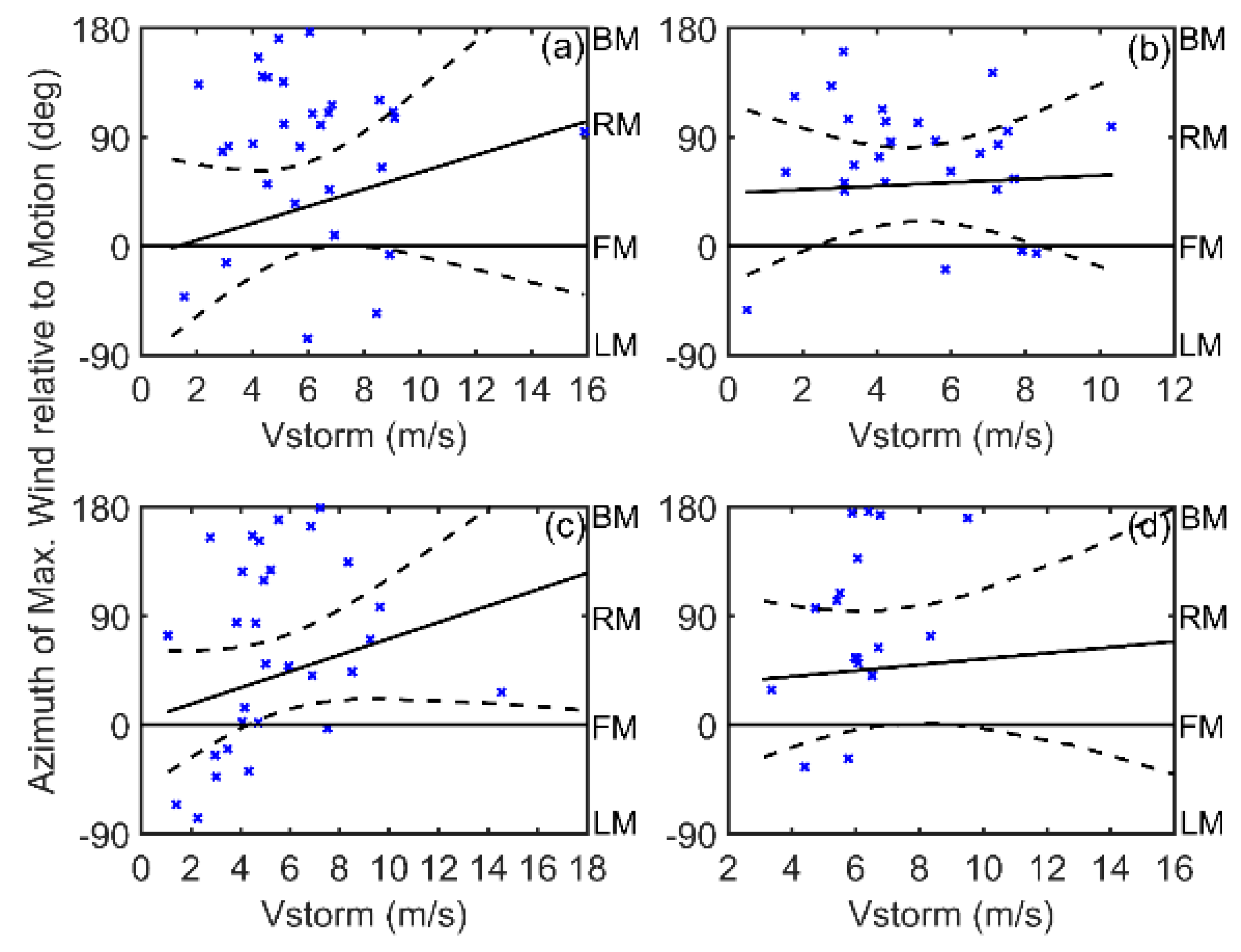
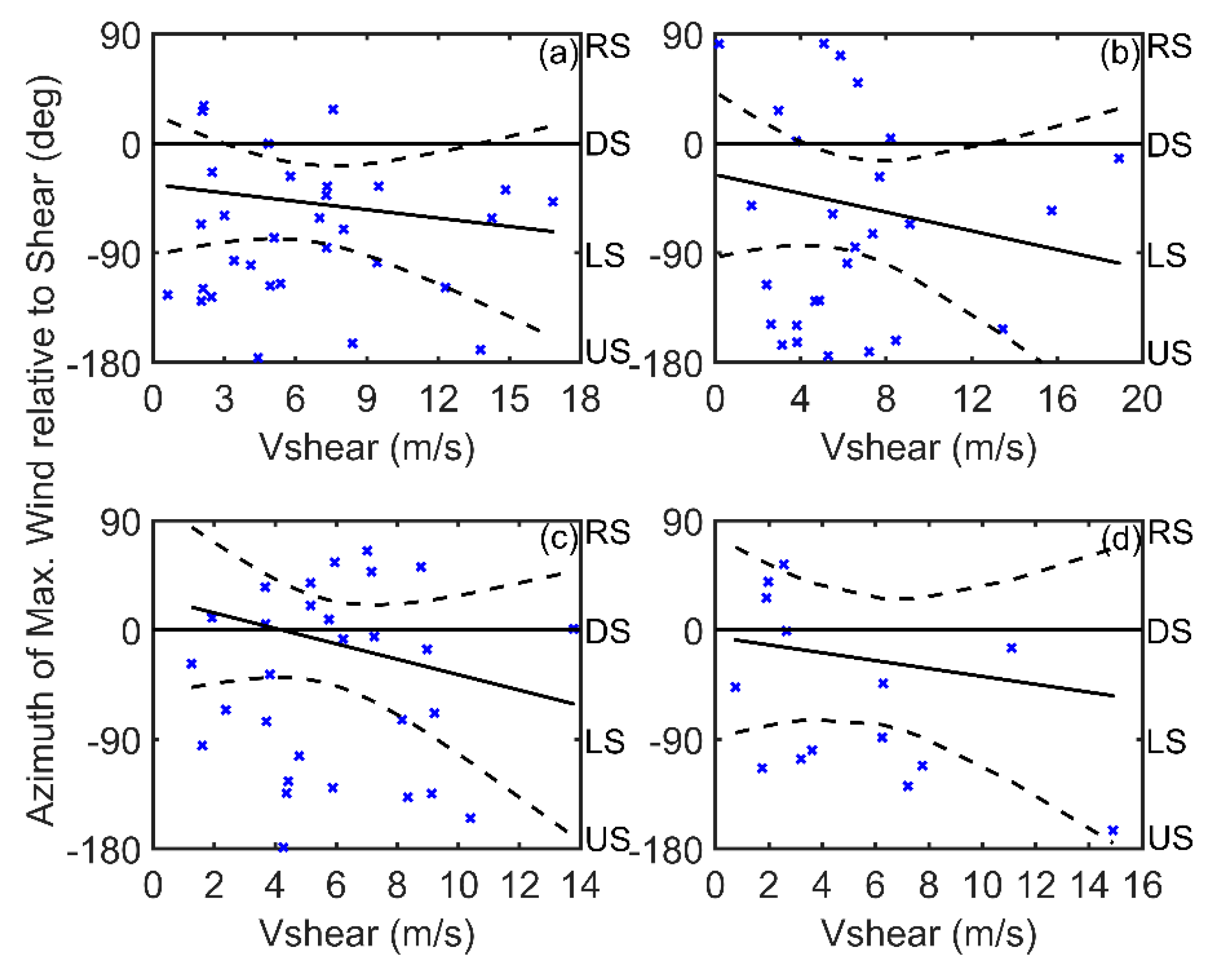
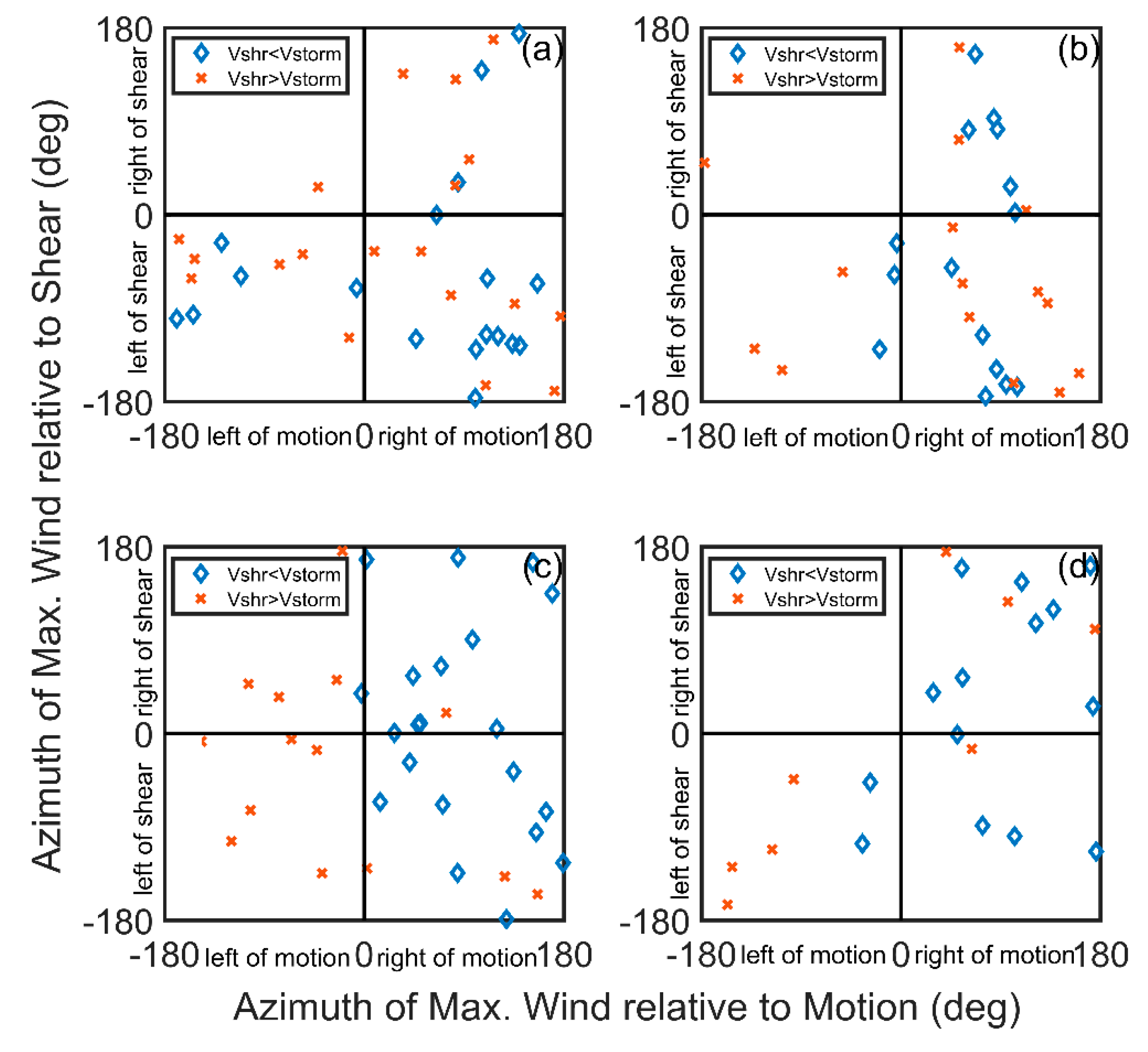
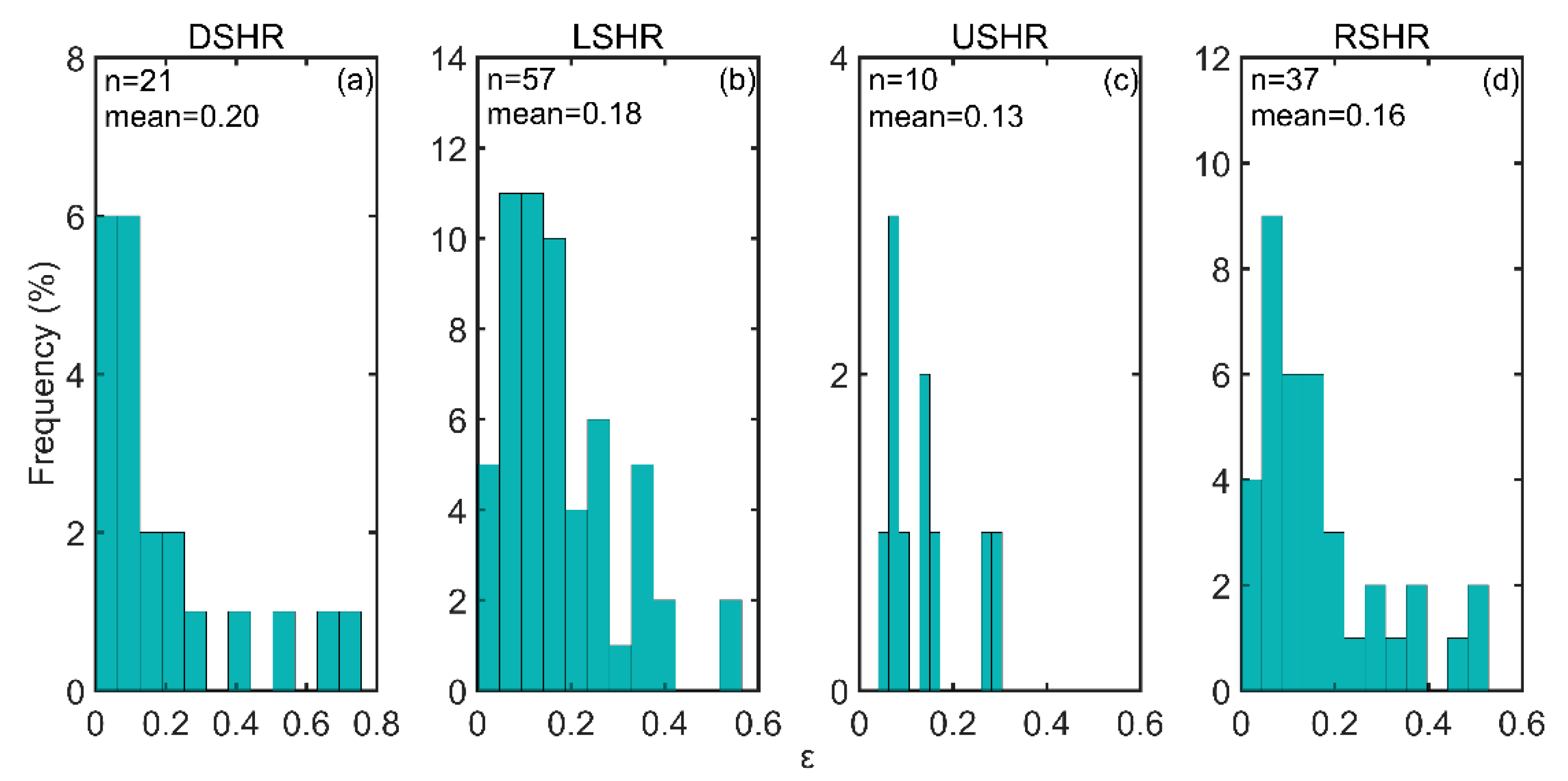
The relationship between the asymmetry parameter (ε) and the dominant factors that influence it were examined, such as the environmental vertical wind shear, storm movement, and intensity. First, TC samples were divided into four groups according to the TC intensity, namely, the tropical storm group (17.2 m/s << 32.6 m/s), typhoon group (32.7 m/s << 41.4 m/s), severe typhoon group (41.5 m/s < < 50.9 m/s), and super typhoon group (> 51.0 m/s). TC samples were also divided into four groups according to the angle difference (), between the storm motion direction,, and wind shear direction, . For the downshear (DSHR) group, wind shear and storm motion directions were equal; the angle difference was || ≤ . For the upshear (USHR) group, the wind shear and storm motion were in the opposite directions; to be specific, the angle difference was || ≥ . When the wind shear was on the right side of the storm motion direction (RSHR) or to the left side of the storm motion direction (LSHR), they were categorized as < < and − < < , respectively.
Several different coordinate systems were used to evaluate the wind asymmetry. These coordinate systems include (1) earth-relative coordinates, in which cardinal directions are designated as North, East, South, and West; (2) motion-relative coordinates, in which cardinal directions are defined as to the front of the storm motion, to the right side of the storm motion, to the rear of the storm motion, and to the left side of the storm motion; and (3) wind shear-relative coordinates, in which the cardinal directions are defined as ‘upshear’, ‘downshear’, left side of shear, and right side of shear.
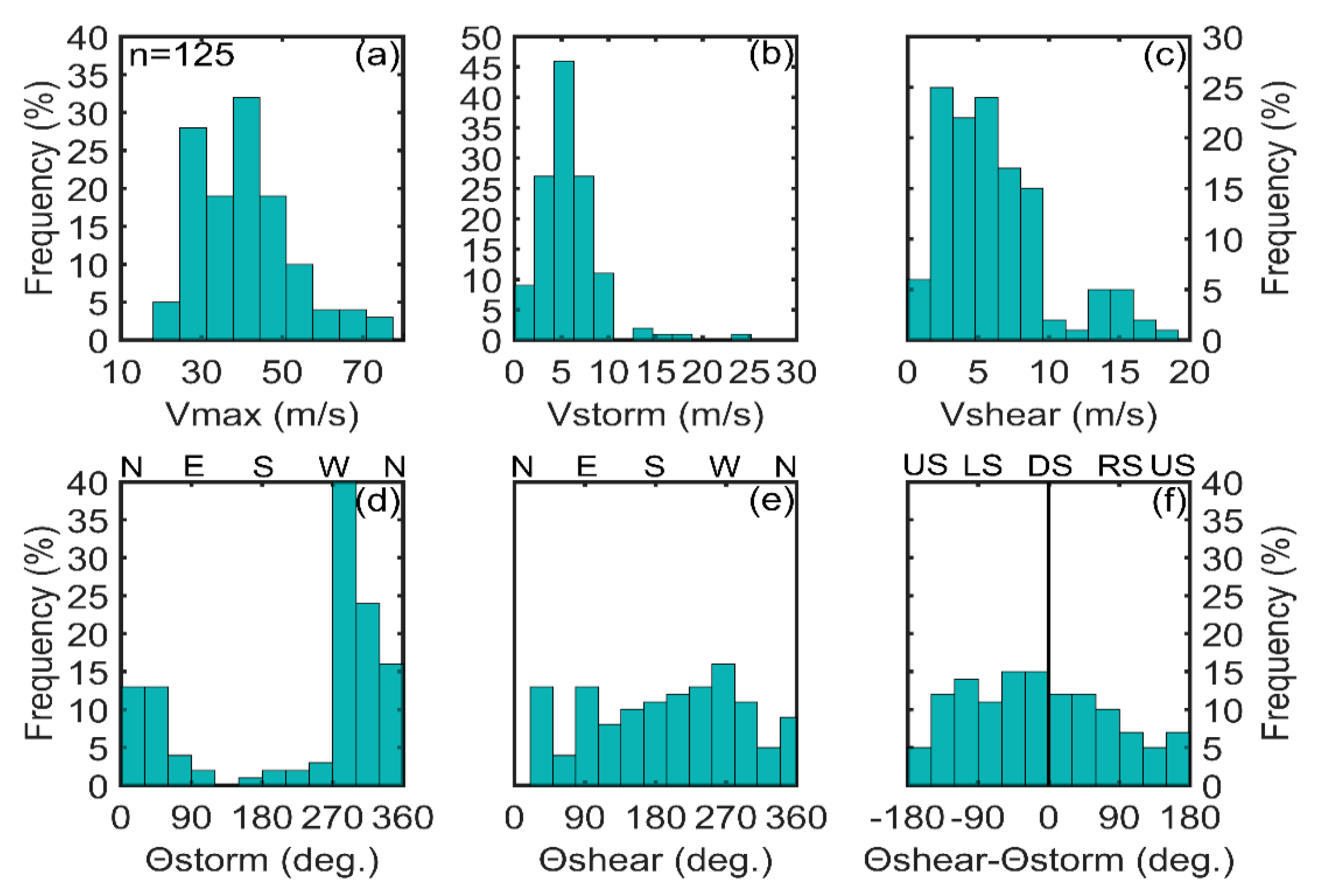
The frequency distributions of some key parameters for the TC samples are shown in
Figure 2. TC intensity (
) was directly derived from the SMAP wind observations.
Figure 2a shows that the TC samples used in this study cover a wide range of TC intensities, from ~20 to 75 m/s. The average TC translation speed (
) and direction (
) over all samples are 5.8 m/s and 231°, respectively. The average environmental vertical wind shear magnitude (
) and direction (
) of the TC samples are 6.15 m/s and 196°, respectively. The range of the angle differences between the wind shear directions and storm motion directions (
) is shown in
Figure 2f.
5. Discussion
Previous studies have shown that both storm motion and environmental vertical wind shear are the primary factors that account for TC surface wind asymmetries [
15,
16,
19,
21,
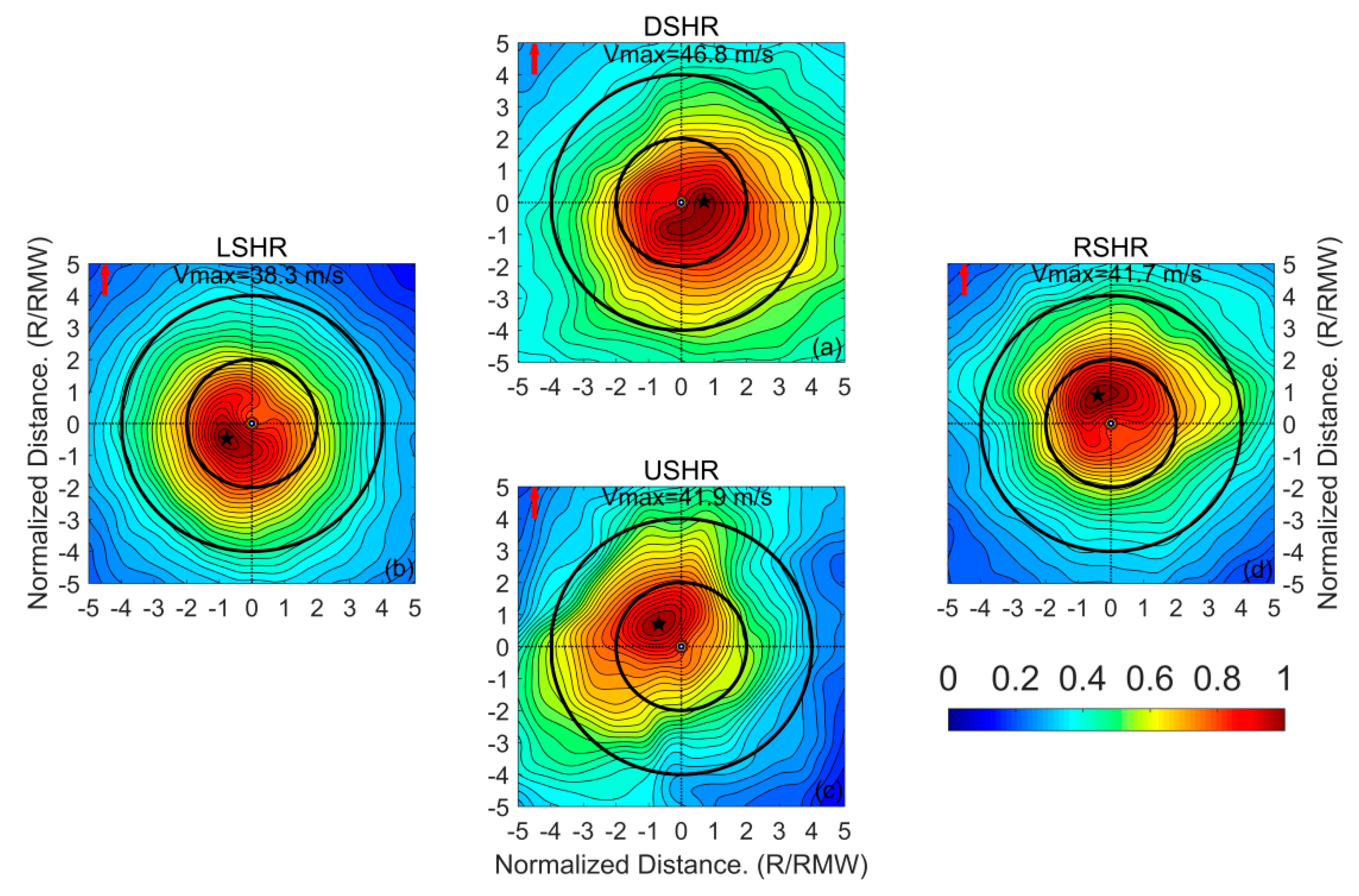
22]. However, it is still not clear which factor has greater influence on the TC asymmetries. In this study, the relationships among TC surface wind asymmetry, storm motion, and vertical wind shear were further explored using SMAP-measured winds. An analysis of composite wind fields of the intensities for tropical storm and typhoon groups show that the location of the maximum wind speed approximately occurs on the left side of the wind shear (
Figure 5a,b), which further corroborates the previous results reported in [
21,
22]. Note that the average maximum wind speeds of the composite wind fields from the SMAP wind data were significantly larger than those derived from scatterometer winds [
21,
22], as shown in
Figure 5c,d, especially for severe typhoons and super typhoons. Moreover, for these two categories, the positions of the maximum wind speed were found to be closer to left of ‘
downshear’ and ‘
upshear’, which are different from those shown in
Figure 5a,b in this study,
Figure 4 in [
21], and
Figure 5 in [
22]. TC structures tend to be more symmetrical for the range from the center to about 4 × RMW, with increasing storm intensity, especially for super typhoons, whether in shear-relative or in motion-relative coordinate frameworks.
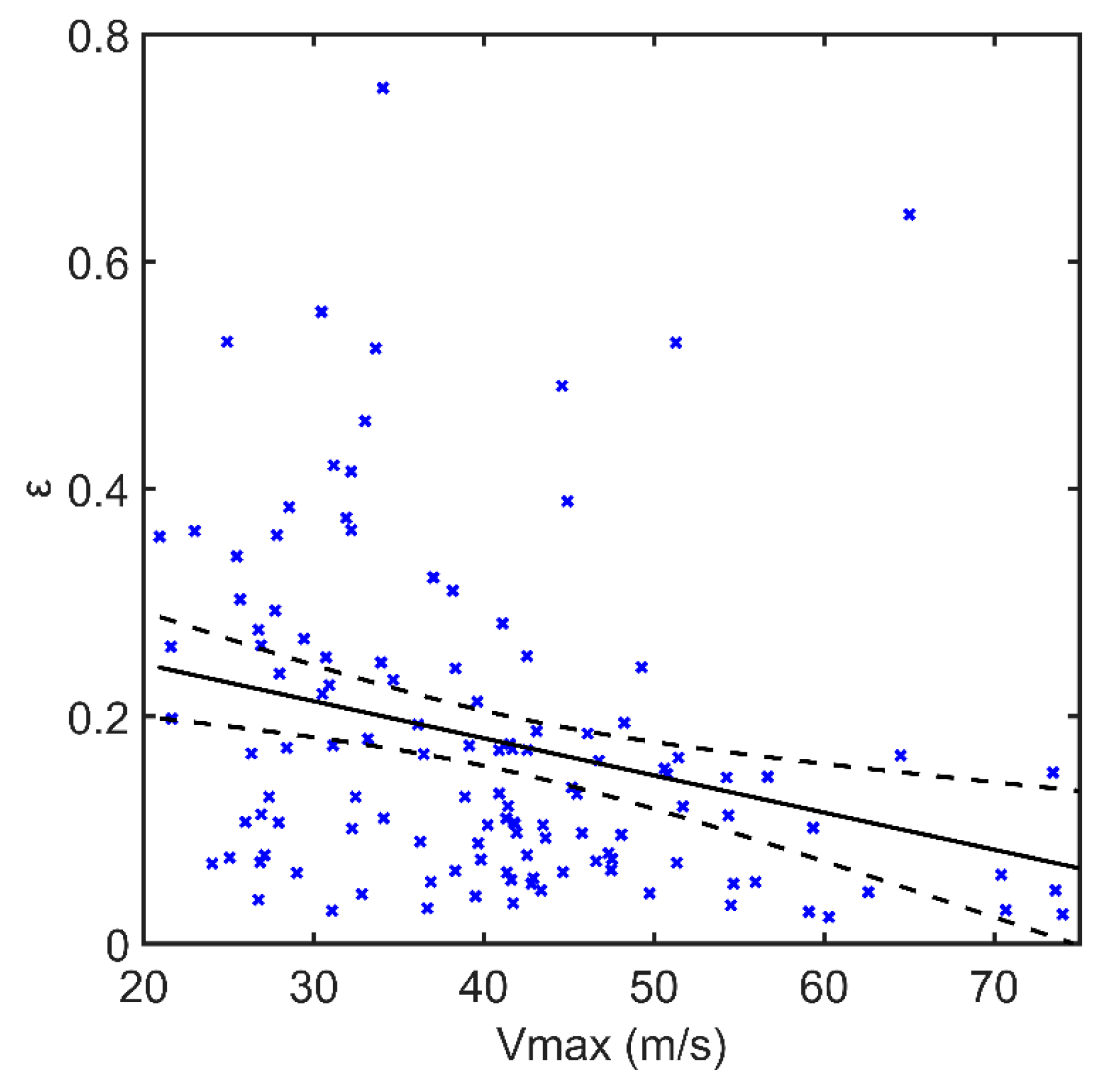
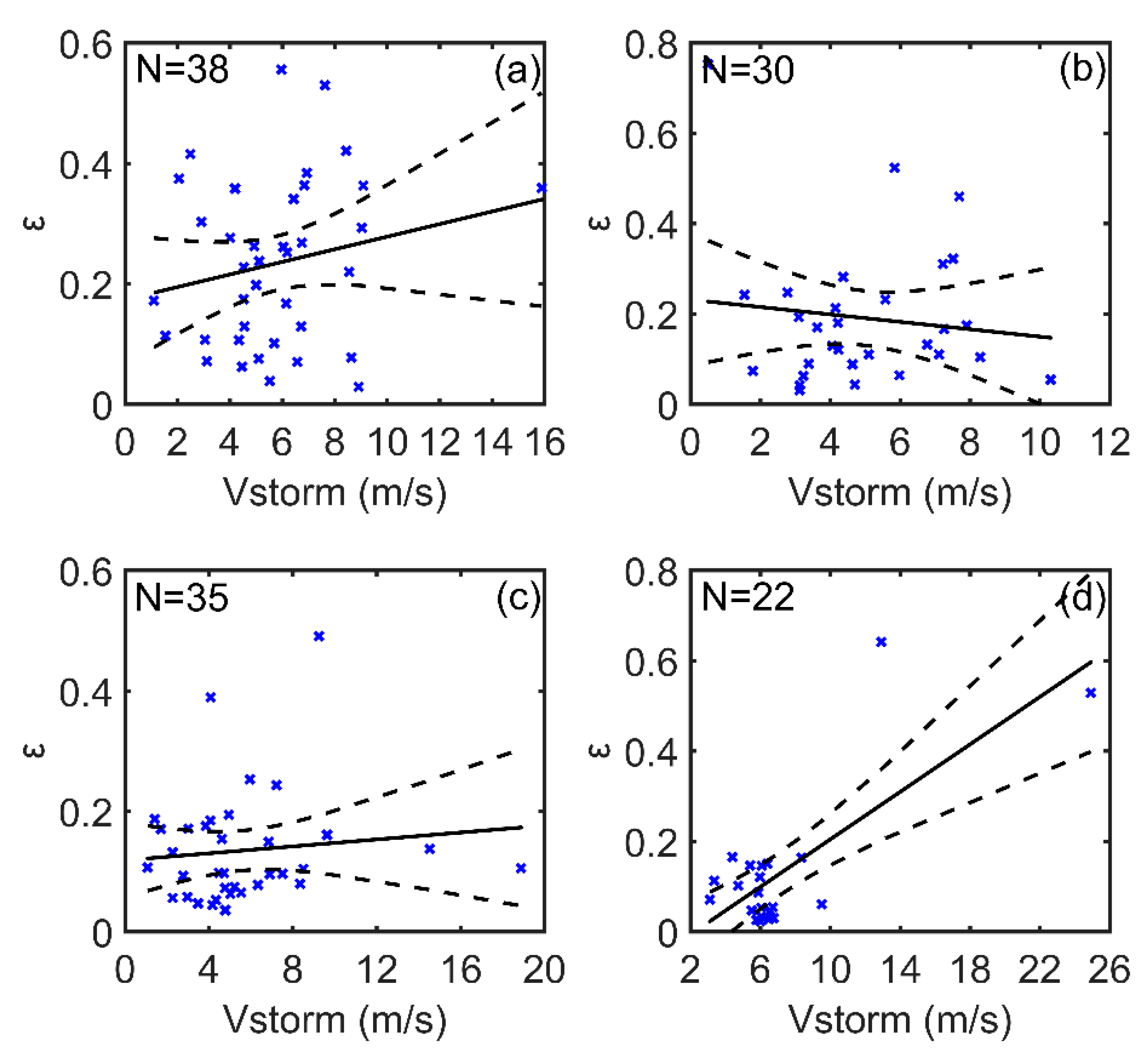
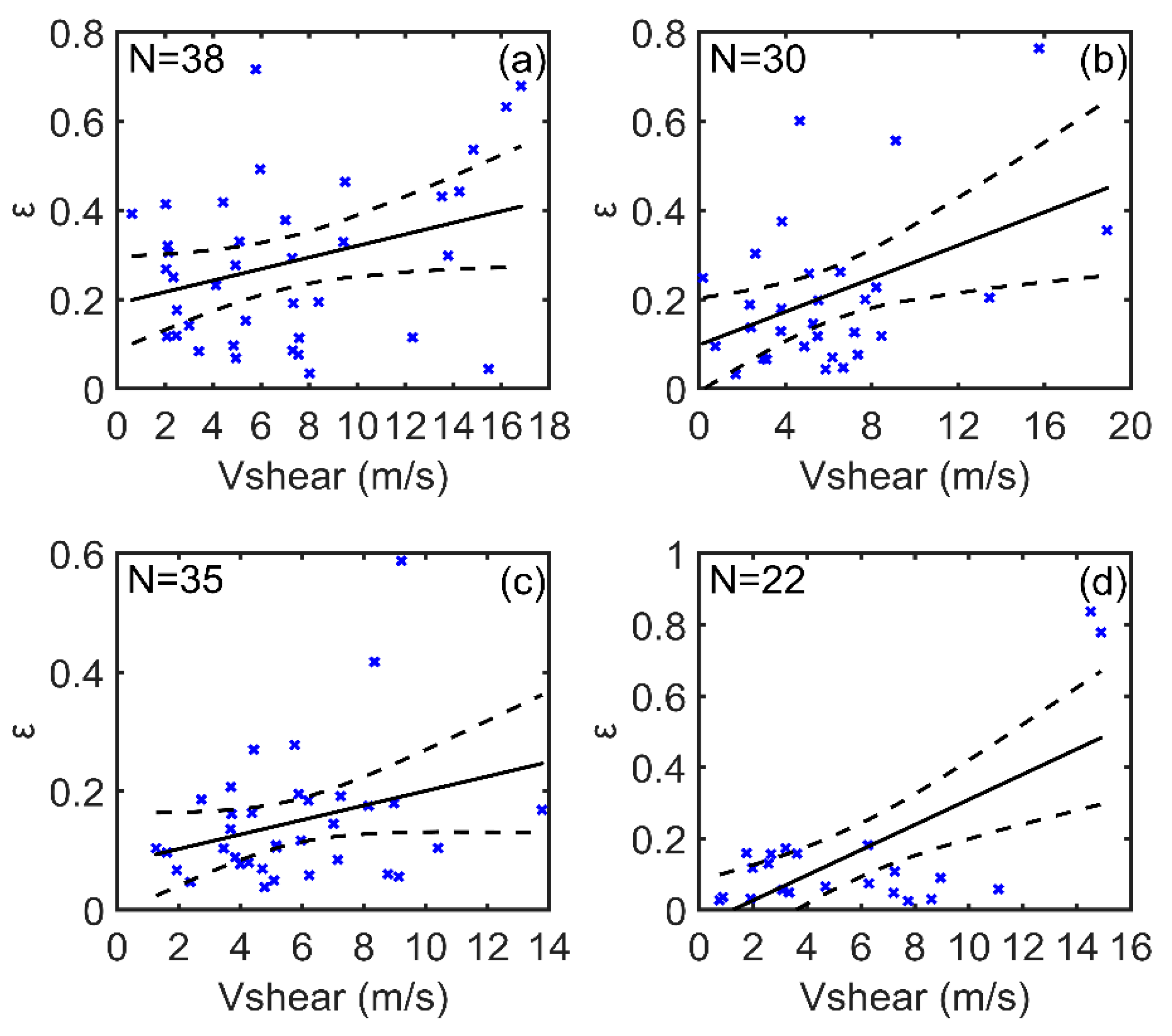
The dependence of TC asymmetries on storm motion and environmental vertical wind shear is probably based on the estimated asymmetric parameter. It was shown that the asymmetry parameter increases with increasing TC translation speed and vertical wind shear magnitude for the tropical storm and super typhoon categories (
Figure 7a,d and
Figure 8a,d); however, this tendency was not given by [
16]. The influence of the angle difference between the storm motion and vertical wind shear on TC asymmetries was also examined by using the composite wind field analysis. The maximum wind speed position rotates on the basis of the angle difference between the storm motion and the wind shear; however, the order of rotation is different from previous studies [
16,
22]. This difference may be due to the different TC intensity ranges between our study and other studies [
16,
22], because [
16] only included hurricane-strength TCs, and in [
22], the maximum wind speeds of TC samples were not as large as those in our study.
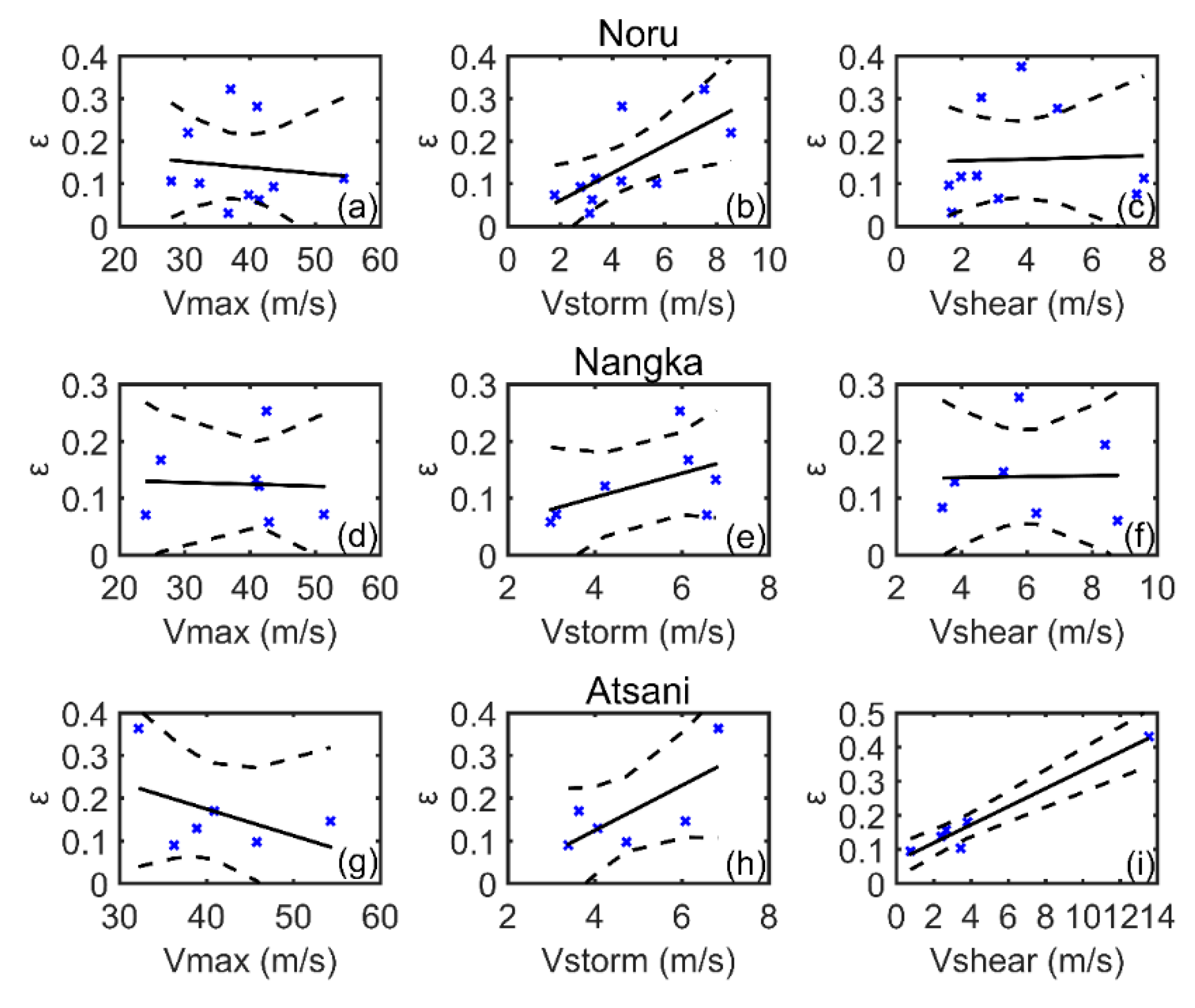
In order to further study the relationship between TC asymmetries and intensity, storm motion, and environmental vertical wind shear, SMAP multi-temporal wind observations of three typical typhoons (Atsani, Nangka, and Noru) were selected from 125 samples to conduct individual case study analyses.
Figure 14 shows the asymmetry parameter versus intensity, translation speed, and environmental vertical wind shear magnitude for each typhoon. As shown in
Figure 14b,e,h, as the translation speed increases, the asymmetry parameter has an obvious increasing tendency for all three typhoons. However, an exception is typhoon Atsani, where the intensity increases, but the asymmetry parameter shows a significant decreasing trend. Additionally, for this case, the asymmetry parameter also increases with the wind shear magnitude, whereas no similar features are found for typhoons Noru and Nangka. The explanation may be that the range of magnitudes for wind shear for these two typhoons (~1.7–7.6 m/s for Noru and ~3.4–8.8 m/s for Nangka) is significantly smaller than that of Atsani (~0.8–13.5 m/s).
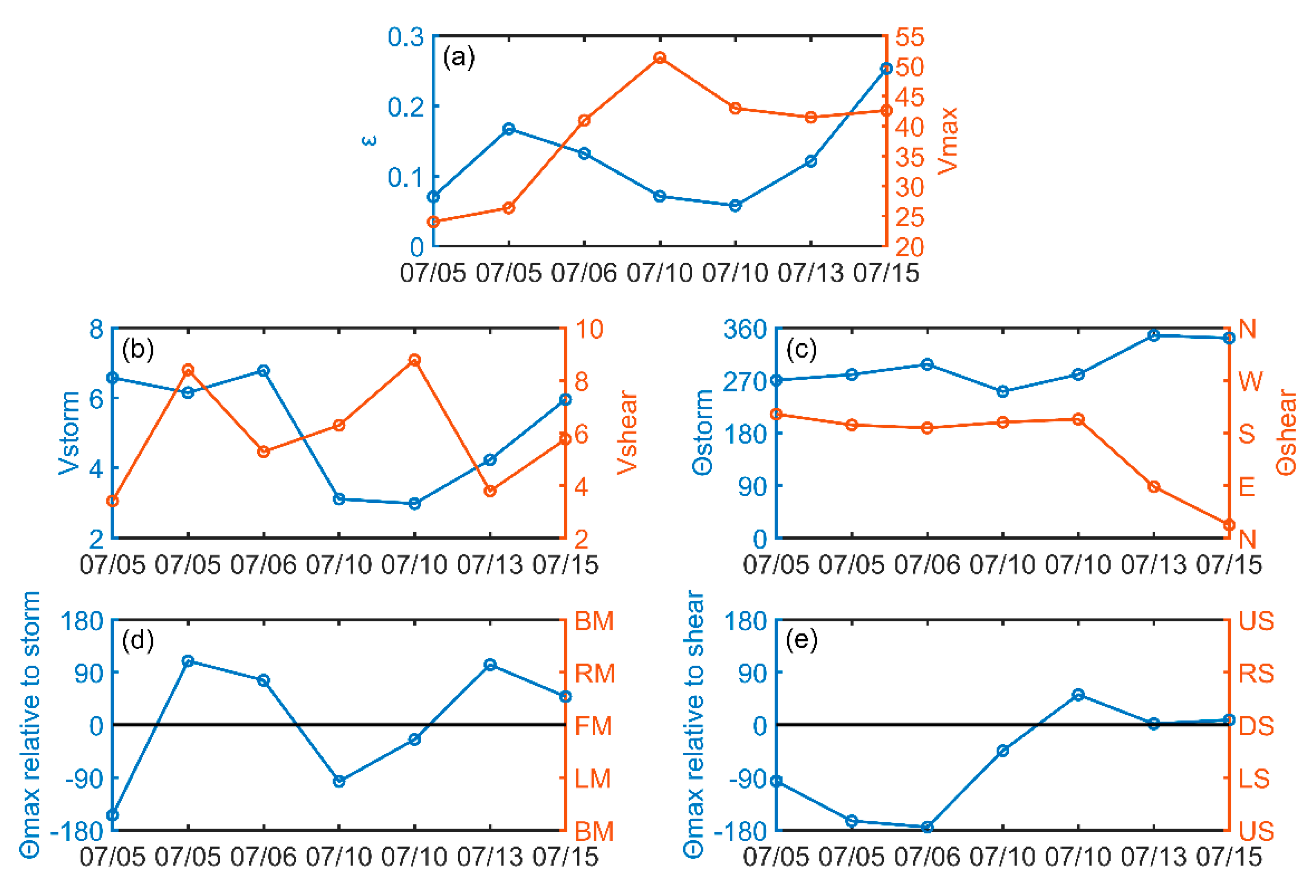
A time series analysis of key parameters of typhoon Nangka was carried out to further investigate the variations of TC surface wind structure. The results are shown in
Figure 15. In the early stage of development (5 July), Nangka was classified as a tropical storm (~24 m/s). It moved westward with a relatively fast translation speed (~6–7 m/s) and a small vertical wind shear (~3.4 m/s); its structure appears to be asymmetric. On 6 July, Nangka was upgraded to a typhoon with a maximum wind speed of about 40.8 m/s. The structure of the surface wind field gradually became symmetrical. On 10 July, Nangka reached the super typhoon level (~51.3 m/s). Subsequently, Nangka began to slowly weaken due to its large vertical wind shear (~8.8 m/s) and the eye became cloud filled. In the evening of 12 July, Nangka commenced to have eyewall replacement and its intensity continued to weaken. As a result, the asymmetric structure again emerged for typhoon Nangka. On 13 July, Nangka started to move northward with a slow translation speed (~4 m/s). Thereafter, the eyewall replacement was completed and Nangka underwent re-intensification between 13 and 15 July.
In general, the largest wind speeds are found in the eyewall on the right side of the typhoons in the northern hemisphere. The typhoon’s motion (forward speed) contributes to the counterclockwise wind speed. In our study, and also in previous investigations [
16,
19,
21,
22], the maximum wind speeds are found to occur mainly on the left side of the wind shear. However, it is difficult to interpret this phenomenon based only on statistical analysis. Based on SMAP wind observations on five different days of typhoon Nangka’s lifecycle, the positions of the maximum wind speed were found to occur four times on the right side of the storm motion (
Figure 15d). Three of these four occurrences corroborate our conclusion that the relative strength between the storm translation speed and the wind shear magnitude affects the position of the maximum wind speed. Namely, the position of the maximum wind speed mostly appears on the right side of the storm motion when the storm translation speed is larger than the magnitude of the wind shear. In the first observation on 10 July, the maximum wind speed position is located on the left side of the storm motion and the wind shear (
Figure 15d,e) because the translation speed (~3 m/s) is relatively smaller than the magnitude of the vertical wind shear (~6.3 m/s). In addition, the TC motion direction and the direction of the wind shear are similar (
Figure 15c), which is in accordance with the conclusion in [
15] that the position of the maximum wind speed occurs on the left side of the storm motion when the angle difference between the storm motion and wind shear is small.
The angle difference between the direction of the storm motion and the direction of the wind shear, and relative strength between the storm translation speed and the wind shear magnitude both have an important influence on the position of the maximum wind speed. The existing TC parametric models [
4,
27,
28] only take into account the impact of the storm motion on the structure of wind field while ignoring the effect of the environmental vertical wind shear. Studies have shown that significant wave heights simulated by numerical ocean wave models using asymmetric wind fields are closer to buoy measurements than those resulting from symmetric wind fields [
29]. Therefore, it is necessary to refine parametric wind field models by incorporating the effect of wind shear on TC asymmetries, thereby providing the potential to improve the accuracy of TC simulations, storm warnings, and risk assessments.
In this study, we used spaceborne radiometer wind data to investigate the effect of storm motion and wind shear on TC wind asymmetry, and moreover, we suggest that the relative strength between the storm translation speed and the wind shear magnitude can affect the location of the maximum wind speed. Compared to spaceborne Ku-band scatterometer winds, L-band SMAP radiometer winds have the advantage that for investigation of TC wind field asymmetry, the radiometer-measured brightness temperatures are largely unaffected by rain and have excellent sensitivity to wind speed when winds are very high. However, due to its coarse resolution, SMAP winds are limited in their ability and cannot accurately resolve the detailed structure of TC storms, such as accurate RMW, or provide reliable radial profiles.
6. Conclusions
The effects of the storm motion and the environmental vertical wind shear on surface wind asymmetry in TCs were investigated by using SMAP observations in the Northwest Pacific Ocean from 2015 to 2017. The great advantage of the SMAP data is that it can provide accurate TC wind speed measurements up to 70 m/s, thereby allowing studies of the wind asymmetry in TCs with a large range in intensity. The asymmetry parameter was estimated by the ratio of the difference between the maximum wind speed and the azimuthal average of the wind speed, relative to the azimuthal average wind speed at the location of the RMW. The results showed that this asymmetry parameter significantly decreases as the TC intensity increases. The results also showed that the degree of surface wind asymmetry increases significantly with increasing TC translation speed for tropical storms and super typhoons; whereas it has little dependence on the storm motion for typhoons and severe typhoons. However, the asymmetry parameter increases with increasing magnitude of the wind shear for all TC intensity groups.
Moreover, the wind maximum tended to occur to the left side of the wind shear direction and to the right side of the storm motion direction in all TC intensity groups. The relative strength between the storm translation speed and the wind shear magnitude also has the potential to affect the location of the maximum wind speed. The position of the maximum wind speed mostly appears to the right side of the storm motion when the storm translation speed is larger than the magnitude of the wind shear. On the contrary, when the storm translation speed is smaller than the wind shear magnitude, the maximum wind speed mostly occurs to the left side of the wind shear direction. The composite analyses show that the wind maximum rotates, in storms where the wind shear is on the left side of the storm motion direction (LSHR), to those in the upshear (USHR) group, to those where wind shear is on the right side of the storm motion direction (RSHR), and to those in the downshear (DSHR) group. A maximum asymmetry exists when the direction of the TC motion is nearly equal to the direction of the wind shear, whereas a minimum asymmetry is found when the directions of motion and wind shear are opposite to each other.