A Decentralized Processing Schema for Efficient and Robust Real-time Multi-GNSS Satellite Clock Estimation
Abstract
1. Introduction
2. Multi-GNSS (Global Navigation Satellite Systems) Clock Estimation
2.1. Undifferenced Observation Model
2.2. Epoch-Differenced Model
2.3. Clock Combination
2.4. Parameter Estimation Methodology
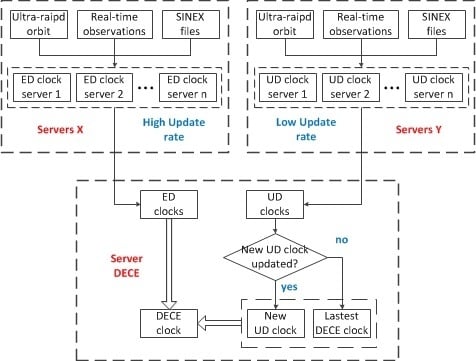
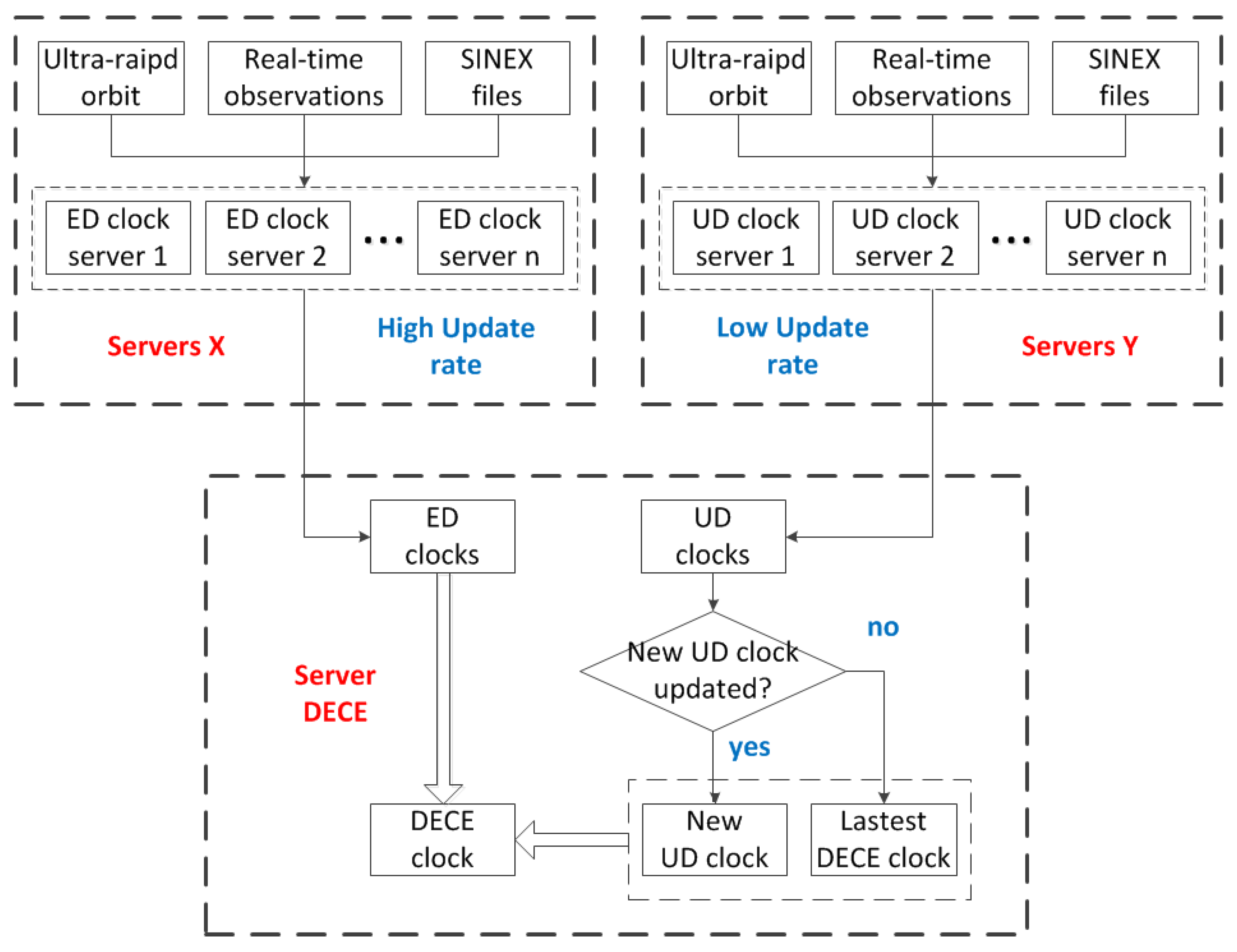
3. Decentralized Clock Estimation (DECE)
4. Real-Time Experimental Evaluation
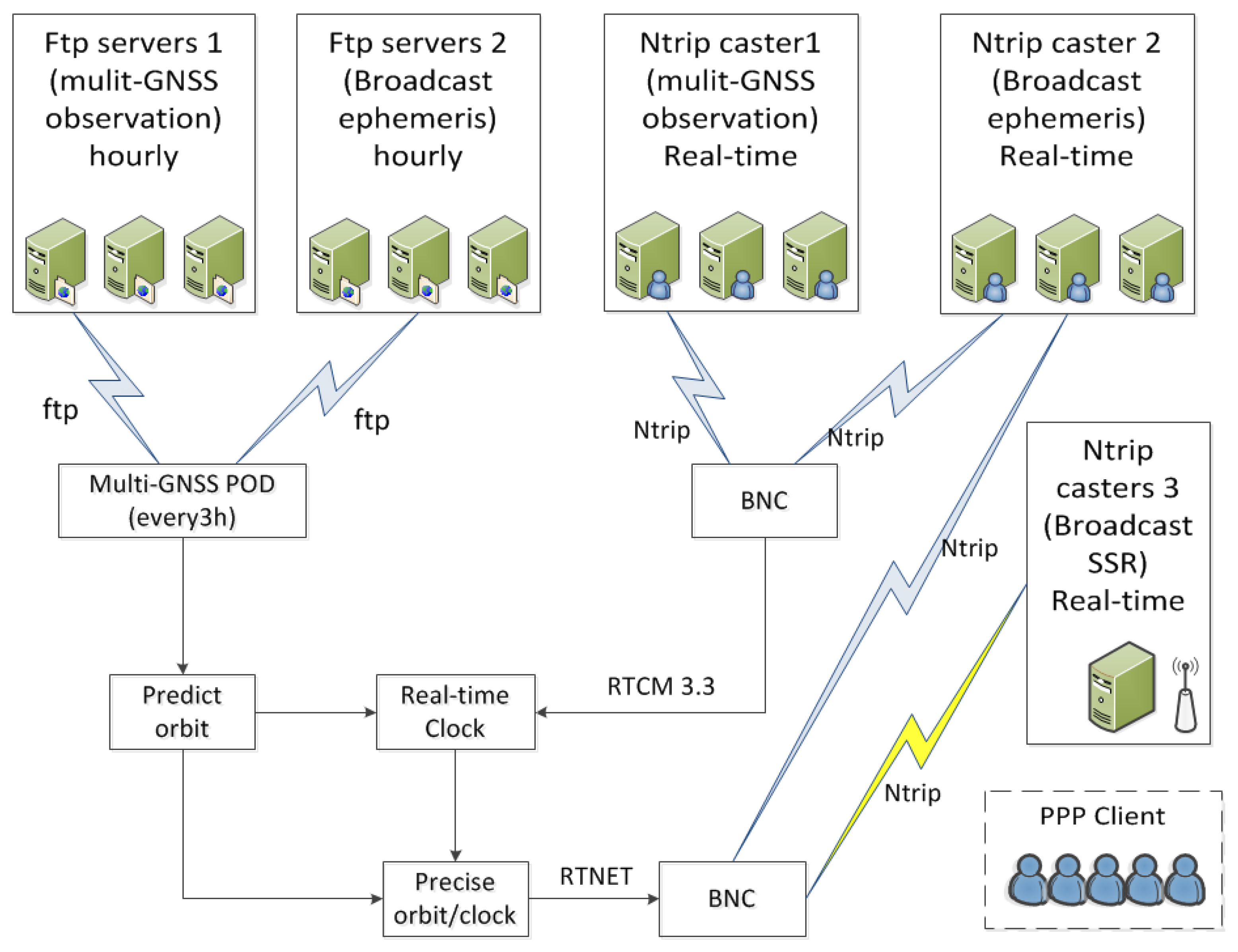
4.1. Data Processing System
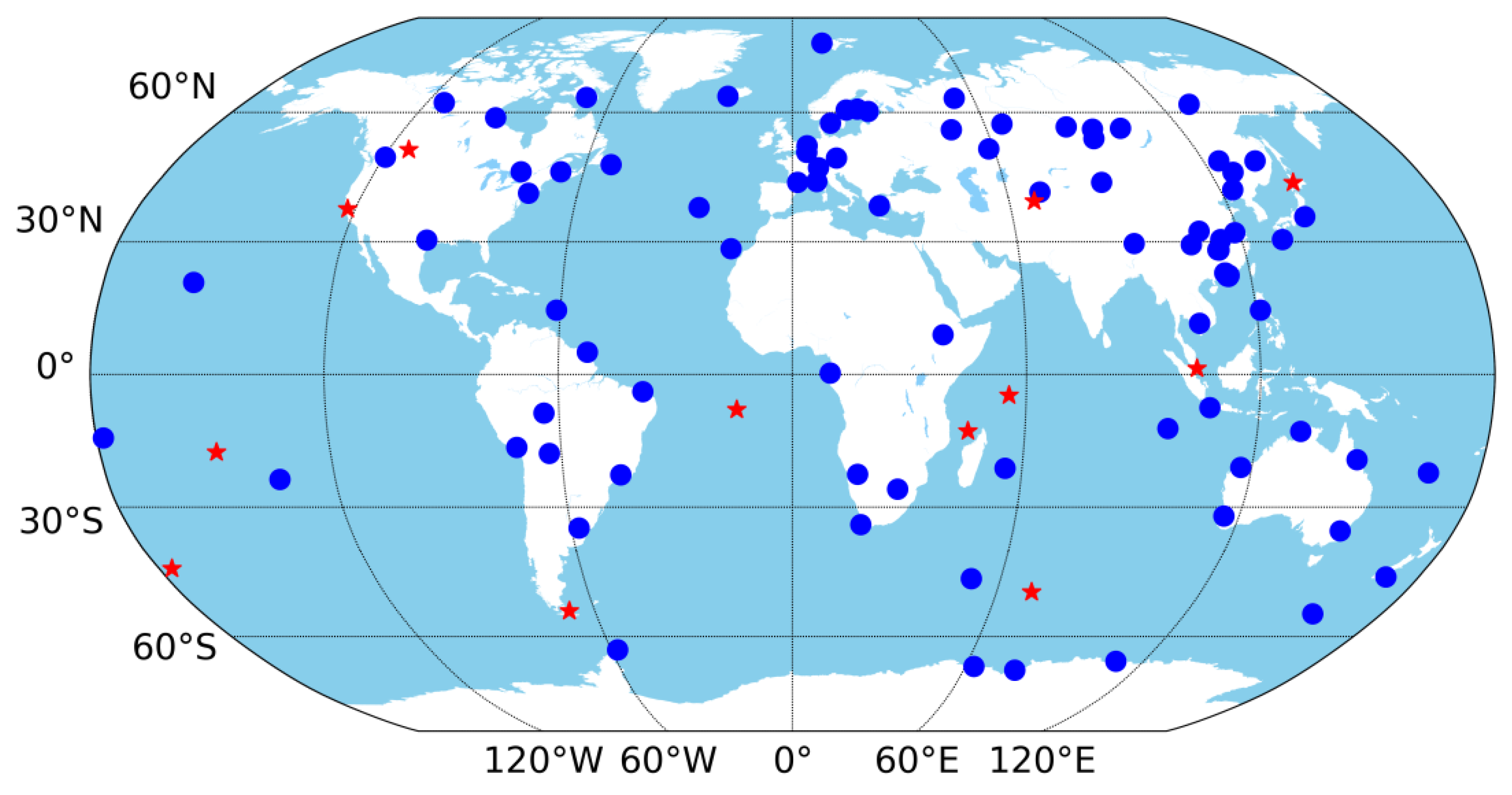
4.2. Data and Network
4.3. Processing Parameters
5. Results
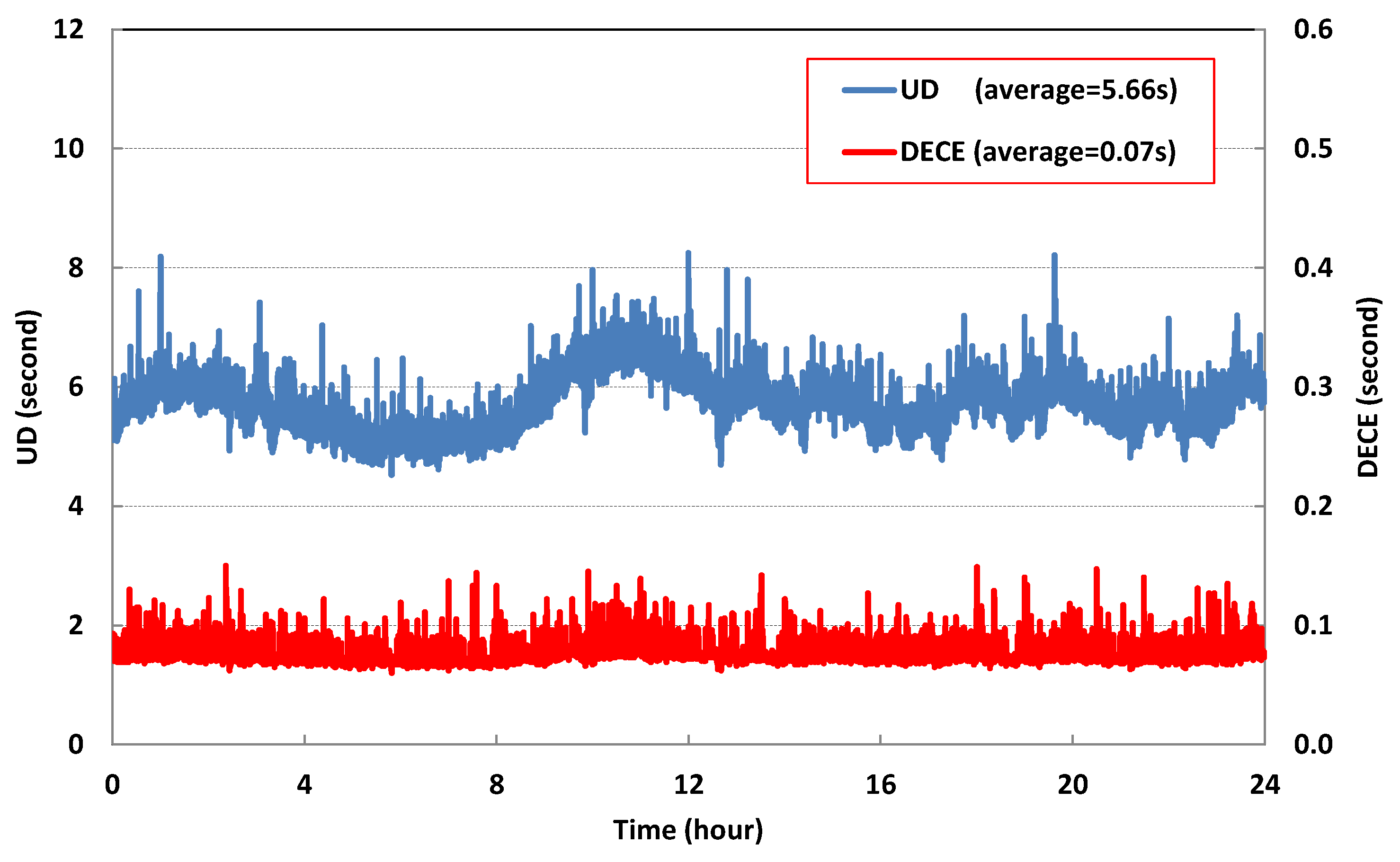
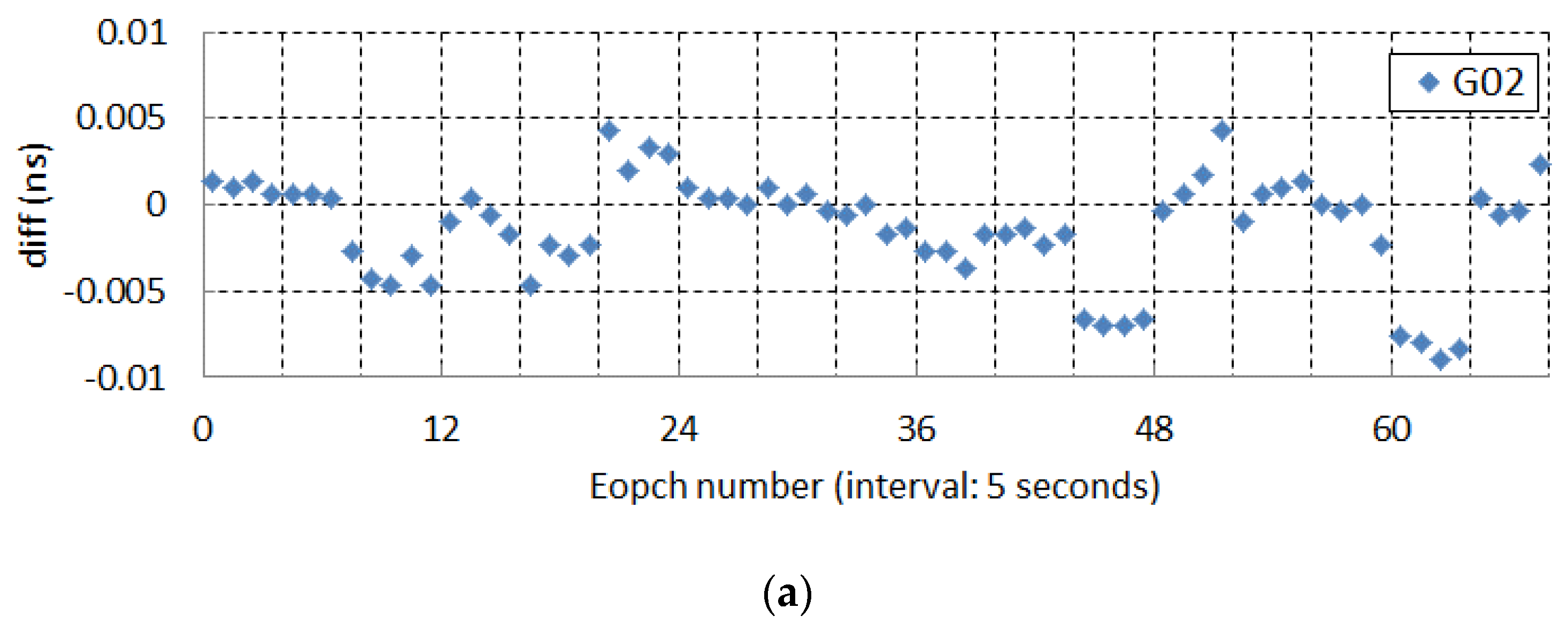
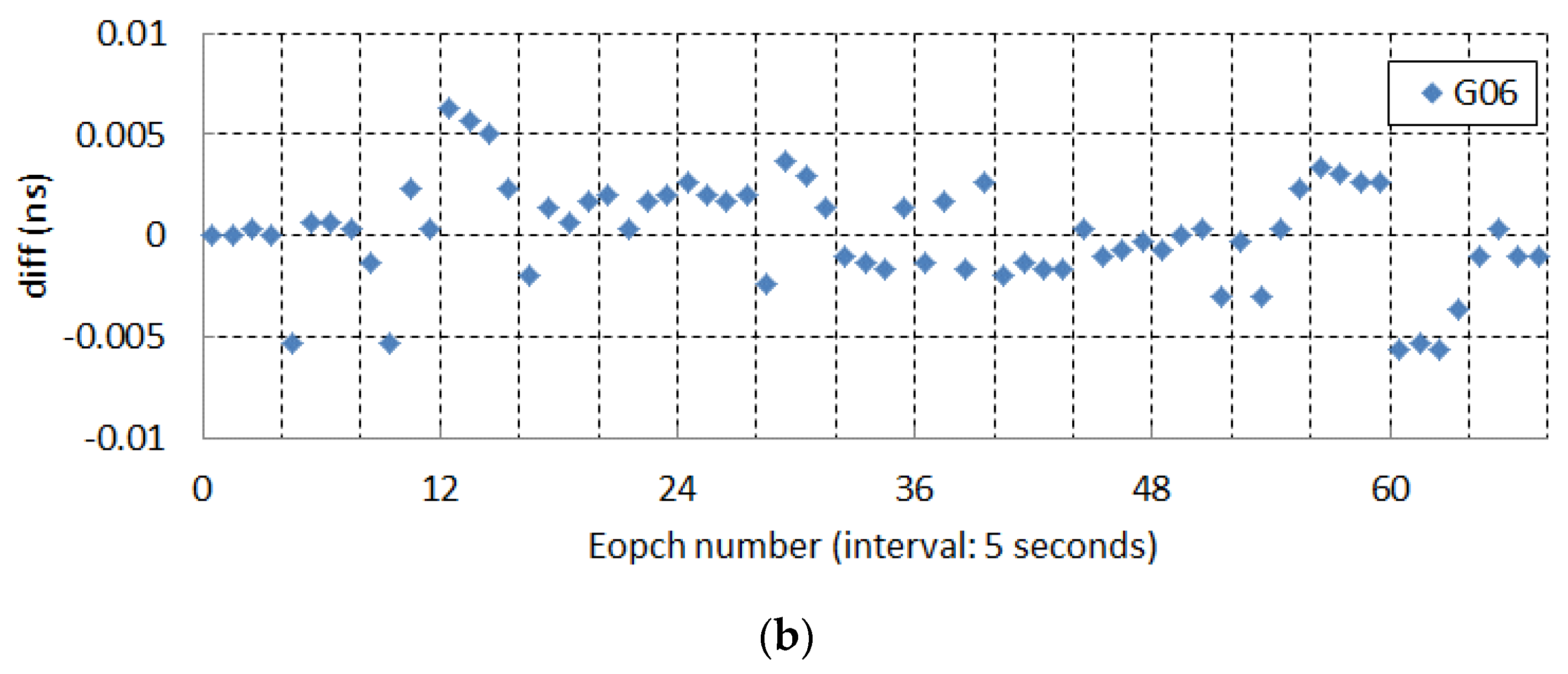
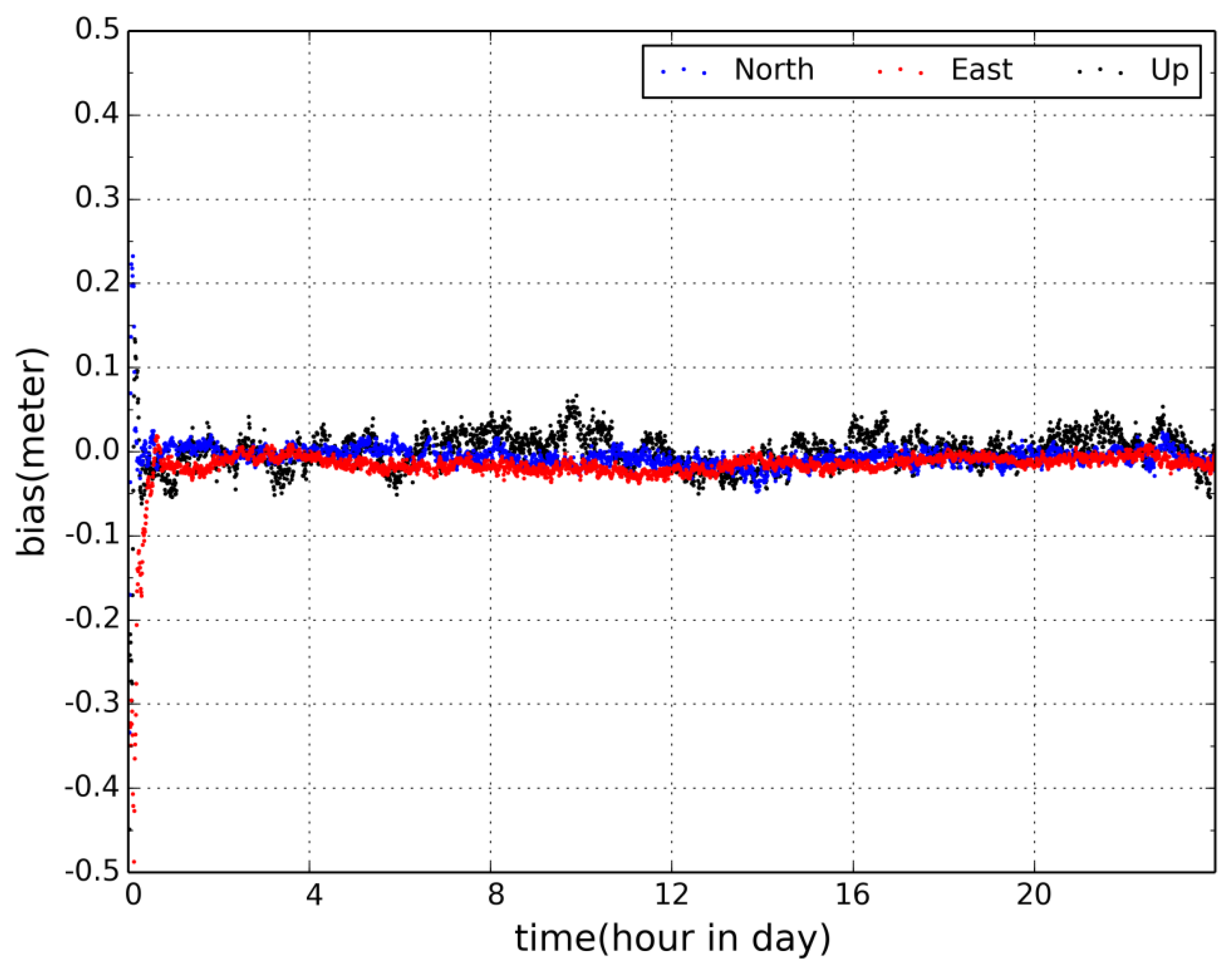
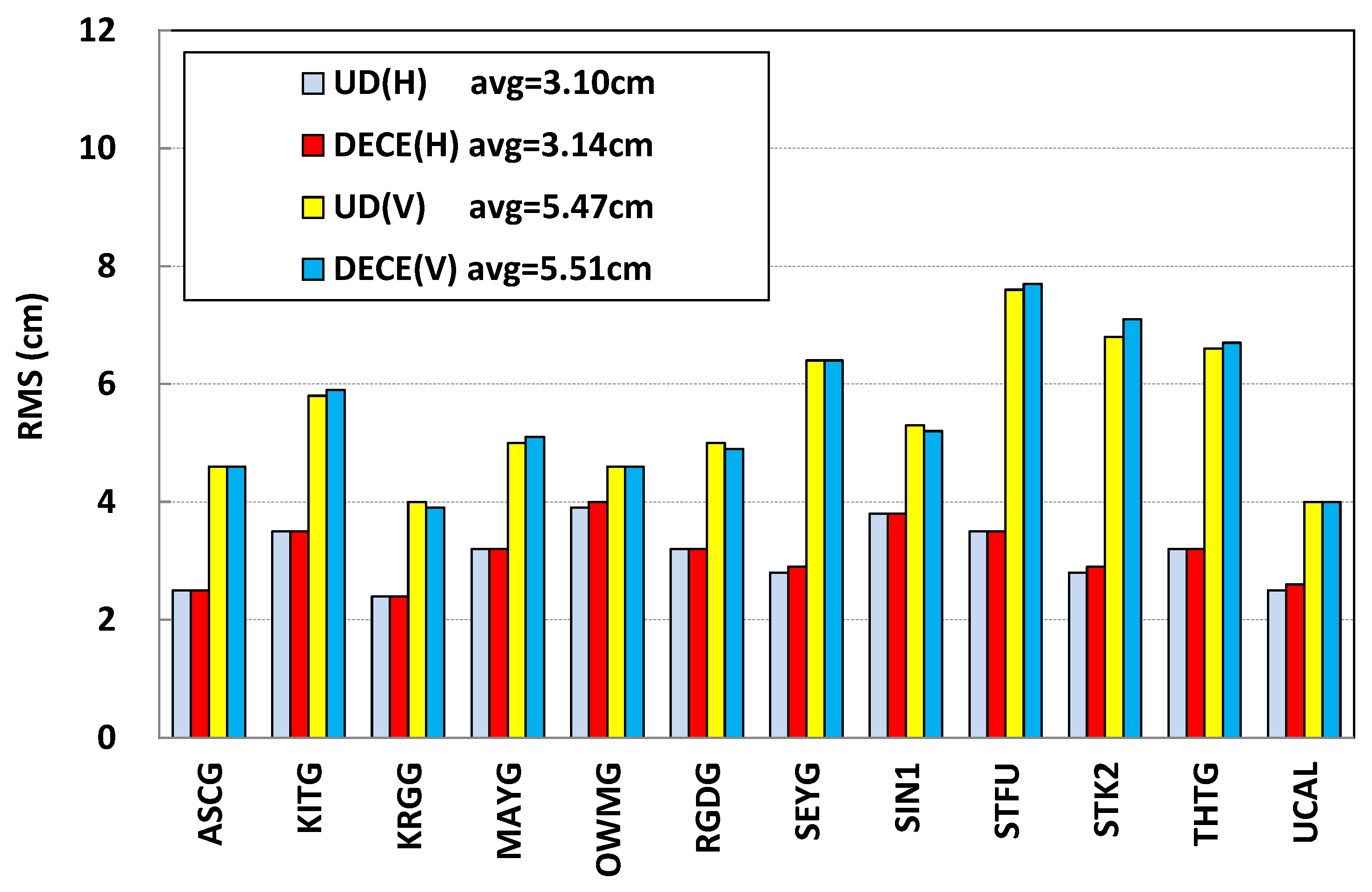
5.1. Decentralized Clock Estimation (DECE) Compared to Undifferenced (UD)
5.2. Decentralized Clock Estimation (DECE) Compared to Post-Processing Products
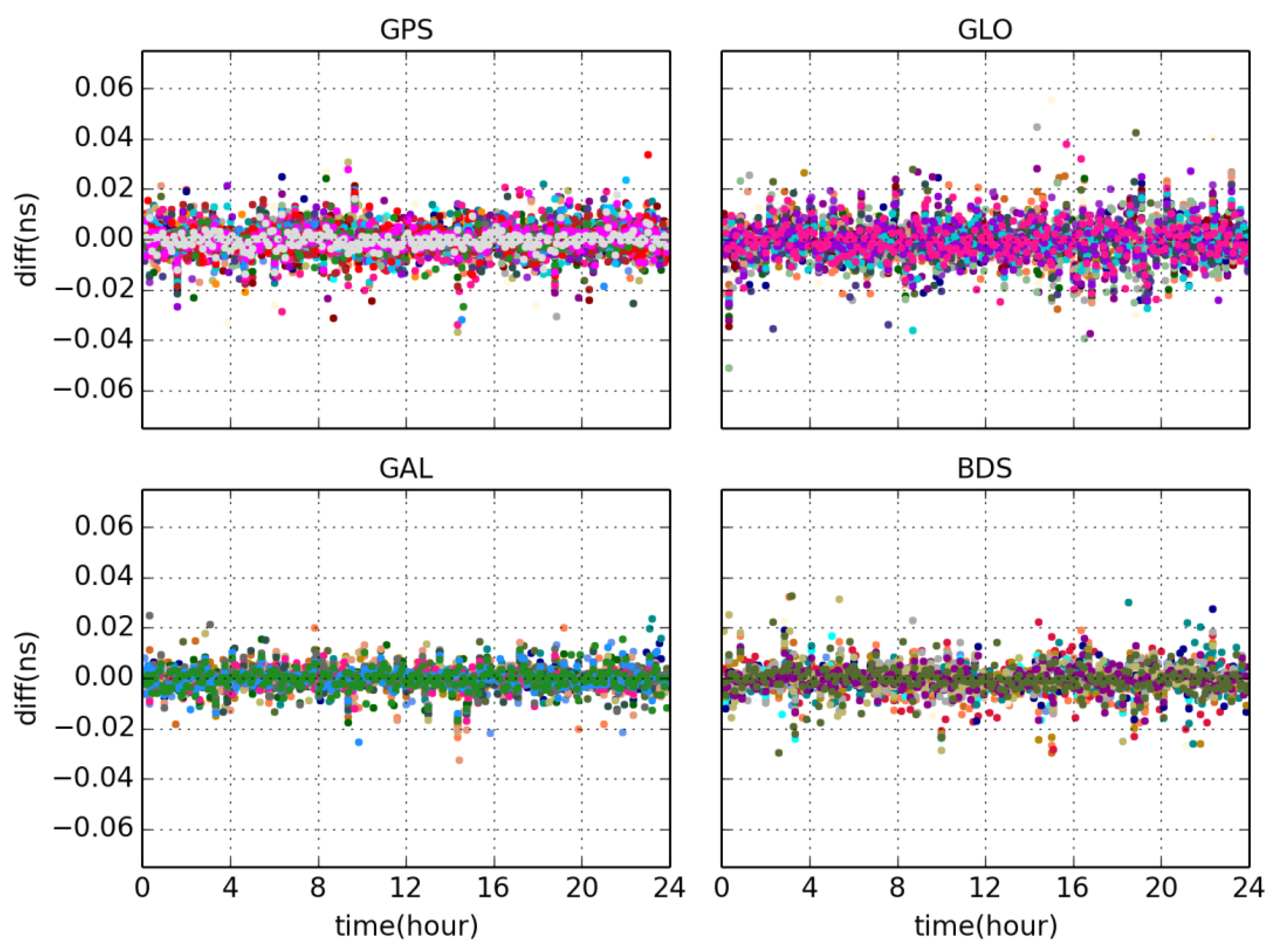
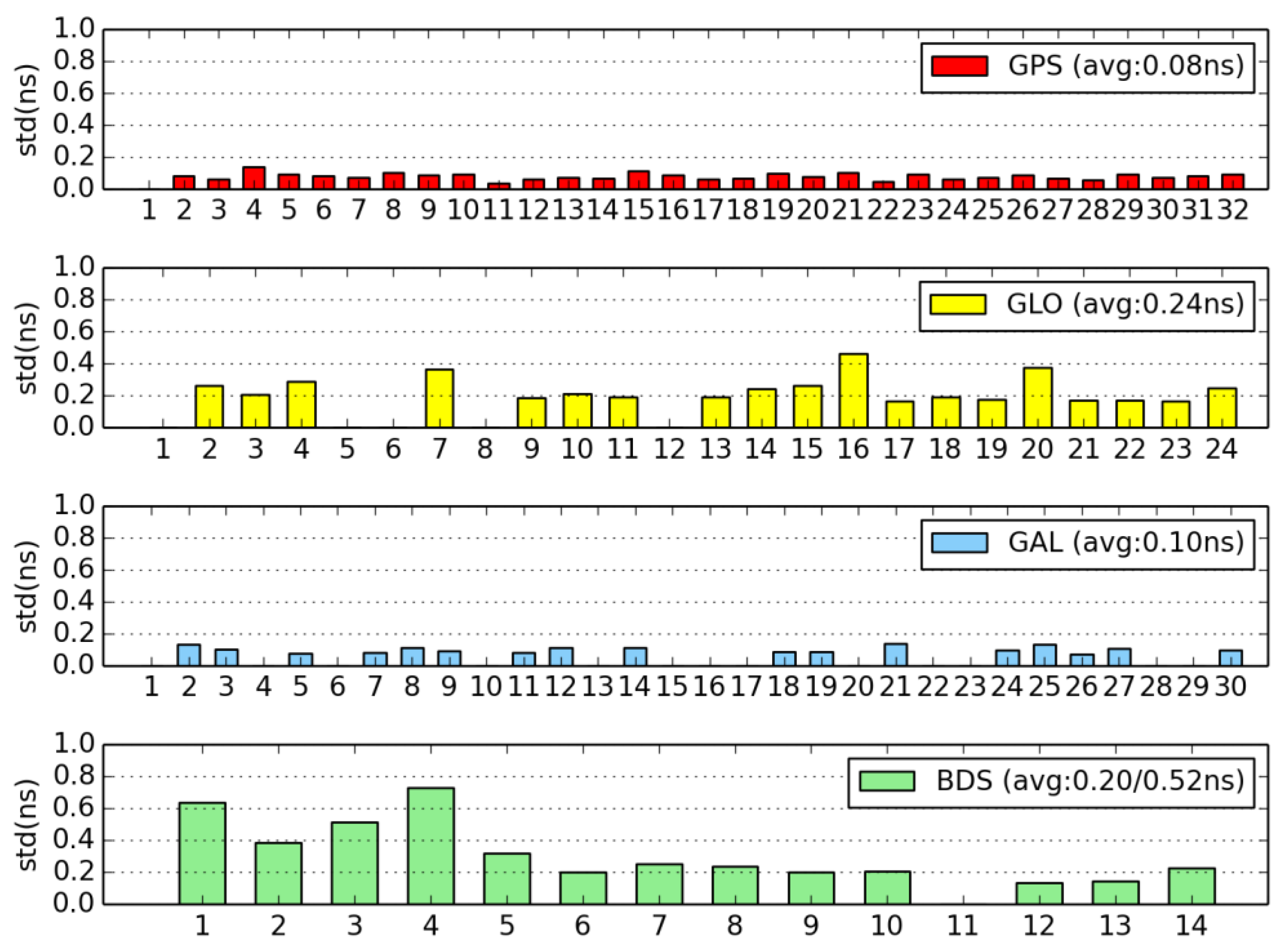
5.2.1. Clock Difference
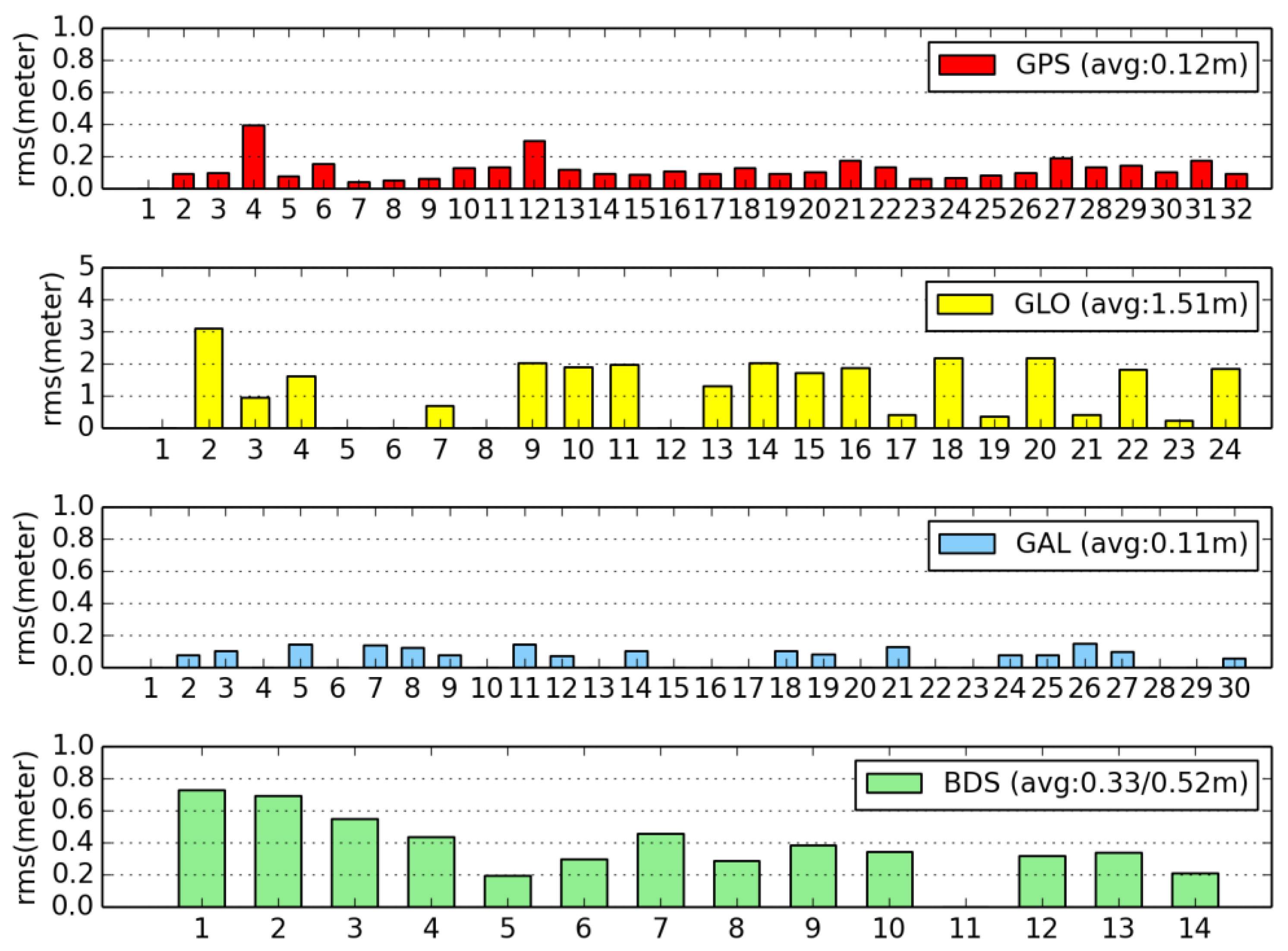
5.2.2. Signal-in-Space Ranging Error (SISRE)
5.3. Precise Point Positioning (PPP) Validation
6. Discussion
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Malys, S.; Jensen, P.A. Geodetic point positioning with GPS carrier beat phase data from the CASA UNO experiment. Geophys. Res. Lett. 1990, 17, 651–654. [Google Scholar] [CrossRef]
- Zumberge, J.F.; Heflin, M.B.; Jefferson, D.C.; Watkins, M.M.; Webb, F.H. Precise point positioning for the efficient and robust analysis of GPS data from large networks. J. Geophys. Res. 1997, 102, 5005–5017. [Google Scholar] [CrossRef]
- Bisnath, S.; Gao, Y. Current state of precise point positioning and future prospects and limitations. In Observing our Changing Earth. International Association of Geodesy Symposia; Sideris, M.G., Ed.; Springer: Berlin/Heidelberg, Germany, 2009; Volume 133. [Google Scholar] [CrossRef]
- Geng, J.; Shi, C.; Ge, M.; Dodson, A.; Lou, Y.; Zhao, Q.; Liu, J. Improving the estimation of fractional-cycle biases for ambiguity resolution in precise point positioning. J. Geodesy 2012, 86, 578–589. [Google Scholar] [CrossRef]
- Ge, M.; Gendt, G.; Rothacher, M.; Shi, C.; Liu, J. Resolution of GPS carrier-phase ambiguities in precise point positioning (PPP) with daily observations. J. Geodesy 2008, 82, 389–399. [Google Scholar] [CrossRef]
- Li, X.; Ge, M.; Dai, X.; Ren, X.; Fritsche, M.; Wickert, J.; Schuh, H. Accuracy and reliability of multi-GNSS real-time precise positioning: GPS, GLONASS, BeiDou, and Galileo. J. Geodesy 2015, 89, 607–635. [Google Scholar] [CrossRef]
- Lou, Y.; Zheng, F.; Gu, S.; Wang, C.; Guo, H.; Feng, Y. Multi-GNSS precise point positioning with raw single-frequency and dual-frequency measurement models. GPS Solut. 2016, 20, 849–862. [Google Scholar] [CrossRef]
- Liu, Y.; Lou, Y.; Ye, S.; Zhang, R.; Song, W.; Zhang, X.; Li, Q. Assessment of PPP integer ambiguity resolution using GPS, GLONASS and BeiDou (IGSO, MEO) constellations. GPS Solut. 2017, 21, 1647–1659. [Google Scholar] [CrossRef]
- Li, X.; Ge, M.; Dousa, J.; Wickert, J. Real-time precise point positioning regional augmentation for large GPS reference networks. GPS Solut. 2014, 18, 61–71. [Google Scholar] [CrossRef]
- Liu, T.; Yuan, Y.; Zhang, B.; Wang, N.; Tan, B.; Chen, Y. Multi-GNSS precise point positioning (MGPPP) using raw observations. J. Geodesy 2017, 91, 253–268. [Google Scholar] [CrossRef]
- RTCM. Radio Technical Commission for Maritime Services (RTCM) Standard 10403.3, Differential GNSS (Global Navigation Satellite Systems) Services; Radio Technical Commission for Maritime Services: Arlington, VA, USA, 2016. [Google Scholar]
- Kouba, J.; Héroux, P. Precise point positioning using IGS orbit and clock products. GPS Solut. 2001, 5, 12–18. [Google Scholar] [CrossRef]
- Griffiths, J.; Ray, J. On the precision and accuracy of IGS orbits. J. Geodesy 2009, 83, 277–278. [Google Scholar] [CrossRef]
- Shi, C.; Guo, S.; Gu, S.; Yang, X.; Gong, X.; Deng, Z.; Ge, M.; Schuh, H. Multi-GNSS satellite clock estimation constrained with oscillator noise model in the existence of data discontinuity. J. Geodesy 2019, 93, 515–528. [Google Scholar] [CrossRef]
- Bock, H.; Dach, R.; Jäggi, A.; Beutler, G. High-rate GPS clock corrections from CODE: Support of 1 Hz applications. J. Geodesy 2009, 83, 1083–1094. [Google Scholar] [CrossRef]
- Zhang, X.; Li, X.; Guo, F. Satellite clock estimation at 1 Hz for realtime kinematic PPP applications. GPS Solut. 2011, 15, 315–324. [Google Scholar] [CrossRef]
- Ge, M.; Chen, J.; Douša, J.; Gendt, G.; Wickert, J. A computationally efficient approach for estimating high-rate satellite clock corrections in realtime. GPS Solut. 2012, 16, 9–17. [Google Scholar] [CrossRef]
- Chen, L.; Zhao, Q.; Hu, Z.; Jiang, X.; Geng, C.; Ge, M.; Shi, C. GNSS global real-time augmentation positioning: Real-time precise satellite clock estimation, prototype system construction and performance analysis. Adv. Space Res. 2017, 61, 367–384. [Google Scholar] [CrossRef]
- Chen, L.; Song, W.; Yi, W.; Shi, C.; Lou, Y.; Guo, H. Research on a method of real-time combination of precise GPS clock corrections. GPS Solut. 2017, 21, 187–195. [Google Scholar] [CrossRef]
- Zhang, W.; Lou, Y.; Gu, S.; Shi, C.; Haase, J.S.; Liu, J. Joint estimation of GPS/BDS real-time clocks and initial results. GPS Solut. 2016, 20, 665–676. [Google Scholar] [CrossRef]
- Gong, X.; Gu, S.; Lou, Y.; Zheng, F.; Ge, M.; Liu, J. An efficient solution of real-time data processing for multi-GNSS network. J. Geodesy 2017, 92, 797–809. [Google Scholar] [CrossRef]
- Laurichesse, D.; Mercier, F.; Berthias, J.P. Real time GPS constellation and clocks estimation using zero-difference integer ambiguity fixing. In Proceedings of the ION ITM 2009, Anaheim, CA, USA, 26–28 January 2009. [Google Scholar]
- Laurichesse, D.; Cerri, L.; Berthias, J.P.; Mercier, F. Real time precise GPS constellation and clocks estimation by means of a Kalman filter. In Proceedings of the ION GNSS 2013, Nashville, TN, USA, 16–20 September 2013. [Google Scholar]
- Mervart, L.; Weber, G. Real-time combination of GNSS orbit and clock correction streams using a Kalman Filter approach. In Proceedings of the ION GNSS 2011, Portland, OR, USA, 20–23 September 2013. [Google Scholar]
- Liu, J.; Ge, M. PANDA Software and its preliminary result of positioning and orbit determination. Wuhan Univ. J. Nat. Sci. 2003, 8, 603–609. [Google Scholar]
- Shi, C.; Zhao, Q.; Geng, J.; Lou, Y.; Ge, M.; Liu, J. Recent development of PANDA software in GNSS data processing. In Proceedings of the SPIE Volume 7285, Wuhan, China, 8–30 December 2008. [Google Scholar]
- Dach, R.; Schaer, S.; Hugentobler, U. Combined multi-system GNSS analysis for time and frequency transfer. In Proceedings of the 20th European Frequency and Time Forum EFTF06, Braunschweig, Germany, 2006. [Google Scholar]
- Bierman, G.J. The treatment of bias in the square-root information filter/smoother. J. Optim. Theory Appl. 1975, 16, 165–178. [Google Scholar] [CrossRef]
- Dai, X.; Lou, Y.; Dai, Z.; Qing, Y.; Li, M.; Shi, C. Real-time precise orbit determination for BDS satellites using the square root information filter. GPS Solut. 2019, 23, 45. [Google Scholar] [CrossRef]
- Ray, J.; Dong, D.; Altamimi, Z. IGS reference frames: Status and future improvements. GPS Solut. 2004, 5, 251–266. [Google Scholar] [CrossRef]
- Rebischung, P.; Altamimi, Z.; Ray, J.; Garayt, B. The IGS contribution to ITRF2014. J. Geodesy 2016, 90, 611–630. [Google Scholar] [CrossRef]
- Stürze, A.; Mervart, L.; Weber, G.; Rülke, A.; Wiesensarter, E.; Neumaier, P. The new version 2.12 of BKG Ntrip Client (BNC). Geophys. Res. Abstr. 2016, 18, 12012. [Google Scholar]
- Gendt, G.; Dick, G.; Reigber, C.H.; Tomassini, M.; Liu, Y.; Ramatschi, M. Demonstration of NRT GPS water vapor monitoring for numerical weather prediction in Germany. J. Meteorol. Soc. Jpn. 2003, 82, 360–370. [Google Scholar]
- Wu, J.; Wu, S.; Hajj, G.; Bertiger, W.; Lichten, S. Effects of antenna orientation on GPS carrier phase. Manuscr. Geodesy 1993, 18, 91–98. [Google Scholar]
- Boehm, J.; Niell, A.; Tregoning, P.; Schuh, H. Global mapping function (GMF): A new empirical mapping function based on numerical weather model data. Geophys. Res. Lett. 2006, 33, L07304. [Google Scholar] [CrossRef]
- Petit, G.; Luzum, B. IERS Conventions 2010; Iers Technical Note 36; Verlag des Bundesamts für Kartographie und Geodäsie: Frankfurt am Main, Germany, 2010; Volume 36, pp. 1–95. [Google Scholar]
- Deng, Z.; Fritsche, M.; Uhlemann, M.; Wickert, J.; Schuh, H. Reprocessing of GFZ Multi-GNSS Product GBM. In Proceedings of the IGS Workshop, Sydney, Australia, 8–12 February 2016; Available online: http://acc.igs.org/workshop2016/presentations/Plenary_01_06.pdf (accessed on 20 February 2016).
- Montenbruck, O.; Steigenberger, P.; Hauschild, A. Broadcast versus precise ephemerides: A multi-GNSS perspective. GPS Solut. 2015, 19, 321–333. [Google Scholar] [CrossRef]
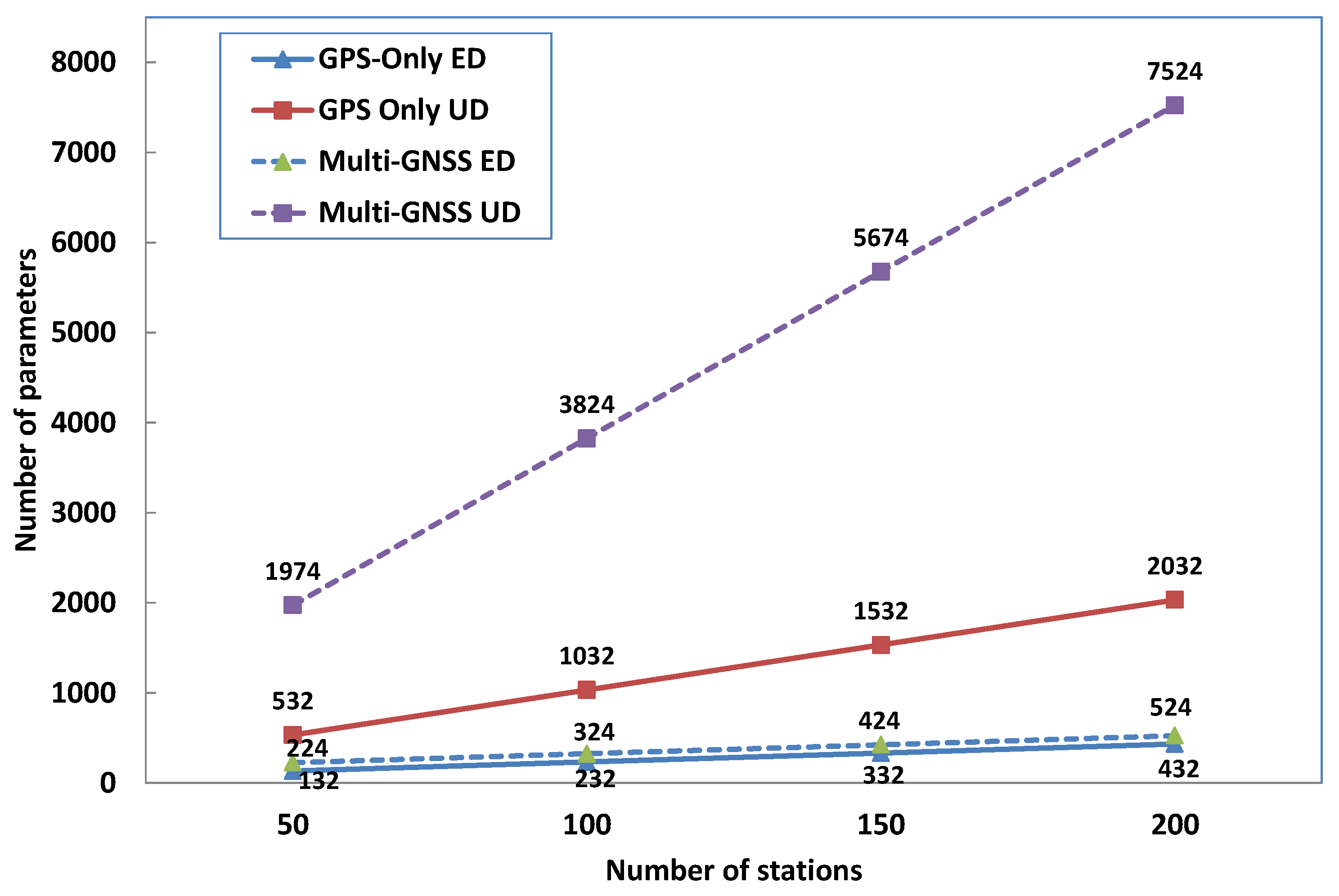
| Item | Parameters Number |
|---|---|
| Receiver clock and Inter-System Bias (ISB) | |
| Satellite clock corrections | |
| Zenith troposphere delay | |
| Undifferenced ambiguity | |
| Total |
| Item | Parameters Number |
|---|---|
| Receiver clocks | |
| Satellite clocks | |
| Zenith troposphere delay | |
| Total |
| Measurement model | |
| Observation | Ionospheric-free combinations of code and phase measurements |
| Sample rate | Undifferenced (UD) 20s/Epoch-differenced (ED) 5s |
| Elevation cutoff angle | 7° |
| Weighting | A priori precision of 0.03 cycles and 3.0 m for raw phase and code, respectively, 1 for E > 30 otherwise 2sin(E) [33] |
| Systematic error | |
| Receiver phase center | igs14.atx(Phase Center Offset (PCO) and Phase Center Variation (PCV) of Galileo and Beidou are corrected as Global Positioning Systems (GPS) |
| Satellite phase center | igs14.atx(PCO and PCV of Galileo and Beidou are corrected as GPS |
| Phase wind up | Corrected [34] |
| Troposphere a priori model | Saastamoinen model for wet and dry hydrostatic delay with Global Mapping Function (GMF) mapping functions without gradient model [35] |
| Solid Earth tides | IERS Conventions 2010 [36] |
| Solid Earth pole tides | IERS Conventions 2010 |
| Ocean tides | IERS Conventions 2010 |
| Relativistic effects | IERS Conventions 2010 |
| Stochastic model | |
| Adjustment method | SRIF |
| Station coordinate | Fixed (from SINEX file or by Position and Navigation Data Analyst (PANDA) GPS-only PPP weekly solutions) |
| Satellite orbit | Fixed (from predicted orbit) |
| Receiver clocks | White noise with a unit weight variance of 9000 m |
| Satellite clocks | White noise with a unit weight variance of 5000 m |
| Ambiguity | Estimated as constant parameters and re-initialized if a cycle slip, loss of lock and other data disruption occurs/None for ED |
| Troposphere | Piecewise constant zenith delay for each station every 2 h with a constraint of 2 cm/√h |
| Inter-System Bias (ISB) | Estimated as constant/None for ED |
| Inter-Frequency Phase Bias (IFB) | Estimated in the orbit determination and corrected as a constant |
| System | a | b |
|---|---|---|
| Global Positioning System (GPS) | 0.98 | 1/41 |
| GLONASS | 0.98 | 1/45 |
| Galileo | 0.98 | 1/61 |
| BeiDou(MEO/IGSO) | 0.98 | 1/54 |
| BeiDou(GEO) | 0.99 | 1/126 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, X.; Gu, S.; Li, P.; Ge, M.; Schuh, H. A Decentralized Processing Schema for Efficient and Robust Real-time Multi-GNSS Satellite Clock Estimation. Remote Sens. 2019, 11, 2595. https://doi.org/10.3390/rs11212595
Jiang X, Gu S, Li P, Ge M, Schuh H. A Decentralized Processing Schema for Efficient and Robust Real-time Multi-GNSS Satellite Clock Estimation. Remote Sensing. 2019; 11(21):2595. https://doi.org/10.3390/rs11212595
Chicago/Turabian StyleJiang, Xinyuan, Shengfeng Gu, Pan Li, Maorong Ge, and Harald Schuh. 2019. "A Decentralized Processing Schema for Efficient and Robust Real-time Multi-GNSS Satellite Clock Estimation" Remote Sensing 11, no. 21: 2595. https://doi.org/10.3390/rs11212595
APA StyleJiang, X., Gu, S., Li, P., Ge, M., & Schuh, H. (2019). A Decentralized Processing Schema for Efficient and Robust Real-time Multi-GNSS Satellite Clock Estimation. Remote Sensing, 11(21), 2595. https://doi.org/10.3390/rs11212595