A Prior Estimation of the Spatial Distribution Parameter of Soil Moisture Storage Capacity Using Satellite-Based Root-Zone Soil Moisture Data
Abstract
1. Introduction
2. Study Area and Data
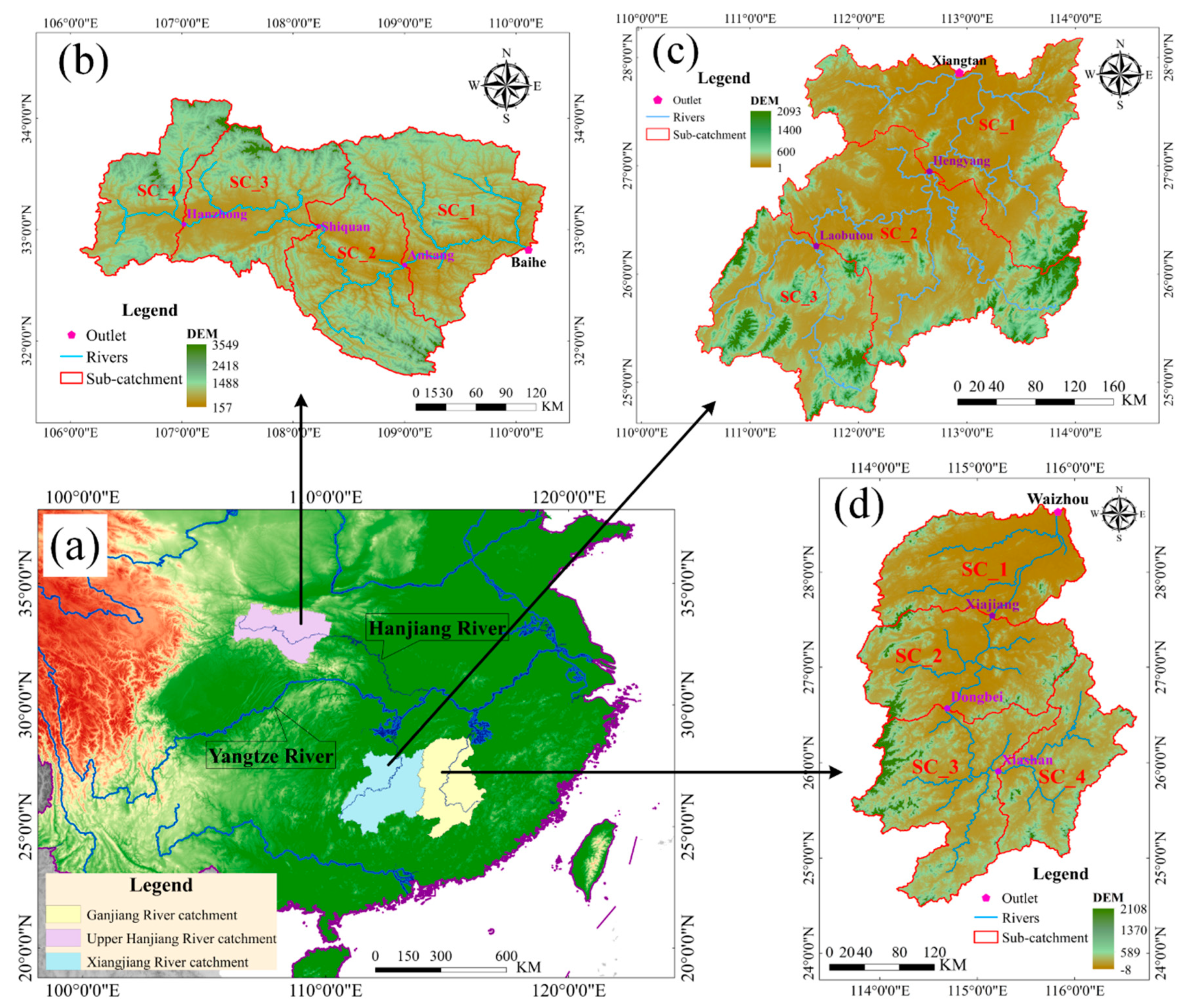
2.1. Study Area
2.1.1. Upper Hanjiang River Catchment
2.1.2. Xiangjiang River Catchment
2.1.3. Ganjiang River Basin
2.2. Data Description
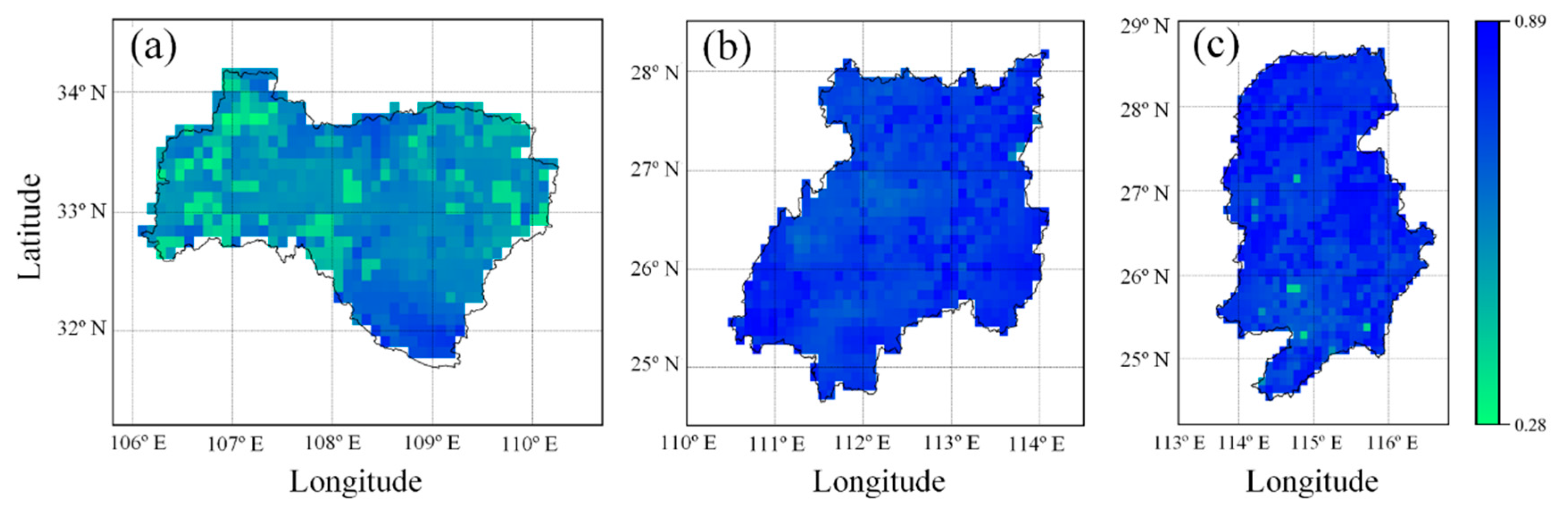
2.3. SMAP Root-Zone Soil Moisture Data
3. Methodology
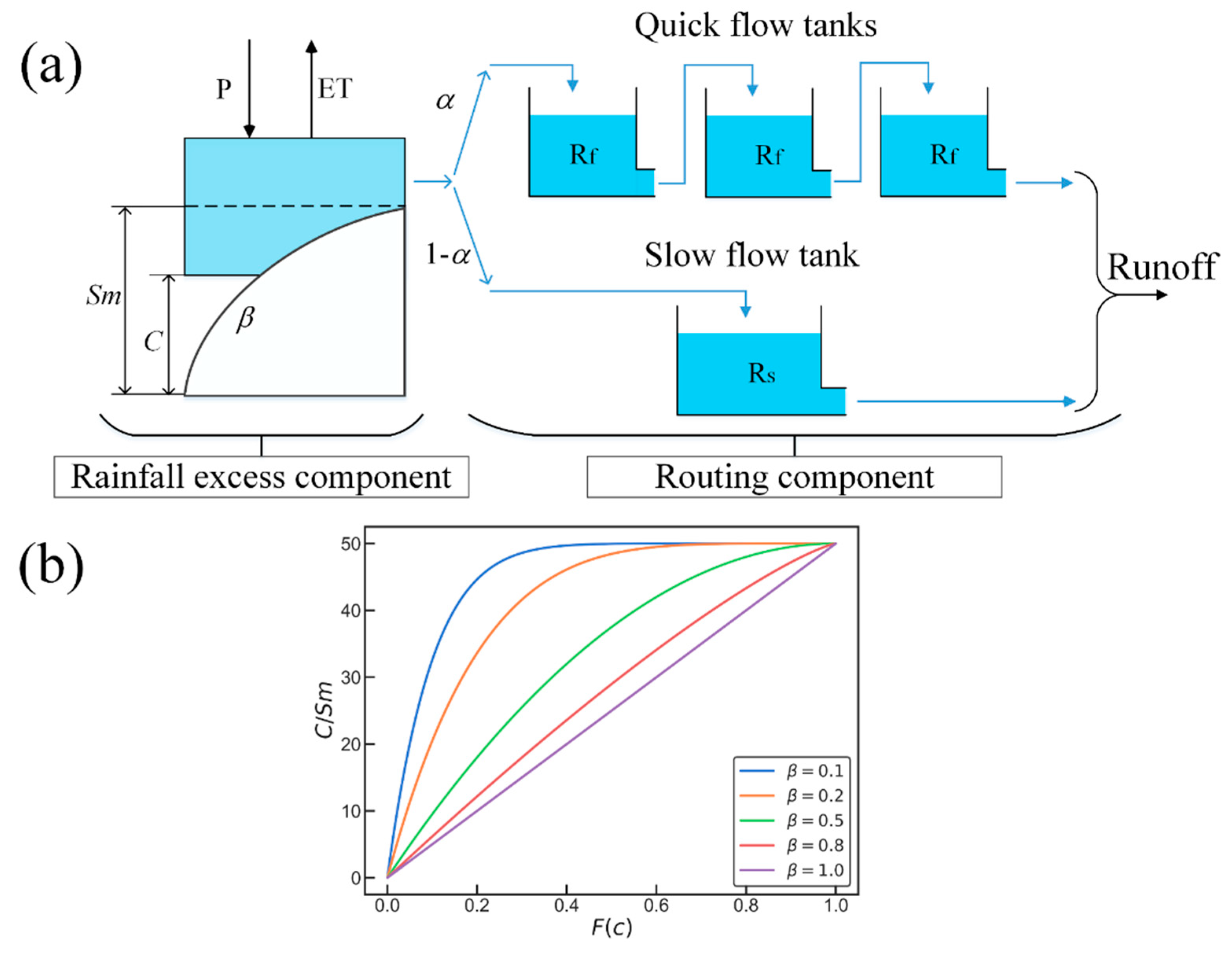
3.1. Structure of Hymod Model
3.2. Semi-Distributed Model Setup
3.3. Prior Estimation of the Degree of Parameter β
3.4. Model Calibration Methodology and Performance Evaluation
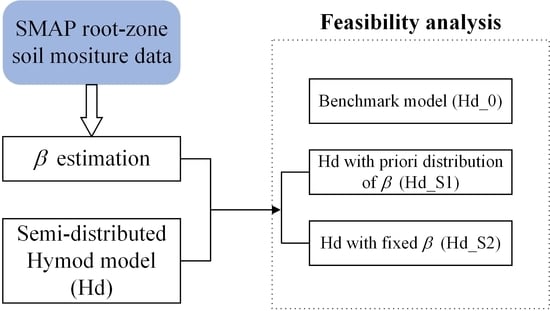
3.5. Experimental Design
4. Results and Discussion
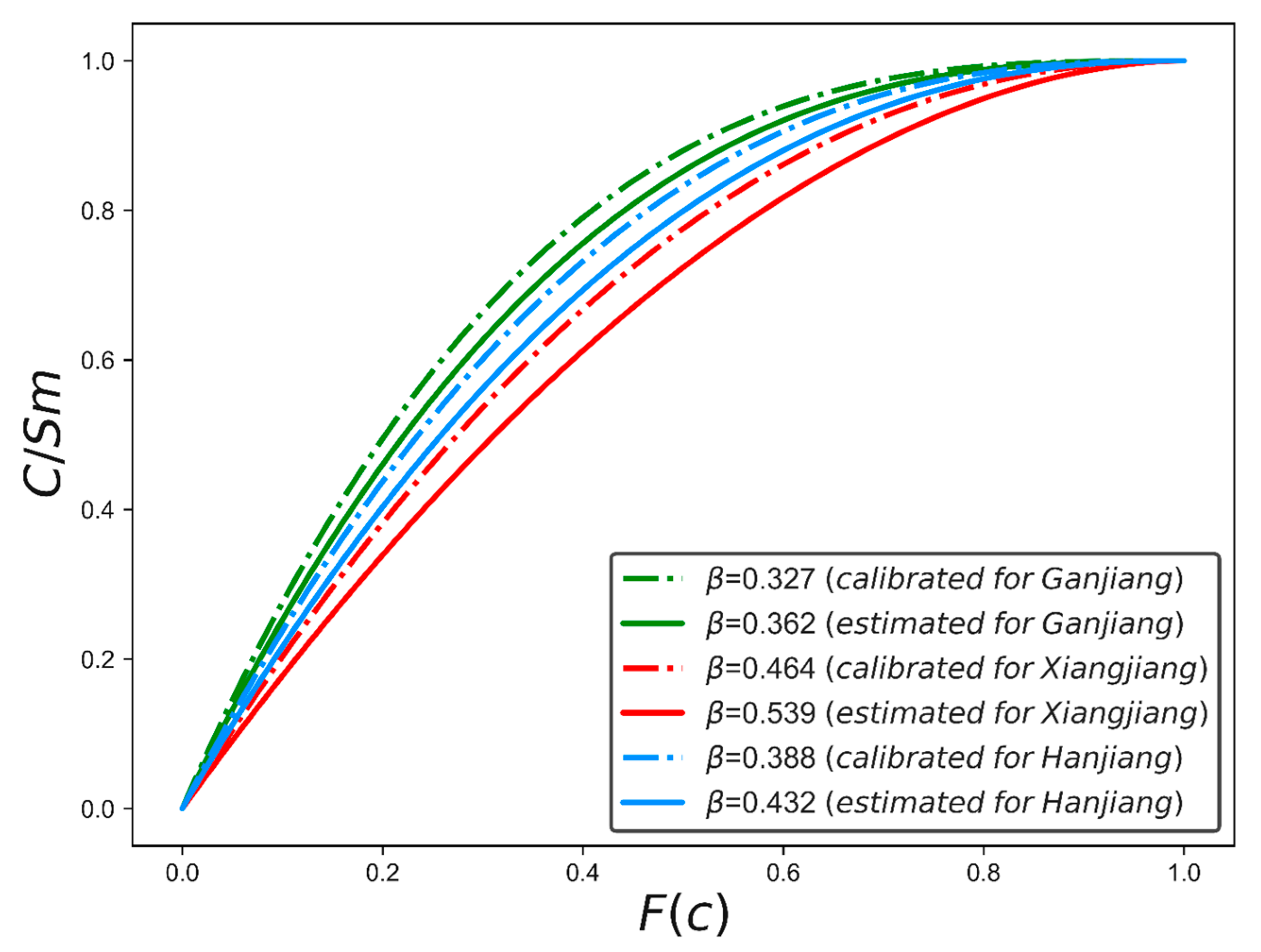
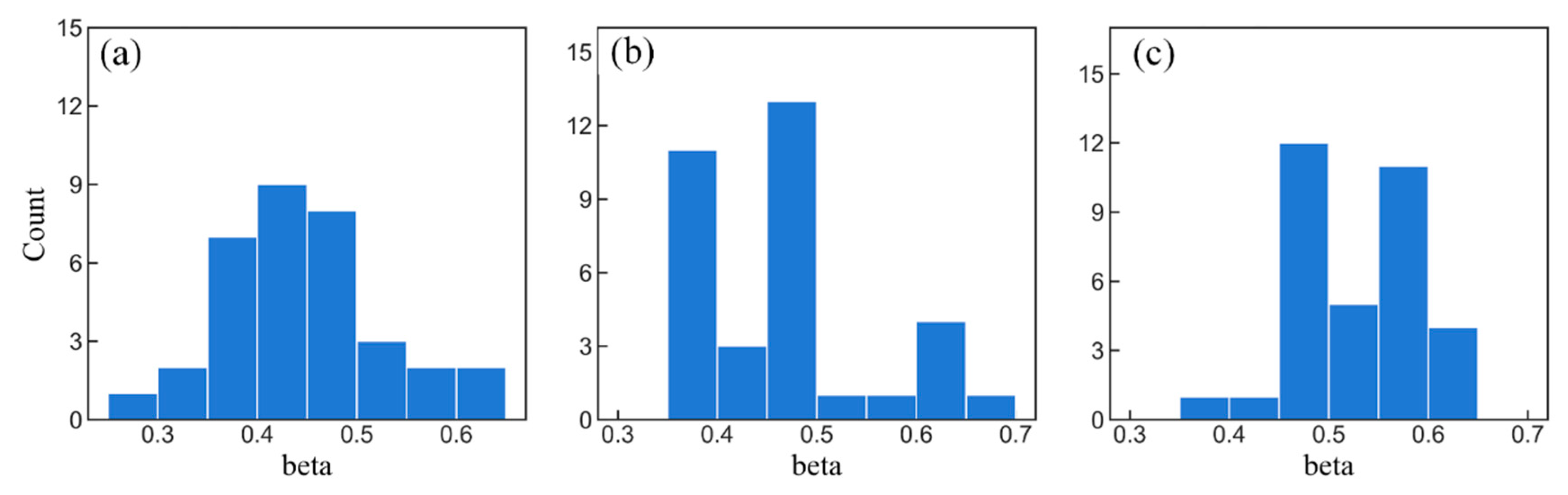
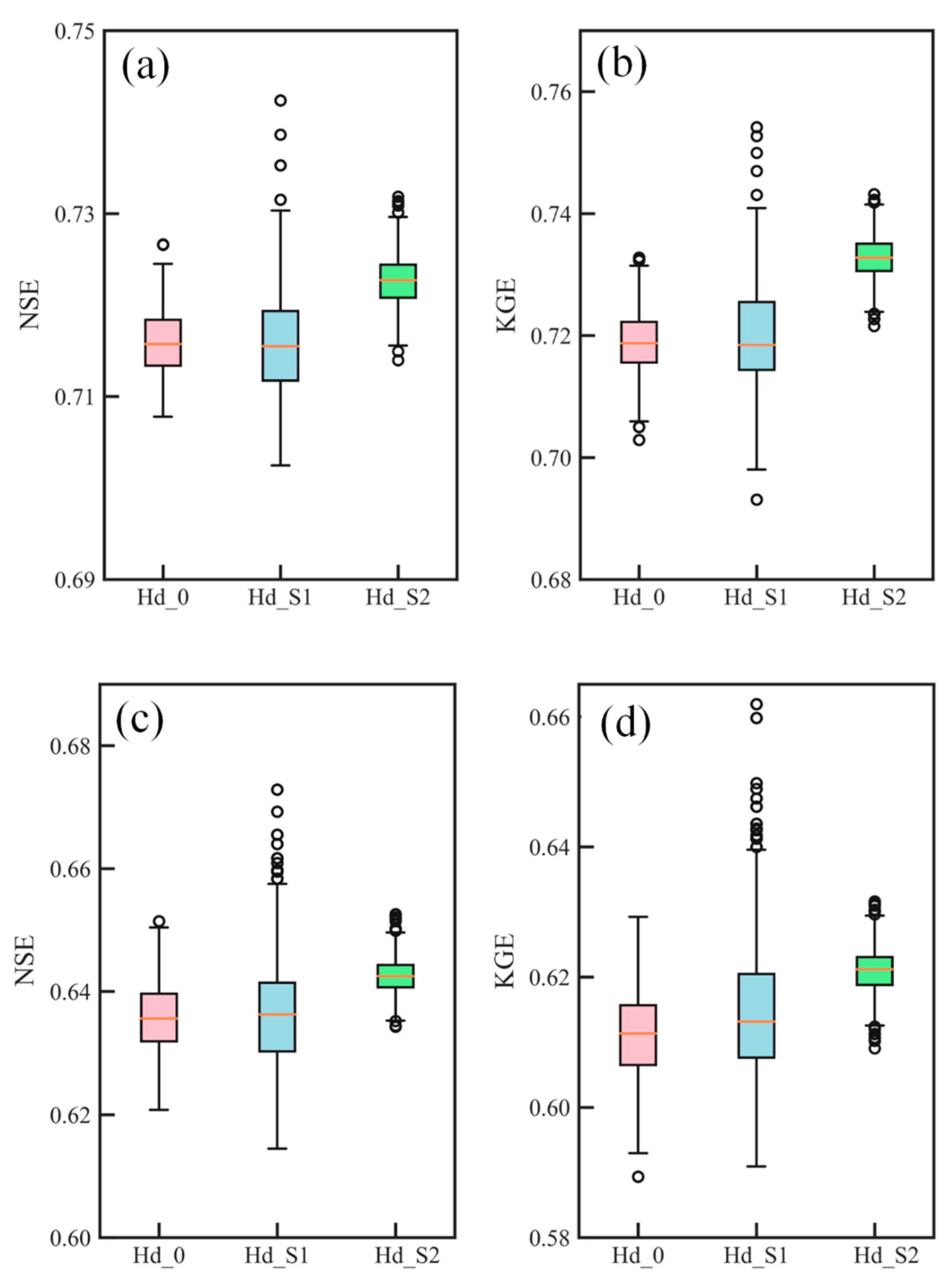
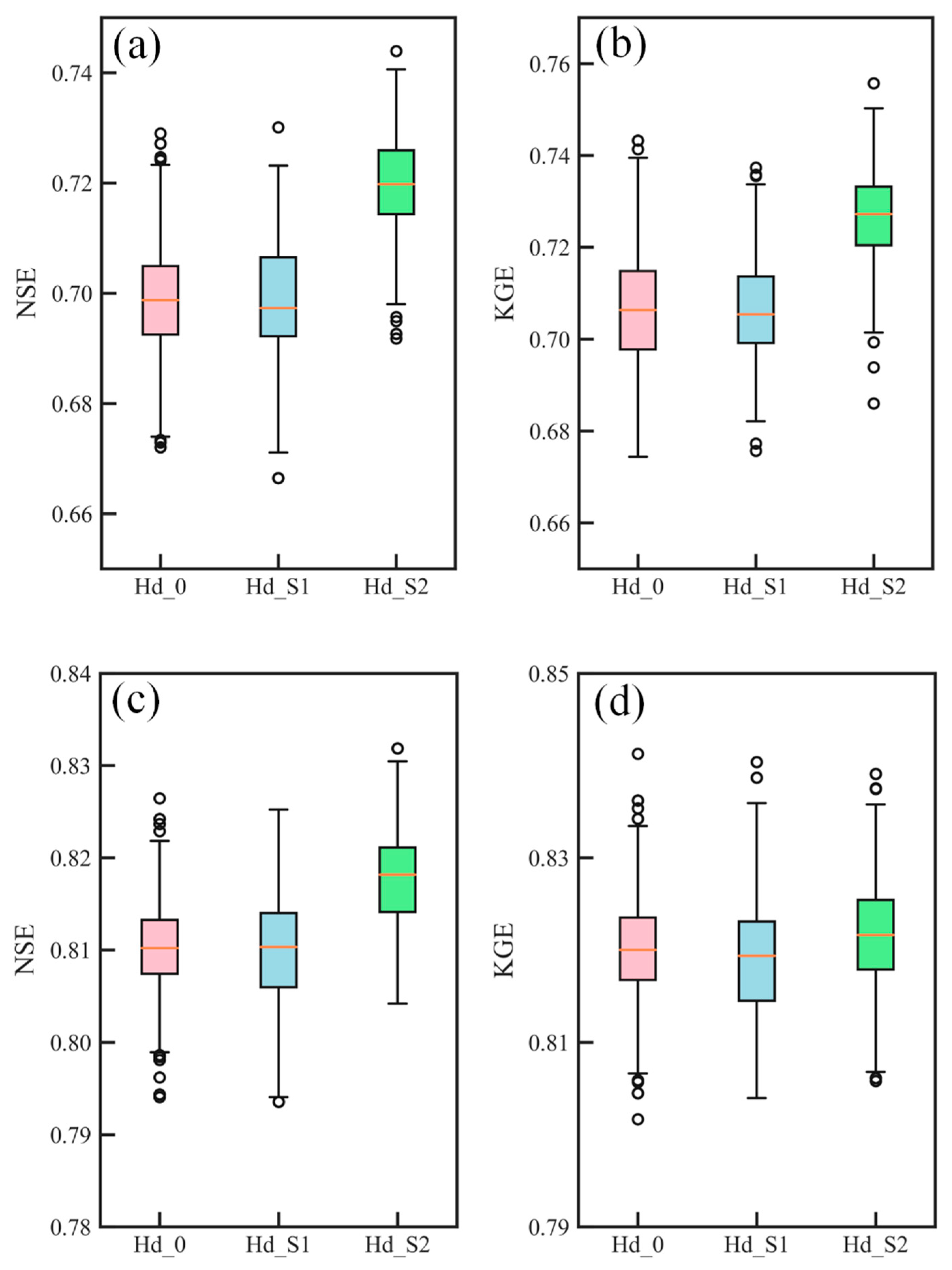
4.1. Results of the Estimated β Value and Its Uncertainty
4.2. Comparison of Model Simulations
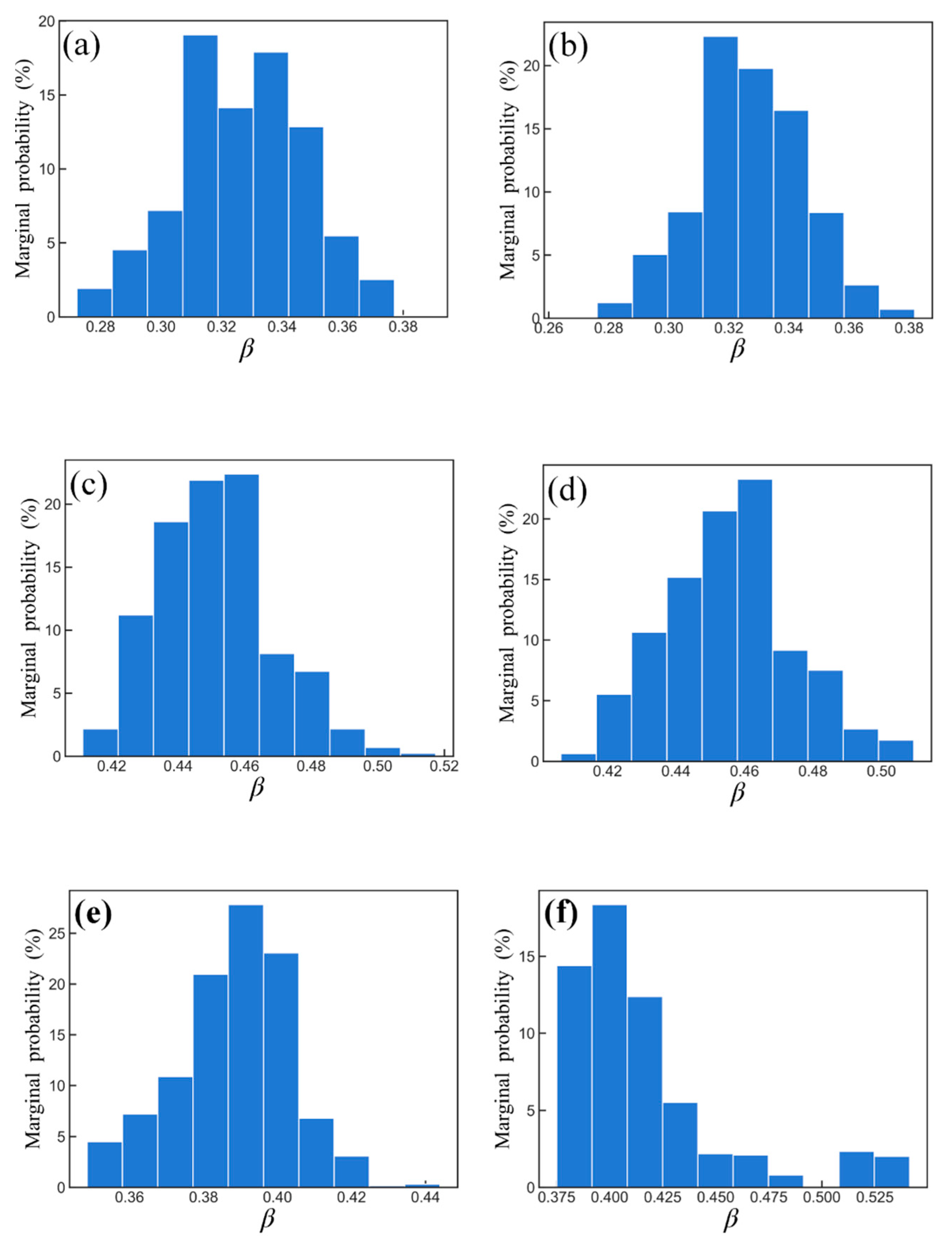
4.3. Analysis of the Posterior Distribution of β
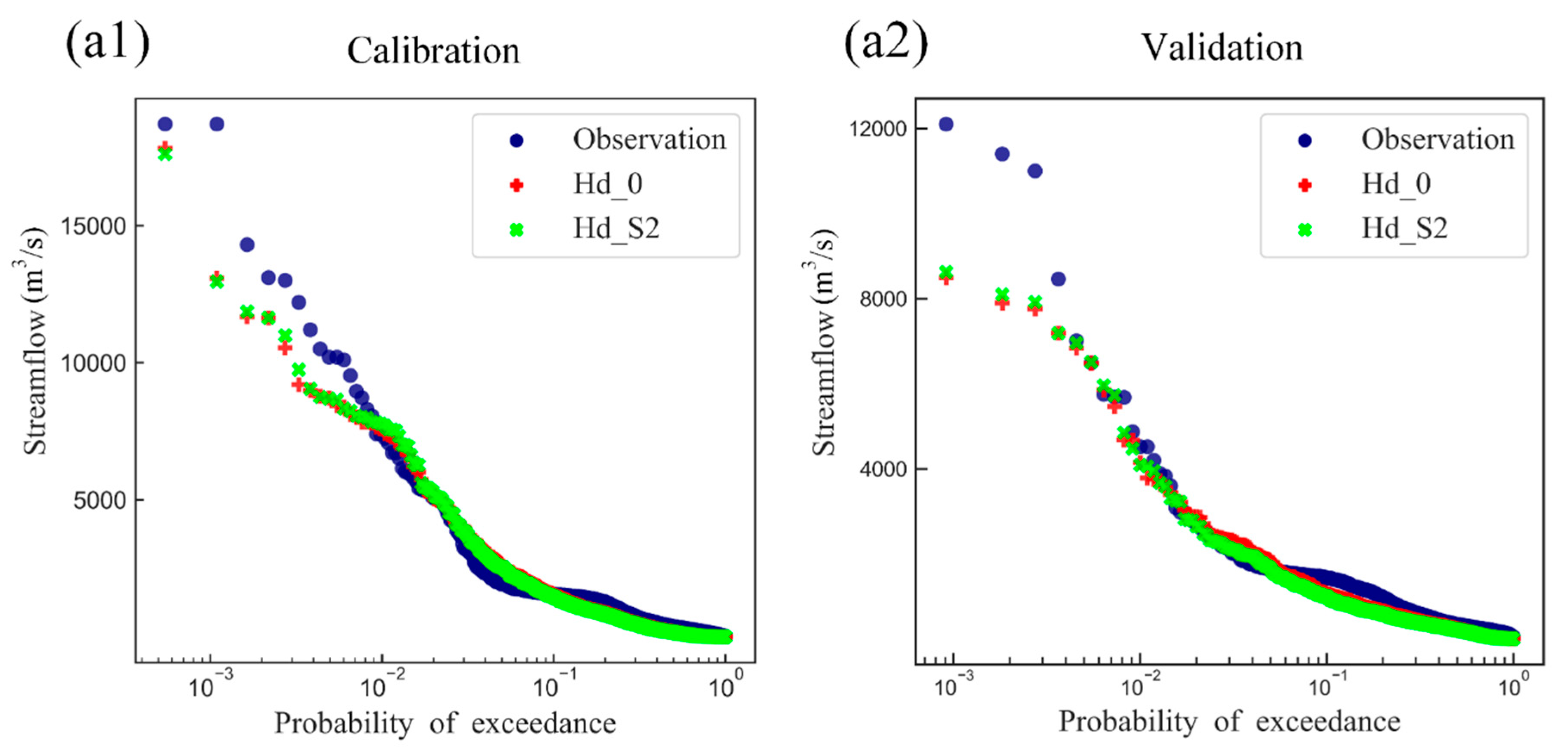
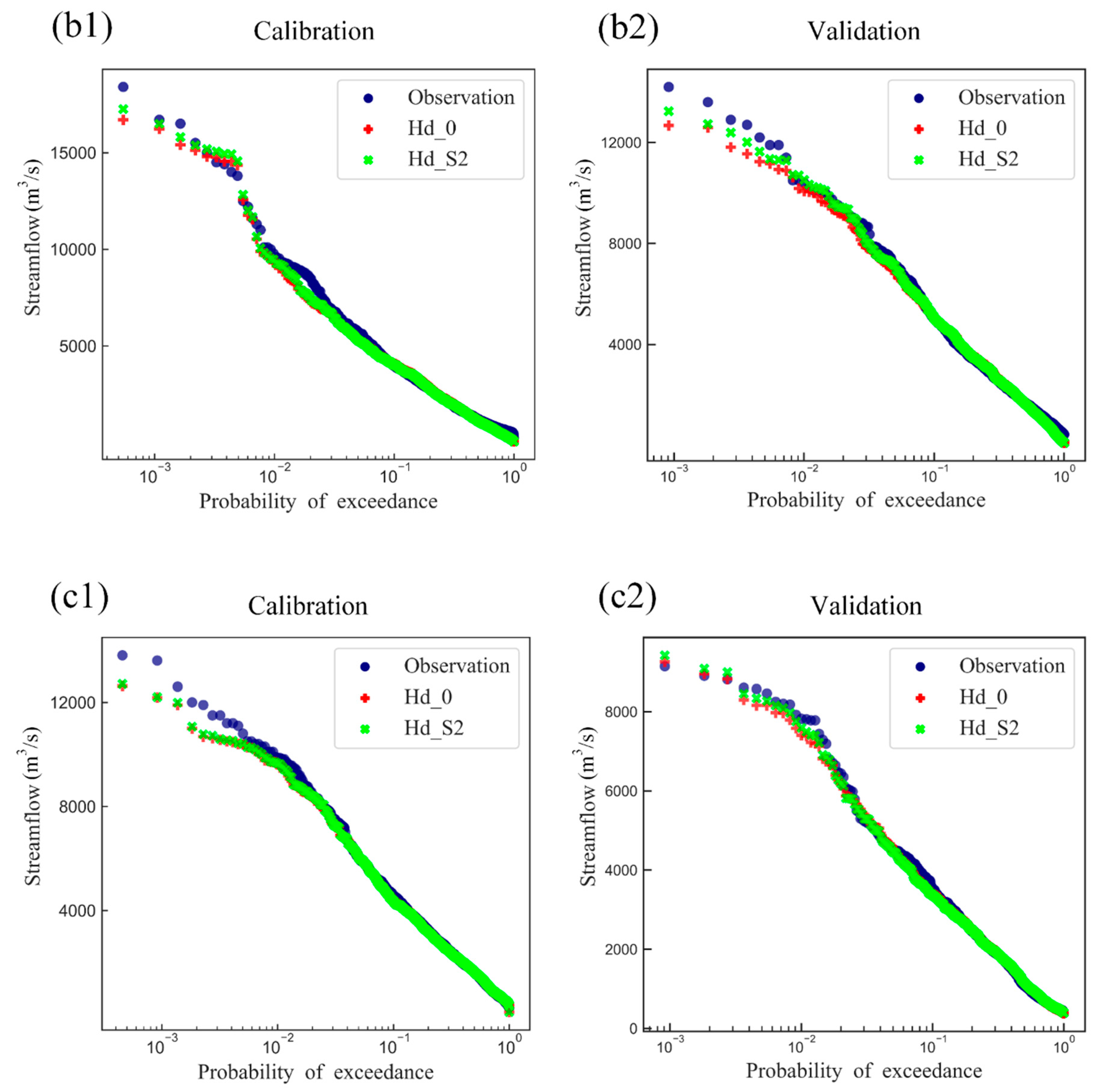
4.4. Streamflow Signature (Flow Duration Curves)
4.5. Impact on Prediction Ability at Ungauged Locations
4.6. Discussion
5. Conclusions
- The different results between calibrated β and estimated β values (0.044 for the Hanjiang River catchment, 0.075 for the Xiangjiang River catchment, and 0.035 for the Ganjiang River catchment) indicated that the method proposed in this study can derive reasonable β values for the Hymod model only based on SMAP soil moisture data before calibration.
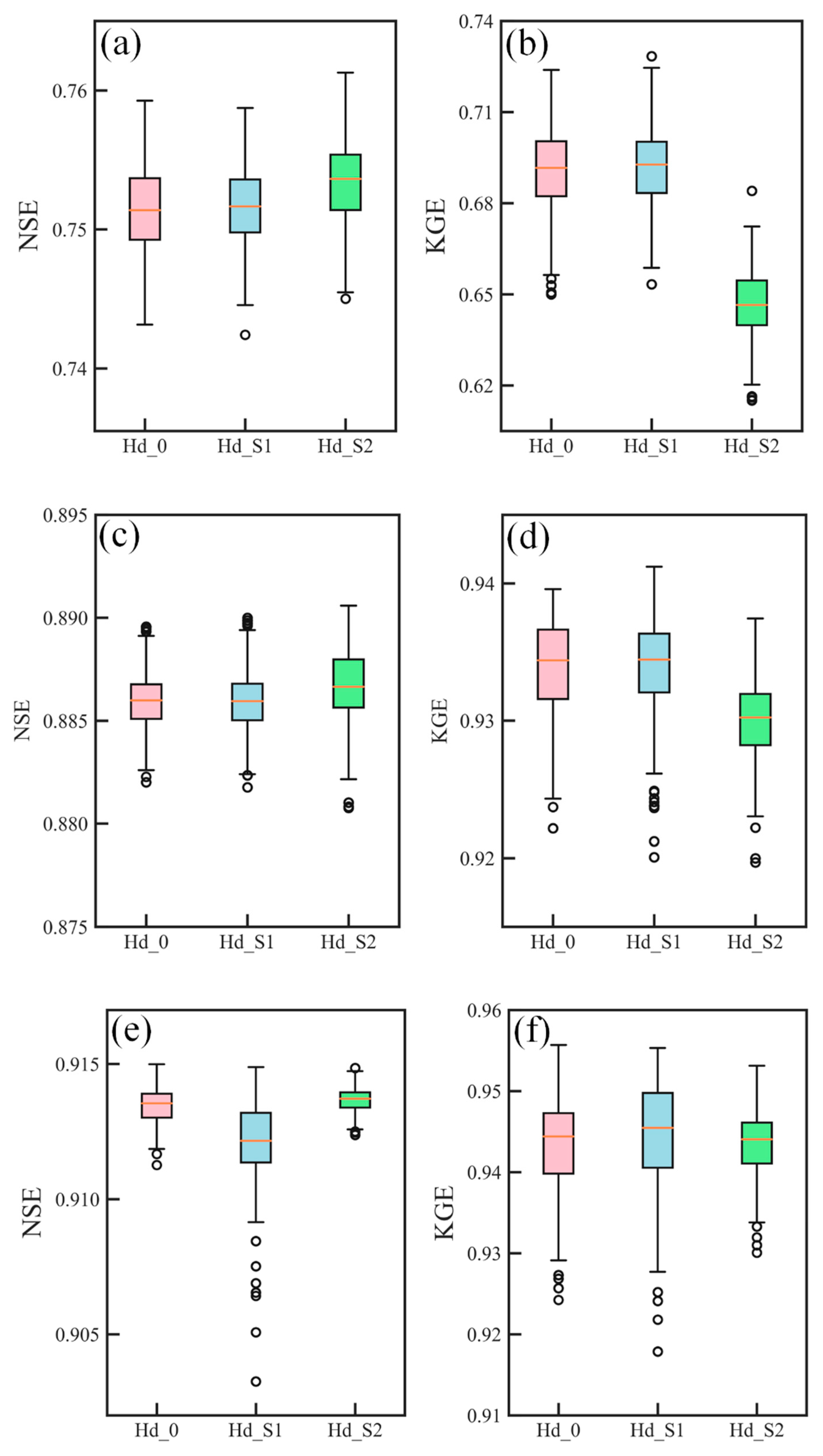
- It was found that both Hd_S1 and Hd_S2 setups both performed well in terms of NSE and KGE that are comparable to the benchmark setup (i.e. Hd_0) in the calibration period. This result indicated that the method proposed can derive a set of feasible values for the β parameter. In the validation period, the transferability of the parameter over time was tested, and a slight improvement was found. This improvement could be explained by the prior estimation of parameter β preventing over-fitting.
- More consistent improvement was generally identified at ungauged neighborhood catchments, with improved NSE values at all four stations. It was demonstrated that the information provided by root-zone soil moisture data was reasonable and increased the robustness of the model. Thus, we highlighted the value of SMAP soil moisture data for finding suitable model parameter sets for the ungauged catchment.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Rakovec, O.; Kumar, R.; Attinger, S.; Samaniego, L. Improving the realism of hydrologic model functioning through multivariate parameter estimation. Water Resour. Res. 2016, 52, 7779–7792. [Google Scholar] [CrossRef]
- Liu, Y.; Weerts, A.; Clark, M.; Hendricks Franssen, H.-J.; Kumar, S.; Moradkhani, H.; Seo, D.-J.; Schwanenberg, D.; Smith, P.; Van Dijk, A. Advancing data assimilation in operational hydrologic forecasting: Progresses, challenges, and emerging opportunities. Hydrol. Earth Syst. Sci. 2012, 16, 3863–3887. [Google Scholar] [CrossRef]
- Yang, H.; Xiong, L.; Ma, Q.; Xia, J.; Chen, J.; Xu, C.-Y. Utilizing satellite surface soil moisture data in calibrating a distributed hydrological model applied in humid regions through a multi-objective Bayesian hierarchical framework. Remote Sens. 2019, 11, 1335. [Google Scholar] [CrossRef]
- Nijzink, R.C.; Almeida, S.; Pechlivanidis, I.G.; Capell, R.; Gustafssons, D.; Arheimer, B.; Parajka, J.; Freer, J.; Han, D.; Wagener, T.; et al. Constraining conceptual hydrological models with multiple information sources. Water Resour. Res. 2018, 54, 8332–8362. [Google Scholar] [CrossRef]
- Brocca, L.; Ciabatta, L.; Massari, C.; Camici, S.; Tarpanelli, A. Soil moisture for hydrological applications: Open questions and new opportunities. Water 2017, 9, 140. [Google Scholar] [CrossRef]
- Srivastava, P.K. Satellite soil moisture: Review of theory and applications in water resources. Water Resour. Manag. 2017, 31, 3161–3176. [Google Scholar] [CrossRef]
- Western, A.W.; Grayson, R.B.; Blöschl, G. Scaling of soil moisture: A hydrologic perspective. Annu. Rev. Earth Planetary. Sci. 2002, 30, 149–180. [Google Scholar] [CrossRef]
- Uber, M.; Vandervaere, J.P.; Zin, I.; Braud, I.; Heisterman, M.; Legout, C.; Molinié, G.; Nord, G. How does initial soil moisture influence the hydrological response? A case study from southern France. Hydrol. Earth Syst. Sci. 2018, 22, 6127–6146. [Google Scholar] [CrossRef]
- Vereecken, H.; Schnepf, A.; Hopmans, J.W.; Javaux, M.; Or, D.; Roose, T.; Vanderborght, J.; Young, M.H.; Amelung, W.; Aitkenhead, M.; et al. Modeling soil processes: Review, key challenges, and new perspectives. Vadose Zone J. 2016, 15, 1–57. [Google Scholar] [CrossRef]
- Wright, A.J.; Walker, J.P.; Pauwels, V.R.N. Identification of hydrologic models, optimized parameters, and rainfall inputs consistent with in situ streamflow and rainfall and remotely sensed soil moisture. J. Hydrometeorol. 2018, 19, 1305–1320. [Google Scholar] [CrossRef]
- Mohanty, B.P.; Cosh, M.H.; Lakshmi, V.; Montzka, C. Soil moisture remote sensing: State-of-the-science. Vadose Zone J. 2017, 16. [Google Scholar] [CrossRef]
- Babaeian, E.; Sadeghi, M.; Jones, S.B.; Montzka, C.; Vereecken, H.; Tuller, M. Ground, proximal, and satellite remote sensing of soil moisture. Rev. Geophys. 2019, 57, 530–616. [Google Scholar] [CrossRef]
- Owe, M.; de Jeu, R.; Holmes, T. Multisensor historical climatology of satellite-derived global land surface moisture. J. Geophys. Res. Earth Surf. 2008, 113, F01002. [Google Scholar] [CrossRef]
- Bartalis, Z.; Wagner, W.; Naeimi, V.; Hasenauer, S.; Scipal, K.; Bonekamp, H.; Figa, J.; Anderson, C. Initial soil moisture retrievals from the METOP-A Advanced Scatterometer (ASCAT). Geophys. Res. Lett. 2007, 34, L20401. [Google Scholar] [CrossRef]
- Kerr, Y.H.; Waldteufel, P.; Wigneron, J.-P.; Delwart, S.; Cabot, F.; Boutin, J.; Escorihuela, M.-J.; Font, J.; Reul, N.; Gruhier, C. The SMOS mission: New tool for monitoring key elements of the global water cycle. Proc. IEEE 2010, 98, 666–687. [Google Scholar] [CrossRef]
- Entekhabi, D.; Njoku, E.G.; O’Neill, P.E.; Kellogg, K.H.; Crow, W.T.; Edelstein, W.N.; Entin, J.K.; Goodman, S.D.; Jackson, T.J.; Johnson, J. The soil moisture active passive (SMAP) mission. Proc. IEEE 2010, 98, 704–716. [Google Scholar] [CrossRef]
- Torres, R.; Snoeij, P.; Geudtner, D.; Bibby, D.; Davidson, M.; Attema, E.; Potin, P.; Rommen, B.; Floury, N.; Brown, M. GMES Sentinel-1 mission. Remote Sens. Environ. 2012, 120, 9–24. [Google Scholar] [CrossRef]
- Peng, J.; Loew, A.; Merlin, O.; Verhoest, N.E. A review of spatial downscaling of satellite remotely sensed soil moisture. Rev. Geophys. 2017, 55, 341–366. [Google Scholar] [CrossRef]
- Bauer-Marschallinger, B.; Freeman, V.; Cao, S.; Paulik, C.; Schaufler, S.; Stachl, T.; Modanesi, S.; Massari, C.; Ciabatta, L.; Brocca, L.; et al. Toward global soil moisture monitoring with sentinel-1: Harnessing assets and overcoming obstacles. IEEE Trans. Geosci. Remote Sens. 2019, 57, 520–539. [Google Scholar] [CrossRef]
- Das, N.N.; Entekhabi, D.; Dunbar, R.S.; Colliander, A.; Chen, F.; Crow, W.; Jackson, T.J.; Berg, A.; Bosch, D.D.; Caldwell, T. The SMAP mission combined active-passive soil moisture product at 9 km and 3 km spatial resolutions. Remote Sens. Environ. 2018, 211, 204–217. [Google Scholar] [CrossRef]
- Montzka, C.; Jagdhuber, T.; Horn, R.; Bogena, H.R.; Hajnsek, I.; Reigber, A.; Vereecken, H. Investigation of SMAP fusion algorithms with airborne active and passive L-band microwave remote sensing. IEEE Trans. Geosci. Remote Sens. 2016, 54, 3878–3889. [Google Scholar] [CrossRef]
- Das, N.N.; Entekhabi, D.; Njoku, E.G.; Shi, J.J.C.; Johnson, J.T.; Colliander, A. Tests of the SMAP combined radar and radiometer algorithm using airborne field campaign observations and simulated data. IEEE Trans. Geosci. Remote Sens. 2014, 52, 2018–2028. [Google Scholar] [CrossRef]
- Song, C.; Jia, L.; Menenti, M. Retrieving high-resolution surface soil moisture by downscaling AMSR-E brightness temperature using MODIS LST and NDVI data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 935–942. [Google Scholar] [CrossRef]
- Srivastava, P.K.; Han, D.; Ramirez, M.R.; Islam, T. Machine learning techniques for downscaling SMOS satellite soil moisture using MODIS land surface temperature for hydrological application. Water Resour. Manag. 2013, 27, 3127–3144. [Google Scholar] [CrossRef]
- Wagner, W.; Dorigo, W.; de Jeu, R.; Fernandez, D.; Benveniste, J.; Haas, E.; Ertl, M. Fusion of active and passive microwave observations to create an essential climate variable data record on soil moisture. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. (ISPRS Ann.) 2012, 7, 315–321. [Google Scholar]
- Massari, C.; Camici, S.; Ciabatta, L.; Brocca, L. Exploiting satellite-based surface soil moisture for flood forecasting in the Mediterranean area: State update versus rainfall correction. Remote Sens. 2018, 10, 292. [Google Scholar] [CrossRef]
- Alvarez-Garreton, C.; Ryu, D.; Western, A.W.; Crow, W.T.; Robertson, D.E. The impacts of assimilating satellite soil moisture into a rainfall–runoff model in a semi-arid catchment. J. Hydrol. 2014, 519, 2763–2774. [Google Scholar] [CrossRef]
- Loizu, J.; Massari, C.; Álvarez-Mozos, J.; Tarpanelli, A.; Brocca, L.; Casalí, J. On the assimilation set-up of ASCAT soil moisture data for improving streamflow catchment simulation. Adv. Water Res. 2018, 111, 86–104. [Google Scholar] [CrossRef]
- Laiolo, P.; Gabellani, S.; Campo, L.; Cenci, L.; Silvestro, F.; Delogu, F.; Boni, G.; Rudari, R.; Puca, S.; Pisani, A.R. Assimilation of remote sensing observations into a continuous distributed hydrological model: Impacts on the hydrologic cycle. In Proceedings of the Geoscience and Remote Sensing Symposium (IGARSS), Milan, Italy, 26–31 July 2015; pp. 1308–1311. [Google Scholar]
- Wanders, N.; Karssenberg, D.; de Roo, A.; de Jong, S.M.; Bierkens, M.F.P. The suitability of remotely sensed soil moisture for improving operational flood forecasting. Hydrol. Earth Syst. Sci. 2014, 18, 2343–2357. [Google Scholar] [CrossRef]
- Chen, F.; Crow, W.T.; Starks, P.J.; Moriasi, D.N. Improving hydrologic predictions of a catchment model via assimilation of surface soil moisture. Adv. Water Res. 2011, 34, 526–536. [Google Scholar] [CrossRef]
- Brocca, L.; Moramarco, T.; Melone, F.; Wagner, W.; Hasenauer, S.; Hahn, S. Assimilation of surface- and root-zone ASCAT soil moisture products into rainfall-runoff modeling. IEEE Trans. Geosci. Remote Sens. 2012, 50, 2542–2555. [Google Scholar] [CrossRef]
- Dharssi, I.; Bovis, K.J.; Macpherson, B.; Jones, C.P. Operational assimilation of ASCAT surface soil wetness at the Met Office. Hydrol. Earth Syst. Sci. 2011, 15, 2729–2746. [Google Scholar] [CrossRef]
- Baguis, P.; Roulin, E. Soil moisture data assimilation in a hydrological model: A case study in Belgium using large-scale satellite data. Remote Sens. 2017, 9, 820. [Google Scholar] [CrossRef]
- Li, Y.; Grimaldi, S.; Pauwels, V.R.N.; Walker, J.P. Hydrologic model calibration using remotely sensed soil moisture and discharge measurements: The impact on predictions at gauged and ungauged locations. J. Hydrol. 2018, 557, 897–909. [Google Scholar] [CrossRef]
- Kundu, D.; Vervoort, R.W.; van Ogtrop, F.F. The value of remotely sensed surface soil moisture for model calibration using SWAT. Hydrol. Process. 2017, 31, 2764–2780. [Google Scholar] [CrossRef]
- López López, P.; Sutanudjaja, E.H.; Schellekens, J.; Sterk, G.; Bierkens, M.F.P. Calibration of a large-scale hydrological model using satellite-based soil moisture and evapotranspiration products. Hydrol. Earth Syst. Sci. 2017, 21, 3125–3144. [Google Scholar] [CrossRef]
- Silvestro, F.; Gabellani, S.; Rudari, R.; Delogu, F.; Laiolo, P.; Boni, G. Uncertainty reduction and parameter estimation of a distributed hydrological model with ground and remote-sensing data. Hydrol. Earth Syst. Sci. 2015, 19, 1727–1751. [Google Scholar] [CrossRef]
- Kunnath-Poovakka, A.; Ryu, D.; Renzullo, L.; George, B. The efficacy of calibrating hydrologic model using remotely sensed evapotranspiration and soil moisture for streamflow prediction. J. Hydrol. 2016, 535, 509–524. [Google Scholar] [CrossRef]
- Reichstein, M.; Camps-Valls, G.; Stevens, B.; Jung, M.; Denzler, J.; Carvalhais, N.; Prabhat. Deep learning and process understanding for data-driven Earth system science. Nature 2019, 566, 195–204. [Google Scholar] [CrossRef]
- Vanderlinden, K.; Vereecken, H.; Hardelauf, H.; Herbst, M.; Martínez, G.; Cosh, M.H.; Pachepsky, Y.A. Temporal stability of soil water contents: A review of data and analyses. Vadose Zone J. 2012, 11. [Google Scholar] [CrossRef]
- Qiu, Z.; Pennock, A.; Giri, S.; Trnka, C.; Du, X.; Wang, H. Assessing soil moisture patterns using a soil topographic index in a humid region. Water Resour. Manag. 2017, 31, 2243–2255. [Google Scholar] [CrossRef]
- Huang, C.; Wang, G.; Zheng, X.; Yu, J.; Xu, X. Simple linear modeling approach for linking hydrological model parameters to the physical features of a river basin. Water Resour. Manag. 2015, 29, 3265–3289. [Google Scholar] [CrossRef]
- Brocca, L.; Melone, F.; Moramarco, T.; Wagner, W.; Naeimi, V.; Bartalis, Z.; Hasenauer, S. Improving runoff prediction through the assimilation of the ASCAT soil moisture product. Hydrol. Earth Syst. Sci. 2010, 14, 1881–1893. [Google Scholar] [CrossRef]
- Maggioni, V.; Houser, P.R. Soil moisture data assimilation. In Data Assimilation for Atmospheric, Oceanic and Hydrologic Applications (Vol. III); Park, S.K., Xu, L., Eds.; Springer International Publishing: Cham, Switzerland, 2017; pp. 195–217. [Google Scholar]
- Zheng, D.; Li, X.; Wang, X.; Wang, Z.; Wen, J.; van der Velde, R.; Schwank, M.; Su, Z. Sampling depth of L-band radiometer measurements of soil moisture and freeze-thaw dynamics on the Tibetan Plateau. Remote Sens. Environ. 2019, 226, 16–25. [Google Scholar] [CrossRef]
- Zhu, Q.; Xuan, W.; Liu, L.; Xu, Y.P. Evaluation and hydrological application of precipitation estimates derived from PERSIANN-CDR, TRMM 3B42V7, and NCEP-CFSR over humid regions in China. Hydrol. Process. 2016, 30, 3061–3083. [Google Scholar] [CrossRef]
- Ma, Q.; Xiong, L.; Liu, D.; Xu, C.-Y.; Guo, S. Evaluating the temporal dynamics of uncertainty contribution from satellite precipitation input in rainfall-runoff modeling using the variance decomposition method. Remote Sens. 2018, 10, 1876. [Google Scholar] [CrossRef]
- Blaney, H.F.; Criddle, W.D. Determining Consumptive Use and Irrigation Water Requirements; US Department of Agriculture: Washington, DC, USA, 1962.
- Zhu, Q.; Luo, Y.; Xu, Y.-P.; Tian, Y.; Yang, T. Satellite soil moisture for agricultural drought monitoring: Assessment of SMAP-derived soil water deficit index in Xiang River Basin, China. Remote Sens. 2019, 11, 362. [Google Scholar] [CrossRef]
- Crow, W.T.; Chen, F.; Reichle, R.H.; Xia, Y. Diagnosing bias in modeled soil moisture/runoff coefficient correlation using the SMAP level 4 soil moisture product. Water Resour. Res. 2019, 55, 7010–7026. [Google Scholar] [CrossRef]
- Reichle, R.H.; Ardizzone, J.V.; Kim, G.-K.; Lucchesi, R.A.; Smith, E.B.; Weiss, B.H. Soil Moisture Active Passive (SMAP) Mission Level 4 Surface and Root Zone Soil Moisture (L4_SM) Product Specification Document; NASA Goddard Space Flight Center: Greenbelt, MD, USA, 2018. [Google Scholar]
- Pathiraja, S.; Marshall, L.; Sharma, A.; Moradkhani, H. Detecting non-stationary hydrologic model parameters in a paired catchment system using data assimilation. Adv. Water Res. 2016, 94, 103–119. [Google Scholar] [CrossRef]
- Alvarez-Garreton, C.; Ryu, D.; Western, A.W.; Su, C.H.; Crow, W.T.; Robertson, D.E.; Leahy, C. Improving operational flood ensemble prediction by the assimilation of satellite soil moisture: Comparison between lumped and semi-distributed schemes. Hydrol. Earth Syst. Sci. 2015, 19, 1659–1676. [Google Scholar] [CrossRef]
- Nijzink, R.; Hutton, C.; Pechlivanidis, I.; Capell, R.; Arheimer, B.; Freer, J.; Han, D.; Wagener, T.; McGuire, K.; Savenije, H.; et al. The evolution of root-zone moisture capacities after deforestation: A step towards hydrological predictions under change? Hydrol. Earth Syst. Sci. 2016, 20, 4775–4799. [Google Scholar] [CrossRef]
- Guo, J.; Zhou, J.; Zou, Q.; Liu, Y.; Song, L. A novel multi-objective shuffled complex differential evolution algorithm with application to hydrological model parameter optimization. Water Resour. Manag. 2013, 27, 2923–2946. [Google Scholar] [CrossRef]
- Moore, R. The probability-distributed principle and runoff production at point and basin scales. Hydrol. Sci. J. 1985, 30, 273–297. [Google Scholar] [CrossRef]
- Boyle, D.P.; Gupta, H.V.; Sorooshian, S. Multicriteria calibration of hydrologic models. In Calibration of Watershed Models; Duan, Q., Gupta, H., Sorooshian, S., Rousseau, A., Turcotte, R., Eds.; AGU: Washington, DC, USA, 2003; pp. 185–196. [Google Scholar]
- Ren-Jun, Z. The Xinanjiang model applied in China. J. Hydrol. 1992, 135, 371–381. [Google Scholar] [CrossRef]
- Wood, E.F.; Lettenmaier, D.P.; Zartarian, V.G. A land-surface hydrology parameterization with subgrid variability for general circulation models. J. Geophys. Res. Atmos. 1992, 97, 2717–2728. [Google Scholar] [CrossRef]
- Moore, R. The PDM rainfall-runoff model. Hydrol. Earth Syst. Sci. 2007, 11, 483–499. [Google Scholar] [CrossRef]
- Gill, M.A. Flood routing by the Muskingum method. J. Hydrol. 1978, 36, 353–363. [Google Scholar] [CrossRef]
- Vrugt, J.A.; ter Braak, C.J.F.; Clark, M.P.; Hyman, J.M.; Robinson, B.A. Treatment of input uncertainty in hydrologic modeling: Doing hydrology backward with Markov chain Monte Carlo simulation. Water Resour. Res. 2008, 44. [Google Scholar] [CrossRef]
- Kunnath-Poovakka, A.; Ryu, D.; Renzullo, L.J.; George, B. Remotely sensed ET for streamflow modelling in catchments with contrasting flow characteristics: An attempt to improve efficiency. Stoch. Environ. Res. Risk Assess. 2018, 32, 1973–1992. [Google Scholar] [CrossRef]
- Broderick, C.; Matthews, T.; Wilby, R.L.; Bastola, S.; Murphy, C. Transferability of hydrological models and ensemble averaging methods between contrasting climatic periods. Water Resour. Res. 2016, 52, 8343–8373. [Google Scholar] [CrossRef]
- Moges, E.; Demissie, Y.; Li, H.Y. Hierarchical mixture of experts and diagnostic modeling approach to reduce hydrologic model structural uncertainty. Water Resour. Res. 2016, 52, 2551–2570. [Google Scholar] [CrossRef]
- Beven, K.; Binley, A. The future of distributed models: Model calibration and uncertainty prediction. Hydrol. Process. 1992, 6, 279–298. [Google Scholar] [CrossRef]
- Gelman, A.; Rubin, D.B. Inference from iterative simulation using multiple sequences. Stat. Sci. 1992, 7, 457–472. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I–A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Gupta, H.V.; Kling, H.; Yilmaz, K.K.; Martinez, G.F. Decomposition of the mean squared error and NSE performance criteria: Implications for improving hydrological modelling. J. Hydrol. 2009, 377, 80–91. [Google Scholar] [CrossRef]
- Euser, T.; Winsemius, H.C.; Hrachowitz, M.; Fenicia, F.; Uhlenbrook, S.; Savenije, H.H.G. A framework to assess the realism of model structures using hydrological signatures. Hydrol. Earth Syst. Sci. 2013, 17, 1893–1912. [Google Scholar] [CrossRef]
- Bahremand, A. HESS Opinions: Advocating process modeling and de-emphasizing parameter estimation. Hydrol. Earth Syst. Sci. 2016, 20, 1433–1445. [Google Scholar] [CrossRef]
- Chouaib, W.; Alila, Y.; Caldwell, P.V. Parameter transferability within homogeneous regions and comparisons with predictions from a priori parameters in the eastern United States. J. Hydrol. 2018, 560, 24–38. [Google Scholar] [CrossRef]
- Hrachowitz, M.; Savenije, H.H.G.; Blöschl, G.; McDonnell, J.J.; Sivapalan, M.; Pomeroy, J.W.; Arheimer, B.; Blume, T.; Clark, M.P.; Ehret, U.; et al. A decade of predictions in ungauged basins (PUB)—A review. Hydrol. Sci. J. 2013, 58, 1198–1255. [Google Scholar] [CrossRef]
- Roy, T.; Gupta, H.V.; Serrat-Capdevila, A.; Valdes, J.B. Using satellite-based evapotranspiration estimates to improve the structure of a simple conceptual rainfall–runoff model. Hydrol. Earth Syst. Sci. 2017, 21, 879–896. [Google Scholar] [CrossRef]
| Sub-Catchment | Upper Hanjiang River | ||
| Hydrological station | Area (km2) | Data period | |
| SC_1 | Baihe | 20,490 | 2008-2017 |
| SC_2 | Ankang | 14,820 | -- |
| SC_3 | Shiquan | 14,476 | -- |
| SC_4 | Hanzhong | 9329 | -- |
| Sub-Catchment | Xiangjiang River | ||
| Hydrological station | Area (km2) | Data period | |
| SC_1 | Xiangtan | 29,518 | 2007-2016 |
| SC_2 | Hengyang | 30,779 | 2007-2016 |
| SC_3 | Laobutou | 21,341 | -- |
| Sub-Catchment | Ganjiang River | ||
| Hydrological station | Area (km2) | Data period | |
| SC_1 | Waizhou | 18,224 | 2000-2009 |
| SC_2 | Xiajiang | 22,493 | 2000-2009 |
| SC_3 | Dongbei | 24,198 | -- |
| SC_4 | Xiashan | 16,033 | -- |
| Parameter | Model Part | Description | Unit | Prior Range |
|---|---|---|---|---|
| Sm | Rainfall excess | Maximum soil moisture storage capacity | mm | 0–500 |
| β | Rainfall excess | The degree of spatial variability of soil moisture storage capacity | -- | 0–2 |
| α | Routing | The split parameter to divide the excess rainfall | -- | 0–1 |
| Rs | Routing | The slow flow residence time of the conceptual linear reservoir | day | 0–0.1 |
| Rf | Routing | The fast flow residence time of three conceptual linear reservoirs | day | 0.1–1 |
| Model Setup | Baihe Station (Hanjiang River) | Xiangtan Station (Xiangjiang River) | Waizhou Station (Ganjiang River) | |||
|---|---|---|---|---|---|---|
| NSE (%) | KGE (%) | NSE (%) | KGE (%) | NSE (%) | KGE (%) | |
| Hd_0 | 82.70 | 81.15 | 89.26 | 93.38 | 92.33 | 95.37 |
| Hd_S1 | 82.70 | 81.35 | 89.26 | 93.45 | 92.31 | 95.73 |
| Hd_S2 | 82.46 | 80.19 | 89.24 | 92.90 | 92.31 | 95.28 |
| Model Setup | Baihe Station (Hanjiang River) | Xiangtan Station (Xiangjiang River) | Waizhou Station (Ganjiang River) | |||
|---|---|---|---|---|---|---|
| NSE (%) | KGE (%) | NSE (%) | KGE (%) | NSE (%) | KGE (%) | |
| Hd_0 | 75.93 | 72.39 | 88.96 | 93.96 | 91.50 | 95.57 |
| Hd_S1 | 75.87 | 72.84 | 89.00 | 94.12 | 91.49 | 95.53 |
| Hd_S2 | 76.13 | 68.41 | 89.06 | 93.74 | 91.49 | 95.31 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tian, Y.; Xiong, L.; Xiong, B.; Zhuang, R. A Prior Estimation of the Spatial Distribution Parameter of Soil Moisture Storage Capacity Using Satellite-Based Root-Zone Soil Moisture Data. Remote Sens. 2019, 11, 2580. https://doi.org/10.3390/rs11212580
Tian Y, Xiong L, Xiong B, Zhuang R. A Prior Estimation of the Spatial Distribution Parameter of Soil Moisture Storage Capacity Using Satellite-Based Root-Zone Soil Moisture Data. Remote Sensing. 2019; 11(21):2580. https://doi.org/10.3390/rs11212580
Chicago/Turabian StyleTian, Yifei, Lihua Xiong, Bin Xiong, and Ruodan Zhuang. 2019. "A Prior Estimation of the Spatial Distribution Parameter of Soil Moisture Storage Capacity Using Satellite-Based Root-Zone Soil Moisture Data" Remote Sensing 11, no. 21: 2580. https://doi.org/10.3390/rs11212580
APA StyleTian, Y., Xiong, L., Xiong, B., & Zhuang, R. (2019). A Prior Estimation of the Spatial Distribution Parameter of Soil Moisture Storage Capacity Using Satellite-Based Root-Zone Soil Moisture Data. Remote Sensing, 11(21), 2580. https://doi.org/10.3390/rs11212580