Pixel Tracking to Estimate Rivers Water Flow Elevation Using Cosmo-SkyMed Synthetic Aperture Radar Data
Abstract
:1. Introduction
2. Rivers Water Flow Elevation Retrieval
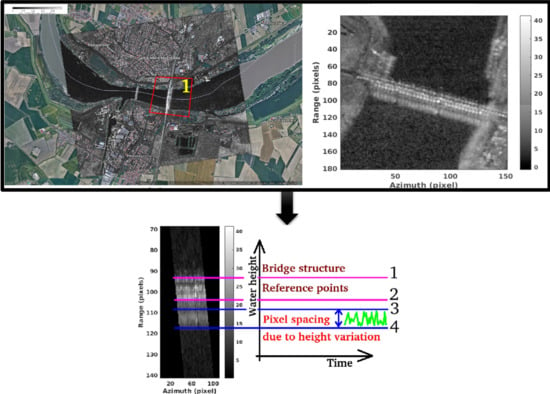
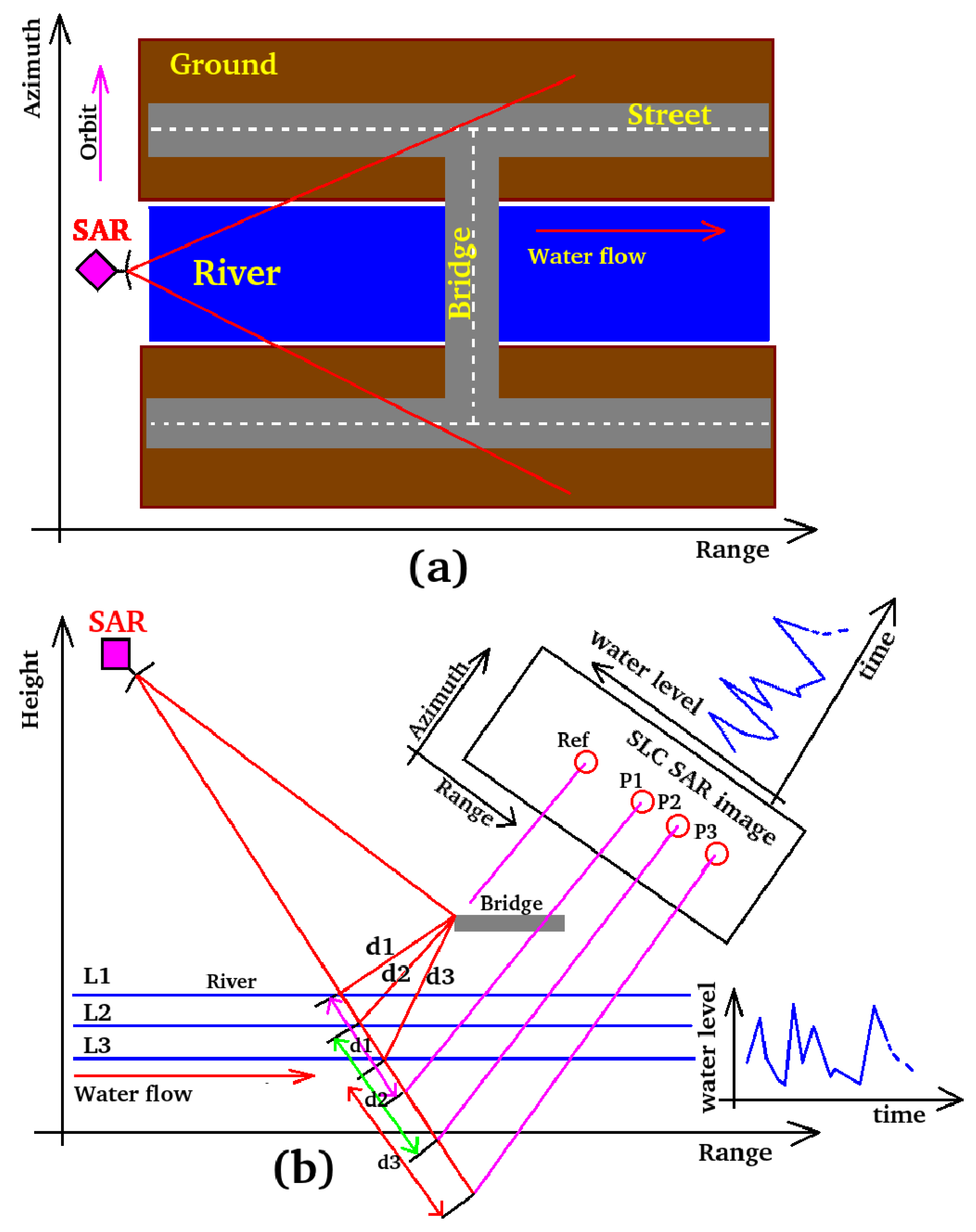
2.1. The Observation Geometry
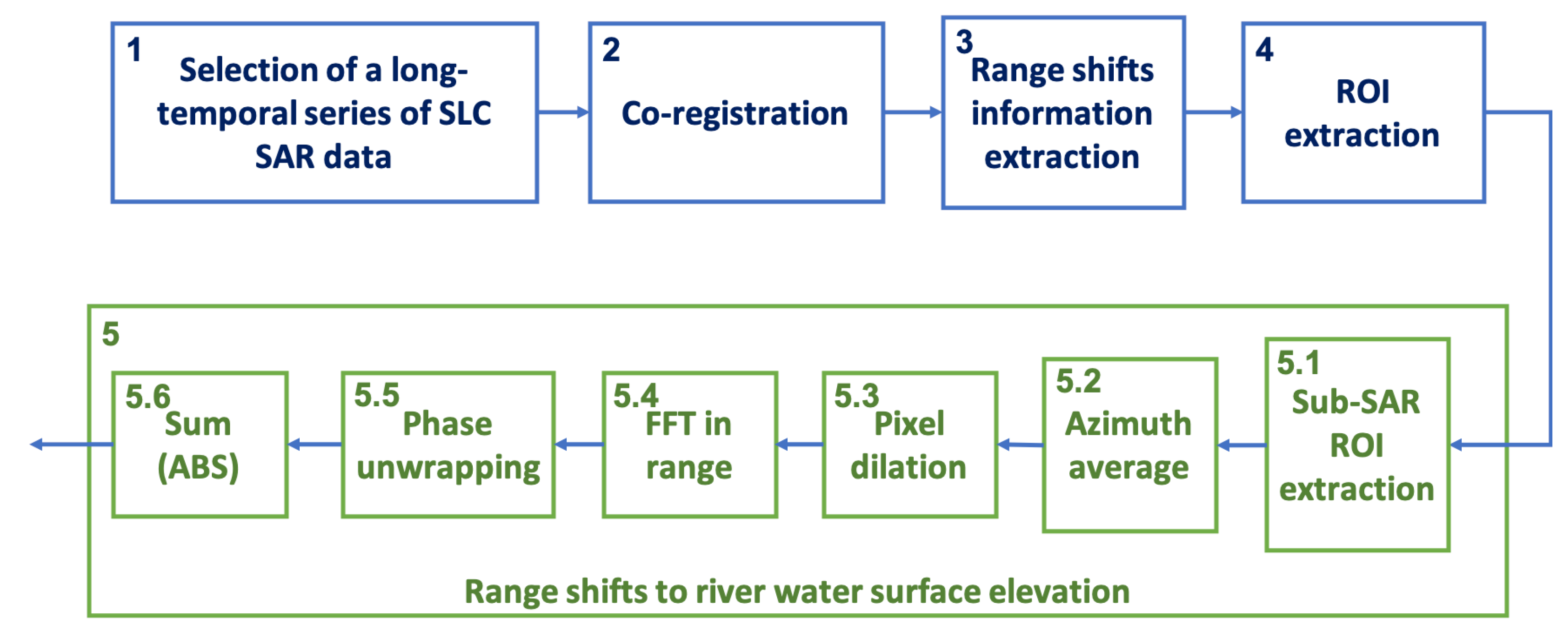
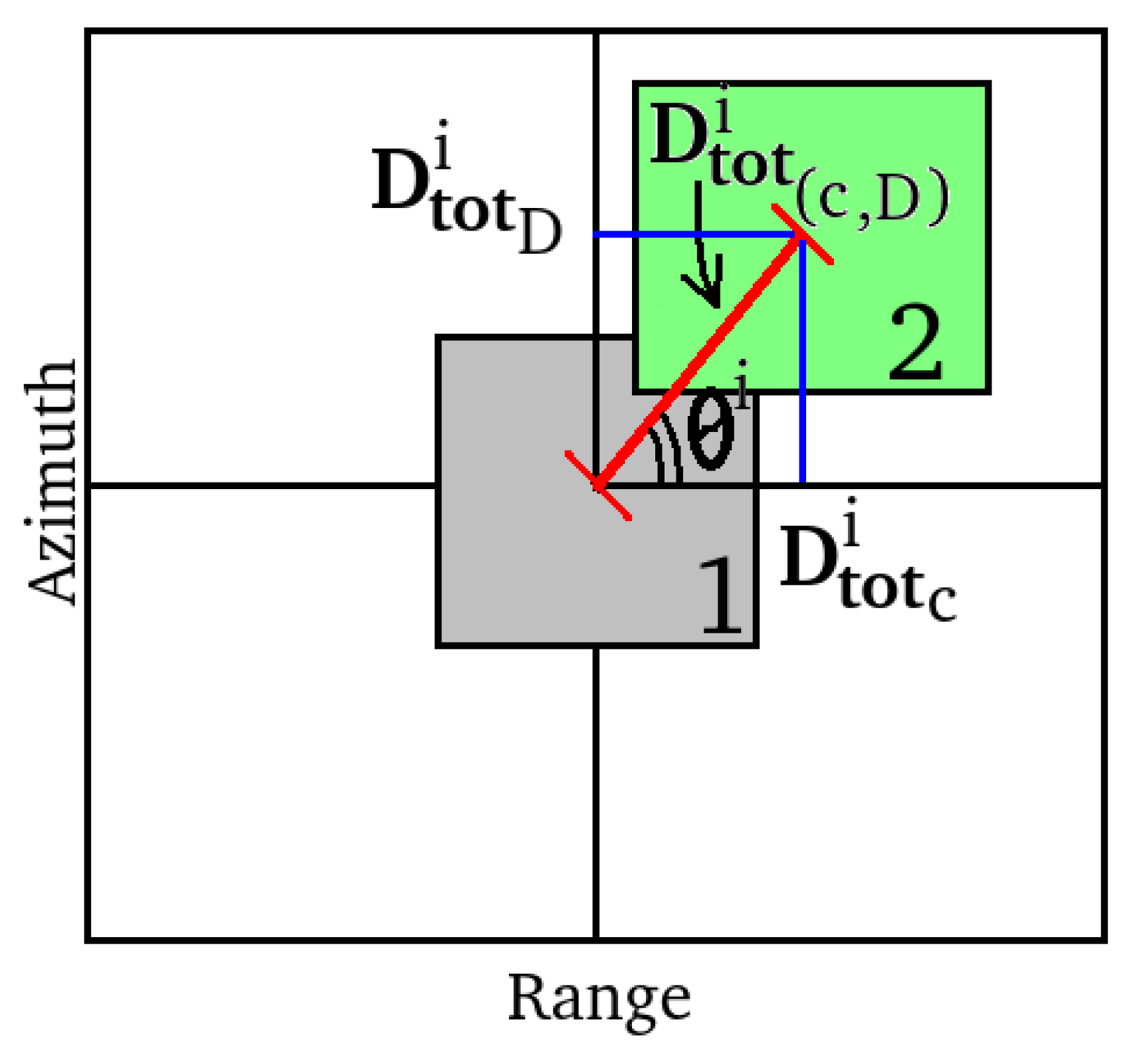
2.2. The Processing Scheme
- A is the backscattering coefficient;
- is the number of pixels of the image along the range;
- is the number of pixels of the image along the azimuth;
- is the chirp resolution;
- is the Doppler resolution;
- is the chirp wavenumber;
- is the Doppler wavenumber;
- is the bandwidth of the transmitted chirp signal;
- is the synthesized Doppler band.
- is the offset component of the signal position presented in (1), generated by the variation of the river water level and detected as a sub-pixel misalignment existing between the first SAR image (master) and the i-th slave SAR image;
- is the offset component generated by the earth displacement when located on highly sloped terrain;
- is the offset caused by residual errors of the satellite orbits;
- is the offset component generated by general attitude and control errors of the flying satellite trajectory;
- and are the contributions accounting for change in the atmospheric and ionospheric dielectric constant and for decorrelation phenomena (spatial, temporal, thermal, etc.), respectively.
3. Test on Simulated Data
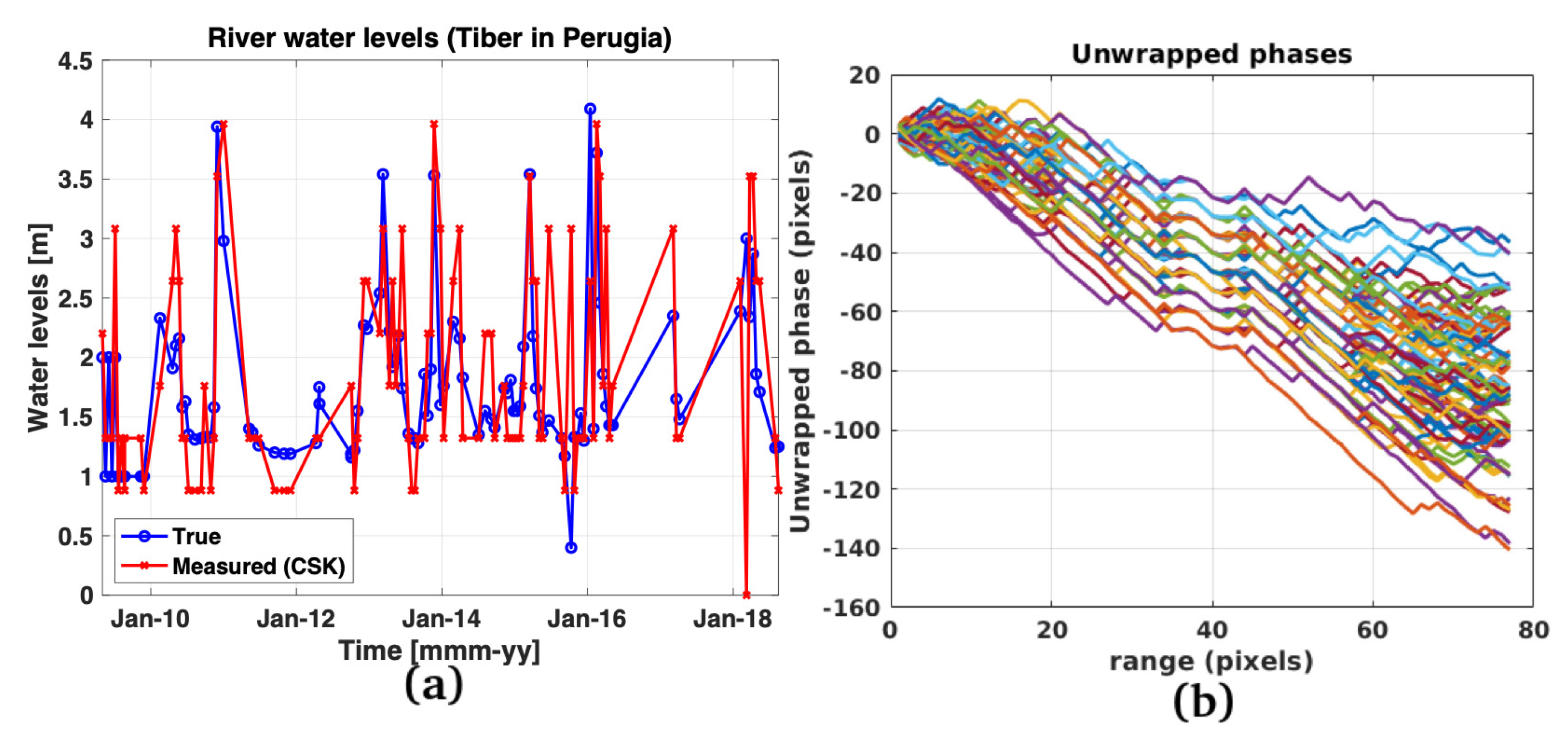
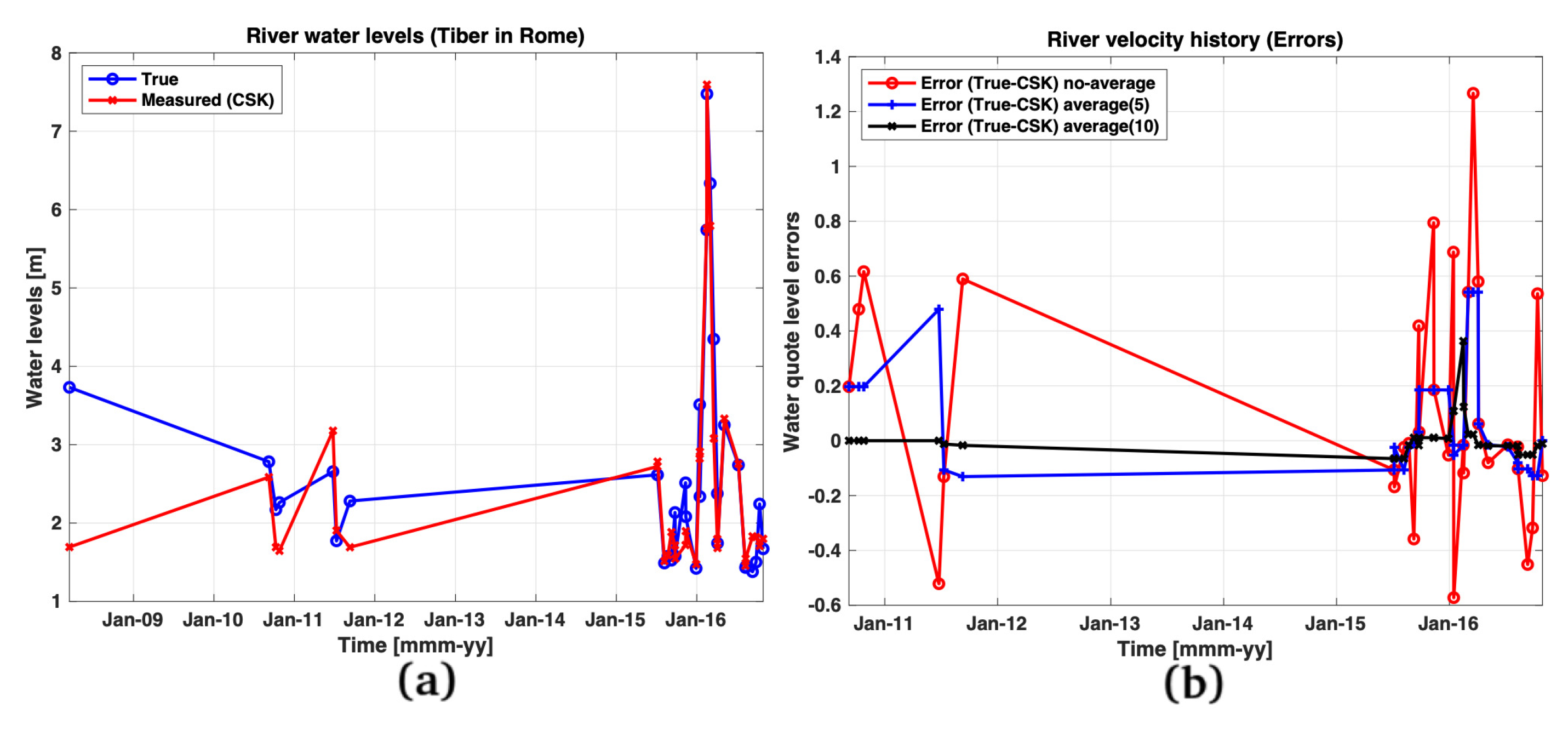
4. Test on Cosmo-SkyMed Data
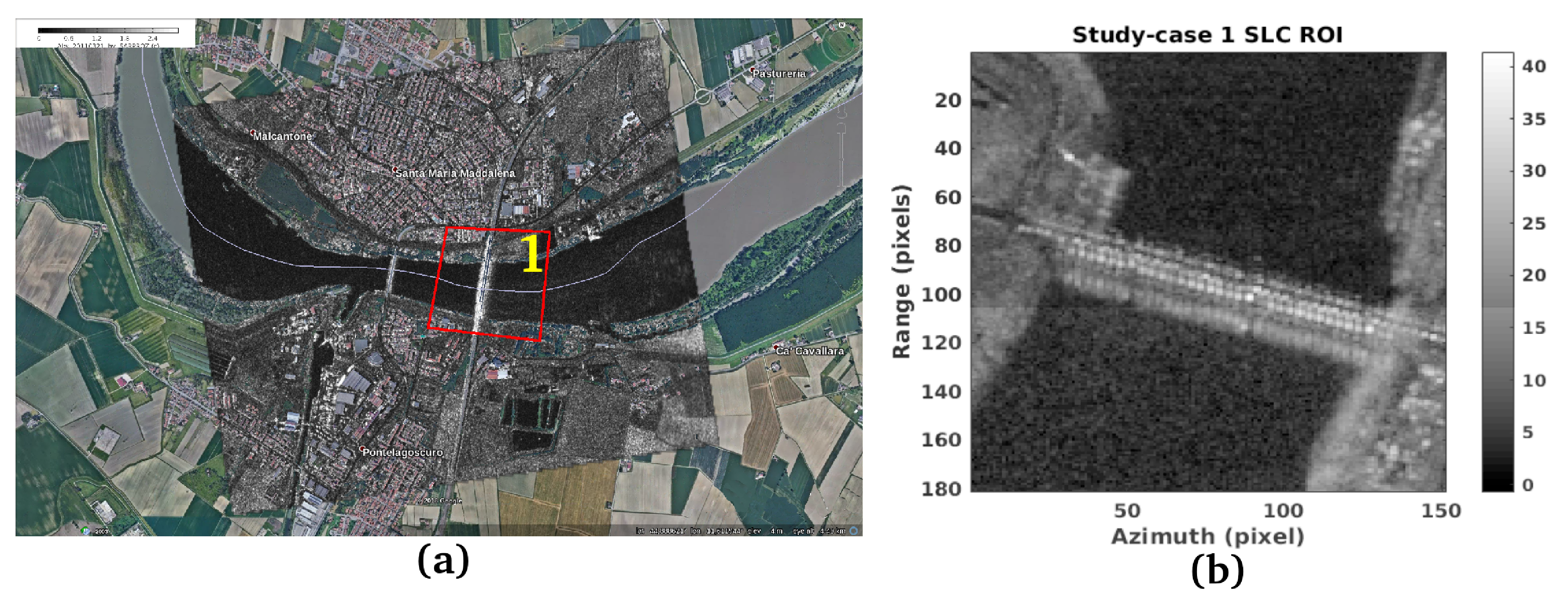
4.1. Case Studies and In-Situ Observations
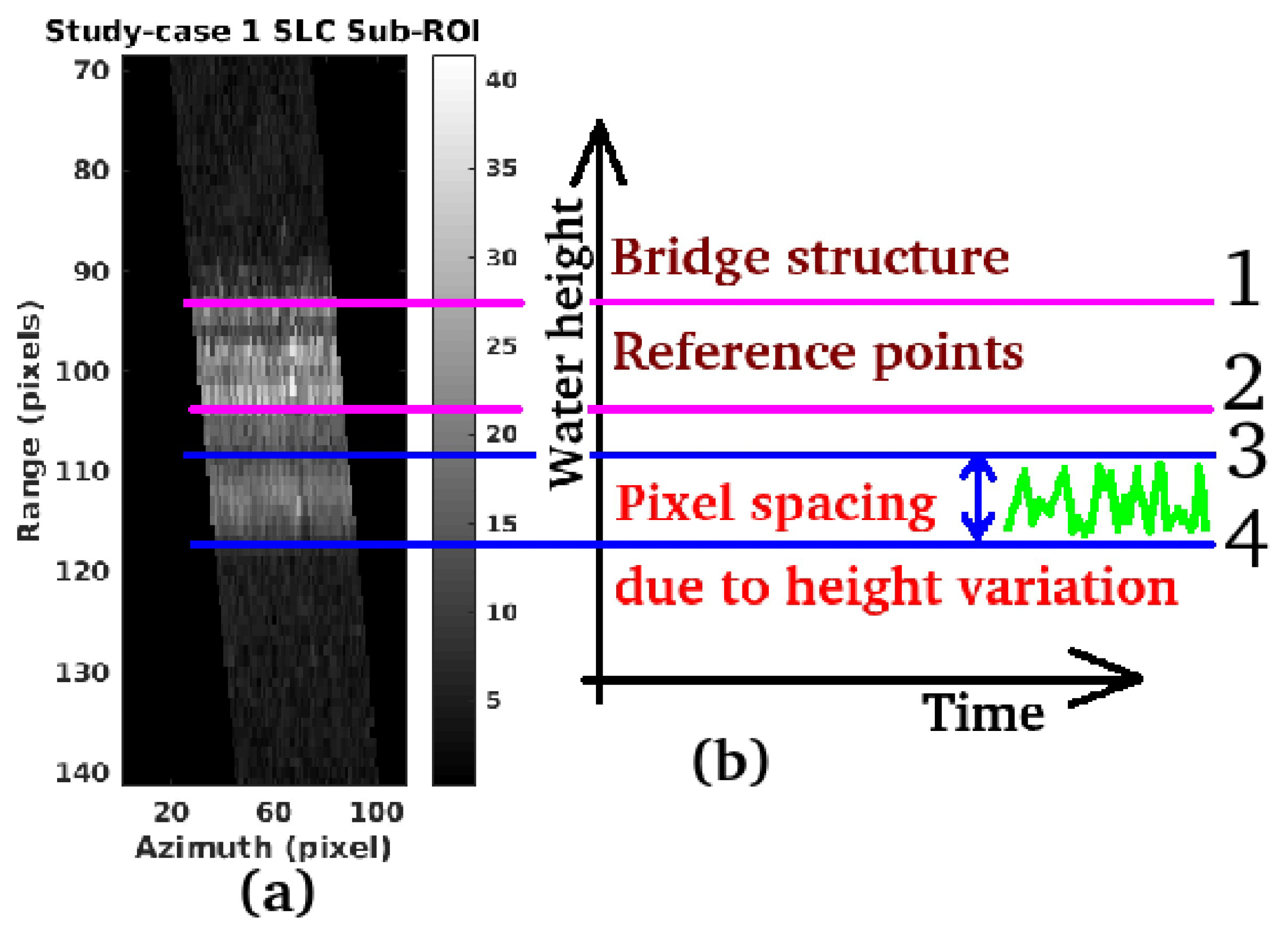
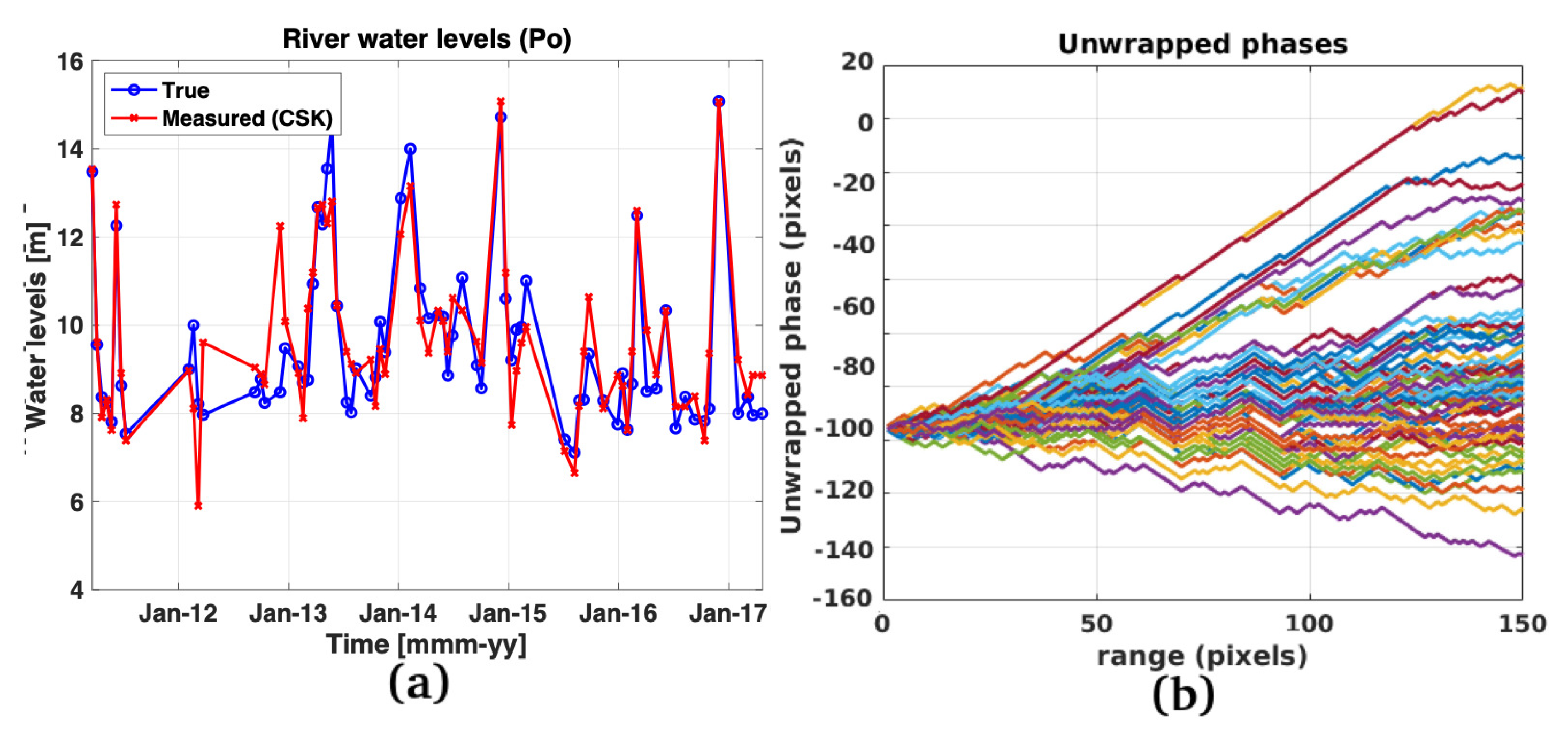
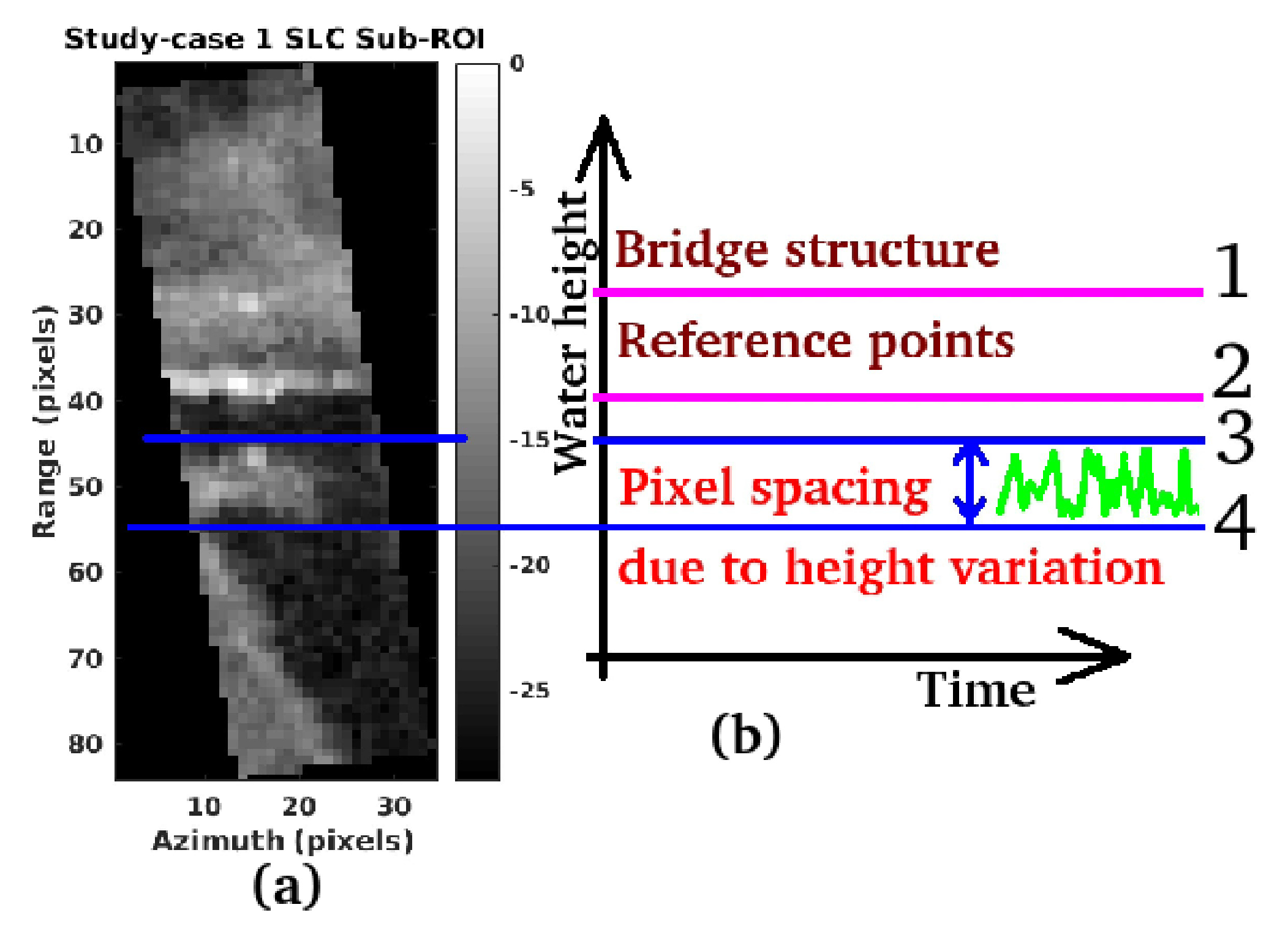
4.2. Experimental Results
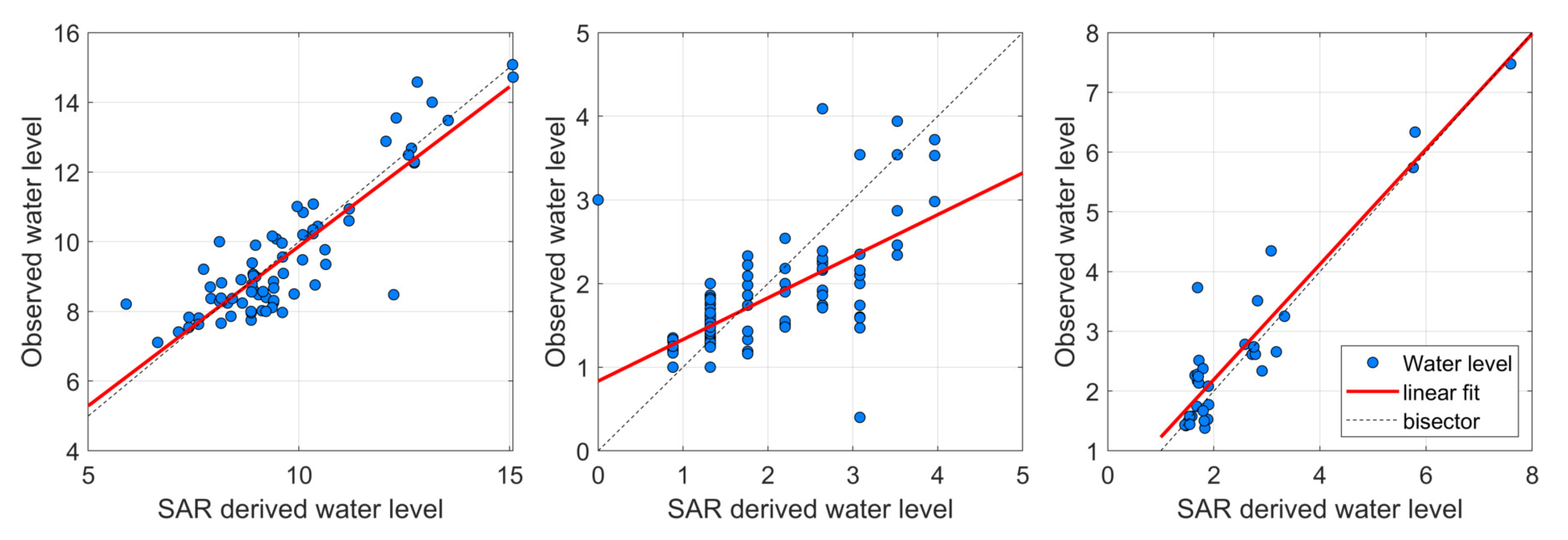
5. Discussion and Performance Assessment
- the Pearsone correlation coefficient (R),
- the Nash-Sutcliffe efficiency (NS) [27],
- the root-mean square error (RMSE), expressed in [m],
- the related root-mean square error (RRMSE), defined as the ratio between the RMSE and the mean of the observed water levels.
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- McGraw-Hill Book Company. Open Channel Hydraulics, Ven Te Chow, 1959: Open Channel Hydraulics; Open Channel Hydraulics, Kogakusha: Tokyo, Japan, 1959. [Google Scholar]
- Hannah, D.M.; Demuth, S.; van Lanen, H.A.J.; Looser, U.; Prudhomme, C.; Rees, G.; Stahl, K.; Tallaksen, L.M. Large-scale river flow archives: Importance, current status and future needs. Hydrol. Process. 2011, 25, 1191–1200. [Google Scholar] [CrossRef]
- Smith, L.C. Satellite remote sensing of river inundation area, stage, and discharge: A review. Hydrol. Process. 1997, 11, 1427–1439. [Google Scholar] [CrossRef]
- Bjerklie, D.M.; Dingman, S.L.; Vorosmarty, C.J.; Bolster, C.H.; Congalton, R.G. Evaluating the potential for measuring river discharge from space. J. Hydrol. 2003, 278, 17–38. [Google Scholar] [CrossRef]
- Bjerklie, D.M.; Moller, D.; Smith, L.C.; Dingman, S.L. Estimating discharge in rivers using remotely sensed hydraulic information. J. Hydrol. 2005, 309, 191–209. [Google Scholar] [CrossRef]
- Bjerklie, D.M. Estimating the bankfull velocity and discharge for rivers using remotely sensed river morphology information. J. Hydrol. 2007, 341, 144–155. [Google Scholar] [CrossRef]
- Koblinsky, C.J.; Clarke, R.T.; Brenner, A.C.; Frey, H. Measurement of River Level Variations with Satellite Altimetry. Water Resour. Res. 1993, 29, 1839–1848. [Google Scholar] [CrossRef]
- Biancamaria, S.; Frappart, F.; Leleu, A.S.; Marieu, V.; Blumstein, D.; Desjonquères, J.D.; Boy, F.; Sottolichio, A.; Valle-Levinson, A. Satellite radar altimetry water elevations performance over a 200 m wide river: Evaluation over the Garonne River. Adv. Space Res. 2016, 59, 128–146. [Google Scholar] [CrossRef]
- Normandin, C.; Frappart, F.; Diepkilé, A.T.; Marieu, V.; Mougin, E.; Blarel, F.; Lubac, B.; Nadine, B.; Abdramane, B. Evolution of the Performances of Radar Altimetry Missions from ERS-2 to Sentinel-3A over the Inner Niger Delta. Remote Sens. 2018, 10, 833. [Google Scholar] [CrossRef]
- Schneider, R.; Tarpanelli, A.; Nielsen, K.; Madsen, H.; Bauer-Gottwein, P. Evaluation of multi-mode Cryosat-2 altimetry data over the Po River against in situ data and a hydrodynamic model. Adv. Water Resour. 2018, 112, 17–26. [Google Scholar] [CrossRef]
- Fu, L.L.; Alsdorf, D.; Rodríguez, E.; Morrow, R.; Mognard, N.; Lambin, J.; Vaze, P.; Lafon, T. The SWOT (Surface Water and Ocean Topography) Mission: Spaceborne Radar Interferometry for Oceanographic and Hydrological Applications. In Proceedings of the OceanObs’09: Sustained Ocean Observations and Information for Society, Venice, Italy, 21–25 September 2009; Hall, J., Harrison, D.E., Stammer, D., Eds.; ESA Publication WPP-306: New York, NY, USA, 2009; Volume 2. [Google Scholar]
- Matgen, P.; Schumann, G.; Henry, J.B.; Hoffmann, L.; Pfister, L. Integration of SAR-derived river inundation areas, high-precision topographic data and a river flow model toward near real-time management. Int. J. Appl. Earth Obs. Geoinf. 2007, 9, 247–263. [Google Scholar] [CrossRef]
- Goldstein, R.M.; Richard, M.; Zebker, H.A. Interferometric radar measurement of ocean surface currents. Nature 1987, 328, 707–709. [Google Scholar] [CrossRef]
- Romeiser, R.; Breit, H.; Eineder, M.; Runge, H.; Flament, P.; De Jong, K.; Vogelzang, J. Current measurements by SAR along-track interferometry from a Space Shuttle. IEEE Trans. Geosci. Remote Sens. 2005, 43, 2315–2324. [Google Scholar] [CrossRef]
- Nitti, D.O.; Hanssen, R.F.; Refice, A.; Bovenga, F.; Nutricato, R. Impact of DEM-assisted coregistration on high-resolution SAR interferometry. IEEE Trans. Geosci. Remote Sens. 2011, 49, 1127–1143. [Google Scholar] [CrossRef]
- Michel, R.; Avouac, J.P.; Taboury, J. Measuring ground displacements from SAR amplitude images: Application to the Landers earthquake. Geophys. Res. Lett. 1999, 26, 875–878. [Google Scholar] [CrossRef]
- Strozzi, T.; Luckman, A.; Murray, T.; Wegmuller, U.; Werner, C.L. Glacier motion estimation using SAR offset-tracking procedures. IEEE Trans. Geosci. Remote Sens. 2002, 40, 2384–2391. [Google Scholar] [CrossRef] [Green Version]
- Casu, F.; Manconi, A. Four-dimensional surface evolution of active rifting from spaceborne SAR data. Geosphere 2016, 12, 697–705. [Google Scholar] [CrossRef] [Green Version]
- Biondi, F. COSMO-SkyMed Staring Spotlight SAR Data for Micro-Motion and Inclination Angle Estimation of Ships by Pixel Tracking and Convex Optimization. Remote Sens. 2019, 11, 766. [Google Scholar] [Green Version]
- Biondi, F.; Addabbo, P.; Clemente, C.; Orlando, D. Micro-Motion Estimation of Maritime Targets Using Pixel Tracking in Cosmo-Skymed Synthetic Aperture Radar Data: An Operative Assessment. Remote Sens. 2019, 11, 1637. [Google Scholar] [CrossRef]
- Oetken, G.; Parks, T.W.; Schussler, H. New results in the design of digital interpolators. IEEE Trans. Acoust. Speech Signal Process. 1975, 23, 301–309. [Google Scholar] [CrossRef]
- Goldstein, R.M.; Zebker, H.A.; Werner, C.L. Satellite radar interferometry: Two-dimensional phase unwrapping. Radio Sci. 1988, 23, 713–720. [Google Scholar] [CrossRef] [Green Version]
- Wang, Z.; Perissin, D.; Lin, H. Subway tunnels identification through Cosmo-SkyMed PSInSAR analysis in Shanghai. In Proceedings of the 2011 IEEE International Geoscience and Remote Sensing Symposium, Vancouver, BC, Canada, 24–29 July 2011. [Google Scholar]
- Ullo, S.L.; Addabbo, P.; Di Martire, D.; Sica, S.; Fiscante, N.; Cicala, L.; Angelino, C.V. Application of DInSAR Technique to High Coherence Sentinel-1 Images for Dam Monitoring and Result Validation Through In Situ Measurements. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 875–890. [Google Scholar] [CrossRef]
- Richards, M.A. Fundamentals of Radar Signal Processing; Tata McGraw-Hill Education: New York, NY, USA, 2005. [Google Scholar]
- Biondi, F.; Clemente, C.; Orlando, D. An atmospheric phase screen estimation strategy based on multi-chromatic analysis for differential interferometric synthetic aperture radar. IEEE Trans. Geosci. Remote Sens. 2019. [Google Scholar] [CrossRef]
- Nash, J.; Sutcliffe, J. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
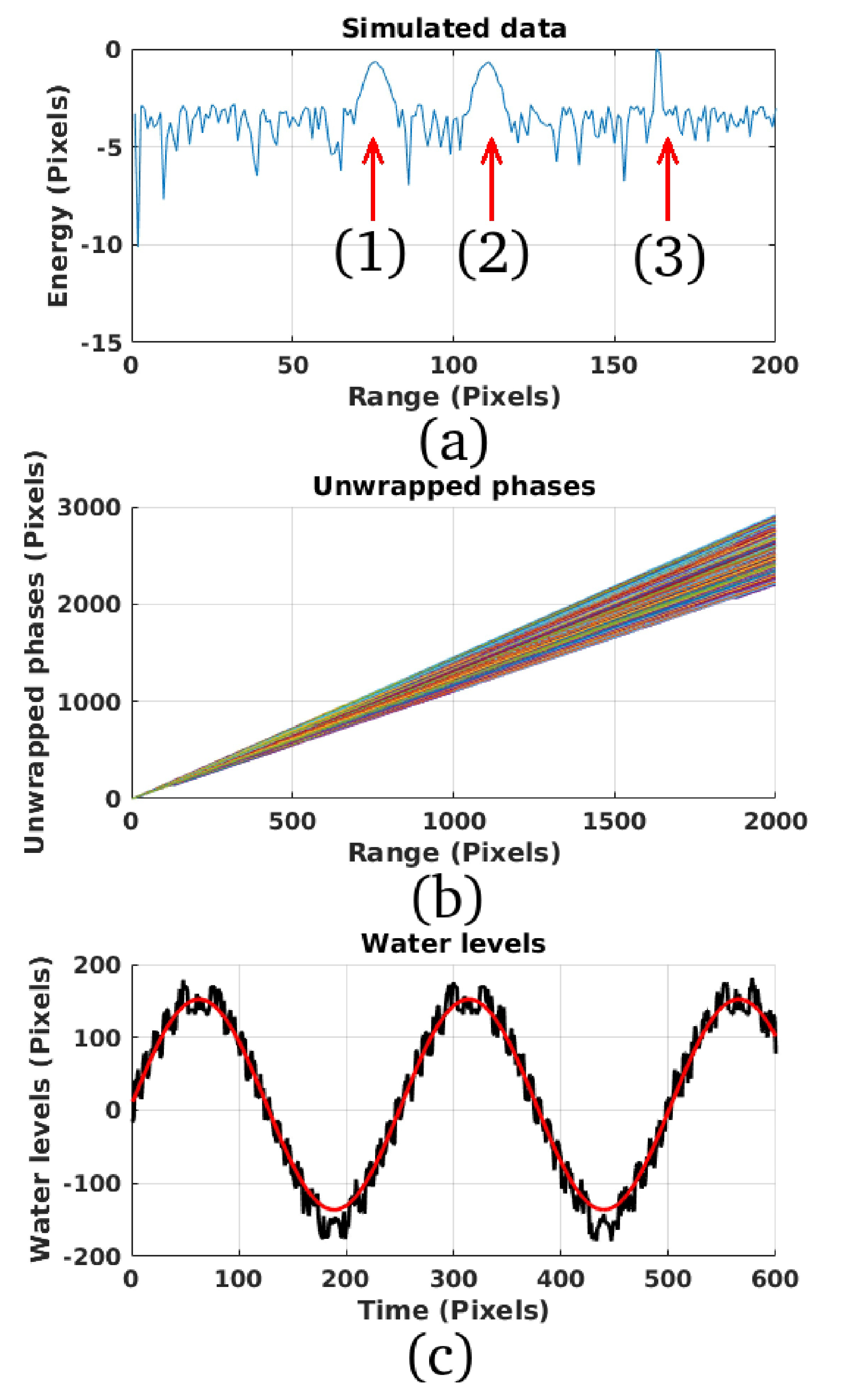
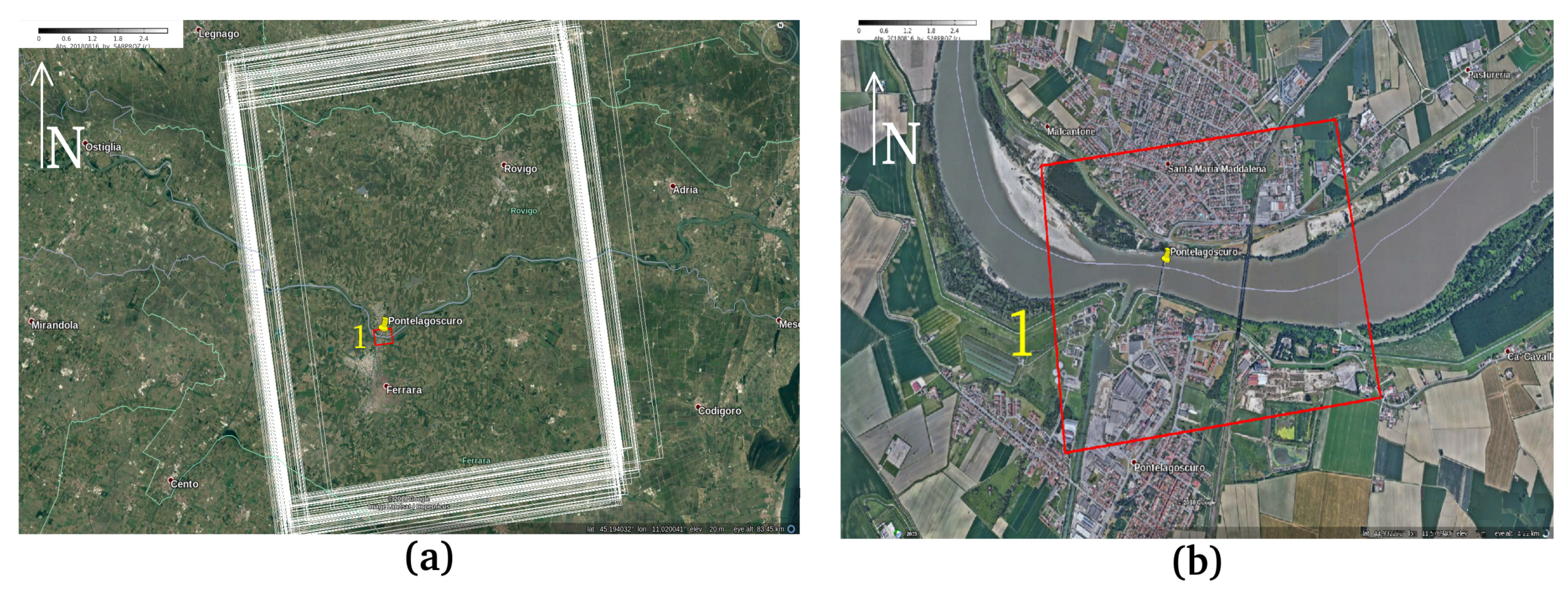
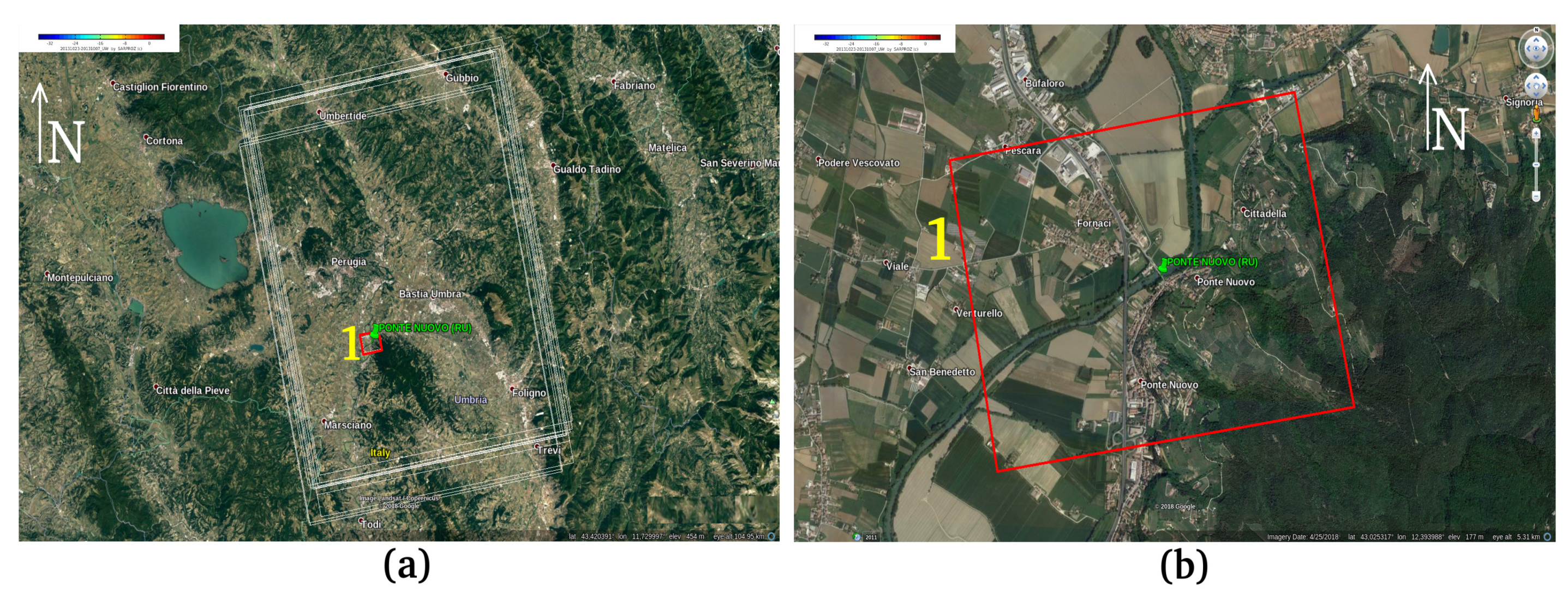
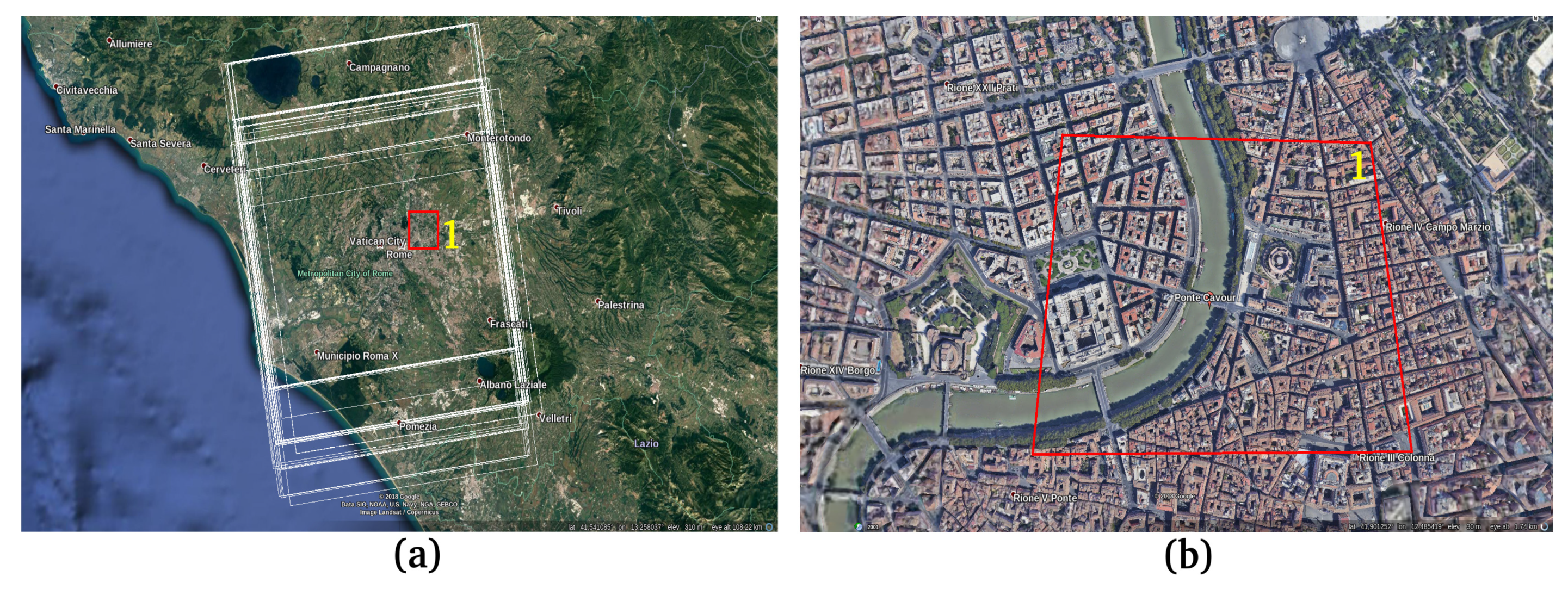


| STATION | RIVER | COORDINATES (WGS-84) | Time of Obs. | Images Number | River Width [m] |
|---|---|---|---|---|---|
| Pontelagoscuro | Po | 445318.84N, 113628.89 E | May 2009–Aug. 2018 | 106 | 340 |
| Ponte Nuovo | Tiber | 4300′37.11 N, 122545.15 E | Mar. 2011–Apr. 2017 | 76 | 60 |
| Ripetta | Tiber | 415417.59 N 122827.84 E | Sept. 2009–Oct. 2016 | 37 | 100 |
| Parameter | Value |
|---|---|
| Initial shifts | Coarse cross-correlation |
| Number of points | 4000 |
| Correlation threshold | 0.8 |
| Oversampling factor | 200 |
| search pixel window | 48x48 pixel |
| Points skimming (minimum points) | 30 |
| Use of DEM | Yes |
| Doppler Centr. Est. Strategy | Polynomials |
| STATION | R | NS | RMSE [m] | RRMSE |
|---|---|---|---|---|
| Pontelagoscuro | 0.88 | 0.77 | 0.91 | 0.10 |
| Ponte Nuovo | 0.65 | −0.03 | 0.68 | 0.39 |
| Ripetta | 0.93 | 0.85 | 0.55 | 0.21 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Biondi, F.; Tarpanelli, A.; Addabbo, P.; Clemente, C.; Orlando, D. Pixel Tracking to Estimate Rivers Water Flow Elevation Using Cosmo-SkyMed Synthetic Aperture Radar Data. Remote Sens. 2019, 11, 2574. https://doi.org/10.3390/rs11212574
Biondi F, Tarpanelli A, Addabbo P, Clemente C, Orlando D. Pixel Tracking to Estimate Rivers Water Flow Elevation Using Cosmo-SkyMed Synthetic Aperture Radar Data. Remote Sensing. 2019; 11(21):2574. https://doi.org/10.3390/rs11212574
Chicago/Turabian StyleBiondi, Filippo, Angelica Tarpanelli, Pia Addabbo, Carmine Clemente, and Danilo Orlando. 2019. "Pixel Tracking to Estimate Rivers Water Flow Elevation Using Cosmo-SkyMed Synthetic Aperture Radar Data" Remote Sensing 11, no. 21: 2574. https://doi.org/10.3390/rs11212574
APA StyleBiondi, F., Tarpanelli, A., Addabbo, P., Clemente, C., & Orlando, D. (2019). Pixel Tracking to Estimate Rivers Water Flow Elevation Using Cosmo-SkyMed Synthetic Aperture Radar Data. Remote Sensing, 11(21), 2574. https://doi.org/10.3390/rs11212574