1. Introduction
Vertical and horizontal forest-structure information is essential for many aspects of global ecosystem studies. For example, the tree height and vegetation gap fraction are the key parameters used to calculate the above ground biomass. Biomass represents the carbon store of forest cover. The accurate assessment of the carbon storage of forest cover over large areas is essential to the quantitative measurement and modeling of the global carbon ecosystem. Three-dimensional forest-structure data represent the different successive stages of forest ecosystems and are good indicators of ecosystem processes, such as natural and anthropogenic disturbances. Further, more accurate knowledge of vertical foliage profiles is essential to obtaining an accurate estimate of light profiles for photosynthesis. In essence, forest-structure data are important for many ecosystem process studies. However, measuring the 3D canopy structure from the ground is difficult and time consuming. Remote estimation of vegetation-structure characteristics is an essential tool for advancing 3D vegetation-structure parameter estimation for many ecosystem modeling studies.
Over many remote sensing measurements, vegetation LiDAR (light detection and ranging) and multi-angular optical remote sensing measurements provide direct and indirect vegetation-structure measurements. The potential use of laser technology to measure tree canopy heights was first documented by Nelson [
1]. Only recently has its potential use been recognized, with more and more airborne and spaceborne LiDAR and multi-angular data available. The global LiDAR data collected using the spaceborne-geoscience laser altimeter system (GLAS) (part of the ICESat mission with a 70 m footprint) are available [
2]. Further, the airborne data collected by the laser vegetation imaging sensor (LVIS) (with a 25 m footprint) over several large areas are better used to characterize vegetation structures [
3]. These data will soon provide vegetation-structure data on a global scale via ICESat measurements [
4] or at large regional scales via LVIS measurements [
5]. Further, many small-footprint LiDAR data, also called terrain LiDAR data, have been collected in many small regions. Many vegetation-structure parameters and ground elevations have been derived from canopy LiDAR data [
6]. For example, canopy height is calculated as the distance between the first significant return above a threshold and the ground [
7,
8,
9,
10,
11]. Airborne LiDAR is more suitable for measuring tree height than ground measurements, especially when the crown cannot be viewed clearly [
12,
13]. Moreover, the LiDAR-derived tree height and gap is used as a true value. Tree canopy size and gap are usually related to photosynthesis, nutrient cycling, energy transfer, and light transmission to the understory vegetation, and these properties affect tree growth. The canopy gap determines the laser echo energy and can be directly calculated by the cumulative laser return from the canopy to the height divided by the total returns from the canopy and the ground, and is adjusted by a ratio to account for the differences in the ground and canopy reflectance at the laser wavelength [
14]. Both the canopy cover and canopy height are parameters describing horizontal and vertical foliage distribution, which provide not only the horizontal structure but also the vertical vegetation-structure data suitable for ecosystem studies.
However, both the spaceborne and airborne LiDAR data can only accurately provide vegetation-structure information at sparse sampling points. Thus, there is a need to find a different, more conventional, remote sensing modality with more complete geographic coverage. Compared with traditional nadir-viewed remote sensing, a multiangular sensor can provide three-dimensional structural information of a forest via different directional observations. Multiangular remote sensing measures the shape of the bidirectional reflectance distribution factor (BRDF), which show links to the canopy’s structure [
15,
16,
17,
18]. Many models have been developed to link vegetation-structure parameters and BRDF [
19,
20]. However, multiangular remote sensing suffers from not being able to directly derive structural canopy measurements in the estimation of biomass without the inversion of these physical models. The geometric-optical BRDF model using spatial variance in single-view thematic mapper images has shown some early success in retrieval of the canopy cover, but biomass and forest-structure parameters were retrieved only with difficulty [
21,
22]. There have been some recent efforts to derive structural information using semi-physical BRDF models to better use advanced MODIS and multiangular imaging spectroradiometer (MISR) sensors on the current EOS-TERRA and AQUA platforms [
23,
24]. Chen, et al. [
25,
26] recently mapped horizontal foliage clumping using the anisotropic indexes, which are the normalized reflectance differences at hot-spot and cold-spot sampling directions. However, these structural data are not directly linked to the parameters important to biomass and vertical light profiles, and the hot-spot and cold-spot reflectance cannot usually be taken by multi-angular sensors, such as MODIS, MISR, and CHIRS(Compact High Resolution Imaging Spectrometer), because the hot-spot’s and cold-spot’s angles always change according to the imaging location and imaging time. Kimes, et al. [
27] developed multivariate linear regression and neural network models to predict the LVIS forest energy height measurements from 28 airborne multiangular imaging spectroradiometer (AirMISR). However, the sensitive angles and bands of the models always change according to different study sites. A universal model or multiangular index without study site restrictions should be developed to retrieve vegetation’s structural parameters using BRDF data.
Taken together, these studies show that canopy structural information is contained in multiangular reflectance measurements, but structural parameters remain difficult to retrieve directly by the inversion of remotely sensed data, especially at coarse spatial scales. However, it is possible to develop a relationship between multiangular data and vegetation-structure parameters based on LiDAR data, using these relationships to map the vegetation-structure parameters from multiangular data. Both the airborne LVIS data and airborne multiangular imaging spectroradiometer (AirMISR) data were collected in several large regions at the same spatial scale for nearly the same period, which facilitated this kind of study. The major purpose of this study was to explore the relationships between vegetation-structure parameters and multiangular data via the anisotropic index, calculated based on the AirMISR data in a Howland conifer forest assessed with airborne LiDAR data.
5. Discussion
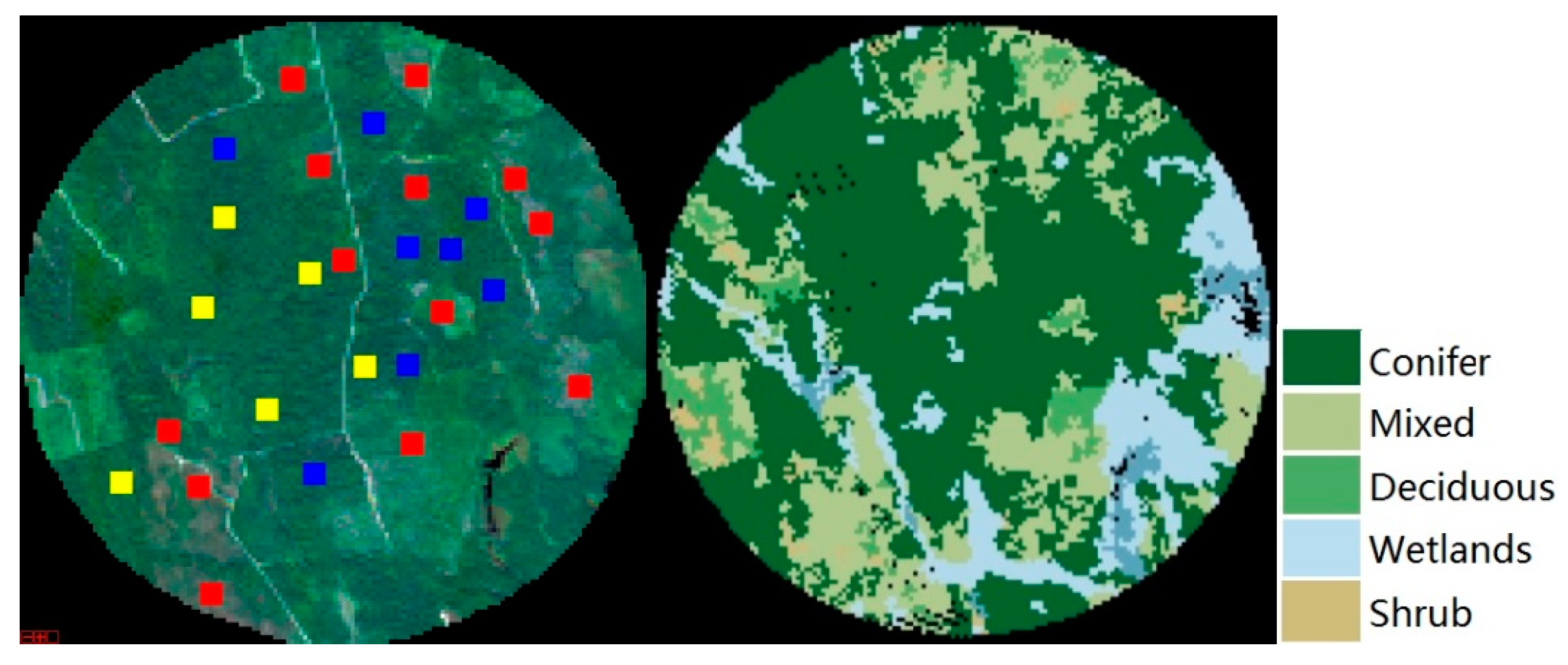
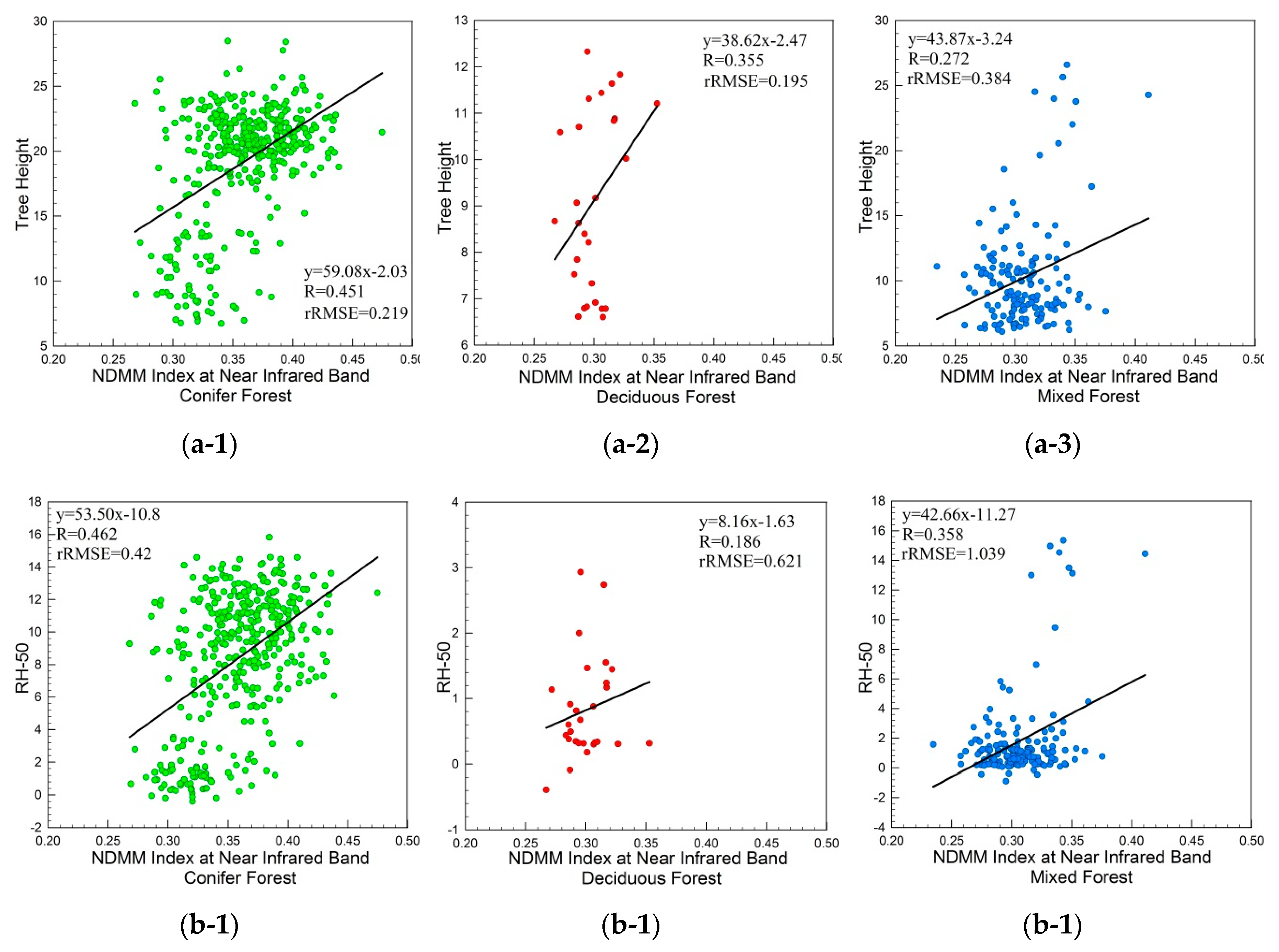
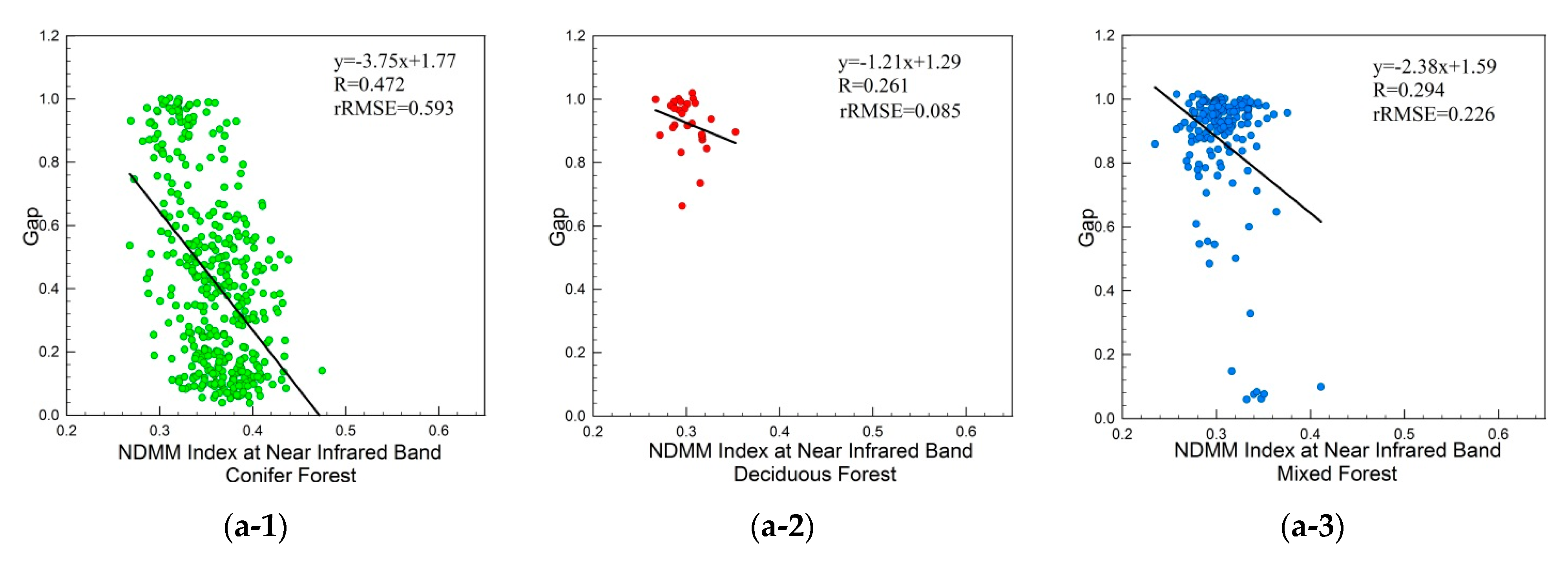
The ratios of the ground’s laser energy returns over the total laser energy returns in
Figure 2(b-1), (a-1) gradually increase, and the tree heights in
Figure 2(b-1),(a-1) gradually decrease. This occurs because under the same site conditions and the same species, when the tree height is small and the canopy width is relatively small, the gaps between the trees and leaves are relatively high. As the trees grow, although some trees die due to intraspecific competition, these gaps decrease with an increase in the canopy’s horizontal and vertical size. Usually, taller trees or trees with larger crown layers are bigger trees that have smaller gaps between their trees and leaves (without human intervention). However, these gaps are not exactly equivalent to the cover. The gaps are three-dimensional parameters used to describe the gaps from the top to the underside of the canopy between the trees, and between the leaves and twigs within the canopy. Moreover, traditional cover only describes the horizontal structure of the canopy. For small and dense trees, their horizontal cover is high, and their gaps are also relatively high because the layer of a small tree canopy is thin, and most LiDAR pulses can penetrate the canopy and return from the ground to the LiDAR sensor.
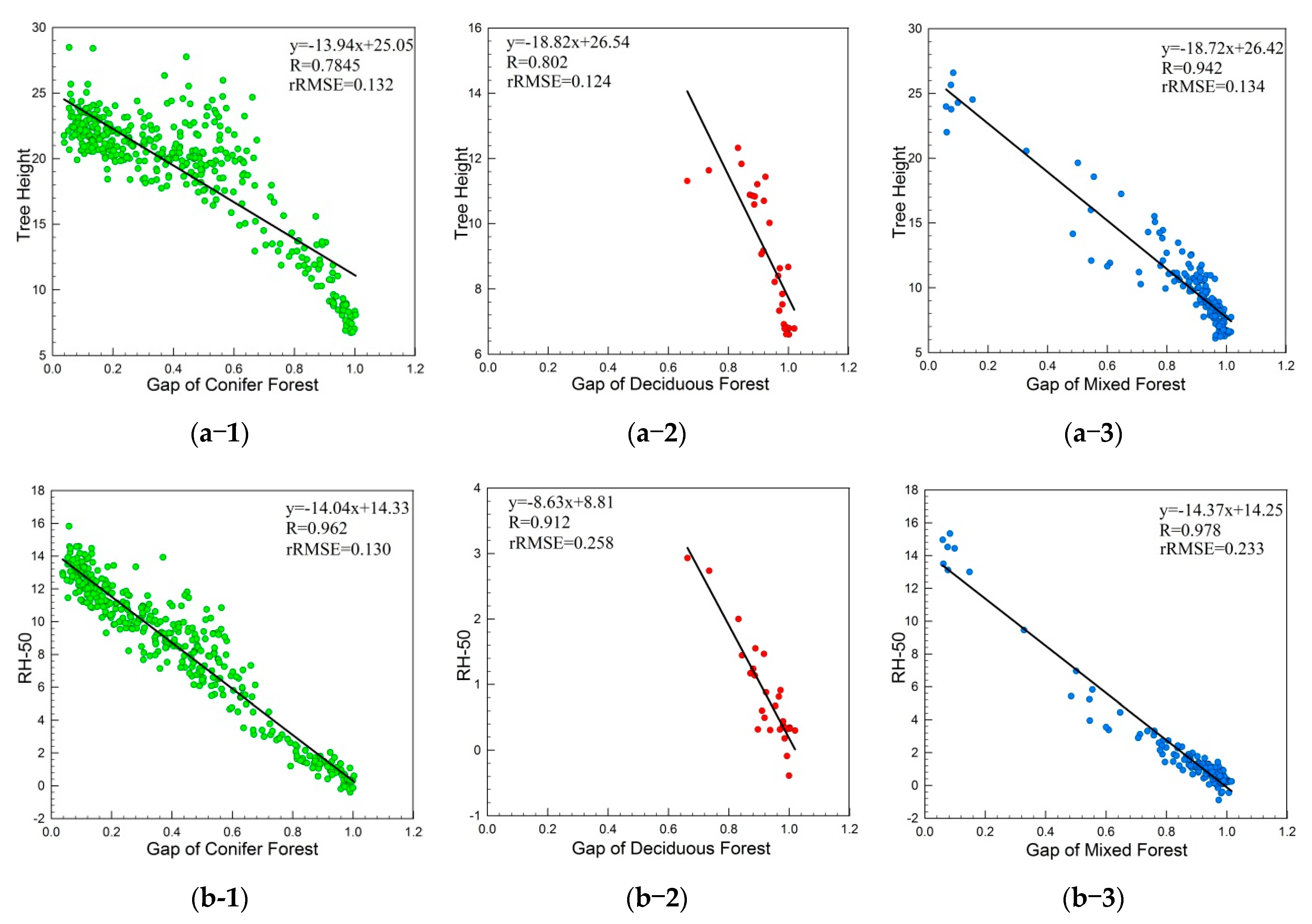
In this paper, three pieces of information were determined from the results. Firstly,
Figure 6 and
Figure 9 show that the relationships between the LiDAR-derived tree height, gap fraction, and NDMM index depend on tree species because the ratio shape for the four components of BRDF changes due to the shadowing effect of the tree canopy, when the sun and viewing directions change. The conifer canopy’s shape is simple and consistent. Its individual canopy is more prominent than that of the deciduous and mixed forests, and there is a better relationship between the NDMM index and canopy structure, which is mainly sensitive to tree height. Secondly,
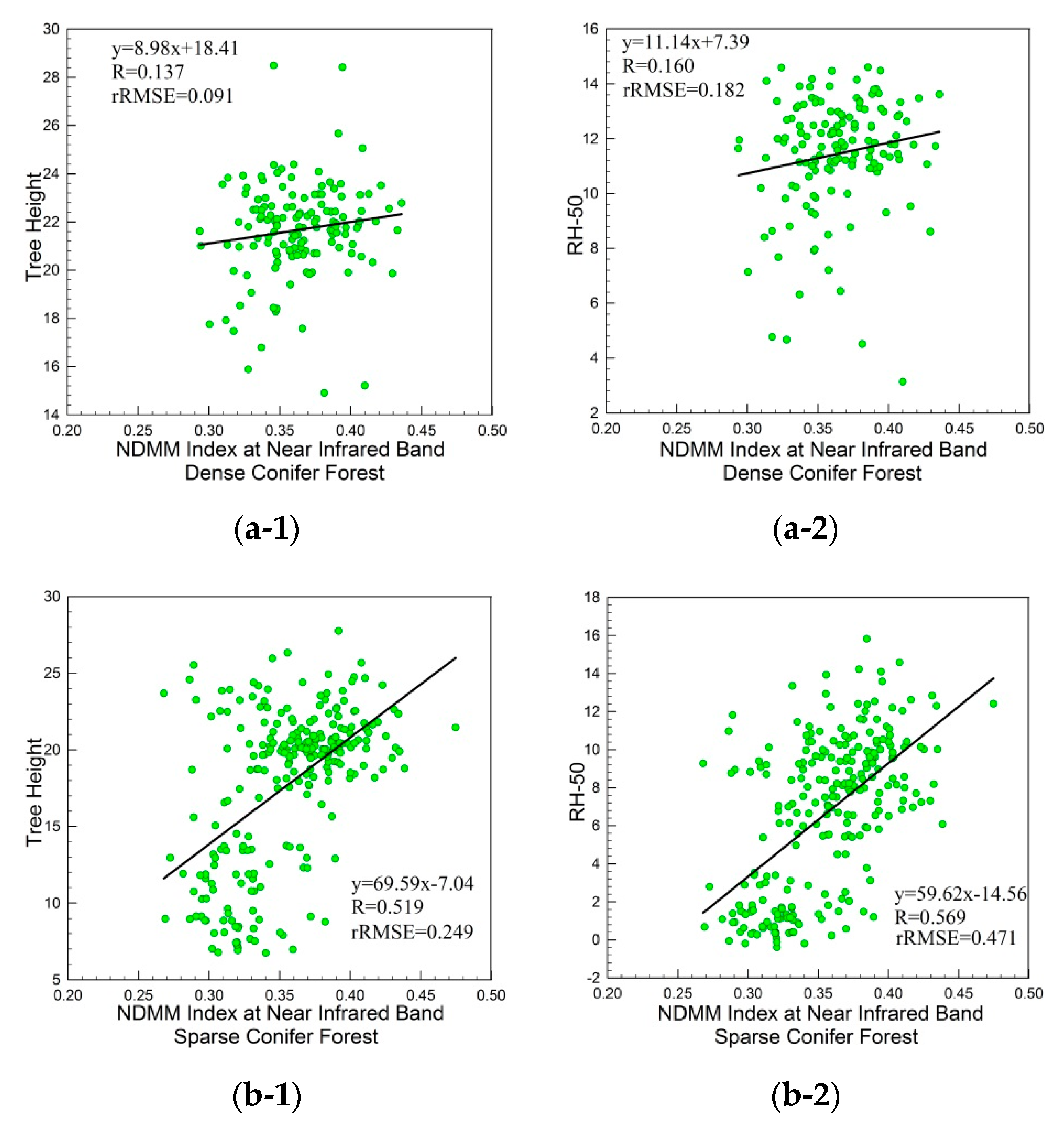
Figure 7 and
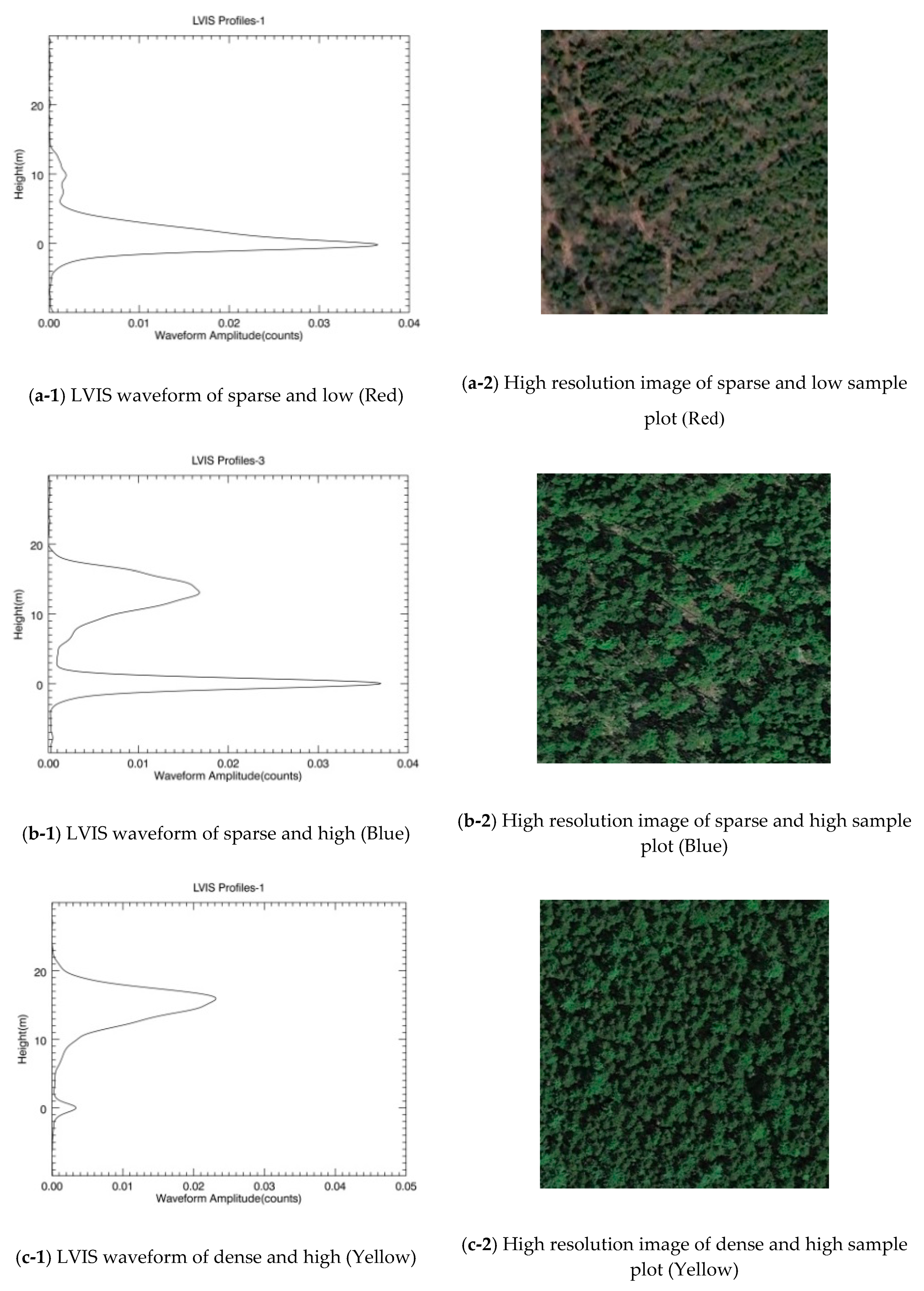
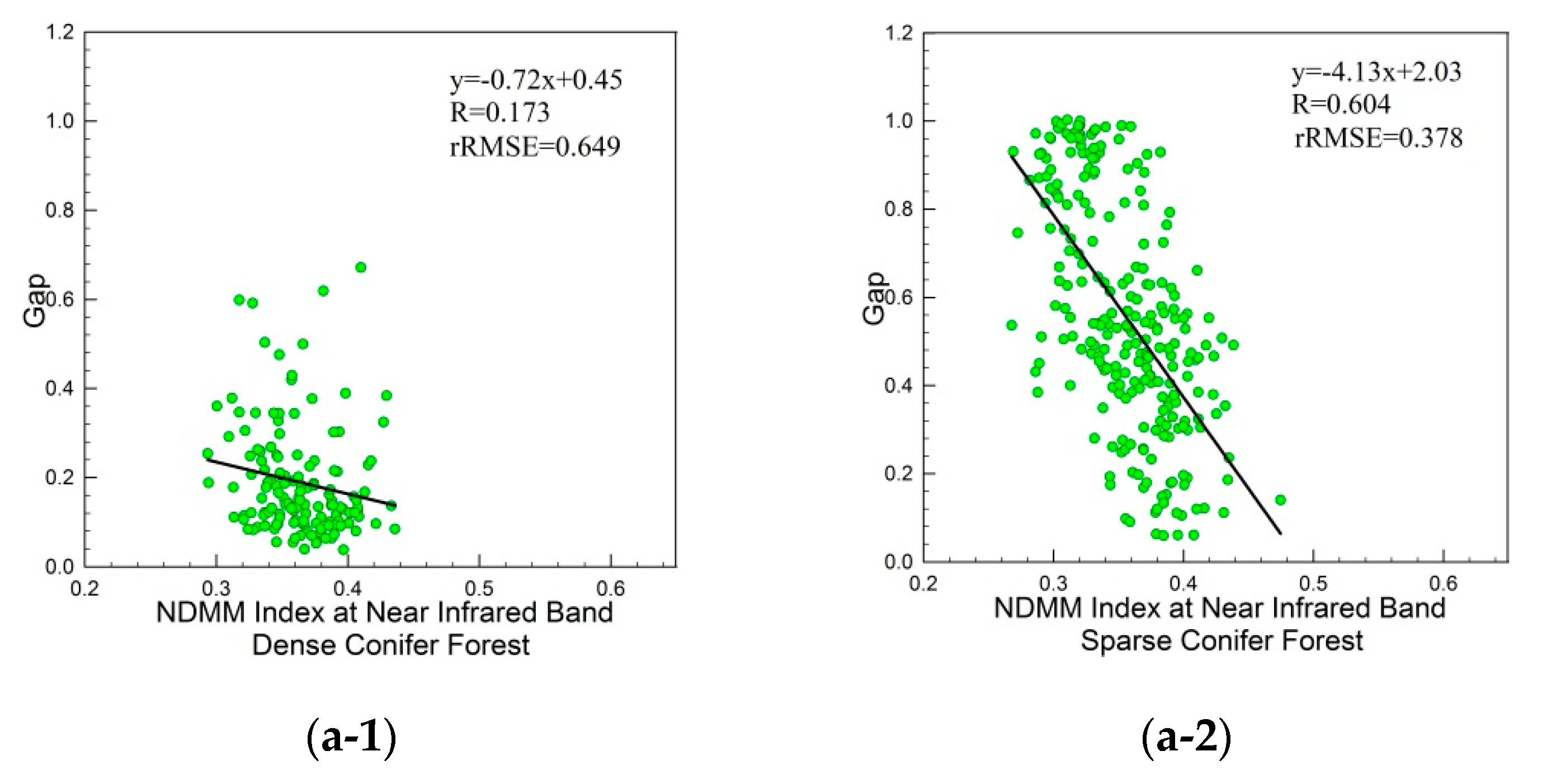
Figure 10 show that these relationships also depend on stand density. The higher the tree height and the larger the NDMM index of the canopy, the lower the tree height and the smaller the NDMM index of the canopy. Especially in the sparse and low (Red) and sparse and high (Blue) research areas, a dark color represents a relatively sparse stand in the tree high map. The NDMM indexes for this region are also small in the thematic NDMM index map. That result shows that the Pearson correlation coefficients between the LiDAR-derived tree height and NDMM index for sparse forest is better than that for density. There is a high overlap between the tree canopies in dense forests, such that the individual tree crowns are not prominent, and the four components cannot vary significantly with the sun and view directions changes. The BRDF curve shape does not change significantly with the zenith angle, and even the NDMM index shows a saturation phenomenon. Because of the high density and overlap, there is intense competition within the tree, which results in a decline of the correlation between tree height and canopy structure parameters. The four components that determine the shape of the BRDF curve have a strong correlation with the tree canopy’s size and distribution, which also determines the relationship between the tree canopy’s structural parameters and the NDMM index. While the stand density is low, the individual tree canopy is prominent, and a change in the four components is sensitive to changes of the zenith angles. The correlation between tree height, gap fraction, and the NDMM index in sparse stands is better than that in dense stands.
Thirdly,
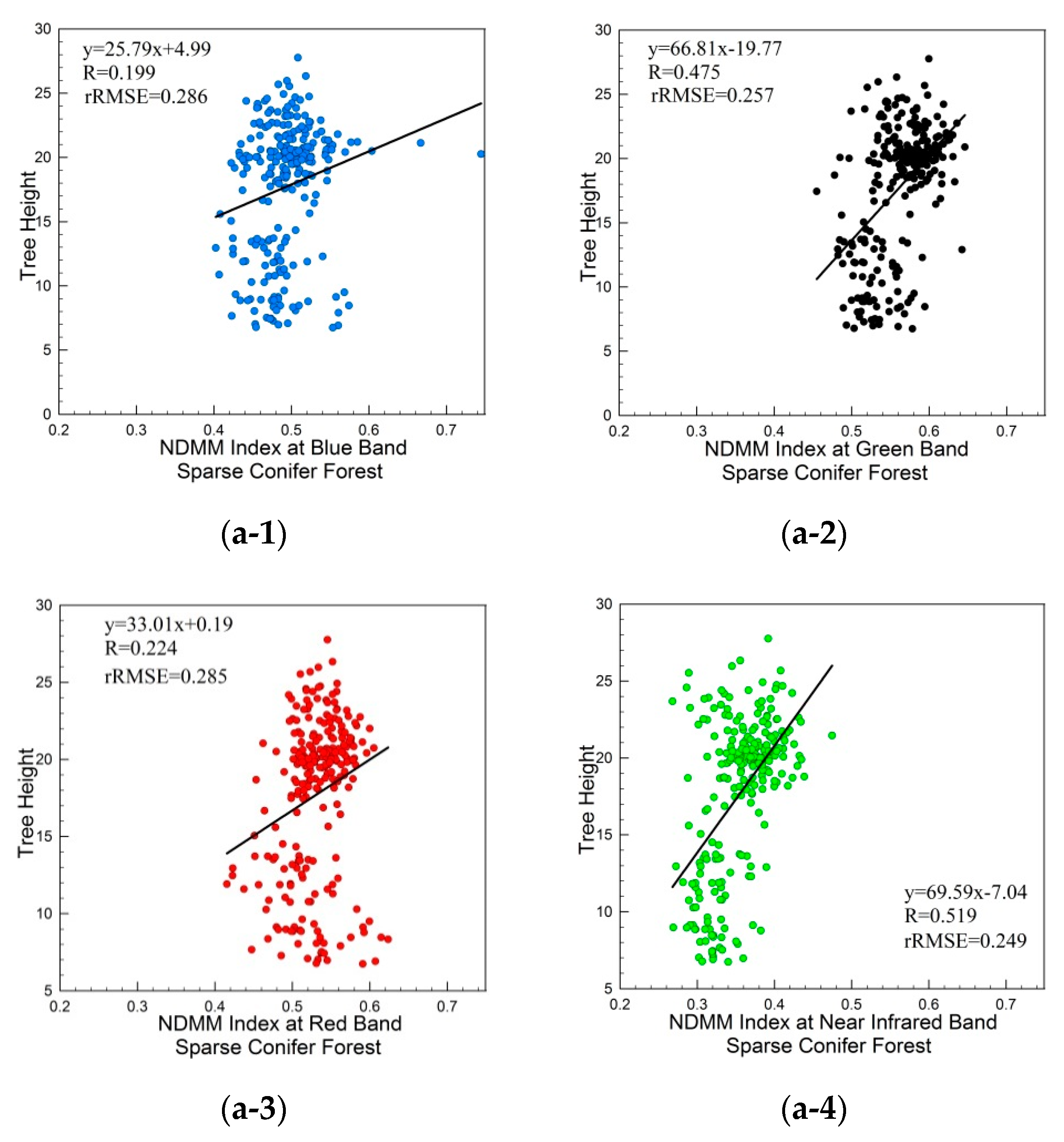
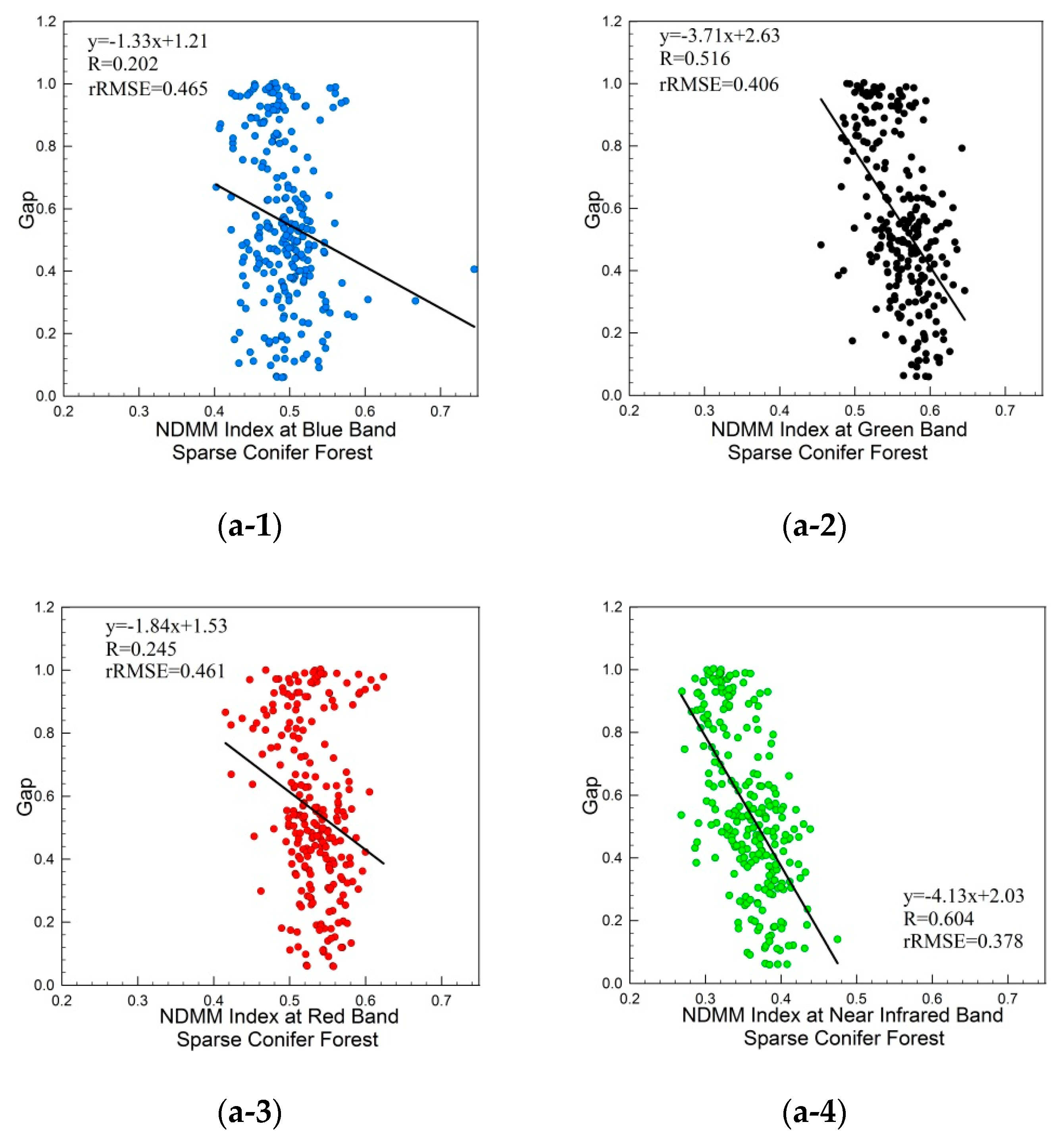
Figure 8 and
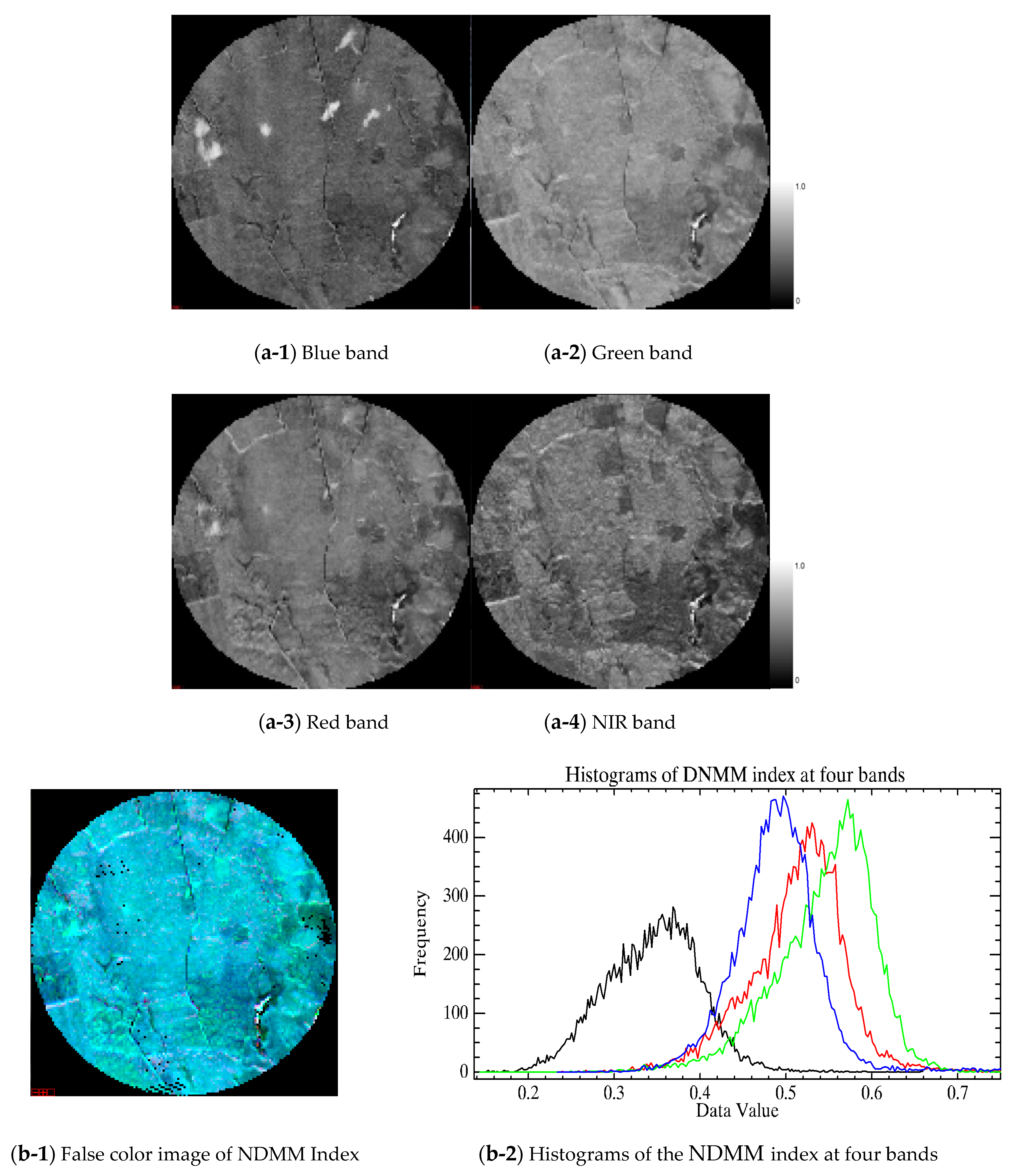
Figure 11 show that the relationships between LiDAR-derived tree height, gap fraction, and NDMM index are also wavelength dependent. Multiple scattering and shadowing are the main reasons for the differences between the near infrared and visible bands. These effects are due to the higher absorption of the green vegetation of red and green bands, and the reflectance of leaves is high, whereas their transmittance and absorption are low at the near-infrared band because the chlorophyll in leaves can perform photosynthesis under sunlight [
32]. The higher single scattering albedo at the near-infrared band leads to more multiple scattering within canopies, among canopies, and between canopies and the background, which results in brighter signatures for all scene components in the near-infrared band than in the blue and red bands. The BRDF value is affected significantly by multi-scatterings between the canopy and backgrounds and among canopies [
33,
34]. The BRDF curves at the near-infrared band are dependent on the ratio of the four components and have a relationship with the tree structure parameters. However, considering orbital imagery, the visible bands with low reflectance are also strongly influenced by shadowing, and at the blue and red bands, the shadowing reflectance is so weak that the BRDF curves at two bands are not dependent on the ration of the four components, so the BRDF shape is not dependent on the canopy structure, and the NDMM index at the blue and red bands is not sensitive to the tree height and gap faction.
Figure 11 also shows a better relationship between the LiDAR-derived tree height and the NDMM index for sparse conifer forests at the near-infrared wavelength than at other visible optical wavelengths, and the NDMM index linearly increases with tree height.
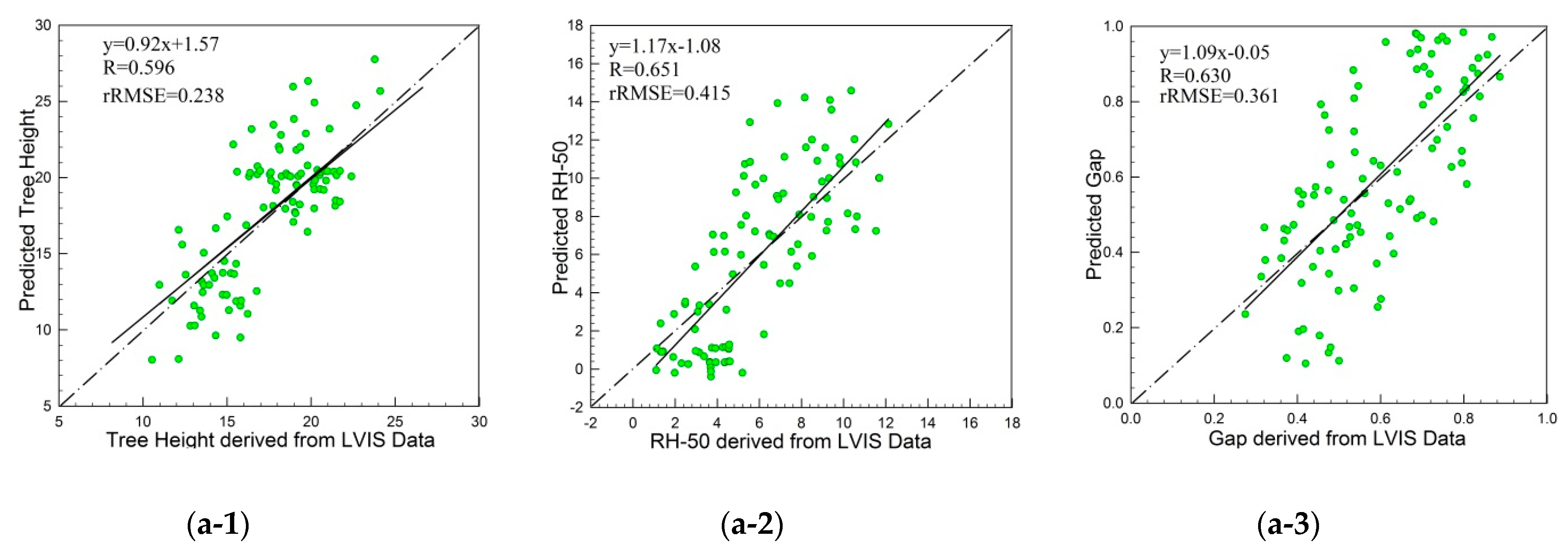
Figure 12 shows the scatterplots for tree height and the gap values derived from LVIS compared to those predicted by the NDMM index at the near-infrared band for sparse confer forests in Howland. In
Figure 12, the dotted line is the 1:1 line, and the solid lines are the scatterplots for the tree height and the gap values derived from LVIS versus those predicted by the NDMM index at the near-infrared band for sparse confer forests in Howland. The LiDAR-derived tree height, gap, and the values predicted by the NDMM index are near the 1:1 line, which indicates that relationships between tree height and gap values are inverted by the NDMM index and LiDAR-derived tree height. The gap values are consistent with the results in
Figure 7(b-1),(b-2) and
Figure 11(a-4). It is known that the BRDF exhibits a half-bowl shape with a peak value in hotspots. That is, when the sun and viewing directions are the same, the higher the tree is and the larger the canopy volume and surface area are, so individual trees are more prominent. There is an increase in the observed sunlit crown components and the relatively bigger canopy; the sunlit crown component is larger than the sunlit background component, which contributes more to the whole BRDF shape. The maximum reflectance value is higher according to the largest area proportion of the sunlit crown component, because the bigger canopy volume and surface area cause the sunlit and shaded crown components to be larger, and the difference between the sunlit and shaded crown components is also larger. The BRDF shows an unsymmetrical shape, with its minimum at an angle in the forward direction (sun and satellite in opposite directions) and its maximum in the backward direction (sun and satellite at the same direction). The differences of the maximum directional reflectance in the forward direction and the minimum directional reflectance in the backward direction are larger and cause the NDMM index to be bigger. On the other hand, with a shorter tree and smaller canopy volume and surface area, there is a decrease in the sunlit crown components observed and a relatively smaller canopy. The difference between sunlit and shaded crown components decreased, so the difference of the maximum directional reflectance in the forward direction and the minimum directional reflectance in the backward direction also decreased and caused the NDMM index to become smaller. As shown in
Figure 7(b-2), when the BRDF value is lower (between 0.25 and 0.35), the height, size, and density of the tree canopy are smaller. However, most of the laser energy transmits through the tree canopy and reaches the background, and the echo energy of the background makes up a large proportion of all the laser echo energy in the footprint, and the RH50 value is less than zero.
Our analysis demonstrates that the NDMM index from visible to near infrared wavelengths increases according to LiDAR-derived tree height and RH50 and decreases with a gap fraction in all three types of forests: conifer, deciduous, and mixed. The BRDF’s shape is directly controlled by the brightness and areal proportions of the sunlit and shaded canopy and background. As the viewing angle changes, these four components are directly related to canopy height and variation, crown size, density, and the spectral properties of the leaves and the background, according to the Geometric Optical-Radiative Transfer (GORT) model. The NDMM index describes the changes in BRDF due to viewing angle differences and is directly linked to vegetation-structure parameters. This study demonstrates a reasonable relationship between BRDF measurements with tree height and the gap fraction derived from LiDAR in sparse conifer forests. However, the multiangular NDMM index used the bidirectional reflection signal of the tree canopy to invert the forest-structure parameters. Moreover, a tree’s canopy is considered to be one of the most important factors that affect the tree’s growth, because a tree canopy intercepts 80% of solar radiation and is the main site of a series of physiological activities, such as photosynthesis, respiration, and transpiration. The size, structure, shape, and spatial distribution of a canopy can directly determine growth vigor, productivity, and overall tree growth. Further, the canopy is one of the main components of individual tree biomass. In particular, the two paramount directional signals, the maximum and minimum angle reflectance, contain the greatest amount of forest canopy information, which is indirectly linked to other forest-structure parameters, such as tree height, forest density, leaf area index (LAI), and even the forest’s biomass.
6. Conclusions
This was an exploratory study to investigate how a single anisotropic index calculated from multiangular measurements is related to the LiDAR-derived vertical structure parameters of vegetation. Based on the result, the physics of the relationships between the multiangular signal and forest canopy structure parameters were studied and assessed using airborne LiDAR data, and multiangular remote sensing data were used to map the forest parameters at larger regions with more complete geographic coverage. We found better relationships between the LiDAR-derived tree height, gap fraction, and NDMM index at the near-infrared band for sparse conifer forests in Howland. The difference between maximum and minimum reflectance from different angles includes the main three-dimensional structural information of a forest canopy. This paper presented a new and potential NDMM index to retrieve the tree heights and gap fractions from multiangular data.
However, for the relationships between the NDMM index and LiDAR-derived tree height, the gap also varies according to tree species, stand density, and wavelength. As the Pearson correlation coefficient between the NDMM index and tree height, the gap fraction shows that the NDMM index for conifer forests is better than those of deciduous and mixed forests. For the relationship between the NDMM index and LiDAR-derived tree height, gap fraction also varies with stand density, and the conifer forest is superior to the dense forest. The results show that the NDMM index at the near-infrared band is better than three other visible bands. Gao, et al. [
24] also showed that an evergreen needle leaf forest has a more constant geometric effect than that of deciduous and mixed forests, and the relationship at blue and red wavelengths is weak, which is consistent with the results of previous studies by Kimes, et al., which show that the relationship at the near infrared wavelength is better.
The BRDF vegetation structure retrieval works better in conifer forests, which indicates that forest biomass retrieval based on the NDMM index can be used to understand how to take advantage of the implied information between multiangular data and forest canopies. In this respect, the feasibility of retrieving the structural properties of a tree canopy from different satellite observations is a challenge. This challenge will provide scientific evidence for more rigorous models. Further studies using GORT models are needed to better understand the physics of the relationships between the NDMM index and the forest canopy’s structural information observed in real airborne LiDAR and AirMISR data. Starting with this paper, better anisotropic factors will be developed to link LiDAR-derived vegetation-structure parameters and multiangular remote sensing data to map vegetation structure parameters at larger regions for carbon cycle studies.