1. Introduction
Precipitation is an important variable in weather and climate research and many other applications. Precipitation data are needed as input for hydrological models, for flood and drought monitoring or for water management in agriculture or power generation. However, estimating precipitation accurately is difficult because of its high spatial and temporal variability. This is especially true for sub-Saharan Africa, where most of the rainfall is produced during the monsoon season by convective rainstorms, which are very localized [
1,
2].
Rain-gauges are the most direct way to measure precipitation. However, the gauge networks in Africa are not dense enough to derive high resolution precipitation estimates. Indeed, the rain-gauge distribution is sparse in many African regions and their number has been decreasing in recent decades [
3]. During the same period, many efforts have been made to derive precipitation estimates from satellite data. Satellites do not measure precipitation directly but have the advantage of covering large areas. This is especially interesting for Africa where gauge networks are sparse and there are also almost no radar observations available.
There is an increasing number of satellite-based rainfall products, providing rainfall estimates at different spatial and temporal resolutions. Most rainfall products use additional sources of data, such as gauge estimates, for bias correction. Bias correction methods focus on correcting the intensity. However, the intensity is not the only possible error in precipitation. Rainfall events are coherent moving systems and, in the case of convective rainstorms, they are also very localized. This can lead to errors in the estimation of the position and shape of the rain events beside the errors in their intensity. For some applications, such as hydrological modeling [
4,
5], flash flood warnings [
6] or data assimilation in a numerical weather model [
7,
8], detecting the correct location of the rain events can be as important as their intensity.
The position errors in weather forecast models, including precipitation, have been taken into account in the field of forecast verification. Several spatial verification approaches have been developed [
9,
10]. They can be divided into four categories: neighborhood, scale-decomposition (e.g., References [
11,
12,
13]), object- (or feature-)based (e.g., References [
14,
15,
16]) and field deformation. In this study, we focus on a method belonging to the latter category. We now give an overview of field deformation method used for weather-related variables. Field deformation methods are based on a spatial mapping or displacement that makes a field (e.g., forecast) more similar to a target field or observation. The deformation is determined by minimizing a cost function. The Feature Calibration and Alignment technique (FCA [
17,
18,
19]) is one of these methods. FCA has also been used for correcting position errors in cloud or water vapor related fields in the framework of data assimilation. For instance, References [
18,
20] corrected position error in a numerical weather model background fields using integrated water vapor measurements from satellite. In Reference [
21], the FCA is used as a prepossessing step of an ensemble-based variational assimilation scheme for (satellite) brightness temperature. Reference [
22] tested this method with several types of observations—integrated water vapor, lower level pressure, brightness temperature and simulated radar reflection. Other feature alignment techniques have been developed and used in data assimilation schemes, such as Reference [
23] (for simulated radar observation), References [
24,
25] (for some idealized cases). The FCA technique has been applied directly to rainfall data in Reference [
19]. They corrected rainfall estimates derived from SSM/I data with ground-based radar estimates. They illustrated the performance of their approach for different types of rainfall events, such as Hurricane Andrew, a squall line in Oklahoma and coastal rainfall in Australia.
Some field deformation methods for spatial verification originate from image processing, such as the optical flow techniques developed in Reference [
26,
27] or in Reference [
28] and evaluated in References [
29,
30]. Image warping has also been used in data assimilation frameworks. Reference [
31] assimilated integrated water vapor from satellite to improve a numerical weather model forecast. However, this method requires the manual selection of pairs of points to perform the image warping. Reference [
32] combined image morphing with an ensemble Kalman filter for a wild fire model. They use an automatic registration technique that only requires two fields to derive the displacement field, without any manual specification needed. Using the same morphing and registration method, a morphing fast Fourier transform (FFT) EnKF for radar precipitation is described in Reference [
33]. However, this morphing FFT EnKF is not implemented and applied to rainfall data.
This present study investigates the use of the morphing approach for the position correction of rainfall estimates, using the approach proposed by References [
32,
33]. While the goal of Reference [
33] was to derive a method to assimilate radar precipitation into a numerical weather model, we aim to correct the position error of satellite-based precipitation estimates using gauge measurements. We apply the morphing approach to real precipitation data, namely the (non-gauge adjusted) IMERG-Late estimates and the new Trans-African Hydro-Meteorological Observatory (TAHMO) gauge network.
The morphing and automatic registration methods, including the case of irregularly spaced observations, are described in
Section 2. The morphing approach is applied to two cases. The first case uses synthetic rainfall events represented by ellipses (
Section 3.1). The second case is a real rainfall event occurring in southern Ghana during the monsoon season (
Section 3.2). Both the convergence of the automatic registration and the performance of the warping are examined in
Section 4. The results of the two cases are compared and discussed in
Section 5, before the conclusion in
Section 6.
2. Methodology
In this section, we define the image registration and morphing processes, before focusing on the implementation of an automatic registration procedure. We use the framework described by Reference [
33].
2.1. Definitions
Let
u and
v be two signals (or images) defined on a domain
and
be a mapping function. The goal of
image registration is to determine a spatial mapping
T such that,
,
where
I is the identity function.
There can be several mappings
T that meet the requirement
. Especially in areas without rainfall, the mapping
T is not unique. We define three criteria to characterize one optimal mapping:
That is, the optimal mapping has to be as small, smooth and divergent-free (i.e., it is not shrinking or expanding the field) as possible.
Several approaches have been used to define the optimality of the mapping. For the FCA method applied to precipitation, Reference [
19] use smoothness and barrier conditions. Contrary to our condition on the magnitude (Equation (
2)), their barrier does not impact small scale displacements. Using the FCA for data assimilation, References [
20,
22] added two more constraints, one on the magnitude and one on the divergent. Reference [
25] did not use any magnitude or barrier approach and only had constraints on the gradient and the divergence. Our constraints on the magnitude and on the smoothness are the same as those used in Reference [
32]. Constraints on the divergence were used in several similar field distortion methods [
20,
22,
25]. Thus, we also added a third constraint on the divergence in order to observe its impact. A short sensitivity study on the impact of these three coefficient is presented in
Appendix B.
Image warping is the distortion of an image based on a spatial transformation of the domain. Warping can be used to transform an image into another one by using the spatial mapping
T obtained from the registration method. The mapping
T is gradually applied to the original image
u as follows:
Warping works well when the residual
is small, which is not the case when the images
u and
v have different intensities for example. It is a spatial transformation. It only acts on the coordinates, it does not modify the intensity of the image
u. On the other hand,
Cross-dissolving only acts on the intensity. It fades two images
u and
v into each other:
Image morphing combines warping and cross-dissolving to account for both the spatial distortion and the difference in intensity:
where
r is the residual:
With this formula of , we obtain and .
2.2. Automatic Registration
The spatial mapping T used for the image morphing is determined by the image registration. Several registration methods are available. However, many of them require to define manually a set of corresponding points from the images u and v. We are interested in an automatic registration procedure that only needs the images u and v as inputs without any extra specifications. This requires the images to be similar enough for the automatic registration procedure to work.
We use the method described by Reference [
33] based on the minimization of a cost function
J with respect to the mapping
T. The cost function can be divided in two terms (Equation (
9)). The first one (
) represents the mapping error between the displaced original signal
and the target signal
v. The second one (
) is a background term that consists of the three criteria for ‘optimal’ mapping given in Equations (2)–(4). These three criteria are used as weak constraints.
where
,
and
are three coefficients determined empirically and
is the
norm.
The minimization problem is solved iteratively, for T defined on increasingly fine grids. The iterative approach has two advantages. It helps reduce the computational cost and avoids the local minima problem (see below).
In our application, the domain D is rectangular. It can be represented by different uniform grids. The regular grid on which u, v and are given is called the pixel grid. The mapping function T is defined on a set of coarser grids (), called morphing grids. It is then represented by two gridded arrays (one for and one for ). The grids are uniform grids (for ) covering the domain D. For , the mapping T discretized on is noted .
The signals u and v, and so the observation term of the cost function, are discretized on the pixel grid . The background term is discretized on the morphing grid . We use the second order central scheme except at the boundaries where the first order backward or forward schemes are used. We use bilinear interpolation to estimate the value of u and v on the distorted grid (e.g., ) and to interpolate T on the different morphing grids .
The finest morphing grid does not need to be the same as the pixel grid . On the contrary, it is computationally advantageous when the morphing grid has a much coarser resolution. When the number of nodes of the morphing grids is much smaller than the number of nodes n of the pixel grid, solving the minimization problem on the set of morphing grids is less computationally expensive than to solve it for T defined on the high resolution pixel grid .
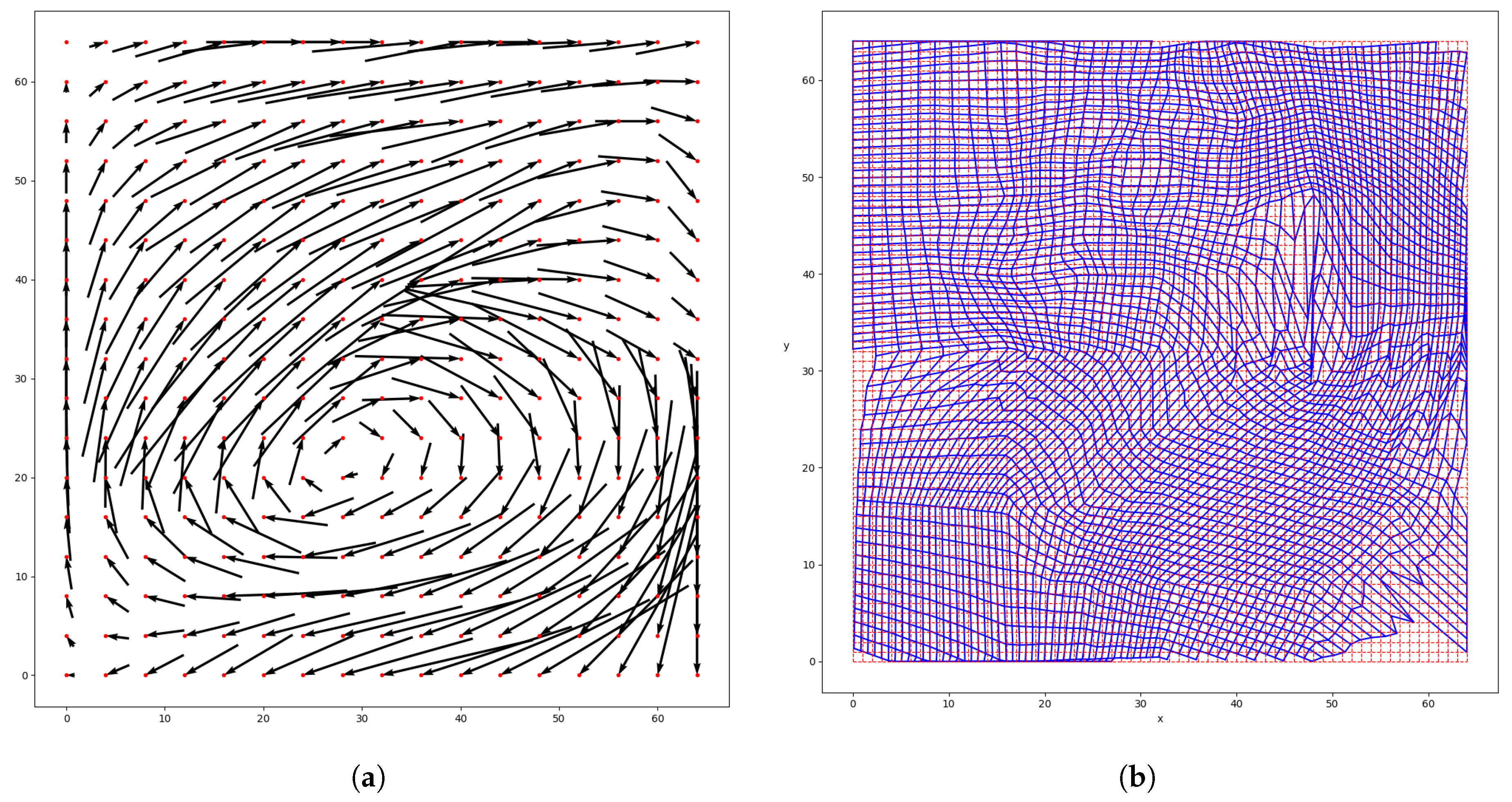
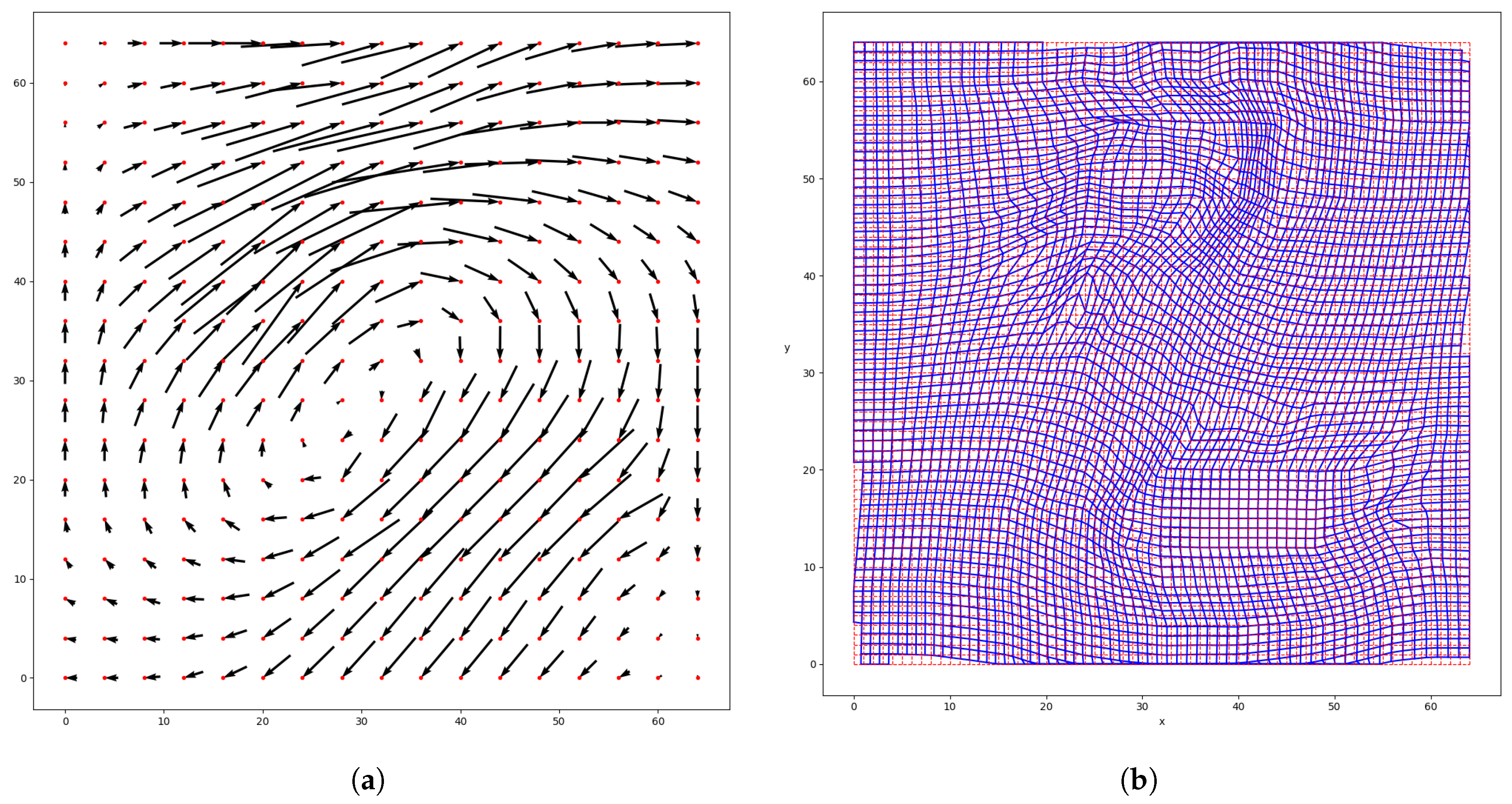
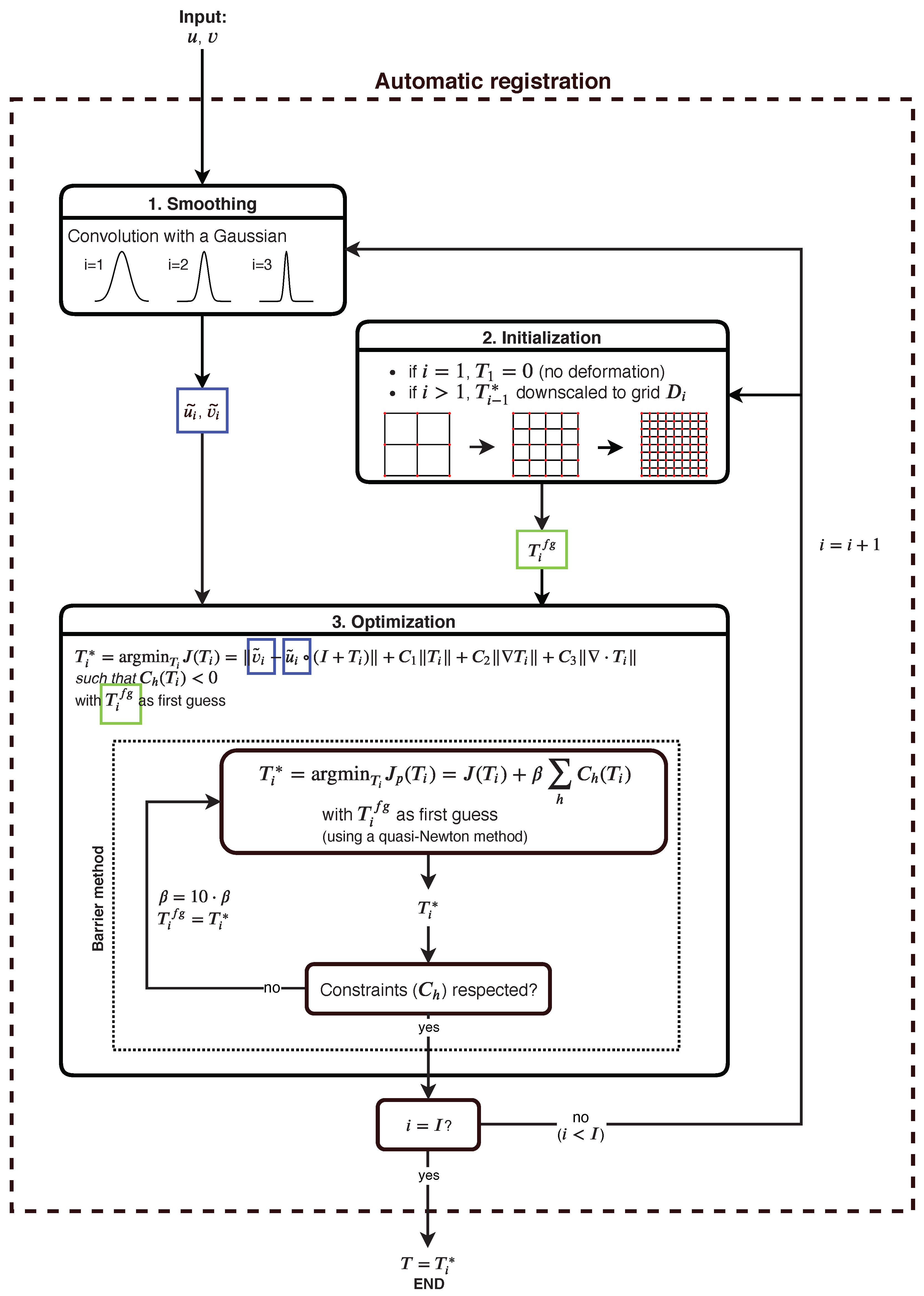
Algorithm
The algorithm iterates over the morphing grids
(
), starting on the coarsest 3-by3 grid
, until it reaches the finest morphing grid
. For each iteration, the three main steps are similar to those in Reference [
32] and are illustrated in
Figure 1.
Smoothing of the images
u and
v: the images are smoothed by convolution with a 2D-Gaussian
where
. The finer the grid
is, the narrower the Gaussian is. Thus, for small
i, the fine features are ignored and the focus is given to the large-scale ones. When
i increases, more and more fine features are taken into account. This way,
for small
i will make the larger features match. Then, for increasing
i, more and more detailed images are matched.
The cost function J is often non-convex with respect to T and so can have several local minima. The smoothing combined with the hierarchy of grids reduce the local minima problem. They ensure that the large-scale features are fitting first, hence avoiding local minima.
After the smoothing, the two fields are normalized such that their maximum is the same. The images obtained after smoothing and normalization are noted as and .
Initialization: solving the minimization problem on grid requires a first guess . For , is set to zeros, that is, no deformation. For , the mapping obtained by solving the minimization problem on grid is interpolated into the grid and used as the first guess .
Optimization: The actual minimization problem to be solved is based on the smoothed fields, that is,
. Contrary to Reference [
32], we solved the minimization problem for all the nodes at the same time.
There is a number of inequality constraints on this minimization problem, due to our requirements of invertibility. An iterative barrier approach is used to transform this constrained minimization problem into an unconstrained one [
34,
35]. In the barrier approach, the minimization is applied to a penalized cost function
, where
are the constraint functions and
the barrier coefficient (over which we iterate when the constraints are not respected). The constraints and the minimization method are described with more details in
Appendix A.
2.3. Dealing with Irregularly Spaced Observations
The automatic registration algorithm described above assumes that both signals u and v are on the same regular grid. However, in practice, one might deal with irregularly spaced observations, such as rain-gauge data.
In such a case, the observations are interpolated on the same regular grid, using kriging (details about the kriging are given in
Section 3.2). In the remainder of the article, we will refer to the gauge interpolation as “kriging”, while “interpolation” will refer to the bi-linear interpolation used in the automatic registration and morphing. The cost function
J fro Equation (
9) is modified to take the unequal coverage of the domain into account. A mask function
M is added in the first term of
J:
were · is the element-wise matrix multiplication. The mask function is defined such that it is equal to 1 in a given perimeter around the observations and zero everywhere else. So, the difference
for the grid points far from any observation does not weigh in the cost function
J.
5. Discussion
5.1. Convergence
The automatic registration algorithm converges for both the synthetic and the real (Southern Ghana) case. However, some differences can be noticed when comparing the optimization results shown in
Table 1 and
Table 3.
The minimization method (L-BFGS-B) needs more iterations for the synthetic than for the real case for all steps i except for . Iterations on the coefficient were needed for step and for the synthetic case, while the real case needed it for its finer step . The real case is noisier than the synthetic one, but the displacement between the field u and v is more straightforward. Indeed, for the synthetic case, the mapping T has to describe both a rotation and a shear. For the real case, the mapping T only has to represent a translation. On the coarser grids, the translation does not violate the constraints on the barrier. On the other hand, a rotation is more likely to violate the constraints and so to require iterations on on coarser grids too. This shows that the number of iterations of both the minimization and barrier method depends on the input fields u and v, especially on the mapping complexity. It also depends on the coefficients , and , but the influence of the chosen coefficient values is limited (results not shown here).
For the synthetic case, the decrease in the cost function is more important for the first steps. This can be explained by better first guesses for the finer grids. On the contrary, for the real case, the decrease is more important in the last steps. While the events were identical in the synthetic case, they have different shapes in the real one. On the coarser grid, these differences are masked by the strong smoothing. They become more visible on the finer grid on which there is less smoothing. The sharper features being more sensitive to small position errors results in a higher cost function. The finer morphing grids allow the mapping to take the shape difference into account, on top of the position error. The reduction of the cost function is thus becoming more important.
The intermediate mappings
give information about the impact of the steps
. They were evaluated by looking at the MAE of the warped fields
(
Table 2 and
Table 4). In the real case, most of the MAE decrease is reached after the first iteration (divided by around 2). The decrease after the subsequent iterations is more marginal. The mapping on the coarser morphing grid
is already able to capture reasonably well the displacement, that is, the translation toward the South-West. Thus, the finer morphing grids induce less improvement. In the synthetic case, the MAE is improved greatly after the first iteration too (divided by 7). However, the subsequent iterations continue to decrease the MAE (divided by 3 after step 2 and by 2 after step 3). The first morphing grids are too coarse to describe accurately the complex displacement, which combine a rotation and a shear. Hence, increasing the resolution of the morphing grids improves the mapping
and thus the MAE. The more complex the displacement is, the finer the morphing grid needs to be and so the higher
I has to be (i.e., the more steps
i we need).
The computational time increases exponentially with the number of steps i. All computations shown here were done on a personal computer. For the synthetic case, the first four steps (i.e., i = 1, 2, 3 and 4) were completed in approximately 2 min, while the fifth iteration () needed between 4 to 10 min (depending on the computer computational capacity). The real case requires fewer iterations than the synthetic one and so a shorter computational time (∼1 min for and ∼4 min for ).
5.2. Validation
The automatic registration procedure converged, for both the synthetic and the real cases. It has been shown that the error between the two original fields was considerably reduced by applying the mapping
T, even without bias adjustment (i.e., the warped field
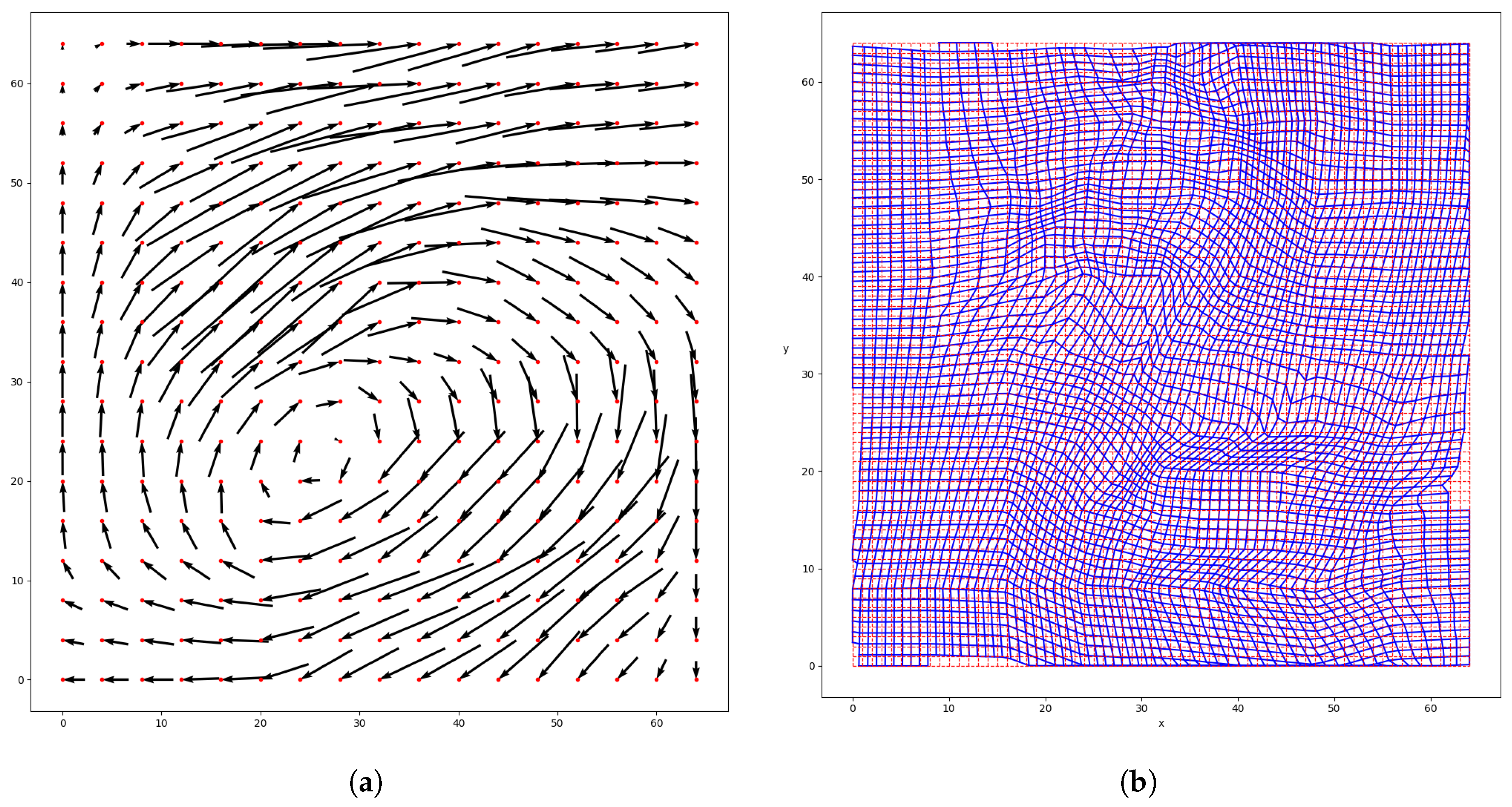
). An issue encountered in the synthetic case was the grid distortion near the domain boundary (
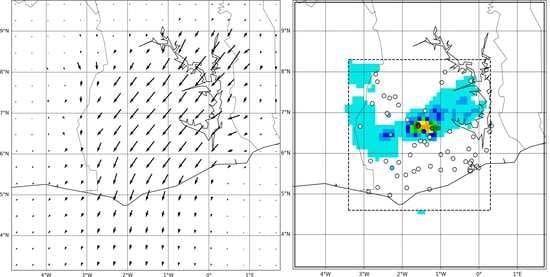
Figure 7). Some inconsistencies can appear when the rainfall events are close to the boundary. This was solved in the real case by adding a padding area, filled with zero precipitation, around the domain. This padding area enables the mapping to have a smooth transition from the largest displacement near the events to (almost) none near the new extended boundary (
Figure 9a).
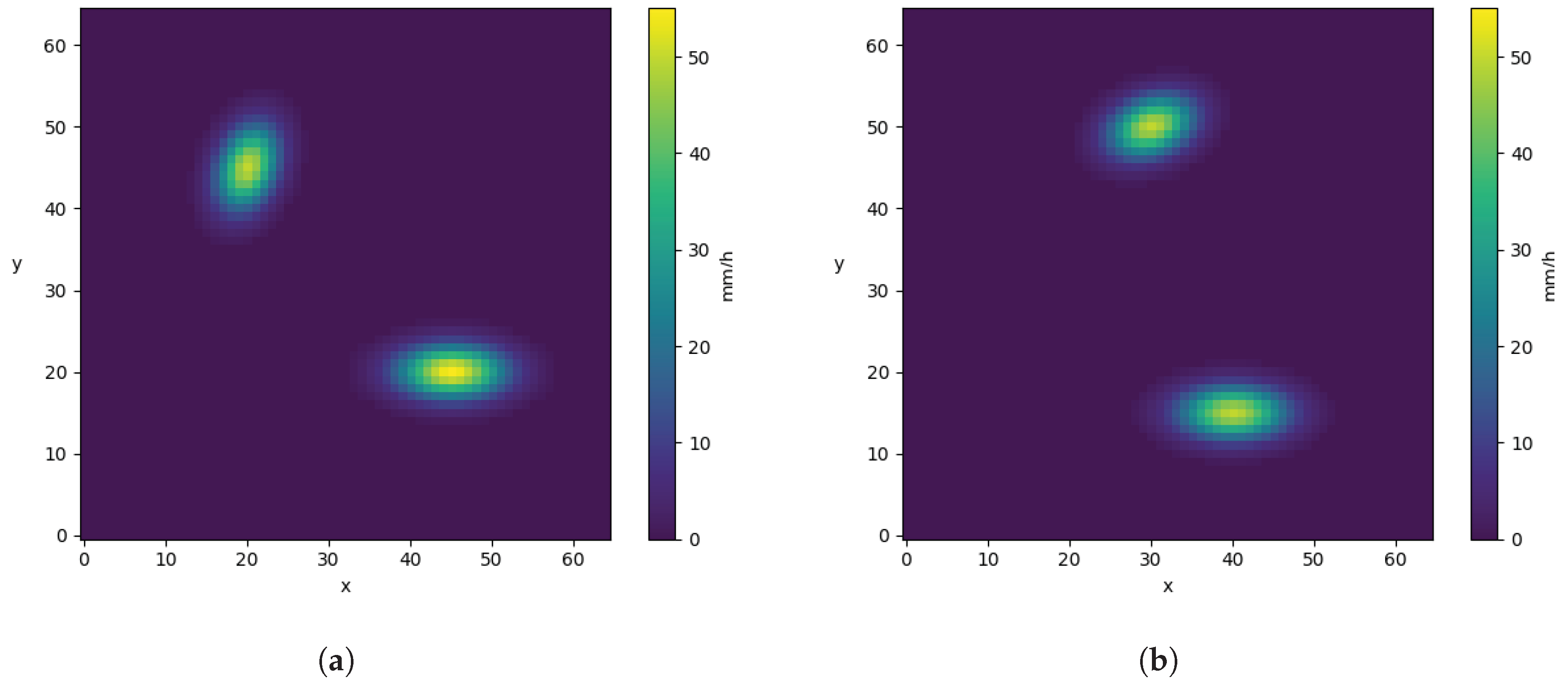
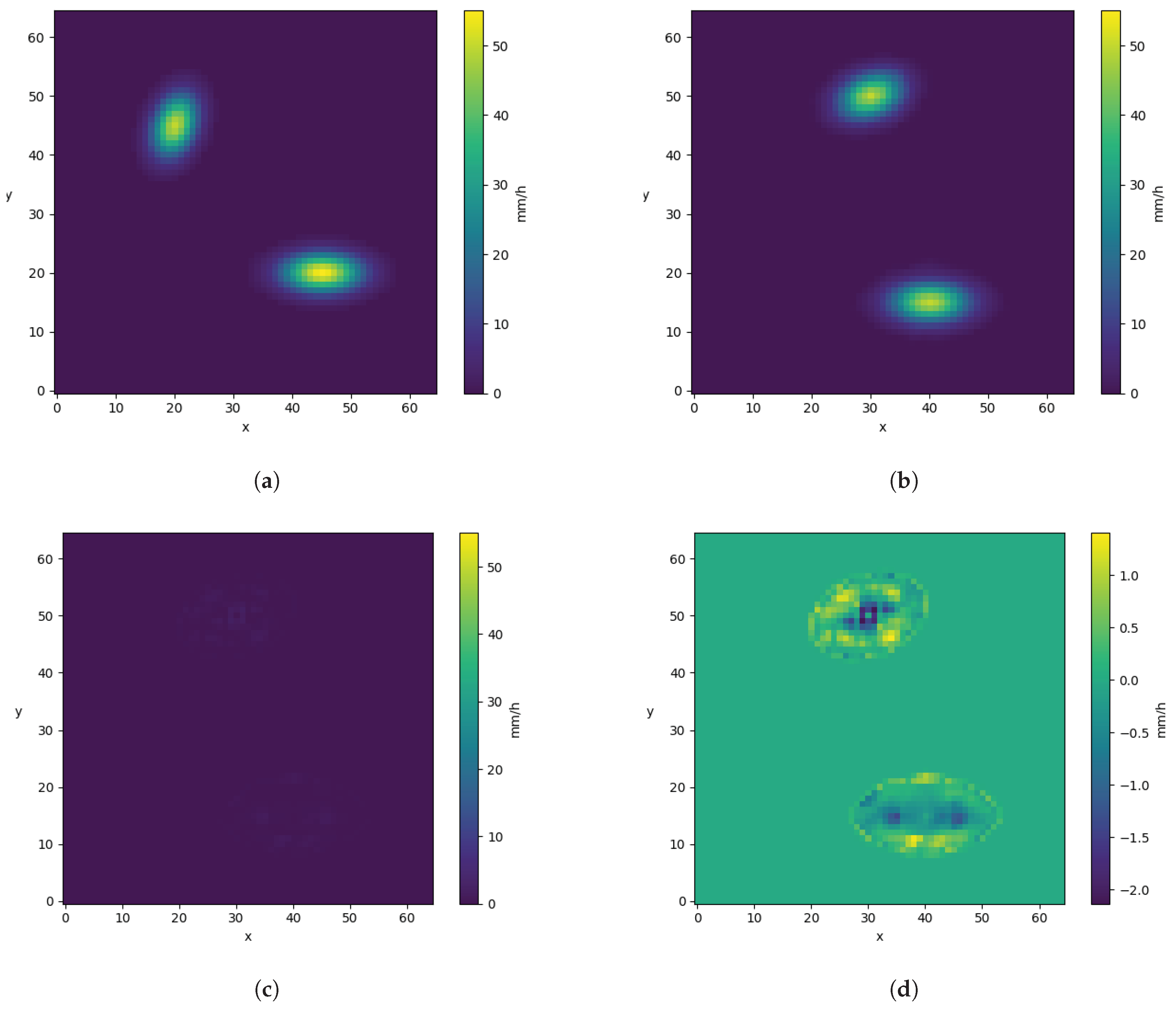
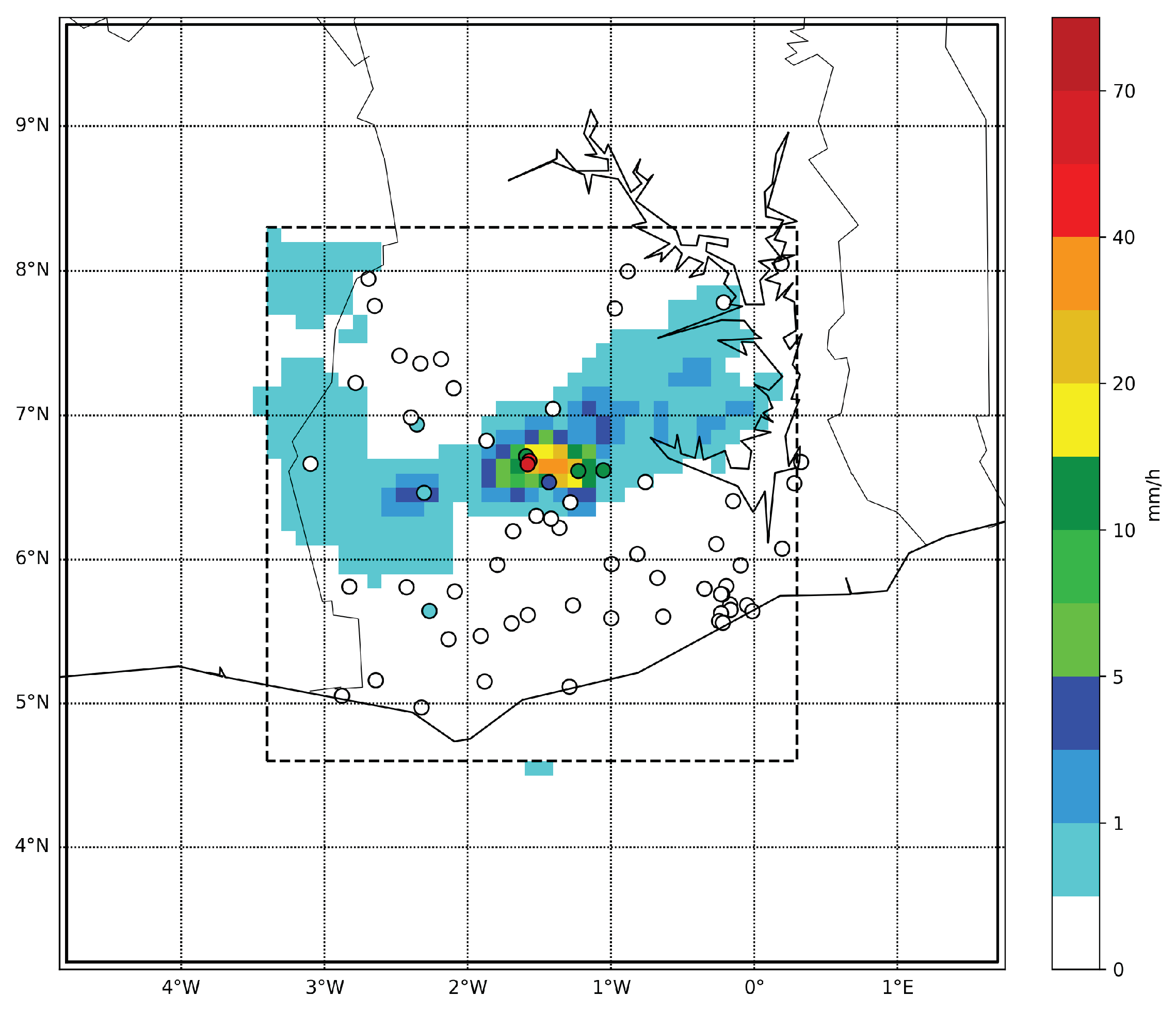
The automatic registration produced reasonable coordinate mapping in these two cases. However, problems can arise if the dissimilarity between the two original fields are too strong. We do not have a method to quantify this problem beforehand. However, there are some minimum conditions, such as having the same number of events in both fields or the proximity of these events. The smoothing steps of the registration algorithm can also be increased or decreased to allow the events to move further or not. In this study, we did not push to the cases to the extreme to determine a feasibility threshold. The goal of this article was to prove the applicability of registration and morphing to precipitation data. A next step would be to apply it to other cases, including different rainfall regimes.
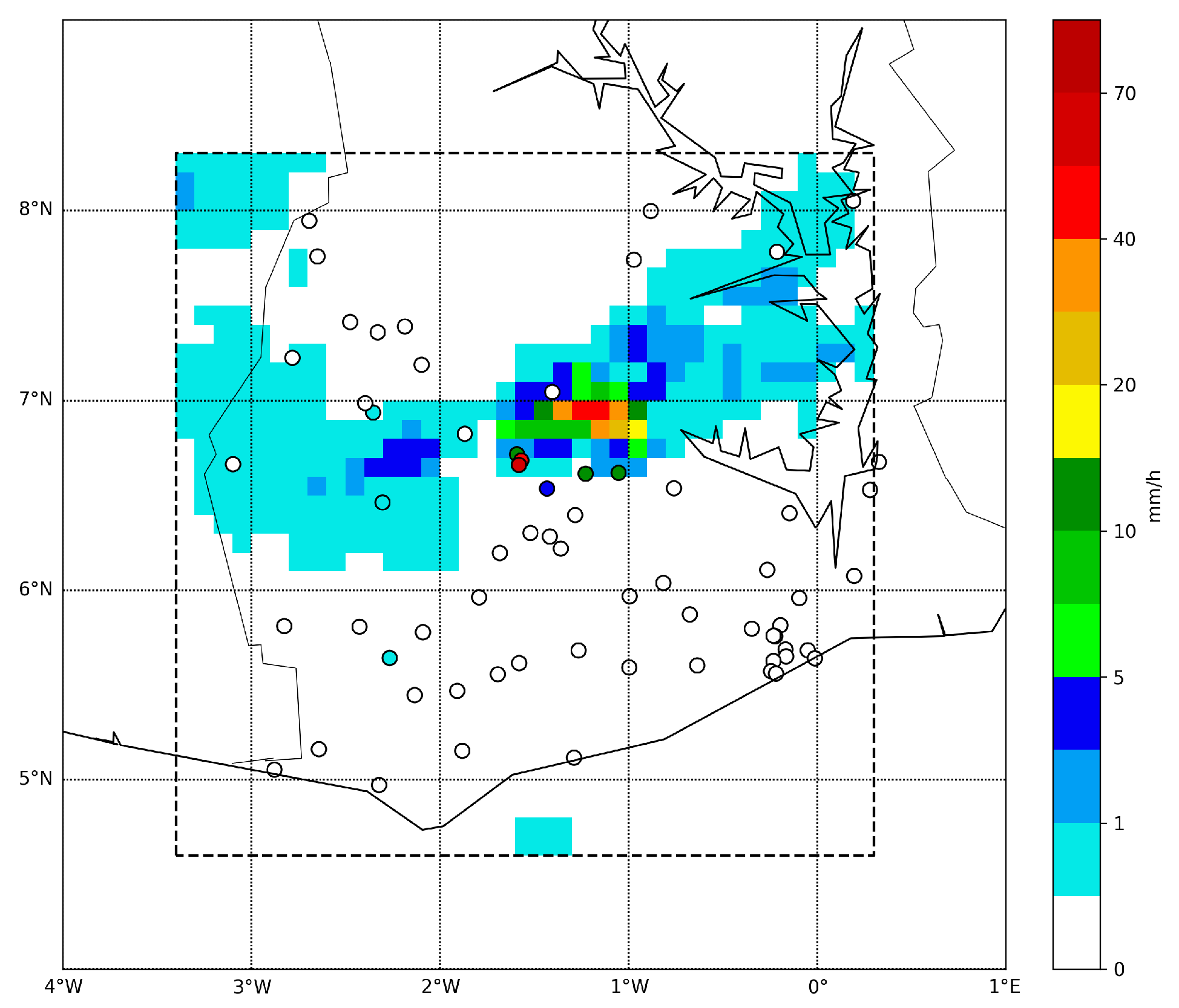
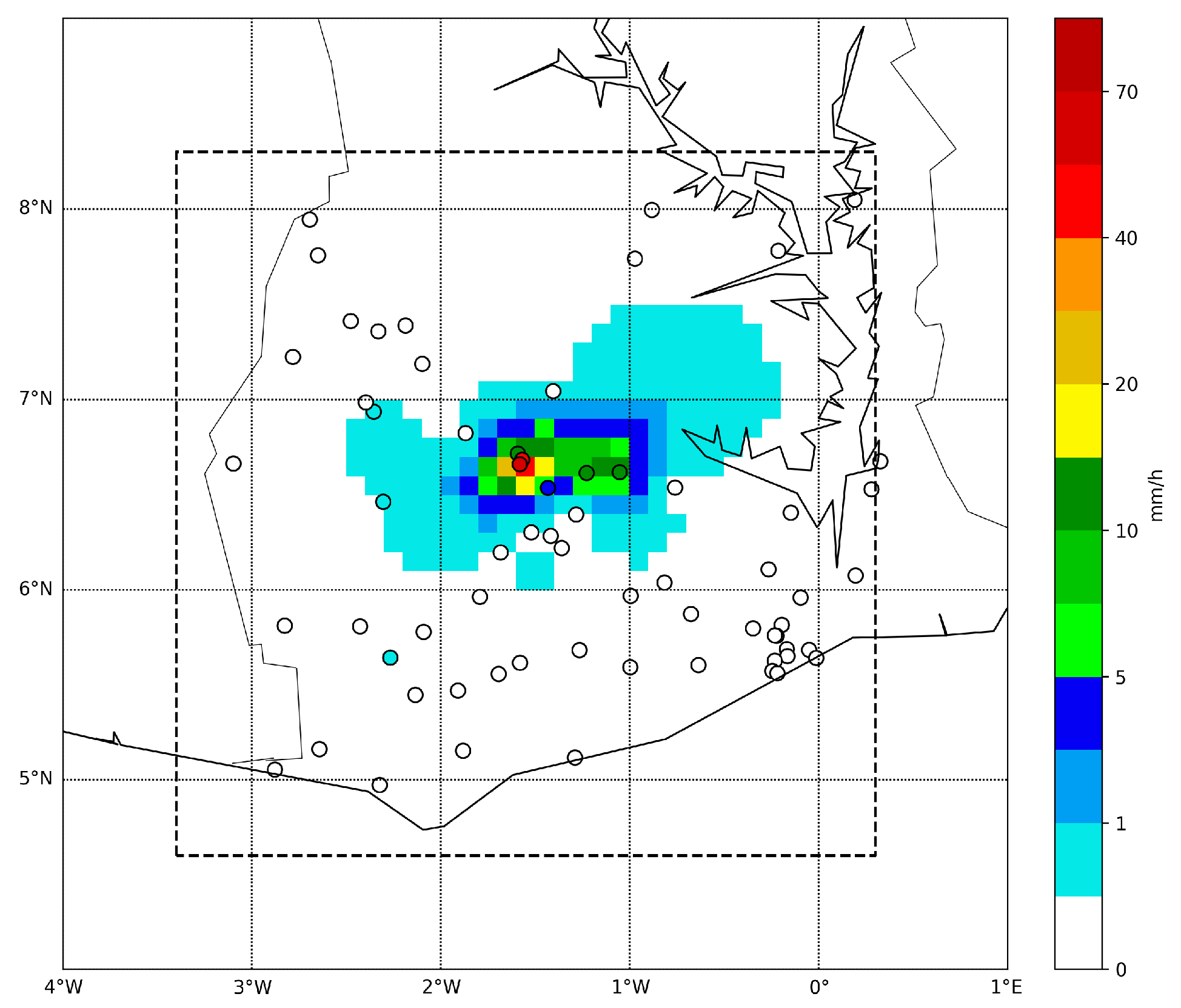
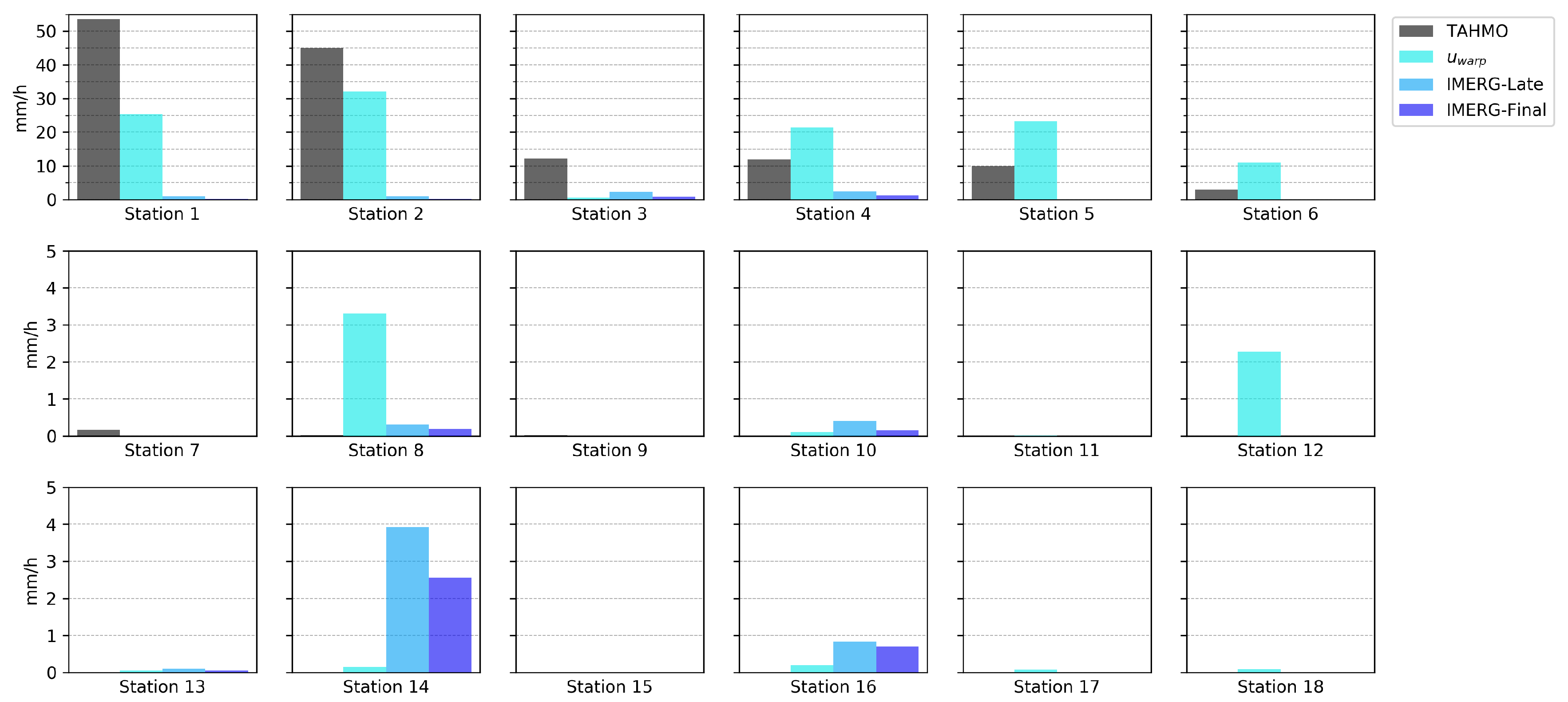
The warping succeeded in correcting the general position error between the fields
u and
v in both cases. In the real case, the shape of the event is different in the original fields. One can notice that the shape of the event is slightly altered by the mapping, but the internal structure stayed similar. The peak (rainfall above 20 mm/h) is larger in the field
u than in the target field
v, but the event (rainfall above 1 mm/h) has a larger longitudinal spread according to
v (see
Figure 4 and
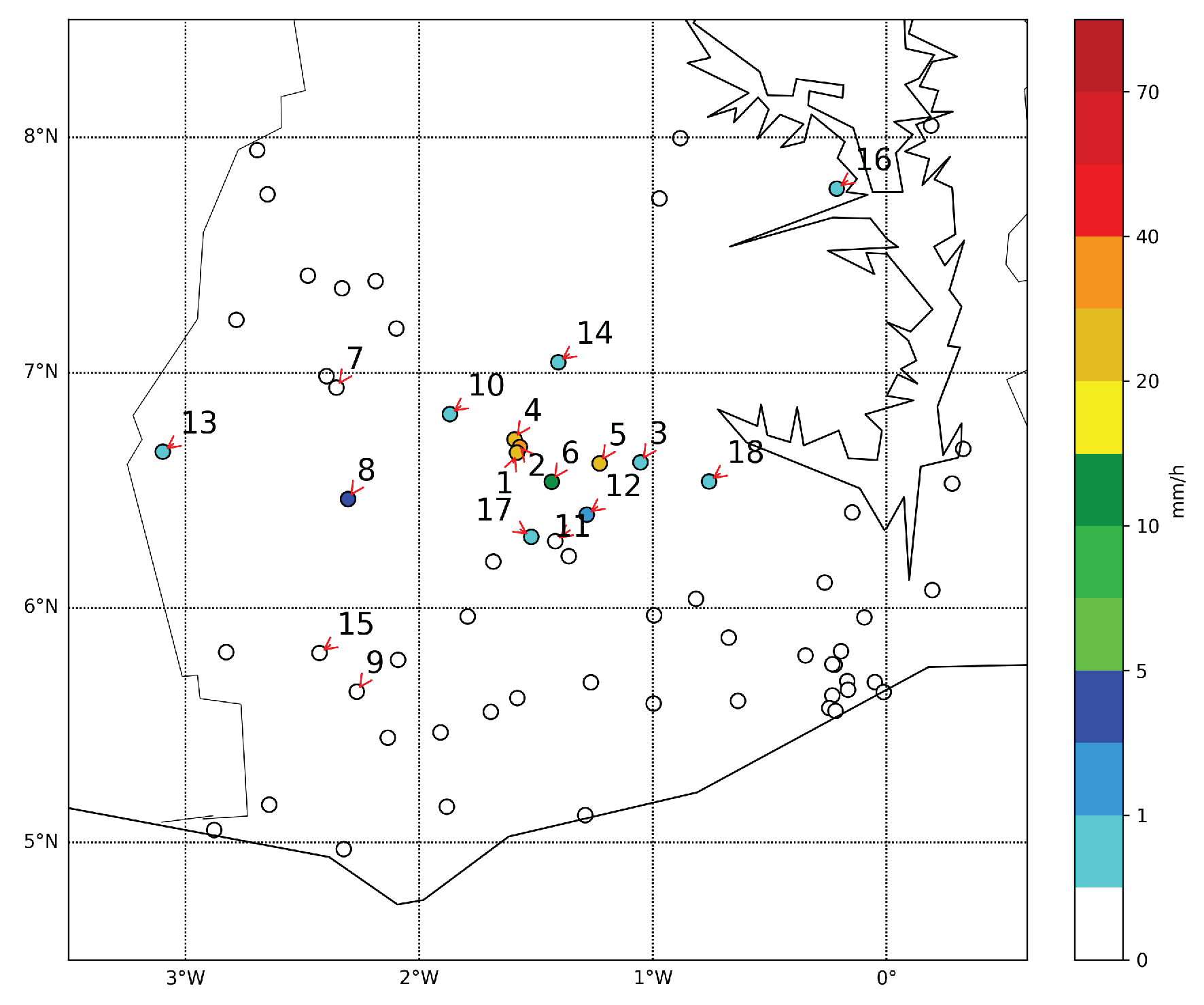
Figure 5). This can explain some of the intensity differences at the station location (
Figure 12). The stations 4 to 6 are in the center of the event, the station 4 is especially very close to the peak (stations 1 and 2). The overestimation by the warped field is related to the larger peak in the field
u. Similarly, the underestimation at station 3 and the overestimation at station 12 is due to their location near the edge of the event. Stations 3 and 12 are located close to the East edge and South edge of the event respectively and so are affected by the spread difference of the event according to
u and
v.
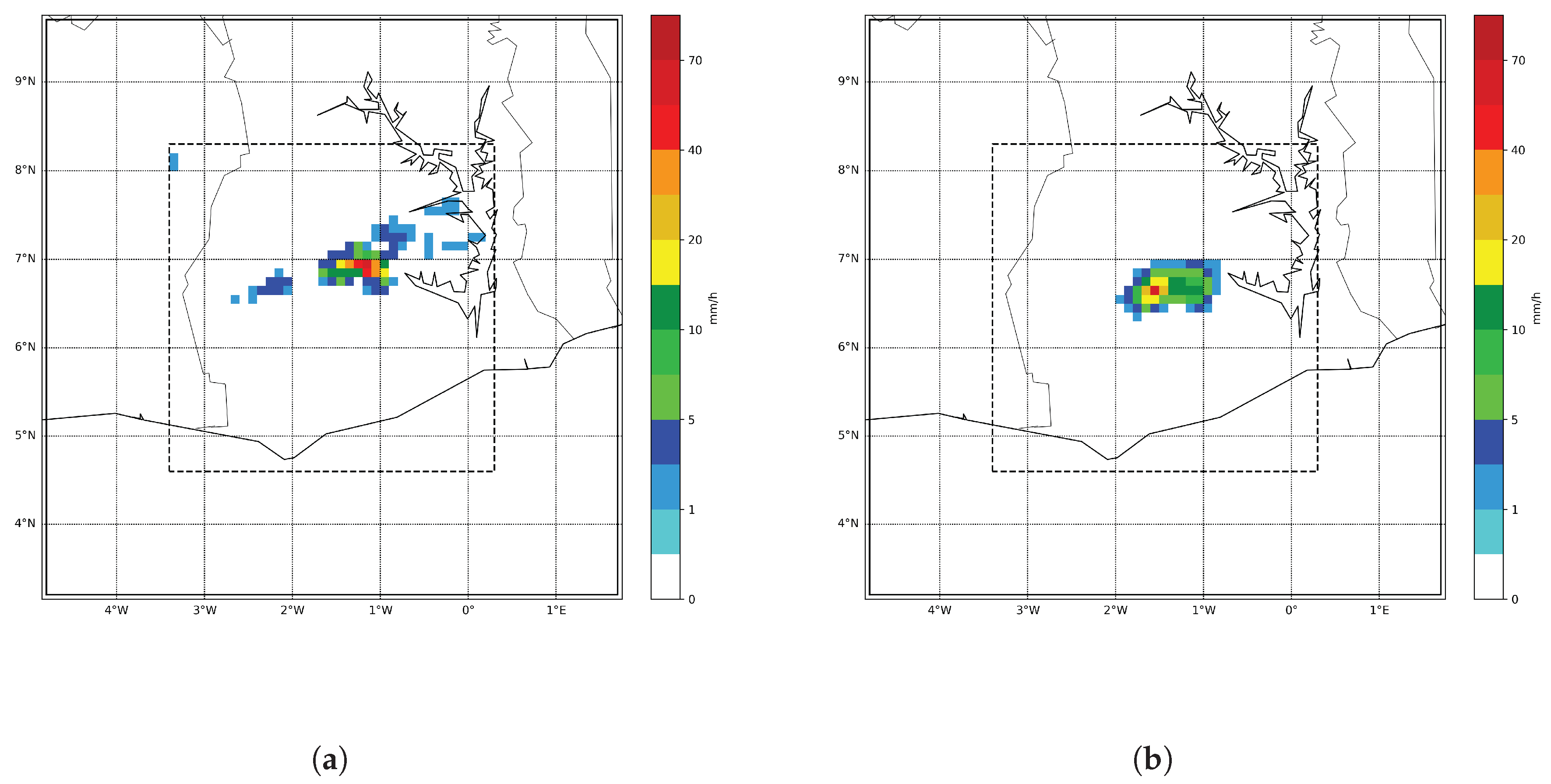
The morphing has been evaluated only for the synthetic case.
Table 2 shows the added advantages of morphing over warping. The MAE of the warped signal is larger by factor 2 on domain
and by a factor of 2.7 on domain
compared to the MAE of the morphed signal. This important difference is due to the intensity difference between the lower event in
u and the one in
v. However, this advantage decreases when the intensity difference decreases. When the intensity is the same for the two fields, warping is more advantageous. Without difference in intensity, the residual
r in the morphing formula Equation (
7) is unnecessary and only add numeric errors (because of the inverse transform
and the extra linear interpolation). The morphing was not tested for the real case because of the irregular nature of the observations. The uncertainty of the kriged field is high in large part of the domain where no gauges are available. We made assumptions on the spatial mapping through the three criteria for optimality. This allowed us to correct the position through the entire domain. However, we can not make similar assumptions for the intensity.
5.3. Applications
In this paper, we corrected a satellite-based precipitation estimate based on gauge measurements. This position correction could be particularly useful to pre-process satellite rainfall data for applications needing accurate rain event positioning. Image morphing can take both the position and the intensity into account but we do not recommend to correct both at the same time. The morphed estimate would then be comparable to the kriged gauge field, without any advantage of the more detailed spatial structure of the satellite observations. A two-step approach is preferred, with first the position correction using the warping and then a bias correction such as the additive-multiplicative one used by IMERG-Final. Such position correction could be particularly beneficial as a pre-processing step for hydrological modelling applications. Rainfall data is an important input for hydrological models and can have a large impact on their accuracy [
41,
42]. The correct positioning of rainfall events can be as crucial as their intensities, especially for the localized events.
The morphing can also be applied to rainfall fields from other sources, such as a numerical model. It can then be used for data assimilation. Two approaches are possible. The position correction can be applied as a first step before the usual data assimilation on the intensity [
22,
24]. It is also possible to assimilate both intensity and distortion at the same time, represented respectively by the residual
r and the mapping
T [
32,
33]. In the second case one can take full advantage of the morphing formulation. In this paper, we did not perform data assimilation as it was described in References [
32,
33]. Instead, we used a similar method to theirs to correct the position in a satellite-based estimate using gauge data. There are three main differences between our method and the morphing described in References [
32,
33]. First, they used two penalty terms to ensure the smoothness of the displacement field (based on its magnitude and gradient), we add a third penalty term based on the divergence. Second, they solved the minimization problem for one grid point at a time (i.e., they have several 1D minimization problems), while we solve it for all the grid points together (i.e., we have one multi-variable minimization problem). Finally, we extend the method to non-gridded observations. Contrary to radar data, the gauge measurements used in our study case are irregularly spaced (i.e., non-gridded). In Reference [
33], the framework for assimilating radar rainfall using morphing is described but is not actually applied to real rainfall data.
The main limitation of image morphing is in fact the limitations of the automatic registration. As discussed above, it can fail if the fields are too dissimilar. It is also influenced by the three regulation coefficients , and . For example, in the case of a low intensity event, the regulation terms in can dominate the cost function, not allowing the rain event to move. In this paper, we explore the feasibility of image morphing for position correction in precipitation estimates. However, we have not pushed to the extreme the cases to quantify its limits. This paper is meant as a proof-of-concept. The next step will be to extend the study to other cases, involving different rainfall regimes. Extreme cases should be included to determine the boundary within which the automatic registration succeeds
6. Conclusions
We have investigated the use of a morphing approach for the gauge-adjustment of satellite-based rainfall estimates with respect to position error. The morphing method, adapted from Reference [
32], has been applied to two cases. Synthetic rainfall events, represented by ellipses, have been used to test the automatic registration and the morphing method. The second case, a convective rainfall event in southern Ghana, showed the potential of the method when applied to real, noisy precipitation data. We applied the position correction such that the gauge data were downscaled while keeping the high spatial variability of the satellite-based product. The rain events estimated by IMERG-Late were spatially shifted to match the gauge data. The morphing method can take both the intensity and the position of the rain events into account. This is an advantage compared to the traditional gauge-adjustment methods that are only looking at the intensity bias.
The automatic registration is able to represent different types of distortions. However, its performance of the registration depends on the degree of difference between the fields u and v and on the regulation coefficients. The more complex the distortion between the fields is, the more computationally expensive the registration is. For example, in the case of a simple distortion (such as a translation), it is possible to choose a smaller number of steps I. The minimization method at each step would also need fewer iterations. On the other hand, if the fields are too dissimilar, the registration can fail. The regulation coefficients also influence both the convergence and the result of the registration.
This paper explores the use of an image morphing method to correct location errors in precipitation estimates. The next step will be to extend the study to other case studies, including different rainfall regimes. It should also be pushed to more extreme cases to determine the method’s limitations more precisely. For example, the regulation coefficients have been chosen empirically in this study. A next step will be to develop a more robust way to select them, for example by defining adaptive coefficients.