Satellite Retrieval of Downwelling Shortwave Surface Flux and Diffuse Fraction under All Sky Conditions in the Framework of the LSA SAF Program (Part 1: Methodology)
Abstract
1. Introduction
2. Method
2.1. Definition of Retrieved Quantities
2.1.1. Downwelling Surface Shortwave Radiation
2.1.2. Diffuse Fraction
2.1.3. Equivalent Aerosol Optical Depth at 550 nm
2.1.4. Opacity Index
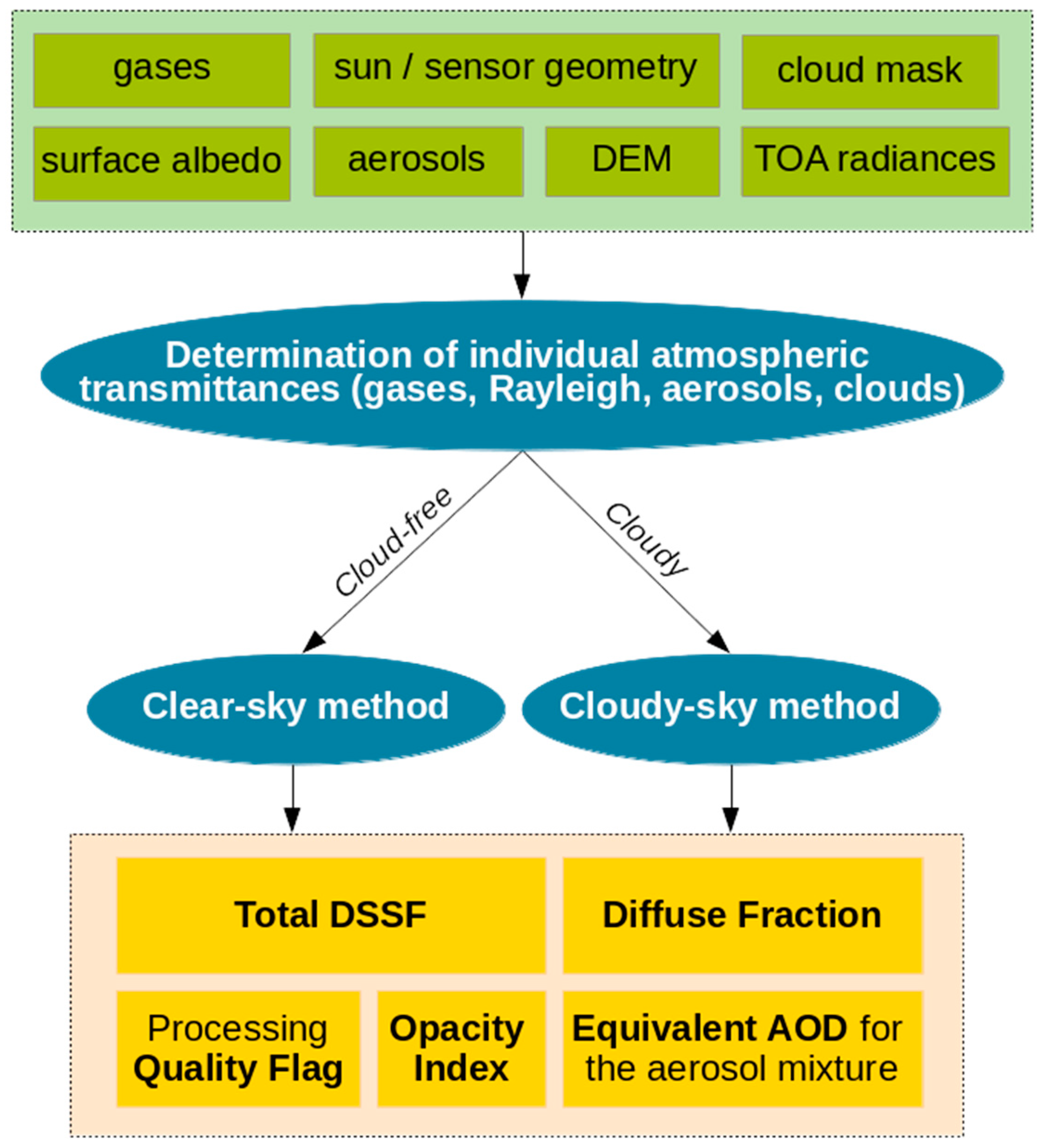
2.2. Overview of the Retrieval Method
3. Input Data
3.1. TOA Data
3.1.1. Satellite TOA Radiance
3.1.2. TOA Incoming Sun Radiation
3.2. Surface Characteristics
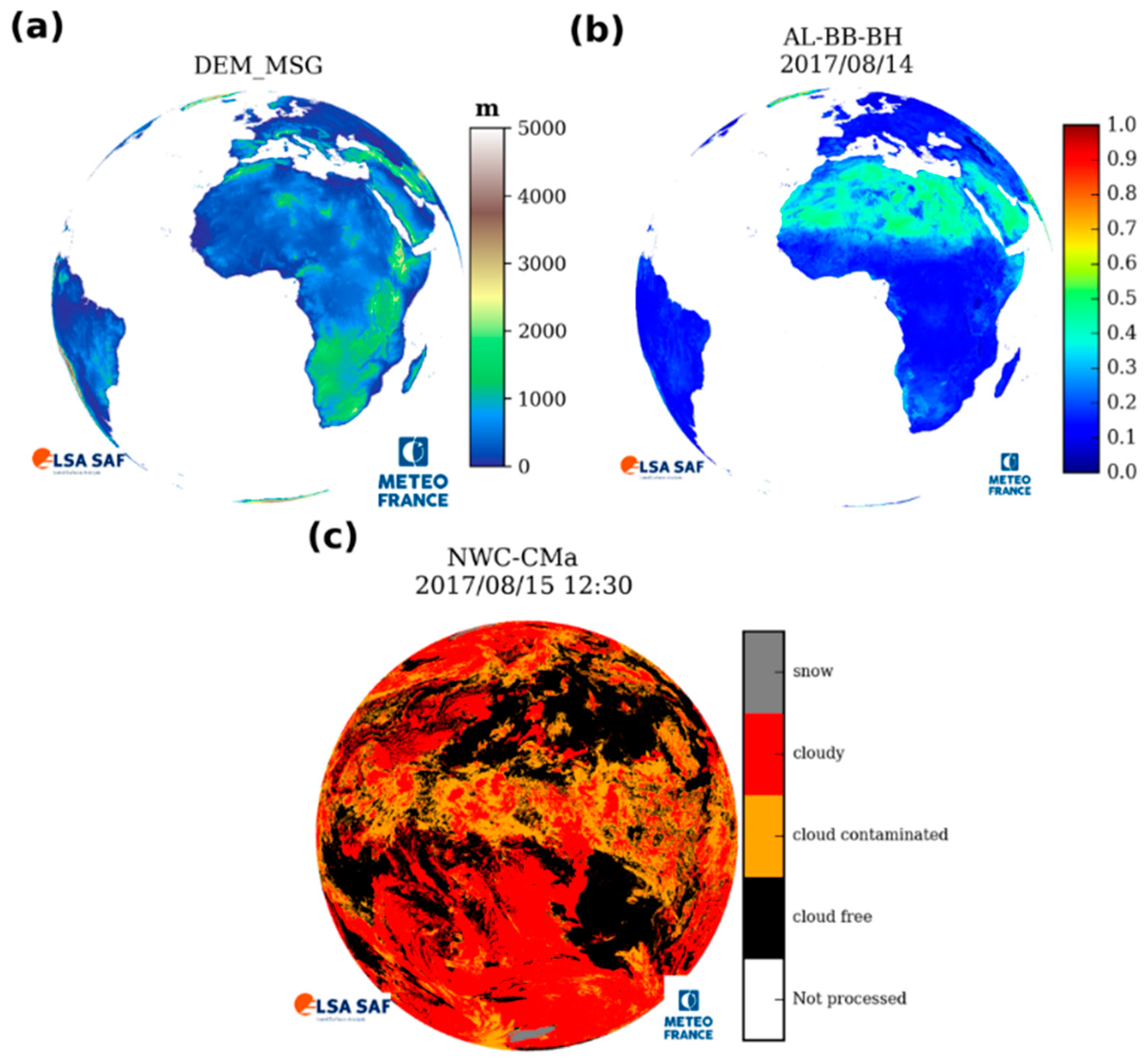
3.2.1. Digital Elevation Models
3.2.2. Land Surface Albedo
3.3. Atmospheric Characteristics
3.3.1. Cloudiness
3.3.2. H2O and O3 Columnar Content Modeling
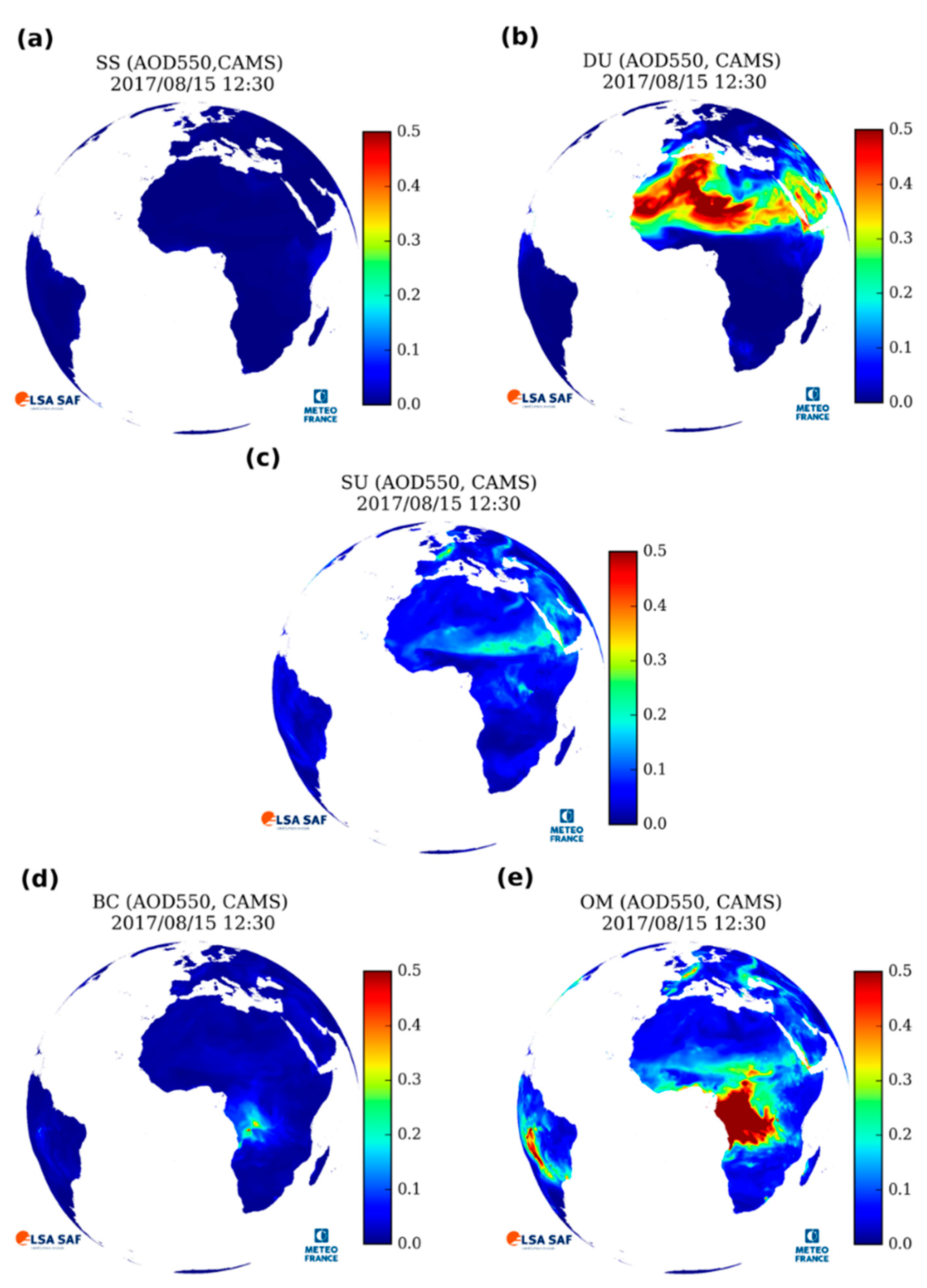
3.3.3. Aerosol Optical Depth and Speciation
3.3.4. Aerosol Optical Properties (Look Up Table)
3.4. Summary of the Input Data
4. Algorithm Description
4.1. Diffuse and Direct Transmittance Contributions of the Individual Atmospheric Components
4.1.1. Gas Transmittances
4.1.2. Rayleigh Direct and Diffuse Transmittances
4.1.3. Aerosols Transmittances and Spherical Albedos
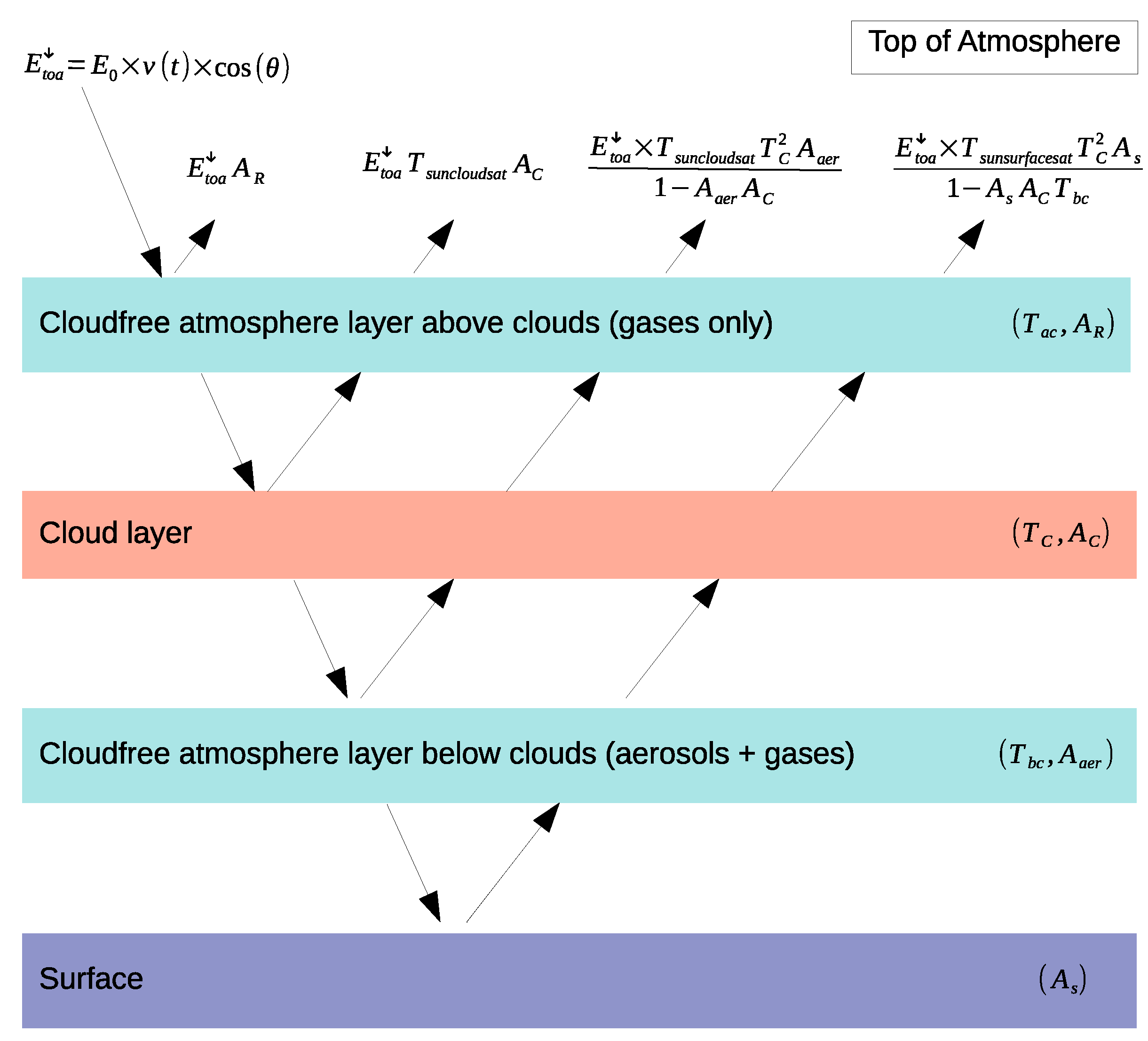
4.1.4. Total Cloud-Free Atmospheric Transmittance
4.1.5. Total Cloudy-Sky Atmospheric Transmittance
4.2. Algorithm Description: Clear-Sky Case
4.2.1. Description
4.2.2. Total DSSF for Clear-Sky Case
4.2.3. Equivalent AOD, Diffuse Fraction and Opacity Index for Clear-Sky Case
4.3. Algorithm Description: Cloudy-Sky Case
4.3.1. Description
4.3.2. Total DSSF in Cloudy Conditions
4.3.3. Equivalent AOD, Diffuse Fraction and Opacity Index for Cloudy Case
5. Results
5.1. Overview of the Output Variables
- total DSSF, named ‘DSSF_TOT’ in the MDSSFTD product;
- diffuse DSSF fraction, named ‘FRACTION_DIFFUSE’;
- equivalent spectral AOD at 550 nm for the current aerosol load, named ‘AOD’;
- the opacity of the atmosphere, named ‘OPACITY_INDEX’;
- processing quality flags, named ‘Q_FLAG’.
5.2. Comparison with the Previous LSA SAF DSSF Product Version
5.3. Known Issues and Limitations
5.4. Access to the Code Sources and Data Policy
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ramanathan, V.; Cess, R.D.; Harrison, E.F.; Minnis, P.; Barkstrom, B.R.; Ahmad, E.; Hartmann, D. Cloud-Radiative Forcing and Climate: Results from the Earth Radiation Budget Experiment. Science 1989, 243, 57–63. [Google Scholar] [CrossRef] [PubMed]
- Dickinson, R.E. Land surface processes and climate–Surface albedos and energy balance. Adv. Geophys. 1983, 25, 305–353. [Google Scholar]
- Mitchell, K.E.; Lohmann, D.; Houser, P.R.; Wood, E.F.; Schaake, J.C.; Robock, A.; Cosgrove, B.A.; Sheffield, J.; Duan, Q.; Luo, L.; et al. The multi-institution North American Land Data Assimilation System (NLDAS): Utilizing multiple GCIP products and partners in a continental distributed hydrological modeling system. J. Geophys. Res. Space Phys. 2004, 109, D7. [Google Scholar] [CrossRef]
- Ferranti, L.; Viterbo, P. The European Summer of 2003: Sensitivity of Soil Water Initial Conditions. J. Clim. 2006, 19, 3659–3680. [Google Scholar] [CrossRef]
- Carrer, D.; Lafont, S.; Roujean, J.-L.; Calvet, J.-C.; Meurey, C.; Le Moigne, P.; Trigo, I.F.; Trigo, I. Incoming Solar and Infrared Radiation Derived from METEOSAT: Impact on the Modeled Land Water and Energy Budget over France. J. Hydrometeorol. 2012, 13, 504–520. [Google Scholar] [CrossRef]
- Carrer, D.; Roujean, J.-L.; Lafont, S.; Calvet, J.-C.; Boone, A.; Decharme, B.; Delire, C.; Gastellu-Etchegorry, J.-P.; Gastellu-Etchegorry, J. A canopy radiative transfer scheme with explicit FAPAR for the interactive vegetation model ISBA-A-gs: Impact on carbon fluxes. J. Geophys. Res. Biogeosciences 2013, 118, 888–903. [Google Scholar] [CrossRef]
- Mercado, L.M.; Bellouin, N.; Sitch, S.; Boucher, O.; Huntingford, C.; Wild, M.; Cox, P.M. Impact of changes in diffuse radiation on the global land carbon sink. Nature 2009, 458, 1014. [Google Scholar] [CrossRef]
- O’Sullivan, M.; Rap, A.; Reddington, C.L.; Spracklen, D.V.; Gloor, M.; Buermann, W. Small global effect on terrestrial net primary production due to increased fossil fuel aerosol emissions from East Asia since the turn of the century. Geophys. Res. Lett. 2016, 43, 8060–8067. [Google Scholar] [CrossRef]
- Blanc, P.; Espinar, B.; Geuder, N.; Gueymard, C.; Meyer, R.; Pitz-Paal, R.; Reinhardt, B.; Renné, D.; Sengupta, M.; Wald, L.; et al. Direct normal irradiance related definitions and applications: The circumsolar issue. Sol. Energy 2014, 110, 561–577. [Google Scholar] [CrossRef]
- Geiger, B.; Meurey, C.; Lajas, D.; Franchisteguy, L.; Carrer, D.; Roujean, J.-L. Near real-time provision of downwelling shortwave radiation estimates derived from satellite observations. Meteorol. Appl. 2008, 15, 411–420. [Google Scholar] [CrossRef]
- Bishop, J.K.B.; Rossow, W.B. Spatial and temporal variability of global surface solar irradiance. J. Geophys. Res. Space Phys. 1991, 96, 16839–16858. [Google Scholar] [CrossRef]
- Darnell, W.L.; Staylor, W.F.; Gupta, S.K.; Denn, F.M. Estimation of Surface Insolation Using Sun-Synchronous Satellite Data. J. Clim. 1988, 1, 820–835. [Google Scholar] [CrossRef]
- Dedieu, G.P.; Deschamps, P.; Kerr, Y. Satellite estimation of solar irradiance at the surface of the earth and of surface albedo using a physical model applied to METEOSAT data. J. Clim. Appl. Meteorol. 1987, 26, 79–87. [Google Scholar] [CrossRef]
- Gautier, C.; Landsfeld, M. Surface Solar Radiation Flux and Cloud Radiative Forcing for the Atmospheric Radiation Measurement (ARM) Southern Great Plains (SGP): A Satellite, Surface Observations, and Radiative Transfer Model Study. J. Atmos. Sci. 1997, 54, 1289–1307. [Google Scholar] [CrossRef]
- Cano, D.; Monget, J.; Albuisson, M.; Guillard, H.; Regas, N.; Wald, L. A method for the determination of the global solar radiation from meteorological satellite data. Sol. Energy 1986, 37, 31–39. [Google Scholar] [CrossRef]
- Li, Z.; Leighton, H.G. Global climatologies of the solar radiation budgets at the surface and in the atmosphere from 5 years of ERBE data. J. Geophys. Res. 1993, 98, 4919–4930. [Google Scholar] [CrossRef]
- Masuda, K.; Leighton, H.G.; Li, Z. A New Parameterization for the Determination of Solar Flux Absorbed at the Surface from Satellite Measurements. J. Clim. 1995, 8, 1615–1629. [Google Scholar] [CrossRef]
- Moser, W.; Raschke, E. Incident Solar Radiation over Europe Estimated from METEOSAT Data. J. Clim. Appl. Meteorol. 1984, 23, 166–170. [Google Scholar] [CrossRef]
- Pinker, R.T.; Ewing, J.A. Modeling Surface Solar Radiation: Model Formulation and Validation. J. Clim. Appl. Meteorol. 1985, 24, 389–401. [Google Scholar] [CrossRef]
- Pinker, R.T.; Laszlo, I. Modeling Surface Solar Irradiance for Satellite Applications on a Global Scale. J. Appl. Meteorol. 1992, 31, 194–211. [Google Scholar] [CrossRef]
- Tarpley, J.D. Estimating Incident Solar Radiation at the Surface from Geostationary Satellite Data. J. Appl. Meteorol. 1979, 18, 1172–1181. [Google Scholar] [CrossRef]
- Whitlock, C.H.; Charlock, T.P.; Staylor, W.F.; Pinker, R.T.; Laszlo, I.; Ohmura, A.; Gilgen, H.; Konzelman, T.; DiPasquale, R.C.; Moats, C.D.; et al. First Global WCRP Shortwave Surface Radiation Budget Dataset. Bull. Am. Meteorol. Soc. 1995, 76, 905–922. [Google Scholar] [CrossRef]
- Romano, F.; Cimini, D.; Cersosimo, A.; Di Paola, F.; Gallucci, D.; Gentile, S.; Geraldi, E.; LaRosa, S.; Nilo, S.T.; Ricciardelli, E.; et al. Improvement in Surface Solar Irradiance Estimation Using HRV/MSG Data. Remote Sens. 2018, 10, 1288. [Google Scholar] [CrossRef]
- Gallucci, D.; Romano, F.; Cersosimo, A.; Cimini, D.; Di Paola, F.; Gentile, S.; Geraldi, E.; LaRosa, S.; Nilo, S.T.; Ricciardelli, E.; et al. Nowcasting Surface Solar Irradiance with AMESIS via Motion Vector Fields of MSG-SEVIRI Data. Remote. Sens. 2018, 10, 845. [Google Scholar] [CrossRef]
- Ineichen, P. High Turbidity Solis Clear Sky Model: Development and Validation. Remote Sens. 2018, 10, 435. [Google Scholar] [CrossRef]
- Ruiz-Arias, J.A.; Alsamamra, H.; Tovar-Pescador, J.; Pozo-Vazquez, D. Proposal of a regressive model for the hourly diffuse solar radiation under all sky conditions. Energy Convers. Manag. 2010, 51, 881–893. [Google Scholar] [CrossRef]
- Rigollier, C.; Lefèvre, M.; Wald, L. The method Heliosat-2 for deriving shortwave solar radiation from satellite images. Sol. Energy 2004, 77, 159–169. [Google Scholar] [CrossRef]
- Ineichen, P. Long Term HelioClim-3 Global, Beam and Diffuse Irradiance Validation. 2016. Available online: https://archive-ouverte.unige.ch/unige:81915/ (accessed on 26 June 2019).
- Trigo, I.F.; DaCamara, C.C.; Viterbo, P.; Roujean, J.L.; Olesen, F.; Barroso, C.; Camacho-de-Coca, F.; Carrer, D.; Freitas, S.C.; García-Haro, J.; et al. The Satellite Application Facility on Land Surface Analysis. Int. J. Remote Sens. 2011, 32, 2725–2744. [Google Scholar] [CrossRef]
- Schmetz, J.; Pili, P.; Tjemkes, S.; Just, D.; Kerkmann, J.; Rota, S.; Ratier, A. An Introduction to Meteosat Second Generation (MSG). Bull. Am. Meteorol. Soc. 2002, 83, 977–992. [Google Scholar] [CrossRef]
- Ineichen, P.; Barroso, C.S.; Geiger, B.; Hollmann, R.; Marsouin, A.; Mueller, R. Satellite Application Facilities irradiance products: hourly time step comparison and validation over Europe. Int. J. Remote Sens. 2009, 30, 5549–5571. [Google Scholar] [CrossRef]
- Roerink, G.; Bojanowski, J.; De Wit, A.; Eerens, H.; Supit, I.; Leo, O.; Boogaard, H. Evaluation of MSG-derived global radiation estimates for application in a regional crop model. Agric. For. Meteorol. 2012, 160, 36–47. [Google Scholar] [CrossRef]
- Moreno, A.; Gilabert, M.; Camacho, F.; Martínez, B. Validation of daily global solar irradiation images from MSG over Spain, Renew. Energy 2013, 60, 332–342. [Google Scholar]
- Bevan, S.L.; North, P.R.; Los, S.O.; Grey, W.M. A global dataset of atmospheric aerosol optical depth and surface reflectance from AATSR. Remote Sens. Environ. 2012, 116, 199–210. [Google Scholar] [CrossRef]
- Lubin, D.; Woodbridge, E.; Collins, W.; Zalpuri, K.S.; Jayaraman, A.; Ramachandran, S.; Ramanathan, V.; Collins, W.D. Direct observations of aerosol radiative forcing over the tropical Indian Ocean during the January-February 1996 pre-INDOEX cruise. J. Geophys. Res. Space Phys. 1998, 103, 13827–13836. [Google Scholar]
- Satheesh, S.K.; Ramanathan, V. Large differences in tropical aerosol forcing at the top of the atmosphere and Earth’s surface. Nature 2000, 405, 60–63. [Google Scholar] [CrossRef]
- Cherian, R.; Quaas, J.; Salzmann, M.; Wild, M. Pollution trends over Europe constrain global aerosol forcing as simulated by climate models. Geophys. Res. Lett. 2014, 41, 2176–2181. [Google Scholar] [CrossRef]
- Drame, M.S.; Ceamanos, X.; Roujean, J.L.; Boone, A.; Lafore, J.P.; Carrer, D.; Geoffroy, O. On the Importance of Aerosol Composition for Estimating Incoming Solar Radiation: Focus on the Western African Stations of Dakar and Niamey during the Dry Season. Atmosphere 2015, 6, 1608–1632. [Google Scholar] [CrossRef]
- Gelaro, R.; McCarty, W.; Suárez, M.J.; Todling, R.; Molod, A.; Takacs, L.; Wargan, K. The Modern-Era Retrospective Analysis for Research and Applications, Version 2 (MERRA-2). J. Clim. 2017, 30, 5419–5454. [Google Scholar] [CrossRef]
- Rémy, S.; Kipling, Z.; Flemming, J.; Boucher, O.; Nabat, P.; Michou, M.; Bozzo, A.; Ades, M.; Huijnen, V.; Benedetti, A.; et al. Description and evaluation of the tropospheric aerosol scheme in the Integrated Forecasting System (IFS-AER, cycle 45R1) of ECMWF. Geosci. Model Dev. Discuss. 2019. [Google Scholar] [CrossRef]
- Chan, K.L.; Wiegner, M.; Flentje, H.; Mattis, I.; Wagner, F.; Gasteiger, J.; Geiß, A. Evaluation of ECMWF-IFS (version 41R1) operational model forecasts of aerosol transport by using ceilometer network measurements. Geosci. Model Dev. 2018, 11, 3807–3831. [Google Scholar] [CrossRef]
- Carrer, D.; Ceamanos, X.; Six, B.; Roujean, J.-L. AERUS-GEO: A newly available satellite-derived aerosol optical depth product over Europe and Africa. Geophys. Res. Lett. 2014, 41, 7731–7738. [Google Scholar] [CrossRef]
- Xu, H.; Ceamanos, X.; Roujean, J.-L.; Carrer, D.; Xue, Y. Can satellite-derived aerosol optical depth quantify the surface aerosol radiative forcing? Atmos. Res. 2014, 150, 151–167. [Google Scholar] [CrossRef]
- Oumbe, A.; Qu, Z.; Blanc, P.; Lefèvre, M.; Wald, L.; Cros, S. Decoupling the effects of clear atmosphere and clouds to simplify calculations of the broadband solar irradiance at ground level. Geosci. Model Dev. 2014, 7, 1661–1669. [Google Scholar] [CrossRef]
- World Meteorological Organization (WMO). Measurement of sunshine duration. In WMO-No. 8–Guide to Meteorological Instruments and Methods of Observation; WMO: Geneva, Switzerland, 2006. [Google Scholar]
- Meftah, M.; Dewitte, S.; Irbah, A.; Chevalier, A.; Conscience, C.; Crommelynck, D.; Janssen, E.; Mekaoui, S. SOVAP/Picard, a spaceborne Radiometer to Measure the Total Solar Irradiance. Sol. Phys. 2014, 289, 1885–1899. [Google Scholar] [CrossRef]
- Spencer, J.W. Fourier series representation of the position of the sun. Search 1971, 2, 172. [Google Scholar]
- Carrer, D.; Roujean, J.-L.; Meurey, C. Comparing operational MSG/SEVIRI land surface albedo products from Land SAF with ground measurements and MODIS. IEEE Trans. Geosci. Remote Sens. 2010, 48, 1714–1728. [Google Scholar] [CrossRef]
- Carrer, D.; Moparthy, S.; Lellouch, G.; Ceamanos, X.; Pinault, F.; Freitas, S.C.; Trigo, I.F. Land Surface Albedo Derived on a Ten Daily Basis from Meteosat Second Generation Observations: The NRT and Climate Data Record Collections from the EUMETSAT LSA SAF. Remote Sens. 2018, 10, 1262. [Google Scholar] [CrossRef]
- NWC SAF. User Manual for the Cma, CT, CTTH, CMIC Products of NWC SAF/GEO: Scientific Part, version v2016; NWC SAF, 2016; Available online: http://www.nwcsaf.org/Downloads/GEO/2018/Documents/Scientific_Docs/NWC-CDOP3-GEO-MF-CMS-SCI-UM-Cloud_v1.0.pdf (accessed on 28 October 2019).
- Derrien, M.; Le Gléau, H. MSG/SEVIRI cloud mask and type from SAFNWC. Int. J. Remote Sens. 2005, 26, 4707–4732. [Google Scholar] [CrossRef]
- Koepke, P.; Hess, M.; Schult, I.; Shettle, E.P. Global Aerosol Data Set; Tech. Rep. 243; Max-Planck-Institut für Meteorologie: Hamburg, Germany, 1997. [Google Scholar]
- Ceamanos, X.; Carrer, D.; Roujean, J.-L. Improved retrieval of direct and diffuse downwelling surface shortwave flux in cloudless atmosphere using dynamic estimates of aerosol content and type: application to the LSA-SAF project. Atmos. Chem. Phys. Discuss. 2014, 14, 8209–8232. [Google Scholar] [CrossRef]
- Mayer, B.; Kylling, A. Technical note: The libRadtran software package for radiative transfer calculations – description and examples of use. Atmos. Chem. Phys. 2005, 5, 1855–1877. [Google Scholar] [CrossRef]
- Psiloglou, B.E.; Kambezidis, H.D. Performance of the mete-orological radiation model during the solar eclipse of 29 March 2006. Atmos. Chem. Phys. 2007, 7, 6047–6059. [Google Scholar] [CrossRef]
- Kambezidis, H.D. Current Trends in Solar Radiation Modeling: The Paradigm of MRM. J. Fundam. Renew. Energy Appl. 2016, 6, e106. [Google Scholar] [CrossRef]
- Kambezidis, H.D.; Psiloglou, B.E.; Karagiannis, D.; Dumka, U.C.; Kaskaoutis, D.G. Meteorological radiation model (mrm v6.1): Improvements in diffuse radiation estimates and a new approach for implementation of cloud products. Renew. Sustain. Energy Rev. 2017, 74, 616–637. [Google Scholar] [CrossRef]
- Psiloglou, B.E.; Santamouris, M.; Asimakopoulos, D.N. Predicting the broadband transmittance of the uniformly mixed gases (CO2, CO, N2O, CH4 and O2) in the atmosphere, for solar radiation models. Renew. Energy 1995, 6, 63–70. [Google Scholar] [CrossRef]
- Kasten, F.; Young, A.T. Revised optical air mass tables and approximation formula. Appl. Opt. 1989, 28, 4735–4738. [Google Scholar] [CrossRef]
- Psiloglou, B.E.; Santamouris, M.; Asimakopoulos, D.N. On broadband Rayleigh scattering in the atmosphere for solar radiation modelling. Renew. Energy 1995, 6, 429–433. [Google Scholar] [CrossRef]
- Bird, R.E.; Hulstrom, R.L. Simplified Clear Sky Model for Direct and Diffuse Insolation on Horizontal Surfaces (No. SERI/TR-642-761); Solar Energy Research Inst.: Golden, CO, USA, 1981. [Google Scholar]
- Mengüç, M.P.; Viskanta, R. Comparison of radiative transfer approximations for a highly forward scattering planar medium. J. Quant. Spectrosc. Radiat. Transf. 1983, 29, 381–394. [Google Scholar] [CrossRef]
- Ceamanos, X.; Carrer, D.; Roujean, J.-L. An efficient approach to estimate the transmittance and reflectance of a mixture of aerosol components. Atmos. Res. 2014, 137, 125–135. [Google Scholar] [CrossRef]
- Lacis, A.A.; Hansen, J. A Parameterization for the Absorption of Solar Radiation in the Earth’s Atmosphere. J. Atmos. Sci. 1974, 31, 118–133. [Google Scholar] [CrossRef]
- Gautier, C.; Diak, G.; Masse, S. A simple physical model to estimate incident solar radiation at the surface from GOES satellite data. J. Clim. Appl. Meteor. 1980, 19, 1005–1012. [Google Scholar] [CrossRef]
- Brisson, A.; Le Borgne, P.; Marsouin, A. Development of Algorithms for Surface Solar Irradiance Retrieval at O&SI SAF Low and Mid Latitude; Météo-France/CMS: Lannion, France, 1999. [Google Scholar]
- Clerbaux, N.; Bertrand, C.; Caprion, D.; Depaepe, B.; Dewitte, S.; Gonzalez, L.; Ipe, A. Narrowband-to-Broadband Conversions for SEVIRI. In Proceedings of the 2005 EUMETSAT Meteorological Satellite Conference, Dubrovnik, Croatia, 19–23 September 2005; pp. 351–357. [Google Scholar]
- Manalo-Smith, N.; Smith, G.L.; Tiwari, S.N.; Staylor, W.F. Analytic forms of bi-directional reflectance functions for application to Earth radiation budget studies. J. Geophys. Res. 1998, 103, 19733–19751. [Google Scholar] [CrossRef]
- Ocean & Sea Ice SAF. Surface Solar Irradiance Product Manual; Version 1.5; Ocean & Sea Ice SAF, 2005. [Google Scholar]
- Reindl, D.T.; Beckman, W.A.; Duffie, J.A. Diffuse fraction correlations. Sol. Energy 1990, 45, 1–7. [Google Scholar] [CrossRef]
- Gueymard, C.A.; Ruiz-Arias, J.A.; Gueymard, C. Extensive worldwide validation and climate sensitivity analysis of direct irradiance predictions from 1-min global irradiance. Sol. Energy 2016, 128, 1–30. [Google Scholar] [CrossRef]
- Oumbe, A.; Qu, Z.; Blanc, P.; Bru, H.; Lefèvre, M.; Wald, L. 2012: Modeling circumsolar irradiance to adjust beam irradiances from radiative transfer models to measurements. In Proceedings of the EMS Annual Meeting 2012, Lodz, Poland, 10–14 September 2012. [Google Scholar]
- Carrer, D.; Moparthy, S.; Vincent, C.; Ceamanos, X.; Freitas, S.; Trigo, I. Satellite Retrieval of Downwelling Shortwave Surface Flux and Diffuse Fraction under all Sky Conditions in the Framework of the LSA SAF Program (Part 2: Evaluation). Remote Sens. 2019. Submitted. [Google Scholar]
- Psiloglou, B.; Kambezidis, H.; Kaskaoutis, D.; Karagiannis, D.; Polo, J. Comparison between MRM simulations, CAMS and PVGIS databases with measured solar radiation components at the Methoni station, Greece. Renew. Energy 2020, 146, 1372–1391. [Google Scholar] [CrossRef]




| INSO | WASO | SOOT | SSALL | MIALL | |
|---|---|---|---|---|---|
| Type of particles | Insoluble | Water-soluble | Soot | Sea Salt | Mineral Dust |
| at 500 nm | 0.72 | 0.98 | 0.23 | 1.0 | 0.83 |
| hygroscopic | No | yes | No | Yes | No |
| Input Category | Input Description and Source | Clear-Sky Method | Cloudy-Sky Method |
|---|---|---|---|
| Atmosphere | MSG SEVIRI TOA radiances | - | X |
| Geometry | Solar zenith angle (MSG ancillary data) | X | X |
| Atmosphere | Cloud mask (NWC SAF) | X | X |
| Atmosphere | GADS aerosols components database [52] | X | X |
| Atmosphere | Atmospheric forecasts of O3 and H2O gases content from CAMS/ECMWF, interpolated to SEVIRI grid and to 15-min resolution | X | X |
| Atmosphere | Atmospheric forecasts of AOD per aerosol type, from CAMS/ECMWF, interpolated to SEVIRI grid | X | X |
| Surface | MSG Shortwave Daily Land Surface Albedos (MDAL, LSA SAF) | X | X |
| Surface | USGS DEM interpolated to SEVIRI resolution and atmospheric fields DEM interpolated to SEVIRI resolution | X | X |
| Atmosphere | Aerosol Optical Properties LUT (SIRAMix) | X | X |
| Gases | |||||
|---|---|---|---|---|---|
| H2O | 3.0140 | 119.300 | 0.6440 | 5.8140 | Variable (see Section 3.3.2) |
| O3 | 0.2554 | 6107.26 | 0.2040 | 0.4710 | Variable (see Section 3.3.2) |
| CO2 | 0.0721 | 377.890 | 0.5855 | 3.1709 | 350 |
| CO | 0.0062 | 243.670 | 0.4246 | 1.7222 | 0.075 |
| N2O | 0.0326 | 107.413 | 0.5501 | 0.9093 | 0.28 |
| CH4 | 0.0192 | 166.095 | 0.4221 | 0.7186 | 1.60 |
| O2 | 0.0003 | 476.934 | 0.4892 | 0.1261 | 2.095 × 105 |
| GADS Aerosol Components | INSO | WASO | SOOT | SSALL | MIALL |
|---|---|---|---|---|---|
| Z (km) | 8 | 8 | 8 | 1 | 2 |
| HTOL (Km) | 2 | 2 | 2 | 2 | 6 |
| GADS Aerosol Components | INSO | WASO | SOOT | SSALL | MIALL |
|---|---|---|---|---|---|
| α | 0.002 | 0.057 | 0.047 | 0.009 | 0.002 |
| β | 1.022 | 0.646 | 0.711 | 0.961 | 0.977 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Carrer, D.; Ceamanos, X.; Moparthy, S.; Vincent, C.; C. Freitas, S.; Trigo, I.F. Satellite Retrieval of Downwelling Shortwave Surface Flux and Diffuse Fraction under All Sky Conditions in the Framework of the LSA SAF Program (Part 1: Methodology). Remote Sens. 2019, 11, 2532. https://doi.org/10.3390/rs11212532
Carrer D, Ceamanos X, Moparthy S, Vincent C, C. Freitas S, Trigo IF. Satellite Retrieval of Downwelling Shortwave Surface Flux and Diffuse Fraction under All Sky Conditions in the Framework of the LSA SAF Program (Part 1: Methodology). Remote Sensing. 2019; 11(21):2532. https://doi.org/10.3390/rs11212532
Chicago/Turabian StyleCarrer, Dominique, Xavier Ceamanos, Suman Moparthy, Chloé Vincent, Sandra C. Freitas, and Isabel F. Trigo. 2019. "Satellite Retrieval of Downwelling Shortwave Surface Flux and Diffuse Fraction under All Sky Conditions in the Framework of the LSA SAF Program (Part 1: Methodology)" Remote Sensing 11, no. 21: 2532. https://doi.org/10.3390/rs11212532
APA StyleCarrer, D., Ceamanos, X., Moparthy, S., Vincent, C., C. Freitas, S., & Trigo, I. F. (2019). Satellite Retrieval of Downwelling Shortwave Surface Flux and Diffuse Fraction under All Sky Conditions in the Framework of the LSA SAF Program (Part 1: Methodology). Remote Sensing, 11(21), 2532. https://doi.org/10.3390/rs11212532






