Assessment of IMERG Precipitation Estimates over Europe
Abstract
1. Introduction
2. Data and Methodology
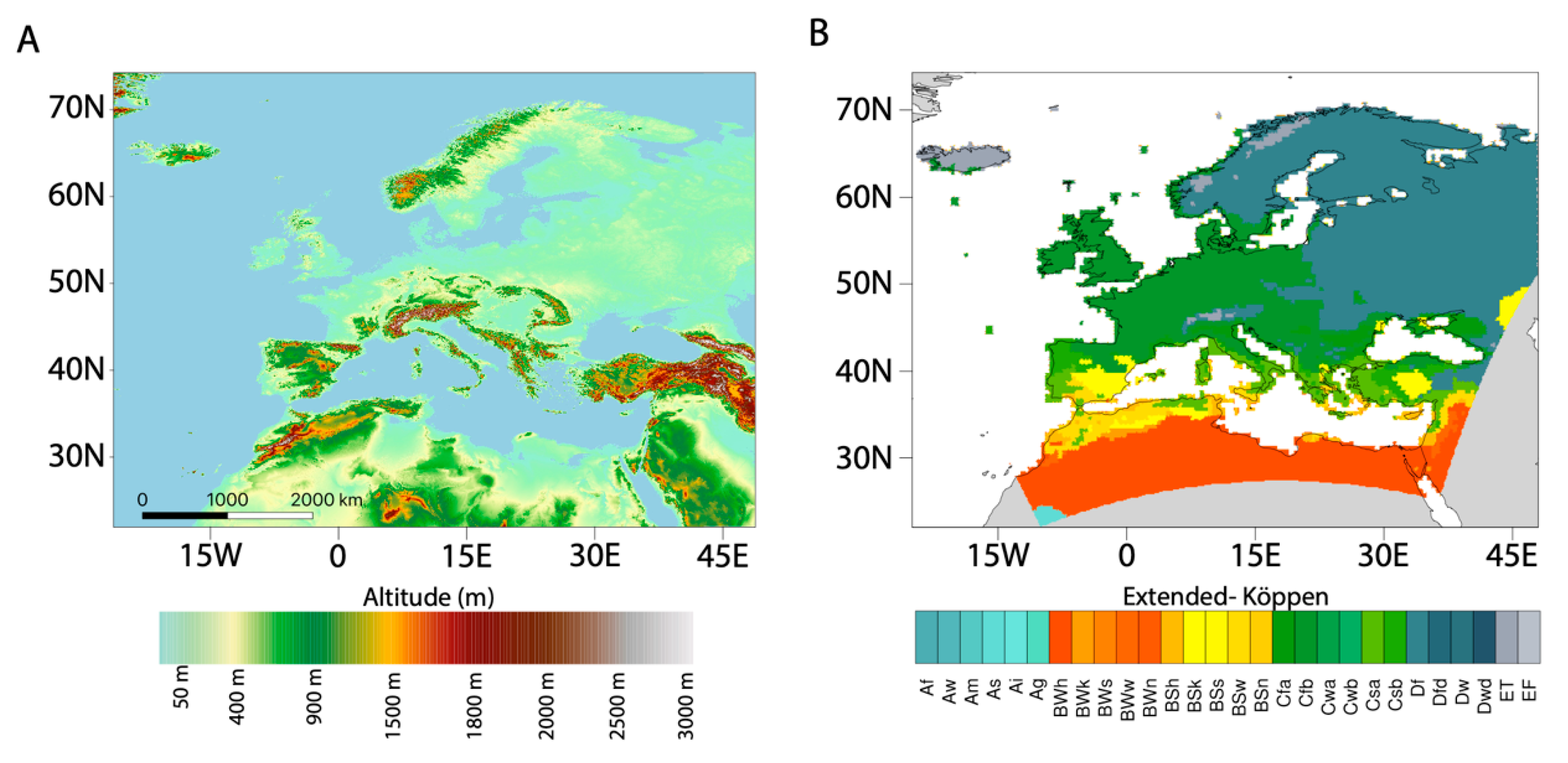
2.1. Study Area
2.2. Datasets
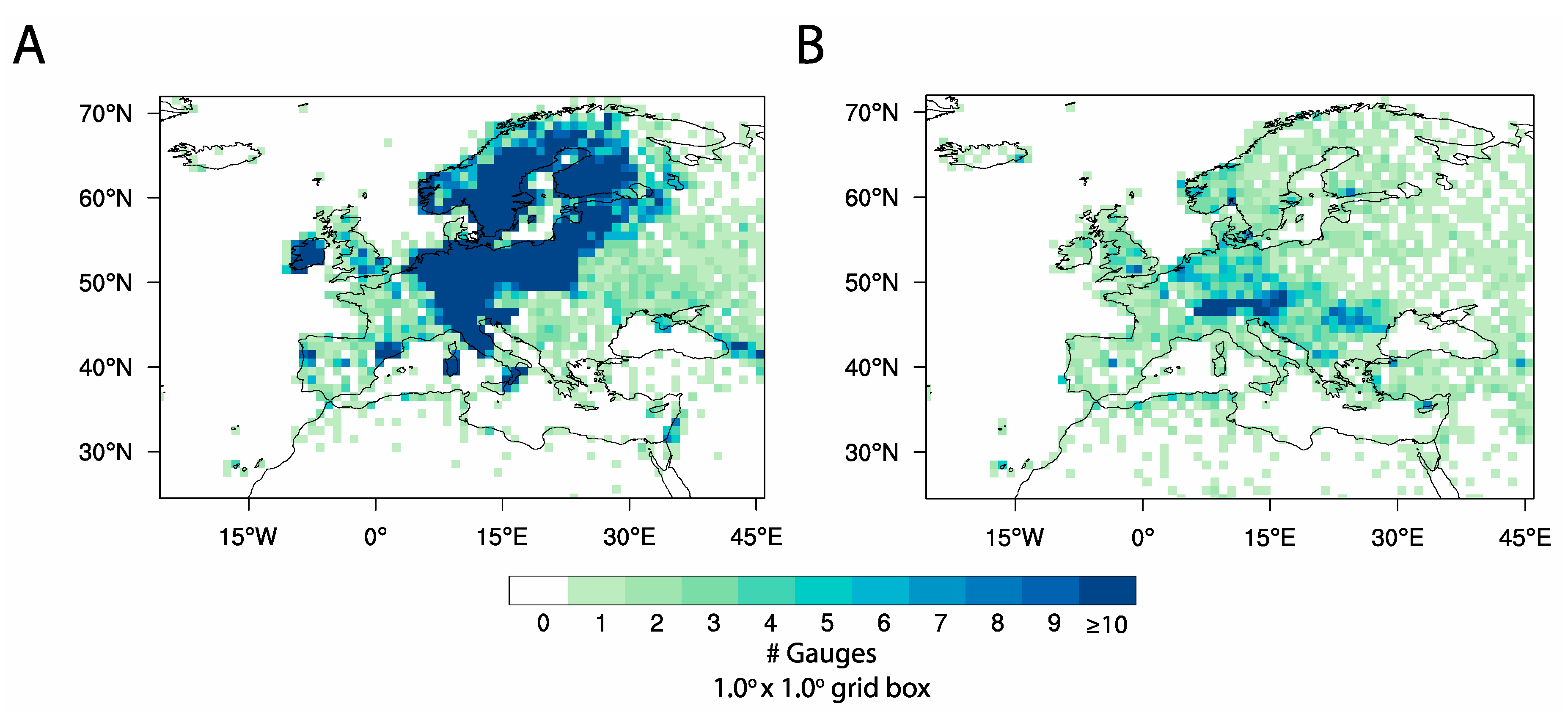
2.2.1. Surface Reference Dataset: E-OBS
2.2.2. GPCC
2.2.3. IMERG
2.3. Metrics
3. Results and Discussion
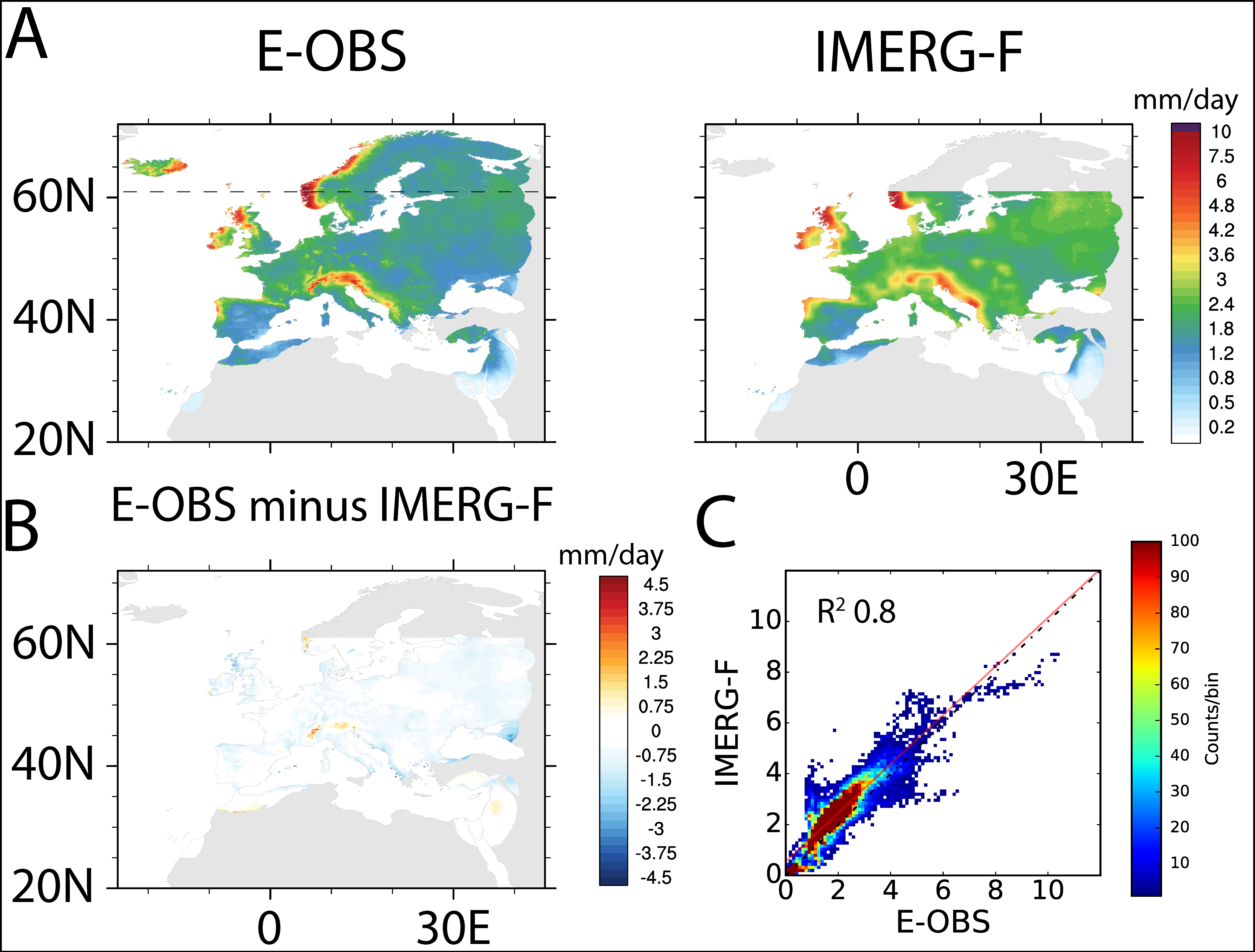
3.1. Comparisons
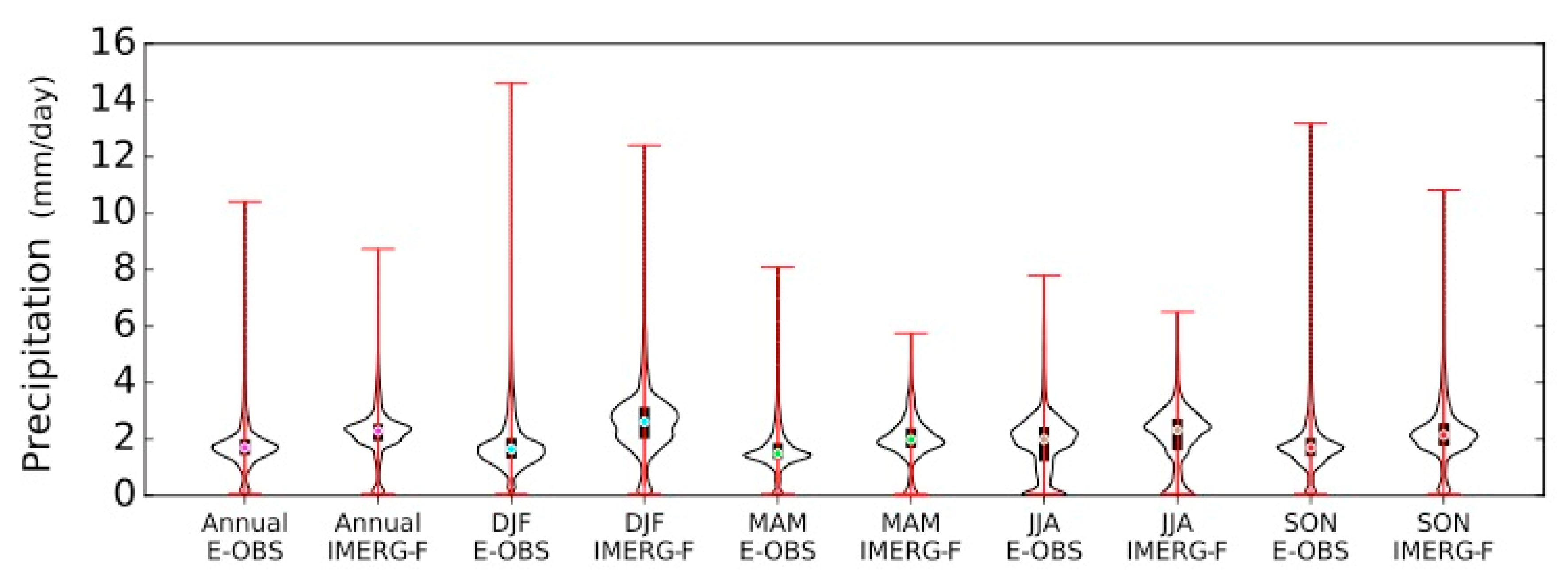
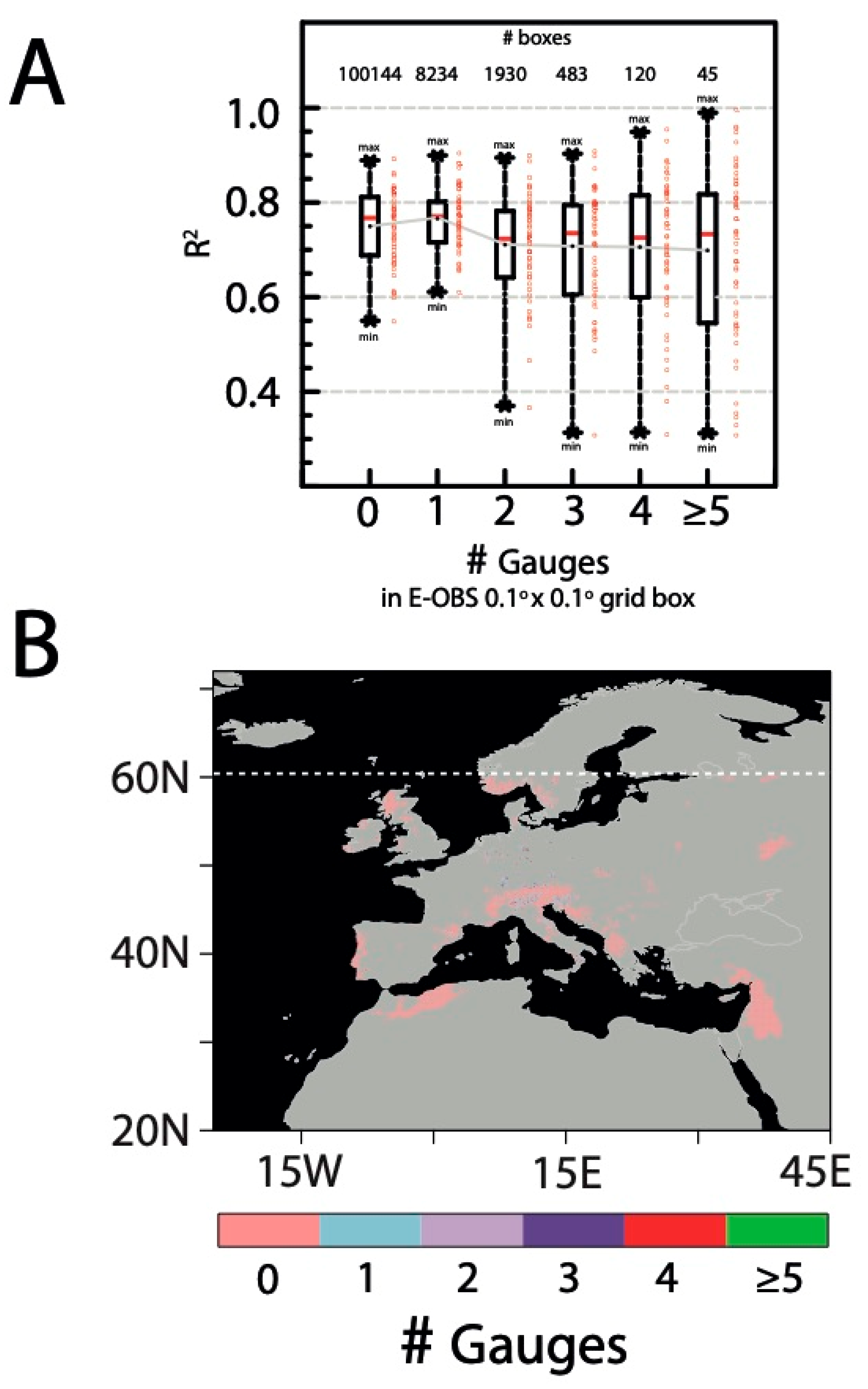
3.1.1. Annual and Seasonal Validation
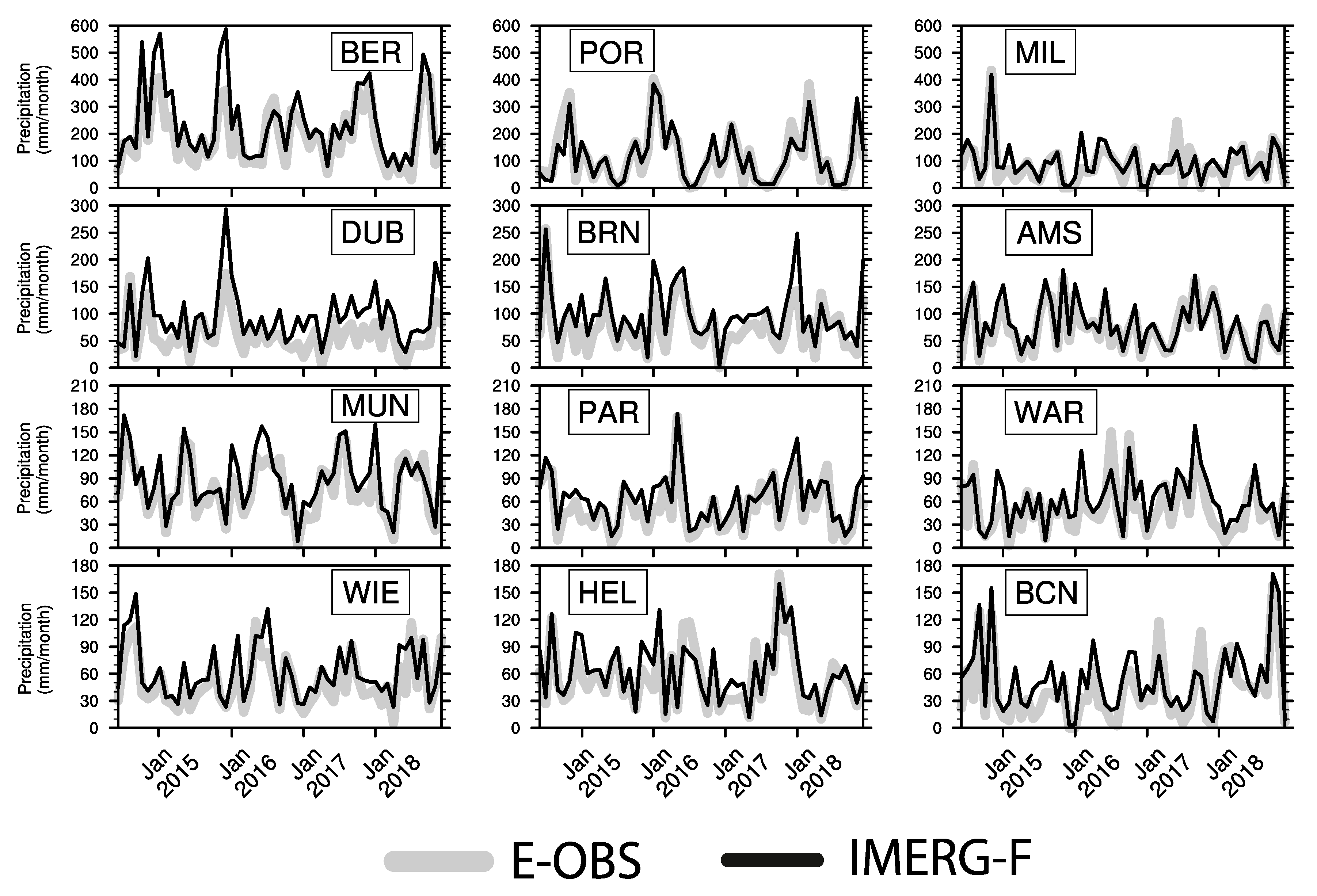
3.1.2. Monthly Time Series
3.2. IMERG Calibration
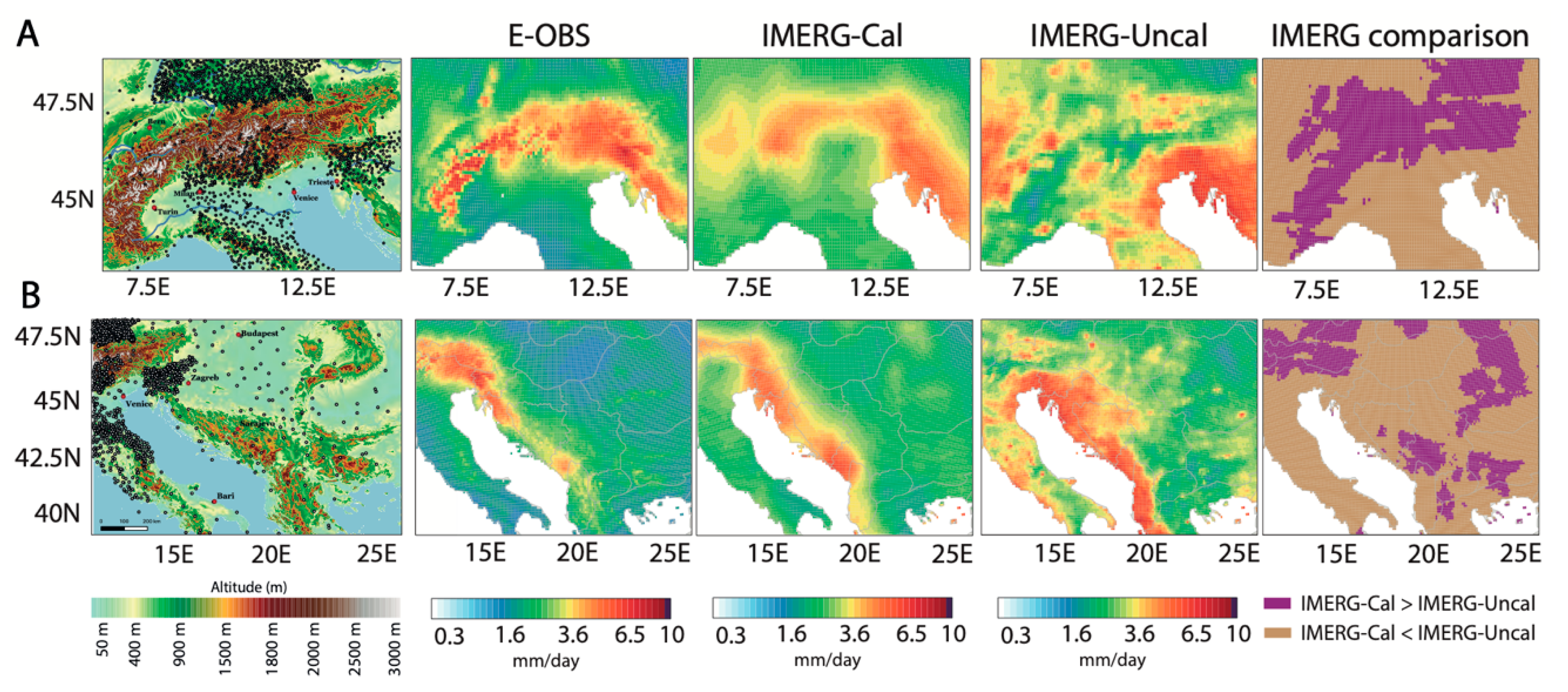
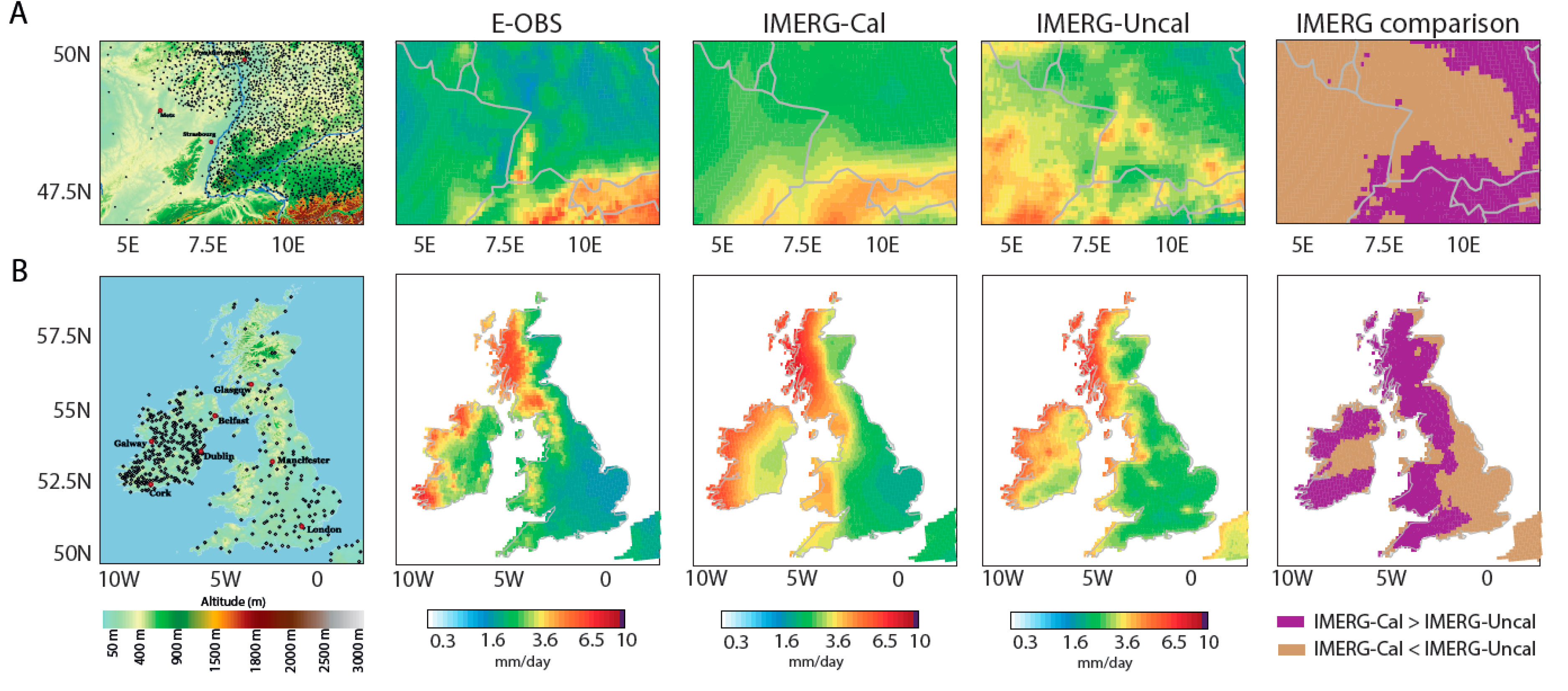
3.3. Discrepancies between E-OBS and IMERG
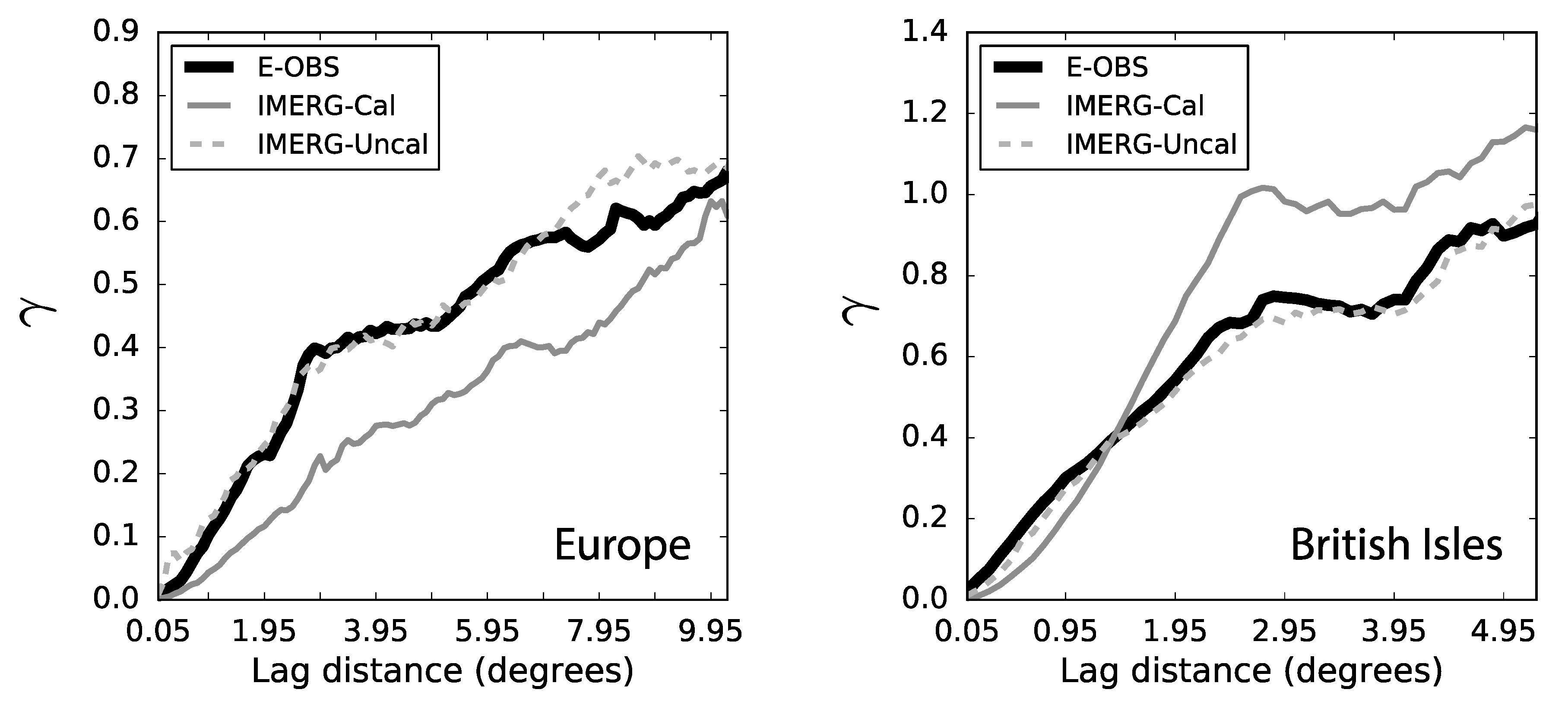
3.3.1. Overview of Areas of Discrepancy
3.3.2. Alps and Adriatic Sea
3.3.3. British Isles and Rhine
3.3.4. Corsica
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Tapiador, F.J.; Navarro, A.; Levizzani, V.; García-Ortega, E.; Huffman, G.J.; Kidd, C.; Kucera, P.A.; Kummerow, C.D.; Masunaga, H.; Petersen, W.A.; et al. Global precipitation measurements for validating climate models. Atmos. Res. 2017, 197, 1–20. [Google Scholar] [CrossRef]
- Ricciardelli, E.; Di Paola, F.; Gentile, S.; Cersosimo, A.; Cimini, D.; Gallucci, D.; Geraldi, E.; Larosa, S.; Nilo, S.T.; Ripepi, E.; et al. Analysis of Livorno Heavy Rainfall Event: Examples of Satellite-Based Observation Techniques in Support of Numerical Weather Prediction. Remote Sens. 2018, 10, 1549. [Google Scholar] [CrossRef]
- Lu, D.; Yong, B. Evaluation and Hydrological Utility of the Latest GPM IMERG V5 and GSMaP V7 Precipitation Products over the Tibetan Plateau. Remote Sens. 2018, 10, 2022. [Google Scholar] [CrossRef]
- Tapiador, F.J.; Roca, R.; Del Genio, A.; Dewitte, B.; Petersen, W.; Zhang, F. Is Precipitation a Good Metric for Model Performance? Bull. Amer. Meteor. Soc. 2019, 100, 223–233. [Google Scholar] [CrossRef]
- Michaelides, S.; Levizzani, V.; Anagnostou, E.; Bauer, P.; Kasparis, T.; Lane, J.E. Precipitation: Measurement, remote sensing, climatology and modeling. Atmos. Res. 2009, 94, 512–533. [Google Scholar] [CrossRef]
- Michaelides, S. Editorial for Special Issue “Remote Sensing of Precipitation”. Remote Sens. 2019, 11, 389. [Google Scholar] [CrossRef]
- Kidd, C.; Becker, A.; Huffman, G.J.; Muller, C.L.; Joe, P.; Skofronick-Jackson, G.; Kirschbaum, D.B. So, how much of the Earth’s surface is covered by rain gauges? Bull. Am. Meteorol. Soc. 2017, 98, 69–78. [Google Scholar] [CrossRef]
- Michelson, D.B. Systematic correction of precipitation gauge observations using analyzed meteorological variables. J. Hydrol. 2004, 290, 161–177. [Google Scholar] [CrossRef]
- Peterson, T.C.; Easterling, D.R.; Karl, T.R.; Groisman, P.; Nicholls, N.; Plummer, N.; Torok, S.; Auer, I.; Boehm, R.; Gullett, D.; et al. Homogeneity adjustments of in situ atmospheric climate data: A review. Int. J. Climatol. 1998, 18, 1493–1517. [Google Scholar] [CrossRef]
- Kidd, C. Satellite rainfall climatology: A review. Int. J. Climatol. 2001, 21, 1041–1066. [Google Scholar] [CrossRef]
- Sanò, P.; Panegrossi, G.; Casella, D.; Marra, A.C.; D’Adderio, L.P.; Rysman, J.F.; Dietrich, S. The Passive Microwave Neural Network Precipitation Retrieval (PNPR) Algorithm for the CONICAL Scanning Global Microwave Imager (GMI) Radiometer. Remote Sens. 2018, 10, 1122. [Google Scholar] [CrossRef]
- Stampoulis, D.; Anagnostou, E.N. Evaluation of Global Satellite Rainfall Products over Continental Europe. J. Hydrometeorol. 2012, 13, 588–603. [Google Scholar] [CrossRef]
- Kucera, P.A.; Ebert, E.E.; Turk, F.J.; Levizzani, V.; Kirschbaum, D.; Tapiador, F.J.; Loew, A.; Borsche, M. Precipitation from space: Advancing earth system science. Bull. Am. Meteorol. Soc. 2013, 94, 365–375. [Google Scholar] [CrossRef]
- Hou, A.Y.; Kakar, R.K.; Neeck, S.; Azarbarzin, A.A.; Kummerow, C.D.; Kojima, M.; Oki, R.; Nakamura, K.; Iguchi, T. The global precipitation measurement mission. Bull. Am. Meteorol. Soc. 2014, 95, 701–722. [Google Scholar] [CrossRef]
- Levizzani, V.; Bauer, P.; Turk, F.J. Measuring Precipitation from Space: EURAINSAT and the Future; Advances in Global Change Research; Springer: Dordrecht, The Netherlands, 2007; ISBN 978-1-4020-5834-9. [Google Scholar]
- Sun, Q.; Miao, C.; Duan, Q.; Ashouri, H.; Sorooshian, S.; Hsu, K.-L. A Review of Global Precipitation Data Sets: Data Sources, Estimation, and Intercomparisons. Rev. Geophys. 2018, 56, 79–107. [Google Scholar] [CrossRef]
- Huffman, G.J.; Bolvin, D.T.; Nelkin, E.J.; Wolff, D.B.; Adler, R.F.; Gu, G.; Hong, Y.; Bowman, K.P.; Stocker, E.F. The TRMM Multisatellite Precipitation Analysis (TMPA): Quasi-Global, Multiyear, Combined-Sensor Precipitation Estimates at Fine Scales. J. Hydrometeorol. 2007, 8, 38–55. [Google Scholar] [CrossRef]
- Kubota, T.; Shige, S.; Hashizume, H.; Aonashi, K.; Takahashi, N.; Seto, S.; Hirose, M.; Takayabu, Y.N.; Ushio, T.; Nakagawa, K.; et al. Global Precipitation Map Using Satellite-Borne Microwave Radiometers by the GSMaP Project: Production and Validation. IEEE Trans. Geosci. Remote Sens. 2007, 45, 2259–2275. [Google Scholar] [CrossRef]
- Huffman, G.J.; Bolvin, D.T.; Nelkin, E.J. Day 1 IMERG Final Run Release Notes; NASA: Washington, DC, USA, 2015; p. 9. [Google Scholar]
- Skofronick-Jackson, G.; Kirschbaum, D.; Petersen, W.; Huffman, G.; Kidd, C.; Stocker, E.; Kakar, R. The Global Precipitation Measurement (GPM) mission’s scientific achievements and societal contributions: Reviewing four years of advanced rain and snow observations. Q. J. R. Meteorol. Soc. 2018, 144, 27–48. [Google Scholar] [CrossRef]
- Prakash, S.; Mitra, A.K.; Pai, D.S.; AghaKouchak, A. From TRMM to GPM: How well can heavy rainfall be detected from space? Adv. Water Resour. 2016, 88, 1–7. [Google Scholar] [CrossRef]
- Omranian, E.; Sharif, H.O.; Tavakoly, A.A. How well can Global Precipitation Measurement (GPM) capture hurricanes? Case study: Hurricane harvey. Remote Sens. 2018, 10, 1150. [Google Scholar] [CrossRef]
- Khan, S.; Maggioni, V. Assessment of Level-3 Gridded Global Precipitation Mission (GPM) Products Over Oceans. Remote Sens. 2019, 11, 255. [Google Scholar] [CrossRef]
- Wu, L.; Xu, Y.; Wang, S. Comparison of TMPA-3B42RT Legacy Product and the Equivalent IMERG Products over Mainland China. Remote Sens. 2018, 10, 1778. [Google Scholar] [CrossRef]
- Mahmoud, M.T.; Al-Zahrani, M.A.; Sharif, H.O. Assessment of global precipitation measurement satellite products over Saudi Arabia. J. Hydrol. 2018, 559, 1–12. [Google Scholar] [CrossRef]
- Rozante, J.R.; Vila, D.A.; Barboza Chiquetto, J.; Fernandes, A.D.A.; Souza Alvim, D. Evaluation of TRMM/GPM Blended Daily Products over Brazil. Remote Sens. 2018, 10, 882. [Google Scholar] [CrossRef]
- Retalis, A.; Katsanos, D.; Tymvios, F.; Michaelides, S. Validation of the first years of GPM operation over Cyprus. Remote Sens. 2018, 10, 1520. [Google Scholar] [CrossRef]
- Gaona, M.F.R.; Overeem, A.; Leijnse, H.; Uijlenhoet, R. First-Year Evaluation of GPM Rainfall over the Netherlands: IMERG Day 1 Final Run (V03D). J. Hydrometeorol. 2016, 17, 2799–2814. [Google Scholar] [CrossRef]
- Ramsauer, T.; Weiß, T.; Marzahn, P. Comparison of the GPM IMERG Final Precipitation Product to RADOLAN Weather Radar Data over the Topographically and Climatically Diverse Germany. Remote Sens. 2018, 10, 2029. [Google Scholar] [CrossRef]
- Sungmin, O.S.; Foelsche, U.; Kirchengast, G.; Fuchsberger, J.; Tan, J.; Petersen, W.A. Evaluation of GPM IMERG Early, Late, and Final rainfall estimates using WegenerNet gauge data in Southeastern Austria. Hydrol. Earth Syst. Sci. 2017, 21, 6559–6572. [Google Scholar]
- Tapiador, F.J.; Navarro, A.; García-Ortega, E.; Merino, A.; Sánchez, J.L.; Kummerow, C.D. The Contribution of Rain Gauges in the Calibration of the GPM-IMERG Product. Results from the First Validation over Spain. J. Hydrometeorol. 2019. under review. [Google Scholar]
- Tapiador, F.J.; Moreno, R.; Navarro, A.; Sánchez, J.L.; García-Ortega, E. Climate classifications from regional and global climate models: Performaces for present climate estimates and expected changes in the future at high spatial resolution. Atmos. Res. 2019, 228, 107–121. [Google Scholar] [CrossRef]
- Köppen, W. Versuch einer Klassifikation der Klimate, vorzugsweise nach ihren Beziehungen zur Pflanzenwelt. Geogr. Zeitschrift 1900, 6, 657–679. [Google Scholar]
- Cornes, R.C.; van der Schrier, G.; van den Besselaar, E.J.M.; Jones, P.D. An Ensemble Version of the E-OBS Temperature and Precipitation Data Sets. J. Geophys. Res. Atmos. 2018, 123, 9391–9409. [Google Scholar] [CrossRef]
- Haylock, M.R.; Hofstra, N.; Tank, A.M.G.K.; Klok, E.J.; Jones, P.D.; New, M. A European daily high-resolution gridded data set of surface temperature and precipitation for 1950–2006. J. Geophys. Res. Atmos. 2008, 113. [Google Scholar] [CrossRef]
- Klok, E.J.; Tank, A.M.G.K. Updated and extended European dataset of daily climate observations. Int. J. Climatol. 2009, 29, 1182–1191. [Google Scholar] [CrossRef]
- Hofstra, N.; Haylock, M.; New, M.; Jones, P.D. Testing E-OBS European high-resolution gridded data set of daily precipitation and surface temperature. J. Geophys. Res. Atmos. 2009, 114. [Google Scholar] [CrossRef]
- Kotlarski, S.; Keuler, K.; Christensen, O.B.; Colette, A.; Déqué, M.; Gobiet, A.; Goergen, K.; Jacob, D.; Lüthi, D.; Van Meijgaard, E.; et al. Regional climate modeling on European scales: A joint standard evaluation of the EURO-CORDEX RCM ensemble. Geosci. Model Dev. 2014, 7, 1297–1333. [Google Scholar] [CrossRef]
- Spinoni, J.; Naumann, G.; Vogt, J.V.; Barbosa, P. The biggest drought events in Europe from 1950 to 2012. J. Hydrol. Reg. Stud. 2015, 3, 509–524. [Google Scholar] [CrossRef]
- Caroletti, G.N.; Coscarelli, R.; Caloiero, T. Validation of Satellite, Reanalysis and RCM Data of Monthly Rainfall in Calabria (Southern Italy). Remote Sens. 2019, 11, 1625. [Google Scholar] [CrossRef]
- Nastos, P.T.; Kapsomenakis, J.; Douvis, K.C. Analysis of precipitation extremes based on satellite and high-resolution gridded data set over Mediterranean basin. Atmos. Res. 2013, 131, 46–59. [Google Scholar] [CrossRef]
- Retalis, A.; Katsanos, D.; Michaelides, S. Precipitation climatology over the Mediterranean Basin—Validation over Cyprus. Atmos. Res. 2016, 169, 449–458. [Google Scholar] [CrossRef]
- Schneider, U.; Finger, P.; Meyer-Christoffer, A.; Rustemeier, E.; Ziese, M.; Becker, A. Evaluating the Hydrological Cycle over Land Using the Newly-Corrected Precipitation Climatology from the Global Precipitation Climatology Centre (GPCC). Atmosphere 2017, 8, 52. [Google Scholar] [CrossRef]
- Huffman, G.J.; Bolvin, D.; Braithwaite, D.; Hsu, K.-L.; Joyce, R.; Kidd, C.; Nelkin, E.; Sorooshian, S.; Tan, J.; Xie, P. Integrated Multi-Satellite Retrievals for GPM (IMERG) Technical Documentation; NASA/GSFC: Greenbelt, MD, USA, 2018. [Google Scholar]
- Kummerow, C.D. GPROF2017 Version 1; NASA/GSFC: Greenbelt, MD, USA, 2017. [Google Scholar]
- Cook, R.D.; Weisberg, S. Residuals and Influence in Regression; Chapman and Hall: New York, NY, USA, 1982. [Google Scholar]
- Copernicus Emergency Management Service. EMSR108: Landslides and Floods in Northern Italy; European Commission Joint Research Centre: Brussels, Belgium, 2014. [Google Scholar]
- Guo, H.; Chen, S.; Bao, A.; Behrangi, A.; Hong, Y.; Ndayisaba, F.; Hu, J.; Stepanian, P.M. Early assessment of Integrated Multi-satellite Retrievals for Global Precipitation Measurement over China. Atmos. Res. 2016, 176, 121–133. [Google Scholar] [CrossRef]
- Houze, R.A. Orographic effects on precipitating clouds. Rev. Geophys. 2012, 50. [Google Scholar] [CrossRef]
- Maggioni, V.; Nikolopoulos, E.I.; Anagnostou, E.N.; Borga, M. Modeling Satellite Precipitation Errors Over Mountainous Terrain: The Influence of Gauge Density, Seasonality, and Temporal Resolution. IEEE Trans. Geosci. Remote Sens. 2017, 55, 4130–4140. [Google Scholar] [CrossRef]
- Krakauer, N.Y.; Pradhanang, S.M.; Lakhankar, T.; Jha, A.K. Evaluating Satellite Products for Precipitation Estimation in Mountain Regions: A Case Study for Nepal. Remote Sens. 2013, 5, 4107–4123. [Google Scholar] [CrossRef]
- Wen, Y.; Behrangi, A.; Lambrigtsen, B.; Kirstetter, P.-E. Evaluation and uncertainty estimation of the latest radar and satellite snowfall products using SNOTEL measurements over mountainous regions in western United States. Remote Sens. 2016, 8, 904. [Google Scholar] [CrossRef]
- Hirpa, F.A.; Gebremichael, M.; Hopson, T. Evaluation of High-Resolution Satellite Precipitation Products over Very Complex Terrain in Ethiopia. J. Appl. Meteor. Climatol. 2009, 49, 1044–1051. [Google Scholar] [CrossRef]
- Gabella, M.; Speirs, P.; Hamann, U.; Germann, U.; Berne, A. Measurement of precipitation in the Alps using dual-polarization C-Band ground-based radars, the GPMSpaceborne Ku-Band Radar, and rain gauges. Remote Sens. 2017, 9, 1147. [Google Scholar] [CrossRef]
- Asong, Z.E.; Razavi, S.; Wheater, H.S.; Wong, J.S. Evaluation of Integrated Multisatellite Retrievals for GPM (IMERG) over Southern Canada against Ground Precipitation Observations: A Preliminary Assessment. J. Hydrometeorol. 2017, 18, 1033–1050. [Google Scholar] [CrossRef]
- Herrera, S.; Kotlarski, S.; Soares, P.M.M.; Cardoso, R.M.; Jaczewski, A.; Gutiérrez, J.M.; Maraun, D. Uncertainty in gridded precipitation products: Influence of station density, interpolation method and grid resolution. Int. J. Climatol. 2019, 39, 3717–3729. [Google Scholar] [CrossRef]
- Hofstra, N.; New, M.; McSweeney, C. The influence of interpolation and station network density on the distributions and trends of climate variables in gridded daily data. Climate Dyn. 2010, 35, 841–858. [Google Scholar] [CrossRef]



| Precipitation (mm/day) | Number of Gauges Per Pixel | |||||
|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | 5 | |
| 0 to < 0.1 | 0.05 | 0.04 | 0.03 | 0.1 | 0.05 | 0.35 |
| 0.1 to < 2.5 | 0.52 | 0.58 | 0.58 | 0.54 | 0.53 | 0.59 |
| 2.5 to < 5.0 | 0.20 | 0.24 | 0.22 | 0.22 | 0.19 | 0.27 |
| 5.0 to < 10.0 | 0.25 | 0.31 | 0.20 | 0.22 | 0.32 | 0.28 |
| ≥10.0 | 0.43 | 0.44 | 0.32 | 0.55 | 0.67 | * |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Navarro, A.; García-Ortega, E.; Merino, A.; Sánchez, J.L.; Kummerow, C.; Tapiador, F.J. Assessment of IMERG Precipitation Estimates over Europe. Remote Sens. 2019, 11, 2470. https://doi.org/10.3390/rs11212470
Navarro A, García-Ortega E, Merino A, Sánchez JL, Kummerow C, Tapiador FJ. Assessment of IMERG Precipitation Estimates over Europe. Remote Sensing. 2019; 11(21):2470. https://doi.org/10.3390/rs11212470
Chicago/Turabian StyleNavarro, Andrés, Eduardo García-Ortega, Andrés Merino, José Luis Sánchez, Christian Kummerow, and Francisco J. Tapiador. 2019. "Assessment of IMERG Precipitation Estimates over Europe" Remote Sensing 11, no. 21: 2470. https://doi.org/10.3390/rs11212470
APA StyleNavarro, A., García-Ortega, E., Merino, A., Sánchez, J. L., Kummerow, C., & Tapiador, F. J. (2019). Assessment of IMERG Precipitation Estimates over Europe. Remote Sensing, 11(21), 2470. https://doi.org/10.3390/rs11212470









