Turbulence Measurements with Dual-Doppler Scanning Lidars
Abstract
1. Introduction
2. Background
2.1. Generalities
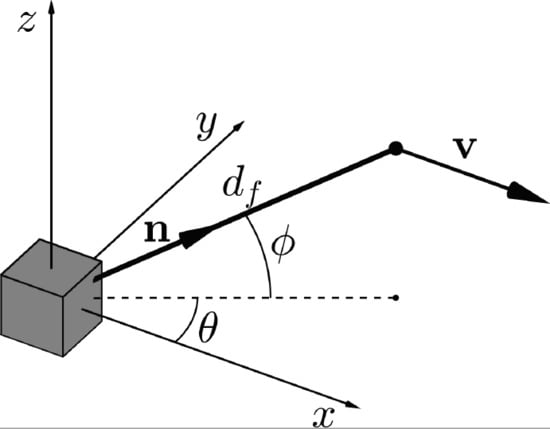
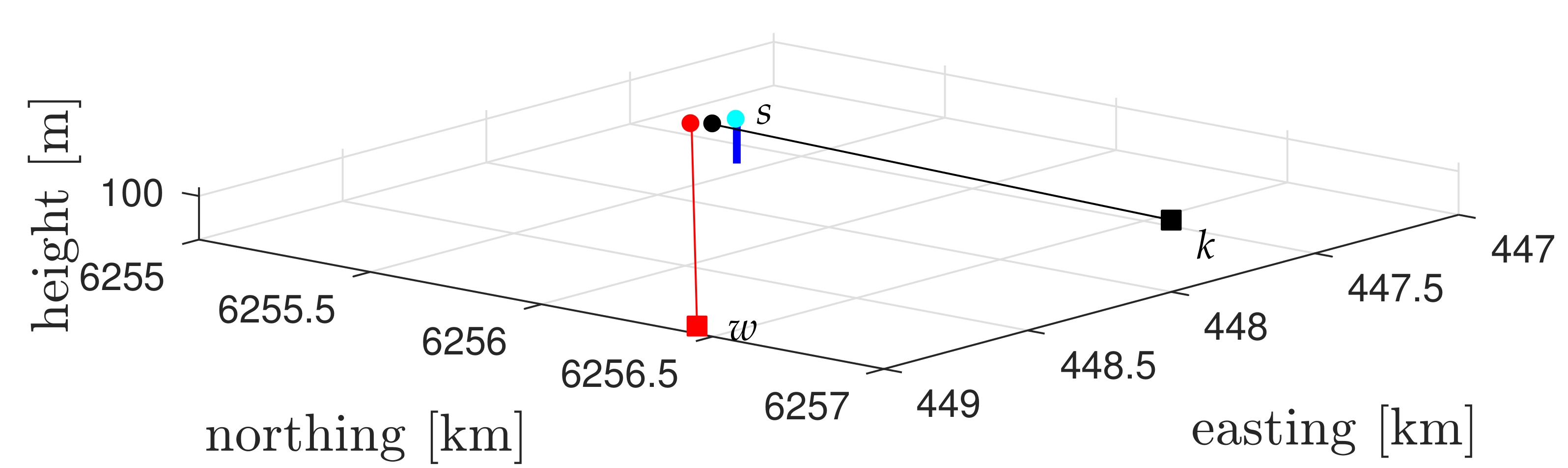
2.2. Dual-Doppler Scanning System
2.2.1. Direct Velocity and Variance Computations
2.2.2. Indirect Variance Computations
3. Experimental Campaign
3.1. Description
3.2. Data Handling and Filtering
- We analyzed the 20-Hz sonic anemometer measurements within each 10-min period and filtered out the 10-min periods where more than 1% of the 20-Hz data within each 10-min showed a sonic status signal lower than two. This procedure resulted in 2574 10-min periods for the analysis.
- We computed the mean horizontal wind speed and wind direction, linearly interpolated the voids in each 10-min time series due to the sonic status filter, performed azimuth and tilt rotations to the sonic anemometer velocity components to have the u-velocity component aligned with the 10-min mean wind direction, and calculated the u- and v-velocity variances.
- We also transformed the sonic anemometer velocities to estimate the sonic-based radial velocities on the WindScanners beams’ directions and computed the mean and variance of both radial velocities.
- We retrieved the WindScanners’ radial velocities within each 10-min interval and filtered out scans where the carrier-to-noise ratio (CNR) was either below dB or above dB. This procedure tries to avoid inaccurate scans and those where hard targets were hit (e.g., the mast). We only analyzed 10-min periods if both lidars showed at least 1000 scans per 10-min interval (out of ≈1200). This left us with 1982 10-min periods for analysis.
- We used the algorithm by Goring and Nikora [34] to detect spikes in the radial velocity time series and filtered out those for each lidar. Again, we only analyzed 10-min periods if both lidars showed at least 1000 scans per 10-min interval (out of ≈1200). This left us with 1939 10-min periods for analysis.
- We computed mean and variances on both WindScanners radial velocities, reconstructed the east and north velocity components from these radial velocities and thus the wind direction assuming . We rotated these velocity components to estimate u (aligned with the mean horizontal wind) and v the crosswind, and estimated their variances.
4. Results
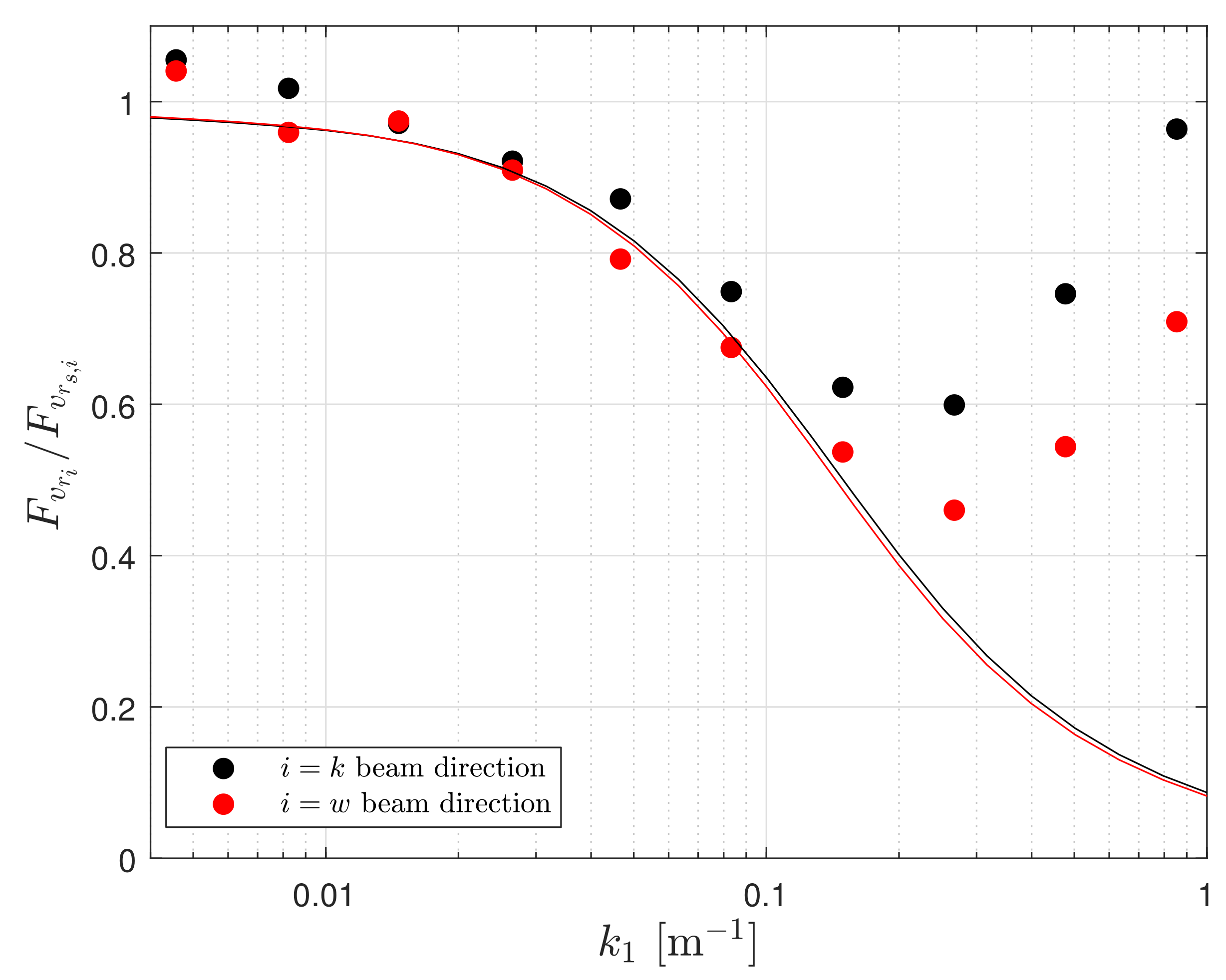
4.1. Radial Velocity Spectra Estimation
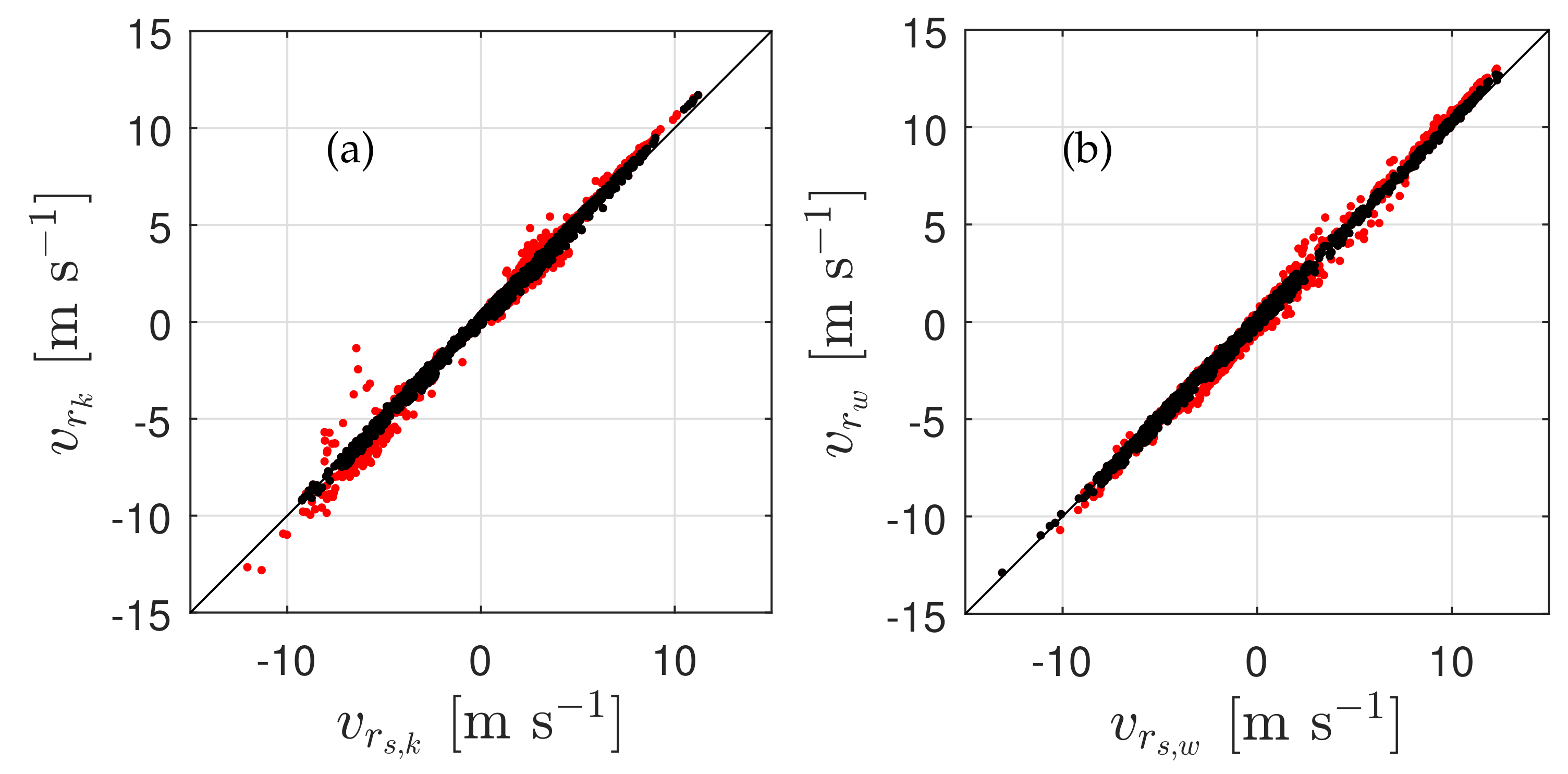
4.2. Radial Velocities
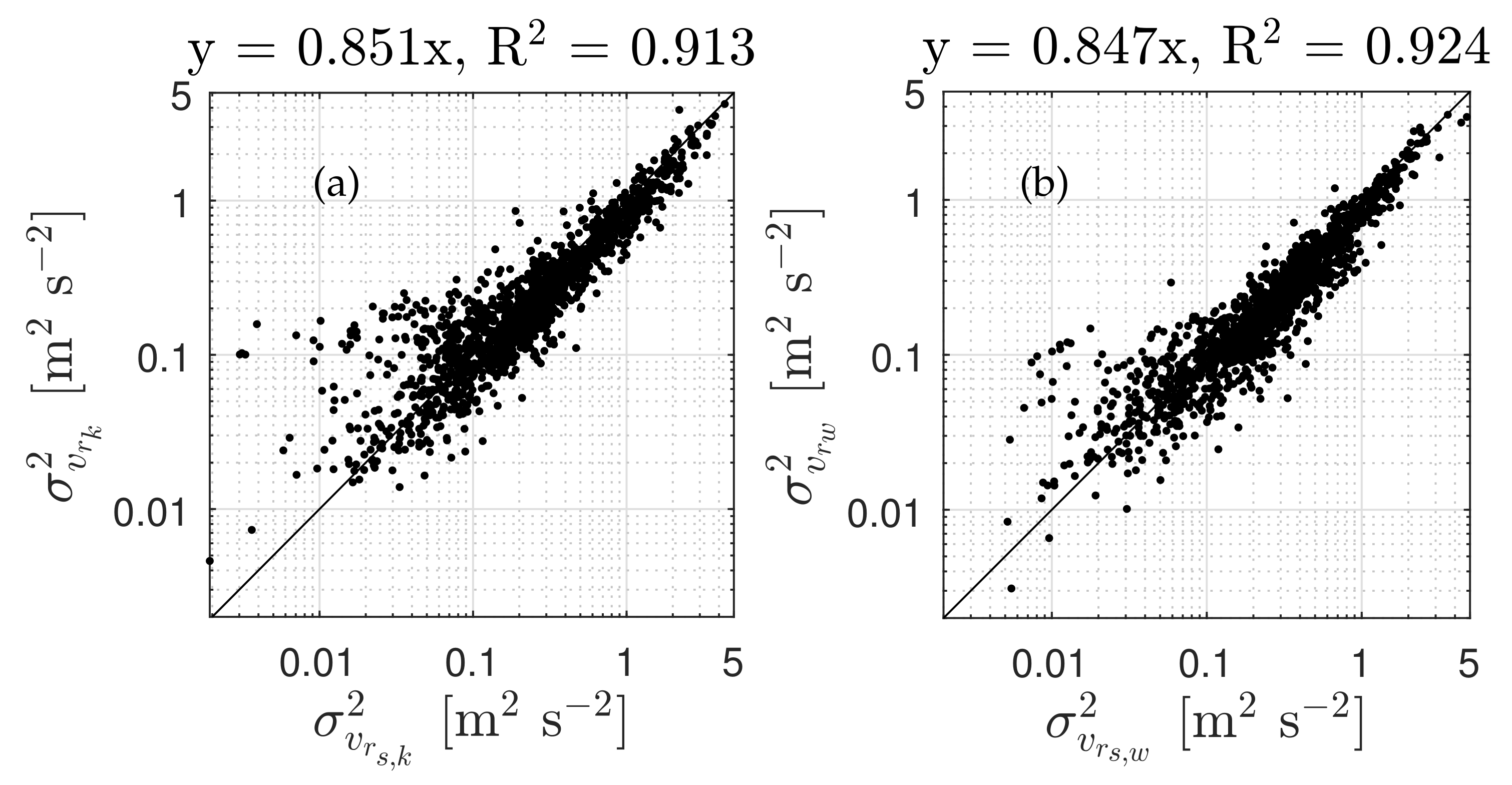
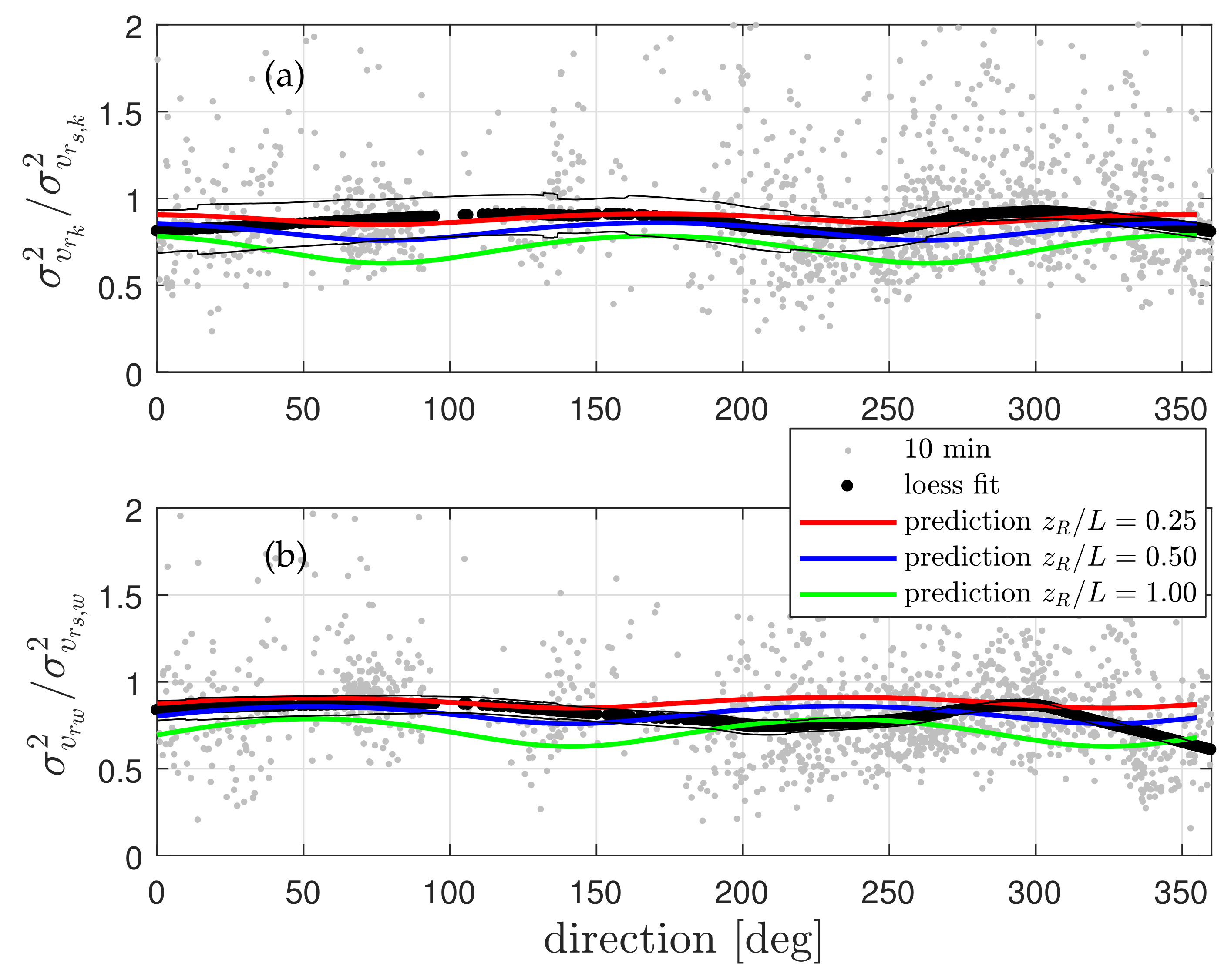
4.3. Radial Velocity Variance
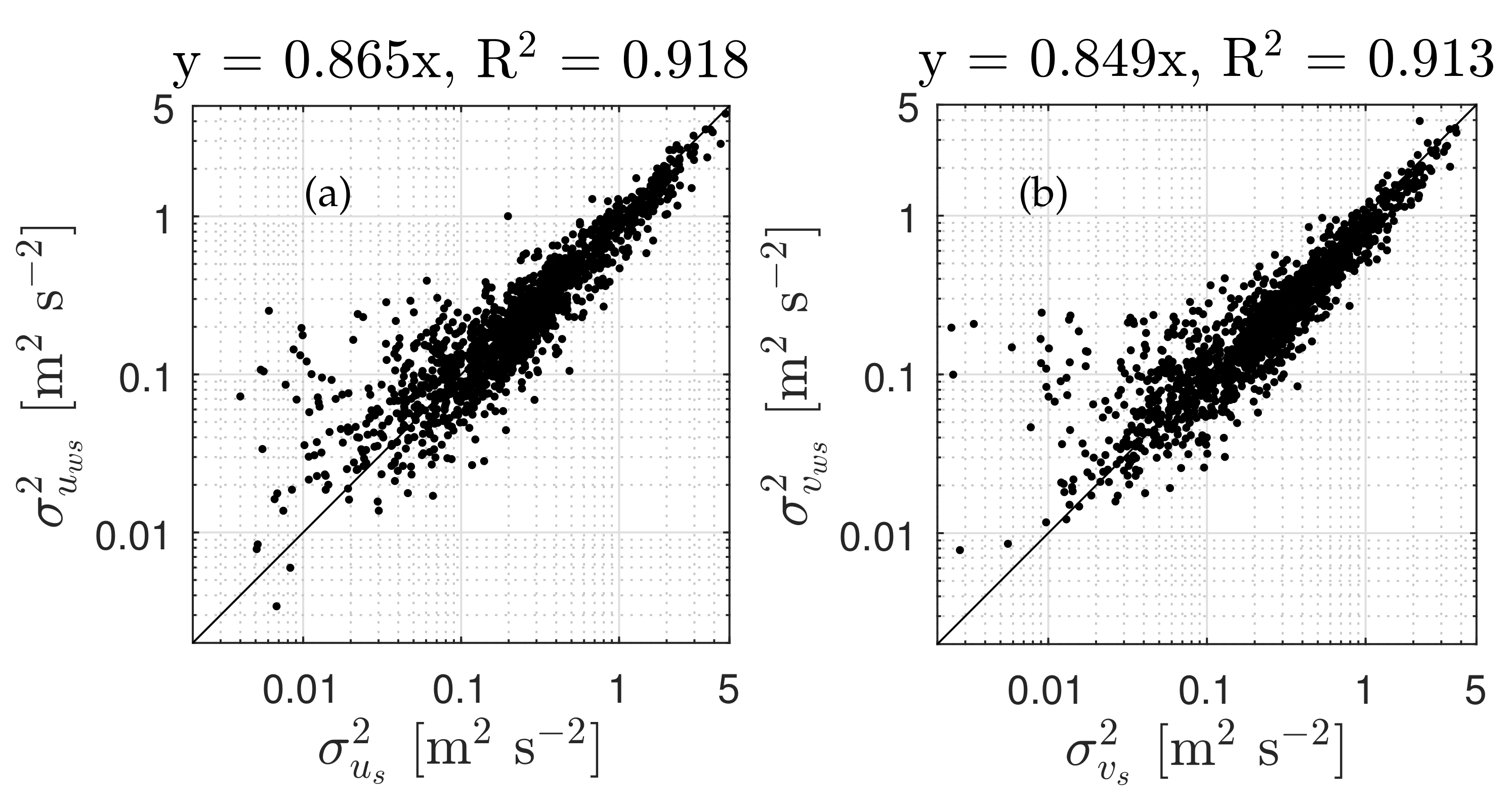
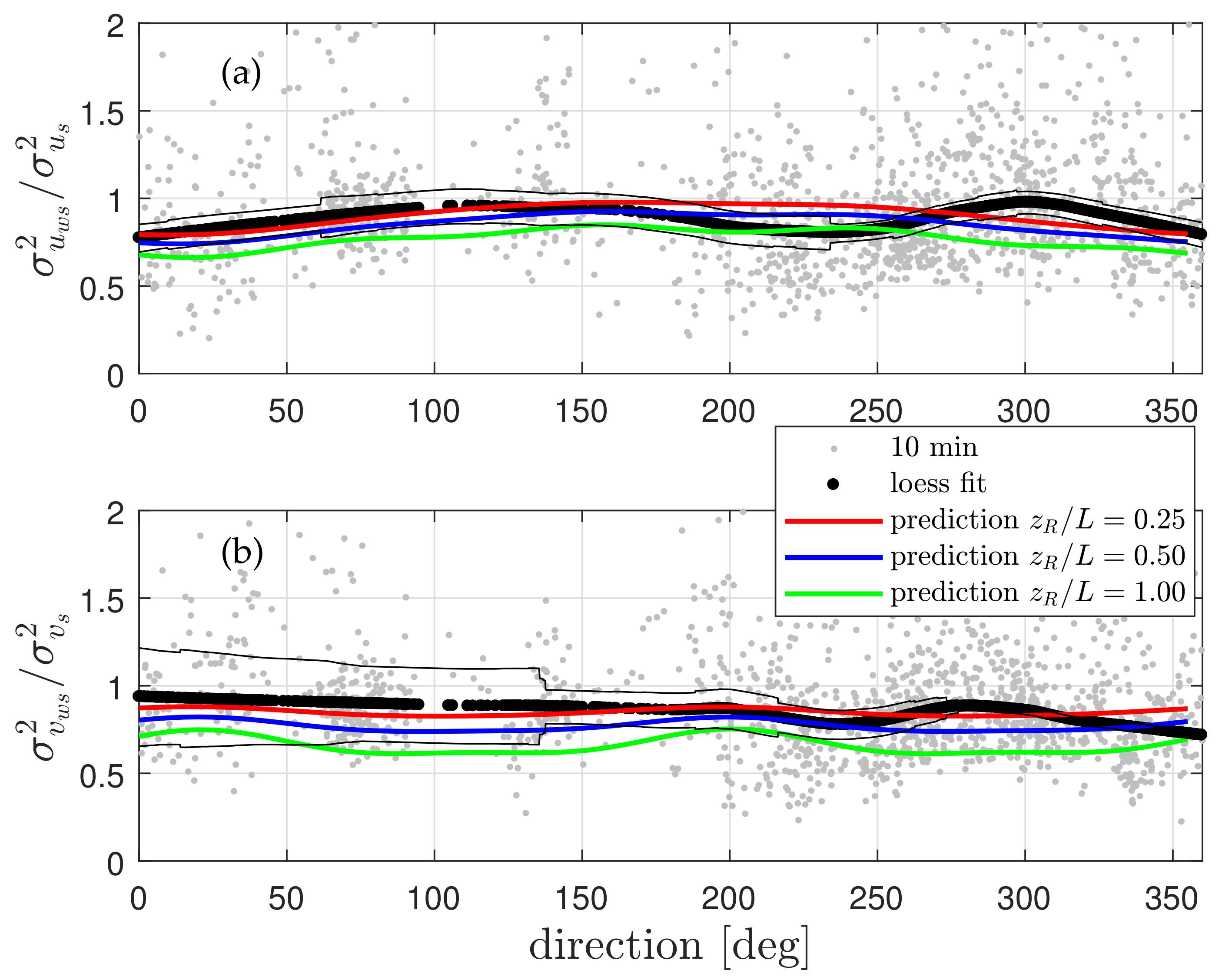
4.4. Velocity-Component Variances
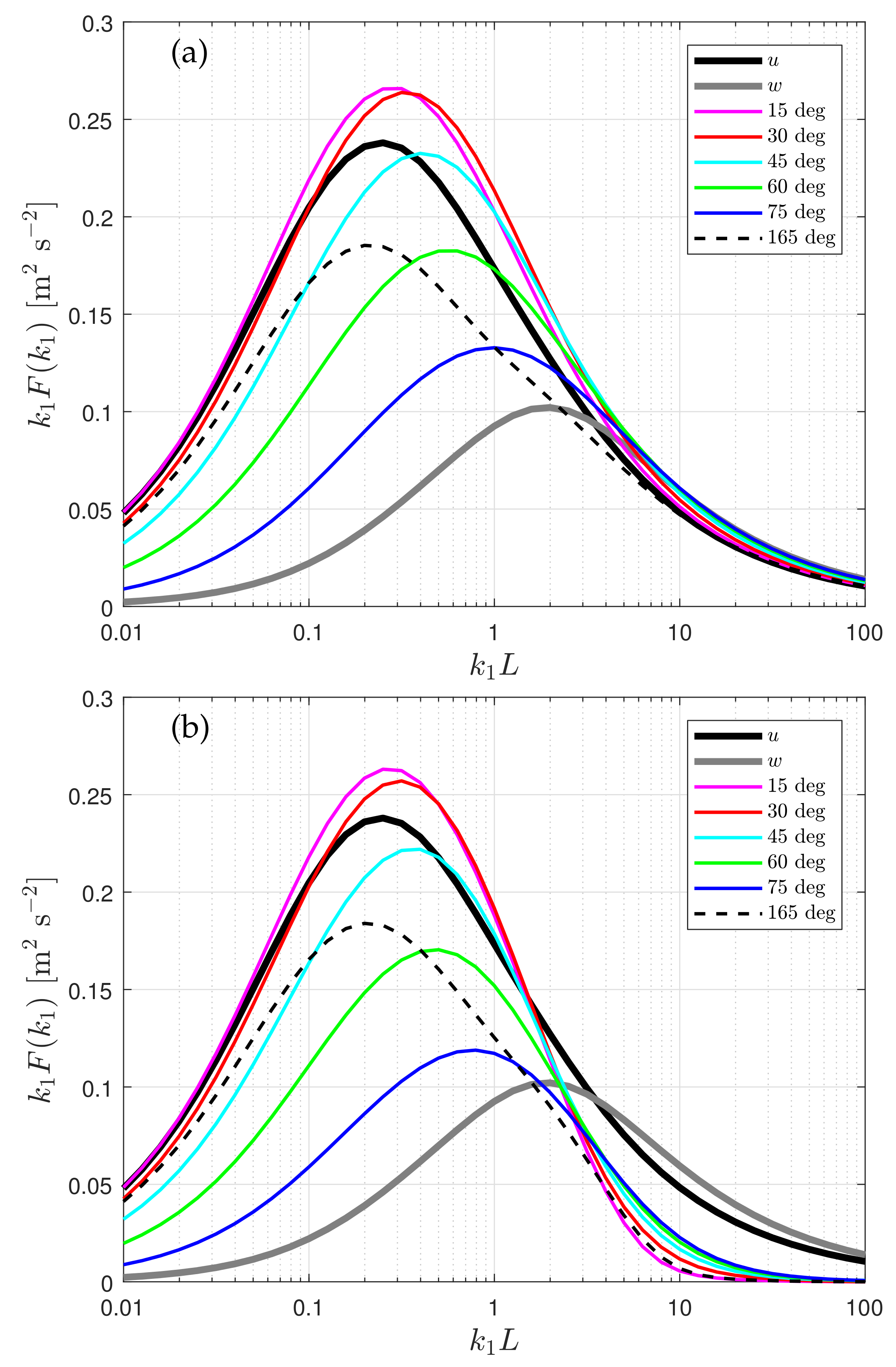
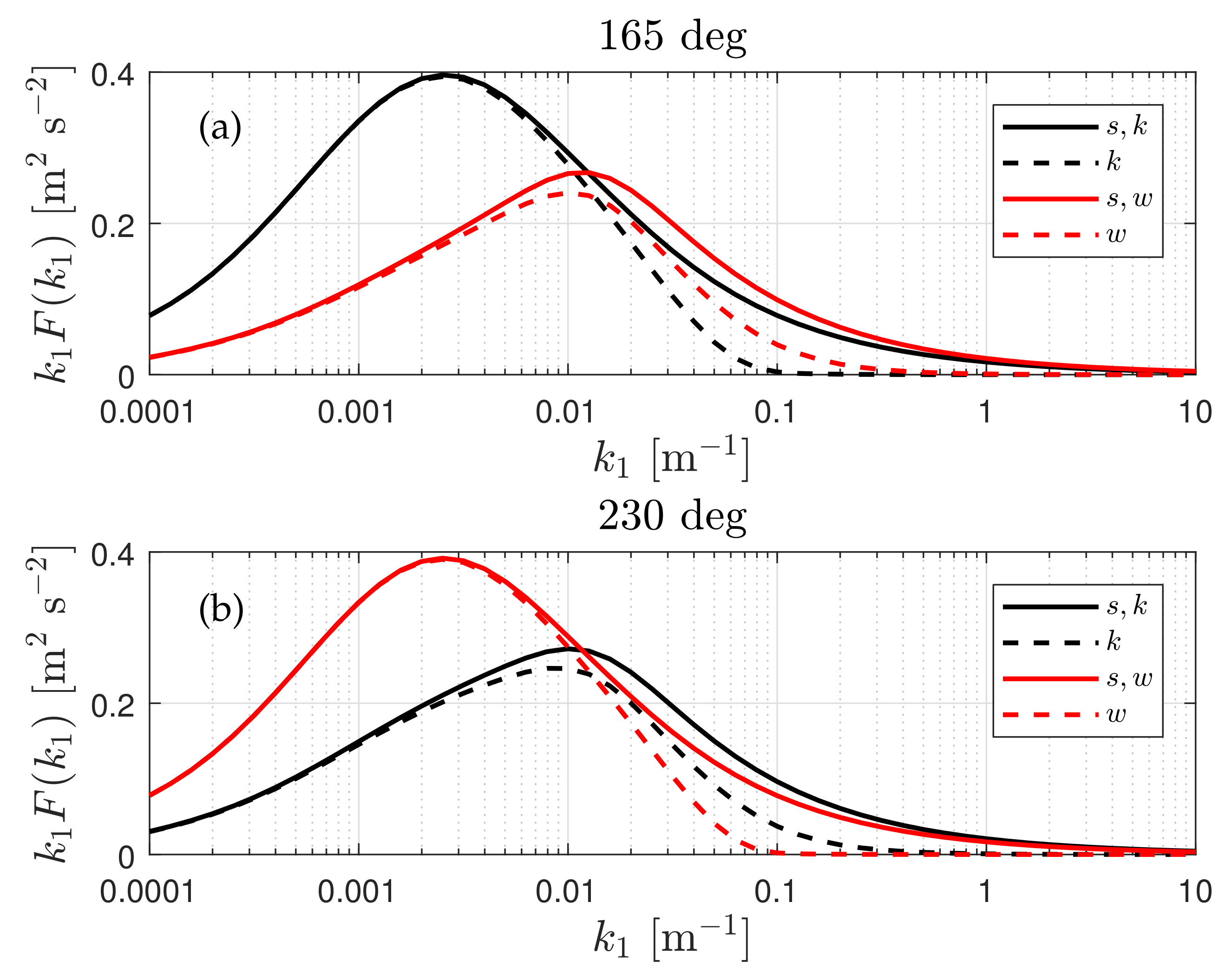
4.5. Radial Velocity Spectra
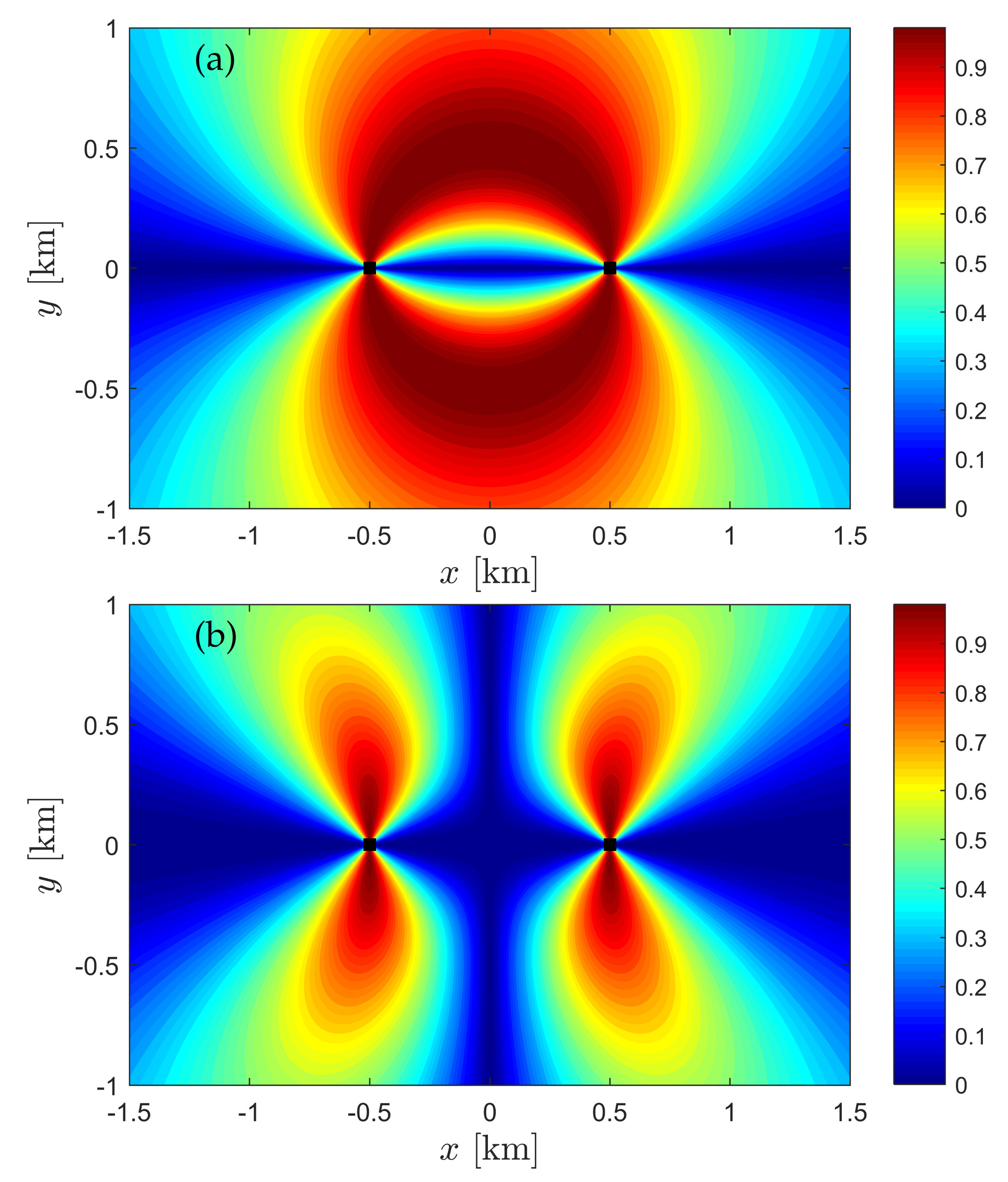
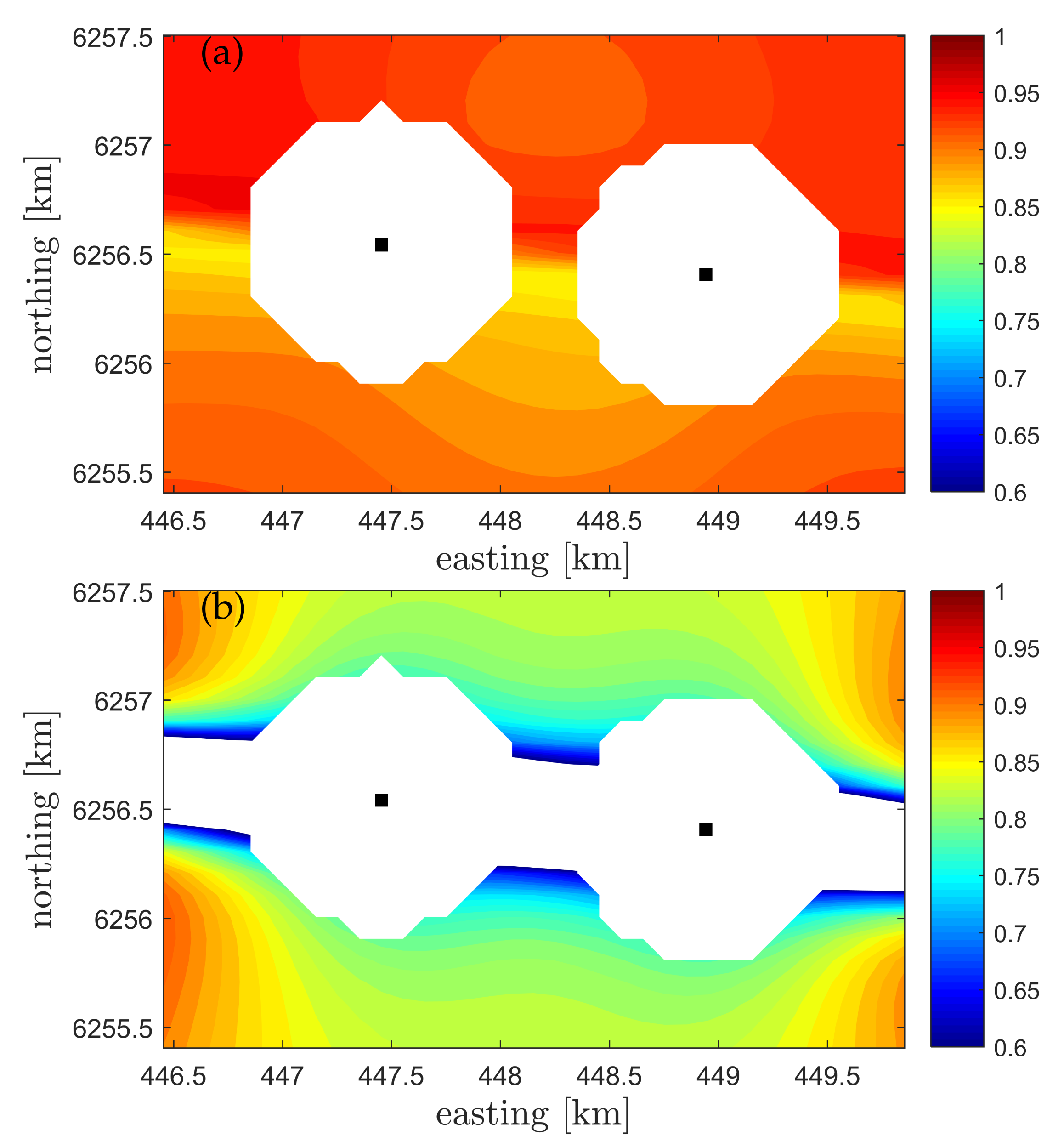
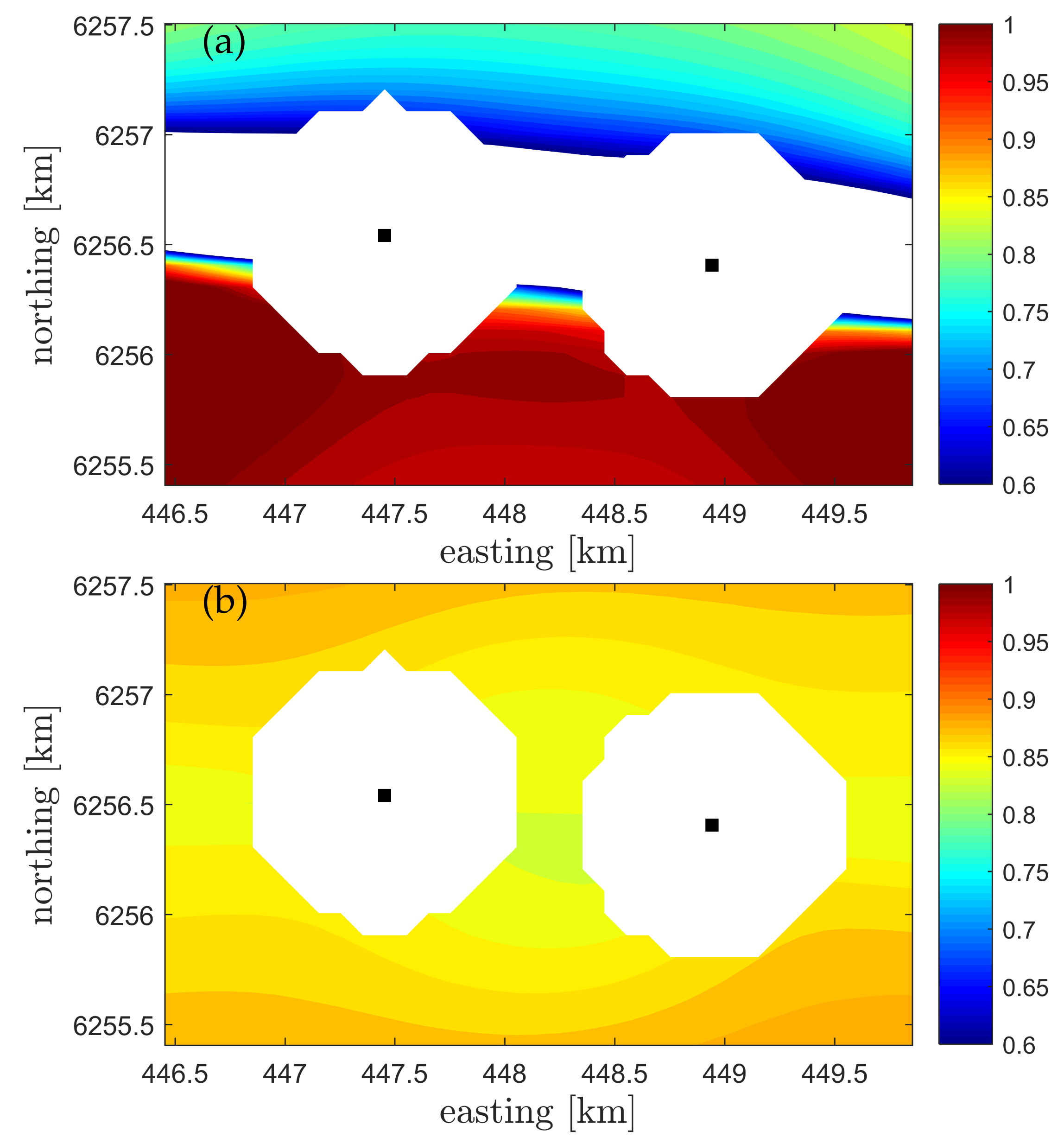
4.6. Spatial Behavior of Velocity-Variance Biases
5. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Chan, P.W. Generation of an Eddy Dissipation Rate Map at the Hong Kong International Airport Based on Doppler Lidar Data. J. Atmos. Ocean. Technol. 2011, 28, 37–49. [Google Scholar] [CrossRef]
- Oude Nijhuis, A.C.P.; Thobois, L.P.; Barbaresco, F.; de Haan, S.; Dolfi-Bouteyre, A.; Kovalev, D.; Krasnov, O.A.; Vanhoenacker-Janvier, D.; Wilson, R.; Yarovoy, A.G. Wind Hazard and Turbulence Monitoring at Airports with Lidar, Radar, and Mode-S Downlinks: The UFO Project. Bull. Am. Meteorol. Soc. 2018, 99, 2275–2293. [Google Scholar] [CrossRef]
- Frehlich, R.; Hannon, S.M.; Henderson, S.W. Coherent Doppler Lidar Measurements of Wind Field Statistics. Bound.-Layer Meteorol. 1998, 86, 233–256. [Google Scholar] [CrossRef]
- Lothon, M.; Lenschow, D.H.; Mayor, S.D. Doppler lidar measurements of vertical velocity spectra in the convective planetary boundary layer. Boundary-Layer Meteorol. 2009, 132, 205–226. [Google Scholar] [CrossRef]
- Barlow, J.F.; Dunbar, T.M.; Nemitz, E.G.; Wood, C.R.; Gallaguer, M.W.; Davies, F.; O’Connor, E.; Harrison, R.M. Boundary layer dynamics over London, UK, as observed using Doppler lidar during REPARTEE-II. Atmos. Chem. Phys. 2011, 11, 2111–2125. [Google Scholar] [CrossRef]
- Smalikho, I.N.; Banakh, V.A.; Pichugina, Y.L.; Brewer, W.A.; Banta, R.M.; Lundquist, J.K.; Kelley, N.D. Lidar investigation of atmosphere effect on a wind turbine wake. J. Atmos. Ocean. Technol. 2013, 30, 2554–2570. [Google Scholar] [CrossRef]
- Pichugina, Y.L.; Brewer, W.A.; Banta, R.M.; Choukulkar, A.; Clack, C.T.M.; Marquis, M.C.; McCarty, B.J.; Weickmann, A.M.; Sandberg, S.P.; Marchbanks, R.D.; et al. Properties of the offshore low level jet and rotor layer wind shear as measured by scanning Doppler Lidar. Wind Energ. 2017, 20, 987–1002. [Google Scholar] [CrossRef]
- Floors, R.; Peña, A.; Lea, G.; Vasiljevic, N.; Simon, E.; Courtney, M. The RUNE experiment–A database of remote-sensing observations of near-shore winds. Remote Sens. 2016, 8, 884. [Google Scholar] [CrossRef]
- Mann, J.; Angelou, N.; Arnqvist, J.; Callies, D.; Cantero, E.; Arroyo, R.C.; Courtney, M.; Cuxart, J.; Dellwik, E.; Gottschall, J.; et al. Complex terrain experiments in the New European Wind Atlas. Philos. Trans. R. Soc. A 2017, 375, 20160101. [Google Scholar] [CrossRef]
- Wagner, R.; Vignaroli, A. Power Curve Measurement with a Sector Scanning Lidar from the TP and a Nacelle Lidar at Greater Gabbard; Technical Report DTU Wind Energy GG I-0016 (EN); DTU Wind Energy: Roskilde, Denmark, 2015. [Google Scholar]
- Mann, J.; Cariou, J.P.; Courtney, M.S.; Parmentier, R.; Mikkelsen, T.; Wagner, R.; Lindelöw, P.; Sjöholm, M.; Enevoldsen, K. Comparison of 3D turbulence measurements using three staring wind lidars and a sonic anemometer. Meteorol. Z. 2009, 18, 135–140. [Google Scholar] [CrossRef]
- Pauscher, L.; Vasiljevic, N.; Callier, D.; Lea, G.; Mann, J.; Klaas, T.; Hieronimus, J.; Gottschall, J.; Schwesig, A.; Kühn, M.; et al. An inter-comparison study of multi- and DBS lidar measurements in complex terrain. Remote Sens. 2016, 8, 782. [Google Scholar] [CrossRef]
- Barthelmie, R.J.; Doubrawa, P.; Wang, H.; Pryor, S.C. Defining wake characteristics from scanning and vertical full- scale lidar measurements. J. Phys. Conf. Ser. 2016, 753, 032034. [Google Scholar] [CrossRef]
- Iungo, G.V.; Porté-Agel, F. Volumetric Lidar Scanning of Wind Turbine Wakes under Convective and Neutral Atmospheric Stability Regimes. J. Atmos. Ocean. Technol. 2014, 31, 2035–2048. [Google Scholar] [CrossRef]
- Valldecabres, L.; Peña, A.; Courtney, M.; von Bremen, L.; Kühn, M. Very short-term forecast of near-coastal flow using scanning lidars. Wind Energ. Sci 2018, 3, 313–327. [Google Scholar] [CrossRef]
- Calamia, J. Where the wind blows. New Sci. 2017, 234, 31–33. [Google Scholar] [CrossRef]
- Fernando, H.J.S.; Mann, J.; Palma, J.M.L.M.; Lundquist, J.K.; Barthelmie, R.J.; Belo-Pereira, M.; Brown, W.O.J.; Chow, F.K.; Gerz, T.; Hocut, C.M.; et al. The Perdigao: Peering into microscale details of mountain winds. Bull. Am. Meteorol. Soc. 2019, 100, 799–819. [Google Scholar] [CrossRef]
- Witze, A. World’s largest wind-mapping project spins up in Portugal. Nat. News 2017, 542, 282. [Google Scholar] [CrossRef]
- Wildmann, N.; Vasiljevic, N.; Gerz, T. Wind turbine wake measurements with automatically adjusting scanning trajectories in a multi-Doppler lidar setup. Atmos. Meas. Tech. 2018, 11, 3801–3814. [Google Scholar] [CrossRef]
- Menke, R.; Vasiljević, N.; Hansen, K.S.; Hahmann, A.N.; Mann, J. Does the wind turbine wake follow the topography? A multi-lidar study in complex terrain. Wind Energ. Sci 2018, 3, 681–691. [Google Scholar] [CrossRef]
- Barthelmie, R.J.; Pryor, S.C. Automated wind turbine wake characterization in complex terrain. Atmos. Meas. Tech. 2019, 12, 3463–3484. [Google Scholar] [CrossRef]
- Rodrigues, C.V.; Palma, J.M.L.M.; Vasiljević, N.; Courtney, M.; Mann, J. Coupled simulations and comparison with multi-lidar measurements of the wind flow over a double-ridge. J. Phys. Conf. Ser. 2016, 753, 032025. [Google Scholar] [CrossRef]
- Palma, J.M.L.M.; Lopes, A.S.; Gomes, V.M.C.; Rodrigues, C.V.; Menke, R.; Vasiljević, N.; Mann, J. Unravelling the wind flow over highly complex regions through computational modeling and two-dimensional lidar scanning. J. Phys. Conf. Ser. 2019, 1222, 012006. [Google Scholar] [CrossRef]
- Menke, R.; Vasiljević, N.; Mann, J.; Lundquist, J.K. Characterization of flow recirculation zones at the Perdigão site using multi-lidar measurements. Atmos. Chem. Phys. 2019, 19, 2713–2723. [Google Scholar] [CrossRef]
- Karagali, I.; Mann, J.; Dellwik, E.; Vasiljević, N. New European Wind Atlas: The sterild balconies experiment. J. Phys. Conf. Series 2018, 1037, 052029. [Google Scholar] [CrossRef]
- Mann, J.; Peña, A.; Bingöl, F.; Wagner, R.; Courtney, M.S. Lidar scanning of momentum flux in and above the surface layer. J. Atmos. Ocean. Technol. 2010, 27, 959–976. [Google Scholar] [CrossRef]
- Mann, J. The spatial structure of neutral atmospheric surface-layer turbulence. J. Fluid Mech. 1994, 273, 141–168. [Google Scholar] [CrossRef]
- Peña, A.; Mann, J.; Dimitrov, N. Turbulence characterization from a forward-looking nacelle lidar. Wind Energ. Sci 2017, 2, 133–152. [Google Scholar] [CrossRef]
- Vasiljevic, N.; Lea, G.; Courtney, M. A Data Set for Comparison of Sector-Scan and Dual-Doppler Retrievals of Horizontal Wind Speed and Wind Direction Made Using Multiple Scanning Lidars; Technical University of Denmark: Roskilde, Denmark, 2018. [Google Scholar] [CrossRef]
- Simon, E. Determination of an Optimum Sector Size for Plan Position Indicator Measurements Using a Long Range Cohorent Scanning Atmospheric Doppler LiDAR. Master’s Thesis, Uppsala University, Uppsala, Sweden, 2015. [Google Scholar]
- Vasiljevic, N.; Lea, G.; Courtney, M.; Cariou, J.P.; Mann, J.; Mikkelsen, T. Long-Range WindScanner System. Remote Sens. 2016, 8, 896. [Google Scholar] [CrossRef]
- Metek GmbH. Flow Distortion Correction for 3-D Flows as Measured by METEK’s Ultrasonic Anemometer USA-1; Metek GmbH: Stonehouse, UK, 2004. [Google Scholar]
- Peña, A.; Dellwik, E.; Mann, J. A method to assess the accuracy of sonic anemometer measurements. Atmos. Meas. Tech. 2019, 12, 237–252. [Google Scholar] [CrossRef]
- Goring, D.G.; Nikora, V.I. Despiking acoustic Doppler velocimeter data. J. Hydraul. Eng. 2002, 128, 117–126. [Google Scholar] [CrossRef]
- Cleveland, W.S.; Devlin, S.J. Locally Weighted Regression: An Approach to Regression Analysis by Local Fitting. J. Am. Stat. Assoc. 1988, 83, 596–610. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peña, A.; Mann, J. Turbulence Measurements with Dual-Doppler Scanning Lidars. Remote Sens. 2019, 11, 2444. https://doi.org/10.3390/rs11202444
Peña A, Mann J. Turbulence Measurements with Dual-Doppler Scanning Lidars. Remote Sensing. 2019; 11(20):2444. https://doi.org/10.3390/rs11202444
Chicago/Turabian StylePeña, Alfredo, and Jakob Mann. 2019. "Turbulence Measurements with Dual-Doppler Scanning Lidars" Remote Sensing 11, no. 20: 2444. https://doi.org/10.3390/rs11202444
APA StylePeña, A., & Mann, J. (2019). Turbulence Measurements with Dual-Doppler Scanning Lidars. Remote Sensing, 11(20), 2444. https://doi.org/10.3390/rs11202444