Spatial and Seasonal Patterns in Vegetation Growth-Limiting Factors over Europe
Abstract
1. Introduction
2. Materials and Methods
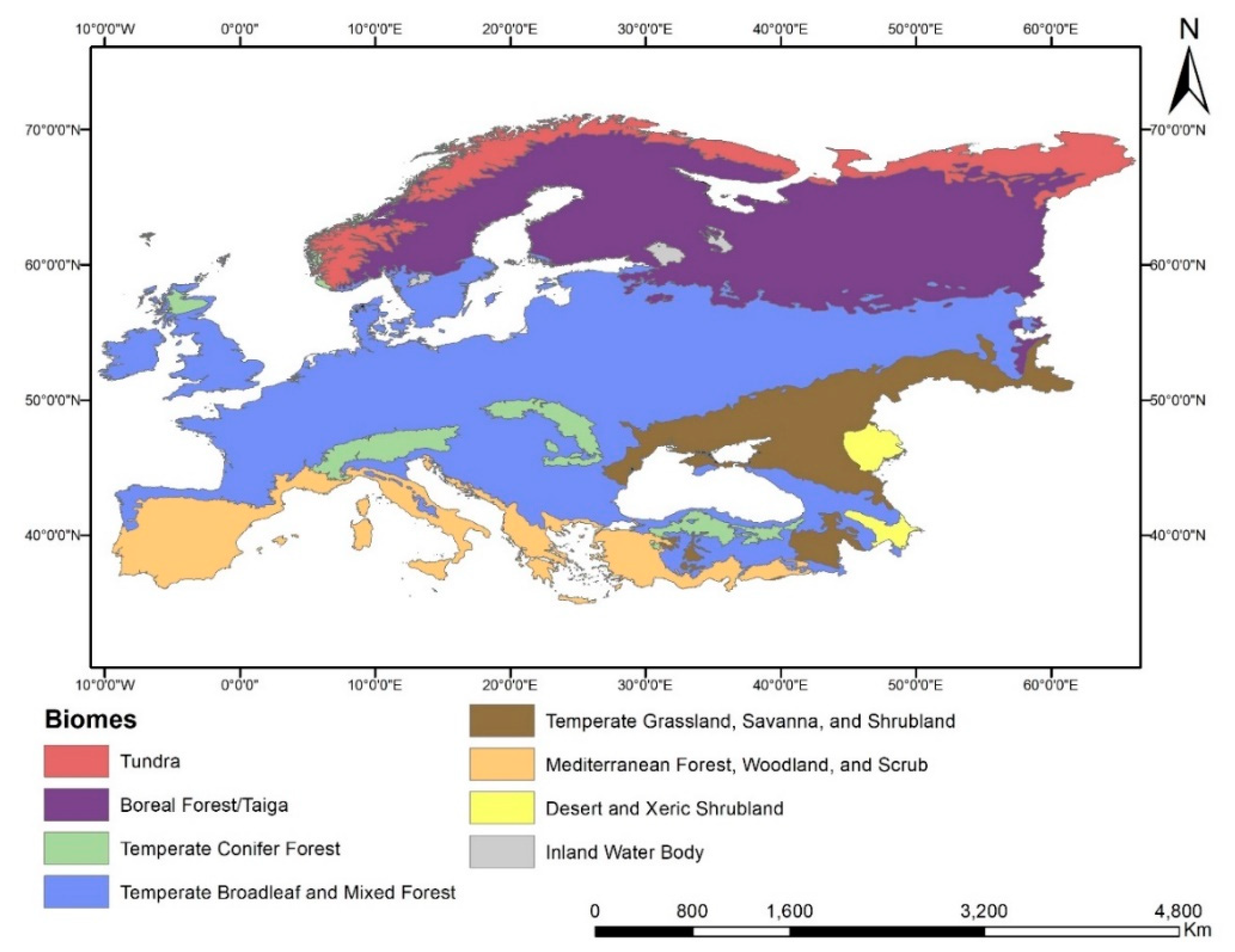
2.1. Study Area
2.2. MODIS Data Sources and Analyses
2.3. LST–NDVI Relation Analyses at Pan-European and Biome Scales
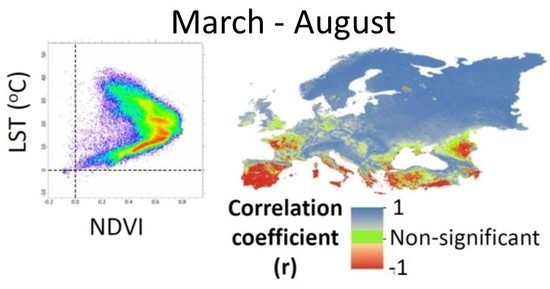
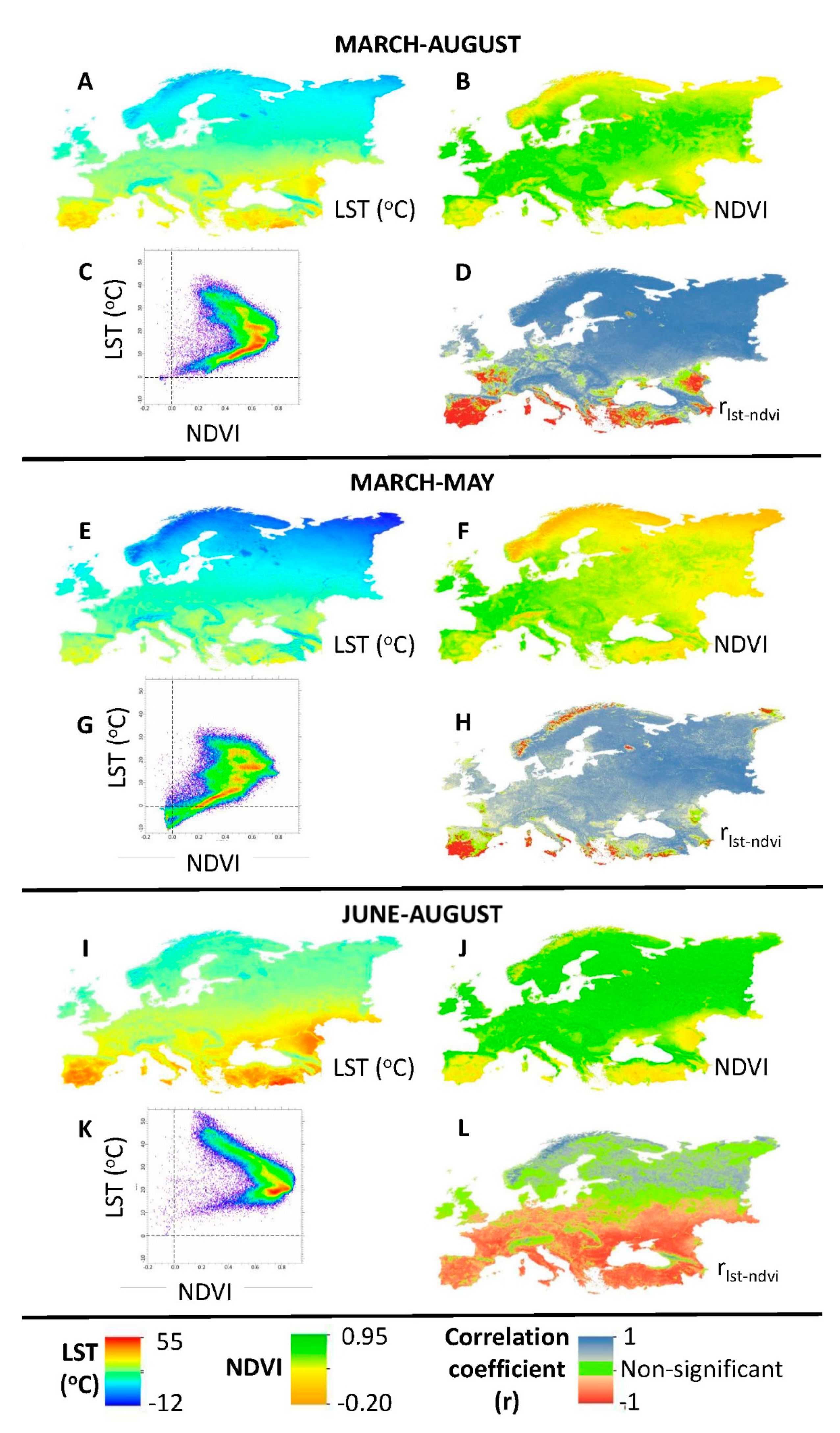
3. Results
3.1. LST–NDVI Correlation Dynamics
3.2. Biome-Specific LST–NDVI Relations
4. Discussion
4.1. Energy Balance Perspective
4.2. European Biomes and Vegetation Growth-Limiting Factors
4.3. Relation to LST–NDVI Models
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Greenberg, J.A.; Santos, M.J.; Dobrowski, S.Z.; Vanderbilt, V.C.; Ustin, S.L. Quantifying environmental limiting factors on tree cover using geospatial data. PLoS ONE 2015, 10, e0114648. [Google Scholar] [CrossRef]
- Bellard, C.; Bertelsmeier, C.; Leadley, P.; Thuiller, W.; Courchamp, F. Impacts of climate change on the future of biodiversity. Ecol. Lett. 2012, 15, 365–377. [Google Scholar] [CrossRef]
- Churkina, G.; Running, S.W. Contrasting climatic controls on the estimated productivity of global terrestrial biomes. Ecosystems 1998, 1, 206–215. [Google Scholar] [CrossRef]
- Nemani, R.R.; Keeling, C.D.; Hashimoto, H.; Jolly, W.M.; Piper, S.C.; Tucker, C.J.; Myneni, R.B.; Running, S.W. Climate-driven increases in global terrestrial net primary production from 1982 to 1999. Science 2003, 300, 1560–1563. [Google Scholar] [CrossRef]
- Wang, K.C.; Dickinson, R.E. A review of global terrestrial evapotranspiration: Observation, modeling, climatology, and climatic variability. Rev. Geophys. 2012, 50, RG2005. [Google Scholar] [CrossRef]
- Fensholt, R.; Langanke, T.; Rasmussen, K.; Reenberg, A.; Prince, S.D.; Tucker, C.; Scholes, R.J.; Le, Q.B.; Bondeau, A.; Eastman, R.; et al. Greenness in semi-arid areas across the globe 1981–2007—An earth observing satellite based analysis of trends and drivers. Remote Sens. Environ. 2012, 121, 144–158. [Google Scholar] [CrossRef]
- Mutiibwa, D.; Strachan, S.; Albright, T. Land surface temperature and surface air temperature in complex terrain. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 4762–4774. [Google Scholar] [CrossRef]
- Phan, T.N.; Kappas, M.; Nguyen, K.T.; Tran, T.P.; Tran, Q.V.; Emam, A.R. Evaluation of MODIS land surface temperature products for daily air surface temperature estimation in northwest Vietnam. Int. J. Remote Sens. 2019, 40, 5544–5562. [Google Scholar] [CrossRef]
- Zeng, L.L.; Wardlow, B.D.; Tadesse, T.; Shan, J.; Hayes, M.J.; Li, D.R.; Xiang, D.X. Estimation of daily air temperature based on MODIS land surface temperature products over the corn belt in the US. Remote Sens. 2015, 7, 951–970. [Google Scholar] [CrossRef]
- Camberlin, P.; Martiny, N.; Philippon, N.; Richard, Y. Determinants of the interannual relationships between remote sensed photosynthetic activity and rainfall in tropical Africa. Remote Sens. Environ. 2007, 106, 199–216. [Google Scholar] [CrossRef]
- Ding, M.J.; Zhang, Y.L.; Liu, L.S.; Zhang, W.; Wang, Z.F.; Bai, W.Q. The relationship between NDVI and precipitation on the Tibetan plateau. J. Geogr. Sci. 2007, 17, 259–268. [Google Scholar] [CrossRef]
- Kang, L.J.; Di, L.P.; Deng, M.X.; Shao, Y.Z.; Yu, G.N.; Shrestha, R. Use of geographically weighted regression model for exploring spatial patterns and local factors behind NDVI-precipitation correlation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 4530–4538. [Google Scholar] [CrossRef]
- Prihodko, L.; Goward, S.N. Estimation of air temperature from remotely sensed surface observations. Remote Sens. Environ. 1997, 60, 335–346. [Google Scholar] [CrossRef]
- Sun, L.; Sun, R.; Li, X.W.; Liang, S.L.; Zhang, R.H. Monitoring surface soil moisture status based on remotely sensed surface temperature and vegetation index information. Agric. For. Meteorol. 2012, 166, 175–187. [Google Scholar] [CrossRef]
- Wan, Z.; Wang, P.; Li, X. Using MODIS land surface temperature and normalized difference vegetation index products for monitoring drought in the southern great plains, USA. Int. J. Remote Sens. 2004, 25, 61–72. [Google Scholar] [CrossRef]
- Anbazhagan, S.; Paramasivam, C.R. Statistical correlation between land surface temperature (LST) and vegetation index (NDVI) using multi-temporal landsat tm data. Int. J. Adv. Earth Sci. Eng. 2016, 5, 333–346. [Google Scholar]
- Ferrelli, F.; Cisneros, M.A.H.; Delgado, A.L.; Piccolo, M.C. Spatial and temporal analysis of the LST-NDVI relationship for the study of land cover changes and their contribution to urban planning in Monte Hermoso, Argentina. Doc. D Anal. Geogr. 2018, 64, 25–47. [Google Scholar] [CrossRef]
- Tan, K.C.; Lim, H.S.; MatJafri, M.Z.; Abdullah, K. A comparison of radiometric correction techniques in the evaluation of the relationship between LST and NDVI in landsat imagery. Environ. Monit. Assess. 2012, 184, 3813–3829. [Google Scholar] [CrossRef]
- Vorovencii, I. A multi-temporal landsat data analysis of land use and land cover changes on the land surface temperature. Int. J. Environ. Pollut. 2015, 56, 109–128. [Google Scholar] [CrossRef]
- Wang, H.; Li, X.B.; Long, H.L.; Xu, X.; Bao, Y. Monitoring the effects of land use and cover type changes on soil moisture using remote-sensing data: A case study in China’s Yongding River basin. Catena 2010, 82, 135–145. [Google Scholar] [CrossRef]
- Nemani, R.R.; Running, S.W. Estimation of regional surface-resistance to evapotranspiration from NDVI and thermal-IR AVHRR data. J. Appl. Meteorol. 1989, 28, 276–284. [Google Scholar] [CrossRef]
- Stisen, S.; Sandholt, I.; Norgaard, A.; Fensholt, R.; Eklundh, L. Estimation of diurnal air temperature using msg seviri data in West Africa. Remote Sens. Environ. 2007, 110, 262–274. [Google Scholar] [CrossRef]
- Han, L.J.; Wang, P.X.; Yang, H.; Liu, S.M.; Wang, J.D. Study on NDVI-TS space by combining LAI and evapotranspiration. Sci. China Ser. D Earth Sci. 2006, 49, 747–754. [Google Scholar] [CrossRef]
- Dall’Olmo, G.; Karnieli, A. Monitoring phenological cycles of desert ecosystems using NDVI and LST data derived from NOAA-AVHRR imagery. Int. J. Remote Sens. 2002, 23, 4055–4071. [Google Scholar] [CrossRef]
- Holzman, M.E.; Rivas, R.; Piccolo, M.C. Estimating soil moisture and the relationship with crop yield using surface temperature and vegetation index. Int. J. Appl. Earth Obs. Geoinf. 2014, 28, 181–192. [Google Scholar] [CrossRef]
- Carlson, T.N.; Petropoulos, G.P. A new method for estimating of evapotranspiration and surface soil moisture from optical and thermal infrared measurements: The simplified triangle. Int. J. Remote Sens. 2019, 40, 7716–7729. [Google Scholar] [CrossRef]
- Schultz, P.A.; Halpert, M.S. Global analysis of the relationships among a vegetation index, precipitation and land-surface temperature. Int. J. Remote Sens. 1995, 16, 2755–2777. [Google Scholar] [CrossRef]
- Lambin, E.F.; Ehrlich, D. The surface temperature-vegetation index space for land cover and land-cover change analysis. Int. J. Remote Sens. 1996, 17, 463–487. [Google Scholar] [CrossRef]
- Nemani, R.; Running, S. Land cover characterization using multitemporal red, near-IR, and thermal-IR data from NOAA/AVHRR. Ecol. Appl. 1997, 7, 79–90. [Google Scholar]
- Tateishi, R.; Ebata, M. Analysis of phenological change patterns using 1982–2000 advanced very high resolution radiometer (AVHRR) data. Int. J. Remote Sens. 2004, 25, 2287–2300. [Google Scholar] [CrossRef]
- Julien, Y.; Sobrino, J.A.; Verhoef, W. Changes in land surface temperatures and NDVI values over europe between 1982 and 1999. Remote Sens. Environ. 2006, 103, 43–55. [Google Scholar] [CrossRef]
- Karnieli, A.; Bayasgalan, M.; Bayarjargal, Y.; Agam, N.; Khudulmur, S.; Tucker, C.J. Comments on the use of the vegetation health index over Mongolia. Int. J. Remote Sens. 2006, 27, 2017–2024. [Google Scholar] [CrossRef]
- Sun, D.L.; Kafatos, M. Note on the ndvi-lst relationship and the use of temperature-related drought indices over North America. Geophys. Res. Lett. 2007, 34. [Google Scholar] [CrossRef]
- Karnieli, A.; Agam, N.; Pinker, R.T.; Anderson, M.; Imhoff, M.L.; Gutman, G.G.; Panov, N.; Goldberg, A. Use of NDVI and land surface temperature for drought assessment: Merits and limitations. J. Clim. 2010, 23, 618–633. [Google Scholar] [CrossRef]
- Marzban, F.; Sodoudi, S.; Preusker, R. The influence of land-cover type on the relationship between NDVI-LST and LST-T-air. Int. J. Remote Sens. 2018, 39, 1377–1398. [Google Scholar] [CrossRef]
- Olson, D.M.; Dinerstein, E.; Wikramanayake, E.D.; Burgess, N.D.; Powell, G.V.N.; Underwood, E.C.; D’Amico, J.A.; Itoua, I.; Strand, H.E.; Morrison, J.C.; et al. Terrestrial ecoregions of the world: A new map of life on earth. Bioscience 2001, 51, 933–938. [Google Scholar]
- Stockli, R.; Vidale, P.L. European plant phenology and climate as seen in a 20-year AVHRR land-surface parameter dataset. Int. J. Remote Sens. 2004, 25, 3303–3330. [Google Scholar] [CrossRef]
- Chrysoulakis, N.; Grimmond, S.; Feigenwinter, C.; Lindberg, F.; Gastellu-Etchegorry, J.P.; Marconcini, M.; Mitraka, Z.; Stagakis, S.; Crawford, B.; Olofson, F.; et al. Urban energy exchanges monitoring from space. Sci. Rep. 2018, 8, 11498. [Google Scholar] [CrossRef]
- Wilson, K.; Goldstein, A.; Falge, E.; Aubinet, M.; Baldocchi, D.; Berbigier, P.; Bernhofer, C.; Ceulemans, R.; Dolman, H.; Field, C.; et al. Energy balance closure at fluxnet sites. Agric. For. Meteorol. 2002, 113, 223–243. [Google Scholar] [CrossRef]
- Gastellu-Etchegorry, J.P.; Lauret, N.; Yin, T.G.; Landier, L.; Kallel, A.; Malenovsky, Z.; Al Bitar, A.; Aval, J.; Benhmida, S.; Qi, J.B.; et al. Dart: Recent advances in remote sensing data modeling with atmosphere, polarization, and chlorophyll fluorescence. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 2640–2649. [Google Scholar] [CrossRef]
- Moderow, U.; Aubinet, M.; Feigenwinter, C.; Kolle, O.; Lindroth, A.; Molder, M.; Montagnani, L.; Rebmann, C.; Bernhofer, C. Available energy and energy balance closure at four coniferous forest sites across Europe. Theor. Appl. Climatol. 2009, 98, 397–412. [Google Scholar] [CrossRef]
- Stoy, P.C.; Mauder, M.; Foken, T.; Marcolla, B.; Boegh, E.; Ibrom, A.; Arain, M.A.; Arneth, A.; Aurela, M.; Bernhofer, C.; et al. A data-driven analysis of energy balance closure across fluxnet research sites: The role of landscape scale heterogeneity. Agric. For. Meteorol. 2013, 171, 137–152. [Google Scholar] [CrossRef]
- Bonan, G.B. Forests and climate change: Forcings, feedbacks, and the climate benefits of forests. Science 2008, 320, 1444–1449. [Google Scholar] [CrossRef] [PubMed]
- Baldocchi, D.D.; Xu, L.K.; Kiang, N. How plant functional-type, weather, seasonal drought, and soil physical properties alter water and energy fluxes of an oak-grass savanna and an annual grassland. Agric. For. Meteorol. 2004, 123, 13–39. [Google Scholar] [CrossRef]
- Teuling, A.J.; Seneviratne, S.I.; Stockli, R.; Reichstein, M.; Moors, E.; Ciais, P.; Luyssaert, S.; van den Hurk, B.; Ammann, C.; Bernhofer, C.; et al. Contrasting response of European forest and grassland energy exchange to heatwaves. Nat. Geosci. 2010, 3, 722–727. [Google Scholar] [CrossRef]
- Parmesan, C. Ecological and evolutionary responses to recent climate change. Ann. Rev. Ecol. Evol. Syst. 2006, 37, 637–669. [Google Scholar] [CrossRef]
- Watson, J.E.M.; Iwamura, T.; Butt, N. Mapping vulnerability and conservation adaptation strategies under climate change. Nat. Clim. Chang. 2013, 3, 989–994. [Google Scholar] [CrossRef]
- Eigenbrod, F.; Gonzalez, P.; Dash, J.; Steyl, I. Vulnerability of ecosystems to climate change moderated by habitat intactness. Glob. Chang. Biol. 2015, 21, 275–286. [Google Scholar] [CrossRef]
- Thuiller, W.; Lavorel, S.; Araujo, M.B.; Sykes, M.T.; Prentice, I.C. Climate change threats to plant diversity in europe. Proc. Natl. Acad. Sci. USA 2005, 102, 8245–8250. [Google Scholar] [CrossRef]
- Vautard, R.; Gobiet, A.; Sobolowski, S.; Kjellstrom, E.; Stegehuis, A.; Watkiss, P.; Mendlik, T.; Landgren, O.; Nikulin, G.; Teichmann, C.; et al. The European climate under a 2 degrees C global warming. Environ. Res. Lett. 2014, 9, 034006. [Google Scholar] [CrossRef]
- Turco, M.; Rosa-Canovas, J.J.; Bedia, J.; Jerez, S.; Montavez, J.P.; Llasat, M.C.; Provenzale, A. Exacerbated fires in mediterranean europe due to anthropogenic warming projected with non-stationary climate-fire models. Nat. Commun. 2018, 1–9, 3821. [Google Scholar] [CrossRef] [PubMed]
- Bayarjargal, Y.; Karnieli, A.; Bayasgalan, M.; Khudulmur, S.; Gandush, C.; Tucker, C.J. A comparative study of noaa-avhrr derived drought indices using change vector analysis. Remote Sens. Environ. 2006, 105, 9–22. [Google Scholar] [CrossRef]
- McVicar, T.R.; Bierwirth, P.N. Rapidly assessing the 1997 drought in Papua New Guinea using composite AVHRR imagery. Int. J. Remote Sens. 2001, 22, 2109–2128. [Google Scholar] [CrossRef]
- Kogan, F.N. Application of vegetation index and brightness temperature for drought detection. Adv. Space Res. 1995, 15, 91–100. [Google Scholar] [CrossRef]
- Kogan, F.; Guo, W. Early detection and monitoring droughts from NOAA environmental satellites. In Use of Satellite and In-Situ Data to Improve Sustainability; Kogan, F., Powell, A.M., Fedorov, O., Eds.; Springer: Berlin/Heidelberg, Germany, 2011; p. 11. [Google Scholar]
- Amalo, L.F.; Hidayat, R.; Sulma, S. Analysis of agricultural drought in East Java using vegetation health index. Agrivita 2018, 40, 63–73. [Google Scholar] [CrossRef]
- Bento, V.A.; Trigo, I.F.; Gouveia, C.M.; DaCamara, C.C. Contribution of land surface temperature (TCI) to vegetation health index: A comparative study using clear sky and all-weather climate data records. Remote Sens. 2018, 10, 1324. [Google Scholar] [CrossRef]
- Skakun, S.; Kussul, N.; Shelestov, A.; Kussul, O. The use of satellite data for agriculture drought risk quantification in ukraine. Geomat. Nat. Hazards Risk 2016, 7, 901–917. [Google Scholar] [CrossRef]
- Kogan, F. Early drought detection, monitoring and assessment of crop losses from space: Global approach—art. No. 641209. In Disaster Forewarning Diagnostic Methods and Management; Kogan, F., Habib, S., Hegde, V.S., Matsuoka, M., Eds.; SPIE: Bellingham, WA, USA, 2006; Volume 6412, p. 41209. [Google Scholar]
- Kogan, F.N. Global drought watch from space. Bull. Am. Meteorol. Soc. 1997, 78, 621–636. [Google Scholar] [CrossRef]
- Kogan, F.N. World droughts in the new millennium from AVHRR-based vegetation health indices. EOS 2002, 83, 557–563. [Google Scholar] [CrossRef]
- Carlson, T. An overview of the “triangle method” for estimating surface evapotranspiration and soil moisture from satellite imagery. Sensors 2007, 7, 1612–1629. [Google Scholar] [CrossRef]
- Sandholt, I.; Rasmussen, K.; Andersen, J. A simple interpretation of the surface temperature/vegetation index space for assessment of surface moisture status. Remote Sens. Environ. 2002, 79, 213–224. [Google Scholar] [CrossRef]
- Petropoulos, G.; Carlson, T.N.; Wooster, M.J.; Islam, S. A review of T-S/VI remote sensing based methods for the retrieval of land surface energy fluxes and soil surface moisture. Prog. Phys. Geogr. 2009, 33, 224–250. [Google Scholar] [CrossRef]
- Garcia, M.; Fernandez, N.; Villagarcia, L.; Domingo, F.; Puigdefaabregas, J.; Sandholt, I. Accuracy of the temperature-vegetation dryness index using MODIS under water-limited vs. Energy-limited evapotranspiration conditions. Remote Sens. Environ. 2014, 149, 100–117. [Google Scholar] [CrossRef]

| rlst–ndvi | |||
|---|---|---|---|
| Positive Correlation | Negative Correlation | Non-Significant Pixels | |
| (%) | (%) | (%) | |
| March–August | |||
| Tundra | 96 | 4 | 0 |
| Boreal forest/taiga | 100 | 0 | 0 |
| Temperate broadleaf and mixed forest | 89 | 5 | 6 |
| Temperate conifer forest | 92 | 4 | 4 |
| Temperate grassland, savanna, and shrubland | 75 | 9 | 16 |
| Mediterranean forest, woodland, and scrub | 23 | 66 | 11 |
| Desert and xeric shrubland | 16 | 71 | 13 |
| March–May | |||
| Tundra | 75 | 15 | 10 |
| Boreal forest/taiga | 99 | 0 | 1 |
| Temperate broadleaf and mixed forest | 97 | 1 | 2 |
| Temperate conifer forest | 96 | 1 | 3 |
| Temperate grassland, savanna, and shrubland | 96 | 1 | 3 |
| Mediterranean forest, woodland, and scrub | 44 | 32 | 24 |
| Desert and xeric shrubland | 52 | 10 | 38 |
| June–August | |||
| Tundra | 57 | 4 | 39 |
| Boreal forest/taiga | 60 | 1 | 39 |
| Temperate broadleaf and mixed forest | 5 | 64 | 31 |
| Temperate conifer forest | 13 | 42 | 45 |
| Temperate grassland, savanna, and shrubland | 0 | 97 | 3 |
| Mediterranean forest, woodland, and scrub | 0 | 94 | 6 |
| Desert and xeric shrubland | 1 | 88 | 11 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Karnieli, A.; Ohana-Levi, N.; Silver, M.; Paz-Kagan, T.; Panov, N.; Varghese, D.; Chrysoulakis, N.; Provenzale, A. Spatial and Seasonal Patterns in Vegetation Growth-Limiting Factors over Europe. Remote Sens. 2019, 11, 2406. https://doi.org/10.3390/rs11202406
Karnieli A, Ohana-Levi N, Silver M, Paz-Kagan T, Panov N, Varghese D, Chrysoulakis N, Provenzale A. Spatial and Seasonal Patterns in Vegetation Growth-Limiting Factors over Europe. Remote Sensing. 2019; 11(20):2406. https://doi.org/10.3390/rs11202406
Chicago/Turabian StyleKarnieli, Arnon, Noa Ohana-Levi, Micha Silver, Tarin Paz-Kagan, Natalya Panov, Dani Varghese, Nektarios Chrysoulakis, and Antonello Provenzale. 2019. "Spatial and Seasonal Patterns in Vegetation Growth-Limiting Factors over Europe" Remote Sensing 11, no. 20: 2406. https://doi.org/10.3390/rs11202406
APA StyleKarnieli, A., Ohana-Levi, N., Silver, M., Paz-Kagan, T., Panov, N., Varghese, D., Chrysoulakis, N., & Provenzale, A. (2019). Spatial and Seasonal Patterns in Vegetation Growth-Limiting Factors over Europe. Remote Sensing, 11(20), 2406. https://doi.org/10.3390/rs11202406