Characterizing Seasonally Rainfall-Driven Movement of a Translational Landslide using SAR Imagery and SMAP Soil Moisture
Abstract
:1. Introduction
2. Landslide Location and Geological Settings
3. Materials and Methods
3.1. SAR Interferometry for Landslide Time-Series Mapping
3.2. Thickness Inversion
3.3. Time Lags
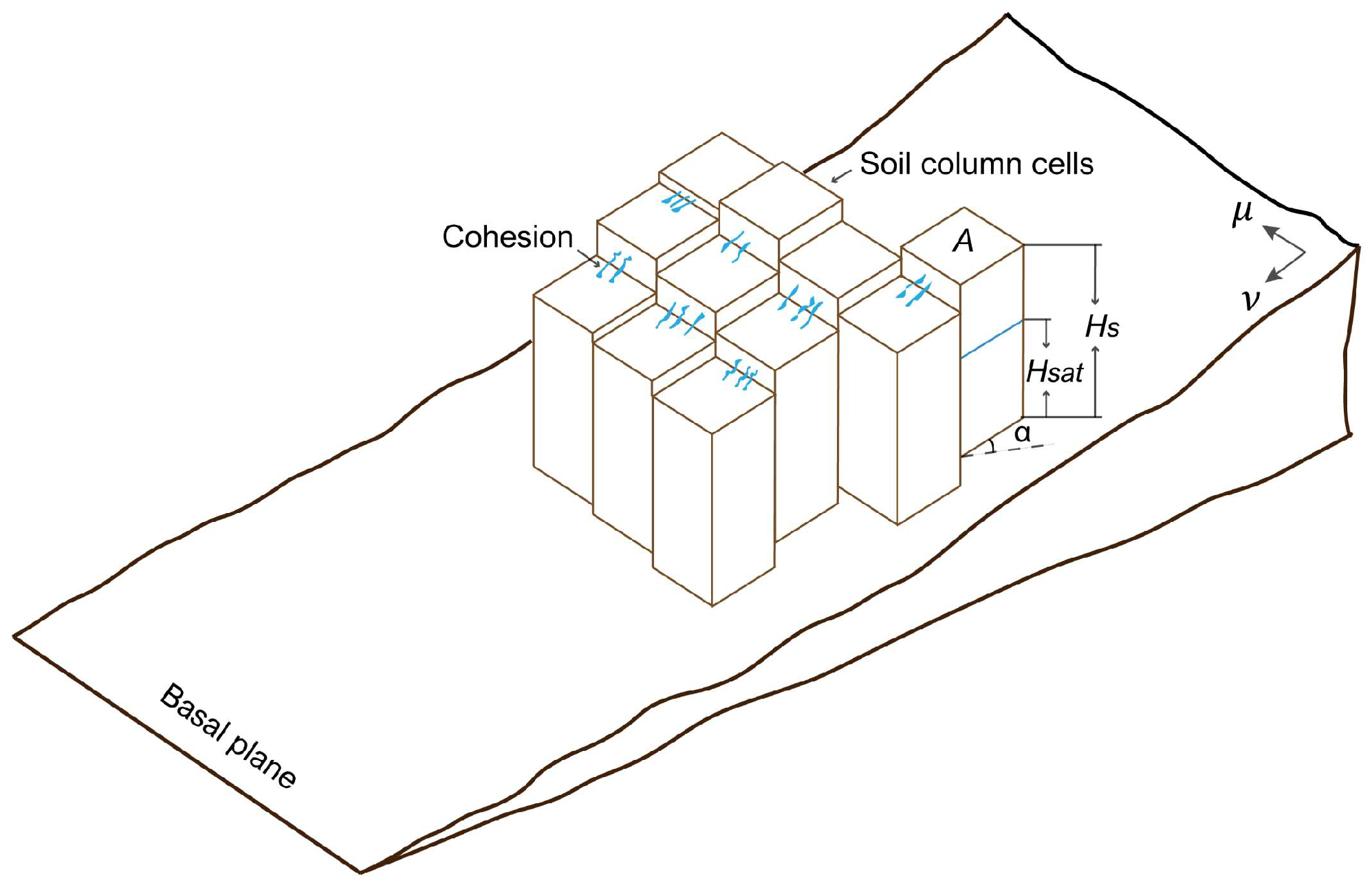
3.4. Failure Depth Using Limit Equilibrium Analysis
4. Results
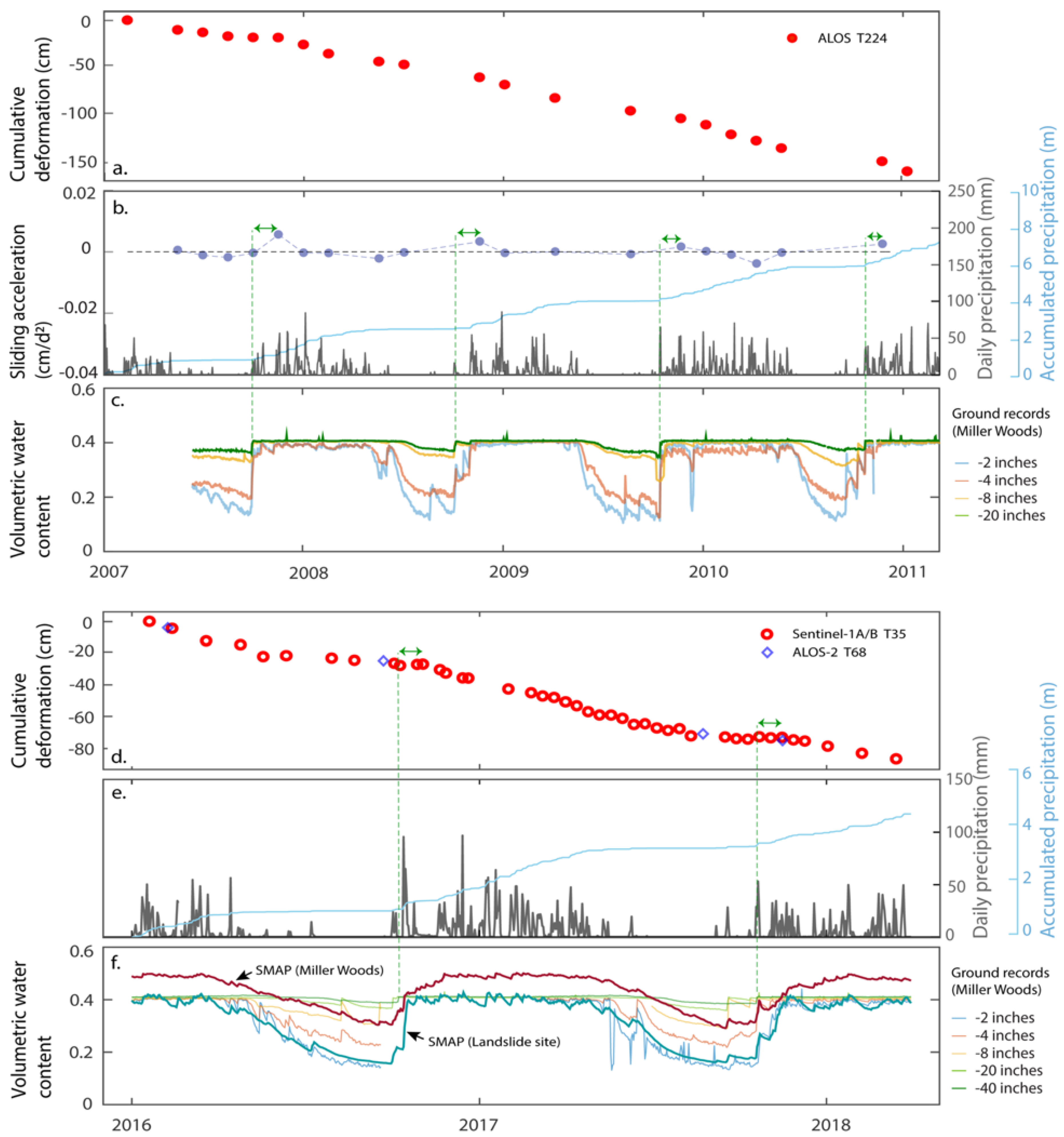
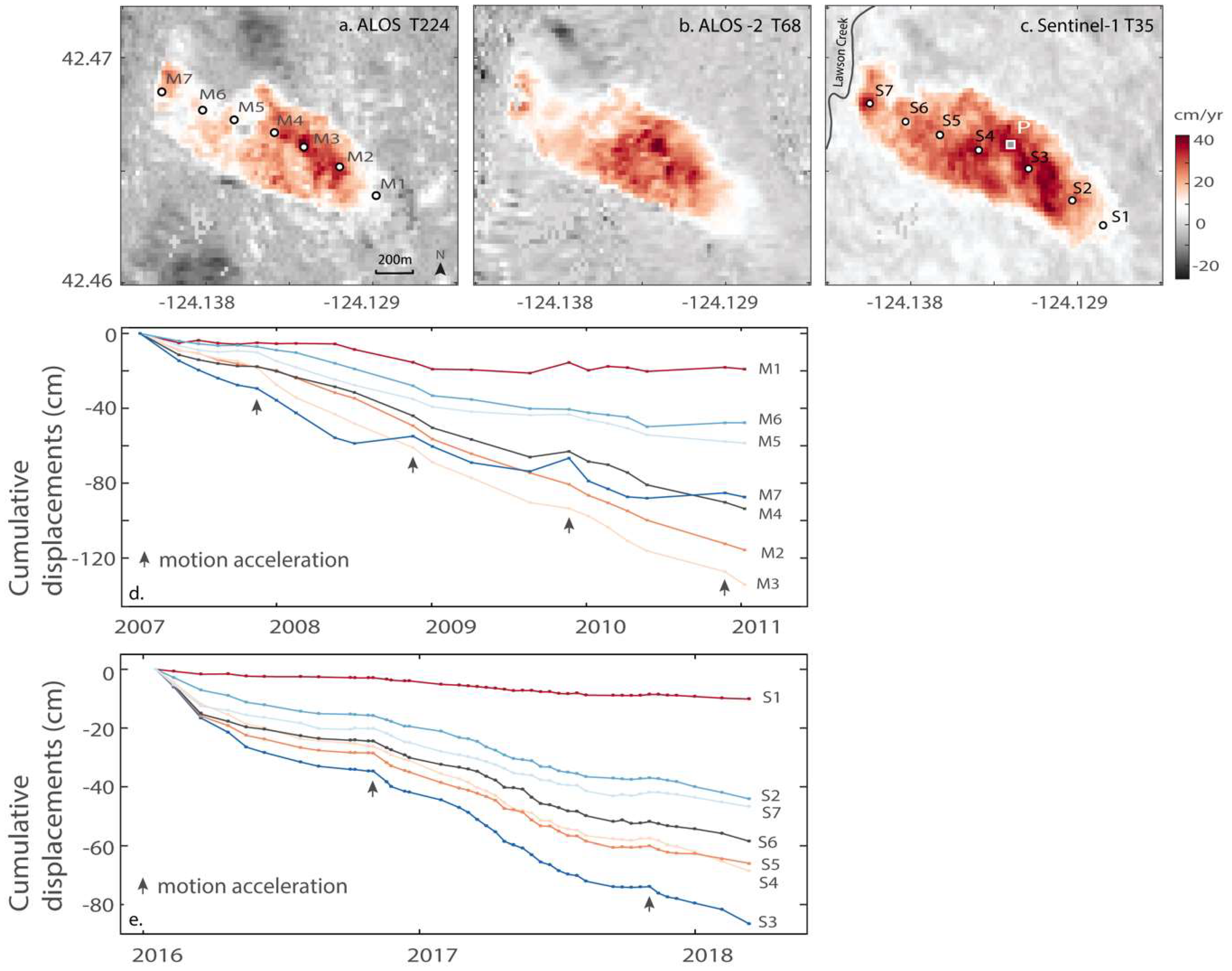
4.1. Time-Series Displacements and Annual Deformation Rates
4.2. Time Retardation to Seasonal Precipitation
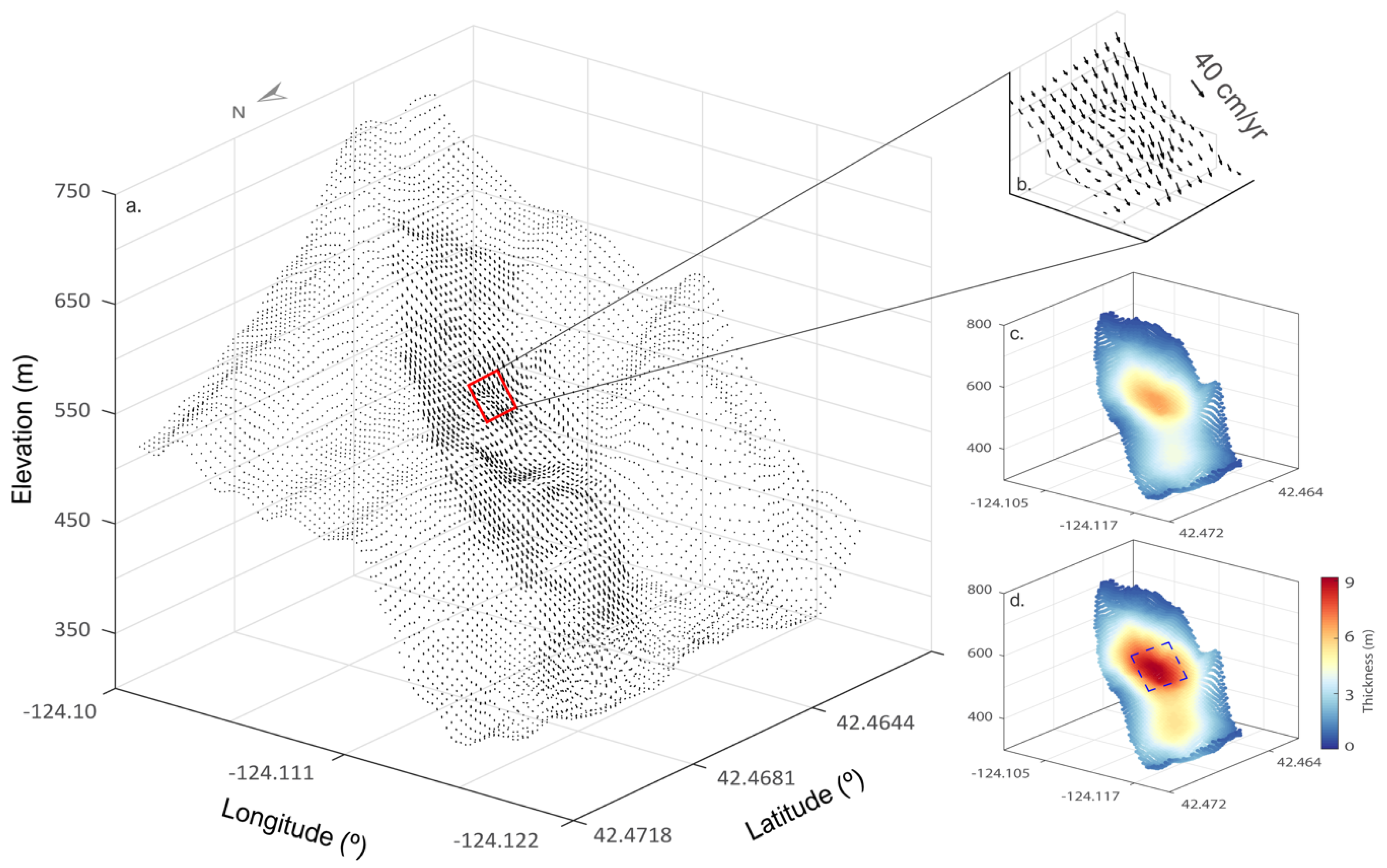
4.3. Basal Depths and Volume Inferred from InSAR Observations
4.4. Failure Depths from Limit Equilibrium Analysis
4.5. Potential for Estimating Hydraulic Parameters
5. Discussion
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Wartman, J.; Montgomery, D.R.; Anderson, S.A.; Keaton, J.R.; Benoît, J.; dela Chapelle, J.; Gilbert, R. The 22 March 2014 Oso landslide, Washington, USA. Geomorphology 2016, 253, 275–288. [Google Scholar] [CrossRef]
- Iverson, R.M.; George, D.L.; Allstadt, K.; Reid, M.E.; Collins, B.D.; Vallance, J.W.; Schilling, S.P.; Godt, J.W.; Cannon, C.M.; Magirl, C.S.; et al. Landslide mobility and hazards: Implications of the 2014 Oso disaster. Earth Planet Sci. Lett. 2015, 412, 197–208. [Google Scholar] [CrossRef]
- Hilley, G.E.; Bürgmann, R.; Ferretti, A.; Novali, F.; Rocca, F. Dynamics of slow-moving landslides from permanent scatterer analysis. Science 2004, 304, 1952–1955. [Google Scholar] [CrossRef] [PubMed]
- Tong, X.; Schmidt, D. Active movement of the Cascade landslide complex in Washington from a coherence-based InSAR time series method. Remote Sens. Environ. 2016, 186, 405–415. [Google Scholar] [CrossRef]
- Liu, P.; Li, Z.; Hoey, T.; Kincal, C.; Zhang, J.; Zeng, Q.; Muller, J.P. Using advanced InSAR time series techniques to monitor landslide movements in Badong of the Three Gorges region, China. Int. J. Appl. Earth Obs. Geoinf. 2013, 21, 253–264. [Google Scholar] [CrossRef]
- Jebur, M.N.; Pradhan, B.; Tehrany, M.S. Detection of vertical slope movement in highly vegetated tropical area of Gunung pass landslide, Malaysia, using L-band InSAR technique. Geosci. J. 2014, 18, 61–68. [Google Scholar] [CrossRef]
- Schlögel, R.; Doubre, C.; Malet, J.P.; Masson, F. Landslide deformation monitoring with ALOS/PALSAR imagery: A D-InSAR geomorphological interpretation method. Geomorphology 2015, 231, 314–330. [Google Scholar] [CrossRef]
- Nikolaeva, E.; Walter, T.R.; Shirzaei, M.; Zschau, J. Landslide observation and volume estimation in central Georgia based on L-band InSAR. Nat. Hazards Earth Syst. Sci. 2014, 14, 675–688. [Google Scholar] [CrossRef] [Green Version]
- Aryal, A.; Brooks, B.A.; Reid, M.E. Landslide subsurface slip geometry inferred from 3-D surface displacement fields. Geophys. Res. Lett. 2015, 42, 1411–1417. [Google Scholar] [CrossRef]
- Booth, A.M.; Lamb, M.P.; Avouac, J.P.; Delacourt, C. Landslide velocity, thickness, and rheology from remote sensing: La Clapière landslide, France. Geophys. Res. Lett. 2013, 40, 4299–4304. [Google Scholar] [CrossRef]
- Iverson, R.M.; Major, J.J. Rainfall, ground-water flow, and seasonal movement at Minor Creek landslide, northwestern California: Physical interpretation of empirical relations. Geol. Soc. Am. Bull. 1987, 99, 579–594. [Google Scholar] [CrossRef]
- Reid, M.E. A pore-pressure diffusion model for estimating landslide-inducing rainfall. J. Geol. 1994, 102, 709–717. [Google Scholar] [CrossRef]
- Baum, R.L.; Reid, M.E. Geology, hydrology, and mechanics of a slow-moving. Clay Shale Slope Instab. 1995, 10, 79. [Google Scholar]
- Bogaard, T.A.; Greco, R. Landslide hydrology: From hydrology to pore pressure. Wires Water 2016, 3, 439–459. [Google Scholar] [CrossRef]
- Berti, M.; Simoni, A. Field evidence of pore pressure diffusion in clayey soils prone to landsliding. J. Geophys. Res.-Earth 2010, 115. [Google Scholar] [CrossRef] [Green Version]
- Berti, M.; Simoni, A. Observation and analysis of near-surface pore-pressure measurements in clay-shales slopes. Hydrol. Process. 2012, 26, 2187–2205. [Google Scholar] [CrossRef]
- Iverson, R.M. Landslide triggering by rain infiltration. Water Resour. Res. 2000, 36, 1897–1910. [Google Scholar] [CrossRef] [Green Version]
- Rutt, I.C.; Hagdorn, M.; Hulton, N.R.J.; Payne, A.J. The Glimmer community ice sheet model. J. Geophys. Res.-Earth 2009, 114. [Google Scholar] [CrossRef] [Green Version]
- Burns, W.J. Statewide Landslide Information Database for Oregon [SLIDO], Release 3.2: Oregon Department of Geology and Mineral Industries, Geodatabase. 2014. Available online: http://www.oregongeology.org/sub/slido (accessed on 30 March 2019).
- Werner, C.; Wegmüller, U.; Strozzi, T.; Wiesmann, A. Gamma SAR and interferometric processing software. In Proceedings of the ERS-ENVISAT Symposium, Gothenburg, Sweden, 16–20 October 2000; Volume 1620. [Google Scholar]
- Berardino, P.; Fornaro, G.; Lanari, R.; Sansosti, E. A new algorithm for surface deformation monitoring based on small baseline differential SAR interferograms. IEEE Trans. Geosci. Remote Sens. 2002, 40, 2375–2383. [Google Scholar] [CrossRef] [Green Version]
- Delbridge, B.G.; Bürgmann, R.; Fielding, E.; Hensley, S.; Schulz, W.H. Three-dimensional surface deformation derived from airborne interferometric UAVSAR: Application to the Slumgullion Landslide. J. Geophys. Res. Solid Earth 2016, 121, 3951–3977. [Google Scholar] [CrossRef] [Green Version]
- Hu, X.; Lu, Z.; Pierson, T.C.; Kramer, R.; George, D.L. Combining InSAR and GPS to Determine Transient Movement and Thickness of a Seasonally Active Low-Gradient Translational Landslide. Geophys. Res. Lett. 2018, 45, 1453–1462. [Google Scholar] [CrossRef]
- Cascini, L.; Fornaro, G.; Peduto, D. Advanced low-and full-resolution DInSAR map generation for slow-moving landslide analysis at different scales. Eng. Geol. 2010, 112, 29–42. [Google Scholar] [CrossRef]
- Grant, M.; Boyd, S.; Ye, Y. CVX: Matlab Software for Disciplined Convex Programming. 2008. Available online: http://cvxr.com/cvx/ (accessed on 1 April 2019).
- Priest, G.R.; Schulz, W.H.; Ellis, W.L.; Allan, J.A.; Niem, A.R.; Niem, W.A. Landslide stability: Role of rainfall-induced, laterally propagating, pore-pressure waves. Environ. Eng. Geosci. 2011, 17, 315–335. [Google Scholar] [CrossRef]
- Van Genuchten, M.T. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef]
- Mualem, Y. A new model for predicting the hydraulic conductivity of unsaturated porous media. Water Resour. Res. 1976, 12, 513–522. [Google Scholar] [CrossRef] [Green Version]
- Lehmann, P.; Or, D. Hydromechanical triggering of landslides: From progressive local failures to mass release. Water Resour. Res. 2012, 48. [Google Scholar] [CrossRef]
- Brooks, R.; Corey, T. Hydraulic Properties of Porous Media. In Hydrology Papers 3; Colorado State University: Fort Collins, CO, USA, 1964; Volume 24, p. 37. [Google Scholar]
- USDA. Soil Survey of Curry County, Oregon. 1994. Available online: https://www.nrcs.usda.gov/Internet/FSE_MANUSCRIPTS/oregon/OR015/0/Curry.pdf (accessed on 1 April 2019).
- USDA. National Cooperative Soil Survey Soil Characterization Data. 2019. Available online: https://ncsslabdatamart.sc.egov.usda.gov (accessed on 25 March 2019).
- Pachepsky, Y.; Park, Y. Saturated hydraulic conductivity of US soils grouped according to textural class and bulk density. Soil Sci. Soc. Am. J. 2015, 79, 1094–1100. [Google Scholar] [CrossRef]
- Wasowski, J. Inclinometer and piezometer record of the 1995 reactivation of the Acquara-Vadoncello landslide, Italy. In Proceedings of the Engineering Geology: A global view from the Pacific Rim, Vancouver, BC, Canada, 21–25 September 1998; Volume 3, pp. 1697–1704. [Google Scholar]
- Gould, J.P. A study of shear failure in certain Tertiary marine sediments. In Proceedings of the Research Conference on Shear Strength of Cohesive Soils, Boulder, CO, USA, 13–17 June 1960; pp. 615–641. [Google Scholar]
- Mainsant, G.; Larose, E.; Brönnimann, C.; Jongmans, D.; Michoud, C.; Jaboyedoff, M. Ambient seismic noise monitoring of a clay landslide: Toward failure prediction. J. Geophys. Res. Earth Surf. 2012, 117. [Google Scholar] [CrossRef] [Green Version]
- Iverson, R.M. A constitutive equation for mass-movement behavior. J. Geol. 1985, 93, 143–160. [Google Scholar] [CrossRef]
- Van Asch, T.W.; Malet, J.P.; Bogaard, T.A. The effect of groundwater fluctuations on the velocity pattern of slow-moving landslides. Nat. Hazards Earth Syst. Sci. 2009, 9, 739–749. [Google Scholar] [CrossRef] [Green Version]
- Malet, J.P.; Maquaire, O. Black marl earthflows mobility and long-term seasonal dynamic in southeastern France. In Proceedings of the 1st International Conference on Fast Slope Movements, Naples, Italy, 14–16 May 2003; pp. 333–340. [Google Scholar]
- Lu, N.; Godt, J.W.; Wu, D.T. A closed-form equation for effective stress in unsaturated soil. Water Resour. Res. 2010, 46. [Google Scholar] [CrossRef]
- Rawls, W.J.; Brakensiek, D.L.; Saxtonn, K.E. Estimation of soil water properties. Trans. ASABE 1982, 25, 1316–1320. [Google Scholar] [CrossRef]
- Hall, D.E.; Long, M.T.; Remboldt, M.D. Slope Stability Reference Guide for National Forests in the United States; United States Department of Agriculture, Forest Service: Washington, DC, USA, 1994.
- Alto, J.V. Engineering Properties of Oregon and Washington Coast Range Soils. Master’s Thesis, Oregon State University, Corvallis, OR, USA, 1981. [Google Scholar]
- MnDOT (Minnesota Department of Transportation). MnDOT Pavement Design Manual. 2007. Available online: http://www.dot.state.mn.us/materials/pvmtdesign/docs/2007manual/Chapter_3-2.pdf (accessed on 5 April 2019).
- Ouyang, Z.; Mayne, P.W. Effective friction angle of clays and silts from piezocone penetration tests. Can. Geotech. J. 2017, 55, 1230–1247. [Google Scholar] [CrossRef]
- Jeong, S.; Lee, K.; Kim, J.; Kim, Y. Analysis of rainfall-induced landslide on unsaturated soil slopes. Sustainability 2017, 9, 1280. [Google Scholar] [CrossRef]
- Thunder, B. The Hydro-Mechanical Analysis of an Infiltration-Induced Landslide Along I-70 in Summit County, CO; Colorado School of Mines: Golden, CO, USA, 2016. [Google Scholar]
- Msilimba, G.G.A.C. A Comparative Study of Landslides and Geohazard Mitigation in Northern and Central Malawi. Doctor’s Dissertation, University of the Free State, Bloemfontein, South Africa, 2007. [Google Scholar]
- Lambe, T.W.; Whitman, R.V. Soil Mechanics Si Version; John Wiley & Sons: New York, NY, USA, 2008. [Google Scholar]
- Madson, A.; Fielding, E.; Sheng, Y.; Cavanaugh, K. High-Resolution Spaceborne, Airborne and in Situ Landslide Kinematic Measurements of the Slumgullion Landslide in Southwest Colorado. Remote Sens. 2019, 11, 265. [Google Scholar] [CrossRef]
- Rosen, P.A.; Hensley, S.; Wheeler, K.; Sadowy, G.; Miller, T.; Shaffer, S.; Muellerschoen, R.; Jones, C.; Zebker, H.; Madsen, S. UAVSAR: A new NASA airborne SAR system for science and technology research. In Proceedings of the 2006 IEEE Conference on Radar, Verona, NY, USA, USA, 24–27 April 2006. [Google Scholar]
- Iverson, R.M.; Reid, M.E.; Iverson, N.R.; LaHusen, R.G.; Logan, M.; Mann, J.E.; Brien, D.L. Acute sensitivity of landslide rates to initial soil porosity. Science 2000, 290, 513–516. [Google Scholar] [CrossRef] [PubMed]
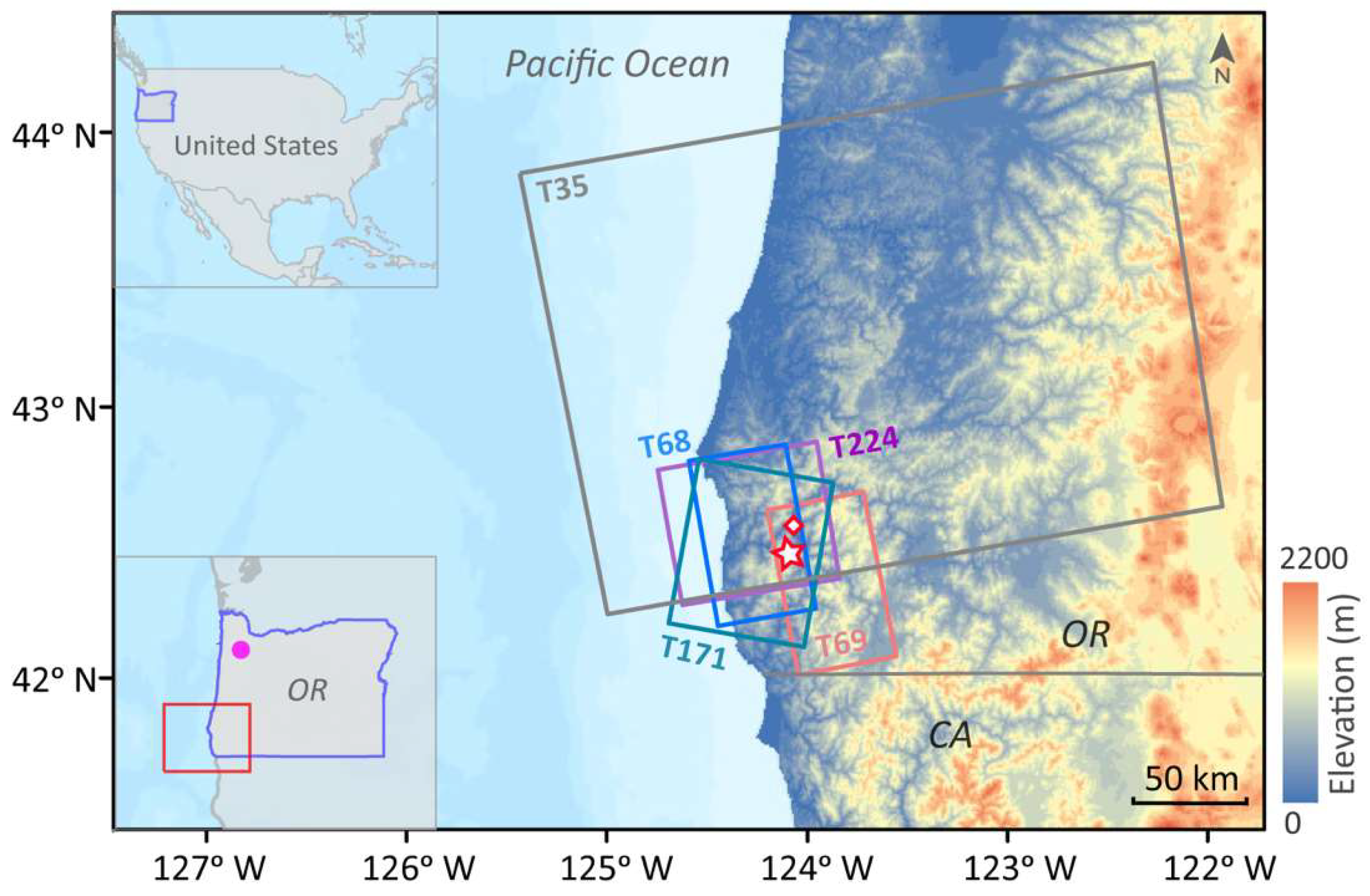
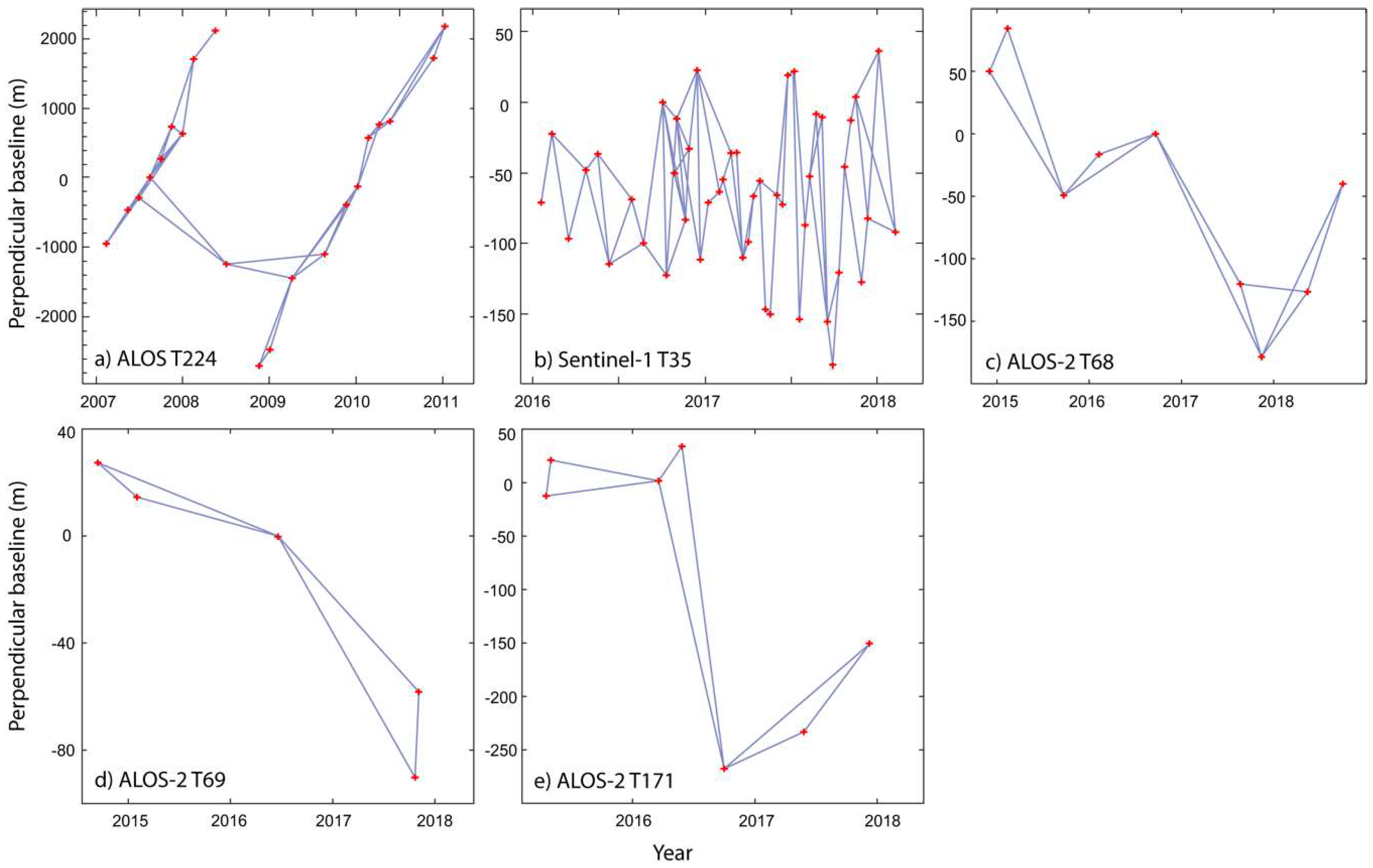
| Radar Satellites | Tracks | Flying Directions | Time Span | Usages |
|---|---|---|---|---|
| Sentinel-1A/B | T35 | Ascending | 2016–2018 | Time-series mapping/surface velocity inversion |
| ALOS | T224 | Ascending | 2007–2011 | Time-series mapping |
| ALOS-2 | T68 | Ascending | 2015–2018 | Time-series mapping/surface velocity inversion |
| T69 | Ascending | 2014–2018 | Surface velocity inversion | |
| T171 | Descending | 2015–2018 | Surface velocity inversion |
| Soil Types | Data Samples | Saturated Hydraulic Conductivity (m/s) | ||
|---|---|---|---|---|
| 25% Quartiles | 75% Quartiles | Geometric Mean | ||
| Silt loam | 58 | 3.6 10−6 | 2.8 10−5 | 1.0 10−5 |
| Silty clay loam | 18 | 1.2 10−6 | 1.6 10−5 | 6.7 10−6 |
| Clay loam | 17 | 4.2 10−6 | 1.6 10−5 | 7.5 10−6 |
| Sandy loam | 127 | 6.6 10−6 | 4.1 10−5 | 1.8 10−5 |
| Silty clay * | - | 1.4 10−6–4.2 10−7 | ||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, Y.; Kim, J.; George, D.L.; Lu, Z. Characterizing Seasonally Rainfall-Driven Movement of a Translational Landslide using SAR Imagery and SMAP Soil Moisture. Remote Sens. 2019, 11, 2347. https://doi.org/10.3390/rs11202347
Xu Y, Kim J, George DL, Lu Z. Characterizing Seasonally Rainfall-Driven Movement of a Translational Landslide using SAR Imagery and SMAP Soil Moisture. Remote Sensing. 2019; 11(20):2347. https://doi.org/10.3390/rs11202347
Chicago/Turabian StyleXu, Yuankun, Jinwoo Kim, David L. George, and Zhong Lu. 2019. "Characterizing Seasonally Rainfall-Driven Movement of a Translational Landslide using SAR Imagery and SMAP Soil Moisture" Remote Sensing 11, no. 20: 2347. https://doi.org/10.3390/rs11202347
APA StyleXu, Y., Kim, J., George, D. L., & Lu, Z. (2019). Characterizing Seasonally Rainfall-Driven Movement of a Translational Landslide using SAR Imagery and SMAP Soil Moisture. Remote Sensing, 11(20), 2347. https://doi.org/10.3390/rs11202347







