3.1. Description of Synoptic Characteristics
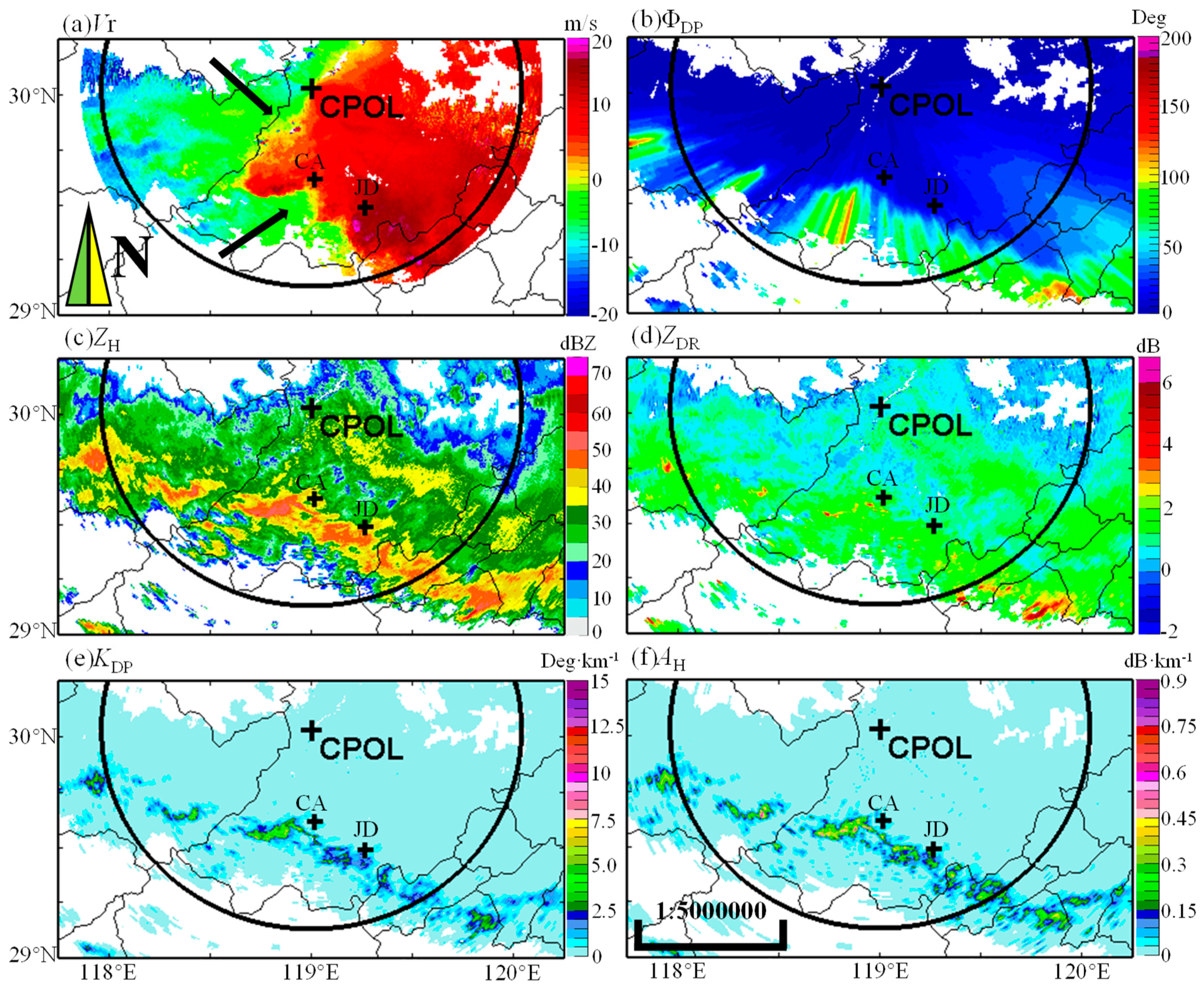
According to the wind directions (bold arrows) depicted in
Figure 5a, there was a quasi-stationary front, and sustained moisture convergence led to persistent convection. The Φ
DP measurements, which passed through the convective rainstorms in many radial directions, exceeded 100° (
Figure 5b), and they were directly responsible for the large
KDP values shown in
Figure 5e. According to posterior analysis, these rainstorms had high concentrations of moderately-sized raindrops, and they were intrinsically related to the sustained moisture convergence along the quasi-stationary front. Consequently, the rainstorms showed a northwestern distribution along this front, supported by the large-scale environment.
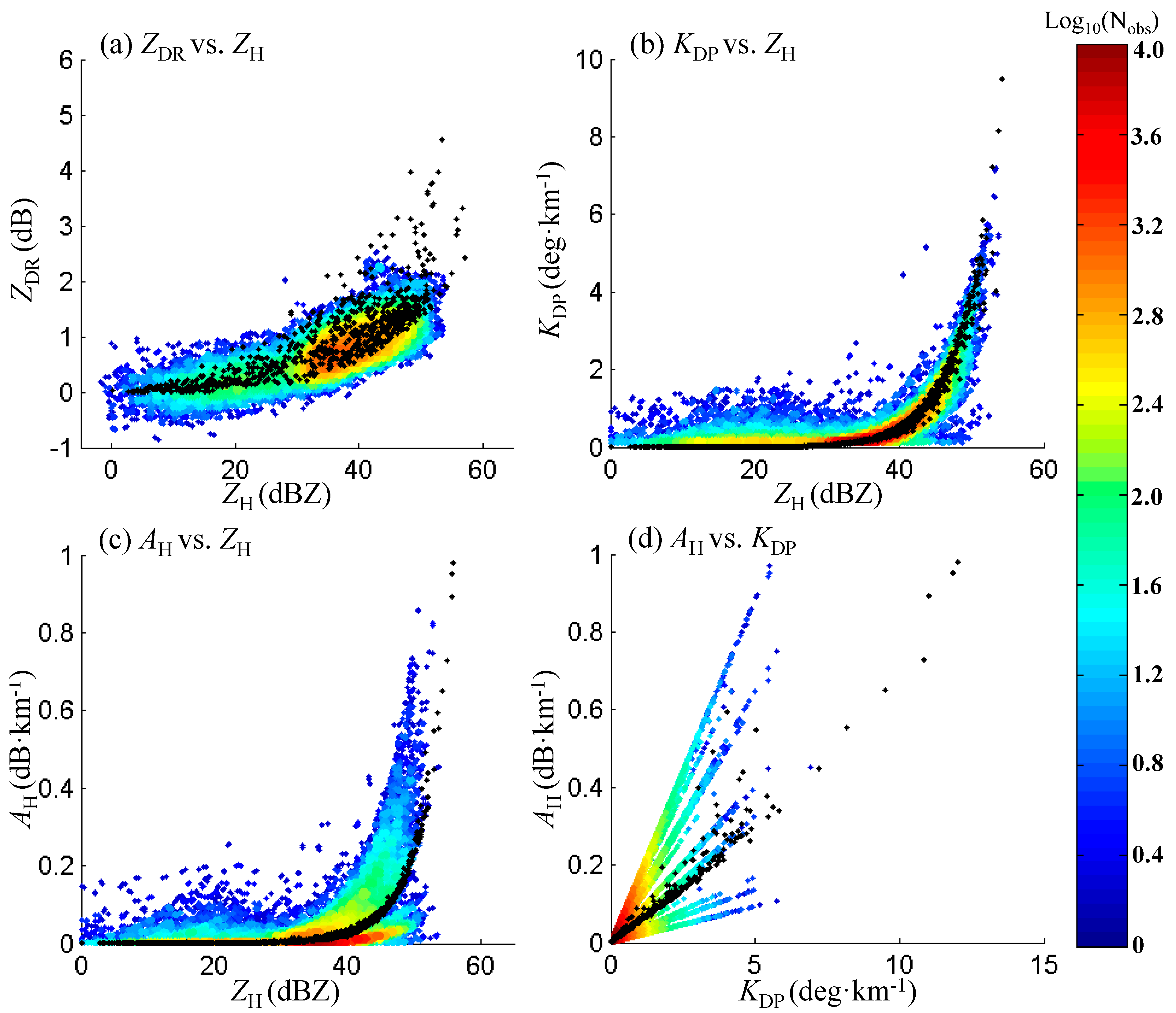
For the posterior analysis, the consistency between
ZH,
ZDR, and
KDP shown in
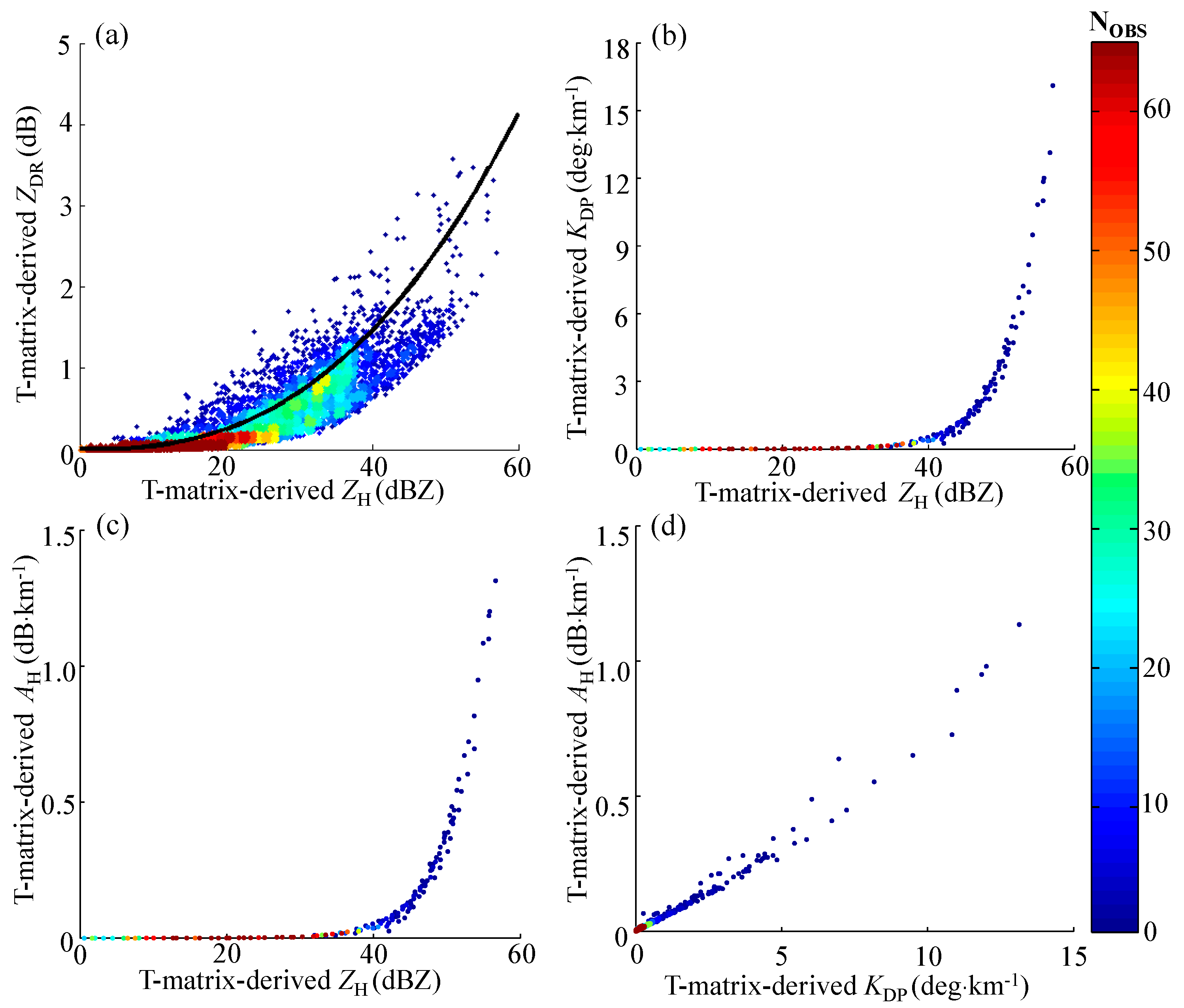
Figure 5c–e was first verified through the scattergram in
Figure 6 to check their quality. The T-matrix-derived
ZH,
ZDR, and
KDP dataset depicted in
Figure 3 was also overlaid on the scattergrams shown in
Figure 6 (black dots) for comparison. It can be seen that the scattergram of radar-observed
ZDR vs.
ZH presented in
Figure 6a agrees well with the T-matrix-derived
ZDR–
ZH distributions shown in
Figure 3a, and
ZDR presented an obvious exponentially increasing tendency as
ZH increased, which coincides with the scattering characteristics of the oblate liquid raindrops. The scattergram of radar-observed
KDP and Z
H derived from
Figure 5c,e is also consistent with the T-matrix-derived counterparts shown in
Figure 3b, and the large
ZH measurements agree well with the large
KDP estimates. The consistency between
ZH,
ZDR, and
KDP demonstrates that the attenuation correction and calibration of
ZH and
ZDR were good. However, radar-observed
AH was not completely consistent with Z
H, as depicted in
Figure 6c, and the black T-matrix-derived dots of
AH vs.
ZH just passed through the center area of radar-observed distribution of
AH vs.
ZH. Some radar-observed
AH values were larger than the T-matrix-derived dots of
AH, while others were smaller, particularly when
ZH exceeded 40 dBZ.
AH related to
KDP in a linear form as
AH = α
KDP with α ranging from 0.03 to 0.18, which can be seen from the ratios between
AH and
KDP shown in
Figure 6d. That is, the combination of
AH and α together was consistent with attenuation-corrected
ZH measurements. In addition, the range of
AH was relatively small, and the high altitudes (1.6–2.1 km) of the CPOL radar measurements by radar-observed
AH may be very different from their surface counterparts.
Some microphysical information about the rainstorms can accordingly be deduced. Assuming the gamma model and neglecting the possible uncertainty induced by parameter
u, the polynomial relationship between the median volume diameter (
D0) and
ZDR and the exponential relationship between the liquid water content (LWC, g·m
−3) and
KDP, which were fitted using the localized DSD dataset during the monsoon season of Hangzhou [
30] and the normalized concentration of raindrops
Nw (mm
−1·m
−3) presented in Ryzhkov et al. (2014) and Testud et al. (2001) [
23,
37], respectively, can be represented as
where
ρw is the water density (1 g·cm
−3 at 4℃), and
Dm (mm) stands for the mean volume diameter of the DSD. It is clearly seen that only a small part of
ZDR measurements in
Figure 5d and
Figure 6a exceeded 2 dB along the area with positive and negative
Vr pairs, which was mainly related to the convective updraft area. Instead, most
ZDR measurements of these rainstorms were featured by Z
H > 20 dBZ and 0.25 dB ≤ Z
DR ≤ 2dB, within which the
D0 of most DSD rarely exceeded 2 mm according to Equation (4), and moderately-sized raindrops with 1 mm ≤
D0 ≤ 2 mm may be the dominant hydrometeors of these rainstorms. However, the southwestern convergence area shown in
Figure 5c was featured by
KDP > 1 deg·km
−1 with a maximum of 8 deg·km
−1, which can also be seen in
Figure 6b. Therefore, the LWC within the rainstorm was higher than 1 g·m
−3 and it increased linearly if
KDP exceeded 1 deg·km
−1. The value of
Dm in Equation (6) was also expected to be less than 2 mm, and
Nw was at least larger than 5000 mm
−1m
−3 if
KDP became larger than 1 deg·km
−1, which implied that a high concentration of moderately-sized raindrops within the convective rainstorms was the microphysical reason for this waterlogging disaster. Furthermore, a similar rainfall pattern persisted for more than 3 h over the study area. The radar retrieved rainfall field was indispensable for the decision-making related to this disaster warning.
3.3. Comparison of Different Radar QPE Approaches
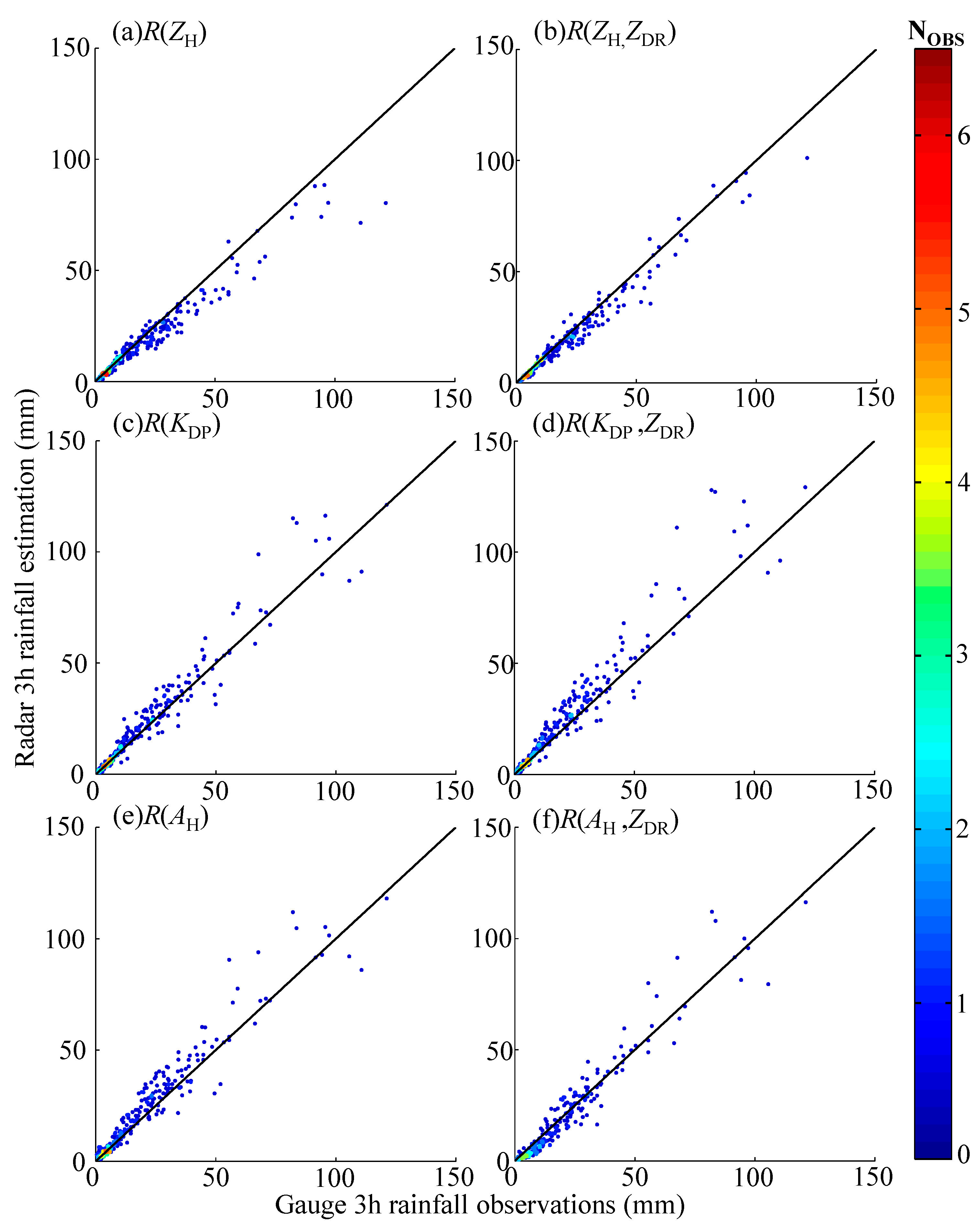
By utilizing the rainfall rate relationships in Equations (3a)–(3f), six radar-based 3-h rainfall accumulation fields at 0500 UTC on 1 June 2016 were obtained, as shown in
Figure 7. At the same time, the scatter between radar 3-h estimates and gauge 3-h observations are also depicted in
Figure 8 to show the relative differences between radar estimates and gauge measurements.
Although the shape of these rainfall fields of
R(
ZH) in
Figure 7a is similar to that of the others, the score of
R(
ZH) in
Table 1 shows that
R(
ZH) seriously underestimated the rainfall center field. This phenomenon can be clearly seen in
Figure 8a, particularly when the gauge 3-h rainfall measurement exceeded 40 mm, and the negative deviation of radar estimates from gauge measurements was more serious with higher rainfall amounts. It can also be seen from
Figure 4a that more scatter dots were found above the black curve when
ZH exceeded 50 dBZ, which implies the potential underestimation of
R(
ZH) in the rainfall center with higher
ZH measurements. Such uncertainties may result from the absence of separate size information (such as
D0 and
Dm) and the concentration information (
Nw) of raindrops within the rainstorms, because
ZH was a composite radar moment of these two factors.
Compared with
R(
ZH), the scores of
R(
ZH,
ZDR) in
Table 1 all improved. Moreover, the radar–gauge data pairs in
Figure 8b are more uniformly scattered along the diagonal line (i.e., y = x) than those in
Figure 8a. This result indicates that combining the potential raindrop shape information through
ZDR was more effective than the single
ZH utilization, as it mitigated this deficiency of
ZH. However,
R(
ZH,
ZDR) is still underestimated since the negative
ENM values and more scatter dots distributed below the diagonal line can be observed in
Figure 8b.
It is hard to say
R(
KDP) performed better than
R(
ZH) from the
ERMS comparison in
Table 1; however, the scattergram of of
R(
ZH) in
Figure 8a was more distributed below the diagonal line in
Figure 8a than the scattergram of
R(
KDP) in
Figure 8c. The latter was more uniformly distributed along the diagnoal line, espically in the range of 0–75 mm, where the scattergram of
R(
AH) was more distributed above the diagonal line in
Figure 8e. Based on this,
R(
KDP) performed best among single-parameter retrievals. Except for the immunity of
KDP to attenuation and wet radome effects, the superiority of
R(
KDP) to the other two single-parameter radar estimates can be attributed to the fact that
KDP was more directly and cohesively associated with LWC [
38], which is represented by the aforementioned Equation (5). However, there are more scatter dots distributed above the diagonal line in
Figure 8c when the 3-h gauge measurements exceeded 75 mm, which apparently accounts for the overestimation of
R(
KDP) in the rainfall center area.
R(
KDP, Z
DR) further integrated the raindrop shape information through
ZDR; however, the scores of
R(
KDP, Z
DR) were actually inferior to those of
R(
KDP) shown in
Table 1, and the overestimation effect seemed more serious in
Figure 8d than that in
Figure 8c. This indicates that additional incorporation of
ZDR is not effective for
R(
KDP, Z
DR), at least in this event, and that the basic equational form of
ZDR and
KDP in
R(
KDP, Z
DR) may account for this phenomenon. It was noticed that
R(
KDP, Z
DR) in Schneebeli and Berne [
20] assumed the exponent of
KDP to be a constant of 1 and just fitted the parameters related to
ZDR, which may better utilize the nearly linear relation between
KDP and LWC according to Equation (5). In addition, it is better to make the
ZDR-related component of
R(
KDP, Z
DR) play a micro-adjusting role if the
KDP-related component of
R(
KDP, Z
DR) can perform at least as well as
R(
KDP). Actually,
KDP contains shape information in a less straightforward way than Z
DR, since oblateness is always required when radar wave passes through a rainstorm and a spherical particle would have
KDP = 0 regardless of its size, this partly explains why the addition of
ZDR cannot significantly improve
R(
KDP).
R(
AH) performed worse than
R(
KDP) based on all evaluation scores. Although
AH was also not sensitive to the negative effects on
ZH (see
Section 1), the calculation of
AH in Equation (1a) includes Φ
DP and the original radar measured
ZH, and
AH was less associated with rainfall rate than
KDP.
R(
AH) was also inferior to
R(
ZH) according to the
ERMS and
ECC scores; however, according to the
ENM scores shown in
Table 1 and the scattergrams shown in
Figure 4a,c,
R(
AH) tended to overestimate, especially at higher rainfall rates; in contrast,
R(
ZH) tended to underestimate in similar patterns. For convenience, radar-observed
KDP vs.
ZH and
AH vs. Z
H, shown in
Figure 6b,c, respectively, can be compared to see the differences between
KDP and
AH. For the same
ZH values, radar-observed
KDP vs. Z
H shows less difference (about ±0.5 deg·km
-1) from T-matrix-derived
KDP vs. Z
H in
Figure 6b. In contrast, radar-observed
AH vs.
ZH suffers from a relatively wider distribution difference (about ±0.3 dB·km
-1 and more positive deviation with Z
H > 40 dBZ) from T-matrix-derived
AH vs.
ZH in
Figure 6c. That is, radar-observed
AH seemed to be overestimated more than
KDP in some radar beams. An unobserved microphysical transition may occur during the falling process of the hydrometeors from the altitude of 1.6–2 km to the surface, then caused the large difference between radar-observed
AH and its surface counterparts.
In addition,
R(
AH,
ZDR) performed best of the six radar QPE estimators with respect to the
ENM and
ERMS scores shown in
Table 1. Essentially, it is not straightforward to resolve the performance differences between
R(
KDP,
ZDR) and
R(
AH,
ZDR), since
AH and
KDP have similar characteristics. They are often related through
AH = α
KDP. Therefore, we aimed to decompose their mathematical formulas into two parts (see
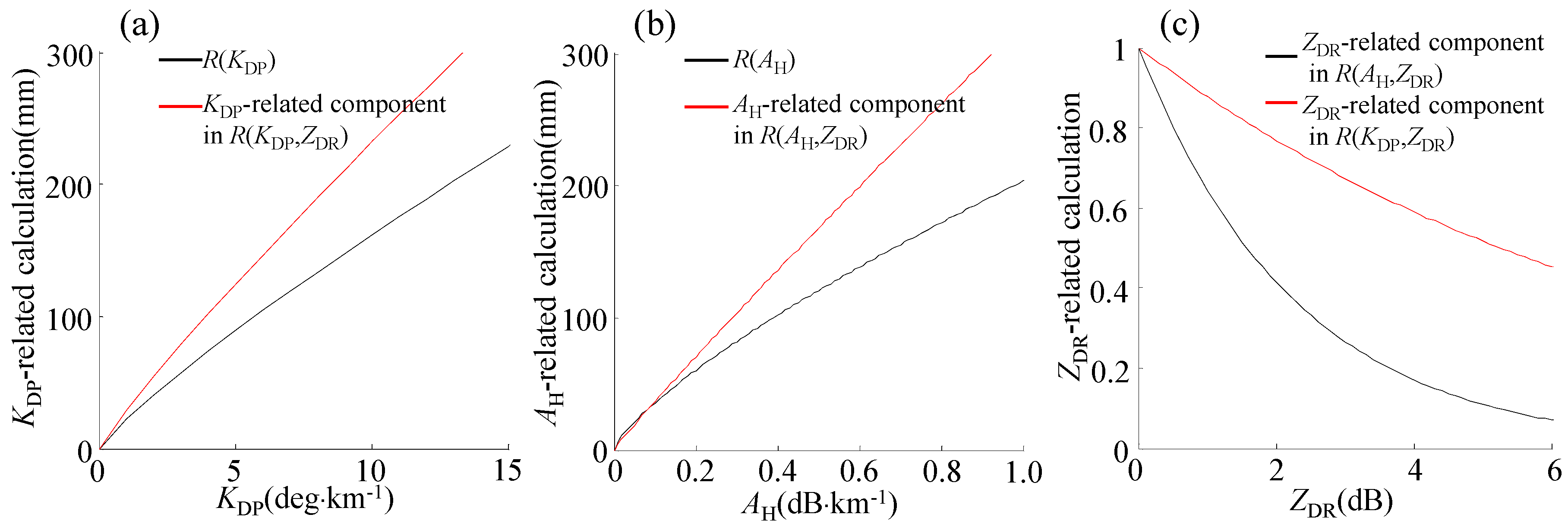
Figure 9). In particular,
R(
KDP,
ZDR) consists of
KDP- and
ZDR-related components, whereas
R(
AH,
ZDR) consists of
AH- and
ZDR-related components. Since the
KDP- and
AH-related calculations behave similarly (see
Figure 9a,b), the
ZDR-related components play a dominant role in the differences. We noticed that
R(
KDP, Z
DR) is more associated with overestimation compared with
R(
AH,
ZDR), and the
ZDR-related calculation in
R(
AH,
ZDR) decreases more quickly than that of
R(
KDP, Z
DR) (see
Figure 9c). All in all, the differences between
R(
KDP, Z
DR) and
R(
AH,
ZDR) are more related to the
ZDR-related component. Besides,
Figure 8f shows that many scatter dots were distributed below the diagonal line when gauge measurements were less than 10 mm, and these underestimates may partly compromise the overestimates when the 3-h gauge measurements exceeded 75 mm, which was an important reason for the superior scores of
R(
AH,
ZDR).
The comparison between different radar QPE approaches showed that
R(
KDP) performs best of all the single-parameter radar QPE estimators in the range 0–75mm, and
R(
AH, Z
DR) performs best with respect to
ENM scores. However, this result cannot be declared just based on the statistical scores. Not all polarimetric radar QPE estimators, such as
R(
KDP,
ZDR), can obtain superior statistical scores to
R(
ZH). Instead, the detailed scatter distributions in
Figure 8c–f show that
R(
KDP),
R(
KDP,
ZDR),
R(
AH), and
R(
AH,
ZDR) were all overestimated when gauge measurements exceeded 50 mm. This indicates that manually alternating polarimetric radar variables cannot always obtain better performances. The rainfall center area is worthy of further investigation to reveal some negative factors, which seriously affect the practical performance of these polarimetric radar QPE algorithms.
3.4. Time Series Analysis
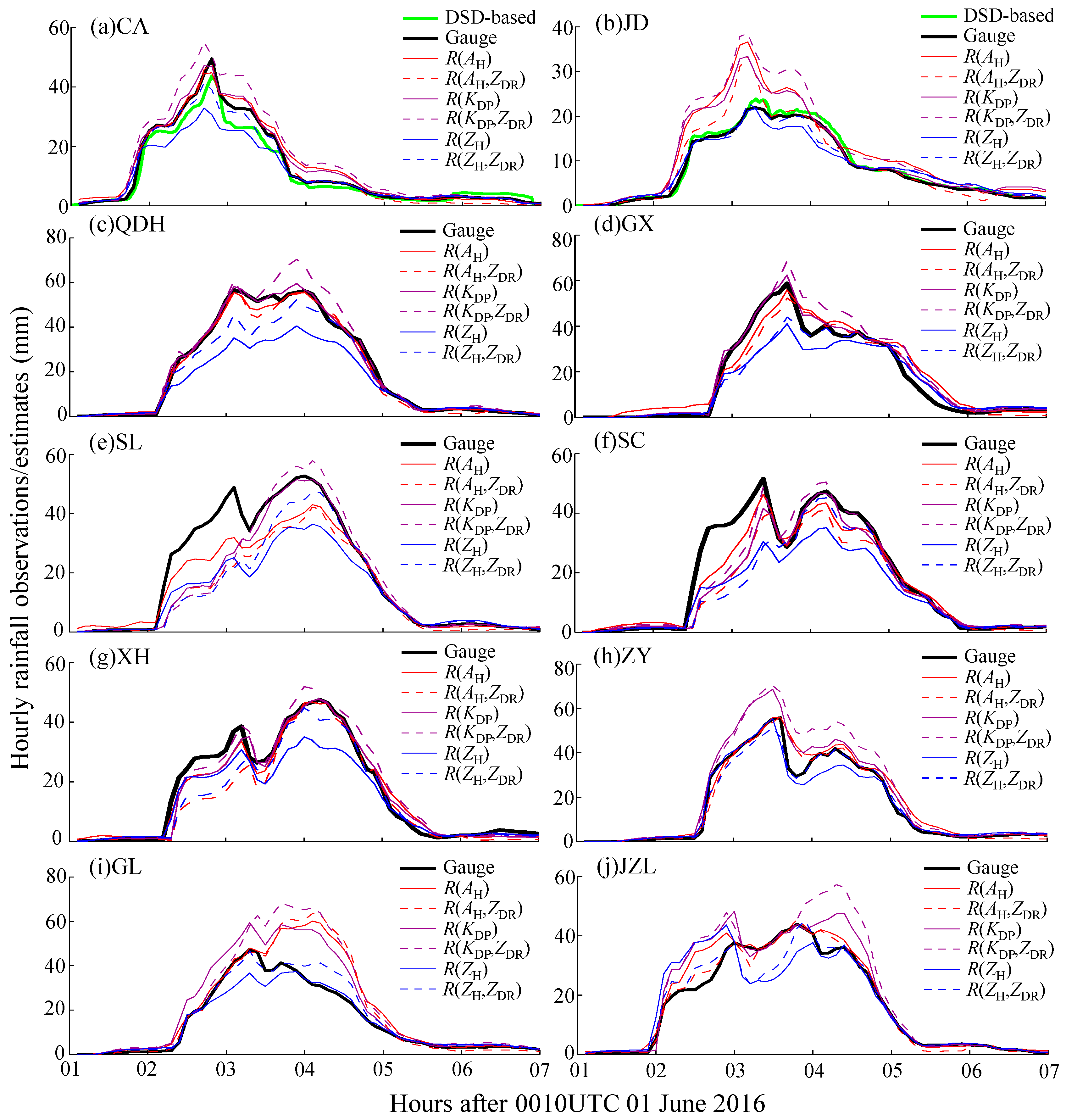
Gauge-measured, DSD-based, and radar-estimated hourly rainfall time series from ten meteorological stations, which are located within the rainfall center area shown in
Figure 7, are shown in
Figure 10. Although only CA and JD stations were used to observe the DSD dataset, the near agreement of DSD-based and gauge-measured hourly rainfall (bold black and green lines) shown in
Figure 10a,b verifies the high quality of these gauge measurements; therefore, the gauge-measured rainfall time series of the other eight stations can also provide good surface reference rainfall for radar estimates too. Moreover, some typical error characteristics related to different radar rainfall patterns can be directly reflected through these temporal rainfall series.
Figure 10a shows a good positive example that nearly all radar-estimated rainfall series at CA station were in good accordance with the gauge-measured rainfall series with an exception of
R(
ZH), which was underestimated at 0200–0400 UTC. The time series at QDH at 0200–0500 UTC shown in
Figure 10c and that at GX at 0300–0500 UTC shown in
Figure 10d were very similar to those shown in
Figure 10a. They can be assumed to have similar rainfall patterns. Although the optimum rainfall retrieval relationship is necessary for a good rainfall estimator, the small deviation between the radar-estimated rainfall series of
R(
AH),
R(
KDP),
R(
ZH,
ZDR),
R(
AH,
ZDR) and the gauge-measured rainfall series in
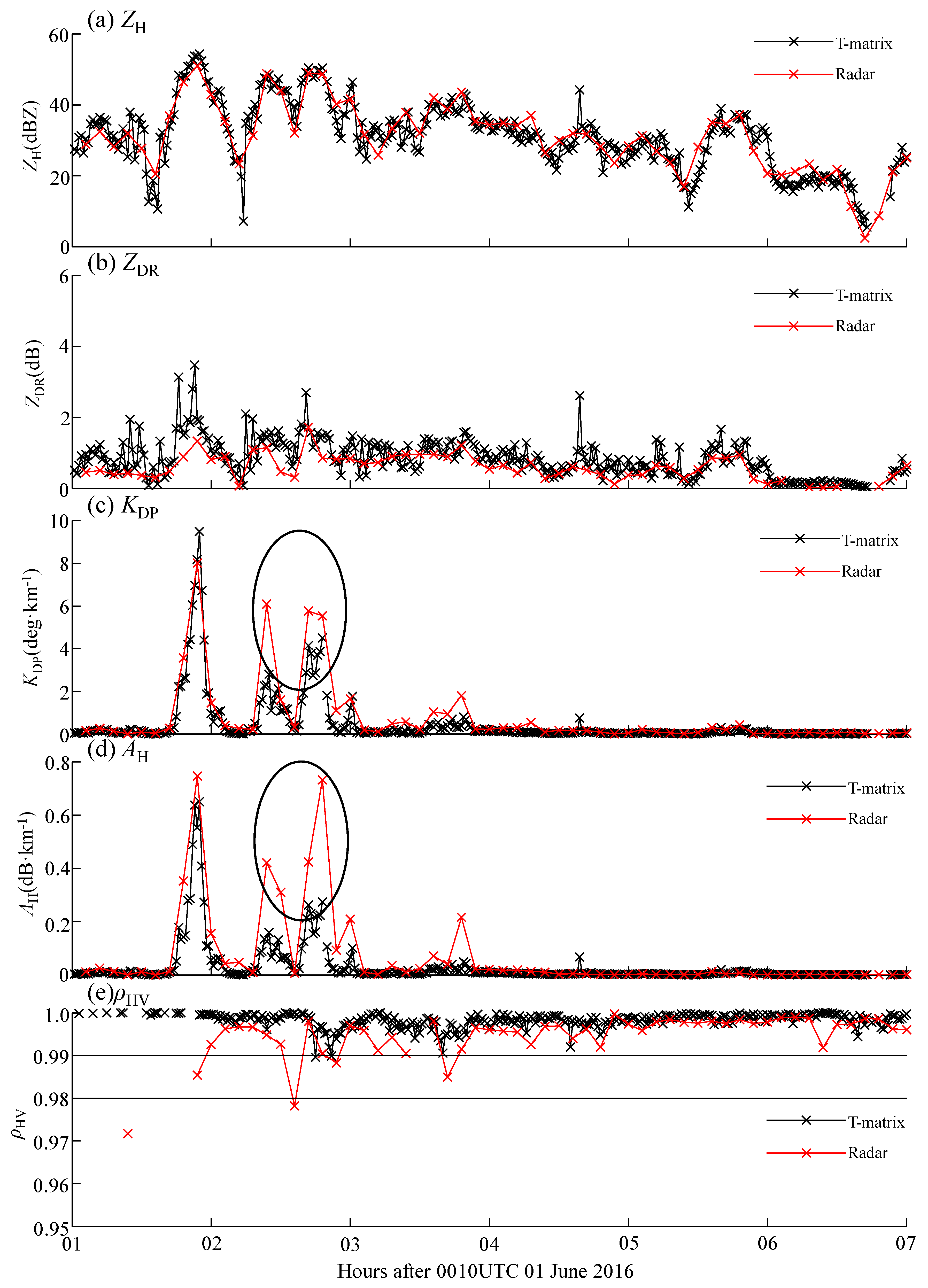
Figure 10a can also be attributed to the consistency between the radar-observed series of
ZH,
ZDR, KDP, and
AH and their T-matrix-derived counterparts in
Figure 11a,c,e,g. Furthermore, most radar-observed and T-matrix-derived
ρHV values exceed 0.99 in
Figure 11i, which indicates that radar observed pure liquid hydrometeors up in the air are similar to those near the surface. Accordingly, the ellipses depicted in
Figure 11c,d implies that the overestimated
KDP and
AH values observed by radar can account for their overestimated rainfall near 0200 UTC in
Figure 10a too. On the contrary, the large deviation of
R(
ZH) from the gauge rainfall series can be attributed to the inadequate
R(
ZH) relationship, as described in
Section 3.3.
The overestimation of the time series of
R(
AH),
R(
KDP),
R(
KDP,
ZDR),
R(
AH,
ZDR) at JD station at 0300–0400 UTC (
Figure 10b), at ZY station at 0400–0500 UTC (
Figure 10h), at GL station at 0300–0500 UTC (
Figure 10i), and at JZL station at 0340–0440 UTC feature similar rainfall patterns. In contrast, the rainfall series estimated by
R(
ZH) and
R(
ZH,
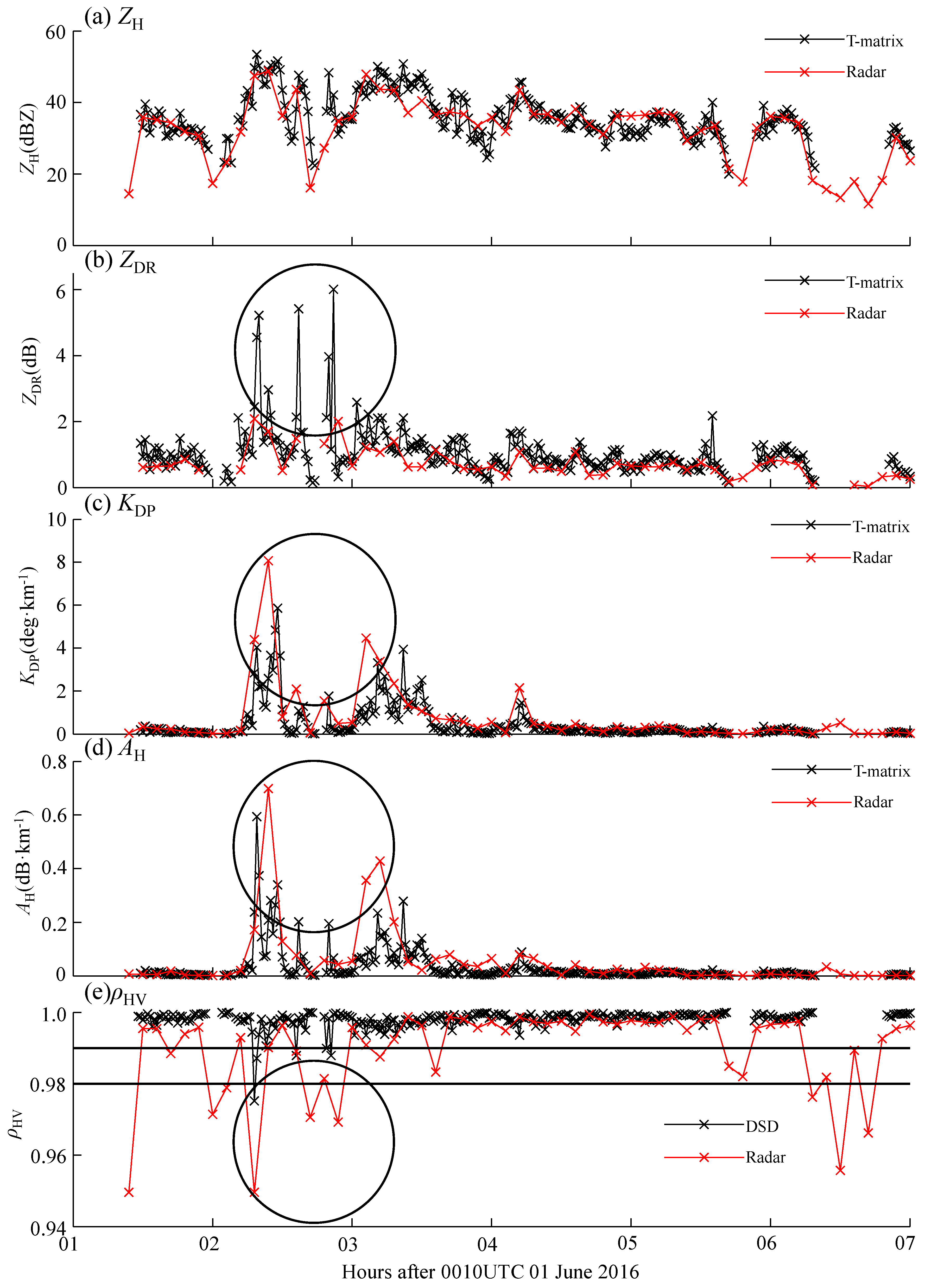
ZDR) agreed well with the gauge rainfall series in these time intervals. Some characteristics can be deduced from the data timeseries of JD station in
Figure 12. The difference of
ρHV depicted in
Figure 12e indicates the hydrometeors in the radar beams and near the surface were microphysically different, namely, some solid hydrometeors may exist in the upper air, but only liquid hydrometeors fell on the surface. Thus, there existed an unobserved microphysical transition before the solid hydrometeors falling on the ground. The large
ZDR values near the surface in
Figure 12b corresponded to big raindrops at the start of the showers; however, radar-observed
ZDR values were all less than 2 dB during this period, which indicates the diameter of the hydrometeors in the air were still smaller than 2 mm and the Mie scattering effects were not obvious in some radar volumes. Therefore, radar-observed
KDP and
AH in
Figure 12c,d may be overestimated than expected if the contribution of the solid hydrometeors was not separated successfully from Φ
DP. The reason for the small biases between radar-observed
ZH and surface-T-matrix-derived Z
H in
Figure 12a can be ascribed to the fact that a large raindrop can account for a large number of little raindrops, namely, more large raindrops were observed near the surface than in the upper air, which had been verified by the large bias of
ZDR. Consequently, radar-observed Z
H and T-matrix-derived Z
H might coincidently agree with each other and
R(
ZH) did not deviate far from the gauge-measured/DSD-based hourly rainfall series during this time period. Simultaneously, the
ZDR-related calculations hardly reduced the overestimation caused by the
AH-related or
KDP-related calculations of
R(
AH,
ZDR) and
R(
KDP,
ZDR) during the same period. Instead,
R(
ZH,
ZDR) outperformed the other five radar QPE estimators and its rainfall time series was most similar to the gauge-measured and DSD-based hourly rainfall series of JD station.
The time series of all radar estimates at SL and SC stations were all underestimated at 0200–0330, as shown in
Figure 10e,f. The rainstorm system, which was featured abundant moisture (see
Figure 5), moved along the northwest direction and successively affected SL, XH, and SC stations. These radar rainfall underestimations were caused by showers at the start of the major rainstorm. The detailed information of
ZH,
ZDR, and
KDP, as well as the six-minute rainfall measurements at these three stations are all listed in
Table 2, where the radar captured only one peak value each of
ZH, Z
DR, and
KDP at SL and SC stations. However, the CPOL radar captured two peak values each of
ZH, Z
DR, and
KDP at XH station. Through comparing the six-minute rainfall recordings from the gauges, SL, XH, and SC were found to have two peak values of Z
H, Z
DR, and
KDP each. That is, the CPOL radar failed to detect the second peak values of
ZH, Z
DR, and
KDP at SL and SC stations due to the rapid development and movement of the shower in front of the rainstorm. As a result, all radar estimates at SL and SC tended to underestimate the hourly rainfall accumulations, and this underestimation lasted for about one hour.
Figure 10h demonstrates another typical pattern where
R(
AH) and
R(
AH,
ZDR) were both superior to
R(
KDP) and
R(
KDP,
ZDR) and the latter two were both overestimated at 0230–0500 UTC. Since the optimal rainfall retrieval relationships were used, the performance difference was mainly attributed to the different characteristics of
AH and
KDP.
AH is often estimated through
AH =
αKDP. In addition, the reconstructed Φ
DP calculated through the fitting process (
KDP fitting) or ZPHI processing (
AH) should both be similar to the filtered Φ
DP. Hence, it can be concluded that the major difference between
AH and
KDP is in the coefficient
α, which is adjustable in [
r0,
rm]. Moreover, for the same ΔΦ
DP (
r0,
rm), it is well known that the difference in
will not affect the
AH because
AH is also immune to attenuation, miscalibration, PBB, and wet radome issues. Based on Equation (1a), coefficient
α must be different in the process in order to maintain such a statement. In the pure liquid rain scenario, both
KDP and
AH were expected to increase as the attenuation corrected
ZH increased. For the mixed phase hydrometeors in the melting layer, both
KDP and
AH tended to be near-zero if ΔΦ
DP (
r0,
rm) could be constrained by a small value during the estimation process; otherwise, they might be overestimated if ΔΦ
DP (
r0,
rm) was large, which is similar to the pure rain scenario.
Furthermore, due to the changes in coefficient
α, the consistency between
AH and
ZH is not as strong as that between
KDP and Z
H and/or
ZDR (for details on the self-consistency of polarimetric radar measurements, see [
39]). To further support such a conclusion,
Figure 6 shows that the radar-observed
KDP vs. Z
H (
Figure 6b) measurements are consistent with the T-matrix-derived scattergram of
KDP vs. Z
H. However, the radar-observed scattergram of
AH vs. Z
H (
Figure 6c) is not as consistent. Instead, there is an obvious divergence when
ZH exceeds 40 dBZ, which is more obvious than that of
KDP vs. Z
H in
Figure 6b. Such divergence is further investigated using
Figure 6c, which led to the separation of the radar-observed scattergram of
AH vs. Z
H into three categories:
(i) Radar-observed data overlap with the T-matrix-derived data: Radar-observed
AH values within the range gates are nearly the same as T-matrix-derived
AH. Using the optimal
R(
AH) relationships, unbiased
R(
AH) is expected compared with the
R calculated directly from DSD and surface gauge rainfall measurements (see
Figure 4e).
(ii) Radar-observed data above the T-matrix-derived data: These radar-observed
AH values are potentially higher than the ideal observations near the surface, which is caused by the contamination of some small-sized melting hydrometeors with the diameter less than 2 mm. These radar-observed
AH values may further cause the overestimation of
R(
AH) if radar-observed
AH values are directly applied (
Figure 4e). Due to the narrow range of
AH, a little deviation may introduce a large difference in
R(
AH). As such, a correction procedure for
AH may be required.
(iii) Radar-observed data below the T-matrix-derived data: This is dominated by the near-zero AH values, and their range gates are more associated with the melting mixed phase hydrometers. Although can be large in [r0, rm], ΔΦDP (r0, rm) may be small in Equation (1a) due to the non-negative constraint imposed on AH estimation, the coefficient α can adjust the non- part of Equation (1a), resulting in reconstructed ΦDP close to the filtered ΦDP.
3.5. Discussion
The statistical comparison in
Section 3.3 actually gives an overall view of the error characteristics of these radar QPE estimators. More error information about each radar QPE estimator can be seen by comparing the time series of radar rainfall estimates with gauge rainfall measurements. This shows that the optimum rainfall rate relationships and the consistency between radar measurements and their surface counterparts are both indispensable, and the relative superiority of polarimetric radar QPE estimators is closely related to the specific rainfall patterns. The following should be noted:
(i) Regionally optimal rainfall estimation relationships are the basis for radar QPE. The C-band relations for
R(
ZH),
R(
AH), and
R(
KDP) provided in this paper are significantly different from those given in [
23,
40,
41]. Similar comparable results may be not expected if the same equation parameters are directly implemented for severe rainfall events in this paper, because they may be representative of different localized precipitation characteristics, which intrinsically varies around the world. This is the reason why individual equations of
R(
ZH),
R(
AH), and
R(
KDP) are always necessary for different locations; (ii)
R(
ZH) is not always an optimal option for polarimetric radar. However, it was observed that
R(
ZH) is not always inferior to other rainfall estimators, and
R(
ZH) really performed best at 0100–0310 UTC (
Figure 10b) and at 0100–0340 UTC (
Figure 10h), where the time series of
R(
ZH) tended to overlap with the gauge time series in these specific temporal intervals. Besides, the overestimation effects caused by the melting layers on
R(Z
H) can be solved by some bright band identification procedure, and more adequate
R(Z
H) relationships suitable for severe rainfall scenario or self-adaptive
R(Z
H) relationships may further enhance the performance of
R(Z
H). Therefore,
ZH is still useful for the range gates where
KDP or
AH is abnormally higher.
(iii) In this paper,
R(
ZH,
ZDR) is a positive example of
ZDR utilization and it performs better than
R(
ZH) in many of the time series depicted in
Figure 10. Comparing the mathematical forms of
R(
ZH) and
R(
ZH,
ZDR), the integration with
ZDR really mitigates some underestimation of
R(
ZH). In contrast,
R(
KDP, Z
DR) presented more overestimates than
R(
KDP), which implies that integrating Z
DR with
KDP through current mathematical form may not be effective. In addition, although
R(
AH,
ZDR) obtained the best
ENM scores, it underestimated in light rainfall scenarios more seriously than
R(
AH). Some regional correction upon the rainfall field derived from
R(
KDP, Z
DR) and
R(
AH,
ZDR) may be necessary to improve their performance.
(iv) The melting layer not only causes the overestimation of R(ZH) but can also introduce overestimation to R(AH) and R(KDP). If radar-observed KDP or AH were contaminated by the melting layer but the hydrometeors near the surface were not, R(KDP) and R(AH) might be overestimated. Although the α coefficient can adjust to mitigate some bias of R(AH), which helps it to outperform R(KDP), the overestimation related to R(AH) remains serious. Some correction procedures aiming to make radar-observed AH or KDP more approximate to the counterparts of surface hydrometers have shown promise for future use; however, some statistical prior knowledge on the regional rainfall characteristics may be necessary during this process.
(v) The convective rainstorms with a quick moving speed may cause all radar QPE estimators to be underestimated if the radar failed to capture the full view of the rainstorm. Such rainfall patterns correspond to the initial developing phase of the rainstorms. The low-cost gap-filling X-band radar network may help to instantly observe such rainstorms in their initial developing phase. The phased array radar supporting quick VCP scanning strategy also helps to provide high temporal resolution dataset for such rainstorms. Both are promising to make the monitoring of rainstorms more spatiotemporally seamless for radar QPE retrievals.
Dynamic composition of the different radar QPE estimators is a promising trend, and all of the different radar rainfall estimators can be comprehensively utilized in this way. However, the optimal and representative relationships incorporating a variety of rainfall characteristics over a target area, the high-quality radar measurements similar to the counterparts of surface hydrometeors, and the detailed composition forms of these radar QPE estimators are all important factors that make the ultimate rainfall estimation results efficient in practical operations. None of the abovementioned issues can be neglected during this process and they are worthy of further investigation in the future.