Bidirectional Convolutional LSTM Neural Network for Remote Sensing Image Super-Resolution
Abstract
1. Introduction
2. Materials and Methods
2.1. Datasets and Metrics
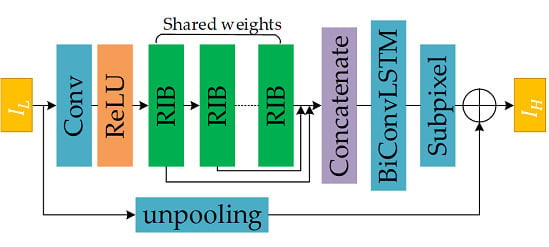
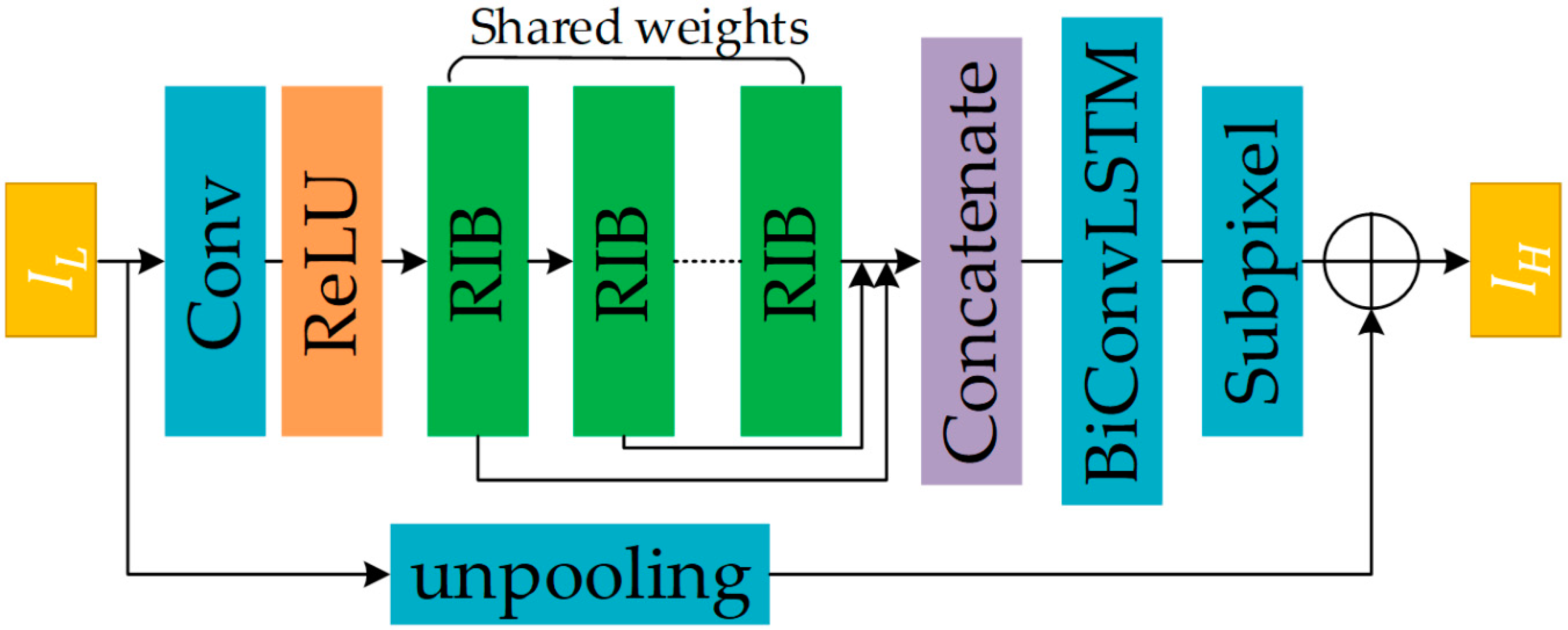
2.2. Network Structure
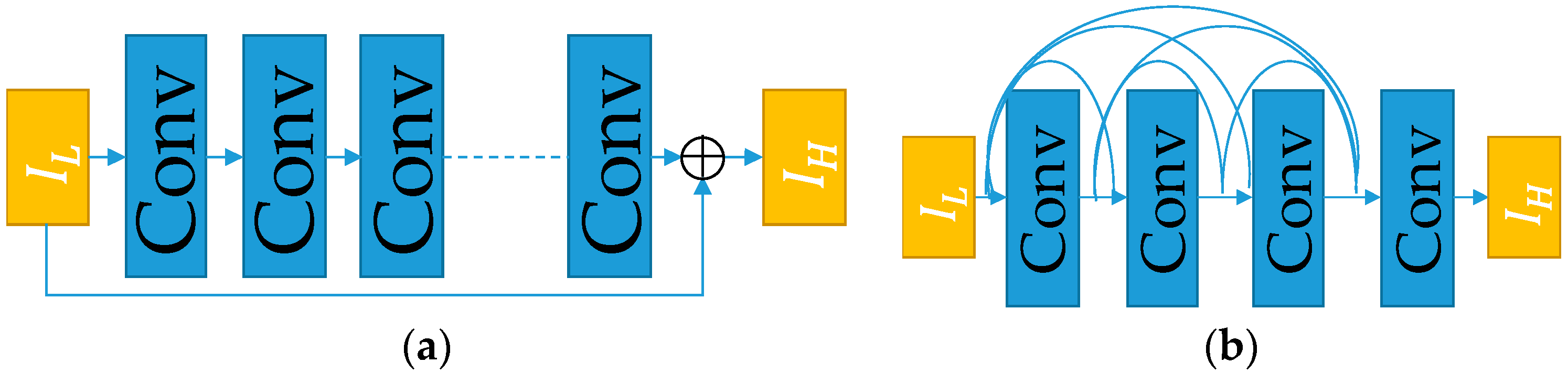
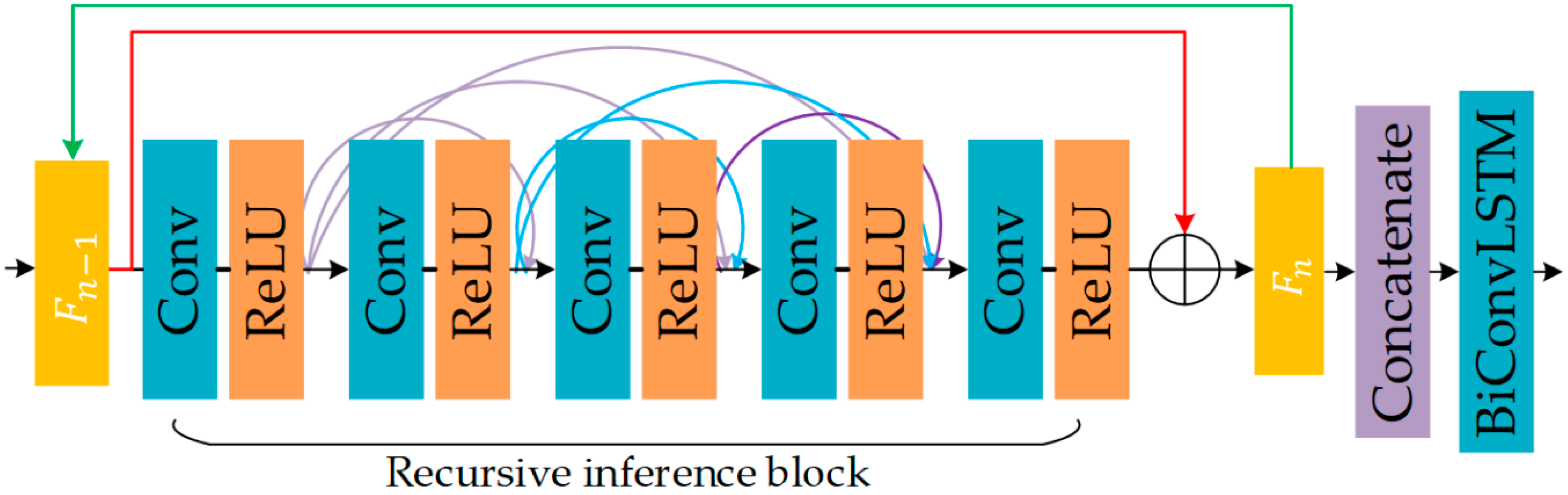
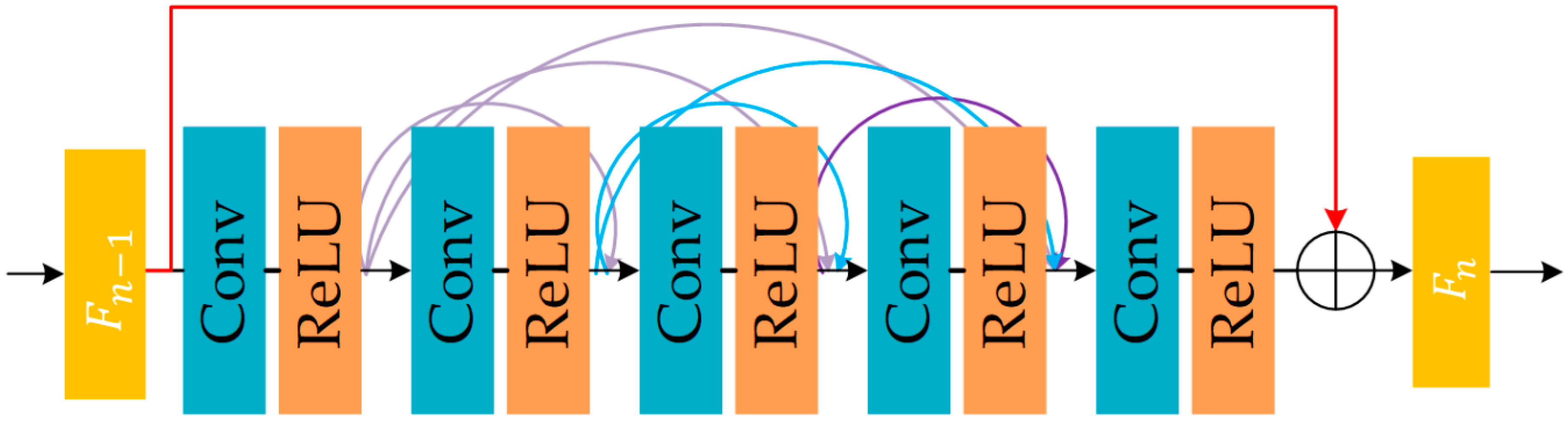
2.3. Recursive Inference Block
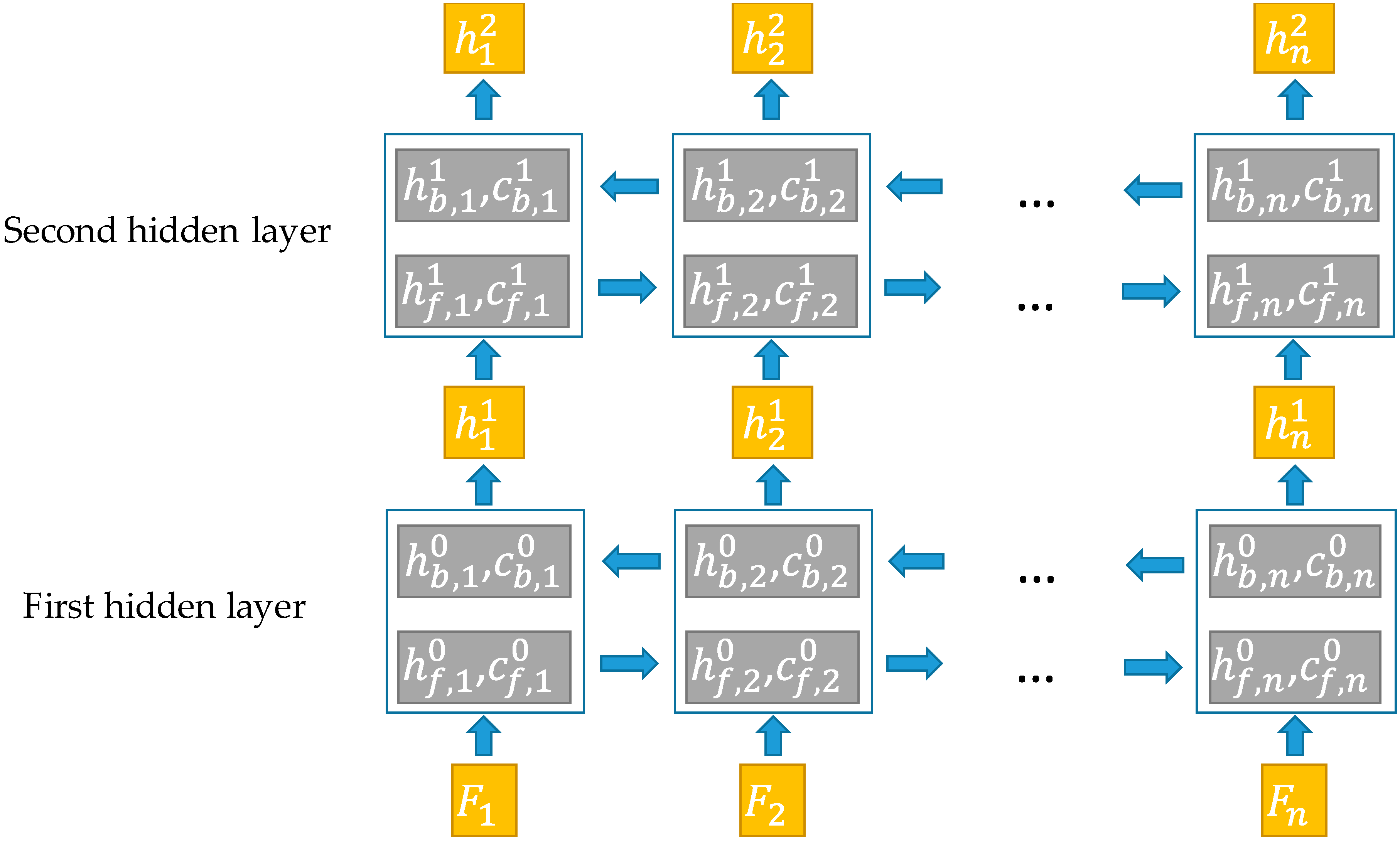
2.4. BiConvLSTM
2.5. Global Residual Path
3. Results
3.1. Implementation Details
3.2. Study of Recursive Inference Block
3.3. Study of BiConvLSTM
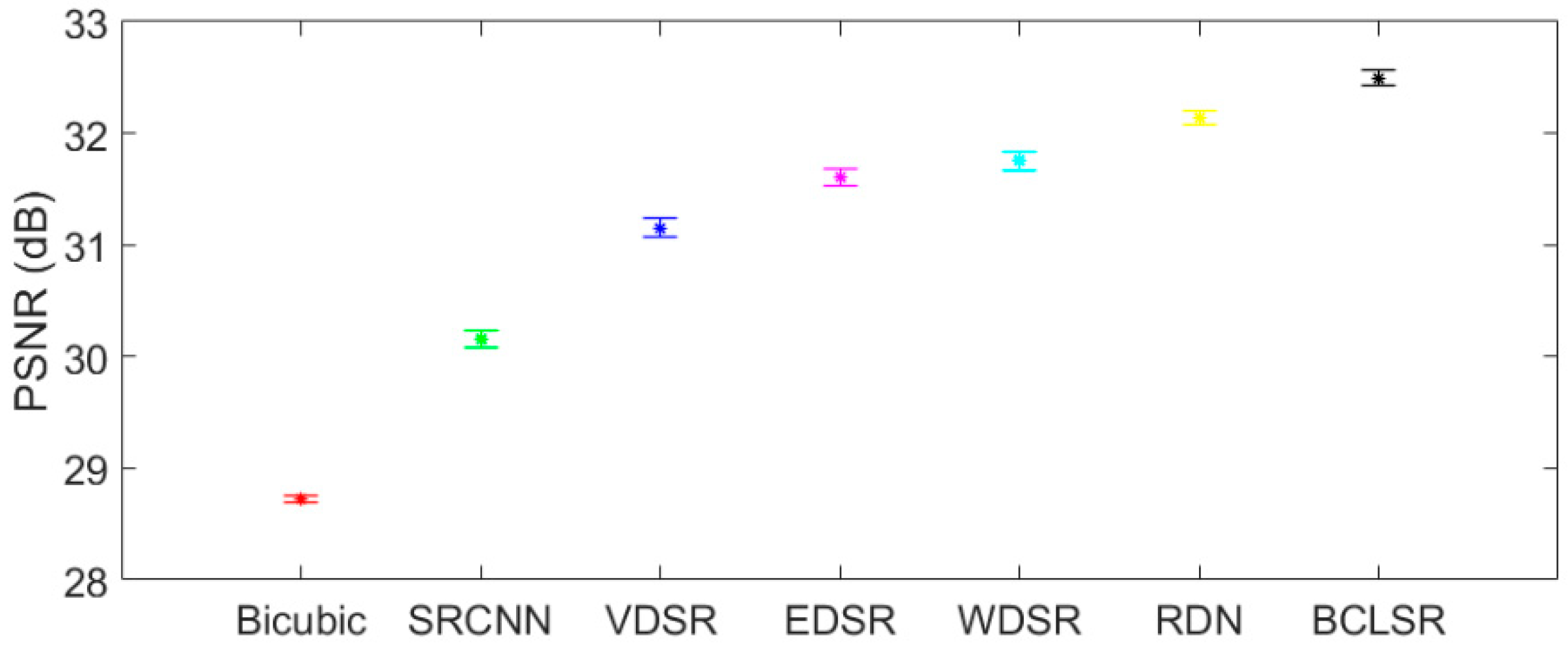
3.4. Result Comparison
3.5. Cross-Validation Experiments
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Merino, M.T.; Nunez, J. Super-resolution of remotely sensed images with variable-pixel linear reconstruction. IEEE Trans. Geosci. Remote Sens. 2007, 45, 1446–1457. [Google Scholar] [CrossRef]
- Yang, D.; Li, Z.; Xia, Y.; Chen, Z. Remote sensing image super-resolution: Challenges and approaches. In Proceedings of the 2015 IEEE International Conference on Digital Signal Processing (DSP), Singapore, 21–24 July 2015; pp. 196–200. [Google Scholar]
- Harris, J.L. Diffraction and resolving power. JOSA 1964, 54, 931–936. [Google Scholar] [CrossRef]
- Goodman, J.W. Introduction to Fourier optics; McGraw-Hill: San Francisco, CA, USA, 2005. [Google Scholar]
- Tsai, R. Multiframe image restoration and registration. Adv. Comput. Vis. Image Process. 1984, 1, 317–339. [Google Scholar]
- Yang, J.; Wright, J.; Huang, T.S.; Ma, Y. Image super-resolution via sparse representation. IEEE Trans. Image Process. 2010, 19, 2861–2873. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Wu, W.; Dai, Y.; Yang, X.; Yan, B.; Lu, W. Remote sensing images super-resolution based on sparse dictionaries and residual dictionaries. In Proceedings of the 2013 IEEE 11th International Conference on Dependable, Autonomic and Secure Computing, Chengdu, China, 21–22 December 2013; pp. 318–323. [Google Scholar]
- Zhang, H.; Huang, B. Scale conversion of multi sensor remote sensing image using single frame super resolution technology. In Proceedings of the 2011 19th International Conference on Geoinformatics, Shanghai, China, 24–26 June 2011; pp. 1–5. [Google Scholar]
- Czaja, W.; Murphy, J.M.; Weinberg, D. Superresolution of Noisy Remotely Sensed Images Through Directional Representations. IEEE Geosci. Remote Sens. Lett. 2018, 1–5. [Google Scholar] [CrossRef]
- Ahi, K. Mathematical modeling of THz point spread function and simulation of THz imaging systems. IEEE Trans. Terahertz Sci. Technol. 2017, 7, 747–754. [Google Scholar] [CrossRef]
- Ahi, K. A method and system for enhancing the resolution of terahertz imaging. Measurement 2019, 138, 614–619. [Google Scholar] [CrossRef]
- Chernomyrdin, N.V.; Frolov, M.E.; Lebedev, S.P.; Reshetov, I.V.; Spektor, I.E.; Tolstoguzov, V.L.; Karasik, V.E.; Khorokhorov, A.M.; Koshelev, K.I.; Schadko, A.O. Wide-aperture aspherical lens for high-resolution terahertz imaging. Rev. Sci. Instrum. 2017, 88, 014703. [Google Scholar] [CrossRef]
- Chernomyrdin, N.V.; Schadko, A.O.; Lebedev, S.P.; Tolstoguzov, V.L.; Kurlov, V.N.; Reshetov, I.V.; Spektor, I.E.; Skorobogatiy, M.; Yurchenko, S.O.; Zaytsev, K.I. Solid immersion terahertz imaging with sub-wavelength resolution. Appl. Phys. Lett. 2017, 110, 221109. [Google Scholar] [CrossRef]
- Nguyen Pham, H.H.; Hisatake, S.; Minin, O.V.; Nagatsuma, T.; Minin, I.V. Enhancement of spatial resolution of terahertz imaging systems based on terajet generation by dielectric cube. Apl Photonics 2017, 2, 056106. [Google Scholar] [CrossRef]
- Dong, C.; Loy, C.C.; He, K.; Tang, X. Learning a deep convolutional network for image super-resolution. In Proceedings of the European conference on computer vision, Zurich, Switzerland, 6–12 September 2014; pp. 184–199. [Google Scholar]
- Kim, J.; Kwon Lee, J.; Mu Lee, K. Accurate image super-resolution using very deep convolutional networks. In Proceedings of the IEEE conference on computer vision and pattern recognition, Las Vegas, NV, USA, 26 June–1 July 2016; pp. 1646–1654. [Google Scholar]
- Lim, B.; Son, S.; Kim, H.; Nah, S.; Mu Lee, K. Enhanced deep residual networks for single image super-resolution. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Honolulu, HI, USA, 21–26 July 2017; pp. 136–144. [Google Scholar]
- Yu, J.; Fan, Y.; Yang, J.; Xu, N.; Wang, Z.; Wang, X.; Huang, T. Wide activation for efficient and accurate image super-resolution. arXiv 2018, arXiv:1808.08718. Available online: https://arxiv.org/abs/1808.08718 (accessed on 21 December 2018).
- Dong, C.; Loy, C.C.; Tang, X. Accelerating the super-resolution convolutional neural network. In Proceedings of the European conference on computer vision, Amsterdam, The Netherlands, 8–16 October 2016; pp. 391–407. [Google Scholar]
- Shi, W.; Caballero, J.; Huszár, F.; Totz, J.; Aitken, A.P.; Bishop, R.; Rueckert, D.; Wang, Z. Real-time single image and video super-resolution using an efficient sub-pixel convolutional neural network. In Proceedings of the IEEE conference on computer vision and pattern recognition, Las Vegas, NV, USA, 26 June–1 July 2016; pp. 1874–1883. [Google Scholar]
- Ahn, N.; Kang, B.; Sohn, K.-A. Image super-resolution via progressive cascading residual network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Salt Lake City, UT, USA, 18–22 June 2018; pp. 791–799. [Google Scholar]
- Kim, J.; Kwon Lee, J.; Mu Lee, K. Deeply-recursive convolutional network for image super-resolution. In Proceedings of the IEEE conference on computer vision and pattern recognition, Las Vegas, NV, USA, 26 June–1 July 2016; pp. 1637–1645. [Google Scholar]
- Tai, Y.; Yang, J.; Liu, X. Image super-resolution via deep recursive residual network. In Proceedings of the IEEE conference on computer vision and pattern recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 3147–3155. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE conference on computer vision and pattern recognition, Las Vegas, NV, USA, 26 June–1 July 2016; pp. 770–778. [Google Scholar]
- Ledig, C.; Theis, L.; Huszár, F.; Caballero, J.; Cunningham, A.; Acosta, A.; Aitken, A.; Tejani, A.; Totz, J.; Wang, Z. Photo-realistic single image super-resolution using a generative adversarial network. In Proceedings of the IEEE conference on computer vision and pattern recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 4681–4690. [Google Scholar]
- Ran, Q.; Xu, X.; Zhao, S.; Li, W.; Du, Q. Remote sensing images super-resolution with deep convolution networks. Multimed. Tools Appl. 2019, 1–17. [Google Scholar] [CrossRef]
- Huang, G.; Liu, Z.; Van Der Maaten, L.; Weinberger, K.Q. Densely connected convolutional networks. In Proceedings of the IEEE conference on computer vision and pattern recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 4700–4708. [Google Scholar]
- Tong, T.; Li, G.; Liu, X.; Gao, Q. Image super-resolution using dense skip connections. In Proceedings of the IEEE International Conference on Computer Vision, Venezia, Italy, 22–29 October 2017; pp. 4799–4807. [Google Scholar]
- Zhang, Y.; Tian, Y.; Kong, Y.; Zhong, B.; Fu, Y. Residual dense network for image super-resolution. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 2472–2481. [Google Scholar]
- Tai, Y.; Yang, J.; Liu, X.; Xu, C. Memnet: A persistent memory network for image restoration. In Proceedings of the IEEE International Conference on Computer Vision, Venezia, Italy, 22–29 October 2017; pp. 4539–4547. [Google Scholar]
- Ahn, N.; Kang, B.; Sohn, K.-A. Fast, accurate, and lightweight super-resolution with cascading residual network. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 252–268. [Google Scholar]
- Wang, X.; Yu, K.; Wu, S.; Gu, J.; Liu, Y.; Dong, C.; Qiao, Y.; Change Loy, C. Esrgan: Enhanced super-resolution generative adversarial networks. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018. [Google Scholar]
- Haris, M.; Shakhnarovich, G.; Ukita, N. Deep back-projection networks for super-resolution. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 1664–1673. [Google Scholar]
- Sajjadi, M.S.; Vemulapalli, R.; Brown, M. Frame-recurrent video super-resolution. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 6626–6634. [Google Scholar]
- Huang, Y.; Wang, W.; Wang, L. Bidirectional recurrent convolutional networks for multi-frame super-resolution. In Proceedings of the Advances in Neural Information Processing Systems, Montréal, QC, Canada, 7–12 December 2015; pp. 235–243. [Google Scholar]
- Huang, Y.; Wang, W.; Wang, L. Video super-resolution via bidirectional recurrent convolutional networks. IEEE Trans. on pattern Anal. Mach. Intell. 2017, 40, 1015–1028. [Google Scholar] [CrossRef] [PubMed]
- Guo, J.; Chao, H. Building an end-to-end spatial-temporal convolutional network for video super-resolution. In Proceedings of the Thirty-First AAAI Conference on Artificial Intelligence, San Francisco, CA, USA, 4–10 February 2017. [Google Scholar]
- Liao, Q.; Poggio, T. Bridging the gaps between residual learning, recurrent neural networks and visual cortex. arXiv 2016, arXiv:1604.03640. Available online: https://arxiv.org/abs/1604.03640 (accessed on 13 April 2016).
- Chen, Y.; Jin, X.; Kang, B.; Feng, J.; Yan, S. Sharing Residual Units Through Collective Tensor Factorization To Improve Deep Neural Networks. In Proceedings of the Twenty-Seventh International Joint Conference on Artificial Intelligence (IJCAI-18), Stockholm, Sweden, 13–19 July 2018; pp. 635–641. [Google Scholar]
- Han, W.; Chang, S.; Liu, D.; Yu, M.; Witbrock, M.; Huang, T.S. Image super-resolution via dual-state recurrent networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 1654–1663. [Google Scholar]
- Hua, Y.; Mou, L.; Zhu, X.X. Recurrently exploring class-wise attention in a hybrid convolutional and bidirectional LSTM network for multi-label aerial image classification. ISPRS J. Photogramm. Remote Sens. 2019, 149, 188–199. [Google Scholar] [CrossRef]
- Liu, Q.; Zhou, F.; Hang, R.; Yuan, X. Bidirectional-convolutional LSTM based spectral-spatial feature learning for hyperspectral image classification. Remote Sens. 2017, 9, 1330. [Google Scholar]
- Mou, L.; Bruzzone, L.; Zhu, X.X. Learning spectral-spatial-temporal features via a recurrent convolutional neural network for change detection in multispectral imagery. IEEE Trans. Geosci. Remote Sens. 2018, 57, 924–935. [Google Scholar] [CrossRef]
- Seydgar, M.; Alizadeh Naeini, A.; Zhang, M.; Li, W.; Satari, M. 3-D Convolution-Recurrent Networks for Spectral-Spatial Classification of Hyperspectral Images. Remote Sens. 2019, 11, 883. [Google Scholar] [CrossRef]
- Mou, L.; Ghamisi, P.; Zhu, X.X. Deep recurrent neural networks for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2017, 55, 3639–3655. [Google Scholar] [CrossRef]
- Liebel, L.; Körner, M. Single-image super resolution for multispectral remote sensing data using convolutional neural networks. ISPRS-International Archives of the Photogrammetry. Remote Sens. Spat. Inf. Sci. 2016, 41, 883–890. [Google Scholar]
- Mundhenk, T.N.; Konjevod, G.; Sakla, W.A.; Boakye, K. A large contextual dataset for classification, detection and counting of cars with deep learning. In Proceedings of the European Conference on Computer Vision, Amsterdam, The Netherlands, 8–16 October 2016; pp. 785–800. [Google Scholar]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef] [PubMed]
- Xingjian, S.; Chen, Z.; Wang, H.; Yeung, D.-Y.; Wong, W.-K.; Woo, W.-c. Convolutional LSTM network: A machine learning approach for precipitation nowcasting. In Proceedings of the Advances in Neural Information Processing Systems, Montréal, QC, Canada, 7–12 December 2015; pp. 802–810. [Google Scholar]
- Hanson, A.; PNVR, K.; Krishnagopal, S.; Davis, L. Bidirectional Convolutional LSTM for the Detection of Violence in Videos. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018. [Google Scholar]
- BCLSR. Available online: https://github.com/ChangYunPeng/BCLSR.git (accessed on 25 June 2019).
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Yang, J.; Zhao, Y.; Yi, C.; Chan, J.C.-W. No-reference hyperspectral image quality assessment via quality-sensitive features learning. Remote Sens. 2017, 9, 305. [Google Scholar] [CrossRef]
- Mittal, A.; Soundararajan, R.; Bovik, A.C. Making a “completely blind” image quality analyzer. IEEE Signal Process. Lett. 2012, 20, 209–212. [Google Scholar] [CrossRef]
- Mittal, A.; Moorthy, A.K.; Bovik, A.C. No-reference image quality assessment in the spatial domain. IEEE Trans. Image Process. 2012, 21, 4695–4708. [Google Scholar] [CrossRef] [PubMed]
- Carranza-García, M.; García-Gutiérrez, J.; Riquelme, J.C. A Framework for Evaluating Land Use and Land Cover Classification Using Convolutional Neural Networks. Remote Sens. 2019, 11, 274. [Google Scholar] [CrossRef]







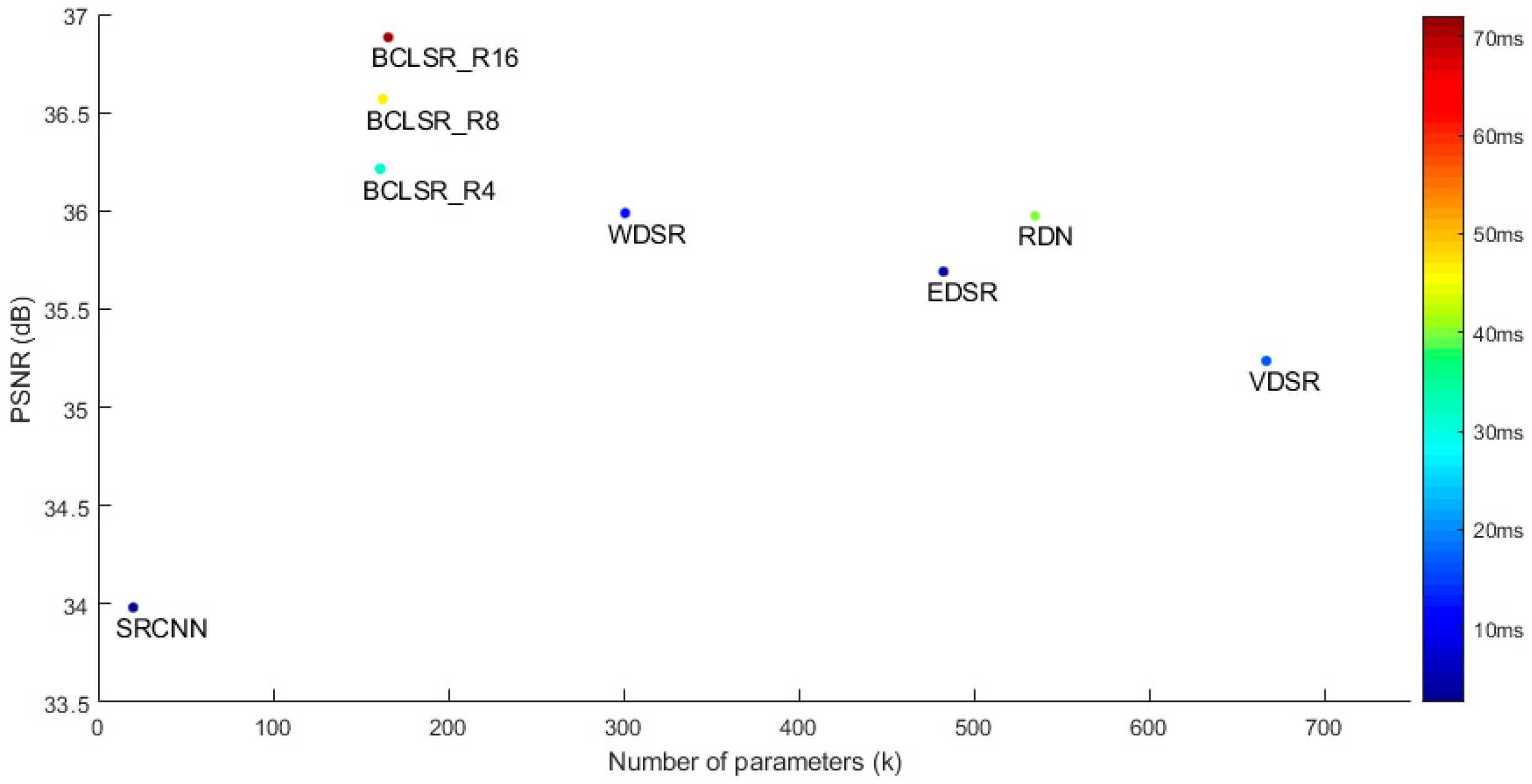

| Recursion | PSNR (dB) | SSIM | Processing Time (s) |
|---|---|---|---|
| 2 | 35.9383 | 0.9621 | 0.0193 |
| 4 | 36.2135 | 0.9632 | 0.0322 |
| 8 | 36.5686 | 0.9641 | 0.0469 |
| 16 | 36.8825 | 0.9650 | 0.0721 |
| 32 | 37.0531 | 0.9652 | 0.1398 |
| Fusion Strategy | PSNR (dB) | SSIM |
|---|---|---|
| Without fusion | 35.9637 | 0.9571 |
| Add | 35.9522 | 0.9565 |
| Concate | 36.0312 | 0.9573 |
| BiConvLSTM | 36.2135 | 0.9632 |
| Dataset | Scale | Bicubic | SRCNN [15] | VDSR [16] | EDSR [17] | WDSR [18] | RDN [29] | Ours |
|---|---|---|---|---|---|---|---|---|
| multi | ×2 | 22.3621/0.7298 | 24.6636/0.8524 | 25.7425/0.8541 | 26.2432/0.8576 | 26.9592/0.8654 | 27.0114/0.8661 | 28.0520/0.8794 |
| ×3 | 21.9478/0.7148 | 24.1481/0.8361 | 24.8528/0.8436 | 25.6459/0.8493 | 26.3841/0.8567 | 26.3419/0.8589 | 27.1440/0.8633 | |
| ×4 | 21.6421/0.7194 | 23.7349/0.8219 | 24.1731/0.8368 | 24.5481/0.8419 | 25.1729/0.8485 | 25.1691/0.8490 | 25.9240/0.8538 | |
| pan | ×2 | 23.4583/0.7605 | 26.8830/0.8523 | 27.8478/0.8624 | 27.9691/0.8731 | 28.5572/0.8874 | 28.5426/0.8852 | 29.4159/0.8925 |
| ×2 | 22.9761/0.7384 | 26.2414/0.8142 | 26.8993/0.8632 | 27.2823/0.8659 | 27.9147/0.8745 | 28.0278/0.8751 | 28.9123/0.8798 | |
| ×4 | 21.7494/0.7129 | 25.6932/0.7942 | 25.7667/0.8223 | 25.8215/0.8434 | 26.5937/0.8512 | 26.6042/0.8551 | 26.9434/0.8672 | |
| COWC | ×2 | 30.5916/0.9154 | 33.9821/0.9521 | 35.2361/0.9598 | 35.6907/0.9623 | 35.9886/0.9625 | 35.9746/0.9636 | 36.8825/0.9650 |
| ×3 | 29.1484/0.8241 | 31.4164/0.8542 | 31.9672/0.8764 | 32.4897/0.8954 | 32.9545/0.9078 | 33.0746/0.9103 | 33.9843/0.9286 | |
| ×4 | 28.8461/0.7987 | 30.1873/0.8073 | 31.0381/0.8531 | 31.5901/0.8862 | 31.6792/0.8891 | 31.7273/0.8934 | 32.5528/0.8952 |
| Dataset | Scale | Bicubic | SRCNN [15] | VDSR [16] | EDSR [17] | WDSR [18] | RDN [29] | Ours |
|---|---|---|---|---|---|---|---|---|
| multi | ×2 | 49.0127 | 45.9521 | 42.8894 | 40.0320 | 38.5421 | 37.2690 | 35.5900 |
| ×3 | 53.1440 | 50.1416 | 49.7040 | 48.9662 | 45.7588 | 44.8927 | 43.2459 | |
| ×4 | 61.3699 | 58.9284 | 55.0017 | 53.2863 | 51.9466 | 50.6996 | 49.3648 | |
| pan | ×2 | 46.7117 | 42.2646 | 40.4815 | 39.7721 | 34.9061 | 35.9469 | 32.6524 |
| ×3 | 55.6381 | 52.46823 | 49.6719 | 47.2730 | 44.8361 | 43.3989 | 41.6488 | |
| ×4 | 59.3537 | 56.7083 | 53.6317 | 52.3405 | 49.1415 | 48.4533 | 47.1435 | |
| COWC | ×2 | 38.2804 | 35.7388 | 34.8030 | 32.6975 | 30.9478 | 29.4001 | 28.1540 |
| ×3 | 46.5723 | 45.5027 | 41.3250 | 40.9971 | 35.7353 | 36.1159 | 34.1814 | |
| ×4 | 52.1886 | 48.4841 | 45.7582 | 43.9544 | 41.6560 | 40.3677 | 38.3023 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chang, Y.; Luo, B. Bidirectional Convolutional LSTM Neural Network for Remote Sensing Image Super-Resolution. Remote Sens. 2019, 11, 2333. https://doi.org/10.3390/rs11202333
Chang Y, Luo B. Bidirectional Convolutional LSTM Neural Network for Remote Sensing Image Super-Resolution. Remote Sensing. 2019; 11(20):2333. https://doi.org/10.3390/rs11202333
Chicago/Turabian StyleChang, Yunpeng, and Bin Luo. 2019. "Bidirectional Convolutional LSTM Neural Network for Remote Sensing Image Super-Resolution" Remote Sensing 11, no. 20: 2333. https://doi.org/10.3390/rs11202333
APA StyleChang, Y., & Luo, B. (2019). Bidirectional Convolutional LSTM Neural Network for Remote Sensing Image Super-Resolution. Remote Sensing, 11(20), 2333. https://doi.org/10.3390/rs11202333