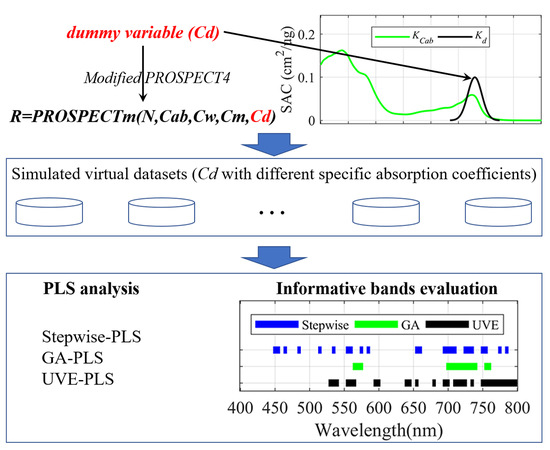
Evaluation of Informative Bands Used in Different PLS Regressions for Estimating Leaf Biochemical Contents from Hyperspectral Reflectance
Abstract
1. Introduction
2. Materials and Methods
2.1. Experimental Designs and Data for Calibration and Validation
2.1.1. PROSPECT-4 Modification
2.1.2. Experimental Design and Database Generation
2.2. PLS Analysis
2.2.1. Stepwise-PLS
2.2.2. GA-PLS
- Forming an initial population of variable sets randomly;
- Fitting a PLS regression model to each variable set, and then evaluating the performance with leave-one-out cross-validation;
- Selecting a collection of variable sets with higher performance to survive until the next “generation”;
- Generating new variable sets by crossover (50% probability in this study) and mutation (1% probability in this study) for each variable;
- Using the surviving and modified variable sets as inputs in step 2, and repeating steps 2–5 for a preset number of times (200 in this study).
2.2.3. Uninformative Variable Elimination with PLS (UVE-PLS)
2.2.4. Evaluation of Different PLSR Models
3. Results
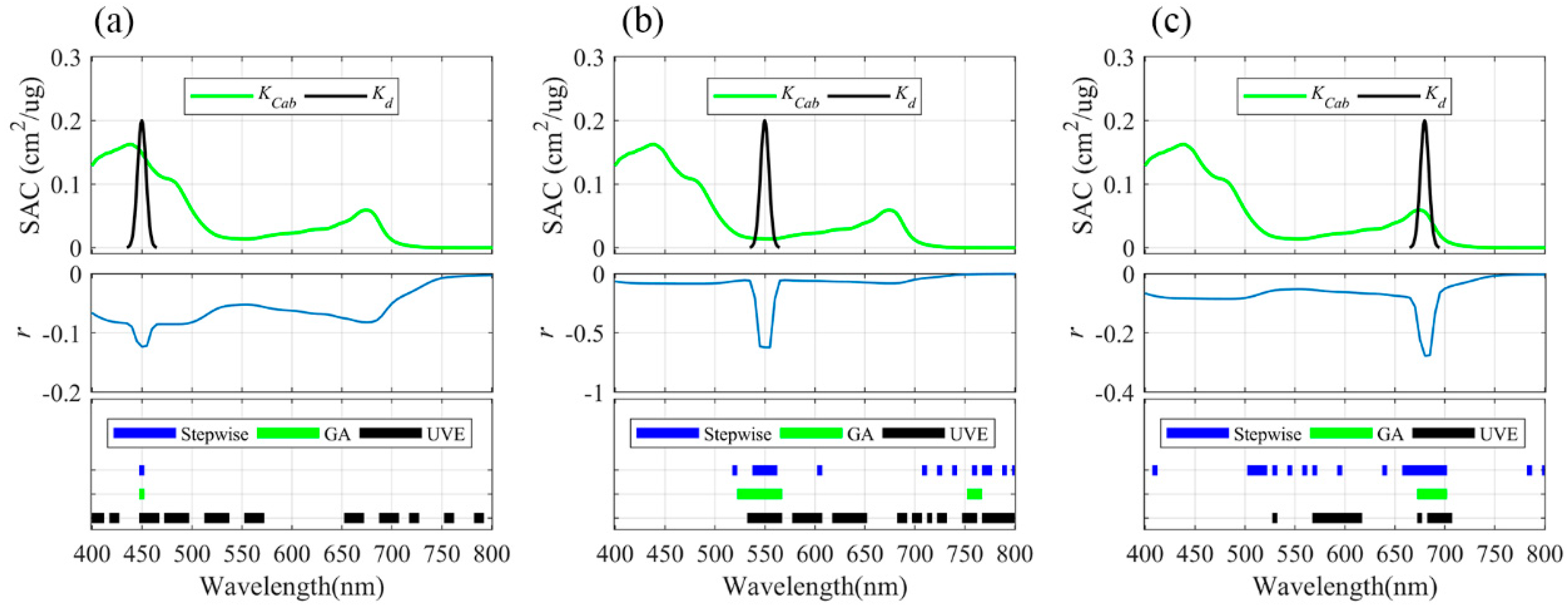
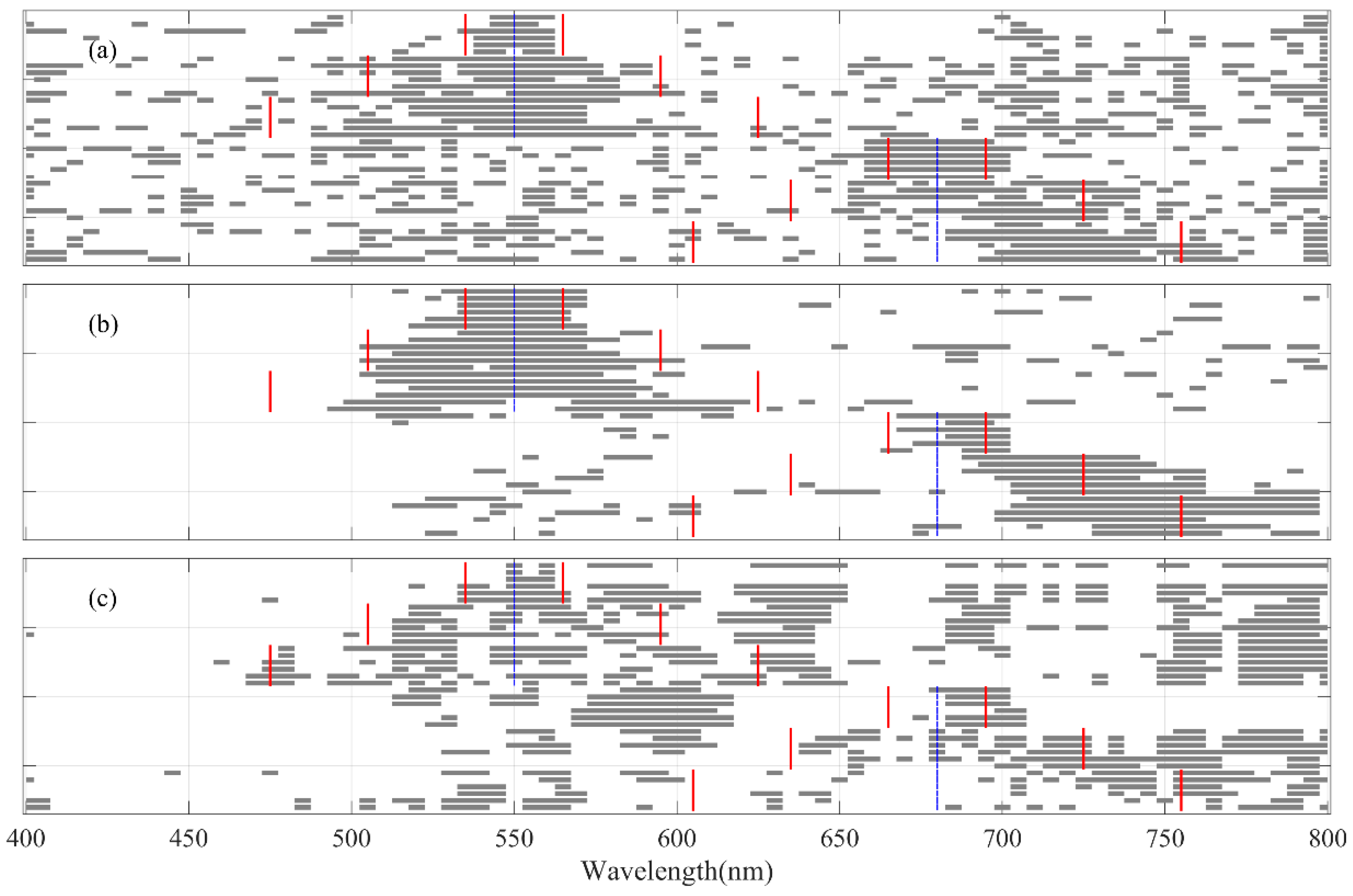
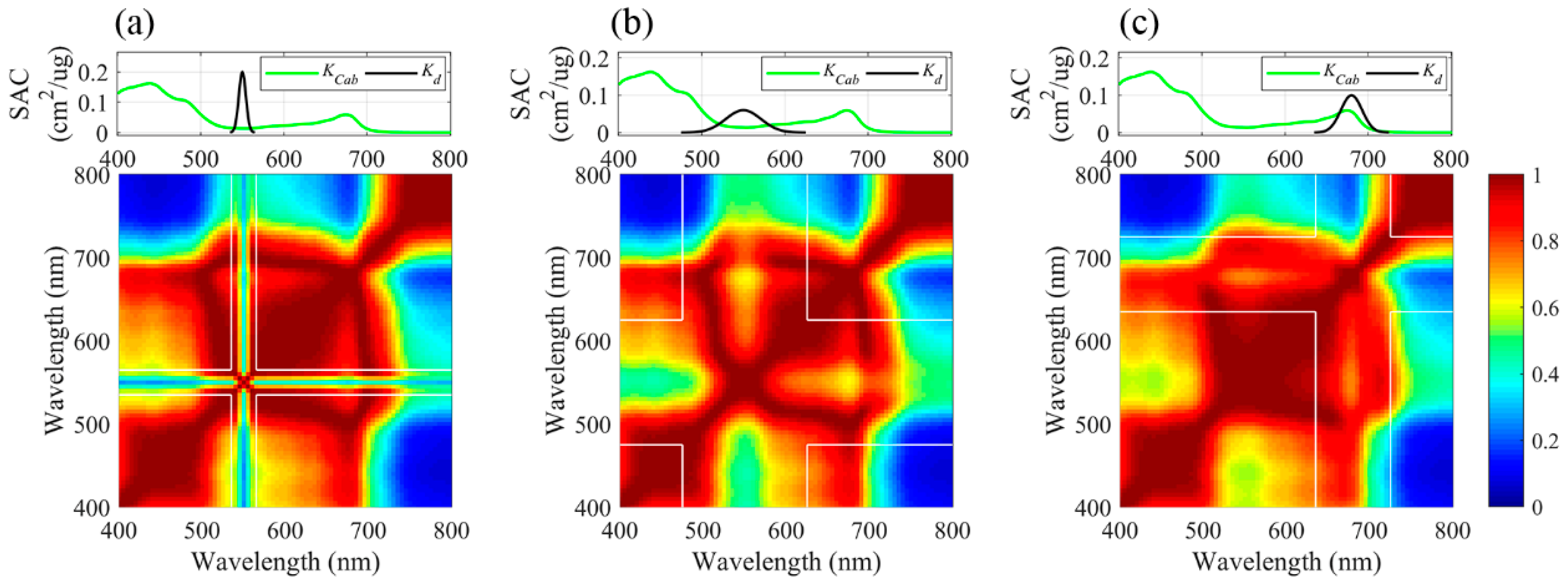
3.1. Informative Bands Selected for PLSR Models under Different Absorption Peak Locations
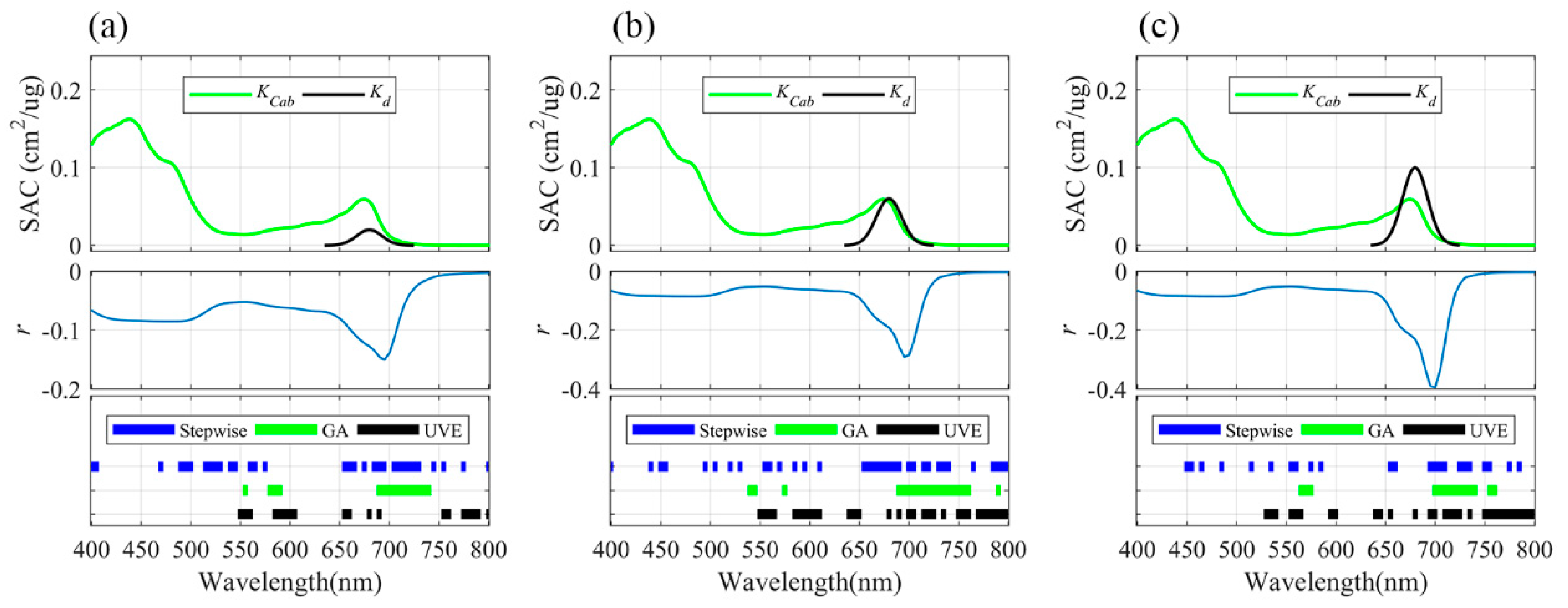
3.2. Informative Bands Selected for PLSR Models under Different Absorption Intensities
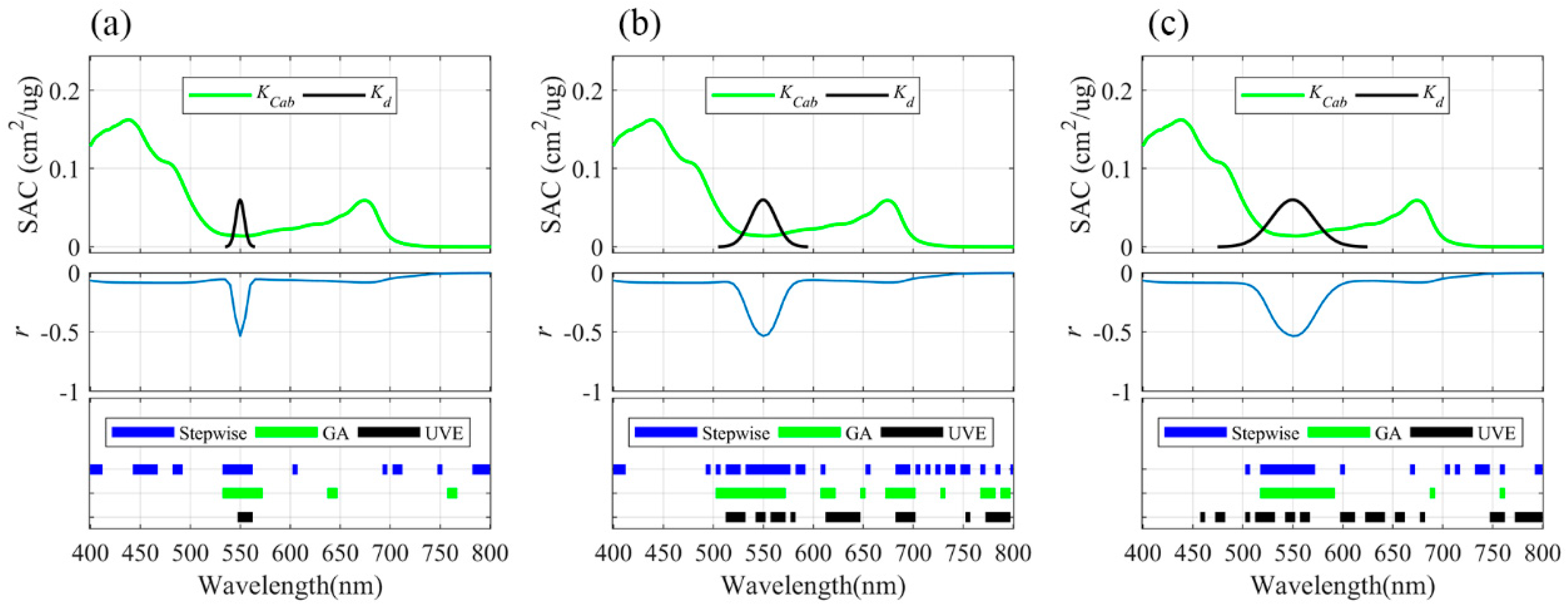
3.3. Informative Bands Selected for PLSR Models under Different Absorption Half-Widths
3.4. Statistical Criteria of Different PLSR Models for Estimating Cd
4. Discussion
4.1. Collinearity among Reflectance Values
4.2. Informative Bands Selected by Different Methods for Leaf Biochemical Parameters
4.3. Performance of PLS Models for Field-Measured Datasets
4.4. Advantages and Disadvantages of PLS Models for estimating Leaf Biochemical Contents
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Verrelst, J.; Camps-Valls, G.; Muñoz-Marí, J.; Rivera, J.P.; Veroustraete, F.; Clevers, J.G.P.W.; Moreno, J. Optical remote sensing and the retrieval of terrestrial vegetation bio-geophysical properties—A review. ISPRS J. Photogramm. Remote Sens. 2015, 108, 273–290. [Google Scholar] [CrossRef]
- Kawamura, K.; Watanabe, N.; Sakanoue, S.; Lee, H.J.; Inoue, Y.; Odagawa, S. Testing genetic algorithm as a tool to select relevant wavebands from field hyperspectral data for estimating pasture mass and quality in a mixed sown pasture using partial least squares regression. Grassl. Sci. 2010, 56, 205–216. [Google Scholar] [CrossRef]
- Kira, O.; Linker, R.; Gitelson, A. Non-destructive estimation of foliar chlorophyll and carotenoid contents: Focus on informative spectral bands. Int. J. Appl. Earth Obs. Geoinf. 2015, 38, 251–260. [Google Scholar] [CrossRef]
- Yi, Q.; Jiapaer, G.; Chen, J.; Bao, A.; Wang, F. Different units of measurement of carotenoids estimation in cotton using hyperspectral indices and partial least square regression. ISPRS J. Photogramm. Remote Sens. 2014, 91, 72–84. [Google Scholar] [CrossRef]
- Hansen, P.M.; Schjoerring, J.K. Reflectance measurement of canopy biomass and nitrogen status in wheat crops using normalized difference vegetation indices and partial least squares regression. Remote Sens. Environ. 2003, 86, 542–553. [Google Scholar] [CrossRef]
- Féret, J.-B.; François, C.; Gitelson, A.; Asner, G.P.; Barry, K.M.; Panigada, C.; Richardson, A.D.; Jacquemoud, S. Optimizing spectral indices and chemometric analysis of leaf chemical properties using radiative transfer modeling. Remote Sens. Environ. 2011, 115, 2742–2750. [Google Scholar] [CrossRef]
- Yu, K.; Lenz-Wiedemann, V.; Chen, X.; Bareth, G. Estimating leaf chlorophyll of barley at different growth stages using spectral indices to reduce soil background and canopy structure effects. ISPRS J. Photogramm. Remote Sens. 2014, 97, 58–77. [Google Scholar] [CrossRef]
- Yu, K.; Gnyp, M.L.; Gao, L.; Miao, Y.; Chen, X.; Bareth, G. Estimate Leaf Chlorophyll of Rice Using Reflectance Indices and Partial Least Squares. Photogramm. Fernerkund. Geoinf. 2015, 2015, 45–54. [Google Scholar] [CrossRef]
- Yu, K.-Q.; Zhao, Y.-R.; Zhu, F.-L.; Li, X.-L.; He, Y. Mapping of Chlorophyll and SPAD Distribution in Pepper Leaves During Leaf Senescence Using Visible and Near-Infrared Hyperspectral Imaging. Trans. ASABE 2016, 59, 13. [Google Scholar] [CrossRef]
- Pan, W.-J.; Wang, X.; Deng, Y.-R.; Li, J.-H.; Chen, W.; Chiang, J.Y.; Yang, J.-B.; Zheng, L. Nondestructive and intuitive determination of circadian chlorophyll rhythms in soybean leaves using multispectral imaging. Sci. Rep. 2015, 5, 11108. [Google Scholar] [CrossRef]
- Huang, Z.; Turner, B.J.; Dury, S.J.; Wallis, I.R.; Foley, W.J. Estimating foliage nitrogen concentration from HYMAP data using continuum removal analysis. Remote Sens. Environ. 2004, 93, 18–29. [Google Scholar] [CrossRef]
- Darvishzadeh, R.; Skidmore, A.; Schlerf, M.; Atzberger, C.; Corsi, F.; Cho, M. LAI and chlorophyll estimation for a heterogeneous grassland using hyperspectral measurements. ISPRS J. Photogramm. Remote Sens. 2008, 63, 409–426. [Google Scholar] [CrossRef]
- Atzberger, C.; Guérif, M.; Baret, F.; Werner, W. Comparative analysis of three chemometric techniques for the spectroradiometric assessment of canopy chlorophyll content in winter wheat. Comput. Electron. Agric. 2010, 73, 165–173. [Google Scholar] [CrossRef]
- Ryu, C.; Suguri, M.; Umeda, M. Multivariate analysis of nitrogen content for rice at the heading stage using reflectance of airborne hyperspectral remote sensing. Field Crop. Res. 2011, 122, 214–224. [Google Scholar] [CrossRef]
- Fu, Y.; Yang, G.; Wang, J.; Song, X.; Feng, H. Winter wheat biomass estimation based on spectral indices, band depth analysis and partial least squares regression using hyperspectral measurements. Comput. Electron. Agric. 2014, 100, 51–59. [Google Scholar] [CrossRef]
- Huang, X.; Xu, Q.-S.; Liang, Y.-Z. PLS regression based on sure independence screening for multivariate calibration. Anal. Methods 2012, 4, 2815–2821. [Google Scholar] [CrossRef]
- Wu, Q.; Wang, J.; Wang, C.; Xu, T. Study on the optimal algorithm prediction of corn leaf component information based on hyperspectral imaging. Infrared Phys. Technol. 2016, 78, 66–71. [Google Scholar] [CrossRef]
- Chen, H.; Chen, T.; Zhang, Z.; Liu, G. Variable Selection Using Adaptive Band Clustering and Physarum Network. Algorithms 2017, 10, 73. [Google Scholar] [CrossRef]
- Wang, Z.; Kawamura, K.; Sakuno, Y.; Fan, X.; Gong, Z.; Lim, J. Retrieval of Chlorophyll-a and Total Suspended Solids Using Iterative Stepwise Elimination Partial Least Squares (ISE-PLS) Regression Based on Field Hyperspectral Measurements in Irrigation Ponds in Higashihiroshima, Japan. Remote Sens. 2017, 9, 264. [Google Scholar] [CrossRef]
- Wang, Z.X.; He, Q.; Wang, J. Comparison of different variable selection methods for partial least squares soft sensor development. In Proceedings of the 2014 American Control Conference, Portland, OR, USA, 4–6 June 2014; pp. 3116–3121. [Google Scholar]
- De Groot, P.J.; Swierenga, H.; Postma, G.J.; Melssen, W.J.; Buydens, L.M.C. Effect on the Partial Least-Squares Prediction of Yarn Properties Combining Raman and Infrared Measurements and Applying Wavelength Selection. Appl. Spectrosc. 2003, 57, 642–648. [Google Scholar] [CrossRef]
- Mehmood, T.; Liland, K.H.; Snipen, L.; Sæbø, S. A review of variable selection methods in Partial Least Squares Regression. Chemom. Intell. Lab. Syst. 2012, 118, 62–69. [Google Scholar] [CrossRef]
- Centner, V.; Massart, D.-L.; de Noord, O.E.; de Jong, S.; Vandeginste, B.M.; Sterna, C. Elimination of Uninformative Variables for Multivariate Calibration. Anal. Chem. 1996, 68, 3851–3858. [Google Scholar] [CrossRef] [PubMed]
- Cai, W.; Li, Y.; Shao, X. A variable selection method based on uninformative variable elimination for multivariate calibration of near-infrared spectra. Chemom. Intell. Lab. Syst. 2008, 90, 188–194. [Google Scholar] [CrossRef]
- Fung, T.; Yan Ma, H.F.; Siu, W.L. Band Selection Using Hyperspectral Data of Subtropical Tree Species. Geocarto Int. 2003, 18, 3–11. [Google Scholar] [CrossRef]
- Schmitt, N.; Ployhart, R.E. Estimates of cross-validity for stepwise regression and with predictor selection. J. Appl. Psychol. 1999, 84, 50. [Google Scholar] [CrossRef]
- Leardi, R.; Boggia, R.; Terrile, M. Genetic algorithms as a strategy for feature selection. J. Chemom. 1992, 6, 267–281. [Google Scholar] [CrossRef]
- Jin, J.; Wang, Q. Selection of informative spectral bands for PLS models to estimate foliar chlorophyll content using hyperspectral reflectance. IEEE Trans. Geosci. Remote Sens. 2018, 1–9. [Google Scholar] [CrossRef]
- Feret, J.-B.; François, C.; Asner, G.P.; Gitelson, A.A.; Martin, R.E.; Bidel, L.P.R.; Ustin, S.L.; le Maire, G.; Jacquemoud, S. PROSPECT-4 and 5: Advances in the leaf optical properties model separating photosynthetic pigments. Remote Sens. Environ. 2008, 112, 3030–3043. [Google Scholar] [CrossRef]
- Le Maire, G.; François, C.; Soudani, K.; Berveiller, D.; Pontailler, J.-Y.; Bréda, N.; Genet, H.; Davi, H.; Dufrêne, E. Calibration and validation of hyperspectral indices for the estimation of broadleaved forest leaf chlorophyll content, leaf mass per area, leaf area index and leaf canopy biomass. Remote Sens. Environ. 2008, 112, 3846–3864. [Google Scholar] [CrossRef]
- Le Maire, G.; François, C.; Dufrêne, E. Towards universal broad leaf chlorophyll indices using PROSPECT simulated database and hyperspectral reflectance measurements. Remote Sens. Environ. 2004, 89, 1–28. [Google Scholar] [CrossRef]
- Wang, Q.; Li, P. Identification of robust hyperspectral indices on forest leaf water content using PROSPECT simulated dataset and field reflectance measurements. Hydrol. Process. 2012, 26, 1230–1241. [Google Scholar] [CrossRef]
- Li, P.; Wang, Q. Retrieval of Leaf Biochemical Parameters Using PROSPECT Inversion: A New Approach for Alleviating Ill-Posed Problems. IEEE Trans. Geosci. Remote Sens. 2011, 49, 2499–2506. [Google Scholar] [CrossRef]
- Qiu, F.; Chen, J.M.; Ju, W.; Wang, J.; Zhang, Q.; Fang, M. Improving the PROSPECT Model to Consider Anisotropic Scattering of Leaf Internal Materials and Its Use for Retrieving Leaf Biomass in Fresh Leaves. IEEE Trans. Geosci. Remote Sens. 2018, 1–18. [Google Scholar] [CrossRef]
- Jin, J.; Wang, Q. Informative bands used by efficient hyperspectral indices to predict leaf biochemical contents are determined by their relative absorptions. Int. J. Appl. Earth Obs. Geoinf. 2018, 73, 616–626. [Google Scholar] [CrossRef]
- Jacquemoud, S.; Baret, F. PROSPECT: A model of leaf optical properties spectra. Remote Sens. Environ. 1990, 34, 75–91. [Google Scholar] [CrossRef]
- Tsai, F.; Philpot, W. Derivative Analysis of Hyperspectral Data. Remote Sens. Environ. 1998, 66, 41–51. [Google Scholar] [CrossRef]
- Eng, D.; Baranoski, G.V.G. The Application of Photoacoustic Absorption Spectral Data to the Modeling of Leaf Optical Properties in the Visible Range. IEEE Trans. Geosci. Remote Sens. 2007, 45, 4077–4086. [Google Scholar] [CrossRef]
- Hosgood, B.; Jacquemoud, S.; Andreoli, G.; Verdebout, J.; Pedrini, G.; Schmuck, G. Leaf Optical Properties Experiment 93 (LOPEX93); European Commission—Joint Research Centre EUR 16095 EN: Ispra, Italy, 1994; p. 20. [Google Scholar]
- Anatoly, G.; Alexei, S. Generic Algorithms for Estimating Foliar Pigment Content. Geophys. Res. Lett. 2017, 44, 9293–9298. [Google Scholar] [CrossRef]
- Dian, Y.; Le, Y.; Fang, S.; Xu, Y.; Yao, C.; Liu, G. Influence of Spectral Bandwidth and Position on Chlorophyll Content Retrieval at Leaf and Canopy Levels. J. Indian Soc. Remote Sens. 2016, 44, 583–593. [Google Scholar] [CrossRef]
- Ustin, S.L.; Gitelson, A.A.; Jacquemoud, S.; Schaepman, M.; Asner, G.P.; Gamon, J.A.; Zarco-Tejada, P. Retrieval of foliar information about plant pigment systems from high resolution spectroscopy. Remote Sens. Environ. 2009, 113, S67–S77. [Google Scholar] [CrossRef]
- Main, R.; Cho, M.A.; Mathieu, R.; O’Kennedy, M.M.; Ramoelo, A.; Koch, S. An investigation into robust spectral indices for leaf chlorophyll estimation. ISPRS J. Photogramm. Remote Sens. 2011, 66, 751–761. [Google Scholar] [CrossRef]
- Norgaard, L.; Saudland, A.; Wagner, J.; Nielsen, J.P.; Munck, L.; Engelsen, S.B. Interval Partial Least-Squares Regression (iPLS): A Comparative Chemometric Study with an Example from Near-Infrared Spectroscopy. Appl. Spectrosc. 2000, 54, 413–419. [Google Scholar] [CrossRef]
- Dorigo, W.A.; Zurita-Milla, R.; de Wit, A.J.W.; Brazile, J.; Singh, R.; Schaepman, M.E. A review on reflective remote sensing and data assimilation techniques for enhanced agroecosystem modeling. Int. J. Appl. Earth Obs. Geoinf. 2007, 9, 165–193. [Google Scholar] [CrossRef]
- Andersen, C.M.; Bro, R. Variable selection in regression—A tutorial. J. Chemom. 2010, 24, 728–737. [Google Scholar] [CrossRef]
- Draper, N.R.; Smith, H. Applied Regression Analysis; John Wiley & Sons: Hoboken, NJ, USA, 1998. [Google Scholar]
- Yu, T.; Yu, G.; Li, P.-Y.; Wang, L.J.S. Citation impact prediction for scientific papers using stepwise regression analysis. Scientometrics 2014, 101, 1233–1252. [Google Scholar] [CrossRef]
- Lu, D.M.; Song, K.S.; Li, L.; Liu, D.W.; Li, S.H.; Wang, Y.D.; Wang, Z.M.; Xu, J.P.; Du, J.; Jia, M.M. Training a GA-PLS Model for Chl-a Concentration Estimation over Inland Lake in Northeast China. Procedia Environ. Sci. 2010, 2, 842–851. [Google Scholar] [CrossRef]
- Leardi, R. Application of genetic algorithm–PLS for feature selection in spectral data sets. J. Chemom. 2000, 14, 643–655. [Google Scholar] [CrossRef]
- Leardi, R.; Lupiáñez González, A. Genetic algorithms applied to feature selection in PLS regression: How and when to use them. Chemom. Intell. Lab. Syst. 1998, 41, 195–207. [Google Scholar] [CrossRef]
- Hasegawa, K.; Miyashita, Y.; Funatsu, K. GA Strategy for Variable Selection in QSAR Studies: GA-Based PLS Analysis of Calcium Channel Antagonists. J. Chem. Inf. Comput. Sci. 1997, 37, 306–310. [Google Scholar] [CrossRef]
- McQuarrie, A.D.R.; Tsai, C.-L. Regression and Time Series Model Selection; World Scientific: Singapore, 1998. [Google Scholar]
- Hurvich, C.M.; Tsai, C.-L. Regression and Time Series Model Selection in Small Samples. Biometrika 1989, 76, 297–307. [Google Scholar] [CrossRef]
- Wold, S.; Ruhe, A.; Wold, H.; Dunn, W.J., III. The Collinearity Problem in Linear Regression. The Partial Least Squares (PLS) Approach to Generalized Inverses. SIAM J. Sci. Stat. Comput. 1984, 5, 735–743. [Google Scholar] [CrossRef]
- Chong, I.-G.; Jun, C.-H. Performance of some variable selection methods when multicollinearity is present. Chemom. Intell. Lab. Syst. 2005, 78, 103–112. [Google Scholar] [CrossRef]
- Wang, Y.; Huang, S.; Liu, D.; Wang, B. Research Advance on Band Selection-Based Dimension Reduction of Hyperspectral Remote Sensing Images. In Proceedings of the 2012 2nd International Conference on Remote Sensing, Environment and Transportation Engineering, Nanjing, China, 1–3 June 2012; pp. 1–4. [Google Scholar]
- Ting, J.-A.; D’Souza, A.; Vijayakumar, S.; Schaal, S. Efficient Learning and Feature Selection in High-Dimensional Regression. Neural Comput. 2010, 22, 831–886. [Google Scholar] [CrossRef] [PubMed]
- Tibshirani, R. Regression Shrinkage and Selection via the Lasso. J. R. Stat. Soc. Ser. B (Methodol.) 1996, 58, 267–288. [Google Scholar] [CrossRef]
- Kazarlis, S.A.; Bakirtzis, A.G.; Petridis, V. A genetic algorithm solution to the unit commitment problem. IEEE Trans. Power Syst. 1996, 11, 83–92. [Google Scholar] [CrossRef]
- Yang, J.; Honavar, V. Feature Subset Selection Using a Genetic Algorithm. In Feature Extraction, Construction and Selection: A Data Mining Perspective; Liu, H., Motoda, H., Eds.; Springer: Boston, MA, USA, 1998; pp. 117–136. [Google Scholar]
- Imanishi, J.; Sugimoto, K.; Morimoto, Y. Detecting drought status and LAI of two Quercus species canopies using derivative spectra. Comput. Electron. Agric. 2004, 43, 109–129. [Google Scholar] [CrossRef]
- Brown, A.J.; Sutter, B.; Dunagan, S. The MARTE VNIR Imaging Spectrometer Experiment: Design and Analysis. Astrobiology 2008, 8, 1001–1011. [Google Scholar] [CrossRef]
- Brown, A.J.; Hook, S.J.; Baldridge, A.M.; Crowley, J.K.; Bridges, N.T.; Thomson, B.J.; Marion, G.M.; de Souza Filho, C.R.; Bishop, J.L. Hydrothermal formation of Clay-Carbonate alteration assemblages in the Nili Fossae region of Mars. Earth Planet. Sci. Lett. 2010, 297, 174–182. [Google Scholar] [CrossRef]
- Inoue, Y.; Sakaiya, E.; Zhu, Y.; Takahashi, W. Diagnostic mapping of canopy nitrogen content in rice based on hyperspectral measurements. Remote Sens. Environ. 2012, 126, 210–221. [Google Scholar] [CrossRef]
- Hong, S.; Minzan, L.; Yane, Z.; Yong, Z.; Haihua, W. Detection of Corn Chlorophyll Content Using Canopy Spectral Reflectance. Sens. Lett. 2010, 8, 134–139. [Google Scholar] [CrossRef]
| Peak Location | Intensity | Half-Width | Stepwise-PLS | GA-PLS | UVE-PLS | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| NRMSE | R2 | AICc | NRMSE | R2 | AICc | NRMSE | R2 | AICc | |||
| 450 | 0.02 | 10 | 0.35 | 0.02 | 3.88 | 0.35 | 0.01 | 3.90 | 0.34 | 0.11 | 3.85 |
| 450 | 0.02 | 30 | 0.35 | 0.04 | 3.88 | 0.35 | 0.01 | 3.89 | 0.33 | 0.12 | 3.96 |
| 450 | 0.02 | 50 | 0.35 | 0.01 | 3.89 | 0.28 | 0.39 | 3.43 | 0.22 | 0.61 | 3.00 |
| 450 | 0.04 | 10 | 0.35 | 0.02 | 3.88 | 0.35 | 0.01 | 3.91 | 0.34 | 0.07 | 3.90 |
| 450 | 0.04 | 30 | 0.35 | 0.02 | 3.88 | 0.35 | 0.01 | 3.89 | 0.34 | 0.11 | 3.85 |
| 450 | 0.04 | 50 | 0.34 | 0.11 | 3.80 | 0.18 | 0.75 | 2.54 | 0.08 | 0.95 | 0.93 |
| 450 | 0.06 | 10 | 0.35 | 0.02 | 3.88 | 0.36 | 0.01 | 3.90 | 0.35 | 0.03 | 3.89 |
| 450 | 0.06 | 30 | 0.35 | 0.03 | 3.87 | 0.35 | 0.01 | 3.89 | 0.32 | 0.19 | 3.74 |
| 450 | 0.06 | 50 | 0.33 | 0.15 | 3.75 | 0.08 | 0.95 | 0.91 | 0.07 | 0.96 | 0.84 |
| 450 | 0.10 | 10 | 0.35 | 0.01 | 3.89 | 0.36 | 0.01 | 3.90 | 0.34 | 0.06 | 3.90 |
| 450 | 0.10 | 30 | 0.35 | 0.03 | 3.87 | 0.35 | 0.03 | 3.88 | 0.34 | 0.11 | 3.94 |
| 450 | 0.10 | 50 | 0.15 | 0.83 | 2.27 | 0.07 | 0.96 | 0.75 | 0.18 | 0.75 | 2.56 |
| 450 | 0.20 | 10 | 0.35 | 0.02 | 3.88 | 0.35 | 0.02 | 3.88 | 0.34 | 0.06 | 3.99 |
| 450 | 0.20 | 30 | 0.34 | 0.09 | 3.82 | 0.35 | 0.02 | 3.89 | 0.33 | 0.14 | 3.84 |
| 450 | 0.20 | 50 | 0.07 | 0.97 | 0.68 | 0.11 | 0.90 | 1.61 | 0.05 | 0.98 | 0.12 |
| 450 | 0.30 | 10 | 0.34 | 0.08 | 3.83 | 0.35 | 0.01 | 3.88 | 0.35 | 0.03 | 3.99 |
| 450 | 0.30 | 30 | 0.34 | 0.10 | 3.81 | 0.35 | 0.02 | 3.88 | − | − | − |
| 450 | 0.30 | 50 | 0.07 | 0.96 | 0.79 | 0.13 | 0.86 | 1.96 | 0.10 | 0.93 | 1.38 |
| 550 | 0.02 | 10 | 0.10 | 0.92 | 1.42 | 0.06 | 0.97 | 0.54 | 0.18 | 0.74 | 2.66 |
| 550 | 0.02 | 30 | 0.05 | 0.98 | −0.01 | 0.06 | 0.97 | 0.51 | 0.04 | 0.99 | −0.26 |
| 550 | 0.02 | 50 | 0.04 | 0.98 | −0.11 | 0.04 | 0.99 | −0.44 | 0.03 | 0.99 | −0.64 |
| 550 | 0.04 | 10 | 0.09 | 0.94 | 1.17 | 0.07 | 0.96 | 0.68 | 0.22 | 0.63 | 2.92 |
| 550 | 0.04 | 30 | 0.05 | 0.98 | 0.14 | 0.07 | 0.96 | 0.67 | 0.05 | 0.98 | 0.02 |
| 550 | 0.04 | 50 | 0.04 | 0.98 | −0.16 | 0.05 | 0.98 | −0.11 | 0.04 | 0.98 | −0.14 |
| 550 | 0.06 | 10 | 0.06 | 0.97 | 0.42 | 0.07 | 0.96 | 0.78 | 0.22 | 0.63 | 2.92 |
| 550 | 0.06 | 30 | 0.05 | 0.98 | 0.24 | 0.06 | 0.97 | 0.38 | 0.06 | 0.97 | 0.37 |
| 550 | 0.06 | 50 | 0.04 | 0.99 | −0.60 | 0.04 | 0.98 | −0.22 | 0.05 | 0.98 | 0.11 |
| 550 | 0.10 | 10 | 0.07 | 0.96 | 0.78 | 0.08 | 0.95 | 1.01 | 0.10 | 0.92 | 1.50 |
| 550 | 0.10 | 30 | 0.06 | 0.98 | 0.29 | 0.08 | 0.95 | 0.87 | 0.06 | 0.97 | 0.54 |
| 550 | 0.10 | 50 | 0.07 | 0.96 | 0.85 | 0.05 | 0.98 | 0.16 | 0.09 | 0.94 | 1.23 |
| 550 | 0.20 | 10 | 0.08 | 0.94 | 1.09 | 0.09 | 0.93 | 1.26 | 0.08 | 0.95 | 1.14 |
| 550 | 0.20 | 30 | 0.06 | 0.97 | 0.59 | 0.11 | 0.91 | 1.64 | 0.06 | 0.97 | 0.56 |
| 550 | 0.20 | 50 | 0.09 | 0.94 | 1.28 | 0.09 | 0.93 | 1.32 | 0.08 | 0.95 | 1.04 |
| 550 | 0.30 | 10 | 0.10 | 0.92 | 1.43 | 0.09 | 0.93 | 1.24 | 0.08 | 0.94 | 1.14 |
| 550 | 0.30 | 30 | 0.07 | 0.96 | 0.79 | 0.10 | 0.92 | 1.42 | 0.07 | 0.96 | 0.80 |
| 550 | 0.30 | 50 | 0.09 | 0.94 | 1.33 | 0.10 | 0.92 | 1.41 | 0.09 | 0.94 | 1.23 |
| 680 | 0.02 | 10 | 0.12 | 0.88 | 1.80 | 0.20 | 0.69 | 2.79 | 0.13 | 0.86 | 2.01 |
| 680 | 0.02 | 30 | 0.03 | 0.99 | −0.98 | 0.05 | 0.98 | 0.08 | 0.20 | 0.69 | 2.81 |
| 680 | 0.02 | 50 | 0.02 | 1.00 | −2.04 | 0.02 | 1.00 | −1.58 | 0.02 | 1.00 | −1.96 |
| 680 | 0.04 | 10 | 0.15 | 0.82 | 2.35 | 0.28 | 0.39 | 3.41 | 0.15 | 0.83 | 2.21 |
| 680 | 0.04 | 30 | 0.02 | 1.00 | −1.50 | 0.04 | 0.98 | −0.26 | 0.02 | 1.00 | −1.48 |
| 680 | 0.04 | 50 | 0.02 | 1.00 | −1.56 | 0.03 | 0.99 | −1.19 | 0.02 | 1.00 | −2.19 |
| 680 | 0.06 | 10 | 0.10 | 0.93 | 1.40 | 0.20 | 0.70 | 2.74 | 0.15 | 0.82 | 2.27 |
| 680 | 0.06 | 30 | 0.03 | 0.99 | −1.23 | 0.02 | 1.00 | −1.89 | 0.02 | 1.00 | −2.02 |
| 680 | 0.06 | 50 | 0.02 | 1.00 | −1.86 | 0.02 | 1.00 | −1.57 | 0.02 | 1.00 | −1.80 |
| 680 | 0.10 | 10 | 0.13 | 0.87 | 1.94 | 0.20 | 0.69 | 2.74 | 0.35 | 0.02 | 3.92 |
| 680 | 0.10 | 30 | 0.03 | 0.99 | −1.23 | 0.02 | 1.00 | −2.02 | 0.02 | 1.00 | −1.98 |
| 680 | 0.10 | 50 | 0.02 | 1.00 | −1.93 | 0.03 | 0.99 | −1.23 | 0.02 | 1.00 | −2.04 |
| 680 | 0.20 | 10 | 0.08 | 0.95 | 0.91 | 0.26 | 0.48 | 3.26 | 0.13 | 0.87 | 1.91 |
| 680 | 0.20 | 30 | 0.02 | 1.00 | −1.47 | 0.02 | 1.00 | −1.89 | 0.02 | 1.00 | −1.87 |
| 680 | 0.20 | 50 | 0.03 | 0.99 | −1.08 | 0.02 | 1.00 | −1.97 | 0.02 | 1.00 | −1.34 |
| 680 | 0.30 | 10 | 0.10 | 0.92 | 1.52 | 0.25 | 0.52 | 3.18 | 0.15 | 0.82 | 2.27 |
| 680 | 0.30 | 30 | 0.02 | 1.00 | −2.09 | 0.02 | 1.00 | −1.72 | 0.02 | 1.00 | −1.71 |
| 680 | 0.30 | 50 | 0.03 | 0.99 | −0.94 | 0.02 | 1.00 | −2.00 | 0.04 | 0.99 | −0.52 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jin, J.; Wang, Q. Evaluation of Informative Bands Used in Different PLS Regressions for Estimating Leaf Biochemical Contents from Hyperspectral Reflectance. Remote Sens. 2019, 11, 197. https://doi.org/10.3390/rs11020197
Jin J, Wang Q. Evaluation of Informative Bands Used in Different PLS Regressions for Estimating Leaf Biochemical Contents from Hyperspectral Reflectance. Remote Sensing. 2019; 11(2):197. https://doi.org/10.3390/rs11020197
Chicago/Turabian StyleJin, Jia, and Quan Wang. 2019. "Evaluation of Informative Bands Used in Different PLS Regressions for Estimating Leaf Biochemical Contents from Hyperspectral Reflectance" Remote Sensing 11, no. 2: 197. https://doi.org/10.3390/rs11020197
APA StyleJin, J., & Wang, Q. (2019). Evaluation of Informative Bands Used in Different PLS Regressions for Estimating Leaf Biochemical Contents from Hyperspectral Reflectance. Remote Sensing, 11(2), 197. https://doi.org/10.3390/rs11020197