Optical Classification of the Remote Sensing Reflectance and Its Application in Deriving the Specific Phytoplankton Absorption in Optically Complex Lakes
Abstract
1. Introduction
2. Data and Methods
2.1. Field-Measured Datasets
2.2. Sentinel-3A/OLCI Images
2.3. Optical Classification of the Remote Sensing Reflectance
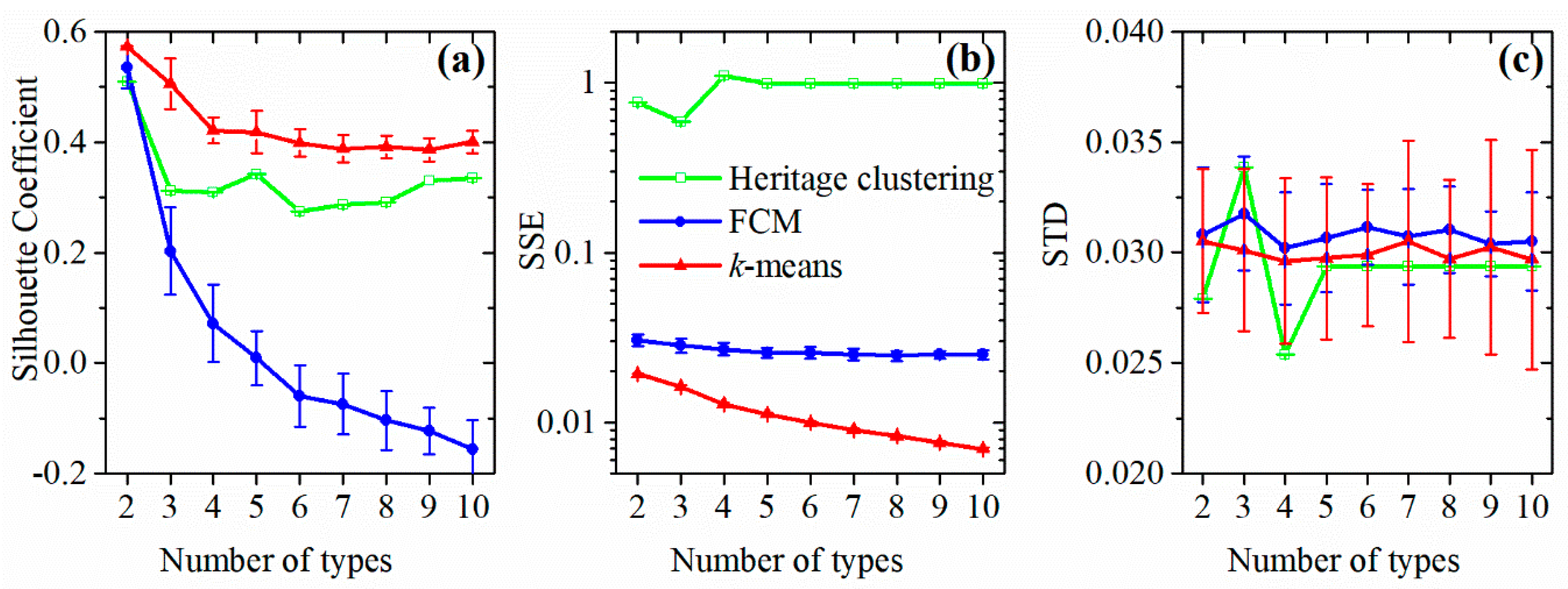
2.3.1. Clustering the Optical Water Types Based on the Field Rrs(Λ)
2.3.2. Type-labeling of the Satellite Rrs(λ)
2.4. Bio-Optical Algorithms Under Evaluation
3. Results
3.1. Optical Classification of the Remote Sensing Reflectance
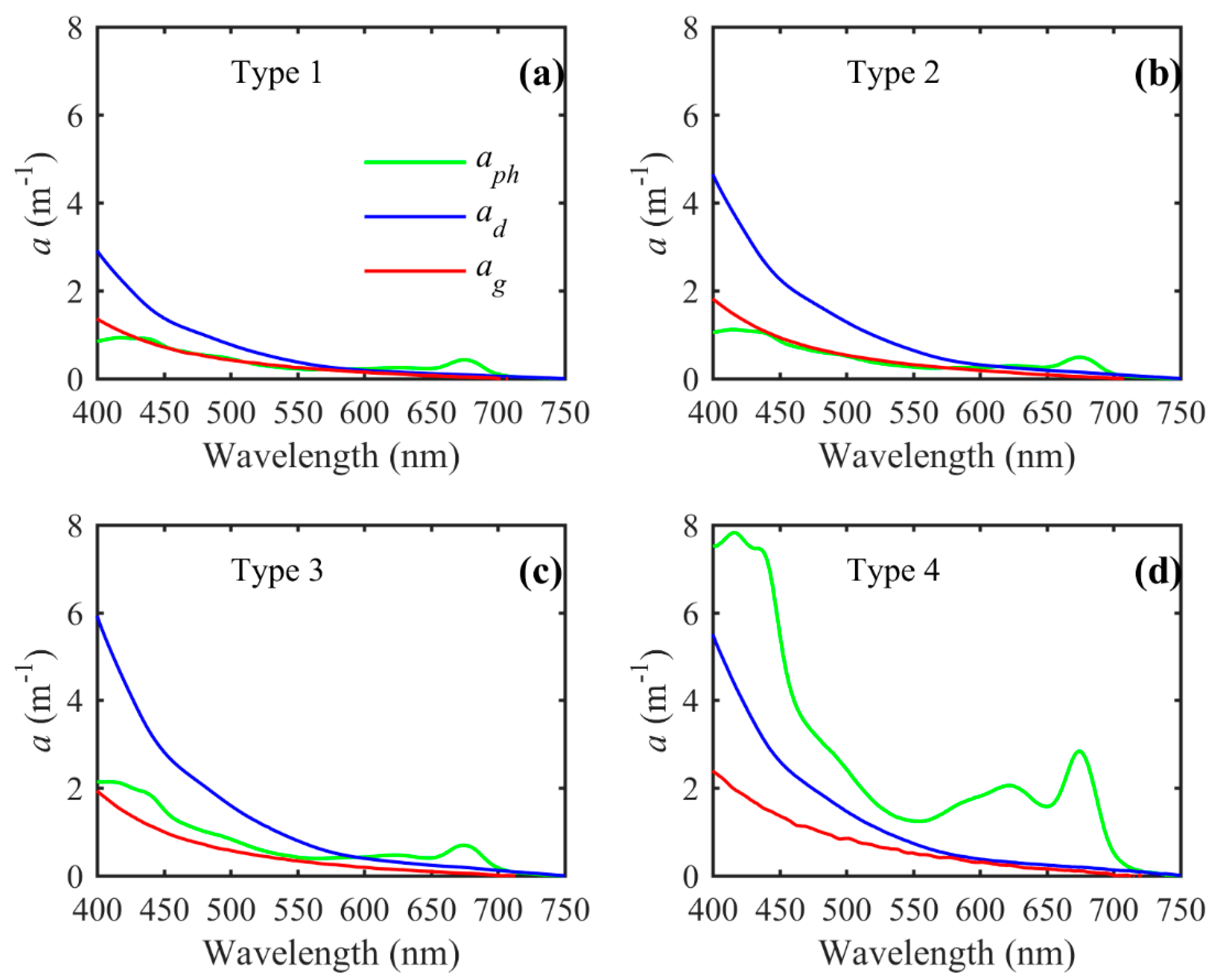
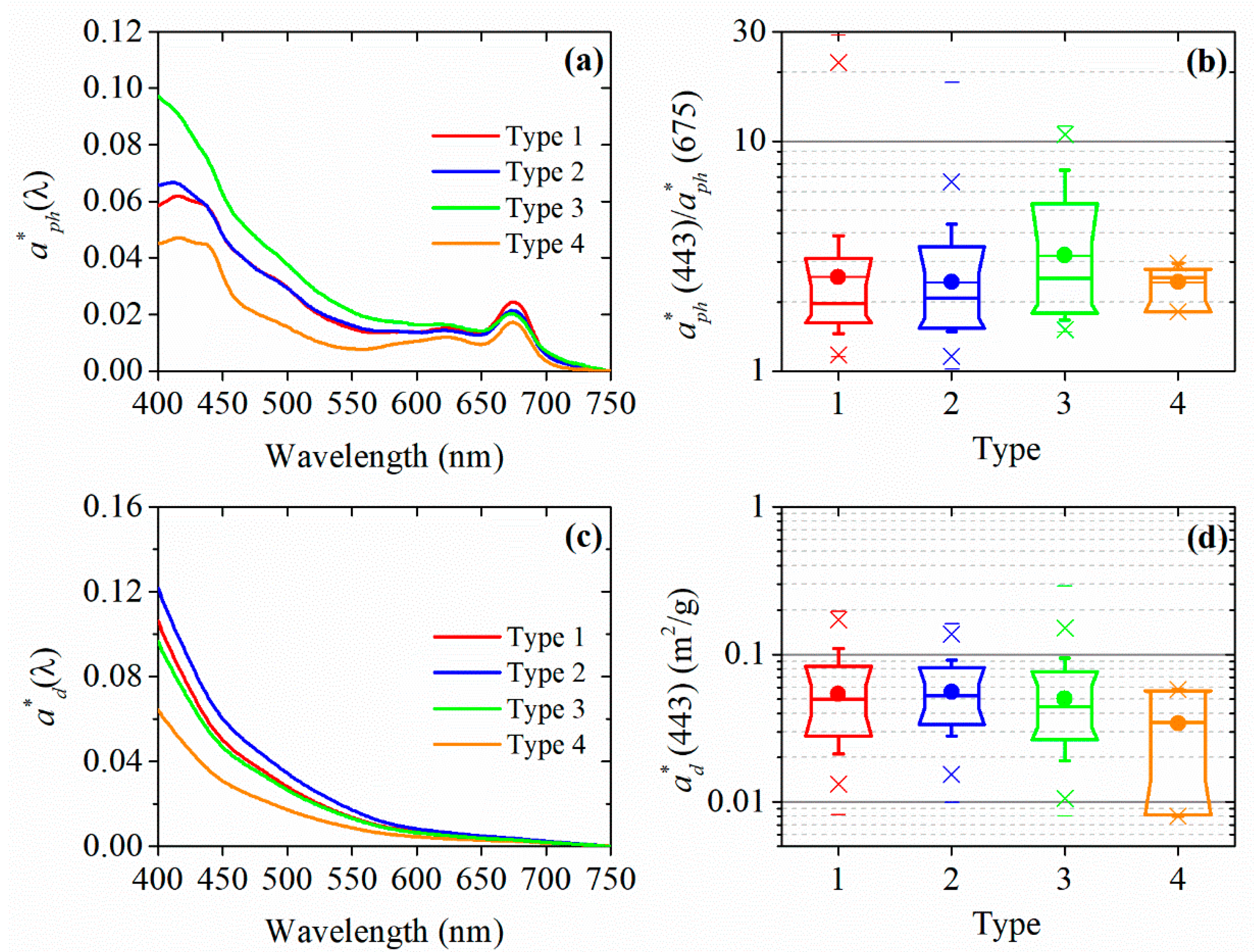
3.2. Bio-Optical Characteristics of OWTs
3.3. Application to the aph*(443) Estimation
3.3.1. Model Validation
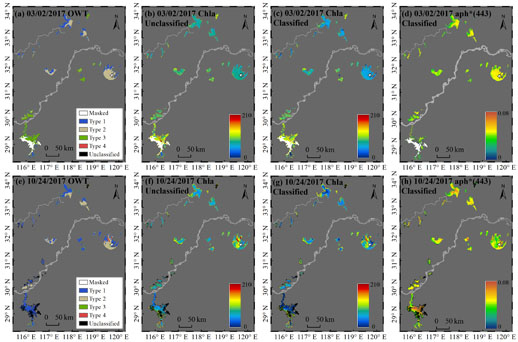
3.3.2. Application to the Satellite OLCI Data
4. Discussion
5. Conclusion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Bootsma, H.A. Oceans, lakes, and inland seas: A virtual issue on the large lakes of the world. Limnol. Oceanogr. 2018, 27, 87–88. [Google Scholar] [CrossRef]
- Duan, H.; Tao, M.; Loiselle, S.A.; Zhao, W.; Cao, Z.; Ma, R.; Tang, X. MODIS observations of cyanobacterial risks in a eutrophic lake: Implications for long-term safety evaluation in drinking-water source. Water Res. 2017, 122, 455–470. [Google Scholar] [CrossRef] [PubMed]
- Hou, X.; Feng, L.; Duan, H.; Chen, X.; Sun, D.; Shi, K. Fifteen-year monitoring of the turbidity dynamics in large lakes and reservoirs in the middle and lower basin of the Yangtze River, China. Remote Sens. Environ. 2017, 190, 107–121. [Google Scholar] [CrossRef]
- Le, C.; Li, Y.; Zha, Y.; Sun, D.; Yin, B. Validation of a Quasi-Analytical Algorithm for Highly Turbid Eutrophic Water of Meiliang Bay in Taihu Lake, China. IEEE Trans. Geosci. Remote Sens. 2009, 47, 2492–2500. [Google Scholar] [CrossRef]
- Meler, J.; Ostrowska, M.; Ficek, D.; Zdun, A. Light absorption by phytoplankton in the southern Baltic and Pomeranian lakes: Mathematical expressions for remote sensing applications. Oceanologia 2017, 59, 195–212. [Google Scholar] [CrossRef]
- Mélin, F.; Vantrepotte, V.; Clerici, M.; D’Alimonte, D.; Zibordi, G.; Berthon, J.F.; Canuti, E. Multi-sensor satellite time series of optical properties and chlorophyll-a concentration in the Adriatic Sea. Prog. Oceanogr. 2011, 91, 229–244. [Google Scholar] [CrossRef]
- Hubert, L.; Lubac, B.; Dessailly, D.; Duforet-Gaurier, L.; Vantrepotte, V. Effect of inherent optical properties variability on the chlorophyll retrieval from ocean color remote sensing: An in situ approach. Opt. Express 2010, 18, 20949–20959. [Google Scholar] [CrossRef]
- Dall’Olmo, G.; Gitelson, A.A. Effect of bio-optical parameter variability and uncertainties in reflectance measurements on the remote estimation of chlorophyll-a concentration in turbid productive waters: Modeling results. Appl. Opt. 2006, 45, 3577–3592. [Google Scholar] [CrossRef]
- Le, C.; Li, Y.; Zha, Y.; Sun, D.; Huang, C.; Zhang, H. Remote estimation of chlorophyll a in optically complex waters based on optical classification. Remote Sens. Environ. 2011, 115, 725–737. [Google Scholar] [CrossRef]
- Lubac, B.; Loisel, H. Variability and classification of remote sensing reflectance spectra in the eastern English Channel and southern North Sea. Remote Sens. Environ. 2007, 110, 45–58. [Google Scholar] [CrossRef]
- Vantrepotte, V.; Loisel, H.; Dessailly, D.; Mériaux, X. Optical classification of contrasted coastal waters. Remote Sens. Environ. 2012, 123, 306–323. [Google Scholar] [CrossRef]
- Moore, T.S.; Campbell, J.W.; Feng, H. A fuzzy logic classification scheme for selecting and blending satellite ocean color algorithms. IEEE Trans. Geosci. Remote Sens. 2001, 39, 1764–1776. [Google Scholar] [CrossRef]
- Neukermans, G.; Reynolds, R.A.; Stramski, D. Optical classification and characterization of marine particle assemblages within the western Arctic Ocean. Limnol. Oceanogr. 2016, 61, 1472–1494. [Google Scholar] [CrossRef]
- Prieur, L.; Sathyendranath, S. An optical classification of coastal and oceanic waters based on the specific spectral absorption curves of phytoplankton pigments, dissolved organic matter, and other particulate materials 1. Limnol. Oceanogr. 1981, 26, 671–689. [Google Scholar] [CrossRef]
- Shi, K.; Li, Y.; Zhang, Y.; Li, L.; Lv, H.; Song, K. Classification of Inland Waters Based on Bio-Optical Properties. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 543–561. [Google Scholar] [CrossRef]
- Spyrakos, E.; O’Donnell, R.; Hunter, P.D.; Miller, C.; Scott, M.; Simis, S.G.H.; Neil, C.; Barbosa, C.C.F.; Binding, C.E.; Bradt, S.; et al. Optical types of inland and coastal waters. Limnol. Oceanogr. 2018, 63, 846–870. [Google Scholar] [CrossRef]
- Zhang, F.; Li, J.; Shen, Q.; Zhang, B.; Wu, C.; Wu, Y.; Wang, G.; Wang, S.; Lu, Z. Algorithms and Schemes for Chlorophyll a Estimation by Remote Sensing and Optical Classification for Turbid Lake Taihu, China. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 350–364. [Google Scholar] [CrossRef]
- Hieronymi, M.; Müller, D.; Doerffer, R. The OLCI Neural Network Swarm (ONNS): A Bio-Geo-Optical Algorithm for Open Ocean and Coastal Waters. Front. Mar. Sci. 2017, 4. [Google Scholar] [CrossRef]
- Mélin, F.; Vantrepotte, V. How optically diverse is the coastal ocean? Remote Sens. Environ. 2015, 160, 235–251. [Google Scholar] [CrossRef]
- Ben Mustapha, Z.; Alvain, S.; Jamet, C.; Loisel, H.; Dessailly, D. Automatic classification of water-leaving radiance anomalies from global SeaWiFS imagery: Application to the detection of phytoplankton groups in open ocean waters. Remote Sens. Environ. 2014, 146, 97–112. [Google Scholar] [CrossRef]
- Moore, T.S.; Campbell, J.W.; Dowell, M.D. A class-based approach to characterizing and mapping the uncertainty of the MODIS ocean chlorophyll product. Remote Sens. Environ. 2009, 113, 2424–2430. [Google Scholar] [CrossRef]
- Eleveld, M.; Ruescas, A.; Hommersom, A.; Moore, T.; Peters, S.; Brockmann, C. An Optical Classification Tool for Global Lake Waters. Remote Sens. 2017, 9, 420. [Google Scholar] [CrossRef]
- Moore, T.S.; Dowell, M.D.; Bradt, S.; Verdu, A.R. An optical water type framework for selecting and blending retrievals from bio-optical algorithms in lakes and coastal waters. Remote Sens. Environ. 2014, 143, 97–111. [Google Scholar] [CrossRef] [PubMed]
- Reinart, A.; Herlevi, A.; Arst, H.; Sipelgas, L. Preliminary optical classification of lakes and coastal waters in Estonia and south Finland. J. Sea Res. 2003, 49, 357–366. [Google Scholar] [CrossRef]
- Moore, T.S.; Dowell, M.D.; Franz, B.A. Detection of coccolithophore blooms in ocean color satellite imagery: A generalized approach for use with multiple sensors. Remote Sens. Environ. 2012, 117, 249–263. [Google Scholar] [CrossRef]
- Torrecilla, E.; Stramski, D.; Reynolds, R.A.; Millán-Núñez, E.; Piera, J. Cluster analysis of hyperspectral optical data for discriminating phytoplankton pigment assemblages in the open ocean. Remote Sens. Environ. 2011, 115, 2578–2593. [Google Scholar] [CrossRef]
- Alimonte, D.D.; Melin, F.; Zibordi, G.; Berthon, J. Use of the novelty detection technique to identify the range of applicability of empirical ocean color algorithms. IEEE Trans. Geosci. Remote Sens. 2003, 41, 2833–2843. [Google Scholar] [CrossRef]
- Moore, T.S.; Campbell, J.W.; Feng, H. Characterizing the uncertainties in spectral remote sensing reflectance for SeaWiFS and MODIS-Aqua based on global in situ matchup data sets. Remote Sens. Environ. 2015, 159, 14–27. [Google Scholar] [CrossRef]
- Sun, D.; Hu, C.; Qiu, Z.; Cannizzaro, J.P.; Barnes, B.B. Influence of a red band-based water classification approach on chlorophyll algorithms for optically complex estuaries. Remote Sens. Environ. 2014, 155, 289–302. [Google Scholar] [CrossRef]
- Sun, D.; Li, Y.; Wang, Q.; Gao, J.; Le, C.; Huang, C.; Gong, S. Hyperspectral Remote Sensing of the Pigment C-Phycocyanin in Turbid Inland Waters, Based on Optical Classification. IEEE Trans. Geosci. Remote Sens. 2013, 51, 3871–3884. [Google Scholar] [CrossRef]
- Xue, K.; Zhang, Y.; Duan, H.; Ma, R. Variability of light absorption properties in optically complex inland waters of Lake Chaohu, China. J. Great Lakes Res. 2017, 43, 17–31. [Google Scholar] [CrossRef]
- Cao, Z.; Duan, H.; Feng, L.; Ma, R.; Xue, K. Climate- and human-induced changes in suspended particulate matter over Lake Hongze on short and long timescales. Remote Sens. Environ. 2017, 192, 98–113. [Google Scholar] [CrossRef]
- Mueller, J.L.; McClain, C.R.; Fargion, G.S.; Bidigare, R.; Trees, C.; Balch, W.; Dore, J.; Drapeau, D.; Karl, D.; Van, L. Ocean optics protocols for satellite ocean color sensor validation, revision 5, volume V: Biogeochemical and bio-optical measurements and data analysis protocols. NASA Tech. Memo 2003, 211621, 36. [Google Scholar]
- Mobley, C.D. Estimation of the remote-sensing reflectance from above-surface measurements. Appl. Opt. 1999, 38, 7442–7455. [Google Scholar] [CrossRef] [PubMed]
- Mobley, C.D. Polarized reflectance and transmittance properties of windblown sea surfaces. Appl. Opt. 2015, 54, 4828–4849. [Google Scholar] [CrossRef] [PubMed]
- Gitelson, A.A.; Dall’Olmo, G.; Moses, W.; Rundquist, D.C.; Barrow, T.; Fisher, T.R.; Gurlin, D.; Holz, J. A simple semi-analytical model for remote estimation of chlorophyll-a in turbid waters: Validation. Remote Sens. Environ. 2008, 112, 3582–3593. [Google Scholar] [CrossRef]
- Werdell, P.J.; Franz, B.A.; Bailey, S.W.; Feldman, G.C.; Boss, E.; Brando, V.E.; Dowell, M.; Hirata, T.; Lavender, S.J.; Lee, Z.; et al. Generalized ocean color inversion model for retrieving marine inherent optical properties. Appl. Opt. 2013, 52, 2019–2037. [Google Scholar] [CrossRef] [PubMed]
- Qi, L.; Hu, C.; Duan, H.; Cannizzaro, J.; Ma, R. A novel MERIS algorithm to derive cyanobacterial phycocyanin pigment concentrations in a eutrophic lake: Theoretical basis and practical considerations. Remote Sens. Environ. 2014, 154, 298–317. [Google Scholar] [CrossRef]
- Mitchell, B.G. Algorithms for determining the absorption-coefficient of aquatic particulates using the Quantitative Filter Technique (Qft). Proc. SPIE Int. Soc. Opt. Eng. 1990, 1302, 137–148. [Google Scholar]
- Pope, R.M.; Fry, E.S. Absorption spectrum (380–700 nm) of pure water. II. Integrating cavity measurements. Appl. Opt. 1997, 36, 8710–8723. [Google Scholar] [CrossRef]
- Binding, C.; Jerome, J.; Bukata, R.; Booty, W. Spectral absorption properties of dissolved and particulate matter in Lake Erie. Remote Sens. Environ. 2008, 112, 1702–1711. [Google Scholar] [CrossRef]
- Babin, M.; Stramski, D.; Ferrari, G.M.; Claustre, H.; Bricaud, A.; Obolensky, G.; Hoepffner, N. Variations in the light absorption coefficients of phytoplankton, nonalgal particles, and dissolved organic matter in coastal waters around Europe. J. Geophys. Res 2003, 108. [Google Scholar] [CrossRef]
- Ylöstalo, P.; Kallio, K.; Seppälä, J. Absorption properties of in-water constituents and their variation among various lake types in the boreal region. Remote Sens. Environ. 2014, 148, 190–205. [Google Scholar] [CrossRef]
- Xue, K.; Zhang, Y.; Ma, R.; Duan, H. An approach to correct the effects of phytoplankton vertical nonuniform distribution on remote sensing reflectance of cyanobacterial bloom waters. Limnol. Oceanogr. Methods 2017, 15, 302–319. [Google Scholar] [CrossRef]
- Vermote, E.F.; Tanre, D.; Deuze, J.L.; Herman, M.; Morcette, J.J. Second Simulation of the Satellite Signal in the Solar Spectrum, 6S: An overview. IEEE Trans. Geosci. Remote Sens. 1997, 35, 675–686. [Google Scholar] [CrossRef]
- Burns, P.; Nolin, A. Using atmospherically-corrected Landsat imagery to measure glacier area change in the Cordillera Blanca, Peru from 1987 to 2010. Remote Sens. Environ. 2014, 140, 165–178. [Google Scholar] [CrossRef]
- Feng, L.; Hu, C.; Chen, X.; Tian, L.; Chen, L. Human induced turbidity changes in Poyang Lake between 2000 and 2010: Observations from MODIS. J. Geophys. Res. Ocean. 2012, 117. [Google Scholar] [CrossRef]
- Shen, M.; Duan, H.; Cao, Z.; Xue, K.; Loiselle, S.; Yesou, H. Determination of the Downwelling Diffuse Attenuation Coefficient of Lake Water with the Sentinel-3A OLCI. Remote Sens. 2017, 9, 1246. [Google Scholar] [CrossRef]
- Brockmann, C.; Doerffer, R.; Peters, M.; Kerstin, S.; Embacher, S.; Ruescas, A. Evolution of the C2RCC neural network for Sentinel 2 and 3 for the retrieval of ocean colour products in normal and extreme optically complex waters. In Proceedings of the Living Planet Symposium, Prague, Czech Republic, 9–13 May 2016; p. 54. [Google Scholar]
- Steinmetz, F.; Deschamps, P.-Y.; Ramon, D. Atmospheric correction in presence of sun glint: Application to MERIS. Opt. Express 2011, 19, 9783–9800. [Google Scholar] [CrossRef]
- Bi, S.; Li, Y.; Wang, Q.; Lyu, H.; Liu, G.; Zheng, Z.; Du, C.; Mu, M.; Xu, J.; Lei, S. Inland Water Atmospheric Correction Based on Turbidity Classification Using OLCI and SLSTR Synergistic Observations. Remote Sens. 2018, 10, 1002. [Google Scholar] [CrossRef]
- Shannon, C.E. A Mathematical Theory of Communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Gilerson, A.A.; Gitelson, A.A.; Zhou, J.; Gurlin, D.; Moses, W.; Ioannou, I.; Ahmed, S.A.J.O.E. Algorithms for remote estimation of chlorophyll-a in coastal and inland waters using red and near infrared bands. Opt. Express 2010, 18, 24109–24125. [Google Scholar] [CrossRef] [PubMed]
- Letelier, R.M.; Abbott, M.R. An analysis of chlorophyll fluorescence algorithms for the Moderate Resolution Imaging Spectrometer (MODIS). Remote Sens. Environ. 1996, 58, 215–223. [Google Scholar] [CrossRef]
- Gower, J.; King, S.; Borstad, G.; Brown, L. Detection of intense plankton blooms using the 709 nm band of the MERIS imaging spectrometer. Int. J. Remote Sens. 2005, 26, 2005–2012. [Google Scholar] [CrossRef]
- Qi, L.; Hu, C.; Duan, H.; Barnes, B.B.; Ma, R. An EOF-based algorithm to estimate chlorophyll a concentrations in Taihu Lake from MODIS land-band measurements: Implications for near real-time applications and forecasting models. Remote Sens. 2014, 6, 10694–10715. [Google Scholar] [CrossRef]
- Bricaud, A.; Babin, M.; Morel, A.; Claustre, H. Variability in the chlorophyll-specific absorption coefficients of natural phytoplankton: Analysis and parameterization. J. Geophys. Res. Ocean. 1995, 100, 13321–13332. [Google Scholar] [CrossRef]
- Vantrepotte, V.; Loisel, H.; Mélin, F.; Desailly, D.; Duforêt-Gaurier, L. Global particulate matter pool temporal variability over the SeaWiFS period (1997–2007). Geophys. Res. Lett. 2011, 38. [Google Scholar] [CrossRef]
- Jackson, T.; Sathyendranath, S.; Mélin, F. An improved optical classification scheme for the Ocean Colour Essential Climate Variable and its applications. Remote Sens. Environ. 2017, 203, 152–161. [Google Scholar] [CrossRef]
- Qin, P.; Simis, S.G.; Tilstone, G.H. Radiometric validation of atmospheric correction for MERIS in the Baltic Sea based on continuous observations from ships and AERONET-OC. Remote Sens. Environ. 2017, 200, 263–280. [Google Scholar] [CrossRef]
- Melin, F.; Vantrepotte, V.; Chuprin, A.; Grant, M.; Jackson, T.; Sathyendranath, S. Assessing the fitness-for-purpose of satellite multi-mission ocean color climate data records: A protocol applied to OC-CCI chlorophyll-a data. Remote Sens Env. 2017, 203, 139–151. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, M.; Qin, B.; Van Der Woerd, H.J.; Li, J.; Li, Y. Modeling remote-sensing reflectance and retrieving chlorophyll-a concentration in extremely turbid case-2 waters (Lake Taihu, China). IEEE Trans. Geosci. Remote Sens. 2009, 47, 1937–1948. [Google Scholar] [CrossRef]
- Babin, M.; Stramski, D. Variations in the mass-specific absorption coefficient of mineral particles suspended in water. Limnol. Oceanogr. 2004, 49, 756–767. [Google Scholar] [CrossRef]
- Le, C.; Li, Y.; Zha, Y.; Sun, D. Specific absorption coefficient and the phytoplankton package effect in Lake Taihu, China. Hydrobiologia 2009, 619, 27–37. [Google Scholar] [CrossRef]
- Yoshimura, K.; Zaitsu, N.; Sekimura, Y.; Matsushita, B.; Fukushima, T.; Imai, A. Parameterization of chlorophyll a-specific absorption coefficients and effects of their variations in a highly eutrophic lake: A case study at Lake Kasumigaura, Japan. Hydrobiologia 2012, 691, 157–169. [Google Scholar] [CrossRef]
- Sun, D.; Li, Y.; Wang, Q.; Le, C.; Lv, H.; Huang, C.; Gong, S. Specific inherent optical quantities of complex turbid inland waters, from the perspective of water classification. Photochem. Photobiol. Sci. 2012, 11, 1299–1312. [Google Scholar] [CrossRef] [PubMed]
- Zheng, G.; Stramski, D. A model based on stacked-constraints approach for partitioning the light absorption coefficient of seawater into phytoplankton and non-phytoplankton components. J. Geophys. Res. Ocean. 2013, 118, 2155–2174. [Google Scholar] [CrossRef]
- Lee, Z.; Ahn, Y.-H.; Mobley, C.; Arnone, R. Removal of surface-reflected light for the measurement of remote-sensing reflectance from an above-surface platform. Opt. Express 2010, 18, 26313–26324. [Google Scholar] [CrossRef]
- Bernardo, N.; Alcântara, E.; Watanabe, F.; Rodrigues, T.; Carmo, A.; Gomes, A.; Andrade, C. Glint Removal Assessment to Estimate the Remote Sensing Reflectance in Inland Waters with Widely Differing Optical Properties. Remote Sens. 2018, 10, 1655. [Google Scholar] [CrossRef]



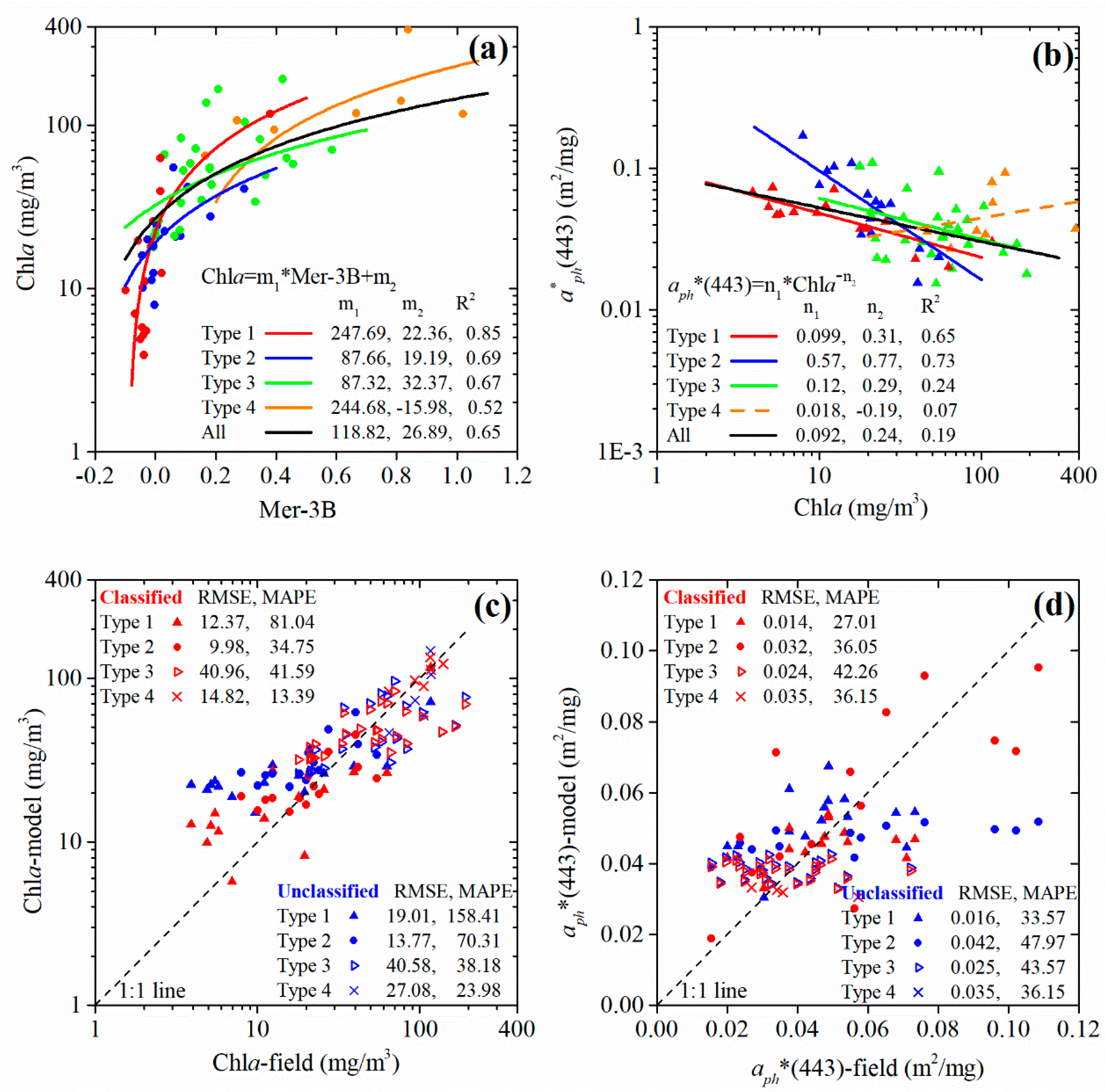
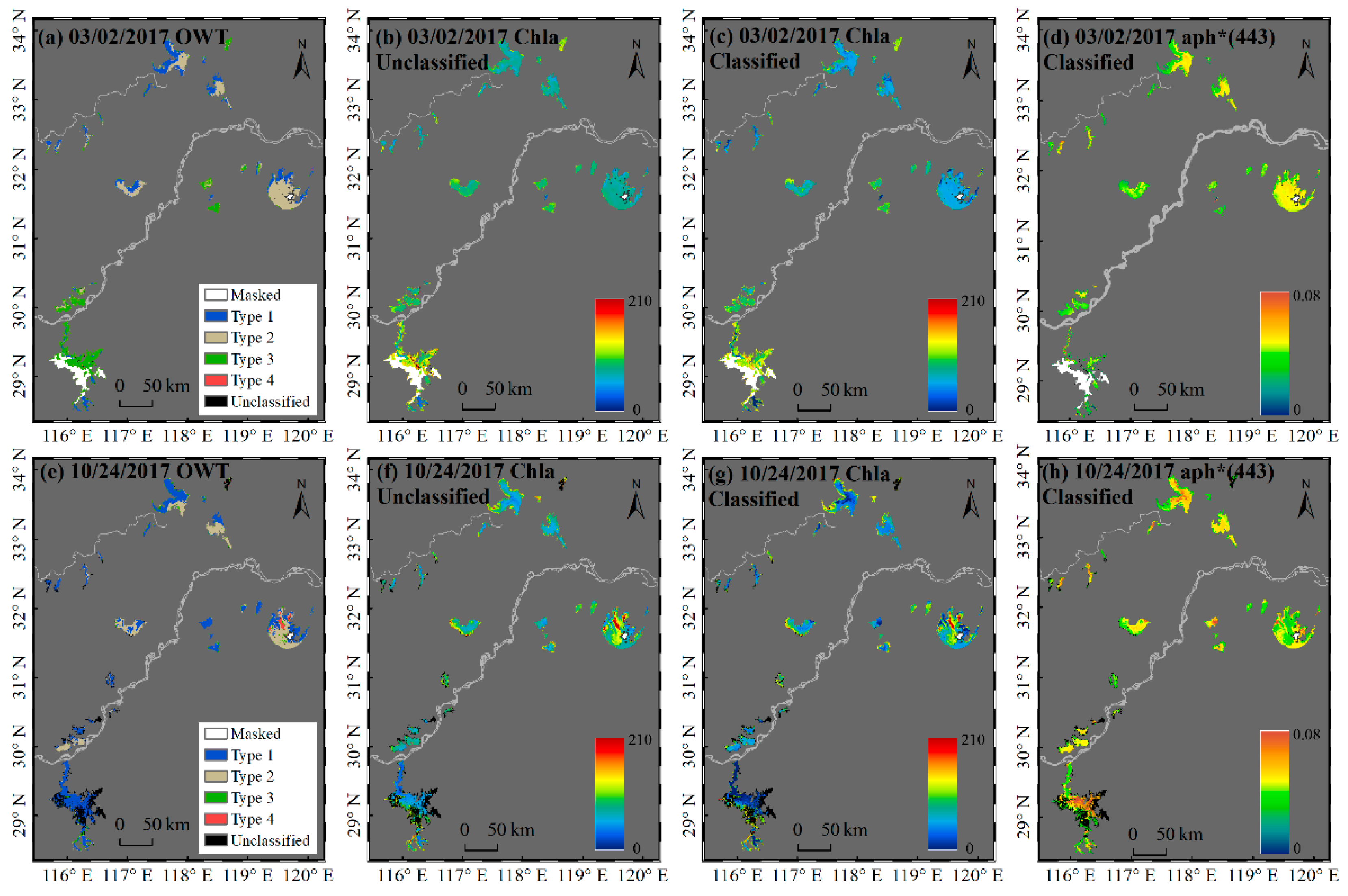

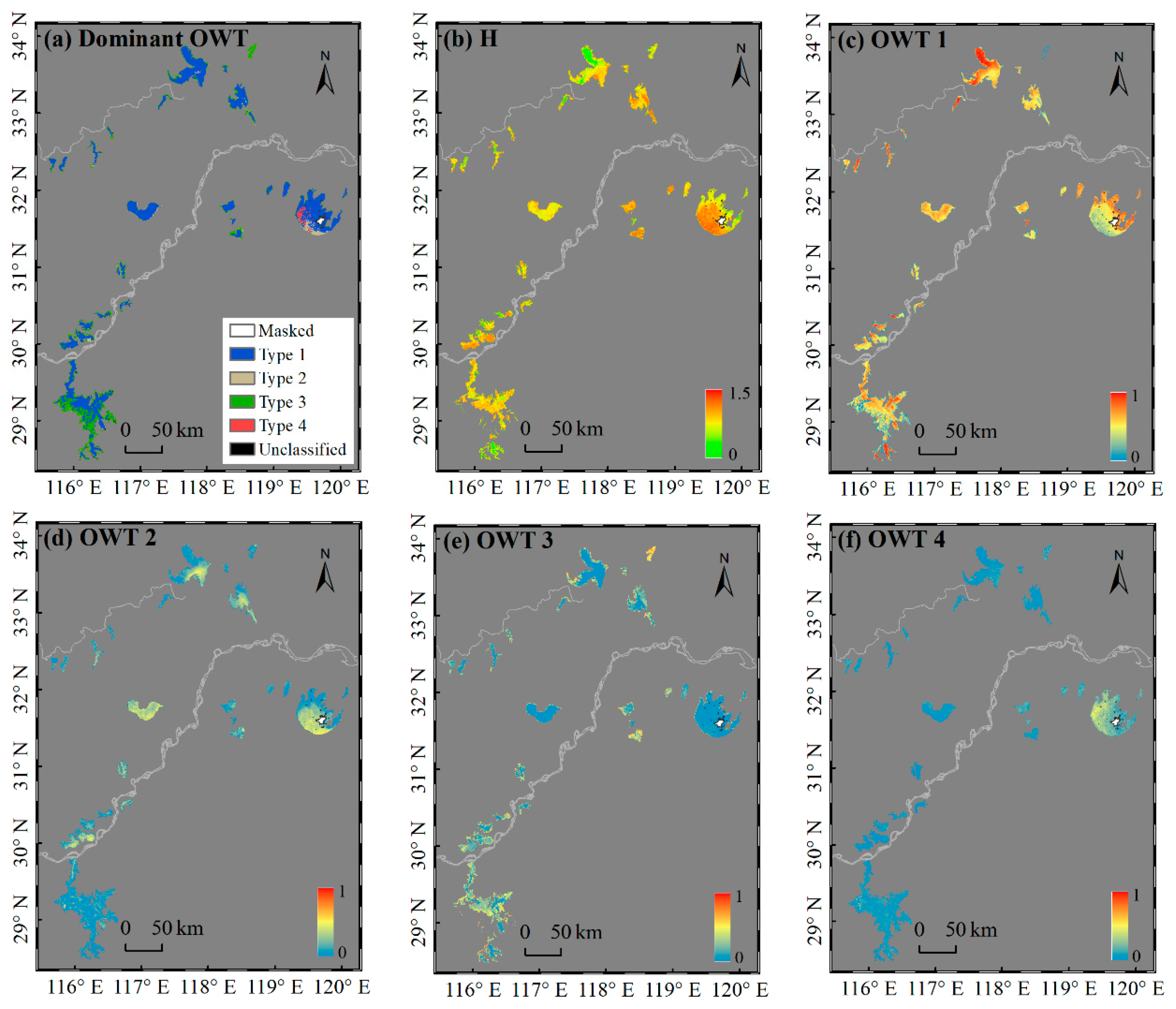
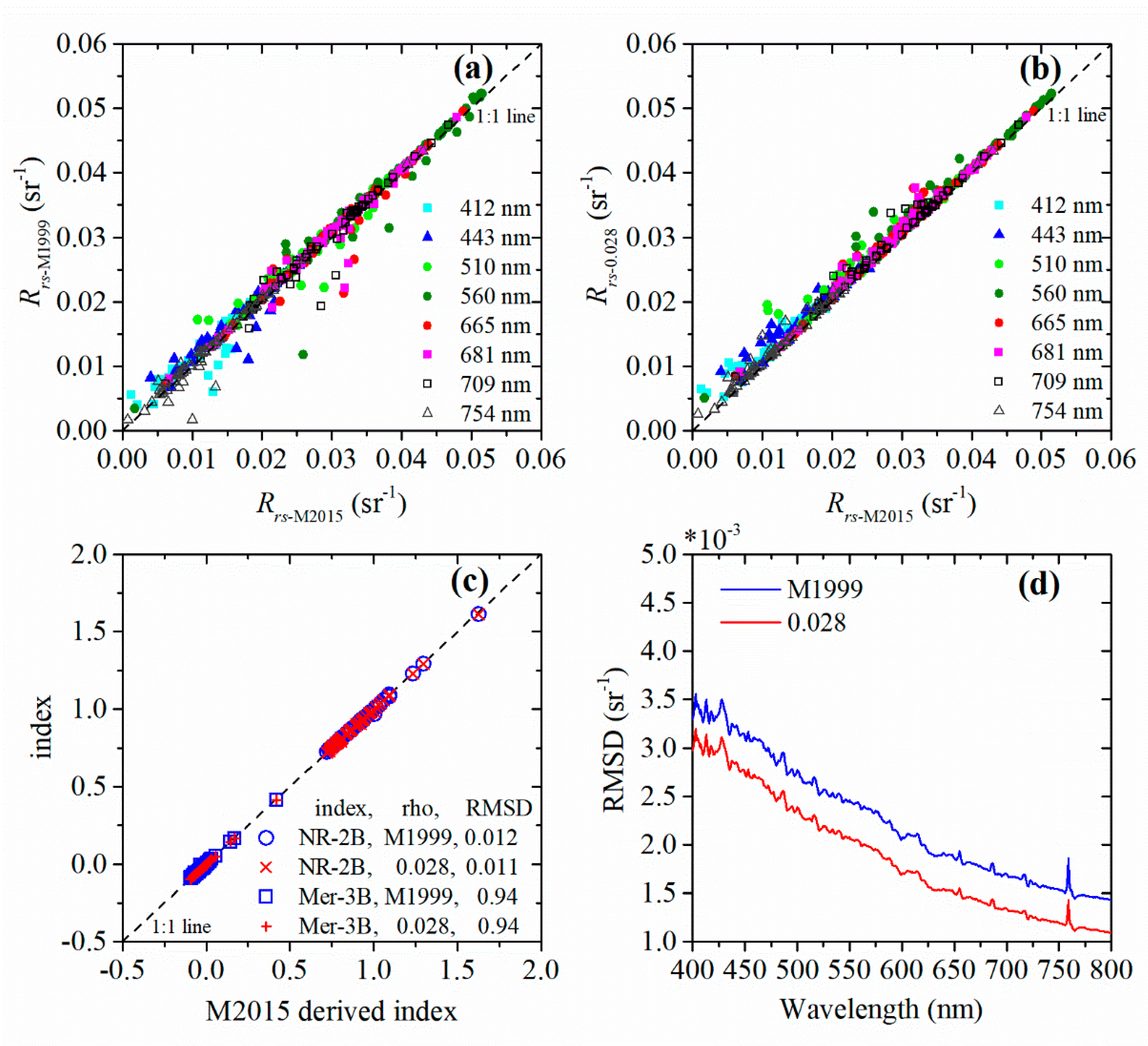
| All N = 535 | Type 1 N = 162 | Type 2 N = 194 | Type 3 N = 168 | Type 4 N = 11 | |
|---|---|---|---|---|---|
| Chla | 31.77 ± 36.86 | 19.30 ± 13.57 | 26.56 ± 25.56 | 41.47 ± 37.21 | 163.08 ± 101.26 |
| 0.70–382.03 | 1.27–85.64 | 0.70–165.84 | 0.71–157.05 | 70.41–382.03 | |
| SPM | 48.87 ± 30.31 | 30.37 ± 11.48 | 45.07 ± 20.23 | 68.85 ± 36.88 | 91.82 ± 45.22 |
| 5.00–245.00 | 5.00–73.33 | 5.00–150.00 | 10.67–245.00 | 20.00–210.67 | |
| SPIM | 37.13 ± 27.16 | 21.44 ± 12.67 | 37.86 ± 18.67 | 50.91 ± 36.39 | 47.88 ± 29.78 |
| 0.50–232.00 | 0.50–73.00 | 6.00–110.00 | 4.00–232.00 | 1.33–96.00 | |
| SPOM | 16.77 ± 16.04 | 12.18 ± 7.35 | 15.23 ± 12.99 | 20.63 ± 18.27 | 51.12 ± 44.11 |
| 1.00–173.33 | 2.67–50.00 | 1.00–120.00 | 1.00–107.00 | 16.00–173.33 | |
| a(443) | 4.67 ± 2.25 | 3.15 ± 0.80 | 4.49 ± 1.22 | 5.96 ± 2.32 | 11.27 ± 5.13 |
| 1.02–20.86 | 1.02–5.61 | 2.06–11.41 | 2.24–16.18 | 5.34–20.86 | |
| aph(443) | 1.31 ± 1.56 | 0.86 ± 0.46 | 0.99 ± 0.80 | 1.76 ± 1.63 | 6.91 ± 5.17 |
| 0.16–17.88 | 0.16–3.09 | 0.18–5.50 | 0.20–13.12 | 1.80–17.88 | |
| ad(443) | 2.40 ± 1.37 | 1.52 ± 0.58 | 2.49 ± 0.80 | 3.11 ± 1.86 | 2.88 ± 1.84 |
| 0.34–10.41 | 0.34–2.97 | 0.51–5.50 | 0.39–10.41 | 0.59–5.66 | |
| ag(443) | 0.98 ± 0.60 | 0.78 ± 0.45 | 1.02 ± 0.70 | 1.10 ± 0.51 | 1.48 ± 0.75 |
| 0.16–7.10 | 0.16–2.50 | 0.28–7.10 | 0.28–4.04 | 0.73–3.18 | |
| aph(443)/ap(443) | 0.34 ± 0.18 | 0.36 ± 0.15 | 0.27 ± 0.15 | 0.36 ± 0.21 | 0.65 ± 0.22 |
| 0.06–0.97 | 0.13–0.76 | 0.06–0.83 | 0.07–0.92 | 0.31–0.97 | |
| ag(443)/a(443) | 0.22 ± 0.11 | 0.25 ± 0.11 | 0.23 ± 0.10 | 0.21 ± 0.10 | 0.15 ± 0.08 |
| 0.05–0.62 | 0.05–0.60 | 0.06–0.62 | 0.05–0.55 | 0.06–0.37 |
| NR-2B | Mer-3B | MCI | |||||||
|---|---|---|---|---|---|---|---|---|---|
| R2 | RMSE (mg/m3) | MAPE (%) | R2 | RMSE (mg/m3) | MAPE (%) | R2 | RMSE (mg/m3) | MAPE (%) | |
| Type 1 | 0.53 | 9.30 | 40.53 | 0.66 | 7.32 | 34.19 | 0.35 | 10.93 | 47.04 |
| Type 2 | 0.86 | 9.70 | 39.52 | 0.88 | 9.79 | 40.33 | 0.63 | 15.37 | 53.60 |
| Type 3 | 0.63 | 23.35 | 68.26 | 0.64 | 22.99 | 59.12 | 0.60 | 25.03 | 69.11 |
| Type 4 | 0.18 | 87.59 | 42.91 | 0.01 | 96.13 | 51.70 | 0.07 | 92.92 | 47.24 |
| All data | 0.66 | 21.78 | 71.34 | 0.51 | 28.57 | 104.90 | 0.61 | 23.35 | 56.23 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xue, K.; Ma, R.; Wang, D.; Shen, M. Optical Classification of the Remote Sensing Reflectance and Its Application in Deriving the Specific Phytoplankton Absorption in Optically Complex Lakes. Remote Sens. 2019, 11, 184. https://doi.org/10.3390/rs11020184
Xue K, Ma R, Wang D, Shen M. Optical Classification of the Remote Sensing Reflectance and Its Application in Deriving the Specific Phytoplankton Absorption in Optically Complex Lakes. Remote Sensing. 2019; 11(2):184. https://doi.org/10.3390/rs11020184
Chicago/Turabian StyleXue, Kun, Ronghua Ma, Dian Wang, and Ming Shen. 2019. "Optical Classification of the Remote Sensing Reflectance and Its Application in Deriving the Specific Phytoplankton Absorption in Optically Complex Lakes" Remote Sensing 11, no. 2: 184. https://doi.org/10.3390/rs11020184
APA StyleXue, K., Ma, R., Wang, D., & Shen, M. (2019). Optical Classification of the Remote Sensing Reflectance and Its Application in Deriving the Specific Phytoplankton Absorption in Optically Complex Lakes. Remote Sensing, 11(2), 184. https://doi.org/10.3390/rs11020184