Synthesis of Vegetation Indices Using Genetic Programming for Soil Erosion Estimation
Abstract
1. Introduction
2. Related Work
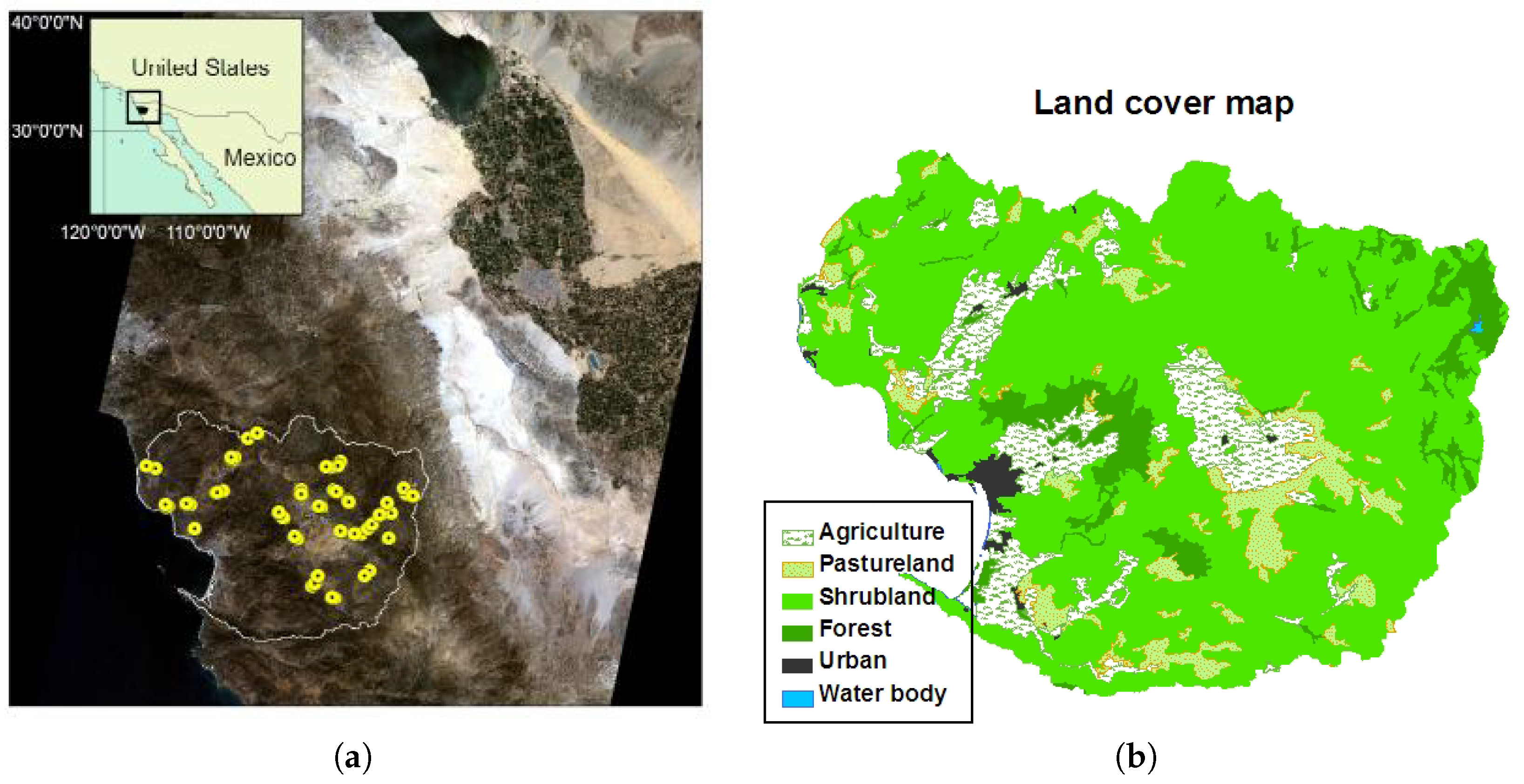
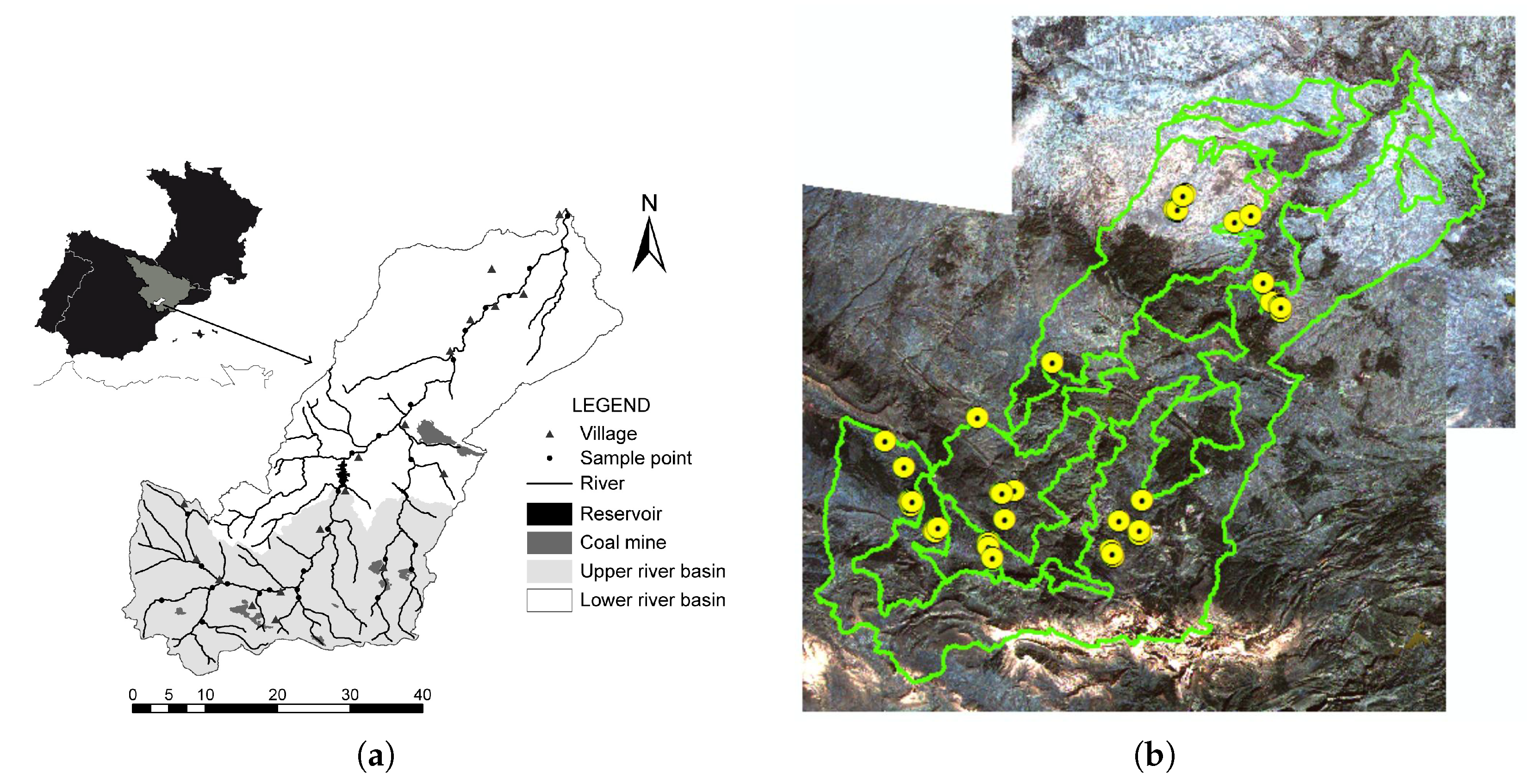
3. Study Area
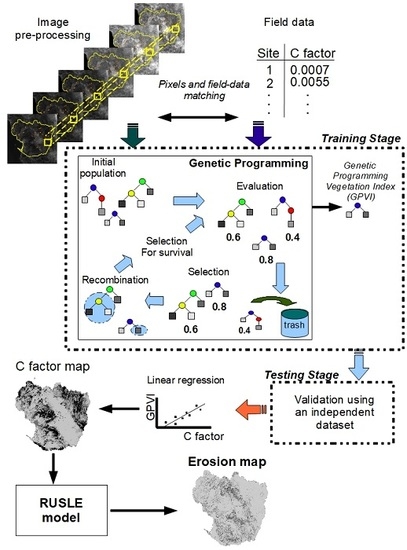
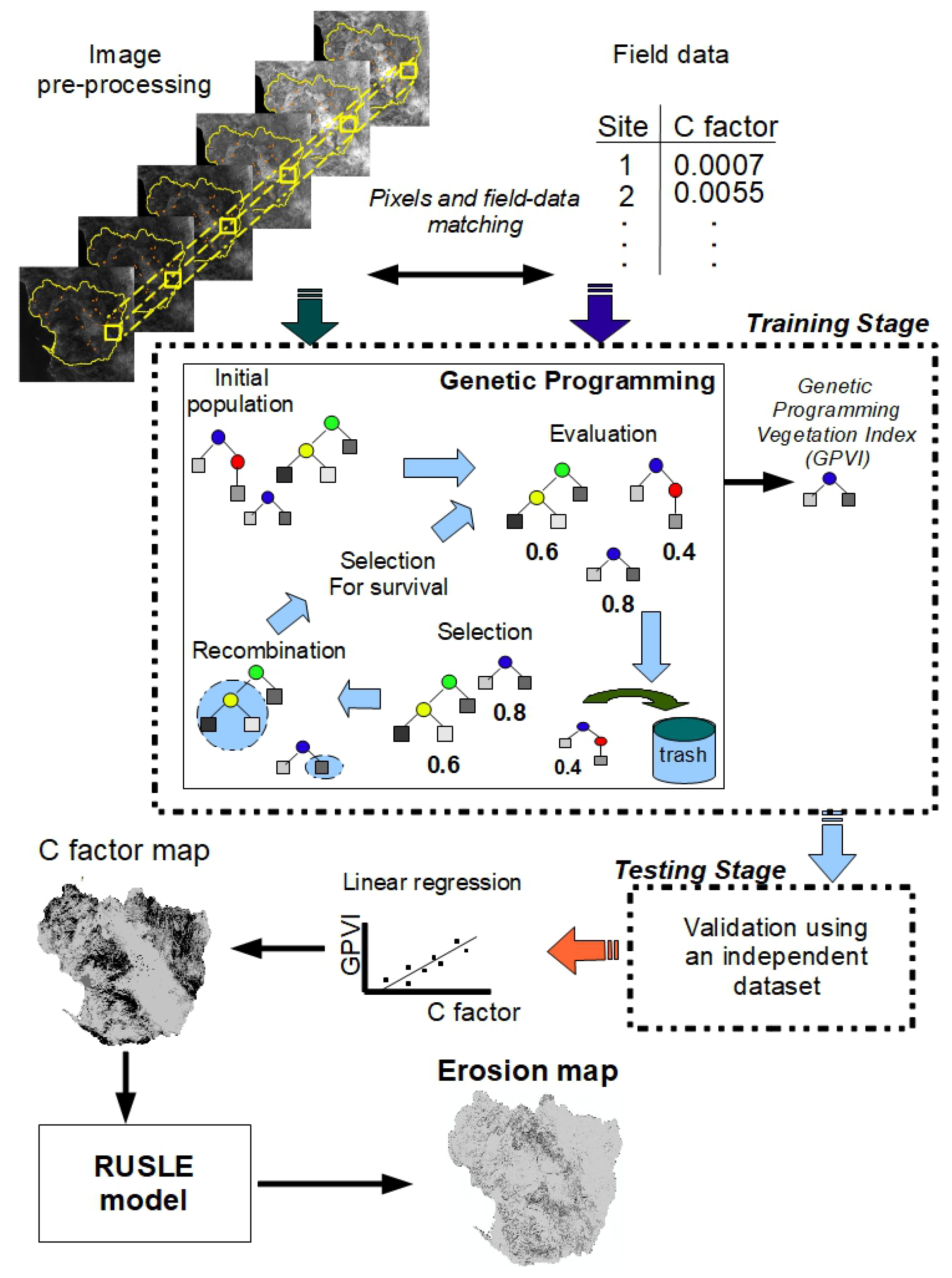
4. Methodology
4.1. Collecting Field Samples
- Superficial cover percentage (g). This was visually determined from 10 cm around a dropped weight, otherwise known as the micro-plot. Each micro-plot was labeled with one of five different classifications according to the percentage of ground covered by vegetation or rocks: 0 = 0–1%, 1 = 1–25%, 2 = 25–50%, 3 = 50–75%, and 4 = 75–100%.
- Percentage (p) and height (h) of aerial vegetation cover. The percentage, p, is obtained using a similar method as for the superficial cover percentage: labeling a micro-plot according to the same five classifications. However, the center of the micro-plot is not defined by a dropped weight, but by the wire from which it hangs. The height, h, of the aerial cover for the sampling point is defined by the plant or its ramifications that are closest to the ground (without touching it) and touch the wire.
- Roughness (r) and underground biomass (b). Roughness, r, is evaluated according to the empirical method proposed by [41] and Tables 5-5 and 5-6 from the RUSLE manual [7]. Underground biomass, b, is inferred using the primary productivity method defined by [45]. For this study, b was assumed to be uniform.
4.2. Satellite Image Acquisition and Correction
- Radiometric correction diminishes the effects of sensor miscalibration. It also corrects the distortions caused by the angle between the Sun and the satellite over the study area. In order to correct the images produced by the satellite, researchers employ the parameters and methodology published by NASA for instrument recalibration and pixel reflectance values [49]. Figure 4a shows two non-corrected images that were taken at different times; by applying the radiometric correction (Figure 4c), the pixel values are normalized, and the results are comparable.
- Geometric correction adjusts the satellite images to the geographic coordinate system. To perform this adjustment, Ground Control Points (GCP) located in the study area were obtained from the U.S. Geological Survey (USGS) website [46].
4.3. Associating Satellite Images and Field Data
4.4. Applying Conventional VIs
4.5. Applying the Genetic Programming Algorithm
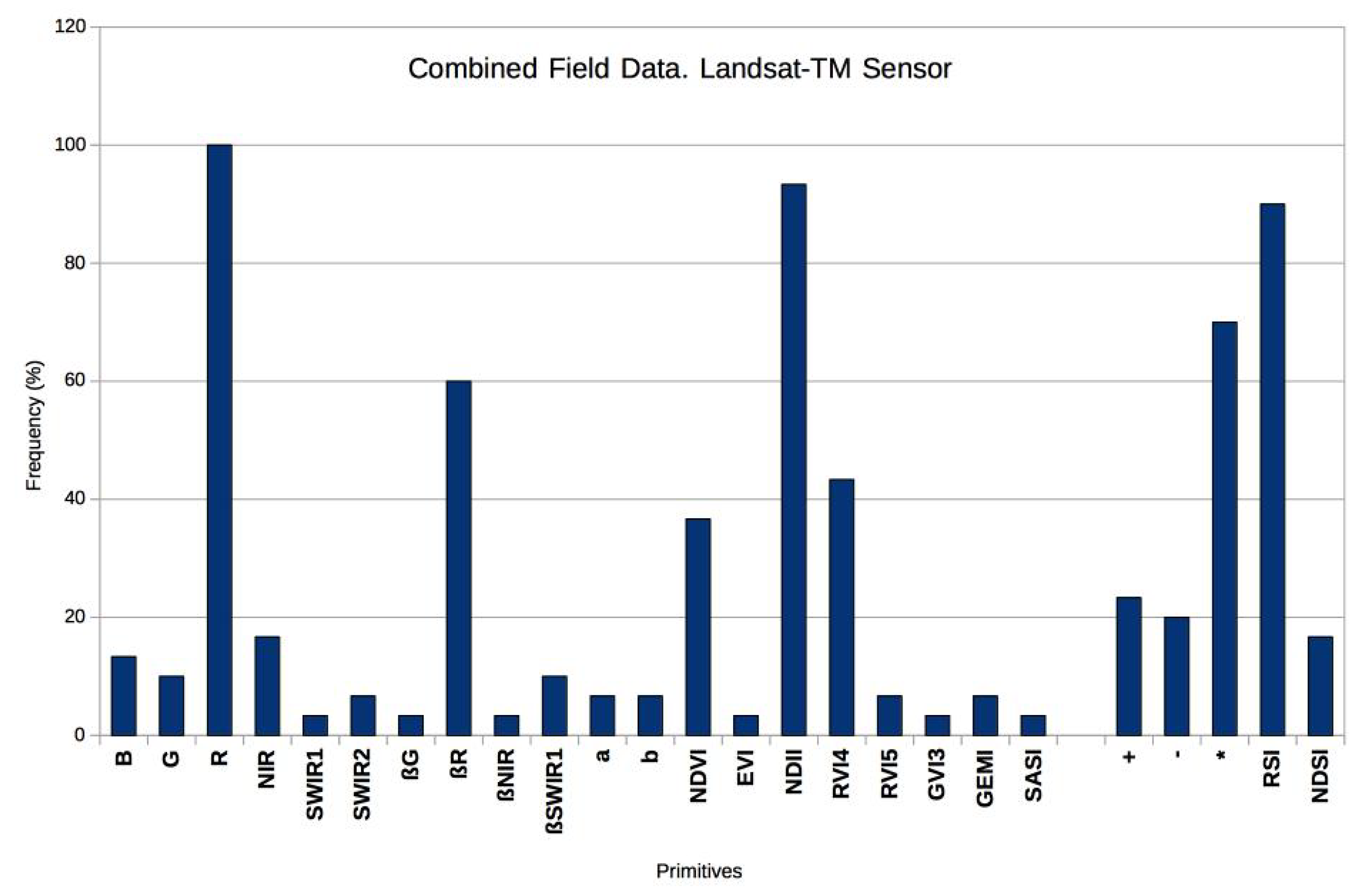
4.5.1. Definition of the Terminal and Function Sets
- Spectral bands represent the median value of the pixel window defined in Section 4.3, which was extracted from each satellite image band: Blue (B), Green (G), Red (R), Near-Infrared (NIR), Shortwave Infrared 1 (SWIR1), and Shortwave Infrared 2 (SWIR2).
- Spectral angles are the angles formed by each vertex in the electromagnetic spectrum for the satellite image [68]. For example, corresponds to the combination of pixels from the B, G, and R bands. The formula for this angle is:where a, b, and c are the Euclidean distances between the vertices of the angle formed by B, G, and R, respectively. Formula (3) is applied for each angle.
- Soil line parameters: This is the relationship between the R and NIR bands [70]. When these bands are graphed in a dispersion graph, they tend to group pixels above a numeric threshold, which is called the soil line. For this study, the slope and the intersect of the soil line are included in the primitives’ set as a and b in Table 3.
- Best-performing conventional VIs: The five better performing conventional VIs in Section 4.4 were selected. This performance is based in statistical significance [71], which is the probability that an index has a random correlation value . For scientific research, the most common statistical significance value is 5%, which means that is significant if there is a 5% or less probability that the index has happened by chance. The statistical significance, , for the correlation coefficient, r, of a sample with N data is [71]:The field samples from both watersheds were used in this research, so the sample size for the training dataset was . Therefore, correlation coefficients greater than 0.39 will be statistically significant for this experiment.Besides the five indices, it was decided to include the and indices since these are the most used for scientific applications.
- Arithmetic operators: The function set is formed by the basic arithmetic operators (+, −, and ×) since these are the operators usually employed for VIs. For this work, division (/) is substituted by the compound operator Ratio Spectral Index (RSI) (see below).
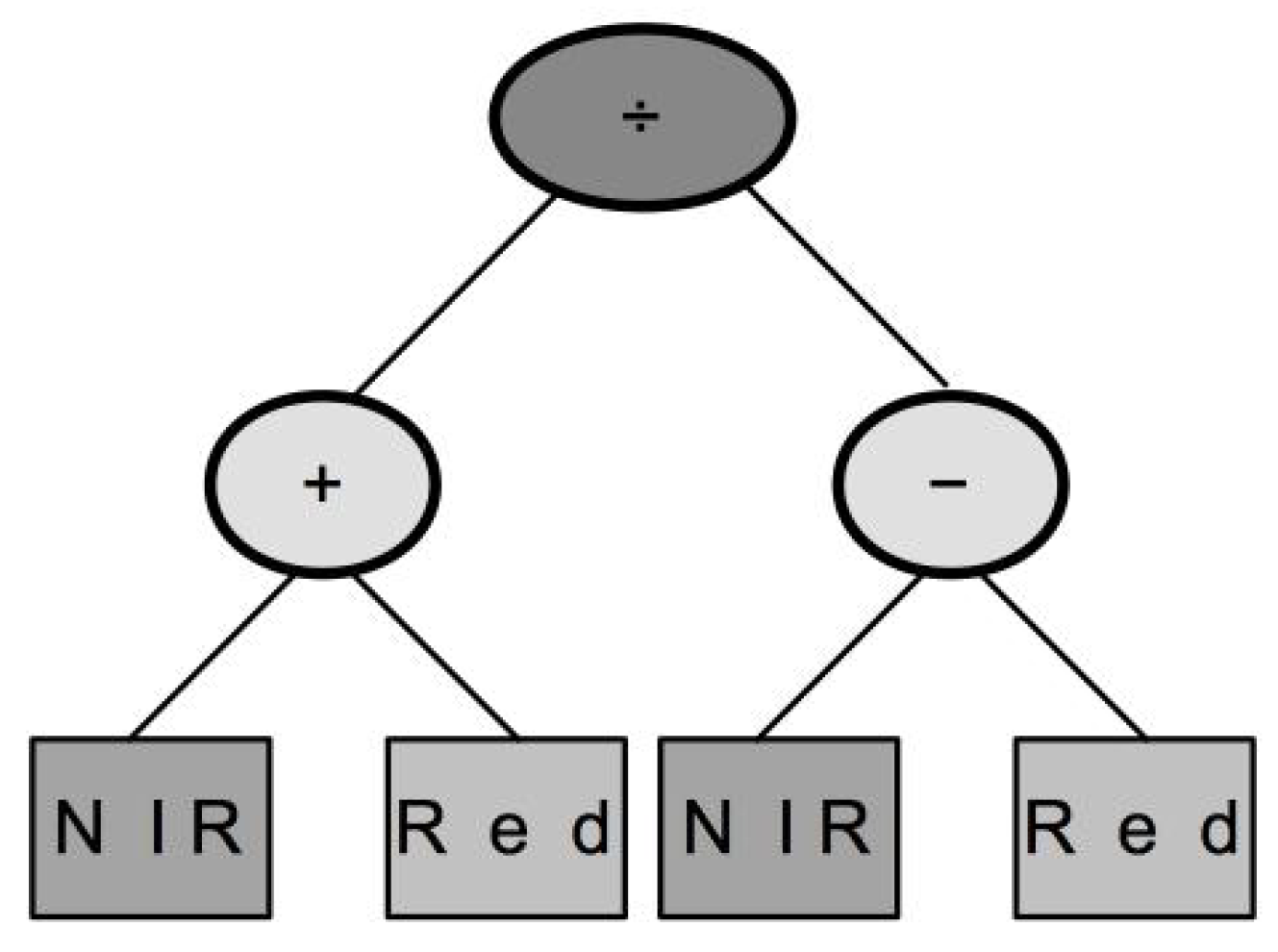
- Compound operators: These represent complete arithmetic structures that have been previously defined. This research includes two of the most-employed indices, NDVI and RVI. The first structure is the Normalized Difference Spectral Index (NDSI) [72], which corresponds to NDVI; while the second structure is the Ratio Spectral Index (RSI), which corresponds to RVI. The definitions for these structures are:where is the pixel reflectance value in band k.
4.5.2. Fitness Function
4.5.3. Control Parameters and Stop Criteria
4.6. Results’ Evaluation
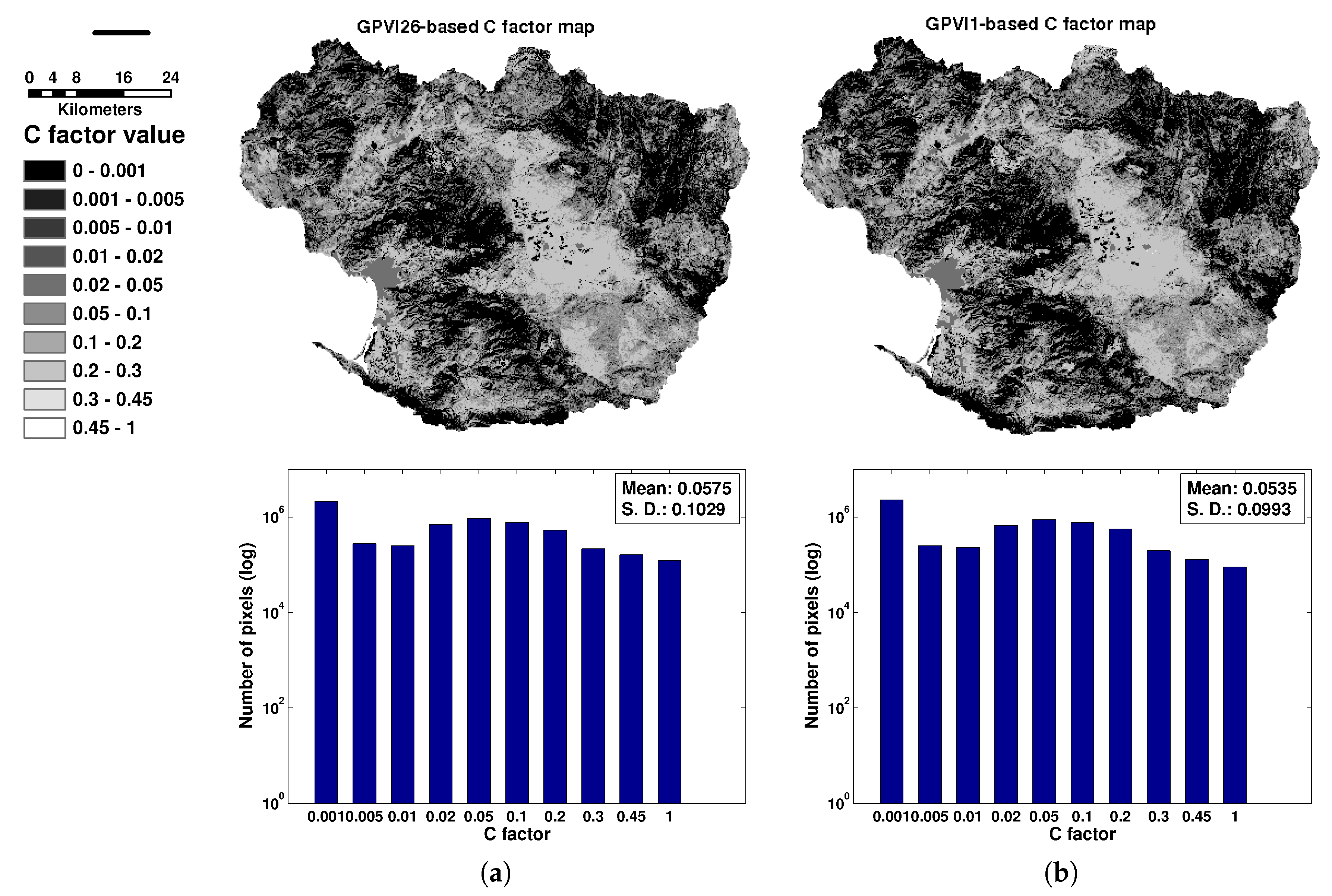
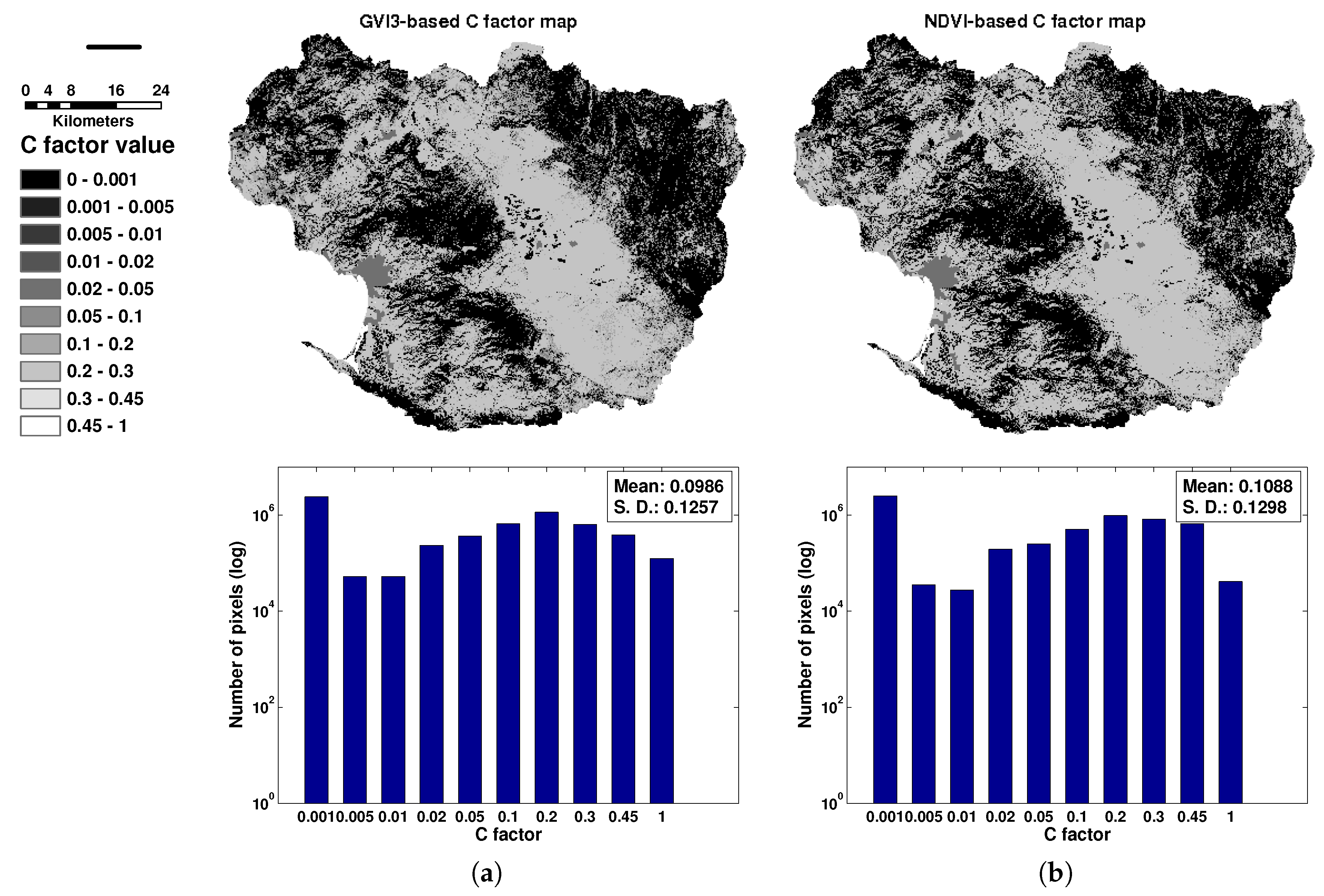
4.7. Generating the C Factor Map and the Erosion Map
5. Experiments and Results
5.1. Implementing the GP Algorithm
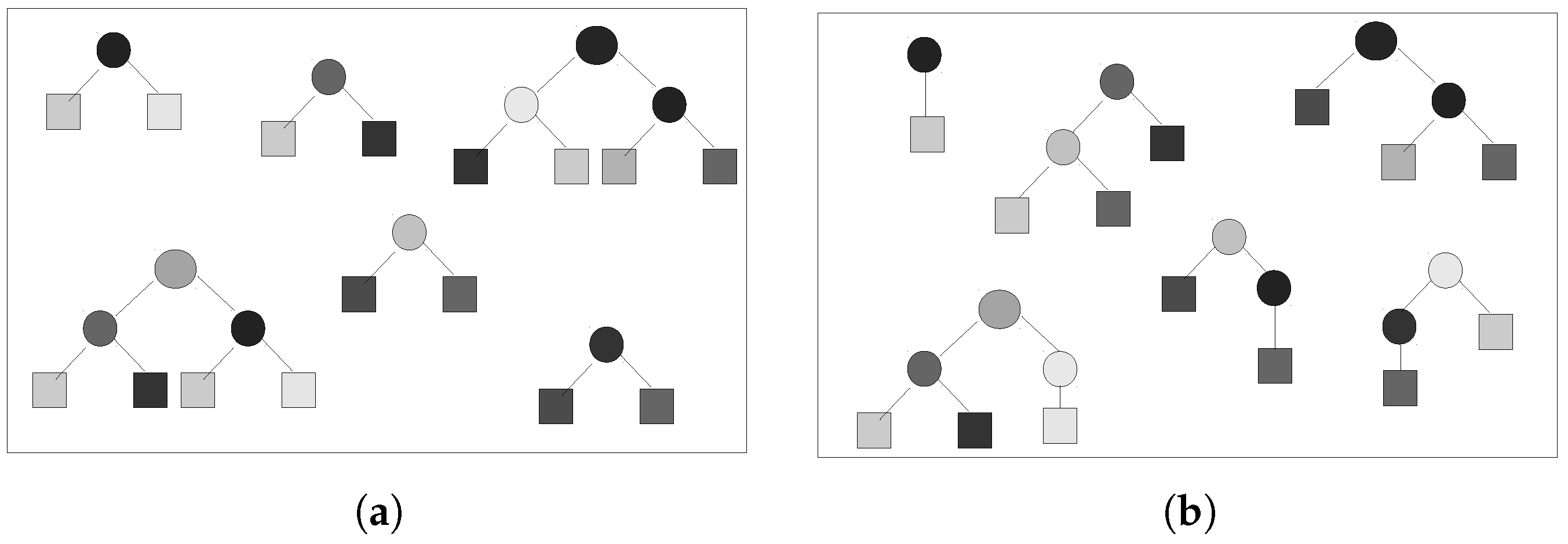
- Initial population: This section generates the initial population and evaluates it according to the fitness function (correlation coefficient) defined in Section 4.5. Population individuals may be generated according to one of three methods: full, grow, and ramped half-and-half. For the full method, the syntactic tree will include all possible nodes at each level (Figure 6a). The grow method generates a random number of nodes at each level, which may generate unbalanced trees (Figure 6b). The ramped Half-and-half method generates half of the tree using the full method and the other half using the grow method. This research employs this last method because it generates trees with a wide variety of sizes and shapes.
- New generation criteria: This section creates a new generation of individuals (children) by either applying genetic mutation operators or crossover (genetic reproduction) to the individuals of the previous population (parents). The following methods may be used to select the next generation’s parents: roulette, stochastic universal sampling, tournament, and lexicographic parsimony pressure tournament [35]. This last method is a special case of the tournament method where competing individuals with the same performance, following the fitness function, are selected according to the one that has the least complexity or the fewer number of nodes. This gives the advantage to simpler VIs that compete against conventional indices and is the reason why lexicographic parsimony pressure tournament was selected as the new generation method.Once the parents have been selected, either mutation or crossover is applied depending on a user-defined probability parameter. Usually, the mutation’s probability is lower than the crossover’s. For this experiment, the crossover probability was 0.7, while the mutation probability was 0.3. The new individuals were evaluated according to the fitness function, and then, these individuals and the best parents became the parents for the next generation. For this research, only the best individual in each generation was preserved for the next generation; this is called the elitist parameter. This procedure was repeated until a stop criteria was met, which for this research was when 50 generations had been produced. This number was employed because the algorithm stopped producing better individuals after 35 iterations.
- Population management: Also called a code bloat in GP parlance, it limits the complexity of individuals. Three parameters are used to define this section: tree depth, maximum dynamic depth, and real maximum depth. If a new individual has a depth greater than the one defined at the beginning, the individual is automatically discarded regardless of the performance provided by the fitness function. This avoids an uncontrolled growth of the syntactic trees that generate the population. The tree depth has two possible values: strict means that the previous rule always applies, while dynamic allows one to preserve individuals that have a better performance than any other previous individual. The dynamic approach verifies that the new individual’s depth is greater than the maximum dynamic depth, but smaller than the real maximum depth. In such a case, the algorithm allows the new individual to survive and sets the maximum dynamic depth to the new individual’s depth value. If later on, there is a better individual with a smaller depth, the previous individual is discarded, and the maximum dynamic depth moves down to the new individual’s depth. In this research, individuals represent a VI in a syntactic tree. Figure 5 shows that the depth of the NDVI syntactic tree was three. The greater the depth of the tree, the greater the complexity; therefore, it is desirable that the GP-synthesized indices have a similar complexity to the conventional indices. Thus, the maximum dynamic depth was set to three, and the real maximum depth to four.
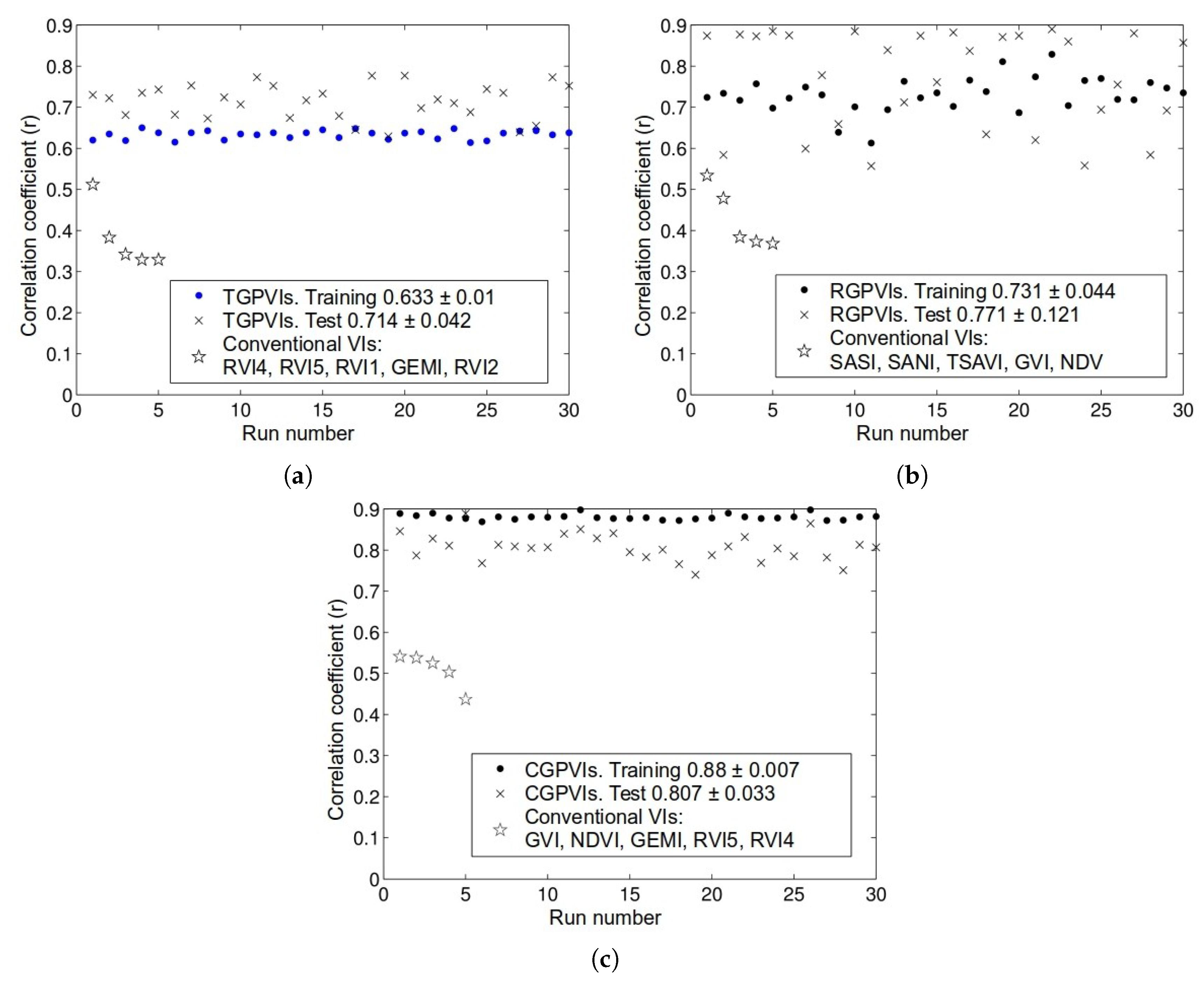
5.2. Methodology Performance Analysis
- The synthesized indices from one watershed produce a good approximation when applied to the other watershed.
- The combined synthesized indices from both watersheds produce a good approximation when they are later applied to each watershed.
5.2.1. First Hypothesis
5.2.2. Second Hypothesis
5.3. Erosion Rate Analysis for the Todos Santos Watershed
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Vrieling, A. Satellite remote sensing for water erosion assessment: A review. CATENA 2006, 65, 2–18. [Google Scholar] [CrossRef]
- Brady, N.C.; Weil, R.R. The Nature and Properties of Soils, 4th ed.; Pearson-Prentice Hall: Upper Saddle River, NJ, USA, 2008; p. 550. [Google Scholar]
- Ananda, J.; Herath, G. Soil erosion in developing countries: A socio-economic appraisal. J. Environ. Manag. 2003, 68, 343–353. [Google Scholar] [CrossRef]
- de Jong, S. Applications of Reflective Remote Sensing for Land Degradation Studies in a Mediterranean Environment. Ph.D. Thesis, Universiteit Utrecht, Utrecht, The Netherlands, 1994. [Google Scholar]
- van der Meer, F.D.; de Jong, S.M. Imaging Spectrometry. Basic Principles and Prospective Applications; Kluwer Academic Publishers: Dordrecht, The Netherlands, 2001. [Google Scholar]
- Flanagan, D.C.; Nearing, M.A. USDA—Water Erosion Prediction Project. Hillslope Profile and Watershed Model Documentation; NSERL Report; USDA-ARS National Soil Erosion Research Laboratory: Washington, DC, USA, 1995; Volume 10.
- Renard, K.; Foster, G.; Weesies, G. Predicting Soil Erosion by Water: A Guide to Conservation Planning with the Revised Universal Soil Loss Equation (RUSLE); U.S. Department of Agriculture: Washington, DC, USA, 1996; Volume 703.
- Wischmeier, W.; Smith, D. Predicting Rainfall Erosion Losses: A Guide to Conservation Planning; U.S. Department of Agriculture: Washington, DC, USA, 1978; Volume 537.
- Borrelli, P.; Robinson, D.A.; Fleischer, L.R.; Lugato, E.; Ballabio, C.; Alewell, C.; Meusburger, K.; Modugno, S.; Schütt, B.; Ferro, V.; et al. An assessment of the global impact of 21st century land use change on soil erosion. Nat. Commun. 2017, 8, 2013. [Google Scholar] [CrossRef] [PubMed]
- Inoue, Y.; Olioso, A. Estimating dynamics of ecosystem CO2 flux and biomass production in agricultural field by synergy of process model and remotely sensed signature. J. Geophys. Res. Atmos. 2006, 111. [Google Scholar] [CrossRef]
- Kurzweil, R. The Age of Intelligent Machines; MIT Press: Cambridge, MA, USA, 1990. [Google Scholar]
- Congalton, R.G.; Balogh, M.; Bell, C.; Green, K.; Milliken, J.A.; Toman, R. Mapping and Monitoring Agricultural Crops and Other Land Cover in the Lower Colorado River Basin. Photogramm. Eng. Remote Sens. 1998, 64, 1107–1113. [Google Scholar]
- Asner, G.P.; Lobell, D.B. A biogeophysical approach for automated SWIR unmixing of soils and vegetation. Remote Sens. Environ. 2000, 74, 99–112. [Google Scholar] [CrossRef]
- Benz, U.C.; Hofmann, P.; Willhauck, G.; Lingenfelder, I.; Heynen, M. Multi-resolution, object-oriented fuzzy analysis of remote sensing data for GIS-ready information. ISPRS J. Photogramm. Remote Sens. 2003, 58, 239–258. [Google Scholar] [CrossRef]
- Guerschman, J.P.; Hill, M.J.; Renzullo, L.J.; Barrett, D.J.; Marks, A.S.; Botha, E.J. Estimating fractional cover of photosynthetic vegetation, non-photosynthetic vegetation and bare soil in the Australian tropical savanna region upscaling the EO-1 Hyperion and MODIS sensors. Remote Sens. Environ. 2009, 113, 928–945. [Google Scholar] [CrossRef]
- Tucker, C.J. Red and Photographic infrared linear combinations for monitoring vegetation. Remote Sens. Environ. 1979, 8, 127–150. [Google Scholar] [CrossRef]
- Van der Knijff, J.; Jones, R.; Montanarella, L. Soil Erosion Risk Assessment in Italy; European Soil Bureau, European Commission: Brussels, Belgium, 1999. [Google Scholar]
- Van der Knijff, J.; Jones, R.; Montanarella, L. Soil Erosion Risk Assessment in Europe; European Soil Bureau, European Commission: Brussels, Belgium, 2000. [Google Scholar]
- Mondal, A.; Khare, D.; Kundu, S. Impact assessment of climate change on future soil erosion and SOC loss. Nat. Hazards 2016, 82, 1515–1539. [Google Scholar] [CrossRef]
- Kourgialas, N.N.; Koubouris, G.C.; Karatzas, G.P.; Metzidakis, I. Assessing water erosion in Mediterranean tree crops using GIS techniques and field measurements: The effect of climate change. Nat. Hazards 2016, 83, 65–81. [Google Scholar] [CrossRef]
- Gupta, S.; Kumar, S. Simulating climate change impact on soil erosion using RUSLE model—A case study in a watershed of mid-Himalayan landscape. J. Earth Syst. Sci. 2017, 126, 43. [Google Scholar] [CrossRef]
- Amanambu, A.C.; Li, L.; Egbinola, C.N.; Obarein, O.A.; Mupenzi, C.; Chen, D. Spatio-temporal variation in rainfall-runoff erosivity due to climate change in the Lower Niger Basin, West Africa. Catena 2019, 172, 324–334. [Google Scholar] [CrossRef]
- Saadoud, D.; Hassani, M.; Peinado, F.J.M.; Guettouche, M.S. Application of fuzzy logic approach for wind erosion hazard mapping in Laghouat region (Algeria) using remote sensing and GIS. Aeolian Res. 2018, 32, 24–34. [Google Scholar] [CrossRef]
- Mangiarotti, S.; Mazzega, P.; Jarlan, L.; Mougin, E.; Baup, F.; Demarty, J. Evolutionary bi-objective optimization of a semi-arid vegetation dynamics model with NDVI and σ0 satellite data. Remote Sens. Environ. 2008, 112, 1365–1380. [Google Scholar] [CrossRef]
- Makkeasorn, A.; Chang, N.; Li, J. Seasonal change detection of riparian zones with remote sensing images and genetic programming in a semi-arid watershed. J. Environ. Manag. 2009, 90, 1069–1080. [Google Scholar] [CrossRef] [PubMed]
- Smith, M.O.; Ustin, S.L.; Adams, J.B.; Gillespie, A. Vegetation in deserts: I. a regional measure of abundance from multispectral images. Remote Sens. Environ. 1990, 31, 1–26. [Google Scholar] [CrossRef]
- Rizeei, H.M.; Saharkhiz, M.A.; Pradhan, B.; Ahmad, N. Soil erosion prediction based on land cover dynamics at the Semenyih watershed in Malaysia using LTM and USLE models. Geocarto Int. 2016, 31, 1158–1177. [Google Scholar] [CrossRef]
- Yang, X. Deriving RUSLE cover factor from time-series fractional vegetation cover for hillslope erosion modelling in New South Wales. Soil Res. 2014, 52, 253–261. [Google Scholar] [CrossRef]
- Puente, C.; Olague, G.; Smith, S.V.; Bullock, S.H.; Hinojosa-Corona, A.; González-Botello, M.A. A genetic programming approach to estimate vegetation cover in the context of soil erosion assessment. Photogramm. Eng. Remote Sens. 2011, 77, 363–376. [Google Scholar] [CrossRef]
- Trabucchi, M.; Puente, C.; Comin, F.A.; Olague, G.; Smith, S.V. Mapping erosion risk at the basin scale in a Mediterranean environment with opencast coal mines to target restoration actions. Reg. Environ. Chang. 2012, 12, 675–687. [Google Scholar] [CrossRef]
- Nicu, I.C. Application of analytic hierarchy process, frequency ratio, and statistical index to landslide susceptibility: An approach to endangered cultural heritage. Environ. Earth Sci. 2018, 77, 79. [Google Scholar] [CrossRef]
- Smith, S.V.; Bullock, S.H.; Hinojosa-Corona, A.; Franco-Vizcaíno, E.; Escoto-Rodríguez, M.; Kretzschmar, T.G.; Farfán, L.M.; Salazar-Ceseña, J.M. Soil Erosion and Significance for Carbon Fluxes in a Mountainous Mediterranean-Climate Watershed. Ecol. Appl. 2007, 17, 1379–1387. [Google Scholar] [CrossRef] [PubMed]
- Symeonakis, E.; Drake, N. Monitoring desertification and land degradation over sub-Saharan Africa. Int. J. Remote Sens. 2004, 25, 573–592. [Google Scholar] [CrossRef]
- Zhao, J.; Vanmaercke, M.; Chen, L.; Govers, G. Vegetation cover and topography rather than human disturbance control gully density and sediment production on the Chinese Loess Plateau. Geomorphology 2016, 274, 92–105. [Google Scholar] [CrossRef]
- Poli, R.; Langdon, W.B.; McPhee, N.F. A Field Guide to Genetic Programming. 2008. Available online: http://www.gp-field-guide.org.uk (accessed on 13 January 2019).
- Koppen, W. Die Klimate der erde, Grundi der Klimakunde; De Gryter: Berlin/Leipzig, Germany, 1923. [Google Scholar]
- Comision Nacional Forestal (CONAFOR). 2008. Available online: http://www.gob.mx/conafor (accessed on 13 January 2019).
- Comision Nacional del Agua (CNA). 2017. Available online: http://smn.cna.gob.mx/es/informacion-climatologica-ver-estado?estado=bc (accessed on 13 January 2019).
- Folly, A.; Bronsveld, M.C.; Clavaux, M. A Knowledge-based Approach for C-factor Mapping in Spain using Landsat TM and GIS. Int. J. Remote Sens. 1996, 17, 2401–2415. [Google Scholar] [CrossRef]
- Xiao, X.; Gertner, G.; Wang, G.; Anderson, A. Optimal sampling scheme for estimation landscape mapping of vegetation cover. Landsc. Ecol. 2004, 20, 375–387. [Google Scholar] [CrossRef]
- González-Botello, M.; Bullock, S. Erosion-reducing cover in semi-arid shrubland. J. Arid Environ. 2012, 84, 19–25. [Google Scholar] [CrossRef]
- González Botello, M.A. Estimaciones de la Cobertura Vegetal y del Suelo en el Noroeste de Baja California y su Aplicación a la Modelación de la Erosión. Master’s Thesis, Facultad de Ciencias, Universidad Autónoma de Baja California, Ensenada, Baja California, Mexico, 2010. [Google Scholar]
- Bauer, H. The statistical analysis of chaparral and other plant communities by means of transect samples. Ecology 1943, 24, 45–60. [Google Scholar] [CrossRef]
- Zippin, D.B.; Vanderwier, J.M. Scrub community descriptions of the Baja California peninsula, Mexico. Madroño 1994, 41, 85–119. [Google Scholar]
- Weltz, M.A.; Renard, K.G.; Simanton, J.R. Revised Universal Soil Loss Equation for western rangeland. In Symposium of Strategies for Classification and Management of Native Vegetation for Food Production in Arid Zones; USDA-GTR: Tuczon, AZ, USA, 1987. [Google Scholar]
- U.S. Geological Survery (USGS). The Global Visualization Viewer. 2017. Available online: http://glovis.usgs.gov/ (accessed on 13 January 2019).
- Instituto Geografico Nacional (Spain). 2017. Available online: https://blogpnt.wordpress.com/ (accessed on 13 January 2019).
- Vincent, R.K. Fundamentals of Geological and Environmental Remote Sensing; Prentice Hall: Upper Sadle River, NJ, USA, 1997; p. 370. [Google Scholar]
- Chander, G.; Markham, B. Revised LANDSAT-5 TM radiometric calibration procedures and postcalibrationdynamic ranges. IEEE Trans. Geosci. Remote Sens. 2003, 41, 2674–2677. [Google Scholar] [CrossRef]
- Jordan, C.F. Derivation of leaf area index from quality of light on the forest floor. Ecology 1969, 50, 663–666. [Google Scholar] [CrossRef]
- Rouse, J.W.; Haas, R.H.; Schell, J.A.; Deering, D.W. Monitoring vegetation systems in the great plains with ERTS. In Third ERTS Symposium; NASA: Washington, DC, USA, 1973; pp. 309–317. [Google Scholar]
- Crippen, R.E. Calculating the Vegetation Index Faster. Remote Sens. Environ. 1990, 34, 71–73. [Google Scholar] [CrossRef]
- Lillesand, T.M.; Kiefer, R.W. Remote Sensing and Image Interpretation, 2nd ed.; John Wiley and Sons: New York, NY, USA, 1987; p. 721. [Google Scholar]
- Huete, A.R. A Soil-Adjusted Vegetation Index (SAVI). Remote Sens. Environ. 1988, 25, 295–309. [Google Scholar] [CrossRef]
- Major, D.J.; Baret, F.; Guyot, G. A ratio vegetation index adjusted for soil brightness. Int. J. Remote Sens. 1990, 11, 727–740. [Google Scholar] [CrossRef]
- Qi, J.; Chehbouni, A.; Huete, A.R.; Kerr, Y.H. Modified Soil Adjusted Vegetation Index (MSAVI). Remote Sens. Environ. 1994, 48, 119–126. [Google Scholar] [CrossRef]
- Baret, F.; Guyot, G.; Major, D. TSAVI: A vegetation index which minimizes soil brightness effects on LAI or APAR estimation. In Proceedings of the 12th Canadian Symposium on Remote Sensing IGARSS 1990, Vancouver, BC, Canada, 10–14 July 1990. [Google Scholar]
- Rondeaux, O.; Steven, M.; Baret, F. Optimization of Soil-Adjusted Vegetation Index. Remote Sens. Environ. 1996, 55, 95–107. [Google Scholar] [CrossRef]
- Clevers, J.G.P.W. The derivation of a simplified reflectance model for the estimation of leaf area index. Remote Sens. Environ. 1988, 35, 53–70. [Google Scholar] [CrossRef]
- Richardson, A.; Wieoand, C. Distinguishing vegetation from soil background information. Photogramm. Eng. Remote Sens. 1977, 43, 541–552. [Google Scholar]
- Pinty, B.; Verstraete, M.M. GEMI: A Non-Linear Index to Monitor Global Vegetation from Satellites. Vegetatio 1992, 101, 15–20. [Google Scholar] [CrossRef]
- Kaufman, Y.J.; Tanre, D. Atmospherically resistant vegetation index (ARVI) for EOS-MODIS. IEEE Trans. Geosci. Remote Sens. 1992, 30, 261–270. [Google Scholar] [CrossRef]
- Liu, H.Q.; Huete, A. A feedback based modification of the NDVI to minimize canopy background and atmospheric noise. IEEE Trans. Geosci. Remote Sens. 1995, 33, 457–465. [Google Scholar]
- Crist, E.P.; Cicone, R.C. Application of the tasseled cap concept to simulated thematic mapper data. Photogramm. Eng. Remote Sens. 1984, 50, 343–352. [Google Scholar]
- Gao, B. NDWI—A normalized difference water index for remote sensing of vegetation liquid water from space. Remote Sens. Environ. 1996, 58, 257–266. [Google Scholar] [CrossRef]
- Hunt, E.R.; Rock, B.N. Detection of changes in leaf water content using near and middle-infrared reflectances. Remote Sens. Environ. 1989, 33, 43–54. [Google Scholar]
- Fensholt, R.; Sandholt, I. Derivation of a shortwave infrared water stress index from MODIS near- and shortwave infrared data in a semiarid environment. Remote Sens. Environ. 2003, 87, 111–121. [Google Scholar] [CrossRef]
- Khana, S.; Palacios-Orueta, A.; Whiting, M.L.; Ustin, S.L.; Riaño, D.; Litago, J. Develoment of angle indexes for soil moisture estimation, dry matter detection and land-cover discrimination. Remote Sens. Environ. 2007, 109, 154–165. [Google Scholar] [CrossRef]
- Olague, G.; Trujillo, L. Evolutionary-computer-assisted design of image operators that detect interest points using genetic programming. Image Vis. Comput. 2011, in press. [Google Scholar] [CrossRef]
- Sabins, F.F. Remote Sensing: Principles and Interpretation, 3rd ed.; Freeman: New York, NY, USA, 1997. [Google Scholar]
- Lowry, R. Concepts and Applications of Inferential Statistics; Vassar College: Poughkeepsie, NY, USA, 2005. [Google Scholar]
- Inoue, Y.; Peñuelas, J.; Miyata, A.; Mano, M. Normalized difference spectral indices for estimating photosynthetic efficiency and capacity at a canopy scale derived from hyperspectral and CO2 flux measurements in rice. Remote Sens. Environ. 2008, 112, 156–172. [Google Scholar] [CrossRef]
- Silva, S.; Almeida, J. Gplab-a genetic programming toolbox for matlab. In Proceedings of the Nordic MATLAB Conference (NMC-2003), Copenhagen, Denmark, 21–22 October 2005; pp. 273–278. [Google Scholar]
- Koza, J.R. Genetic Programing: On the Programming of Computers by Means of Natural Selection; MIT Press: Cambridge, MA, USA, 1992; p. 840. [Google Scholar]
- De Jong, S. Derivation of vegetative variables from a Landsat TM image for modelling soil erosion. Earth Surf. Process. Landf. 1994, 19, 165–178. [Google Scholar] [CrossRef]
- Asis, A.M.; Omasa, K. Estimation of Vegetation Parameter for Modeling Soil Erosion using Linear Spectral Mixture Analysis of Landsat ETM data. ISPRS J. Photogramm. Remote Sens. 2007, 62, 309–324. [Google Scholar] [CrossRef]
- Lin, C.; Lin, W.; Chou, W. Soil erosion prediction and sediment yield estimation: The Taiwan experience. Soil Tillage Res. 2002, 68, 143–152. [Google Scholar] [CrossRef]
- Lu, H.; Prosser, I.P.; Moran, C.J.; Gallant, J.C.; Priestly, G.; Stevenson, J.G. Predicting sheetwash and rill erosion over Australian continent. Aust. J. Remote Sens. 2003, 41, 1037–1062. [Google Scholar] [CrossRef]
- Streck, N.A.; Rundquist, D.; Connot, J. Estimating Residual Wheat Dry Matter from RemoteSensing Measurements. Photogramm. Eng. Remote Sens. 2002, 68, 1193–1201. [Google Scholar]
- Matsuchita, B.; Yang, W.; Chen, J.; Onda, Y.; Qiu, G. Sensitivity of the Enhanced Vegetation Index (EVI) and Normalized Difference Vegetation Index (NDVI) to Topographic Effects: A Case Study in High-Density Cypress Forest. Sensors 2007, 7, 2636–2651. [Google Scholar] [CrossRef] [PubMed]
- Renard, K.G.; Freimund, J.R. Using monthly precipitation data to estimate the R-factor in the revised USLE. J. Hydrol. 1994, 157, 287–306. [Google Scholar] [CrossRef]
- Griffin, M.L.; Beasley, D.B.; Fletcher, J.G.; Foster, G.R. Estimating soil loss on topographically nonuniform field and farm units. J. Soil Water Conserv. 1988, 43, 326–331. [Google Scholar]
- Moore, I.D.; Wilson, J.P. Length-slope factors for the Revised Universal Soil Loss Equation: Simplified method of estimation. J. Soil Water Conserv. 1992, 47, 423–428. [Google Scholar]
- Instituto Nacional de Estadística y Geografía (INEGI). Digital Elevation Models. 2017. Available online: http://www.beta.inegi.org.mx/app/geo2/elevacionesmex/ (accessed on 13 January 2019).
- Instituto Nacional de Estadística y Geografía (INEGI). Soil Charts. 2017. Available online: https://www.inegi.org.mx/temas/mapas/edafologia/ (accessed on 13 January 2019).
- Karydas, C.G.; Panagos, P.; Gitas, I.Z. A classification of water erosion models according to their geospatial characteristics. Int. J. Digit. Earth 2014, 7, 229–250. [Google Scholar] [CrossRef]


| Band | Name | Wavelength |
|---|---|---|
| 1 | Blue light (B) | 0.45–0.52 m |
| 2 | Green light (G) | 0.53–0.60 m |
| 3 | Red light (R) | 0.63–0.69 m |
| 4 | Near-Infrared (NIR) | 0.76–0.90 m |
| 5 | Shortwave Infrared Channel 1 (SWIR1) | 1.55–1.75 m |
| 6 | Thermal Infrared (TIR) | 10.4–12.5 m |
| 7 | Shortwave Infrared Channel 2 (SWIR2) | 2.08–2.35 m |
| Indices | Equation | Ref. |
|---|---|---|
| RVI1 | [50] | |
| RVI2 | based on [50] | |
| RVI3 | based on [50] | |
| RVI4 | based on [50] | |
| RVI5 | based on [50] | |
| RVI6 | based on [50] | |
| NDVI | [51] | |
| IPVI | [52] | |
| DVI | [53] | |
| SAVI | where L is a correction factor between 0 and 1 | [54] |
| SAVI2 | where m and bare the slope and intercept of the soil line. These parameters are used in the next six indices as well | [55] |
| MSAVI | same that SAVI, but | [56] |
| MSAVI2 | [56] | |
| TSAVI | [57] | |
| OSAVI | [58] | |
| WDVI | [59] | |
| PVI | [60] | |
| GEMI | where | [61] |
| ARVI | ; where | [62] |
| EVI | where . | [63] |
| GVI1 | [64] | |
| GVI2 | [64] | |
| GVI3 | [64] | |
| NDWI | [65] | |
| NDII | [66] | |
| SIWSI | [67] | |
| ANIR | where a, b, and c are Euclidean distances between R, NIR and SWIR | [68] |
| SASI | where is defined like , but a, b, and c are Euclidean distances between NIR, SWIR1 and SWIR2 | [68] |
| SANI | is defined like in SASI | [68] |
| Elements | Description |
|---|---|
| Terminals | |
| B, G, R NIR, SWIR1, SWIR2 | Satellite image’s spectral bands |
| Calculated spectral angles from the available bands | |
| RVI1, RVI2, RVI4, RVI5 GEMI, NDVI, EVI | Best-performing conventional indices |
| a, b | Slope and the intersect of the soil line |
| Functions | |
| +, −, × | Arithmetic operators |
| NDSI, RSI | Compound operators |
| Todos Santos | Rio Martin | |
|---|---|---|
| Todos Santos | 0.633 ± 0.01 | 0.323 ± 0.010 |
| Max. 0.65 | Max. 0.363 | |
| Min. 0.614 | Min. 0.290 | |
| Rio Martin | 0.329 ± 0.11 | 0.731 ± 0.044 |
| Max. 0.401 | Max. 0.829 | |
| Min. 0.137 | Min. 0.613 |
| Index | GVI3 | NDVI | GEMI | RVI5 | RVI4 | SASI | NDII | OSAVI | RVI1 | TSAVI |
|---|---|---|---|---|---|---|---|---|---|---|
| 0.541 | 0.538 | 0.525 | 0.503 | 0.437 | 0.349 | 0.341 | 0.328 | 0.309 | 0.302 |
| Index | Formula | Dif. | ||
|---|---|---|---|---|
| CGPVI1 | 0.887 | 0.849 | 0.037 | |
| CGPVI2 | 0.884 | 0.787 | 0.097 | |
| CGPVI3 | 0.890 | 0.828 | 0.061 | |
| CGPVI4 | 0.878 | 0.811 | 0.067 | |
| CGPVI5 | 0.861 | 0.899 | 0.038 | |
| CGPVI6 | 0.869 | 0.768 | 0.102 | |
| CGPVI7 | 0.881 | 0.813 | 0.068 | |
| CGPVI8 | 0.875 | 0.809 | 0.066 | |
| CGPVI9 | 0.881 | 0.805 | 0.075 | |
| CGPVI10 | 0.880 | 0.807 | 0.073 | |
| CGPVI11 | 0.882 | 0.840 | 0.042 | |
| CGPVI12 | 0.898 | 0.851 | 0.048 | |
| CGPVI13 | 0.879 | 0.829 | 0.050 | |
| CGPVI14 | 0.878 | 0.840 | 0.038 | |
| CGPVI15 | 0.877 | 0.795 | 0.083 | |
| CGPVI16 | 0.879 | 0.783 | 0.096 | |
| CGPVI17 | 0.873 | 0.801 | 0.072 | |
| CGPVI18 | 0.872 | 0.766 | 0.105 | |
| CGPVI19 | 0.876 | 0.740 | 0.136 | |
| CGPVI20 | 0.878 | 0.788 | 0.090 | |
| CGPVI21 | 0.890 | 0.809 | 0.081 | |
| CGPVI22 | 0.881 | 0.832 | 0.049 | |
| CGPVI23 | 0.877 | 0.769 | 0.108 | |
| CGPVI24 | 0.878 | 0.804 | 0.074 | |
| CGPVI25 | 0.881 | 0.785 | 0.096 | |
| CGPVI26 | 0.898 | 0.865 | 0.033 | |
| CGPVI27 | 0.872 | 0.782 | 0.090 | |
| CGPVI28 | 0.873 | 0.751 | 0.122 | |
| CGPVI29 | 0.881 | 0.813 | 0.068 | |
| CGPVI30 | 0.882 | 0.807 | 0.075 |
| Method employed to calculate C | Erosion (Mg·km·year) |
|---|---|
| Field data | |
| Indices generated from field data from the Todos Santos and Rio Martin watersheds | |
| CGPVI26 | |
| CGPVI1 | |
| GVI3 | |
| Spectral classification method | |
| Spectral classification method | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Puente, C.; Olague, G.; Trabucchi, M.; Arjona-Villicaña, P.D.; Soubervielle-Montalvo, C. Synthesis of Vegetation Indices Using Genetic Programming for Soil Erosion Estimation. Remote Sens. 2019, 11, 156. https://doi.org/10.3390/rs11020156
Puente C, Olague G, Trabucchi M, Arjona-Villicaña PD, Soubervielle-Montalvo C. Synthesis of Vegetation Indices Using Genetic Programming for Soil Erosion Estimation. Remote Sensing. 2019; 11(2):156. https://doi.org/10.3390/rs11020156
Chicago/Turabian StylePuente, Cesar, Gustavo Olague, Mattia Trabucchi, P. David Arjona-Villicaña, and Carlos Soubervielle-Montalvo. 2019. "Synthesis of Vegetation Indices Using Genetic Programming for Soil Erosion Estimation" Remote Sensing 11, no. 2: 156. https://doi.org/10.3390/rs11020156
APA StylePuente, C., Olague, G., Trabucchi, M., Arjona-Villicaña, P. D., & Soubervielle-Montalvo, C. (2019). Synthesis of Vegetation Indices Using Genetic Programming for Soil Erosion Estimation. Remote Sensing, 11(2), 156. https://doi.org/10.3390/rs11020156