Detecting Targets above the Earth’s Surface Using GNSS-R Delay Doppler Maps: Results from TDS-1
Abstract
1. Introduction
2. TDS-1 Satellite GNSS-R Data
3. Analyses of Possible Causes
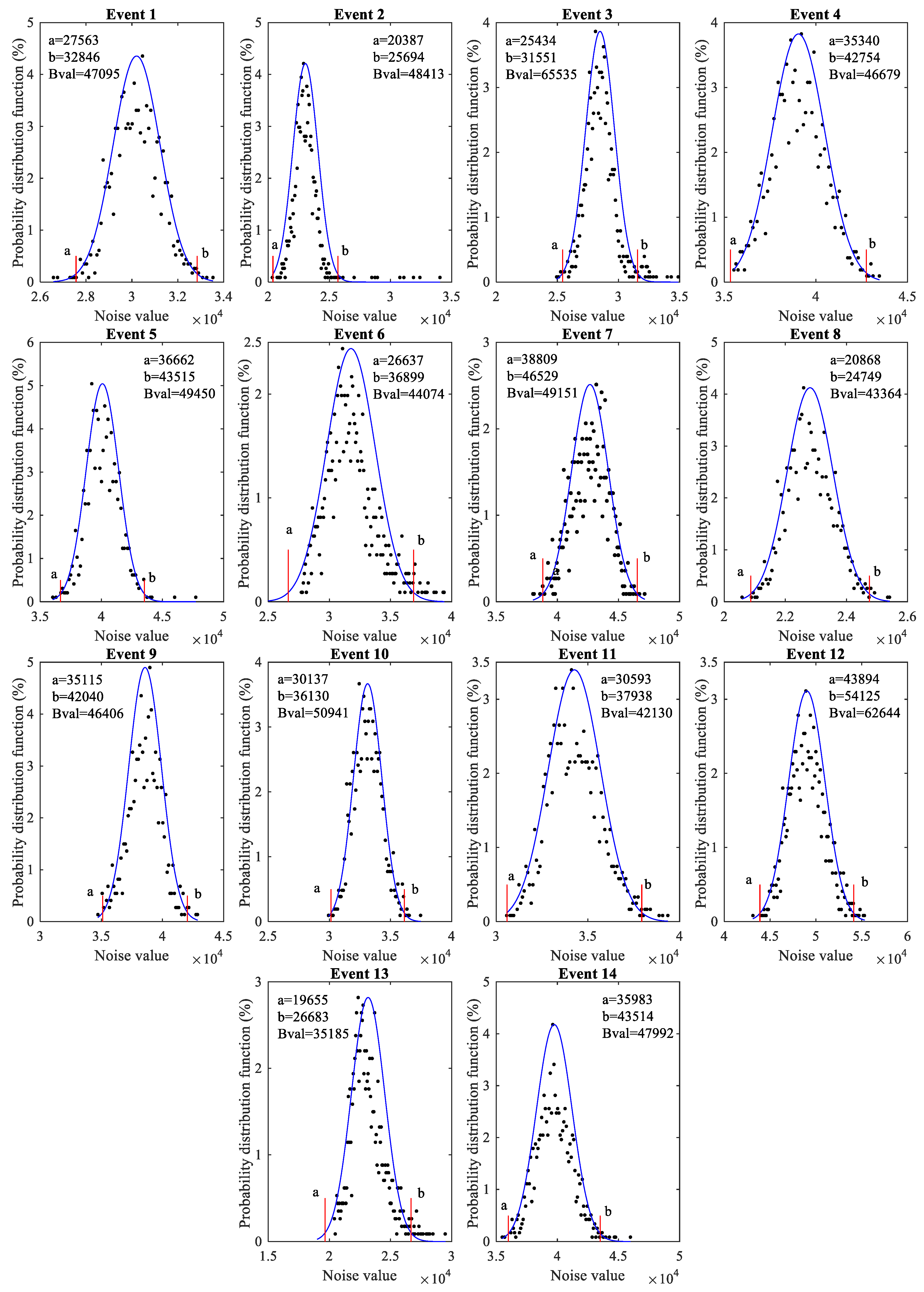
3.1. Random Noise
3.2. DDM Generator Losing Tracking
3.3. Leakage of Direct Signal
3.4. Aliasing
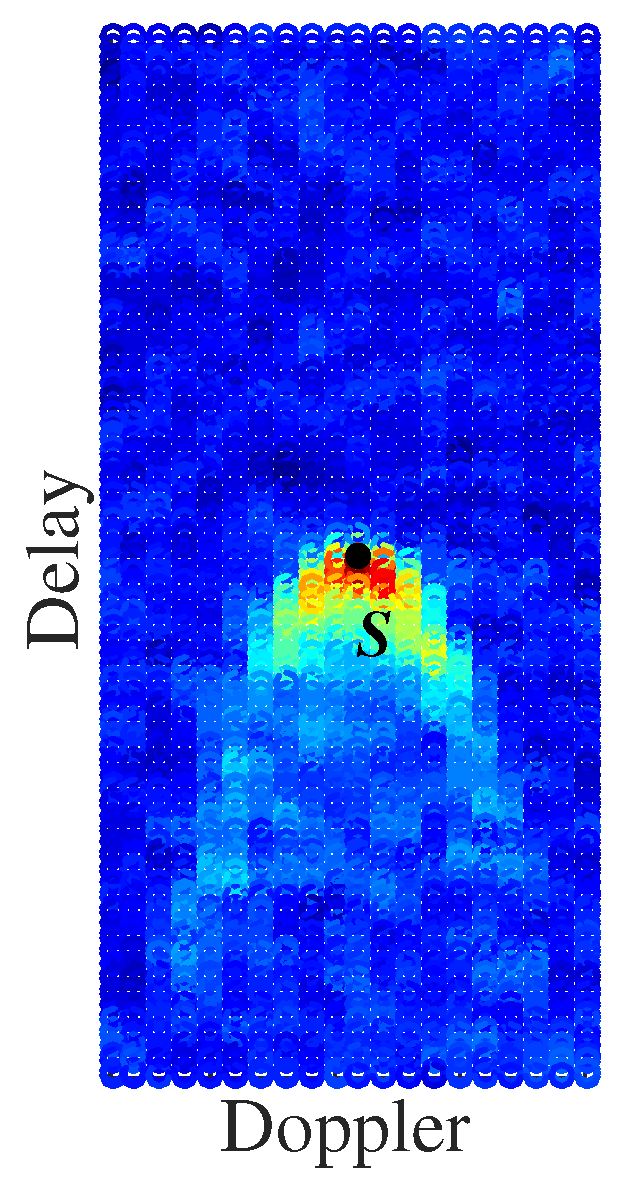
3.5. Reflections from an Earth’s Surface Target
3.6. GNSS Radio-Occultation
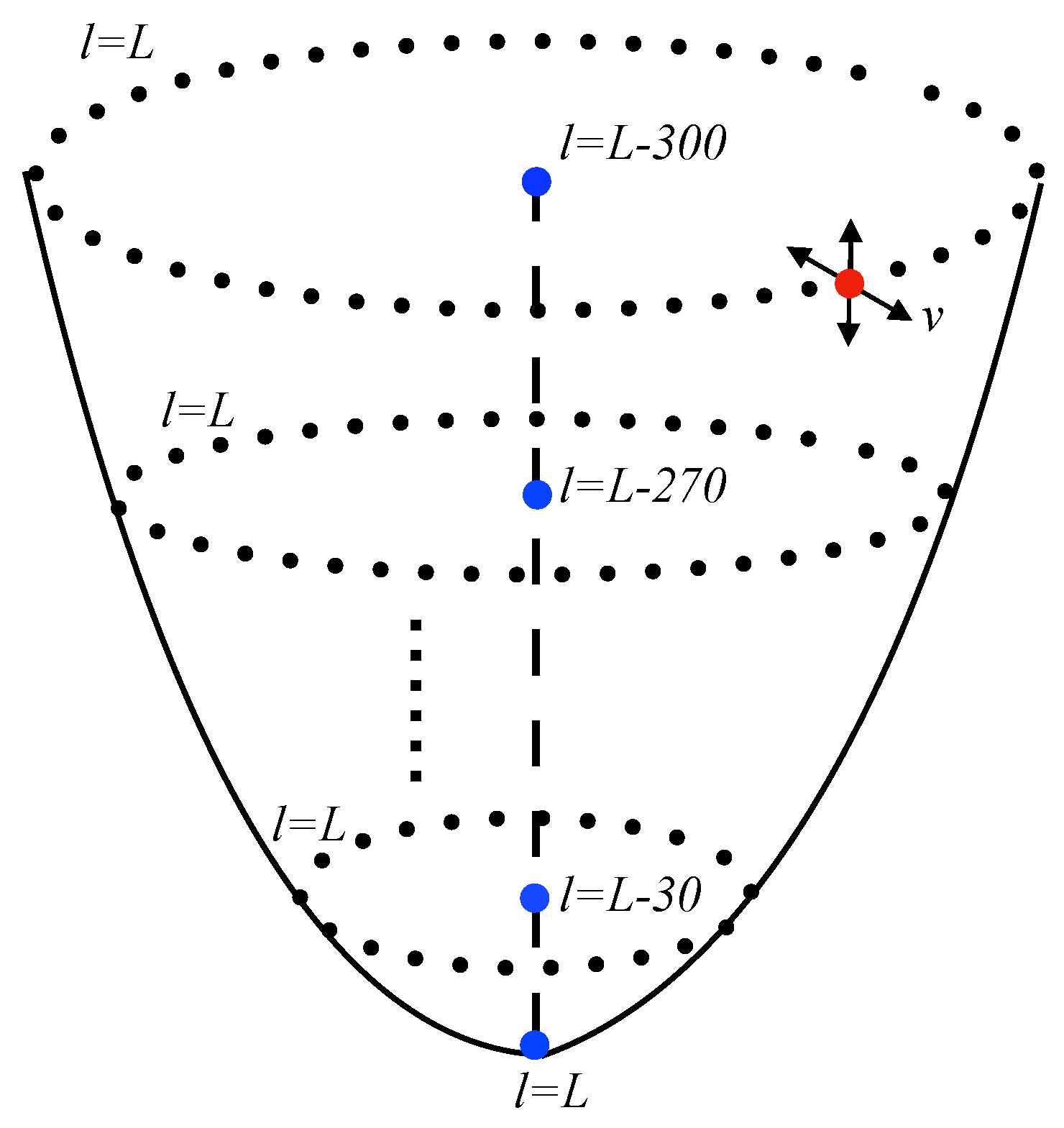
4. Object Positioning
5. Results Analyses
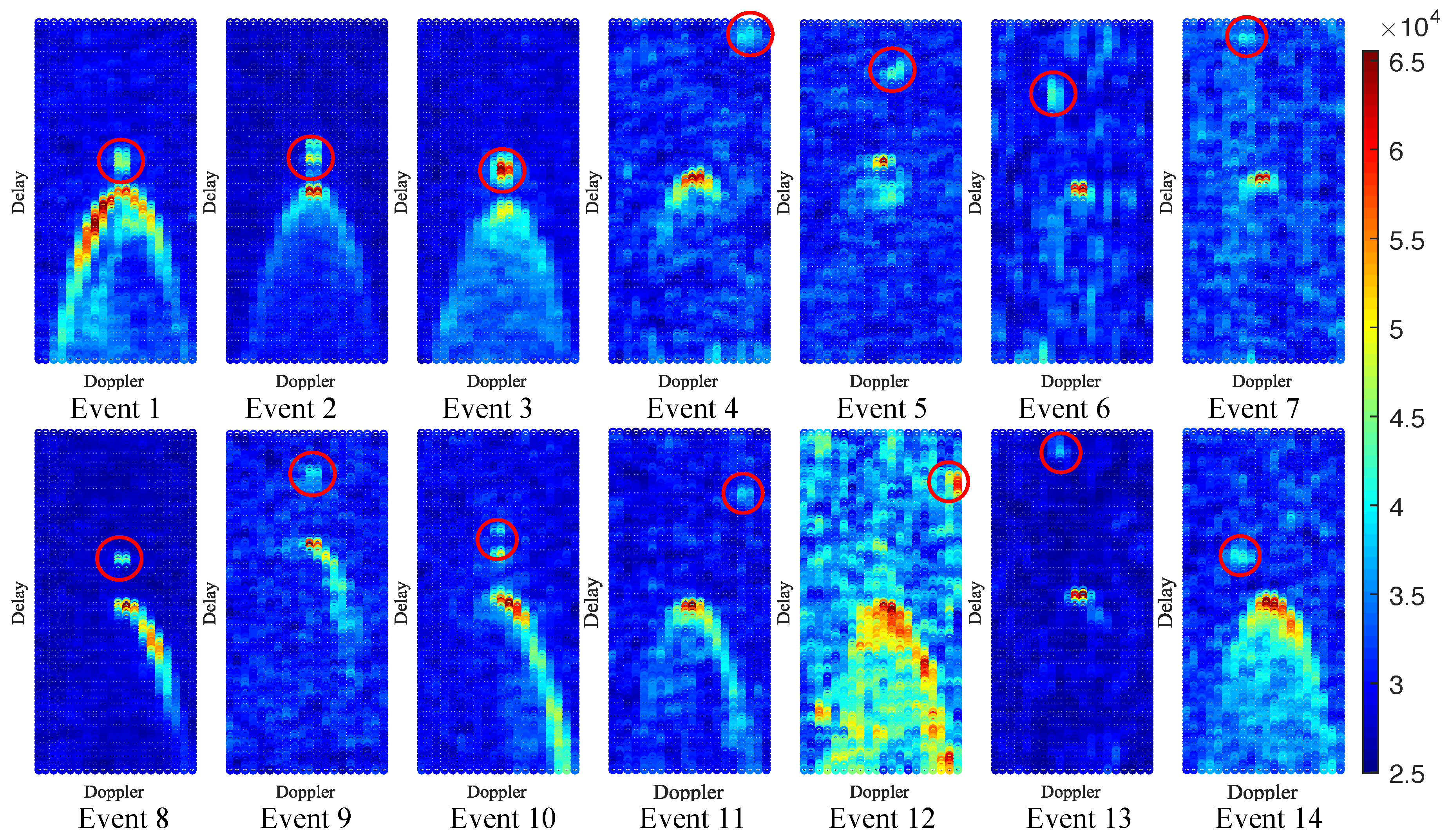
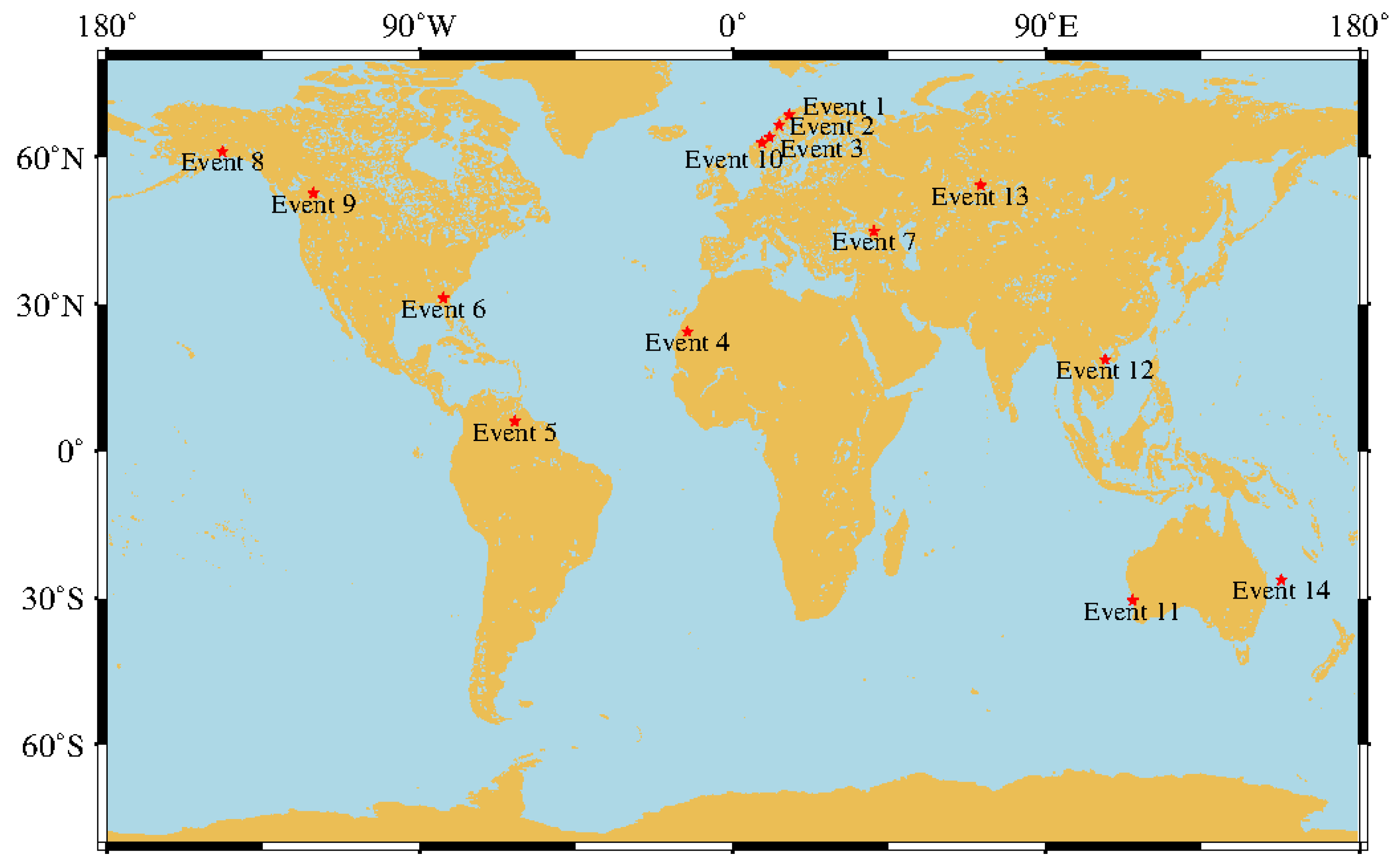
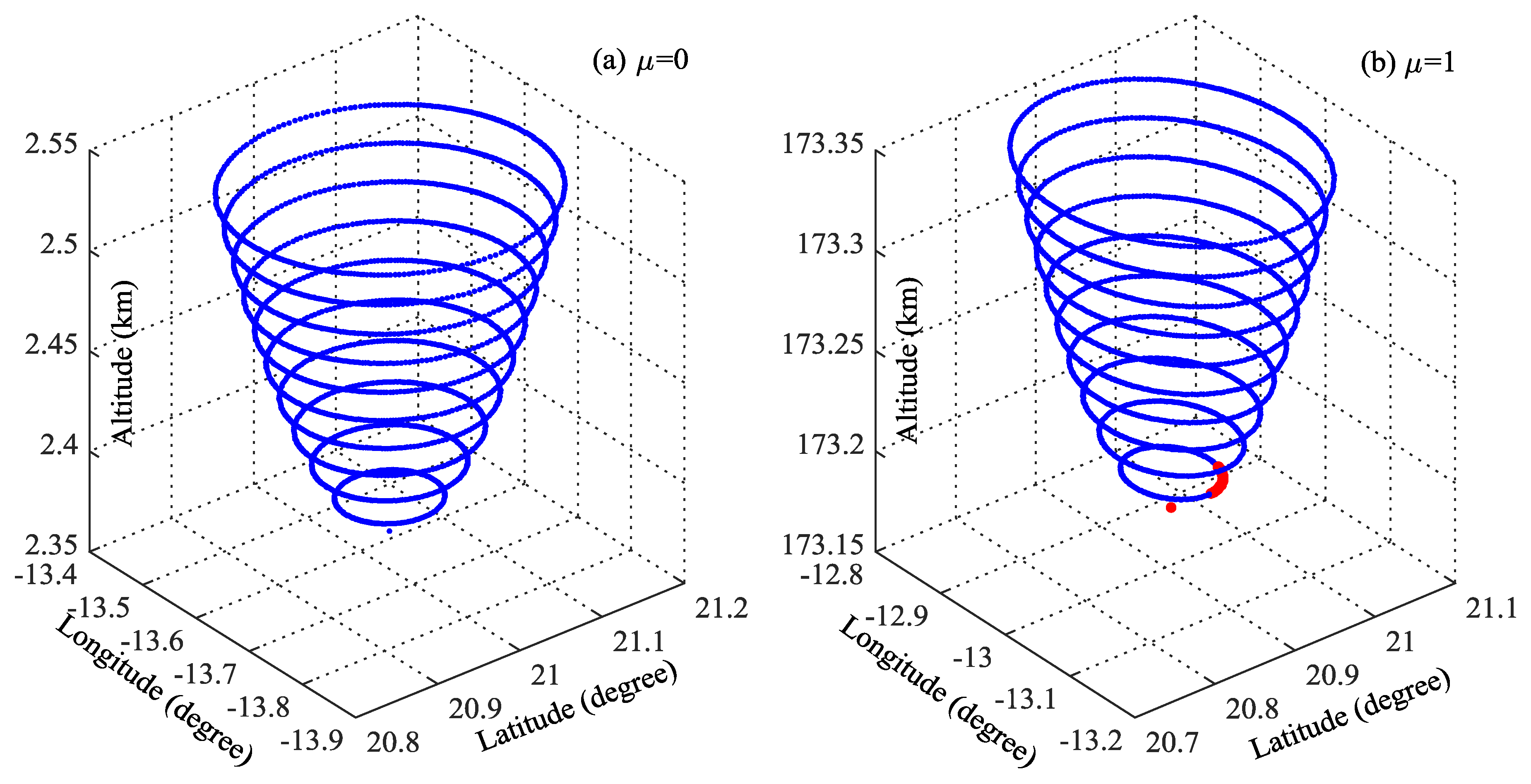
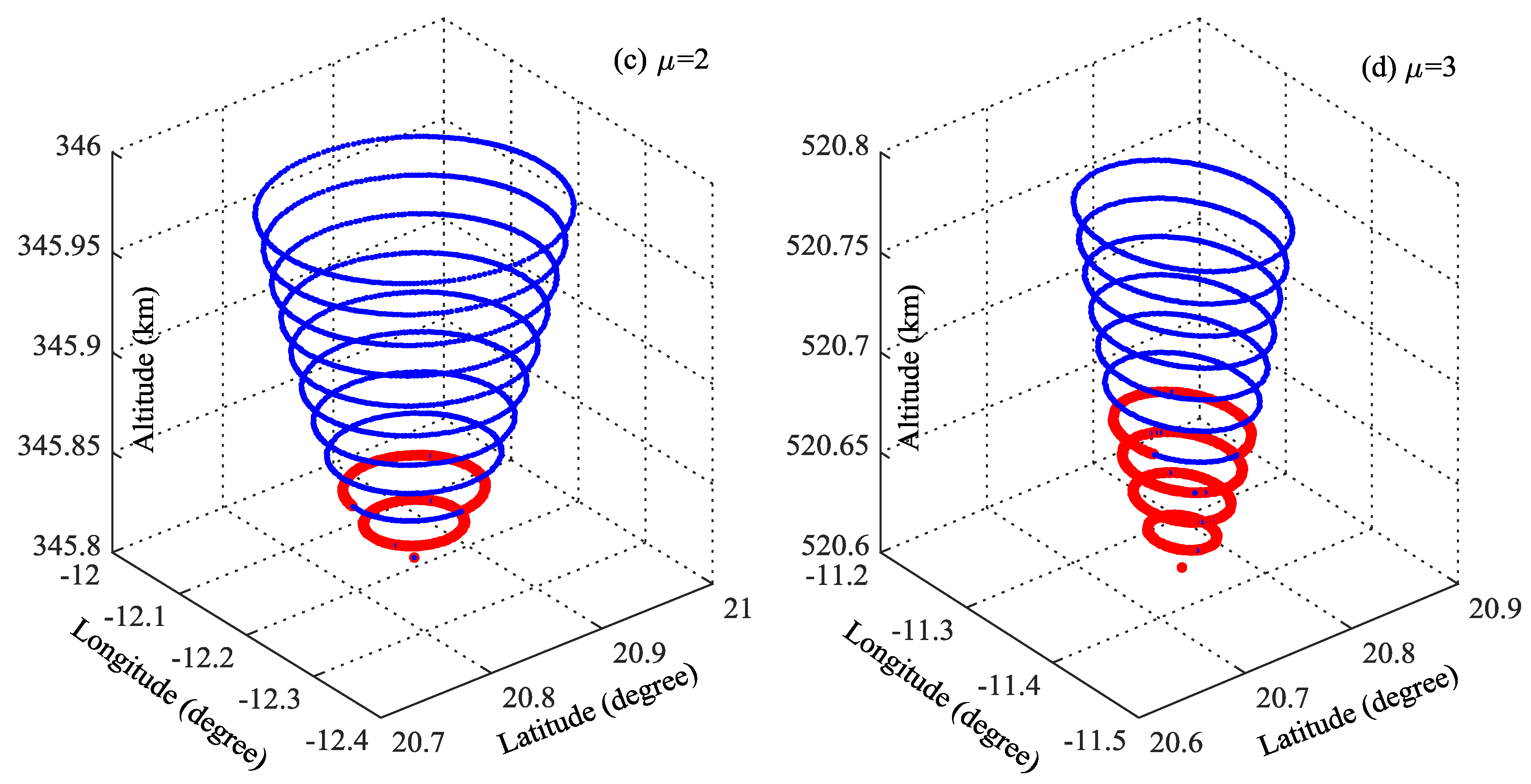
5.1. Target Position Retrieval
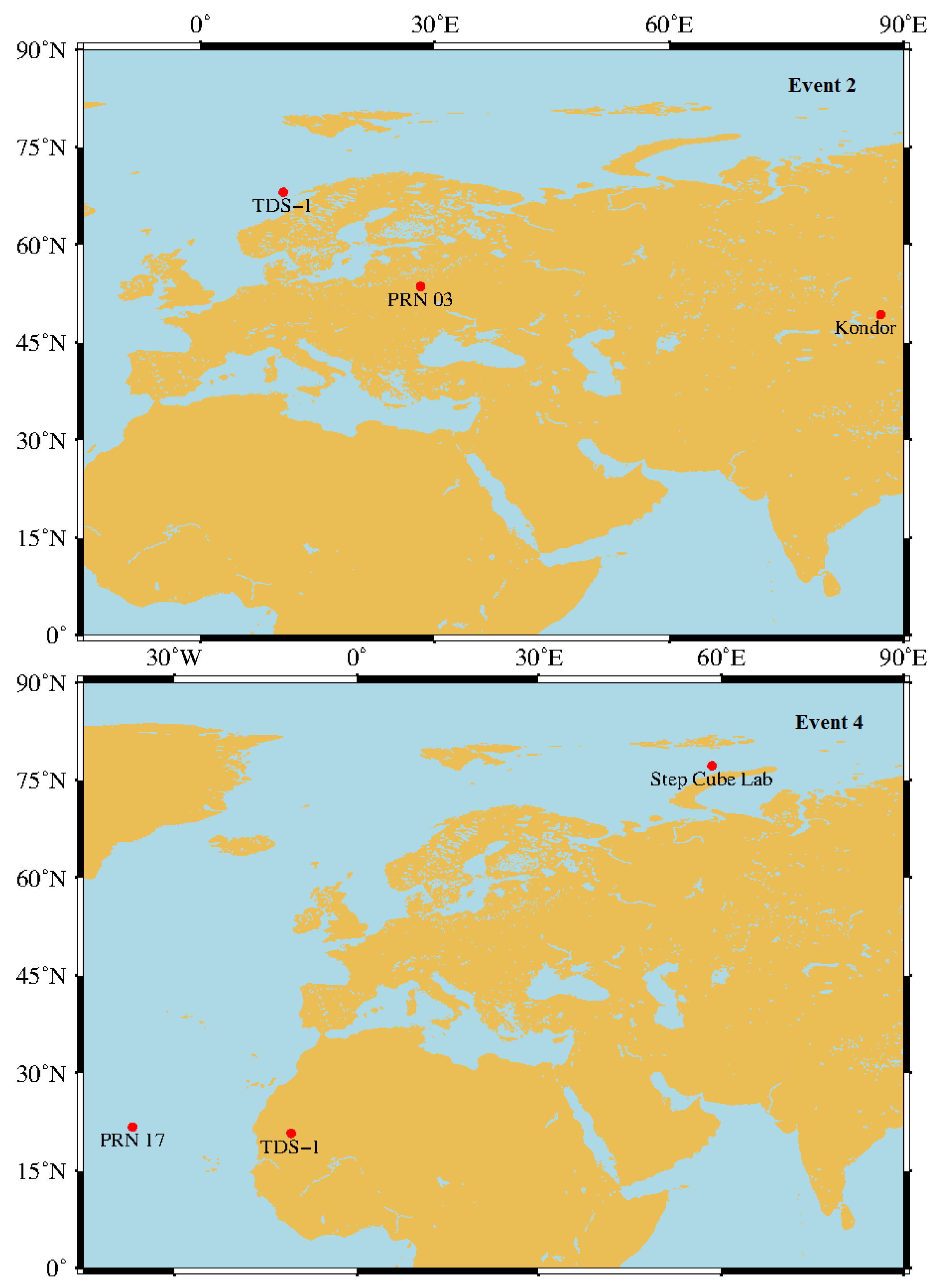
5.2. Verification of Suspected Objects
6. Conclusions and Remarks
Author Contributions
Funding
Conflicts of Interest
References
- Hall, C.; Cordey, R. Multistatic scatterometry. In Proceedings of the IGARSS, Edinburgh, UK, 12–16 September 1988; pp. 561–562. [Google Scholar]
- Martin-Neira, M.; Caparrini, M.; Font-Rossello, J.; Lannelongue, S.; Vallmitjana, C.S. The PARIS concept: An experimental demonstration of sea surface altimetry using GPS reflected signals. IEEE Trans. Geosci. Remote Sens. 2001, 39, 142–150. [Google Scholar] [CrossRef]
- Garrison, J.L.; Komjathy, A.; Zavorotny, V.U.; Katzberg, S.J. Wind speed measurement using forward scattered GPS signals. IEEE Trans. Geosci. Remote Sens. 2002, 40, 50–65. [Google Scholar] [CrossRef]
- Rius, A.; Aparicio, J.M.; Cardellach, E.; Martín-Neira, M.; Chapron, B. Sea surface state measured using GPS reflected signals. Geophys. Res. Lett. 2002, 29, 37-1–37-4. [Google Scholar] [CrossRef]
- Gleason, S. Remote Sensing of Ocean, ICE and land Surfaces Using Bistatically Scattered GNSS Signals from Low Earth Orbit. Ph.D Thesis, University of Surrey, London, UK, 2006. [Google Scholar]
- Unwin, M.; Jales, P.; Tye, J.; Gommenginger, C.; Foti, G.; Rosello, J. Spaceborne GNSS-reflectometry on TechDemoSat-1: Early mission operations and exploitation. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2016, 9, 4525–4539. [Google Scholar] [CrossRef]
- Ruf, C.S.; Gleason, S.; Jelenak, Z.; Katzberg, S.; Ridley, A.; Rose, R.; Scherrer, J.; Zavorotny, V. The CYGNSS nanosatellite constellation hurricane mission. In Proceedings of the IGARSS, Munich, Germany, 22–27 July 2012; pp. 214–216. [Google Scholar]
- Wickert, J.; Cardellach, E.; Martín-Neira, M.; Bandeiras, J.; Bertino, L.; Andersen, O.B.; Camps, A.; Catarino, N.; Chapron, B.; Fabra, F. GEROS-ISS: GNSS reflectometry, radio occultation, and scatterometry onboard the international space station. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2016, 9, 4552–4581. [Google Scholar] [CrossRef]
- Martín-Neira, M.; Li, W.; Andrés-Beivide, A.; Ballesteros-Sels, X. “Cookie”: A satellite concept for GNSS remote sensing constellations. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2016, 9, 4593–4610. [Google Scholar] [CrossRef]
- Høeg, P.; Fragner, H.; Dielacher, A.; Zangerl, F.; Koudelka, O.; Beck, P.; Wickert, J. PRETTY: Grazing altimetry measurements based on the interferometric method. In Proceedings of the 5th Workshop on ARSI, Noordwijk, The Netherlands, 12–14 September 2017. [Google Scholar]
- Cardellach, E.; Wickert, J.; Baggen, R.; Benito, J.; Camps, A.; Catarino, N.; Chapron, B.; Dielacher, A.; Fabra, F.; Flato, G. GNSS transpolar earth reflectometry exploring system (G-TERN): Mission concept. IEEE Access 2018, 6, 13980–14018. [Google Scholar] [CrossRef]
- Martin-Neira, M. A passive reflectometry and interferometry system (PARIS): Application to ocean altimetry. ESA J. 1993, 17, 331–355. [Google Scholar]
- Treuhaft, R.N.; Lowe, S.T.; Zuffada, C.; Chao, Y. 2-cm GPS altimetry over Crater Lake. Geophys. Res. Lett. 2001, 28, 4343–4346. [Google Scholar] [CrossRef]
- Hu, C.; Benson, C.; Rizos, C.; Qiao, L. Single-pass sub-meter space-based GNSS-R ice altimetry: Results from TDS-1. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2017, 10, 3782–3788. [Google Scholar] [CrossRef]
- Li, W.; Cardellach, E.; Fabra, F.; Rius, A.; Ribó, S.; Martín-Neira, M. First spaceborne phase altimetry over sea ice using TechDemoSat-1 GNSS-R signals. Geophys. Res. Lett. 2017, 44, 8369–8376. [Google Scholar] [CrossRef]
- Masters, D.; Zavorotny, V.; Katzberg, S.; Emery, W. GPS signal scattering from land for moisture content determination. In Proceedings of the IGARSS, Honolulu, HI, USA, 24–28 July 2000; pp. 3090–3092. [Google Scholar]
- Chew, C.; Small, E.E.; Larson, K.M. An algorithm for soil moisture estimation using GPS-interferometric reflectometry for bare and vegetated soil. GPS Solut. 2015, 20, 525–537. [Google Scholar] [CrossRef]
- Garrison, J.L.; Katzberg, S.J.; Hill, M.I. Effect of sea roughness on bistatically scattered range coded signals from the Global Positioning System. Geophys. Res. Lett. 1998, 25, 2257–2260. [Google Scholar] [CrossRef]
- Germain, O.; Ruffini, G.; Soulat, F.; Caparrini, M.; Chapron, B.; Silvestrin, P. The Eddy Experiment: GNSS-R speculometry for directional sea-roughness retrieval from low altitude aircraft. Geophys. Res. Lett. 2004, 31, L21307. [Google Scholar] [CrossRef]
- Zavorotny, V.U.; Voronovich, A.G. Scattering of GPS signals from the ocean with wind remote sensing application. IEEE Trans. Geosci. Remote Sens. 2000, 38, 951–964. [Google Scholar] [CrossRef]
- Foti, G.; Gommenginger, C.; Jales, P.; Unwin, M.; Shaw, A.; Robertson, C.; Roselló, J. Spaceborne GNSS reflectometry for ocean winds: First results from the UK TechDemoSat-1 mission. Geophys. Res. Lett. 2015, 42, 5435–5441. [Google Scholar] [CrossRef]
- Carreno-Luengo, H.; Camps, A.; Querol, J.; Forte, G. First results of a GNSS-R experiment from a stratospheric balloon over boreal forests. IEEE Trans. Geosci. Remote Sens. 2016, 54, 2652–2663. [Google Scholar] [CrossRef]
- Yu, K.; Li, Y.; Chang, X. Snow depth estimation bsed on combination of pseudorange and carrier phase of GNSS dual-frequency signals. IEEE Trans. Geosci. Remote Sens. 2019, 57, 1817–1828. [Google Scholar] [CrossRef]
- Camps, A.; Park, H.; Foti, G.; Gommenginger, C. Ionospheric effects in GNSS-reflectometry from space. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2016, 9, 5851–5861. [Google Scholar] [CrossRef]
- Alonso-Arroyo, A.; Zavorotny, V.U.; Camps, A. Sea ice detection using UK TDS-1 GNSS-R data. IEEE Trans. Geosci. Remote Sens. 2017, 55, 4989–5001. [Google Scholar] [CrossRef]
- Li, C.; Huang, W.; Gleason, S. Dual antenna space-based GNSS-R ocean surface mapping: Oil slick and tropical cyclone sensing. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2015, 8, 425–435. [Google Scholar] [CrossRef]
- Yu, K. Tsunami-wave parameter estimation using GNSS-based sea surface height measurement. IEEE Trans. Geosci. Remote Sens. 2015, 53, 2603–2611. [Google Scholar] [CrossRef]
- Di Simone, A.; Park, H.; Riccio, D.; Camps, A. Sea target detection using spaceborne GNSS-R delay-Doppler maps: Theory and experimental proof of concept using TDS-1 data. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2017, 10, 4237–4255. [Google Scholar] [CrossRef]
- Gao, C.; Yang, D.; Hong, X.; Xu, Y.; Wang, B.; Zhu, Y. Experimental results about traffic flow detection by using GPS reflected signals. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2018, 11, 5076–5087. [Google Scholar] [CrossRef]
- Howard, D.; Roberts, S.; Brankin, R. Target detection in SAR imagery by genetic programming. Adv. Eng. Softw. 1999, 30, 303–311. [Google Scholar] [CrossRef]
- Bekkerman, I.; Tabrikian, J. Target detection and localization using MIMO radars and sonars. IEEE Trans. Signal Process. 2006, 54, 3873–3883. [Google Scholar] [CrossRef]
- UCS Satellite Database. 2019. Available online: https://www.ucsusa.org/nuclear-weapons/space-weapons/satellite-database (accessed on 1 April 2019).
- Mashburn, J.; Axelrad, P.; Lowe, S.T.; Larson, K.M. Global ocean altimetry with GNSS reflections from TechDemoSat-1. IEEE Trans. Geosci. Remote Sens. 2018, 56, 4088–4097. [Google Scholar] [CrossRef]
- MERRByS Product Manual-GNSS Reflectometry on TDS-1 with the SGR-ReSI. 2019. Available online: http://merrbys.co.uk/wp-content/uploads/2018/02/MERRByS-Product-Manual-V4.pdf (accessed on 3 December 2018).
- Andersen, O.; Knudsen, P.; Kenyon, S.; Factor, J.; Holmes, S. The DTU13 global marine gravity field—First evaluation. In Proceedings of the OSTST, Boulder, CO, USA, 8–11 October 2013; pp. 1–14. [Google Scholar]
- Lyons, R.G. Periodic sampling. In Understanding Digital Signal Processing, 3rd ed.; Pearson Education, Inc.: Boston, MA, USA, 2011; pp. 48–110. [Google Scholar]
- Yu, K.; Rizos, C.; Burrage, D.; Dempster, A.G.; Zhang, K.; Markgraf, M. An overview of GNSS remote sensing. EURASIP J. Adv. Signal Process 2014, 1, 134. [Google Scholar] [CrossRef]
- Vallado, D.; Crawford, P. SGP4 orbit determination. In Proceedings of the AIAA/AAS Astrodynamics Specialist Conference and Exhibit, Honolulu, HI, USA, 18–21 August 2008. [Google Scholar] [CrossRef]
- Two Line Element Data. 2019. Available online: www.space-track.org/ (accessed on 30 April 2019).
- Hajj, G.A.; Zuffada, C. Theoretical description of a bistatic system for ocean altimetry using the GPS signal. Radio Sci. 2003, 38, 1089. [Google Scholar] [CrossRef]
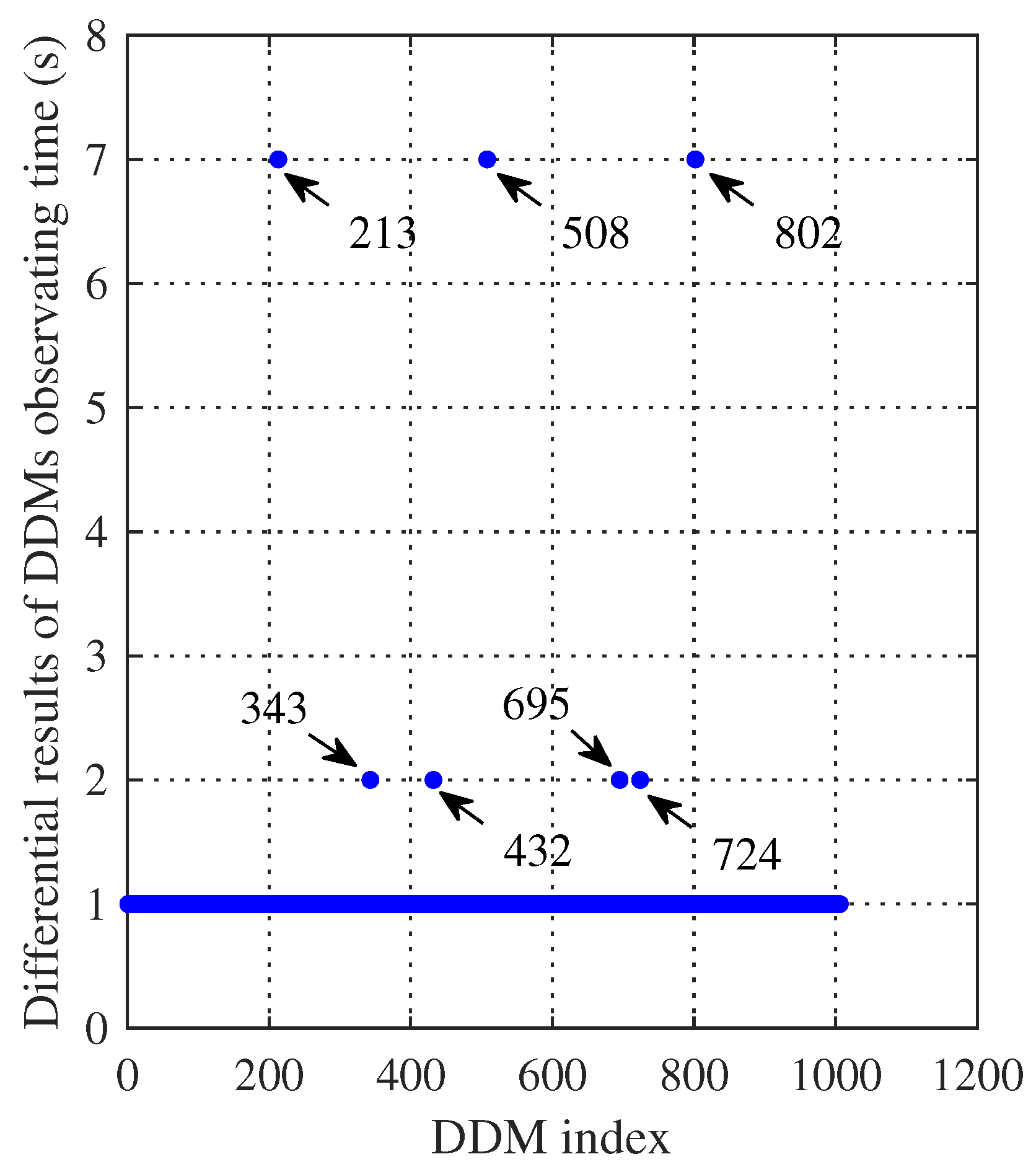
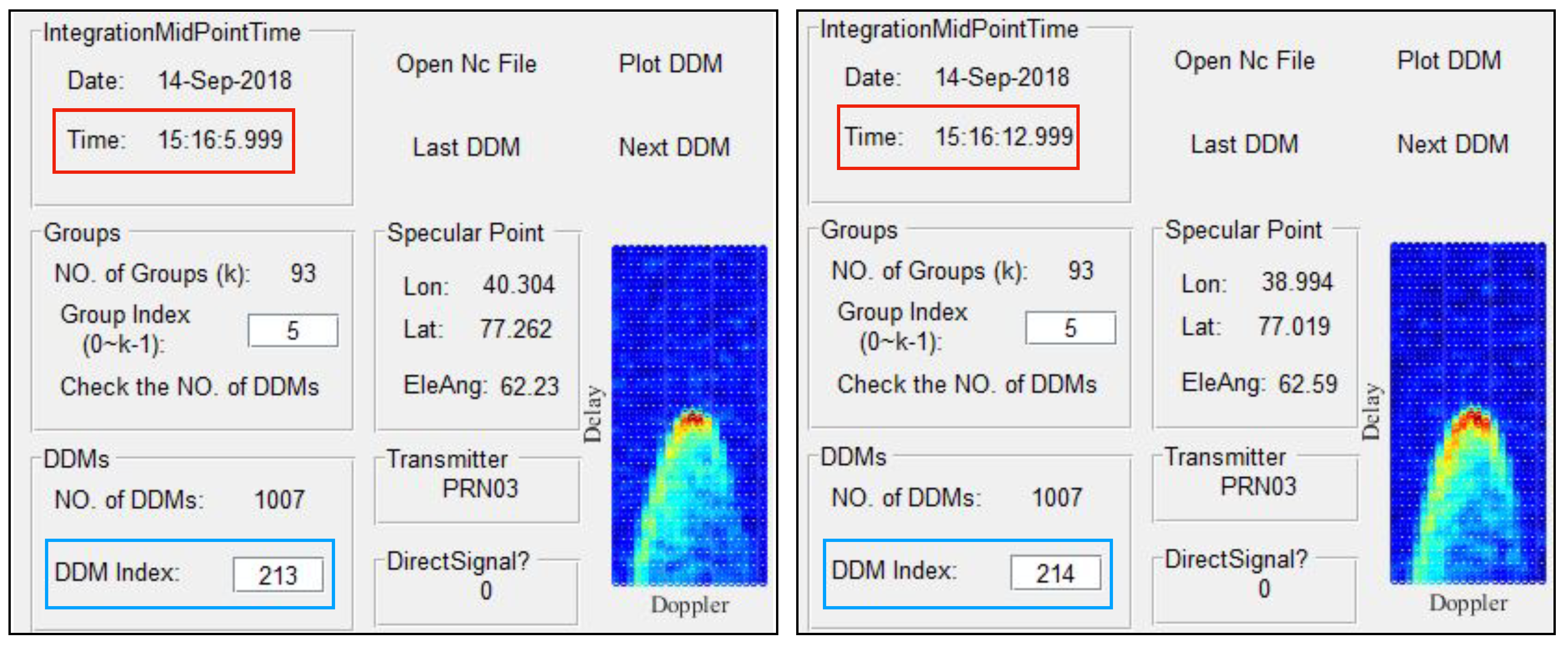
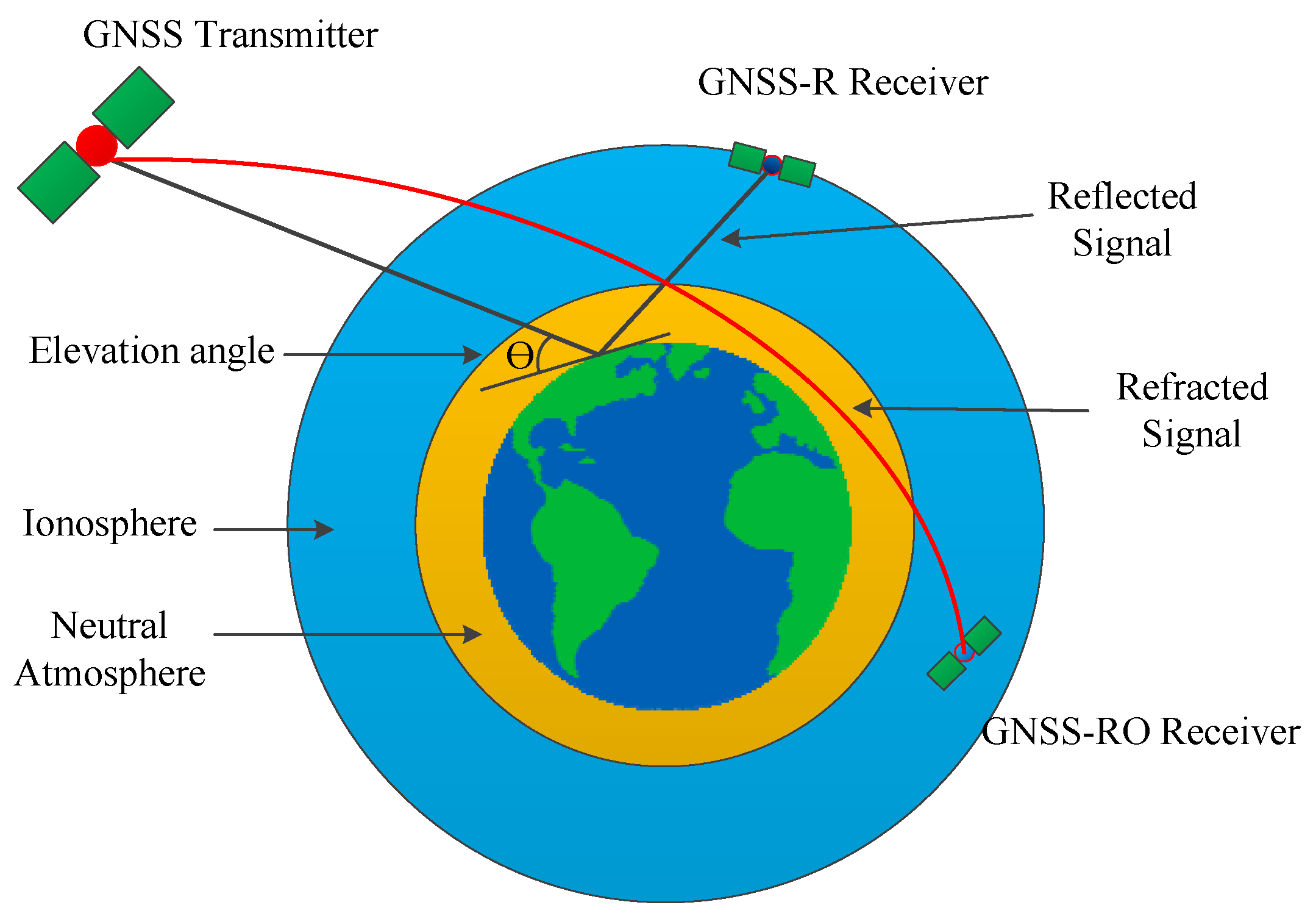
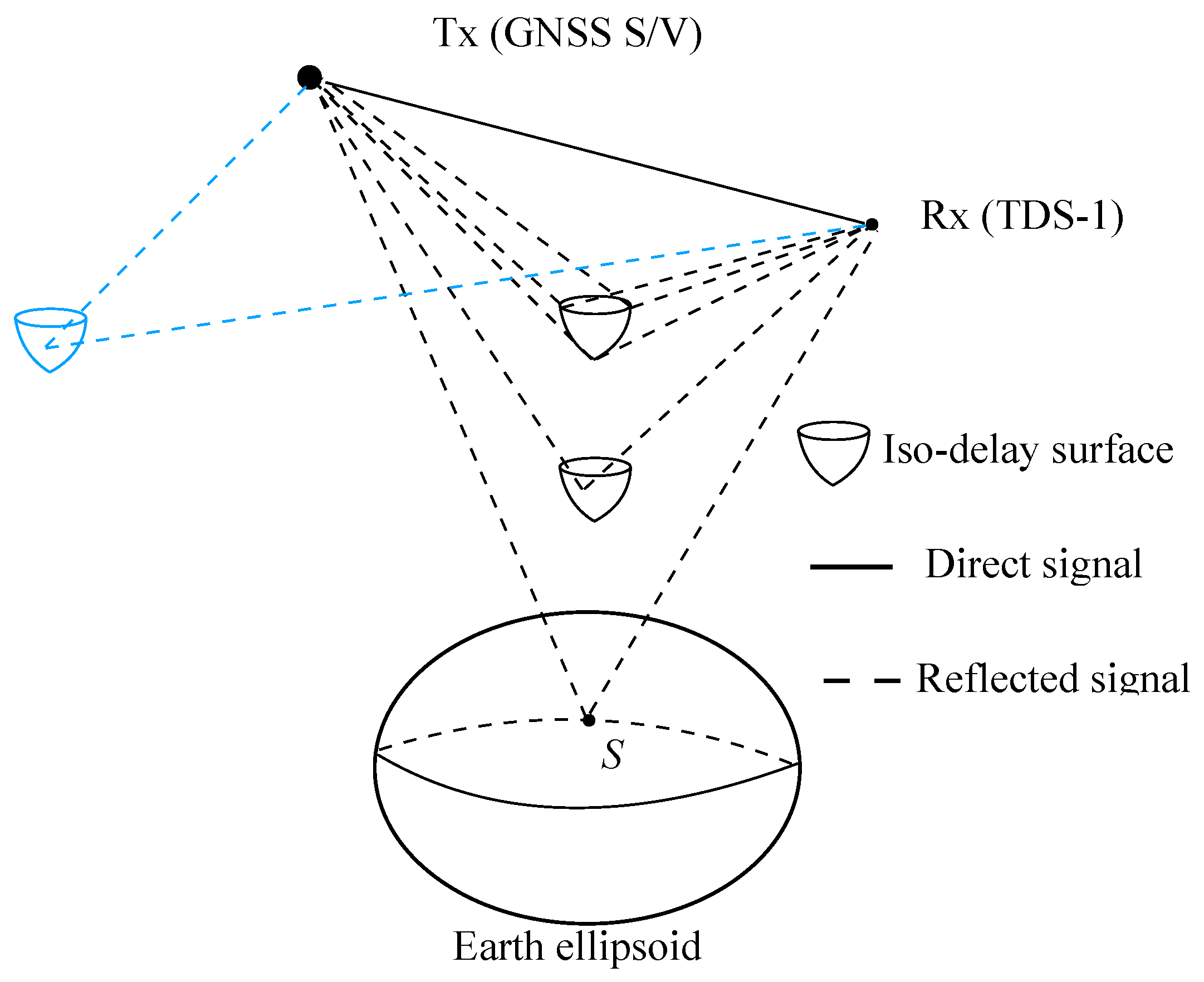
| Elevation | Column No. of | “DirectSignal | Track ID | Observation | |
|---|---|---|---|---|---|
| Angle | Bright Point | InDDM” | in Dataset | Time | |
| Event 1 | 71 | 11 | False | 20180914H18Group05 | 15-19-26.999 |
| Event 2 | 72 | 11 | False | 20180914H18Group05 | 15-20-07.999 |
| Event 3 | 73 | 11 | False | 20180914H18Group05 | 15-20-58.999 |
| Event 4 | 64 | 17 | False | 20180914H18Group08 | 15-33-15.999 |
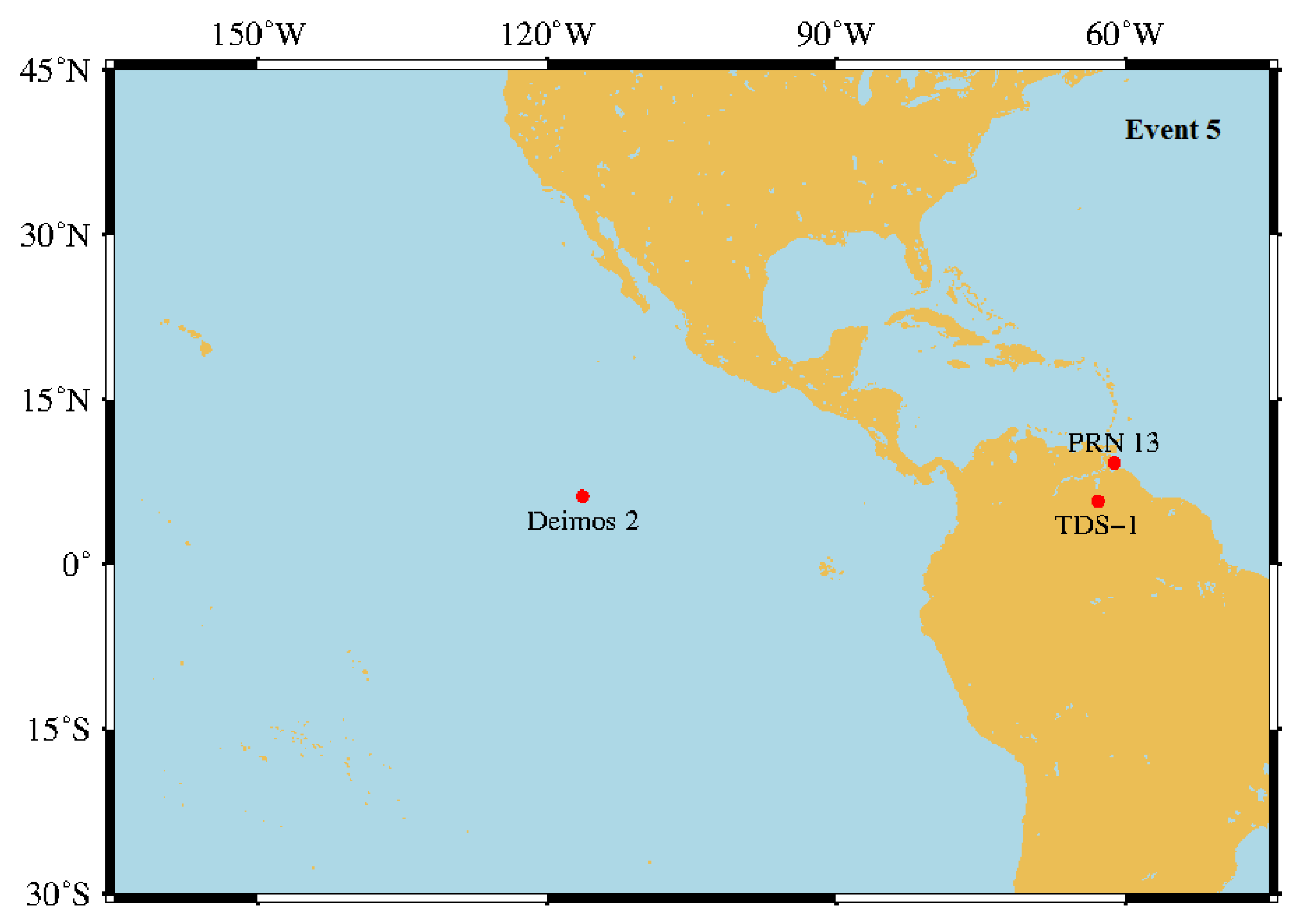
| Event 5 | 85 | 12 | False | 20180914H18Group51 | 18-51-51.999 |
| Event 6 | 59 | 8 | False | 20180914H18Group82 | 20-21-29.999 |
| Event 7 | 67 | 8 | False | 20180915H00Group27 | 23-09-16.999 |
| Event 8 | 67 | 11 | False | 20180915H00Group52 | 01-05-40.999 |
| Event 9 | 77 | 11 | False | 20180915H00Group32 | 23-30-54.999 |
| Event 10 | 76 | 11 | False | 20180915H00Group49 | 00-51-30.999 |
| Event 11 | 61 | 17 | False | 20180915H06Group53 | 06-22-39.999 |
| Event 12 | 66 | 20 | False | 20180915H06Group78 | 07-46-53.999 |
| Event 13 | 73 | 9 | False | 20180915H12Group25 | 10-51-09.999 |
| Event 14 | 59 | 8 | False | 20180915H18Group30 | 16-39-04.999 |
| (km) | (Hz) | (Hz) | (Hz) | |
|---|---|---|---|---|
| Event 1 | 273.1 | 6703 | 1701 | 0 |
| Event 2 | 284.4 | 4726 | 1177 | 0 |
| Event 3 | 292.6 | 2242 | 518 | 0 |
| Event 4 | 186.7 | 2081 | 453 | 3000 |
| Event 5 | 54.7 | −3114 | −745 | 500 |
| Event 6 | 116.3 | 15812 | 3826 | −1500 |
| Event 7 | 221.1 | −6864 | −1595 | −1500 |
| Event 8 | 224.1 | 5715 | 1418 | 0 |
| Event 9 | 22.4 | −5668 | −1622 | 0 |
| Event 10 | 15.1 | −8527 | −2079 | 0 |
| Event 11 | 156.7 | 2087 | 730 | 3000 |
| Event 12 | 211.8 | −14858 | −3780 | 4500 |
| Event 13 | 290.8 | −3627 | −1052 | −1000 |
| Event 14 | 119.4 | −80 | −173 | −1500 |
| Name and NORAD ID | (km) | (Hz) | Altitude (km) | |
|---|---|---|---|---|
| Event 2 | Kondor (39194) | 0.495 | 607 | 459.5 |
| Event 4 | Step Cube Lab (43138) | 0.458 | 568 | 505.9 |
| Event 5 | Deimos 2 (40013) | 0.653 | 1046 | 616.4 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, C.; Benson, C.; Park, H.; Camps, A.; Qiao, L.; Rizos, C. Detecting Targets above the Earth’s Surface Using GNSS-R Delay Doppler Maps: Results from TDS-1. Remote Sens. 2019, 11, 2327. https://doi.org/10.3390/rs11192327
Hu C, Benson C, Park H, Camps A, Qiao L, Rizos C. Detecting Targets above the Earth’s Surface Using GNSS-R Delay Doppler Maps: Results from TDS-1. Remote Sensing. 2019; 11(19):2327. https://doi.org/10.3390/rs11192327
Chicago/Turabian StyleHu, Changjiang, Craig Benson, Hyuk Park, Adriano Camps, Li Qiao, and Chris Rizos. 2019. "Detecting Targets above the Earth’s Surface Using GNSS-R Delay Doppler Maps: Results from TDS-1" Remote Sensing 11, no. 19: 2327. https://doi.org/10.3390/rs11192327
APA StyleHu, C., Benson, C., Park, H., Camps, A., Qiao, L., & Rizos, C. (2019). Detecting Targets above the Earth’s Surface Using GNSS-R Delay Doppler Maps: Results from TDS-1. Remote Sensing, 11(19), 2327. https://doi.org/10.3390/rs11192327







