Abstract
Many wetlands are characterized by a vegetation cover of variable height and density over time. Tracking spatio-temporal changes in inundation patterns of these wetlands remains a challenge for remote sensing. Water In Wetlands (WIW) was predicted using a dichotomous partitioning of reflectance values encoded based on ground-truth (n = 4038) and optical-space derived (n = 7016) data covering all land cover types (n = 17) found in the Rhône delta, southern France. The models were developed with spectral data from Sentinel 2, Landsat 7, and Landsat 8 sensors, hence providing a monitoring tool that covers a 35-year period (same sensor for Landsat 5 and 7). A single model combining the near infrared (NIR ≤ 0.1558 to 0.1804, depending on sensors) and short-wave infrared (SWIR2 ≤ 0.0871 to 0.1131) wavelengths was identified by three independent analyses, each one using a different satellite. Overall accuracy of water maps ranged from 89% to 94% for the training samples and from 90% to 94% for the validation samples, encompassing standard water indices that systematically underestimate flooding duration under vegetation cover. Sentinel 2 provided the highest performance with a kappa coefficient of 0.82 for both samples. Such tool will be most useful for monitoring the water dynamics of seasonal wetlands, which are particularly sensitive to climate change while providing multiple services to humankind. Considering the high temporal resolution of Sentinel 2 (every 5 days), cumulative water maps built with the WIW logical rule could further be used for mapping a wide range of wetlands which are either periodically or permanently flooded.
1. Introduction
Ecosystem monitoring with replicable remotely-sensed methods offers the distinct advantage of repeated, homogeneous coverage of large areas, with little extra effort [1,2,3,4]. This allows the development of time series datasets at coherent spatial scale irrespective of site accessibility. Application of remotely-sensed techniques for wetland mapping and monitoring has received a lot of attention [5,6,7] due to this ecosystem’s decline and contribution to human well-being [8,9]. Wetland classifications have been performed with a multitude of sensors (aerial, multispectral, and synthetic aperture radar SAR) under a wide array of parametric and non-parametric statistical approaches using pixel- and object-based algorithms [5,10,11,12,13,14]. Among spectral bands, the near infrared (NIR) and red edge (RE) have been identified as the most useful for delineating wetland types [5,6,7,11,15,16], along with short-wave infrared (SWIR) bands, which are sensitive to both soil and vegetation moisture [6,17]. Thermal infrared (TIR) bands have also been used successfully to distinguish water bodies from vegetation and soil covers [6,7], as well as for identifying inundated wetlands [6,18]. With microwave bands, optimal values for incidence angles, wavelengths, and polarizations differ according to wetland vegetation types, with longer wavelengths performing better in forested wetlands [14]. What stands out from the abundant literature reviews on the remote mapping of wetlands is that, owing to the diversity of their vegetation morphologies, which are highly dynamic and often hard to discriminate from that of terrestrial ecosystems, there is no standard methodology to map wetlands on a large scale [6,19]. However, because hydroperiod is a prime factor influencing biodiversity and the services provided by aquatic ecosystems [20,21], surface water area is often used as a proxy in remote sensing to identify wetlands or estimate spatio-temporal changes in their extent [22,23,24,25].
Although supervised classifications based on spectral analysis have been useful for accurately and repeatedly mapping water bodies [26,27,28], the application of spectral indices has gained popularity because they are considered less restrictive and more reproducible, especially for applications at large or on global scale [4,29]. Several spectral indices have been developed to monitor surface water areas using satellite imagery [25,30,31,32,33,34,35,36,37]. They generally use the near infrared (NIR) and/or short-wave infrared (SWIR) bands because water absorbs most radiation at NIR wavelengths and beyond, in contrast to other landscape features [33,38]. Their increasing applications under various situations has led to several modifications to improve classification accuracy, especially relative to the misclassification of turbid waters [39] or the noise caused by built-up land and shadow [22,40]. For instance, the NIR band in the Normalized Difference Water Index (NDWI) developed in 1996 [37] was replaced by the SWIR band in 2006 to reduce disturbances related to built-up lands giving rise to the Modified NDWI [36]. Under the same reasoning, it was further suggested to calculate the MNDWI using the band SWIR2 instead of SWIR1 [22]. An Automated Water Extraction Index (AWEI) has been proposed under two versions to reduce misclassifications related to either shadow or built-up land [31]. A comprehensive comparison of the performance of these water indices using Landsat scenes from Australia revealed that most indices tend to underestimate water presence, being affected by water color and the presence of non-water features in a pixel [41]. Considering the unique spectral characteristics of water bodies in the visible and infrared wavelengths, the application of fixed thresholds to spectral bands remains a valuable approach for delineating aquatic ecosystems [40,42]. Arguments against threshold-based methods is that they do not necessarily perform as well outside the areas where they were developed [25]. Although water indices are considered as more stable because they use band ratios, recent studies have revealed similar shortcomings when water maps are confronted with ground-truth data, imposing the use of specific thresholds (different from 0) to increase classification accuracy [22,41].
Because of its particular climate characterized by an annual water deficit, many wetlands of the Mediterranean basin are flooded only seasonally [43]. In this area, wetlands colonized by reeds, bulrushes, and other emergent plants provide sheltered refuges for wildlife and primary resources for industry and local populations [44]. The biodiversity and socio-economic value of these wetlands primarily rely on the timing and duration of inundation [45]. Increased water stress predicted under climate change projections [46,47,48,49] will negatively affect ecosystem services (provision of food, building materials, recreational activities, etc.) and biodiversity (e.g., reduction of suitable feeding, spawning, nesting and nursery grounds to birds, amphibians and fish) [8,50,51]. Accordingly, failure to detect water presence under vegetation could lead to errors in the (1) classification of wetland habitats; (2) detection of changes in wetland functions; (3) assessment in water resource use, availability or management; and (4) extrapolation of wetland biodiversity and services [19,46,52].
Detection of water under wetland vegetation has received little attention in the development of remote sensing algorithms and indices using optical data [25,26]. Vegetation growth inhibits optical sensors in variable ways, depending on the plant species, by interfering with water detection [25,26,53,54]. With radar sensors, emergent vegetation presents differences in surface roughness and increases the amount of backscattered radiation from inundated surfaces, making the discrimination of land and vegetated wetlands problematic [24,54]. Long wavelength SAR sensors with small incidence angles can penetrate vegetation more successfully, but the signal that is partially blocked by the vegetation creates a specific backscatter response due to double-bounce scattering [55]. Because vegetation growth and structure will induce different scattering mechanisms [54,55,56,57], the ability to detect surface water will vary across space and time being influenced by vegetation morphology and phenology [14,58].
Several studies have recently tested the performance of standard spectral indices for surface water detection under various situations in terms of terrain and sensor [22,40,41,59]. Capitalizing on a solid ground-truth sample, this study aims at identifying what are currently the best options for detecting surface water, with special attention to water under dense vegetation cover. However, instead of individually testing the water and non-water classification accuracy of each index relative to ground-truth data as previously done [22,40,41,59], this study uses a data mining approach to identify what performs best among water indices, vegetation indices, and spectral bands used alone or in combination, using decision trees as classifiers. This work was carried out with the optical sensors of Sentinel 2, Landsat 7, and Landsat 8. The recent launch of Sentinel 2 satellites provides scenes of relevant spectral, spatial, and temporal resolution for monitoring wetlands routinely and at no cost. Although Landsat data have lower temporal and spatial resolutions, they were also selected because of their exceptional data archive that enables long-term trend assessments.
2. Materials and Methods
2.1. Ground-Truth Data
The diversity and dynamics of Camargue wetlands make it an ideal case study for testing the performance of water detection methods under different types of vegetation cover. The Camargue or Rhône delta is a 145,300 ha alluvial plain located in southern France that rarely surpasses 5 m elevation. It is comprised of a network of wetland habitats including ponds, lagoons, freshwater open and reed marshes, halophilous scrubs (Salicornia marshes), salt pans, and rice fields (Figure 1). The variety of human uses associated with wetlands combined with the natural water deficit (−700 mm annually) on one hand and the possibility of water pumping from the Rhône river on the other hand, produce a variety of hydrological conditions at any time of the year (Figure 2).
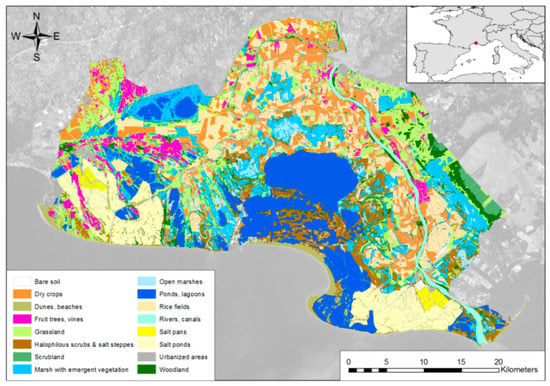
Figure 1.
Simplified land cover map of the Camargue Unesco Man and Biosphere reserve built from maps provided by the Syndicat Mixte de Camargue gardoise and Parc naturel régional de Camargue based on orthophotographs of 2011 and 2016, respectively.
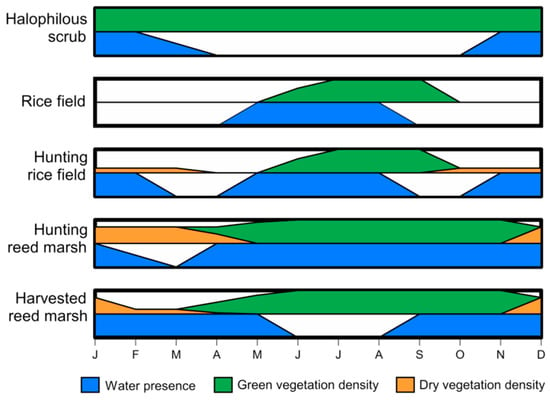
Figure 2.
Monthly hydroperiod and vegetation development for different wetland types in relation to human uses in Camargue.
Between 20 April and 27 October 2017, 480 points were monitored for water presence/absence within lagoons, salt marsh, reed beds, and grasslands. These measurement points were distributed every 60 m along 29 transects. Most transects were sampled two or three times during this period in order to obtain data under wet and dry conditions. Some 1115 additional measures of water level were obtained from a monitoring programme initiated in 2001 in the largest reed bed of the Camargue. This wetland is divided into 37 independent hydrological units covered more or less homogenously with common reed Phragmites australis which can grow up to 1.5–3 m tall depending on salinity. Water levels were measured bi-monthly or monthly at piezometers buried 50 cm into the ground at the marsh edge. A number of studies collected data on water levels in the middle of these hydrological units and these measures, calibrated with the associated piezometer [26,43,60], were the ones used in this study. For each hydrological unit, mean water level at one point randomly selected in emergent vegetation was extrapolated once or twice a month at the time of passage of a satellite under the assumption that water levels vary linearly over time. To overcome the insensitivity of the data associated with micro-topography, points with water levels estimated between −5 and 5 cm were discarded from the analysis. Because early classification attempts with Sentinel 2 misclassified dune areas as flooded, 454 dry points were sampled in the dunes during the summer of 2016, and these points were systematically reported on the two scenes corresponding to the period of field sampling.
2.2. Optical Data
To increase the performance and transferability of this work, water measures in wetlands were complemented by optical data extracted from 50 random points selected in each of the 17 main land cover types (n = 850) of the Camargue. Information on water presence/absence was derived from five SPOT-5 scenes of 2015 by applying the Modified Index of Free Water (MIFW, [26]), which provides an overall accuracy of 88% for detecting water in Camargue wetlands. The five scenes of SPOT-5 were selected to match dates at which scenes could be provided by the Operational Land Imager (OLI) of Landsat 8 (Table 1), allowing us to transfer the water presence/absence information of the 850 reference points to the five Landsat 8 scenes. A new model to detect Water In Wetlands (WIW) using field and optical data was then developed with Landsat 8. The resulting water masks were used to extract and transfer the reference point data (n = 850) to five Sentinel 2 scenes of the same dates. A similar reasoning was followed to obtain optical data for 6 scenes provided by the Enhanced Thematic Mapper Plus (ETM+) of Landsat 7 in 2014 from the Landsat 8 water mask. To compensate for the failure of the Landsat 7 ETM+ scan line corrector since May 2003, the number of optical reference points was increased twofold for each land cover type with this satellite. The number of scenes used for data transfer between satellites corresponds to the maximum number of clear images that coincide in time (within three days maximum), while covering all seasons. Considering the satellite timelines and the fact that Landsat 7 used the same sensors as Landsat 5 TM (from 1984 to 2011), the three models developed in this study provide a water monitoring tool for several upcoming years extending 35 years back.

Table 1.
Satellite sensors and spectral bands used in this study with their spatial and temporal resolutions.
2.3. Development of the Water In Wetlands (WIW) Logical Rule
A supervised classification was performed in the Rpart (Recursive PARTitioning, [61]) package in R software. Reference field and optical data points were encoded as 0 for water absence and 1 for water presence. Classification algorithms included the reflectance value of spectral bands listed in Table 1, as well as 9 current water indices or equations and 13 indices used in image analysis which are listed in Table 2. Several classifiers were created iteratively by progressively varying (at every 5%) the value of prior probabilities of the presence and absence of water classes. The classifier that was the least complex with the highest rate of good classification was selected. A cross-validation procedure called CV1-0 [62], for pruning with 10 subsets as well as iterative runs of the algorithm [63] for the selection of the cost complexity parameter and the prior parameter for imbalanced samples, was used. A random selection of 30% of all points was excluded from the sample and used for (independent) validation. In addition, a second validation was performed by comparing the classification rates from all of the points (training and validation) by separating the ground-truth from the optical-space based data.

Table 2.
Indices used as potential model variable in dichotomous partitioning for classifying water presence in wetlands.
2.4. Validation of the Water In Wetlands (WIW) Logical Rule
A binary mask of water presence based on the most accurate classifiers with each satellite was created with the raster calculator (Spatial Analyst) of ArcGIS version 10 (ESRI). Using the zonal statistics tool (Spatial Analyst) of ArcGIS, the values of the validation points (1 for water presence and 0 for water absence) were extracted to build an error matrix for estimating omission errors, commission errors, overall accuracy, and Kappa coefficient [22]. These statistics were also calculated for 8 standard water indices or equations found in the literature based on the training and validation reference points used in this study. The annual water masks, obtained by combining monthly water masks when applying the WIW and three water indices having the highest classification accuracy with our dataset, were also computed for qualitative visual validation based on local expert knowledge.
3. Results
3.1. Optimal Classifiers for Detecting Water In Wetlands (WIW) According to Satellites
Although based on different ground-truth and optical-based data, the binary trees resulting from the data mining process were highly similar among satellites. Two single spectral bands from Landsat and Sentinel sensors were preferred over the various existing water indices for detecting water in wetlands according to the following thresholds:
| Landsat 8 | : | WIW = NIR ≤ 0.1735 and SWIR2 ≤ 0.1035 |
| Landsat 5, 7 | : | WIW = NIR ≤ 0.1558 and SWIR2 ≤ 0.0871 |
| Sentinel 2 | : | WIW = NIR ≤ 0.1804 and SWIR2 ≤ 0.1131 |
Threshold values identified by the classifiers differed slightly from one satellite to another, resulting from the diversity of sensors (Table 1) and the different ground-truth data used to fit their time coverage. Details on the samples used for training and validation of the classifiers as well as accuracy estimates are provided in Table 3. Overall accuracy was highest with Sentinel 2 (94.1%) followed by Landsat 7 (93.0%) and Landsat 8 (89.2%). Omission errors were lower for predicting water absence (9% for Landsat 8, 3% for Landsat 7, and 4% for Sentinel 2) than water presence (respectively 19%, 20%, and 15%). Kappa coefficients on the training and validation samples were, respectively, 0.63 and 0.68 for Landsat 8, 0.82 and 0.78 for Landsat 7, and 0.82 and 0.82 for Sentinel 2. All classifiers behaved similarly with all datasets, with classification accuracy for training and validation samples not varying by more than 1.3%. Field data were better classified than data extrapolated from water masks for Landsat 7 and Sentinel 2, reaching 97% of correct classification with S2.

Table 3.
Optimal classifiers for predicting water presence with error matrix and calculation of overall accuracy (%OA) according to land cover types for each satellite.
3.2. Classification Accuracy According to Landcover Types
Predictive accuracy according to land cover classes was also quite similar across satellites (Table 3). Dry habitats were typically well classified, and the low omission errors were probably overestimated due to potentially false data in the training samples which were entirely based on remotely-sensed transferred data. A good example of this are the buildings from Landsat 7 scenes, of which 4% were “misclassified” as flooded areas. Model performance was lower for sand, with around 90% of good classification. Wet habitats with permanent or temporary waters were typically less well classified (≈85%), mostly due to omission errors of water presence. Wet habitats containing tall vegetation, which were our main targets in this study, were correctly classified at 83% (Landsat 8), 85% (Landsat 7), and 89% (Sentinel 2). Riparian vegetation was rather well classified even though the training data were remotely-sensed and identified as dry areas in the training sample. As a consequence, the omission rate when the habitats are flooded can reach up to 55% with Sentinel 2. Another particular case is that of canals and rivers, which were well classified at only 75% with Landsat 8.
3.3. Coherence of Resulting Water Masks
More important than the statistics is the coherence of the water maps produced with our predictive classifiers relative to “real” habitat hydrology [19]. Permanent and seasonal wetlands, as well as dry natural areas were all correctly identified based on visual interpretation and expert knowledge (Figure 1 and Figure 3). The differing management strategies (flooding durations) of embanked units were easily recognizable on the resulting water maps, similarly to hydrology of rectangular rice fields, which are flooded for four to five months a year. A strong decrease in rice cropped areas was further easily detected when comparing the maps built with Landsat 7 scenes to the more recent satellite images (Figure 3). Such decrease is in accordance with data from the French Rice Centre reporting 20479 hectares of rice in 2001 [77], compared to 11349 ha in 2017 [78]. The Landsat 7 classifier provided longer flooding durations compared to Landsat 8 and Sentinel 2 due to discrepancies in the amount of rainfall among the three periods considered (Figure 3a–c). The annual water maps were created with at least one image per month. However, given the availability of cloud-free scenes from Landsat 7 and 8, images from different successive calendar years were combined. The sum of rainfalls in the month preceding the 12 scenes corresponded to 651 mm for Landsat 7, 393 mm for Landsat 8, and 474 mm for Sentinel 2, based on data from a local meteorological station. A closer look at the September–December period, when Mediterranean wetlands are flooded again, is shown in Figure 4. The period covered by Landsat 7 (from 26 August 2002 to 31 December 2002) was characterized by strong rainfalls cumulating 328 mm compared to 67mm for Landsat 8 (from 27 August 2017 to 16 December 2017) and 89 mm for Sentinel 2 (from 27 August 2017 to 24 December 2017). These precipitations translated into the inundation of natural and agricultural systems of which the progression is easily detected on the successive Landsat 7 scenes (Figure 4). Actually, the impact of a wet month preceding scene acquisition is clearly visible when comparing scenes on a monthly basis, irrespective of the satellite used.
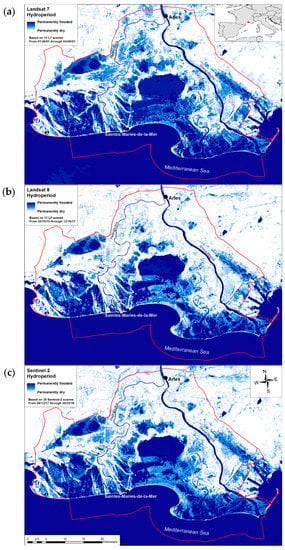
Figure 3.
Annual water masks resulting from application of the WIW logical rule on (a) Landsat 7, (b) Landsat 8 and (c) Sentinel 2 satellites.
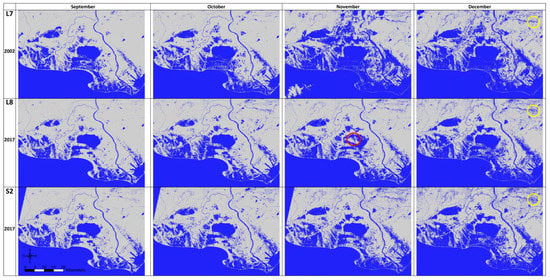
Figure 4.
Impact of precipitations received in the month preceding scene acquisition from September through December based on single water masks (one scene per month showing water presence/absence) produced with Landsat 7 (328 mm in 2002), Landsat 8 (67 mm in 2017) and Sentinel 2 (89 mm in 2017). The red circle refers to noises caused by waves on a windy day, while the yellow circles enclose misclassifications due to shadows in a mountainous area.
With all satellites, uneven slopes facing north of a small mountain range located north west of the study area were sometimes misclassified as flooded (Figure 4). These misclassifications arise from the end of autumn to winter and disappear progressively from winter to early spring. On a few occasions, some permanent waters in large lagoons were identified as dry (see November scenes of Landsat 8 in Figure 4). This situation occurred systematically under strong winds (above 100 km/h) according to data from a local meteorological station.
3.4. Impact of Radiometric Corrections and Satellite Sensors on Classifier Accuracy
Considering that atmospheric corrections affect the reflectance value of a pixel, they can influence classification accuracy based on reflectance thresholds. The effect of correction methods on overall accuracy was tested with Sentinel 2. The original model, obtained with 2A level scenes from THEIA (WIW = B8a ≤ 0.1804 and B12 ≤ 0.1131) was compared with models using 1A level scenes provided by the Sentinel products exploitation platform (PEPS) of Copernicus and scenes corrected with the Semi-Automatic Classification Plug-in (SCP) in QGIS. The models obtained were very similar to the original (SCP: B8a ≤ 0.1798 and B12 ≤ 0.1143; PEPS: B8a ≤ 0.1839 and B12 ≤ 0.1269), as was their overall accuracy with 93.9% (SCP) and 93.1% (PEPS) compared to 94.1% for the original classifier. For any land cover class, omission or commission errors did not vary by more than 1% from the original classification, except for halophilous scrubs for which omission errors increased by 5.3% (SCP) and 3.6% (PEPS) due to misclassification of ten dry-ground points (Table 4).

Table 4.
Difference in % overall accuracy according to the original satellite used for classification and the radiometric correction used for Sentinel 2 when applying the WIW logical rule.
Considering that the WIW logical rules differed little among satellites, their performance was tested across satellites. All models performed well with all satellite sensors (Table 4). Actually, the model developed with Landsat 7 performed better with Landsat 8 than the model originally built with Landsat 8. While the overall accuracy was rather similar, discrepancies were sometimes observed according to land cover classes. For instance, classification accuracy of bare ground and halophilous scrubs decreased by more than 10% when the Sentinel 2 model was applied to Landsat 7 scenes. Application of any model to Sentinel 2 provided, however, a roughly similar overall accuracy. Water maps were coherent and similar, the only perceptible divergence being an overall slight increase or decrease in the annual flooding durations. Results issued from the Landsat 7 model applied to Landsat 8 scenes or from the Sentinel 2 model applied to Landsat 8 can be considered as identical as they were only very marginally different.
3.5. Performance of the WIW Logical Rule Relative to Other Water Indices
Performance of the WIW equation (based on independent validation data only) was compared to eight water indices found in the literature using all field and optical reference points extracted from Landsat 7, Landsat 8 and Sentinel 2 scenes (Table 5). The Kappa coefficients were systematically higher with the WIW logical rule and differences among methods were especially marked with Sentinel 2 scenes. The resulting water masks were computed on twelve Sentinel 2 scenes from December 2017 through November 2018 using the four methods providing the highest Kappa coefficient values (Figure 5).

Table 5.
Kappa values obtained when applying spectral water indices found in the literature to Sentinel 2 (S2), Landsat 7 (L7) and Landsat 8 (L8) scenes using the ground-truth and optical data available in this study.
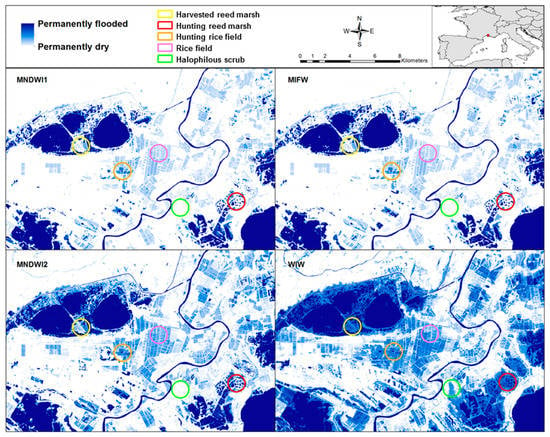
Figure 5.
Annual water mask obtained with 12 monthly scenes of Sentinel 2 (from December 2017 to November 2018) when applying the water indices having the highest Kappa values in Table 5.
The MNDWI1 and MIFW indices could detect water in rice fields only before rice growth (area in pink circle on Figure 5) or after rice harvest (darker area in orange circle on Figure 5). Likewise, water in reed vegetation was detected only inside open-water areas of hunting marshes (small dark areas in red circle) or after reed harvest in winter (right part in the yellow circle). It appears that the MIFW index, which was developed with SPOT-5 sensors for detecting water under vegetation (used here with 0 as threshold value to improve Kappa coefficient), does not perform better than other water indices when used with Sentinel 2. The MNDWI2 succeeds partially in detecting water under vegetation, but its performance with Landsat 8 is particularly low (Table 5). Only the WIW equation provides duration of flooding that reflects real inundation patterns for all habitat types (shown in Figure 2): Water is detected similarly in non-harvested and harvested reed marsh (left vs. right part in yellow circle), demonstrating that vegetation coverage does not interfere with water detection; rice fields are considered as flooded during most of the period of rice growth (pink circle); and water can be detected under dense cover of halophilous scrubs (darker area in green circle). These plant formations, which grow in depressions that are flooded during a few winter months by rainfalls, are misclassified as permanently dry with the other three indices (Figure 5).
4. Discussion
In contrast to current water indices, the logical rule presented in this paper for detecting Water In Wetlands (WIW) performs equally well in the absence or presence of vegetation above the water surface. Seasonal wetlands are ecologically and economically important ecosystems that are particularly sensitive to climate change [46]. A robust tool for monitoring annual and seasonal trends in their hydrology is needed by practitioners interested in the conservation of these vulnerable ecosystems because hydrology is a prime factor affecting their biodiversity and contribution to humankind [8,43]
Although based on independent field and remotely-sensed data in differing proportions, as well as various satellite sensors and different time periods, dichotomous partitioning with Landsat 7, Landsat 8, and Sentinel 2 led to the same logical rule for predicting water presence. In all cases, the near-infrared band (NIR) was first selected, followed by the second shortwave-infrared band (SWIR2). None of the standard water indices found in the literature were selected by our models for detecting water in wetlands. Although an increased performance of water indices has been obtained recently by adding specific threshold values or by using them in combination with vegetation indices [22,41,59], applying simple threshold values to the NIR and SWIR2 bands appeared to provide better results in this study. Switching the threshold values among satellites or using different atmospheric correction methods provided similar water maps, suggest that our approach is robust and replicable. Furthermore, when applied to a Sentinel 2 scene of the Doñana marshes in southern Spain [79], the WIW logical rules provides a Kappa coefficient of similar value (0.84) to the one obtained for the Camargue wetlands. Overall, Sentinel 2 scenes systematically provide better classifications, presumably because of their higher spatial resolution compared to Landsat sensors. All models performed better than the water index previously developed in Camargue with Spot 5 which used a combination of green and SWIR wavelengths (MIFW index, [26]). The Spot-5 sensor had a single SWIR band that was located in the lower wavelength (1.58–1.75 μm), corresponding to the SWIR1 of the satellites used in this study and not selected in our classifiers.
A closer look at the classification tree reveals that areas which reflect heat back into the atmosphere such as dry ground with little (e.g., mud flats) or no (e.g., road, buildings) vegetation are discarded by the reflectance values of the near infrared radiation. In a second step, the combined action of the short infrared penetrating the vegetation, its absorption by water and reflection by the ground is useful for identifying flooded areas, even under vegetation cover. Penetration of the NIR and SWIR wavelengths (800 and 2700 nm) through organic matter has several applications [80]. It has been shown that SWIR penetration capacity increases with increasing wavelengths [81,82]. In our case, it seems that the SWIR band behaves as in reflectography, the process used to highlight charcoal drawing underlying master paintings. According to this technique, a light source is used to illuminate the painting and the SWIR passes through the paint, being reflected by the canvas and absorbed by the charcoal. The optimal wavelength for passing through all paint layers is around 2 μm [83], similarly to the SWIR2 bands selected in the WIW logical rule. It is noteworthy to mention that the only existing water index that can detect water under vegetation (MNDWI2) also uses SWIR2 wavelengths.
The main types of flooded vegetation in the Camargue correspond to grasses (e.g., rice), succulent shrubs (e.g., Arthrocnemum, Salicornia, Salsola), trees (Tamarix sp.), and beds of emergent plants having variable height and density such as Ludwigia spp., club-rush, rush, sedge, fen-sedge, and common reed [84]. Based on visual interpretation of the water maps, the WIW logical rule performs equally well with all these types of vegetation. Apart from the MNDWI2 that can detect water in the early stage of vegetation growth, all water indices tested in this study failed to detect water under all types of vegetation cover. The particular case of hunting reed marshes is interesting because all water indices could detect permanent water in areas free of vegetation that are managed for ducks, but none of them could detect water into the reeds surrounding these pools which are also flooded for most of the year. Likewise, water under halophilous scrubs, which are a common habitat in Camargue, went completely undetected in all water indices.
Standard water indices applied to our dataset had nevertheless Kappa coefficients generally above 0.6. Kappa coefficients are considered as the most robust method to measure classification accuracy because they take into account the possibility of the agreement occurring by chance alone. However, their calculation remains limited to the reference and validation points provided by the observer. Accordingly, a high Kappa coefficient does not necessarily mean that the map is accurate. Originally, only optical-space derived data (from SPOT 5 to Landsat 8 and then other satellites, see methods) were used in this study to develop the WIW equation. Such an approach provided good overall accuracy and Kappa coefficients but the resulting water maps were wrong when confronted with ground-truth knowledge. Conventional statistical methods are not designed to deal with erroneous data. When using inaccurate training data, misclassifications (e.g., sampling points for which the reflectance value is located outside the confidence interval of the studied variable) are discarded from the original group of data. This contributes to reducing the confidence intervals of the original dataset and the data marginally correctly classified are suppressed to optimize good classifications. While such procedure gives a high potential for good statistical results, it amplifies the original model’s flaws. In our case, when the original model correctly classified water presence or absence only half the time for a specific land cover class, the following water model then systematically misclassified this land cover type. Our solution was to add ground-truth data on water presence in the training sample for those land cover classes that were identified as providing false results. This allowed us to restore the original confidence interval of the dataset by increasing the number of points lying outside its limit values. This approach provided satisfactory results because the water maps were coherent with reality and the final models provided high classification accuracy.
With all satellites, uneven slopes facing north of a small mountain range located outside the study area were misclassified as flooded during the winter months. Since all satellites were passing over the Camargue in the late morning (between 10:10 and 10:40 CET), this confusion is probably associated with shadows caused by the winter sun that is too low to light the northern face of the mountains. This problem has previously been reported with most water detection methods and can be solved by combining spectral indices or adding elevation data [23,31]. On a few occasions, some permanent waters in a large and deep lagoon were identified as dry by all satellites. Considering that these scenes were systematically acquired under the condition of strong winds (> 100 km/h), these artifacts were probably caused by strong waves causing foam on the water surface. Such phenomenon is, however, unlikely to occur in shallow or seasonal wetlands.
5. Conclusions
The Camargue or Rhône delta comprises a high diversity of natural and human-modified habitats. The method developed in this study for detecting Water In Wetland (WIW) is hence likely to be applicable to many other wetland areas, especially around the Mediterranean Basin where similar types of landscapes are found. It would be interesting to test its performance under subtropical and tropical climates where wetland vegetation is more luxuriant and stratified, such as in the Everglades [25]. Automated methods for defining optimal thresholds would certainly increase performance of the WIW of which the main strength is to rely on high shortwave infrared wavelengths (SWIR2). Considering that our models were transferable from one satellite to the other, it seems likely that they would perform equally well with other satellites should they have SWIR and NIR sensors of comparable wavelengths. The model developed with Landsat 7 is probably the most robust for use with other satellites given its high performance with Landsat 8 and Sentinel 2, which is attributed to the wider acceptance range of its NIR sensor. Considering that Landsat 5 uses exactly the same sensors as Landsat 7, application of the WIW logical rule will permit territorial planners, wetland managers, and environmental scientists to follow water dynamics back to 35 years ago and, hopefully, for many years into the future with Sentinel 2, Landsat 8, and other satellites.
The definition of wetlands provided by the Ramsar Convention is very inclusive [85]: “…wetlands are areas of marsh, fen, peatland or water, whether natural or artificial, permanent or temporary, with water that is static or flowing, fresh, brackish or salt, including areas of marine water the depth of which at low tide does not exceed six metres.” Considering the high temporal resolution of Sentinel 2 scenes (every 5 days), cumulative water maps built with the WIW logical rule could further be used for mapping a wide range of wetlands which are either periodically or permanently flooded. Such approach could be a good substitute to wetland mapping based on their vegetation characteristics and would further enable the monitoring of hydrology, in addition to wetland extent and location. Flooding dynamics have important implications for multiple services provided by wetlands (e.g., flood mitigation, water purification, wildlife habitat, and recreational potential), including carbon and methane cycling [8,86].
Author Contributions
Conceptualization, G.L., A.D. and J.C.; methodology, A.D., C.M., G.L. and J.C.; data acquisition, C.M., A.G. and J.C.; data analysis, C.M. and G.L.; data curation, L.W. and G.L.; writing—original draft preparation, L.R & G.L.; writing—review and editing, B.P.; visualization, L.W.; supervision, G.L.; funding acquisition, B.P, A.D., A.G.
Funding
This study was supported by ECOPOTENTIAL (GL, LW, CM, BP) and SWOS (AG), two projects funded by the European Union’s Horizon 2020 research and innovation programme, under grant agreement no. 641762 and 642088, and by the Agence de l’Eau Rhône Méditerranée Corse (GLE, JC, LW, BP).
Acknowledgments
We are grateful to Nadège Popoff, Rémy Tiné and Samuel Hilaire for collecting in-situ data on water levels and to Philippe Isenmann (Parc Naturel Régional de Camargue) and Clarisse Brochier (Syndicat Mixte Camargue Gardoise) for providing the land cover maps of the Camargue.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- Al-Azab, M.; El-Shorbagy, W.; Al-Ghais, S. Oil Pollution and its Environmental Impact in the Arabian Gulf Region, 1st ed.; Elsevier Science: Amsterdam, The Netherlands, 2005; Volume 3, ISBN 9780080457802. [Google Scholar]
- Aires, F.; Papa, F.; Prigent, C. A long-term, high-resolution wetland dataset over the Amazon Basin, downscaled from a multiwavelength retrieval using SAR data. J. Hydrometeorol. 2012, 14, 594–607. [Google Scholar] [CrossRef]
- Pettorelli, N.; Laurance, W.F.; O’Brien, T.G.; Wegmann, M.; Nagendra, H.; Turner, W. Satellite remote sensing for applied ecologists: Opportunities and challenges. J. Appl. Ecol. 2014, 51, 839–848. [Google Scholar] [CrossRef]
- Pekel, J.-F.; Cottam, A.; Gorelick, N.; Belward, A.S. High-resolution mapping of global surface water and its long-term changes. Nature 2016, 540, 418–422. [Google Scholar] [CrossRef] [PubMed]
- Ozesmi, S.L.; Bauer, M.E. Satellite remote sensing of wetlands. Wetl. Ecol. Manag. 2002, 10, 381–402. [Google Scholar] [CrossRef]
- Mahdavi, S.; Salehi, B.; Granger, J.; Amani, M.; Brisco, B.; Huang, W. Remote sensing for wetland classification: A comprehensive review. GIScience Remote Sens. 2018, 55, 623–658. [Google Scholar] [CrossRef]
- Amani, M.; Salehi, B.; Mahdavi, S.; Brisco, B. Spectral analysis of wetlands using multi-source optical satellite imagery. ISPRS J. Photogramm. Remote Sens. 2018, 144, 119–136. [Google Scholar] [CrossRef]
- Finlayson, C.M.; D’Cruz, R.; Davidson, N.; Millennium Ecosystem Assessment (Program); World Resources Institute. Ecosystems and Human Well-Being: Wetlands and Water: Synthesis; World Resources Institute: Washington, DC, USA, 2005; ISBN 978-1-56973-597-8. [Google Scholar]
- Davidson, N.C. How much wetland has the world lost? Long-term and recent trends in global wetland area. Mar. Freshw. Res. 2014, 65, 934. [Google Scholar] [CrossRef]
- Dronova, I. Object-based image analysis in wetland research: A review. Remote Sens. 2015, 7, 6380–6413. [Google Scholar] [CrossRef]
- Adam, E.; Mutanga, O.; Rugege, D. Multispectral and hyperspectral remote sensing for identification and mapping of wetland vegetation: A review. Wetl. Ecol. Manag. 2010, 18, 281–295. [Google Scholar] [CrossRef]
- Tiner, R.W.; Lang, M.W.; Klemas, V. Remote Sensing of Wetlands: Applications and Advances; CRC Press Taylor & Francis Group: Boca Raton, FL, USA, 2015; ISBN 978-1-4822-3735-1. [Google Scholar]
- Gallant, A. The challenges of remote monitoring of wetlands. Remote Sens. 2015, 7, 10938–10950. [Google Scholar] [CrossRef]
- Henderson, F.M.; Lewis, A.J. Radar detection of wetland ecosystems: A review. Int. J. Remote Sens. 2008, 29, 5809–5835. [Google Scholar] [CrossRef]
- Schmidt, K.S.; Skidmore, A.K. Spectral discrimination of vegetation types in a coastal wetland. Remote Sens. Env. 2003, 85, 92–108. [Google Scholar] [CrossRef]
- Mutanga, O.; Adam, E.; Cho, M.A. High density biomass estimation for wetland vegetation using WorldView-2 imagery and random forest regression algorithm. Int. J. Appl. Earth Obs. Geoinf. 2012, 18, 399–406. [Google Scholar] [CrossRef]
- Crist, E.P.; Cicone, R.C. A Physically-Based Transformation of Thematic Mapper Data—The TM Tasseled Cap. IEEE Trans. Geosci. Remote Sens. 1984, 3, 256–263. [Google Scholar] [CrossRef]
- Leblanc, M.; Lemoalle, J.; Bader, J.-C.; Tweed, S.; Mofor, L. Thermal remote sensing of water under flooded vegetation: New observations of inundation patterns for the ‘Small’ Lake Chad. J. Hydrol. 2011, 404, 87–98. [Google Scholar] [CrossRef]
- Perennou, C.; Guelmami, A.; Paganini, M.; Philipson, P.; Poulin, B.; Strauch, A.; Tottrup, C.; Truckenbrodt, J.; Geijzendorffer, I.R. Chapter Six—Mapping Mediterranean wetlands with remote sensing: A good-looking map is not always a good map. In Advances in Ecological Research; Bohan, D.A., Dumbrell, A.J., Woodward, G., Jackson, M., Eds.; Next Generation Biomonitoring: Part 1; Academic Press: Cambridge, MA, USA, 2018; Volume 58, pp. 243–277. [Google Scholar]
- Boavida, M.-J. Wetlands: Most relevant structural and functional aspects. Limnetica 1999, 17, 57–63. [Google Scholar]
- Coops, H.; Hosper, S.H. Water-level management as a tool for the restoration of shallow lakes in the Netherlands. Lake Reserv. Manag. 2002, 18, 293–298. [Google Scholar] [CrossRef]
- Acharya, T.D.; Subedi, A.; Lee, D.H. Evaluation of Water Indices for Surface Water Extraction in a Landsat 8 Scene of Nepal. Sensors 2018, 18, 2580. [Google Scholar] [CrossRef]
- Donchyts, G.; Schellekens, J.; Winsemius, H.; Eisemann, E.; van de Giesen, N. A 30 m Resolution Surface Water Mask Including Estimation of Positional and Thematic Differences Using Landsat 8, SRTM and OpenStreetMap: A Case Study in the Murray-Darling Basin, Australia. Remote Sens. 2016, 8, 386. [Google Scholar] [CrossRef]
- Bourgeau-Chavez, L.L.; Smith, K.B.; Brunzell, S.M.; Kasischke, E.S.; Romanowicz, E.A.; Richardson, C.J. Remote monitoring of regional inundation patterns and hydroperiod in the Greater Everglades using Synthetic Aperture Radar. Wetlands 2005, 25, 176. [Google Scholar] [CrossRef]
- Jones, J.W. Efficient Wetland Surface Water Detection and Monitoring via Landsat: Comparison with in situ Data from the Everglades Depth Estimation Network. Remote Sens. 2015, 7, 12503–12538. [Google Scholar] [CrossRef]
- Davranche, A.; Poulin, B.; Lefebvre, G. Mapping flooding regimes in Camargue wetlands using seasonal multispectral data. Remote Sens. Environ. 2013, 138, 165–171. [Google Scholar] [CrossRef]
- Beeri, O.; Phillips, R.L. Tracking palustrine water seasonal and annual variability in agricultural wetland landscapes using Landsat from 1997 to 2005. Glob. Chang. Biol. 2007, 13, 897–912. [Google Scholar] [CrossRef]
- Huang, C.; Chen, Y.; Wu, J. Mapping spatio-temporal flood inundation dynamics at large river basin scale using time-series flow data and MODIS imagery. Int. J. Appl. Earth Obs. Geoinf. 2014, 26, 350–362. [Google Scholar] [CrossRef]
- Aires, F.; Miolane, L.; Prigent, C.; Pham, B.; Fluet-Chouinard, E.; Lehner, B.; Papa, F. A global dynamic long-term inundation extent dataset at high spatial resolution derived through downscaling of satellite observations. J. Hydrometeorol. 2017, 18, 1305–1325. [Google Scholar] [CrossRef]
- Adell, C.; Puech, C. L’analyse spatiale des plans d’eau extraits par télédétection satellitale permet-elle de retrouver la marque cynégétique en Camargue? Bull. Société Fr. Photogrammétrie Télédétection 2003, 172, 76–86. [Google Scholar]
- Feyisa, G.L.; Meilby, H.; Fensholt, R.; Proud, S.R. Automated Water Extraction Index: A new technique for surface water mapping using Landsat imagery. Remote Sens. Environ. 2014, 140, 23–35. [Google Scholar] [CrossRef]
- Gao, B. NDWI—A normalized difference water index for remote sensing of vegetation liquid water from space. Remote Sens. Environ. 1996, 58, 257–266. [Google Scholar] [CrossRef]
- Kordelas, G.A.; Manakos, I.; Aragonés, D.; Díaz-Delgado, R.; Bustamante, J. Fast and Automatic Data-Driven Thresholding for Inundation Mapping with Sentinel-2 Data. Remote Sens. 2018, 10, 910. [Google Scholar] [CrossRef]
- Shen, L.; Li, C. Water body extraction from Landsat ETM+ imagery using adaboost algorithm. In Proceedings of the 2010 18th International Conference on Geoinformatics, Beijing, China, 18–20 June 2010; pp. 1–4. [Google Scholar]
- Singh, K.V.; Setia, R.; Sahoo, S.; Prasad, A.; Pateriya, B. Evaluation of NDWI and MNDWI for assessment of waterlogging by integrating digital elevation model and groundwater level. Geocarto Int. 2015, 30, 650–661. [Google Scholar] [CrossRef]
- Xu, H. Modification of normalised difference water index (NDWI) to enhance open water features in remotely sensed imagery. Int. J. Remote Sens. 2006, 27, 3025–3033. [Google Scholar] [CrossRef]
- McFeeters, S.K. The use of the Normalized Difference Water Index (NDWI) in the delineation of open water features. Int. J. Remote Sens. 1996, 17, 1425–1432. [Google Scholar] [CrossRef]
- Díaz-Delgado, R.; Aragonés, D.; Afán, I.; Bustamante, J. Long-Term Monitoring of the Flooding Regime and Hydroperiod of Doñana Marshes with Landsat Time Series (1974–2014). Remote Sens. 2016, 8, 775. [Google Scholar] [CrossRef]
- Sun, F.; Sun, W.; Chen, J.; Gong, P. Comparison and improvement of methods for identifying waterbodies in remotely sensed imagery. Int. J. Remote Sens. 2012, 33, 6854–6875. [Google Scholar] [CrossRef]
- Zhou, Y.; Dong, J.; Xiao, X.; Xiao, T.; Yang, Z.; Zhao, G.; Zou, Z.; Qin, Y. Open surface water mapping algorithms: A comparison of water-related spectral indices and sensors. Water 2017, 9, 256. [Google Scholar] [CrossRef]
- Fisher, A.; Flood, N.; Danaher, T. Comparing Landsat water index methods for automated water classification in eastern Australia. Remote Sens. Environ. 2016, 175, 167–182. [Google Scholar] [CrossRef]
- Acharya, T.; Lee, D.; Yang, I.; Lee, J. Identification of Water Bodies in a Landsat 8 OLI Image Using a J48 Decision Tree. Sensors 2016, 16, 1075. [Google Scholar] [CrossRef]
- Lefebvre, G.; Germain, C.; Poulin, B. Contribution of rainfall vs. water management to Mediterranean wetland hydrology: Development of an interactive simulation tool to foster adaptation to climate variability. Environ. Model. Softw. 2015, 74, 39–47. [Google Scholar] [CrossRef]
- Poulin, B. Reedbed management and conservation in Europe: Introduction. In Wildlife, Land and People: Priorities for the 21st Century; Field, R., Warren, R.J., Okarma, H., Sievert, P.R., Eds.; Wildlife Society: Bethesda, MD, USA, 2001; pp. 378–381. [Google Scholar]
- Russi, D.; ten Brink, P.; Farmer, A.; Badura, T.; Coates, D.; Förster, J.; Kumar, R.; Davidson, N. The Economics of Ecosystems and Biodiversity for Water and Wetlands; IEEP, Ramsar Secretariat: London, UK; Gland, Switzerland, 2013. [Google Scholar]
- Lefebvre, G.; Redmond, L.; Germain, C.; Palazzi, E.; Terzago, S.; Willm, L.; Poulin, B. Predicting the vulnerability of seasonally-flooded wetlands to climate change across the Mediterranean Basin. Sci. Total Environ. 2019, 692, 546–555. [Google Scholar] [CrossRef]
- Giorgi, F. Climate change hot-spots. Geophys. Res. Lett. 2006, 33, L08707. [Google Scholar] [CrossRef]
- Giorgi, F.; Lionello, P. Climate change projections for the Mediterranean region. Glob. Planet. Chang. 2008, 63, 90–104. [Google Scholar] [CrossRef]
- Dubrovský, M.; Hayes, M.; Duce, P.; Trnka, M.; Svoboda, M.; Zara, P. Multi-GCM projections of future drought and climate variability indicators for the Mediterranean region. Reg. Environ. Chang. 2014, 14, 1907–1919. [Google Scholar] [CrossRef]
- Postel, S.; Carpenter, S. Freshwater ecosystem services. In Nature’s Services: Societal Dependence on Natural Ecosystems; Island Press: Washington, DC, USA, 1997; pp. 195–214. ISBN 978-1-59726-775-5. [Google Scholar]
- TEEB. The Economics of Ecosystems and Biodiversity: Ecological and Economic Foundations, 1st ed.; Earthscan, Pushpam Kumar: London, UK; Washington, DC, USA, 2010; ISBN 978-1-84971-212-5. [Google Scholar]
- Poulin, B.; Davranche, A.; Lefebvre, G. Ecological assessment of Phragmites australis wetlands using multi-season SPOT-5 scenes. Remote Sens. Environ. 2010, 114, 1602–1609. [Google Scholar] [CrossRef]
- Horritt, M.S.; Mason, D.C.; Luckman, A.J. Flood boundary delineation from Synthetic Aperture Radar imagery using a statistical active contour model. Int. J. Remote Sens. 2001, 22, 2489–2507. [Google Scholar] [CrossRef]
- Cazals, C.; Rapinel, S.; Frison, P.-L.; Bonis, A.; Mercier, G.; Mallet, C.; Corgne, S.; Rudant, J.-P. Mapping and Characterization of Hydrological Dynamics in a Coastal Marsh Using High Temporal Resolution Sentinel-1A Images. Remote Sens. 2016, 8, 570. [Google Scholar] [CrossRef]
- Jensen, K.; McDonald, K.; Podest, E.; Rodriguez-Alvarez, N.; Horna, V.; Steiner, N. Assessing L-Band GNSS-Reflectometry and Imaging Radar for Detecting Sub-Canopy Inundation Dynamics in a Tropical Wetlands Complex. Remote Sens. 2018, 10, 1431. [Google Scholar] [CrossRef]
- Hess, L.L.; Melack, J.M.; Novo, E.M.L.M.; Barbosa, C.C.F.; Gastil, M. Dual-season mapping of wetland inundation and vegetation for the central Amazon basin. Remote Sens. Environ. 2003, 87, 404–428. [Google Scholar] [CrossRef]
- White, L.; Brisco, B.; Dabboor, M.; Schmitt, A.; Pratt, A. A collection of SAR methodologies for monitoring wetlands. Remote Sens. 2015, 7, 7615–7645. [Google Scholar] [CrossRef]
- Tsyganskaya, V.; Martinis, S.; Marzahn, P.; Ludwig, R. SAR-based detection of flooded vegetation—A review of characteristics and approaches. Int. J. Remote Sens. 2018, 39, 2255–2293. [Google Scholar] [CrossRef]
- Rokni, K.; Ahmad, A.; Selamat, A.; Hazini, S. Water feature extraction and change detection using multitemporal Landsat imagery. Remote Sens. 2014, 6, 4173–4189. [Google Scholar] [CrossRef]
- Poulin, B.; Lefebvre, G.; Allard, S.; Mathevet, R. Reed harvest and summer drawdown enhance bittern habitat in the Camargue. Biol. Conserv. 2009, 142, 689–695. [Google Scholar] [CrossRef]
- Therneau, T.M.; Atkinson, E.J. An Introduction to Recursive Partitioning Using the RPART Routines; Mayo Foundation: Scottsdale, AZ, USA, 2019; p. 60. [Google Scholar]
- Esposito, F.; Malerba, D.; Semeraro, G.; Tamma, V. The effects of pruning methods on the predictive accuracy of induced decision trees. Appl. Stoch. Models Bus. Ind. 1999, 15, 277–299. [Google Scholar] [CrossRef]
- Breiman, L. Classification and Regression Trees, 1st ed.; Routledge: New York, NY, USA, 1984; ISBN 978-1-315-13947-0. [Google Scholar]
- Rikimaru, A.; Roy, P.S.; Miyatake, S. Tropical forest cover density mapping. Trop. Ecol. 2002, 43, 39–47. [Google Scholar]
- Richardson, A.J.; Everitt, J.H. Using spectral vegetation indices to estimate rangeland productivity. Geocarto Int. 1992, 7, 63–69. [Google Scholar] [CrossRef]
- Gond, V.; Bartholomé, E.; Ouattara, F.; Nonguierma, A.; Bado, L. Surveillance et cartographie des plans d’eau et des zones humides et inondables en régions arides avec l’instrument VEGETATION embarqué sur SPOT-4. Int. J. Remote Sens. 2004, 25, 987–1004. [Google Scholar] [CrossRef]
- Crippen, R.E. Calculating the vegetation index faster. Remote Sens. Environ. 1990, 34, 71–73. [Google Scholar] [CrossRef]
- Huntjr, E.; Rock, B. Detection of changes in leaf water content using Near- and Middle-Infrared reflectances. Remote Sens. Environ. 1989, 30, 43–54. [Google Scholar] [CrossRef]
- Rouse, J., Jr.; Haas, R.H.; Schell, J.A.; Deering, D.W. Monitoring vegetation systems in the Great Plains with ERTS. In NASA Goddard Space Flight Center 3d ERTS-1 Symposium; NASA: Washington, DC, USA, 1974; Volume 1, pp. 309–317. [Google Scholar]
- Rondeaux, G.; Steven, M.; Baret, F. Optimization of soil-adjusted vegetation indices. Remote Sens. Environ. 1996, 55, 95–107. [Google Scholar] [CrossRef]
- Lillesand, T.M.; Kiefer, R.W. Remote Sensing and Image Interpretation, 2nd ed.; Wiley: New York, NY, USA, 1987; ISBN 978-0-471-84517-1. [Google Scholar]
- Huete, A.R. A soil-adjusted vegetation index (SAVI). Remote Sens. Environ. 1988, 25, 295–309. [Google Scholar] [CrossRef]
- Pearson, R.L.; Miller, L.D. Remote mapping of standing crop biomass for estimation of the productivity of the short-grass Prairie, Pawnee National Grasslands, Colorado. In Proceedings of the 8th International Symposium on Remote Sensing of Environment, Ann Arbor, MI, USA, 2–6 October 1972; pp. 1357–1381. [Google Scholar]
- Broge, N.H.; Leblanc, E. Comparing prediction power and stability of broadband and hyperspectral vegetation indices for estimation of green leaf area index and canopy chlorophyll density. Remote Sens. Environ. 2001, 76, 156–172. [Google Scholar] [CrossRef]
- Caillaud, L.; Guillaumont, B.; Manaud, F. Essai de discrimination des modes d’utilisation des marais maritimes par analyse multitemporelle d’images spot. Application aux marais maritimes du Centre Ouest. 1987. Available online: https://archimer.ifremer.fr/doc/00446/55728/ (accessed on 20 September 2019).
- Kameyama, S.; Yamagata, Y.; Nakamura, F.; Kaneko, M. Development of WTI and turbidity estimation model using SMA — application to Kushiro Mire, eastern Hokkaido. Jpn. Remote Sens. Environ. 2001, 77, 1–9. [Google Scholar] [CrossRef]
- Centre Français du Riz. Bilan de la campagne 2006 et résultats variétaux. 2007. [Google Scholar]
- Centre Français du Riz. Bilan de la Campagne 2017 et résultats variétaux. 2018. [Google Scholar]
- Kordelas, G.A.; Manakos, I.; Lefebvre, G.; Poulin, B. Automatic inundation mapping using Sentinel-2 data applicable to both Camargue and Doñana wetlands. Remote Sens.
- De Oliveira, G.A.; Bureau, S.; Renard, C.M.-G.C.; Pereira-Netto, A.B.; de Castilhos, F. Comparison of NIRS approach for prediction of internal quality traits in three fruit species. Food Chem. 2014, 143, 223–230. [Google Scholar] [CrossRef] [PubMed]
- Daffara, C.; Pampaloni, E.; Pezzati, L.; Barucci, M.; Fontana, R. Scanning multispectral IR reflectography SMIRR: An advanced tool for art diagnostics. Acc. Chem. Res. 2010, 43, 847–856. [Google Scholar] [CrossRef] [PubMed]
- Delaney, J.K.; Thoury, M.; Zeibel, J.G.; Ricciardi, P.; Morales, K.M.; Dooley, K.A. Visible and infrared imaging spectroscopy of paintings and improved reflectography. Herit. Sci. 2016, 4, 6. [Google Scholar] [CrossRef]
- van Asperen de Boer, J.R. Infrared reflectography: A method for the examination of paintings. Appl. Opt. 1968, 7, 1711–1714. [Google Scholar] [CrossRef]
- Tamisier, A.; Grillas, P. A review of habitat changes in the Camargue: An assessment of the effects of the loss of biological diversity on the wintering waterfowl community. Biol. Conserv. 1994, 70, 39–47. [Google Scholar] [CrossRef]
- Davis, T.J. The Ramsar Convention Manual: A Guide to the Convention on Wetlands; Ramsar Convention Bureau: Gland, Switzerland, 1997. [Google Scholar]
- Schlesinger, W.H.; Bernhardt, E.S. Biogeochemistry: An Analysis of Global Change, 3rd ed.; Elsevier, Academic Press: Amsterdam, The Netherlands; Boston, MA, USA, 2013; ISBN 978-0-12-385874-0. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).