K-Matrix: A Novel Change-Pattern Mining Method for SAR Image Time Series
Abstract
1. Introduction
- (1)
- preprocessing of SAR images;
- (2)
- comparison between two images;
- (3)
- thresholding of the image change indicator.
- (1)
- A novel two-step framework to mine the change patterns of SAR image time series.
- (2)
- An efficient change detection approach based on the distance matrix for SAR image time series.
- (3)
- An unsupervised clustering algorithm, called K-Matrix, for the distance matrix to extract the change patterns.
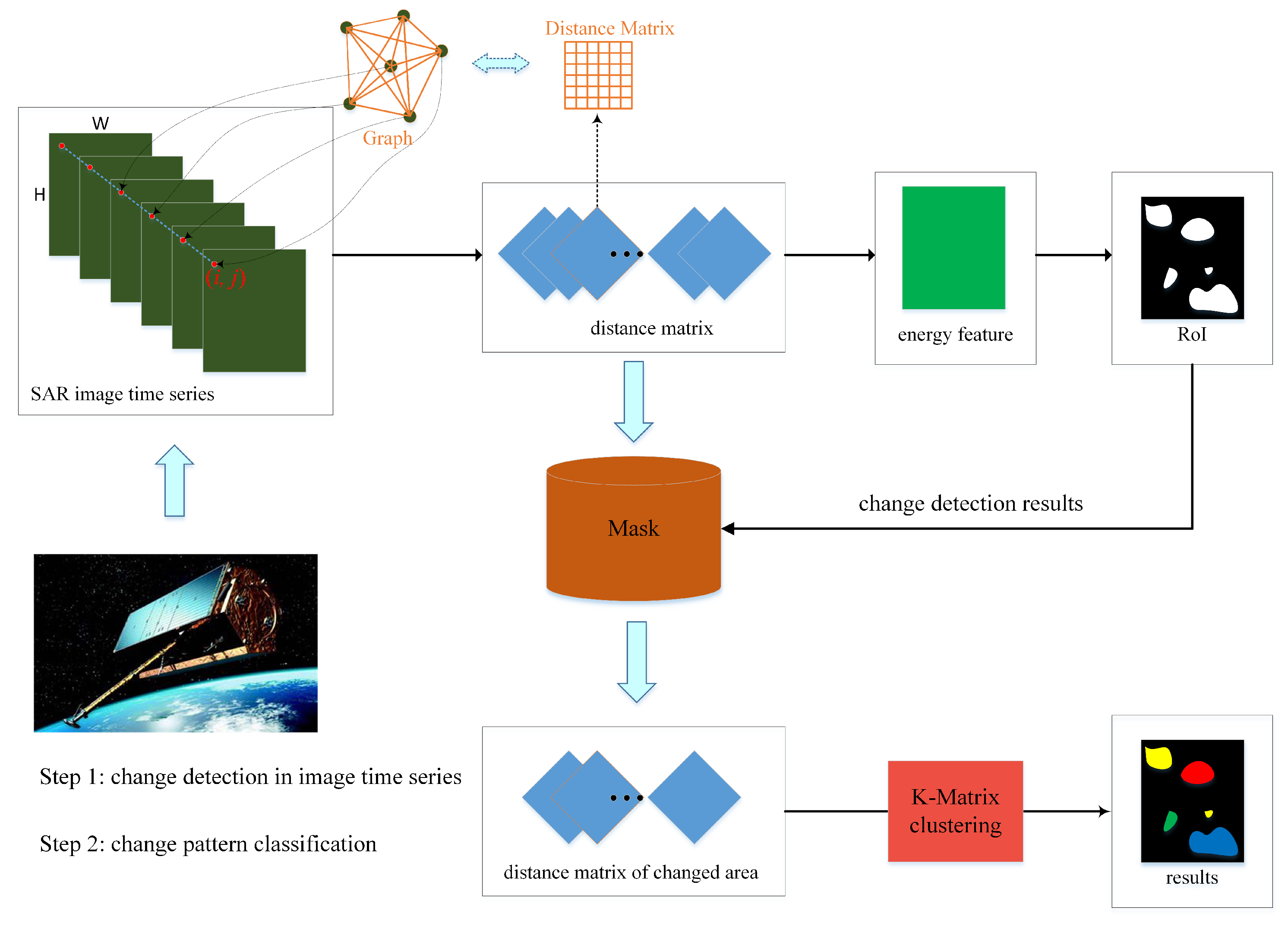
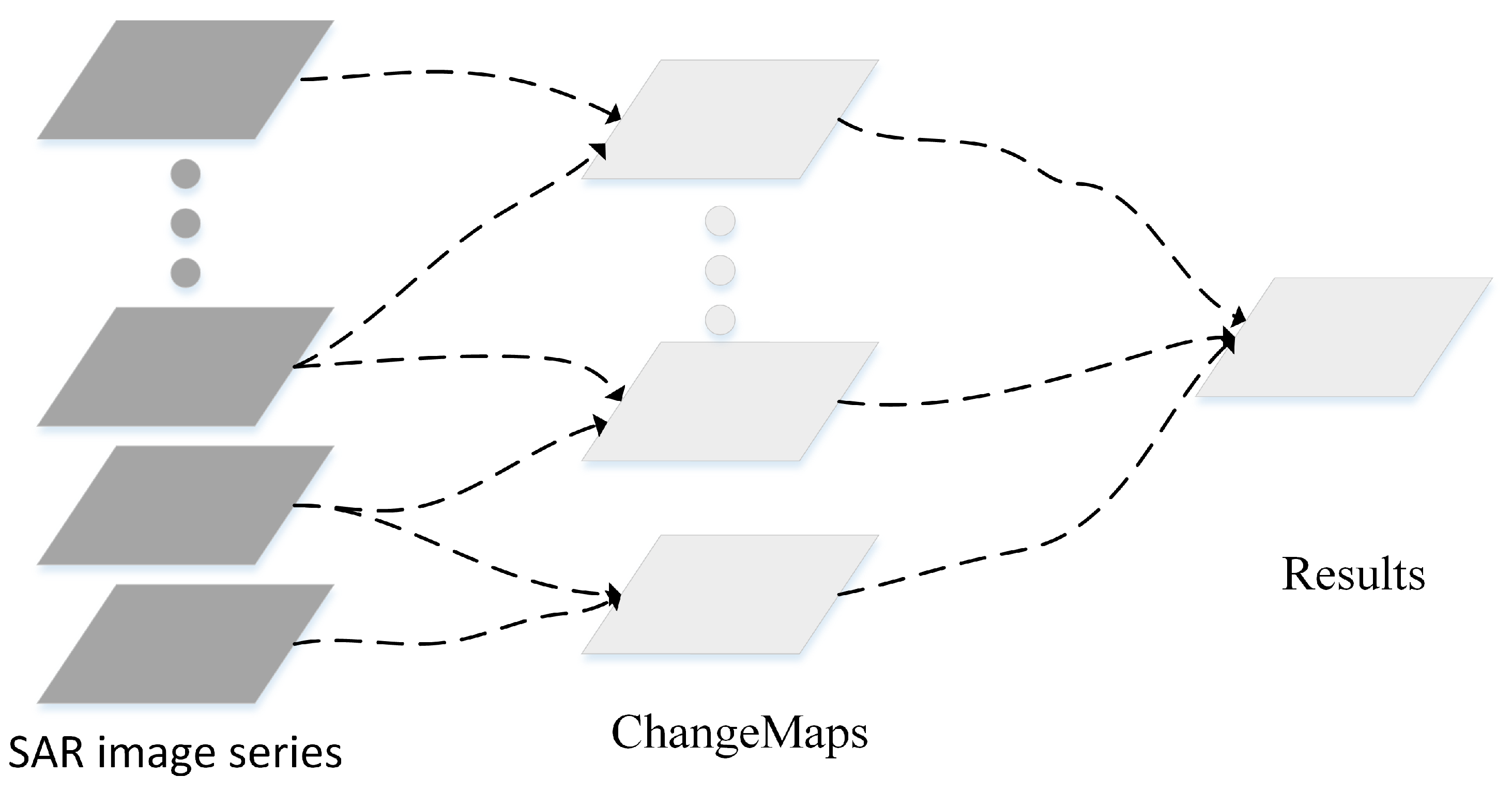
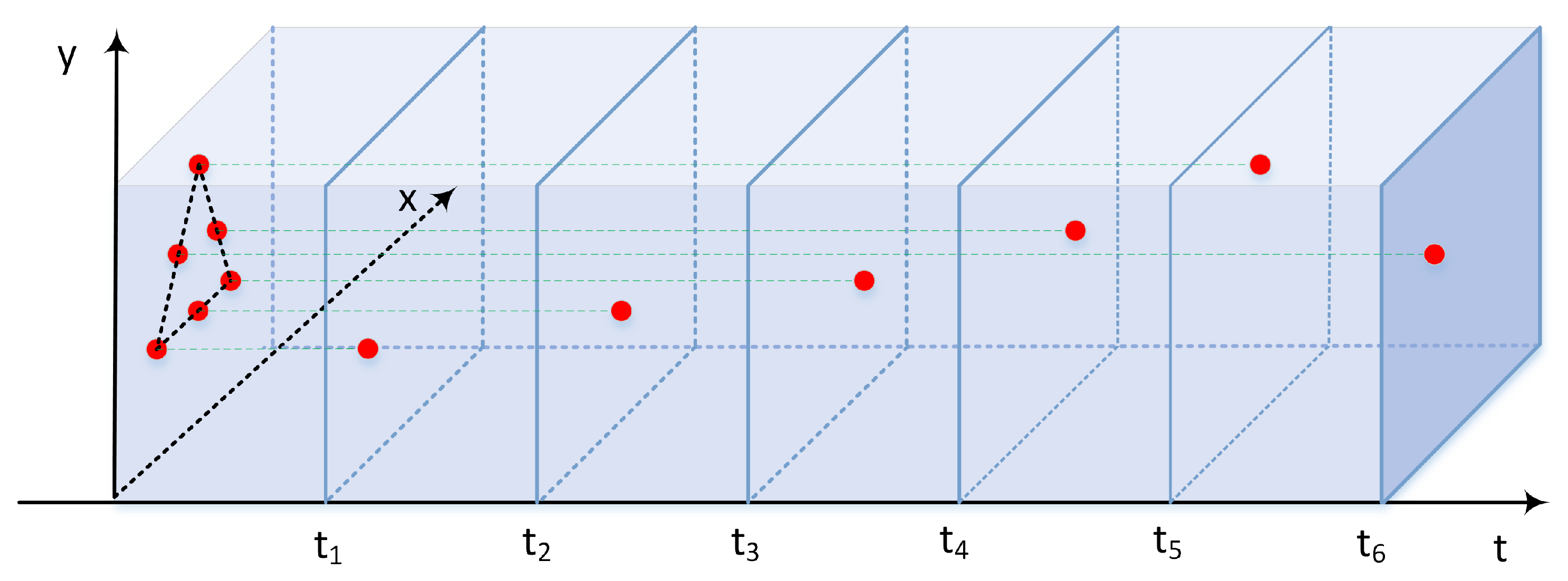
2. Methodology
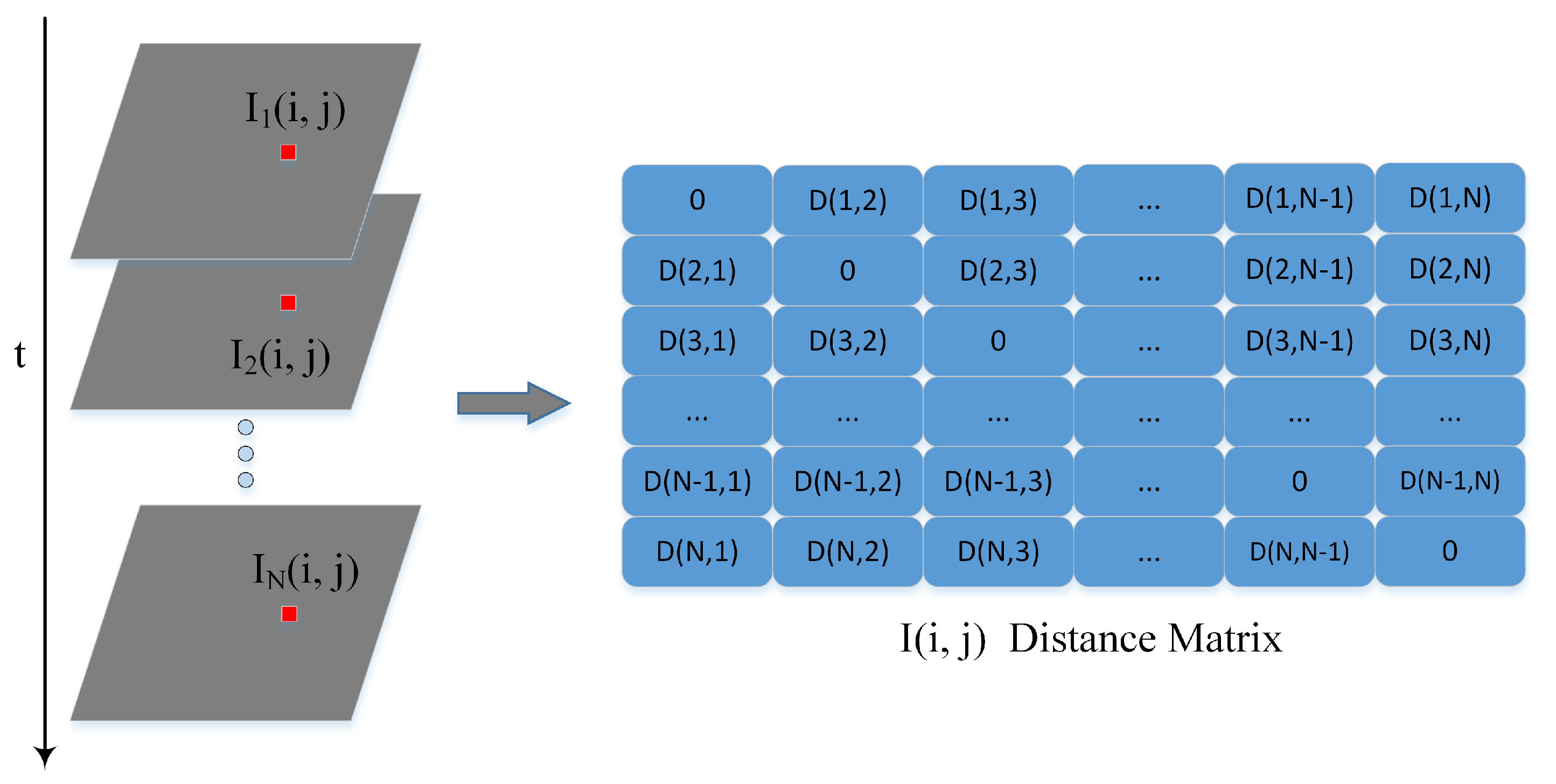
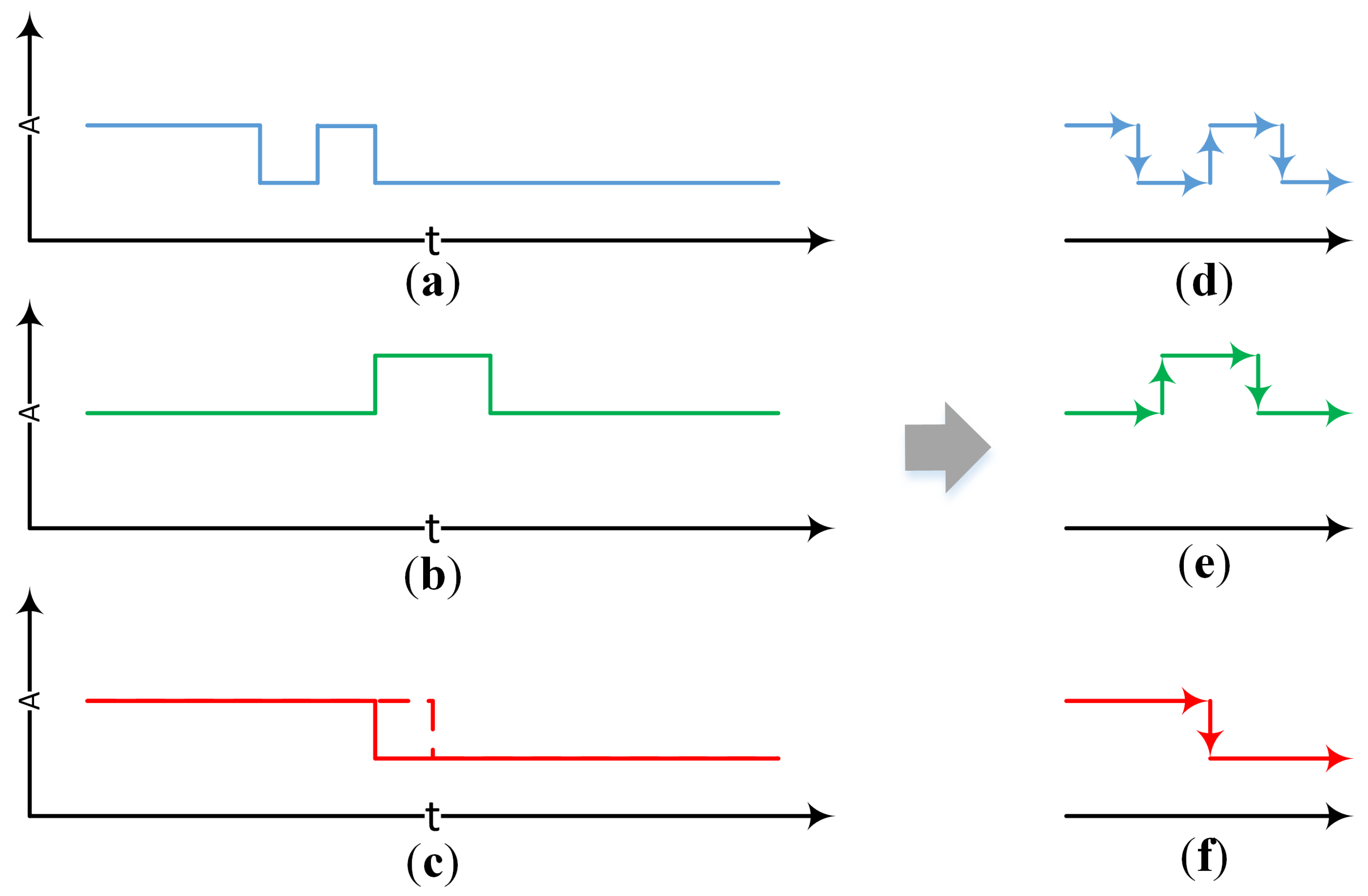
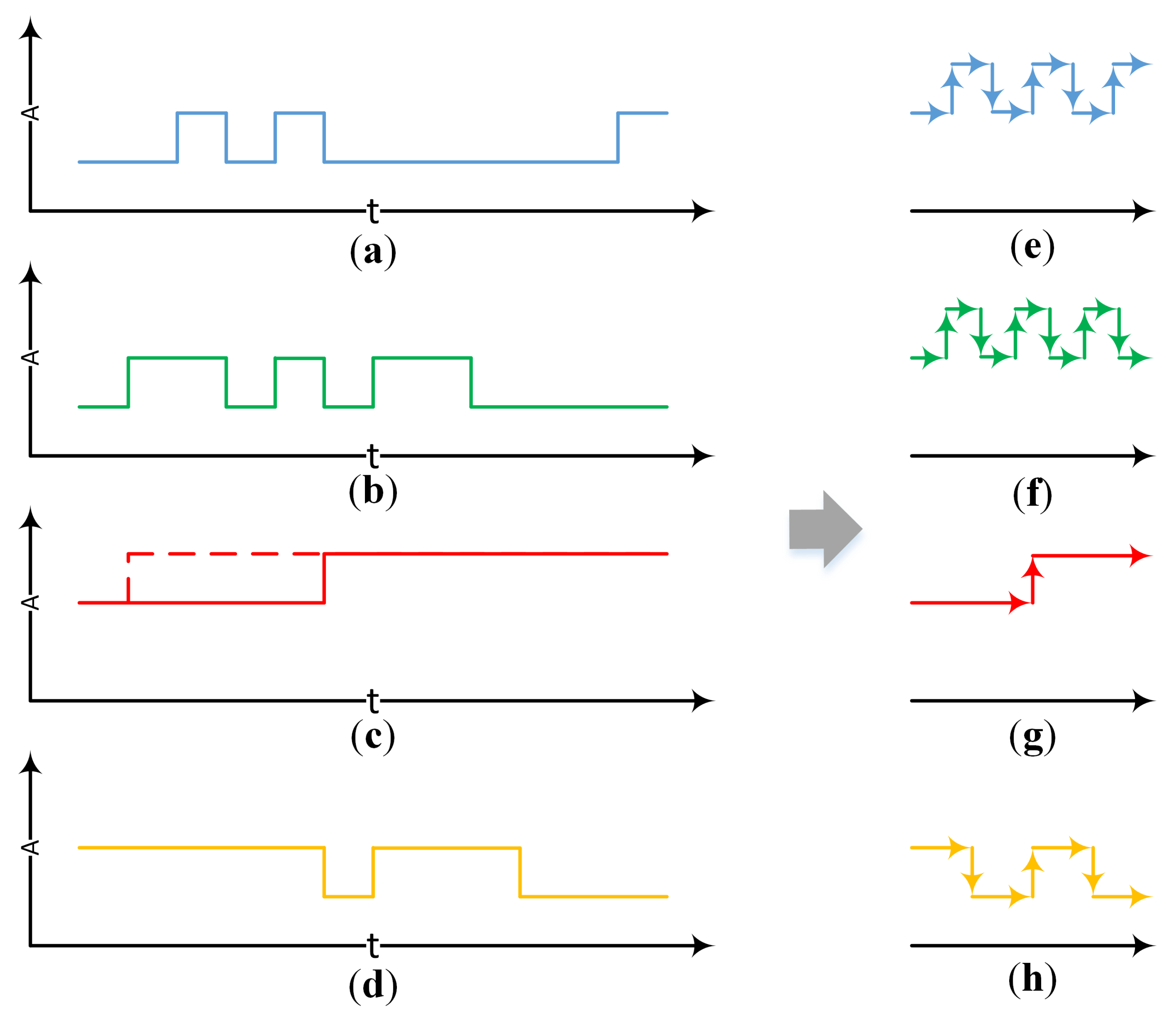
2.1. Change Detection in SAR Image Time Series
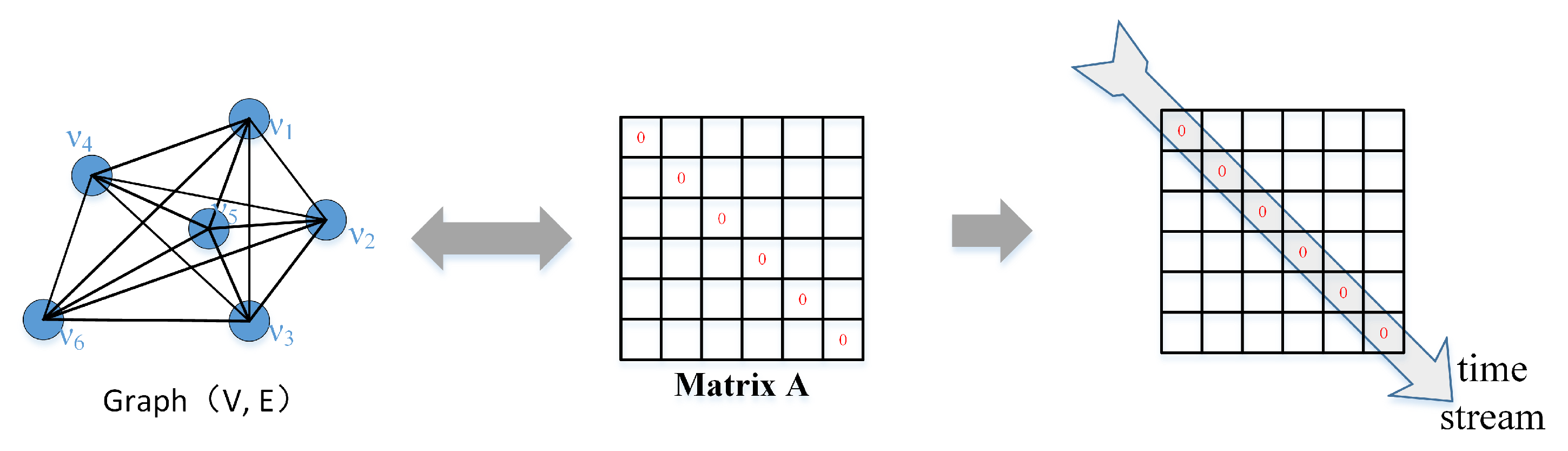
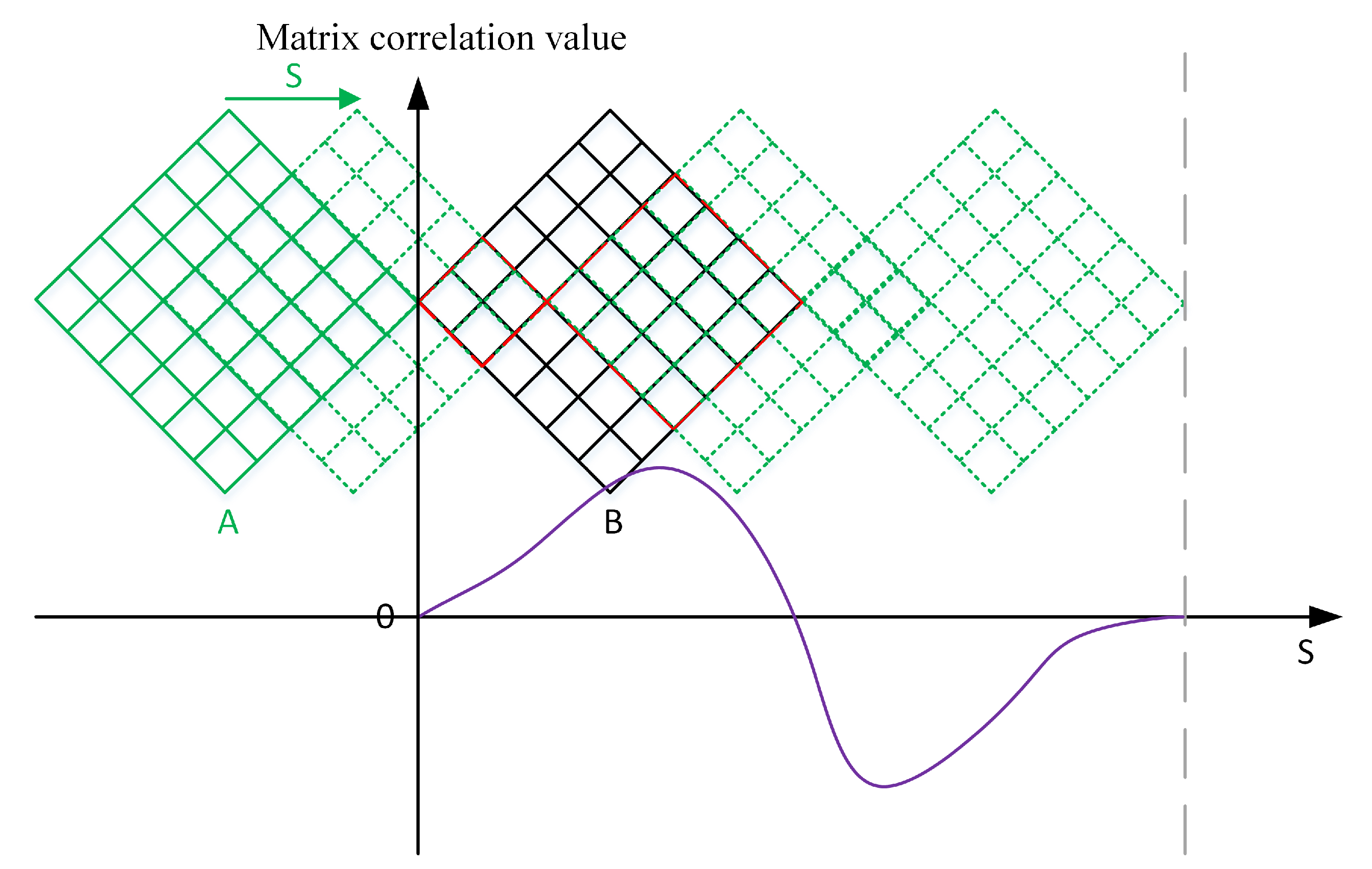
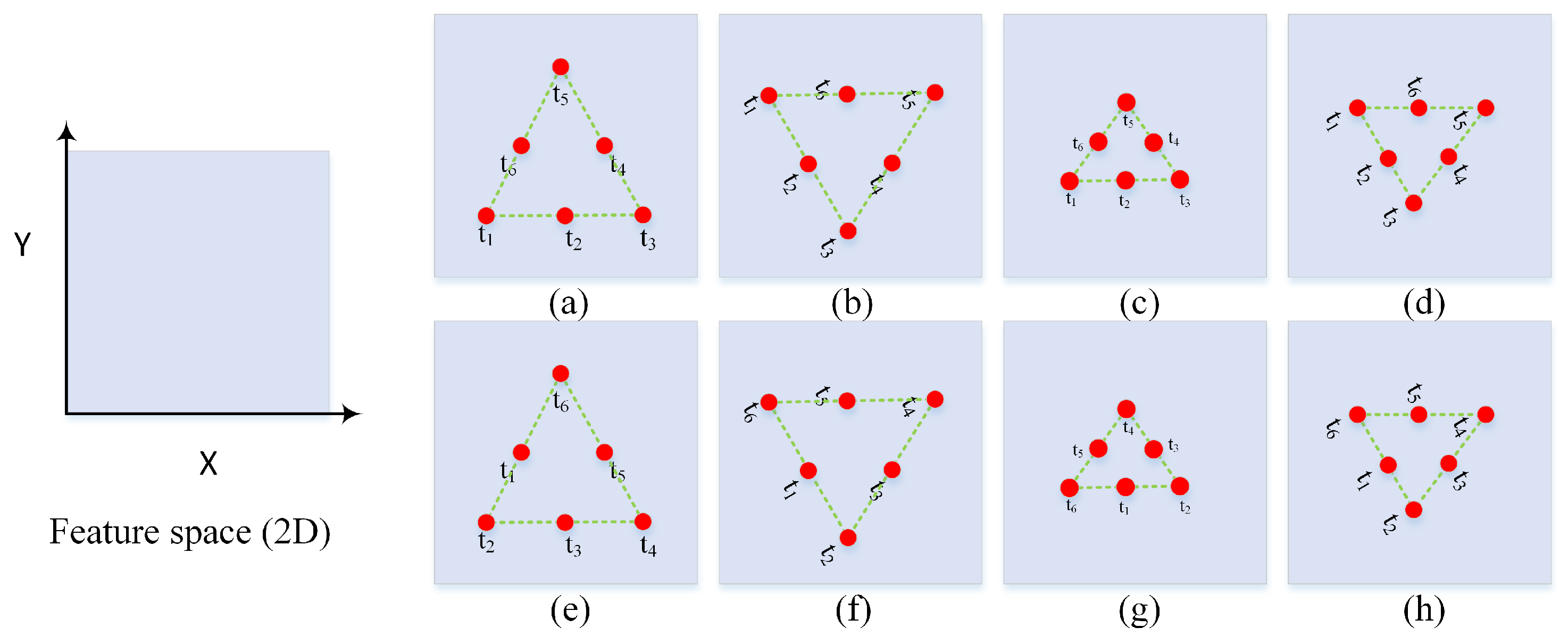
2.2. K-Matrix Clustering Algorithm
3. Experiment
3.1. Description of Datasets
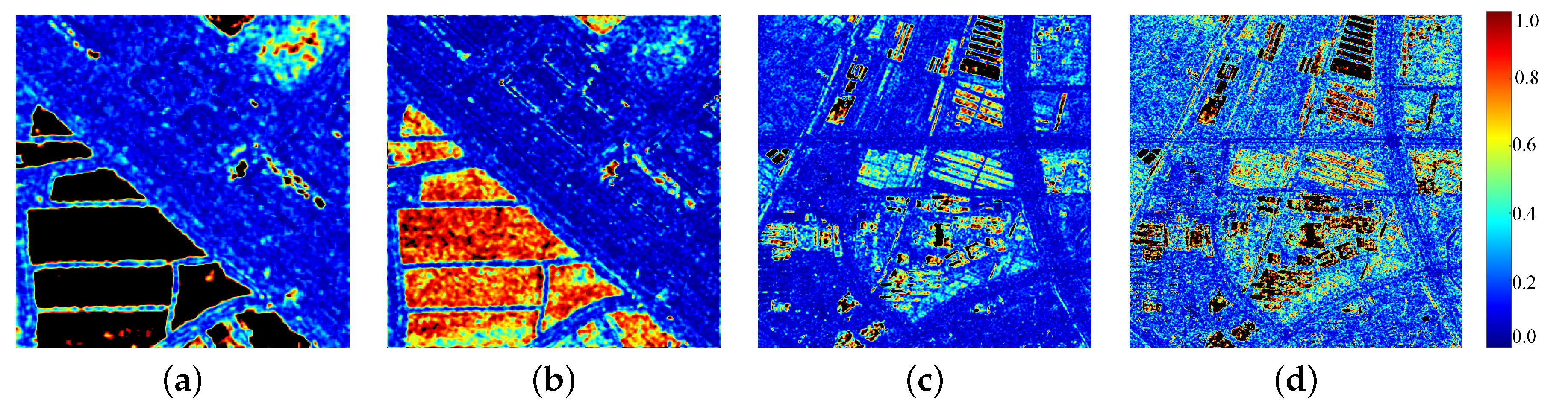
3.2. Change Detection in SAR Image Time Series
3.3. Change-Pattern Mining
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
References
- Lu, D.; Mausel, P.; Moran, E.F. Change detection techniques. Int. J. Remote Sens. 2004, 25, 2365–2407. [Google Scholar] [CrossRef]
- Quegan, S.; Toan, T.L.; Yu, J.J.; Ribbes, F.; Floury, N. Multitemporal ERS SAR analysis applied to forest mapping. IEEE Trans. Geosci. Remote Sens. 2000, 38, 741–753. [Google Scholar] [CrossRef]
- Muro, J.; Canty, M.J.; Conradsen, K.; Huttich, C.; Nielsen, A.A.; Skriver, H.; Remy, F.; Strauch, A.; Thonfeld, F.; Menz, G. Short-Term Change Detection in Wetlands Using Sentinel-1 Time Series. Remote Sens. 2016, 8, 795. [Google Scholar] [CrossRef]
- Chen, F.; Lasaponara, R.; Masini, N. An overview of satellite synthetic aperture radar remote sensing in archaeology: From site detection to monitring. J. Cult. Herit. 2017, 23, 5–11. [Google Scholar] [CrossRef]
- Brunner, D.; Bruzzone, L.; Lemoine, G. Change detection for earthquake damage assessment in built-up areas using very high resolution optical and SAR imagery. IEEE Int. Geosci. Remote Sens. Symp. 2010, 1, 3210–3213. [Google Scholar]
- Bovolo, F.; Bruzzone, L. A Split-Based Approach to Unsupervised Change Detection in Large-Size Multitemporal Images: Application to Tsunami-Damage Assessment. IEEE Trans. Geosci. Remote Sens. 2007, 45, 1658–1670. [Google Scholar] [CrossRef]
- Gamba, P.; Dellacqua, F.; Lisini, G. Change Detection of Multitemporal SAR Data in Urban Areas Combining Feature-Based and Pixel-Based Techniques. IEEE Trans. Geosci. Remote Sens. 2006, 44, 2820–2827. [Google Scholar] [CrossRef]
- Heine, I.; Jagdhuber, T.; Itzerott, S. Classification and Monitoring of Reed Belts Using Dual-Polarimetric TerraSAR-X Time Series. Remote Sens. 2016, 8, 552. [Google Scholar] [CrossRef]
- Brown, W.M. Synthetic Aperture Radar. IEEE Trans. Aerosp. Electron. Syst. 1967, 2, 217–229. [Google Scholar] [CrossRef]
- Yang, W.; Zhong, N.; Yan, T.; Yang, X. Classification of Polarimetric SAR Images Based on the Riemannian Manifold. J. Radars 2017, 6, 43-3-441. [Google Scholar]
- Bruzzone, L.; Bovolo, F. A Novel Framework for the Design of Change-Detection Systems for Very-High-Resolution Remote Sensing Images. Proc. IEEE 2013, 101, 609–630. [Google Scholar] [CrossRef]
- Gao, F.; Liu, X.; Dong, J.; Zhong, G.; Jian, M. Change Detection in SAR Images Based on Deep Semi-NMF and SVD Networks. Remote Sens. 2017, 9, 435. [Google Scholar] [CrossRef]
- Hu, H.; Ban, Y. Unsupervised Change Detection in Multitemporal SAR Images Over Large Urban Areas. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 3248–3261. [Google Scholar] [CrossRef]
- Argenti, F.; Lapini, A.; Bianchi, T.; Alparone, L. A Tutorial on Speckle Reduction in Synthetic Aperture Radar Images. IEEE Geosci. Remote Sens. Mag. 2013, 1, 6–35. [Google Scholar] [CrossRef]
- Deledalle, C.; Denis, L.; Poggi, G.; Tupin, F.; Verdoliva, L. Exploiting Patch Similarity for SAR Image Processing: The nonlocal paradigm. IEEE Signal Process. Mag. 2014, 31, 69–78. [Google Scholar] [CrossRef]
- Deledalle, C.; Denis, L.; Tabti, S.; Tupin, F. MuLoG, or How to Apply Gaussian Denoisers to Multi-Channel SAR Speckle Reduction? IEEE Trans. Image Process. 2017, 26, 4389–4403. [Google Scholar] [CrossRef]
- Singh, A. Digital change detection techniques using remotely sensed data. Int. J. Remote Sens. 1989, 10, 989–1003. [Google Scholar] [CrossRef]
- Rignot, E.; Van Zyl, J.J. Change detection techniques for ERS-1 SAR data. IEEE Trans. Geosci. Remote Sens. 1993, 31, 896–906. [Google Scholar] [CrossRef]
- Lombardo, P.; Oliver, C.J. Maximum likelihood approach to the detection of changes between multitemporal SAR images. IEE Proc.-Radar Sonar Navig. 2001, 148, 200–210. [Google Scholar] [CrossRef]
- Inglada, J.; Mercier, G. A New Statistical Similarity Measure for Change Detection in Multitemporal SAR Images and Its Extension to Multiscale Change Analysis. IEEE Trans. Geosci. Remote Sens. 2011, 45, 1432–1445. [Google Scholar] [CrossRef]
- Yang, W.; Song, H.; Huang, X.; Xu, X.; Liao, M. Change Detection in High-Resolution SAR Images Based on Jensen–Shannon Divergence and Hierarchical Markov Model. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 3318–3327. [Google Scholar] [CrossRef]
- Ostu, N. A threshold selection method from gray-level histograms. IEEE Trans. Syst. Man Cybern. 1978, 9, 62–66. [Google Scholar]
- Kittler, J.; Illingworth, J. Minimum error thresholding. Pattern Recognit. 1986, 19, 41–47. [Google Scholar] [CrossRef]
- Bazi, Y.; Bruzzone, L.; Melgani, F. An unsupervised approach based on the generalized Gaussian model to automatic change detection in multitemporal SAR images. IEEE Trans. Geosci. Remote Sens. 2005, 43, 874–887. [Google Scholar] [CrossRef]
- Moser, G.; Serpico, S.B. Generalized minimum-error thresholding for unsupervised change detection from SAR amplitude imagery. IEEE Trans. Geosci. Remote Sens. 2006, 44, 2972–2982. [Google Scholar] [CrossRef]
- Schulz, K. Change detection in time series of high resolution SAR satellite images. Proc. SPIE Int. Soc. Opt. Eng. 2012, 8538, 06. [Google Scholar]
- Yuan, J.; Lv, X.; Dou, F.; Yao, J. Change Analysis in Urban Areas Based on Statistical Features and Temporal Clustering Using TerraSAR-X Time-Series Images. Remote Sens. 2019, 11, 926. [Google Scholar] [CrossRef]
- Atto, A.M.; Trouve, E.; Berthoumieu, Y.; Mercier, G. Multidate Divergence Matrices for the Analysis of SAR Image Time Series. IEEE Trans. Geosci. Remote Sens. 2013, 51, 1922–1938. [Google Scholar] [CrossRef]
- Quin, G.; Pinel-Puyssegur, B.; Nicolas, J.; Loreaux, P. MIMOSA: An Automatic Change Detection Method for SAR Time Series. IEEE Trans. Geosci. Remote Sens. 2014, 52, 5349–5363. [Google Scholar] [CrossRef]
- Lê, T.T.; Atto, A.M.; Trouvé, E.; Solikhin, A.; Pinel, V. Change detection matrix for multitemporal filtering and change analysis of SAR and PolSAR image time series. ISPRS J. Photogramm. Remote Sens. 2015, 107, 64–76. [Google Scholar] [CrossRef]
- Su, X.; Deledalle, C.; Tupin, F.; Sun, H. NORCAMA: Change analysis in SAR time series by likelihood ratio change matrix clustering. ISPRS J. Photogramm. Remote Sens. 2015, 101, 247–261. [Google Scholar] [CrossRef]
- Paparrizos, J.; Gravano, L. k-Shape: Efficient and Accurate Clustering of Time Series. Int. Conf. Manag. Data 2015, 45, 1855–1870. [Google Scholar]
- Hansen, P.; Jaumard, B. Cluster analysis and mathematical programming. Math. Program. 1997, 79, 191–215. [Google Scholar] [CrossRef]
- Golub, G.H.; Van, L.; Charles, F. Matrix Computations, 3rd ed.; JHU Press: Baltimore, MD, USA, 1996. [Google Scholar]
- Su, X.; Deledalle, C.A.; Tupin, F.; Sun, H. SAR image change detection by likelihood ratio test in multitemporal time series. In Proceedings of the IGARSS 2013, Melbourne, VIC, Australia, 21–26 July 2013. [Google Scholar]
- Boldt, M.; Schulz, K. Change detection in high resolution SAR images: Amplitude based activity map compared with CoVAmCoh analysis. In Proceedings of the IEEE Geoscience and Remote Sensing Symposium, Munich, Germany, 22–27 July 2012; pp. 3803–3806. [Google Scholar]









© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peng, D.; Pan, T.; Yang, W.; Li, H.-C. K-Matrix: A Novel Change-Pattern Mining Method for SAR Image Time Series. Remote Sens. 2019, 11, 2161. https://doi.org/10.3390/rs11182161
Peng D, Pan T, Yang W, Li H-C. K-Matrix: A Novel Change-Pattern Mining Method for SAR Image Time Series. Remote Sensing. 2019; 11(18):2161. https://doi.org/10.3390/rs11182161
Chicago/Turabian StylePeng, Dong, Ting Pan, Wen Yang, and Heng-Chao Li. 2019. "K-Matrix: A Novel Change-Pattern Mining Method for SAR Image Time Series" Remote Sensing 11, no. 18: 2161. https://doi.org/10.3390/rs11182161
APA StylePeng, D., Pan, T., Yang, W., & Li, H.-C. (2019). K-Matrix: A Novel Change-Pattern Mining Method for SAR Image Time Series. Remote Sensing, 11(18), 2161. https://doi.org/10.3390/rs11182161






