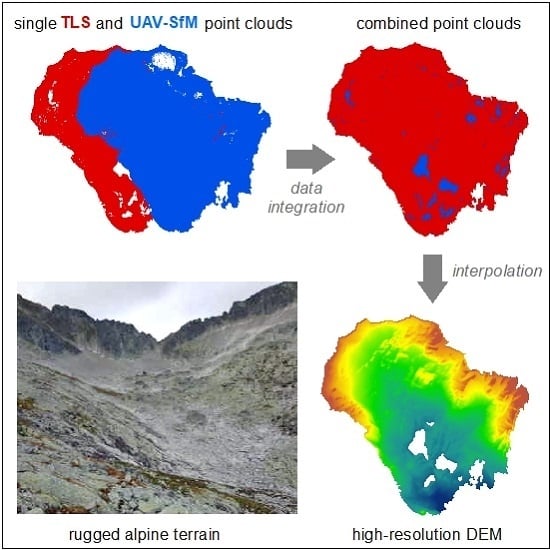
1. Introduction
Capturing terrain topography with a high spatial detail has become a common task in many research and engineering applications, which require sampling land surface heights (elevations) with spatial density and measurement precision in the order of millimeters to centimeters [
1,
2,
3,
4]. Currently, the most commonly used remote sensing methods for such a fine-scale 3D mapping comprise terrestrial laser scanning (TLS)—i.e., terrestrial lidar [
5,
6]—and close-range photogrammetry based on image matching by structure from motion, typically based on unmanned aerial vehicles as the sensor platforms (UAV-SfM) [
7,
8,
9,
10]. The main benefit of the technologies is in fast data acquisition and high accuracy—several millimeters for TLS [
11,
12,
13] and several centimeters for UAV-SfM [
14,
15,
16]. The achievable ultra-high spatial resolution provides means for analysing structural properties of rock outcrops [
17,
18], landslide dynamics [
19], relative age of landforms [
20], soil erosion [
21], biomass [
22], 3D city modelling [
23] or archaeology [
24]. Several studies [
25,
26,
27,
28] compared the accuracy of point clouds generated by TLS and UAV-SfM and/or digital elevation models (DEMs) derived from these sources of point clouds but without their integration into a single point cloud to generate a DEM.
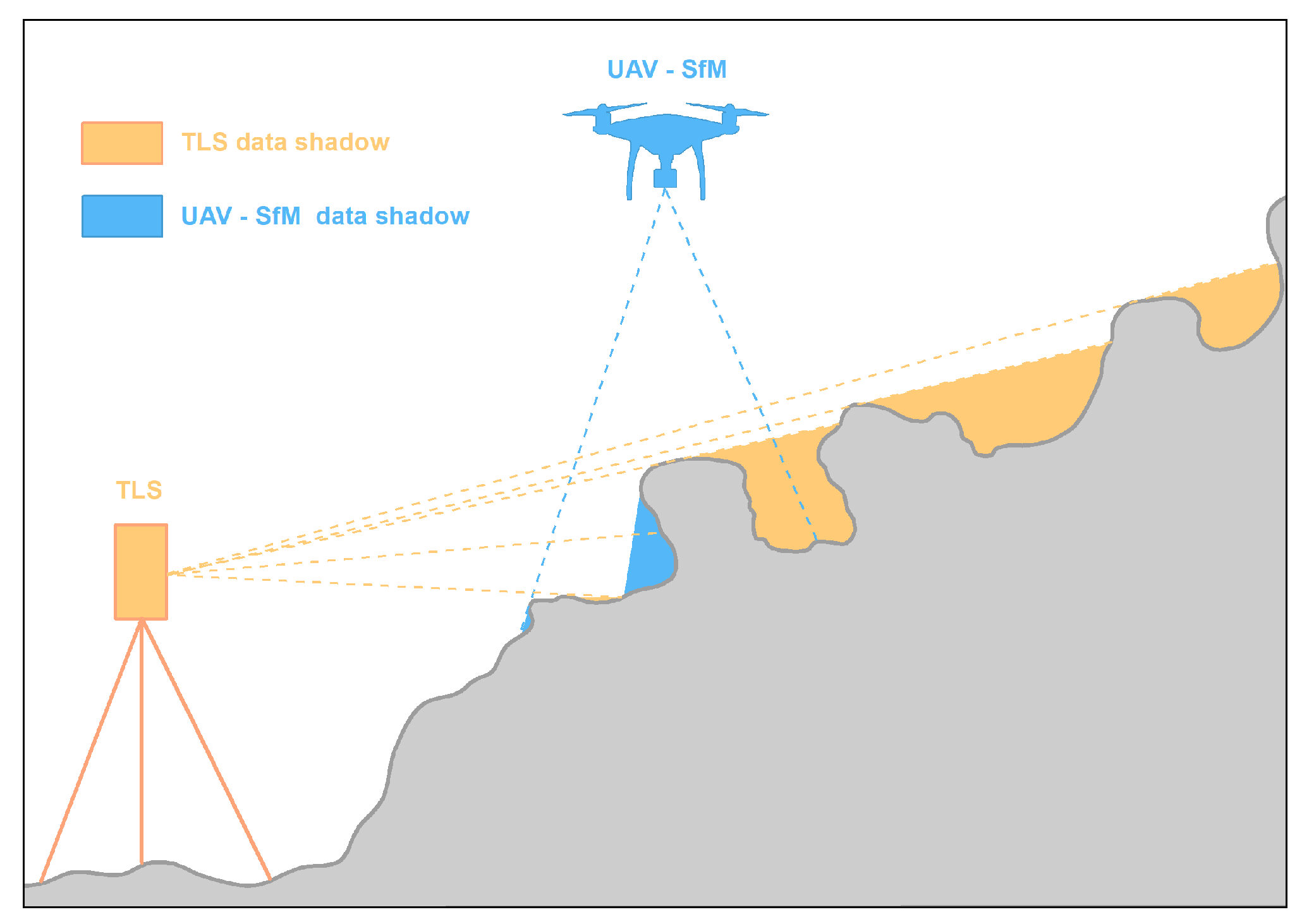
The general advantage of laser scanning over photogrammetry is in the ability of sampling several kinds of surfaces (e.g., top of vegetation canopy, inter-canopy surfaces, and ground) which are in the line of sight of the laser beam until impermeable surface restrains further penetration of the laser energy. UAV-SfM has become a low-cost alternative to TLS, generating point clouds with comparable accuracies to TLS albeit with the limitation of sampling the top surface in the field of view. Either way, in cases where TLS or UAV-SfM are used separately, data shadows originate in areas which are obscured in the sensor’s field of view [
23,
29] (
Figure 1). Complementing the unsampled areas with the surface altitude measurements is possible by sensing the area from multiple positions and different viewing perspectives by changing the location of the sensor. Zhang and Lin [
30] provide a systematic overview of the lidar and photogrammetric data fusion. Cawood et al. [
7] showed there is no exclusive method for capturing complex 3D geometry in the case study of 3D modelling a large boulder with distinct geological structural features. Combination of TLS and UAV-SfM provided the most satisfying results to capture the geometric complexity of the object of interest for structural analysis. A similar approach of combining different viewing geometry of TLS and photogrammetry was demonstrated in 3D modelling of a historical city by [
23]. Planning the data collection in the mentioned studies concerned environments with a relatively easy access for the technology and the surveying personnel.
Deglaciated alpine landscape with landforms of different size, shape and verticality (
Figure 2) pose a serious challenge for mapping with high sampling density and homogenous data coverage. Also, such areas are often inaccessible by convenient means of transportation such as a car or a helicopter and often access by foot is the sole option. Therefore, survey equipment has to be manually carried to reach the area of interest. In addition, the weather can change quickly, and the survey plan needs to be adapted accordingly. In many countries, alpine landscapes are protected areas of outstanding natural beauty with legal constraints for human activities and movement.
In many developed countries across the globe airborne lidar or photogrammetric data exist and the datasets are publicly available on a state-wide level. However, for pronounced rugged alpine areas, the spatial resolution and measurement accuracy of the existing digital elevation datasets can be still insufficient for specific tasks requiring very high accuracy and spatial resolutions. For example, Podgórski et al. [
31] report that steep slopes in alpine areas introduce large errors in the TanDEM-X DEM dataset. For this reason, custom remote sensing data need to be acquired, mostly with UAV-SfM or TLS. Such high-resolution DEMs are often required for snow cover modelling [
32,
33], analysis of glacial morphogenesis [
34], land surface dynamics [
35,
36] and associated land surface processes such as water flows and avalanches.
Several studies demonstrated the use of UAV-SfM for mapping rugged terrains such as alpine mountains [
32], coastal cliffs [
14], or volcanos [
37]. However, these studies put the focus on validation of the UAV-SfM datasets and not on the integration of UAV-SfM with TLS point clouds. Iterative closest points (ICP) algorithm has become a popular method in mutual orientation of two spatially overlapping point clouds (i.e., point cloud registration). Combination of 3D point clouds from UAV-SfM and TLS with ICP was demonstrated for 3D building models and heritage sites [
23,
38,
39]. The obvious advantage of this approach is a substantial reduction of data shadows and availability of photographic images for photorealistic visualisation. In these cases, the mapped scenes contained many objects with regular shapes allowing the achievement of a higher level of accuracy than in natural rugged alpine landscapes with much more complex morphology.
The alpine terrain exhibits many dynamic geomorphologic phenomena associated with mass movement such as landslides, erosion and rockfalls that frequently alter terrain surface morphology. Recording the effect of these processes requires a flexible mapping workflow which results in the digital elevation dataset having sufficient spatial detail and measurement accuracy for capturing the fine-scale morphology. In this paper, we hypothesise that the challenging task of 3D mapping the rugged alpine topography can be efficiently achieved with the combined use of TLS and UAV-SfM. We demonstrate this by our suggested workflow involving acquisition of 3D data by the two remote sensing techniques, data processing and combining the data into a final point cloud, DEM, and a 3D mesh surface. This approach is applied in a small study area comprising nested glacial cirques in the Tatry Mountains, the highest range of the Carpathians. The ultimate goal of the presented work is to generate a fine-scale 3D representation of the terrain surface applicable in geomorphological research of rugged alpine topography. The final 3D point cloud is made available for other studies via a 3D interactive web-interface as sharing and accessibility of the 3D spatial data is important to communicate the scientific outcomes. We also compare the generated DEM with other available DEM datasets for the mapped area. The presented workflow is transferable to other similar rugged environments to be used for high resolution geomorphological monitoring and mapping of small areas in the rugged alpine terrain.
2. Materials and Methods
2.1. Area of Interest
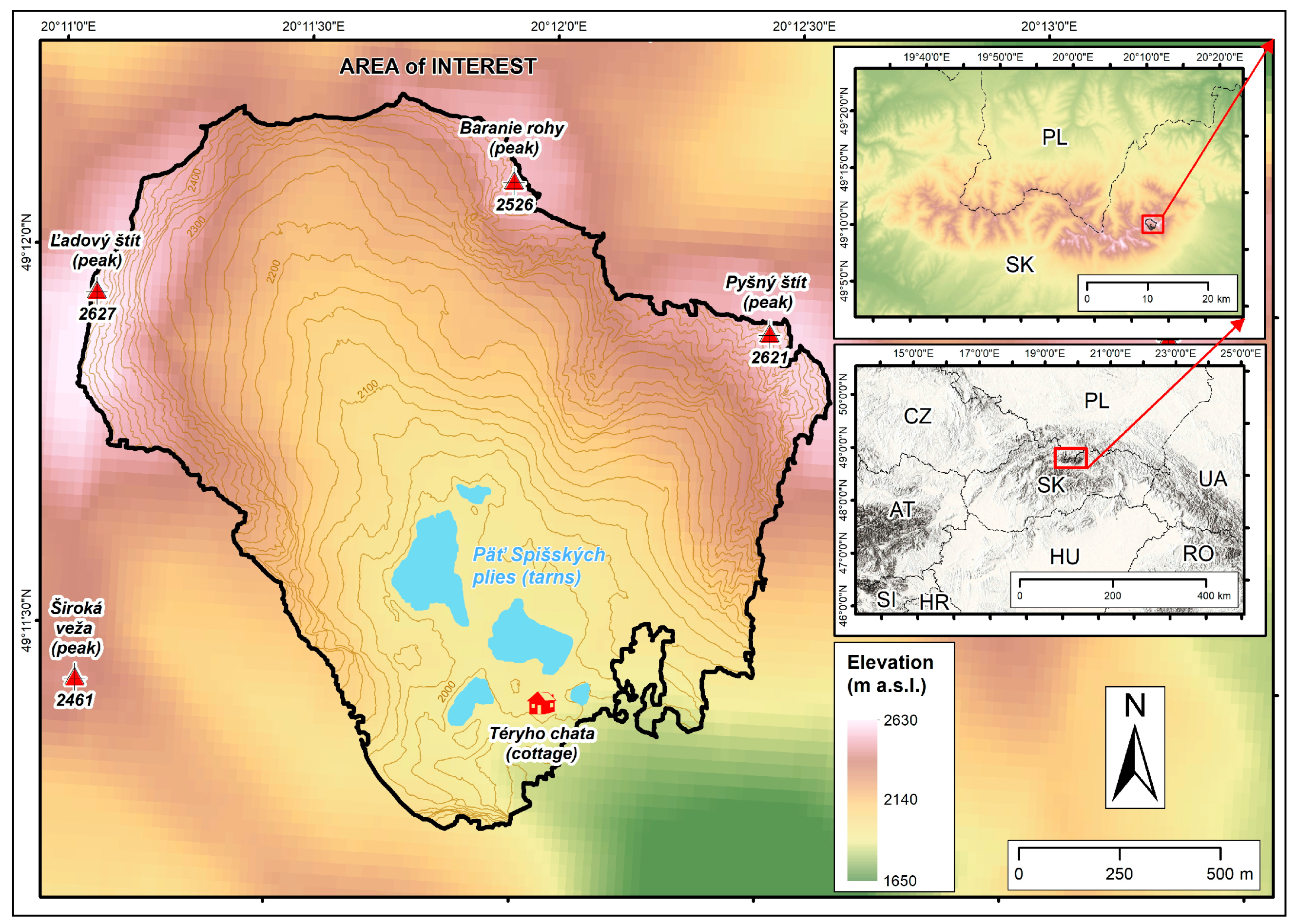
The area of interest is located in Vysoké Tatry (High Tatras)—the central part of the Tatry Mountains, where the Carpathians reach the highest elevation, displaying the most pronounced glacial morphology in the mountain range (
Figure 2). The contemporary topography of High Tatras resulted from alpine glaciation altering with deglaciation stages in the Pleistocene while the massif has undergone a relatively rapid and continuous tectonic uplift since the Pliocene [
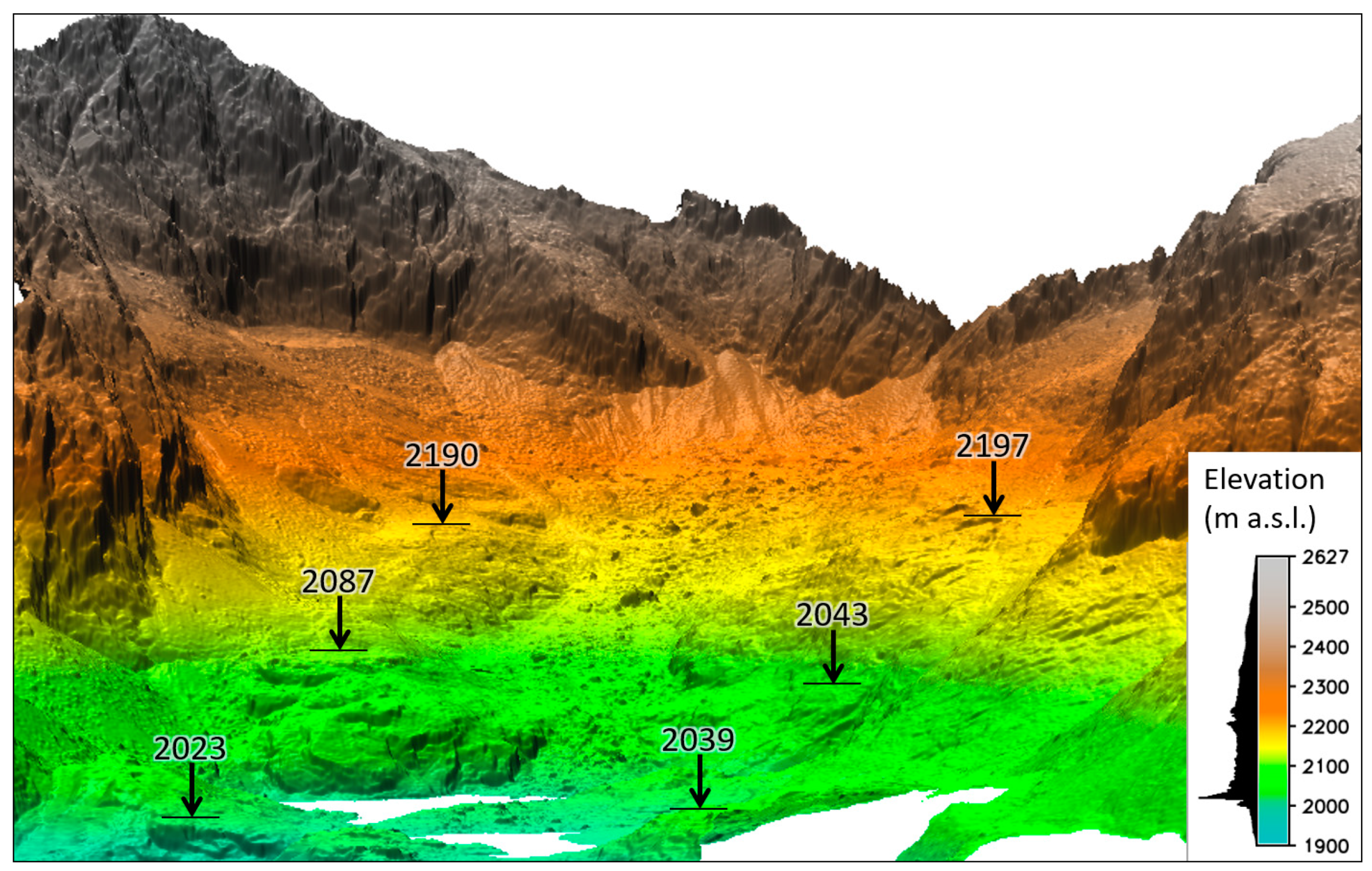
40]. The glaciers carved ∼600–900-m-deep troughs and cirques with steep slopes separated by sharp ridges and peaks in altitudes from ∼2500 to 2655 m above sea level (m a.s.l.).
In particular, the area, which was subject to the remote sensing survey, comprises about 2 km
2 of the upper part of the Malá Studená dolina valley (
Figure 3). It is a glacial cirque incised into the southern part of the crystalline core consisting of biotite granodiorite-tonalite to muscovite-biotite granodiorite [
41]. There are three compound cirques surrounded by headwalls up to 500 m high which form the upper part of the valley. The distinct glacial morphology of the area is modified by prominent gravity and cryogenic depositions forming extensive talus cones descending from the lower sections of the headwalls and ablation till and nivation ridges covering the central parts of the cirques floor. The bottoms of the cirques are situated at ∼2000 and 2190 m a.s.l., respectively. The depression parts of the cirques are filled with water forming five partially interconnected glacial lakes (tarns) from which the stream of Malý Studený potok flows out into the valley [
42]. Rock steps up to 400 m high represent the transition from compound cirques down to the trough at the southeast edge of the area of interest.
Climate conditions of High Tatras are specific, determined by transition of ocean to continental climate which combines with the climate of high altitudes. The average annual temperature in the area of interest is −2.5 °C and temperatures not exceeding 0 °C occur approximately 160 days a year [
43]. The average annual rainfall of 1870 mm per year is the highest in the region and most precipitation falls in the form of snow. The snow cover remains in the area for approximately 180 days a year [
43]. Such a climate allows only for a limited grass cover with rare clusters of mountain pine; therefore, the majority of the terrain is exposed bedrock or scree.
Almost the entire extent of the Tatry Mountains is protected by law as a national park (TANAP) with the highest level of natural protection in Slovakia [
44]. Moreover, the surveyed area is a part of specially protected natural reserve of Studené doliny for being a refuge of various plant and zoological species and for outstanding natural beauty. Therefore, human activities are limited and road access by car is restricted to lower parts of the mountains up to about 1500 m a.s.l. with tourist resorts. Upper parts are accessible only by foot via trails or elsewhere with mountaineering equipment and special permission. The mountain cottage of Téryho chata is situated in the south of the area of interest providing accommodation and refuge in case of bad weather or mountain rescue throughout the year. For this reason, a number of human activities such as supplying mountain cottages, treatment and transporting wounded by rescuers have been hampered.
2.2. Data Collection
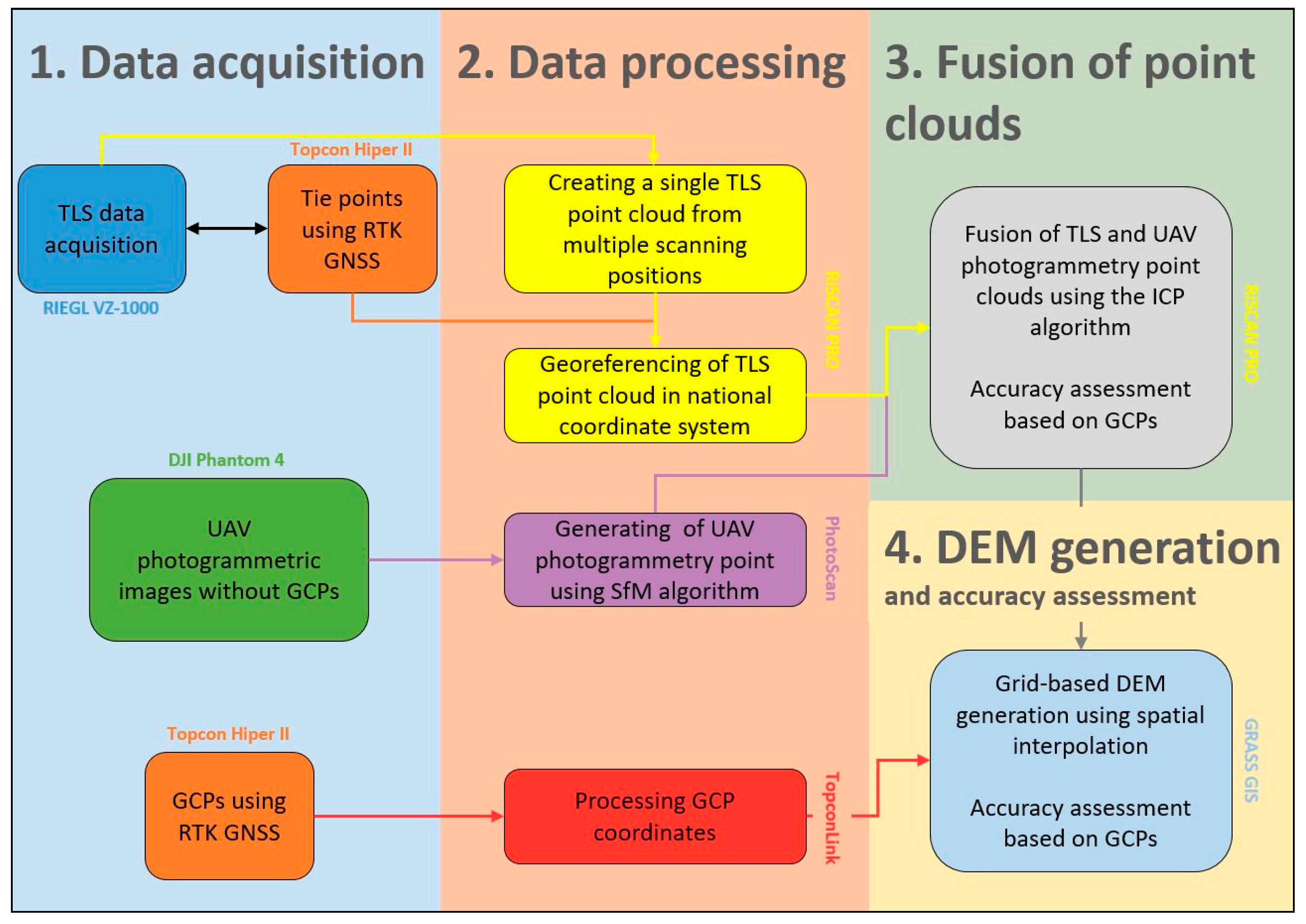
The study area was mapped in two separate mapping campaigns in September and October 2017. Four persons were involved in carrying the necessary instruments and performing the field work. The weight of surveying equipment and accessories was about 50 kg in total and had to be hand-delivered walking for about 3 h using the existing tourist trail. The equipment comprised two dual-frequency GNSS receivers Topcon Hyper II, a Riegl VZ-1000 long range laser scanner with an integrated Nikon D-700 camera, an UAV quadcopter DJI Phantom 4 with an integrated 12-megapixel FC330 camera (focal length 3.61 mm) mounted on 3-axes gimbal.
Careful planning preceded the work in the mountains. We analysed available orthoimagery on Google Earth, and national DEM (DMR3) was used to do a preliminary assessment of the visibility for optimal placement of the laser scanner and for determining optimal paths for transport between the intended scanner positions. Once in the field, the preliminary plan had to be modified in some cases for safety of transportation between scanner positions. The laser scanner was preferably placed on stable, exposed bedrock or large boulders avoiding scree debris surface so that the device remained stable during scanning and the scanner field of view was as wide as possible. In addition, the terrestrial laser scanner was tested, especially its range, scanning duration at various settings and transport options in rugged terrain. The maximum recorded range of the scanner was 1500 m and the dispersion of point measurements at such a distance was approximately 0.6 m. The planning also involved consideration of the weather. We aimed for clear sky, calm wind and no snow conditions to perform the work in a single campaign. First, the site was surveyed during 13 and 14 September 2017 when the snow cover was at minimum that year. The sky was clear; the maximum air temperature was about 15 °C. The wind speed was 8–12 m/s which was at the upper limit for flying the UAV. The land surface was dry which was favourable for TLS. The field work began at 13:00 setting up a GNSS base station near the cottage of Téryho chata. Position of the base station was located by real-time kinematic (RTK) GNSS positioning with a mobile broadband connection to the network of the Slovak real-time positioning service (SKPOS) within the national S-JTSK03 coordinate system (EPSG code: 5514) with vertical datum Baltic after adjustment (Bpv). The overall accuracy of the RTK GNSS positioning ranged between 1–2 cm (1σ). The baseline to the closest SKPOS base station in Gánovce was 20 km southeast. Meanwhile, the TLS and UAV-SfM surveys had begun.
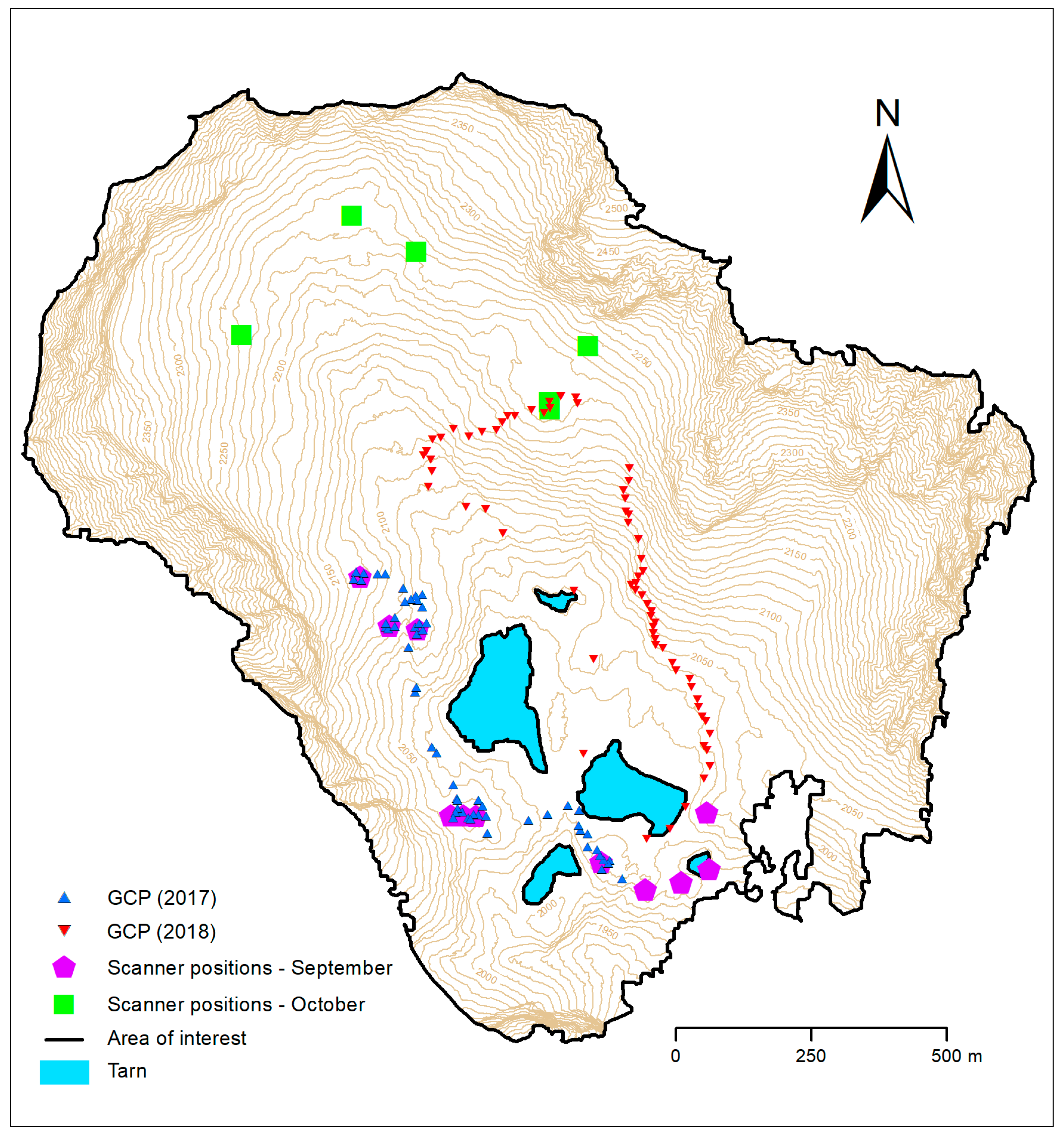
The RTK GNSS positioning was used to locate 104 ground control points (GCPs) on the terrain, free bedrock or large boulders. There were 4 black and white checker board markers (20 cm by 20 cm) distributed at a distance of 5–10 m around 4 scan positions and their central point was measured with the RTK GNSS. By this means, 16 tie points originated for transforming the TLS data into the national coordinate system. In addition, there were 21 GCPs collected during the campaign in September 2017 between the TLS positions (
Figure 4). The rapidly varying weather conditions, especially, increasing wind speed, induced another campaign one month later to supplement the data voids with new measurements. Therefore, another survey campaign was performed on 19 October 2017. The mapping involved TLS and UAV-SfM without positioning any GCPs with GNSS. Additional 67 GCPs were collected with RTK GNSS in July 2018 to supplement the GCPs dataset with validation points (
Figure 4).
2.3. Terrestrial Laser Scanning
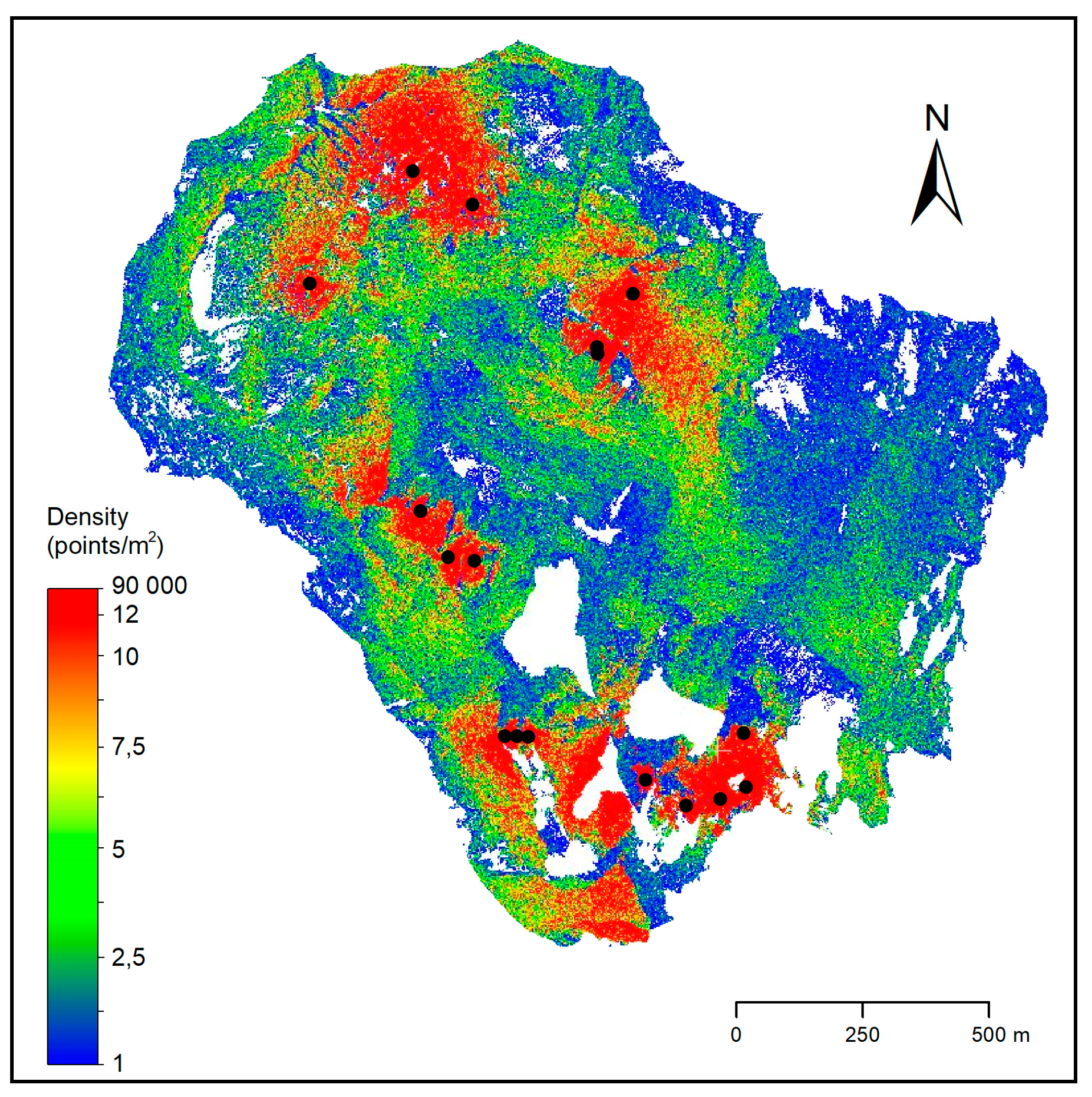
Data collection with TLS in the September campaign began with a position near the cottage of Téryho chata in the south and continued to the northwest up toward the valley head. Selection of the consecutive position of the scanner considered terrain ruggedness and accessibility so that possible data shadows are eliminated and sufficient spatial overlap of point clouds from two adjacent positions is ensured. Therefore, the separation of positions was not regular (
Figure 4); the scanner was preferably located on sites where it was possible to efficiently map larger parts of the area of interest. To ensure an optimal coverage of the area by point measurements, different settings of the scanner were used for laser scanning. Given the spatial extent of the area of interest, scanning from 6 positions with a 70 kHz pulse repetition rate (PRR) and scanning range of more than 1400 m was performed. For some positions, scanning with 300 kHz PRR and a range of 450 m or with 150 kHz PRR and a range of 950 m were used to densify data at overlap positions. In total, TLS was performed from 15 positions during the first campaign in September 2017 which were supplemented by 7 scan positions in October 2017 (
Figure 4). The scanning positions were distributed in the south, west and north of the area of interest which was limited by the accessibility and safe transport of the equipment.
Figure 5 maps the data coverage from each scanning position for both dates of the TLS survey where data voids can be seen as white areas. The reasons of data shadows are to do with terrain occlusion or poor reflection of the laser light from the surface of water or snow.
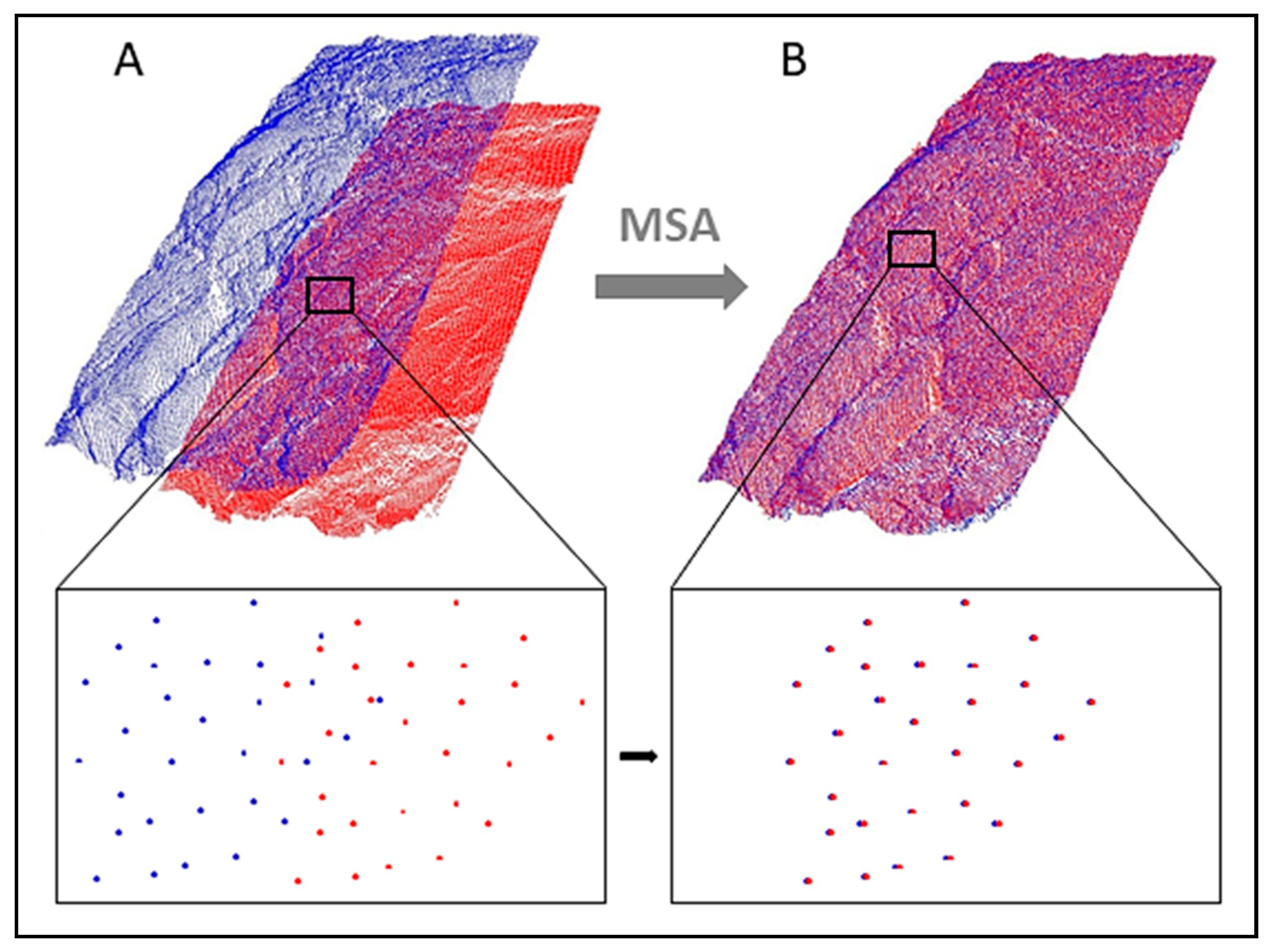
Raw TLS data was processed in the RiSCAN PRO software. First, the individual point clouds (scans) acquired from each scanning position were assigned RGB values representing natural colour from the photographs taken with the camera integrated on the scanner. The information on colour helped in interpretation of the points and in finding and co-locating the objects of interest in the following procedure of mutual orientation of the scans (registration). The registration was performed between two or more overlapping point clouds based on identical points. This procedure consisted of two steps: manual and automatic registration. The Riegl VZ-1000 terrestrial laser scanner comprises an integrated GPS receiver that measures geographic coordinates of the scanner position with accuracy of several decimeters to meters. The in-built magnetic compass provides measurement of the azimuth towards magnetic north. Measurements of the two devices are used for coarse placing of the individual scans in a global (common) coordinate system and coarse orientation of the scans. This feature facilitates and speeds up finding identical points of the spatially overlapping TLS point clouds in the following step of the coarse registration. The procedure requires at least 4 identical points to be identified between two overlapping scans. This principle also works with automatic registration that is implemented as the Multi Station Adjustment (MSA) in RiSCAN PRO. Based on the selected parameters, the MSA generates polydata. These are the points identified as identical in the areas of overlap for two or more scans being mutually registered. The MSA method uses the iterative closest points (ICP) algorithm which minimises the 3D distance between the polydata points by translating and/or rotating the entire point cloud along X, Y, and Z axes until the least possible distance between the polydata points is reached [
39,
45,
46] (
Figure 6). The TLS point clouds (scans) were registered in such a way that the position and orientation of the first scan were locked and the second scan was translated and rotated until the smallest standard deviation was reached with respect to the polydata of first scan. After registration, the position and orientation of the first and second scan was locked and the position and orientation of the third scan was adjusted by the MSA. The procedure continued in this way until all scans were registered as precisely as possible in a common coordinate system. Finally, the position and orientation of all scans was unlocked apart from the central scan which remained locked, and the MSA was performed again to redistribute the adjustment error more evenly within the point cloud.
For georeferencing the final TLS point cloud, central points of the 16 black and white checker board targets placed within the scanned scenes were manually identified and they were assigned with the coordinates measured by the RTK GNSS method. By this means, the final TLS point cloud was transformed from the global coordinate system (Cartesian WGS84) into the national projection coordinate system (EPSG: 5514) with the Bpv vertical datum.
For the data voids still present in the TLS point cloud another campaign was performed on 19 October 2017. The mapping involved TLS and UAV-SfM methods. The TLS was performed in the northern part of the valley from 7 scan positions to increase the point density in this area. The MSA method in the RiSCAN PRO software was used to mutually register the acquired TLS point clouds as was described earlier. The resulting October TLS point cloud was oriented with respect to the September TLS point cloud and thus georeferenced in the national coordinate system. A unified TLS point cloud originated.
As the last step, the final TLS point cloud was cleaned by manually removing the noise points (e.g., reflections from water table or dust particles in the air) and the points representing the building of the Téryho chata cottage. The area under the building was kept unsampled but the terrain under the building was approximated by the interpolation function in the production of the final DEM. In the area of interest, there is virtually no vegetation cover which could effectively occlude the terrain surface for the emitted laser light. Point returns from occasional patches of low grass, moss or individual dwarf pine trees present in the lower parts of the area were inspected. We decided that applying vegetation filter is not required to remove the non-ground returns as the height difference between top parts of the grass or dwarf pines and the ground was below 0.2 m.
2.4. UAV Digital Photogrammetry
The UAV-SfM method provides a different, vertical to subvertical, viewing angle which increases the capability of mapping in areas of pronounced vertical relief obscured for TLS where data shadows originated (
Figure 1). The UAV-SfM method also supplements the point data with orthoimagery. We decided to fly the UAV in the manual mode despite the fact that the system is capable of flying according to a pre-set trajectory and camera settings. The main reason was the safety of flight, i.e., to have a direct control over the UAV during the flight in case of wind gusts and uncertain visibility of GPS satellites in such a pronounced vertical relief of the mapped area (over 600 m). There were two 20-min flights performed in September 2017, taking 352 images in total covering the entire area of interest and its surroundings with an average spatial resolution of 17 cm. The average flying height relative to the take-off position near the cottage of Téryho chata was 464 m. The range between the UAV and the terrain was at least 100 m. In October 2017, the UAV was manually flown at a lower average flight height of 258 m taking 618 images with average spatial resolution of 9.5 cm covering 80% of the area of interest. The acquired imagery was processed in the Agisoft PhotoScan software resulting in 3D point clouds and orthoimagery. Almost 13 million and 90 million points were extracted from the September and October image collections, respectively. The data were georeferenced in the WGS84 geographic coordinate system (EPSG: 4326) based on the positioning data recorded by the on-board GPS antenna for the image exposures. More details on the settings and output statistics of the data processing are found in the reports provided as
Supplementary files (UAV reports S2).
2.5. TLS and UAV-SfM Data Fusion
Both independently acquired datasets locally contained data shadows (voids) or sparse coverage which could be reduced by fusing the TLS and UAV-SfM point clouds. The assumption in this procedure was that the TLS data are internally registered (mutually oriented) with a higher level of accuracy than the UAV-SfM points. While the TLS point cloud was georeferenced using GCPs, there were no GCPs acquired for such georeferencing of the UAV-SfM data. The reasons were practical as placing the GCPs targets in the area of interest and measuring their location with GNSS would have to be done before flying the UAV. This case would require additional manpower or more time which was not feasible in such a rugged terrain. Mapping by UAVs is strongly influenced by weather conditions since flying in strong wind and rain is very problematic and also dangerous. Fog or low altitude cloudiness decrease the visibility of land surface. In High Tatras and other similar alpine areas, the weather can change very quickly. Therefore, it was preferred to perform the UAV-SfM data collection as soon as possible and the generated point clouds were georeferenced in the national coordinate system by registering them on the already georeferenced final TLS point cloud with the MSA method in the RiSCAN PRO software.
First, coarse registration based on 4 manually identified points was performed to place the UAV-SfM and TLS point clouds closer together in the 3D space reaching standard deviation of mutual displacement between the two point clouds of 0.5 m. Afterwards, the application of the MSA automatic registration method followed. The MSA method identified only several tens of identical points (i.e., polydata) between the TLS and UAV-SfM point clouds in areas of markedly differing point densities. The automatic registration process was performed in several steps, with each step further reducing the values of the search window parameters and the point cloud rotation angle [
39,
45,
46]. By decreasing the values of these parameters, the registration error was reduced from decimeters to several centimeters. The UAV-SfM dataset contained less morphological detail than the TLS point dataset as the point density was much lower in the UAV-SfM data. Hence, further reduction of the standard deviation of mutual adjustment reached the limits at several centimeters. For this reason, the UAV-SfM points were used for the fusion with the final TLS point cloud only in the areas larger than 2 m
2 where no spatial coverage of the TLS points existed. In this way, the elevation points covered the areas of TLS data shadows. There was no vegetation present in such places.
The point cloud resulting from the TLS and UAV-SfM fusion was decimated with a 0.5 m spacing of 3D distance in the Cloud Compare software to homogenise the diverse spatial density of points and to reduce data redundancy for the DEM generation procedure. The final point cloud thus contained 4 points/m2. The colour information was kept with the pre-decimated TLS data, but it was removed from the decimated TLS point cloud as it provided mixed colours from two different TLS campaigns. After the point cloud fusion, the points were assigned with the RGB colour from the orthoimagery, which provided consistent colour information across the area with higher resolution (0.17 cm) than the final point cloud had (0.5 m).
2.6. Generating a Digital Elevation Model
The point cloud is a discontinuous digital representation of the mapped land surface, which is not directly applicable for modelling phenomena and processes in the landscape. Typically, point clouds are used as input data for generating continuous raster-based DEMs. We considered the final point cloud as the representation of terrain surface (ground) as there was limited number of above-ground features present in the area of interest and the point cloud was subject to filtering (
Section 2.3 and
Section 2.5). Therefore, we will further use the term DEM to refer to a digital terrain model instead of digital surface model (DSM). In our case, we preferred spatial interpolation procedure generating smooth continuous DEM surface instead of direct conversion of point elevations to raster grid. The method used is implemented as the parallelised v.surf.rst module in the open-source GRASS GIS 7.6.1 software [
47,
48]. The module uses regularised spline with tension and smoothing [
49,
50] for interpolating the input height values into centres of a raster grid. The used interpolation tool allows for fine tuning the spline interpolation function via a set of parameters controlling the stiffness and exactness (smoothness) of the resulting surface. The default parameters were changed in the case of the tension parameter to 20, the smoothing parameter to 0.8 and the minimum distance between points to 0.4 m. The final DEM was interpolated in a squared grid of 0.5 m grid cell-size which corresponded to the density of the final, spatially homogenised (i.e., decimated) point cloud.
The DEM data structure reaches limitations in modelling pronounced verticality of land surface, which often occurs in rugged alpine terrain or in caves [
51]. Therefore, we also generated a 3D vector-based surface model (i.e., polyhedral mesh) using the Poisson reconstruction [
52] implemented in the Cloud Compare software.
2.7. Comparison with Other Freely Available DEM Datasets
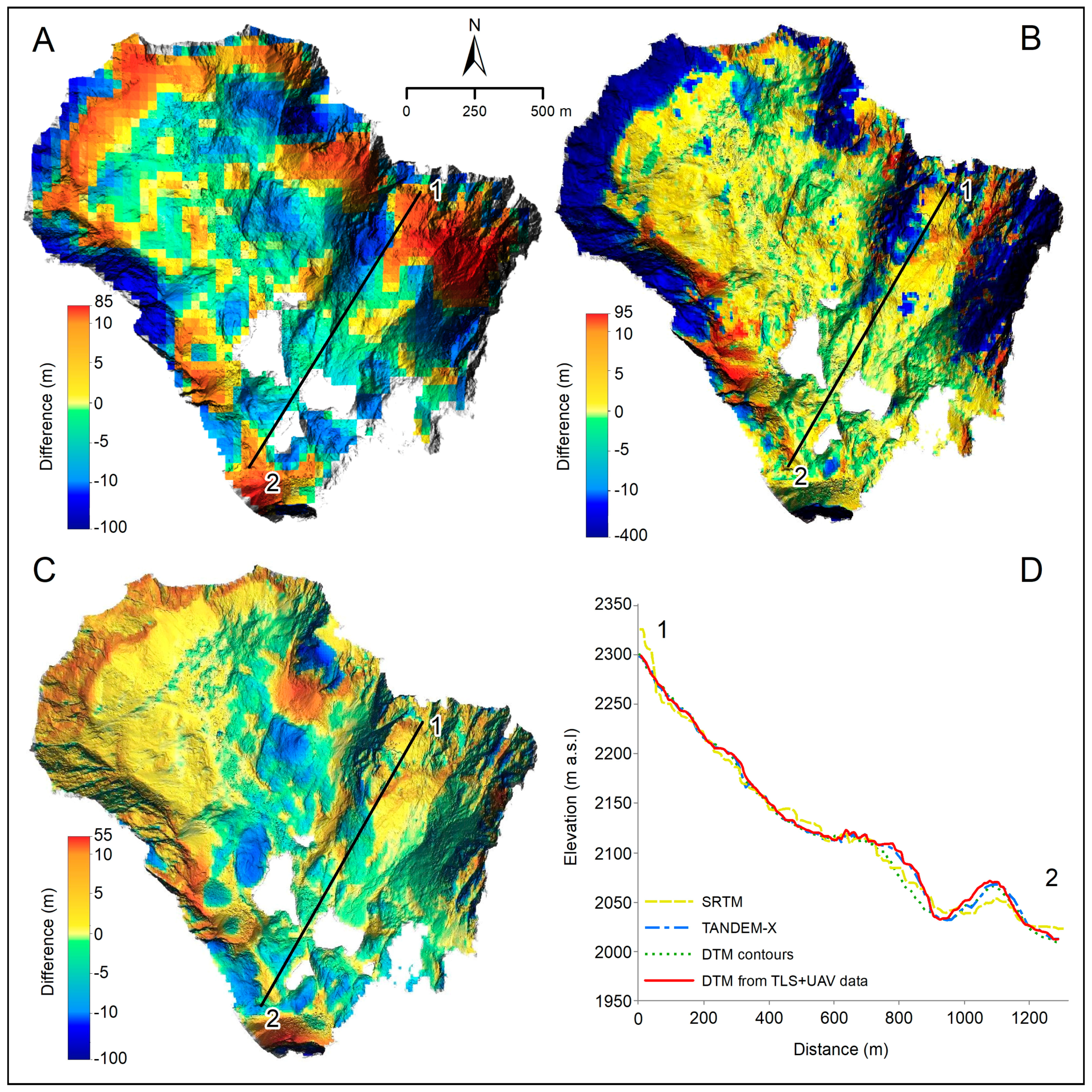
The extreme morphology of the area of interest has been captured by other publicly available DEM data sources. To support the relevance of the performed research, we selected three datasets and calculated vertical differences with respect to the final DEM derived from the fused TLS and UAV-SfM data. The following DEM products were used: SRTM (SRTMGL1-V003) DEM, TanDEM-X, and the national DMR3 DEM. The SRTM dataset [
53] was acquired with 1 arc-second spatial resolution on global scale in 2000 by synthetic aperture radar (SAR) interferometry during a single shuttle radar topographic mission. Further details on data SRTM data acquisition are reported in [
54]. The SRTM data have been widely used for land surface analysis across various disciplines and they were validated for different kinds of topographies [
55]. The spatial resolution in the area of interest is about 27 m for the SRTM data used. Additionally, the overall vertical error in the final product is below 9 m [
55].
The TanDEM-X data were acquired by radar interferometry with a constellation of two satellites between 2010–2014 with repeated data acquisition (at least twice up to four passes) [
56]. The DEM product was made available since September 2016. This DEM product is a new generation global DEM providing resolution of 0.4 arc second which can be seen as one of the most consistent, highly accurate and completest global DEM data sets of the Earth surface. Global assessment summarised by [
57,
58,
59] reports overall vertical accuracy below 2 m which is subject to land cover and surface slope angle on local scale.
The third DEM dataset involved in the comparison was the national DMR3 DEM derived from vectorised contours from topographic maps at 1:10,000 and 1:25,000 scale and interpolated into a grid of 10 m by 10 m cell-size. The dataset was provided by the Geodetic and Cartographic Institute of the Slovak Republic.
The final TLS-UAV-SfM DEM was resampled to match the original resolution of each of the three compared DEMs: 30 m for SRTM, 12 m for TanDEM-X and 10 m cell size for DMR3, respectively. The elevations were unified into a common WGS84 geodetic datum with ellipsoidal heights. Afterwards, the resampled final DEM was subtracted from the compared DEM in a map algebra operation using the r.mapcalc module and the statistics of the elevation residuals were calculated with the r.univar module in GRASS GIS, respectively.
4. Discussion
The presented approach of combined use of TLS and UAV-SfM data in mapping rugged alpine terrain has several advantages. It provides a valuable flexibility in periodic mapping of small alpine areas, which is not economically and practically feasible by standard airborne laser scanning and photogrammetric methods. It provides more homogeneous spatially distributed point clouds which is important for creation of a DEM with spatially consistent quality using spatial interpolation. It should be emphasised that the generated dense point clouds are valuable and unique for the area in terms of geometric accuracy and the captured level of detail. To date, national elevation datasets of such alpine areas in Slovakia were acquired by aerial photogrammetry and vectorised topographic contours with spatial resolution of several meters. Other data available for the region comprise even coarser datasets such as the TanDEM-X DEM and the SRTM DEM derived by interferometric radar with a global coverage. These datasets are smoothed in some places or they contain noise in comparison with the final DEM resampled to the equivalent resolutions. This outcome hampers the applicability of the SRTM and TanDEM-X data in very detailed geomorphological research of the study area. Similar accuracy issues were observed in other areas with extremely rugged terrain [
31,
67].
Coarse DEMs are insufficient for analysing the rugged alpine morphology and for abundant presence of loose sediments of different sizes ranging from small scree to large boulders. Especially, it holds for detailed analysis and modelling of shallow recent land surface processes, such as runoff, bioturbation or solifluction which operate on a finer spatial scale than the coarse DEMs represent. Conversely, the high-resolution DEM created by the TLS and UAV-SfM data fusion can be used to identify and analyse a wide range of specific landforms and geomorphologic processes. It opens new possibilities for multiscale geomorphic modelling and segmentation leading to reveal a comprehensive nested hierarchy of landforms and land surface processes [
68]. Indeed, a generalised (i.e., spatially coarser) DEM can suit the analysis of massive landforms and processes. However, using such a less detailed DEM is not the appropriate solution since the DEM is generalised in a random (i.e., erroneous or uncontrolled) fashion which causes the altitude and derived values of geomorphometric parameters to be distorted or biased. On the other hand, a high resolution and accurate DEM can be generalised in a controlled fashion providing a better solution for geomorphological research across multiple scales.
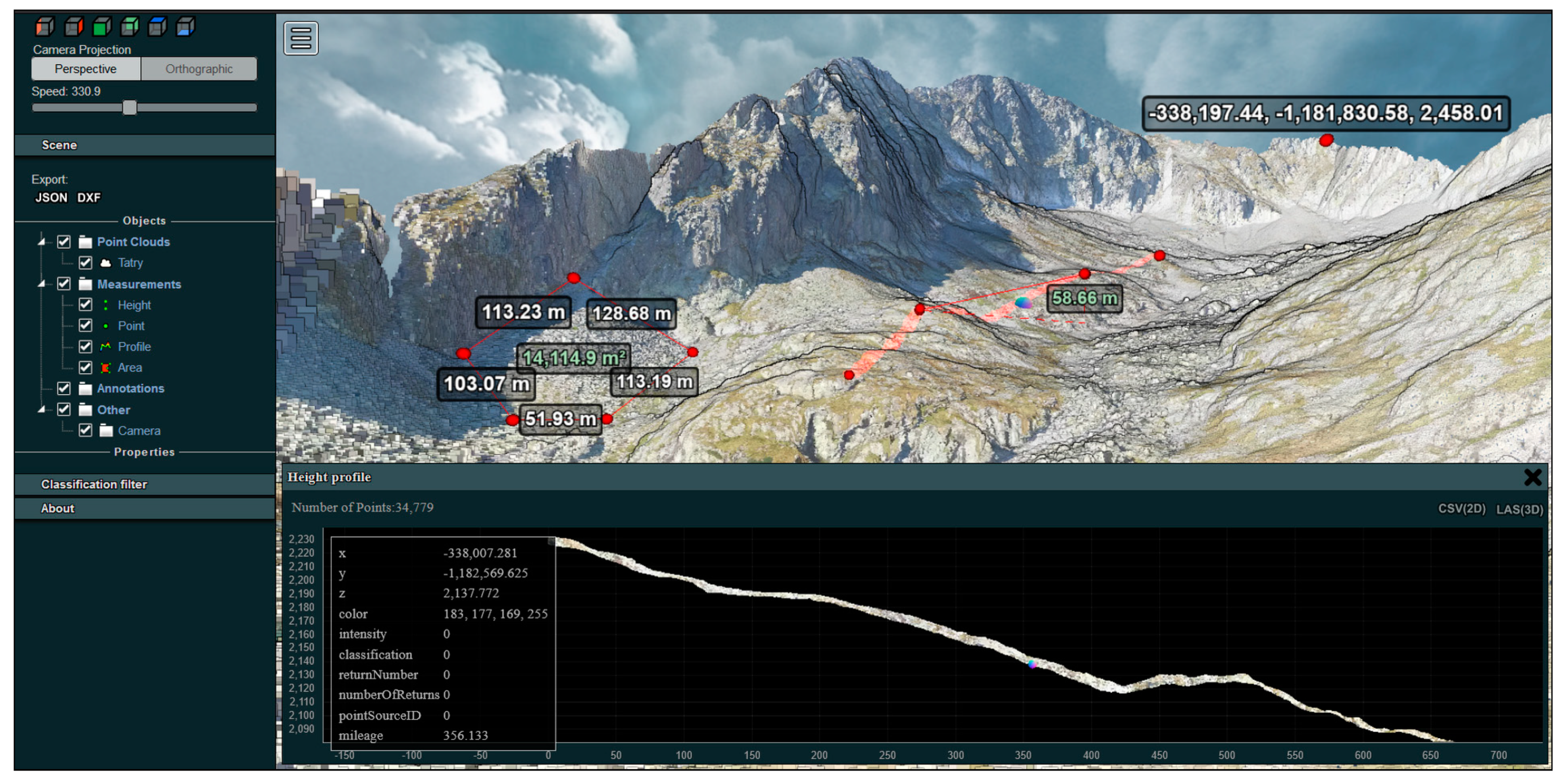
The orthophoto images can be used for photorealistic 3D visualization such as for 3D city models. The 3D point data could be used for modelling and planning search and rescue operations since the area is popular among tourists and mountaineers. The generated web-based tool enhances communication of the results. It is a user-friendly environment providing means for non-specialists to draw cross-sections, and conduct various types of 3D measurement, changing the displayed characteristics or extracting the 3D points for custom purposes (e.g., 3D printing).
The proposed approach also has limitations. It requires extensive field work with several hours of surveying depending on the extent of the area with limited accessibility by a car or other means for convenient transport of the required equipment. A long-range laser scanner, such as Riegl VZ-1000, has a clear advantage and saves a lot of time during surveying. However, its approximate weight of 12 kg complicates transport of the scanner and selection of optimal scanning position, especially in areas accessible only by foot and with considerable difficulties. Therefore, safer positions were preferred compromising the field of view.
The combined use of TLS and UAV-SfM was feasible as there is very limited vegetation cover in the area of interest, comprising occasional patches of grass and dwarf pine in the lower parts. Both methods generate most favourable representation of terrain unless dense vegetation, boulders, or buildings occlude the terrain surface. While TLS can penetrate vegetation cover into some extent, slant viewing angles from terrestrial platform, such as tripod, restrain the laser from reaching the ground through grass, dwarf coniferous trees. Reaching a uniform or homogenous point coverage with TLS is strongly limited by the number of scanning positions, their constellation, and mutual distance. The point density decreases with increasing range from the scanner. Large boulders of glacial moraines are abundant with TLS data shadows. In such cases, the vertical perspective of UAV-SfM helps to sample data but vegetation still occludes the ground. Shadows cast by the boulders or steep walls deteriorate the capability of the SfM method to find corresponding points in the shadowed parts where, on the other hand, TLS is applicable since it is an active remote sensing method. It is important to target the point density to the purpose of the resulting data. In our case, 0.5 m minimal spacing across the area was considered sufficient to represent the terrain topography.
Also, the surveying by UAVs or TLS depends on favourable meteorological conditions which can quickly turn into harsh weather in the mountains. In turn, the weather affects accuracy of surveying. Therefore, the use of these mapping methods requires careful planning and quick realization. Time of day and seasonality are other factors which can affect especially the quality of UAV-SfM data for differing light conditions. UAV mapping in October generated more points than in September, suggesting that October data captured the landscape with a higher level of detail. However, with regard to horizontal and, in particular, vertical accuracy, the data obtained in September could be more accurate. Ideally, capturing the imagery should be performed about noon with sky covered by clouds which disperse the sun light evenly. Meeting such requirements becomes often not feasible in planning the survey in a remote and hardly accessible area. In our case, the shadows cast by the pronounced terrain features were longer in the morning of the October campaign covering larger areas than during the flight about noon of the September campaign. In October, the sun is considerably lower above the horizon than in September which in combination with the NW–SE orientation of the valley made the terrain illuminated unevenly. Such an uneven illumination of the terrain caused lower vertical and horizontal accuracy of the October point cloud overall.
The limitation of a DEM in representing the alpine topography manifests in areas of extremely steep rock walls or overhangs. This is because a single DEM cell can represent only a single land surface elevation value. Although 3D point data were recorded for such forms, they are averaged in the DEM interpolation procedure resulting in a single elevation value per cell. The solution for analysing geomorphometric properties of such specific landforms is in modelling the surface as a 3D mesh.
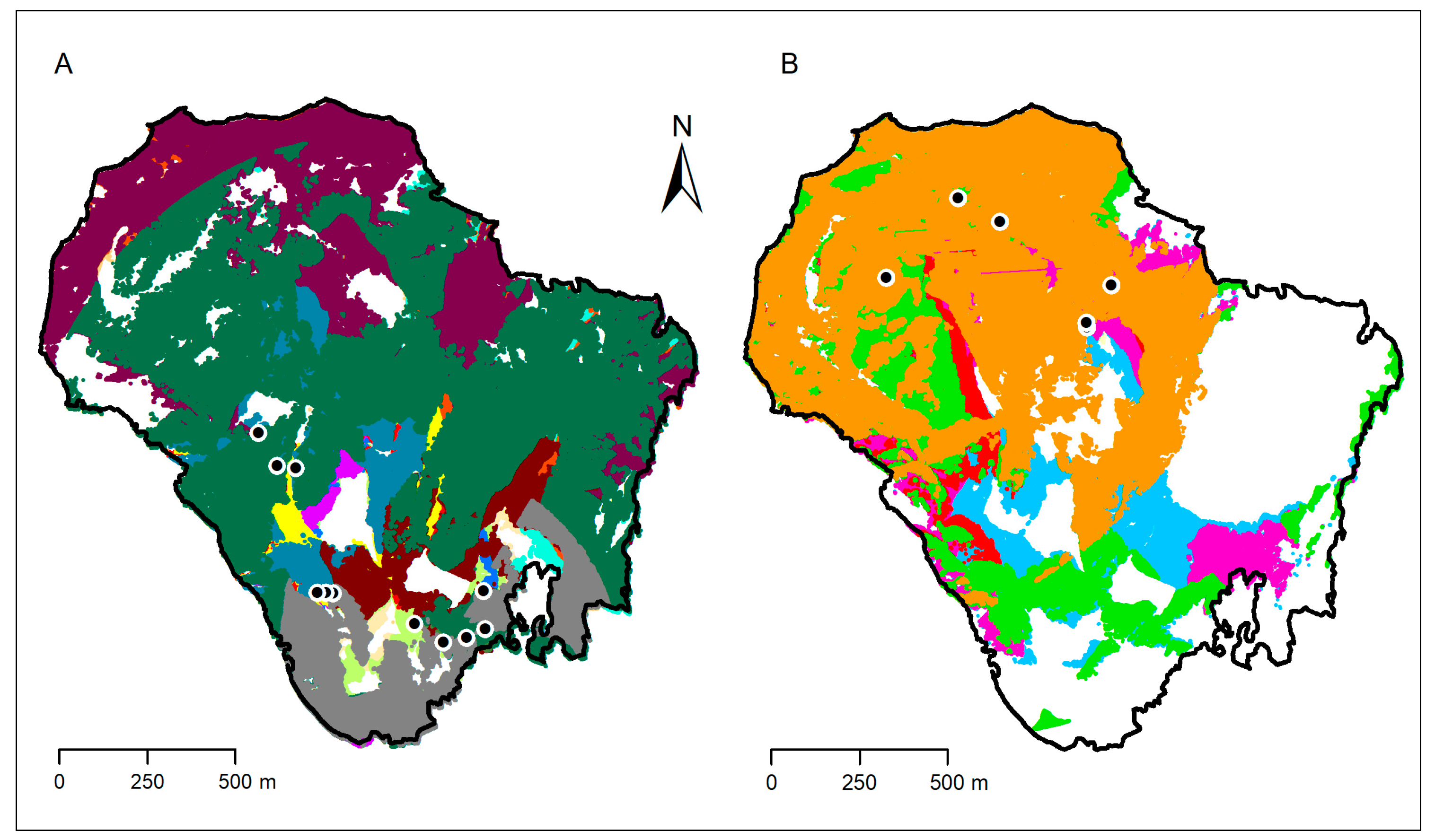
Figure 15 compares the derived elevation gradient (i.e., slope angle) for the DEM surface (
Figure 15A) and 3D mesh surface (
Figure 15B). One drawback of such a 3D data structure is that it has to be created and analysed in a specialised 3D software (e.g., Cloud Compare, Meshlab, Geomagic Wrap) as contemporary GIS software are not fully adapted to use 3D mesh for spatial modelling, and raster DEM modelling is still preferred.
5. Conclusions
Rugged alpine areas are dynamic landscapes with diverse geomorphologic forms and processes which require recurrent mapping with high accuracy and spatial detail. This study showed that currently available DEMs derived from radar remote sensing such as SRTM and TanDEM-X have varying accuracy especially in very steep slopes that limit their use in detailed geomorphological mapping in rugged alpine areas. Moreover, monitoring dynamic geomorphologic phenomena requires recurrent surveys depending on the occurrence of the event. The TLS and UAV-SfM technologies provide a flexibility needed to monitor small dynamic areas.
We proposed a methodology for an effective integration of TLS and UAV-SfM point clouds and production of a high-resolution DEM. In this methodology, the UAV point cloud supplements the more accurate TLS point cloud in areas with insufficient TLS data coverage. This approach greatly reduces data shadows present in the 3D point clouds produced solely by a single mapping technique, and it provides means for 3D mapping of extremely steep slopes and overhangs frequently present in the rugged alpine terrain. The accuracy and flexibility of the approach enable mapping the effects of dynamic geomorphologic processes such as landslides, erosion or rockfall that has been impossible so far with existing DEM data or traditional mapping techniques.
The fused 3D point cloud and calculated DEM for the Malá Studená dolina valley in the High Tatras currently represent the most detailed representation of rough alpine terrain in Slovakia. It has no data shadows apart from water bodies. The accuracy of the iterative closest point adjustment of the UAV-SfM and TLS point clouds was in the order of several centimeters but internal consistency of the TLS data was in the order of millimeters. The resulting DEM with a spatial resolution of 0.5 m provides a valuable dataset for mapping of any geomorphologic forms and terrain effects of dynamic geomorphologic process in this area. This product is also suitable for multiscale land surface analysis and segmentation [
67]. The nested hierarchy of landforms and land surface processes can be captured only by a very accurate, complete, and spatially consistent DEM from which credible geomorphometric variables can be derived. In comparison to publicly available DEMs, this approach also opens up a possibility to map extremely rugged alpine terrain features such as vertical walls and overhangs, representing them appropriately via 3D mesh. New visualization tools such as Potree can be used conveniently by researchers, natural protection authorities, mountain rescuers and the general public to explore a final 3D point cloud via a web-browser.