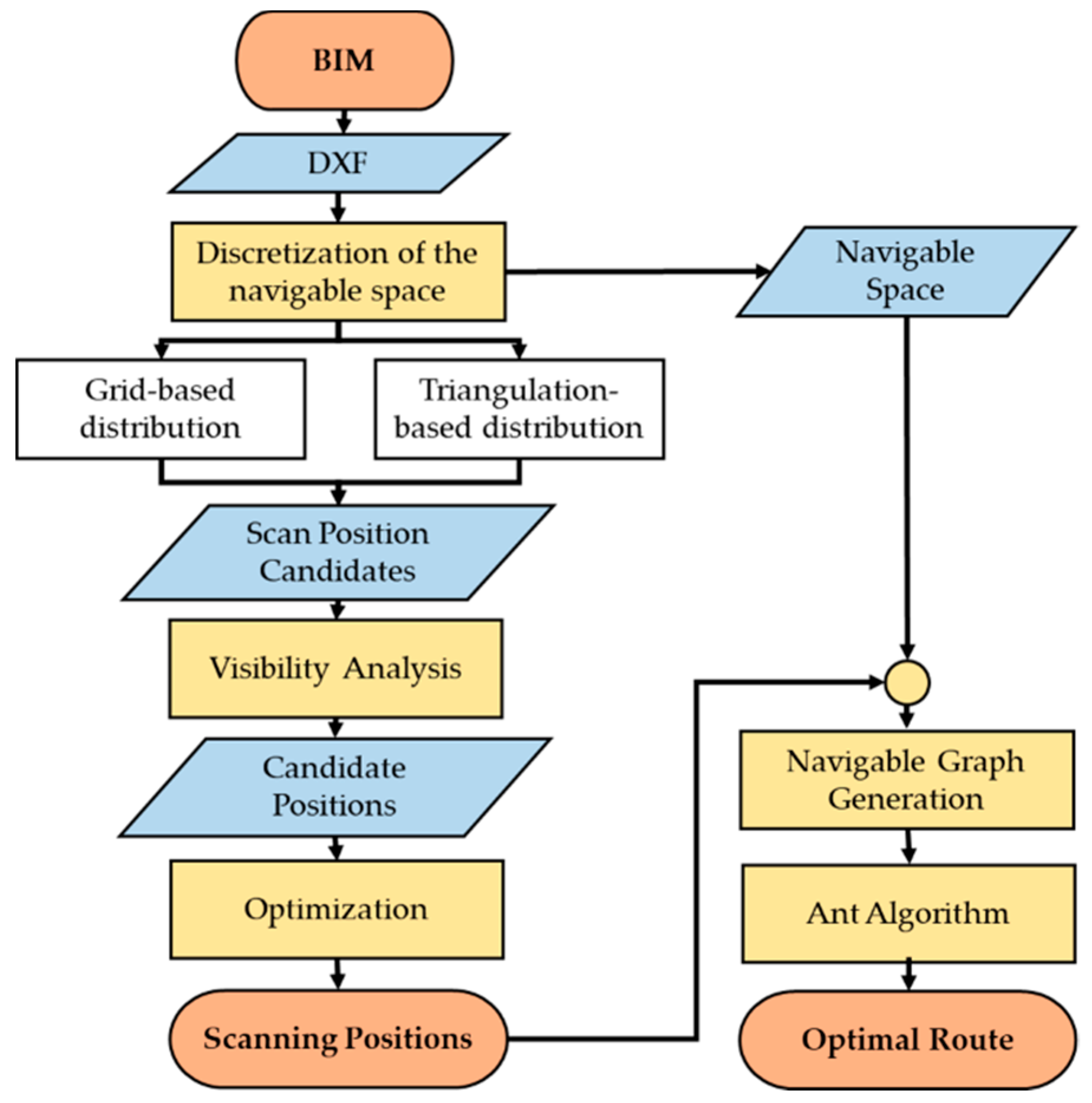
Figure 1.
General workflow of the method.
Figure 1.
General workflow of the method.
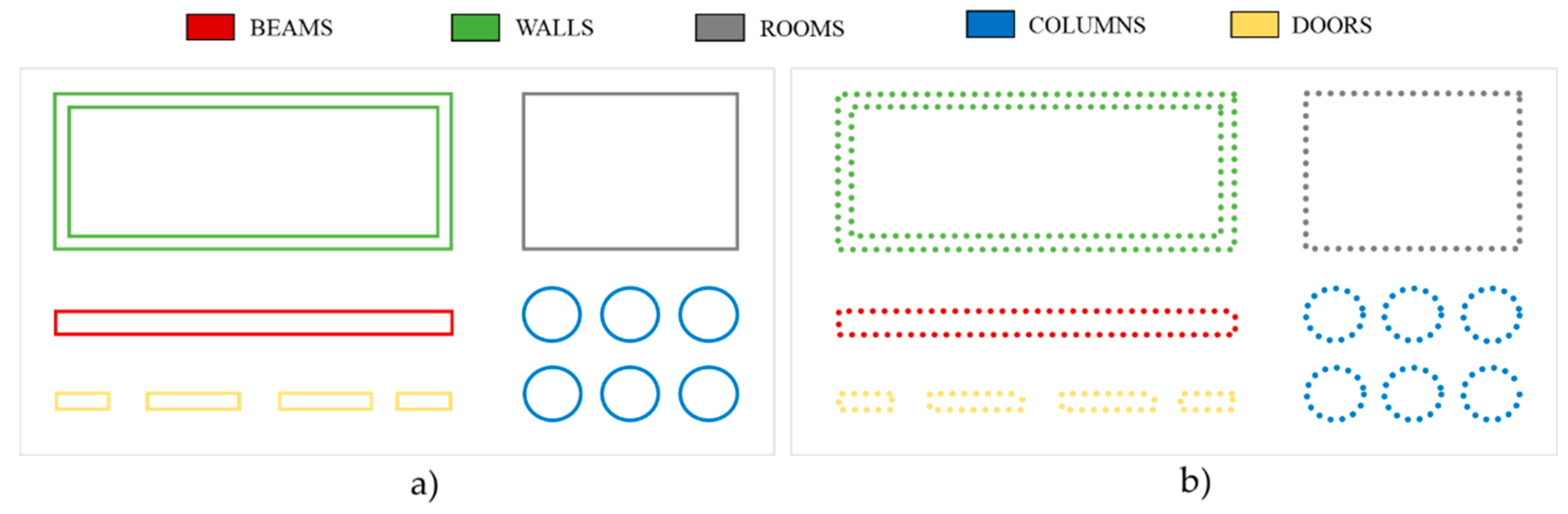
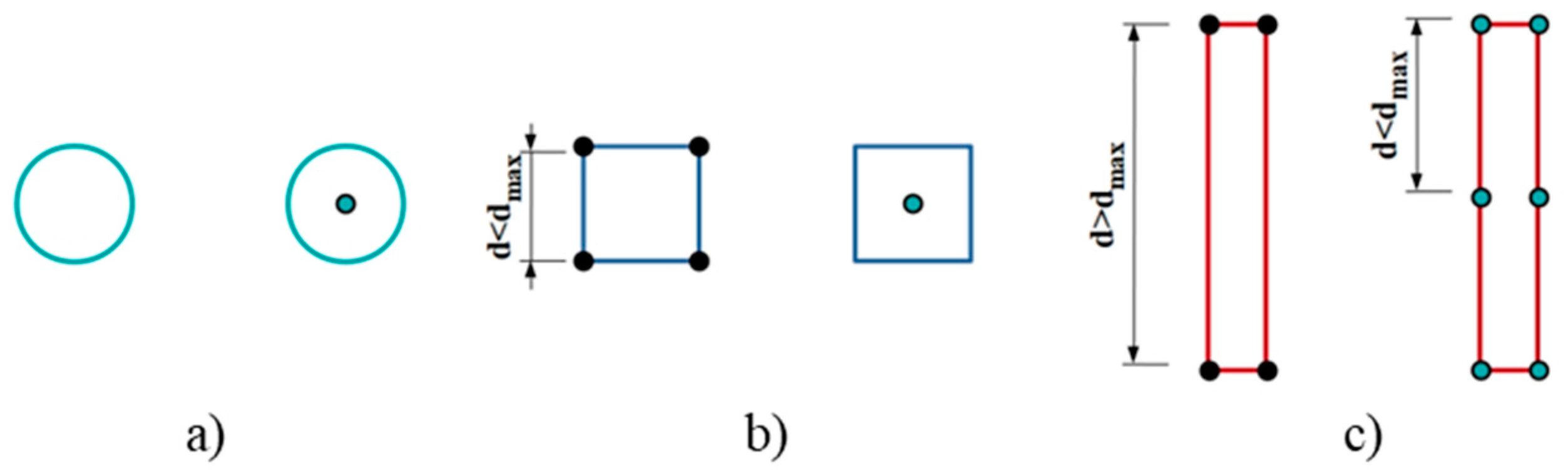
Figure 2.
(a) Building elements considered in this work, (b) elements after discretization in equidistant points.
Figure 2.
(a) Building elements considered in this work, (b) elements after discretization in equidistant points.
Figure 3.
Geometric representation of navigable space (a) in case of the existence of holes and columns (blue lines), (b) in case of the existence of rooms.
Figure 3.
Geometric representation of navigable space (a) in case of the existence of holes and columns (blue lines), (b) in case of the existence of rooms.
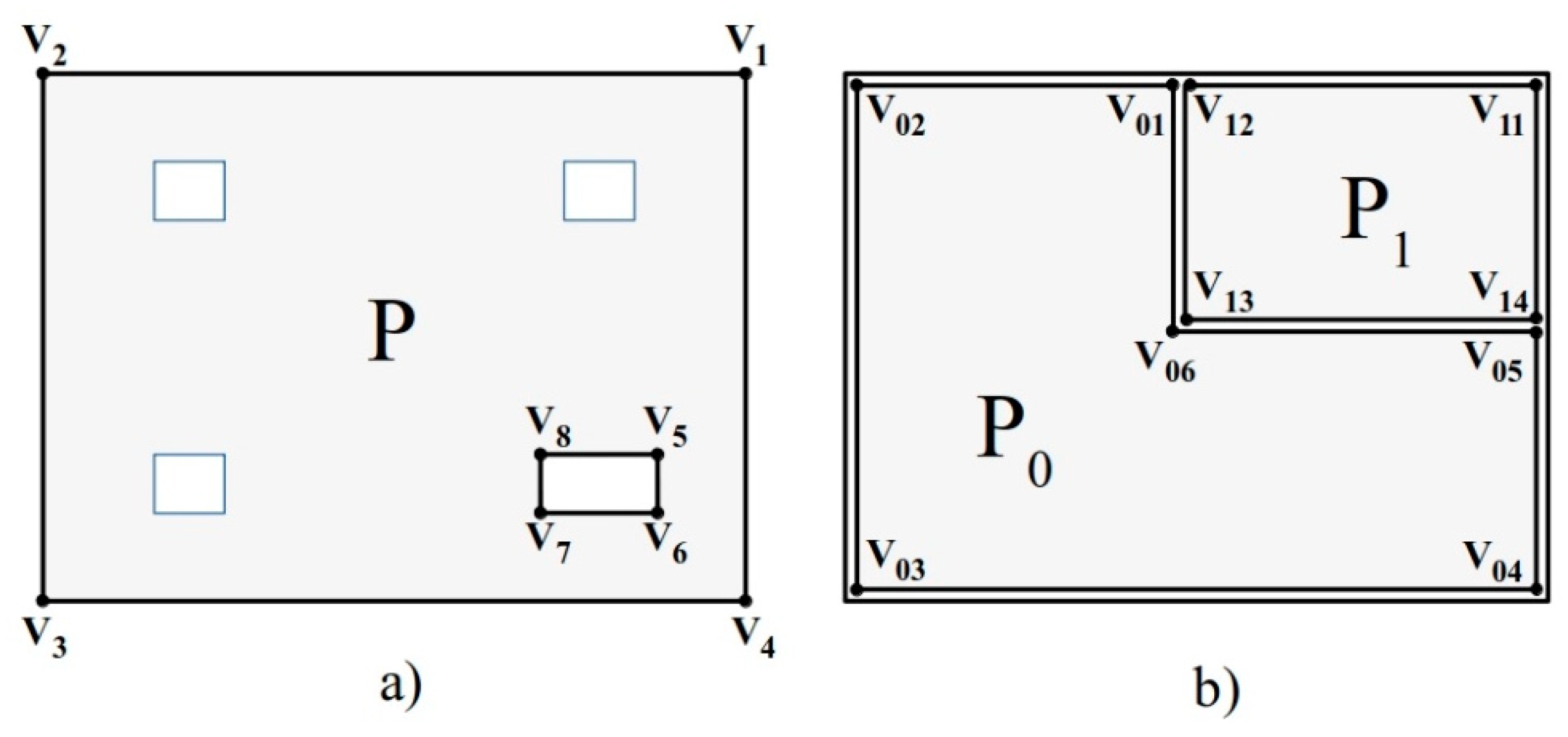
Figure 4.
Schema of discretization process when using a grid-based structure (a) in case of the existence of one floor space including a hole and three columns (blue lines) (b) in case of the existence of rooms. Final candidate positions are in green, while discarded candidate positions are in red. Local coordinate systems are represented.
Figure 4.
Schema of discretization process when using a grid-based structure (a) in case of the existence of one floor space including a hole and three columns (blue lines) (b) in case of the existence of rooms. Final candidate positions are in green, while discarded candidate positions are in red. Local coordinate systems are represented.
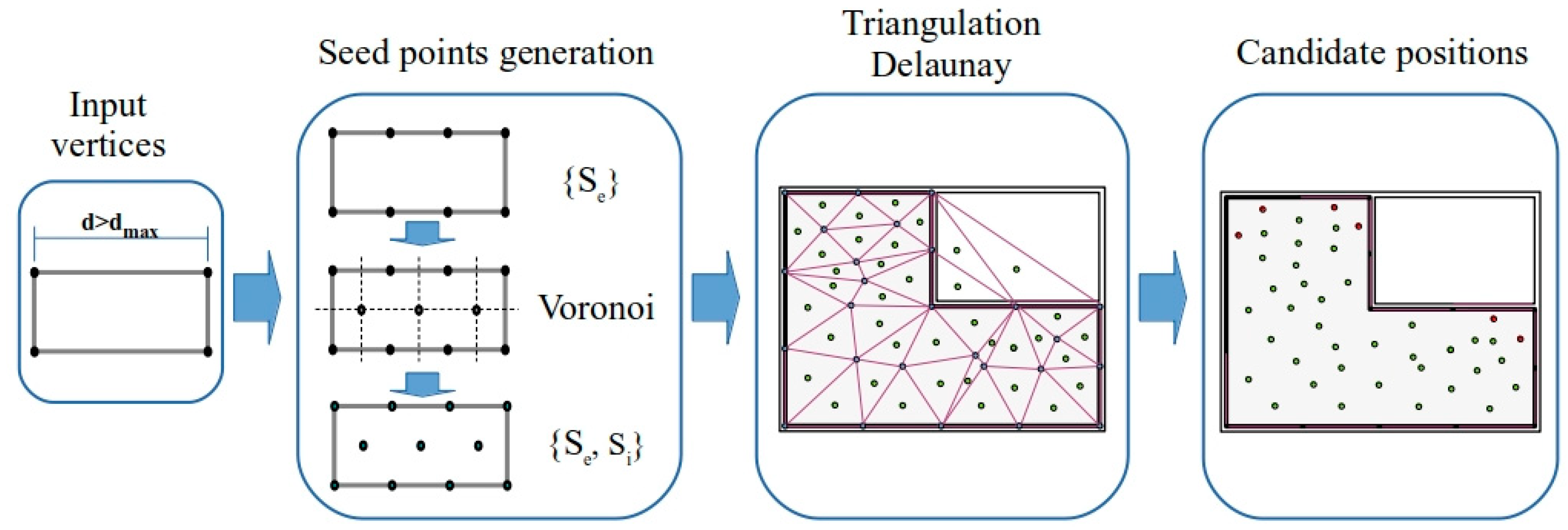
Figure 5.
Workflow of the triangulation process.
Figure 5.
Workflow of the triangulation process.
Figure 6.
Generation of seed points Se (in blue) for triangulation process for: (a) column, (b) polygon with side < dmin and (c) polygon with side < dmin.
Figure 6.
Generation of seed points Se (in blue) for triangulation process for: (a) column, (b) polygon with side < dmin and (c) polygon with side < dmin.
Figure 7.
Navigable space is partitioned by applying Delaunay triangulation process. (a) Since the polygon that contains navigable space may be concave, some positions obtained after the division can fall out of navigable space (orange). Small triangles are discarded according the parameters lmin and αmin (yellow). (b) A filtering process is conducted to retrieve positions are inside navigable space (points generated by Voronoi process are included). Subsequently, points near obstacles are discarded (red) according to the defined security distance.
Figure 7.
Navigable space is partitioned by applying Delaunay triangulation process. (a) Since the polygon that contains navigable space may be concave, some positions obtained after the division can fall out of navigable space (orange). Small triangles are discarded according the parameters lmin and αmin (yellow). (b) A filtering process is conducted to retrieve positions are inside navigable space (points generated by Voronoi process are included). Subsequently, points near obstacles are discarded (red) according to the defined security distance.
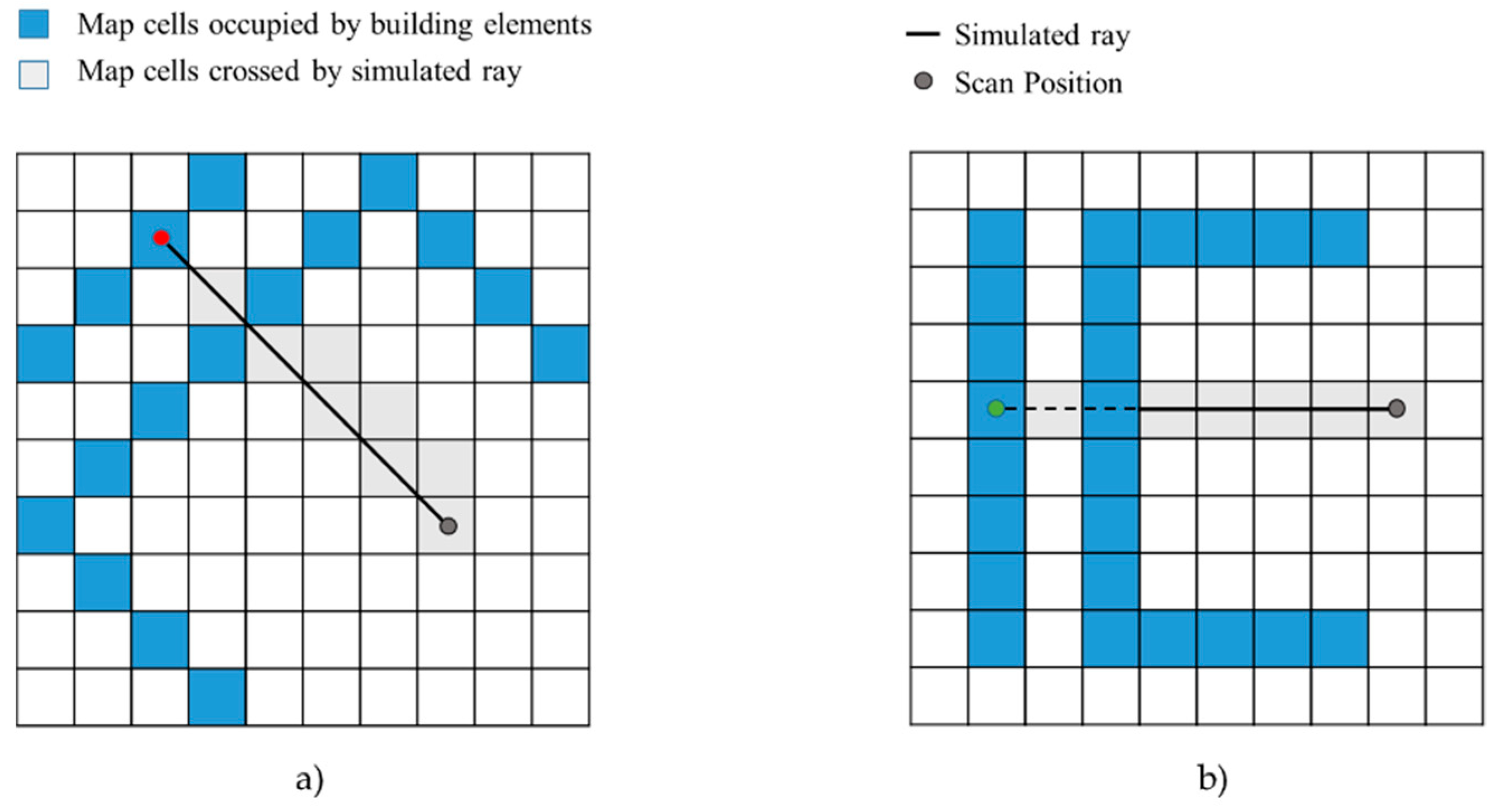
Figure 8.
Bresenham algorithm is used to determinate the map cells that are crossed by simulated beam (gray) in visibility analysis. (a) target cell (red) is wrongly classified as visible since it is not occluded by other cells representing building elements, (b) target point (green) is correctly classified as occluded in the ray-casting process.
Figure 8.
Bresenham algorithm is used to determinate the map cells that are crossed by simulated beam (gray) in visibility analysis. (a) target cell (red) is wrongly classified as visible since it is not occluded by other cells representing building elements, (b) target point (green) is correctly classified as occluded in the ray-casting process.
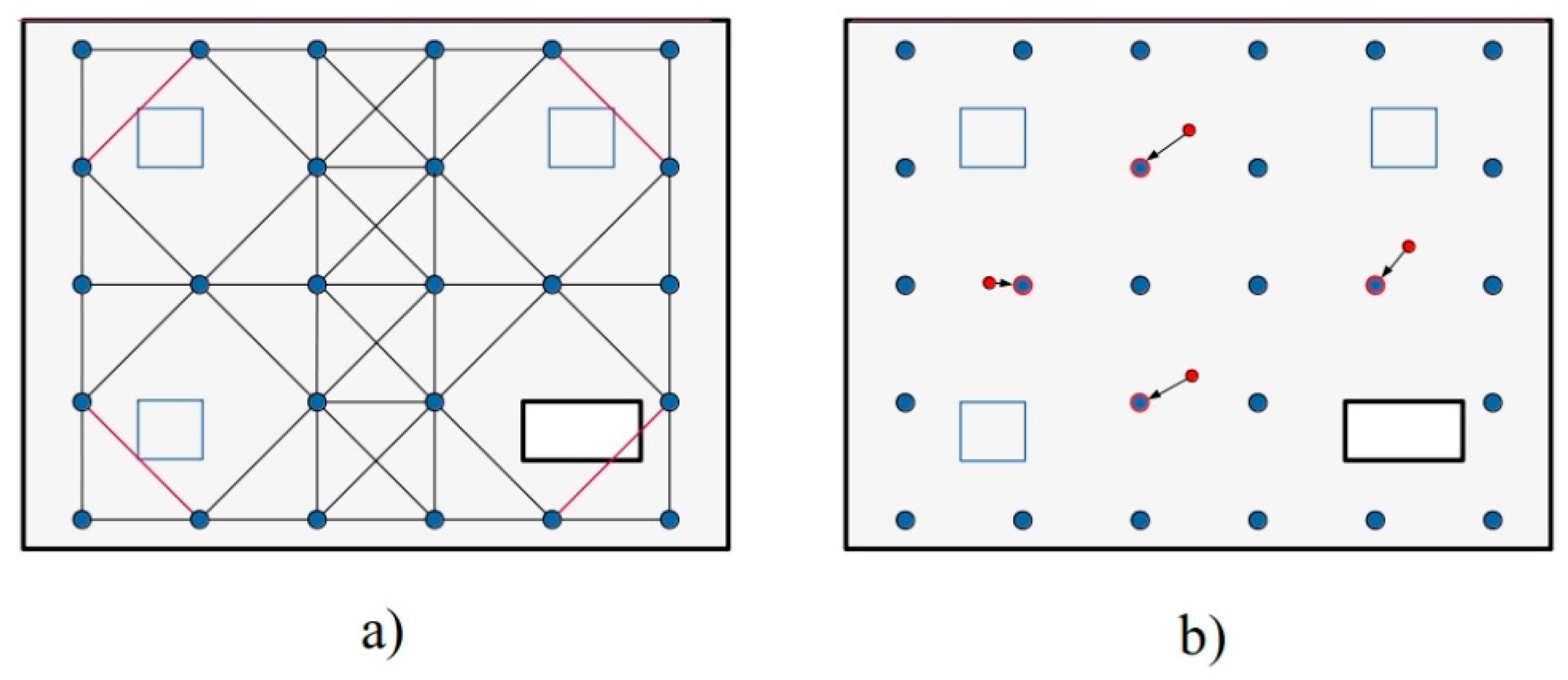
Figure 9.
Scan optimization process is carried out from candidate positions (green points) to obtain scanning positions (red points). In each iteration the candidate position is selected which maximizes the theoretically acquirable surface (red lines). The black lines represent the surface theoretically acquired from the previously selected positions.
Figure 9.
Scan optimization process is carried out from candidate positions (green points) to obtain scanning positions (red points). In each iteration the candidate position is selected which maximizes the theoretically acquirable surface (red lines). The black lines represent the surface theoretically acquired from the previously selected positions.
Figure 10.
(a) Graph nodes are 8-connected by edges and the ones intersecting with any no-navigable space are removed (magenta). (b) Scanning positions (red points) are relocated to nearest nodes to them (blue points with red contour).
Figure 10.
(a) Graph nodes are 8-connected by edges and the ones intersecting with any no-navigable space are removed (magenta). (b) Scanning positions (red points) are relocated to nearest nodes to them (blue points with red contour).
Figure 11.
(a) A navigable graph composed by navigable (blue) and scanning (red) nodes is generated. Then, navigable nodes are abstracted from graph and (b) a simpler one is represented only with scanning nodes (red).
Figure 11.
(a) A navigable graph composed by navigable (blue) and scanning (red) nodes is generated. Then, navigable nodes are abstracted from graph and (b) a simpler one is represented only with scanning nodes (red).
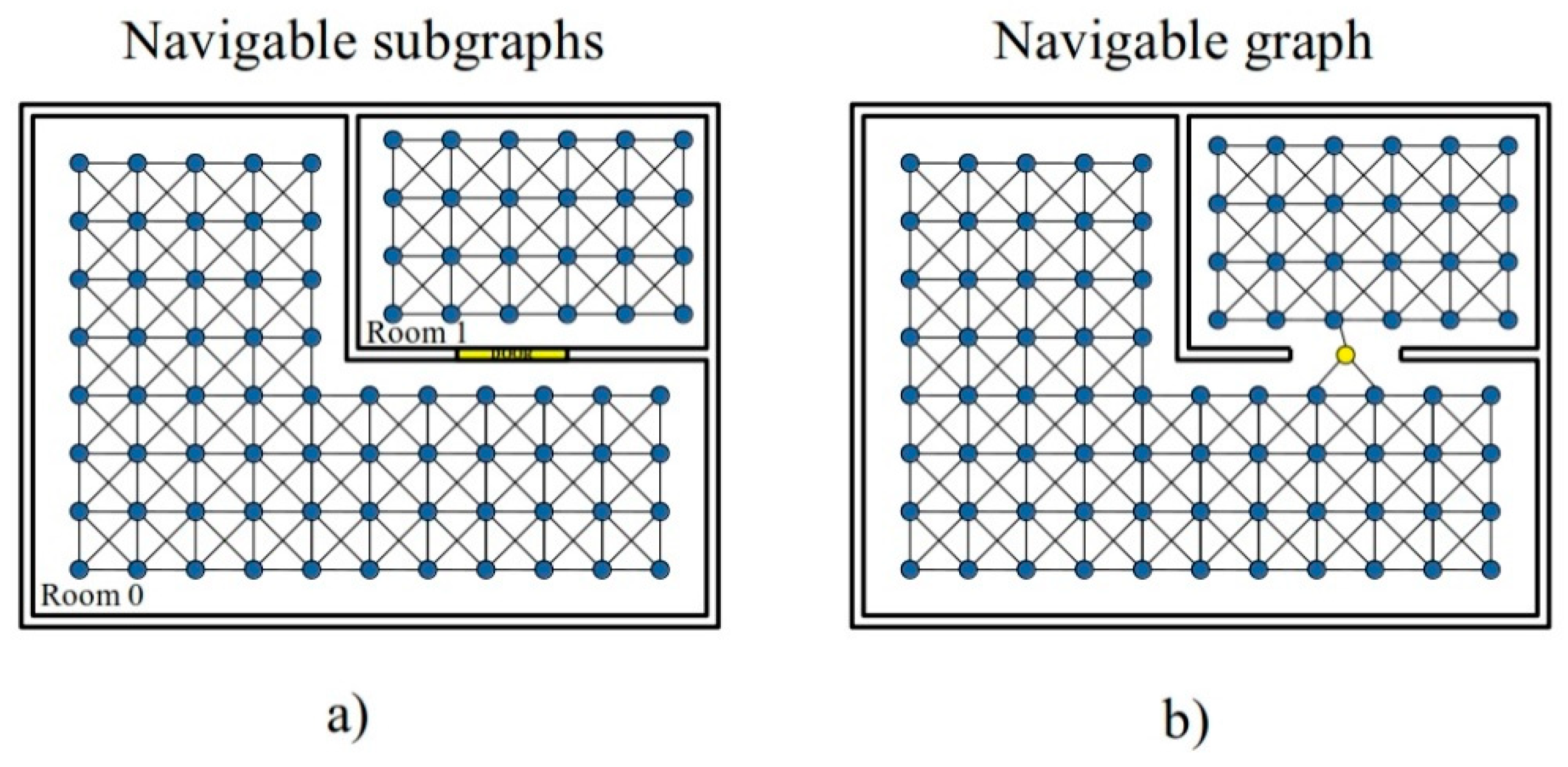
Figure 12.
(a) A subgraph is generated separately for each room. (b) The global graph consists of all subgraphs joined by new nodes corresponding to door positions (yellow).
Figure 12.
(a) A subgraph is generated separately for each room. (b) The global graph consists of all subgraphs joined by new nodes corresponding to door positions (yellow).
Figure 13.
(a) Input BIM model. (b) DXF model of case study 1 and (b) DXF model of case study 2.
Figure 13.
(a) Input BIM model. (b) DXF model of case study 1 and (b) DXF model of case study 2.
Figure 14.
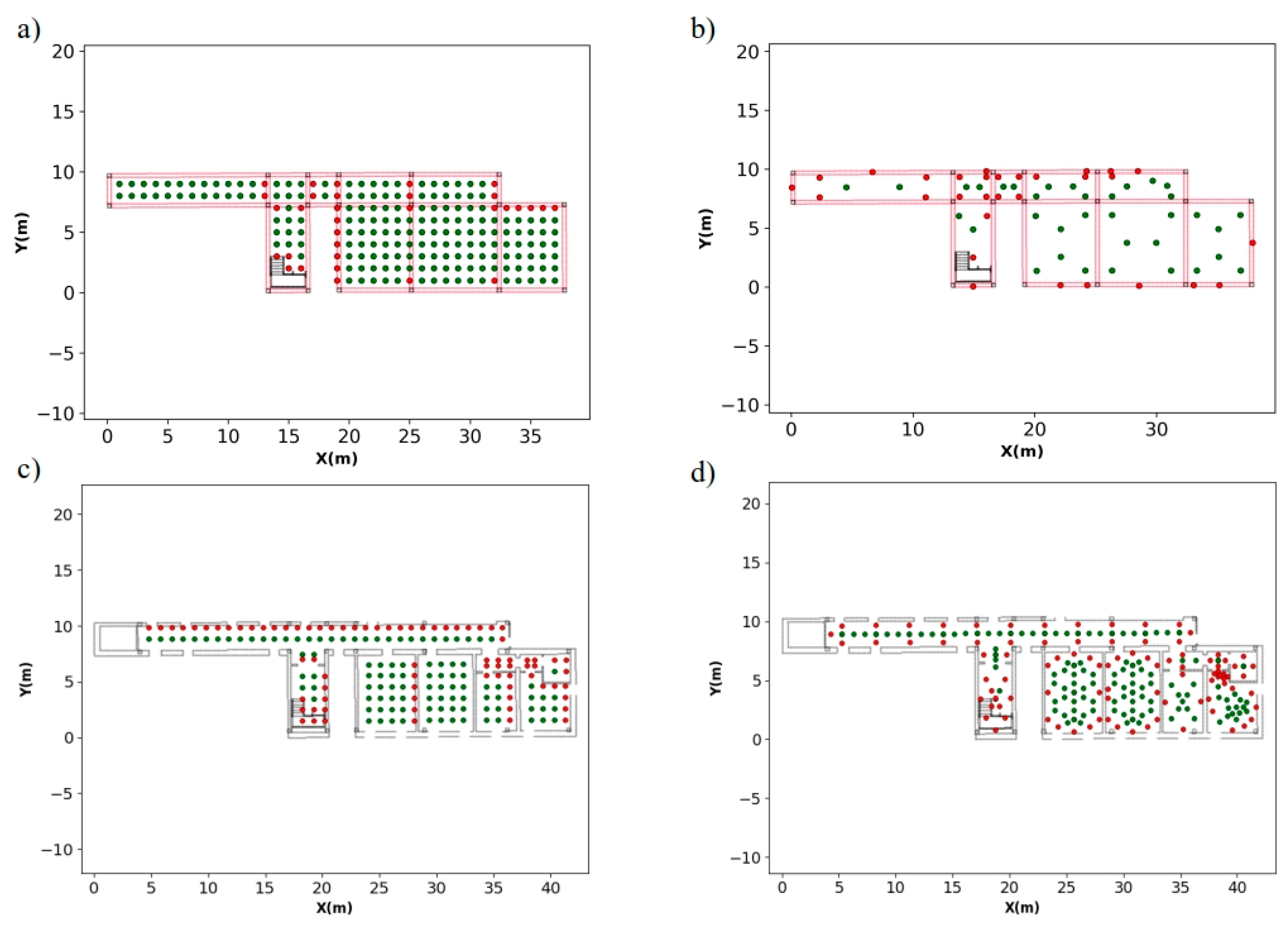
Candidate positions generated by both discretization methods in case study 1: (a) grid-based method in structural phase, (b) triangulation-based method in structural phase, (c) grid-based method with rooms and (d) triangulation-based method with rooms. Horizontal and vertical elements are displayed in magenta and black respectively. Green points represent position reachable by robotic system, unreachable positions are depicted in red.
Figure 14.
Candidate positions generated by both discretization methods in case study 1: (a) grid-based method in structural phase, (b) triangulation-based method in structural phase, (c) grid-based method with rooms and (d) triangulation-based method with rooms. Horizontal and vertical elements are displayed in magenta and black respectively. Green points represent position reachable by robotic system, unreachable positions are depicted in red.
Figure 15.
Candidate positions generated by both discretization methods in case study 2.
Figure 15.
Candidate positions generated by both discretization methods in case study 2.
Figure 16.
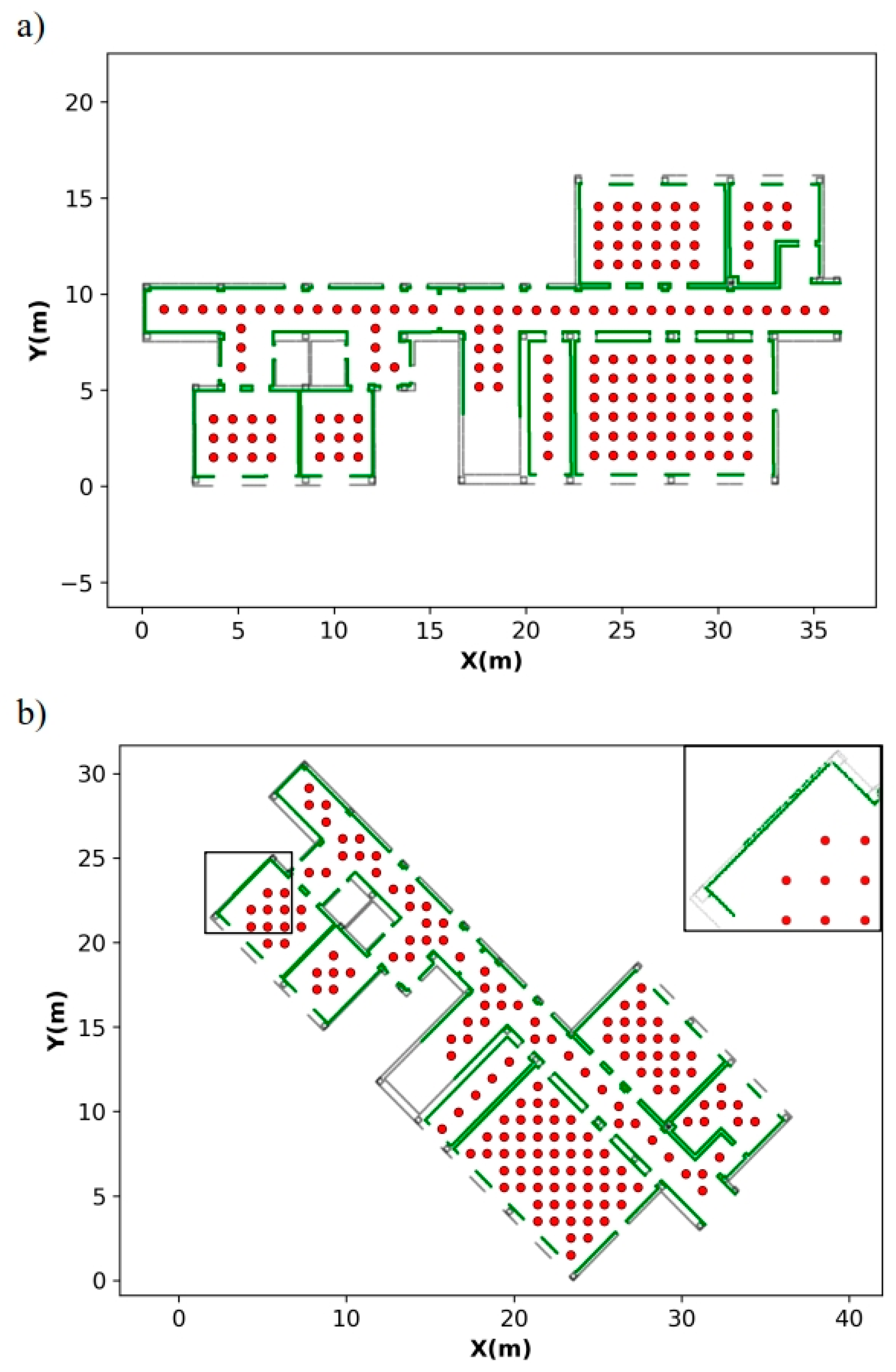
Visibility analysis results obtained from candidates generated in case study 1: (a) grid-based candidate distribution in structural phase, (b) triangulation-based candidate distribution in structural phase, (c) grid-based candidate distribution with rooms and (d) triangulation-based candidate distribution with rooms. Elements determined as visible for analysis process are depicted in green, black points represent no visible elements.
Figure 16.
Visibility analysis results obtained from candidates generated in case study 1: (a) grid-based candidate distribution in structural phase, (b) triangulation-based candidate distribution in structural phase, (c) grid-based candidate distribution with rooms and (d) triangulation-based candidate distribution with rooms. Elements determined as visible for analysis process are depicted in green, black points represent no visible elements.
Figure 17.
Visibility analysis results obtained from candidates generated in case study 2.
Figure 17.
Visibility analysis results obtained from candidates generated in case study 2.
Figure 18.
Visibility analysis of case study 1 original (a) and rotated (b). Visible elements are coloured in green, while black zones correspond to areas of element to be acquired are not visible from any candidate position.
Figure 18.
Visibility analysis of case study 1 original (a) and rotated (b). Visible elements are coloured in green, while black zones correspond to areas of element to be acquired are not visible from any candidate position.
Figure 19.
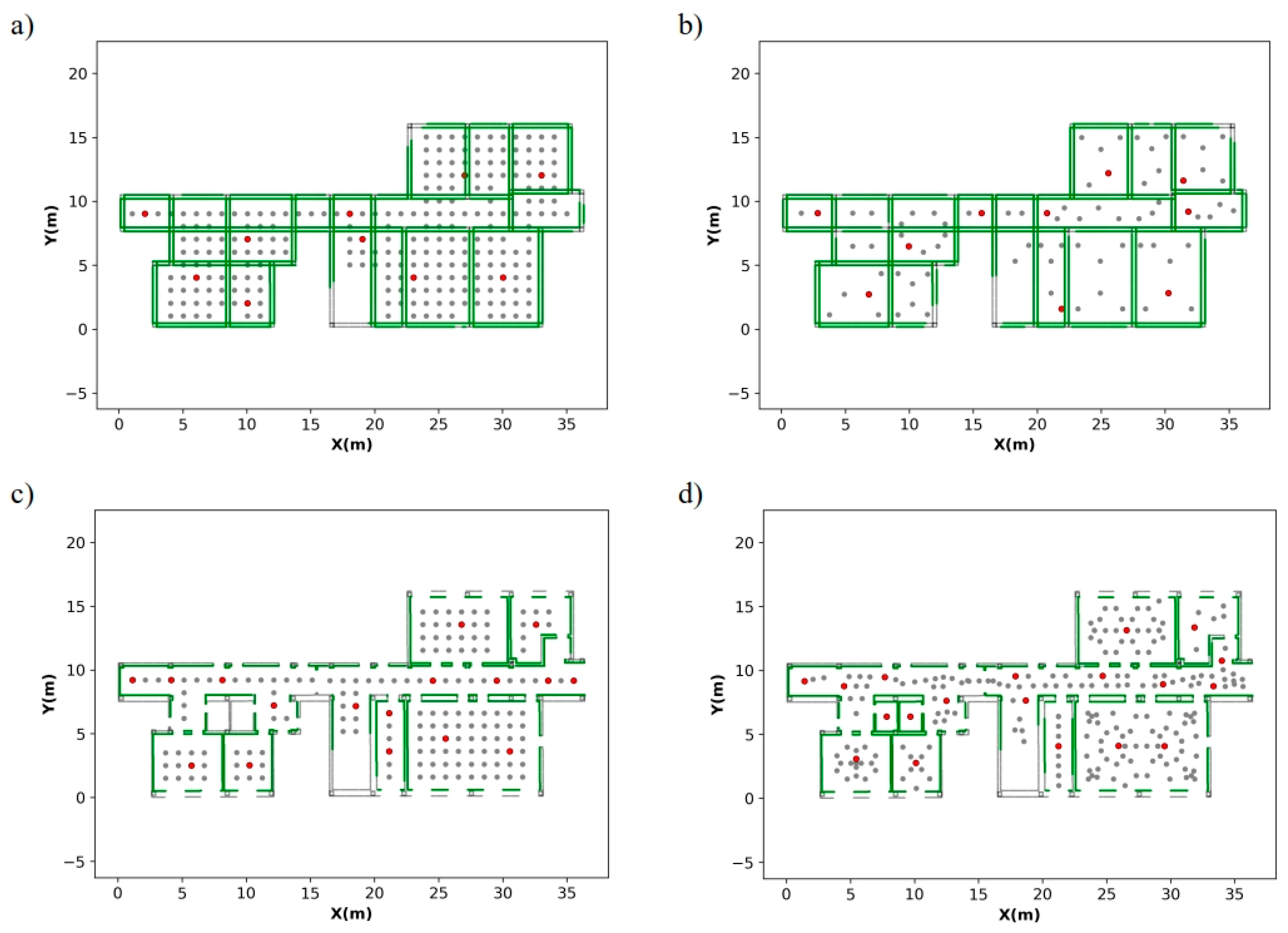
Optimization scan position result in case study 1: (a) grid-based method, (b) triangulation-based method, (c) grid-based with scan positions in doors and (d) triangulation-based method with scan positions in doors. Color code: scan positions (red points), candidates scan positions (gray points), acquired elements (green), non-acquired elements (black).
Figure 19.
Optimization scan position result in case study 1: (a) grid-based method, (b) triangulation-based method, (c) grid-based with scan positions in doors and (d) triangulation-based method with scan positions in doors. Color code: scan positions (red points), candidates scan positions (gray points), acquired elements (green), non-acquired elements (black).
Figure 20.
Optimization scan position result in case study 2.
Figure 20.
Optimization scan position result in case study 2.
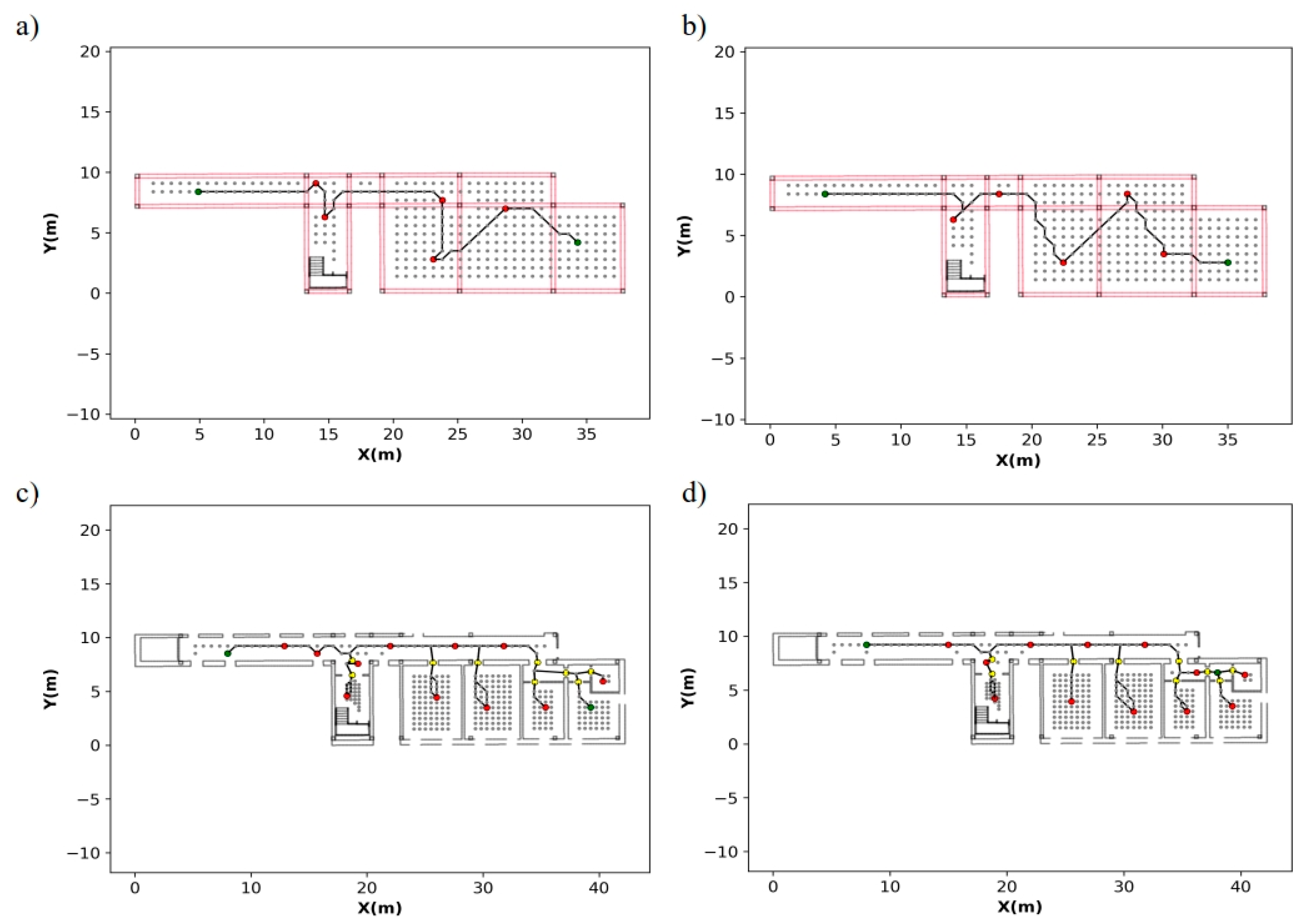
Figure 21.
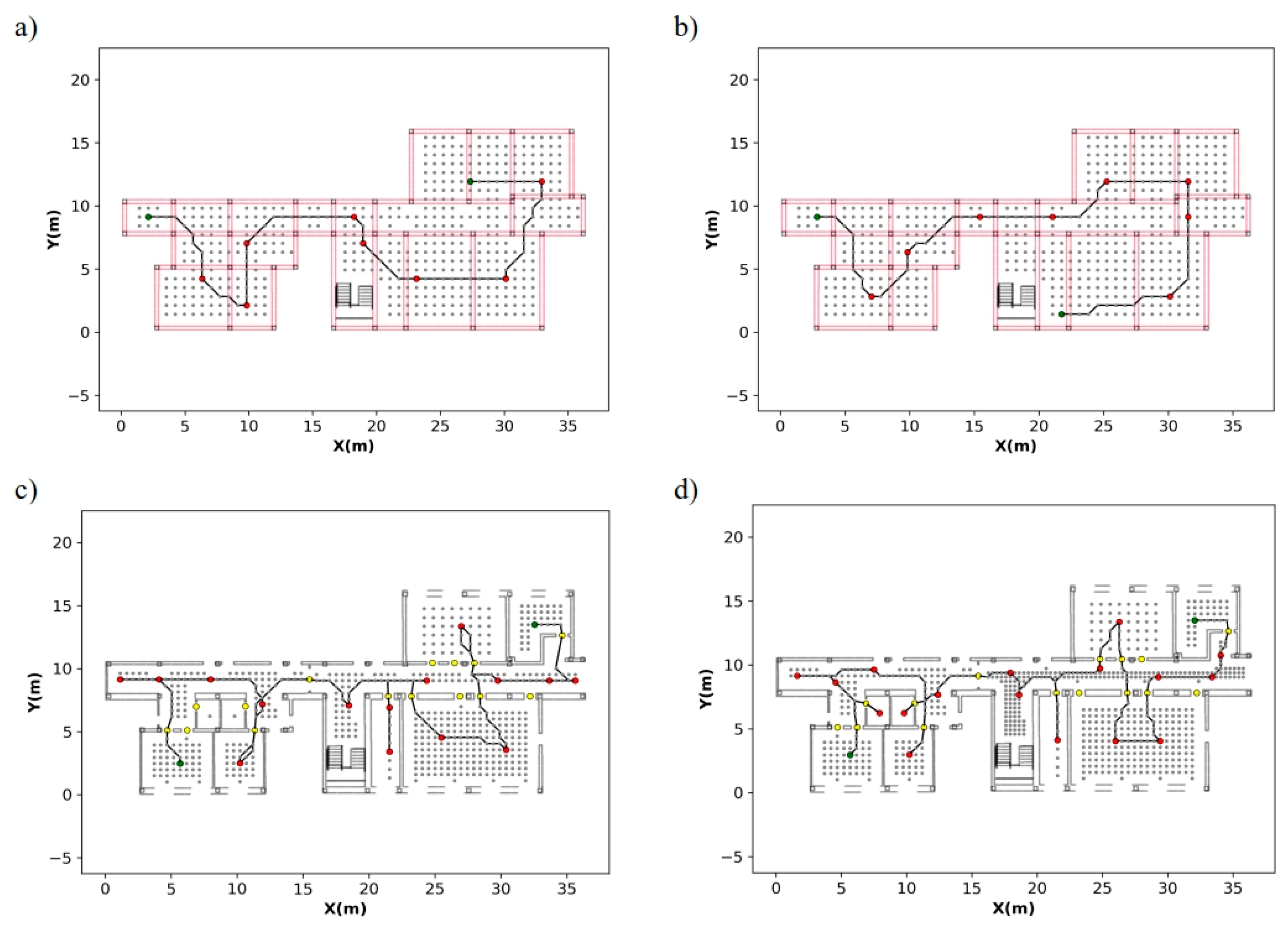
Optimal route calculated in case study 1 whose scanning positions were obtained by: (a) grid-based method in structural phase, (b) triangulation-based method in structural phase, (c) grid-based method with rooms and (d) triangulation-based method with rooms. Horizontal and vertical elements are displayed in magenta and black respectively. Green points represent start and end scanning position, the remaining ones are depicted in red.
Figure 21.
Optimal route calculated in case study 1 whose scanning positions were obtained by: (a) grid-based method in structural phase, (b) triangulation-based method in structural phase, (c) grid-based method with rooms and (d) triangulation-based method with rooms. Horizontal and vertical elements are displayed in magenta and black respectively. Green points represent start and end scanning position, the remaining ones are depicted in red.
Figure 22.
Optimal route calculated in case study 2.
Figure 22.
Optimal route calculated in case study 2.
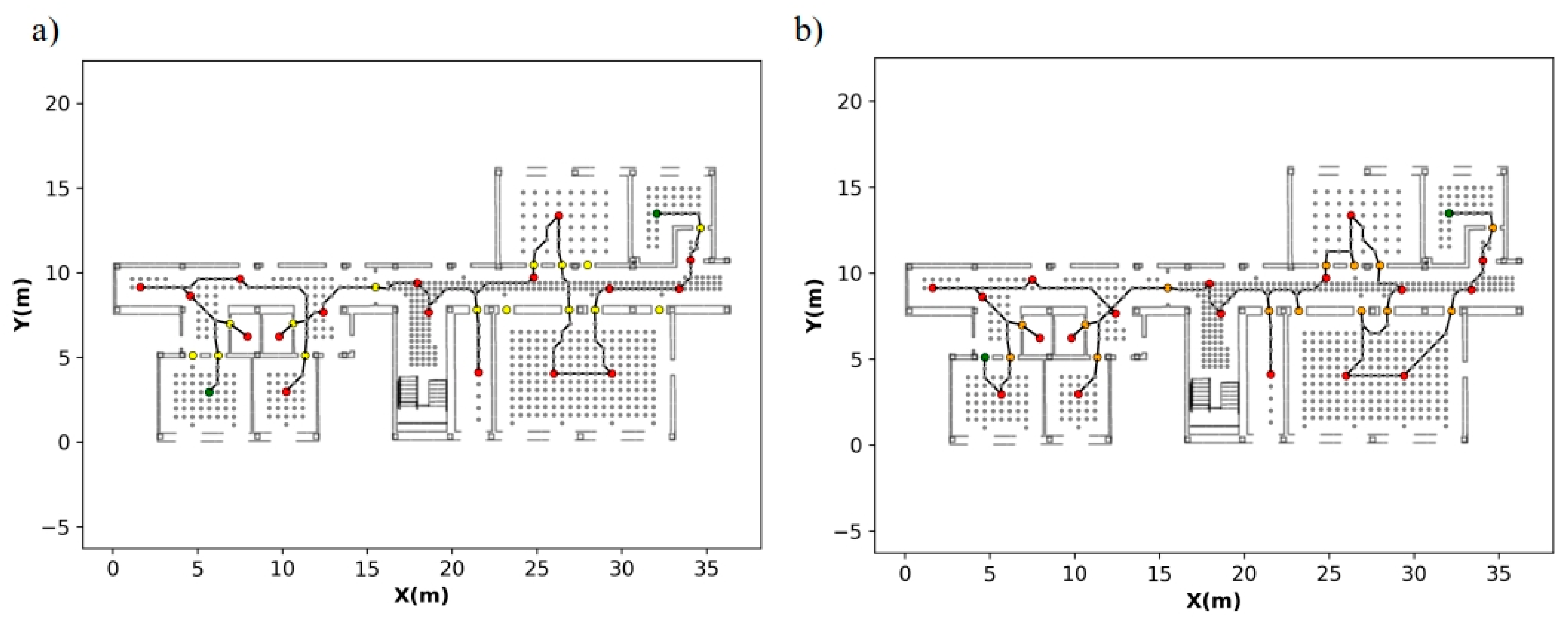
Figure 23.
Optimal route calculated in case study 1 with scan positions at doorways in (a) and without scan position at doorways in (b). Color code: scan positions (red points), graph nodes (gray points), start-end positions (green points), scanning-door positions (orange).
Figure 23.
Optimal route calculated in case study 1 with scan positions at doorways in (a) and without scan position at doorways in (b). Color code: scan positions (red points), graph nodes (gray points), start-end positions (green points), scanning-door positions (orange).
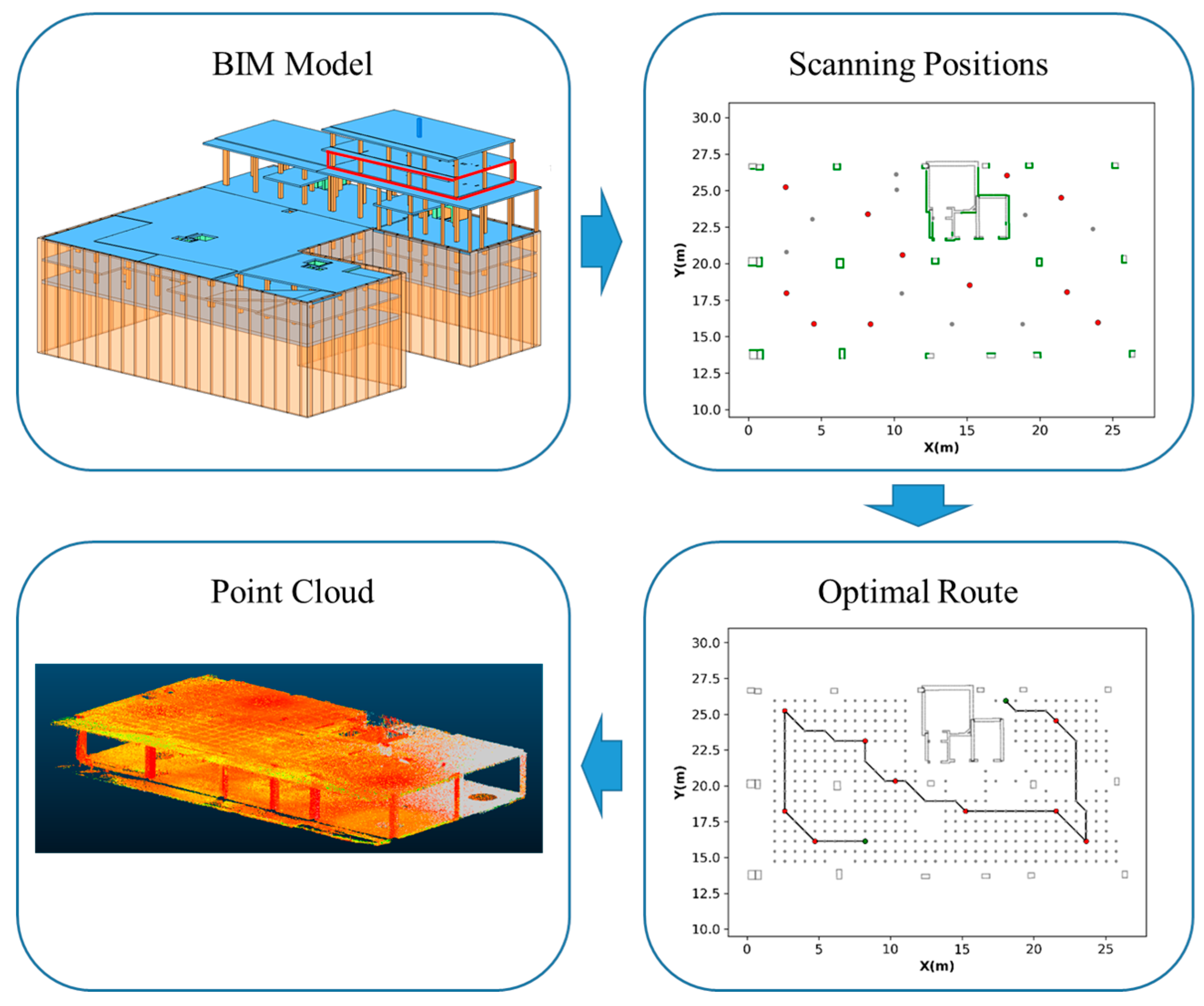
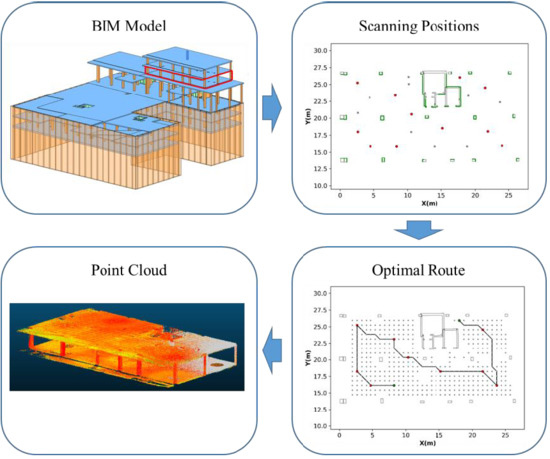
Figure 24.
Workflow of the entire process from Building Information Model (BIM) to the acquired point cloud tracking scanning plan generated by the proposed algorithm.
Figure 24.
Workflow of the entire process from Building Information Model (BIM) to the acquired point cloud tracking scanning plan generated by the proposed algorithm.
Table 1.
Input parameters.
Table 1.
Input parameters.
| Type of Parameter | Parameter | Abbreviation | Value |
|---|
| | Discretization resolution | ddis | 50 mm |
| | Laser range | r | 5 m |
| | Field of view | v | 360º |
| General | Security Distance | dsec | 0.7 m |
| | Coverage | cmin | 90% |
| Specifics | Resolution grid | rgrid | 1.0 m |
| Door accessibility | door_access | 0.7 m |
| Doors as scanning position | door_scan | True/False |
Table 2.
Number of units of discretization.
Table 2.
Number of units of discretization.
| Scenario | BEAMS | COLUMNS | STAIRS | WALLS | TOTAL |
|---|
| Case 1 (Structural) | 9066 | 1038 | 891 | - | 10995 |
| Case 1 (Rooms) | - | 1038 | 891 | 6296 | 8225 |
| Case 2 (Structural) | 6044 | 491 | 682 | - | 7217 |
| Case 2 (Rooms) | - | 491 | 682 | 5690 | 6863 |
Table 3.
Results distribution of candidate positions.
Table 3.
Results distribution of candidate positions.
| Case of Study | Scenario | Distribution | Number of Candidates | Reachable Candidates | Time (s) |
|---|
| Case 1 | Structural | Grid-based | 374 | 247 | 0.83 |
| Triangulation-based | 131 | 80 | 0.33 |
| Rooms | Grid-based | 297 | 163 | 0.83 |
| Triangulation-based | 368 | 229 | 1.06 |
| Case 2 | Structural | Grid-based | 214 | 182 | 0.80 |
| Triangulation-based | 65 | 35 | 1.10 |
| Rooms | Grid-based | 183 | 105 | 0.79 |
| Triangulation-based | 233 | 138 | 0.68 |
Table 4.
Results of visibility analysis.
Table 4.
Results of visibility analysis.
| Scenario | Units To Be Acquired | Method | Candidate Positions | Visible Units | Time (s) | Avg. Time (s) |
|---|
| Case 1 (structural) | 10104 | Grid-based | 247 | 9864 | 15.66 | 0.063 |
| Triangulation-based | 80 | 9714 | 4.73 | 0.059 |
| Case 2 (structural) | 6535 | Grid-based | 182 | 6230 | 7.73 | 0.042 |
| Triangulation-based | 35 | 6173 | 1.53 | 0.043 |
| Case 1 (Rooms) | 7334 | Grid-based | 163 | 3940 | 2.45 | 0.015 |
| Triangulation-based | 229 | 4260 | 3.78 | 0.017 |
| Case 2 (Rooms) | 6181 | Grid-based | 105 | 3193 | 1.69 | 0.016 |
| Triangulation-based | 138 | 3417 | 2.18 | 0.016 |
Table 5.
Comparison between different l_rng in structural phase of case study 1.
Table 5.
Comparison between different l_rng in structural phase of case study 1.
| | l_rng | 5 m | 10 m |
|---|
| Grid-based | units of visible elements | 9864 units | 9967 units |
| time consumed | 15.66 s | 89.59 s |
| Triangulation-based | units of visible elements | 9714 units | 9963 units |
| time consumed | 4.73 s | 21.18 s |
Table 6.
Results of optimization process.
Table 6.
Results of optimization process.
| Scenario | Method | Candidate Positions | Scanning Positions | Acquired (%) | Time (s) |
|---|
| Case 1 (structural) | Grid-based | 247 | 10 | 90.67 | 1.94 |
| Triangulation-based | 80 | 10 | 90.71 | 0.58 |
| Case 2 (structural) | Grid-based | 182 | 7 | 90.48 | 0.92 |
| Triangulation-based | 35 | 7 | 90.07 | 0.17 |
| Case 1 (Rooms) | Grid-based | 163 | 17 | 90.36 | 1.36 |
| Triangulation-based | 229 | 19 | 90.71 | 2.19 |
| Case 2 (Rooms) | Grid-based | 105 | 13 | 92.48 | 0.71 |
| Triangulation-based | 138 | 14 | 90.31 | 0.97 |
Table 7.
Results optimal route calculation.
Table 7.
Results optimal route calculation.
| Scenario | Method | Scanning Positions | Time Graph Generation (s) | Route Distance (m) | Time Route Calculation (s) |
|---|
| Case 1 (structural) | Grid-based | 10 | 2.35 | 55.61 | 0.15 |
| Triangulation-based | 10 | 2.38 | 57.02 | 0.15 |
| Case 2 (structural) | Grid-based | 7 | 1.58 | 42.42 | 0.06 |
| Triangulation-based | 7 | 1.55 | 44.59 | 0.05 |
| Case 1 (Rooms) | Grid-based | 17 | 3.02 | 103.99 | 0.63 |
| Triangulation-based | 19 | 4.27 | 100.34 | 0.94 |
| Case 2 (Rooms) | Grid-based | 13 | 1.87 | 88.10 | 0.29 |
| Triangulation-based | 14 | 1.89 | 87.27 | 0.35 |