Mapping Growing Stem Volume of Chinese Fir Plantation Using a Saturation-based Multivariate Method and Quad-polarimetric SAR Images
Abstract
1. Introduction
2. Study Area and Datasets
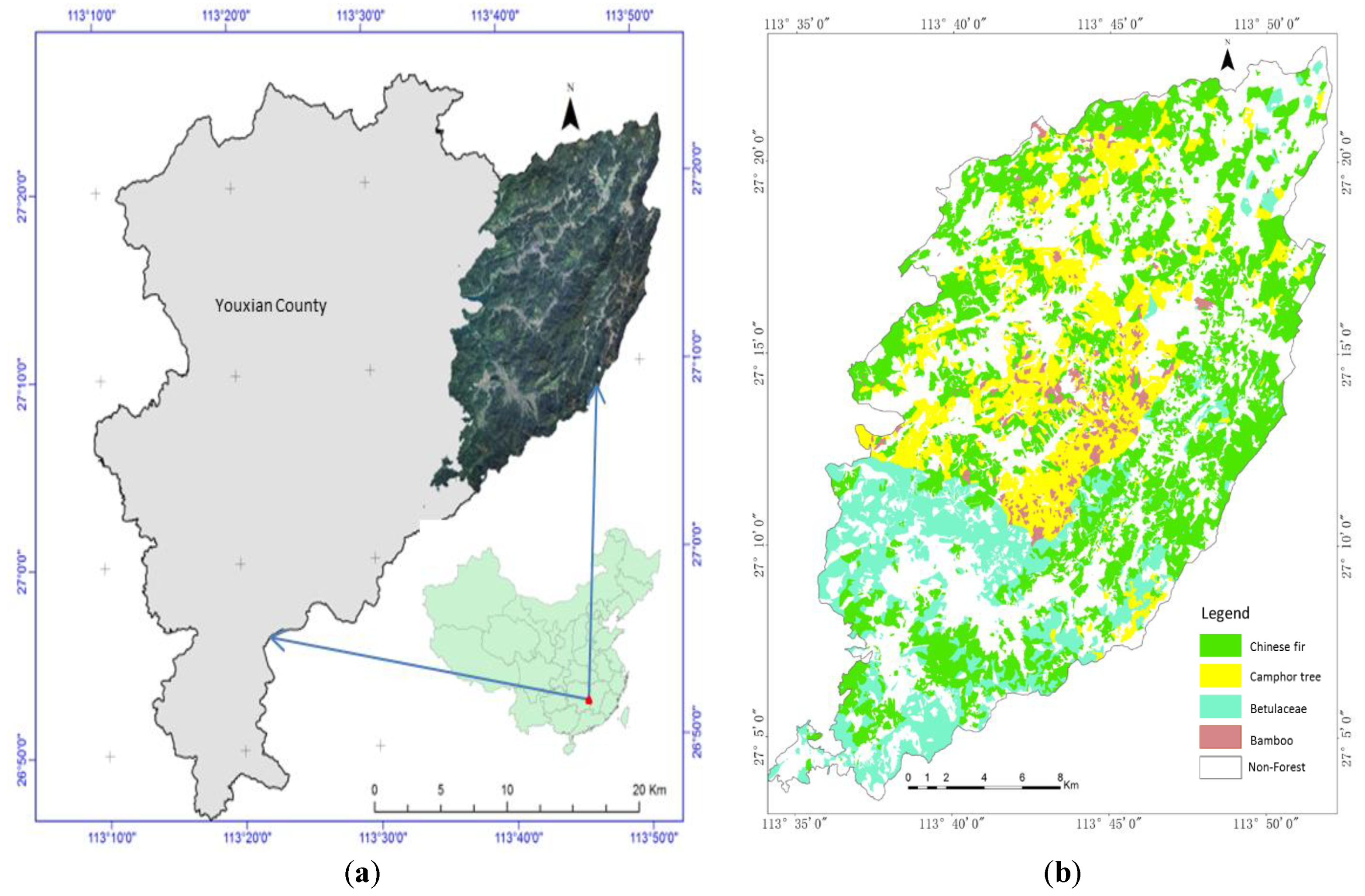
2.1. Study Area
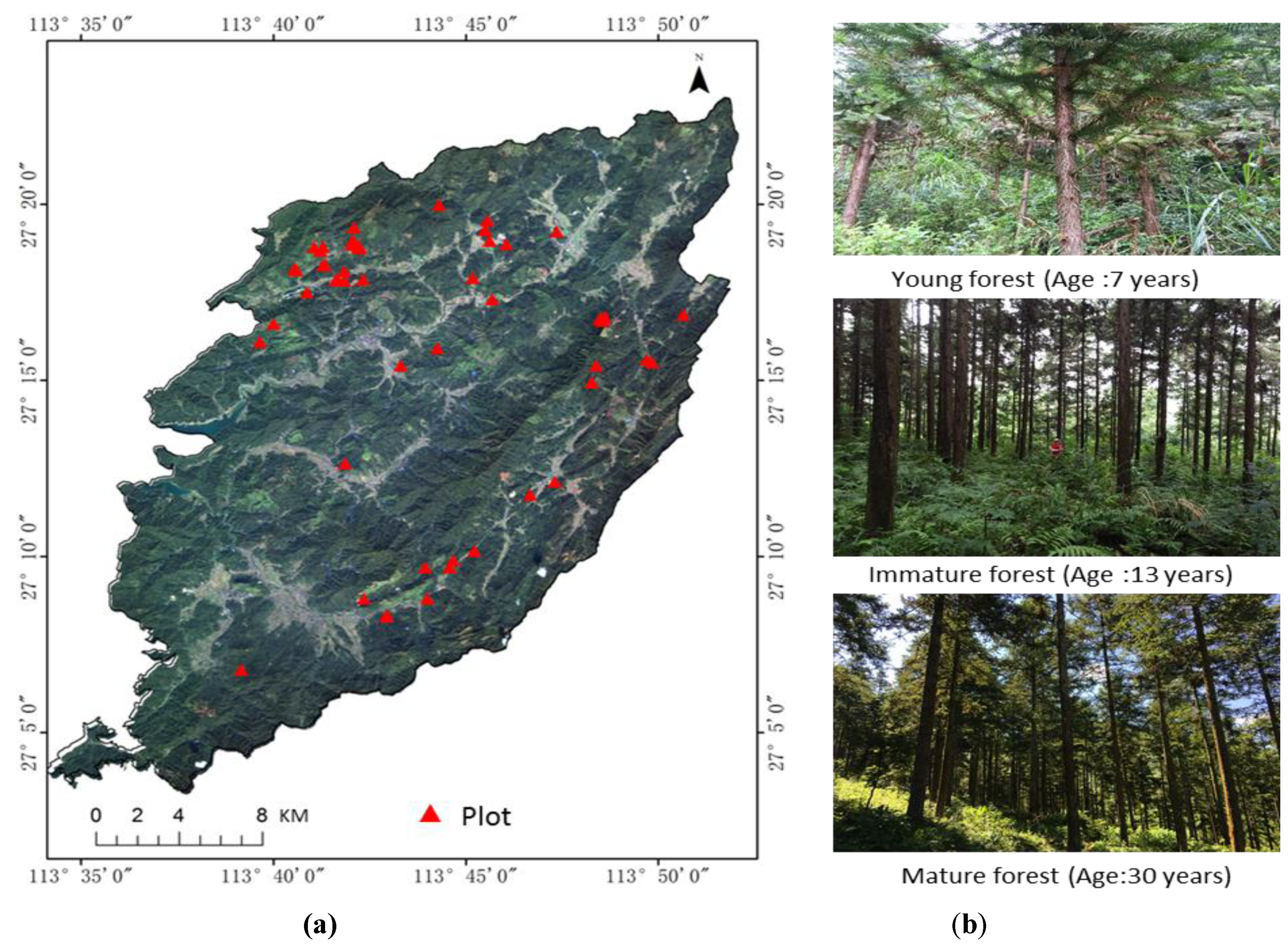
2.2. Ground Data Collection and Processing
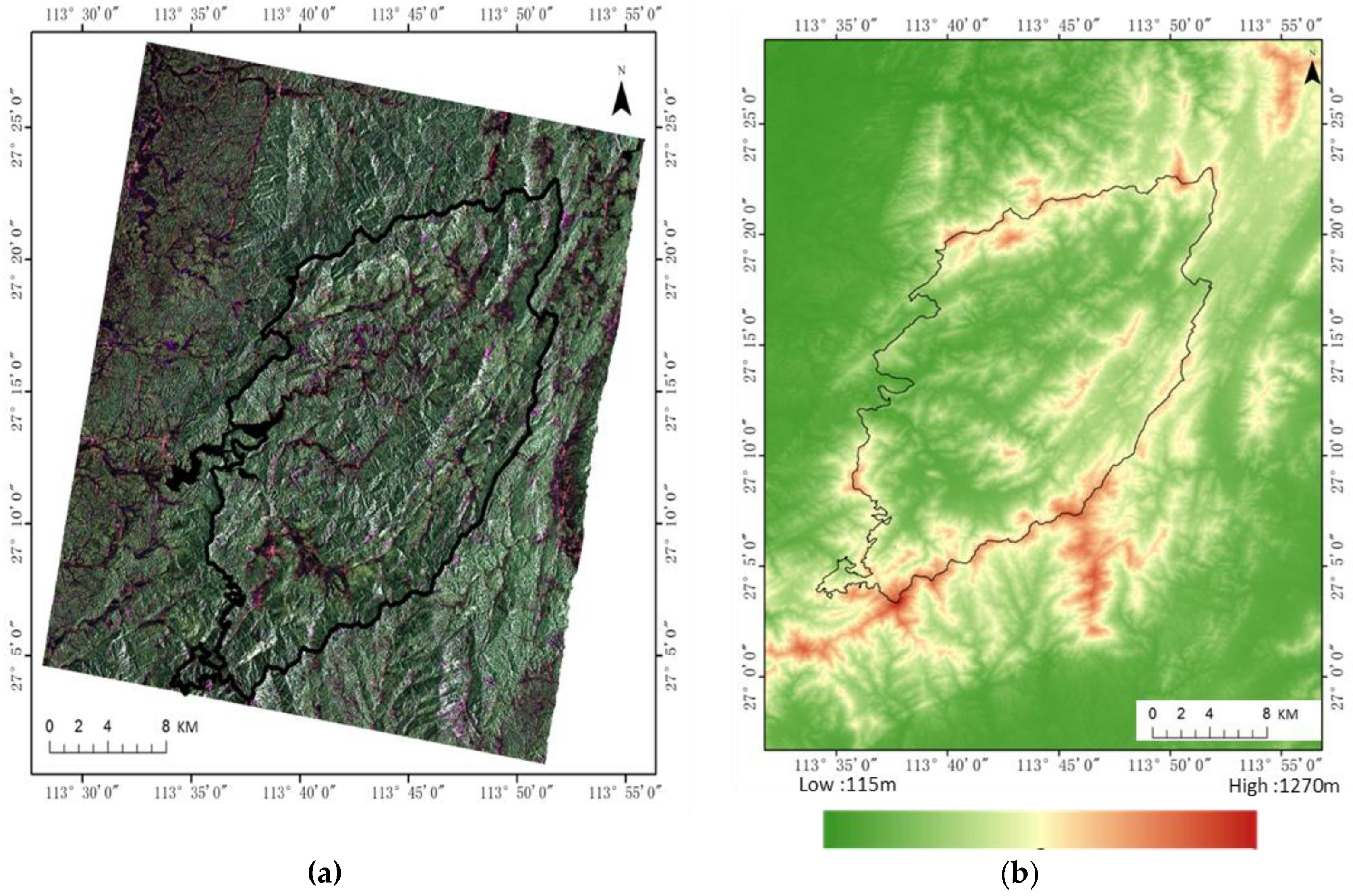
2.3. Quad-Polarimetric SAR Data and Digital Elevation Model (DEM)
3. Methods
3.1. SAR Data Pre-processing
3.2. Retrival of Polarimetric Characteristics
3.3. Forest GSV Estimation
4. Results
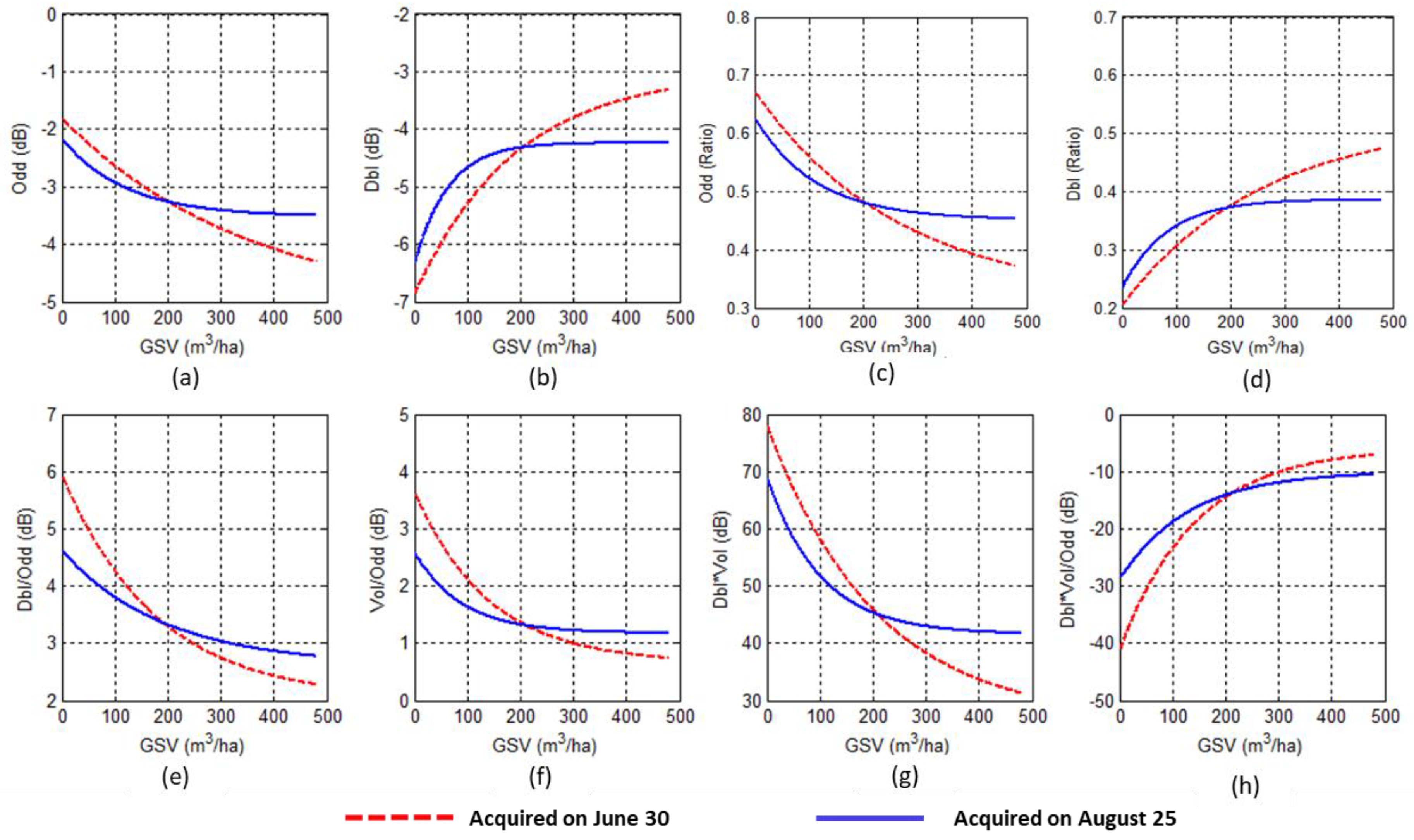
4.1. Polarimetric Characteristics
4.2. Saturation Level of Planted Forest
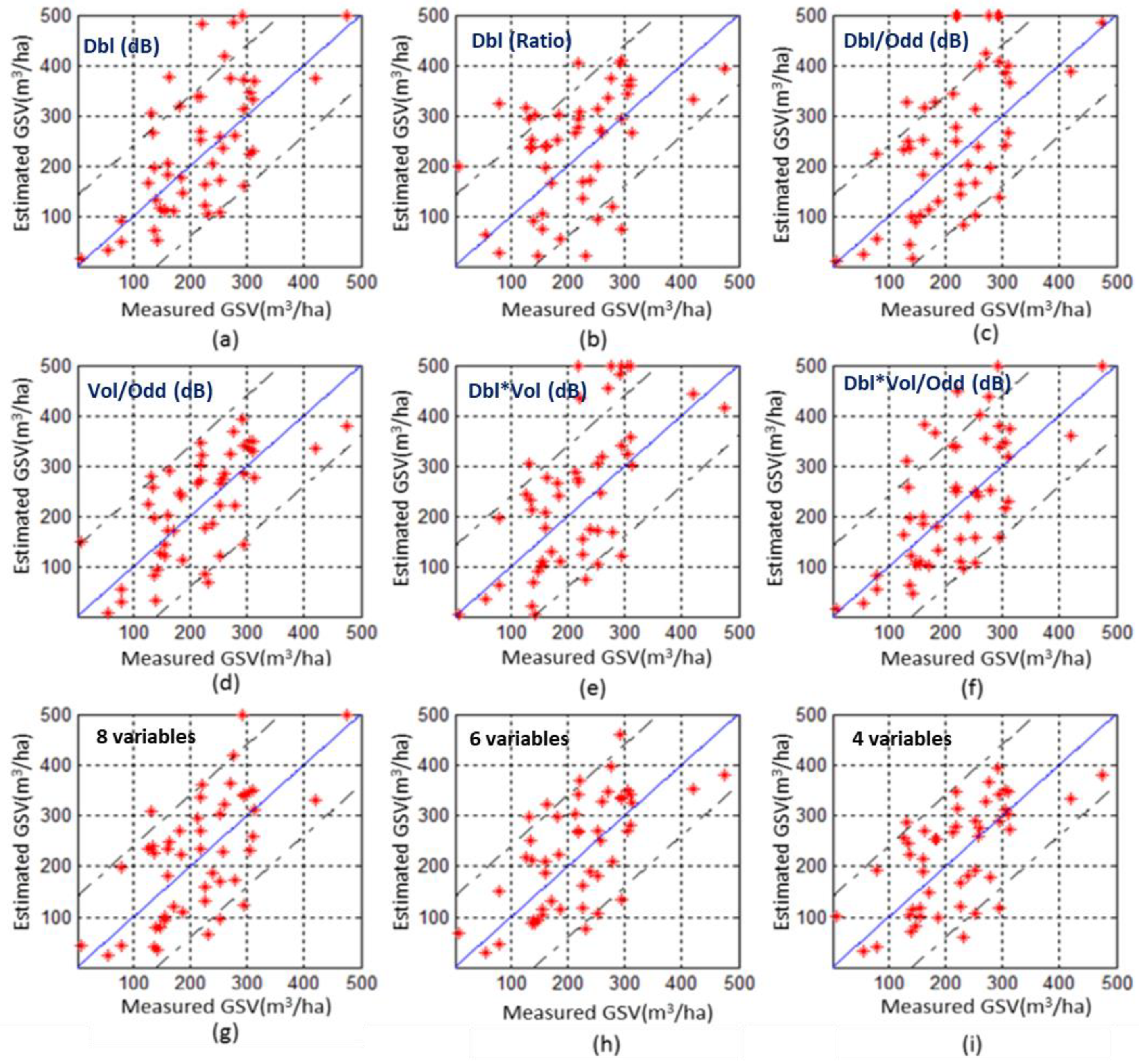
4.3. Forest GSV Estimated by the Univariate Method
4.4. Forest GSV Estimated by the Saturation-Based Multivariate Method
5. Discussion
5.1. Polarimetric Characteristics Related to Tree Species
5.2. Saturation Level of Forest GSV
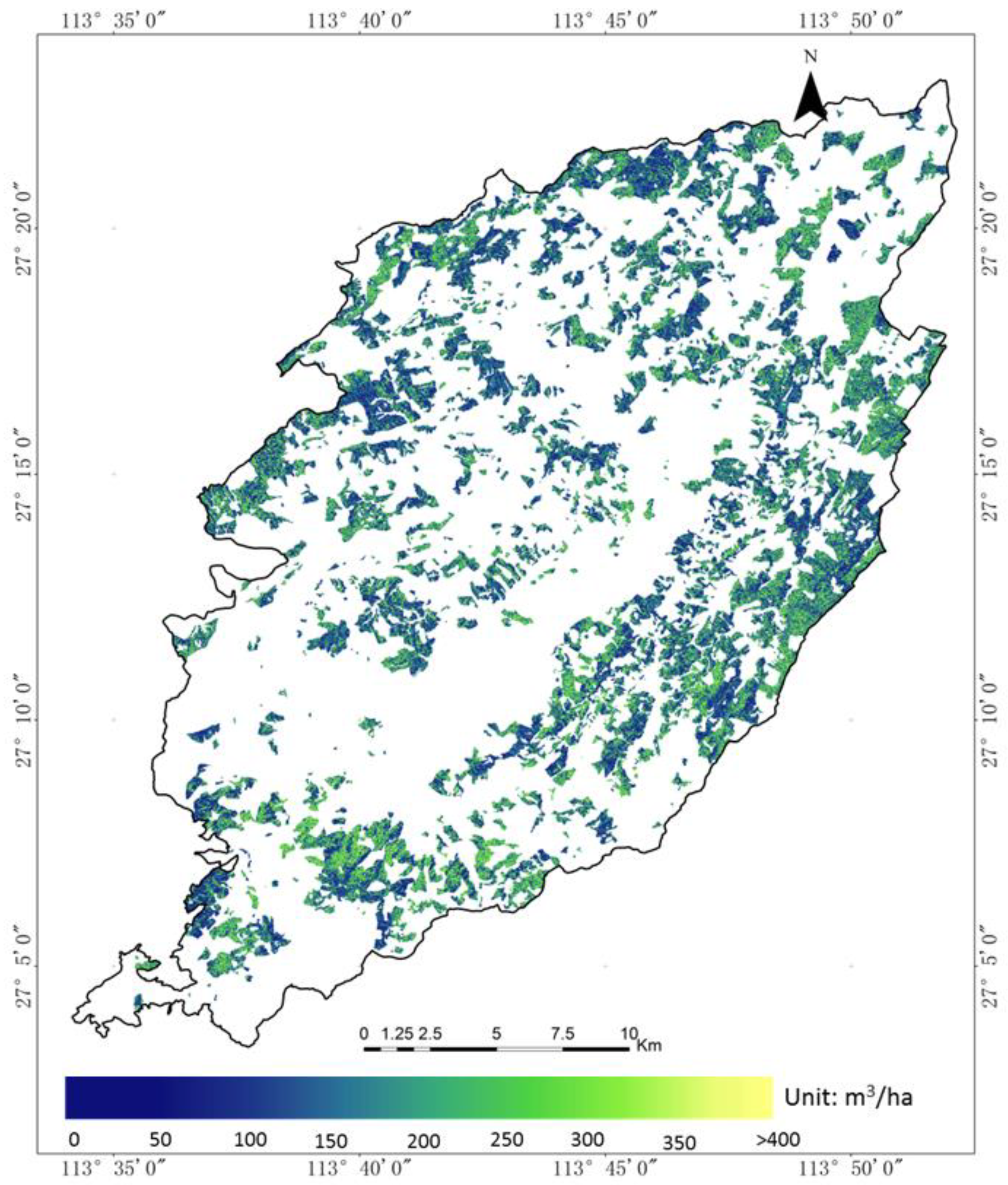
5.3. Estimated GSV of Chinese Fir Plantation
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Di Cosmo, L.; Gasparini, P.; Tabacchi, G. A national-scale, stand-level model to predict total above-ground tree biomass from growing stock volume. For. Ecol. Manag. 2016, 361, 269–276. [Google Scholar] [CrossRef]
- Krejza, J.; Světlík, J.; Bedná, P. Allometric relationship and biomass expansion factors (BEFs) for above- and below-ground biomass prediction and stem volume estimation for ash (Fraxinus excelsior L.) and oak (Quercus robur L.). Trees 2017, 31, 1303–1316. [Google Scholar] [CrossRef]
- Wijaya, A.; Kusnadi, S.; Gloaguen, R.; Heilmeier, H. Improved strategy for estimating stem volume and forest biomass using moderate resolution remote sensing data and GIS. J. For. Res.-JPN 2010, 21, 1–12. [Google Scholar] [CrossRef]
- Mathieu, R.; Naidoo, L.; Cho, M.A.; Leblon, B.; Main, R. Toward structural assessment of semi-arid African savannahs and woodlands: The potential of multitemporal polarimetric RADARSAT-2 fine beam images. Remote Sens. Environ. 2013, 138, 215–231. [Google Scholar] [CrossRef]
- Silva, C.A.; Klauberg, C.; Hudak, A.T.; Vierling, L.A.; Liesenberg, V.; Carvalho, S.P.C.E.; Rodriguez, L.C.E. A principal component approach for predicting the stem volume in Eucalyptus plantations in Brazil using airborne LiDAR data. Forestry 2016, 89, 422–433. [Google Scholar] [CrossRef]
- Abdullahi, S.; Kugler, F.; Pretzsch, H. Prediction of stem volume in complex temperate forest stands using TanDEM-X SAR data. Remote Sens. Environ. 2016, 174, 197–211. [Google Scholar] [CrossRef]
- Chowdhury, T.A.; Thiel, C.; Schmullius, C.; Stelmaszczukgórska, M. Polarimetric Parameters for Growing Stock Volume Estimation Using ALOS PALSAR L-Band Data over Siberian Forests. Remote Sens. 2013, 5, 5725–5756. [Google Scholar] [CrossRef]
- Iizuka, K.; Tateishi, R. Simple Relationship Analysis between L-Band Backscattering Intensity and the Stand Characteristics of Sugi and Hinoki Trees. Adv. Remote Sens. 2014, 3, 219–234. [Google Scholar] [CrossRef]
- Joshi, N.; Mitchard, E.T.A.; Brolly, M.; Schumacher, J.; Fernándezlanda, A.; Johannsen, V.K.; Marchamalo, M.; Fensholt, R. Understanding ‘saturation’ of radar signals over forests. Sci. Rep. 2017, 7, 3505. [Google Scholar] [CrossRef]
- Antropov, O.; Rauste, Y.; Ahola, H.; Hame, T. Stand-Level Stem Volume of Boreal Forests from Spaceborne SAR Imagery at L-Band. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2013, 6, 35–44. [Google Scholar] [CrossRef]
- Thiel, C.; Schmullius, C. The potential of ALOS PALSAR backscatter and InSAR coherence for forest growing stock volume estimation in Central Siberia. Remote Sens. Environ. 2016, 173, 258–273. [Google Scholar] [CrossRef]
- Stelmaszczuk-Górska, M.; Rodriguez-Veiga, P.; Ackermann, N.; Thiel, C.; Balzter, H.; Schmullius, C. Non-Parametric Retrieval of Aboveground Biomass in Siberian Boreal Forests with ALOS PALSAR Interferometric Coherence and Backscatter Intensity. J. Imaging 2016, 2, 1. [Google Scholar] [CrossRef]
- Santoro, M.; Schmullius, C.; Pathe, C.; Schwilk, J. Pan-boreal mapping of forest growing stock volume using hyper-temporal Envisat ASAR ScanSAR backscatter data. In Proceedings of the 2012 IEEE International Geoscience and Remote Sensing Symposium, Munich, Germany, 22–27 July 2012. [Google Scholar]
- Santoro, M.; Eriksson, L.; Askne, J.; Schmullius, C. Assessment of stand-wise stem volume retrieval in boreal forest from JERS-1 L-band SAR backscatter. Int. J. Remote Sens. 2006, 27, 3425–3454. [Google Scholar] [CrossRef]
- Fransson, J.E.S. Estimation of stem volume in boreal forests using ERS-1 C-and JERS-1 L-band SAR data. Int. J. Remote Sens. 1999, 20, 123–137. [Google Scholar] [CrossRef]
- Santoro, M.; Beer, C.; Cartus, O.; Schmullius, C.; Shvidenko, A.; Mccallum, I.; Wegmüller, U.; Wiesmann, A. Retrieval of growing stock volume in boreal forest using hyper-temporal series of Envisat ASAR ScanSAR backscatter measurements. Remote Sens. Environ. 2011, 115, 490–507. [Google Scholar] [CrossRef]
- Santoro, M.; Cartus, O.; Fransson, J.E.S.; Shvidenko, A.; Mccallum, I.; Hall, R.J.; Beaudoin, A.; Beer, C.; Schmullius, C. Estimates of Forest Growing Stock Volume for Sweden, Central Siberia, and Québec Using Envisat Advanced Synthetic Aperture Radar Backscatter Data. Remote Sens. 2013, 5, 4503–4532. [Google Scholar] [CrossRef]
- Santoro, M.; Askne, J.; Smith, G.; Fransson, J.E.S. Stem volume retrieval in boreal forests from ERS-1/2 interferometry. Remote Sens. Environ. 2002, 81, 19–35. [Google Scholar] [CrossRef]
- Santoro, M.; Shvidenko, A.; McCallum, I.; Askne, J.; Schmullius, C. Properties of ERS-1/2 coherence in the Siberian boreal forest and implications for stem volume retrieval. Remote Sens. Environ. 2007, 106, 154–172. [Google Scholar] [CrossRef]
- Chowdhury, T.A.; Thiel, C.; Schmullius, C. Growing stock volume estimation from L-band ALOS PALSAR polarimetric coherence in Siberian forest. Remote Sens. Environ. 2014, 155, 129–144. [Google Scholar] [CrossRef]
- Thiel, C.; Schmullius, C. Impact of Tree Species on Magnitude of PALSAR Interferometric Coherence over Siberian Forest at Frozen and Unfrozen Conditions. Remote Sens. 2014, 6, 1124–1136. [Google Scholar] [CrossRef]
- Thiel, C.; Schmullius, C. Investigating ALOS PALSAR interferometric coherence in central Siberia at unfrozen and frozen conditions: Implications for forest growing stock volume estimation. Can. J. Remote Sens. 2013, 39, 232–250. [Google Scholar] [CrossRef]
- Karila, K.; Vastaranta, M.; Karjalainen, M.; Kaasalainen, S. Tandem-X interferometry in the prediction of forest inventory attributes in managed boreal forests. Remote Sens. Environ. 2015, 159, 259–268. [Google Scholar] [CrossRef]
- Cloude, S.R.; Zebker, H. Polarisation: Applications in Remote Sensing. Phys. Today 2010, 63, 53–54. [Google Scholar]
- Lee, J.S.; Pottier, E. Polarimetric Radar Imaging: Basics to Applications, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]
- Freeman, A.; Durden, S.L. A three-component scattering model for polarimetric SAR data. IEEE Trans. Geosci. Remote Sens. 1998, 36, 963–973. [Google Scholar] [CrossRef]
- Freeman, A. Fitting a two-component scattering model to polarimetric SAR data from forests. IEEE Trans. Geosci. Remote Sens. 2007, 45, 2583–2592. [Google Scholar] [CrossRef]
- Yamaguchi, Y.; Moriyama, T.; Ishido, M.; Yamada, H. Four-component scattering model for polarimetric SAR image decomposition. IEEE Trans. Geosci. Remote Sens. 2005, 43, 1699–1706. [Google Scholar] [CrossRef]
- Kobayashi, S.; Omura, Y.; Sangangoie, K.; Widyorini, R.; Kawai, S.; Supriadi, B.; Yamaguchi, Y. Characteristics of Decomposition Powers of L-Band Multi-Polarimetric SAR in Assessing Tree Growth of Industrial Plantation Forests in the Tropics. Remote Sens. 2012, 4, 3058–3077. [Google Scholar] [CrossRef]
- Antropov, O.; Rauste, Y.; Hame, T. Volume scattering modeling in PolSAR decompositions: Study of ALOS PALSAR data over boreal forest. IEEE Trans. Geosci. Remote Sens. 2011, 49, 3838–3848. [Google Scholar] [CrossRef]
- Huang, L.Y.; Yan, Q.L.; Gao, T.; Zhu, J.J. Estimation on stock volume of plantation forests using ALOS PALSAR images: A case study of Larix principis-rupprechtii plantations in Saihanba Forest Farm. Chin. J. Ecol. 2015, 34, 2401–2409. [Google Scholar]
- Kobayashi, S.; Omura, Y.; Sanga-Ngoie, K.; Yamaguchi, Y.; Widyorini, R.; Fujita, M.S.; Supriadi, B.; Kawai, S. Yearly Variation of Acacia Plantation Forests Obtained by Polarimetric Analysis of ALOS PALSAR Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 8, 5294–5304. [Google Scholar] [CrossRef]
- Yuan, J.; Li, Y.M.; Liu, C.L.; Zha, X.F. Leave-One-Out Cross-Validation Based Model Selection for Manifold Regularization; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Askne, J.; Santoro, M.; Smith, G.; Fransson, J.E.S. Multitemporal repeat-pass SAR interferometry of boreal forests. IEEE Trans. Geosci. Remote Sens. 2005, 43, 1219–1228. [Google Scholar] [CrossRef]
- Pulliainen, J.; Engdahl, M.; Hallikainen, M. Feasibility of multi-temporal interferometric SAR data for stand-level estimation of boreal forest stem volume. Remote Sens. Environ. 2003, 85, 397–409. [Google Scholar] [CrossRef]
- Gonçalves, F.G.; Santos, J.R.; Treuhaft, R.N. Stem volume of tropical forests from polarimetric radar. Int. J. Remote Sens. 2011, 32, 503–522. [Google Scholar] [CrossRef]
- Olesk, A.; Praks, J.; Antropov, O.; Zalite, K.; Arumäe, T.; Voormansik, K. Interferometric SAR Coherence Models for Characterization of Hemiboreal Forests Using TanDEM-X Data. Remote Sens. 2016, 8, 700. [Google Scholar] [CrossRef]
- Zhang, H.; Zhu, J.; Wang, C.; Lin, H.; Long, J.; Zhao, L.; Fu, H.; Liu, Z. Forest Growing Stock Volume Estimation in Subtropical Mountain Areas Using PALSAR-2 L-Band PolSAR Data. Forests 2019, 10, 276. [Google Scholar] [CrossRef]
- Wang, C.; Wang, L.; Fu, H.; Xie, Q.; Zhu, J.; Wang, C.; Wang, L.; Fu, H.; Xie, Q.; Zhu, J. The Impact of Forest Density on Forest Height Inversion Modeling from Polarimetric InSAR Data. Remote Sens.-Basel 2016, 8, 291. [Google Scholar] [CrossRef]
- Wagner, W.; Luckman, A.; Vietmeier, J.; Tansey, K.; Balzter, H.; Schmullius, C.; Davidson, M.; Gaveau, D.; Gluck, M.; Toan, T.L. Large-scale mapping of boreal forest in SIBERIA using ERS tandem coherence and JERS backscatter data. Remote Sens. Environ. 2003, 85, 125–144. [Google Scholar] [CrossRef]
- Wang, Z.M.; Zhang, W.Q.; Yue, C.R.; Liu, Q. Estimation of Forest Growing Stock Based on TerraSAR-X and ALOS PALSAR Data:a Case Study in Mengla County of Yunnan Province. J. Zhejiang For. Sci. Technol. 2018, 38, 38–42. [Google Scholar]
- Yang, M.; Wang, Y.; Zhang, X. Study on the model for estimating forest volume of Chinese fir based on bi-source remote sensing data. J. Nanjing For. Univ. 2016, 40, 107–114. [Google Scholar]
- Dong, G.; Jian, Y.; Peng, Y.; Chao, W.; Hong, Z. Forest characteristic detection with Pol-SAR. J. Tsinghua Univ. 2003, 43, 953–956. [Google Scholar]
- Xi, F. Density, storage and distribution of carbon in Chinese fir plantation at fast growing stage. Sci. Silv. Sin. 2002, 38, 14–19. [Google Scholar]
- Zhang, X.; Zhang, J.; Duan, A. Compatibility of Stand Volume Model for Chinese Fir Based on Tree-Level and Stand-Level. Sci. Silv. Sin. 2014, 50, 82–87. [Google Scholar]
- Zheng, D.; Hu, G.; Chen, P.; Gong, Z. The Selection and Error Analysis of the Angle Gauge Constant in the Chinese-fir Plantation at Different Ages. For. Resour. Manag. 2006, 2, 74–78. [Google Scholar]
- Quegan, S.; Dutra, L.V. SAR Calibration and Principal Component Analysis. In Proceedings of the Third Airborne Synthetic Aperture Radar (AIRSAR) Workshop, Pasadena, CA, USA, 1 August 1991. [Google Scholar]
- Freeman, A. Calibration of linearly polarized polarimetric SAR data subject to Faraday rotation. IEEE Trans. Geosci. Remote Sens. 2004, 42, 1617–1624. [Google Scholar] [CrossRef]
- Chen, J.; Quegan, S. Calibration of Spaceborne CTLR Compact Polarimetric Low-Frequency SAR Using Mixed Radar Calibrators. IEEE Trans. Geosci. Remote Sens. 2011, 49, 2712–2723. [Google Scholar] [CrossRef]
- Quegan, S.; Lomas, M. The interaction between calibration and Faraday rotation estimates from SAR. In Proceedings of the EUSAR European Conference on Synthetic Aperture Radar, Berlin, Germany, 3–5 June 2014. [Google Scholar]
- Mohanty, S.; Singh, G.; Yamaguchi, Y. Faraday rotation correction and total electron content estimation using ALOS-2/PALSAR-2 full polarimetric SAR data. In Proceedings of the 2016 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016. [Google Scholar]
- Kimura, H.; Mizuno, T.; Papathanassiou, K.P.; Hajnsek, I. Improvement of polarimetric SAR calibration based on the Quegan algorithm. In Proceedings of the IEEE International Geoscience & Remote Sensing Symposium, Anchorage, AK, USA, 20–24 September 2004. [Google Scholar]
- Lee, J.S.; Schuler, D.L.; Ainsworth, T.L. Polarimetric SAR data compensation for terrain azimuth slope variation. IEEE Trans. Geosci. Remote Sens. 2000, 38, 2153–2163. [Google Scholar]
- Schuler, D.L.; Lee, J.S.; Grandi, G.D. Measurement of topography using polarimetric SAR images. IEEE Trans. Geosci. Remote Sens. 1996, 34, 1266–1277. [Google Scholar] [CrossRef]
- Lee, J.S.; Schuler, D.L.; Ainsworth, T.L.; Krogager, E.; Kasilingam, D.; Boerner, W.M. On the estimation of radar polarization orientation shifts induced by terrain slopes. IEEE Trans. Geosci. Remote Sens. 2002, 40, 30–41. [Google Scholar]
- Yi, X.; Hoffmeyer, P.D.; Narayanan, R.M.; Curtis, J.O. Signal processing aspects of polarimetric random noise radar data for shallow subsurface imaging. In Proceedings of the International Geoscience & Remote Sensing Symposium, Lincoln, NE, USA, 31–31 May 1996. [Google Scholar]
- Cloude, S.R.; Pottier, E. A review of target decomposition theorems in radar polarimetry. IEEE Trans. Geosci. Remote Sens. 1996, 34, 498–518. [Google Scholar] [CrossRef]
- Cameron, W.L.; Leung, L.K. Feature motivated polarization scattering matrix decomposition. In Proceedings of the IEEE International Radar Conference, Arlington, VA, USA, 7–10 May 1990. [Google Scholar]
- Xu, F.; Jin, Y.Q. Deorientation theory of polarimetric scattering targets and application to terrain surface classification. IEEE Trans. Geosci. Remote Sens. 2005, 43, 2351–2364. [Google Scholar]
- Loew, A.; Mauser, W. Generation of geometrically and radiometrically terrain corrected SAR image products. Remote Sens. Environ. 2007, 106, 337–349. [Google Scholar] [CrossRef]
- Logan, T.A.; Nicoll, J.; Laurencelle, J.; Hogenson, K.; Gens, R.; Buechler, B.; Barton, B.; Shreve, W.; Stern, T.; Drew, L. Radiometrically Terrain Corrected ALOS PALSAR Data Available from the Alaska Satellite Facility. In Proceedings of the AGU Fall Meeting, San Francisco, CA, USA, 15–19 December 2014. [Google Scholar]

| Authors | Data | Area | Forest Type | Model | Saturation (m3/ha) | RMSE (m3/ha) | RRMSE (%) |
|---|---|---|---|---|---|---|---|
| Santoro (2002) [18] | C-band ERS-1/2 (coherence) | Sweden | Boreal coniferous, | Semi-Empirical Model | Max: 350 | Min:22 Max:152 | Not estimated |
| Santoro (2006) [14] | L-band JERS-1 (backscatter) | Sweden, Finland Siberia | Boreal coniferous, | Semi-Empirical Model | Min: 100 Max: 300 | Min: 36 Max: 152 | Min: 25% Max:68% |
| Pulliainen (2003) [35] | C band ERS-1/2 (coherence) | Finland | Norway spruce/Scots pine | Semi-Empirical Model | Not estimated | Not estimated | Max:48% |
| Askne (2005) [34] | C band ERS-1/2 (coherence) | Finland | boreal coniferous species | Semi-Empirical Model Interferometric HUT Model | Not estimated | Not estimated | Not estimated |
| Antropov (2013) [10] | ALOS PALSAR dual polarization (backscatter) | Finland | mixed forest. | Semi-Empirical Model | 150–200 | Min: 40 Max: 66 | Min: 42% Max:63% |
| Chowdhury (2013) [7] | ALOS PALSAR Quad polarization (backscatter) | Central Siberia | mixed forest. | Semi-Empirical Model | Min: 80 Max: 595 | Not estimated | Not estimated |
| Chowdhury (2014) [20] | ALOS PALSAR Quad polarization (coherence) | Central Siberia | mixed forest. | Semi-Empirical Model | 250 | Min: 33 Max: 42 | Not estimated |
| Age Group | Number of Plots | Average DBH of Plot (cm) | Average Height of Plot (m) | Average GSV (m3/ha) | Range of GSV (m3/ha) |
|---|---|---|---|---|---|
| Seedlings (DBH < 5 cm) | 1 | 4.01 | 3.23 | 0 | 0 |
| Young forest (DBH > 5 cm) | 4 | 8.72 | 6.15 | 98 | 55–126 |
| immature forest | 19 | 17.58 | 12.17 | 200 | 78–303 |
| Near Mature forest | 7 | 18.51 | 14.15 | 216 | 140–300 |
| Mature forest | 15 | 22.41 | 15.17 | 268 | 135–480 |
| Over mature forest | 4 | 23.73 | 18.64 | 291 | 259–321 |
| Variables | Data Acquired on 30 June | Data Acquired on 25 August | ||
|---|---|---|---|---|
| R | P-Value | R | P-Value | |
| Odd (dB) | −0.56 | 0.000 | −0.48 | 0.000 |
| Dbl (dB) | 0.70 | 0.000 | 0.53 | 0.000 |
| Vol (dB) | 0.44 | 0.002 | 0.21 | 0.154 |
| Odd (Ratio) | −0.57 | 0.000 | −0.42 | 0.000 |
| Dbl (Ratio) | 0.69 | 0.000 | 0.40 | 0.000 |
| Vol (Ratio) | 0.45 | 0.001 | 0.25 | 0.074 |
| Dbl/Odd | −0.57 | 0.000 | −0.48 | 0.001 |
| Vol/Odd | −0.63 | 0.000 | −0.53 | 0.000 |
| Dbl*Vol | −0.71 | 0.000 | −0.48 | 0.000 |
| Dbl*Vol/Odd | 0.62 | 0.000 | 0.50 | 0.000 |
| Image of 30 June 2016 | Image of 25 August 2016 | |||||
|---|---|---|---|---|---|---|
| Variable | βs | βn | k | βs | βn | k |
| Odd(dB) | −5.15 | −1.80 | 349.84 | −3.53 | −2.16 | 121.74 |
| Dbl(dB) | −3.01 | −6.88 | 188.13 | −4.24 | −6.37 | 62.38 |
| Odd(Ratio) | 0.31 | 0.67 | 268.95 | 0.45 | 0.63 | 113.69 |
| Dbl(Ratio) | 0.52 | 0.20 | 260.88 | 0.39 | 0.23 | 82.84 |
| Dbl/Odd | 2.01 | 5.95 | 179.22 | 2.60 | 4.63 | 193.71 |
| Vol/Odd | 0.64 | 3.66 | 140.05 | 1.17 | 2.59 | 89.80 |
| Dbl*Vol | 26.18 | 78.20 | 206.42 | 41.50 | 69.07 | 101.79 |
| Dbl*Vol/Odd | −5.93 | −41.30 | 141.05 | −10.07 | −28.83 | 130.81 |
| Variable | Image of 30 June 2016 | Image of 25 August 2016 | ||||||
|---|---|---|---|---|---|---|---|---|
| R2 | RMSE (m3/ha) | RRMSE (%) | Notes | R2 | RMSE (m3/ha) | RRMSE (%) | Notes | |
| Odd (dB) | 0.59 | 81.40 | 40.36 | * | 0.57 | 90.37 | 46.20 | * |
| Dbl (dB) | 0.64 | 69.19 | 33.94 | 0.51 | 80.03 | 39.17 | * | |
| Odd (Ratio) | 0.57 | 78.30 | 38.27 | * | 0.24 | 68.67 | 36.89 | ** |
| Dbl (Ratio) | 0.66 | 69.09 | 35.07 | 0.27 | 81.73 | 40.32 | ** | |
| Dbl/Odd | 0.62 | 75.62 | 31.13 | * | 0.39 | 125.70 | 56.60 | ** |
| Vol/Odd | 0.53 | 71.13 | 33.70 | * | 0.62 | 78.35 | 38.61 | * |
| Dbl*Vol | 0.66 | 71.65 | 31.80 | * | 0.47 | 76.27 | 37.30 | ** |
| Dbl*Vol/Odd | 0.59 | 71.04 | 35.14 | 0.52 | 74.06 | 41.67 | * | |
| Acquired Date | Number of Variables | Average of Errors (m3/ha) | Std of Errors (m3/ha) | RMSE (m3/ha) | RRMSE (%) |
|---|---|---|---|---|---|
| 30 June 2016 | 8 Variables | 67.42 | 31.01 | 74.06 | 35.09 |
| 6 Variables | 58.85 | 29.77 | 65.79 | 29.64 | |
| 4 Variables | 61.89 | 34.21 | 70.53 | 30.88 | |
| 25 August 2016 | 8 Variables | 58.67 | 35.80 | 78.49 | 36.23 |
| 6 Variables | 66.72 | 35.01 | 80.15 | 38.84 | |
| 4 Variables | 68.52 | 35.15 | 88.81 | 44.70 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Long, J.; Lin, H.; Wang, G.; Sun, H.; Yan, E. Mapping Growing Stem Volume of Chinese Fir Plantation Using a Saturation-based Multivariate Method and Quad-polarimetric SAR Images. Remote Sens. 2019, 11, 1872. https://doi.org/10.3390/rs11161872
Long J, Lin H, Wang G, Sun H, Yan E. Mapping Growing Stem Volume of Chinese Fir Plantation Using a Saturation-based Multivariate Method and Quad-polarimetric SAR Images. Remote Sensing. 2019; 11(16):1872. https://doi.org/10.3390/rs11161872
Chicago/Turabian StyleLong, Jiangping, Hui Lin, Guangxing Wang, Hua Sun, and Enping Yan. 2019. "Mapping Growing Stem Volume of Chinese Fir Plantation Using a Saturation-based Multivariate Method and Quad-polarimetric SAR Images" Remote Sensing 11, no. 16: 1872. https://doi.org/10.3390/rs11161872
APA StyleLong, J., Lin, H., Wang, G., Sun, H., & Yan, E. (2019). Mapping Growing Stem Volume of Chinese Fir Plantation Using a Saturation-based Multivariate Method and Quad-polarimetric SAR Images. Remote Sensing, 11(16), 1872. https://doi.org/10.3390/rs11161872








