Spatio–temporal Assessment of Drought in Ethiopia and the Impact of Recent Intense Droughts
Abstract
1. Introduction
2. Study Area and Data
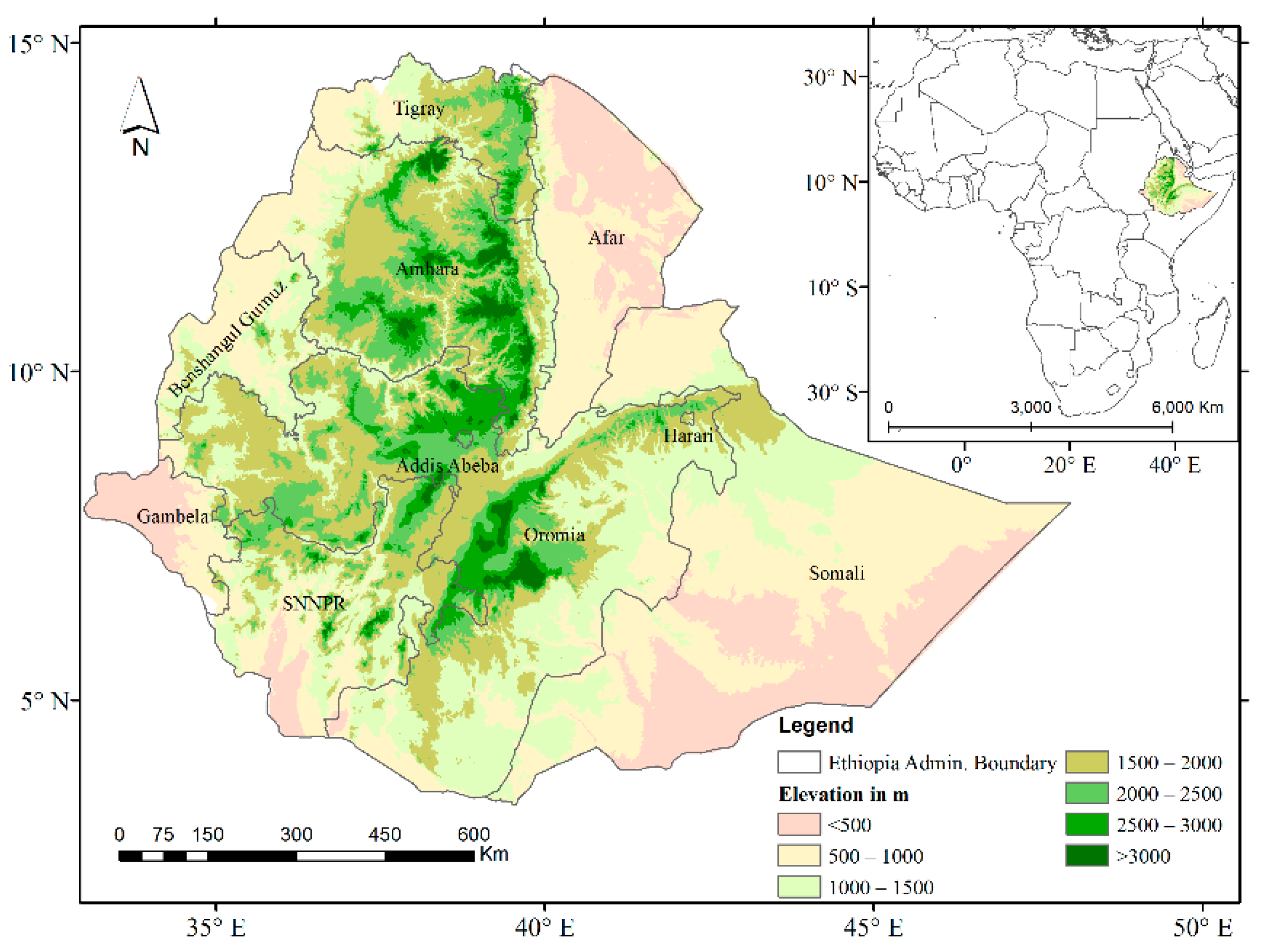
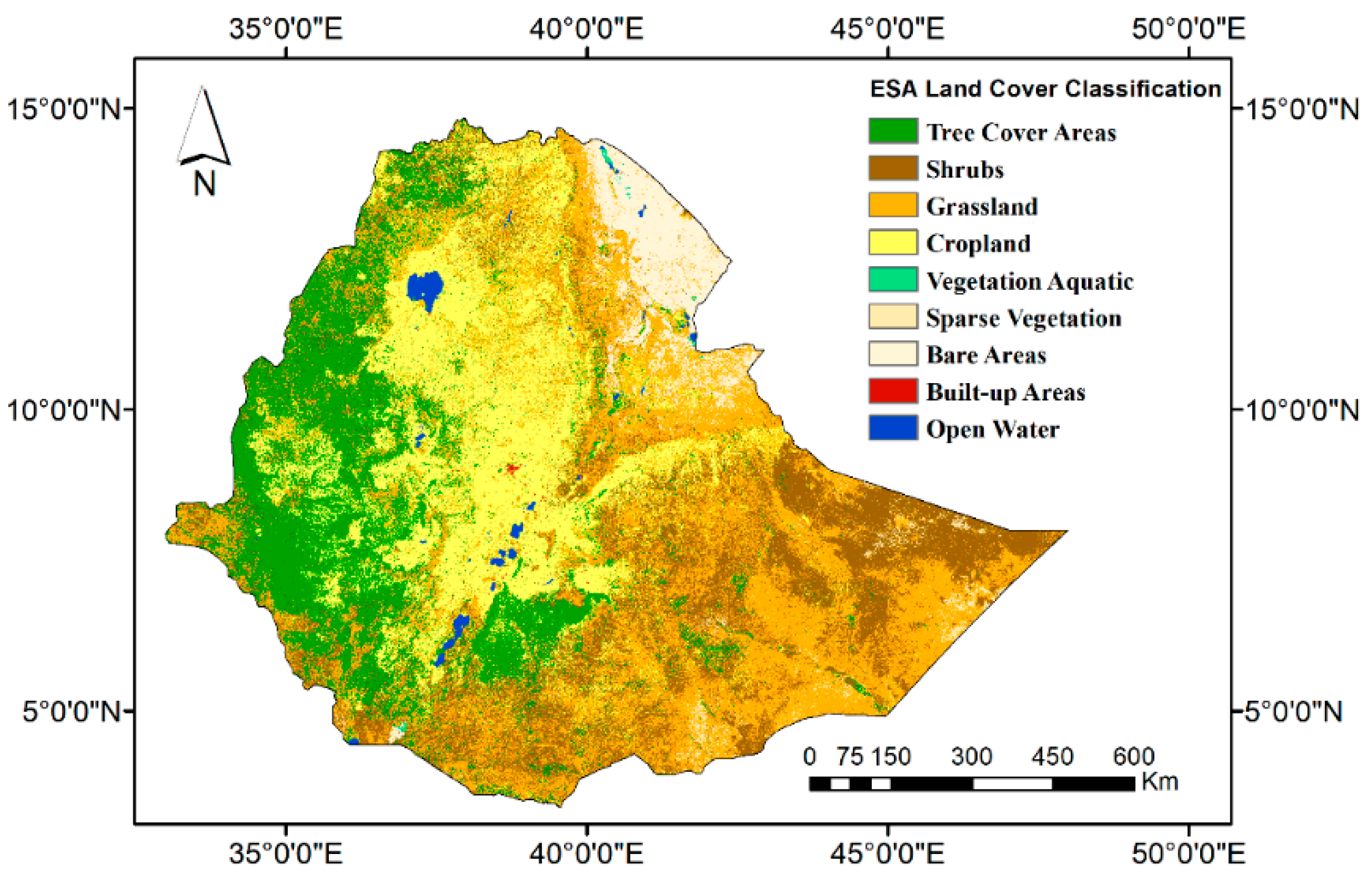
2.1. Study Area
2.2. Datasets
3. Methodology
3.1. Identification of Drought
3.2. Mann–Kendall Trend Analysis
3.3. Multiple Linear Regression
4. Results and Discussion
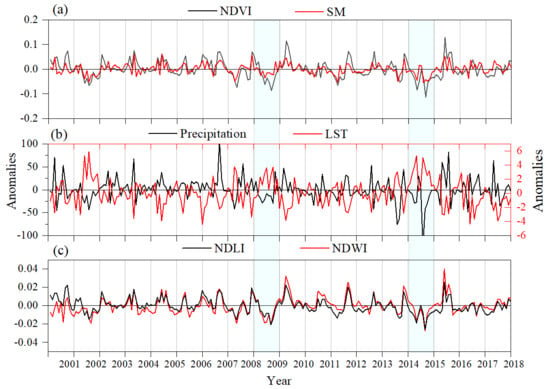
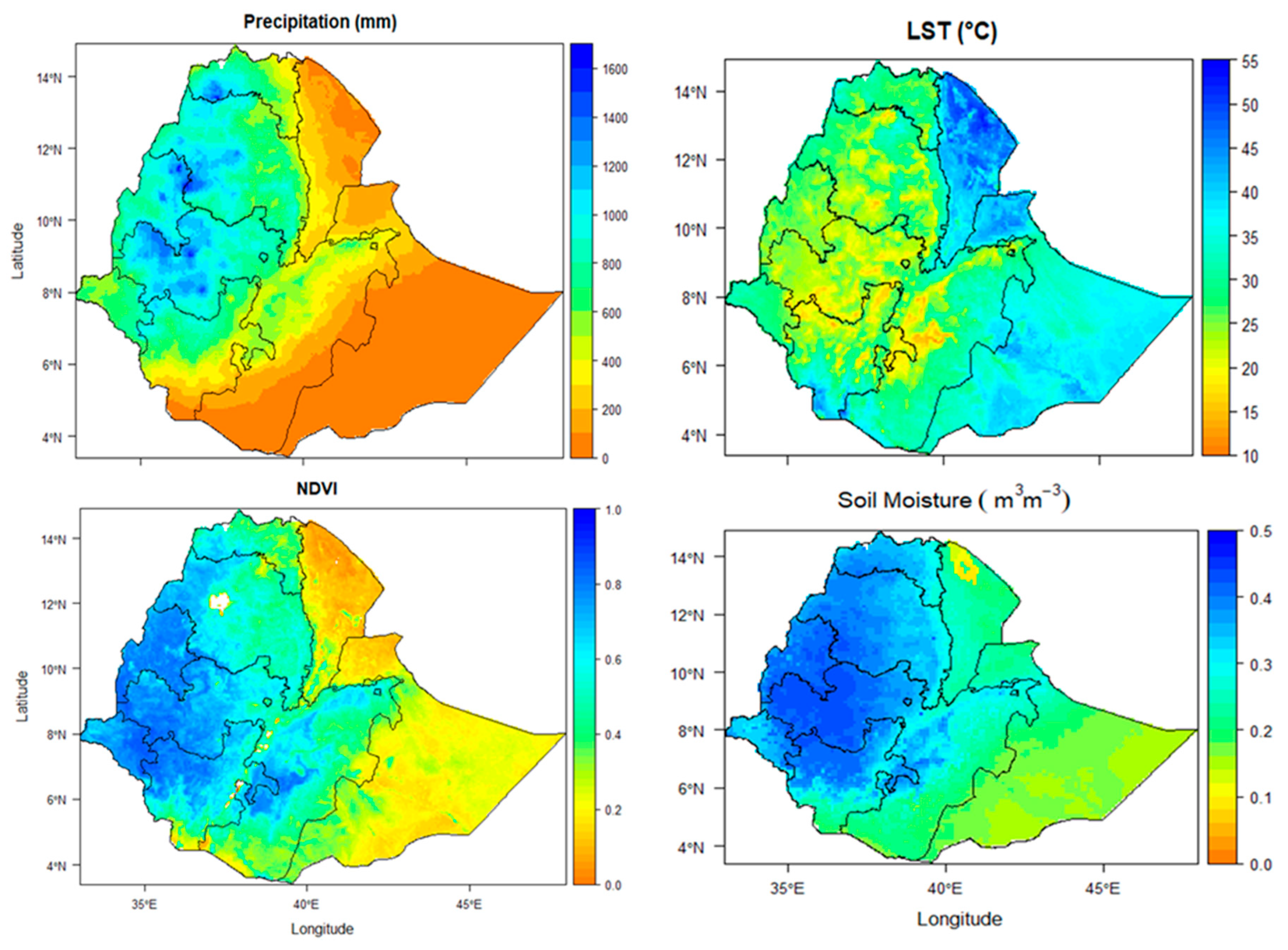
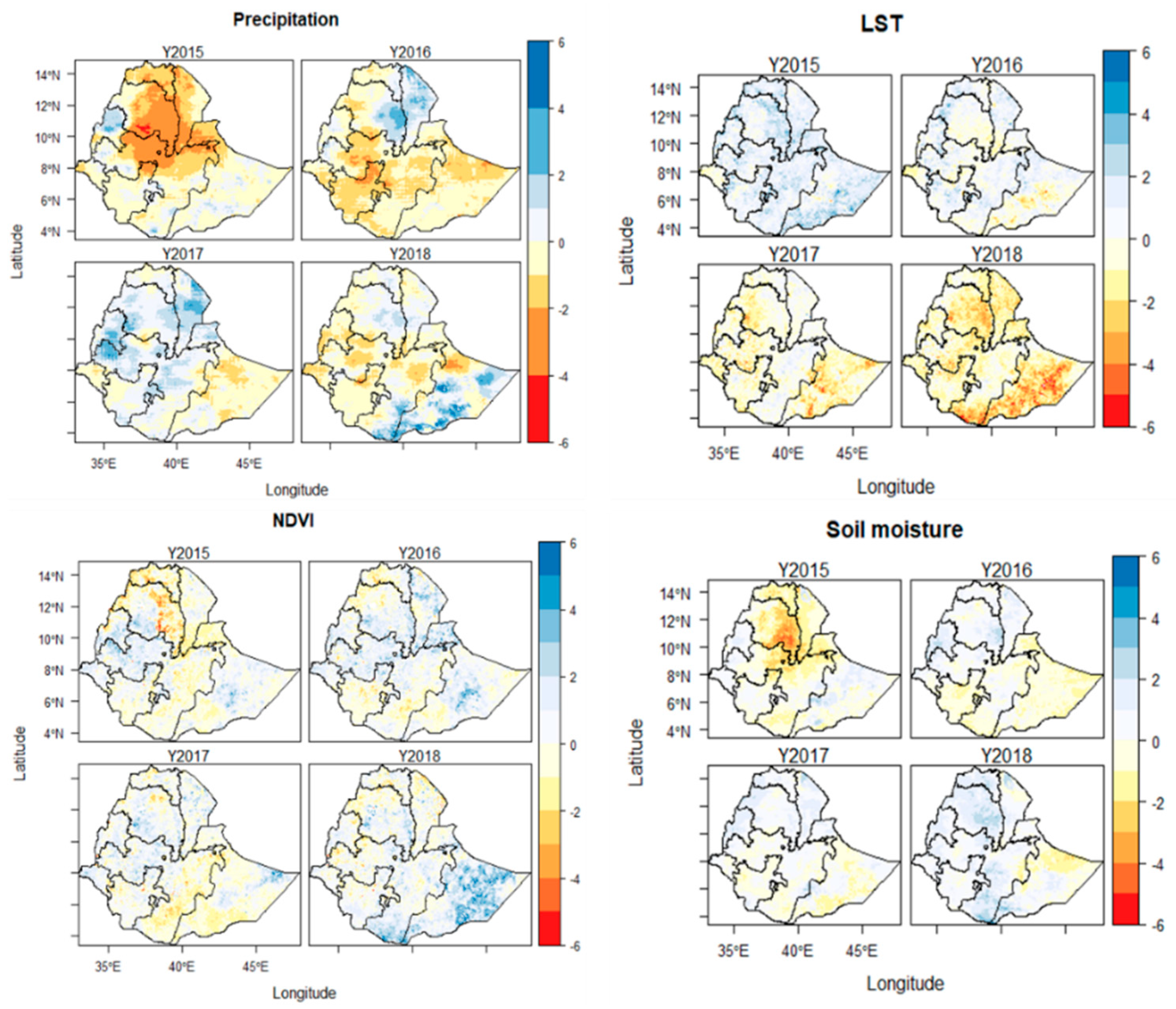
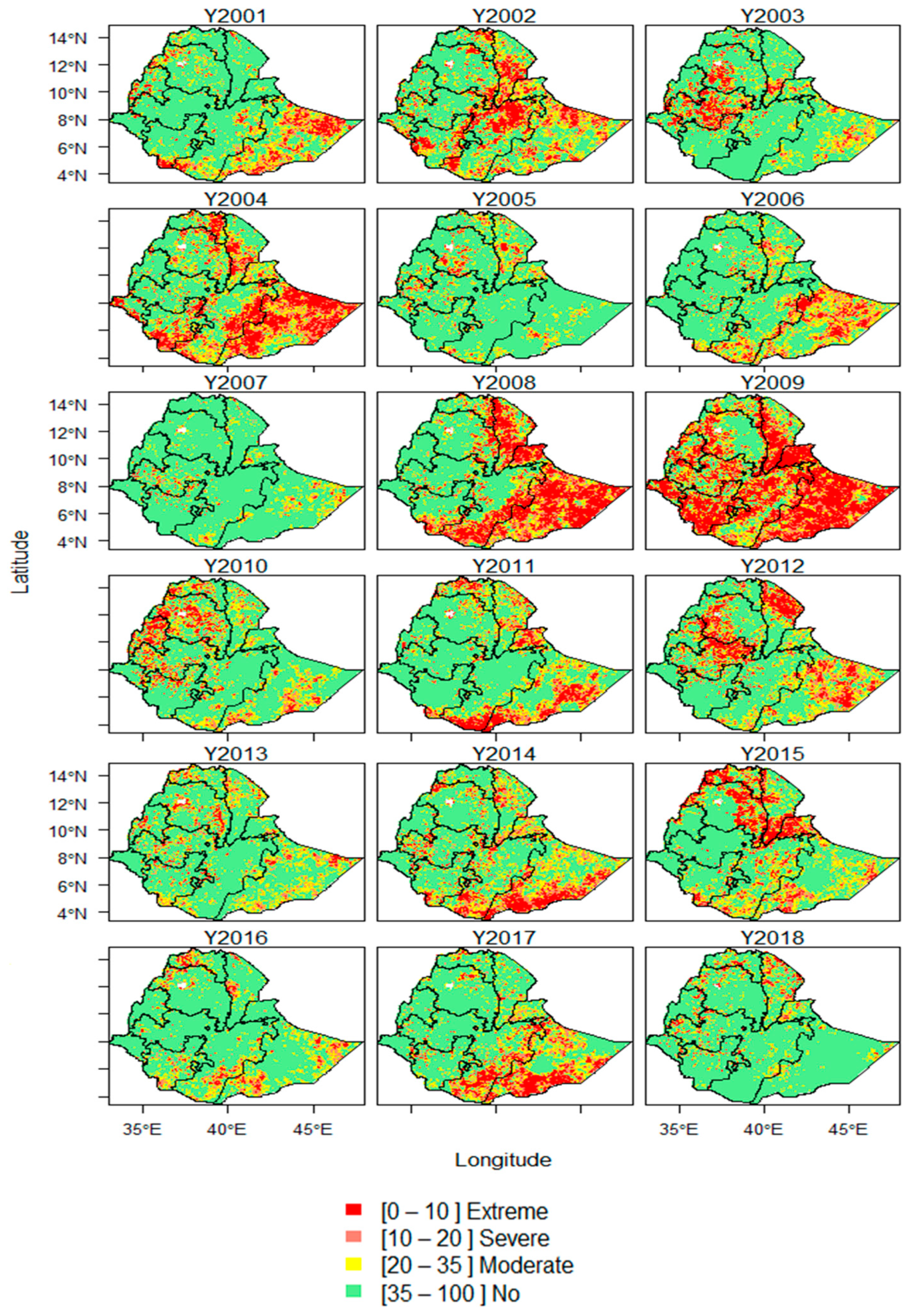
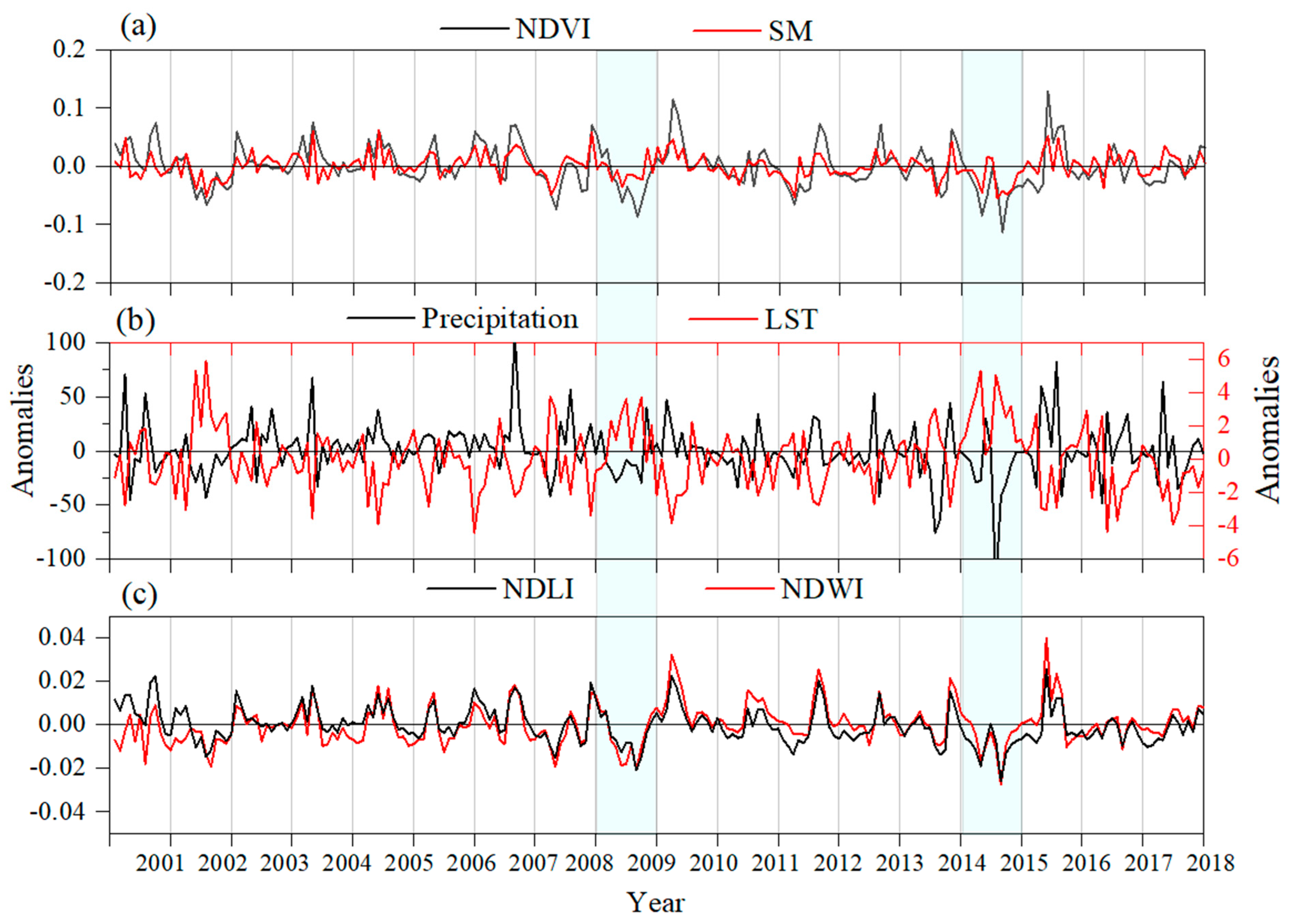
4.1. Drought Patterns Based on VCI
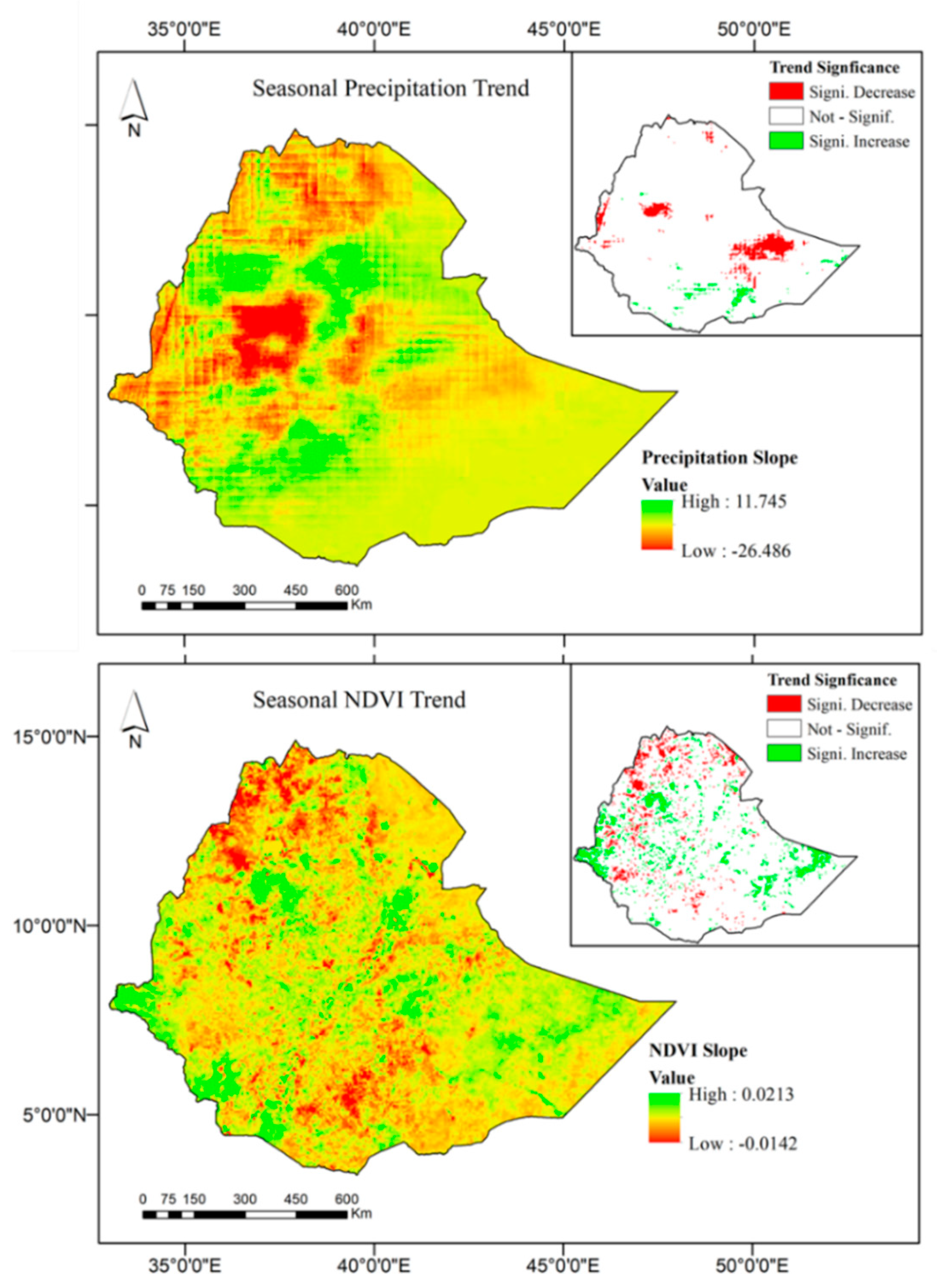
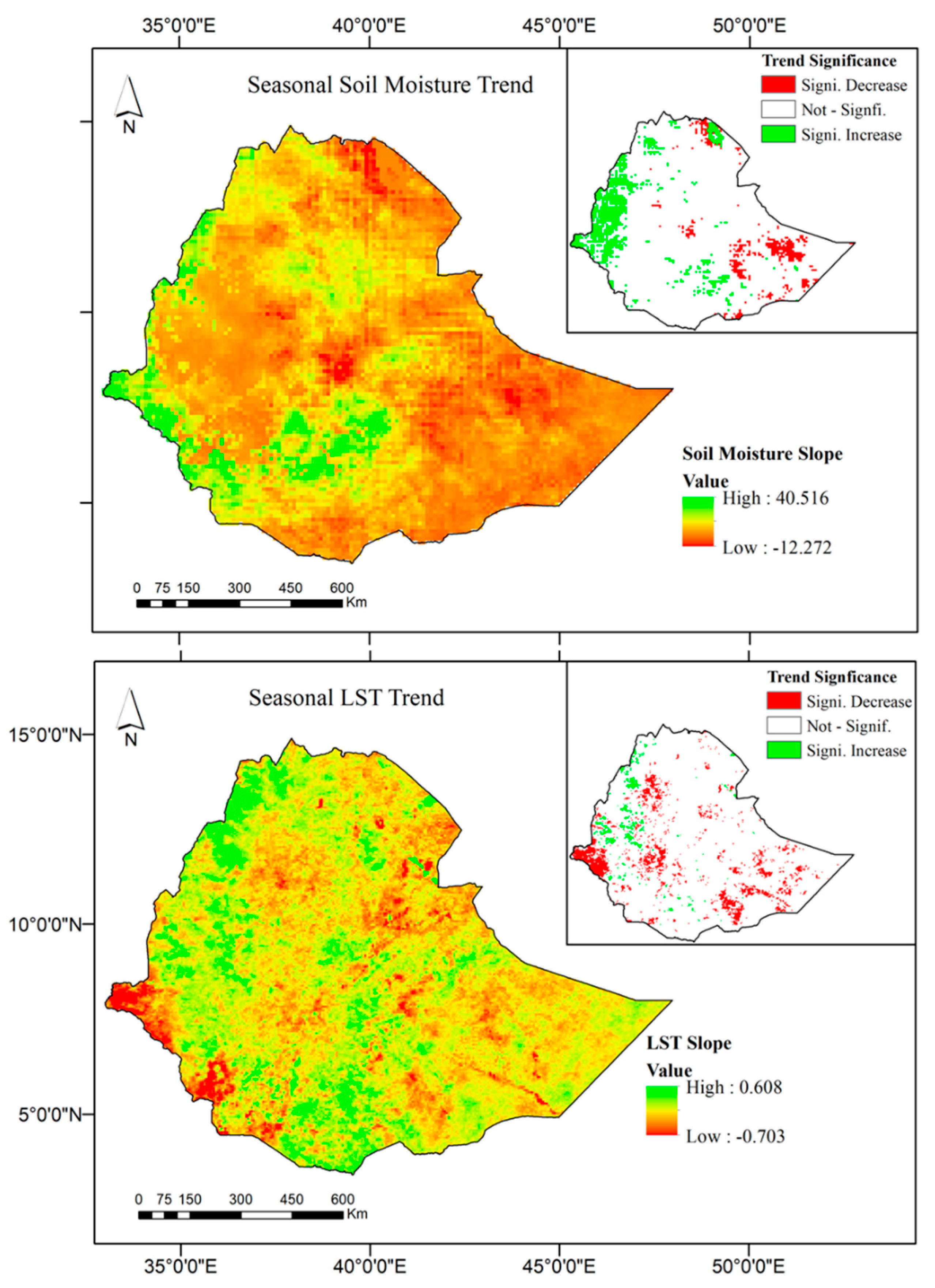
4.2. Spatial and Temporal Trends
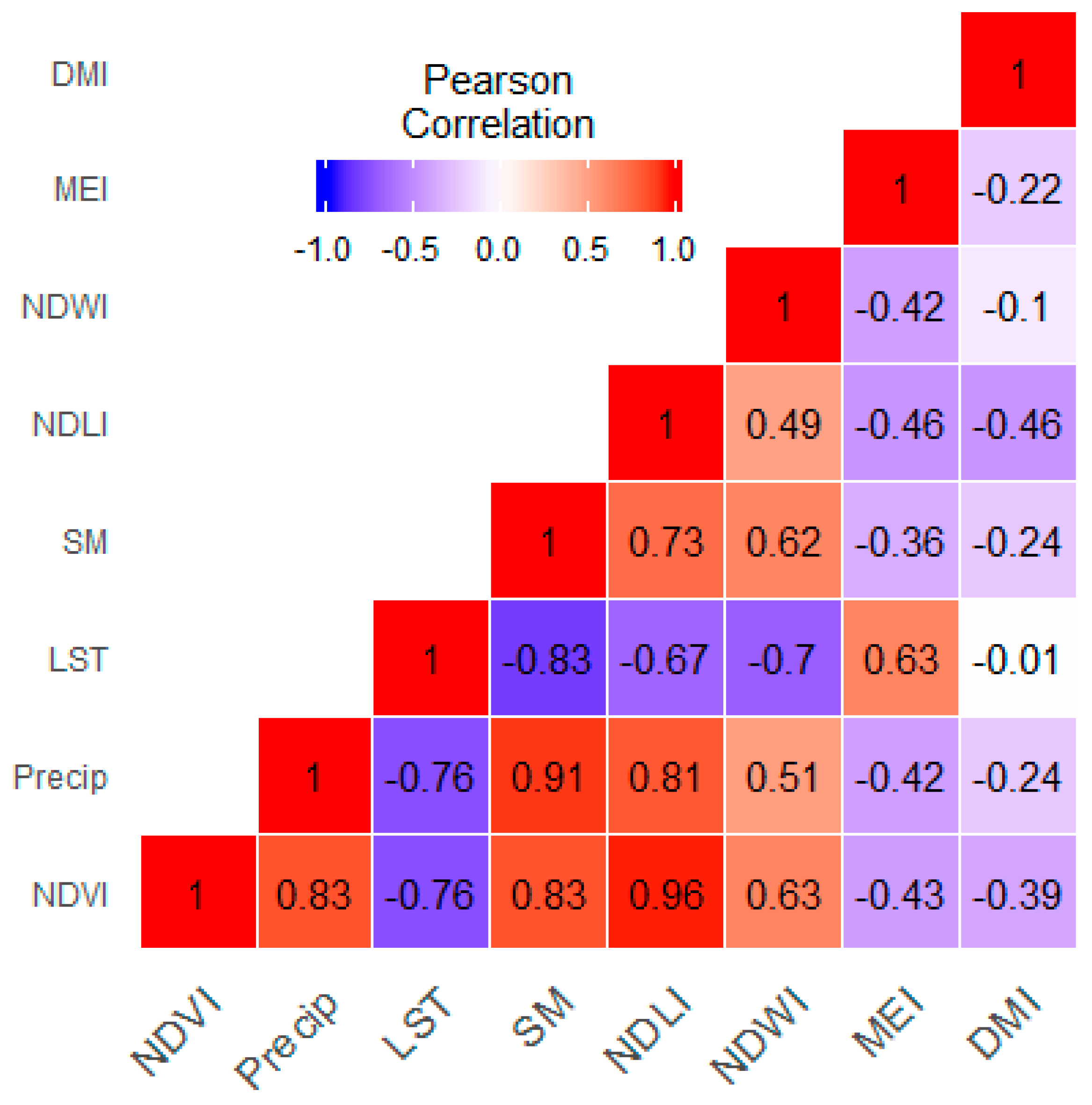
4.3. Multi Linear Regression and Correlation Statistics
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Singh, N.P.; Bantilan, C.; Byjesh, K. Vulnerability and policy relevance to drought in the semi-arid tropics of Asia—A retrospective analysis. Weather Clim. Extrem. 2014, 3, 54–61. [Google Scholar] [CrossRef]
- Nguyen, A.K.; Liou, Y.-A.; Li, M.-H.; Tran, T.A. Zoning eco-environmental vulnerability for environmental management and protection. Ecol. Indic. 2016, 69, 100–117. [Google Scholar] [CrossRef]
- Liou, Y.-A.; Nguyen, A.K.; Li, M.-H. Assessing spatiotemporal eco-environmental vulnerability by Landsat data. Ecol. Indic. 2017, 80, 52–65. [Google Scholar] [CrossRef]
- Nguyen, K.A.; Liou, Y.A. Global mapping of eco-environmental vulnerability from human and nature disturbances. Sci. Total Environ. 2019, 664, 995–1004. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, K.-A.; Liou, Y.-A. Mapping global eco-environment vulnerability due to human and nature disturbances. Methods X 2019, 6, 862–875. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, K.-A.; Liou, Y.-A.; Terry, J.P. Vulnerability of Vietnam to typhoons: A spatial assessment based on hazards, exposure and adaptive capacity. Sci. Total Environ. 2019, 682, 31–46. [Google Scholar] [CrossRef] [PubMed]
- Sitorus, E.; Nguyen, K.A.; Liou, Y.A. Forest fire impact on and vulnerability assessment of eco-environment in tropical rainforest: A case study of leuser ecosystem-Aceh, Indonesia. In AGU Fall Meeting Abstracts; 2018; Available online: http://adsabs.harvard.edu/abs/2018AGUFMGH23B1095S (accessed on 12 April 2019).
- Cheng, C.-H.; Nnadi, F.; Liou, Y.-A. Energy budget on various land use areas using reanalysis data in Florida. Adv. Meteorol. 2014, 2014, 1–13. [Google Scholar] [CrossRef]
- Hayes, M.; Svoboda, M.D.; Wardlow, B.D.; Anderson, M.; Kogan, F. Drought monitoring:Historical and current perspectives. In Remote Sensing of Drought: Innovative Monitoring Approaches; CRC Press: Boca Raton, FL, USA, 2012; pp. 1–19. [Google Scholar]
- Kuri, F.; Murwira, A.; Murwira, K.S.; Masocha, M. Predicting maize yield in Zimbabwe using dry dekads derived from remotely sensed Vegetation Condition Index. Int. J. Appl. Earth Obs. Geoinf. 2014, 33, 39–46. [Google Scholar] [CrossRef]
- Jiao, W.; Zhang, L.; Chang, Q.; Fu, D.; Cen, Y.; Tong, Q. Evaluating an enhanced vegetation condition index (VCI) based on VIUPD for drought monitoring in the continental United States. Remote Sens. 2016, 8, 224. [Google Scholar] [CrossRef]
- Townshend, J.R.G.; Justice, C.O. Analysis of the dynamics of African vegetation using the normalized difference vegetation index. Int. J. Remote Sens. 1986, 7, 1435–1445. [Google Scholar] [CrossRef]
- Kogan, F.N. Droughts of the late 1980s in the United States as derived from NOAA polar-orbiting satellite data. Bull. Am. Meteorol. Soc. 1995, 76, 655–668. [Google Scholar] [CrossRef]
- Dorjsuren, M.; Liou, Y.-A.; Cheng, C.-H. Time series MODIS and in situ data analysis for Mongolia drought. Remote Sens. 2016, 8, 509. [Google Scholar] [CrossRef]
- Tadesse, T.; Demisse, G.B.; Zaitchik, B.; Dinku, T. Satellite-based hybrid drought monitoring tool for prediction of vegetation condition in Eastern Africa: A case study for Ethiopia. Water Resour. Res. 2014, 50, 2176–2190. [Google Scholar] [CrossRef]
- Mckee, T.B.; Doesken, N.J.; Kleist, J. The relationship of drought frequency and duration to time scales. In Proceedings of the 8th Conference on Applied Climatology, Anaheim, CA, USA, 17–22 January 1993; American Meteorological Society: Boston, MA, USA, 1993; pp. 179–184. [Google Scholar]
- Rouse, J., Jr.; Haas, R.H.; Schell, J.A.; Deering, D.W. Monitoring vegetation systems in the Great Plains with ERTS, Third ERTS Symposium. NASA 1973, 1, 309–317. [Google Scholar]
- Gebrehiwot, T.; Van der Veen, A.; Maathuis, B. Governing agricultural drought: Monitoring using the vegetation condition index. Ethiop. J. Environ. Stud. Manag. 2016, 9, 354. [Google Scholar] [CrossRef]
- Cheng, C.-H.; Nnadi, F.; Liou, Y.-A. A Regional Land Use Drought Index for Florida. Remote Sens. 2015, 7, 17149–17167. [Google Scholar] [CrossRef]
- Wu, D.; Qu, J.J.; Hao, X. Agricultural drought monitoring using MODIS-based drought indices over the USA Corn Belt. Int. J. Remote Sens. 2015, 36, 5403–5425. [Google Scholar] [CrossRef]
- Liu, K.; Su, H.; Tian, J.; Li, X.; Wang, W.; Yang, L.; Liang, H. Assessing a scheme of spatial-temporal thermal remote-sensing sharpening for estimating regional evapotranspiration. Int. J. Remote Sens. 2018, 39, 3111–3137. [Google Scholar] [CrossRef]
- Wan, Z.; Wang, P.; Li, X. Using MODIS Land Surface Temperature and Normalized Difference Vegetation Index products for monitoring drought in the southern Great Plains, USA. Int. J. Remote Sens. 2004, 25, 61–72. [Google Scholar] [CrossRef]
- Du, L.; Tian, Q.; Yu, T.; Meng, Q.; Jancso, T.; Udvardy, P.; Huang, Y. A comprehensive drought monitoring method integrating MODIS and TRMM data. Int. J. Appl. Earth Obs. Geoinf. 2013, 23, 245–253. [Google Scholar] [CrossRef]
- Mutowo, G.; Chikodzi, D. Remote sensing based drought monitoring in Zimbabwe. Disaster Prev. Manag. An Int. J. 2014, 23, 649–659. [Google Scholar] [CrossRef]
- Rojas, O.; Vrieling, A.; Rembold, F. Assessing drought probability for agricultural areas in Africa with coarse resolution remote sensing imagery. Remote Sens. Environ. 2011, 115, 343–352. [Google Scholar] [CrossRef]
- Anderson, W.B.; Zaitchik, B.F.; Hain, C.R.; Anderson, M.C.; Yilmaz, M.T.; Mecikalski, J.; Schultz, L. Towards an integrated soil moisture drought monitor for East Africa. Hydrol. Earth Syst. Sci. 2012, 16, 2893–2913. [Google Scholar] [CrossRef]
- Masih, I.; Maskey, S.; Mussá, F.E.F.; Trambauer, P. A review of droughts on the African continent: A geospatial and long-term perspective. Hydrol. Earth Syst. Sci. 2014, 18, 3635–3649. [Google Scholar] [CrossRef]
- Yang, S.; Meng, D.; Gong, H.; Li, X.; Wu, X. Soil drought and vegetation response during 2001–2015 in North China based on GLDAS and MODIS data. Adv. Meteorol. 2018, 2018, 1–14. [Google Scholar] [CrossRef]
- Tsegay Wolde-Georgis. El Niño and Drought Early Warning in Ethiopia. Internet J. Afr. Stud. 1997. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=1589710 (accessed on 16 March 2019).
- Edossa, D.C.; Babel, M.S.; Das Gupta, A. Drought analysis in the Awash River Basin, Ethiopia. Water Resour. Manag. 2010, 24, 1441–1460. [Google Scholar] [CrossRef]
- Kumar, B.G. Ethiopian famines 1973–1985: A case-study. Polit. Econ. Hunger 1990, 2, 173–216. [Google Scholar]
- Gore, T.; Hillier, D. Climate Change and Future Impacts on Food Security. Oxfam Policy Pract. Agric. Food L. 2011, 11, 57–62. [Google Scholar]
- Ayalew, D.; Tesfaye, K.; Mamo, G.; Yitaferu, B.; Bayu, W. Variability of rainfall and its current trend in Amhara region, Ethiopia. Afr. J. Agric. Res. 2012, 7, 1475–1486. [Google Scholar]
- Schmidt, W.; Peter Uhe, A.; Kimutai, J.; Otto, F.; Cullen, H. Climate and Development Knowledge Network and World Weather Attribution Initiative Raising Risk Awareness; Royal Netherlands Meteorological Institute: De Bilt, The Netherlands, 2017; pp. 2016–2017. [Google Scholar]
- Funk, C.; Peterson, P.; Landsfeld, M.; Pedreros, D.; Verdin, J.; Shukla, S.; Husak, G.; Rowland, J.; Harrison, L.; Hoell, A. The climate hazards infrared precipitation with stations—A new environmental record for monitoring extremes. Sci. Data 2015, 2, 150066. [Google Scholar] [CrossRef] [PubMed]
- Philip, S.; Kew, S.F.; Jan van Oldenborgh, G.; Otto, F.; O’Keefe, S.; Haustein, K.; King, A.; Zegeye, A.; Eshetu, Z.; Hailemariam, K.; et al. Attribution Analysis of the Ethiopian Drought of 2015. J. Clim. 2018, 31, 2465–2486. [Google Scholar] [CrossRef]
- USAID. El niño in Ethiopia, A Real-Time Review of Impacts and Responses2015-2016; USAID: Washington, DC, USA, 2016. Available online: https://www.agri-learning-ethiopia.org/wp-content/uploads/2016/06/AKLDP-El-Nino-Review-March-2016 (accessed on 28 May 2019).
- Camberlin, P. Rainfall anomalies in the source region of the Nile and their connection with the Indian summer monsoon. J. Clim. 1997, 10, 1380–1392. [Google Scholar] [CrossRef]
- Korecha, D.; Sorteberg, A. Validation of operational seasonal rainfall forecast in Ethiopia. Water Resour. Res. 2013, 49, 7681–7697. [Google Scholar] [CrossRef]
- Liou, Y.-A.; Le, M.S.; Chien, H. Normalized difference latent heat index for remote sensing of land surface energy fluxes. IEEE Trans. Geosci. Remote Sens. 2019, 57, 1423–1433. [Google Scholar] [CrossRef]
- Worqlul, A.W.; Jeong, J.; Dile, Y.T.; Osorio, J.; Schmitter, P.; Gerik, T.; Srinivasan, R.; Clark, N. Assessing potential land suitable for surface irrigation using groundwater in Ethiopia. Appl. Geogr. 2017, 85, 1–13. [Google Scholar] [CrossRef]
- Viste, E.; Korecha, D.; Sorteberg, A. Recent drought and precipitation tendencies in Ethiopia. Theor. Appl. Climatol. 2013, 112, 535–551. [Google Scholar] [CrossRef]
- Terefe, T.; Mengistu, G. Spatial and temporal variability of summer rainfall over Ethiopia from observations and a regional climate model experiment climate model experiments. Theor. Appl. Climatol. 2012, 111, 665–681. [Google Scholar]
- Seleshi, Y.; Camberlin, P. Recent changes in dry spell and extreme rainfall events in Ethiopia. Theor. Appl. Climatol. 2006, 83, 181–191. [Google Scholar] [CrossRef]
- Liebmann, B.; Hoerling, M.P.; Funk, C.; Bladé, I.; Dole, R.M.; Allured, D.; Quan, X.; Pegion, P.; Eischeid, J.K. Understanding recent eastern horn of africa rainfall variability and change. J. Clim. 2014, 27, 8630–8645. [Google Scholar] [CrossRef]
- Gebrehiwot, T.; van der Veen, A.; Maathuis, B. Spatial and temporal assessment of drought in the Northern highlands of Ethiopia. Int. J. Appl. Earth Obs. Geoinf. 2011, 13, 309–321. [Google Scholar] [CrossRef]
- Birhane, E.; Ashfare, H.; Fenta, A.A.; Hishe, H.; Gebremedhin, M.A.; Solomon, N. Land use land cover changes along topographic gradients in Hugumburda national forest priority area, Northern Ethiopia. Remote Sens. Appl. Soc. Environ. 2019, 13, 61–68. [Google Scholar] [CrossRef]
- Larbi, I.; Hountondji, F.; Annor, T.; Agyare, W.; Mwangi Gathenya, J.; Amuzu, J.; Larbi, I.; Hountondji, F.C.C.; Annor, T.; Agyare, W.A.; et al. Spatio-temporal trend analysis of rainfall and temperature extremes in the Vea Catchment, Ghana. Climate 2018, 6, 87. [Google Scholar] [CrossRef]
- Muthoni, F.K.; Odongo, V.O.; Ochieng, J.; Mugalavai, E.M.; Mourice, S.K.; Hoesche-Zeledon, I.; Mwila, M.; Bekunda, M. Long-term spatial-temporal trends and variability of rainfall over Eastern and Southern Africa. Theor. Appl. Climatol. 2019, 137, 1869–1882. [Google Scholar] [CrossRef]
- McNally, A.; Arsenault, K.; Kumar, S.; Shukla, S.; Peterson, P.; Wang, S.; Funk, C.; Peters-Lidard, C.D.; Verdin, J.P. A land data assimilation system for sub-Saharan Africa food and water security applications. Sci. Data 2017, 4, 170012. [Google Scholar] [CrossRef]
- Saji, N.H.; Goswami, B.N.; Vinayachandran, P.N.; Yamagata, T. A dipole mode in the tropical Indian Ocean. Nature 1999, 401, 360–363. [Google Scholar] [CrossRef]
- LIU, W.T.; KOGAN, F.N. Monitoring regional drought using the Vegetation Condition Index. Int. J. Remote Sens. 1996, 17, 2761–2782. [Google Scholar] [CrossRef]
- Winkler, L.; Gessner, U.; Hochschild, V. Identifying droughts affecting agrictlture in Africa based on remote sensing time series between 2000-2016: Rainfall anomalies and vegetation condition in the context of ENSO. Remote Sens. 2017, 9, 831. [Google Scholar] [CrossRef]
- Measho, S.; Chen, B.; Trisurat, Y.; Pellikka, P.; Guo, L.; Arunyawat, S.; Tuankrua, V.; Ogbazghi, W.; Yemane, T. Spatio-temporal analysis of vegetation dynamics as a response to climate variability and drought patterns in the Semiarid Region, Eritrea. Remote Sens. 2019, 11, 724. [Google Scholar] [CrossRef]
- Baniya, B.; Tang, Q.; Xu, X.; Haile, G.G.; Chhipi-Shrestha, G. Spatial and temporal variation of drought based on satellite derived vegetation condition index in Nepal from 1982. Sensors 2019, 19, 430. [Google Scholar] [CrossRef]
- De Jong, R.; de Bruin, S.; de Wit, A.; Schaepman, M.E.; Dent, D.L. Analysis of monotonic greening and browning trends from global NDVI time-series. Remote Sens. Environ. 2011, 115, 692–702. [Google Scholar] [CrossRef]
- Sobrino, J.A.; Julien, Y. Global trends in NDVI-derived parameters obtained from GIMMS data. Int. J. Remote Sens. 2011, 32, 4267–4279. [Google Scholar] [CrossRef]
- Julien, Y.; Sobrino, J.A.; Mattar, C.; Ruescas, A.B.; Jiménez-Muñoz, J.C.; Sòria, G.; Hidalgo, V.; Atitar, M.; Franch, B.; Cuenca, J. Temporal analysis of normalized difference vegetation index (NDVI) and land surface temperature (LST) parameters to detect changes in the Iberian land cover between 1981 and 2001. Int. J. Remote Sens. 2011, 32, 2057–2068. [Google Scholar] [CrossRef]
- Sen, P.K. Estimates of the regression coefficient based on Kendall’s Tau. J. Am. Stat. Assoc. 1968, 63, 1379–1389. [Google Scholar] [CrossRef]
- Tian, F.; Wang, Y.; Fensholt, R.; Wang, K.; Zhang, L.; Huang, Y. Remote sensing mapping and evaluation of NDVI trends from synthetic time series obtained by blending landsat and MODIS data around a coalfield on the Loess Plateau. Remote Sens. 2000, 5, 4255–4279. [Google Scholar] [CrossRef]
- Ravindrababu, S.; Ratnam, M.; Basha, G.; Liou, Y.-A.; Reddy, N. Large anomalies in the tropical upper troposphere lower stratosphere (UTLS) trace gases observed during the Extreme 2015–2016 El Niño Event by using satellite measurements. Remote Sens. 2019, 11, 687. [Google Scholar] [CrossRef]
- Anyamba, A.; Glennie, E.; Small, J.; Anyamba, A.; Glennie, E.; Small, J. Teleconnections and Interannual Transitions as Observed in African Vegetation: 2015. Remote Sens. 2018, 10, 1038. [Google Scholar] [CrossRef]
- Cochrane, L.; Bekele, Y.W. Average crop yield (2001–2017) in Ethiopia: Trends at national, regional and zonal levels. Data Br. 2018, 16, 1025–1033. [Google Scholar] [CrossRef]
- Korecha, D.; Barnston, A.G.; Korecha, D.; Barnston, A.G. Predictability of June–September rainfall in Ethiopia. Mon. Weather Rev. 2007, 135, 628–650. [Google Scholar] [CrossRef]
- Workie, T.G.; Debella, H.J. Climate change and its effects on vegetation phenology across ecoregions of Ethiopia. Glob. Ecol. Conserv. 2018, 13, e00366. [Google Scholar] [CrossRef]
- Yan, D.; Xu, T.; Girma, A.; Yuan, Z.; Weng, B.; Qin, T.; Do, P.; Yuan, Y.; Yan, D.; Xu, T.; et al. Regional Correlation between precipitation and vegetation in the Huang-Huai-Hai River Basin, China. Water 2017, 9, 557. [Google Scholar] [CrossRef]
- Zhao, W.; Zhao, X.; Zhou, T.; Wu, D.; Tang, B.; Wei, H. Climatic factors driving vegetation declines in the 2005 and 2010 Amazon droughts. PLoS ONE 2017, 12, e0175379. [Google Scholar] [CrossRef]
- Degefu, M.A.; Rowell, D.P.; Bewket, W. Teleconnections between Ethiopian rainfall variability and global SSTs: Observations and methods for model evaluation. Meteorol. Atmos. Phys. 2017, 129, 173–186. [Google Scholar] [CrossRef]
- Greenland, S.; Senn, S.J.; Rothman, K.J.; Carlin, J.B.; Poole, C.; Goodman, S.N.; Altman, D.G. Statistical tests, P values, confidence intervals, and power: A guide to misinterpretations. Eur. J. Epidemiol. 2016, 31, 337–350. [Google Scholar] [CrossRef]
- Wu, D.; Zhao, X.; Liang, S.; Zhou, T.; Huang, K.; Tang, B.; Zhao, W. Time-lag effects of global vegetation responses to climate change. Glob. Chang. Biol. 2015, 21, 3520–3531. [Google Scholar] [CrossRef]
| Data | Source | Characteristics |
|---|---|---|
| Precipitation | CHIRPS | Monthly precipitation at 0.05 × 0.05 from Jan. 2001 to Dec. 2018 |
| NDVI | MODIS | Monthly NDVI at 250 m from Jan. 2001 to Dec. 2018 |
| LST | MODIS | Monthly LST at 1 km from Jan. 2001 to Dec. 2018 |
| NDWI | MODIS | Estimated from surface reflectance at 500 m from Jan. 2001 to Dec. 2018 |
| NDLI | MODIS | Estimated from surface reflectance at 500 m from Jan. 2001 to Dec. 2018 |
| Soil Moisture | FLDAS Noah | Monthly soil moisture (0–10cm) at 0.10 × 0.10 from Jan. 2001 to Dec. 2018 |
| MEI | NOAA | Monthly MEI time series from Jan. 2001 to Dec. 2018 |
| DMI | JAMSTEC | Monthly DMI time series from Jan. 2001 to Dec. 2018 |
| VCI Percentage | Drought Severity Level |
|---|---|
| >35 | No drought |
| 20–35 | Moderate drought |
| 10–20 | Severe drought |
| <10 | Extreme drought |
| Variable | Estimate | Std. Error | t-Value | p-Value | Sig | VIF |
|---|---|---|---|---|---|---|
| Precip. | −2.215 × 10−5 | 3.788 × 10−5 | −0.585 | 0.5594 | 2.387 | |
| LST | 4.577 × 10−4 | 6.140 × 10−4 | 0.745 | 0.456 | 3.433 | |
| SM | 5.505 × 10−2 | 6.104 × 10−2 | 0.902 | 0.368 | 4.622 | |
| NDLI | 3.697 | 1.363 × 10−1 | 27.125 | <2.00 × 10−16 | *** | 3.407 |
| NDWI | 0.528 | 1.097 × 10−1 | 4.813 | 2.86 × 10−6 | *** | 2.804 |
| MEI | −1.470 × 10−3 | 7.704 × 10−4 | −1.909 | 0.0576 | . | 1.089 |
| DMI | −4.552 × 10−4 | 5.439 × 10−3 | −0.187 | 0.852 | 1.099 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liou, Y.-A.; Mulualem, G.M. Spatio–temporal Assessment of Drought in Ethiopia and the Impact of Recent Intense Droughts. Remote Sens. 2019, 11, 1828. https://doi.org/10.3390/rs11151828
Liou Y-A, Mulualem GM. Spatio–temporal Assessment of Drought in Ethiopia and the Impact of Recent Intense Droughts. Remote Sensing. 2019; 11(15):1828. https://doi.org/10.3390/rs11151828
Chicago/Turabian StyleLiou, Yuei-An, and Getachew Mehabie Mulualem. 2019. "Spatio–temporal Assessment of Drought in Ethiopia and the Impact of Recent Intense Droughts" Remote Sensing 11, no. 15: 1828. https://doi.org/10.3390/rs11151828
APA StyleLiou, Y.-A., & Mulualem, G. M. (2019). Spatio–temporal Assessment of Drought in Ethiopia and the Impact of Recent Intense Droughts. Remote Sensing, 11(15), 1828. https://doi.org/10.3390/rs11151828