Ocean Optical Profiling in South China Sea Using Airborne LiDAR
Abstract
1. Introduction
2. Materials and Methods
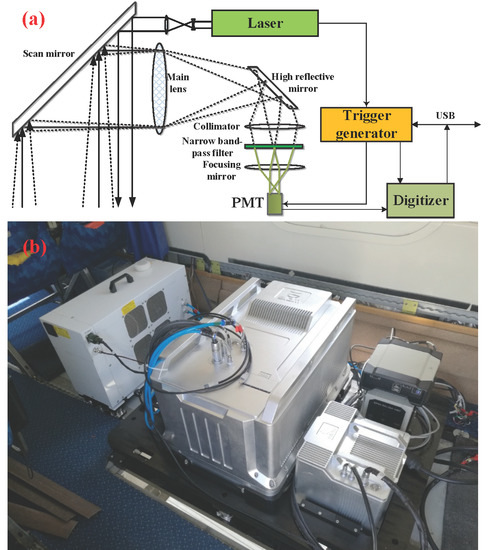
2.1. LiDAR System Design
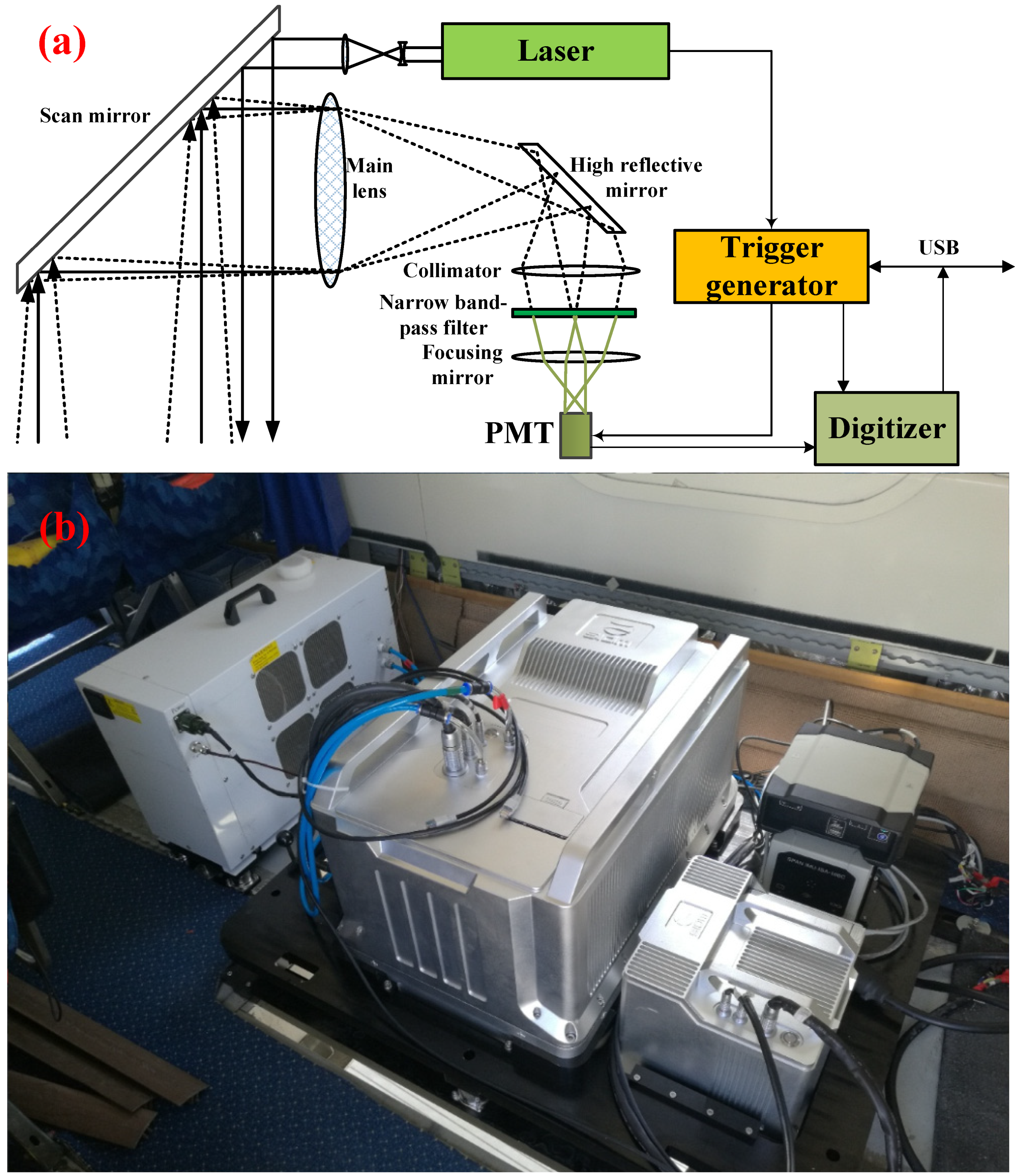
2.2. LiDAR Flight Experiments
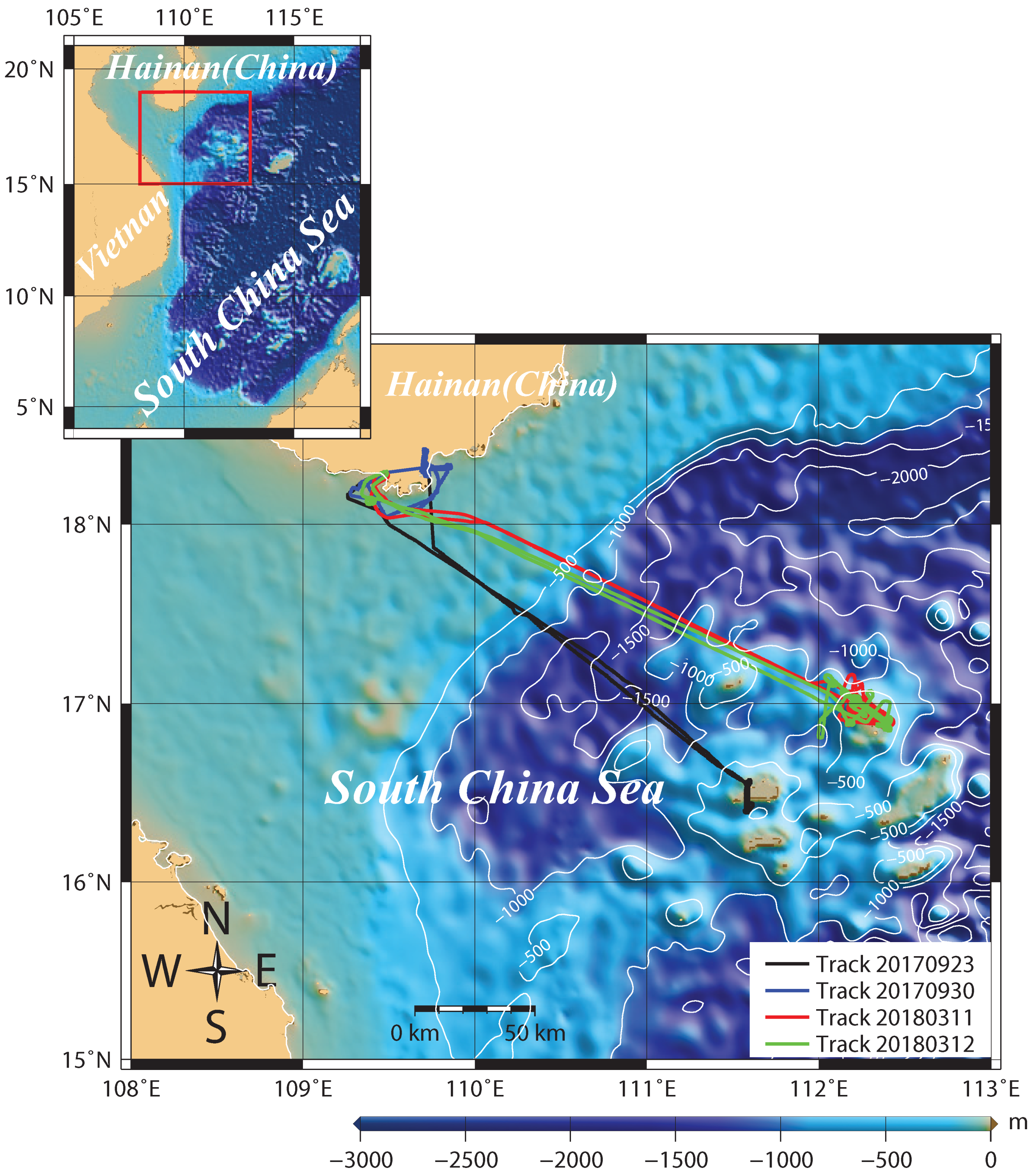
2.3. LiDAR Inversion Method
2.4. Evaluation Method
3. Results
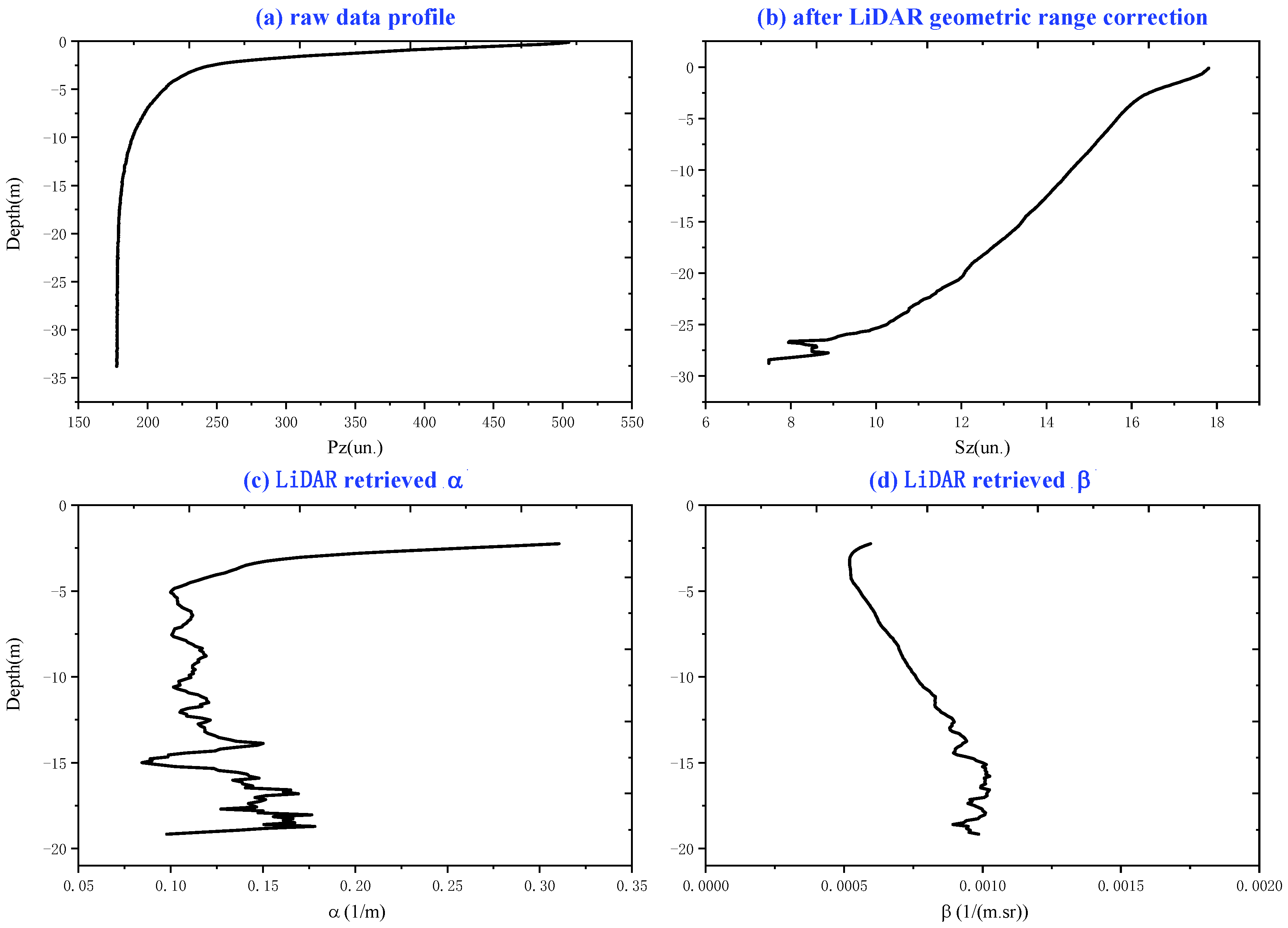
3.1. An Example of the LiDAR Processing Results in Each Procedure
3.2. Validation of the LiDAR Inversion Method
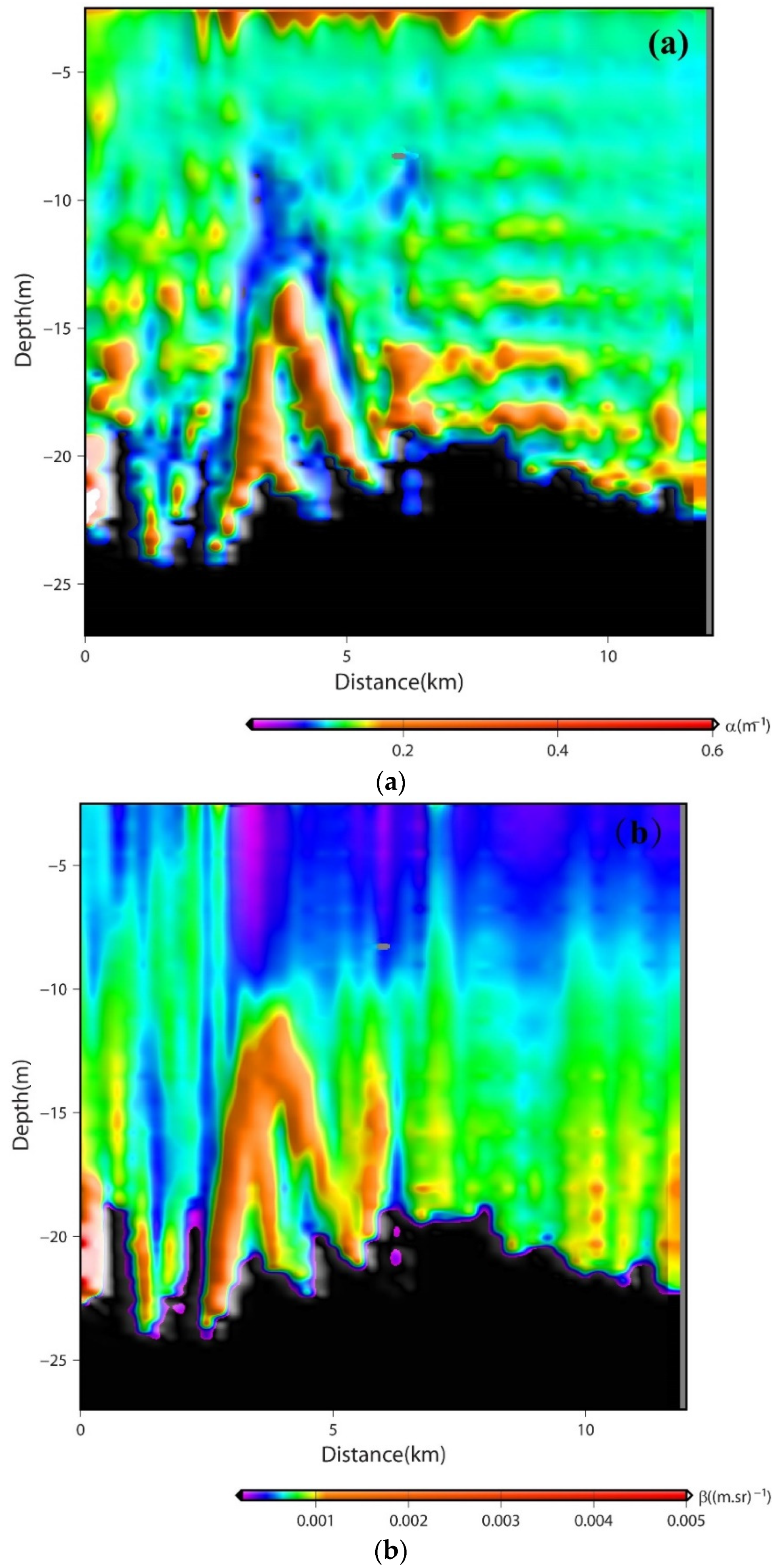
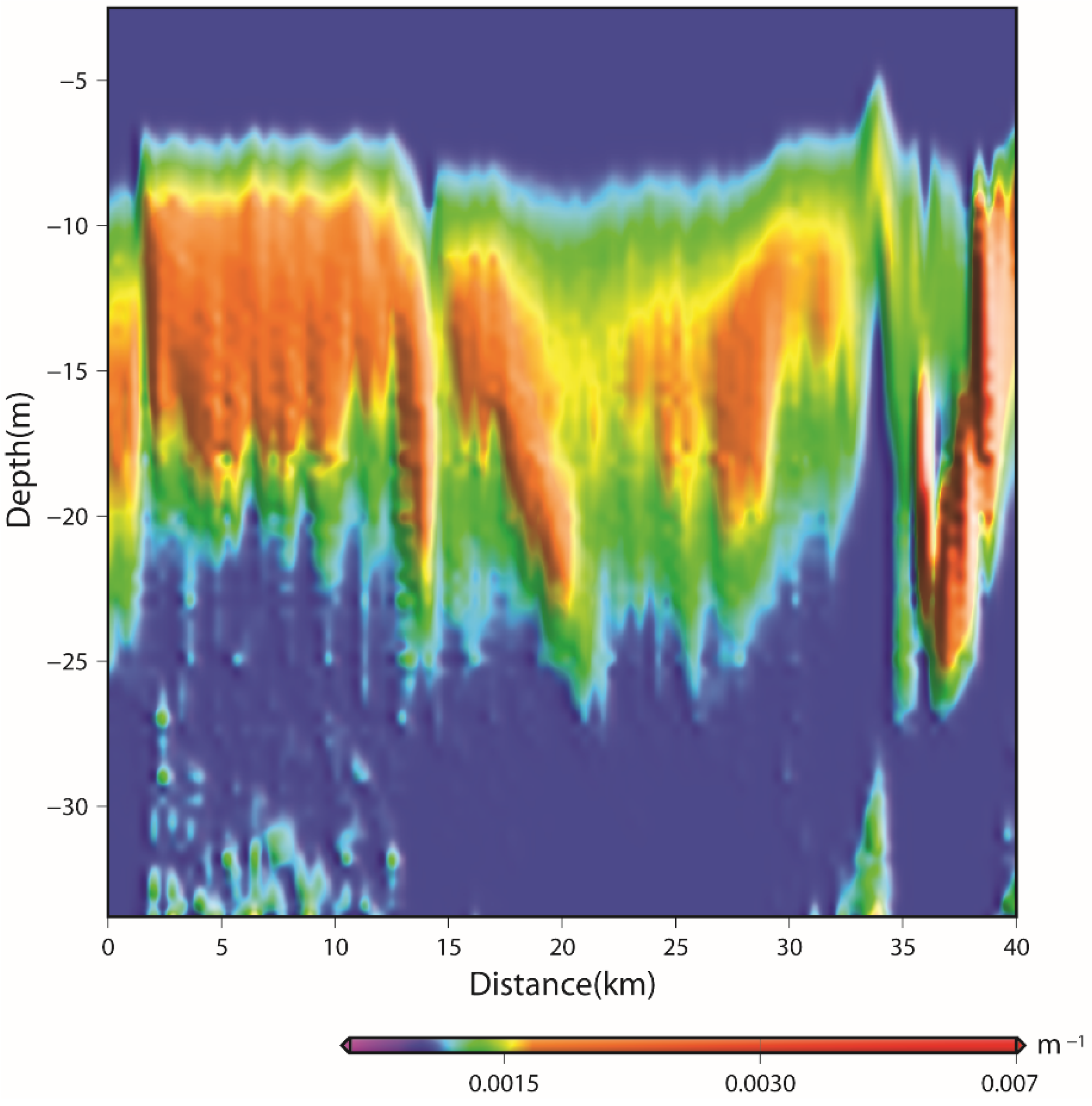
3.3. LiDAR Inversion Profile Distribution along LiDAR Flight Tracks
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Hostetler, C.A.; Behrenfeld, M.J.; Hu, Y.; Hair, J.W.; Schulien, J.A. Spaceborne Lidar in the Study of Marine Systems. Annu. Rev. Mar. Sci. 2018, 10, 121–147. [Google Scholar] [CrossRef] [PubMed]
- Behrenfeld, M.J.; Hu, Y.; O’Malley, R.T.; Boss, E.S.; Hostetler, C.A.; Siegel, D.A.; Sarmiento, J.L.; Schulien, J.; Hair, J.W.; Lu, X. Annual boom–bust cycles of polar phytoplankton biomass revealed by space-based lidar. Nat. Geosci. 2016, 10, 18. [Google Scholar] [CrossRef]
- Richter, K.; Maas, H.-G. An Approach to Determining Turbidity and Correcting for Signal Attenuation in Airborne Lidar Bathymetry. J. Photogramm. Remote Sens. Geoinf. Sci. 2017, 85, 31–40. [Google Scholar] [CrossRef]
- Saylam, K.; Brown, R.A.; Hupp, J.R. Assessment of depth and turbidity with airborne Lidar bathymetry and multiband satellite imagery in shallow water bodies of the Alaskan North Slope. Int. J. Appl. Earth Obs. Geoinf. 2017, 58, 191–200. [Google Scholar] [CrossRef]
- Lee, J.H.; Churnside, J.H.; Marchbanks, R.D.; Donaghay, P.L.; Sullivan, J.M. Oceanographic lidar profiles compared with estimates from in situ optical measurements. Appl. Opt. 2013, 52, 786–794. [Google Scholar] [CrossRef]
- Kokhanenko, G.P.; Balin, Y.S.; Penner, I.E.; Shamanaev, V.S. Lidar and in situ measurements of the optical parameters of water surface layers in Lake Baikal. Atmos. Ocean. Opt. 2011, 24, 478–486. [Google Scholar] [CrossRef]
- Churnside, J.; Hair, J.; Hostetler, C.; Scarino, A. Ocean Backscatter Profiling Using High-Spectral-Resolution Lidar and a Perturbation Retrieval. Remote Sens. 2018, 10, 2003. [Google Scholar] [CrossRef]
- Concannon, B.M.; Prentice, J.E. LOCO with a Shipboard Lidar. 2008. [Google Scholar]
- Churnside, J.H.; Marchbanks, R.D. Subsurface plankton layers in the Arctic Ocean. Geophys. Res. Lett. 2015, 42, 4896–4902. [Google Scholar] [CrossRef]
- Liu, H.; Chen, P.; Mao, Z.; Pan, D.; He, Y. Subsurface plankton layers observed from airborne lidar in Sanya Bay, South China Sea. Opt. Express 2018, 26, 29134–29147. [Google Scholar] [CrossRef]
- Arnone, R.; Derada, S.; Ladner, S.; Trees, C. Probing the subsurface ocean processes using ocean LIDARS. In Proceedings of the SPIE—The International Society for Optical Engineering, Baltimore, MD, USA, 12 June 2012; Volume 8372, p. 21. [Google Scholar] [CrossRef]
- Churnside, J. Lidar signature from bubbles in the sea. Opt. Express 2010, 18, 8294–8299. [Google Scholar] [CrossRef]
- Churnside, J.D.; Marchbanks, R.H.; Lee, J.; Shaw, J.; Weidemann, A.L.; Donaghay, P. Airborne lidar detection and characterization of internal waves in a shallow Fjord. J. Appl. Remote Sens. 2012, 6, 3611. [Google Scholar] [CrossRef]
- Roddewig, M.R.; Pust, N.J.; Churnside, J.H.; Shaw, J.A. Dual-polarization airborne lidar for freshwater fisheries management and research. Opt. Eng. 2017, 56, 031221. [Google Scholar] [CrossRef]
- Roddewig, M.R.; Churnside, J.; Hauer, F.R.; Williams, J.; Bigelow, P.; Koel, T.; Shaw, J. Airborne lidar detection and mapping of invasive lake trout in Yellowstone Lake. Appl. Opt. 2018, 57, 4111–4116. [Google Scholar] [CrossRef] [PubMed]
- Churnside, J.H.; Marchbanks, R.D. Inversion of oceanographic profiling lidars by a perturbation to a linear regression. Appl. Opt. 2017, 56, 5228–5233. [Google Scholar] [CrossRef] [PubMed]
- Hair, J.W.; Hostetler, C.A.; Cook, A.L.; Harper, D.B.; Ferrare, R.A.; Mack, T.L.; Welch, W.; Izquierdo, L.R.; Hovis, F.E. Airborne High Spectral Resolution Lidar for profiling aerosol optical properties. Appl. Opt. 2008, 47, 6734–6752. [Google Scholar] [CrossRef] [PubMed]
- Dawson, K.W.; Meskhidze, N.; Josset, D.; Gassó, S. Spaceborne observations of the lidar ratio of marine aerosols. Atmos. Chem. Phys. 2015, 15, 3241–3255. [Google Scholar] [CrossRef]
- Kunz, G.J.; de Leeuw, G. Inversion of lidar signals with the slope method. Appl. Opt. 1993, 32, 3249–3256. [Google Scholar] [CrossRef] [PubMed]
- Fernald, F.G. Analysis of atmospheric lidar observations: Some comments. Appl. Opt. 1984, 23, 652–653. [Google Scholar] [CrossRef]
- Klett, J.D. Stable analytical inversion solution for processing lidar returns. Appl. Opt. 1981, 20, 211–220. [Google Scholar] [CrossRef]
- Churnside, J.H.; Sullivan, J.M.; Twardowski, M.S. Lidar extinction-to-backscatter ratio of the ocean. Opt. Express 2014, 22, 18698–18706. [Google Scholar] [CrossRef]
- Chen, P.; Pan, D.; Mao, Z.; Liu, H. Semi-analytic Monte Carlo radiative transfer model of laser propagation in inhomogeneous sea water within subsurface plankton layer. Opt. Laser Technol. 2019, 111, 1–5. [Google Scholar] [CrossRef]
- Mitchell, B.G.; Kahru, M.; Wieland, J.; Stramska, M. Determination of spectral absorption coefficients of particles, dissolved material and phytoplankton for discrete water samples. Nasa Tech. Memo. 2002, 125–153. [Google Scholar]
- Kopilevich, Y.I.; Surkov, A.G. Mathematical modeling of the input signals of oceanological lidars. J. Opt. Technol. 2008, 75, 321–326. [Google Scholar] [CrossRef]
- Chen, P.; Pan, D.; Mao, Z.; Liu, H. A Feasible Calibration Method for Type 1 Open Ocean Water LiDAR Data Based on Bio-Optical Models. Remote Sens. 2019, 11, 172. [Google Scholar] [CrossRef]
- Sullivan, J.M.; Twardowski, M.S. Angular shape of the oceanic particulate volume scattering function in the backward direction. Appl. Opt. 2009, 48, 6811–6819. [Google Scholar] [CrossRef] [PubMed]
- PinEiro, G.; Perelman, S.; Guerschman, J.P.; Paruelo, J.M. How to evaluate models: Observed vs. predicted or predicted vs. observed? J. Ecol. Model. 2008, 216, 316–322. [Google Scholar] [CrossRef]
- Gordon, H.R. Interpretation of airborne oceanic lidar: Effects of multiple scattering. Appl. Opt. 1982, 21, 2996–3001. [Google Scholar] [CrossRef] [PubMed]
- Walker, R.E.; McLean, J.W. Lidar equations for turbid media with pulse stretching. Appl. Opt. 1999, 38, 2384–2397. [Google Scholar] [CrossRef]
- Churnside, J.H. Review of profiling oceanographic lidar. Opt. Eng. 2014, 53, 051405. [Google Scholar] [CrossRef]
- Winker, D.; Pelon, J.; Coakley, J., Jr.; Ackerman, S.; Charlson, R.; Colarco, P.; Flamant, P.; Fu, Q.; Hoff, R.; Kittaka, C. The CALIPSO mission: A global 3D view of aerosols and clouds. Bull. Am. Meteorol. Soc. 2010, 91, 1211–1230. [Google Scholar] [CrossRef]
- Boss, E.; Pegau, W.S. Relationship of light scattering at an angle in the backward direction to the backscattering coefficient. Appl. Opt. 2001, 40, 5503–5507. [Google Scholar] [CrossRef] [PubMed]
- Chami, M.; Marken, E.; Stamnes, J.; Khomenko, G.; Korotaev, G. Variability of the relationship between the particulate backscattering coefficient and the volume scattering function measured at fixed angles. J. Geophys. Res. Ocean 2006, 111. [Google Scholar] [CrossRef]
- Zhang, X.; Boss, E.; Gray, D.J. Significance of scattering by oceanic particles at angles around 120 degree. Opt. Express 2014, 22, 31329–31336. [Google Scholar] [CrossRef] [PubMed]
- Whitmire, A.L.; Pegau, W.S.; Karp-Boss, L.; Boss, E.; Cowles, T.J. Spectral backscattering properties of marine phytoplankton cultures. Opt. Express 2010, 18, 15073–15093. [Google Scholar] [CrossRef] [PubMed]
- Churnside, J.H.; Marchbanks, R.D.; Lembke, C.; Beckler, J. Optical backscattering measured by airborne lidar and underwater glider. Remote Sens. 2017, 9, 379. [Google Scholar] [CrossRef]
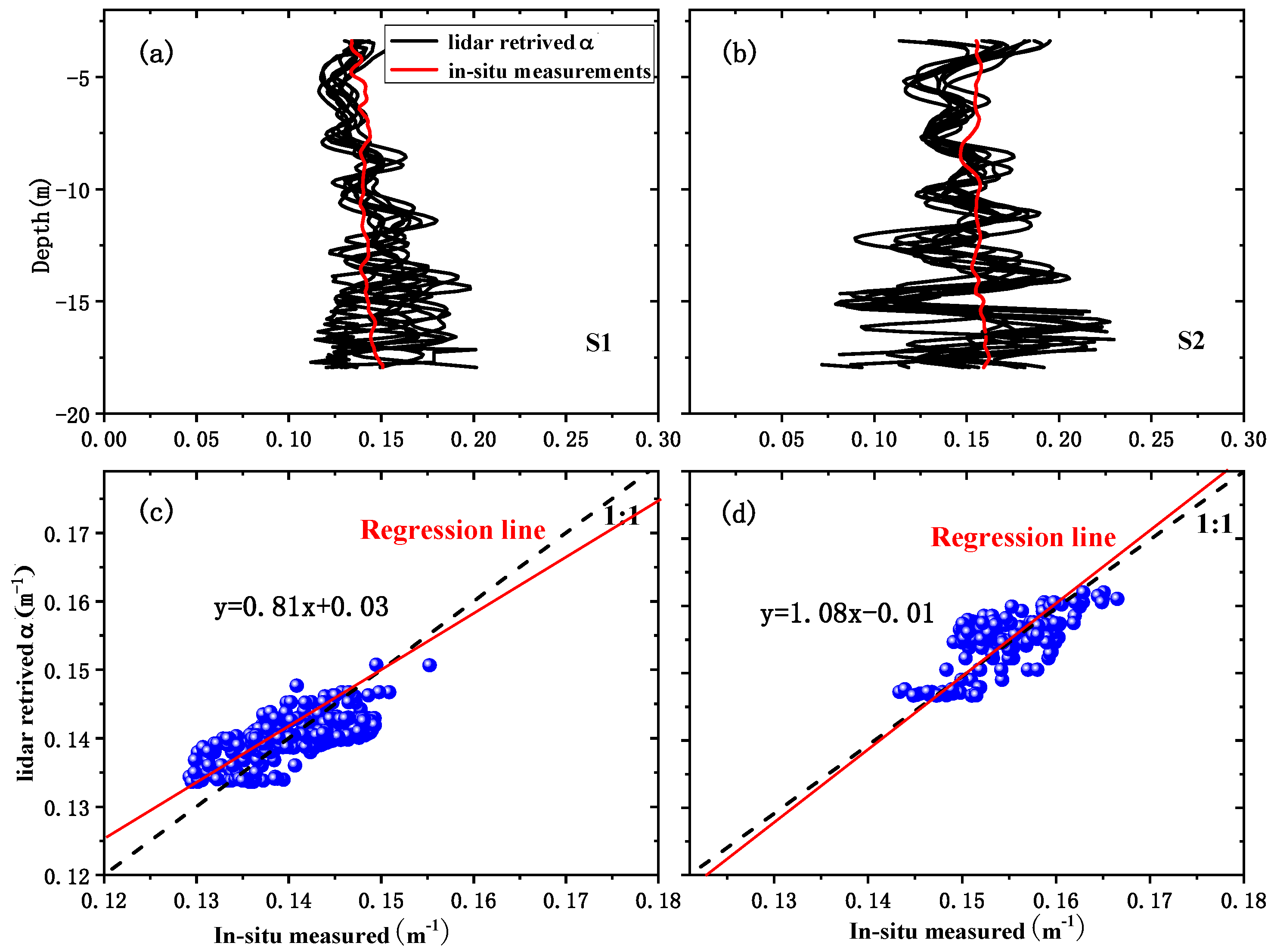
| Station | Number | Min | Max | R | MAE | RMSE | NRMSD |
|---|---|---|---|---|---|---|---|
| 1 | 260 | 0.128 | 0.143 | 0.67 | 7.1% | 0.012 | 8.54% |
| 2 | 130 | 0.156 | 0.166 | 0.70 | 9.7% | 0.018 | 11.55% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, P.; Pan, D. Ocean Optical Profiling in South China Sea Using Airborne LiDAR. Remote Sens. 2019, 11, 1826. https://doi.org/10.3390/rs11151826
Chen P, Pan D. Ocean Optical Profiling in South China Sea Using Airborne LiDAR. Remote Sensing. 2019; 11(15):1826. https://doi.org/10.3390/rs11151826
Chicago/Turabian StyleChen, Peng, and Delu Pan. 2019. "Ocean Optical Profiling in South China Sea Using Airborne LiDAR" Remote Sensing 11, no. 15: 1826. https://doi.org/10.3390/rs11151826
APA StyleChen, P., & Pan, D. (2019). Ocean Optical Profiling in South China Sea Using Airborne LiDAR. Remote Sensing, 11(15), 1826. https://doi.org/10.3390/rs11151826